Characteristic identification of seismogenic electromagnetic anomalies based on station electromagnetic impedance

The main components of seismo-electromagnetic research are the deep underground electromagnetic seismogenic environment, electromagnetic field changes at different stages of the seismogenic process, and the physical mechanism and change rules of electromagnetic properties of the earth’s interior. Traditional electric and magnetic methods mainly analyze the single field change of the geoelectric field, geomagnetic field, or resistivity at frequencies less than 1 Hz. These do not include the extremely low-frequency band that is sensitive to seismic events, so it is difficult to obtain the characteristics of time-spatial variations and propagation characteristics precursors. In comparison, magnetotelluric stations observe magnetotelluric fields containing seismogenic-induced electromagnetic disturbances, and the observation frequency band is wide. In this paper, the three-dimensional numerical simulation method is used to calculate the magnetotelluric apparent resistivity anomaly generated by resistivity changes in the seismogenic zone, and the forward algorithm of arbitrarily orientated dipole source in layered earth is used to simulate the response of low-frequency pre-earthquake electromagnetic radiation. The magnetotelluric response including seismogenic resistivity anomaly and pre-earthquake electromagnetic radiation is obtained using the field component composition method. The frequency characteristics and spatial distribution characteristics of apparent resistivity anomalies are systematically analyzed, and the results are of important significance for the observation, data processing, and identification and analysis of seismic electromagnetic anomalies in different seismogenic processes.

1 Introduction

Physical quantities that can be related to electromagnetic anomalies in the earthquake developing process mainly include earth resistivity, geomagnetic field, geoelectric field, electromagnetic induction field, and electromagnetic radiation (Zhao et al., 2022). In a deep underground electromagnetic seismogenic environment, changes in the electromagnetic field in the seismogenic process, and the physical mechanism and change characteristics of electromagnetic properties of the earth’s interior are the main contents of seismo-electromagnetic research (Mao, 1986). Since the 1960s, there has been systematic research and observations of seismogenic electromagnetic phenomena in China. Observation stations have been successively set up in key earthquake risk areas for long-term observation of the geomagnetic field, geoelectric field, earth resistivity, magnetotelluric field, and electromagnetic radiation (Pan, 1998), recording a large number of electromagnetic precursors (Huang et al., 2017). In 2018, the experimental satellite Zhang Heng No.1 was launched for seismic electromagnetic monitoring in China; from this, a space-ground joint seismic electromagnetic monitoring system was established (Zhang et al., 2020). During this period, there has been theoretical and experimental research on the mechanism of earthquake electromagnetic precursors, distribution laws and propagation characteristics, correlation with seismic activity, and information extraction (Huang, 2002; Ma, 2002; Wang et al., 2005; Ding, 2009; Gao and Hu, 2010; Du, 2011; Huang et al., 2015; Ren et al., 2015; 2016; Zhou et al., 2017). These results confirm that the earthquake preparation process does cause electromagnetic anomalies, summarize the characteristics of temporal and spatial variations of seismic electromagnetic anomalies, and use numerical simulations to try to explain the generation mechanism and propagation selective phenomena of seismic electromagnetic signals and focus on numerical simulation research on the mechanism of earthquake electromagnetic co-seismic or post-earthquake attenuation (Gao et al., 2016; Hu et al., 2011), but there is still a lack of strong quantitative explanations for the identification characteristics of electromagnetic anomalies caused by the seismogenesis process.

The early earthquake precursor observation and data analysis methods in China have mainly used traditional electrical and magnetic methods to observe the changes in the geoelectric field, geomagnetic field ($\le$ 1 Hz), or the earth direct current (DC) resistivity. It is difficult to obtain the time-spatial change and propagation characteristics of seismo-electromagnetic precursor from these observation data including no ultra-low frequency (ULF)/extremely low frequency (ELF) band signals which may be more sensitive to seismic events. At the same time, individual field component is easily affected by the changes in the earth’s electromagnetic environment and by human activity. Because these changes and disturbances are random events, they cause great difficulty in the identification of seismic electromagnetic anomalies. During the period 2007–2009, 12 magnetotelluric stations were set to observe the alternating geo-electromagnetic field, the data is mainly used for the study of electromagnetic field background changes (Zhao et al., 2010; Fan et al., 2013), and less for extracting seismic electromagnetic anomaly information (Gao et al., 2010; 2013). During 2011–2015, an ELF electromagnetic observation network for seismic anomaly monitoring has been set up (with the support of major national science and technology infrastructure projects) in the capital circle and the southern section of the North-South Earthquake Belts, which makes it possible to use magnetotelluric impedance for seismic electromagnetic anomaly monitoring. This network can not only observe natural source signals for magnetotelluric sounding, but it can also receive signals of a given frequency regularly sent by a long-distance high-power transmitter to improve the signal-to-noise ratio of the natural source in the low energy window frequency band and reduce the error of the data. Then the apparent resistivity and other observational data will have a higher sensitivity to the anomalies of the underground resistivity structure (Zhao et al., 2012).

The magnetotelluric sounding method based on the principle of electromagnetic induction has the characteristics of the wide frequency band and multi-component observation. Using magnetotelluric data from stations to identify and extract seismic electromagnetic anomaly information has the following advantages. 1) In data processing, the ratio of the mutually orthogonal electric and magnetic field is used to obtain the electromagnetic impedance of the earth and then the apparent resistivity and impedance phase information. This method can automatically eliminate the influence of magnetotelluric field changes of any frequency caused by the change of the earth’s electromagnetic environment. 2) Reliable regional background resistivity information at different depths can be obtained from long-term observations by the network, which is convenient for identifying and extracting resistivity anomalies. 3) The seismogenic resistivity anomaly has the characteristic of slow change over a long time, which is easy to distinguish from human activity and local spatial change. 4) Allows for better comprehensive analysis, the electromagnetic impedance anomaly of a magnetotelluric station not only includes the change in the resistivity of the underlying earth formation caused by stress change and fracture development in the adjacent areas but also includes the electromagnetic radiation information generated by pressure in the rock formation.

In many cases, the earth can be represented as a horizontally stratified medium with homogeneous and isotropic properties in each layer (Wait, 1951). In this paper, we introduce a three-dimensional low resistivity anomaly in the horizontally layered stratum model designed to simulate the change of the earth’s resistivity in the seismogenic zone, the electromagnetic impedance response in a large spatial range is calculated and its characteristics with frequency and space variation have been analyzed. Assuming that the electromagnetic radiation in the seismogenic region is equivalent to the vector electric dipole radiation source, the electromagnetic impedance response of electric dipole of different orientations is calculated and its characteristics of responses are analyzed. Finally, the dipole source response and magnetotelluric response are synthesized to simulate the observed response of the seismic electromagnetic anomaly by the magnetotelluric stations. From the perspective of 3D numerical simulation, we analyze the characteristics of an electromagnetic anomaly caused by earth resistivity changes and electromagnetic radiation during the pre-seismic period and propose methods to identify and extract different seismic electromagnetic anomalies. This will then provide theoretical support for extremely low-frequency electromagnetic observations used to monitor seismic electromagnetic anomalies.

2 Model design

This study concentrates on observations and processing of magnetotelluric data within a limited spatial area. Based on the one-dimensional (1D) horizontal layered stratum model, the 3D low resistivity anomaly is added to the high resistivity stratum to simulate the resistivity change caused by fracture development in the seismogenic area. The electromagnetic radiation generated by the sudden change of stress in the seismogenic center area before the earthquake is simulated with an inclined electric dipole source at depth.

The designed model structure is shown in Figure 1, where we use the x-y-z rectangular coordinate system with z = 0 at the ground surface and positive upward. Figure 1A shows the x-z resistivity section at y = 0 (shown by the dotted line in Figure 1B) of the horizontally layered model with a 3D low resistivity anomaly. Figure 1B is an x-y slice of resistivity at a depth of 10 km (as shown by the dotted line in Figure 1A), showing the plane structure of the 3D low resistivity anomaly. The top earth layer is a low-resistance cover layer with a thickness of $h_1=2km$ and resistivity of ${\rho }_1=20\mathrm{\Omega }m$. The second layer is a high resistance intermediate layer, with a thickness of $h_2=23km$ and resistivity of ${\rho }_2={10}^4\mathrm{\Omega }m$. The bottom of the model (lower crust) is a low resistivity half space (h₃→∞) with the resistivity of ${\rho }_3=10\mathrm{\Omega }m$. The atmosphere is above the ground surface and its resistivity is set to ${\rho }_0={10}^{12}\mathrm{\Omega }m.$ The embedded 3D low-resistivity anomaly is a flat, low-resistivity wedge-shaped body located in the middle of the high-resistivity layer of the model. The core region of the 3D body is a low resistivity (10 $\mathrm{\Omega }m$) cuboid with a length (y-direction) of 105 km, a width (x-direction) of 25 km, and a height (z-direction) of 4 km, centered at (0, 0, −10 km) to simulate the seismogenic core area extending along the fault zone. The resistivity outside the cuboid core increases by 20, 30, 50, 100, and 300 Ωm in steps of 5 km along the x-axis, and the extension range reaches ±37.5 km in the x-direction. The resistivity along the y-axis increases as the same as in the x-direction but by 10 km spatial steps, forming two triangular anomalous bodies whose resistivity gradually increases as distance in the x-direction from the center point in the x-y plane. This structure is used to simulate the change of the formation resistivity near the seismogenic core area. The buried inclined electric dipole (small white arrow in Figure 1A), which simulates the electromagnetic radiation source, is located at (0, 0, −10 km), with an azimuth of θ=0° and inclination of φ=30 $°$. Unless otherwise specified, the permeability parameter and dielectric constant are set to ${\mu }_0=4\pi \times {10}^{-7}H/m$ and ${\epsilon }_0=8.85418\times {10}^{-12}F/m$, respectively.

FIGURE 1

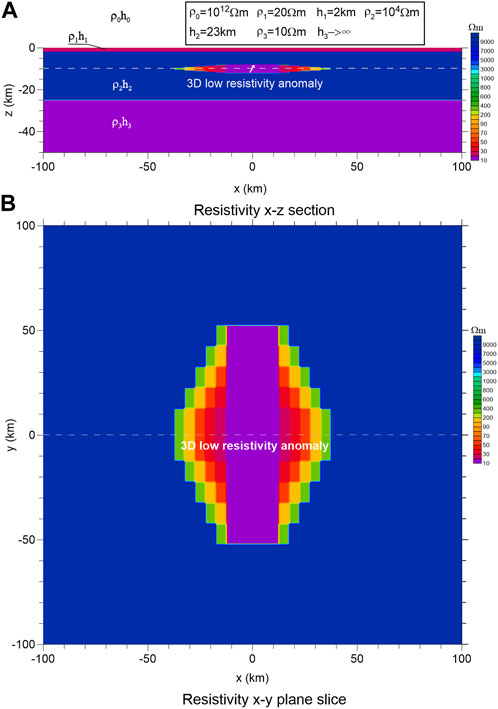
FIGURE 1. Horizontal layered and 3D low resistivity anomaly model using the x-y-z rectangular coordinate system with z=0 at the ground surface and positive upward (A) Is the resistivity x-z section, and (B) is the resistivity x-y plane slice at a depth of 10 km (z = −10 km).

3 3D magnetotelluric response simulation

Using 3D simulation software to calculate the magnetotelluric response of the horizontally layered model with the 3D low resistivity anomaly shown in Figure 1, we can obtain the apparent resistivity and phase information of the xy and yx components at the ground observation site. Figure 2 shows contour maps of the apparent resistivity of the two principal component elements with frequencies of 0.1, 0.05, and 0.01 Hz, respectively. Because the model structure is symmetrical, we only show quadrant 1 (with x=0–400 km and y=0–300 km) to investigate the distribution of electromagnetic impedance response. In Figure 2, white ladder lines are used to mark the corresponding positions and boundaries of the 3D low resistivity anomalous body at depth. Different color scales are used in contour maps because the amplitude of different frequency responses varies greatly.

FIGURE 2

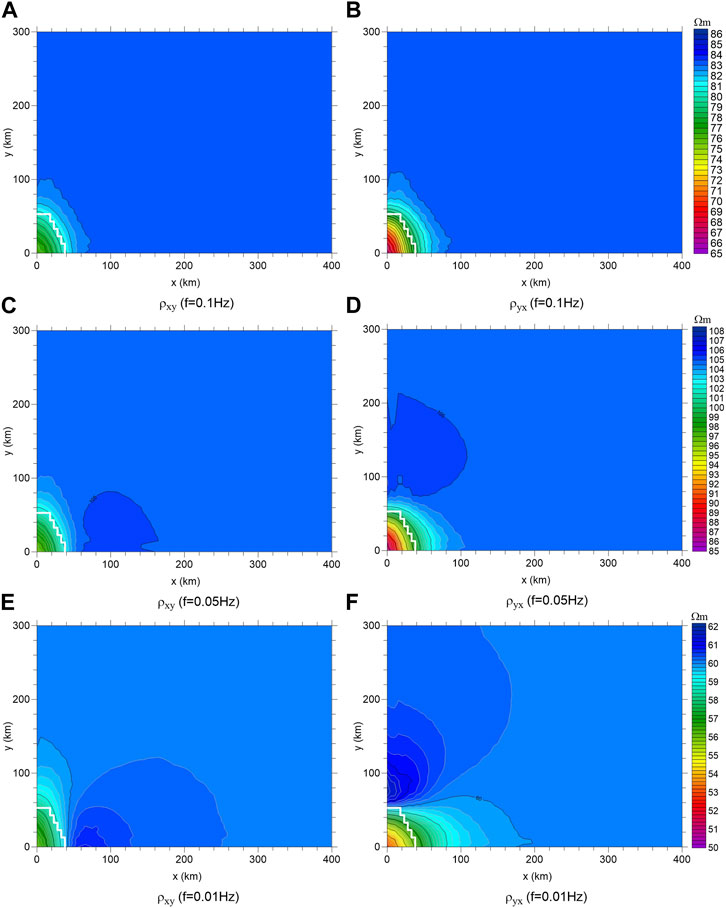
FIGURE 2. Contour maps of the spatial distribution of the apparent resistivity of the two principal components of the 3D model. (A,C,E) are the ρ_xy at the frequency of 0.1 Hz, 0.05 Hz, 0.01 Hz respectively; (B,D,F) are the ρ_yx at the frequency of 0.1 Hz, 0.05 Hz, 0.01 Hz respectively.

It can be seen from Figure 2 that 1) generally, the existence of a 3D low resistivity anomaly causes the apparent resistivity value above and near the 3D body to be significantly reduced. 2) The amplitude of the apparent resistivity anomaly is largest just above the 3D low resistivity body, and gradually decreases to background value with increasing distance from the boundary of the 3D low resistivity body, and the attenuation distance increases with decreasing frequency. For example, the distance of the ${\rho }_{\mathrm{y}\mathrm{x}}$ anomaly decrease to zero on the x-axis is about 80 km when f=0.1 Hz, and about 180 km when f=0.01 Hz 3) The maximum amplitude of the apparent resistivity anomaly occurs at a lower frequency, that because the top surface of the 3D low resistivity anomaly body is buried at a depth of 8 km and has a low-resistivity overburden with a thickness of 2 km, as shown in Figure 1A. 4) Compared with ${\rho }_{\mathrm{x}\mathrm{y}}$; ${\rho }_{\mathrm{y}\mathrm{x}}$ has a larger apparent resistivity value, apparent resistivity anomaly amplitude, and anomaly distribution range, which may be because the electrical principal axis of the 3D low resistivity anomaly body is in the y-direction, and ${\rho }_{\mathrm{y}\mathrm{x}}$ closer to the response of TM (transverse magnetic) polarization mode. 5) When f=0.05 Hz, the decay rate of ${\rho }_{\mathrm{x}\mathrm{y}}$ in the x-direction, outside the 3D low resistivity anomaly, becomes faster and shows a small enhancement (positive anomaly) after attenuating to zero. With the frequency reduced to f=0.01 Hz, the apparent resistivity anomaly outside the 3D low resistivity anomaly has changed from negative to positive, and the amplitude and extension range of the positive anomaly has increased. Correspondingly, a similar phenomenon occurs in the y-direction for ${\rho }_{\mathrm{y}\mathrm{x}}$, and the amplitude and coverage of positive anomalies are larger than that of ${\rho }_{\mathrm{x}\mathrm{y}}$.

To quantitatively evaluate the sensitivity of the magnetotelluric response observed at the stations to the seismogenic resistivity anomaly, Figure 3 shows the ratio curve of the responses of the measuring sites at different offsets along the radial x) direction and axial y) direction of the 3D low resistivity anomaly to the responses of the 1D horizontal layered model of the corresponding measuring sites. The offsets of the measuring sites are 0, 10, 25, 50, 100, 200, and 400 km, respectively. The curve with a ratio of 1 represents the response of a 1D layered model, which is not disturbed by the 3D low resistivity anomaly. If the ratio is larger than 1, the apparent resistivity value increases, making this a positive anomaly. A ratio less than 1 indicates that the apparent resistivity value decreases, that is, a negative anomaly. Because the model contains the 3D low resistivity anomaly, the ratio curve should be dominated by negative anomalies, and how much the ratio deviates from 1 is the amplitude of the anomaly. The apparent resistivity ratio curve in Figure 3 shows that: 1) The influence of 3D low resistivity anomaly begins in the low-frequency band below 5 Hz. 2) In the frequency band of about 1∼5 Hz, the apparent resistivity ratio curve shows a positive abnormal overshoot, which is the intrinsic characteristic of the magnetotelluric response. The amplitude of overshoot is largest at zero offsets (up to about 7%) and decreases with an increasing offset; is approaching zero for x offset is greater than or equal to 50 km and while y offset is greater than or equal to 100 km. 3) Generally, in the low-frequency band below 1Hz, the ratio curve is dominated by negative anomalies, and the amplitude of the negative anomaly decreases with increasing offset distance. At the same offset distance, the amplitude of the ${\rho }_{xy}/{\rho }_{1D}$ curve is less than the amplitude of the ${\rho }_{yx}/{\rho }_{1D}$ curve. For example, at zero offset distance, there is a maximum negative anomaly near the frequency of about 0.13 Hz, the ratio of the ${\rho }_{xy}/{\rho }_{1D}$ can reach about −11% and the ratio of the ${\rho }_{yx}/{\rho }_{1D}$ can reach about −25%. 4) In the frequency band below 0.1 Hz, the ratio curve of ${\rho }_{xy}/{\rho }_{1D}$ with an offset of greater than or equal to 50 km along the x-axis shows a small positive anomaly. When the ${\rho }_{xy}/{\rho }_{1D}$ offset is 50 km, the maximum positive anomaly reaches about 2.5%, and the positive anomaly amplitude decreases rapidly with the increasing offset. When the ${\rho }_{yx}/{\rho }_{1D}$ offset along the y-axis is equal to 50 km, a small positive anomaly appears at about 0.013 Hz, and the amplitude is close to 2%. When the offset is equal to 100 km, the ${\rho }_{yx}/{\rho }_{1D}$ curve starts to show a positive anomaly at about 0.1 Hz, with an amplitude of about 2%, which decreases rapidly to zero with the further increasing offset. 5) It should be pointed out that the boundaries of the 3D anomalous body are at 37.5 km in the +x direction and 52.5 km in the +y direction, that is, the overshoot anomaly in the frequency band of 1–5 Hz can only be identified within the range of the 3D body; while identifiable weak positive anomalies for the low-frequency band below 0.1 Hz may only appear in the area outside the anomalous body.

FIGURE 3

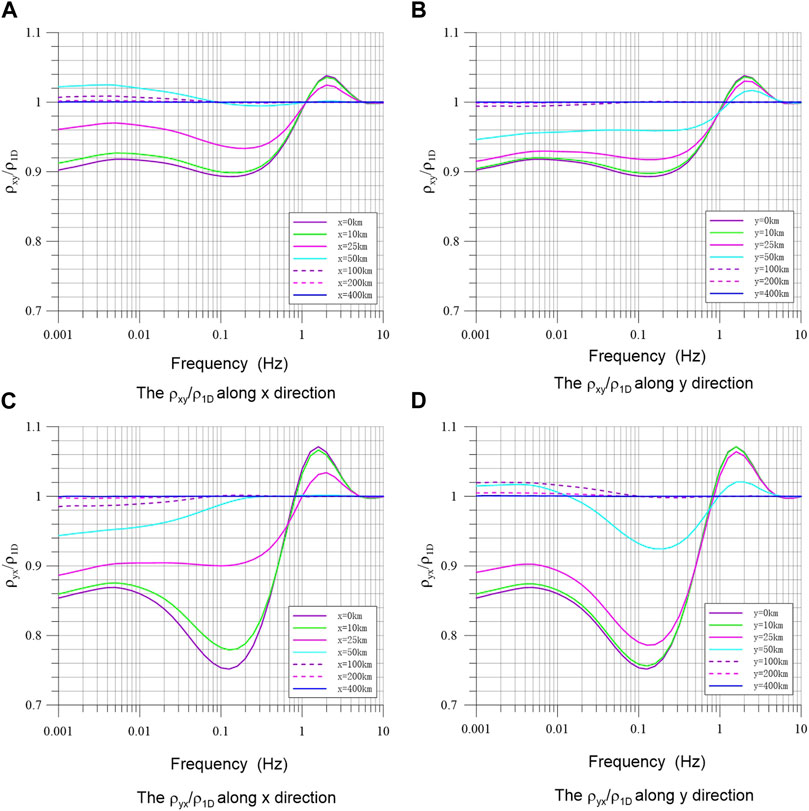
FIGURE 3. Apparent resistivity ratio of the three-dimensional model to one-dimensional layered model for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy/ρ_1D along x and y direction respectively; (C) and (D) are the ρ_xy/ρ_1D along x and y direction respectively.

The apparent resistivity method is one of the earliest geophysical methods used for earthquake precursor monitoring in China. After years of observation and research, Qian et al. (1982) and Zhang et al. (1996) successively summarized the characteristics of the apparent resistivity anomaly before earthquakes: 1) The apparent resistivity anomaly before earthquakes can be divided into a long-trend anomaly and impending anomaly. 2) Before the earthquake, the apparent resistivity is mostly a decreasing anomaly, though some increasing changes have also been observed. The anomaly amplitude decreases with increasing epicenter distance. 3) Before the earthquake, the long trend anomaly extends outward from the epicenter area, extending out to 150 km. 4) The anomalies are directional. 5) The standard deviation of the monthly average value of the active source apparent resistivity observation method should be less than 0.5%. If the apparent resistivity has a continuous multipoint trend change and the amplitude exceeds 3 times the standard error, it can be identified as the anomaly. Our simulation results described above provide a theoretical basis for the characteristics of the apparent resistivity anomaly in the seismogenic area summarized by precursors and verify the identification rule of the resistivity anomaly.

4 Response simulation of electric dipole source in the earth

The electromagnetic responses of the electric dipole source in the horizontally layered earth are calculated using the algorithm by Hu et al. (2023), and the propagation characteristics of the electric dipole source radiation field in earth and its influence on ground observations have been investigated. For comparative studies, the responses of a horizontal and an incline electric dipole in uniform earth and horizontally layered earth are calculated and analyzed respectively.

4.1 Response of an electric dipole source in a uniform earth

An x-direction horizontal electric dipole source (azimuth angle $\theta$ =0 $°$, dip angle $\phi$ =0 $°$), and an inclined electric dipole source (azimuth angle $\theta$ =0 $°$, dip angle $\phi$ =30 $°$) are set to located at a depth of 10 km in a uniform earth with the resistivity of 10⁴ Ωm. The apparent resistivity and phase are calculated for observation sites at the earth’s surface with 25, 50, 100, 200, and 400 km offset in the x-direction and y-direction respectively. Figure 4 shows the curves of apparent resistivity and phase excited by a horizontal electric dipole source and observed at the earth’s surface with different offsets. Figures 4A, B show the apparent resistivity ${\rho }_{xy}$ (above) and phase ${\phi }_{xy}$ curve (below), and Figures 4C, D show the ${\rho }_{yx}$ and ${\phi }_{yx}$ with different offsets in the x- and y-directions respectively. In general, all apparent resistivity and phase curves show similar variation patterns with frequency and offset but have slightly different changing rates. When the frequency is high enough, the dipole source field meets the far-field condition, the apparent resistivity value obtained is close to the true resistivity value (10⁴ Ωm) of the medium, and the impedance phase is about 45 $°$, which is a typical plane wave electromagnetic response. When the frequency is low enough, the apparent resistivity and phase of the dipole source field response have typical near-field characteristics, meaning that with decreasing frequency, the apparent resistivity sharply increases, while the impedance phase correspondingly decreases to zero. Curves of ${\rho }_{yx}$ and ${\phi }_{yx}$ along the x direction have almost the same pattern and values as curves along the y direction for the corresponding offset, this means the ${\rho }_{yx}$ and ${\phi }_{yx}$ responses excited by horizontal electric dipole have spatial symmetry in the x-y plane; while the ${\rho }_{xy}$ and ${\phi }_{xy}$ responses along x direction show slightly different variation rates and frequency feature from responses along the y direction, this indicates the ${\rho }_{xy}$ and ${\phi }_{xy}$ responses have no symmetry in the x-y plane.

FIGURE 4

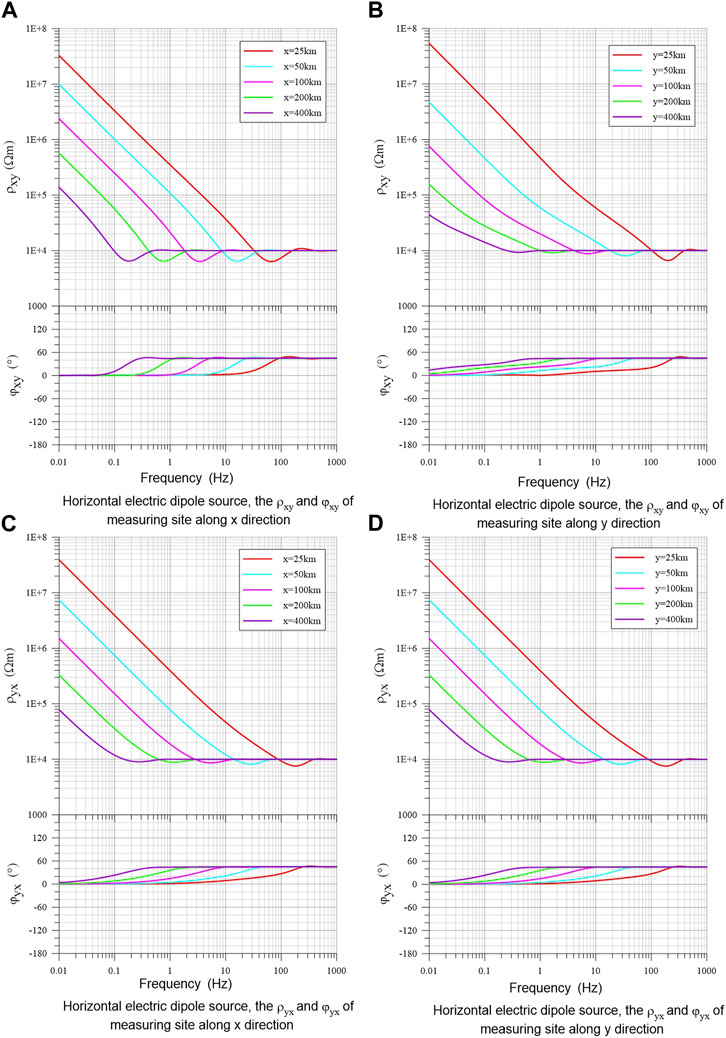
FIGURE 4. Apparent resistivity and phase response of a horizontal dipole source in a homogeneous earth for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy and φ_xy of measuring sites along x and y direction respectively; (C) and (D) are the ρ_yx and φ_yx of measuring sites along x and y direction respectively.

For the field responses of horizontal electric dipole source, the area with an offset greater than $\sqrt{2}\lambda$ (λ-wavelength) can be regarded as the far field, while the area with an offset less than $\lambda /\sqrt{2}$ as the near field. As the frequency decreases, the apparent resistivity starts to deviate from the far-field value at the frequency corresponding to wavelength ${\lambda }_f\approx d/\sqrt{2}$, where d is the offset along x or y direction; and increases exponentially at the frequency corresponding to wavelength ${\lambda }_n\approx d\sqrt{2}$, indicating of near field response pattern. The apparent resistivity response at the transition zone between frequencies corresponding to ${\lambda }_f$ and ${\lambda }_n$ shows somewhat complicated variations, first increasing slightly, and then returning to the far-field value at the frequency corresponding to wavelength ${\lambda }_t\approx d$, and then decreases slightly. The impedance phase starts to deviate slightly by 45 $°$ at the frequency corresponding to ${\lambda }_f$, and recovers to the far-field value at the frequency corresponding to ${\lambda }_t$, then decreases slowly to zero as decreasing frequency.

Since the impedance response of the vertical electric dipole source does not have plane wave characteristics as defined by the field responses observed on the ground, it is not presented here. For the field of an inclined dipole source in the earth, the field responses observed on the ground will be affected by the vertical source field, which is much different from the field of a simple horizontal dipole source. Figure 5 shows the curves of apparent resistivity and phase excited by a 30° inclined electric dipole source at 10 km deep from the earth’s surface, Figures 5A, B show ${\rho }_{xy}$ and ${\phi }_{xy}$ curves, and Figures 5C, D show ${\rho }_{yx}$ and ${\phi }_{yx}$ responses observed at earth surface with different offsets in the x- and y-directions respectively. The basic features of apparent resistivity and phase responses of the inclined dipole mainly follow the typical response patterns of the horizontal dipole with frequencies and offsets. The curves of ${\rho }_{xy}$, ${\phi }_{xy}$ along the y-direction, and ${\rho }_{yx}$, ${\phi }_{yx}$ along x-direction do not show much effect by vertical dipole responses; while responses of ${\rho }_{xy}$, ${\phi }_{xy}$ along x-direction show some effect of vertical dipole especially for small offsets; but responses of ${\rho }_{yx}$, ${\phi }_{yx}$ have been severely affected by vertical dipole responses. It can be seen from Figure 5D that the ${\rho }_{yx}$ and ${\phi }_{yx}$ curves in the y-direction show oscillating feature in the far field zone with decreasing amplitude as frequency. The responses of the horizontal electric dipole source also oscillate, though the amplitude is very small and difficult to identify. Thus one of the effects of the vertical source field is to amplify this oscillation. The apparent resistivity response in the transition zone shows a negative overshot with a large amplitude at the frequency corresponding to ${\lambda }_t$. The impedance phase curve also shows a small amplitude oscillation in the high-frequency band of the far field; starts rising rapidly from close to 45° approaching +180° at the frequency corresponding to ${\lambda }_f$, and drops sharply toward −180° at the frequency corresponding to ${\lambda }_t$; and then rises to zero slowly. It can be seen that the frequency characteristics and spatial distribution characteristics of magnetotelluric responses observed on the ground may become extremely complex if an arbitrarily orientated electric dipole source at depth exists at the same time.

FIGURE 5

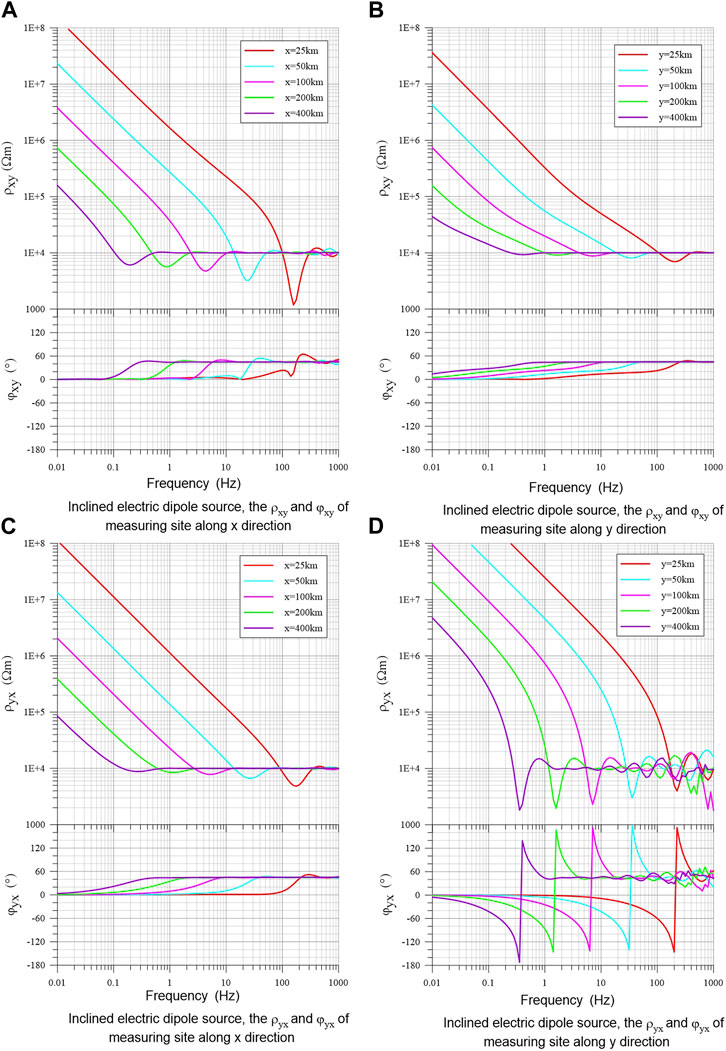
FIGURE 5. Apparent resistivity and phase response of an inclined dipole source in a homogeneous earth for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy and φ_xy of measuring sites along x and y direction respectively; (C) and (D) are the ρ_yx and φ_yx of measuring sites along x and y direction respectively.

4.2 Response of electric dipole source in the three-layer model.

The frequency characteristics of apparent resistivity and phase response of electric dipole in layered earth medium may become complex due to the difference in sensitivity of different frequencies to different depths. Figure 6 shows the apparent resistivity and phase curves of the horizontal electric dipole source with different offsets along the x - and y-directions in the three-layer earth model. Note that the impedance phases of the two principal component elements have been corrected to the 45 $°$ baseline. The parameters of the three-layer model are set and described in Figure 1A, and the horizontal dipole source in the x-direction is located at a depth of 10 km. In general, the near- and far-field characteristics of the frequency response excited by the horizontal electric dipole source shown in Figure 6 are still obvious for both apparent resistivity and phase curves. That is, in the high-frequency band, the apparent resistivity value tends to the resistivity of the surface layer, and the impedance phase tends to 45 $°$; however, in the low-frequency band, the apparent resistivity increases sharply and the phase decreases to zero. The shape of the frequency response curve becomes complex due to the influence of different resistivity layers, especially the conductive cover layer, and it is difficult to define the far/near field transition frequency as well as the oscillation and jump of the phase curve. Figure 6A shows the most complex changes of the ${\rho }_{xy}$ and ${\phi }_{xy}$ curves in the x-direction. Although the far-field apparent resistivity value is about 20 $\mathrm{\Omega }\mathrm{m}$, the frequency from the far-field to the transition zone is not much different from the transition frequency as shown in Figure 4 for resistive half-space, especially for large offsets where the resistive layer below the surface has dominant effects. For small offsets (<100 km), the apparent resistivity rises to a certain extent, then starts to decline, and then rises again in the near field zone; this may be a reflection of the layered electrical structure. The smaller the offset, the greater the amplitude of the apparent resistivity rises, with a maximum of about 3000 Ωm which is approaching the resistivity of 10⁴ $\mathrm{\Omega }\mathrm{m}$ for the resistive layer. With increasing offset, the amplitude and frequency band of the formation change effect decreases, and the near-field influence characteristics become prominent. The far-field value of ${\phi }_{xy}$ is about 45 $°$, showing a jump to +180 $°$ at the transition section, and then gradually return to zero. The jump in corresponding frequency is lower than the phase jump frequency of the uniform high-resistance earth in Figure 4. Figure 6B shows the response of the ${\rho }_{xy}$ and ${\phi }_{xy}$ in the y-direction. Compared with the ${\rho }_{xy}$ and ${\phi }_{xy}$ response in the x direction, the apparent resistivity responses have the same variation pattern, but the variation amplitude of the curve is smaller. The change of phase curve is gentle, and shows characteristics of dipole source response; only the curve with an offset of 25 km appears a positive jump at transition frequency. The curves of ${\rho }_{yx}$ and ${\phi }_{yx}$ in the x- and y-direction as shown in Figures 6C, D reflect the basic characteristics of the dipole source response and again show perfect symmetry. The frequency of the apparent resistivity and phase curves with different offset distances from the far field zone to the transition zone is close to the response of the homogeneous resistive earth as shown in Figure 4. After entering the near-field zone, the apparent resistivity curve rises slowly, and then rises at a similar rate near 1 Hz, approaching 10⁴ Ωm for all offsets. When the offset is 400 km, the apparent resistivity shows a large negative overshot and the phase shows a jump in the transition zone.

FIGURE 6

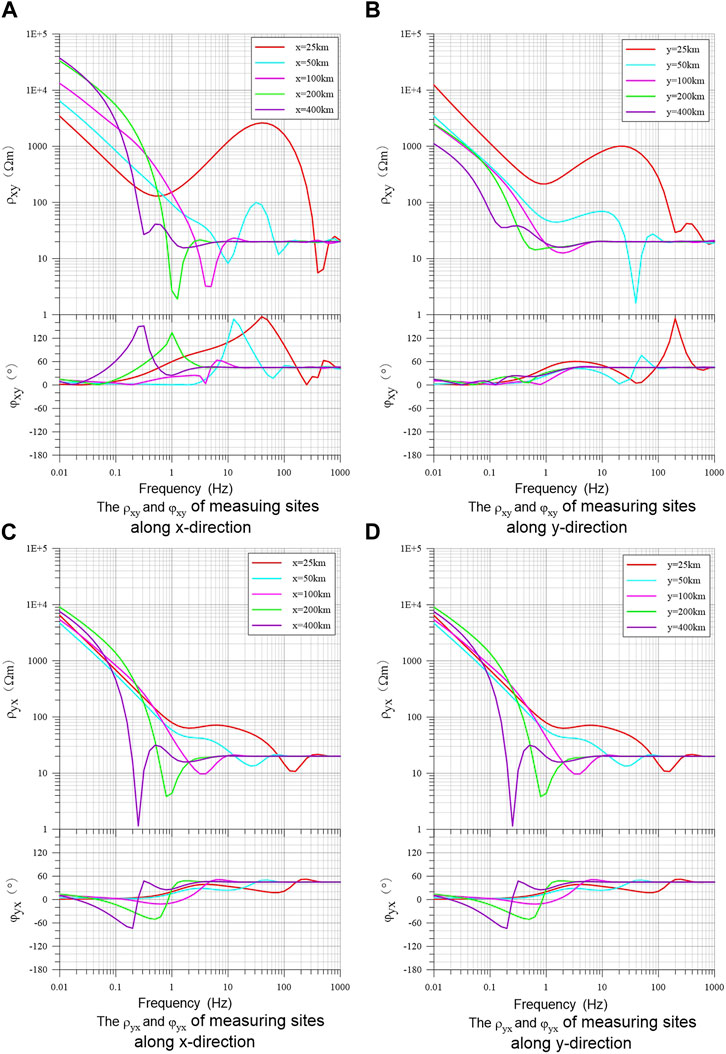
FIGURE 6. Apparent resistivity and phase curves of the horizontal electric dipole source in a three-layer earth model for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy and φ_xy of measuring sites along x and y direction respectively; (C) and (D) are the ρ_yx and φ_yx of measuring sites along x and y direction respectively.

It can be seen from the above analyses that the electromagnetic response of the horizontal electric dipole source in the layered stratum can reflect the basic characteristics of the dipole source field. However, because of the influence of layered electrical structure, the frequency response curves in different directions, differing offsets, and polarization modes may have complex shapes and variation characteristics. To better understand the spatial distribution characteristics of the electromagnetic response of the horizontal electric dipole source, Figure 7 shows the x-y plane distribution of the apparent resistivity (${\rho }_{xy}and{\rho }_{yx}$) of the horizontal electric dipole source at 100, 10, and 1 Hz, respectively; and the plotting range is the same as in Figure 2. The white arrow in Figure 7 indicates the position of the horizontal electric dipole source in the earth. It can be seen that the spatial distribution form of ${\rho }_{xy}$ is complex. First, the apparent resistivity in the corresponding rectangular neighborhood above the dipole source increases sharply towards the center of the dipole, and the lower the frequency, the larger the range of resistivity increases. For example, when the frequency is 100 Hz, the range of resistivity increase is a rectangular area composed of $x\approx \pm 35km$ and $y\approx \pm 30km$. However, when the frequency is 1 Hz, it is an area composed of $x\approx \pm 170km$ and $y\approx \pm 90km$, and the shape of the regional boundary is complex. Second, at the periphery of the area with a sharp increase in resistivity, a trough with decreased resistivity appears, corresponding to the negative overshoot of the apparent resistivity curve in Figure 6. The lower the frequency, the wider the wave trough, and, by extension, the greater the reduction in the resistivity value. Moreover, because the Ex and Hy components of the dipole source response have amplitude crossing zero and phase jump from positive to negative (or from negative to positive) at the azimuth of $\phi$ =35 $°$, the resistivity anomaly of ${\rho }_{xy}$ changes in the vicinity of the line that starts from the center of the dipole source and extends at an azimuth angle of 35 $°$. From the source center to the outside, the resistivity near the 35 $°$ line is larger than that of the adjacent area, forming a high resistivity strip extending outward, and the extended distance is far greater than the aforementioned rectangular area scale with sharply increasing resistivity. With further increase in distance, the resistivity near the extension line is slightly smaller than that in the neighborhood. It can be seen from Figure 7C with a frequency of 10 Hz that the x boundary of the rectangular domain with sharply increased resistivity is about x $\approx$ 50km, and the high resistivity anomaly zone along the 35 $°$ line extends to x $\approx$ 150 km. Meaning, that if the station is located near the extension line, the electromagnetic anomaly can be observed further away from the seismogenic center. Since the Ey and Hx components of the dipole source response change continuously with the azimuth angle; ${\rho }_{yx}$ has a simple and symmetrical spatial distribution. The resistivity increases sharply in the circle centered on the dipole source, and the radius of the circle increases with decreasing frequency. Since the earth model is not a homogeneous half-space, it cannot be characterized by the wavelength corresponding to a certain formation resistivity value. From the near source range in Figure 7 that is greater than the surface resistivity value (20 Ωm), it can be seen that the radius is about 23 km when f =100 Hz, 55 km when f = 10 Hz, and 135 km when f = 1 Hz. It can also be seen from Figure 7 that the apparent resistivity ${\rho }_{yx}$ shows a small change in oscillation amplitude in the far-field area, and the period of the oscillation decreases first and then increases with the increasing offset, which may be caused by a change of apparent resistivity with offset. Because the wavelength becomes longer at low frequencies, it is difficult to identify the oscillation period of the low-frequency response in the displayed space. ${\rho }_{xy}$ also has similar oscillation characteristics, but the 180 $°$ shift is generated with the 35 $°$ line as the boundary; that is, both sides of the 35 $°$ line correspond to peaks and troughs. The amplitude of the oscillation in the far-field area is not large, which may not be noticed in the processing of actual observation data and anomaly identification.

FIGURE 7

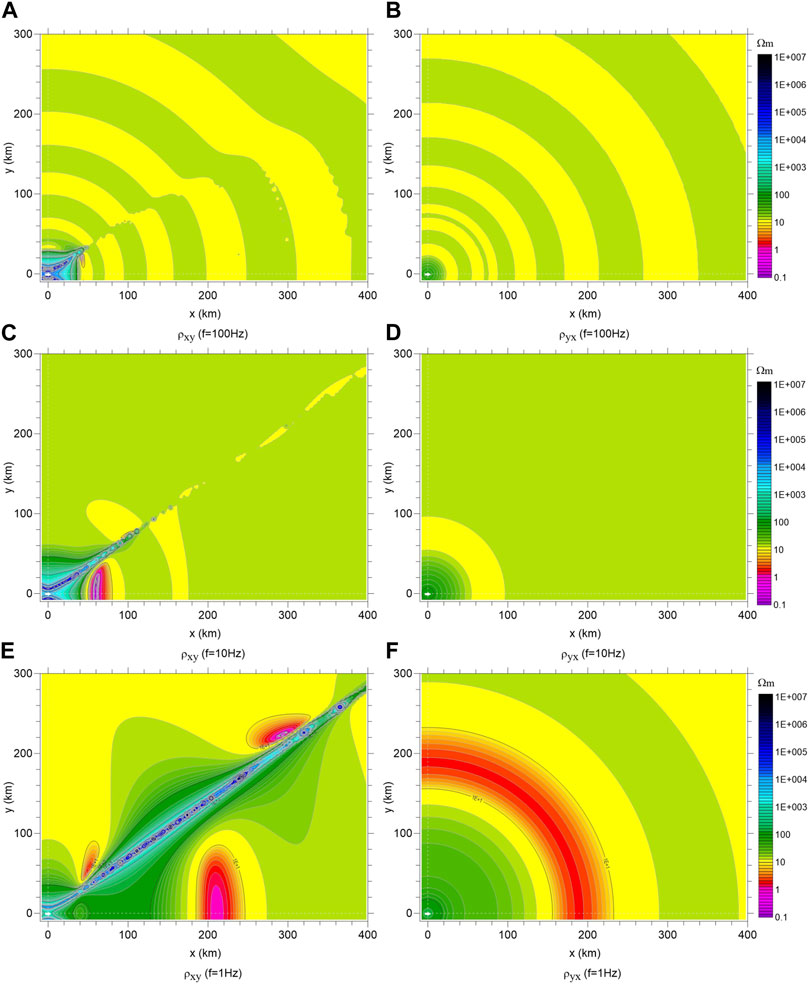
FIGURE 7. Contour plots in the x-y plane of apparent resistivity response of the x-direction horizontal electric dipole source in a three-layer earth. (A,C,E) are the ρ_xy at the frequency of 100 Hz, 10 Hz, 1 Hz respectively; (B,D,F) are the ρ_yx at the frequency of 100 Hz, 10 Hz, 1 Hz respectively.

Figure 8 shows the apparent resistivity and phase curves of the x-direction inclined (φ=30 $°$) dipole in the three-layer earth with different offsets in the x- and y-directions. Compared with the response of the horizontal electric dipole source shown in Figure 6, the response excited by the vertical electric dipole source, except the ${\rho }_{xy}$ of the y-direction, has very different curve shapes and amplitudes in other components. In general, the response curve of a tilted electric dipole source is more complex with frequency. The apparent resistivity response of the tilted dipole source exhibits a large amplitude variation pattern in the near-field zone, first reaching a high value, then decreasing slowly, and finally exhibiting an oscillating pattern with increasing frequency. The near-field maximum amplitude is much higher (at least one to two orders) than the response of the corresponding horizontal electric dipole source. For example, the x-direction’s ${\rho }_{xy}$ increase to greater than 10⁵ Ωm, the x-direction’s ${\rho }_{yx}$ increases to greater than 10⁴ Ωm, and the y-direction’s ρ_yx increase to greater than 10⁶ Ωm. The turning frequency of the apparent resistivity curve corresponding to ${\lambda }_n$ is about an order of magnitude higher than the turning frequency of the horizontal dipole source. The small amplitude oscillation in the far-field area is more prominent, that is, the amplitude change is greater, and the period is more obvious. The ${\rho }_{yx}$ value along the y-direction in the far-field zone does not reflect the resistivity of the surface layer but is closer to the value of the second layer (10⁴ Ωm). The phase curves for ${\phi }_{xy}and{\phi }_{yx}$ along the x-direction and ${\phi }_{xy}$ along y-direction oscillate slightly near the 45 $°$ line when they are in the far-field area, and when they enter the near-field area, there is a jump of +180 $°\mathrm{t}\mathrm{o}$-180 $°$, and then gradually trend to 0 $°.$ In the far-field region, ${\phi }_{yx}$ along the y-direction also oscillates rapidly.

FIGURE 8

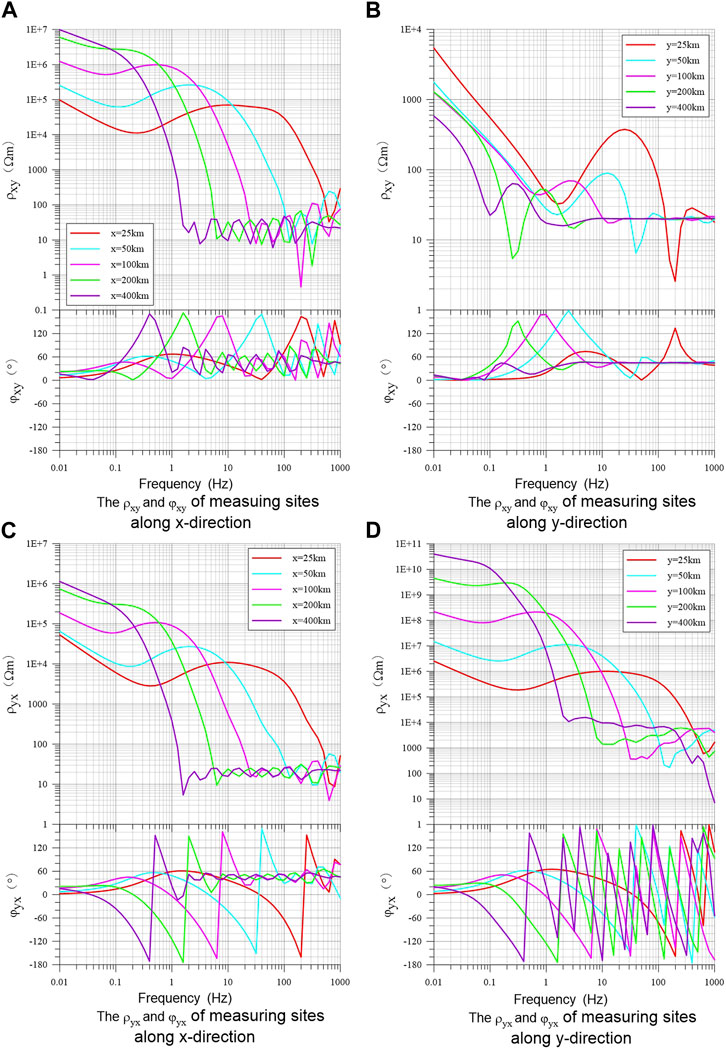
FIGURE 8. Apparent resistivity and phase curves of an inclined electric dipole source in three-layer earth for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy and φ_xy of measuring sites along x and y direction respectively; (C) and (D) are the ρ_yx and φ_yx of measuring sites along x and y direction respectively.

Figure 9 shows the plane distribution of the apparent resistivity of the inclined electric dipole source. To facilitate comparison, the same contour color scale as in Figure 7 is used. Compared with Figure 7, it can be seen that 1) the apparent resistivity of the inclined electric dipole source is much higher than that of the horizontal electric dipole source. 2) The area of near-source area apparent resistivity enhancement is much larger than the response of a simple horizontal dipole source. Taking ${\rho }_{xy}$ of f = 10 Hz as an example, the boundary in the x-direction of the simple horizontal electric dipole source is 50 km, while the boundary of the inclined electric dipole source is 160 km. 3) Because of the effect of vertical electric dipole source response, a resistivity anomaly band is formed for ${\rho }_{yx}$ response in the y-direction; that means the plane distribution ${\mathrm{o}\mathrm{f}\rho }_{yx}$ for inclined dipole response no longer has simple symmetry. 4) The oscillation amplitude in the far-field area is larger than that of the simple horizontal dipole source, and the oscillation amplitude is even larger near the anomalous extension zone.

FIGURE 9

FIGURE 9. Contour plots in the x-y plane of apparent resistivity response of an inclined electric dipole source in a three-layer earth. (A,C,E) are the ρ_xy at the frequency of 100 Hz, 10 Hz, 1 Hz respectively; (B,D,F) are the ρ_yx at the frequency of 100 Hz, 10 Hz, 1 Hz respectively.

It can be seen from the apparent resistivity response of the tilt dipole source in the earth that when the radiation source contains vertical components, the amplitude and spatial range of the apparent resistivity anomaly in the near-field zone are greatly enhanced. Compared with the response of a simple horizontal electric dipole source, the amplitude of the high resistance anomaly is about 2–5 orders of magnitude higher. For the same offset, the frequency of the near-field zone anomaly increases by about an order of magnitude. The spatial range of near-field zone anomaly is about 3 times larger (taking 10 Hz response as an example). It can be seen that the vertical component of seismogenic electromagnetic radiation can greatly increase the detectability of anomalies.

5 Magnetotelluric response with dipole radiation in the earth

The behaviors of the magnetotelluric response of the 3D anomaly of earth resistivity and the dipole response of buried electric dipole radiation source in the seismogenic zone have been presented in previous sections. We now discuss the magnetotelluric responses when the 3D anomalous body and radiation dipole exist at the same time while the magnetotelluric observation is carried on.

In the process of seismogenesis, the formation resistivity in a specific range may be reduced because of the development and expansion of micro-fractures in the earth caused by the accumulation of stress. This earth resistivity change can cause the apparent resistivity decrease in the low-frequency band (less than 1 Hz) and can be observed by magnetotelluric stations in a certain range outside the seismogenic area. As the time of the earthquake approaches, the resistivity anomalies may have the characteristics of gradually enhancing and expanding. The abrupt change of ground stress before an earthquake may also lead to electromagnetic radiation, but the spatial scope will be more limited to the vicinity of the fault. However, only in the short time before an earthquake, the stress is strong enough to generate an anomalous electromagnetic field in the far field (Du et al., 2004). For long-term monitoring stations, magnetotelluric field changes caused by different types of anomalies may be observed separately or simultaneously in different stages of earthquake preparation. If there is electromagnetic radiation before the earthquake, the field components observed at the station are the superposition of the magnetotelluric field and electromagnetic radiation field components. Because of the randomness of the amplitude and change of the magnetotelluric field, the processing and analysis of single-field data are not practical when processing observational data. Instead, it is mainly through obtaining the power spectrum of each field quantity and defining the ratio of the electromagnetic field quantity, or the impedance element, to characterize the changing relationship of the apparent resistivity with frequency. If low-frequency electromagnetic radiation is generated by the earthquake preparation, the radiation field strength must reach a certain strength before it can have a significant impact on the superimposed total field, which is reflected in the magnetotelluric response where the apparent resistivity systematically deviates from the background value.

To show the influence of the resistivity anomaly and radiation source in the earth on the magnetotelluric response, Figure 10 shows the ratio of the apparent resistivity of the 3D anomaly body and the inclined dipole source to the apparent resistivity of the 1D layered earth model. The structure and parameters of the model are shown in Figure 1. The buried depth of the electric dipole source in the earth is 10 km, the dip angle is 30 $°$, the source moment (the product of current change and rupture length) is I $\bullet$ dl=10¹¹A $\bullet$ m, and the equal source moment is used for all frequencies; Figure 10A shows the ratio curve of the apparent resistivity of the 1D layered model to ${\rho }_{xy}$ with different offsets along the x-axis: the offsets are x=25, 50, 100, 200, and 400 km, respectively. It can be seen from Figure 10A that the ${\rho }_{xy}$ response along x direction containing electromagnetic radiation for small offsets (<100 km) presents a positive anomaly with a large amplitude peak (with a maximum of 450) in the medium-frequency band (0.1–50 Hz); small positive and negative variations can be identified at the frequencies (e.g., >40 Hz for the response of 25 km offset) corresponding to the transition zone. As the offset distance increases, the abnormal peak value decreases rapidly and the anomaly of the transition zone shifts to a lower frequency. For the source moment used, the apparent resistivity anomaly with an offset greater than 100 km is weak, and almost no identifiable anomaly for responses of 400 km offset. It can be seen that the influence of the dipole radiation source observed at a magnetotelluric station is more different from the dipole source response itself shown in Figure 8, and cannot be simply identified as the near- or far-field zone for different offsets. Figure 10B shows the ratio curve of ${\rho }_{xy}$ along the y-direction to the apparent resistivity of the 1D layered model with different offsets. The response of 25 km offset shows a prominent peak of apparent resistivity enhancement with the maximum ratio of 3,800 at about 1Hz, but smoothly reducing to ∼0.6 for frequency less than 0.1 Hz. The variation of ratio curves of other offsets is small and difficult to identify for the response of offset greater than 100 km.

FIGURE 10

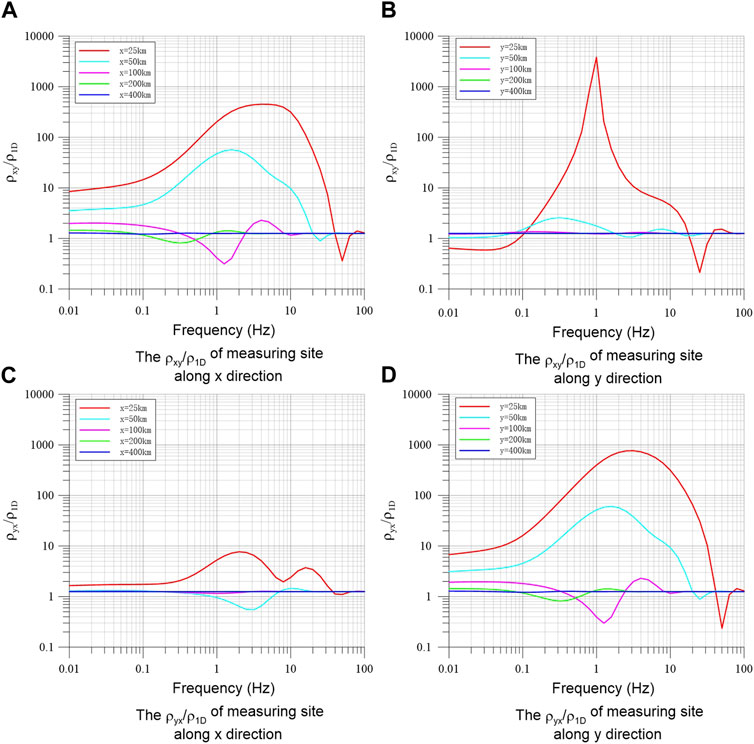
FIGURE 10. Ratio of the apparent resistivity of the 3D anomaly body together with inclined dipole source in the earth to the apparent resistivity of the 1D layered earth model for measuring sites of different offsets along x- and y-direction. (A) and (B) are the ρ_xy/ρ_1D of measuring sites along x and y direction respectively; (C) and (D) are the ρ_yx/ρ_1D of measuring sites along x and y direction respectively.

Figure 10C shows the ratio curve of ${\rho }_{yx}$ along the x-axis with different offsets to the apparent resistivity of the 1D layered model. It can be seen that the ${\rho }_{yx}$ anomaly generated by the electromagnetic radiation source is mainly in the middle-frequency band, but the amplitude is far less than the ${\rho }_{xy}$ anomaly. It is difficult to identify anomalies in the ratio curve with offsets greater than 50 km. The characteristics of the ${\rho }_{yx}$ anomaly with differing offsets along the y-direction (Figure 10D) are much similar to those of the ${\rho }_{xy}$ anomaly along the x-direction (Figure 10A), with only a slight difference in anomaly amplitude, especially for the response of short offset.

Figure 11 shows the spatial distribution of the ratio of the apparent resistivity calculated by superposition of the magnetotelluric response of the 3D low resistance anomaly and the x-direction inclined dipole source response in the layered earth model to the apparent resistivity of the 1D layered earth model, for frequencies of 10, 1 and 0.01 Hz, respectively. The range of the drawings is the same as that in Figure 9. The small white arrows in Figure 11 indicate the position of the electric dipole source in the earth, and the white step lines indicate the boundary of the 3D low resistance anomaly. It can be seen from the plot that the apparent resistivity change caused by the dipole radiation source at depth occurs in the area near the source, and the closer the source, the greater the anomaly. The apparent resistivity far away from the source is almost unchanged (the ratio is equal to 1). The anomaly in the intermediate frequency band has the maximum amplitude enhancement anomaly and a strong reduction anomaly (the ratio is far less than 1). The amplitude of the medium frequency band (f = 1 Hz) anomaly is the largest (0.01–30,000 times), and the expansion range is also large. The anomaly of ${\rho }_{xy}$ is mainly observed in a sector area in the x direction, and ${\rho }_{yx}$ in the y direction, with large amplitude enhancement from the dipole center and gradually decay to 1 at the radius of about 100 km and then reduce to a minimum of 0.01 at the radius of about 165 km. The amplitude of the high-frequency band and low-frequency band is relatively small, and the anomalous extension range is also small. The maximum amplitude of f = 10 Hz anomaly (Figures 11A, B) is ∼8,000 times, and the sector radius is about 75 km. The maximum amplitude of f = 0.01 Hz anomaly (Figures 11E, F) is ∼20 times, and the sector radius is about 95 km.

FIGURE 11

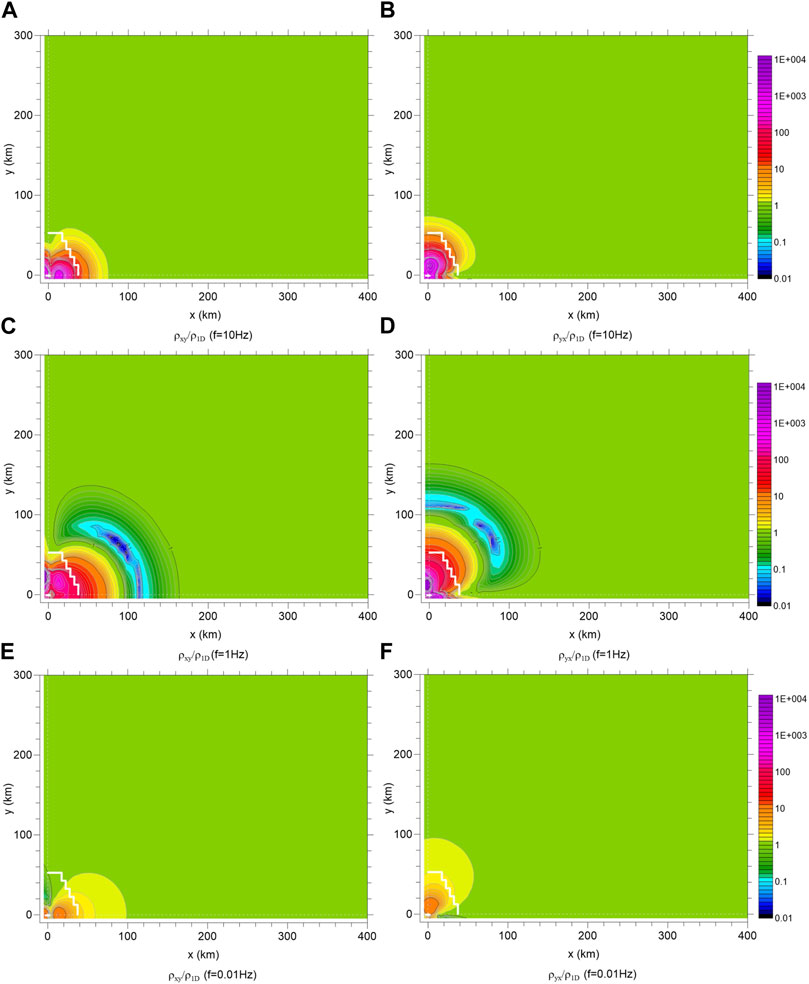
FIGURE 11. Contour plots of the ratio of apparent resistivity with 3D anomaly body together with inclined dipole source to the apparent resistivity of the 1D layered model. (A,C,E) are the ρ_xy/ρ_1D at the frequency of 10 Hz, 1 Hz, 0.01 Hz respectively; (B,D,F) are the ρ_yx/ρ_1D at the frequency of 10 Hz, 1 Hz, 0.01 Hz respectively.

6 Discussion and conclusion

It can be seen from the analysis of the above simulations that the observational data of magnetotelluric stations may contain seismogenic electromagnetic anomaly information. The characteristics of different types of seismic electromagnetic anomalies in magnetotelluric impedance response can be summarized as follows. In the seismogenic process, the change of formation resistivity (seismogenic resistivity anomaly) can produce a recognizable low-frequency (less than 1 Hz) apparent resistivity anomaly in magnetotelluric data. The anomaly is mainly a reduction of apparent resistivity from the normal value, and small amplitude enhancement anomalies may also be observed at various spatial sites. Although the amplitude of the anomaly is small, it may also be detected hundreds of kilometers (more than 200 km) away from the seismogenic center. However, if there is a low-frequency electromagnetic radiation anomaly at the same time, the influence of seismogenic low resistance anomaly may be completely masked in the low-frequency band due to the strong anomaly generated by dipole radiation in the seismogenic area. The anomaly produced by low-frequency electromagnetic radiation before earthquakes are characterized by a sharp increase of the apparent resistivity in the near-field zone, the phase approaching zero, and strong amplification of the anomaly by the presence of vertical source dipole components.

The influence of electromagnetic radiation before earthquakes included in magnetotelluric data on apparent resistivity depends on the proportion of each component of the radiation field in the spectral intensity of each component of the corresponding magnetotelluric field and will show different frequency and spatial characteristics from the response of a pure dipole source. For example, the response of a simple dipole source can be simply divided into a far-field zone and a near-filed zone according to frequency or offset, while the response of a dipole source radiation field contained in magnetotelluric data to apparent resistivity shows frequency selectivity, that is, anomalous amplitudes in the high-frequency and low-frequency bands are small, and the abnormal amplitude in the medium frequency band (0.1–50 Hz in this example) is largely due to the weak energy window of magnetotelluric field. In space, the response of the pure dipole source shows a small amplitude oscillation in the far-field area, which is difficult to identify in the magnetotelluric data. The manifestation of electromagnetic radiation in magnetotelluric response before earthquakes are mainly from the apparent resistivity enhancement anomaly with strong amplitude, and the anomaly amplitude decreases with the distance from the radiation source, but the apparent resistivity reduction anomaly with large amplitude may also appear for the data of different observation sites and different frequencies. The magnitude and spatial range of the influence of electromagnetic radiation on apparent resistivity before earthquakes are related to the intensity of the radiation sources. The stronger the radiation field intensity is, the larger the amplitude of apparent resistivity anomaly, and the wider the distribution range of anomaly. The calculation result of the source moment 10¹¹A $\bullet$ m is given in this paper. The actual earthquake case may have even stronger electromagnetic radiation, for example, the Wenchuan earthquake reached 10¹³A $\bullet$ m (Li et al., 2018), and so the station farther from the seismogenic center can also detect the electromagnetic radiation anomaly.

The algorithm for 3D magnetotelluric modeling has adopted the strategy of magnetic field normalization for field component calculation, and the calculated strength for each field component may be different from the actual spectral intensity of each component measured at the station. However, the basic characteristics of electromagnetic radiation before earthquakes simulated by an electric dipole source in magnetotelluric response are valid.

In summary, electromagnetic impedance responses of a 3D low-resistance anomalous body which is used to simulate the resistivity change of strata in the seismogenic region, and an electric dipole which is used to simulate the seismogenic radiation source in horizontally layered earth model have been calculated, and the characteristics of electromagnetic impedance response with frequency and space over a large area have been analyzed quantitatively. The simulation results show that: 1) Visual resistivity anomalies of the 3D resistivity anomalous body appear in the frequency band below 5 Hz, with negative anomalies dominating in the frequency band below 1 Hz. The amplitude of the negative anomaly decreases with the increase of the offset distance, and the anomaly can be identified over 200 km. The measured data show that the resistivity often presents an abnormal decline feature before the earthquake, and the numerical simulation in this paper provides a theoretical basis for this phenomenon. 2) The vector electric dipole radiation source is equivalent to the electromagnetic radiation in the seismogenic region, and calculating and analyzing the electromagnetic impedance response. It is found that the component of tilted electromagnetic radiation in the y-direction will greatly enhance the detectability of electromagnetic anomalies. 3) Considering the electromagnetic radiation and the change of resistivity in the seismogenic area comprehensively, it is found that the medium frequency band (0.1–50 Hz) is the dominant frequency band for seismic electromagnetic anomalies. Around 1 Hz, the anomaly is more obvious and can be detected at a large spatial range.

The obtained results are of great significance for the observation of seismic electromagnetic anomalies, data processing, and analysis of the identification of electromagnetic anomalies in different seismogenic processes. In the future, we can analyze and compare data changes during earthquakes by combining measurement data from 30 ELF stations in the metropolitan area and the North-South seismic zone in China.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

YF drafted the manuscript and the figures with the guidance of WH. All authors contributed to the completion of procedures, and discussion of this study, and provided feedback on the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 41574064), Basic Research Funds from the Institute of Geology, China Earthquake Administration (No. IGCEA2002), and the Beijing Natural Science Foundation Project (No. 8212045).

Acknowledgments

The authors would like to express gratitude to EditSprings (https://www.editsprings.cn) for the expert linguistic services. We acknowledge the constructive reviews of the reviewers, and the useful summary and review by the editor JL. We also thank Professor PH (China Earthquake Network Center) for her guidance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ding, J. H. (2009). Geomagnetic diurnal earthquake prediction method and earthquake cases. Beijing: Seismological Press.

Google Scholar

Du, A. M., Zhou, Z. J., Xu, W. Y., and Yang, S. F. (2004). Generation mechanisms of ULF electromagnetic emissions before the M_L=7.1 earthquake at Hetan of Xin Jiang. Chin. J. Geophys. 47, 832–837. http://www.geophy.cn/article/id/cjg_555.

CrossRef Full Text | Google Scholar

Du, X. B. (2011). Two types of changes in apparent resistivity in earthquake prediction. Sci. China Earth Sci. 54 (1), 145–156. doi:10.1007/s11430-010-4031-y

CrossRef Full Text | Google Scholar

Fan, Y., Tang, J., Zhao, G. Z., Wang, L. F., Wu, J. X., Li, X. S., et al. (2013). Schumann resonances variation observed from Electromagnetic monitoring stations. Chin. J. Geophys. 56, 2369–2377. doi:10.6038/cjg20130723

CrossRef Full Text | Google Scholar

Gao, S. D., Tang, J., Du, X. B., Liu, X. F., Su, Y. G., Chen, Y. P., et al. (2010). The change characteristics of electromagnetic field before to after Wenchuan Ms8.0 earthquake. Chin. J. Geophys. 53, 512–525. doi:10.3969/j.issn.0001-5733.2010.03.005

CrossRef Full Text | Google Scholar

Gao, S. D., Tang, J., and Sun, W. H. (2013). Electromagnetic anomaly before the Yingjiang M_S5.8 and Myanmar M_S7.2 earthquakes. Chin. J. Geophys. 56, 1538–1548. doi:10.6038/cjg20130512

CrossRef Full Text | Google Scholar

Gao, Y., and Hu, H. (2010). Seismoelectromagnetic waves radiated by a double couple source in a saturated porous medium. Geophys J. Int. 181, 873–896. doi:10.1111/j.1365-246x.2010.04526.x

CrossRef Full Text | Google Scholar

Gao, Y., Harris, M., Wen, J., Huang, Y., Twardzik, C., Chen, X., et al. (2016). Modeling of the coseismic electromagnetic fields observed during the 2004 Mw 6.0 Parkfield earthquake. Geophy. Res. Lett. 43, 620–627. doi:10.1002/2015GL067183

CrossRef Full Text | Google Scholar

Hu, H., and Gao, Y. (2011). Electromagnetic field generated by a finite fault due to electrokinetic effect. J. Geophy. Res. 116, B08302. doi:10.1029/2010JB007958

CrossRef Full Text | Google Scholar

Hu, K. Y., Hu, W. B., and Huang, Q. H. (2023). The electromagnetic wave fields induced by dipoles in the horizontally stratified medium. Chin. J. Geophys. 8, 1–12. Available at: https://doi.org/10.6038/cjg2023Q0775 (Accessed February 22, 2023). doi:10.6038/cjg2023Q0775

CrossRef Full Text | Google Scholar

Huang, F. Q., Li, M., Ma, Y. C., Han, Y. Y., Tian, L., Yan, W., et al. (2017). Studies on earthquake precursors in China: A review for recent 50 years. Geodesy Geodyn. 8, 1–12. doi:10.1016/j.geog.2016.12.002.geog.2016.12.002

CrossRef Full Text | Google Scholar

Huang, Q. H. (2002). One possible generation mechanism of co-seismic electric signals. Proc. Jpn. Acad. Ser. B 78, 173–178. doi:10.2183/pjab.78.173

CrossRef Full Text | Google Scholar

Huang, Q. H., Ren, H. X., Zhang, D., and Chen, Y. J. (2015). Medium effect on the characteristics of the coupled seismic and electromagnetic signals. Proc. Jpn. Acad. Ser. B 91, 17–24. doi:10.2183/pjab.91.17.91.17

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., Wang, Z. P., Lu, J., Tan, H. D., and Zhang, X. T. (2018). Estimating the equivalent dipole of the 2008 wenchuan M_s8.0 earthquake using observed electromagnetic ground signals. Earthquake 38, 49–60. http://dizhen.ief.ac.cn/CN/Y2018/V38/I1/49.

Google Scholar

Ma, Q. (2002). The boundary element method for 3-D dc resistivity modeling in layered Earth. Geophysics 67, 610–617. doi:10.1190/1.1468622

CrossRef Full Text | Google Scholar

Mao, T. N. (1986). Present status of electric-magnetic studies in earthquake science in China. Earthq. Res. China 30, 31–35. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD198603005.htm.

Google Scholar

Pan, H. W. (1998). Development and prospects of the earthquake electromagnetic observation system in China. Earthquake 18, 115–119. http://dizhen.ief.ac.cn/CN/Y1998/V18/IS1/115.

Google Scholar

Qian, F. Y., Zhao, Y. L., Yu, M. M., Wang, Z. X., Liu, X. W., and Chang, S. M. (1982). Anomalous variation of apparent resistivity before earthquakes. Sci. China Earth Sci. 9, 831–839. http://www.cnki.com.cn/Article/CJFDTotal-ZBDZ198202004.htm.

Google Scholar

Ren, H., Huang, Q., and Chen, X. (2016). Existence of evanescent electromagnetic waves resulting from seismoelectric conversion at a solid–porous interface. Geophys J. Int. 204, 147–166. doi:10.1093/gji/ggv400

CrossRef Full Text | Google Scholar

Ren, H., Wen, J., Huang, Q., and Chen, X. (2015). Electrokinetic effect combined with surface-charge assumption: A possible generation mechanism of coseismic EM signals. Geophys J. Int. 200, 837–850. doi:10.1093/gji/ggu435

CrossRef Full Text | Google Scholar

Wait, J. R. (1951). The magnetic dipole over the horizontally stratified Earth. Can. J. Phys. 29, 577–592. doi:10.1139/p51-060

CrossRef Full Text | Google Scholar

Wang, J. J., Zhao, G. Z., Zhan, Y., Zhuo, X. J., Tang, J., Guan, H. P., et al. (2005). Observations and studies on EM phenomena caused by earthquake in China. J. Geodesy Geodyn. 25, 11–21.

Google Scholar

Zhang, H. K., Shen, Q. X., Wu, W., Zhao, Y. L., and Mao, T. E. (1996). Research on dynamic prediction method of apparent resistivity in earthquake. Acta Seismol. Sin. 18, 340–345. https://www.dzxb.org/article/id/2e00a835-f6c7-47d4-8269-58f665298c71.

Google Scholar

Zhang, X. M., Qian, J. D., Sheng, X. H., Liu, J., Wang, Y. L., Huang, J. P., et al. (2020). The seismic application progress in electromagnetic satellite and future development. Earthquake 40, 18–37. doi:10.12196/j.ISSN.1000-3274.2020.02.002

CrossRef Full Text | Google Scholar

Zhao, G. Z., Wang, L. F., Tang, J., Chen, X. B., Zhan, Y., Xiao, Q. B., et al. (2010). New experiments of CSELF electromagnetic method for earthquake monitoring. Chin. J. Geophys. 53, 479–486. doi:10.3969/j.issn.0001-5733.2010.03.002

CrossRef Full Text | Google Scholar

Zhao, G. Z., Wang, L. F., Zhan, Y., Tang, J., Xiao, Q. B., Chen, X. B., et al. (2012). A new electromagnetic technique for Earthquake monitoring CSELF and the first observational network. Seismol. Geol. 34, 576–585. doi:10.3969/j.issn.0253-4967.2012.04.004

CrossRef Full Text | Google Scholar

Zhao, G. Z., Zhang, X. M., Cai, J. T., Zhan, Y., Ma, Q. Z., Tang, J., et al. (2022). A review of seismo-electromagnetic research in China. Sci. China Earth Sci. 65, 1229–1246. doi:10.1007/s11430-021-9930-5

CrossRef Full Text | Google Scholar

Zhou, C., Liu, Y., Zhao, S. F., Liu, J., Zhang, X. M., Huang, J. P., et al. (2017). An electric field penetration model for seismo-ionospheric research. Adv. Space Res. 60, 2217–2232. doi:10.1016/j.asr.2017.08.007

CrossRef Full Text | Google Scholar