Seismic random noise suppression using improved CycleGAN

Random noise adversely affects the signal-to-noise ratio of complex seismic signals in complex surface conditions and media. The primary challenges related to processing seismic data have always been reducing the random noise and increasing the signal-to-noise ratio. In this study, we propose an improved cycle-consistent generative adversarial network (CycleGAN) seismic random noise suppression method. First, the generator replaces the original cycle-consistent generative adversarial network generator network structure with the Unet structure combined with the Resnet structure in order to increase the diversity of seismic data feature extraction and decrease the loss of seismic data details. Second, in order to improve the network’s stability, the feature extraction effect, the event texture preservation effect, and the signal-to-noise ratio, the Least Square GAN (LSGAN) square difference loss is used in place of the conventional generative adversarial network cross-entropy loss. The feasibility of the proposed method was confirmed using model and real seismic data, both of which demonstrated that the improved cycle-consistent generative adversarial network method effectively suppressed random noise in seismic data. In addition, the denoising effect was superior to both the widely used FX deconvolution denoising method and original cycle-consistent generative adversarial network denoising method.

1 Introduction

Seismic data frequently include a substantial amount of random noise, owing to the influences of surface conditions, environmental interference, and anthropogenic factors. The process of seismic acquisition in the field results in the superposition of random noise and effective signals in the seismic data, which negatively impacts the data’s signal-to-noise ratio and the precision of its processing and interpretation. Wide frequency bands, ambiguous apparent velocities, and indefinable propagation directions are all characteristics of such random noise. It is challenging to accurately predict and efficiently remove random noise using current conventional methods. Therefore, a major problem in seismic data processing is the suppression of random noise and improving the signal-to-noise ratio in seismic data (Zhang et al., 2005). Currently, model- and data-driven denoising methods comprise the random noise suppression techniques for seismic data. By creating a data distribution model, model-driven seismic data denoising predicts the actual scenario that contains noisy data. Filtering, sparse transformation, and modal decomposition are frequently applied in model-driven seismic data denoising.

Filtering-based seismic data denoising removes the components associated with the noise by designing various filters, thereby enabling good sorting of the effective signal and noise in the time-space, frequency, or frequency-wavenumber. Band-pass, median (Guan et al., 2005; Wang et al., 2012), frequency-domain, and frequency-wavenumber domain filtering are commonly used for earthquake data. Predictive filtering (Gulunay, 1986; Abma and Claerbout, 1997) is another technique that builds predictive filters for noise reduction using the predictability of seismic signals in the frequency and time-space domains. Seismic data denoising based on sparse transformation (Sacchi et al., 1998; Gaci, 2014; Górszczyk et al., 2014; Lari and Gholami, 2014; Zhai, 2014; Xue et al., 2017; Chen and Song, 2018; Tang et al., 2018; Dalai et al., 2019) uses the characteristics of the difference in coefficient amplitudes between the effective signal and the noise in the transform domain. Typically, the noise corresponds to a low-value coefficient, while the effective signal corresponds to a high-value coefficient. The method involves filtering out the low-value coefficients corresponding to the noise and retaining the corresponding high-value coefficients of the signal using the hard or soft threshold method. The denoised signal is then obtained through inverse transformation. Seismic data denoising based on mode decomposition considers that the mode of the effective signal is similar to that of the original signal, while the mode of the noise signal differs widely from the original signal. Therefore, the noise in the signal is separated by mode decomposition, which suppresses the random noise in the seismic data (Chen, 2016; Liu et al., 2017; Yu and Ma, 2018; Zhou and Zhu, 2019). However, model-driven methods are not very versatile, and algorithms are often designed for specific data. When a new data type is encountered, current methods may no longer be applicable.

A representative class of algorithms in data-driven industries is deep learning, which has yielded very impressive performance across many fields owing to the advent of big data and the advancement of computing power. Deep learning approaches aim to use a trained model to predict unknown data after allowing the model to learn the data characteristics at various depths (Liu et al., 2018; Luo et al., 2020; Zhang et al., 2021; Ye et al., 2022). Deep learning techniques have been applied widely and successfully in seismic exploration (Oliveira et al., 2018; Wang and Chen, 2019; Dong and Li, 2020; Liu et al., 2022; Yang et al., 2022; Zhang et al., 2022). Wang et al. (2019) proposed a CNN denoising framework for seismic data based on data generation and augmentation, which can better suppress random noise and protect effective signals. CNNs denoise the signal by extracting the texture features from the seismic noise data. However, as the neural network’s layer count rises, it becomes easier to experience gradient explosion and overfitting, which limits denoising effectiveness (Liang et al., 2020). The use of neural networks in seismic data denoising is also constrained by their slow training speeds and for the large number of seismic data samples required. The emergence of generative adversarial networks (GANs) has partially solved these issues (Goodfellow et al., 2014). In order to train, GANs use an unsupervised learning technique that is widely applicable to both unsupervised and semi-supervised learning. Compared to other neural network models, GANs can produce seismic data that is clearer and more realistic (Wang et al., 2020). By incorporating cyclic consistency loss, CycleGAN (Zhu et al., 2017), a GAN variant, more effectively realizes the network adversarial learning process. Some researchers have successfully applied CycleGAN to the field of seismic exploration through their research (Kaur et al., 2019; Huang et al., 2022). In the area of seismic data denoising, Si et al. (2020) successfully attenuated ground rolls in seismic data using CycleGAN and Conditional GAN. Wu and Zhang (2021) demonstrated the superior denoising effect of CycleGAN by applying the original CycleGAN to seismic data random noise suppression, contrasting it with the conventional denoising method. CycleGAN was first applied to the denoising of desert seismic data by Li et al. (2020), resolving the issue that most denoising algorithms were unable to effectively suppress the noise in desert seismic data due to its particular characteristics. Ma et al. (2022) integrated the attention module into CycleGAN and proposed that ACGNet be used to denoise seismic data, thereby improving the efficiency of seismic data denoising. Li and Wang (2021) proposed a CycleGAN based on residual learning (RCGAN) for noise suppression of seismic data, achieving high quality denoising effect but still having shortcomings in detail characterization. In contrast to the method of Li and Wang (2021), we use a Unet structure in the CycleGAN generator to further improve the denoising effect on seismic data.

Based on the original CycleGAN used by Wu and Zhang (2021), an enhancement was made in order to further increase the suppression capability of random noise in seismic data. In order to enhance the random noise suppression effect of seismic data to a greater extent, reduce the loss of seismic data details, and better retain effective signals in seismic data, the generator in the original CycleGAN was improved to use the U-Net structure (Ronneberger et al., 2015) and ResNet structure (He et al., 2016). The traditional GAN cross entropy loss is replaced by the Least Square GAN square variance loss, which enhances the feature extraction effect, increases network stability, and yields better in-phase axis texture preservation effect and higher signal-to-noise ratio. Denoising tests were performed on model and real seismic data using FX deconvolution denoising method, the original CycleGAN denoising method used by Wu and Zhang (2021) and improved CycleGAN denoising method, which confirmed the denoising effect of the proposed method.

2 Methods

2.1 Residual network principle

Before the advent of ResNet, popular neural network models such as AlexNet (Krizhevsky et al., 2012) and VGG (Simonyan et al., 2014) learned the target features more effectively by simply stacking the number of neural network layers (Figure 1A). However, when the number of neural network layers reaches a certain depth, issues such as gradient disappearance, gradient explosion, and overfitting will occur, resulting in network degradation, lower training accuracy, and lower test accuracy. By adding a residual module, ResNet addresses network degradation by reducing gradient disappearance, gradient explosion, and overfitting caused by an excessively large number of neural network layers.

FIGURE 1

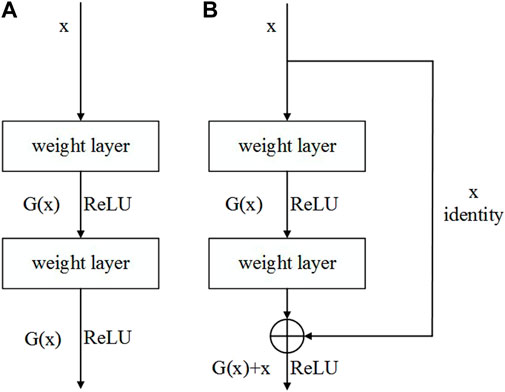
FIGURE 1. Comparison of the two different module structures: (A) convolution module and (B) residual module.

The basic structure of the residual module is shown in Figure 1B. Assuming that the neural network’s input is x, its predicted output is H(x), and its actual output is G(x). Unlike the conventional convolution module A structure, in the residual network, the input x can be directly passed to the output as the initial result by skip connections, and the output result becomes H(x) = G(x) + x. This is equivalent to the residual module changing the learning target and no longer learning a complete output, but instead learning the difference between the target value H(x) and x, (i.e., the residual G(x) = H(x) - x).

The biggest difference between ResNet and other CNNs is the addition of identity mapping. If the neural network contains more network layers than the recommended number, the residual network will train the redundant layers to G(x)=0, which means that their inputs and outputs are the same, thereby changing the network into an identity map. Gradient explosion or disappearance during network training can be avoided by using the identity mapping function, which allows the network to quickly transfer the gradient value from deeper to shallower layers. Therefore, adding more layers to the network will not result in network degradation, thereby enhancing the stability and effectiveness of the network training process.

2.2 CycleGAN principle and improvement of loss function

GANs differ from regular neural networks, as they comprise generator and discriminator networks. GANs originated from the two-person zero-sum game in game theory. Through cooperative games, both the generator and the discriminator improve at their respective functions. The value of the loss function decreases over time as the model parameters are continuously optimized and iterated during training, eventually reaching Nash equilibrium, which is a state of equilibrium in the game process.

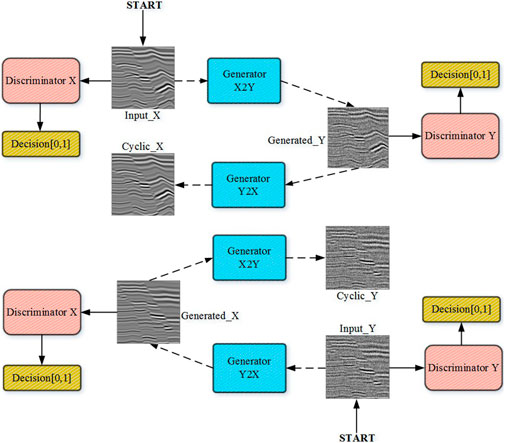
CycleGAN was enhanced based on GANs and contains two generators and two discriminators. Cycle consistency was the central concept. The data Generated_Y can then obtain the same data Cyclic_X as the data Input_X through the generator Y2X (Figure 2). This ensures that Input_X is consistent with Cyclic_X, which is equivalent to making the data cycle back to the starting point and maintaining its consistency. The original data is Domain X, the target data is Domain Y, the generator that transfers data from Domain X to data in Domain Y is G, and the generator that transfers data from data in domain Y to data in domain X is F. The discriminator that determines whether or not the data belongs to Domain X and is real is D_X, and the discriminator that determines whether or not the data belongs to Domain Y and is real is D_Y.

FIGURE 2

FIGURE 2. Working principle of CycleGAN.

First the loss that corresponds to cycle consistency is defined, also known as the cycle-consistency loss. The representation of CycleGAN is as follows to guarantee cycle consistency:

When converting from data in Domain X to data in Domain Y:

$x\to G\left(x\right)\to F\left(G\left(x\right)\right)\approx x$

When converting from data in Domain Y to data in Domain X:

$y\to G\left(y\right)\to F\left(G\left(y\right)\right)\approx y$

This can be stated as a mathematical formula:

$L_{cyc}\left(G,F\right)=E_{x\sim P_{data}\left(x\right)}\left[{‖F\left(G\left(x\right)\right)-x‖}_1\right]+E_{y\sim P_{data}\left(y\right)}\left[{‖G\left(F\left(x\right)\right)-y‖}_1\right](1)$

GAN loss is the loss function corresponding to a regular GAN, in addition to the formula corresponding to cycle-consistency loss. The loss function of the GAN composed of G and D_Y is:

$L_{GAN}\left(G,D_Y,X,Y\right)=E_{y\sim P_{data}\left(y\right)}\left[\mathit{log}{D}_Y\left(y\right)\right]+E_{x\sim P_{data}\left(x\right)}\left[\mathit{log}\left(1-D_Y\left(G\left(x\right)\right)\right)\right](2)$

The loss function of a GAN composed of F and D_X is:

$L_{GAN}\left(F,D_X,Y,X\right)=E_{x\sim P_{data}\left(x\right)}\left[\mathit{log}{D}_X\left(x\right)\right]+E_{y\sim P_{data}\left(y\right)}\left[\mathit{log}\left(1-D_X\left(G\left(y\right)\right)\right)\right](3)$

Instead of the conventional GAN loss, we propose to use the least square GAN squared difference loss. Traditional GAN generates less accurate results if cross entropy is used as the loss function, as the generator will stop optimizing the data that the discriminator believes to be true, even if they differ from the real data. This yields seismic data with a low quality, and its denoising effect is not readily apparent. The improved CycleGAN method proposed herein uses the least square GAN to replace the objective function of a traditional GAN, using the squared difference as the loss instead of the Log-likelihood to improve the feature extraction effect and obtain better in - phase axis texture preserving effect. Its formula is as follows:

$L_{LSGAN}\left(G,D_Y,X,Y\right)=E_{y\sim P_{data}\left(y\right)}\left[{\left(D_Y\left(y\right)-1\right)}^2\right]+E_{x\sim P_{data}\left(x\right)}\left[D_Y{\left(G\left(x\right)\right)}^2\right](4)$

$L_{LSGAN}\left(F,D_X,Y,X\right)=E_{x\sim P_{data}\left(x\right)}\left[{\left(D_X\left(x\right)-1\right)}^2\right]+E_{y\sim P_{data}\left(y\right)}\left[D_X{\left(G\left(y\right)\right)}^2\right](5)$

When these three components are added together, the total loss objective function of CycleGAN is obtained:

$L\left(G,F,D_X,D_Y\right)=L_{LSGAN}\left(G,D_Y,X,Y\right)+L_{LSGAN}\left(F,D_X,Y,X\right)+\lambda L_{cyc}\left(G,F\right)(6)$

2.3 Improved CycleGAN structure

2.3.1 Generator structure

We made the following improvements to the CycleGAN generator to improve the model’s denoising effect on seismic data.

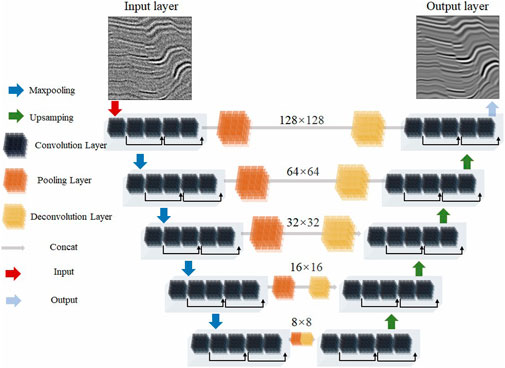
(1) The generator used the U-Net structure to increase the precision of seismic data generation. Encoder and decoder sub-networks comprise the U-Net structure. The encoder sub-network examines the input seismic data and determines its useful signal features. The decoder network can perform end-to-end training and learns the distinctive information of seismic data at various scales. By fusing the shallow low-level features of the encoder with the deep high-level features of the decoder, skip connections between layers with equal resolutions can enhance the denoising effect on seismic data.

(2) A residual network was used in the generator to better preserve the semantics of the seismic data. To ensure that the output seismic data retains the same useful information and accuracy as the input seismic data, a residual network structure was used in the CycleGAN generator to strengthen the relationship between the input and output seismic data.

(3) The generator was trained using historical data that was cached. The seismic data produced by the previous generator is the historical data that was cached, which can improve seismic data generation, stabilize the model, and reduce vibrations during training. These improvements enhance the effect of denoising on seismic data.

In this study, the encoder and decoder sub-networks comprise the generator (Figure 3). The encoder sub-network transforms input 128 × 128 seismic data into 8 × 8 data feature information. The convolution kernel size was set to 4 × 4, and the stride was set to 1. Five sets of residual blocks were included in the encoder sub-network, each of which had five convolutional layers and one pooling layer. To preserve the characteristic information of the seismic data, the size of the seismic data was compressed to half of the size of the previous operation, while the number of channels of the corresponding seismic data was double that of the previous residual block operation. The decoder sub-network upsampled the 8 × 8 data feature information produced by the encoder to 128 × 128 seismic data. The sub-network was composed of four groups of residual blocks, each of which was composed of one deconvolution layer and five convolution layers. In accordance with the encoding process, the upsampled size of the feature data was doubled after each residual operation, and the number of feature data channels was reduced by half of that of the previous residual operation. The final output was determined by a convolutional layer with 1 × 1 kernel size, a stride of 1, and using the tanh activation function.

FIGURE 3

FIGURE 3. Improved CycleGAN generator network structure used in this study.

2.3.2 Discriminator structure

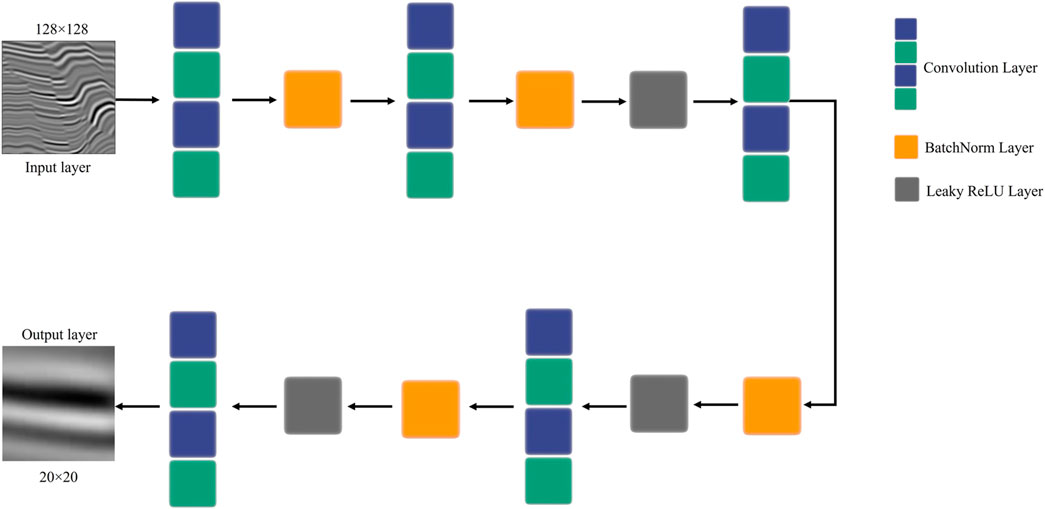
The output of the original GAN discriminator, which represents the outcome of discriminating the input data as a whole, is a True or False vector. The value of X_ij, which PatchGAN (Isola et al., 2016) generates as an N × N matrix, denotes the likelihood that each matrix is true. The discriminator’s final output is the average value of X_ij; therefore, the GAN output produced in this manner is known as PatchGAN. In this study, PatchGAN was used to enhance the accuracy and resolution of the output seismic data, which enhances the model’s denoising capacity.

In this study, the discriminator used PatchGAN (Figure 4). The input size of the discriminator network was the same as that of the generator network (128 × 128), the convolution kernel size was set to 4 × 4, and the step size was set to 1. The Leaky ReLU activation function with batch standardization and a slope of 0.2 was applied after each convolution process to produce a 20 × 20 seismic data matrix. The value of each element in the matrix denotes the probability that a particular portion of the seismic data input used by the discriminator is real.

FIGURE 4

FIGURE 4. Improved CycleGAN discriminator network structure used in this study.

2.4 Experimental procedure

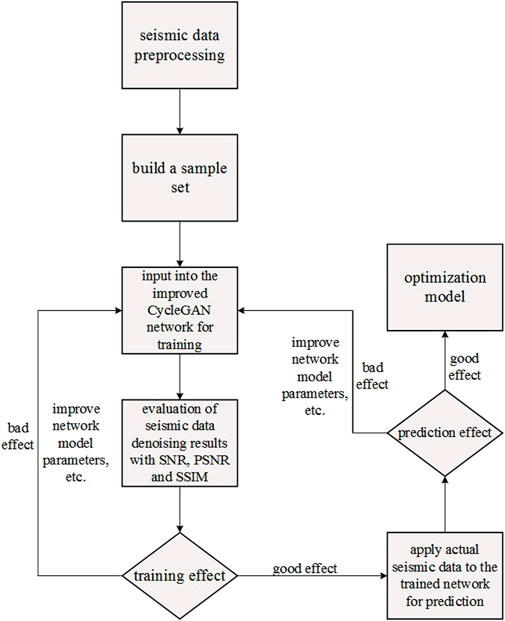
The experimental workflow used in this study is shown in Figure 5. A sample set of seismic data was created for network training after a series of pre-processing steps, which included normalizing and standardizing the seismic data. The improved CycleGAN network was trained using a sample set of original seismic data, as well as a sample set of seismic data with added random noise. The final results of the seismic data denoising process were evaluated and analyzed using signal-to-noise ratio (SNR), peak SNR (PSNR), and structural similarity (SSIM) quantitative parameter indicators. It was necessary to change the network parameters, retrain, and test until an optimized network model was attained if the training and testing results were unsatisfactory.

FIGURE 5

FIGURE 5. Experimental workflow chart of this study.

In this study, model and real seismic data were used to verify the denoising effect of the improved CycleGAN network. To evaluate the denoising effect, quantitative indicators were added, in addition to qualitative analysis. As evaluation indicators for data denoising, SNR (Zhang et al., 2009), PSNR (Netravali, 1995), and SSIM (Wang et al., 2004) were used.

$SNR=\frac{E_s}{E_n}=\frac{{\displaystyle \sum }_{i=0}^{N-1}{s}^2\left(t\right)}{{\displaystyle \sum }_{i=0}^{N-1}{\left[g\left(t\right)-s\left(t\right)\right]}^2}(7)$

The SNR is the ratio of the effective signal energy to the noise energy, which is the square of the amplitude ratio. E_s is the energy of the effective signal, E_n is the energy of the noise, s(t) is the energy of the effective signal, and g(t) is the energy of the denoised signal. Generally, the denoising effect improves and the residual noise energy of the denoised signal decreases as the SNR increases.

The root mean square error is expressed by the following:

$MSE=\frac{1}{mn}{\displaystyle \sum }_{i=0}^{m-1}{\displaystyle \sum }_{j=0}^{n-1}{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2(8)$

where I is the seismic data without random noise, K is the seismic data with random noise, and m and n are the data sizes among them. After obtaining the root mean square error, the PSNR is expressed as:

$PSNR=201\mathrm{g}\frac{{\left(2^n-1\right)}^2}{\sqrt{MSE}}(9)$

Generally, higher PSNR values indicate a more obvious denoising effect.

$SSIM\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)}(10)$

where x and y are seismic data with random noise and the denoised results, respectively; μ_x is the mean of x; μ_y is the mean of y; σ2 x and σ2 y are the variances of x and y, respectively; and σ_xy is the covariance of x and y. C₁ and C₂ are constants that maintain the stability of the structure, i.e., the denominator is guaranteed to be non-zero. Generally, larger SSIM values indicate higher data similarity.

3 Results and discussion

3.1 Model data test

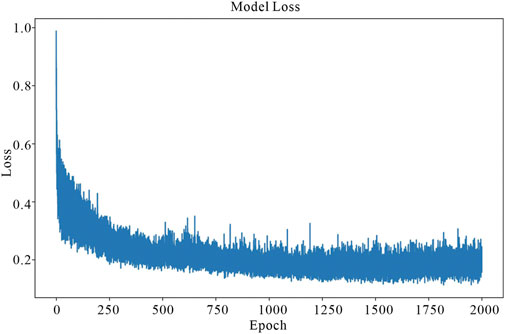
The model data in this study simulated the generation of seismic datasets using the methods of Wu et al. (2020), which produced synthetic 3D seismic data that is similar to real seismic data (Figure 6). To create a two-dimensional data sample, 128 data traces were selected in the crossline direction and 128 sampling points were selected in the time direction. Then, 2,600 data traces were selected in the inline direction as the sample set, to which random noise was added to create 2,600 groups of sample sets. As shown in Figure 7, there was no 1:1 correspondence between the original model sample data and the model sample data that contained random noise (SNR is 0.2673). After a series of data pre-processing operations that included data normalization and standardization, the sample set was input into the improved CycleGAN. Training was performed in the network, and the final training effect was tested. The ratio of the training dataset to the test dataset was set to 8:2. The final test results were compared with those of FX deconvolution denoising method and original CycleGAN denoising methods. For comparison, the SNR, PSNR, and SSIM were used as evaluation indicators for the data denoising effect. During training, we set the initial learning rate to 0.0002, used the Adam optimization algorithm, and set the number of epochs to 2000. A dedicated computer (Intel Xeon Gold5188) with 3584 CUDA cores, 16 GB of video memory, and an NVIDIA Tesla P100 graphics card was used to train the model. Figure 8 shows the improved CycleGAN loss function curve. It can be seen that the network converges after about 1,500 epochs. The denoising effect is shown in Figure 9.

FIGURE 6

FIGURE 6. 3D model of the seismic data.

FIGURE 7

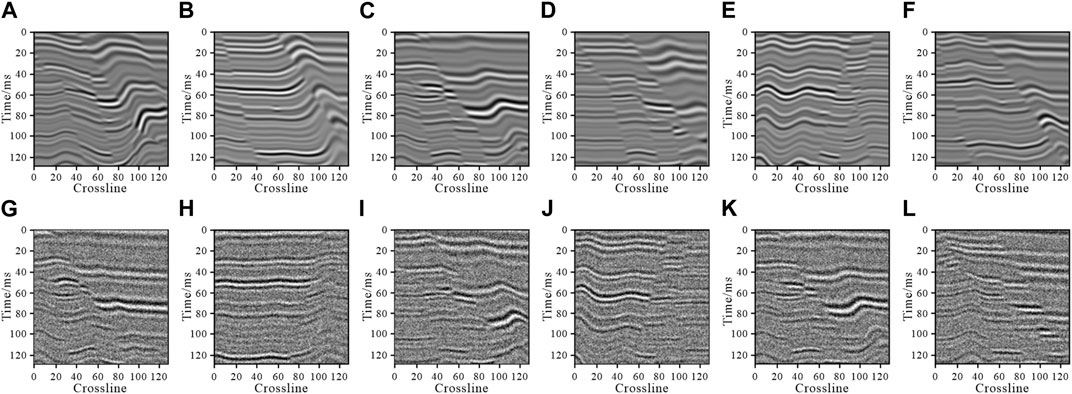
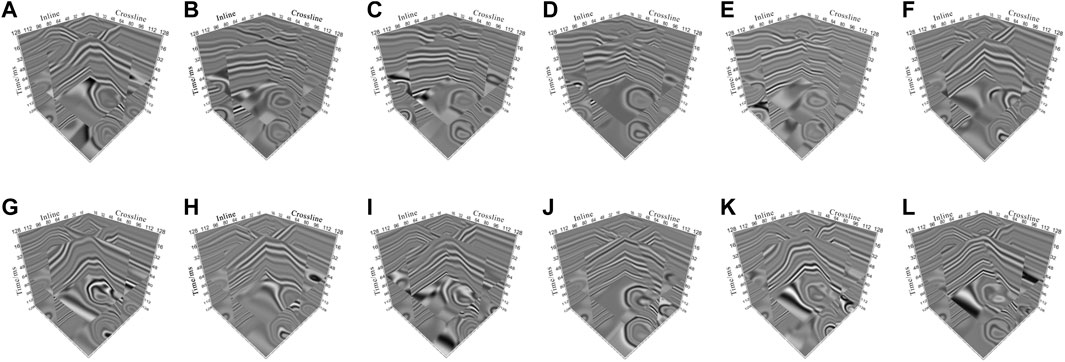
FIGURE 7. Examples of model seismic data training samples. (A–F) Original model data and (G–L) model data with random noise.

FIGURE 8

FIGURE 8. Improved CycleGAN loss function curve.

FIGURE 9

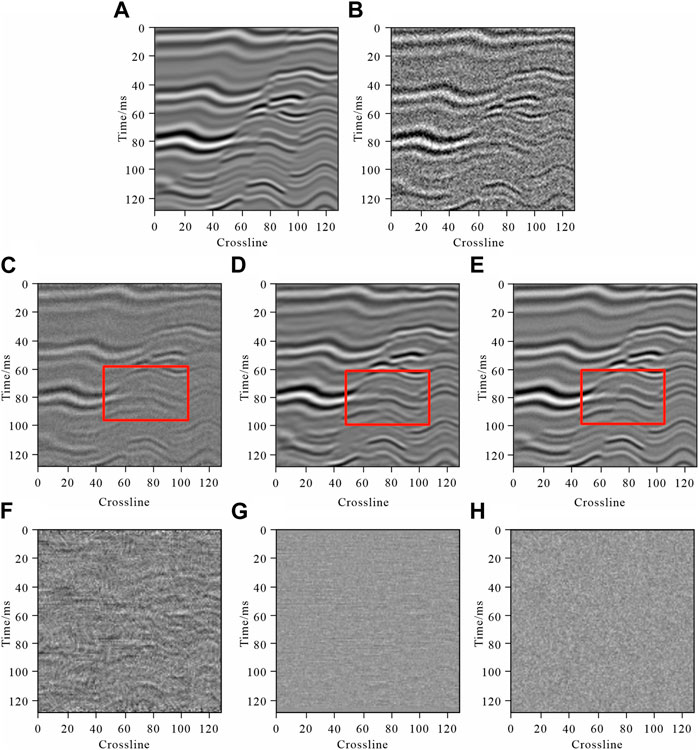
FIGURE 9. Experimental results for the model seismic data. (A) Original model data, (B) model data with random noise, (C) denoising effect of FX deconvolution method, (D) denoising effect of the original CycleGAN method, and (E) denoising effect of the improved CycleGAN method, (F) noise removal by FX deconvolution method, (G) noise removal by the original CycleGAN method, and (H) noise removal by the improved CycleGAN method developed herein.

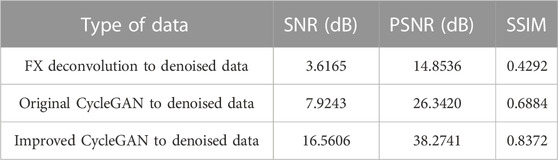
Although some random noise was removed from the denoised data produced by FX deconvolution denoising method, the overall denoising effect was not clear and some random noise persisted, which masked the useful information contained in the seismic data (Figure 9). Subsequent interpretation of the seismic data presented challenges. The original CycleGAN method still had an ambiguity issue in the description of the effective information details after the random noise was removed; however, the denoising effect was improved significantly compared to that of FX deconvolution denoising method. The improved CycleGAN network clarified the event information of the seismic data output by the generator and enhanced the texture features by combining the U-Net and ResNet structures. To improve the final data output quality, the PatchGAN discriminator was used to separate each detail of the data output by the generator. The seismic data event information obtained by the improved CycleGAN denoising method was clearer and the texture features were more obvious compared to FX deconvolution denoising method and original CycleGAN denoising methods (red box in Figure 9). The improved CycleGAN denoising method also had better denoising and effective information retention effects on the seismic data (Table 1).

TABLE 1

TABLE 1. Comparison of denoising effects on the model seismic data.

3.2 Real data test

We use publicly accessible three-dimensional seismic data from the Netherlands F3, which were collected in the offshore North Sea region and comprise a large dataset. Figure 10 shows the crossline (100–611) and inline (300–683) direction ranges, as well as the time range (1,337–1,848 ms) and sampling interval (4 ms). To create a two-dimensional sample of the data, 384 lines of data were selected in the inline direction and 512 sampling points were selected in the time direction. Then, 120 data lines were selected in the crossline direction as the sample set. The sample data were expanded to a total of 1,000 sample sets using operations including up and down flip, left and right flip, and interpolation. A specific amount of random noise was then added to the sample data to create 1,000 sample sets with random noise. The improved CycleGAN network was trained using the sample datasets mentioned above. Another section with substantial random noise added to the seismic data was also tested.

FIGURE 10

FIGURE 10. 3D real seismic data used in this study.

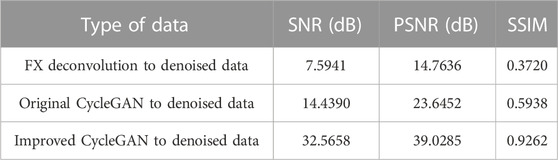
Figure 11 demonstrates that FX deconvolution denoising method did reduce some of the random noise to a certain extent, issues like masked event information and fuzzy texture details were still present. The denoising effect of the original CycleGAN method was significantly enhanced compared to that of FX deconvolution denoising method on the real seismic data. Although a substantial amount of random noise was eliminated, issues with the detailed characterization of the seismic data remained, as well as discontinuous issues, unclear expressions of the in-phase axis information, and lost texture detail features. In addition to having a better effect on removing random noise from the real seismic data, the improved CycleGAN method proposed herein also better expressed the intricate features of the real seismic data. The improved CycleGAN method depicted the event axis information more clearly and continuously, the event edge information restoration effect was improved, and the texture detail features were clearer and richer (red box in Figure 11). In addition, the improved CycleGAN method retained more useful information for the real seismic data and had a more noticeable denoising effect than FX deconvolution denoising method and original CycleGAN denoising method (Table 2).

FIGURE 11

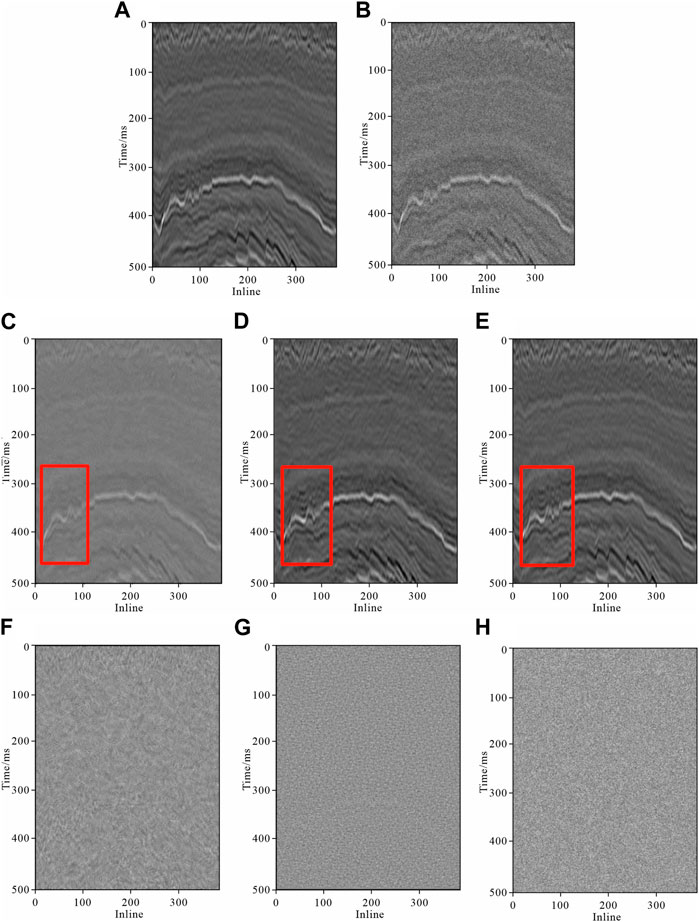
FIGURE 11. Experimental results for the real seismic data. (A) Real seismic data, (B) real seismic data with random noise, (C) denoising effect of FX deconvolution method, (D) denoising effect of the original CycleGAN method, (E) denoising effect of the improved CycleGAN method, (F) noise removal by FX deconvolution method, (G) noise removal by the original CycleGAN method, and (H) noise removal by the improved CycleGAN method developed herein.

TABLE 2

TABLE 2. Comparison of denoising effects on the real seismic data.

4 Conclusion

In this study, we proposed an improved CycleGAN random noise suppression method for seismic data. By using the U-Net and ResNet structures, the proposed method enhanced the generator in the original CycleGAN method to maximize the retention of useful information from the input seismic data and strengthened the output seismic data. The method’s ability to retain details improved the denoising effect. The objective loss function employs Least Square GAN square variance loss to enhance the effect of feature extraction and enhance network stability. The improved CycleGAN method proposed herein was then compared to FX deconvolution denoising method and original CycleGAN denoising method, and was verified as suppressing random noise using both model and real seismic data. Comparing the SNR, PSNR, and SSIM enabled an objective quantitative analysis of these denoising techniques, while viewing images of the denoising effect allowed for a subjective qualitative analysis. When the improved CycleGAN method was applied, the event information was more continuous and clear, the texture features were more noticeable, and the ability to retain local detailed features was greater, demonstrating its viability for reducing random noise in seismic data.

However, the model that was applied in this study was trained using only a portion of the data from the same region, making it challenging to produce better results when dealing with more and various types of complex seismic data. To increase the model’s capacity for generalization, more diverse types of seismic data must be used for training.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: GL, RD, and LZ; methodology: SS and RD; software: SS, YZ, and SZ; writing—original draft preparation: SS; writing—review and editing: GL, RD, LZ, YZ, SZ, JZ, and JY; visualization: SS. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the: Major Research Plan on West-Pacific Earth System Multispheric Interactions, Grant No. 92058213; Natural Science Foundation of Shandong Province, Grant No. ZR2022QD087; National Natural Science Foundation of China, Grant Nos 41676039 and 41930535.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abma, R., and Claerbout, J. (1997). Lateral prediction for noise attenuation by t-x and f-x techniques. Geophysics 60 (6), 1887–1896. doi:10.1190/1.1443920

CrossRef Full Text | Google Scholar

Chen, W., and Song, H. (2018). Automatic noise attenuation based on clustering and empirical wavelet transform. J. Appl. Geophys. 159, 649–665. doi:10.1016/j.jappgeo.2018.09.025

CrossRef Full Text | Google Scholar

Chen, Y. K. (2016). Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter. Geophys. J. Int. 206 (1), 457–469. doi:10.1093/gji/ggw165

CrossRef Full Text | Google Scholar

Dalai, B., Kumar, P., and Yuan, X. (2019). De-noising receiver function data using the Seislet Transform. Geophys. J. Int. 217 (3), 2047–2055. doi:10.1093/gji/ggz135

CrossRef Full Text | Google Scholar

Dong, X. T., and Li, Y. (2020). Denoising the optical fiber seismic data by using convolutional adversarial network based on loss balance. IEEE Trans. Geoscience Remote Sens. 59 (12), 10544–10554. doi:10.1109/TGRS.2020.3036065

CrossRef Full Text | Google Scholar

Gaci, S. (2014). The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces. IEEE Trans. Geosciences Remote Sens. 52 (8), 4558–4563. doi:10.1109/TGRS.2013.2282422

CrossRef Full Text | Google Scholar

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2672–2680.

Google Scholar

Górszczyk, A., Adamczyk, A., and Malinowski, M. (2014). Application of curvelet denoising to 2D and 3D seismic data - practical considerations. J. Appl. Geophys. 105, 78–94. doi:10.1016/j.jappgeo.2014.03.009

CrossRef Full Text | Google Scholar

Guan, X. P., Zhao, L. X., and Tang, Y. Q. (2005). Hybrid filtering method for image denoising. Chin. J. Image Graph. Ser. A 10 (3), 332–337. doi:10.3969/j.issn.1006-8961.2005.03.013

CrossRef Full Text | Google Scholar

Haskell, B. G., and Netravali, A. N. (1995). Digital pictures: Representation, compression, and standards. Plenum Press.

Google Scholar

He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, June 2016, 770–778. doi:10.1109/CVPR.2016.90

CrossRef Full Text | Google Scholar

Huang, Y. B., Huang, J. P., and Ma, Y. Y. (2022). A fast least-squares reverse time migration method using cycle-consistent generative adversarial network. Front. Earth Sci. 10, 967828. doi:10.3389/feart.2022.967828

CrossRef Full Text | Google Scholar

Isola, P., Zhu, J. Y., Zhou, T., and Efros, A. (2016). Image-to-Image translation with conditional adversarial networks. IEEE Conf. Comput. Vis. Pattern Recognit., 1125–1134. doi:10.1109/CVPR.2017.632

CrossRef Full Text | Google Scholar

Kaur, H., Pham, N., and Fomel, S. (2019). “Seismic data interpolation using CycleGAN,” in SEG technical program expanded abstracts (SAN Antonio, TX: Society of Exploration Geophysicists), 2202–2206. doi:10.1190/segam2019-3207424.1

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. (2012)., 25. New York, NY, USA: Curran Associates Inc. December 3-8, Harrahs and Harveys, Lake Taho.ImageNet classification with deep convolutional neural networksNIPS

Google Scholar

Lari, H., and Gholami, A. (2014). Curvelet-TV regularized Bregman iteration for seismic random noise attenuation. J. Appl. Geophys. 109, 233–241. doi:10.1016/j.jappgeo.2014.08.005

CrossRef Full Text | Google Scholar

Li, W. D., and Wang, J. (2021). Residual learning of cycle-GAN for seismic data denoising. Ieee Access 9, 11585–11597. doi:10.1109/ACCESS.2021.3049479

CrossRef Full Text | Google Scholar

Li, Y., Wang, H. Z., and Dong, X. T. (2020). The denoising of desert seismic data based on cycle-GAN with unpaired data training. IEEE Geoscience Remote Sens. Lett. 18 (11), 2016–2020. doi:10.1109/LGRS.2020.3011130

CrossRef Full Text | Google Scholar

Liang, J. J., Wei, J. J., and Jiang, Z. F. (2020). Generative adversarial networks GAN overview. J. Forntiers Comput. Sci. Technol. 14 (1), 1–17.

Google Scholar

Liu, J., Cao, J. X., Ding, W. N., Zhou, P., and Cheng, M. (2022). Research on reservoir porosity prediction method based on bidirectional long-term and short-term memory neural network. Prog. Geophys. 1–9.

Google Scholar

Liu, J., Lu, W., and Zhang, P. (2018). “Random noise attenuation using convolutional neural networks,” in Proceedings of the 80th EAGE Conference and Exhibition, Copenhagen, Denmark, June 2018, 1–5.

CrossRef Full Text | Google Scholar

Liu, W., Cao, S., and Wang, Z. (2017). Application of variational mode decomposition to seismic random noise reduction. J. Geophys. Eng. 14 (4), 888–898. doi:10.1093/jge/aa6b28

CrossRef Full Text | Google Scholar

Luo, R. Z., and Li, Y. Y. (2020). A random noise suppression method for seismic data based on RUnet convolutional neural network. Geophys. Prospect. Petroleum 59 (1), 51–59. CNKI:SUN:SYWT.0.2020-01-007.

Google Scholar

Ma, H. T., Ba, H., Li, Y., Zhao, Y. X., and Wu, N. (2022). Unpaired training: Optimize the seismic data denoising model without paired training data. Geophysics 88 (1), 1–73. doi:10.1190/geo2022-0224.1

CrossRef Full Text | Google Scholar

Necati, G. (1986). Fxdecon and complex wiener prediction filter. Seg. Tech. Program Expand. Abstr. 5 (1), 404–405. doi:10.1190/1.1893128

CrossRef Full Text | Google Scholar

Oliveira, D., Ferreira, R. S., Silva, R., and Brazil, E. V. (2018). Interpolating seismic data with conditional generative adversarial networks. IEEE Geoscience Remote Sens. Lett. 15 (12), 1952–1956. doi:10.1109/LGRS.2018.2866199

CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention (Berlin, Germany: Springer), 234–241.

CrossRef Full Text | Google Scholar

Sacchi, M., Ulrych, T., and Walker, C. (1998). Interpolation and extrapolation using a high-resolution discrete Fourier transform. IEEE Trans. Signal Process. 46 (1), 31–38. doi:10.1109/78.651165

CrossRef Full Text | Google Scholar

Si, X., Yuan, Y. J., Ping, F. Y., Zheng, Y., and Feng, L. Y. (2020). “Ground roll attenuation based on conditional and cycle generative adversarial networks,” in SEG 2019 workshop: Mathematical Geophysics: Traditional vs learning (Beijing, China: Society of Exploration Geophysicists), 595–798. doi:10.1190/iwmg2019_23.1

CrossRef Full Text | Google Scholar

Simonyan, K., and Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. Available at: https://arxiv.org/abs/1409.1556.

Google Scholar

Tang, N., Zhao, X., Li, Y., and Zhu, D. (2018). Adaptive threshold shearlet transform for surface microseismic data denoising. J. Appl. Geophys. 153, 64–74. doi:10.1016/j.jappgeo.2018.03.019

CrossRef Full Text | Google Scholar

Wang, F., and Chen, S. (2019). Residual learning of deep convolutional neural network for seismic random noise attenuation. IEEE Geosciences Remote Sens. Lett. 16 (8), 1314–1318. doi:10.1109/LGRS.2019.2895702

CrossRef Full Text | Google Scholar

Wang, H. Z., Li, Y., and Dong, X. T. (2020). Generative adversarial network for desert seismic data denoising. IEEE Trans. Geoscience Remote Sens. 59 (8), 7062–7075. doi:10.1109/TGRS.2020.3030692

CrossRef Full Text | Google Scholar

Wang, W., Gao, J. H., Chen, W. C., and Zhu, Z. Y. (2012). Random noise attenuation method based on structural adaptive median filter. Chin. J. Geophys. 55 (5), 1732–1741. CNKI:SUN:DQWX.0.2012-05-031.

Google Scholar

Wang, Y. Q., Lu, W. K., Liu, J. L., Zhang, M., and Miao, Y. K. (2019). Seismic random noise suppression based on data augmentation and CNN. Chin. J. Geophys. 62 (1), 13. doi:10.6038/cjg2019M0385

CrossRef Full Text | Google Scholar

Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 13 (4), 600–612. doi:10.1109/tip.2003.819861

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X. F., and Zhang, H. X. (2021). A random noise suppression method for seismic data based on cyclic consistent generative adversarial networks. Oil Geophys. Prospect. 56 (5), 958–968. +923-924. doi:10.13810/j.cnki.issn.1000-7210.2021.05.003

CrossRef Full Text | Google Scholar

Wu, X. M., Geng, Z. C., Shi, Y. Z., Pham, N., Fomel, S., and Caumon, G. (2020). Building realistic structure models to train convolutional neural networks for seismic structural interpretation. Geophysics 85 (4), WA27–WA39. doi:10.1190/geo2019-0375.1

CrossRef Full Text | Google Scholar

Xue, Y. R., Man, M. X., Zu, S. H., Chang, F. L., and Chen, Y. K. (2017). Amplitude-preserving iterative deblending of simultaneous source seismic data using high-order Radon transform. J. Appl. Geophys. 139, 79–90. doi:10.1016/j.jappgeo.2017.02.010

CrossRef Full Text | Google Scholar

Yang, J. Q., Lin, N. T., Zhang, K., Tian, G. P., and Cui, Y. (2022). Hyperparametric selection and evaluation of deep neural network models: A case study of feature extraction of multi-wave seismic response in an oil-gas reservoir. Geophys. Prospect. Petroleum 61 (2), 236–244.

Google Scholar

Ye, Z., Zhang, Z., Wünnemann, B., Liu, W., Li, H., Shi, Z., et al. (2022). High-precision downward continuation of the potential field based on the D-Unet network. Front. Earth Sci. 10, 897055. doi:10.3389/feart.2022.897055

CrossRef Full Text | Google Scholar

Yu, S., and Ma, J. (2018). Complex variational mode decomposition for slop-preserving denoising. Denoising. IEEE Trans. Geosciences Remote Sens. 56 (1), 586–597. doi:10.1109/TGRS.2017.2751642

CrossRef Full Text | Google Scholar

Zhai, M. Y. (2014). Seismic data denoising based on the fractional Fourier transformation. J. Appl. Geophys. 109, 62–70. doi:10.1016/j.jappgeo.2014.07.012

CrossRef Full Text | Google Scholar

Zhang, J. H., Lv, N., Tian, L. Y., and Lei, L. (2005). A comprehensive review of seismic data denoising methods. Oil Geophys. Prospect. (S1), 121–127+138. doi:10.3969/j.issn.1004-2903.2005.04.032

CrossRef Full Text | Google Scholar

Zhang, J. H., Zang, S. T., Zhou, Z. X., Jing, W., Shan, L. Y., Hui, J. R., et al. (2009). Quantitative computation and comparison of S/N ratio in seismic data. Oil Geophys. Prospect. 44 (4), 481–486.

Google Scholar

Zhang, Y. J., Wang, D. D., Ding, R. W., Yang, J., Zhao, L. H., Zhao, S., et al. (2022). An intelligent recognition method for low-grade fault based on attention mechanism and encoder–decoder network structure. Energies 15 (21), 8098. doi:10.3390/en15218098

CrossRef Full Text | Google Scholar

Zhang, Z., Liao, X., Cao, Y., Hou, Z., Fan, X., Xu, Z., et al. (2021). Joint gravity and gravity gradient inversion based on deep learning. Chin. J. Geophys. (in Chinese) 64, 1435–1452. doi:10.6038/cjg2021O0151

CrossRef Full Text | Google Scholar

Zhou, Y., and Zhu, Z. (2019). A hybrid method for noise suppression using variational mode decomposition and singular spectrum analysis. Journal of Applied Geophysics 161, 105–115. doi:10.1016/j.jappgeo.2018.10.025

CrossRef Full Text | Google Scholar

Zhu, J. Y., Park, T., Isola, P., and Efros, A. A. (2017). “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, October 2017, 2242–2251. IEEE. doi:10.1109/iccv.2017.244

CrossRef Full Text | Google Scholar