Rock physics and machine learning comparison: elastic properties prediction and scale dependency

Rock physics diagnostics (RPD) established based upon the well data are used to deterministically predict elastic properties of rocks from measured petrophysical rock parameters. However, with the recent advances in statistical methods, machine learning (ML) can help to build a shortcut between raw well data and rock properties of interest. Several studies have reported the comparison of rock physics and machine learning methods for the prediction of rock properties, but the scale dependence of the ML models was never investigated. This study aims at comparing the results from rock physics and machine learning models for predicting elastic properties such as bulk density (ρ_b), P-wave velocity (V_p), S-wave velocity (V_s), as well as Poisson’s ratio (v) and acoustic impedance (I_p) in a well from the Gulf of Mexico (GOM) in two different scale scenarios: the well log and seismic scales. The well data under examination was split into training and testing subsets to optimize and test the developed ML models. The RPD approach was also used to validate and compare the accuracy of predicted elastic properties. Backus averaging was later applied to upscale the well data to the seismic scale to examine the scale dependence and prediction accuracy of aforementioned physics-driven and data-driven approaches. Results show that RPD and ML methods provided consistent results at both well log and seismic scales, suggesting the scale independence of both approaches. Moreover, ML models showed better estimation of rock properties due to their “apparent” match with measured data at both scales compared to the RPD approach where a significant mismatch between measured and predicted rock properties was found in the reservoir section of the well. However, by conducting further quality control of the sonic data, it was found that the measured Poisson’s ratio was extremely high in the gas-saturated interval. Hence, the prediction from ML models in this particular case cannot be trusted as ML models were trained based on poor-quality well data with non-realistic V_s and v values. Such an issue, however, could be identified and corrected using RPD as presented in this study. We demonstrate the importance of incorporating domain knowledge, i.e., rock physics, to check data quality and validate results from data-driven models.

1 Introduction

As a branch of earth sciences, seismic rock physics integrates the multiscale subsurface data for predicting various properties of porous rocks through mathematical models frequently called “rock physics transforms.” Particularly, these transforms relate elastic properties (e.g., bulk density, P- and S-wave seismic velocity, Poisson’s ratio, P-wave impedance) to petrophysical rock properties (e.g., porosity, mineralogy) and their conditions (e.g., pore fluid, stress). Rock physics diagnostics (RPD) is the process of establishing the transform between the aforementioned rock properties (Dvorkin et al., 2014). The objective of RPD is to find a rock physics transform (model) that quantitatively explains the well data by predicting the elastic properties strictly through mathematical and physics-based relations. Moreover, RPD is useful to conduct the quality control (QC) of the well data as well as describe the texture of sedimentary rocks based on established rock physics transform (Avseth et al., 2010). The obtained elastic properties are then used to derive or “forward model” the expected seismic signatures of measured rock properties. The arsenal of developed rock physics models (such as the soft sand, stiff sand, constant cement, etc.) is available to conduct such modeling (Avseth et al., 2005; Mavko et al., 2020). A number of RPD studies have been conducted to predict rock properties from the well and seismic data (Alabbad et al., 2021; Gogoi and Chatterjee, 2021). The stiff sand model established from RPD was used to build a rock physics template to diagnose a consolidated sand reservoir (Ali et al., 2020). Suleymanov et al. (2021) employed RPD to derive seismic reflections in a tight gas sandstone reservoir. RPD was also performed by Wollner et al. (2017) to correct erroneously measured S-wave velocity curves. Moreover, Dvorkin and Wollner (2017) investigated the scale dependence of rock physics transforms at the seismic scale, where rock physics transforms were found to be scale-independent. By means of RPD, the well data can be quantitatively explained and then corrected, as needed, not only at the wireline scale but also at the seismic scale.

RPD is strictly based on physics-based relations to link petrophysical and elastic rock properties. However, one of the main drawbacks of the RPD approach is that the input data employed in rock physics transforms may not be of good quality, particularly for the total porosity, mineralogy, and water saturation, resulting in erroneous estimation of rock properties. Often, these volumetric rock properties are calculated by petrophysicists in a process that is prone to uncertainty and undesired artifacts. For example, the clay content and saturation curves calculated from gamma ray and resistivity data, respectively, are based on empirical relations that require certain fitting parameters, which in turn may introduce uncertainty and then carried away in RPD. The derivation of petrophysical input parameters certainly requires expertise and can be time-consuming.

Increasingly, researchers have made efforts to predict rock properties from the well data by employing machine learning (ML) and deep learning (DL) methods. Machine learning and deep learning algorithms have been employed in many domains of geosciences, including rock physics (Das et al., 2019; Weinzierl and Wiese, 2021; Xiong et al., 2021; Suleymanov et al., 2022a), reservoir characterization (Elkatatny et al., 2018; Gowida et al., 2019) and seismic interpretation (Di et al., 2018; Wang et al., 2018). Based on available data and the proposed task, the subsurface data coming from seismic, drilling, and well logging operations can serve as input parameters to predict the rock properties of interest. For example, Tariq et al. (2016) employ the well data for predicting compressional and shear travel times, while Suleymanov et al. (2022b) predict sonic travel times but using drilling data. However, few studies reported the comparison of rock physics and machine learning methods for the prediction of elastic properties from well log data. As an example, Jiang et al. (2020) demonstrated the applicability of machine learning in rock physics analysis. Particularly, the rock physics modeling workflow was used to generate 30 synthetic well logs to train and validate machine learning models, while the measured well log data was used to test the developed data-driven models. Azadpour et al. (2020) used the combination of rock physics and machine learning approaches to predict S-wave velocity, which improved the prediction accuracy compared to the routine Xu-Payne (2009) model. Elastic properties, such as V_p and V_s, were also predicted from regression analysis performed per facies with porosity and clay volume used as input parameters (Avseth et al., 2021). However, the applicability of machine learning methods for predicting elastic properties at the seismic scale is not well understood yet. That is, the scale dependence of the machine learning results is yet to be investigated.

This research focuses on applying rock physics and machine learning methods to predict elastic properties, namely, bulk density (ρ_b), P-wave velocity (V_p), S-wave velocity (V_s), as well as Poisson’s ratio (v) and acoustic impedance (I_p) from the well data in the Gulf of Mexico (GOM). In particular, we examine the applicability of RPD versus three different ML models, such as artificial neural networks (ANN), functional networks (FN), and support vector machines (SVM), to predict elastic properties. Well log data such as total porosity, gamma ray, and deep resistivity logs were used as inputs to simulate the petrophysical input parameters employed in rock physics models, namely, porosity, mineralogy, and pore fluid, respectively. Moreover, we investigate whether the results obtained from machine learning are scale-dependent or not (i.e., applicable at both well log and seismic scales). Predicted elastic properties were evaluated based on correlation coefficient (R) and average absolute percentage error (AAPE) between measured and predicted values in these two methods. Finally, we discuss the advantages and limitations of physics-driven and data-driven approaches during the prediction of rock properties.

2 Materials and methods

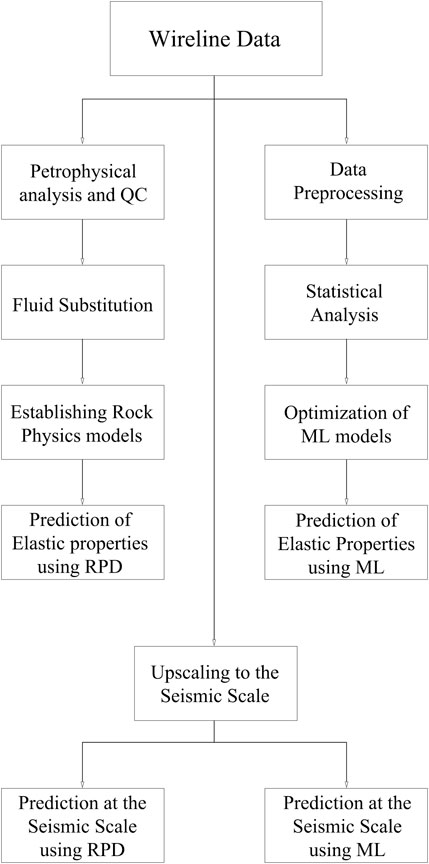
This research primarily incorporates the petrophysical analysis to delineate the reservoir intervals in the well data. Once this analysis was conducted, the well data were employed by physics-driven and data-driven methods to predict elastic parameters of rocks. First, RPD was used as a physics-based approach to relate petrophysical and elastic properties of sedimentary rocks. Alternatively, ML was employed as a data-driven approach for predicting the same elastic properties at the well log scale. Next, the measured well data and the obtained results were upscaled to the seismic scale to investigate the scale dependence and accuracy of both approaches. Figure 1 summarizes the workflow used in this study, and details are included in the following sections.

FIGURE 1

FIGURE 1. Workflow of this study.

2.1 Well data

As the first step, the petrophysical interpretation of the well data was conducted to evaluate the physical properties of porous rocks. Figure 2 illustrates the well data under examination from the Mississippi basin in the Gulf of Mexico (GOM), which incorporates a conventional suite of wireline logs such as gamma ray, resistivity, bulk density, and sonic logs. According to the petrophysical analysis of the well data, several depth intervals describe high-porosity gas sand from a clastic depositional environment. From the available wireline data, our main objective was to conduct rock physics and machine learning analyses in the lower part of the well interval (starting from 14.2 kft depth) and compare the obtained results from physics-driven and data-driven approaches. The remaining upper interval, in turn, was used to optimize machine learning models prior to applying them in the lower part of the well interval to validate developed models. Figure 3 illustrates the well data interval used in both rock physics and machine learning modeling.

FIGURE 2

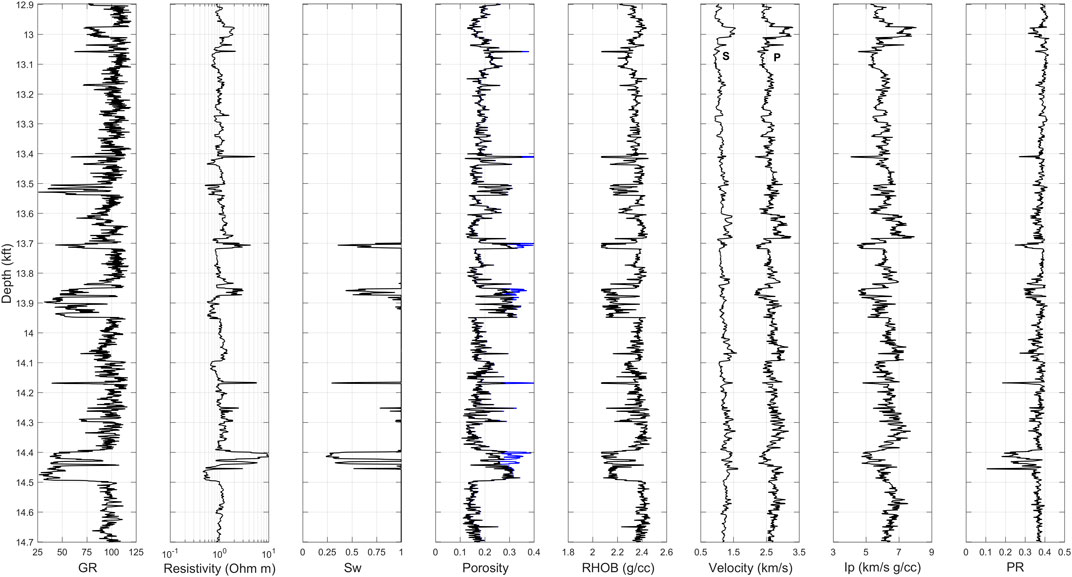
FIGURE 2. Well log data from GOM dataset. From left to right: gamma ray, resistivity, saturation, porosity (total porosity is black, density-derived porosity assuming full water saturation is blue), bulk density, velocities (S-wave velocity on left, P-wave velocity on right), P-wave impedance, and Poisson’s ratio.

FIGURE 3

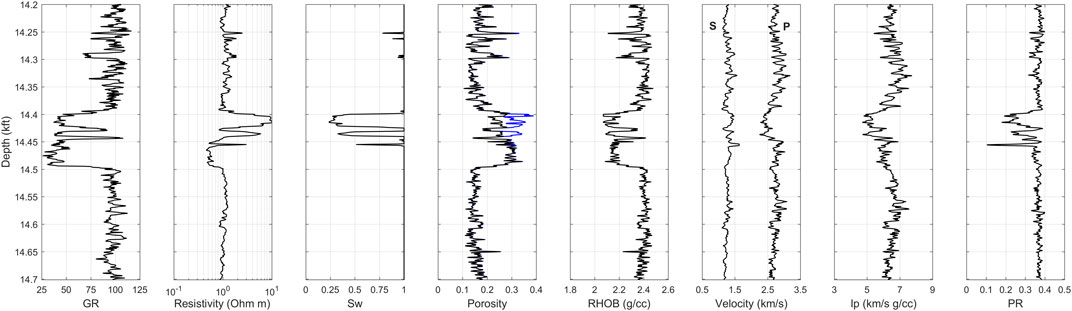
FIGURE 3. Same as Figure 2 but displaying only the well interval employed in rock physics and machine learning.

2.1.1 Total porosity

The total porosity is one of the critical inputs in rock physics modeling controlling the elastic response of rocks. Therefore, we quantify the total porosity from the measured bulk density as the density-derived porosity:

$\varphi =\left({\rho }_s-{\rho }_b\right)/\left({\rho }_s-{\rho }_f\right)(1)$

where ${\rho }_s$ is the density of the mineral matrix, ${\rho }_b$ is the measured bulk density, and ${\rho }_f$ is the density of the pore fluid. By assuming the density of the fluid 1.00 g/cc, and the density of mineral matrix 2.65 g/cc, Eq. (1) becomes:

${\varphi }_{\rho }=\left(2.65-{\rho }_b\right)/\left(2.65-1.00\right)(2)$

The resultant porosity assuming this full water saturation is shown in Figure 2 (blue curve). However, a more accurate estimation of the total porosity can be obtained from another physics-based equation. It can be calculated as Eq. (2), but now using the density of the pore fluid as a saturation-weighted average of those of water and gas as shown below:

${\rho }_f=S_w{\rho }_w-\left(1-S_w\right){\rho }_g(3)$

As a result, the total porosity becomes:

${\varphi }_t=\left(2.65-{\rho }_b\right)/\left(2.65-{\rho }_f\right)(4)$

2.1.2 Clay content

Mineralogy is another critical input in rock physics modeling. The modeling assumes that only two minerals are present in the well data under examination: quartz and clay. One of the common ways of obtaining the clay content from well log data is a linear transformation from the gamma-ray (GR) log (Dvorkin et al., 2014). The readings acquired from the GR tool are crucial to identify the presence of shale in the formations. The clay content can be determined from the selected pure-quartz (GR_min) and pure-shale (GR_max) points or baselines in the GR log profile. In this study, GR readings such as 30 and 115 API were selected as GR_min and GR_max, respectively. The resulting clay content was calculated from the GR log as follows:

$C=\frac{G{R}_{\mathit{log}}-G{R}_{\min }}{G{R}_{\max }-G{R}_{\min }}(5)$

2.1.3 Acoustic impedance and Poisson’s ratio

In exploration geophysics, the contrast of acoustic impedance determines seismic reflections of subsurface formations. Acoustic impedance is a vital parameter that relates rock petrophysical and elastic properties. According to the data available, the acoustic impedance was calculated from the well data as the product of the bulk density and seismic velocity (either P- or S-wave velocity) measured on the same porous rock:

$I_p={\rho }_b{V}_p(6)$

$I_s={\rho }_b{V}_s(7)$

Poisson’s ratio, on the other hand, is the ratio of various elastic moduli or elastic-wave velocities. Essentially, Poisson’s ratio is the ratio of lateral strain to the axial strain (Bachrach et al., 2000). Based on available wireline data, the Poisson’s ratio was derived as a function of elastic wave velocities:

$v=\frac{1}{2}\frac{{V_p}^2/V_s^2-2}{{V_p}^2/V_s^2-1}(8)$

The calculated impedances (I_p and I_s) and Poisson’s ratio (v) can be found in Figure 2.

2.2 Rock physics diagnostics

We employ RPD as the physics-driven methodology, which allows to predict the elastic properties of rocks from the well or core data through developed rock physics models (Dvorkin et al., 2014). RPD can be used not only for the quantitative interpretation of the rock elastic properties but also to provide a qualitative explanation of these properties in terms of rock texture, including the grain size sorting, pore space geometry, degree of cementation, and the effect of clay (Avseth et al., 2010; Salih et al., 2021; Salih et al., 2023). Schematically, RPD is employed in two steps: (i) a theoretical fluid substitution transform is used to replace the pore fluid in the entire well data interval to a common pore fluid, formation brine, and (ii) by cross-plotting the wet (fluid substituted) velocities versus total porosity data with theoretical rock physics model curves superimposed upon these data. Next, these cross-plots are usually color-coded by a third variable indicative of the clay content, which in turn, validates the relevancy of the rock physics model for the well data under examination.

2.2.1 Fluid substitution

Fluid substitution is an integral part of rock physics analysis. It allows to observe the difference between measured and modeled elastic properties when the pore fluids and their saturations are theoretically changed. Essentially, this step is performed to eliminate the impact of pore fluids variations and thus focus on the pure effect of texture and mineralogy on rock elastic properties. In rock physics, Gassmann’s (1951) fluid substitution is a theoretical transform that can help to investigate various pore fluid and saturation scenarios at their in-situ conditions. This transform primarily employs the fluid properties computed from Batzle-Wang (1992) equations to arrive at bulk modulus and seismic velocities of the rock saturated with a particular pore fluid. The main outputs from Batzle-Wang (1992) equations are the bulk modulus and the density of the pore fluid such as gas and water. Table 1 summarizes the fluid properties obtained from Batzle-Wang (1992) formulations applied at the reservoir pressure and temperature.

TABLE 1

TABLE 1. Rock and fluid properties used in theoretical fluid substitution.

The rock and fluid properties used in Gassmann’s (1951) equations are listed in Table 1.

2.2.2 Rock physics models (transforms)

As a velocity-porosity science, rock physics provides physics-based relations between the elastic-wave velocity and the measured porosity in the well or laboratory (Dvorkin, 2021). This operation can be inversely implemented to arrive at the porosity of the subsurface formations from known seismic attributes. A number of rock physics models were developed to relate these petrophysical and elastic properties of rocks. The time average equation, introduced by Wyllie et al. (1956), is among the first rock physics transforms relating velocity to porosity:

$\frac{1}{V_p}=\frac{1-\varphi }{V_{ps}}+\frac{\varphi }{V_{pf}}(9)$

where $V_{ps}$ is the velocity in the mineral phase, and $V_{pf}$ is the velocity in the fluid phase. However, this transform suffers from the unrealistic simplicity of the model. The model idealizes a porous rock as a combination of mineral and fluid phases in terms of layers. The velocity in this transform is calculated as the sum of travel times of minerals and fluids. Nevertheless, in nature, the rock is a composite of varying-sized and irregularly shaped grains and pores (Kerimov, 2018). The empirical equation introduced by Raymer et al. (1980) is another historical equation that provides a relation between the velocity and porosity of the rock.

$V_p={\left(1-\varphi \right)}^2{V}_{ps}+\varphi V_{pf}(10)$

Compared to Wyllie et al. (1956) time average equation, this rock physics transform is more accurate for consolidated rocks. By using the same functional form, Dvorkin (2008b) showed that S-wave velocity can be estimated as well (excluding friable sands):

$V_s={\left(1-\varphi \right)}^2{V}_{ss}\sqrt{\frac{\left(1-\varphi \right){\rho }_s}{\left(1-\varphi \right){\rho }_s+\varphi {\rho }_f}}(11)$

Where $V_{ss}$ is the S-wave velocity in the mineral phase, ${\rho }_s$ and ${\rho }_f$ are the density of the mineral phase and the pore fluid, respectively.

In addition to the aforementioned velocity-porosity models, Mavko et al. (2020) present a number of rock physics models for various lithologies, including unconsolidated and consolidated sandstones, carbonates, and other sediments. These models can be generally classified as inclusion models and grain-based models. If the model is relevant to well data, it can significantly contribute to the prediction of the rock texture. In inclusion models, the pore space is represented as inclusions, typically observed in carbonate rocks (Fournier et al., 2018; Jaballah et al., 2021; Teillet et al., 2021). However, in grain-based models, the rock is represented as a combination of ideally rounded and identically shaped grain packs. Since the rock under examination is sandstone (binary mixture of quartz and clay minerals), we examine some of the widely used granular effective medium (GEM) models that are usually applied to rocks from clastic environments. The concept of critical porosity introduced by Nur et al. (1998) is employed in all grain-based models, mainly in sandstones. In addition; Hertz-Mindlin (1949) contact theory is used to provide elastic properties of the grain packs in these models. The soft-sand, stiff-sand, and constant-cement models are among these models. The soft-sand model is also called a friable sand model. This model assumes that the porosity of the sand grain pack decreases as a result of the presence of other small rock fragments (Dvorkin and Nur, 1996). The stiff-sand model, however, implies that the porosity decrease is accompanied by a diagenetic trend due to cement formation and accumulation observed in grain contacts (Mavko et al., 2009). The constant cement model assumes that the initial cementation is present in the sand grain pack, but the further porosity decrease is accompanied by the deposition of non-cementing particles (rock fragments) in the pore space (Avseth et al., 2000). The illustration of these theories is presented in Figure 4.

FIGURE 4

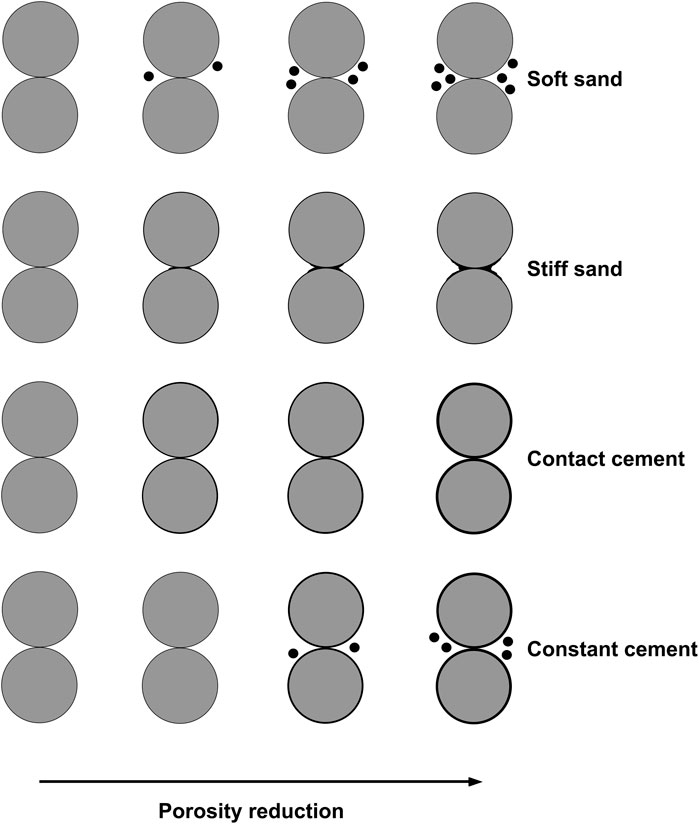
FIGURE 4. Theoretical rock physics models illustrating porosity reduction from left to right. From top to bottom: soft sand model, stiff sand model, contact cement model, and constant cement model. Modified from Dvorkin (2021).

2.3 Upscaling

From seismic exploration to well logging to core analysis, the scale of investigation of subsurface formations varies dramatically from kft to ft. The multiscale subsurface data are typically used to characterize various rock properties. One way to bring the multiscale subsurface data to a common scale is upscaling (Partyka et al., 2000). Upscaling is a technique that allows finding the common or “effective” properties of heterogeneous rocks. During this process, the wireline and core data are usually upscaled to a seismic scale so that the obtained rock properties can be compared and extrapolated, if needed, to the prospects away from the well location and correlated with seismic data. In geophysics, Backus (1962) averaging method is widely used to produce effective rock properties at the seismic scale. Particularly, arithmetic average and harmonic average were used to upscale petrophysical (clay content and porosity) and elastic parameters, respectively. In this study, we used the upscaling technique to investigate the validity of RPD versus ML approaches when the results are being upscaled at the seismic scale.

3 Results

3.1 Rock physics diagnostics

3.1.1 Fluid substitution

The first rock physics transform applied to well data under examination was Gassmann’s (1951) fluid substitution. As stated in the previous section, the lower part of the well interval was used for rock physics analysis. Figure 5 indicates that a theoretically substituted pore fluid, 100% saturated brine, impacted the elastic response of porous rocks in the reservoir section of the well. Based on the obtained results, the sensitivity of elastic properties to pore fluid saturation is obvious in the upper part of the high-porosity reservoir interval. Moreover, by plotting the impedance (I_p) versus porosity as presented in Figure 6, we notice that a low-porosity high-impedance domain of the cross-plot describes water-saturated rocks, while hydrocarbon-saturated rocks have high porosity (ϕ > 0.2) and an I_p that is predominantly below 5.5 km/s g/cc.

FIGURE 5

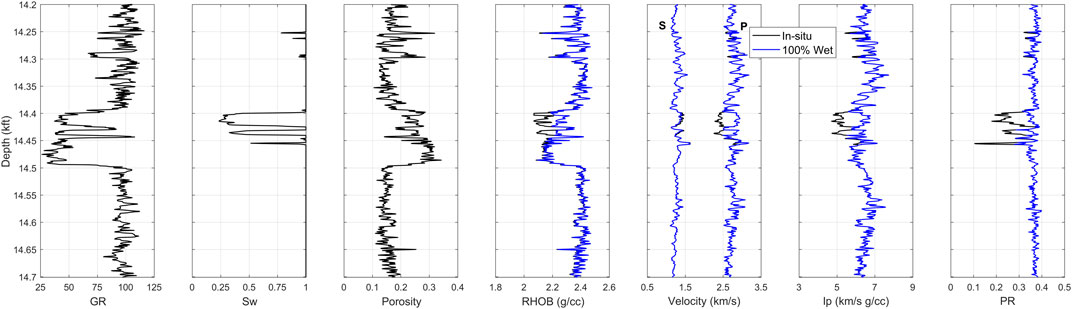
FIGURE 5. Measured (black) and computed (blue) elastic properties of rocks for 100% water saturation.

FIGURE 6

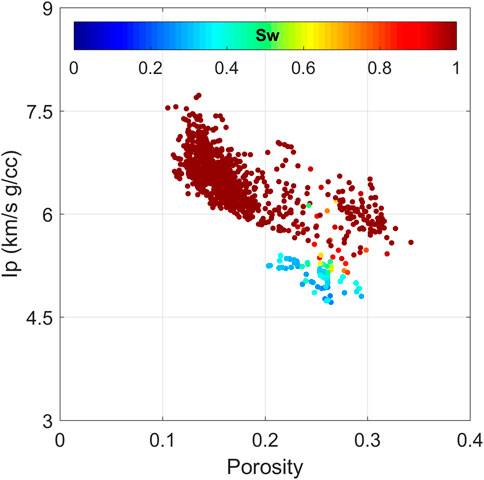
FIGURE 6. Cross-plot of P-wave impedance vs total porosity color coded by water saturation at in-situ conditions.

3.1.2 Rock physics modeling

As the second step in RPD, our objective was to establish the rock physics model which quantitatively explains the well data. By making the cross-plots between 100% wet velocity and total porosity, as shown in Figure 7, as well as color-coding the data by the GR-derived clay content, the corresponding transform between rock properties can be found with rock physics model curves superimposed on this cross-plot. The success of the model is defined by the consistency of the model curves and the well data color-coded by the clay content. Among the available arsenal of rock physics models, we examine four different velocity-porosity-mineralogy transforms: Raymer-Dvorkin, soft-sand, stiff-sand, and constant-cement models. The inputs in all these models are essentially the porosity, mineralogy, and pore fluid. However, aforementioned models (except the Raymer-Dvorkin model) require additional inputs, namely, the critical porosity, differential pressure, shear correction factor, and coordination number. The properties of individual minerals (quartz and clay) are listed in Table 1. The critical porosity was 0.4, the shear correction factor was 1, and the differential pressure was 30 MPa which is the average reservoir pressure. The only input which was different in these models was the coordination number. For the soft-sand and stiff-sand models, the coordination number was 6, while for the constant-cement model, it was 12. Figure 7 shows the application of these models on velocity-porosity-mineralogy cross-plots. In particular, the model curves (each representing a 20% clay content increment from top to bottom) are superimposed on the color-coded data. Based on plotted cross-plots, the constant-cement model was most relevant to well data under examination. This can be confirmed by the fact that the top curve (0% clay content) and bottom curve (100% clay content) are consistent with the color-coded clay content in the data. Thus, the constant-cement model was established as a rock physics transform to quantitatively predict elastic properties of rocks.

FIGURE 7

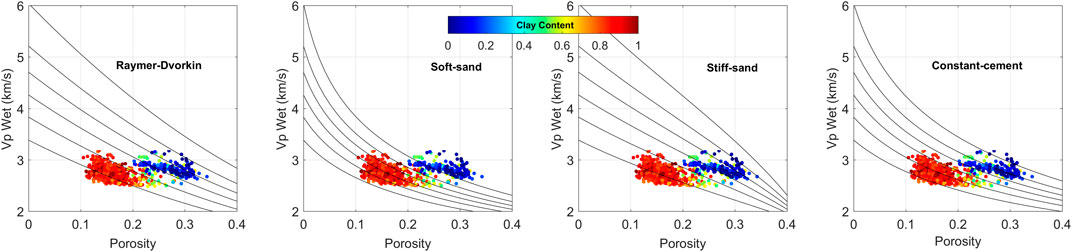
FIGURE 7. Cross-plots of wet-rock velocity vs the total porosity color coded by GR-derived clay content for the 14.2–14.7 kft depth interval. Model curves are from the Raymer-Dvorkin, soft-sand, stiff-sand, and constant-cement models. The upper and lower curves are for pure quartz and clay mineralogy, respectively. The different curves represent the variable mineralogy (clay and quartz) with 20% clay increment and starting from 0% clay (100% quartz) in the upper most curve.

We use the selected constant-cement model to predict elastic properties from the available petrophysical properties. This operation can be achieved using the following inputs: the total porosity, clay content, and water saturation. The RPD-based prediction of elastic properties is presented in Figure 8 using the clay content computed from the GR log. According to the obtained predictions, the resulting elastic properties match the overall trends of the measured profiles but fail to accurately reproduce them. In particular, the RPD-based approach showed lower accuracy in reproducing the measured V_p, V_s, and v curves, especially within the reservoir zone (Figure 8). The evaluation of predicted elastic attributes was based on correlation coefficient (R) and average absolute percentage error (AAPE) between measured and predicted rock properties. Table 2 shows the quantitative performance indicators for results from this approach, with the AAPE ranging between 4% and 10%.

FIGURE 8

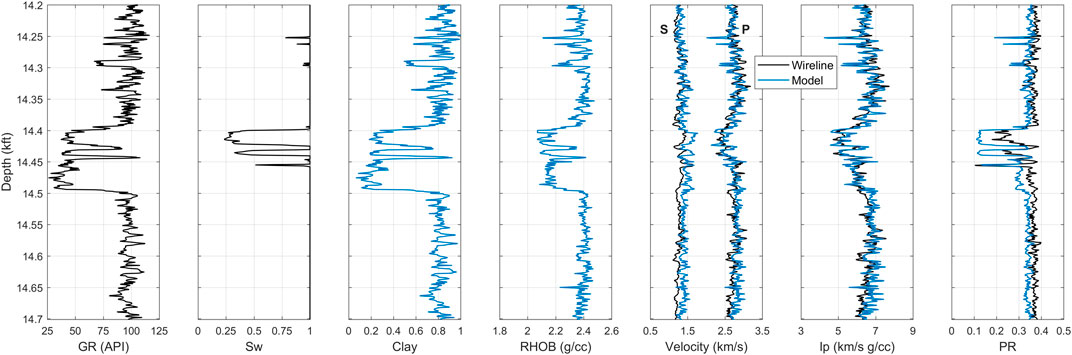
FIGURE 8. Measured and predicted well log curves in 14.2–14.7 kft depth interval: GR, saturation, clay content (predicted from GR log), bulk density, velocity (P-wave velocity on right and S-wave velocity on left). The black curves are for the measured data and blue ones for the rock physics model. Elastic properties are predicted from the constant-cement model.

TABLE 2

TABLE 2. Quantitative performance of the established rock physics model for predicted elastic properties.

3.2 Machine learning analysis

3.2.1 Data description, pre-processing, and statistical analysis

Machine learning models were trained and tested with 2610 data points in the upper part of the well interval and validated with 1003 data points in the remaining depth interval. The latter was used in RPD, as we demonstrated above. The total porosity, gamma-ray, and resistivity curves were selected as machine learning model inputs to represent the petrophysical parameters employed in rock physics models, namely, the porosity, mineralogy, and pore fluid, respectively. The idea behind selecting the gamma-ray log was to provide indirect information about the mineralogy, particularly shale and non-shale sedimentary rocks. Similarly, the resistivity log was used as pore fluid indicator, especially between hydrocarbon and water-saturated rocks. The bulk density, P- and S-wave velocities were selected as outputs in machine learning models as our primary goal was to compare the predicted elastic properties from rock physics and data-driven modeling.

Data preprocessing was conducted as a first stage towards obtaining successful data-driven models. This step is usually performed through statistical analysis, feature scaling, removal of duplicates, outliers, and any other unrealistic values observed in the dataset. However, statistical analysis showed that the well data under examination was of high quality, which excluded any data removal. Moreover, statistical analysis of the well data showed a good distribution of the data, which is crucial for developing successful data-driven models.

3.2.2 Optimization of ML models

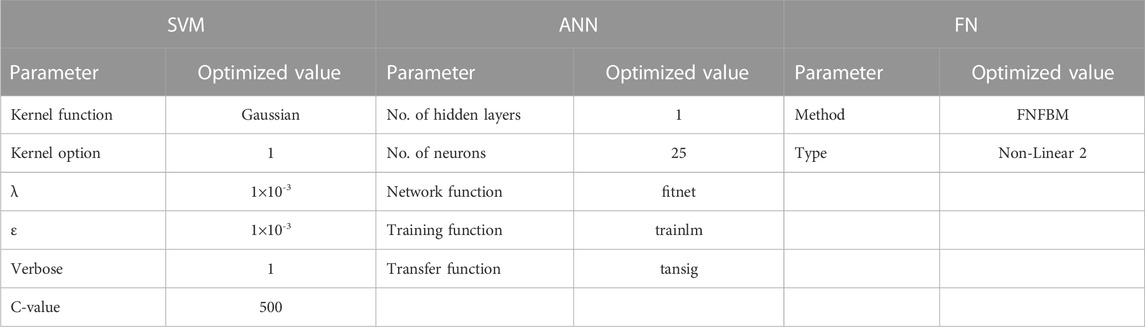
A traditional approach to finding the optimum model parameters in ML is based on hyperparameter tuning. This step allows observing which combination of model parameters is the most appropriate for achieving a high prediction performance. By employing the upper part of the well log data, hyperparameter tuning was conducted to find the optimum parameters of the data-driven models. The upper part of the well data was randomly distributed by a 70:30 data ratio for the model training and testing purposes. Each machine learning model consists of several adjustable parameters tuned to obtain accurate output predictions. In the ANN model, the adjustable parameters are the number hidden of layers and neurons, as well as network, training, and transfer functions. The FN model consists of method and type model parameters. The SVM model, in turn, can be tuned using the kernel function, epsilon (ε), kernel option, lambda (λ), C-value, and verbose parameters. The quality of the developed models was determined by R and AAPE. Table 3 presents the optimized parameters of the developed ANN, FN, and SVM models for predicting the elastic properties of rocks.

TABLE 3

TABLE 3. Optimized parameters of machine learning models.

3.2.3 Prediction from ML models

Once the ML models were optimized through hyperparameter tuning, they were used for predicting elastic properties of rocks from another depth interval unseen during the development and optimization of data-driven models. In ML, this step can also be termed the validation stage. In this study, we select the lower part of the well interval (Figure 3) to validate the optimized ML models since both intervals consist of similar lithology and pore fluids. The idea behind selecting the lower interval was to compare the results from RPD and ML, as the former was conducted on the bottom part of the well interval. The predicted outputs, such as ρ_b, V_p, V_s, as well as the v and I_p (computed from predicted outputs), are presented in Figure 9. The measured rock properties are shown by black, while the predicted ones are shown by red curves. Moreover, the quantitative performance of ANN, FN, and SVM models is presented in terms of R and AAPE values in Table 4. Compared to the RPD-based approach, data-driven models showed better estimation of elastic properties, as presented in Table 4. The AAPE did not exceed 3% when using ML (Table 4), while the error reached up to 10% for RPD (Table 2). Among these models, the ANN model produced slightly more accurate predictions of elastic properties than FN and SVM models.

FIGURE 9

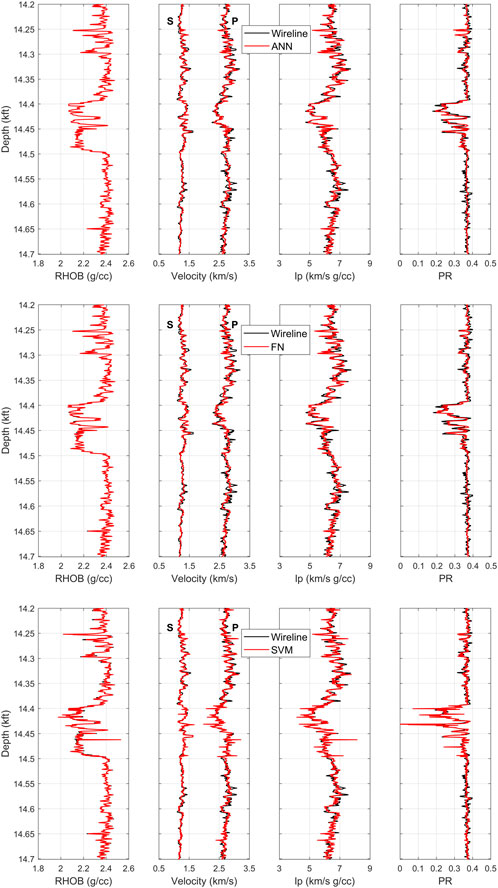
FIGURE 9. Measured and predicted well log curves in 14.2–14.7 kft depth interval. From left to right: bulk density, velocity (P-wave velocity on right and S-wave velocity on left), P-wave impedance, and Poisson’s ratio. The black curves are for the measured data and red ones for the machine learning models. Elastic properties were predicted from ANN (top), FN (middle), and SVM (bottom) models.

TABLE 4

TABLE 4. Quantitative performance of machine learning models for predicting elastic attributes at the well log scale.

3.3 Prediction at the seismic scale

The scale dependence of rock physics and machine learning models was investigated at the seismic scale. The idea here was to determine if the models produced based on well log data can be used for prediction at the seismic scale. To achieve this, we first upscaled the measured well data using the Backus (1962) averaging method to arrive at the seismic scale. Then, the upscaled wireline data were used in rock physics and machine learning analyses to predict elastic properties, but once again, at the seismic scale.

According to the Widess (1973) discussion of the limit of resolvable thickness from seismic data, if the value of wavelength $\left(\lambda \right)$ divided by eight $\left(\lambda /8\right)$ is less than thin bed thickness, then such a feature is resolvable. The equation below was used to calculate the wavelength:

$\lambda =\frac{V_{p\left(mean\right)}}{freq}(12)$

where $V_{p\left(mean\right)}$ is the mean value of measured P-wave velocity (2.72 km/s), $freq$ is the frequency at the reservoir level. By assuming the frequency at the reservoir level of 30 Hz, the wavelength of 297 ft was computed and later divided by 8 to generate a resolvable window size. As a result, the window size of 37 ft was computed for the well data under examination. The resolvable window size was used during Backus (1962) averaging of rock properties. In other words, every 37 ft of the well interval was averaged to produce a single or “effective” value rock property instead of 74 values (2 data points per foot). Figure 10 shows the results from Backus (1962) averaging method.

FIGURE 10

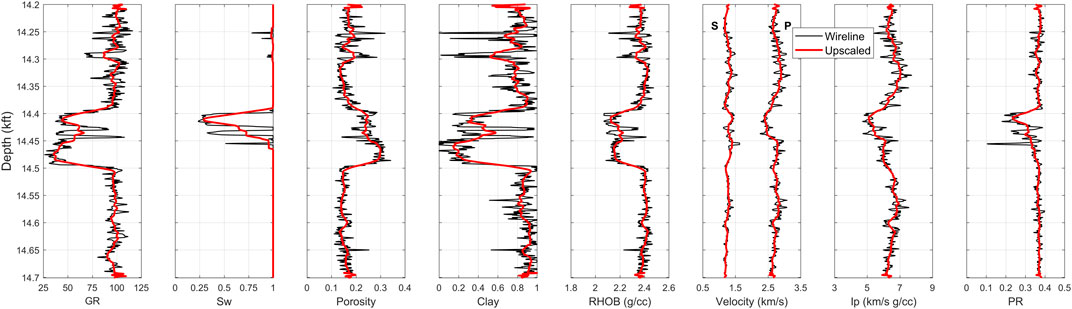
FIGURE 10. Measured and Backus-upscaled well log curves in 14.2–14.7 kft depth interval. The colors are black for the measured data and red for the Backus-upscaled data.

During the upscaling process, the arithmetic mean was used for the gamma-ray, water saturation, porosity, clay content, and bulk density. The remaining elastic properties (Figure 10) were averaged from the elastic moduli computed as harmonic mean. The Backus-upscaled well data showed good agreement with the overall trends from the original well log data (Figure 10). In particular, the upscaled clay content is still consistent with the gamma-ray curve, even at the seismic scale. As observed in Figure 10, the fine-scale variations in properties are not captured during the upscaling process, which is reasonable when the well data are averaged. Nevertheless, this feature did not prevent identifying the reservoir and non-reservoir zones at the seismic scale.

To investigate the applicability of rock physics and machine learning models at the seismic scale, the upscaled well data were used in rock physics and machine learning analyses. Here we do not show step-by-step processes for predicting elastic properties from the upscaled well data as we demonstrated rock physics and machine learning techniques in previous sections (same procedure). However, we present the results obtained from these physics-driven and data-driven methods. Figure 11 demonstrates the results obtained from RPD (top) and ANN, FN, and SVM machine learning models.

FIGURE 11

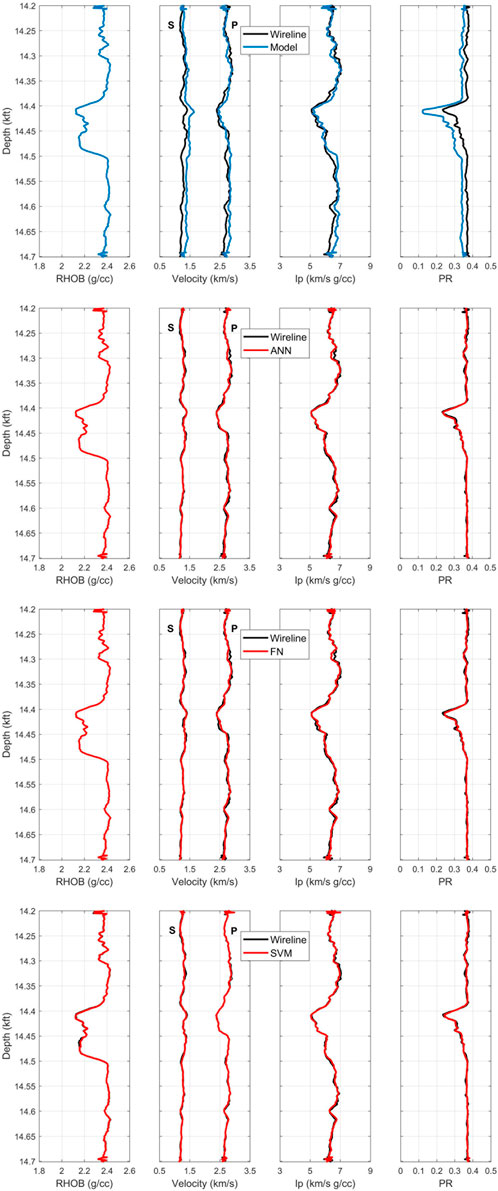
FIGURE 11. Backus-upscaled and predicted well log curves for 14.2–14.7 kft depth interval. The colors are black for the measured data and red for the machine learning models. The top figure is from rock physics model, the rest are from machine learning models. Elastic properties were predicted from constant-cement (rock physics), ANN, FN, and SVM (machine learning) models at the seismic scale.

According to qualitative and quantitative results presented in Figure 11 and Table 5, the prediction accuracy of ρ_b remained high during rock physics and machine learning modeling with R of 0.999 and AAPE of less than 0.1% at the seismic scale. It is interesting to note that rock physics and machine learning models performed relatively better (higher R and lower AAPE) at the seismic scale compared to the well log scale, as suggested by the results presented in Tables 4 and 5. Such results, in addition to those presented in Figure 11, suggest that ML prediction of elastic properties seems to be scale-independent. However, the rock physics-based estimation of rock properties still showed a significant mismatch within the reservoir interval at the seismic scale (Figure 11). In the discussion below, we investigate and provide an explanation for such discrepancy, especially in the V_s and v prediction when applying RPD.

TABLE 5

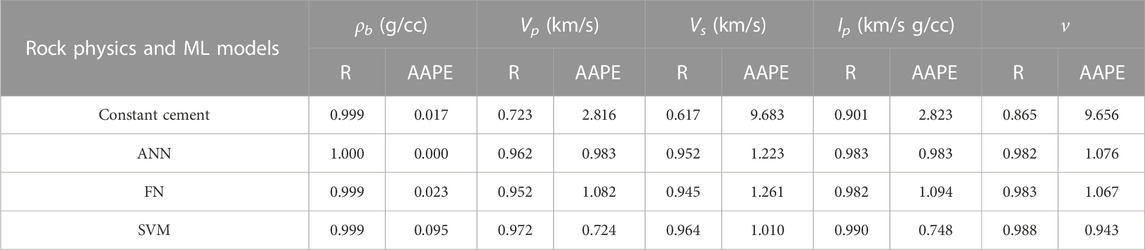
TABLE 5. Quantitative performance of rock physics and machine learning models for predicting elastic properties at the seismic scale.

4 Discussion

4.1 Prediction accuracy and data quality

Poisson’s ratio is an important quality indicator of the measured sonic data in the well. Typically, the range of Poisson’s ratio is 0.10–0.20 for the gas sand (Knight et al., 1998). However, as presented in Figure 3, the calculated Poisson’s ratio in the reservoir section of the well varied between 0.20 and 0.40. By conducting the quality control of the sonic data using V_p/V_s ratio, it was found that the measured V_s was of poor quality as the ratio was higher than 2, which is unreasonable for the sandstone formations. Needless to say, that the poor quality of V_s data is a common case during well logging operations. This data quality issue urged us to ask: how to perform quality control (QC) on the V_s data or how we can confirm that the poor-quality V_s was the main reason behind the large discrepancy observed during the prediction of V_s and v (using RPD) in the reservoir section of the well?

Earlier studies showed that RPD could be used to check the consistency and quality of V_s data (Wollner et al., 2017). This was done by using an approach that was detailed by Dvorkin et al. (2014). First, the measured V_p data and the established constant-cement model can be used to invert for a sonic-derived clay content. Such clay content, when used as an input in the constant-cement model, should accurately reproduce the measured V_p data. The hypothesis is that if this model, with V_p-derived clay content, can accurately predict V_p, then it should also reproduce V_s. In this case, any major discrepancy between the measured and predicted V_s suggests an issue with the V_s data quality. This is because V_p and V_s will not be physically consistent, where the latter is frequently of lower quality and higher uncertainty.

Figure 12 demonstrates the results from RPD when V_p-derived clay content was used as an input in the constant cement model. The sonic-derived clay content followed similar trends of GR log and GR-derived clay content. By this method, the exact match between measured and predicted elastic properties was observed for the ρ_b, V_p, and I_p. Of course, such a perfect match was expected, given that the clay content was estimated based on V_p. However, the important task here was to check whether such an approach will reproduce the measured V_s and v. Figure 12 shows that this approach (red curves) reproduced the measured V_s reasonably well except at the reservoir interval (14.4 kft–14.5 kft), similar to the earlier approach that used GR-derived clay content (blue curves). The significant discrepancy in predicting v still persists even after using the V_p-derived clay content. In particular, the predicted v shows values between 0.1 and 0.2 in the gas sand which are physically more reasonable than the values obtained from the measured V_s. Such observations support the argument that the V_s data within the reservoir zone is of poor quality and that the measured V_s cannot be trusted in that depth interval. Table 6 lists the accuracy of predicted elastic properties in terms of R and AAPE values.

FIGURE 12

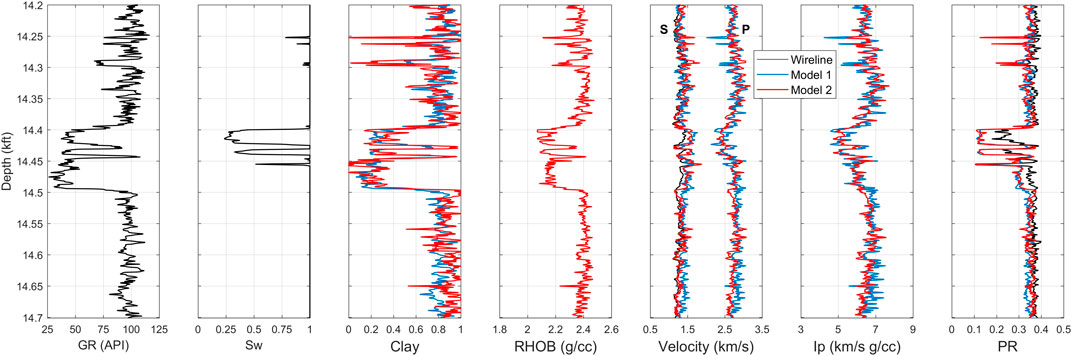
FIGURE 12. Measured and predicted well log curves in 14.2–14.7 kft depth interval: GR, saturation, clay content, bulk density, velocity (P-wave velocity on right and S-wave velocity on left). The black curves are for the measured data, blue one for rock physics model with GR-derived clay content, and red ones for the rock physics model with V_p-derived clay content. Elastic properties are predicted from the constant-cement model.

TABLE 6

TABLE 6. Quantitative performance of the established rock physics model for predicted elastic properties in Figure 12.

The above discussion suggests that while ML models resulted in lower prediction errors, especially for V_s, such approach fails to account for issues in the data without the use of rock physics analysis. It is true that the use of ML models for the prediction of elastic properties does not require the calculation of clay content and water saturation, as GR and resistivity data can be used directly. This perhaps is the main advantage of ML approach over RPD, which requires the calculation of petrophysical properties and has its own associated uncertainty, as mentioned earlier. Nevertheless, our results showed that the prior use of RPD to QC the data is crucial to avoid training the ML models with poor-quality data resulting in unrealistic predictions. Relying on ML prediction without involving RPD can lead to improper estimation of elastic properties despite the “apparent match” with the measured data during the training and testing phases. RPD, on the other hand, has the power not only to identify data quality issues, but also to correct them.

4.2 Scale dependence

According to Figure 11 and Table 5, it is evident that ML models produced an excellent agreement with the measured data at both well log and seismic scales. This suggests that the ML models are scale independent as the prediction accuracy of rock properties remained high at the seismic scale. In other words, the same ML models established and used at the well log scale can be used to predict the elastic properties at the seismic scale through Backus (1962) averaging. Such a conclusion also applies to the RPD results as shown above (Figure 11) and suggested by earlier work (Dvorkin & Wollner, 2017). Overall, the estimation of rock properties at the seismic scale was slightly better than at the well log scale for both RPD and ML (Tables 2, 4, and 5). This might be explained by the smoother nature of the upscaled data (Figure 11), in which small-scale variations within the well log data were lost during the upscaling process. Thus, the difference between rock physics and machine learning results was reduced at the seismic scale, as observed in Figure 12 and Table 5.

5 Conclusion

The physics behind any estimation or prediction is crucial for validating developed physics-driven and data-driven models. The deterministic method presented in this study, RPD, heavily relies on the physics behind the prediction of rock properties. The well data from GOM were used to estimate and compare the accuracy of predicted elastic rock properties from rock physics and machine learning models in two different scale scenarios: the well log and seismic scales. The mineralogy of the subsurface was assumed as a binary mixture of quartz and clay minerals. The constant cement model was later established to predict elastic rock properties. Based on presented results from rock physics and machine learning methods, ML models provided better prediction accuracy at the well log and seismic scales compared with the RPD approach. The use of ML for elastic properties prediction was also found to be scale independent, similar to the RPD, as prediction accuracy remained high at the seismic scale. Moreover, the ML method did not require the calculation of petrophysical properties, such as clay content and water saturation, with GR and resistivity data used directly. However, the main limitation of the ML method we found in this study was that it could not capture poor-quality data or correct it as opposed to the RPD method. The poor-quality V_s data resulted in erroneous v values and predictions, even if they showed an excellent agreement. Hence, QC using rock physics analysis has to be conducted prior to applying ML method to eliminate such issues. Thus, this study suggests the importance of incorporating rock physics analysis in machine learning to check the quality of the training data and ensure reasonable predictions.

Data availability statement

The datasets presented in this article are not readily available because the data is confidential. Requests to access the datasets should be directed to vagif.suleymanov1@gmail.com.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was supported by the Center for Integrative Petroleum Research (CIPR) and the College of Petroleum Engineering and Geosciences (CPG) both at the King Fahd University of Petroleum and Minerals (KFUPM).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alabbad, A., Dvorkin, J., Altowairqi, Y., and Duan, Z. F. (2021). Rock physics based interpretation of seismically derived elastic volumes. Front. Earth Sci. 8, 1–14. doi:10.3389/feart.2020.620276

CrossRef Full Text | Google Scholar

Ali, M., Ma, H., Pan, H., Ashraf, U., and Jiang, R. (2020). Building a rock physics model for the formation evaluation of the Lower Goru sand reservoir of the Southern Indus Basin in Pakistan. J. Petroleum Sci. Eng. 194, 107461. doi:10.1016/j.petrol.2020.107461

CrossRef Full Text | Google Scholar

Avseth, P., Dvorkin, J., Mavko, G., and Rykkje, J. (2000). Rock physics diagnostic of North Sea sands: Link between microstructure and seismic properties. Geophys. Res. Lett. 27, 2761–2764. doi:10.1029/1999GL008468

CrossRef Full Text | Google Scholar

Avseth, P., Lehocki, I., Kjøsnes, Ø., and Sandstad, O. (2021). Data-driven rock physics analysis of North Sea tertiary reservoir sands. Geophys. Prospect. 69, 608–621. doi:10.1111/1365-2478.12986

CrossRef Full Text | Google Scholar

Avseth, P., Mukerji, T., Mavko, G., and Dvorkin, J. (2010). Rock-physics diagnostics of depositional texture, diagenetic alterations, and reservoir heterogeneity in high-porosity siliciclastic sediments and rocks - a review of selected models and suggested work flows. Geophysics 75. doi:10.1190/1.3483770

CrossRef Full Text | Google Scholar

Avseth, P., Mukerji, T., and Mavko, G. (2005). Quantitative seismic interpretation. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511600074

CrossRef Full Text | Google Scholar

Azadpour, M., Saberi, M. R., Javaherian, A., and Shabani, M. (2020). Rock physics model-based prediction of shear wave velocity utilizing machine learning technique for a carbonate reservoir, southwest Iran. J. Petroleum Sci. Eng. 195, 107864. doi:10.1016/j.petrol.2020.107864

CrossRef Full Text | Google Scholar

Bachrach, R., Dvorkin, J., and Nur, A. M. (2000). Seismic velocities and Poisson’s ratio of shallow unconsolidated sands. Geophysics 65, 559–564. doi:10.1190/1.1444751

CrossRef Full Text | Google Scholar

Backus, G. E. (1962). Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res. 67, 4427–4440. doi:10.1029/JZ067I011P04427

CrossRef Full Text | Google Scholar

Batzle, M., and Wang, Z. (1992). Seismic properties of pore fluids. Geophysics 57, 1396–1408. doi:10.1190/1.1443207

CrossRef Full Text | Google Scholar

Das, V., Pollack, A., Wollner, U., and Mukerji, T. (2019). Convolutional neural network for seismic impedance inversion. Geophysics 84, R869–R880. doi:10.1190/geo2018-0838.1

CrossRef Full Text | Google Scholar

Di, H., Wang, Z., and AlRegib, G. (2018). Seismic fault detection from post-stack amplitude by convolutional neural networks. Proceedings of the 80th EAGE Conference and Exhibition. Copenhagen, Denmark, June 2019, doi:10.3997/2214-4609.201800733

CrossRef Full Text | Google Scholar

Dvorkin, J., Gutierrez, M. A., and Grana, D. (2014). Seismic reflections of rock properties. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511843655

CrossRef Full Text | Google Scholar

Dvorkin, J. P., and Nur, A. M. (1996). Elasticity of high-porosity sandstones: Theory for two North Sea datasets. Seg. Tech. Program Expand. Abstr. 61, 890–893. doi:10.1190/1.1887538

CrossRef Full Text | Google Scholar

Dvorkin, J. P. (2008). Yet another vs equation. Geophysics 73, E35–E39. doi:10.1190/1.2820604

CrossRef Full Text | Google Scholar

Dvorkin, J. (2021). “Rock physics: Recent history and advances,” in Geophysics and ocean waves studies (London, UK: Intechopen), 1–24. doi:10.5772/intechopen.92161

CrossRef Full Text | Google Scholar

Dvorkin, J., and Wollner, U. (2017). Rock-physics transforms and scale of investigation. Geophysics 82, MR75–MR88. doi:10.1190/GEO2016-0422.1

CrossRef Full Text | Google Scholar

Elkatatny, S., Tariq, Z., Mahmoud, M., and Abdulraheem, A. (2018). New insights into porosity determination using artificial intelligence techniques for carbonate reservoirs. Petroleum 4, 408–418. doi:10.1016/j.petlm.2018.04.002

CrossRef Full Text | Google Scholar

Fournier, F., Pellerin, M., Villeneuve, Q., Teillet, T., Hong, F., Poli, E., et al. (2018). The equivalent pore aspect ratio as a tool for pore type prediction in carbonate reservoirs. AAPG Bull. 102, 1343–1377. doi:10.1306/10181717058

CrossRef Full Text | Google Scholar

Gassmann, F. (1951). “Elasticity of porous media,” in Über die Elastizität poröser Medien (Gesellschaft: Vierteljahrsschrift der Naturforschenden), 96, 1–21.

Google Scholar

Gogoi, T., and Chatterjee, R. (2021). An integrated petrophysical and rock physics analysis for reservoir characterization study in parts of Upper Assam basin, India. Arabian J. Geosciences 14, 1–11. doi:10.1007/S12517-021-08240-7

CrossRef Full Text | Google Scholar

Gowida, A., Elkatatny, S., and Abdulraheem, A. (2019). Application of artificial neural network to predict formation bulk density while drilling. Petrophysics 60, 660–674. doi:10.30632/pjv60n5-2019a9

CrossRef Full Text | Google Scholar

Jaballah, J., Reijmer, J. J. G., El-Husseiny, A., Le Goff, J., Hairabian, A., and Slootman, A. (2021). Physical properties of Cretaceous to Eocene platform-to-basin carbonates from Albania. Mar. Petroleum Geol. 128, 105022. doi:10.1016/j.marpetgeo.2021.105022

CrossRef Full Text | Google Scholar

Jiang, L., Castagna, J. P., Russell, B., and Guillen, P. (2020). Rock physics modeling using machine learning. Thousand Oaks, CA: SEG Technical Program Expanded Abstracts, 2530–2534. doi:10.1190/SEGAM2020-3427097.1

CrossRef Full Text | Google Scholar

Kerimov, A. (2018). “The impact of grain-scale changes in microstructure geometry on effective mechanical and transport properties of granular porous media,” PhD thesis (Stanford, CA: Stanford University). Available at: https://stanford.app.box.com/s/mf7jsipmre8tvg8t38x4wqzpt2ziww9c.

Google Scholar

Knight, R., Dvorkin, J., and Nur, A. (1998). Acoustic signatures of partial saturation. Geophysics 63, 132–138. doi:10.1190/1.1444305

CrossRef Full Text | Google Scholar

Mavko, G., Mukerji, T., and Dvorkin, J. (2009). The rock physics handbook. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511626753

CrossRef Full Text | Google Scholar

Mavko, G., Mukerji, T., and Dvorkin, J. (2020). The rock physics handbook. Cambridge: Cambridge University Press. doi:10.1017/9781108333016

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1949). Compliance of elastic bodies in contact. J. Appl. Mech. 16, 259–268. doi:10.1115/1.4009973

CrossRef Full Text | Google Scholar

Nur, A., Mavko, G., Dvorkin, J., and Galmudi, D. (1998). Critical porosity: A key to relating physical properties to porosity in rocks. Lead. Edge 17, 357. doi:10.1190/1.1437977

CrossRef Full Text | Google Scholar

Partyka, G. A., Thomas, J. B., Turco, K. P., and Hartmann, D. J. (2000). Upscaling petrophysical properties to the seismic scale. Seg. Tech. Program Expand. Abstr. 19, 1636–1638. doi:10.1190/1.1815729

CrossRef Full Text | Google Scholar

Raymer, L. L., Hunt, E. R., and Gardner, J. S. (1980). An improved sonic transit time-to-porosity transform. SPWLA Annu. Logging Symp., 1–13.

Google Scholar

Salih, M., Reijmer, J. J. G., and El-Husseiny, A. (2021). Diagenetic controls on the elastic velocity of the early triassic upper khartam member (khuff formation, central Saudi Arabia). Mar. Petroleum Geol. 124, 104823. doi:10.1016/j.marpetgeo.2020.104823

CrossRef Full Text | Google Scholar

Suleymanov, V., Almumtin, A., Glatz, G., and Dvorkin, J. (2021). “Seismic reflections of rock properties in a clastic environment,” in Proceedings of the SPE Abu Dhabi International Petroleum Exhibition and Conference (ADIPEC), Abu Dhabi, UAE, November 2021. doi:10.2118/207808-MS

CrossRef Full Text | Google Scholar

Suleymanov, V., El-Husseiny, A., Glatz, G., and Dvorkin, J. (2022a). “Rock physics and machine learning analysis of a high-porosity gas sand in the Gulf of Mexico,” in Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, USA, October 2022. doi:10.2118/210191-MS

CrossRef Full Text | Google Scholar

Suleymanov, V., Gamal, H., Elkatatny, S., Glatz, G., and Abdulraheem, A. (2022b). Machine learning models for acoustic data prediction during drilling composite lithology formations. J. Energy Resour. Technol. 144. doi:10.1115/1.4053846

CrossRef Full Text | Google Scholar

Tariq, Z., Elkatatny, S., Mahmoud, M., and Abdulraheem, A. (2016). “A new artificial intelligence based empirical correlation to predict sonic travel time,” in Proceedings of the International Petroleum Technology Conference (IPTC), Bangkok, Thailand, February 2016. doi:10.2523/iptc-19005-ms

CrossRef Full Text | Google Scholar

Teillet, T., Fournier, F., Zhao, L., Borgomano, J., and Hong, F. (2021). Geophysical pore type inversion in carbonate reservoir: Integration of cores, well logs, and seismic data (Yadana field, offshore Myanmar). Geophysics 86, B149–B164. doi:10.1190/geo2020-0486.1

CrossRef Full Text | Google Scholar

Wang, Z., Di, H., Shafiq, M. A., Alaudah, Y., and Alregib, G. (2018). Successful leveraging of image processing and machine learning in seismic structural interpretation: A review. Lead. Edge 37, 451–461. doi:10.1190/TLE37060451.1

CrossRef Full Text | Google Scholar

Weinzierl, W., and Wiese, B. (2021). Deep learning a poroelastic rock-physics model for pressure and saturation discrimination. Geophysics 86, MR53–MR66. doi:10.1190/geo2020-0049.1

CrossRef Full Text | Google Scholar

Widess, M. B. (1973). How thin is a bed? Geophysics 38, 1176–1180. doi:10.1190/1.1440403

CrossRef Full Text | Google Scholar

Wollner, U., Yang, Y., and Dvorkin, J. P. (2017). Rock-physics diagnostics of an offshore gas field. Geophysics 82, MR121–MR132. doi:10.1190/geo2016-0390.1

CrossRef Full Text | Google Scholar

Wyllie, M. R. J., Gregory, A. R., and Gardner, L. W. (1956). Elastic wave velocities in heterogeneous and porous media. Geophysics 21, 41–70. doi:10.1190/1.1438217

CrossRef Full Text | Google Scholar

Xiong, F., Ba, J., Gei, D., and Carcione, J. M. (2021). Data-driven design of wave-propagation models for shale-oil reservoirs based on machine learning. J. Geophys. Res. Solid Earth 126, e2021JB022665. doi:10.1029/2021JB022665

CrossRef Full Text | Google Scholar

Xu, S., and Payne, M. A. (2009). Modeling elastic properties in carbonate rocks. Lead. Edge 28, 66–74. doi:10.1190/1.3064148

CrossRef Full Text | Google Scholar