Thermomechanical modelling of lithospheric slab tearing and its topographic response

Lithospheric slab tearing, the process by which a subducted lithospheric plate is torn apart and sinks into the Earth’s mantle, has been proposed as a cause for surface vertical motions in excess of 100 s of meters. However, little is known about the mechanisms that help initiate and control the propagation of slab tearing and the associated uplift. This study aims to explore these processes by means of 3D thermo-mechanical geodynamic modelling of a slab retreat oblique to a continental margin, using the Gibraltar Arc region (Betic Cordillera) as a scenario for inspiration. Our results suggest that the obliquity of the continental passive margin relative to the subduction trench leads to an asymmetric distribution of subduction forces and strength, facilitating the initiation of slab tearing. The model results predict a lateral migration of the tearing point at a velocity ranging between 38 and 68 cm/yr for a sublithospheric-mantle viscosity of up to 1e+22 Pa s. This fast slab tearing propagation yields uplift rates of 0.23–2.16 mm/yr above the areas where the subducted slab is torn apart, depending on mantle viscosity. Although a more detailed parametric exploration is needed, this range of uplift rates is compatible with the uplift rates required to overcome seaway erosion along the Atlantic-Mediterranean marine corridors during the Late Miocene, as proposed for the onset of the Messinian Salinity Crisis.

Highlights

• A subduction trench arriving diachronously to a continental passive margin facilitates slab tearing of the retreating slab.

• The viscosity of the sublithospheric mantle and the amount of shortening prior to tearing are the key controls on the slab-tearing dynamics.

• Surface uplift rates of 0.23–2.16 mm/yr for the overriding plate are obtained, compatible with those required for blocking the seaways of the Mediterranean Sea as during the onset of Messinian Salinity Crisis.

1 Introduction

The perception that some areas of the continental crust have subsided/uplifted at rates that cannot be explained by crustal thickening or fault activity alone, has pointed the need to other epeirogenic surface uplift mechanisms (England and Molnar, 1990) including dynamic topography or isostatic responses to mass motions. Slab breakoff is among the deep-seated mechanisms invoked to justify the long-wavelength, high rates of surface uplift observed in some continental collision settings (Spakman et al., 1988; Wortel and Spakman, 1992; 2000; Davies and von Blanckenburg, 1995; Van Der Meulen et al., 1998). Uplift in these scenarios is purportedly driven by the cancellation of the negative buoyancy force, the same force that drives slab pull and subduction (e.g., Garcia-Castellanos et al., 2000; Conrad and Lithgow-Bertelloni, 2002; Billen, 2008; Boonma et al., 2019; Jiménez-Munt et al., 2019). Slab breakoff is a process happening at depth within the mantle consisting of the detachment of a subducted oceanic lithospheric slab from the more buoyant continental lithosphere during continental collision. The concept of slab breakoff, as inferred from seismic tomography, was first proposed for the geodynamical evolution of the Mediterranean by Spakman et al. (1988) and Wortel and Spakman (1992). Slab breakoff was then used to explain post-collisional magmatism and exhumation of high-pressure rocks in the European Alps by Davies and von Blanckenburg (1995). Garzanti et al. (2018), and references therein, gave a comprehensive global overview of where slab breakoff has been invoked to explain changes in plate kinematics and tectonic deformation in regions including the Alps (Spakman et al., 1988; Wortel and Spakman, 1992; Davies and von Blanckenburg, 1995; Sinclair, 1997; Fox et al., 2015), the Mediterranean region (Carminati et al., 1998; Wortel and Spakman, 2000; Spakman and Wortel, 2004; Rosenbaum et al., 2008; Chertova et al., 2014; van Hinsbergen et al., 2014; Spakman et al., 2018), the Anatolia-Zagros orogen (Şengör et al., 2003; Faccenna et al., 2006), and Himalaya and Tibet (Jiménez-Munt and Platt, 2006; Van Hinsbergen et al., 2014; Wu et al., 2014; Liang et al., 2016; Qayyum et al., 2022). Many of these studies confirm the hypothesis that a complete slab break off is preceded by the lateral propagation of a slab tear or detachment within the subducted plate (Yoshioka and Wortel, 1995), ascribing short-lived, long-wavelength exhumation events or sudden pulses in sediment supply to this process. This lateral propagation of tearing makes the process of breakoff more gradual and prone to be influenced by the 3D tectonic configuration. The lateral tearing of lithospheric subducted slabs has been invoked to explain a diversity of observations, such as the seismicity pattern in the Vrancea slab (Mitrofan et al., 2016) or the seismic tomography in the South Iberian margin, Apennines and Hellenic arc (Wortel and Spakman, 2000). Previous 3D numerical models of subduction that exhibited slab tearing, such as those by van Hunen and Allen (2011); Duretz et al. (2014); Magni et al. (2017), all investigating a passive margin parallel to the subduction trench, which ended up producing slab tearing in the slab interior rather than on the slab edge. How does this initial tectonic setting condition the slab tearing in the first place? How can other configurations affect the progress of the tearing? How much does slab tearing contribute to the buoyancy-driven isostatic surface uplift? Our study addresses these questions inspired by the geological region of the Gibraltar Arc in the westernmost Mediterranean.

Based on seismic tomographic imaging, Spakman and Wortel (2004) suggested that slab tearing might have occurred in the Gibraltar Arc region as a consequence of the continental convergence between Africa and Iberia and the subsequent slab rollback (Elsasser, 1971; Karig, 1971) declined during early Miocene. The uplift observed in the internal Betic basins after late Tortonian are best constrained from the present elevation of tectonically undeformed Miocene marine sediment in that region (marine to non-marine transition), often above 600 m elevation (Garcés et al., 1998; Iribarren et al., 2009). The biostratigraphic studies by Krijgsman et al. (2018) and van der Schee et al. (2018) revised the age of the uplift and provided a new age constraint on the western Betic intramountain basins to be older than 7.51 Ma (late Tortonian). This has been interpreted as the result of a westward migration of a lateral tear of the hanging slab seen in tomography underneath the Gibraltar Arc (Spakman and Wortel, 2004; Garcia-Castellanos and Villaseñor, 2011; Bezada et al., 2013). Slab tearing occurred in previous thermomechanical models by Chertova et al. (2014) and Spakman et al. (2018), but the cause and timing of slab tearing was not investigated by them. The timing and the topographic response to this tearing process remains poorly constrained.

The uplift of the intramountain basins within the Betics and Rif (Figure 1), possibly caused by the slab tearing, has been linked to the closure of the marine gateway across the Gibraltar Arc during the Late Miocene which led to the partial desiccation of the Mediterranean Sea, (Messinian Salinity Crisis; MSC) (Garcia-Castellanos and Villaseñor, 2011; Coulson et al., 2019; Capella et al., 2020). According to this hypothesis, once the marine gateways closed off due to the regional epeirogenic uplift, it triggered the massive salt accumulation of the MSC (5.96–5.33 Ma), possibly the most abrupt environmental change on Earth since the beginning of the Tertiary.

FIGURE 1

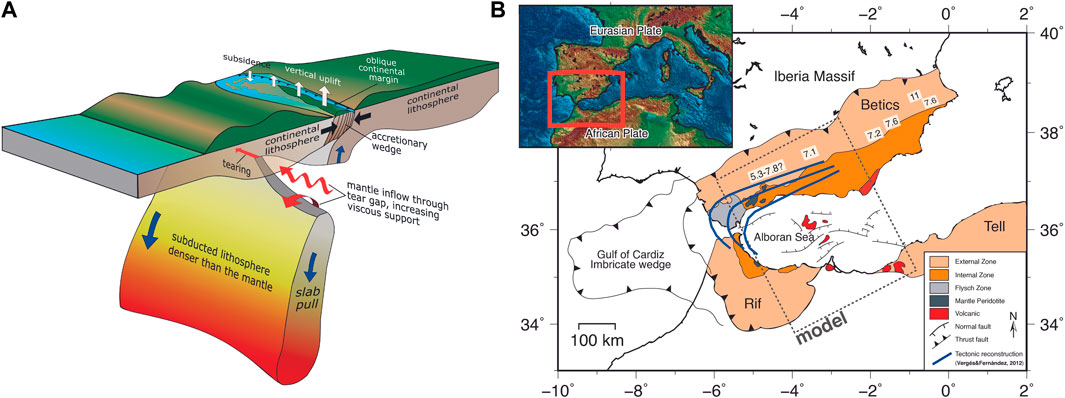
FIGURE 1. (A) An illustration of the lithospheric tearing process and the role of lithospheric buoyancy. (B) Gibraltar Arc region (Vergés and Fernandez, 2012). The inset is a topography-bathymetry map, with our region of interest in the red box. The map displays key units of the Gibraltar Arc System. The blue lines are the reconstruction of the slab rollback. The dashed-grey frame outlines the area and the basic features therein, which the model setup is based on. The model frame is at such angle to encapsulate the stages from the reconstruction that involve slab detachment. The numbers in white rectangles are the ages in Ma of the transition from marine to continental conditions of intramountain basins within the Betics (Iribarren et al., 2009; Krijgsman et al., 2018; van der Schee et al., 2018).

This study aims to understand the lithospheric slab tearing process and the resulting surface uplift using 3D thermomechanical modelling. For this purpose, we design a model setup of convergence between two tectonic plates, one of them being a continental margin attached to an oceanic plate which subducts under a second plate (Figure 2, we try both continent and oceanic structure for this one). This model setup is inspired by the tectonic setting of the westernmost Mediterranean. The tectonic kinematics of this region for the last 35 Myr are controversial (Faccenna et al., 2004; Spakman and Wortel, 2004; Vergés and Fernàndez, 2012) in terms of subduction polarity, the direction of slab retreat, and the exact timing. To study the tearing process, our model setup (Figure 2C) follows those tectonic models implying a subducted slab oblique to the Iberian margin and laterally ending towards the east (Spakman and Wortel, 2004; Vergés and Fernàndez, 2012; Van Hinsbergen et al., 2014; Angrand and Mouthereau, 2021). It is important to note that our study will focus on the tearing process itself during Middle to Late Miocene rather than on the previous evolution of the slab retreat. We address this by testing how different model parameters act on the initiation of the slab tearing and its propagation along the trench and the resulting surface elevation changes (due to viscous flow, temperature evolution, and dynamic topography). In addition, we will provide insights into how the slab tearing dynamics fit within the realm of the western Mediterranean, and how these surface vertical motions may have helped restricting the connections with the Atlantic Ocean during the Messinian Salinity Crisis.

FIGURE 2

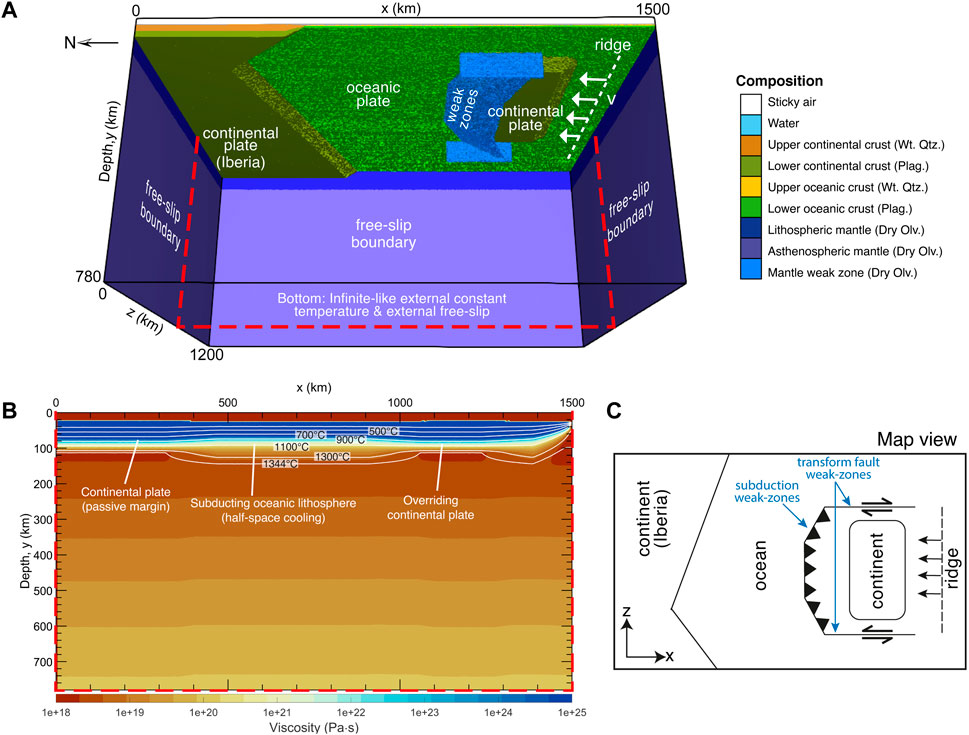
FIGURE 2. Setup of Mod1-reference model. (A) 3D model domain (1,500 × 780 × 1,200 km) with colours representing different compositions. The flow law abbreviations are Wt Qtz.—wet quartzite; Plag. –Plagioclase; and Dry Olv.—Dry Olivine. Convergence is imposed by applying a uniform velocity v of 47 mm yr^-1 until the slab reaches 200 km depth. At that stage we set time as t = 0 and the block velocity v becomes controlled by the sinking slab. (B) Cross-section profile of the viscosity. (C) Map view of the model set up showing the obliquity adopted between the subduction fault and the continental margin.

2 Methods

The modelling in this work is carried out using a 3D thermo-mechanical coupled numerical code, “I3ELVIS” (Gerya, 2013). The code is based on finite-differences and marker-in-cell numerical schemes (Harlow and Welch, 1965; Gerya and Yuen, 2003).

2.1 Governing equations

The governing physical laws such as conservation of mass, conservation of momentum, and heat equation are discretised on a staggered Eulerian grid.

(1) The conservation of mass is described by the continuity equation of an incompressible viscous medium:

$\frac{\partial v_i}{\partial x_i}=0,(1)$

where $v$ is the flow velocity and where i (as well as j shown hereafter) is index, which denotes spatial directions i, j = (x,y, z) in 3D using Einstein notation.

(2) The conservation of momentum is described by the Stokes equation for creeping flow, which states:

$\frac{\partial {\sigma }_{ij}^{\prime }}{\partial x_j}-\frac{\partial P}{\partial x_i}=-\rho \left(T,P,c\right)g_{i,}(2)$

where ${\sigma }_{ij}^{\prime }$ is the deviatoric stress tensor, $P$ denotes the total pressure (Pa), and $g$ is the gravitational acceleration (m/s²). In this form, we consider the extended Boussinesq approximation, where the density $\rho \left(T,P,c\right)$ in the buoyancy term $\rho g_i$ varies locally as a function of temperature (T), pressure (P), and composition (c).

$\rho C_p\frac{DT}{Dt}=\frac{\partial }{\partial x_i}\left(k\frac{\partial T}{\partial x_i}\right)+H_r+H_a+H_L+H_s,(3)$

(3) The heat balance in a convective medium is described by the heat conservation equation, which states:

where $C_p$ is the heat capacity (J/K), $T$ is temperature (K), $k$ denotes thermal conductivity (W/(m·K), which is a function of temperature, pressure, and composition, i.e., k(T, P, c), $H_r$ is radioactive heat production; $H_a$ is adiabatic heat production/consumption; $H_L$ is latent heat production/consumption (due to phase transformation), and $H_s$ is the shear heat production (a product of deviatoric stress and strain rate). More details are provided in Gerya and Yuen (2003), Gerya and Yuen (2007).

For each time step, a fourth order Runge-Kutta scheme is used to spatially advect the markers. The multi-grid method is used to speed up the convergence of the Gauss-Seidel iterative solver.

2.2 Density model and phase changes

The rocks’ densities vary with temperature T (K) and pressure P (Pa) according to the equation of state:

${\rho }_{P,T}={\rho }_0\left[1-\alpha \left(T-T_0\right)+\beta \left(P-P_0\right)\right],(4)$

where ${\rho }_0$ is the reference density at $P_0$ = 1 MPa and $T_0$ = 298.15 K, the coefficient of thermal expansion $\alpha$ = 2×10⁻⁵ 1/K, and the coefficient of compressibility $\beta$ = 6×10⁻¹² 1/Pa. Our models take phase transition of olivine in the mantle into account. As the dry olivine is subjected to greater pressure at depths, it first undergoes exothermic phase transition (∼410 km) and transforms into wadsleyite (Katsura and Ito, 1989). At a greater depth and pressure, the wadsleyite exothermically transforms into ringwoodite (∼520 km), which decompose (endothermically) into bridgmanite (silicate perovskite) at an even greater depth (∼660 km) (Ito et al., 1990). The eclogitization of the subducted oceanic crust (basaltic and gabbroic) is taken into account by linearly increasing the density of the crust with pressure from 0% to 16% in the P-T region between the experimentally determined garnet-in and plagioclase-out phase transitions in basalt (Ito and Kennedy, 1971).

2.3 Visco-plastic rheology

A composite visco-plastic rheology is used that captures the general dynamics of continental convergence and the underlying mantle flow (Gerya and Yuen, 2003; 2007). The ductile rheology is charactesized by a ductile viscosity ${\eta }_{ductile}$ that is approximated by a combination of effective viscosities for diffusion ${\eta }_{diff}$ and dislocation ${\eta }_{disl}$ creep. We assume that the total strain rate is the sum of the strain rates due to diffusion creep and dislocation creep, and that they act in parallel and independently from each other.

$1/{\eta }_{ductile}=1/{\eta }_{diff}+1/{\eta }_{disl}(5)$

(1) In the crust, we assume constant grain size and ${\eta }_{diff}$ and ${\eta }_{disl}$ is computed as:

${\eta }_{diff}=\frac{A}{2{\sigma }_{cr}^{\left(n-1\right)}}\mathit{exp}\left(\frac{E+PV}{RT}\right)(6)$

${\eta }_{disl}=\frac{A^{1/n}}{2}\mathit{exp}\left(\frac{E+PV}{nRT}\right){\dot{\epsilon }}_{II}^{\left(1-n\right)/n}(7)$

where R is gas constant (8.314 J/(K·mol)), P is pressure (Pa), T is temperature (K), ${\dot{\epsilon }}_{\mathrm{I}\mathrm{I}}=\sqrt{\frac{1}{2}{\dot{\epsilon }}_{ij}{\dot{\epsilon }}_{ij}}$ is the second invariant deviatoric strain-rate tensor, σ_cr is the critical stess, A is the pre-exponential factor (Paⁿ·s), E denotes activation energy (J/mol), V is activation volume (J/Pa), and n is the stress exponent of the viscous creep (Table 1).

(2) In the mantle, the ductile creep is implemented with grain size growth and reduction processes. In the case of the mantle, the composite rheology in Eq. 5 still stands,

${\eta }_{diff}=\frac{1}{2}{A_{diff}h}^m\mathit{exp}\left(\frac{E_{diff}+P{V}_{diff}}{RT}\right)(8)$

${\eta }_{disl}=\frac{1}{2}{A}_{disl}^{\frac{1}{n}}\mathit{exp}\left(\frac{E_{disl}+P{V}_{disl}}{nRT}\right){\dot{\epsilon }}_{II}^{\left(1-n\right)/n}(9)$

where, $A_{diff}$ is the experimentally determined pre-exponential factor for diffusion creep (Pa·s) and $A_{disl}$ is pre-exponential factor for dislocation creep (Paⁿ·s), h is grain size (m), m is the grain size exponent (Table 1).

TABLE 1

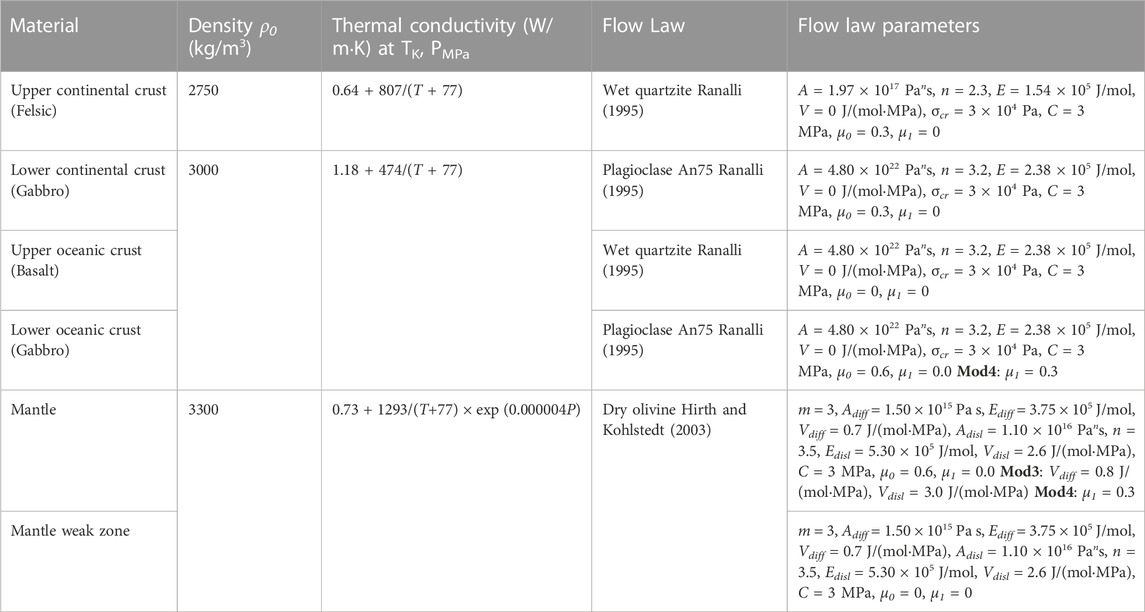
TABLE 1. Material properties used in the numerical experiments. The flow law include: A is the pre-exponential factor; E denotes activation energy; V is activation volume; n is the stress exponent; m is grain size exponent; σ_cr is critical stress or the assumed diffusion-dislocation transition stress; C is the rock compressive strength at p=0 MPa; μ₀ and μ₁ are the initial and final internal coefficients, respectively parameters (Karato and Wu, 1993; Ranalli, 1995; Hirth and Kohlstedt, 2003; Turcotte and Schubert, 2014). The subscripts “diff” and “disl” indicate that those parameters are associated with diffusion and dislocation creep processes, respectively. Mod3 has higher values for mantle activation volume than other models. Mod4 has higher final internal friction coefficient for lower oceanic crust and the mantle. Other properties for all rock types include: heat capacity C_p = 1000 J/(kg·K), thermal expansion α = 2 × 10⁻⁵ 1/K; and compressibility β = 6 × 10⁻¹² 1/Pa.

The viscous rheology is combined with a brittle rheology to compute an effective visco-plastic behavior adopting a Drucker-Prager yielding criterion (e.g., Ranalli, 1995) that effectively accounts for a strain weakening:

${\eta }_{ductile}\le \frac{C+\mu P}{2{\dot{\epsilon }}_{II}}(10)$

$\mu =\left\{\begin{array}{c}{\mu }_0-\gamma {\mu }_{\gamma },\gamma \le {\gamma }_0\\ {\mu }_1,\gamma >{\gamma }_0\end{array}\right.(11)$

$\gamma =\int \sqrt{\frac{1}{2}{\dot{\epsilon }}_{ij\left(plastic\right)}^2}dt(12)$

where $\mu$ is the internal friction coefficient (${\mu }_0$; ${\mu }_1$ are the initial and final internal friction coefficient, respectively), ${\mu }_{\gamma }=\left({\mu }_0-{\mu }_1\right)/{\gamma }_0$ is the rate of faults weakening with integrated plastic strain $\gamma$ (${\gamma }_0$ is the upper strain limit for the fracture-related weakening), C is the rock compressive strength at p = 0, t is time (s), ${\dot{\epsilon }}_{ij\left(\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\right)}$ is the plastic strain rate tensor (Table 1).

2.4 Model setup

The continental convergence is modelled with an incoming continental block, overriding a subducting oceanic plate, which is connected to a stationary continental block through a passive margin (model box located in Figure 1B). The model setup is based on geodynamic settings where an oceanic subducting plate retreats towards an oblique continental passive margin, inspired on the Neogene-to-present southern Iberian margin (e.g., Spakman and Wortel, 2004; Vergés and Fernàndez, 2012; van Hinsbergen et al., 2014). The 3D model domain (Figure 2) measures 1,500 km × 780 km × 1,200 km, with a resolution of 4.6 km× 3.0 km × 4.6 km, in the x, y (vertical), and z directions, respectively (22.1 million elements, 6 markers per element). The 40-km thick continental crust consists of the upper (20 km) and lower (20 km) continental crust, and thinning toward the ocean. The 8-km thick oceanic crust also consists of the upper (basaltic, 3 km) and lower (gabbroic, 5 km) oceanic crust. Partial melting and melt extraction processes are neglected in order to keep our models simplified and the interaction between the slab tearing and the crust isolated.

We use the “wet quartzite” viscous flow law for both the upper continental crust and the upper oceanic crust, while the “Plagioclase An75” describes the behaviour of the lower continental crust and lower oceanic crust (Table 1; Ranalli, 1995). The lithospheric mantle, asthenospheric mantle, and mantle “weak zone” (less viscous mantle material) all have a “dry olivine” rheology (Table 1; Hirth and Kohlstedt, 2003). The weak zone is prescribed in front of the incoming continental plate (Figures 2A,C) to facilitate the subduction initiation (Table 1). Two weak zones are also prescribed on both the eastern and western side of the incoming continental plate as a way to decouple the moving plate from the surrounding oceanic domain (Figures 2A,C).

In the first stage of the experiment, the convergence velocity is prescribed as constant at a vertical plane at x=1,389 km between depths of y=21–147 km (upper lithospheric mantle). This plane is labelled “ridge” in Figure 2C. The first stage of the experiment involves a forced convergence until the slab reach 200 km depth. After the first stage, the obtained thermo-mechanical state is then used as an initial setup for the second stage. In this second stage, the prescribed convergence rate is either removed, so that the slab sinks due to its own weight (Mod1-reference, Mod2, Mod3, and Mod4), or reduced to a lower value of 4 mm/yr (still pushing from the “ridge” at x=1,389 km) resembling the relative convergence rate between Africa and Iberia in the western Mediterranean (Mod5) (Macchiavelli et al., 2017).

2.5 Boundary conditions

The velocity boundary conditions are free slip for the left (x=0 km), right (x= 1,500 km), front (z=0 km), back (z=1,200 km), and top boundaries (y=0 km). The bottom boundary (y=780 km) is open/permeable, allowing rock materials to flow in or out of the model domain. For the bottom boundary, an external outflux boundary implies zero shear stress conditions and constant normal velocity to be satisfied at ∼300 km below the base of the model domain, which ensures the mass conservation within the computational domain (e.g., Burg and Gerya, 2005; Gerya et al., 2008; Li et al., 2013).

The elevation of the lithosphere is calculated dynamically as an internal free surface through a buffer layer of “sticky air” (η_air = 10¹⁸ Pa s, ρ_air = 1 kg/m³) (Gerya and Yuen, 2003; Schmeling et al., 2008; Crameri et al., 2012). It is 22 km thick on top of the continental plate and 25 km on top of the oceanic plate. We implemented a simplified erosion condition in our model, where instantaneous sedimentation limits a trench depth to 8 km below the water level and the instantaneous erosion is prescribed at 8 km above the initial continental crustal surface where rock markers change into sticky-air markers.

The continental geotherm is prescribed as a linear variation from 0°C at the model surface (y≤22 km, air) to 1,344°C the lithosphere-asthenosphere boundary (y=110 km) (Jiménez-Munt et al., 2019; Kumar et al., 2021). The initial thermal structure of the oceanic lithosphere is calculated using the half-space cooling model (e.g., Turcotte and Schubert, 2014) based on a slab age of 110 Ma. The initial adiabatic temperature gradient of 0.5°C/km is prescribed in the asthenospheric mantle (Katsura et al., 2010). For the initial thermal boundary conditions, the upper boundary has a fixed value of 0°C, and zero horizontal heat flux across the vertical boundaries. Similar to the velocity boundary, the bottom thermal boundary is permeable such that the temperature and vertical heat fluxes can vary along the lower boundary. This implies that the constant temperature condition is satisfied at ∼300 km below the bottom of the model box (e.g., Burg and Gerya, 2005; Gerya et al., 2008; Li et al., 2013).

3 Results

All of the experiments incorporate two stages. The first stage consists of forced convergence until the slab reaches 200 km depth. The time when this happens is defined as t=0 in our models. The second stage (t>0) uses the output from the first stage as an initial setup and continues on as the slab undergoes either free-rollback (Mod1-reference, Mod2, Mod3, and Mod4) or fixed convergence velocity (Mod5). Note that time “t” (in Myr) is relative to the beginning of stage 2 for each model.

3.1 Reference model (Mod1-reference)

After the slab has reached the depth of 200 km, the prescribed convergence rate is stopped. As the dense slab continues to sink due to its own negative buoyancy relative to the surrounding mantle (Table 1), the continental margin (Iberia) starts to bend downward and the incoming block overrides the passive margin. At t=3.84–4.10 Myr, the lithospheric thinning/necking started on the slab’s easternmost side (z=800 km) at 120 km depth (Figure 3). Immediately after this necking develops into tearing at 4.24 Myr, the incoming continental block stops due to the collision with the lower-plate continent. The tearing point propagates westward reflecting in the tilted angle of the slab’s top edge as shown in Figure 3E and Figure 4.

FIGURE 3

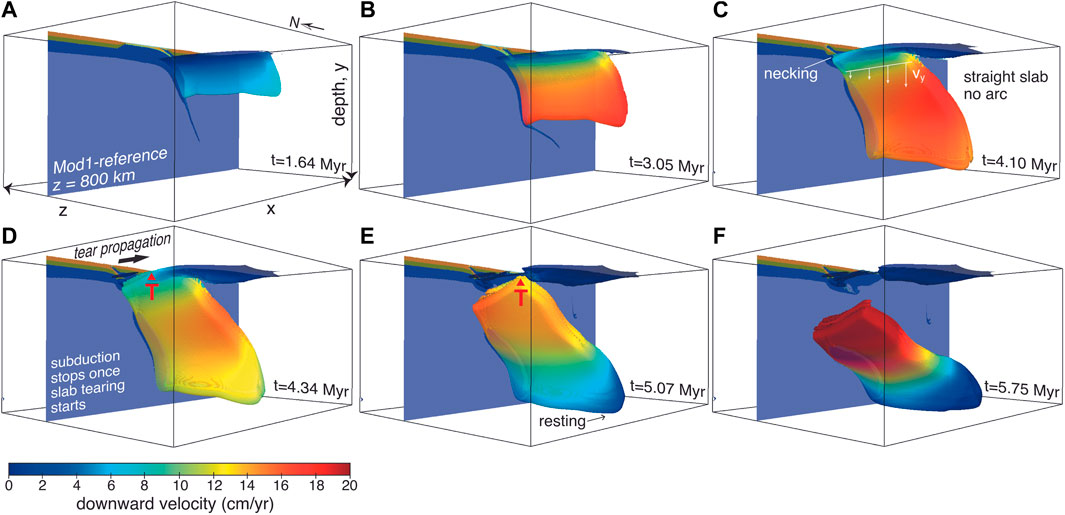
FIGURE 3. The evolution of the slab’s downward velocity (Mod1-reference). The slab structure shown here comes from the temperature isosurface, T = 1,300°C. The cross-section (z = 800 km) shows the lithology/composition (for rock composition colour legends please refer to Figure 2. The red ‘T’ illustrates the position of the slab tear. Prior necking or slab tearing, the slab subducts with little lateral velocity variation across the slab (A, B). Once the necking and the tearing has started, the higher downward velocity now shifted to side of the slab that is still attached (C–E). After the slab is completely detached (F), the slab’s downward velocity regained the lateral uniformity of downward velocity.

FIGURE 4

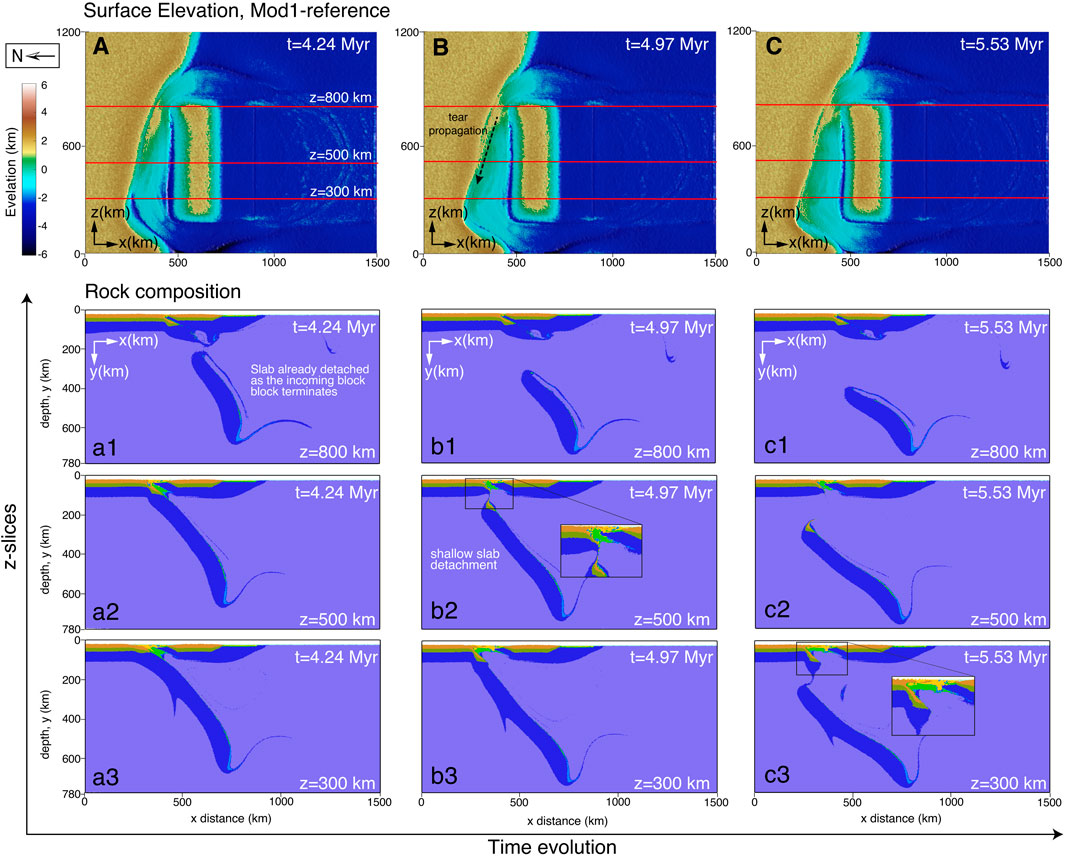
FIGURE 4. Evolution of the reference model (Mod1-reference) shown as surface topography (A, B, C) and lithology (a1-3, b1-3, and c1-3). The colour coding for the lithology slices is the same as in Figure 2. Set (A) show the stage at which the continental-continental collision causes the incoming continental block to stop completely. The slab has already started to detach on the eastern side (z = 800 km) by this point. In Set (B), the slab is half-torn with the attached portion of the slab still exerting slab-pull force. In Set (C), the tearing is approaching the western most side of the slab. Here the tearing/pinching occurs at a deeper depth as the slab still sinks until the arrival of the tearing. The tearing propagates westward as exhibited in a1, b2, and c3 cross-sections.

While the slab is fully attached, the down-dip motion of the slab induces corner flows, and the large slab body induces a large flow around the slab’s edges (Figure 5). The initiation of slab necking and tearing on the eastern side is inherent to our model setup because the slab’s easternmost part is the only region in which the continental-continental convergence occurs (Figure 4a1). As the oceanic plate is fully subducted in the eastern side, slab retreat is inhibited and subduction ends in that area due to the lower density of the upper continental plate continent. This initial slab tearing increases the slab pull on the still attached slab and the slab tear starts propagating westward. Towards the west, the subsequent lithosphere tearing is purely a result of the tearing process that has been set in motion from the east and not a tearing following continental collision. The different amounts of exhumed oceanic crust in the forearc wedge (Figure 4b2, c3) appear to be depending on how large the remaining oceanic domain is in between the southern incoming plate and the northern continental margin. We observe a larger amount of exhumed oceanic crust in the westernmost side (Figure 4c3).

FIGURE 5

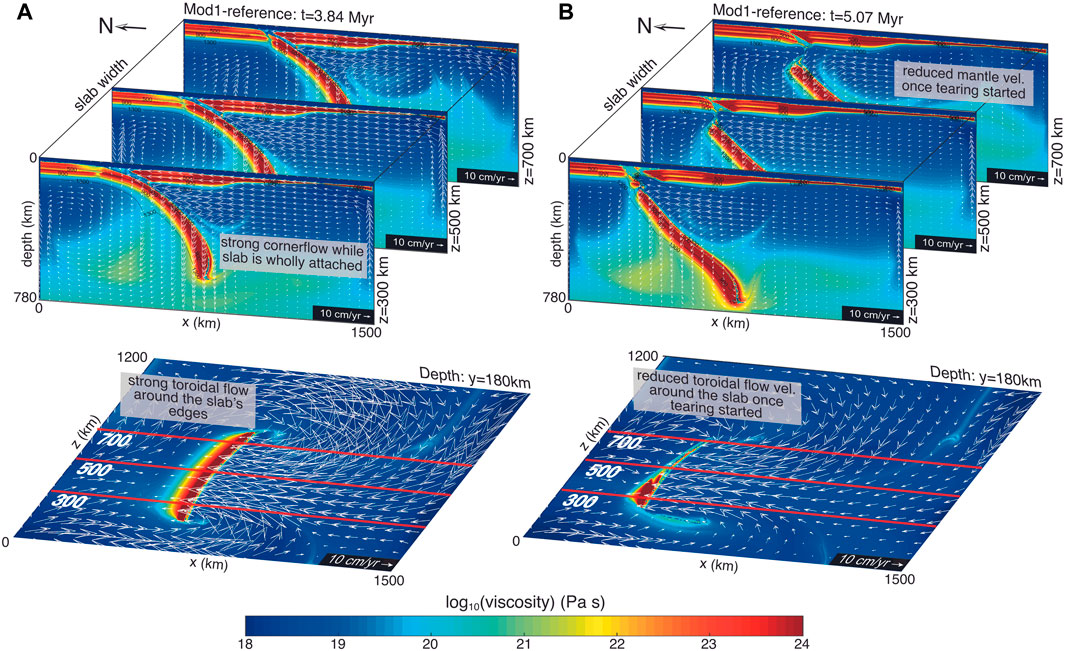
FIGURE 5. Reference model Mod1 viscosity cross-sections and velocity field. The upper panels show the x-y cross-sections from z = 300, 500, and 700 km, while the bottom panels show the x-z cross-sections from the depth y = 180 km, and the red lines correspond to the x-y slices in the panel above. The cross-sections in (A) come from a stage when the lithospheric slab is still wholly attached. The large hanging slab disturbs the mantle flow and causes mantle corner flow to build up, as well as causing strong mantle flow around the slab. The cross-sections in (B) are from the stage after slab tearing has started (on the eastern side). The mantle flow velocity diminishes as the slab-tear window allows the mantle to flow through.

The tearing localises where high stress and strain rate are caused between the buoyant continental part of the plate (upward force) and the negatively buoyant hanging slab (downward force). This initiation of slab tearing is reflected by a sharp surface uplift along the collisional belt, with uplift rate ranges from 0.23 mm/yr to 2.16 mm/yr throughout the tear propagation. The rise in elevation caused by the detachment of the slab affects an ever-increasing area (Figures 4A–C), migrating westward and reflecting the tear propagation. The slab is completely detached after t=5.75 Myr (tearing duration of ∼1.65 Myr).

3.2 Influence of model parameters

3.2.1 Effect of no incoming continental block (Mod2)

The reference model (Mod1-reference) incorporates an incoming buoyant continental block implemented to create a continental-continental collision, which the diachronous collision then led to a one-sided slab tearing. We now move on to investigate how the absence of this incoming buoyant continental block affects the subduction dynamics. Rheologically, Mod2 mimics Mod1-reference but the absence of an incoming continental block creates a continental-oceanic arc. At t=3.48 Myr, the retreating intra-oceanic subduction trench reaches the continental passive margin, after which the trench continues to retreat. After 0.5 Myr, high topography developed over the trench (Supplementary Figure S1A). Here, on the eastern side of the slab, the accumulation of crustal materials above the trench prevented the trench from retreating any further and led to the initiation of slab tearing at t=4.66 Myr. The slab is completely detached by t=5.70 Myr (tearing duration of ∼1.04 Myr). The uplift rate during the tear propagation ranges from 0.71 mm/yr to 1.35 mm/yr. The lack of incoming continental block thus does not prevent the initiation of slab tearing.

In Mod2, where the overriding plate does not incorporate a buoyant continental block, the slab-tearing dynamics are similar to the Mod1 (reference model), likely because both models have the same mantle rheological setup. Mod2’s lack of a buoyant continental block on the overriding plate does not affect the rate of trench retreat that is thus mainly controlled by the negative buoyancy of the oceanic slab and the asthenospheric mantle viscosity. In Mod1-reference, the presence of an incoming buoyant continental block does limit the extent of the forearc region, as illustrated in Figure 6. A less dense body (relative to the surrounding mantle) rises up the subduction channel and thrusts under the overlying crustal materials (Figures 6C,E,F). Uplift of the lighter mantle material in this region is partly driven by the extension related to roll back. The absence of a continental block in Mod2 allows the crustal material to spread farther compared to Mod1, where the spreading is limited by the buoyant continental block.

FIGURE 6

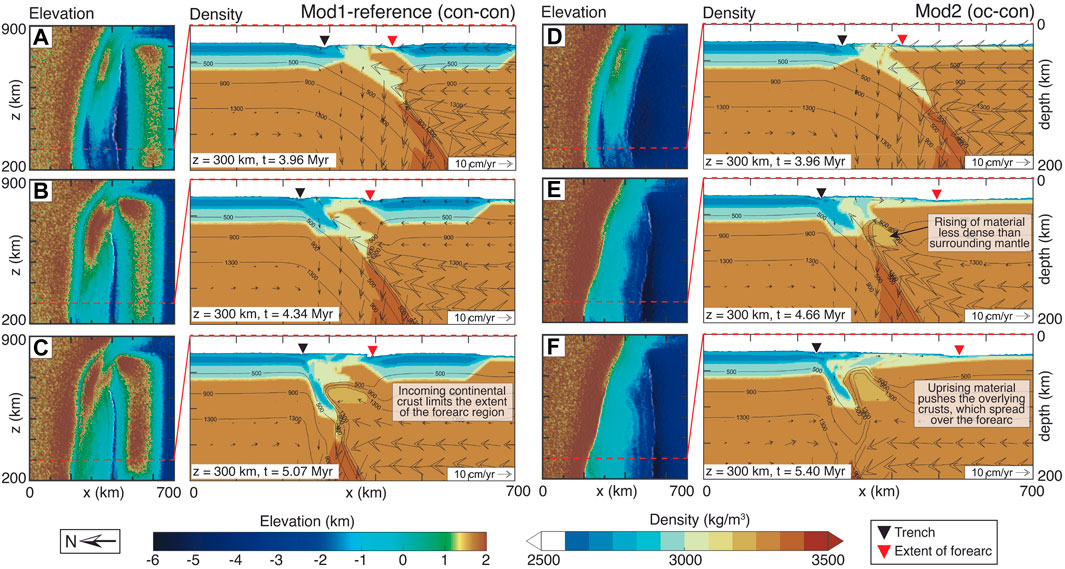
FIGURE 6. Elevation and density evolution for model Mod1-reference (A,B,C) and Mod2 (D,E,F). The density cross-sections are taken from z = 300 km, shown as a red dashed line on each corresponding elevation plot. The black triangle indicates the position of the trench and the red triangle indicates the extent of the forearc. In both models, a body of less density (3,200 kg/m³) than the surrounding mantle exhumes up the subduction channel (C,E,F). The exhumed material thrusts under the overlying crust leading to a raised elevation. In Mod1, the buoyant incoming continental crust (right, southern side of the model) limits the extent of the forearc region to the area in-between the passive margin and the incoming continental crust. In Mod2, the lack of a buoyant continental crust allows the crustal material, which are pushed up by mantle exhumation, to spread over a wider area and extending the forearc region.

3.2.2 Role of mantle viscous rheology

The subduction in the reference model is spontaneous, in the sense that the slab sinks by its own weight causing the subsequent trench retreat. However, the velocity of this process is highly controlled by the viscosity of the mantle and the role of this parameter must be quantively explored. To this purpose we design two model setups (Mod3 and Mod4) in which viscosity is increased relative to the reference setup Mod1.

Mod3 adopts a more viscous mantle, which can be achieved by increasing the ductile viscosity through increasing the activation volume of the mantle (both V_diff and V_disl). This results in slowing down the down-going slab due to the increased resistance of the higher-viscosity sublithospheric mantle. In the model setup Mod1-reference, the prescribed activation volume for the dislocation creep is V_disl=2.6 J/(mol·MPa) and for diffusion creep V_diff=0.7 J/(mol·MPa), and in model Mod3 we use V_disl=3.0 J/(mol·MPa) and V_diff=0.8 J/(mol·MPa) (Table 1). The increased activation volume implies a stronger mantle viscosity increases with pressure (and therefore with depth, Supplementary Figure S2). The evolution of the subduction is similar to the reference model but with much slower rate. For example, when the slab has reached 450 km depth, the slab in Mod1-reference has a maximum downward velocity of 20 cm/yr (t=3.05 Myr) where as Mod3’s maximum downward velocity is 8 cm/yr (t=6.87 Myr). The slab tearing in Mod3 initiated at around t=11.08 Myr as oppose to t=4.34 Myr in the reference model. The surface topography above the initiation of tearing exhibits an elevation of ∼1.5 km (Supplementary Figure S1D), which is similar to Mod1-reference. The uplift rate during the tear propagation ranges from 0.75 mm/yr to 1.68 mm/yr. In Mod3, the slab tear initiated at t=11 Myr and the slab completely detached by t=12.95 Myr (tearing duration of ∼ 2 Myr).

The fast down-going slab, together with the fast trench retreat velocity in the reference model, causes segments of high stress (4–5 MPa) and high strain-rate (10⁻¹⁴–10⁻¹² 1/s) to develop at the depth of greater than 120 km which led to a deeper tearing depth. In Mod3, with a more viscous mantle, the ambient mantle offers less resistance to the incoming of the down-going slab leading to a more gradual and shallow stress build-up focussing within the bending zone of the slab. This shallow stress focussing, at a depth of less than 100 km, led to a shallower tearing compared to the reference model.

Another way to increase the viscosity of the mantle is to increase the brittle viscosity, i.e., the upper visco-plastic limit of viscosity. In Mod4, we increase the final internal friction coefficient (μ₁ in Eq. 11) for the lower oceanic crust and the mantle from 0 in Mod1 to 0.3 in Mod4 (Table 1). By increasing this coefficient, we decrease the strain weakening by a factor of two and we significantly increase the effective visco-plastic viscosity of deformed cold lithospheric mantle at high pressure/depth. As a result, the slab fails to sink down into the ambient mantle on its own due to a high resistance to local brittle/plastic deformation. This lack of slab’s downward velocity also led to the termination of trench retreat all together (Supplementary Figure S3). The slab only reached a depth of 300 km. This rheological setup shows that a lithosphere-averaged effective viscosity higher than 10²⁴ Pa s should prevent slab roll-back and tearing.

3.2.3 Effect of fixed the convergence velocity (Mod5)

In model Mod5, we take the first stage of the reference model (initial push, slab reaches the depth of 200 km) and enters the model into the second stage with an imposed constant convergence. The imposed plate convergence velocity is set to 4 mm/yr to mimic the average convergent velocity between the Iberian and African plates (Macchiavelli et al., 2017). This velocity is much slower than the velocity resulting from the free hanging slab in previous models, consequently it is reducing the slab retreat. Such slow velocity makes thermal diffusion more relevant relative to advection (Boonma et al., 2019) warming the slab up and lowering its density and viscosity, all of which lead to thermal erosion and lithospheric dripping (Supplementary Figure S4). No slab tearing occurs in this model, but instead a lithospheric dripping takes place (Supplementary Figure S4).

The enhanced thermal diffusion that the slab experiences and the long time that the slab spends hanging among the sublithospheric mantle both allow an arcuate (in plan-view) deformed lower-viscosity slab to develop. In the models dominated by slab roll-back (Mod1-reference, Mod2, Mod3, and Mod4), subduction and trench migration stop once the slab reached the passive margin and the tear has started. In Mod5, however, the continuous pushing of the incoming continental block creates a band of high elevation over the arcuate trench (Supplementary Figure S1D).

4 Discussion

4.1 Geometry of the passive margin and slab-tearing dynamics

In this study, we have explored the role in tearing dynamics of an oblique continental passive margin adding asymmetry to the collision process. Magni et al. (2014) used also 3D geodynamic numerical modelling to explain the formation of backarc basins and later a slab window with an along-trench variation in slab buoyancy, localizing extension within the overriding plate. The results from the present study show that the obliquity of the continental passive margin can also introduce an asymmetry in the dynamics of the subducted slab, initiating slab tearing because it promotes a laterally diachronous consumption of the subducted oceanic plate, and facilitating slab tearing in one end of the plate and its lateral propagation. The obliquity of the passive margin relative to the trench axis causes an initial localized contact of the upper plate continent with the edge of the subducted slab in the trench. The resistance of the buoyant continent to subduction, together with the oppositely-directed slab pull, causes the initial break-off of the oceanic part of the plate. This is different from models implementing a continental margin parallel to the subduction trench direction, where the lateral propagation of tearing is initiated differently. Averaging over 500 km distance (from z=300–800 km), the tearing velocities are 42.6 cm/yr in Mod1-reference, 67.6 cm/yr in Mod2, and 37.6 cm/yr in Mod3 (Table 2). Our tear propagation rates fall well within the range of previous estimations: 7–45 cm/yr from the Carpathians’ depocenter migration by Meulenkamp et al. (1996) from the evolution of the Carpathian-Pannonian system whose geological model is constructed using regional chronostratigraphic sequences; and 10–80 cm/yr from 3D numerical modelling of continental collision by van Hunen and Allen (2011). A 3D stress model accounting for rheology, tear length, and force distribution, by Yoshioka and Wortel (1995) obtained a wide range of tear propagation rates between 2 and 94 cm/yr.

TABLE 2

TABLE 2. Comparison between model results.

The 500 km wide slab takes about 2 Myr to completely detach, which is fast compared to the timescales needed for subduction. This velocity is in a similar order of magnitude than the slab tear propagation in the Betics, where the ages of emersion of the intraorogenic basins (the transition from marine to continental conditions) suggests a shift of 300–400 km migration of the uplifting region in a period lasting between 3 and 6 Myr (the ranges indicate uncertainty; Garcia-Castellanos and Villaseñor, 2011). In our results, the main parameter controlling the timing of the tearing is the mantle rheology. The viscosity of the sublithospheric mantle in Mod3 is ≤ 10²² Pa s whereas it is ≤ 10²¹ Pa s in Mod1-reference. The more viscous sublithospheric mantle in Mod3 slowed down the sinking slab, hence the slowest tear-propagating velocity. This tear propagation rate is faster than that obtained in Chertova et al. (2014) and Spakman et al. (2018) based on numerical models and seismic tomography. Because the upper mantle viscosity in their model is similar to ours, the difference might rise from the lack of a sharp jump to higher viscosity below the 640 km discontinuity (lower mantle) in our model, which facilitates slabs to sink down to the bottom of our model box, at −780 km.

The ranges of tearing depth from our models are 80–150 km on the eastern side and 170–200 km on the western side. These ranges are similar to previous numerical modelling studies such as 80–240 km from Freeburn et al. (2017), 95–140 km from Schellart (2017), 100–400 km from Gerya et al. (2004), and 120–145 km from Duretz et al. (2014). The difference in tearing depth could plausibly come from the different rheological setting in each numerical model, as well as different tectonic setup. In the models presented here, the slab’s eastern side has a shallow tearing depth, determined by the weakness in the transition zone between the continental and the oceanic lithosphere. Although tearing is triggered by the first subduction of the continental-oceanic boundary of the upper plate in the East, the tearing thereafter propagates through the subducted oceanic lithosphere, and the transition zone stops having a role. As the tearing propagates westwards, the tearing depth becomes deeper. Two mechanisms favouring tear propagation and possibly making it grow deeper are: (i) the negative buoyancy of the already detached portion of the slab hangs from an ever-decreasing length of the rest of the slab; and (ii) the mantle flow through the slab tear window (Figure 5). A similar pattern is reflected in the tearing depth. On the easternmost side, the tearing tends to occur within the subducted continental lithosphere portion, such that the detached slab pinches out some continental crust. Because the tearing depth is deeper in the west, breakoff tends to localise within the subducted oceanic lithosphere.

4.2 Surface uplift: Isostasy vs. dynamic topography

Two known contributions to surface topography are the isostatic equilibrium of the lithosphere floating atop the mantle and the dynamic topography (Forte et al., 1993) caused by the buoyancy-driven mantle convection exerting vertical stress onto the lithosphere. Dynamic subsidence is generally caused by downward mantle flow (downwelling), while dynamic uplift is caused by upward mantle flow (upwelling).

We aim at differentiating topographic changes relate to tectonic deformation from vertical epeirogenic motions related to mantle/slab tearing by separating these two components of topography in our models. We calculate the isostatic effect adopting a compensation depth of 150 km (128 km below crustal surface, where the lowest values of viscosity are predicted, roughly matching the depth of initial tearing). Figure 7 shows model Mod3’s modelled density distribution and the evolution of the modelled elevation, and the two contributions, the isostatic and the dynamic components. This isostatic elevation is due to the density changes at crustal and lithosphere scales, without accounting the dynamics of the flow associated to slab subduction.

FIGURE 7

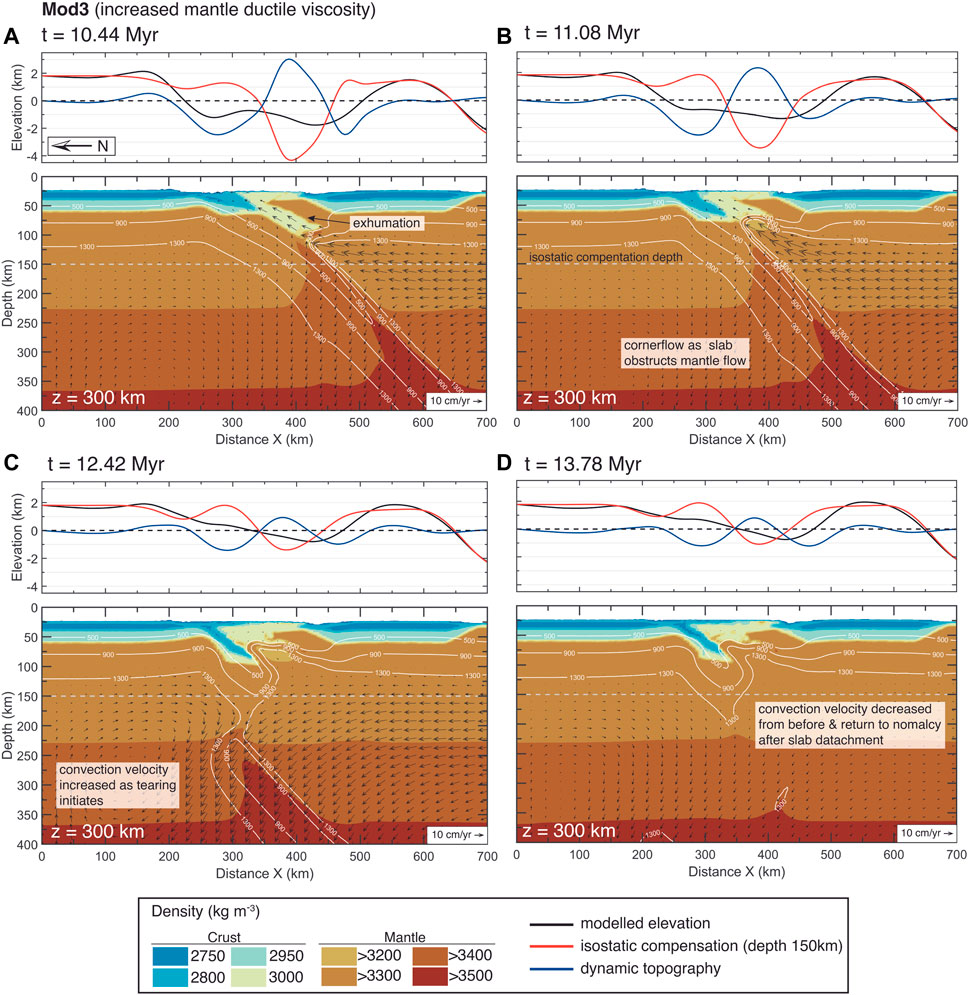
FIGURE 7. Dynamic topography and density for model Mod3 (higher mantle ductile viscosity). The elevation plots (top panels) consist of: 1) total elevation resulting from the model (black); 2) component of elevation corresponding to isostatic compensation of the crust (red); and 3) component related to dynamic topography (blue). The isostatic effect is calculated with a compensation depth of 150 km (∼128 km below crustal surface). The density (kg/m³) distribution (bottom panels) is overlaid with temperature contours of the lithospheric mantle (500°C, 900°C, and 1,300°C). (A) From the stage when the incoming continental block came to a complete stop. (B) Pre-detachment stage with ongoing exhumation of the subducted oceanic crust and corner flow as the slab obstructs mantle flow. (C) During necking and tearing when mantle flow focus on the detaching slab and decrease the convection velocity in the upper part of the mantle. (D) Post-detachment stage when the mantle flow returns to its unperturbed state and convection velocity are reduced (the detached slab is at 450–660 km depth).

The dynamic topography is then obtained from taking the isostatic effect away from the modelled elevation. The dynamic topography shown in Figure 7 appears to be reflecting properly the mantle dynamics. From the dynamic topography results, we can identify the slab pull effect with a subsidence and the corner flow and mantle upwelling with an uplift. Prior to slab tearing, the mantle flowing upwards in the subduction channel corresponds with the high dynamic topography (Figures 7A,B). As tearing begins, the tearing gap allows the mantle flow to go through and this channel upward flow is reduced (Figures 7C,D; Figure 5). While the slab is still attached, the slab-pull force is transmitted up to the crust, producing the subsidence on the passive margin (Figure 7A, x=250–300 km). As the slab starts necking and tearing, this transmission of slab-pull force vanishes, reducing the aforementioned subsidence (Figures 7C,D). The mantle convection decreases when the detached slab is at a depth of 450–660 km (Figure 7D).

We also set out to look at the time-response of surface topography to tearing in the mantle and the possible temporal delay involved. The one-to-one (instantaneous) interpretation has been widely utilised by previous studies (Lithgow-Bertelloni and Silver, 1998; Boschi et al., 2010; Faccenna and Becker, 2010; Faccenna et al., 2014; Gvirtzman et al., 2016; Heller and Liu, 2016; Austermann and Forte, 2019; Ávila and Dávila, 2020). However, the tearing process in our models occurs at a relatively fast velocity, which may make it difficult to capture and quantify this delay. Figure 8 displays the modelled evolution of the topographic response as the slab tearing laterally propagates westward. The incoming continental block collides with the passive margin and subsequently stops. The deformation associated to this continental-continental collision prior to tearing increases elevation by >1 km on the eastern side (z=800 km) (Figures 8A,E). As the tearing process starts at the eastern end, the topography increases by another 300 m. As tearing propagates westwards, this additional elevation propagates in the tearing direction (Figures 8B–E), attaining 500–1,000 m. The increase in surface elevation does not only occur above the tearing point but also in a nearby area, as shown in Figures 8E,F, reflecting the flexural lateral transmission of stresses in response to slab unloading. This is also due to the mantle flow: as the tear gap opens, it triggers higher poloidal flow, inducing trenchward mantle movement. This poloidal flow then induces a basal drag that drives trenchward motions under the two converging plates. The trenchward motion exerts compressional force to the relatively immobile subduction zone hinge, in addition to the opposing related to convergence, leading to an uplift of 0.3–0.8 km even before the arrival of the tear (Figure 8E). As the tearing propagates further westward, the high topography on the eastern side starts to subside by as much as 0.2 km (Figure 8E).

FIGURE 8

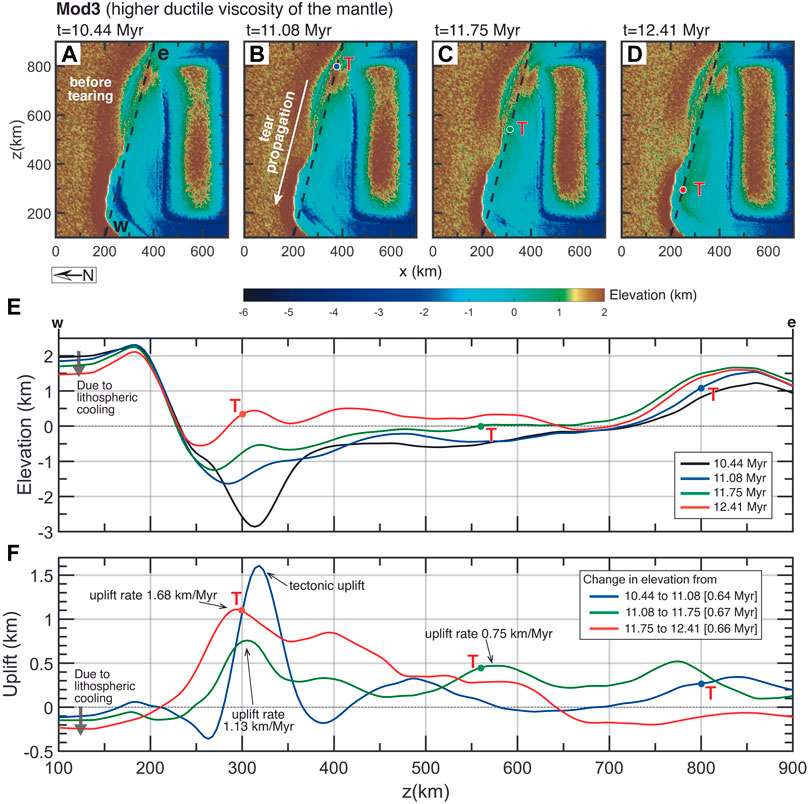
FIGURE 8. Elevation evolution of model Mod3 (higher mantle ductile viscosity). (A), (B), (C), and (D) are map views of the model’s surface elevation evolution with the tear propagating westward. The red ‘T’ indicates the slab-tear position in the subsurface. The dash lines (W–E) in (A) through (D) represent the elevation profiles shown in plot (E). Plot (F) shows the amount of uplift between time steps as the tearing propagates westward. The elevation increases as the tear propagates, with the maximum uplift rate of 1.68 km/Myr in the west. As the tear moves westward, the region toward the east of the profile W-E starts to subside, as shown with the red line in plot (E).

Figure 7 shows how the flow within the mantle changes during the subduction and tearing stages. As the slab subducts further, its volume in the mantle increases, obstructing the mantle flow and giving rise to corner flow in the mantle wedge. This corner flow increases the velocity of mantle convection by 3–10 cm/yr (Figure 7A), supporting the overlaying crust (Figures 7A,B). As the tearing of the slab initiates, it opens up a new pathway for the mantle to quickly flow through to replace the volume previously taken up by the slab (Figure 7C). Tearing causes the unload of the overlying crust (Figure 7C) leading to a rapid isostatic surface uplift as a prominent signature of slab detachment. Meanwhile, the velocity of the corner flow in the mantle wedge is reduced during the slab tearing (Figures 7B,C), decreasing the dynamic contribution to topography at the trench. As the detached slab sinks further down, the bottom of the slab hits the depth of 660–700 km discontinuity, where it becomes flatter (e.g., Figure 3F) while the mantle convection velocity slows down to pre-rollback values (4 cm/yr). This slower velocity reduces the elevation while the crust and the lithospheric mantle begin to thermally equilibrate. Overall, the surface uplift rates observed in our models, as a response to the slab tearing, range from 0.23 to 2.16 mm/yr. These values fall within surface uplift rates obtained from previous numerical modelling studies ranging from as low as 0.10 mm/yr to as high as 2.65 mm/yr (Andrews and Billen, 2009; Duretz et al., 2011).

4.3 Comparison to the tearing process in the Gibraltar Arc

The Neogene tectonic evolution of the western Mediterranean is a topic of controversy and numerous geodynamic mechanisms have been proposed. The currently prevalent models invoke a slab rollback that ends by reaching the south Iberian margin. Some authors consider an originally NW-dipping subduction zone located along the SE borders of Corsica-Sardinia and Balearic promontories (e.g., Rosenbaum et al., 2002; Spakman and Wortel, 2004; van Hinsbergen et al., 2014) where the slab experiences a clockwise rotation of about 180° dragged by roll-back until reaching the southern Iberian margin and creating the arcuate Betic-Rif orogen. An alternative model considers an originally SE-dipping subduction under Africa, then retreating to the northwest and originating the arcuate Betic-Rif fold and thrust belts on Iberian and NW African plates (Vergés and Fernàndez, 2012). Regardless of the precise geodynamic mechanism and kinematics responsible for the formation of the slab, what is relevant to the present study is that these alternative tectonic evolution models agree on the present SE dipping of the slab that rolled back towards the South Iberian margin prior to 6 Ma. Any tectonic model implying 1) a subducting plate laterally ending towards the East, and 2) its earlier consumption by subduction in that edge, would equally justify our initial setup. Therefore, according to our results, any such model would be consistent with slab tearing starting from the eastern end of the slab and leading to the present slab geometry observed in seismic tomography (Figure 9; Spakman and Wortel, 2004; Bezada et al., 2013; Palomeras et al., 2014).

FIGURE 9

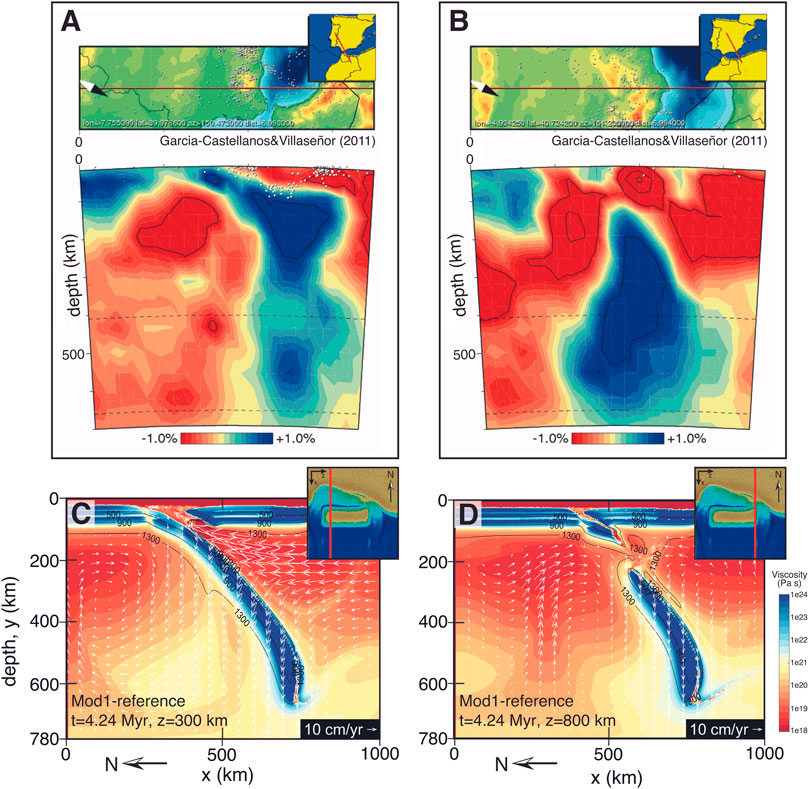
FIGURE 9. Comparison of slab structure from Mod1-reference with the seismic tomography of the western Mediterranean. (A) and (B) are seismic tomographic images from Garcia-Castellanos and Villaseñor (2011) showing the distribution of fast- (blue) and slow-seismic-velocity (red). (C) and (D) are viscosity cross-sections from model Mod1-reference with (C) sliced from z = 300 km, where the subducting slab is still attached and (D) sliced from z = 800 km, where the slab has just started tearing. The subsets in (C) and (D) show the plan-view (x–z) of the surface elevation, and the red lines indicate the position of the corresponding cross-sections. The cross-sections from Mod1-reference resemble, to an extent, the seismic tomography from the western Mediterranean, with the attached portion of the slab on the NW side (A) and the detached slab toward the NE side (B).

Several 3D numerical modelling studies have addressed the geodynamic evolution of the last 35 My of the western Mediterranean (Chertova et al., 2014; Spakman et al., 2018; Capella et al., 2020; Peral et al., 2022). A thermo-mechanical model by Negredo et al. (2020) suggests that sharp lateral thermal and rheological variations across STEP faults following slab-tearing, favours the occurrence of continental delamination. In the present study, the Gibraltar Arc is used as a reference because the relationship between slab tearing and surface uplift has previously been described in this region (Garcia-Castellanos and Villaseñor, 2011; Spakman et al., 2018). In our model, slab tearing initiates at the eastern slab edge, which according to the tectonic evolution envisaged by Vergés and Fernàndez (2012) may have resulted from a subduction polarity change under the transition between the Betic Cordillera and the Balearic Promontory. The uplift rates obtained (0.23 mm/yr to 2.16 mm/yr) are consistent with the rates considered necessary to compensate erosion of a sustained inflow during the first stage of the Messinian Salinity Crisis (Garcia-Castellanos and Villaseñor, 2011). The prevalent gypsum precipitation during this period suggests a reduced connectivity between the Atlantic Ocean and the Mediterranean Sea that has been linked to a competition between tectonic uplift of the seaway and the erosion of the seaway by the inflowing waters. This inflow from the Atlantic Ocean is needed to compensate for evaporation in the Mediterranean and to explain the gypsum accumulation from 5.97 Ma (e.g., Andreetto et al., 2021). This tectonic-erosion competition would explain the persistent but restricted water inflow from the Atlantic into the Mediterranean Sea required to explain the precipitation of gypsum during the first stage of the MSC. The model by Garcia-Castellanos and Villaseñor (2011) also leads to a critical uplift rate in the range of a few mm/yr needed to close the seaways across the Gibraltar Arc. Coulson et al. (2019) incorporated to that model the effect of glacioisostasy in response to sea level changes, lowering the required critical uplift rate to < 1.5 mm/yr.

Regarding the time span of this uplift, previous stratigraphic studies in the intrabetic basins suggested that the age of marine to continental transition (basin emersion) in the region is in the range of 11–8 Ma, younger towards the West (Garcés et al., 1998; Krijgsman et al., 2000; Iribarren et al., 2009). The last of these basins’ emersion was previously dated at 5.3 Ma, which indicates that the duration of tear propagation in the Betics (across 400 km distance) could last as long as 3–5 Myr, yielding a tearing rate of 80–133 km/Myr. Nevertheless, more recent biostratigraphic studies by Krijgsman et al. (2018); van der Schee et al. (2018) dated the age of the latest preserved marine sediment in the Guadalhorce Corridor (Ronda, Antequera and Arcos sedimentary basins) to 7.51 Ma (late Tortonian; westernmost age in Figure 1B). This would narrow down the plausible tear propagation duration to 1–3 Myr, implying a tearing rate of (133–400 km/Myr), a priori more compatible with the outcomes of our reference model (370–670 km/Myr). However, the available constraints on the timing of uplift show more complexity. The Alborán Sea coastal uplift reported by Guerra-Merchán et al. (2014) may have propagated further to the W until 3.2 Ma, leaving marine sediment at present elevations locally above 150 m. Furthermore, in the East, the Lorca Basin may not have become continental as soon as 11 Ma (Figure 1B) but during Messinian times (Carpentier et al., 2020). Moreover, Duggen et al. (2003) link the topographic uplift to the change in volcanic geochemistry between 6.3 and 4.8 Ma, from a subduction-related to a sublithospheric-mantle source. Seismic focal mechanisms suggest that tearing is today ongoing underneath the city of Málaga (Ruiz-Constán et al., 2011; Mancilla et al., 2015), although probably at much slower rates than those during the Messinian, since that location is close to the Guadalhorce Corridor: if the tearing propagation rates were similar to those mentioned above, it would have already affected the entire slab, leading to a break off that is not visible in the available seismic tomography. In summary, the uncertainties in the measured chronology of the intrabetic basin uplift and in the modelling methodology (both in mantle’s viscosity and the initial setup) impede a more detailed comparison between modelled and observed tearing propagation rates.

The uplift of the intramountain basins within the Betics in southern Iberia is higher on the eastern side (Iribarren et al., 2009), where the slab is interpreted to be detached earlier based on seismic tomography (Figure 9B), relative to the western Betics, where the slab still remains attached to Iberia (Figure 9A). Our models predict a similar trend and geometry, with earlier and higher uplift on the eastern side due to a combination of tectonic shortening deformation and to slab tearing, and a smaller and later uplift in the western end of the slab, where it remains attached (at t=4.24 My; Figures 9C,D).

5 Conclusion

Our results support the idea that the lateral ending of the subducting plate and the obliquity of its subduction relative to the continental passive margin favours the initiation of lateral slab tearing. The obliquity favours the consumption of the subducting plate earlier at the slab edge, determining the first contact between slab and continental margin in one side and leading to incipient slab necking. In the setups explored in this paper, this obliquity leads to slab tearing velocities of ∼37.6–67.6 cm/yr (for a lower-mantle viscosity of up to 10²² Pa s) and a surface uplift of 0.5–1.5 km across the forearc region throughout the tearing process.

Within the limited range of model runs presented, lithospheric tearing along the subducting plate does not relate specifically to the process of continental collision or to the obliquity between plate motions, but to the obliquity between the continental margin of the subducting plate and the subduction trench. This obliquity determines in our model which edge of the subducting plate starts tearing first.

The slab tearing depth increases as it propagates along the slab, shallower on the side where the tear initiated (80–150 km in our setups) and deeper tear on the other edge (170–200 km). The speed of slab tearing is geologically fast (370–670 km/Myr, with a duration og 3 Myr in our model scenarios). The key controls on the speed of detachment process are the viscosity of the sublithospheric mantle (low viscosity implying a faster tearing) and the amount of shortening/oceanic subduction prior to tearing (determining the slab pull of the subducted oceanic slab).

We obtain uplift rates ranging from 0.23 to 2.16 mm/yr, compatible with uplift rates needed to achieve an equilibrium between seaway uplift and seaway erosion proposed as responsible for the closure of marine gateways that reduced the water-flow from the Atlantic Ocean into the Mediterranean Sea during the first stage of the Messinian Salinity Crisis.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://doi.org/10.5281/zenodo.4637879.

Author contributions

KB: Methodology, Software, Investigation, Formal analysis, Validation, Writing—Original Draft, Visualisation. DG: Conceptualisation, Resources, Funding acquisition, Supervision, Validation, and Writing—Review and Editing. IJ: Conceptualisation, Resources, Funding acquisition, Supervision, Validation, and Writing—Review and Editing. TG: Methodology, Software, and Writing—Review and Editing.

Funding

This work has been supported by EU Marie Curie Initial Training Network “SUBITOP” (674899-SUBITOP-H2020-MSCA-ITN-2015), the Spanish Government national research program (GeoCAM, PGC 2018–095154-B-I00) and the Generalitat de Catalunya grant (AGAUR 2021 SGR 00410). We thank the Laboratorio de Geodinámica at GEO3BCN-CSIC as well as the Euler Cluster at the Scientific Computing centre at ETH Zürich for providing the computing facilities.

Acknowledgments

We gratefully thank Wim Spakman and Nicolas Riel, and the editors Frederic Mouthereau and Guillermo Booth-Rea for the careful and critical reviews that contributed to clarify and enrich this manuscript. Rob Govers also provided useful comments on a previous version of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1095229/full#supplementary-material

References

Andrews, E. R., and Billen, M. I. (2009). Rheologic controls on the dynamics of slab detachment. Tectonophysics 464 (1–4), 60–69. doi:10.1016/j.tecto.2007.09.004

CrossRef Full Text | Google Scholar

Andreetto, F., Aloisi, G., Raad, F., Heida, H., Flecker, R., Agiadi, K., et al. (2021). Freshening of the Mediterranean Salt Giant: controversies and certainties around the terminal (Upper Gypsum and Lago-Mare) phases of the Messinian Salinity Crisis. Earth-Sci. Reviews 216. doi:10.1016/j.earscirev.2021.103577

CrossRef Full Text | Google Scholar

Angrand, P., and Mouthereau, F. (2021). Evolution of the Alpine orogenic belts in the Western Mediterranean region as resolved by the kinematics of the Europe-Africa diffuse plate boundary. Bsgf - Earth Sci. Bull. 192, 42. doi:10.1051/bsgf/2021031

CrossRef Full Text | Google Scholar

Austermann, J., and Forte, A. M. (2019). The importance of dynamic topography for understanding past sea-level changes. Past. Glob. Chang. Mag. 27 (1). doi:10.22498/pages.27.1.18

CrossRef Full Text | Google Scholar

Ávila, P., and Dávila, F. M. (2020). Lithospheric thinning and dynamic uplift effects during slab window formation, southern Patagonia (45˚-55˚ S). J. Geodyn. 133, 101689. doi:10.1016/j.jog.2019.101689

CrossRef Full Text | Google Scholar

Bezada, M. J., Humphreys, E., Toomey, D., Harnafi, M., Davila, J., and Gallart, J. (2013). Evidence for slab rollback in westernmost Mediterranean from improved upper mantle imaging. Earth Planet. Sci. Lett. 368, 51–60. doi:10.1016/j.epsl.2013.02.024

CrossRef Full Text | Google Scholar

Billen, M. I. (2008). Modeling the dynamics of subducting slabs. Annu. Rev. Earth Planet. Sci. 36, 325–356. doi:10.1146/annurev.earth.36.031207.124129

CrossRef Full Text | Google Scholar

Boonma, K., Kumar, A., Garcia-Castellanos, D., Jiménez-Munt, I., and Fernández, M. (2019). Lithospheric mantle buoyancy: The role of tectonic convergence and mantle composition. Sci. Rep. 9 (1), 17953. doi:10.1038/s41598-019-54374-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Boschi, L., Faccenna, C., and Becker, T. W. (2010). Mantle structure and dynamic topography in the Mediterranean Basin. Geophys. Res. Lett. 37 (20), 20303. doi:10.1029/2010GL045001

CrossRef Full Text | Google Scholar

Burg, J. P., and Gerya, T. V. (2005). The role of viscous heating in Barrovian metamorphism of collisional orogens: Thermomechanical models and application to the Lepontine Dome in the Central Alps. J. Metamorph. Geol. 23 (2), 75–95. doi:10.1111/j.1525-1314.2005.00563.x

CrossRef Full Text | Google Scholar

Capella, W., Spakman, W., Hinsbergen, D. J. J., Chertova, M. V., and Krijgsman, W. (2020). Mantle resistance against Gibraltar slab dragging as a key cause of the Messinian Salinity Crisis. Terra nova. 32 (2), 141–150. doi:10.1111/ter.12442

CrossRef Full Text | Google Scholar

Carminati, E., Wortel, R., Spakman, W., and Sabadini, R. (1998). The role of slab detachment processes in the opening of the Western–central mediterranean basins: Some geological and geophysical evidence. Earth Planet. Sci. Lett. 160 (3–4), 651–665. doi:10.1016/S0012-821X(98)00118-6

CrossRef Full Text | Google Scholar

Carpentier, C., Vennin, E., Rouchy, J. M., Cornée, J. J., Melinte-Dobrinescu, M., Hibsch, C., et al. (2020). Ages and stratigraphical architecture of late Miocene deposits in the Lorca Basin (Betics, SE Spain): New insights for the salinity crisis in marginal basins. Sediment. Geol. 405, 105700. doi:10.1016/j.sedgeo.2020.105700

CrossRef Full Text | Google Scholar

Chertova, M. V., Spakman, W., Geenen, T., van den Berg, A. P., and van Hinsbergen, D. J. J. (2014). Underpinning tectonic reconstructions of the Western Mediterranean region with dynamic slab evolution from 3-D numerical modeling. J. Geophys. Res. Solid Earth 119 (7), 5876–5902. doi:10.1002/2014JB011150

CrossRef Full Text | Google Scholar

Conrad, C. P., and Lithgow-Bertelloni, C. (2002). How mantle slabs drive plate tectonics. Science 298 (5591), 207–209. doi:10.1126/science.1074161

PubMed Abstract | CrossRef Full Text | Google Scholar

Coulson, S., Pico, T., Austermann, J., Powell, E., Moucha, R., and Mitrovica, J. X. (2019). The role of isostatic adjustment and gravitational effects on the dynamics of the Messinian salinity crisis. Earth Planet. Sci. Lett. 525, 115760. doi:10.1016/j.epsl.2019.115760

CrossRef Full Text | Google Scholar

Crameri, F., Schmeling, H., Golabek, G. J., Duretz, T., Orendt, R., Buiter, S. J. H. H., et al. (2012). A comparison of numerical surface topography calculations in geodynamic modelling: An evaluation of the ‘sticky air’ method. Geophys. J. Int. 189 (1), 38–54. doi:10.1111/j.1365-246X.2012.05388.x

CrossRef Full Text | Google Scholar

Davies, J. H., and von Blanckenburg, F. (1995). Slab breakoff: A model of lithosphere detachment and its test in the magmatism and deformation of collisional orogens. Earth Planet. Sci. Lett. 129 (1–4), 85–102. doi:10.1016/0012-821X(94)00237-S

CrossRef Full Text | Google Scholar

Duggen, S., Hoernle, K., van den Bogaard, P., R€upke, L., and Phipps Morgan, J. (2003). Deep roots of the Messinian salinity crisis. Nature 422, 602–606. doi:10.1038/nature01553

PubMed Abstract | CrossRef Full Text | Google Scholar

Duretz, T., Gerya, T. V., and May, D. A. (2011). Numerical modelling of spontaneous slab breakoff and subsequent topographic response. Tectonophysics 502 (1–2), 244–256. doi:10.1016/j.tecto.2010.05.024

CrossRef Full Text | Google Scholar

Duretz, T., Gerya, T. V., and Spakman, W. (2014). Slab detachment in laterally varying subduction zones: 3-D numerical modeling. Geophys. Res. Lett. 41 (6), 1951–1956. doi:10.1002/2014GL059472

CrossRef Full Text | Google Scholar

Elsasser, W. M. (1971). Sea-floor spreading as thermal convection. J. Geophys. Res. 76, 1101–1112. doi:10.1029/jb076i005p01101

CrossRef Full Text | Google Scholar

England, P., and Molnar, P. (1990). Surface uplift, uplift of rocks, and exhumation of rocks. Geology 18 (12), 1173–1177. doi:10.1130/0091-7613(1990)018<1173:SUUORA>2.3.CO;2

CrossRef Full Text | Google Scholar

Faccenna, C., and Becker, T. W. (2010). Shaping mobile belts by small-scale convection. Nature 465 (7298), 602–605. doi:10.1038/nature09064

PubMed Abstract | CrossRef Full Text | Google Scholar

Faccenna, C., Piromallo, C., Crespo-Blanc, A., Jolivet, L., and Rossetti, F. (2004). Lateral slab deformation and the origin of the Western Mediterranean arcs. Tectonics 23 (1). doi:10.1029/2002tc001488

CrossRef Full Text | Google Scholar

Faccenna, C., Bellier, O., Martinod, J., Piromallo, C., and Regard, V. (2006). Slab detachment beneath eastern Anatolia: A possible cause for the formation of the north anatolian fault. Earth Planet. Sci. Lett. 242 (1–2), 85–97. doi:10.1016/J.EPSL.2005.11.046

CrossRef Full Text | Google Scholar

Faccenna, C., Becker, T. W., Miller, M. S., Serpelloni, E., and Willett, S. D. (2014). Isostasy, dynamic topography, and the elevation of the Apennines of Italy. Earth Planet. Sci. Lett. 407, 163–174. doi:10.1016/j.epsl.2014.09.027

CrossRef Full Text | Google Scholar

Forte, A. M., Peltier, W. R., Dziewonski, A. M., and Woodward, R. L. (1993). Dynamic surface topography: A new interpretation based upon mantle flow models derived from seismic tomography. Geophys. Res. Lett. 20 (3), 225–228. doi:10.1029/93GL00249

CrossRef Full Text | Google Scholar

Fox, M., Herman, F., Kissling, E., and Willett, S. D. (2015). Rapid exhumation in the Western Alps driven by slab detachment and glacial erosion. Geology 43 (5), 379–382. doi:10.1130/G36411.1

CrossRef Full Text | Google Scholar

Freeburn, R., Bouilhol, P., Maunder, B., Magni, V., van Hunen, J., Hunen, J. V., et al. (2017). Numerical models of the magmatic processes induced by slab breakoff. Earth Planet. Sci. Lett. 478, 203–213. doi:10.1016/j.epsl.2017.09.008

CrossRef Full Text | Google Scholar

Garcés, M., Krijgsman, W., and Agustí, J. (1998). Chronology of the late turolian deposits of the fortuna basin (SE Spain): Implications for the messinian evolution of the eastern Betics. Earth Planet. Sci. Lett. 163 (1–4), 69–81. doi:10.1016/S0012-821X(98)00176-9

CrossRef Full Text | Google Scholar

Garcia-Castellanos, D., and Villaseñor, A. (2011). Messinian salinity crisis regulated by competing tectonics and erosion at the Gibraltar arc. Nature 480 (7377), 359–363. doi:10.1038/nature10651

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Castellanos, D., Torne, M., and Fernàndez, M. (2000). Slab pull effects from a flexural analysis of the Tonga and Kermadec trenches (Pacific Plate). Geophys. J. Int. 141 (2), 479–484. doi:10.1046/j.1365-246X.2000.00096.x

CrossRef Full Text | Google Scholar

Garzanti, E., Radeff, G., and Malusà, M. G. (2018). Slab breakoff: A critical appraisal of a geological theory as applied in space and time. Earth-Science Rev. 177, 303–319. Elsevier. doi:10.1016/j.earscirev.2017.11.012

CrossRef Full Text | Google Scholar

Gerya, T. V., and Yuen, D. (2003). Characteristics-based marker-in-cell method with conservative finite-differences schemes for modeling geological flows with strongly variable transport properties. Phys. Earth Planet. Inter. 140 (4), 293–318. doi:10.1016/j.pepi.2003.09.006

CrossRef Full Text | Google Scholar

Gerya, T. V., and Yuen, D. (2007). Robust characteristics method for modelling multiphase visco-elasto-plastic thermo-mechanical problems. Phys. Earth Planet. Interiors 163 (1–4), 83–105. doi:10.1016/j.pepi.2007.04.015

CrossRef Full Text | Google Scholar

Gerya, T. V., Yuen, D. A., and Maresch, W. V. (2004). Thermomechanical modelling of slab detachment. Earth Planet. Sci. Lett. 226 (1–2), 101–116. doi:10.1016/j.epsl.2004.07.022

CrossRef Full Text | Google Scholar

Gerya, T. V., Perchuk, L. L., and Burg, J. P. (2008). Transient hot channels: Perpetrating and regurgitating ultrahigh-pressure, high-temperature crust-mantle associations in collision belts. Lithos 103 (1–2), 236–256. doi:10.1016/j.lithos.2007.09.017

CrossRef Full Text | Google Scholar

Gerya, T. V. (2013). Three-dimensional thermomechanical modeling of oceanic spreading initiation and evolution. Phys. Earth Planet. Inter. 214, 35–52. doi:10.1016/j.pepi.2012.10.007

CrossRef Full Text | Google Scholar

Guerra-Merchán, A., Serrano, F., Hlila, R., El Kadiri, K., Sanz de Galdeano, C., and Garcés, M. (2014). Tectono-sedimentary evolution of the peripheral basins of the Alboran Sea in the arc of Gibraltar during the latest Messinian-Pliocene. J. Geodyn. 77, 158–170. ISSN 0264-3707. doi:10.1016/j.jog.2013.12.003

CrossRef Full Text | Google Scholar

Gvirtzman, Z., Faccenna, C., and Becker, T. W. (2016). Isostasy, flexure, and dynamic topography. Tectonophysics 683, 255–271. doi:10.1016/j.tecto.2016.05.041

CrossRef Full Text | Google Scholar

Harlow, F. H., and Welch, J. E. (1965). Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 8 (12), 2182. doi:10.1063/1.1761178

CrossRef Full Text | Google Scholar

Heller, P. L., and Liu, L. (2016). Dynamic topography and vertical motion of the U.S. Rocky Mountain region prior to and during the Laramide orogeny. Bull. Geol. Soc. Am. 128 (5–6), 973–988. doi:10.1130/B31431.1

CrossRef Full Text | Google Scholar

Hirth, G., and Kohlstedt, D. (2003). “Rheology of the upper mantle and the mantle wedge: A view from the experimentalists,” in Inside the subduction factory. 83–105. doi:10.1029/138GM06

CrossRef Full Text | Google Scholar

Iribarren, L., Vergés, J., and Fernàndez, M. (2009). Sediment supply from the betic–rif orogen to basins through Neogene. Tectonophysics 475 (1), 68–84. doi:10.1016/j.tecto.2008.11.029

CrossRef Full Text | Google Scholar

Ito, K., and Kennedy, G. C. (1971). “An experimental study of the basalt-garnet granulite-eclogite transition,” in The structure and physical properties of the Earth’s crust. Editor J. G. Heacock (American Geophysical Union), 14, 303–314. doi:10.1029/GM014p0303

CrossRef Full Text | Google Scholar

Ito, E., Akaogi, M., Topor, L., and Navrotsky, A. (1990). Negative pressure-temperature slopes for reactions formign MgSiO ₃ perovskite from calorimetry. Science 249 (4974), 1275–1278. doi:10.1126/science.249.4974.1275

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiménez-Munt, I., and Platt, J. P. (2006). Influence of mantle dynamics on the topographic evolution of the Tibetan Plateau: Results from numerical modelling. Tectonics 25, TC6002. doi:10.1029/2006TC001963

CrossRef Full Text | Google Scholar

Jiménez-Munt, I., Torne, M., Fernàndez, M., Vergés, J., Kumar, A., Carballo, A., et al. (2019). Deep seated density anomalies across the iberia-africa plate boundary and its topographic response. J. Geophys. Res. Solid Earth 124 (12), 13310–13332. doi:10.1029/2019JB018445

PubMed Abstract | CrossRef Full Text | Google Scholar

Karato, S. I., and Wu, P. (1993). Rheology of the upper mantle: A synthesis. Science 260 (5109), 771–778. doi:10.1126/science.260.5109.771

PubMed Abstract | CrossRef Full Text | Google Scholar

Karig, D. E. (1971). Origin and development of marginal basins in the Western Pacific. J. Geophys. Res. 76, 2542–2561. doi:10.1029/jb076i011p02542

CrossRef Full Text | Google Scholar

Katsura, T., and Ito, E. (1989). The system Mg 2 SiO 4 -Fe 2 SiO 4 at high pressures and temperatures: Precise determination of stabilities of olivine, modified spinel, and spinel. J. Geophys. Res. Solid Earth 94 (B11), 15663–15670. doi:10.1029/JB094iB11p15663

CrossRef Full Text | Google Scholar

Katsura, T., Yoneda, A., Yamazaki, D., Yoshino, T., Ito, E., Suetsugu, D., et al. (2010). Adiabatic temperature profile in the mantle. Phys. Earth Planet. Interiors 183 (1–2), 212–218. doi:10.1016/j.pepi.2010.07.001

CrossRef Full Text | Google Scholar

Krijgsman, W., Garcés, M., Agustı, J., Raffi, I., Taberner, C., and Zachariasse, W. J. (2000). The ‘Tortonian salinity crisis’ of the eastern Betics (Spain). Earth Planet. Sci. Lett. 181 (4), 497–511. doi:10.1016/s0012-821x(00)00224-7

CrossRef Full Text | Google Scholar

Krijgsman, W., Capella, W., Simon, D., Hilgen, F. J., Kouwenhoven, T. J., Meijer, P. T., et al. (2018). The Gibraltar corridor: Watergate of the messinian salinity crisis. Mar. Geol. 403, 238–246. doi:10.1016/j.margeo.2018.06.008

CrossRef Full Text | Google Scholar

Kumar, A., Fernàndez, M., Vergés, J., Torne, M., and Jiménez-Munt, I. (2021). Opposite symmetry in the lithospheric structure of the Alboran and Algerian basins and their margins (Western Mediterranean): Geodynamic implications. J. Geophys. Res. Solid Earth 126 (7). doi:10.1029/2020JB021388

CrossRef Full Text | Google Scholar

Li, Z. H., Xu, Z., Gerya, T., and Burg, J. P. (2013). Collision of continental corner from 3-D numerical modeling. Earth Planet. Sci. Lett. 380, 98–111. doi:10.1016/j.epsl.2013.08.034

CrossRef Full Text | Google Scholar

Liang, X., Chen, Y., Tian, X., Chen, Y. J., Ni, J., Gallegos, A., et al. (2016). 3D imaging of subducting and fragmenting Indian continental lithosphere beneath southern and central Tibet using body-wave finite-frequency tomography. Earth Planet. Sci. Lett. 443, 162–175. doi:10.1016/J.EPSL.2016.03.029

CrossRef Full Text | Google Scholar

Lithgow-Bertelloni, C., and Silver, P. G. (1998). Dynamic topography, plate driving forces and the African superswell. Nature 395 (6699), 269–272. doi:10.1038/26212

CrossRef Full Text | Google Scholar

Macchiavelli, C., Vergés, J., Schettino, A., Fernàndez, M., Turco, E., Casciello, E., et al. (2017). A new southern north atlantic isochron map: Insights into the drift of the iberian plate since the late cretaceous. J. Geophys. Res. Solid Earth 122 (12), 9603–9626. doi:10.1002/2017JB014769

CrossRef Full Text | Google Scholar

Magni, V., Faccenna, C., van Hunen, J., and Funiciello, F. (2014). How collision triggers backarc extension: Insight into Mediterranean style of extension from 3-D numerical models. Geology 42, 511–514. doi:10.1130/G35446.1

CrossRef Full Text | Google Scholar

Magni, V., Allen, M. B., van Hunen, J., Bouilhol, P., Hunen, J. V., Bouilhol, P., et al. (2017). Continental underplating after slab break-off. Earth Planet. Sci. Lett. 474, 59–67. doi:10.1016/j.epsl.2017.06.017

CrossRef Full Text | Google Scholar

Mancilla, F. d. L., Booth-Rea, G., Stich, D., Pérez-Peña, J. V., Morales, J., Azañón, J. M., et al. (2015). Slab rupture and delamination under the Betics and Rif constrained from receiver functions. Tectonophysics 663, 225–237. doi:10.1016/j.tecto.2015.06.028

CrossRef Full Text | Google Scholar

Meulenkamp, J. E., Kováč, M., and Cicha, I. (1996). On Late Oligocene to Pliocene depocentre migrations and the evolution of the Carpathian-Pannonian system. Tectonophysics 266 (1–4), 301–317. doi:10.1016/S0040-1951(96)00195-3

CrossRef Full Text | Google Scholar

Mitrofan, H., Anghelache, M. A., Chitea, F., Damian, A., Cadicheanu, N., and Vişan, M. (2016). Lateral detachment in progress within the Vrancea slab (Romania): Inferences from intermediate-depth seismicity patterns. Geophys. J. Int. 205 (2), 864–875. doi:10.1093/gji/ggv533

CrossRef Full Text | Google Scholar

Negredo, A. M., Mancilla, F. d. L., Clemente, C., Morales, J., and Fullea, J. (2020). Geodynamic modeling of edge-delamination driven by subduction-transform edge propagator faults: The westernmost mediterranean margin (central betic orogen) case study. Front. Earth Sci. 8, 6. doi:10.3389/feart.2020.533392

CrossRef Full Text | Google Scholar

Palomeras, I., Thurner, S., Levander, A., Liu, K., Villasenor, A., Carbonell, R., et al. (2014). Finite-frequency Rayleigh wave tomography of the Western Mediterranean: Mapping its lithospheric structure. Geochem. Geophys. Geosystems 15, 140–160. doi:10.1002/2013gc004861

CrossRef Full Text | Google Scholar

Peral, M. F., Vergés, J., Zlotnik, S., Jiménez-Munt, I., and Jimenez-Munt, I. (2022). Numerical modelling of opposing subduction in the Western Mediterranean. Tectonophysics 830, 229309. doi:10.1016/j.tecto.2022.229309

CrossRef Full Text | Google Scholar

Qayyum, A., Lom, N., Advokaat, E. L., Spakman, W., van der Meer, D. G., and van Hinsbergen, D. J. J. (2022). Subduction and slab detachment under moving trenches during ongoing India-Asia convergence. Geochem. Geophys. Geosystems 23, e2022GC010336. doi:10.1029/2022GC010336

CrossRef Full Text | Google Scholar

Ranalli, G. (1995). Rheology of the Earth. 2nd ed. Springer. ISBN: 978-0-412-54670-9.

Google Scholar

Rosenbaum, G., Lister, G. S., and Duboz, C. (2002). Reconstruction of the tectonic evolution of the Western mediterranean since the oligocene. J. Virtual Explor. 8. doi:10.3809/jvirtex.2002.00053

CrossRef Full Text | Google Scholar

Rosenbaum, G., Gasparon, M., Lucente, F. P., Peccerillo, A., and Miller, M. S. M. S. (2008). Kinematics of slab tear faults during subduction segmentation and implications for Italian magmatism. Tectonics 27 (2). doi:10.1029/2007TC002143

CrossRef Full Text | Google Scholar

Ruiz-Constán, A., Galindo-Zaldívar, J., Pedrera, A., Célérier, B., and Marín-Lechado, C. (2011). Stress distribution at the transition from subduction to continental collision (northwestern and central Betic Cordillera). Geochem. Geophys. Geosyst. 12, Q12002. doi:10.1029/2011GC003824

CrossRef Full Text | Google Scholar

Schellart, W. P. (2017). A geodynamic model of subduction evolution and slab detachment to explain Australian plate acceleration and deceleration during the latest Cretaceous-early Cenozoic. Lithosphere 9 (6), 976–986. doi:10.1130/L675.1

CrossRef Full Text | Google Scholar

Schmeling, H., Babeyko, A. Y., Enns, A., Faccenna, C., Funiciello, F., Gerya, T., et al. (2008). A benchmark comparison of spontaneous subduction models-Towards a free surface. Phys. Earth Planet. Interiors 171 (1–4), 198–223. doi:10.1016/j.pepi.2008.06.028

CrossRef Full Text | Google Scholar

Şengör, A. M. C., Özeren, S., Genç, T., and Zor, E. (2003). East Anatolian high plateau as a mantle-supported, north-south shortened domal structure. Geophys. Res. Lett. 30 (24). doi:10.1029/2003GL017858

CrossRef Full Text | Google Scholar

Sinclair, H. D. (1997). Flysch to molasse transition in peripheral foreland basins: The role of the passive margin versus slab breakoff. Geology 25 (12), 1123–1126. doi:10.1130/0091-7613(1997)025<1123:FTMTIP>2.3.CO;2

CrossRef Full Text | Google Scholar

Spakman, W., and Wortel, R. (2004). “A tomographic view on western mediterranean geodynamics,” in The TRANSMED atlas. The mediterranean region from crust to mantle (Berlin, Heidelberg: Springer Berlin Heidelberg), 31–52. doi:10.1007/978-3-642-18919-7_2

CrossRef Full Text | Google Scholar

Spakman, W., Wortel, M. J. R., and Vlaar, N. J. (1988). The hellenic subduction zone: A tomographic image and its geodynamic implications. Geophys. Res. Lett. 15 (1), 60–63. doi:10.1029/GL015i001p00060

CrossRef Full Text | Google Scholar

Spakman, W., Chertova, M. V., Van Den Berg, A., and van Hinsbergen, D. J. J. J. (2018). Puzzling features of Western Mediterranean tectonics explained by slab dragging. Nat. Geosci. 11 (3), 211–216. doi:10.1038/s41561-018-0066-z

CrossRef Full Text | Google Scholar

Turcotte, D., and Schubert, G. (2014). Geodynamics. Cambridge University Press. doi:10.1017/CBO9780511843877

CrossRef Full Text | Google Scholar

Van Der Meulen, M. J., Meulenkamp, J. E., and Wortel, M. J. R. (1998). Lateral shifts of Apenninic foredeep depocentres reflecting detachment of subducted lithosphere. Earth Planet. Sci. Lett. 154 (1–4), 203–219. doi:10.1016/s0012-821x(97)00166-0

CrossRef Full Text | Google Scholar

van der Schee, M., van den Berg, B. C. J., Capella, W., Simon, D., Sierro, F. J., and Krijgsman, W. (2018). New age constraints on the Western betic intramontane basins: A late tortonian closure of the Guadalhorce corridor? Terra nova. 30 (5), 325–332. doi:10.1111/ter.12347

CrossRef Full Text | Google Scholar

Van Hinsbergen, D. J. J. J., Vissers, R. L. M. M., and Spakman, W. (2014). Origin and consequences of Western Mediterranean subduction, rollback, and slab segmentation. Tectonics 33 (4), 393–419. doi:10.1002/2013TC003349

CrossRef Full Text | Google Scholar

van Hunen, J., and Allen, M. B. (2011). Continental collision and slab break-off: A comparison of 3-D numerical models with observations. Earth Planet. Sci. Lett. 302 (1–2), 27–37. doi:10.1016/j.epsl.2010.11.035

CrossRef Full Text | Google Scholar

Vergés, J., and Fernàndez, M. (2012). Tethys–atlantic interaction along the iberia–africa plate boundary: The betic–rif orogenic system. Tectonophysics 579, 144–172. doi:10.1016/j.tecto.2012.08.032

CrossRef Full Text | Google Scholar

Wortel, R., and Spakman, W. (1992). “Structure and dynamics of subducted lithosphere in the Mediterranean region,” in Proceedings of the koninklijke nederlandse akademie van Wetenschappen/C, 95, 325–347.

Google Scholar

Wortel, M. J. R., and Spakman, W. (2000). Subduction and slab detachment in the mediterranean-carpathian region. Science 290 (5498), 1910–1917. doi:10.1126/science.290.5498.1910

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, F.-Y., Ji, W.-Q., Wang, J.-G., Liu, C.-Z., Chung, S.-L., and Clift, P. D. (2014). Zircon U-Pb and Hf isotopic constraints on the onset time of India-Asia collision. Am. J. Sci. 314 (2), 548–579. doi:10.2475/02.2014.04

CrossRef Full Text | Google Scholar

Yoshioka, S., and Wortel, R. (1995). Three-dimensional numerical modeling of detachment of subducted lithosphere. J. Geophys. Res. 100 (B10), 20223–20244. doi:10.1029/94jb01258

CrossRef Full Text | Google Scholar