Prestack seismic random noise attenuation using the wavelet-inspired invertible network with atrous convolutions spatial pyramid

Convolutional Neural Network (CNN) is widely used in seismic data denoising due to its simplicity and effectiveness. However, traditional seismic denoising methods based on CNN ignore multi-scale features of seismic data in the wavelet domain. The lack of these features will decrease the accuracy of denoising results. To address this barrier, a seismic denoise method based on the wavelet-inspired invertible network with atrous convolutions spatial pyramid (WINNet_ACSP) is proposed. WINNet_ACSP follows the principle of lifting wavelet transform. The proposed method utilizes the redundant orthogonal wavelet transform to obtain frequency multi-scale information from noisy seismic data. Then predict update network (PUNet) extracts spatial multi-scale features of approximate and detailed parts. The sparse driven network (SDN) learns the complex multi-scale information and obtains sparse features. These sparse features are processed to eliminate random noise. Compared to standard convolution, the atrous convolutions spatial pyramid (ACSP) can extract more features. The redundant features are the key to ensure the precision of multi-scale information. Therefore, the introduction of ACSP in PUNet can guarantee the denoising effect of the network. WINNet_ASCP combines the characteristics of wavelet transform and neural network and has a high generalization. Besides, transfer learning is used to overcome the difficulty caused by the training sample size of seismic data. The training process includes pre-training and post-training. The former is trained to obtain the initial denoising network by natural image samples. The latter is trained with a small sample of seismic data to enhance stratigraphic continuity. Finally, the proposed method is tested with synthetic and field data. The experimental results show that the proposed method can effectively remove random noise and reduce the loss of detailed information in prestack seismic data. In the future, we will make further improvements on this basis and conduct experiments on 3D prestack data.

1 Introduction

Random noise can affect the signal-to-noise ratio (SNR) of seismic data. Suppressing random noise and improving the SNR of seismic data is a critical step in seismic signal processing (Kong and Peng, 2015; Saad and Chen, 2020; Zhong et al., 2021). So far, researchers have come up with many methods to suppress random noise. Common methods include predictive filtering (Chen and Ma, 2014; Liu et al., 2020; Wang et al., 2021), mode decomposition (Han and van der Baan, 2015; Gómez and Velis, 2016; Long et al., 2021), low-rank constraints (Anvari et al., 2017; Chen et al., 2017; Huang, 2022), and transform domain (Kesharwani et al., 2022; Xie et al., 2022; Zhang et al., 2022).

Predictive filtering exploits the predictability of seismic data to suppress random noise. Canales and Lu (1993) first time proved the feasibility of predictive filtering technology in seismic data denoising field. Chen and Sacchi (2017) proposed a predictive filtering approach to simultaneously suppress mixed noises. This approach utilizes the hybrid L1/L2 norm to design a robust M-estimate of a special autoregressive moving-average model. The experimental results show that the model can effectively remove the mixed noise. Besides, Liu and Li (2018) proposed an adaptive predictive filtering method for non-stationary seismic signals. This method utilizes streaming characteristics to speed up the computation and uses signal-to-noise orthogonalization to enhance the denoising ability. Experiments on field data demonstrate the superiority of the method.

Mode decomposition-based denoising methods use correlation to separate seismic data into signal and noise components. Cai et al. (2011) utilized empirical mode decomposition to denoise seismic record. The denoising result showed that mode decomposition can suppress random noise. Zhang and Hong (2019) proposed a random noise suppression method based on the complete ensemble empirical mode decomposition. The results show that complete ensemble empirical mode decomposition has high feature recognition ability in complex random desert noise. Wu et al. (2022) uses multivariate variational modal decomposition on the segmented seismic data. This method significantly improves the lateral continuity and SNR of the seismic data.

Low-rank constrained denoising methods utilize seismic data’s low-rank property to remove random noise. Wang et al. (2018) proposed a Hankel low-rank approximate denoising approach. Hankel structure can enhance the seismic low-rank property. The enhanced low-rankness effectively removes random noise. Feng et al. (2021) proposed a denoising method using low-rank tensors. This method applies low-rank constraints to the seismic data tensor and improves the structural similarity of seismic data.

Transform domain-based denoising methods utilize the characteristics of seismic data in different transform domains to attenuate random noise. Zwartjes and Gisolf (2007) used Fourier transform to reconstruct seismic data. The high SNR reconstruction results demonstrate the feasibility of this method. Liang et al. (2018) proposed a denoising method based on the non-subsampled shearlet transform. The results show that the non-subsampled shearlet transform can suppress random noise and retain effective signals. Chen and Song (2018) used wavelet decomposition to decompose seismic data into multiple components. Then different threshold methods are applied to different seismic data components to achieve random noise suppression.

Predictive filtering, mode decomposition, low-rank constraints, and transform domain use the prior information of seismic data to construct suitable optimization strategies. Though these methods have good denoising ability and generalization abilities, denoising results are easily affected by human factors because of their large number of hyperparameters. To reduce the interference of human factors, researchers proposed the learning-based denoising method (Beckouche and Ma, 2014; Chen, 2017; Richardson and Feller, 2019; Yu et al., 2019). Dictionary learning and deep learning are commonly used strategies. Dictionary learning-based denoising methods train appropriate dictionary elements and linearly combine the elements to suppress random noise. Beckouche and Ma (2014) proposed a step-decomposable dictionary learning denoising method. The field data denoising result show that this method has a good denoising performance. Wang and Ma (2019) used the variation of noise variance in space to design a dictionary learning method with adaptive threshold parameters. The introduction of self-adaptation can realize blind denoising of seismic data and obtain signals with a high SNR. Kuruguntla et al. (2021) introduced a double sparse dictionary learning constraint to improve the denoising performance. This method combines the strength of the analytical transform and adaptive transform to suppress mixing noise. Chen et al. (2023) proposed a robust dictionary learning denoising method to reduce the loss of effective signal. This method retrieves leaked seismic signals by introducing a Huber-norm sparse coding model. Synthetic data and field data demonstrate the effectiveness of this method.

The denoising method based on deep learning distinguishes random noise from effective seismic signals by extracting the implicit features of seismic data through a neural network. Zhang et al. (2018) proposed a fast and flexible denoising convolutional neural network (FFDNet) to suppress noise. Numerous experimental results prove that FFDNet can flexibly and efficiently suppress random noise. Yu et al. (2019) attenuated the random and linear noise of complex seismic data using CNN. Experimental results prove the potential applications of CNN in suppression of random, linear, and multiples noise. Guo et al. (2019) proposed a convolutional blind denoising network (CBDNet) to eliminate random noise. The experimental results show that CBDNet can flexibly remove different levels of random noise by introducing a noise level estimation subnetwork. Sang et al. (2020) proposed a denoising method for multidimensional geological structure features based on the end-to-end deep denoising convolutional neural networks (DCNNs). DCNNs have a good denoising ability for complex geological structures, by extracting the characteristics of seismic data in different directions. Yang et al. (2021) proposed a denoising approach for 3-D seismic data by deep skip autoencoder. This approach uses the deep skip autoencoder to extract the waveform features of each seismic data patch. Feng and Li (2021) combined singular value decomposition (SVD) and neural networks to suppress noise interference in distributed acoustic sensing. The introduction of SVD improves the network’ generalization and can accurately represent complex features in seismic data. Dong et al. (2022) utilized a spatial attention mechanism and convolutional neural network to distinguish weakly reflected seismic signals from strong random noise. The spatial attention further strengthens the denoising ability of the convolutional neural network.

Learning-based methods can extract various implicit features of seismic data. Through these implicit features, non-linear mapping of noiseless seismic data and noisy seismic data can be established. However, learning-based methods rarely take into account the advantages of other categories of methods approaches. For example, the wavelet transform threshold-based denoising method proved that the multi-scale features of seismic data can suppress random noise. But learning-based methods do not consider multi-scale information. The lack of multi-scale information results in a limited denoising effect of learning-based methods. To extract more abundant seismic information and improve the denoising effect, a wavelet-inspired invertible network with atrous convolutions spatial pyramid (WINNet_ACSP) is proposed for seismic denoising task. The proposed method consists of the lifting inspired invertible neural network with atrous convolutions spatial pyramid (LINN_ACSP) and sparse driven network (SDN). LINN_ACSP and SDN follow the principle of lifting wavelet transform and soft threshold operation, respectively. Therefore, LINN_ACSP inherits the multi-scale characteristic, sparsity, and perfect reconstruction characteristic of the lifting wavelet transform. Multi-scale features can ensure that the network effectively suppresses random noise. Sparsity can be exploited by soft-thresholding to distinguish random noise. Perfect reconstruction characteristic ensures that effective signals are not leaked. LINN_ACSP can obtain the frequency and spatial multi-scale information of seismic data through the splitting operator, prediction and update network (PUNet). The detail and approximate parts of the seismic data can be obtained by using this multi-scale information. Using the sparse detail part obtained by LINN_ACSP, the SDN learns to denoise the detail coefficients and obtains the denoised detail coefficients. Besides, to overcome the difficulty caused by the training sample size of seismic data, the proposed method utilizes transfer learning for training. Finally, the proposed method and other state-of-the-art methods are tested with synthetic and field seismic data. The experimental results show that the proposed method can effectively remove random noise and reduce the loss of detailed information in prestack seismic data.

2 Methods

Noisy seismic data can be expressed as follows

$\mathit{Y}=\mathit{X}+\mathit{N}(1)$

where $\mathit{Y}$ represents noise-containing seismic data observed in the field, $\mathit{X}$ denotes seismic data, and $\mathit{N}$ indicates additive white Gaussian noise.

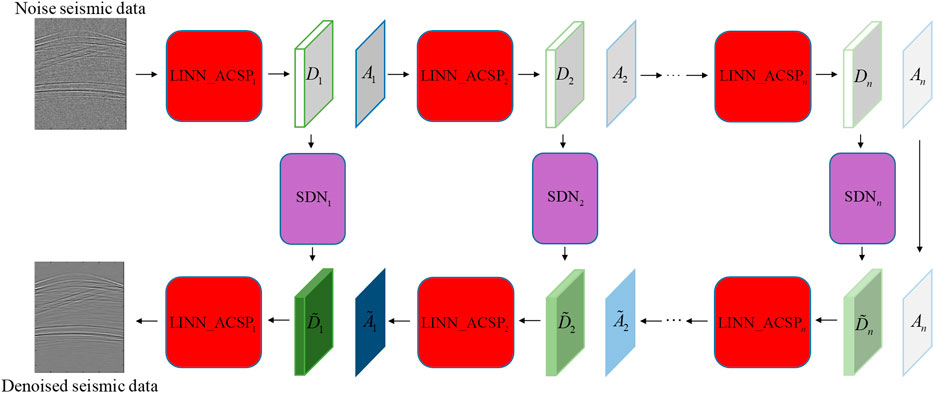
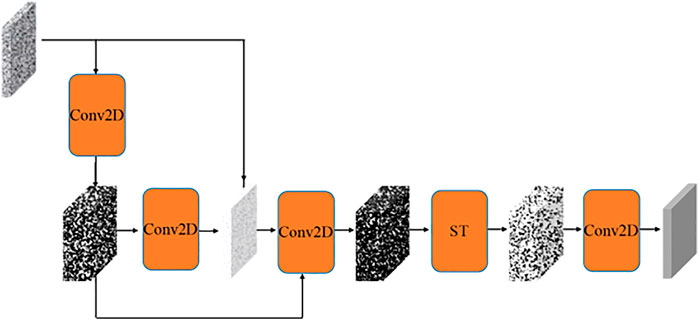
In this work, we propose a method for attenuating prestack seismic random noise using WINNet_ACSP. The LINN can obtain frequency multi-scale features in the wavelet domain (Huang and Dragotti, 2022). Embedding ACSP in LINN can extract spatial multi-scale features of the approximate or detail parts. LINN_ACSP combines the characteristics of wavelet transform and neural networks. The entire network structure of WINNet_ACSP follows the wavelet threshold principle. At the same time, WINNet_ACSP as a neural network can realize non-linear mapping. The network structure of WINNet_ACSP is shown in Figure 1.

FIGURE 1

FIGURE 1. The network structure of WINNet_ACSP.

In Figure 1, LINN_ACSP represents lifting inspired invertible neural networks with atrous convolutions spatial pyramid, SDN denotes the sparse-driven network, D indicates the detail part, representing the boundary information, A is the approximate part, representing the smoothing information, n indicates the n-th scale, and the superscript ∼ indicates the part after denoising.

WINNet_ACSP consists of LINN_ACSP and SDN. The forward pass of LINN_ACSP learns to perform a non-linear redundant transform on seismic data to obtain the multi-scale approximation part and detail part. The SDN learns to denoise the detail coefficients and obtains the denoised detail coefficients. Finally, using the backward pass of LINN_ACSP, the approximate part and the denoised detail part are reconstructed to obtain denoised seismic data.

2.1 LINN_ACSP

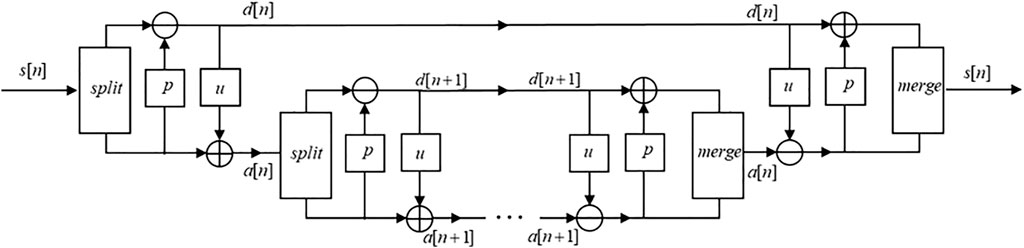
The denoising method based on wavelet transform can well remove the random noise in seismic data (Aghayan et al., 2016). The lifting scheme is known as the second-generation wavelet transform (Sweldens, 1998). The second-generation wavelet transform process can be divided into three steps: split, predict and update. Each step can be reconstructed by changing the direction and sign of the data flow. The splitting and merging process of the lifting scheme wavelet transform is shown in Figure 2.

FIGURE 2

FIGURE 2. Lifting scheme wavelet transform.

In Figure 2, p represents the predict step, u denotes the update step, d [ ] indicates the detail part, a [ ] is the approximate part, s [ ] represents seismic data or approximate part, and n indicates the n-th scale.

However, for the split step, the lifting scheme wavelet transform uses a non-redundant transform. Affected by random noise, the non-redundant transformation will lose some important seismic information. For the prediction and update steps, the lifting scheme wavelet transform utilizes a simple linear formula and cannot accurately represent complex spatial features. For the above problems, some researchers use neural networks to complete the above requirements. LINN_ACSP is an invertible neural network with a structure inspired by the lifting scheme. LINN_ACSP inherits the sparsifying ability, perfect reconstruction characteristics, and multi-scale characteristics of the wavelet transform. Similar to the lifting scheme wavelet transform, LINN_ACSP consists of a splitting/merging operator, and a learnable predict and update network (PUNet).

2.1.1 Splitting/merging operator

LINN_ACSP uses redundant linear operators as a splitting operator, denoted as S. The split operator S is parameterized by a convolution kernel K∈R^c×1×ρ×ρ, where c denotes the number of channels and ρ denotes the spatial filter size.

Using the redundant split operator to process the seismic data, the approximate part and the detail part with frequency multi-scale are obtained, as shown in the following formula

$S\left(\mathit{Y}\right)=\left({\mathit{A}}_1,{\mathit{D}}_1\right)(2)$

where ${\mathit{A}}_1$ represents the approximate part of the first scale, and ${\mathit{D}}_1$ is the detail part of the first scale.

To ensure invertible, the merge operator M is parameterized by the transpose of the convolution kernel corresponding to the split operator. The merge operator reconstructs the approximate part and detailed part into seismic data. It can be defined as

$M\left(\left\{{\mathit{A}}_1,{\mathit{D}}_1\right\}\right)=\mathit{Y}(3)$

where { } is the concatenation operation.

Redundant representation can effectively reduce the leakage of seismic information and improve the stability of reconstruction results. Considering the waveform characteristics of seismic records, the sym2 wavelet is used to construct the convolution kernel K.

2.1.2 PUNet

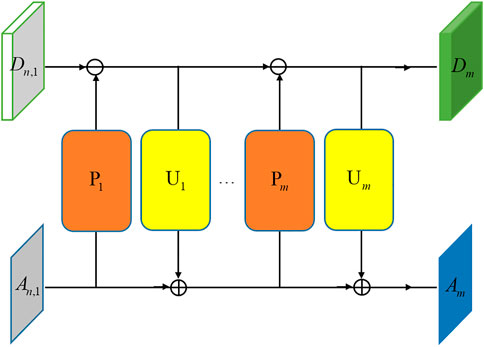
LINN_ACSP uses a learnable convolutional neural network with ACSP to imitate the prediction and update operations in the lifting scheme wavelet transform. This convolutional neural network is named PUNet. PUNet can adaptively learn the corresponding non-linear features of the approximate part and the detailed part. These non-linear features are used to predict the detail part and update the approximate part. Completing one prediction and update process can be called one lifting step. Suppose there are m pairs of PUNet, in the n-th scale. The m times of lifting steps are shown in Figure 3.

FIGURE 3

FIGURE 3. The process of predict and update.

In Figure 3, P represents the predict network, U denotes the update network, and the subscript m indicates the m-th lifting step. This paper sets m = 4.

In the forward transform, the approximate part and the detail part of the seismic data are non-linearly transformed by the neural network into a representation that is easier to denoising. For the approximate part ${\mathit{A}}_n$ and detailed part ${\mathit{D}}_n$ split in the n-th scale, the predict network uses the correlation between the approximate part and the detail part to perform prediction operation on the approximate part. The m-th pairs predict operation can be expressed as

${\mathit{D}}_{n,m}={\mathit{D}}_{n,m-1}-{\mathrm{P}}_{n,m}\left({\mathit{A}}_{n,m-1}\right)(4)$

The purpose of the predict network is to make ${\mathit{D}}_{n,m}$ sparser.

The update network act on the detail part to obtain the update result. Add the updated result and the approximate part to get the adjusted approximate part. The m-th pairs update operation can be expressed as

${\mathit{A}}_{n,m}={\mathit{A}}_{n,m-1}+{\mathrm{U}}_{n,m}\left({\mathit{D}}_{n,m-1}\right)(5)$

The purpose of the update network is to make the approximate part A_n,m smoother.

In the backward transform, the denoised detail part and approximate part are reconstructed back to the original domain by the same set of m pairs PUNet used in the forward transform. The formula is as follows

${\mathit{D}}_{n,m-1}={\mathit{D}}_{n,m}+{\mathrm{P}}_{n,m}\left({\mathit{A}}_{n,m-1}\right)(6)$

${\mathit{C}}_{n,m-1}={\mathit{C}}_{n,m}-{\mathrm{U}}_{n,m}\left({\mathit{D}}_{n,m-1}\right)(7)$

2.1.3 Structure of PUNet

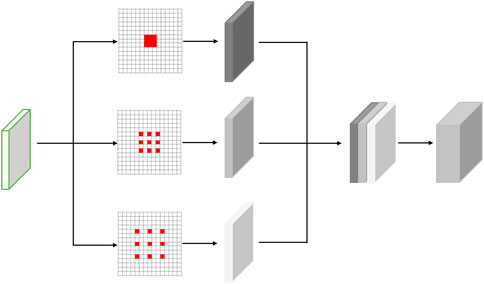
To accurately predict and update the detail and approximate parts, PUNet needs to extract spatial multi-scale features of the detail and approximate parts. So PUNet is constructed by ACSP, residual blocks with depth-wise separable convolution, and the soft-thresholding operator approximated as the activation function. The network structure of PUNet is shown in Figure 4.

FIGURE 4

FIGURE 4. The structure of PUNet.

In Figure 4, ACSP represents atrous convolutions spatial pyramid, RB indicates residual block with depth-wise separable convolution, Conv2D is the 2D convolutional layer, and the subscript j represents j-th RB. This paper sets j = 4.

2.1.3.1 Atrous convolutions spatial pyramid

Atrous convolution is also called dilated convolution. Atrous convolution can change the receptive field by changing the dilation rate without increasing the number of convolution kernel parameters. The convolution kernel of atrous convolution is equivalent to inserting zeros between adjacent filter values in the horizontal or vertical direction of the convolution kernel of standard convolution. As shown in Figure 5, the larger the dilation rate, the larger the receptive field of the atrous convolution.

FIGURE 5

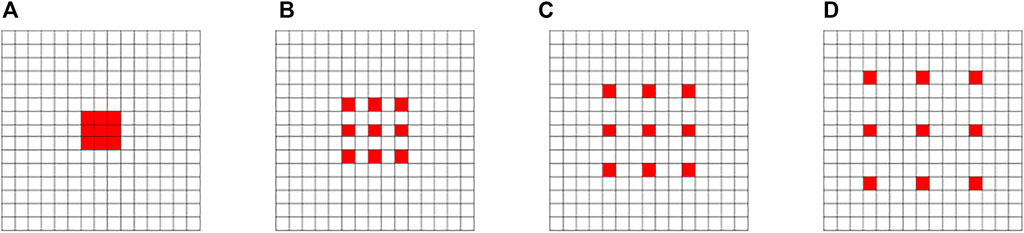
FIGURE 5. Atrous convolution with different dilation rates. (A) Dilation rate of 1; (B) Dilation rate of 2; (C) Dilation rate of 3; (D) Dilation rate of 4.

ACSP contains multiple parallel branches of the atrous convolutions with different dilation rates, shown in Figure 6. ACSP can extract spatial multi-scale features of approximate part and detail part (Ma et al., 2019). These spatial multi-scale features are fused by 1 × 1 convolution and input to the residual block.

FIGURE 6

FIGURE 6. Atrous convolutions spatial pyramid.

2.1.3.2 Residual block with depth-wise separable convolution

The residual block directly stacks the input on the output through the skip connection to realize the feature fusion of the current module and the previous module. Feature fusion can solve the gradient vanishing problem during neural network training. Specifically, the residual block converts the original mappings that need to be learned into residual mappings, as shown in Eq. 8. And residual maps are easier to optimize for neural networks.

$R\left(z\right)=O\left(z\right)-z(8)$

where z represents input features, O(z) indicates original mapping, and R(z) is residual mapping.

So residual learning can improve the stability of the network and allow more layers to be stacked to enhance the learning ability of the network.

Depth-wise separable convolution can reduce residual block parameters and ensure the accuracy of feature extraction by dividing the standard convolution operation into two parts (Chollet, 2017), as shown in Figure 7. The first part is the depth-wise convolution. The second part is the 1 × 1 convolution. Depth-wise convolution performs a separate convolution on each channel. The 1 × 1 convolution integrates all channel information. When the number of channels and the size of the convolution kernel are large, depth-separable convolution can effectively reduce memory and time costs during training.

FIGURE 7

FIGURE 7. Convolution. (A) Standard convolution; (B) Depth-wise separable convolution.

2.1.3.3 Soft-thresholding

The soft-thresholding activation function expression is as Eq. 9

${ST}_{\lambda }\left(z\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left(z\right)\max \left(\left|z\right|-\lambda ,0\right)(9)$

where, ST represents soft-thresholding operations, z is input features, and λ is a hyperparameters.

The soft-thresholding operator can be regarded as a two-sided ReLU function. Therefore, for seismic data with peaks and troughs, the soft-thresholding is more suitable as a non-linearization operator.

2.2 Sparse driven network (SDN)

The sparse driven network (SDN) consists of convolutional layers and soft-threshold sparse operators. For the detail parts at each scale, the denoising operation of the sparse drive network does not directly perform simple soft thresholding on the detail coefficients. The purpose of the sparse-driven network is to first utilize convolutional layers to transform the detail parts at each scale into a domain more suitable for denoising. In this domain, the eigencoefficient of the effective signal is made larger, and the eigencoefficient of random noise is made smaller. All feature coefficients are then processed using a learnable soft threshold operator. Finally, a convolutional layer is used to convert the feature coefficients back to the domain corresponding to the detail part. The network structure of SDN is shown in Figure 8.

FIGURE 8

FIGURE 8. The structure of sparse driven network.

2.3 Network training

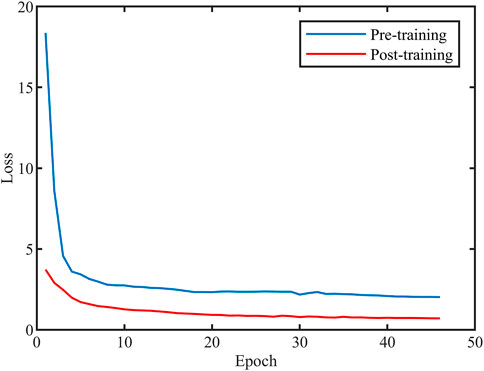
To overcome the problem of the training sample size of seismic data, transfer learning (Pan and Yang, 2009) is used in this paper. The training process is divided into pre-training and post-training. In the pre-training step, a dataset of natural images is used to train the network. The pre-training can teach LINN_ACSP and SDN how to predict updates and denoising, respectively. In the post-training step, a small sample of seismic data is used for training to fine-tune the network. To reduce computer consumption, the dataset size is divided into 50 × 50 as the input of the neural network. The optimizer uses Adaptive Moment Estimation with a learning rate of 0.001 in the pre-training and 0.0001 in the post-training. Figure 9 is the training loss.

FIGURE 9

FIGURE 9. Training loss.

3 Examples and results

3.1 Evaluation of denoising performance

The SNR can directly reflect the quality of denoising results, it is defined as

$\mathrm{S}\mathrm{N}\mathrm{R}=10{\log }_{10}\frac{{‖\mathit{X}‖}_{\mathrm{F}}^2}{{‖\mathit{X}-{\mathit{X}}_{denoise}‖}_F^2}(10)$

where ${\mathit{X}}_{denoise}$ is the estimated or denoised seismic data.

SNR can evaluate the denoising effect of various methods as a whole. However, calculating SNR requires noise-free seismic data. So the SNR cannot be calculated in field seismic data tests. To comprehensively evaluate the denoising results, the F-K spectrum is utilized to evaluate the denoising effect of various methods, too. F-K spectrum can analyze the advantages and disadvantages of various methods in terms of frequency.

3.2 Synthetic two-dimensional (2-D) seismic data

The marmousi2 P wave velocity model was used as the forward model. Combined with the first-order stress-velocity-sound wave equation, 31 shot synthetic data that conform to the law of field seismic data are obtained. The synthetic seismic data of each shot contains 277 traces, each trace has 3,000 sampling points, the sampling interval is 0.5 ms, and the domain frequency range is 20–30 Hz. The 30 shot synthetic seismic data were randomly selected as the post-training dataset. The selected seismic data of each shot is divided into datasets of size 50*50, as the input of the neural network. The remaining one-shot synthetic seismic data, shown in Figure 10, was used to test the denoising effect of the proposed method and other methods. Then AWGN was added to seismic data to generate noisy seismic data with SNR = −2 dB.

FIGURE 10

FIGURE 10. Synthetic Seismic Data. (A) Noise-free data; (B) Noisy data.

To evaluate the denoising effect of the proposed method, three state-of-the-art seismic denoising methods are used for comparison. Figures 11A–D are the denoising results of f-x damped multichannel singular spectrum analysis (DMSSA), SSWT-GoDec method, DnCNN and the proposed method, respectively. Figure 11A shows that the random noise in the sanction of the denoising results based on DMSSA is effectively suppressed. And this method does not cause the waveform distortion of the seismic effective signal. The SNR of the DMSSA is 6.9 dB. Figure 11B contains a lot of random noise, and the waveform of the seismic signal is distorted. The SNR of the SSWT-GoDec is 3.3 dB. Figure 11C shows that DnCNN can suppress random noise, but also weaken the continuity of effective seismic signals. The SNR of the SSWT-GoDec is 4 dB. Figure 11D shows that the proposed method can effectively suppress random noise without causing distortion of the effective seismic signal waveform, nor weakening the continuity of the signal. The SNR of the proposed method is 7.3 dB. This result proves that the use of multi-scale features can improve the denoising effect of the neural network.

FIGURE 11

FIGURE 11. Synthetic seismic data denoising results section. (A) DMSSA; (B) SSWT-GoDec; (C) DnCNN; (D) The proposed method; (E) Removed noise by DMSSA; (F) Removed noise by SSWT-GoDec; (G) Removed noise by DnCNN; (H) Removed noise by the proposed method.

The removed noise section of the above method is shown in Figure 11E–H. Comparing Figure 11E–H the results show that there is obvious seismic reflection information in the whole removed noise section based on SSWT-GoDec and DnCNN. The denoising method based on DMSSA, when affected by random noise, will leak effective signals when recovering high-amplitude seismic signals. Finally, the seismic signal leakage cannot be observed in the removed noise section corresponding to the proposed method. This result demonstrates that the use of multi-scale features can prevent the leakage of valid seismic signals.

Figures 12A, B shows the F-K spectra of clean and noisy seismic data, respectively. Figure 12C–F are the F-K spectrum of the denoising results of the above methods. Figure 12C is the F-K spectrum obtained by DMSSA denoising. Comparing Figures 12A, C, when the frequency is higher than 30 Hz, the amplitude of the F-K spectrum shown in Figure 12C is smaller than the corresponding F-K spectrum of the noise-free seismic data. This result shows that the DMSSA-based denoising method loses high-frequency information, that is, leakage occurs when the seismic signal changes from low amplitude to high amplitude. Figure 12D is the F-K spectrum obtained by SSWT-GoDec denoising. Comparing Figures 12A, D, when the frequency is lower than 20 Hz, the F-K spectrum shown in Figure 12D is less consistent with Figure 12A. This result shows that the denoising method based on SSWT-GoDec will change the low-frequency information, that is, the waveform of the seismic signal is distorted. Figure 14E is the F-K spectrum obtained by DnCNN denoising. Comparing Figures 12A, E, the overall magnitude of the F-K spectrum shown in Figure 12E is lower than that in Figure 12A. The results show that the denoising method based on DnCNN will leak the effective seismic signal. Figure 12F is the F-K spectrum obtained by the proposed method for denoising. Comparing Figures 12A, F, the F-K spectrum shown in Figure 12F has the highest similarity with Figure 12A. The results show that the proposed method can effectively remove random noise and protect critical seismic signals.

FIGURE 12

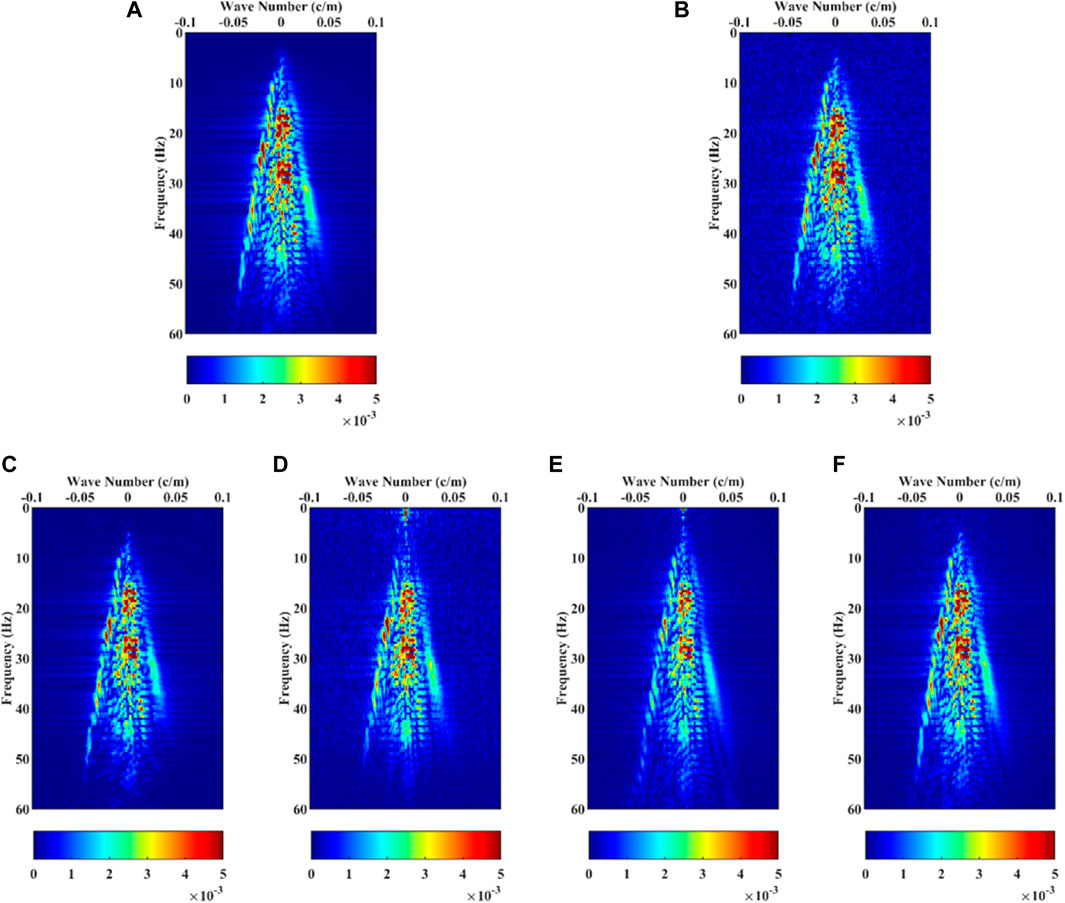
FIGURE 12. The F-K spectrum of the seismic data. (A) Clean data; (B) Noisy data; (C) DMSSA; (D) SSWT-GoDec; (E) DnCNN; (F) The proposed method.

3.3 Application on field seismic data

To verify the effectiveness of the proposed method in field seismic data, the single shot data shown in Figure 13 are used for testing. This single shot data contains 180 traces, each trace has 500 sampling points, and the sampling interval is 0.005 s.

FIGURE 13

FIGURE 13. Field seismic data.

Figure 14 shows the denoising results and removed noise section of the proposed method and other methods, respectively. Observing Figure 14, the results show that the DMSSA-based denoising method will seriously leak the effective signal. SSWT-GoDec-based denoising approach cause waveform distortion and lateral discontinuities. DnCNN-based denoising methods lose effective signals. The proposed method can effectively suppress random noise and retain valid signals.

FIGURE 14

FIGURE 14. Field seismic data denoising results section. (A) DMSSA; (B) SSWT-GoDec; (C) DnCNN; (D) The proposed method; (E) Removed noise by DMSSA; (F) Removed noise by SSWT-GoDec; (G) Removed noise by DnCNN; (H) Removed noise by the proposed method.

Figure 15 shows the F-K spectrum of the field single shot seismic data and denoising results. The F-K spectrum amplitudes of DMSSA and DnCNN denoising results are low, again indicating that the effective signal will leak. The F-K spectrum of the SSWT-GoDec denoising results has a small amplitude in the low frequency part, which confirms the waveform distortion. The amplitude of the F-K spectrum of the denoising result of the proposed method is appropriate and focused. This result proves that the proposed method can effectively suppress random noise and retain important seismic signals.

FIGURE 15

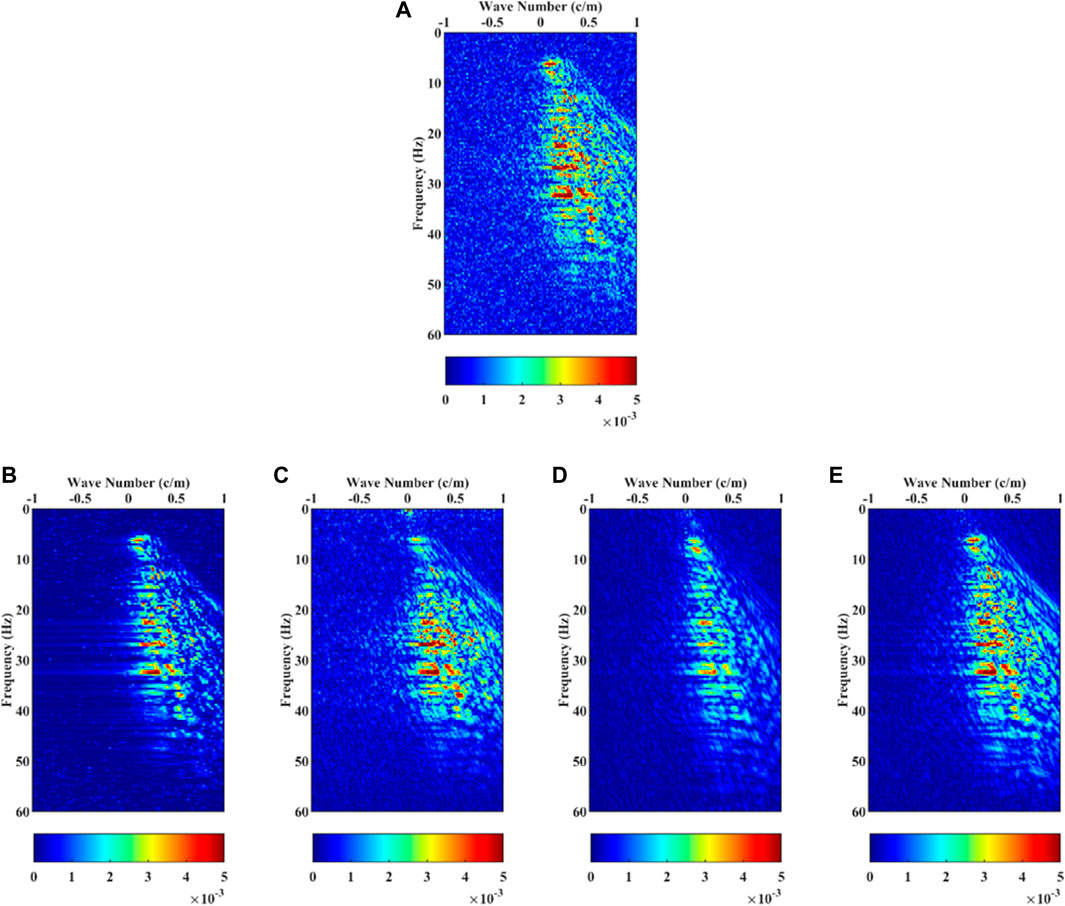
FIGURE 15. The F-K spectrum of the field seismic data. (A) Noisy data; (B) DMSSA; (C) SSWT-GoDec; (D) DnCNN; (E) The proposed method.

4 Conclusion

This paper proposes a denoising method for prestack seismic data using WINNet_ACSP. This method can effectively suppress random noise and prevent the leakage of important seismic information. In the forward pass of WINNet_ACSP, the first step uses a redundant transformation to split the seismic data to obtain frequency multi-scale approximate and detail parts. The second step utilizes a learnable neural network with ACSP to extract spatial features for the approximate or detail parts. The third step uses the sparse drive network to process the coefficients of the detail part. Finally, the denoised seismic data is reconstructed using the backward pass of WINNet_ACSP. The whole denoising process follows the principle of wavelet transformation. The combination of redundant transformation and ACSP can obtain richer multi-scale information. These multi-scale features can effectively suppress random noise and retain important seismic information. Transfer learning divides the training process into pre-training and post-training. The former is trained using natural images. The latter is trained using a small amount of seismic data. Synthetic and field seismic data are utilized to test the proposed method and other methods. The results show that the proposed method can effectively suppress random noise, improve the SNR of seismic data, and prevent the leakage of effective signals. In the future, we will make further improvements on this basis and conduct experiments on 3D prestack data.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LH proposes method and writes manuscript; HW proposes and participates in design research and reviews paper; XW participates in design research and reviews paper. All the authors approved the final version of the manuscript.

Funding

This work was supported by the Natural Science Foundation Project of Sichuan Province under Grant 22NSFSC3773.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aghayan, A., Jaiswal, P., and Siahkoohi, H. R. (2016). Seismic denoising using the redundant lifting scheme. Geophysics 81, V249–V260. doi:10.1190/geo2015-0601.1

CrossRef Full Text | Google Scholar

Anvari, R., Siahsar, M. a. N., Gholtashi, S., Kahoo, A. R., and Mohammadi, M. (2017). Seismic random noise attenuation using synchrosqueezed wavelet transform and low-rank signal matrix approximation. IEEE Trans. Geosci. Remote Sens. 55, 6574–6581. doi:10.1109/tgrs.2017.2730228

CrossRef Full Text | Google Scholar

Beckouche, S., and Ma, J. (2014). Simultaneous dictionary learning and denoising for seismic data. Geophysics 79, A27–A31. doi:10.1190/geo2013-0382.1

CrossRef Full Text | Google Scholar

Cai, H., He, Z., and Huang, D. (2011). Seismic data denoising based on mixed time-frequency methods. Appl. Geophys. 8, 319–327. doi:10.1007/s11770-011-0300-6

CrossRef Full Text | Google Scholar

Canales, L. L., and Lu, L. (1993). “3-D trace interpolation in the fxp domain,” in 63th Annual International Meeting (Tulsa, OK, United States: Society of Exploration Geophysicists), 1174–1176.

Google Scholar

Chen, K., and Sacchi, M. D. (2017). Robust f-x projection filtering for simultaneous random and erratic seismic noise attenuation. Geophys. Prospect. 65, 650–668. doi:10.1111/1365-2478.12429

CrossRef Full Text | Google Scholar

Chen, W., and Song, H. (2018). Automatic noise attenuation based on clustering and empirical wavelet transform. J. Appl. Geophys. 159, 649–665. doi:10.1016/j.jappgeo.2018.09.025

CrossRef Full Text | Google Scholar

Chen, Y., and Ma, J. (2014). Random noise attenuation by fx empirical-mode decomposition predictive filtering. Geophysics 79, V81–V91. doi:10.1190/geo2013-0080.1

CrossRef Full Text | Google Scholar

Chen, Y. (2017). Fast dictionary learning for noise attenuation of multidimensional seismic data. Geophys. J. Int. 209, 21–31. doi:10.1093/gji/ggw492

CrossRef Full Text | Google Scholar

Chen, Y., Zhou, Y., Chen, W., Zu, S., Huang, W., and Zhang, D. (2017). Empirical low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 55, 4696–4711. doi:10.1109/tgrs.2017.2698342

CrossRef Full Text | Google Scholar

Chen, W., Oboué, Y. a. S. I., and Chen, Y. (2023). Retrieving useful signals from highly corrupted erratic noise using robust residual dictionary learning. Geophysics 88, WA55–WA64. doi:10.1190/geo2022-0168.1

CrossRef Full Text | Google Scholar

Chollet, F. O. (2017). “Xception: Deep learning with depthwise separable convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition (IEEE), 1251–1258.

CrossRef Full Text | Google Scholar

Dong, X., Lin, J., Lu, S., Wang, H., and Li, Y. (2022). Multi-scale spatial attention network for seismic data denoising. IEEE Trans. Geosci. Remote Sens. 60, 212. doi:10.1109/TGRS.2022.3178212

CrossRef Full Text | Google Scholar

Feng, J., Liu, X., Li, X., Xu, W., and Liu, B. (2021). Low-rank tensor minimization method for seismic denoising based on variational mode decomposition. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2021.3100262

CrossRef Full Text | Google Scholar

Feng, Q., and Li, Y. (2021). Denoising deep learning network based on singular spectrum analysis—DAS seismic data denoising with multichannel SVDDCNN. IEEE Trans. Geosci. Remote Sens. 60, 1–11. doi:10.1109/tgrs.2021.3071189

CrossRef Full Text | Google Scholar

Gómez, J. L., and Velis, D. R. (2016). A simple method inspired by empirical mode decomposition for denoising seismic data. Geophysics 81, V403–V413. doi:10.1190/geo2015-0566.1

CrossRef Full Text | Google Scholar

Guo, S., Yan, Z., Zhang, K., Zuo, W., and Zhang, L. (2019). “Toward convolutional blind denoising of real photographs,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (IEEE), 1712–1722.

CrossRef Full Text | Google Scholar

Han, J., and Van Der Baan, M. (2015). Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding. Geophysics 80, KS69–KS80. doi:10.1190/geo2014-0423.1

CrossRef Full Text | Google Scholar

Huang, J., and Dragotti, P. L. (2022). WINNet: Wavelet-inspired invertible network for image denoising. IEEE Trans. Image Process. 31, 4377–4392. doi:10.1109/tip.2022.3184845

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, W. (2022). A two-step singular spectrum analysis method for robust low-rank approximation of seismic data. Geophysics 88, V9–V19. doi:10.1190/geo2021-0781.1

CrossRef Full Text | Google Scholar

Kesharwani, A., Aggarwal, V., Singh, S., Br, R., and Kumar, A. (2022). Marine seismic signal denoising using VMD with Hausdorff distance and wavelet transform. J. Def. Model. Simul. 19, 739–746. doi:10.1177/15485129211036044

CrossRef Full Text | Google Scholar

Kong, D., and Peng, Z. (2015). Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 12, 1024–1035. doi:10.1088/1742-2132/12/6/1024

CrossRef Full Text | Google Scholar

Kuruguntla, L., Dodda, V. C., and Elumalai, K. (2021). Study of parameters in dictionary learning method for seismic denoising. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/tgrs.2021.3107541

CrossRef Full Text | Google Scholar

Liang, X., Li, Y., and Zhang, C. (2018). Noise suppression for microseismic data by non-subsampled shearlet transform based on singular value decomposition. Geophys. Prospect. 66, 894–903. doi:10.1111/1365-2478.12576

CrossRef Full Text | Google Scholar

Liu, B., Fu, C., Ren, Y., Zhang, Q., Xu, X., and Chen, Y. (2020). Structural complexity-guided predictive filtering. Geophys. Prospect. 68, 1509–1522. doi:10.1111/1365-2478.12941

CrossRef Full Text | Google Scholar

Liu, Y., and Li, B. (2018). Streaming orthogonal prediction filter in the t-x domain for random noise attenuation. Geophysics 83, F41–F48. doi:10.1190/geo2017-0322.1

CrossRef Full Text | Google Scholar

Long, L., Wen, X., and Lin, Y. (2021). Denoising of seismic signals based on empirical mode decomposition-wavelet thresholding. J. Vib. Control 27, 311–322. doi:10.1177/1077546320926846

CrossRef Full Text | Google Scholar

Ma, J., Dai, Y., and Tan, Y.-P. (2019). Atrous convolutions spatial pyramid network for crowd counting and density estimation. Neurocomputing 350, 91–101. doi:10.1016/j.neucom.2019.03.065

CrossRef Full Text | Google Scholar

Pan, S. J., and Yang, Q. (2009). A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 22, 1345–1359. doi:10.1109/tkde.2009.191

CrossRef Full Text | Google Scholar

Richardson, A., and Feller, C. (2019). Seismic data denoising and deblending using deep learning. arXiv preprint arXiv:1907.01497.

Google Scholar

Saad, O. M., and Chen, Y. (2020). Deep denoising autoencoder for seismic random noise attenuation. Geophysics 85, V367–V376. doi:10.1190/geo2019-0468.1

CrossRef Full Text | Google Scholar

Sang, W., Yuan, S., Yong, X., Jiao, X., and Wang, S. (2020). DCNNs-based denoising with a novel data generation for multidimensional geological structures learning. IEEE Geosci. Remote Sens. Lett. 18, 1861–1865. doi:10.1109/lgrs.2020.3007819

CrossRef Full Text | Google Scholar

Sweldens, W. (1998). The lifting scheme: A construction of second generation wavelets. SIAM J. Math. Anal. 29, 511–546. doi:10.1137/s0036141095289051

CrossRef Full Text | Google Scholar

Wang, C., Zhu, Z., Gu, H., Wu, X., and Liu, S. (2018). Hankel low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 57, 561–573. doi:10.1109/tgrs.2018.2858545

CrossRef Full Text | Google Scholar

Wang, H., Chen, W., Huang, W., Zu, S., Liu, X., Yang, L., et al. (2021). Nonstationary predictive filtering for seismic random noise suppression—a tutorial. Geophysics 86, W21–W30. doi:10.1190/geo2020-0368.1

CrossRef Full Text | Google Scholar

Wang, X., and Ma, J. (2019). Adaptive dictionary learning for blind seismic data denoising. IEEE Geosci. Remote Sens. Lett. 17, 1273–1277. doi:10.1109/lgrs.2019.2941025

CrossRef Full Text | Google Scholar

Wu, G., Liu, G., Wang, J., and Fan, P. (2022). Seismic random noise denoising using mini-batch multivariate variational mode decomposition. Comput. Intell. Neurosci. 2022, 2132732. doi:10.1155/2022/2132732

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, X., Ma, X., Long, H., Ming, Y., and Sun, S. (2022). Curvelet transform-based denoising of resonance interference induced by electrical poles in seismic exploration. Geophys. Geochem. Explor. 46, 474–481. doi:10.11720/wtyht.2022.2411

CrossRef Full Text | Google Scholar

Yang, L., Wang, S., Chen, X., Saad, O. M., Chen, W., Oboué, Y. a. S. I., et al. (2021). Unsupervised 3-D random noise attenuation using deep skip autoencoder. IEEE Trans. Geosci. Remote Sens. 60, 1–16. doi:10.1109/tgrs.2021.3100455

CrossRef Full Text | Google Scholar

Yu, S., Ma, J., and Wang, W. (2019). Deep learning for denoising. Geophysics 84, V333–V350. doi:10.1190/geo2018-0668.1

CrossRef Full Text | Google Scholar

Zhang, K., Zuo, W., and Zhang, L. (2018). FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 27, 4608–4622. doi:10.1109/tip.2018.2839891

CrossRef Full Text | Google Scholar

Zhang, Q., Chen, Y., Zhang, F., and Chen, Y. (2022). Improving receiver function imaging with high-resolution Radon transform. Geophys. J. Int. 230, 1292–1304. doi:10.1093/gji/ggac116

CrossRef Full Text | Google Scholar

Zhang, Z., and Hong, W.-C. (2019). Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dyn. 98, 1107–1136. doi:10.1007/s11071-019-05252-7

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Dong, X., and Wu, N. (2021). Seismic random noise attenuation by applying multiscale denoising convolutional neural network. IEEE Trans. Geosci. Remote Sens. 60, 1–13. doi:10.1109/tgrs.2021.3095922

CrossRef Full Text | Google Scholar

Zwartjes, P., and Gisolf, A. (2007). Fourier reconstruction with sparse inversion. Geophys. Prospect. 55, 199–221. doi:10.1111/j.1365-2478.2006.00580.x

CrossRef Full Text | Google Scholar