- Department of Geology and Geophysics, Woods Hole Oceanographic Institution, Woods Hole, MA, United States
Prior to intrusion, magma migrates through the crustal plumbing system that likely contains layers or columns of crystal mush. To better understand the behavior of the crustal magmatic system during magmatic unrest, it is important to examine the process of melt migration within the crystal mush and the associated evolution in pressure and temperature. In this study I use an analytical model to explore the characteristics of transport of melt, pressure, and heat through an idealized crystal mush layer/column under uniaxial strain condition. The model invokes a thermo-poro-viscoelastic rheology and uses a frequency-domain method to explore two scenarios of magmatic unrest: harmonic perturbation of fluid pressure, and step-rise in fluid pressure at a source location. Several factors influence the transport of melt, pressure and heat, including the thermal-mechanical coupling arising from the mush rheology, the advection of heat by melt flows, the competition between thermal diffusivity and poroelastic diffusivity, and the viscoelastic relaxation of the crystalline framework. One key finding is the development of transport asymmetry: when a background temperature gradient exists, the transport properties become different for propagation along the background thermal gradient and propagation against the background thermal gradient. Analysis on an endmember case shows that the transport asymmetry is associated to the competition between the diffusion and advection of pore pressure, which determines a Peclet number that depends on the temperature difference across the mush and the thermal expansion coefficients. Because the temperature in magma mushes in the crust likely increase with depth, the observed propagation asymmetry suggests some intrinsic difference between a bottom-up vs. a top-down triggering mechanism for magmatic unrest. The results from this study highlight the importance for further exploration for a more complete description of the transport properties in the crystal mush.
1 Background and introduction
Crystal mush is an important component in the current paradigm of crustal igneous architecture, and plays important roles in the mechanical, thermal, and chemical evolution of the crustal magmatic system (Gelman et al., 2013; Bachmann and Huber, 2016; Barboni et al., 2016; Cashman et al., 2017; Karakas et al., 2017; Sparks and Cashman, 2017; Szymanowski et al., 2017; Jackson et al., 2018; Singer et al., 2018; Edmonds et al., 2019; Sparks et al., 2019; Caricchi et al., 2021; Weinberg et al., 2021). Some deformation models suggest that the crystal mush in an individual magmatic reservoir could noticeably influence the reservoir’s response to magmatic events and the resulting surface deformations (Liao et al., 2021; Alshembari et al., 2022; Mullet and Segall, 2022). A recent numerical study by Mullet and Segall (2022) extended the concept of mushy magmatic reservoir to a mush column containing a crystal-poor fluid region, deriving more implications on volcano geodesy. The vertically extensive crystal column explored in Mullet and Segall (2022) has been implied by geophysical observations. For example, under Axial Seamount, seismic reflections suggested the existence of mush layers between melt rich lenses, and geodetic observations led to hypothesis that fluid transport in the mush layers could be responsible for the features in post-eruption seafloor deformation data (Carbotte et al., 2020; Chadwick Jr. et al., 2022). One key feature of a vertically extensive crystal mush column/layer is that it allows for the transport of melt, pressure and heat in the crust, even in the absence of dikes and channels. The transport properties of a mush column could lead to several consequences: For example, melt-rich reservoirs/lenses separated by a crystal mush could become hydraulically connected; if a mush column spans across large temperature difference, convective heat transfer by melt transport could become significant; local perturbations (e.g., change in fluid pressure) could be transmitted along a crystal mush column either upward or downward, allowing for both bottom-up and top-down triggering of magmatic unrest. The physical processes involved in the above-mentioned scenarios could depend on intrinsic or external factors, such as the local tectonic setting, the existence of boundaries and barriers, the physical properties and rheologies of the mush, and the time and spatial scale of the magmatic event.
Here, I explore the transport properties of crystal mush layer/column that result from the intrinsic mush rheology and its physical properties. Following earlier studies, I consider a crystal mush as a continuous system consisting of a contiguous solid phase and a viscous fluid phase (melt) residing in the interstitial pore spaces of the crystalline framework. The migration of melt and transport of pressure and heat in the mush layer occur while retaining the structural integrity of the crystalline framework (i.e., no disaggregation or re-melting). Following Liao (2022), I assume a thermo-poro-visco-elastic mush rheology that describes the deformation, pressurization, melt migration, and temperature evolution in the mush. The quantitative framework centering around the chosen rheology incorporates several physical processes, including the coupling between pore fluid pressurization and solid deformation, the viscoelastic relaxation of the crystalline framework under deviatoric stresses, the generation of thermal stress and pore pressure due to thermal expansion/contraction of fluid and solid, the diffusion of heat, and the advection of heat by porous flows. These physical processes have been studied to limited extent in physical models on mushy magmatic reservoirs, which are now examined in the new context of vertically extensive crystal mush column/layer (Liao et al., 2018; 2021; Liao, 2022).
An endmember of the thermo-poro-viscoelastic rheology is poroelasticity, which has been a popular choice for modeling mushy magmatic reservoirs (Gudmundsson, 2015; Liao et al., 2018; Alshembari et al., 2022; Mullet and Segall, 2022). The concept of poroelastic layer/column has been widely adopted in models on hydrothermal circulation occurring in the water-saturated rock/sediment below the seafloor, which provide a starting point for us to explore the transport properties of crystal mush (Jupp and Schultz, 2004; Crone and Wilcock, 2005; Barreyre et al., 2014; 2022). Poroelastic medium is diffusive, resulting in decaying of perturbations (pressure and fluid velocity) away from their sources (Segall, 2010; Cheng, 2016). This diffusive nature is conveniently represented by a frequency-dependent “skin depth,” which is an e-folding decay length of oscillatory signals (Turcotte and Schubert, 2002). In the context of sub-seafloor hydrothermal systems, the skin depth has been used for estimating the depth of non-negligible fluid transport in response to tidal loading on the seafloor (Jupp and Schultz, 2004). In my analysis, I adopt a similar frequency-domain perspective and begin the exploration by examining the transport of melt, pressure and heat in response to harmonic fluid pressure perturbation at a source location. I then explore one example of broad-band perturbation where fluid pressure at the source evolves in time as a step function. One key finding from our analysis is the non-negligible role of background thermal gradient along the mush column, which could be advected by porous melt flows and result in asymmetric transport of melt, pressure and heat (top-down propagation vs. bottom-up propagation). Section 3.1.1 shows a simplified case of thermo-poro-elasticity, which is used to elucidate the root cause for the observed asymmetric transport of harmonic magmatic signals; Section 3.1.2 shows the effects of additional factors (viscoelastic relaxation and thermal diffusion) on the transport properties; Section 3.2 explores the case of step-rise pressure perturbation and show the effects of viscoelastic relaxation and non-vanishing background temperature gradient. The quantitative approaches are briefly summarized in the next section, and detailed in the Supplementary Appendix S1.
2 Model and approach
Figure 1 shows the geometry of the model. A crystal mush column/layer is modeled as a thermo-poro-viscoelastic material with uniform porosity, permeability, viscosity, and elastic moduli. The model assumes an uniaxial strain condition, where the displacements and fluid velocities only have vertical components. I use the term “magmatic signals” to refer to anomalies in melt content, pore pressure, and temperature that deviate from their background values. Magmatic signals are generated at the source location z = 0 and propagate away from the source into z → ±∞. To elucidate the intrinsic transport characteristics of the crystal mush resulting from its physical properties and rheologies, I do not model the processes that generate magamtic signals, and assume no boundaries in the domain. The material properties of the mush and melts are assumed to be steady in time, hence thermal and chemical processes which could alter these properties (such as crystallinity) are neglected.

FIGURE 1. Schematic of the 1D crystal mush column. The direction of
In the absence of perturbations, the crystal mush column is assumed to be in a state of equilibrium with steady state temperature profile, no fluid flows, and balanced forces. This state is considered the background state signifying the absence of magmatic unrest. The background temperature profile is linear and has a zero or negative temperature gradient for our choice of the direction for
The quantitative framework is detailed in the Supplementary Appendix S1 and briefly summarized here. The thermal-mechanical couplings stated above are reflected by the constitutive relations and evolution equations for melt velocity and temperature, which are similar to those in Liao (2022). The strain-stress relations are (Biot, 1941; Cheng, 2016).
Where the overhead dot ⋅ denotes partial derivative in time, I denotes identity matrix. σij and ϵij are stress and strain tensors of the ensemble material, ϵ is the volumetric strain, P is the pore pressure, T is the temperature variation from its reference value. ζ is the variation of fluid content, defined as the increment of pore fluid volume per un-deformed volume of the mush. μ and η are the shear modulus and shear viscosity of the crystalline framework, α is the Biot coefficient of poroelasticity, and ϕ is the porosity in the mush. βs is the volumetric thermal expansion coefficient for the solid crystals. The thermal expansion coefficient of the gas-rich pore magma βpore encodes the content of exsolved gas, which is assumed to be in the form of disconnected bubbles [see Supplementary Appendix S1 and (Liao, 2022)].
The equilibrium condition, Darcy’s law, mass conservation, and energy conservation are
Where
Following the linear thermo-poro-viscoelastic constitutive relations, Darcy’s law, mass conservation, energy conservation and stress equilibrium condition similar to (Liao, 2022), I derive the evolution equations for pore pressure, fluid velocity, and temperature in the mush column. The perturbations are considered to be small, allowing the evolution equations to be linearized (Kaviany, 2012). The linear equations are then analyzed in frequency space where all quantities are represented by their Fourier transforms. A set of boundary conditions (pressure and/or temperature anomalies at the source, fluid-loading condition at z = 0 and implicit conditions at z = ±∞) allows for the full frequency-domain solutions (i.e., Fourier transforms) for pressure, velocity, and temperature at any given locations. Our frequency-domain approach shares some similarities to approaches based on Laplace transform—a method widely used for studying magma chamber deformation (Dragoni and Magnanensi, 1989; Segall, 2016; Liao et al., 2018; 2021). For the 1D crystal mush problem, a Fourier-transform-based approach has some advantages: first, there are evidence suggesting that some magmatic signals are cyclic/periodic in nature, hence would be easily represented by a superposition of one or multiple harmonic functions (Murphy et al., 2000; Rout et al., 2021); second, a frequency-domain approach could potentially predict characteristics of frequency spectra for key quantities, hence allowing observational data (time series) to be examined under new lenses. Overall, Fourier transform and Laplace transform do not contradict but complement each other, and have been shown to have converging results (Liao et al., 2023).
Two types of perturbations that generate melt migration are explored: single-frequency perturbations generated by harmonic oscillations at z = 0, and broadband perturbations generated by a step increase in fluid pressure at z = 0. In the case of harmonic perturbations, all quantities (velocity, pressure, temperature) are periodic oscillations in time, and the transport properties are characterized by the profiles of oscillation amplitudes and phase lags for −∞ < z < ∞. In the case of broad-band perturbations, time-dependent solutions at specific locations for 0 < z < ∞ are obtained from inverse Fourier transform of the frequency-domain solutions.
3 Findings
3.1 Transport properties of an unbound mush column for harmonic perturbations
In this section, both the top-down and bottom-up transport of harmonic perturbations are shown. The perturbation signals are generated at z = 0 and represented by sinusoidal functions, for example, in pressure
3.1.1 The nature of propagation asymmetry arising from thermal-mechanical coupling
In this Section 1 examine how thermal-mechanical coupling in the crystal mush gives rise to asymmetric propagation (bottom-up vs. top-down) of magmatic signals. The nature of propagation asymmetry is elucidated in a simplified end-member case where there is neither thermal diffusion nor viscoelastic relaxation. This scenario is likely for rapid transport of porous melt occurring on timescales much shorter than thermal diffusion and viscoelastic relaxation. The thermal-mechanical coupling is reflected in two aspects: first, with temperature change, both crystals and pore fluids may expand or contract, resulting in thermal stress or pressurization; second, the background thermal profile is advected by the porous melt flows.
The constrains above lead to the evolution equation for pore pressure
where c is the poroelastic diffusivity, βc is the effective thermal expansion coefficient (see Supplementary Table S1), and DT is the magnitude of the background thermal gradient in the mush column. The constant coefficient γ (see Supplementary Table S1) is determined by the micromechanical properties in the mush. The last term on the left-hand-side of Eq. 3 indicates the extent of thermal-mechanical coupling and would vanish if there is no thermal expansion or no thermal advection (i.e., zero background thermal gradient).
Assuming harmonic oscillations, I solve the simplified evolution Eq. 3 together with two constraints: first, fluid pressure is continuous and the column is loaded by the overpressure at the source z = 0; second, the mush column is not bounded, hence any perturbation signal far from the source (z → ±∞) must vanish. For the given source perturbation P(0) = Poeiωt and the above mentioned boundary conditions, the solution for Eq. 3 is a superposition of terms in the form of eiωt+kz (referred to as sub-wave). The wavenumber k is determined by a dispersion relation and the amplitude for each sub-wave is determined by the boundary conditions. The dispersion relation resulting from the evolution equation is
where λP is the poroelastic skin depth, the dimensionless parameter Δ = βc|DT|λP is the background thermal gradient scaled by
When Δ = 0, (4) recovers the diffusive endmember with solution kPλP = ±(1 + i), and the decay length 1/Re(kp) = λP for both bottom-up and top-down transport (Turcotte and Schubert, 2002; Segall, 2010; Cheng, 2016). When Δ ≠ 0, the decay length 1/Re(k) deviates from λP and becomes different for bottom-up and top-down propagations: the decay length for bottom-up propagations becomes larger than the skin depth, indicating slower decay; The decay length for top-down propagation becomes smaller than the skin depth, indicating faster decay. With increasing Δ, bottom-up transport is further promoted with longer decay length and top-down transport is further suppressed with shorter decay length (Figure 2A).
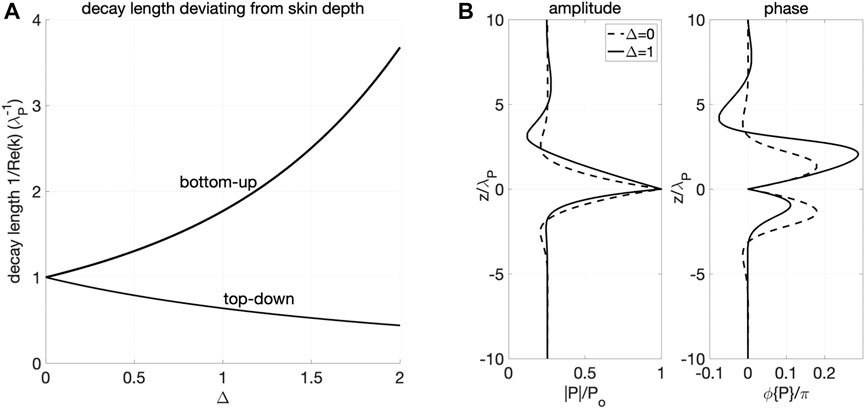
FIGURE 2. (A) Decay lengths associated to dispersion relation (4) as functions of Δ. For any frequency there are two wavenumbers k, with decay length 1/Re(k). The decay lengths are normalized by the poroelastic skin depth
The actual solution for the magmatic signals, such as pressure P(z, t), can be expressed using its Fourier transform
The frequency-domain solution Eq. 5 suggests a time-domain solution, that is a superposition of one decaying traveling wave (first term on the right-hand-side) and one standing oscillation (γeiωt): the traveling wave contributes to melt transport, and the standing oscillation elastically loads the whole column uniformly. When Δ = 0, the solution
The solutions suggest that the root for the asymmetric propagation and the modification of decay lengths lies in the thermal-mechanical coupling (i.e., Δ) that demands both thermal advection and thermal expansion. I postulate the following scenario where pressure increases at the source and expels melt: in the upper domain, melt migration (from the relatively warmer source) increases the local temperature and provides additional pressurization, hence pressure decays slower; for the lower domain, melt migration (from the relatively colder source) reduces local temperature and pressure, hence pressure decays faster. Similar argument can be made when the source depressurizes and sucks melt in: melt migration in the upper domain promotes pressure reduction and allows the negative pressure to persist for longer distance; in the lower domain, the pressure reduction is discounted by thermal expansion and pressurization, hence the negative pressure persists for shorter distance. In both scenarios, the propagation of melt in the upper domain (either towards or away from the source) allows for the pressure anomaly (either positive or negative) to persist for longer distance, hence the observation of longer decay length.
3.1.2 Transport of harmonic perturbations in thermo-poro-viscoelastic mush
The general thermo-poro-viscoelastic mush rheology examined in this section expands the simplified case in Section 3.1.1 by incorporating thermal diffusion (i.e., κT ≠ 0) and (Maxwell) viscoelastic relaxation of the crystalline framework. While the dynamics for the simplified case in Section 3.1.1 is governed by one dimensionless number Δ, the transport of harmonic perturbations in the fully thermo-poro-viscoelastic mush (with non-vanishing thermal diffusivity) is governed by three dimensionless numbers: Δ, R, and De. The ratio R = c/κT reflects the relative rapidness of thermal diffusion. The Deborah number De = ωη/μ reflects the relative rapidness of relaxation (η and μ are the viscosity and instantaneous shear modulus of the crystaline framework). It is worth noting that, although the quantities in out problem have only one degree of freedom and deformation only occurs on the vertical direction, the stress components under the uniaxial-strain condition do not vanish on the horizontal plane, hence the deviatoric stress tensor for the 1D column is not always zero. The non-vanishing deviatoric stress components prompt the viscoelastic creeping of the crystaline matrix, further compressing the pore spaces and increasing the pore pressure. In frequency domain, the quantitative manifestation of the viscoelastic effect is a complex rigidity
For the thermo-poroelastic case (De = R = ∞) examined in Section 3.1.1, the dispersion relation for the wave-form solutions is (4), which predicts two wavenumbers for each frequency. Assuming finite values for De and R, the dispersion relation becomes (see Supplementary Appendix S1 for derivation)
where λP is the poroelastic skin depth,
With non-vanishing thermal diffusion, the solutions for (6) are named k1, k2, k3, and k4, in which k2 and k3 deviate from kP (the poroelastic endmembers with skin depth λP), and k1, k4 deviate from kT (the thermal diffusion endmember). The intrinsic boundary conditions for unbound mush further determine that the sub-waves with wavenumber k1 and k2 exist (i.e., having non-zero amplitudes) in the lower (z < 0) domain, and that the sub-waves with wavenumber k3 and k4 exist in the upper (z > 0) domain. Based on the above observations I therefore refer to the sub-wave
Figure 3 shows examples of the four submodes
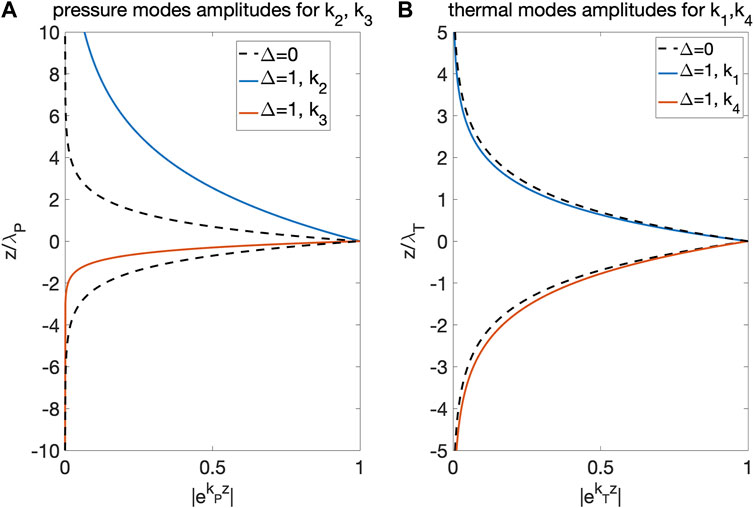
FIGURE 3. Amplitudes of four single submodes
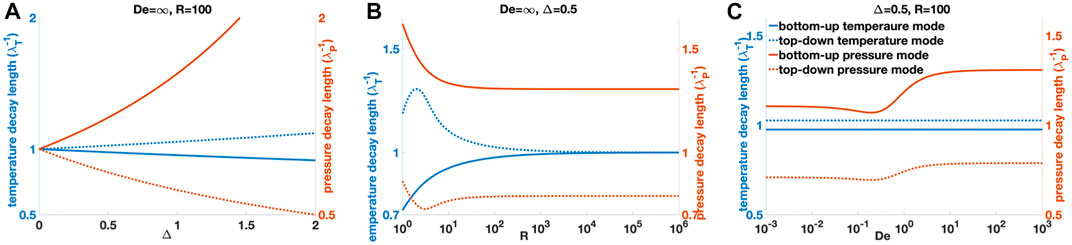
FIGURE 4. Decay length 1/|Re(k)| for all solutions for (6) shown as functions of dimensionless parameters. The decay lengths associated with thermal modes are normalized by the thermal skin depth (left y-axis, blue curves). The decay lengths associated with pressure modes are normalized by the poroelastic skin depth (right y-axis, red curves). Solid lines are decay lengths for bottom-up sub-waves (i.e., against the background thermal gradient); dash lines are decay lengths for top-down sub-waves (i.e., along the background thermal gradient). (A) Shows the decay lengths as functions of Δ which reflects the extent of thermal-mechanical coupling; (B) shows the decay lengths as functions of R, the ratio between poroelastic diffusivity and thermal diffusivity; (C) shows the decay lengths as functions of Deborah number De. When R = ∞, De = ∞, Δ = 0, the system recovers pressure diffusion endmembers with no viscoelastic relaxation, no thermal diffusion, and no thermo-mechanical coupling.
The frequency-domain solutions for pressure, temperature, and melt velocity are expressed as
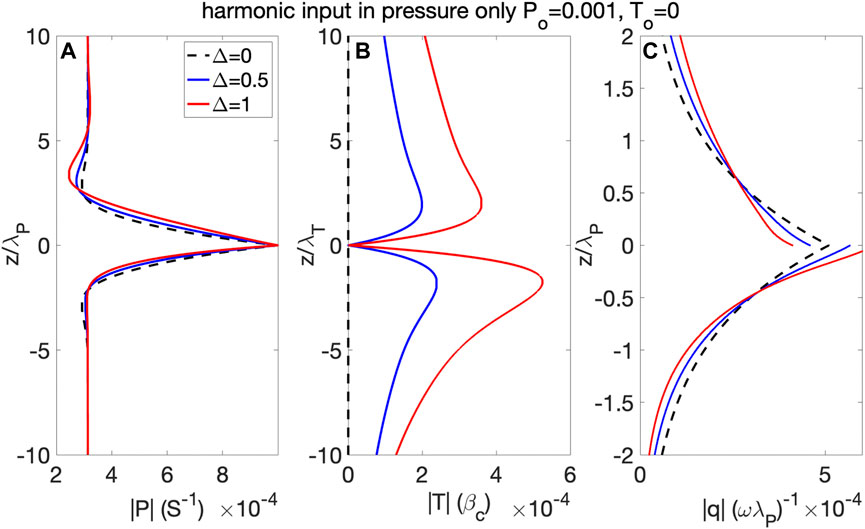
FIGURE 5. Examples of pressure, temperature and velocity oscillation amplitudes
3.2 Propagation of pressure and melt following a step rise in pressure
The frequency-domain approach outlined above can be applied to broad-band perturbations that are not harmonic in time. Two assumptions need to be met for this approximation to be appropriate: first, the perturbations at the source can be represented by their Fourier transforms (continuous and integrable in time); second, the advection of first-order temperature deviation is negligible compared to the advection of the background temperature profile (i.e., linearization of thermal advection is appropriate). These two assumptions preclude some scenarios, such as sporadic magma inputs that are highly discontinuous in time, or large thermal anomalies that overwhelm the background thermal profile. For scenarios suitable for my approach, the perturbations are represented in frequency domain by their Fourier transforms, where each frequency ω generates two wavenumbers in each domain (z > 0 or z < 0) with their complex amplitudes determined by the boundary conditions.
While the method (shown in Supplementary Appendix S1) is generally applicable to source perturbations in both pressure and temperature, or as more complex time-dependent functions, here I consider the simplest broad-band example where pressure is suddenly raised to a constant, positive value while temperature remains unchanged at the source. The frequency-domain method is realized numerically with fast Fourier transform. To ensure that the magmatic signals are integrable, the pressure step increase is represented by a square pulse time-sequence. The pulse has a sufficiently long duration, such that a new steady state develops prior to the end of the pulse. Results are obtained over the time period near the onset of source pressurization and in the upper domain (i.e., only bottom-up transport). The individual effects of viscoelastic relaxation and background thermal gradient on the evolution in pressure and melt velocity are examined.
The detailed derivation for the analytical and numerical approach are shown in Supplementary Appendix S1. The system of equations and dispersion relations are re-derived in dimensionless space, ensuring consistent scaling among all frequencies (see Supplementary Appendix S1). Definition for Δ is given by a general characteristic length (instead of the skin depth for one single frequency). A discrete numerical Fourier transform is applied to the pressure perturbation time sequence, where the complex amplitude for each frequency at the source is then used as a boundary condition in frequency domain. The complex amplitudes for pressure, temperature and velocity at any given location are generated based on the analytical solutions. The resulting frequency-domain solutions are then inverted by a numerical discrete Inverse Fourier Transform code to produce time sequence of the outputs. This frequency-domain approach has been applied in a couple of recent works and shown to be efficient in computational time and a powerful alternative method for time-domain approach (Rucker et al., 2022; Liao et al., 2023).
Figure 6 shows the examples of pressure and melt velocity as functions of time measured at multiple locations in the upper z > 0 domain for a case of isothermal poroelastic mush column (no background thermal gradient and no viscoelastic relaxation). A fluid loading boundary condition is assumed at the source, so the increase in source pressure at time t = 0 instantaneously loads the mush column elastically, resulting in sudden increase of pore pressure at t = 0, that is uniform along the column (Figure 6A). At t > 0, the gradient in pore pressure drives the melt upwards into the mush column and pore pressure further increases at all locations. In comparison, melt transport (reflected by the local fluid velocity) is non-monotonous. For an arbitrary location zo, the local fluid velocity at zo first increases with the build-up of fluid pressure from below zo following the onset of the source pressure increase. With the transport of melt, the pressure above zo increases, which reduces the local fluid pressure gradient hence decreasing melt velocity. The arrival time of the maximum fluid velocity is delayed with increasing distance from the source (Figure 6B).
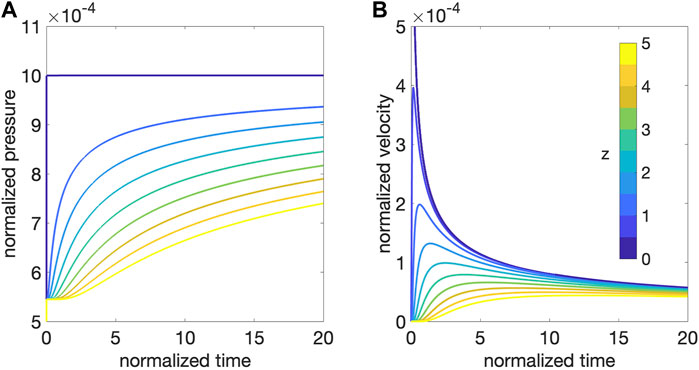
FIGURE 6. Example of pressure (A) and fluid velocity (B) evolution with time at multiple vertical locations obtained from the frequency-domain method. Colored lines show different vertical location (normalized by an arbitrary length scale [l]). Time is normalized by the poroelastic diffusion time [t] = [l]2/c. Pressure in (A) is normalized by the poroelastic storage coefficient S−1; and Darcian velocity in (B) is normalized by the velocity scale [l]/[t]. At the source location z = 0, pressure is elevated at t = 0 and instantaneously transmits to the column via a fluid loading boundary condition. The transport of melt, pressure, and heat are driven by poroelastic diffusion, where there is no background temperature gradient and no viscoelastic relaxation. Other parameters used for (B) include melt bulk modulus Kl = 1 GPa, shear modulus μ = 1 GPa, solid bulk modulus Ks = 10 GPa, porosity ϕ = 0.3, and gas volume fraction in pore melt χ = 0.
The effects of viscoelastic relaxation and thermal coupling on pressure evolution and melt velocity measured at a specific location are shown in Figure 7. A mush column with viscoelastic relaxation (with a relaxation time similar to the poroelastic diffusion time) has faster pressure increase (Figure 7A) and earlier arrival of maximum fluid velocity with reduced magnitude (Figure 7B). The more rapid pressurization in the presence of viscoelastic relaxation is likely due to the additional compression of pore spaces. Because the column is assumed to have uniaxial strain (i.e., no displacement in the horizontal direction), horizontal stress components are non-zero, resulting in non-vanishing deviatoric stress. The deviatoric stress drives the crystalline matrix to deform along the vertical direction, compressing pore spaces. The reduction of melt velocity is consistent with the transport features seen in the case of harmonic perturbation, where viscoelastic relaxation reduces decay length for pressure modes (Figure 4C). The existence of thermal gradient (i.e., transport of fluid from warmer to colder area) causes higher pressure and larger maximum velocity, which are likely due to the additional thermal expansion and pressurization associated to the advection of hotter melt (Figure 7). The thermo-mechanical coupling also causes reduction of fluid velocity in the long term, which indicates a more rapid elimination of local pressure gradient. I postulate that the rapid decrease of pressure gradient is achieved by more efficient pressurization of the whole mush column as shown in Figure 8 and associated movie (Supplementary Material): In the absence of upper boundary (as in the examined case), a pressurization front propagates upwards along the column; below the pressure front, a quasi-steady state develops in the mush segment close to the source, with a nearly linear pressure profile that transport melt at a near-constant velocity. The length of the quasi-static segment increases with time, and along the segment, the (quasi-uniform) pressure gradient is determined by the pressure at the top of the segment and the length of the segment (because at the base of the column the source pressure is held constant). The thermal-mechanical coupling causes faster increase of pressure at the propagation front, and a lengthened quasi-steady segment, both reducing the local pressure gradient close to the source, leading to reduced melt velocity observed in Figure 7B.
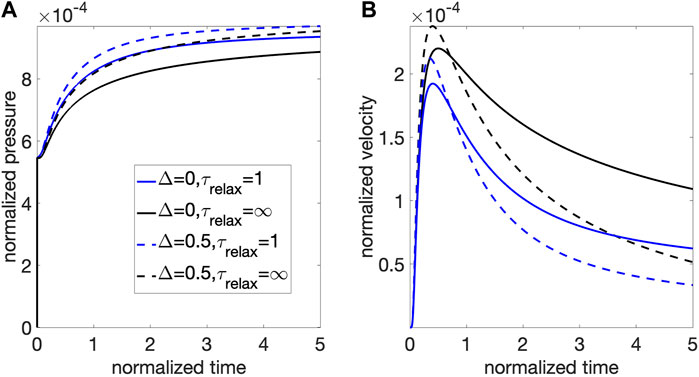
FIGURE 7. Pressure (A) and melt velocity (B) at z = 1 (normalized) shown as functions of time following a step increase in fluid pressure at z = 0. Solid lines correspond to a mush column with no background temperature gradient, dash lines correspond to a mush column with a negative background temperature gradient (hotter at the source). Black lines correspond to a mush column with no viscous relaxation (i.e., infinitely long relaxation time); blue lines correspond to a mush column with viscous relaxation time τrelax = [t] (the poroelastic diffusion time). Other parameters used for (B) include melt bulk modulus Kl = 1 GPa, shear modulus μ = 1 GPa, solid bulk modulus Ks = 10 GPa, porosity ϕ = 0.3, and gas volume fraction in pore melt χ = 0.
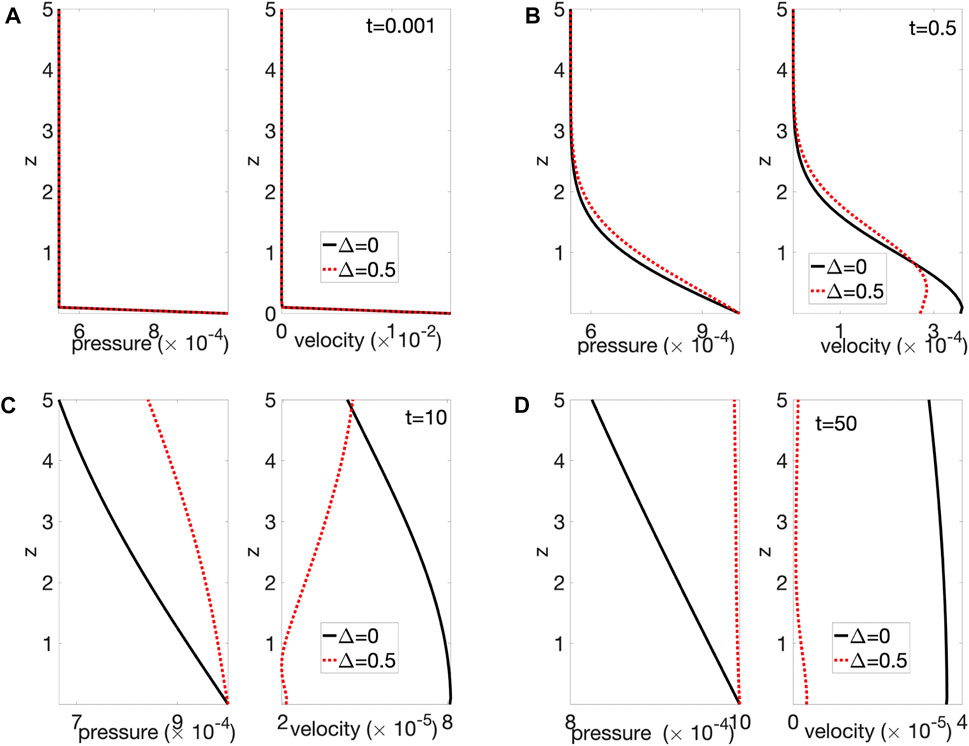
FIGURE 8. Distribution of pore pressure and melt velocity along the mush column at (A) t = 0.001, (B) t = 0.5, (C) t = 10, and (D) t = 50. In each sub-figure, left panel shows to pressure profile, right panel shows melt velocity profile. At time t = 0, the mush column is subjected to a step rise in fluid pressure at the source z = 0. Black solid lines correspond to a poroelastic mush column with Δ = 0; red dash lines corresdpond to a thermo-poro-elastic mush with Δ = 0.5. With the proceeding of time, pressure increases faster for the case with Δ = 0.5, resulting in reduction in pressure gradient and decrease of fluid velocity. Other parameters used for (B) include melt bulk modulus Kl = 1 GPa, shear modulus μ = 1 GPa, solid bulk modulus Ks = 10 GPa, porosity ϕ = 0.3, and gas volume fraction in pore melt χ = 0.
4 Summary and discussions
In this study, I present a model for examining the transport properties of an unbound thermo-poro-viscoelastic mush column under uniaxial strain. The model is based on first principles in continuum mechanics and employs a frequency-domain approach. The mush column is subjected to unrest triggered by harmonic pressure perturbations or a step-rise pressure increase at the source region (z = 0). The fluid pressure anomalies transport melt, pressure and heat from bottom up (from z = 0 to z → ∞) or top down (from z = 0 to z → −∞). If the mush column has a linear background thermal gradient thermal-mechanical coupling (thermal stress and advection of heat), the bottom-up transport and top-down transport become asymmetric, distinguishing a thermo-poro-viscoelastic mush column from a poroelastic column. Our preliminary results suggest that the coexisting mechanical and thermal processes could promote a preferred transport direction for melt, pressure, and heat. Some assumptions are made to simplify the problem and to elucidate the intrinsic transport characteristics resulting from mush rheology. Because of these simplifications, our results are best interpreted as instrinsic properties of mush, rather than applications on actual volcanic systems.
A key finding of the model is the development of transport asymmetry in the mush column, which distinguishes it from a purely diffusive endmember. To understand the root of this observation, I use a simplified case where viscoelastic relaxation and thermal diffusion are infinitely slow. This simplified case sheds light on the nature of the role of thermal-mechanical coupling on the propagation of magmatic signals: together, the background thermal gradient, fluid advection, and thermal expansion contribute to an extra term in the otherwise diffusive governing equation for pressure (e.g., Eq. 3). The pressure and melt velocity evolution hence are driven by diffusion-advection, instead of diffusion alone. In the equation of evolution (3), a steady and virtual “flow field” can be identified, which advects the pressure anomalies at a constant speed Uadv = cβcDT. The time scale associated to this advection along a column with length L is L/Uadv = L/cβcDT where c, βc and DT are the poroelastic diffusivity, effective thermal expansion coefficient, and magnitude of background temperature gradient. The timescale for pressure diffusion is L2/c. The ratio between the advection timescale and diffusion timescale, a Peclet number, is therefore Pe = 1/LβcDT. This Peclet number is identical to the dimensionless background temperature gradient (scaled by L and βc). For a linear temperature profile DT = |δT|/L, where δT is the temperature difference between the two ends of a segment along the mush column with length L. The Peclet number therefore can also be written as
The extent of transport asymmetry observed in the model depends on the physical parameters and the timescale of the forcing associated to the magmatic perturbation. Following previous studies by assuming permeability κ ∈ [10–11, 10–8]m2, magma viscocity ηm = 100 Pa.s, and elastic moduli of the order of GPa, the poroelastic diffusivity c ∈ [3 × 10−5, 0.2]m2/s. For magmatic perturbations with characteristic time from a day to a year, the skin depth ranges from 0.5 m to 1.3 km, and the decay length difference between bottom-up and top-down transport ranges from several cm to hundreds of meters. For longer period forcing, higher permeability, lower melt viscosity, and large temperature gradient (i.e., towards large skin depth), the separation of transport distance is most significant. It is worth noting that, while the transport asymmetry found in this study is an intrinsic characteristic of a mush column with thermal-mechanical coupling, it is unclear if it can manifest in actual observations, as the several neglected factors in our model, such as boundaries, could play more important roles in determine the transport of magmatic signals. It is also worth noting that the transport asymmetry and associated frequency-dependent length scales are results from (thermo)poro(visco)elastic rheology, which is one possible choice of rheology for multi-phase materials; other continuous or discrete description of multiphase rheology, which may be suitable for other geological settings, may lead to different manifestation of thermal-mechanical couplings (Liao et al., 2021).
There are several aspects in the model that request future implementation before it can be applied to more realistic magmatic systems at different volcanoes. The current model assumes an unbound mush column to single out the transport properties independent from boundary effects. This assumption naturally introduces a set of intrinsic boundary conditions (at infinities) that allow only decaying waves in the direction of propagation. In the presence of boundaries, such as fluid lenses, mush-rock interfaces, permeability barriers and discontinuities, the intrinsic boundary conditions are no longer appropriate. In this scenario, the transport of melt, pressure and heat results from the combinations of growing waves and decaying waves, with amplitudes determined by explicit boundary conditions prescribed at each interface. For a mush column in which multiple interfaces reside (such as for Axial Seamount), each segment between adjacent melt lenses needs to be treated with such an approach. For broadband perturbation, an example of pressure step increase is used, simplifying the source mechanism. Some specific examples involving more realistic/complex source mechanisms, such as injection of magma with finite volume and heat, can be applied using the model framework presented here with simple modifications (Liao, 2022). In the current model, one source location is allowed. For systems incorporating multiple source regions, the propagation of magmatic signals would be a superposition of propagation from each individual source, with modification based on specific boundary conditions. The above complexities are potentially more relevant to different magmatic systems and specific unrest events, which could be incorporated into the framework presented here to allow for more comprehensive descriptions on melt assemblage, transport, and hydraulic interactions between difference reservoirs. Most of the processes mentioned above linearly relates pressure, deformation, fluid velocity and temperature, which could be conveniently incorporated into the efficient frequency-domain based model framework. Other time-dependent non-linear processes that alter the crystallinity and/or thermal structure, such as melt-solid reactions, require more complex and time-domain approach (Hu et al., 2022).
Data availability statement
The datasets presented in this study can be found in online repository FigShare at https://doi.org/10.6084/m9.figshare.21954407.v1.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Acknowledgments
The author gives special thank to Paul Segall who helped her with the development of the model, presentation of the findings, and providing editorial suggestions.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2023.1085897/full#supplementary-material
References
Aguilera, C. A. V., 2022, FourierTransform.m. Available at: https://www.mathworks.com/matlabcentral/fileexchange/13327-fouriertransform-m.
Alshembari, R., Hickey, J., Williamson, B. J., and Cashman, K. (2022). Poroelastic mechanical behavior of crystal mush reservoirs: Insights into the spatio-temporal evolution of volcano surface deformation. J. Geophys. Res. Solid Earth 127 (10), e2022JB024332. doi:10.1029/2022jb024332
Bachmann, O., and Huber, C. (2016). Silicic magma reservoirs in the earth’s crust. Am. Mineralogist 101 (11), 2377–2404. doi:10.2138/am-2016-5675
Barboni, M., Boehnke, P., Schmitt, A. K., Harrison, T. M., Shane, P., Bouvier, A.-S., et al. (2016). Warm storage for arc magmas. Proc. Natl. Acad. Sci. 113 (49), 13959–13964. doi:10.1073/pnas.1616129113
Barreyre, T., Escartin, J., Sohn, R., and Cannat, M. (2014). Permeability of the lucky strike deep-sea hydrothermal system: Constraints from the poroelastic response to ocean tidal loading. Earth Planet. Sci. Lett. 408, 146–154. doi:10.1016/j.epsl.2014.09.049
Barreyre, T., Parnell-Turner, R., Wu, J.-N., and Fornari, D. J. (2022). Tracking crustal permeability and hydrothermal response during seafloor eruptions at the east Pacific rise, 9 °50’n. Geophys. Res. Lett. 49 (3), e2021GL095459. doi:10.1029/2021gl095459
Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. doi:10.1063/1.1712886
Carbotte, S. M., Arnulf, A., Spiegelman, M., Lee, M., Harding, A., Kent, G., et al. (2020). Stacked sills forming a deep melt-mush feeder conduit beneath axial seamount. Geology 48 (7), 693–697. doi:10.1130/G47223.1
Caricchi, L., Townsend, M., Rivalta, E., and Namiki, A. (2021). The build-up and triggers of volcanic eruptions. Nat. Rev. 2 (7), 458–476. doi:10.1038/s43017-021-00174-8
Cashman, K. V., Sparks, R. S. J., and Blundy, J. D. (2017). Vertically extensive and unstable magmatic systems: A unified view of igneous processes. Science 355 (6331), eaag3055. doi:10.1126/science.aag3055
Chadwick, W. W., Wilcock, W. S. D., Nooner, S. L., Beeson, J. W., Sawyer, A. M., and Lau, T.-K. (2022). Geodetic monitoring at axial seamount since its 2015 eruption reveals a waning magma supply and tightly linked rates of deformation and seismicity. Geochem. Geophys. Geosystems 23 (1), e2021GC010153. doi:10.1029/2021gc010153
Crone, T. J., and Wilcock, W. S. D. (2005). Modeling the effects of tidal loading on mid-ocean ridge hydrothermal systems. Geochem. Geophys. Geosystems 6 (7). doi:10.1029/2004gc000905
Dragoni, M., and Magnanensi, C. (1989). Displacement and stress produced by a pressurized, spherical magma chamber, surrounded by a viscoelastic shell. Phys. Earth Planet. Interiors 56 (3), 316–328.
Edmonds, M., Cashman, K. V., Holness, M., and Jackson, M. (2019). Architecture and dynamics of magma reservoirs. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 377 (2139), 20180298.
Gelman, S. E., Gutiérrez, F. J., and Bachmann, O. (2013). On the longevity of large upper crustal silicic magma reservoirs. Geology 41 (7), 759–762. doi:10.1130/g34241.1
Gudmundsson, A. (2015). Collapse-driven large eruptions. J. Volcanol. Geotherm. Res. 304, 1–10. doi:10.1016/j.jvolgeores.2015.07.033
Hu, H., Jackson, M. D., and Blundy, J. (2022). Melting, compaction and reactive flow: Controls on melt fraction and composition change in crustal mush reservoirs. J. Petrology 63 (11), egac097. doi:10.1093/petrology/egac097
Jackson, M. D., Blundy, J., and Sparks, R. S. J. (2018). Chemical differentiation, cold storage and remobilization of magma in the earth’s crust. Nature 564, 405–409. doi:10.1038/s41586-018-0746-2
Jupp, T. E., and Schultz, A. (2004). A poroelastic model for the tidal modulation of seafloor hydrothermal systems. J. Geophys. Res. Solid Earth 109, B03105. doi:10.1029/2003jb002583
Karakas, O., Degruyter, W., Bachmann, O., and Dufek, J. (2017). Lifetime and size of shallow magma bodies controlled by crustal-scale magmatism. Nat. Geosci. 10 (6), 446–450. doi:10.1038/ngeo2959
Kaviany, M. (2012). Principles of heat transfer in porous media. New York: Springer Science and Business Media.
Liao, Y., Karlstrom, L., and Erickson, B. A. (2023). History-dependent volcanic ground deformation from broad-spectrum viscoelastic rheology around magma reservoirs. Geophys. Res. Lett. 50 (1), e2022GL101172. doi:10.1029/2022gl101172
Liao, Y., Nimmo, F., and Neufeld, J. A. (2020). Heat production and tidally driven fluid flow in the permeable core of enceladus. J. Geophys. Res. Planets 125 (9), e2019JE006209. doi:10.1029/2019je006209
Liao, Y., Soule, S. A., Jones, M., and Le Mével, H. (2021). The mechanical response of a magma chamber with poroviscoelastic crystal mush. J. Geophys. Res. Solid Earth 126 (4), e2020JB019395. doi:10.1029/2020jb019395
Liao, Y., Soule, S. A., and Jones, M. (2018). On the mechanical effects of poroelastic crystal mush in classical magma chamber models. J. Geophys. Res. Solid Earth 123 (11), 9376–9406. doi:10.1029/2018JB015985
Liao, Y. (2022). The roles of heat and gas in a mushy magma chamber. J. Geophys. Res. Solid Earth 127 (7), e2022JB024357. doi:10.1029/2022jb024357
Mullet, B., and Segall, P. (2022). The surface deformation signature of a transcrustal, crystal mush-dominant magma system. J. Geophys. Res. Solid Earth 127 (5), e2022JB024178. doi:10.1029/2022jb024178
Murphy, M. D., Sparks, R. S. J., Barclay, J., Carroll, M. R., and Brewer, T. S. (2000). Remobilization of andesite magma by intrusion of mafic magma at the soufriere hills volcano, Montserrat, west indies. J. Petrology 41 (1), 21–42. doi:10.1093/petrology/41.1.21
Rout, S. S., Blum-Oeste, M., and Wörner, G. (2021). Long-term temperature cycling in a shallow magma reservoir: Insights from sanidine megacrysts at taápaca volcano, central andes. J. Petrology 62, egab010. doi:10.1093/petrology/egab010
Rucker, C., Erickson, B. A., Karlstrom, L., Lee, B., and Gopalakrishnan, J. (2022). A computational framework for time-dependent deformation in viscoelastic magmatic systems. J. Geophys. Res. Solid Earth 127 (9), e2022JB024506. doi:10.1029/2022jb024506
Segall, P. (2016). Repressurization following eruption from a magma chamber with a viscoelastic aureole. J. Geophys. Res. Solid Earth 121 (12), 8501–8522. doi:10.1002/2016jb013597
Singer, B. S., Le Mével, H., Licciardi, J. M., Córdova, L., Tikoff, B., Garibaldi, N., et al. (2018). Geomorphic expression of rapid holocene silicic magma reservoir growth beneath laguna del maule, Chile. Sci. Adv. 4 (6), eaat1513. doi:10.1126/sciadv.aat1513
Sparks, R. S. J., Annen, C., Blundy, J. D., Cashman, K. V., Rust, A. C., and Jackson, M. D. (2019). Formation and dynamics of magma reservoirs. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 377 (2139), 20180019. doi:10.1098/rsta.2018.0019
Sparks, R. S. J., and Cashman, K. V. (2017). Dynamic magma systems: Implications for forecasting volcanic activity. Elements 13 (1), 35–40. doi:10.2113/gselements.13.1.35
Szymanowski, D., Wotzlaw, J.-F., Ellis, B. S., Bachmann, O., Guillong, M., and von Quadt, A. (2017). Protracted near-solidus storage and pre-eruptive rejuvenation of large magma reservoirs. Nat. Geosci. 10 (10), 777–782. doi:10.1038/ngeo3020
Keywords: magma mush, crystal mush, melt migration, transport properties, heat tranfer, thermal mechanical coupling
Citation: Liao Y (2023) Transport of melt, pressure and heat through a magma mush. Front. Earth Sci. 11:1085897. doi: 10.3389/feart.2023.1085897
Received: 31 October 2022; Accepted: 14 February 2023;
Published: 02 March 2023.
Edited by:
Yan Zhan, The Chinese University of Hong Kong, ChinaReviewed by:
Ying Qi Wong, ETH Zürich, SwitzerlandAlison Claire Rust, University of Bristol, United Kingdom
Copyright © 2023 Liao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Liao, eWxpYW9Ad2hvaS5lZHU=
 Yang Liao
Yang Liao