
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 16 September 2022
Sec. Hydrosphere
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.995874
This article is part of the Research TopicImproved Quantification of Precipitation Over Mountain RegionsView all 4 articles
 Melissa L. Wrzesien1,2,3
Melissa L. Wrzesien1,2,3 Tamlin M. Pavelsky3*
Tamlin M. Pavelsky3* Stefan P. Sobolowski4
Stefan P. Sobolowski4 Laurie S. Huning5,6
Laurie S. Huning5,6 Jonathan S. Cohen7
Jonathan S. Cohen7 Jonathan D. Herman7
Jonathan D. Herman7Cool season precipitation plays a critical role in regional water resource management in the western United States. Throughout the twenty-first century, regional precipitation will be impacted by rising temperatures and changing circulation patterns. Changes to precipitation magnitude remain challenging to project; however, precipitation phase is largely dependent on temperature, and temperature predictions from global climate models are generally in agreement. To understand the implications of this dependence, we investigate projected patterns in changing precipitation phase for mountain areas of the western United States over the twenty-first century and how shifts from snow to rain may impact runoff. We downscale two bias-corrected global climate models for historical and end-century decades with the Weather Research and Forecasting (WRF) regional climate model to estimate precipitation phase and spatial patterns at high spatial resolution (9 km). For future decades, we use the RCP 8.5 scenario, which may be considered a very high baseline emissions scenario to quantify snow season differences over major mountain chains in the western U.S. Under this scenario, the average annual snowfall fraction over the Sierra Nevada decreases by >45% by the end of the century. In contrast, for the colder Rocky Mountains, the snowfall fraction decreases by 29%. Streamflow peaks in basins draining the Sierra Nevada are projected to arrive nearly a month earlier by the end of the century. By coupling WRF with a water resources model, we estimate that California reservoirs will shift towards earlier maximum storage by 1–2 months, suggesting that water management strategies will need to adapt to changes in streamflow magnitude and timing.
Snow accumulation and snowmelt are fundamental components in regional water budgets for mountainous areas. In semi-arid regions, like much of the western United States, mountain snowmelt plays an outsized role in downstream river runoff (Li et al., 2017), highlighting the importance of snow for driving regional water storage (Zhou et al., 2015). Numerous studies have reported historical changes in snow-related variables, including decreased snow accumulation (Mote 2003; Grundstein and Mote 2010; Fyfe et al., 2017; Mote et al., 2018), declining snowfall (Knowles et al., 2006), and earlier spring streamflow peaks (Dettinger et al., 2004; Stewart et al., 2004; Maurer et al., 2007; Schwartz et al., 2017). In addition to studying these historical changes, it is important for local and regional water managers to know how snow resources may continue to change in response to the climate of the coming century to develop new adaptation and operation strategies. Furthermore, to facilitate informed decision-making, a more holistic picture of the hydrologic cycle is required–one in which warming causes changes in precipitation phase that manifest in downstream reservoir management approaches.
While global climate models (GCMs) are useful tools for understanding continental-scale variability and change (Taylor et al., 2012; Knutson et al., 2013; Knutti and Sedláček 2013; Eyring et al., 2016), their coarse grid spacing (on the order of 100 km or larger) limits their use over regions on the scale of a single mountain range or watershed (Maraun et al., 2010). In general, datasets at this resolution underestimate mountain snowpack, often by an order of magnitude (Broxton et al., 2016; Snauffer et al., 2016; Wrzesien et al., 2017, 2019). Therefore, multiple techniques have been developed to downscale GCM output to a more appropriate resolution for regional applications, including statistical downscaling (Barnett et al., 2008; Wang and Zhang 2008; Alder and Hostetler, 2019) and dynamical downscaling through a regional climate model (RCM; Liu et al., 2017; Walton et al., 2017; Wrzesien and Pavelsky 2020). Among the most popular tools for dynamical downscaling is the Weather Research and Forecasting (WRF) RCM, which has been used extensively to study western U.S. hydroclimate (Liu et al., 2017; Musselman et al., 2017, 2018; Letcher and Minder, 2018; Wrzesien et al., 2017, 2018)
To investigate potential future changes to snow accumulation and melt, we must first understand how precipitation may change. However, end-century projections from GCMs for precipitation are often in disagreement with one another and have large intermodel spread (Sillmann et al., 2013; Langenbrunner et al., 2015; Shen et al., 2018; Yazdandoost et al., 2021). Temperature projections, on the other hand, generally have a consensus between models on the sign of the temperature projections, though not necessarily on the magnitude of warming (IPCC et al., 2021). Therefore, it is more feasible to study the changing precipitation phase–particularly the extent to which snowfall will transition to rainfall–since precipitation phase is strongly tied to temperature. By assessing changes to precipitation phase by the end of the twenty-first century, in this study, we aim to understand potential downstream impacts of those changes, including changes to snow accumulation, the length of the snow season, and the timing and magnitude of streamflow. Other studies have evaluated projected changes to snowpack and snowfall (Krasting et al., 2013; Rhoades et al., 2018; Ikeda et al., 2021), shifts from snow to rain (Klos et al., 2014; Rhoades A.et al., 2018; Catalano et al., 2019; McCrary and Mearns, 2019), and related impacts on streamflow (Islam et al., 2019) through dynamical downscaling of GCMs (Rhoades et al., 2018; McCrary and Mearns, 2019), statistical downscaling of GCMs (Klos et al., 2014; Islam et al., 2019), or using a pseudo-global warming approach (PGW; Ikeda et al., 2021). However, the latter two approaches of statistical downscaling and PGW require assumptions about climate stationarity, such as historical spatial patterns in precipitation. These assumptions are avoided by a fully dynamical downscaling approach. Few dynamical studies have mapped the cascading impact of projected changes in precipitation phase through the full water cycle, including snowpack, streamflow, and water management. Therefore, we approach this future water resources challenge with a dynamical, holistic framework to provide a much-needed, yet often unexplored resource management perspective.
Water management is a particularly important topic in semi-arid regions like the western United States (Tidwell et al., 2014). In order to understand the implications of changing precipitation phase for water management, it is essential to accurately simulate precipitation, runoff generation, and the operating policies of downstream reservoirs. This connection is relevant for climate assessment because reservoirs will offset some of the detrimental impacts of snowpack decline, including the seasonal shift in water availability for agriculture (Qin et al., 2020) and the risk of rain-on-snow flood events (Huang et al., 2018). Dynamical downscaling with WRF has previously been linked to reservoir operations models for historical simulations (e.g., Holtzman et al., 2020), though the combination has not yet been used for future projections. We connect a water resources model with high-resolution RCM output to enable detailed estimates of how reservoir system operations may need to adapt due to climate change.
In this paper, we use a multimodel framework to project how future hydroclimate conditions over the western United States may respond to altered precipitation phase in a warming climate. We aim to address three main questions, all related to following the hydrologic process chain, from precipitation to snow accumulation to streamflow to management:
1) To what extent will winter precipitation shift from snowfall to rainfall by the end of the twenty-first century?
2) What impacts will a projected precipitation phase shift have on downstream variables, such as snow and streamflow, both in terms of magnitude and timing?
3) How will reservoir operations be impacted by projected hydroclimatic changes?
To address these questions, we use WRF to downscale two GCMs over the western United States for two decade-long periods–historical and end-century. As part of these WRF simulations, we use a modified version of the Noah-MP land surface model that is designed to provide better simulations of runoff in mountain regions (Holtzman et al., 2020). We then use the resulting WRF/Noah-MP simulations to drive the Operations of Reservoirs in California (ORCA) reservoir operations model, representing selected Sierra Nevada basins (Cohen et al., 2020). Further details on the model setup are described in Section 2, including the bias adjustment procedure for both the GCM data and the streamflow output from WRF and the ORCA model. In Section 3, we present results, and in Section 4, we discuss implications for projected hydroclimatic changes on water resource availability and water management.
We downscale two GCMs using WRF version 4.0.3 (Skamarock et al., 2019) with the Noah land surface model with multi-parameterization options (Noah-MP; Niu et al., 2011). Meteorological forcing data are from the Community Climate System Model version 4 (CCSM4; Gent et al., 2011; Lawrence et al., 2011; Neale et al., 2013) and the Norwegian Earth System Model (NorESM1-M; Bentsen et al., 2012; Iversen et al., 2013), both under a high emissions scenario (RCP 8.5). While it is preferable to generate a multi-model ensemble, the computational costs of running a high resolution regional model for many ensemble members over a domain as large as ours are prohibitively high. CCSM4 and NorESM1-M are chosen due to the fact that they sit near the CMIP5 multi-model ensemble mean (Supplementary Figure S1) for both transient climate response and equilibrium climate sensitivity (IPCC, 2021). For the study domain, NorESM is within 0.34 mm and 0.023°C of the CMIP5 ensemble average for annual precipitation and annual temperature, respectively over the selected historical decade (Supplementary Figure S1); for the end-century period, NorESM is slightly cooler (0.35°C) and slightly wetter (13.45 mm) than the ensemble average. Similarly, CCSM is close to the ensemble average for the western US domain for average temperature (0.022°C), though drier than the ensemble average by 11.74 mm over the historical decade (Supplementary Figure S1). For end-century, CCSM is 0.47°C degrees cooler than the ensemble average and 19.50 mm drier. Results are similar if we subset the CMIP5 GCMs to only consider mountainous regions in the western US study domain.
The choice of RCP8.5 was made in order to provide a physically plausible “worst case” scenario based on a high emissions baseline (van Vuuren et al., 2011). This extreme or upper bound scenario has been widely used in previous snow-related literature (e.g., Musselman et al., 2017, 2018; Rhoades A.et al., 2018; Ullrich et al., 2018; Siirilia-Woodburn et al., 2021). Table 1 includes details on CCSM4 and NorESM1-M. Prior to using either CCSM4 or NorESM1-M as initial and boundary conditions for WRF, we first bias adjust the GCMs; details on the bias adjustment procedure are below in Section 2.2.
Here we use a two-way nested domain, where the outer domain has a spatial resolution of 27 km and the inner domain a resolution of 9 km (Supplementary Figure S2, S3). The 27 km domain covers North America, while the 9 km inner domain zooms in on the western United States and southwestern Canada, from the Pacific Coast to east of the Rocky Mountains. Previous work suggests a model grid cell resolution of <10 km is necessary to accurately reproduce orographic precipitation (Ikeda et al., 2010; Pavelsky et al., 2011; Rasmussen et al., 2011; Minder et al., 2016; Wrzesien et al., 2017; Wrzesien et al., 2018). Although convective processes are not necessarily captured well at this resolution, past work suggests that cool season precipitation in the western U.S. is similar at convection parameterized (∼9 km) and convection permitting (∼3 km) resolutions (Pavelsky et al., 2011; Wrzesien et al., 2017). Here analysis is performed on the 9 km domain.
While we are interested in precipitation patterns across the full western U.S., we will only analyze streamflow in the Sierra Nevada region since the ORCA model is designed for selected Sierra Nevada basins that are critical to California’s water resources. Given the importance of these types of precipitation phase through management studies, we provide a guiding framework for analysis of reservoir operations of other hydrologically-relevant western U.S. basins. Following previous work (Holtzman et al., 2020), we modify Noah-MP to improve streamflow simulations for basins in the Sierra Nevada, including updating the snow capacitance, subsurface flow slope, and depth of subsurface runoff generation. All WRF/Noah-MP modifications are detailed in Table 2. We also apply a statistical aquifer correction algorithm based on comparisons to estimates of full natural flow (FNF), which improves simulated baseflow for basins with headwaters in the Sierra Nevada (Holtzman et al., 2020).
For the WRF setup, we select the following physics schemes: the Thompson et al. (2008) cloud microphysics scheme, the Rapid Radiative Transfer Model longwave scheme (Mlawer et al., 1997), the Dudhia shortwave scheme (Dudhia 1989), the Yonsei University planetary boundary layer scheme (Hong et al., 2006), and the modified Kain–Fritsch convective parameterization for the outer domain (Kain & Fritsch, 1990; Kain & Fritsch, 1993; Kain, 2004). We also apply two-way spectral nudging to wind, geopotential height, temperature, and water vapor mixing ratio; nudging to temperature and moisture are only applied within the free troposphere, following recent literature on nudging for regional climate purposes (Spero et al., 2018, 2014). Previous studies show that applying spectral nudging to bias-corrected GCM forcing data helps to reduce biases introduced from both the GCM and the RCM, particularly climate drifts in the center of the model domain (Wang and Kotamarthi, 2015; Xu and Yang, 2015).
WRF simulations are performed for two separate decadal periods: historical (water years (WYs) 1996–2005) and end-century (WYs 2091–2100). We include an additional year in each decadal simulation for model spin-up (WYs 1995 and 2090), but those years are not included in the analysis presented here. We recognize that it would be desirable to use multidecade averages, but this was not possible due to the computational expense of running WRF. Instead, we performed an analysis to ensure that we selected representative decades in terms of precipitation and temperature relative to the combined historical and RCP8.5 data spanning 1900–2100 from CCSM4. For example, we would not want to use a decade that, through random variability, represented an extreme drought or wet period in the model. For this analysis, we first detrended the data and deseasonalized all data by removing the mean seasonal cycle. Note that this process did not remove seasonality in precipitation or temperature variability. We then compared the decades we chose to all possible 10 year periods for precipitation and temperature (Supplementary Figure S4). We observed that while individual months and occasionally multiple consecutive months fell outside of 1 standard deviation ranges, we did not observe systematic anomalies for either the historical decade or the end century decade from CCSM4. Further, the selected historical decade is in the 69th percentile of historical decadal averages for temperature, and the selected end-century decade is in the 48th percentile of projected decadal averages for temperature. Similarly, the selected historical decade is in the 61st percentile of historical decadal averages for precipitation, and the selected end-century decade is in the 15th percentile of projected decadal averages for precipitation. As such, we feel confident that our results are not substantially affected by the inadvertent selection of a highly anomalous decade.
Both GCMs and RCMs suffer from biases arising from poorly resolved physics, model errors and parameter uncertainty. As such, some form of bias adjustment is often needed prior to downscaled data being used in impacts models. There is no agreed-upon optimal bias adjustment approach, and many create as many problems as they solve (Maraun et al., 2010). One approach that has shown some promise in recent years, and that we apply here, is to adjust the GCM input to the RCM so that large-scale biases inherent to the GCM are at least partly ameliorated. For our WRF forcing data, we use CCSM4 and NorESM1-M simulations that have already been bias adjusted following the Bruyère et al. (2014) method. This method adjusts GCM mean values toward the ERA-Interim (Dee et al., 2011) mean, calculated from the 1981–2005 period. Over the 1981–2005 reference period, GCM 6-hourly data are separated into a monthly mean and a deviation. To calculate the bias-corrected GCM output, the monthly mean from ERA-Interim and the GCM deviation are combined. Therefore, the Bruyère et al. (2014) method corrects for mean errors in the GCM but incorporates the climate variability from the GCM. The following equations are used in the bias adjustment:
In the above equations, the subscript ref stands for the reference period over which the bias adjustment is calculated, the overbar signifies the monthly mean, and the prime signifies the deviation from the mean. For future years, the 6-hourly deviations are applied to monthly means from the historical reference period; that is, deviations from 2006–2100 are applied to ERA-Interim monthly means over 1981–2005.
Bias adjustment is applied to correct the mean bias in 3-D fields and in surface fields. Bias adjusted 3-D fields include geopotential height, wind, temperature, and humidity; surface fields include surface pressure, sea level pressure, sea surface temperature, skin temperature, soil temperature, and soil moisture (Bruyère et al., 2014). This method retains the GCM variability in the initial and lateral boundary conditions for WRF. The Bruyère et al. (2014) method has been applied successfully in other studies to bias adjust GCMs (e.g., Wang and Kotamarthi 2015; Pontoppidan et al., 2018; Wrzesien and Pavelsky, 2020). It must be noted that, due to biases arising from parameterized processes in any chosen RCM, further bias adjustment of the RCM output is still often needed prior to its use in downstream impact modeling (Malek et al., 2022).
Instead of comparing historical and end-century precipitation magnitudes, here we consider how spatial patterns of precipitation phase may change. Specifically, we compare historical values of snowfall fraction, or simply the ratio of snowfall to total precipitation, to end-century values. We calculate cool season (October through March) snowfall fraction and compare the two downscaled GCMs for the historical and end-century periods.
In addition to comparing snow accumulation and peak SWE timing, we also consider how snow cover duration (SCD) may change throughout the twenty-first century. We calculate the maximum continuous SCD for each year in both the historical and end-century decades; for our evaluation, we compare decadal average continuous SCD. Within the literature, a SCD of 2 months or more is generally described as seasonal snow (Sturm et al., 1995); regions with SCD of less than 2 months have intermittent or ephemeral snow. Here we evaluate the end-century projections against the historical simulations to estimate the extent to which SCD may change throughout the western U.S., resulting in some areas shifting from seasonal to ephemeral snow, which can largely impact runoff and water availability timing and magnitude downstream.
Prior to projecting how future streamflow may be affected by changes to precipitation patterns, we first bias adjust the WRF-generated streamflow estimates. We compare historical simulations to estimates of “unimpaired” or “full nature flow” (FNF) for eight Sierra Nevada basins (Huang et al., 2018), which are available for download from the California Data Exchange Center. We include an additional four basins with headwaters in the Sierra Nevada that do not have FNF data available. Basins with sufficient available data were selected, spanning the entire Sierra Nevada, which also matches those analyzed by Holtzmann et al. (2020). FNF values are meant to provide an estimate of what streamflow would be without diversions for irrigation or other human interventions. Over each basin, we compare FNF and WRF decade-averaged hydrographs to calculate a basin-specific percent bias. We average the eight individual percent biases into a Sierra Nevada mean percent bias for each downscaled GCM. This mean bias approach allows us to apply the bias adjustment to all twelve basins of interest (Supplementary Figure S2) and to the end-century decade. WRF/CCSM streamflow estimates are shifted by +15% and WRF/NorESM estimates are shifted by -28%.
Water resources management is represented by the Operations of Reservoirs in California (ORCA) model for selected river basins in the Sierra Nevada (Cohen et al., 2020). This region, like many in the western U.S., must manage substantial intra- and inter-annual variability in precipitation with a complex network of (aging) reservoir infrastructure. Specifically, the model simulates operations of Shasta, Oroville, and Folsom reservoirs, located in the Sacramento, Feather, and American river basins, respectively, as well as the management of water supply infrastructure in the Sacramento-San Joaquin Delta. This system serves multiple purposes, including agricultural water supply and flood control, that are expected to be impacted by snowpack decline. The modeled operating policies are estimated from agency manuals, and they lead to a daily mass balance update in which a target release is determined by the greatest of three minimum operating requirements: environmental flows, flood control releases, and water demand. ORCA is open source (https://github.com/jscohen4/orca) and has been shown to accurately reproduce historical operations in prior work, with the Nash-Sutcliffe Efficiency (NSE) of reservoir storage exceeding 0.8. More simulation details are provided by Cohen et al. (2020).
Here we evaluate the ORCA model with daily inputs from WRF over the historical (WY 1996–2005) and end-century (2091–2100) periods. The input variables include reservoir inflows, SWE, temperature, and precipitation. While prior studies of this system have employed relatively coarse statistically-downscaled GCM projections to determine impacts of climate change (e.g., Robinson et al., 2020; Cohen et al., 2021), the model has not been investigated with high-resolution, dynamically downscaled hydrological inputs and such investigations tend to remain unexplored across large regions of the western U.S. Previous studies such as Qin et al. (2020), indicate that with changing snowmelt timing, alternative water sources and practices are needed for specific applications such as agricultural irrigation. By primarily focusing on reservoir storage, which affects these applications, in this study we determine the extent to which the infrastructure operations may have to compensate for seasonal shifts in runoff timing and potential loss of snowpack, to minimize the potential impacts to millions of people that rely on these reservoirs to deliver water for their domestic, agricultural, and industrial uses.
We first compare decade-averaged annual temperature and annual precipitation from the WRF downscaled estimates to native GCM output for each model (Figure 1 and Figure 2, respectively). Broadly speaking, historical spatial patterns of temperature and precipitation across the western U.S. domain have similarities between the coarse resolution global datasets and the fine resolution WRF estimates. For example, for annual precipitation (Figure 2), we see a local maximum in the Pacific Northwest/Southwest Canada from GCMs and WRF downscaled results. For decade-averaged annual temperature, all datasets have warm temperatures in the desert southwest and colder temperatures in Canada and along the Rocky Mountains. However, neither CCSM nor NorESM appear to have fine enough spatial resolution to capture either cooler temperatures in the Sierra Nevada and Cascade Mountains or orographic enhancement of precipitation in the mountains along the west coast, particularly in NorESM, which has a grid resolution of 1.89° ⨯ 2.5° (∼200 km). Due to finer grid spatial resolution and more realistic topography, WRF simulations result in a more detailed representation of both temperature and precipitation (Wrzesien et al., 2019).
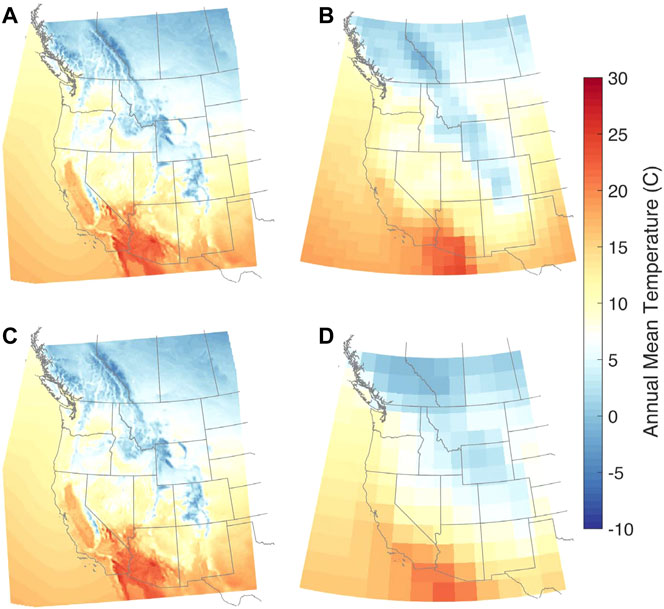
FIGURE 1. Comparison of annual mean temperature, averaged over the historical decade (water years 1996–2005) from (A,B) CCSM4 and (C,D) NorESM1-M. The WRF estimates (A,C) are at 9 km spatial resolution and the GCM estimates (B,D) are at the GCM native resolution.
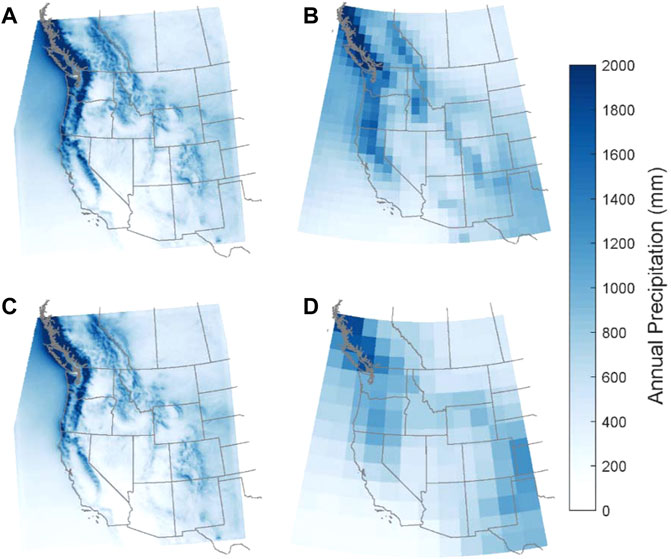
FIGURE 2. As for Figure 1 but for annual precipitation. (A–D) represent WRF/CCSM4, CCSM4, WRF/NorESM1-M, and NorESM1-M, respectively.
Differences between WRF and the GCMs are particularly stark when comparing SWE (Figure 3). While the GCMs do have some snow throughout the domain (e.g., NorESM in Figure 3), magnitudes are much less than expected, particularly when compared to the corresponding WRF simulation. Low SWE magnitudes in a coarse resolution GCM are not unexpected: previous work found that coarser resolution models and reanalysis underestimate mountain snow, often by more than an order of magnitude (Broxton et al., 2016; Snauffer et al., 2016; Wrzesien et al., 2017, 2019). Most notably, the WRF results have large values of SWE (>500 mm) in the Sierra Nevada, Cascades, Colorado Rockies, and southwestern British Columbia, all regions with little to no snow accumulation in the GCM. Based on the WRF simulations, we can appreciate the impact of topography on both precipitation and snow accumulation processes. By design, GCMs with grid resolution ≥1° cannot resolve realistic surface elevations, which may cause biases in surface temperature and precipitation, among other hydroclimate variables. Using WRF to dynamically downscale the GCMs presents a method for translating GCM output onto a finer resolution grid, which is particularly important in regions with complex topography, such as the western United States. Improved topographic and process representations can translate into more realistic precipitation partitioning and SWE amounts, which are needed for understanding the propagating impact of changing SWE on other components of the hydrologic cycle (e.g., evapotranspiration, soil moisture, runoff, streamflow), wildfires, ecology, and socioeconomics (Huning and AghaKouchak, 2020; Siirila-Woodburn et al., 2021).
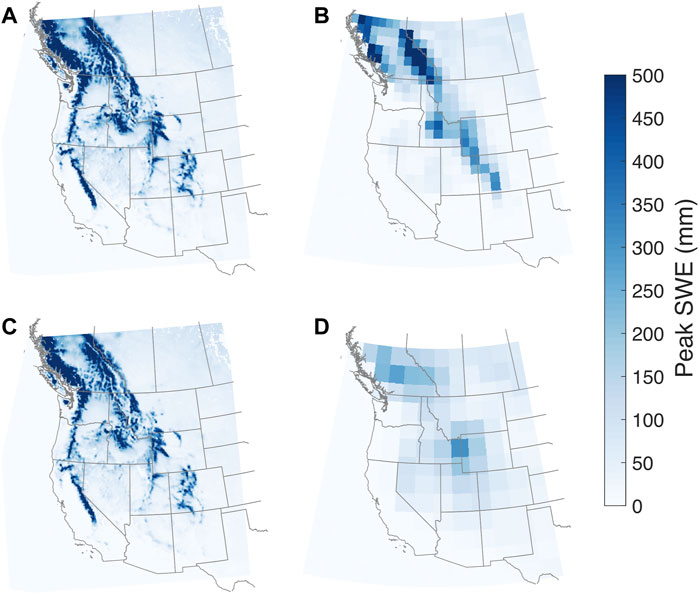
FIGURE 3. As for Figure 1 but for peak snow water equivalent. (A–D) represent WRF/CCSM4, CCSM4, WRF/NorESM1-M, and NorESM1-M, respectively.
We note that the GCMs and WRF have differing rain-snow partitioning schemes, which would impact snowfall and snow accumulation estimates from each model. Both CCSM4 and NorESM1 use the Community Atmosphere Model version 4 (CAM4; Neale et al., 2010) for the atmospheric component of the GCM. In CAM4, the fraction of precipitation that falls as snow is the following function of temperature:
With
To assess how western U.S. hydroclimate may change by 2100, we first compare annual precipitation between our historical and end-century study decades from the two WRF/GCM simulations (Figure 4). The historical decades from each WRF/GCM scenario have similar magnitudes for average annual precipitation (somewhat by design since both GCMs are biased adjusted against ERA-Interim data), but the percent differences by end-century largely diverge. WRF/CCSM and WRF/NorESM exhibit similar spatial patterns of precipitation change, with the Pacific Northwest getting wetter and the desert southwest getting drier, which agree with previous projection studies (Gutzler and Robbins 2011; Kumar et al., 2013; Baker and Huang 2014). The dipole pattern, however, is shifted further south in the WRF/NorESM simulations, with projected precipitation increases as far south as northern Utah and Colorado. A small shift in the dipole could have far-reaching implications. Consider the Upper Colorado River basin: in WRF/CCSM, end-century annual precipitation is projected to have a 7% decrease, while in WRF/NorESM, precipitation is projected to increase by 5%. In already stressed or over-allocated regions such as the Colorado River (Tidwell et al., 2014), a small decrease in precipitation may add further strain to the system and enhance anthropogenic drought across regions where increasing population centers drive increasing water demands and competition for resources (AghaKouchak et al., 2021). It is also important to consider that many arid and/or snow-free regions depend on precipitation and snowmelt-derived water from remote mountainous regions through imported water, meaning that a small change in one location’s precipitation may not just have direct local impacts, but rather widespread implications that cascade through various sectors. Overall, NorESM has larger differences by end-century, with annual precipitation projected to increase by 13%, on average, for all land pixels within the domain, compared to an average increase of less than 1% for CCSM.
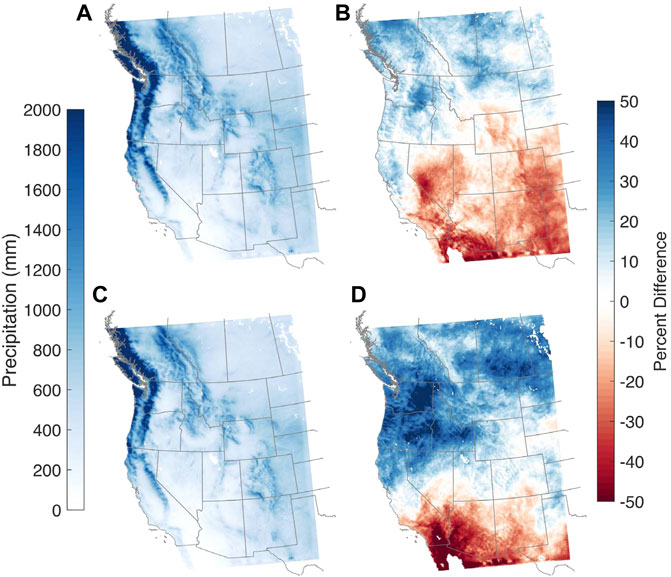
FIGURE 4. Decade-averaged annual precipitation for (A,C) historical decade and (B,D) percent difference by end-century from (A,B) WRF/CCSM and (C,D) WRF/NorESM.
For precipitation phase, we compare projected changes in snowfall fraction, or the ratio of snowfall to total precipitation, between the two WRF experiments (Figure 5). Consistent with warming temperatures, widespread declines in snowfall fraction are projected across the western U.S. and southwestern Canada. Here we consider four major western mountain regions: Sierra Nevada, Cascades, Great Basin, and U.S. Rockies (see Supplementary Figure S2). For these four regions, the cool season snowfall fraction is projected to decline by up to 55% when averaged over each mountain range (Supplementary Table S2). For example, the U.S. Rockies, the coldest range in our study area, are projected to experience snowfall fraction declines of between 28% (WRF/NorESM) and 35% (WRF/CCSM). High elevation regions, such as the Colorado Rockies and the Sierra Nevada, have smaller declines relative to surrounding non-mountain areas due to cooler temperatures. For the four major western mountain regions we consider here, nearly all grid cells are projected to experience decreases to snowfall fraction by end-century, with the largest decreases at the lower elevations (Figure 6); decreases at low elevations are not unexpected since these areas already have the warmest temperatures and tend to have the smallest snow accumulations. Elevations where half of the winter precipitation falls as snow are projected to shift higher; from both downscaled GCMs, the elevation change is projected to be the smallest for the Cascades (+398 m for WRF/CCSM and +313 m for WRF/NorESM), while the change is the largest for the Sierra Nevada (+661 m from WRF/CCSM and +586 m from WRF/NorESM). This elevational increase can be accompanied by a change in the likelihood of rain-on-snow events and flooding potential given the hypsometry of a basin as well as a change in timing and magnitude of mountain water storage. Over the four mountain ranges, the projected increase in elevation is larger in the WRF/CCSM simulations. This potentially suggests that the higher transient climate response of CCSM GCM (1.8 K) compared to NorESM (1.4 K) (IPCC, 2021) manifests as a higher regional warming signal.
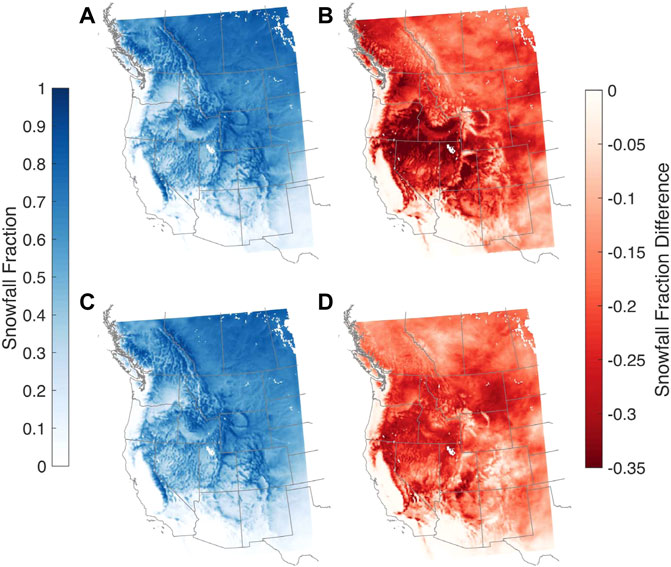
FIGURE 5. As for Figure 4 but for snowfall fraction. (A,B) are for WRF/CCSM and (C,D) are for WRF/NorESM.
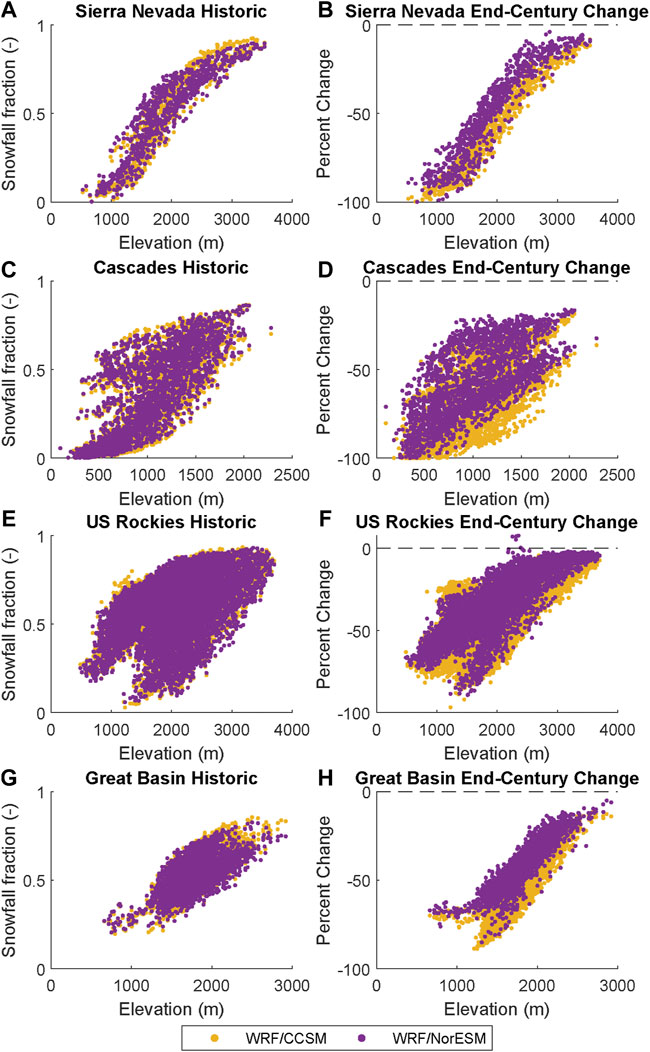
FIGURE 6. (A,C,E,G) Relationship between snowfall fraction and elevation for individual grid cells within four mountain ranges in the western United States for each downscaled GCM simulation (B,D,F,H) Projected snowfall fraction change across elevation.
In addition to snowfall fraction, we compare historical and future estimates for snow accumulation and snow duration. First, we consider how the selected decades compare to the longer record by considering the historical period of 1900–2005 from the CCSM GCM simulation (Supplementary Figure S5). The selected historical decade of 1996–2005 is within expected variability of domain-averaged SWE for the 100+ year period. The selected end-century decade of 2091–2100 is well outside natural variability for the region, suggesting that the differences we consider here between the historical and end-century decades for SWE magnitude and timing are related to impacts of a changing climate.
For snow accumulation, we compare grid cell peak SWE (Figure 7). For most of the model domain, SWE is projected to decline by end-century in both GCM scenarios. When comparing percent difference in SWE by end-century, it is evident, particularly in the Sierra Nevada and the Colorado Rocky Mountains, that higher elevations are projected to have smaller declines than low to mid-elevations; this is similar to snowfall fraction changes and attributable to cooler temperatures at high elevations as compared to surrounding low lying areas.
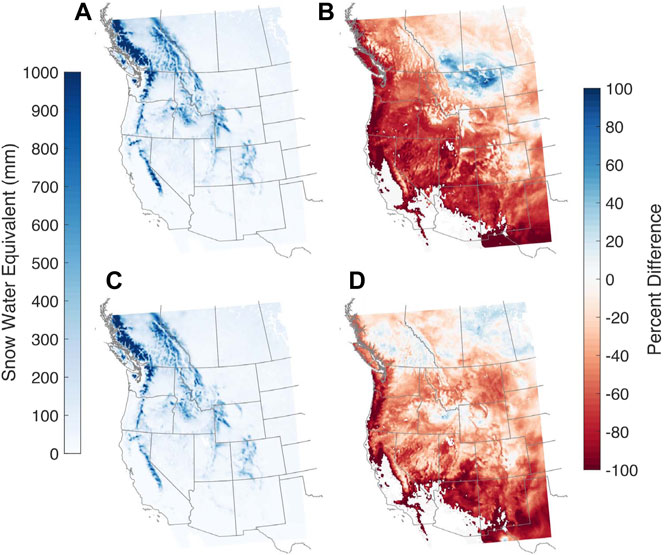
FIGURE 7. As for Figure 4 but for grid-cell peak SWE. (A,B) are for WRF/CCSM and (C,D) are for WRF/NorESM.
Range-wide snow water storage (SWS), or the volume of water stored as snow, is projected to decline by 24–68%, depending on mountain range and GCM (Table 3; Figure 8). In each WRF/GCM simulation, mountains areas of the Great Basin are projected to have the largest percent decline in SWS, while the Cascades and U.S. Rockies are projected to have larger decreases in SWS magnitude. Though both GCM projections suggest decreases to maximum range-scale SWS, declines are larger from WRF/CCSM, with projected decreases up to 40 percentage points larger than WRF/NorESM. Projected end-century SWS values are most similar for the Sierra Nevada, with 7.1 km3 from WRF/CCSM and 7.3 km3 from WRF/NorESM; however, since WRF/CCSM historical simulations have 4.4 km3 more snow in the Sierra Nevada than WRF/NorESM, the end-century changes still are ∼16 percentage point larger in WRF/CCSM.

TABLE 3. Maximum snow water storage (SWS) for western U.S. mountain ranges from CCSM and NorESM downscaled simulations.
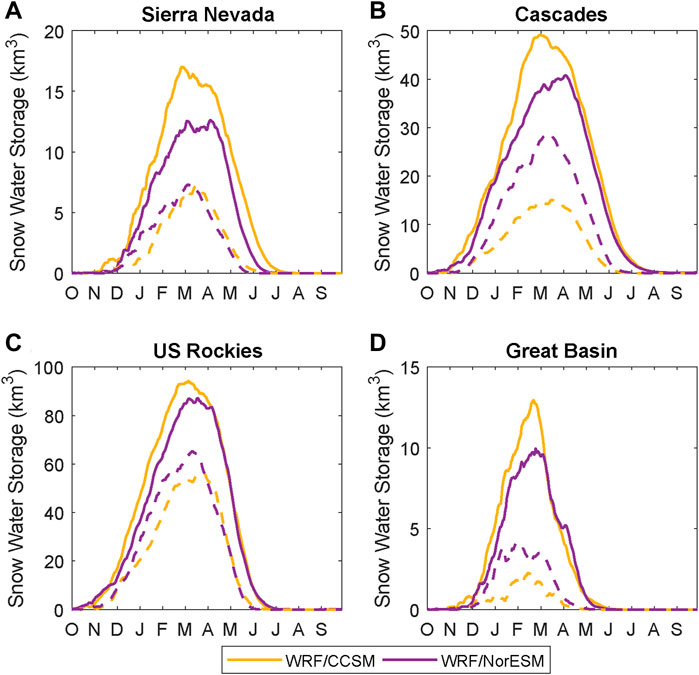
FIGURE 8. Average snow water storage, in km3, for each mountain range from the two downscaled GCMs. Solid lines show SWS averaged over the historical decade, and dashed lines show SWS averaged over the end-century decade. (A–D) show the Sierra Nevada, the Cascades, the US Rockies, and the Great Basin, respectively.
Not only is there likely to be less snow accumulating, but the length of the snow season is projected to change and in the future, seasonal snow may be at-risk of transitioning to ephemeral conditions where snow does not persist (Hatchett 2021). Continuous SCD is projected to have widespread declines across the full model domain (Figure 9); large decreases are projected across high elevation areas, particularly the warm maritime ranges of the Sierra Nevada, Cascades, and southern Coast Mountains of British Columbia, where decreases of 73–75 days from WRF/CCSM are expected (a decline of 45–54 days from WRF/NorESM). The highest elevation areas in the WRF domain (elevation ≥3,000 m) are projected to have SCD declines of 47 and 59 days, on average, by the end century from WRF/CCSM and WRF/NorESM simulations, respectively.
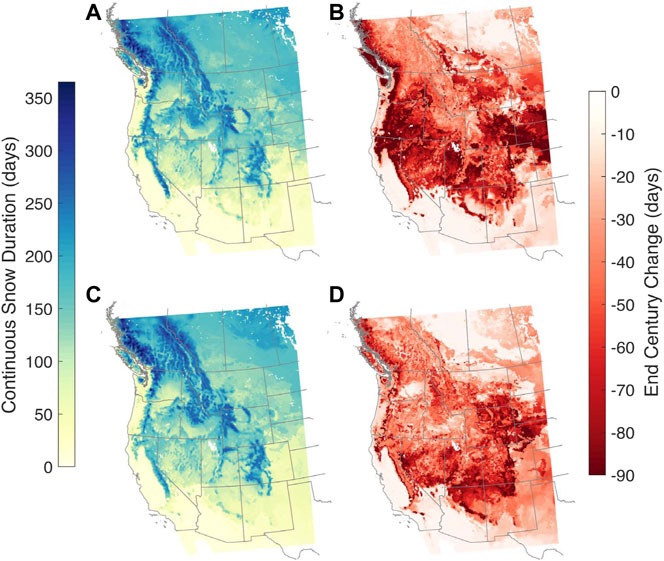
FIGURE 9. As for Figure 4 but for continuous snow duration. (A,B) are for WRF/CCSM and (C,D) are for WRF/NorESM.
To estimate whether there is a relationship between snowfall fraction and snow duration, we compare historical values of snowfall fraction over each mountain range to SCD from the historical and end-century periods (Figure 10). By holding snowfall fraction constant at historical levels, we can compare how SCD changes for the same group of grid cells. When comparing the same mountain grid cells between the historical and end-century decades, we see large decreases in continuous snow duration for all snowfall fraction values. That is, over the same set of grid cells, we project average decreases to the snow season of up to 74 days. Relationships are similar between WRF/CCSM and WRF/NorESM, though snow duration by the end-century tends to be less in WRF/CCSM.
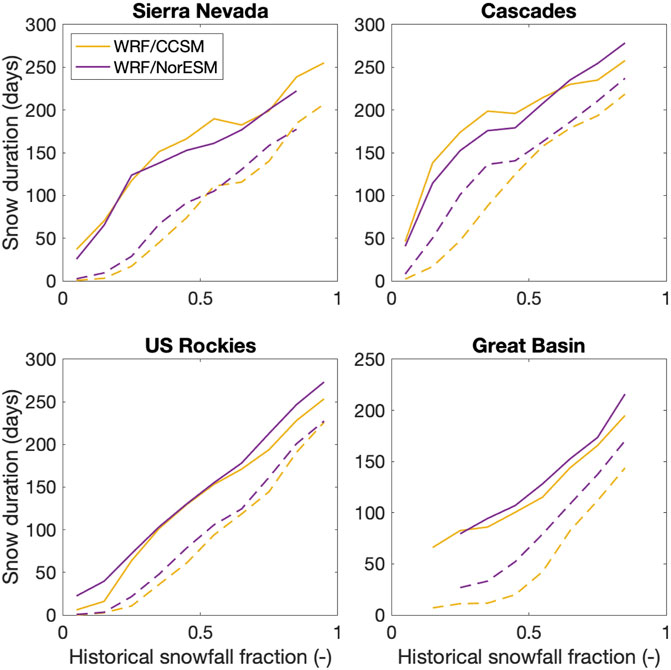
FIGURE 10. Relationship between continuous snow duration and historical values of snowfall fraction for four mountain ranges in the western United States. In all plots, both historical (solid lines) and end-century (dashed lines) relationships are determined with historical snowfall fraction values in order to compare over the same grid cells. Snow duration values correspond to historical and end-century values.
In addition to precipitation and snow accumulation, we consider how streamflow in the Sierra Nevada may be impacted by climate warming. First, we compare WRF-generated streamflow over eight basins in the Sierra Nevada to estimates of full natural flow (FNF) (Figure 11). Since we would not expect GCM output to match observations for a specific year (Taylor et al., 2012), we compare the decade-averaged hydrographs. After bias adjustment, WRF/CCSM and WRF/NorESM are both reasonable compared to FNF for most basins, with NSE values >0.7 for the San Joaquin and Kings basins from both WRF/CCSM and WRF/NorESM; the Kern also has an NSE >0.7 from WRF/CCSM.
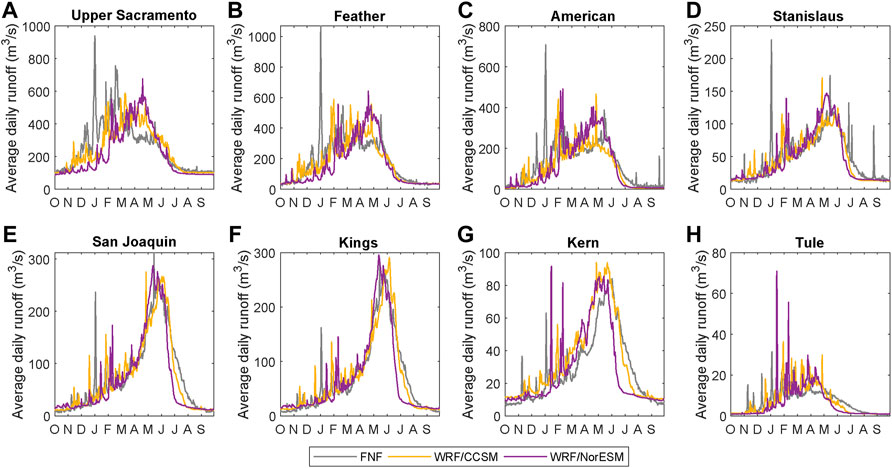
FIGURE 11. (A–H) Historical decade-averaged daily runoff from eight Sierra Nevada basins with available estimates for full natural flow (FNF).
Next, we compare historical and end-century streamflow estimates from downscaled simulations (Figure 12). For all basins, future projections of bias-adjusted streamflow suggest a decrease in spring/early summer streamflow, with an average earlier shift of the streamflow centroid timing of 24 days from WRF/CCSM and 31 days from WRF/NorESM (Supplementary Table S2). Earlier streamflow centroid timing is likely due to a shift in precipitation phase from snowfall to rainfall and corresponding declines in snow accumulation, which also lead to decreased spring and summer streamflow. WRF/NorESM generally shows a shift to earlier centroid timing compared to WRF/CCSM, which may be due to differences in peak SWE timing. In WRF/CCSM, the day of peak SWE in the Sierra Nevada is projected to occur 19 days later versus 30 days earlier in WRF/NorESM. The differences in timing between NorESM and CCSM is particularly evident in the southern Sierra Nevada watersheds, such as the San Joaquin, Kings, and Kaweah. Across all basins, WRF streamflow increases in the winter and spring, likely due to increased cool season rainfall. From WRF/CCSM (WRF/NorESM), average cool season rainfall is projected to increase over the Sierra Nevada by 61% (72%), while cool season total precipitation is projected to increase by only 12% (23%). Though total precipitation may increase over the Sierra Nevada, much of the change can be attributed to snowfall transitioning to rainfall under warmer temperatures. Evidence of this change is also seen in the flashiness of end-century hydrographs, suggesting a fast response between rainfall and streamflow instead of the typical delayed response between snowfall and streamflow, which could pose challenges for flood management.
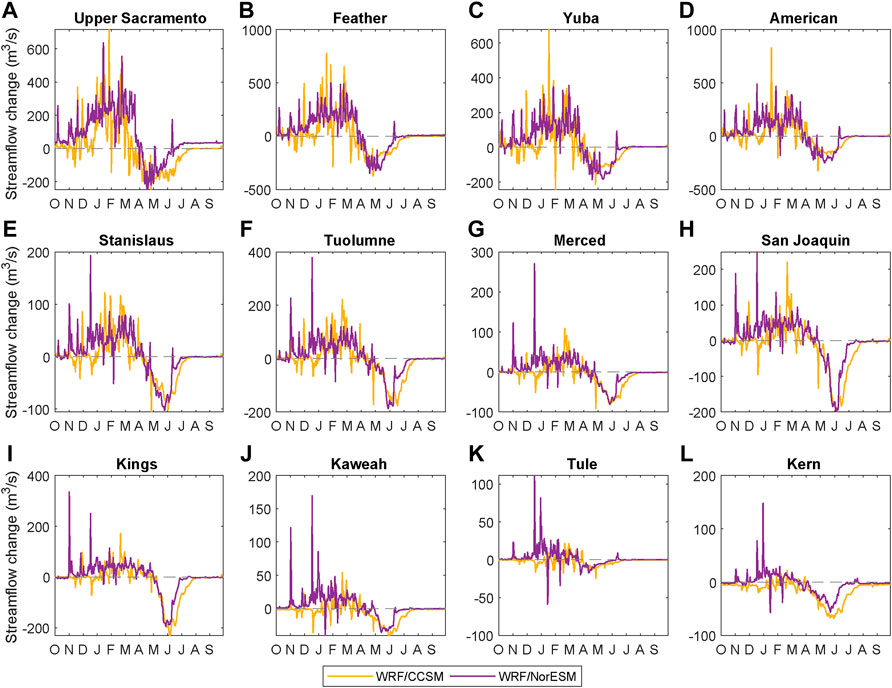
FIGURE 12. (A–L) Differences in decade-averaged daily streamflow between historical and end-century WRF simulations. Positive values indicate increases in streamflow magnitude by end century, while negative values indicate decreases.
When using WRF output to run the ORCA model, we can estimate how reservoir storage may change throughout the twenty-first century (Figure 13). Though both the historical and end-century periods have large interannual variability (Supplementary Figure S6), projections suggest an earlier peak in reservoir storage for Shasta, Oroville, and Folsom in both GCM scenarios. In results driven by WRF/NorESM, maximum springtime storage is projected to increase by end-century in both Shasta and Oroville reservoirs; results from WRF/CCSM, however, show slight declines in reservoir storage following the peak. This analysis assumes that the current system operations remain the same in the future, such that earlier winter inflows may not be stored due to current flood control regulations. The largest projected change comes from WRF/NorESM for Shasta: in nearly every month, the end-century interannual variability is outside the range of the historical interannual variability, likely driven by increased winter/early spring streamflow in the Upper Sacramento basin (Figure 12) and higher inflows into the reservoir (Supplementary Figure S7). While this additional storage would be a benefit for water supply, it would also pose challenges for flood control, with inflows arriving in highly variable, rainfall-driven events rather than the more gradual snowmelt observed historically. In contrast, WRF/CCSM projections show much smaller changes in interannual variability for Shasta between the historical and end-century periods.
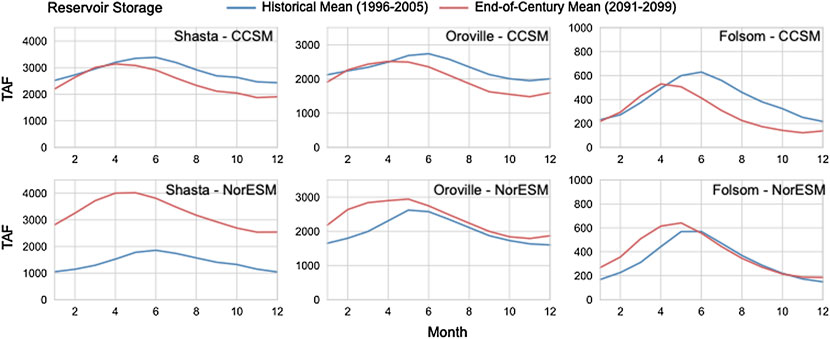
FIGURE 13. Reservoir storage, in thousand acre feet (TAF), for lakes impounded by Shasta, Oroville, and Folsom Dams in the foothills of the Sierra Nevada in California as calculated by the ORCA model. In each plot, the historical mean storage is reported in blue and the end-century mean is reported in red. Shasta Dam is on the Upper Sacramento River, Oroville Dam is on the Feather River, and Folsom Dam is on the American River.
In this study, we dynamically downscale two GCMs with WRF to consider how mountain hydroclimate in the western United States may change by 2100. Outputs from the model simulations indicate how precipitation phase shifts might change precipitation patterns, how a phase shift would impact other hydrological variables, and how reservoir operations would have to respond to a projected precipitation phase shift. We discuss these topics below further.
Precipitation magnitude throughout the twenty-first century is difficult to project, and models often do not agree (Sillmann et al., 2013; Langenbrunner et al., 2015). Indeed, we see that tendency here in the varying precipitation response patterns from the downscaling of the two GCMs in this study (e.g., Figure 4). However, temperature projections tend to have high agreement between models (IPCC, 2021). Therefore, we consider projections of how precipitation phase - specifically snowfall fraction - may change throughout the twenty-first century since the rain-snow threshold is largely temperature dependent. To evaluate precipitation phase, we compare cool season snowfall fraction (Figure 5). For all four mountain ranges, regardless of GCM, snowfall fraction is projected to decline across all elevation bands. Out of all grid cells classified as mountainous, less than 0.05% are projected to have increases in snowfall fraction by 2100 (6 grid cells out of 14,432 total). Shifting from snowfall to rainfall is not unexpected in a warming climate and is in agreement with recent studies on future climate in snow-dominated regions (Krasting et al., 2013; Klos et al., 2014; Rhoades et al., 2018; Ikeda et al., 2021; Siirila-Woodburn et al., 2021). With precipitation phase changes, both WRF/GCM simulations are in agreement in the direction of the change, though snowfall fraction declines are larger in WRF/CCSM.
After assessing precipitation phase, we examine “downstream” impacts - that is, how a shift from snowfall to rainfall impacts snow accumulation, snow duration, and streamflow timing. As expected, decreased snowfall leads to reduced snowpacks. Both end-century WRF simulations have less snow accumulation than the historical period, with declines up to 80% for some mountain ranges. Snowpack declines of this magnitude are consistent with the literature (e.g., Rhoades et al., 2018; Siirila-Woodburn et al., 2021). In the Sierra Nevada and the U.S. Rockies, where much of the snow is critical for the water supply, snow water storage declines are projected in WRF/CCSM to be on the order of -58% and -40%, respectively. For WRF/NorESM projections, snow water storage declines are projected to be on the order of -42% and -25% for the Sierra Nevada and the U.S. Rockies, respectively. Such large declines will impact water resources, possibly straining the water and energy supplies, irrigation, and recreation with severe economic consequences (Sturm et al., 2017).
Beyond snow accumulation magnitude, all ranges are projected to have snow duration decrease by at least 50 days. Sturm et al. (1995) define a seasonal snowpack as persisting for a minimum of 2 months. By end-century, snow cover in much of the Great Basin will no longer meet the seasonal snow criterion: in WRF/CCSM projections, average snow duration will fall to 52 days. Much of eastern Washington/Oregon and southern Utah (Figure 9) may also have annual snow duration decrease below 60 days. Remarkably, the slope of the relationship between snow duration and snowfall fraction remains very similar by end-century (Figure 10), though at lower values of snow duration. This consistency in relationship is even more apparent when we compare the same relationship between snow duration and snowfall fraction, but use each decade’s values for snowfall fraction (Supplementary Figure S8); that is, this evaluation does not compare snow duration over the same set of grid cells for historical and end-century (as we do in Figure 10). By end-century, generally, the shape of the relationship between the two variables remains largely the same. This result suggests that we may be able to estimate snow duration values from snowfall fraction using a single, consistent relationship for each range. For downscaling methods that only consider a handful of variables (e.g., statistical downscaling), this approach may allow for projection of an additional hydroclimatic variable, snow duration. However, we note that our results here are from a 9 km WRF simulation and further study of the stability of this relationship is necessary between historical and end-century at other spatial resolutions.
Following changes to both snow accumulation and melt timing, results indicate that changes to precipitation phase will also impact streamflow. As snowfall shifts to rainfall, the residence time on the surface decreases, resulting in earlier springtime streamflow peaks: streamflow centroid timing occurs 24 31) days earlier by 2,100 in WRF/CCSM (WRF/NorESM) simulations. The shift in WRF/NorESM to earlier streamflow may be due to differences in peak SWE timing; in WRF/CCSM, the day of peak SWE in the Sierra Nevada is projected to occur 19 days later versus 30 days earlier in WRF/NorESM. The differences in timing between NorESM and CCSM is particularly evident in the southern Sierra Nevada watersheds, such as the San Joaquin, Kings, and Kaweah. Changes to streamflow timing will directly impact water management strategies, which are currently based on historical records of snow magnitude and streamflow timing.
Finally, the results of our WRF-forced ORCA simulations to estimate how reservoir operations as Shasta, Oroville, and Folsom show that all reservoirs are projected to have an earlier storage peak, with possible shifts up to 2 months. The earlier peak, often in April by end-century versus historical peaks in June, corresponds to shifts in hydrographs (Figure 12), due to a higher rainfall fraction and earlier snowmelt. Though the largest-magnitude changes to streamflow occur during months with extensive snowmelt, changing summer low flows also likely have an impact on reservoir storage. Though low flows are not a large proportion of total annual streamflow, summer releases from the reservoirs may be reduced by curtailments due to low snowpack under existing operating policies, which could cause carryover storage to increase as seen in Shasta by end-century for NorESM. Using a reservoir system model allows us to track impacts of changing precipitation phase and snow accumulation on reservoir storage under current operating policies, highlighting how water management strategies will need to adapt to not only changes in streamflow magnitude but also in streamflow timing. Further, as demonstrated with Shasta end-century projections, relatively small changes to seasonal inflow patterns can produce outsized changes in projected reservoir storage.
These findings broadly agree with prior assessments of California water resources under climate change, which generally indicate reduced carryover storage (Vicuna and Dracup, 2007; Medellín-Azuara et al., 2008; Ray et al., 2020) and increased flood risk, worsened by the loss of streamflow predictability historically afforded by snowpack (Livneh and Badger, 2020; Liu et al., 2021). This combination of impacts is expected to increase the tension between water supply and flood control operations, indicating the need for operating policies to adapt (Mateus and Tullos, 2017; Cohen et al., 2021). However, this analysis is primarily based on changes in precipitation phase, and does not account for the wider range of disagreement among GCMs in the amount of precipitation and patterns of drying and wetting. This is particularly challenging for the extreme flood and drought events that drive water management decisions (Dottori et al., 2018; Herman et al., 2020). The high-resolution dynamical analysis presented here is a step toward representing the physical drivers of these events and understanding their consequences for reservoir management.
The future projections that we discuss here are useful for considering regional patterns of climate change at finer spatial resolutions than GCMs currently allow. However, it is important to consider the limitations of our approach. First, we only downscale two GCMs and therefore our experiments cannot capture the full range of temperature and precipitation projections from CMIP5 models. Since we select GCMs that are close to the ensemble average for both the historical and end-century decades (Supplementary Figure S1), our results cannot consider how future snowfall or snow mass would respond to a GCM that is hotter, colder, wetter, or drier than the CMIP5 ensemble average. Downscaling more models would likely produce a wider range of future precipitation and snow projections for the western United States, but we cannot make that conclusion without more simulations, which is beyond the scope of this project. Therefore, our conclusions are limited to the results that we see from only two downscaled estimates. Similarly, due to WRF’s high computational cost, multi-decade, multi-model, high-resolution ensemble simulations are not possible. Similar to other studies (Gao et al., 2012; Prein et al., 2017), we only consider decadal snapshots of western U.S. climate throughout the 20th and 21st centuries. While the snapshot approach is useful for understanding potential hydroclimatic changes, recent literature suggests a large ensemble approach is likely the best method for projecting future climate; as computational resources continue to improve, this may be a possible method with WRF. Until then, approaches such as ours, less complex models (e.g., the Intermediate Complexity Atmospheric Research model (Gutmann et al., 2016)), or a hybrid dynamical-statistical downscaling approach (Walton et al., 2015; Sun et al., 2016; Schwartz et al., 2017) are tools that are available for obtaining robust projections of climate change on a mountain range or smaller scale.
Dynamically downscaling GCM projections provides suggestions for how hydroclimatic conditions may change over scales that are more appropriate for local and regional planning. Despite limitations due to the computational cost of downscaling with WRF, we present two potential scenarios for end-century conditions in the western United States. Both models agree on the large-scale thermodynamically driven changes, including decreases to snowfall fraction, decreases to snow duration, declines to peak snow accumulation, and earlier springtime streamflow. Perhaps more importantly from a resource management perspective, we also demonstrate how projected changes to physical variables may impact our water resources through reservoir system simulations. Using tools like WRF and ORCA together is necessary for assessing how the timing and magnitude of local water resources may be affected by climate change. Future work should continue striving for high-resolution climate projections, which are essential for capturing the fine resolution hydroclimatic patterns required for elevation-dependent snow accumulation and melt. Climate change will impact the water resources of the western United States, and downscaled simulations, like the ones we present here, are the first step for understanding how water management strategies will need to adapt.
Publicly available datasets were analyzed in this study. This data can be found here: Bias Corrected CCSM Data: https://rda.ucar.edu/datasets/ds316.1/.
MW co-conceived the idea, conducted the WRF modelling and analysis and drafted the paper; TP co-conceived the idea, edited the paper, and helped obtain the funding; SS contributed expertise in climate modeling; LH contributed expertise in western U.S. hydroclimate; JH conceived the ORCA model and helped obtain the funding; JC developed and executed the ORCA model. All authors edited the paper.
This research was funded by NSF Innovations at the Nexus of Food Energy and Water Systems (INFEWS) grant CNS-1639268 (PI G. Characklis, UNC) and NSF Coupled Natural and Human Systems (CNH) grant 2009726 (PI: J. West, UNC). WRF simulations used the Extreme Science and Engineering Discovery Environment (XSEDE) Stampede2 at the Texas Advanced Computing Center, University of Texas at Austin, through allocation TGATM19008.
Bias adjusted NorESM simulations from M. Pontoppidan.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.995874/full#supplementary-material
AghaKouchak, A., Mirchi, A., Madani, K., Nazemi, A., Alborzi, A., Anjileli, H., et al. (2021). Anthropogenic drought: Definitions, challenges, and opportunities. Rev. Geophys. 59, e2019RG000683. doi:10.1029/2019RG000683 |
Alder, J. R., and Hostetler, S. W. (2019). The dependence of hydroclimate projections in snow-dominated regions of the Western United States on the choice of statistically downscaled climate data. Water Resour. Res. 55 (3), 2279–2300. doi:10.1029/2018wr023458 |
Baker, N. C., and Huang, H.-P. (2014). A comparative study of precipitation and evaporation between CMIP3 and CMIP5 climate model ensembles in semiarid regions. J. Clim. 27, 3731–3749. doi:10.1175/JCLI-D-13-00398.1 |
Barnett, T. P., Pierce, D. W., Hidalgo, H. G., Bonfils, C., Santer, B. D., Das, T., et al. (2008). Human-induced changes in the hydrology of the western United States. Science 319, 1080–1083. doi:10.1126/science.1152538 | |
Bentsen, M., Bethke, I., Debernard, J. B., Iversen, T., Kirkevag, A., Seland, O., et al. (2012). The Norwegian Earth system model, NorESM1-M – Part 1: Description and basic evaluation. Geosci. Model. Dev. Discuss. 5, 2843–2931. doi:10.5194/gmdd-5-2843-2012 |
Broxton, P. D., Zeng, X., and Dawson, N. (2016). Why do global reanalyses and land data assimilation products underestimate snow water equivalent? J. Hydrometeorol. 17, 2743–2761. doi:10.1175/JHM-D-16-0056.1 |
Bruyère, C. L., Done, J. M., Holland, G. J., and Fredrick, S. (2014). Bias corrections of global models for regional climate simulations of high-impact weather. Clim. Dyn. 43, 1847–1856. doi:10.1007/s00382-013-2011-6 |
Catalano, A. J., Loikith, P. C., and Aragon, C. M. (2019). Spatiotemporal variability of twenty-first-century changes in site-specific snowfall frequency over the Northwest United States. Geophys. Res. Lett. 46 (16), 10122–10131. doi:10.1029/2019gl084401 |
Cohen, J. S., Zeff, H. B., and Herman, J. D. (2020). Adaptation of multiobjective reservoir operations to snowpack decline in the western United States. J. Water Resour. Plan. Manag. 146 (12), 04020091. doi:10.1061/(asce)wr.1943-5452.0001300 |
Cohen, J. S., Zeff, H. B., and Herman, J. D. (2021). How do the properties of training scenarios influence the robustness of reservoir operating policies to climate uncertainty? Environ. Model. Softw. 141, 105047. doi:10.1016/J.ENVSOFT.2021.105047 |
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 137, 553–597. doi:10.1002/qj.828 |
Dettinger, M. D., Cayan, D. R., Meyer, M. K., and Jeton, A. E. (2004). Simulated hydrologic responses to climate variations and change in the merced, carson, and American river basins, Sierra Nevada, California, 1900–2099. Clim. Change 62, 283–317. doi:10.1023/B:CLIM.0000013683.13346.4f |
Dottori, F., Szewczyk, W., Ciscar, J.-C., Zhao, F., Alfieri, L., Hirabayashi, Y., et al. (2018). Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Chang. 8 (9), 781–786. doi:10.1038/s41558-018-0257-z |
Dudhia, J. (1989). Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 46, 3077–3107. doi:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., et al. (2016). Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 9, 1937–1958. doi:10.5194/gmd-9-1937-2016 |
Fyfe, J. C., Derksen, C., Mudryk, L., Flato, G. M., Santer, B. D., Swart, N. C., et al. (2017). Large near-term projected snowpack loss over the Western United States. Nat. Commun. 8, 14996–14997. doi:10.1038/ncomms14996 | |
Gao, Y., Fu, J. S., Drake, J. B., Liu, Y., and Lamarque, J.-F. (2012). Projected changes of extreme weather events in the eastern United States based on a high resolution climate modeling system. Environ. Res. Lett. 7, 044025. doi:10.1088/1748-9326/7/4/044025 |
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., et al. (2011). The community climate system model version 4. J. Clim. 24, 4973–4991. doi:10.1175/2011JCLI4083.1 |
Grundstein, A., and Mote, T. L. (2010). Trends in average snow depth across the western United States. Phys. Geogr. 31, 172–185. doi:10.2747/0272-3646.31.2.172 |
Gutmann, E., Barstad, I., Clark, M., Arnold, J., and Rasmussen, R. (2016). The intermediate complexity atmospheric research model (ICAR). J. Hydrometeorol. 17, 957–973. doi:10.1175/JHM-D-15-0155.1 |
Gutzler, D. S., and Robbins, T. O. (2011). Climate variability and projected change in the Western United States: Regional downscaling and drought statistics. Clim. Dyn. 37, 835–849. doi:10.1007/s00382-010-0838-7 |
Hatchett, B. J. (2021). Seasonal and ephemeral snowpacks of the conterminous United States. Hydrology 8, 32. doi:10.3390/hydrology8010032 |
Herman, J. D., Quinn, J. D., Steinschneider, S., Giuliani, M., and Fletcher, S. (2020). Climate adaptation as a control problem: Review and perspectives on dynamic water resources planning under uncertainty. Water Resour. Res. 56 (2). doi:10.1029/2019WR025502 |
Holtzman, N. M., Pavelsky, T. M., Cohen, J. S., Wrzesien, M. L., and Herman, J. D. (2020). Tailoring WRF and noah-MP to improve process representation of Sierra Nevada runoff: Diagnostic evaluation and applications. J. Adv. Model. Earth Syst. 12, e2019MS001832. doi:10.1029/2019MS001832 |
Hong, S. Y., Noh, Y., and Dudhia, J. (2006). A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 134 (9), 2318–2341. doi:10.1175/Mwr3199.1 |
Huang, X., Hall, A. D., and Berg, N. (2018). Anthropogenic warming impacts on today’s Sierra Nevada snowpack and flood risk. Geophys. Res. Lett. 45 (12), 6215–6222. doi:10.1029/2018GL077432 |
Huning, L. S., and AghaKouchak, A. (2020). Global snow drought hot spots and characteristics. Proc. Natl. Acad. Sci. U. S. A. 117, 19753–19759. doi:10.1073/pnas.1915921117 | |
Ikeda, K., Rasmussen, R., Liu, C. H., Gochis, D., Yates, D., Chen, F., et al. (2010). Simulation of seasonal snowfall over Colorado. Atmos. Res. 97 (4), 462–477. doi:10.1016/j.atmosres.2010.04.010 |
Ikeda, K., Rasmussen, R., Liu, C., Newman, A., Chen, F., Barlage, M., et al. (2021). Snowfall and snowpack in the western US as captured by convection permitting climate simulations: Current climate and pseudo global warming future climate. Clim. Dyn. 57, 2191–2215. doi:10.1007/s00382-021-05805-w |
IPCC (2021). “Climate change 2021: The physical science basis,” in Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Editors M. Delmotte, V. P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Bergeret al. (Cambridge, United Kingdom: Cambridge University Press).
Islam, S. U., Curry, C. L., Déry, S. J., and Zwiers, F. W. (2019). Quantifying projected changes in runoff variability and flow regimes of the Fraser River Basin, British Columbia. Hydrol. Earth Syst. Sci. 23 (2), 811–828. doi:10.5194/hess-23-811-2019 |
Iversen, T., Bentsen, M., Bethke, I., Debernard, J. B., Kirkevag, A., Seland, O., et al. (2013). The Norwegian Earth system model, NorESM1-M–Part 2: Climate response and scenario projections. Geosci. Model. Dev. 6, 389–415. doi:10.5194/gmd-6-389-2013 |
Kain, J. S., and Fritsch, J. M. (1990). A one-dimensional entraining detraining plume model and its application in convective parameterization. J. Atmos. Sci. 47 (23), 2784–2802. doi:10.1175/1520-0469(1990)047<2784:Aodepm>2.0.Co;2 |
Kain, J. S., and Fritsch, J. M. (1993). “Convective parameterization for mesoscale models: The Kain-Fritsch scheme,” in The representation of cumulus convection in numerical models (New York, United States: Springer), 165–170. |
Kain, J. S. (2004). The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor. 43 (1), 170–181. doi:10.1175/1520-0450(2004)043<0170:Tkcpau>2.0.Co;2 |
Klos, P. Z., Link, T. E., and Abatzoglou, J. T. (2014). Extent of the rain-snow transition zone in the Western US under historic and projected climate. Geophys. Res. Lett. 41 (13), 4560–4568. doi:10.1002/2014gl060500 |
Knowles, N., Dettinger, M. D., and Cayan, D. R. (2006). Trends in snowfall versus rainfall in the western United States. J. Clim. 19, 4545–4559. doi:10.1175/JCLI3850.1 |
Knutson, T. R., Zeng, F., and Wittenberg, A. T. (2013). Multimodel assessment of regional surface temperature trends: CMIP3 and CMIP5 twentieth-century simulations. J. Clim. 26, 8709–8743. doi:10.1175/JCLI-D-12-00567.1 |
Knutti, R., and Sedláček, J. (2013). Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Chang. 3, 369–373. doi:10.1038/nclimate1716 |
Krasting, J. P., Broccoli, A. J., Dixon, K. W., and Lanzante, J. R. (2013). Future changes in northern hemisphere snowfall. J. Clim. 26 (20), 7813–7828. doi:10.1175/jcli-d-12-00832.1 |
Kumar, S., Merwade, V., Kinter, J. L., and Niyogi, D. (2013). Evaluation of temperature and precipitation trends and long-term persistence in CMIP5 twentieth-century climate simulations. J. Clim. 26, 4168–4185. doi:10.1175/JCLI-D-12-00259.1 |
Langenbrunner, B., Neelin, J. D., Lintner, B. R., and Anderson, B. T. (2015). Patterns of precipitation change and climatological uncertainty among CMIP5 models, with a focus on the midlatitude pacific storm track. J. Clim. 28, 7857–7872. doi:10.1175/JCLI-D-14-00800.1 |
Lawrence, D. M., Oleson, K. W., Flanner, M. G., Thornton, P. E., Swenson, S. C., Lawrence, P. J., et al. (2011). Parameterization improvements and functional and structural advances in version 4 of the community land model. J. Adv. Model. Earth Syst. 3, M03001. doi:10.1029/2011MS00045 |
Letcher, T. W., and Minder, J. R. (2018). The simulated impact of the snow albedo feedback on the large-scale mountain—plain circulation east of the Colorado Rocky Mountains. J. Atmospher. Sci. 75 (3), 755–774. doi:10.1175/JAS-D-17-0166.1 |
Li, D., Wrzesien, M. L., Durand, M., Adam, J., and Lettenmaier, D. P. (2017). How much runoff originates as snow in the Western United States, and how will that change in the future?: Western U.S. Snowmelt-derived runoff. Geophys. Res. Lett. 44, 6163–6172. doi:10.1002/2017GL073551 |
Liu, C., Ikeda, K., Rasmussen, R., Barlage, M., Newman, A. J., Prein, A. F., et al. (2017). Continental-scale convection-permitting modeling of the current and future climate of North America. Clim. Dyn. 49, 71–95. doi:10.1007/s00382-016-3327-9 |
Liu, Z., Herman, J. D., Huang, G., Kadir, T., and Dahlke, H. E. (2021). Identifying climate change impacts on surface water supply in the southern Central Valley, California. Sci. Total Environ. 759, 143429. doi:10.1016/J.SCITOTENV.2020.143429 | |
Livneh, B., and Badger, A. M. (2020). Drought less predictable under declining future snowpack. Nat. Clim. Chang. 10 (5), 452–458. doi:10.1038/s41558-020-0754-8 |
Malek, K., Reed, P., Zeff, H., Hamilton, A., Wrzesien, M., Holtzman, N., et al. (2022). Bias correction of hydrologic projections strongly impacts inferred climate vulnerabilities in institutionally complex water systems. J. Water Resour. Plan. Manag. 148 (1), 04021095. doi:10.1061/(asce)wr.1943-5452.0001493 |
Maraun, D., Wetterhall, F., Ireson, A. M., Chandler, R. E., Kendon, E. J., Widmann, M., et al. (2010). Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 48, RG3003. doi:10.1029/2009RG000314 |
Mateus, M. C., and Tullos, D. (2017). Reliability, sensitivity, and vulnerability of reservoir operations under climate change. J. Water Resour. Plan. Manag. 143 (4), 04016085. doi:10.1061/(ASCE)WR.1943-5452.0000742 |
Maurer, E. P., Stewart, I. T., Bonfils, C., Duffy, P. B., and Cayan, D. (2007). Detection, attribution, and sensitivity of trends toward earlier streamflow in the Sierra Nevada. J. Geophys. Res. 112, D11118. doi:10.1029/2006JD008088 |
McCrary, R. R., and Mearns, L. O. (2019). Quantifying and diagnosing sources of uncertainty in midcentury changes in North American snowpack from NARCCAP. J. Hydrometeorol. 20 (11), 2229–2252. doi:10.1175/jhm-d-18-0248.1 |
Medellín-Azuara, J., Harou, J. J., Olivares, M. A., Madani, K., Lund, J. R., Howitt, R. E., et al. (2008). Adaptability and adaptations of California’s water supply system to dry climate warming. Clim. Change 87 (S1), 75–90. doi:10.1007/s10584-007-9355-z |
Minder, J. R., Letcher, T. W., and Skiles, S. M. (2016). An evaluation of high-resolution regional climate model simulations of snow cover and albedo over the rocky mountains, with implications for the simulated snow-albedo feedback. JGR. Atmos. 121 (15), 9069–9088. doi:10.1002/2016jd024995 |
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A. (1997). Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 102 (14), 16663–16682. doi:10.1029/97jd00237 |
Mote, P. W., Li, S., Lettenmaier, D. P., Xiao, M., and Engel, R. (2018). Dramatic declines in snowpack in the Western US. npj Clim. Atmos. Sci. 1, 2–6. doi:10.1038/s41612-018-0012-1 |
Mote, P. W. (2003). Trends in snow water equivalent in the Pacific Northwest and their climatic causes. Geophys. Res. Lett. 30, 1601. doi:10.1029/2003GL017258 |
Musselman, K. N., Clark, M. P., Liu, C., Ikeda, K., and Rasmussen, R. (2017). Slower snowmelt in a warmer world. Nat. Clim. Chang. 7, 214–219. doi:10.1038/nclimate3225 |
Musselman, K. N., Lehner, F., Ikeda, K., Clark, M. P., Prein, A. F., Liu, C., et al. (2018). Projected increases and shifts in rain-on-snow flood risk over Western North America. Nat. Clim. Chang. 8, 808–812. doi:10.1038/s41558-018-0236-4 |
Neale, R. B., Chen, C. C., Gettelman, A., Lauritzen, P. H., Park, S., Williamson, D. L., et al. (2010). Description of the NCAR community atmosphere model (CAM 5.0). NCAR Tech. Note NCAR/TN-486+ Str. 1 (1), 1
Neale, R. B., Richter, J., Park, S., Lauritzen, P. H., Vavrus, S. J., Rasch, P. J., et al. (2013). The mean climate of the community atmosphere model (CAM4) in forced SST and fully coupled experiments. J. Clim. 26, 5150–5168. doi:10.1175/JCLI-D-12-00236.1 |
Niu, G. Y., Yang, Z. L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., et al. (2011). The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 116 (12), D12109. doi:10.1029/2010jd015139 |
Pavelsky, T. M., Kapnick, S., and Hall, A. (2011). Accumulation and melt dynamics of snowpack from a multiresolution regional climate model in the central Sierra Nevada, California. J. Geophys. Res. 116 (16), D16115. doi:10.1029/2010jd015479 |
Pontoppidan, M., Kolstad, E. W., Sobolowski, S., and King, M. P. (2018). Improving the reliability and added value of dynamical downscaling via correction of large-scale errors: A Norwegian perspective. J. Geophys. Res. Atmos. 123 (21), 11875–11888. doi:10.1029/2018jd028372 |
Prein, A. F., Rasmussen, R. M., Ikeda, K., Liu, C., Clark, M. P., and Holland, G. J. (2017). The future intensification of hourly precipitation extremes. Nat. Clim. Chang. 7, 48–52. doi:10.1038/nclimate3168 |
Qin, Y., Abatzoglou, J. T., Siebert, S., Huning, L. S., AghaKouchak, A., Mankin, J. S., et al. (2020). Agricultural risks from changing snowmelt. Nat. Clim. Chang. 10 (5), 459–465. doi:10.1038/s41558-020-0746-8 |
Rasmussen, R., Liu, C. H., Ikeda, K., Gochis, D., Yates, D., Chen, F., et al. (2011). High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: A process study of current and warmer climate. J. Clim. 24 (12), 3015–3048. doi:10.1175/2010jcli3985.1 |
Ray, P., Wi, S., Schwarz, A., Correa, M., He, M., and Brown, C. (2020). Vulnerability and risk: Climate change and water supply from California’s central valley water system. Clim. Change 161 (1), 177–199. doi:10.1007/S10584-020-02655-Z |
Rhoades, A., Jones, A. D., and Ullrich, P. A. (2018). The changing character of the California Sierra Nevada as a natural reservoir. Geophys. Res. Lett. 45, 13008–13019. doi:10.1029/2018GL080308 |
Rhoades, A. M., Ullrich, P. A., and Zarzycki, C. M. (2018). Projecting 21st century snowpack trends in western USA mountains using variable-resolution CESM. Clim. Dyn. 50, 261–288. doi:10.1007/s00382-017-3606-0 |
Robinson, B., Cohen, J. S., and Herman, J. D. (2020). Detecting early warning signals of long-term water supply vulnerability using machine learning. Environ. Model. Softw. 131, 104781. doi:10.1016/j.envsoft.2020.104781 |
Schwartz, M., Hall, A., Sun, F., Walton, D., and Berg, N. (2017). Significant and inevitable end-of-twenty-first-century advances in surface runoff timing in California’s Sierra Nevada. J. Hydrometeorol. 18, 3181–3197. doi:10.1175/JHM-D-16-0257.1 |
Shen, M., Chen, J., Zhuan, M., Chen, H., Xu, C. Y., and Xiong, L. (2018). Estimating uncertainty and its temporal variation related to global climate models in quantifying climate change impacts on hydrology. J. Hydrology 556, 10–24. doi:10.1016/j.jhydrol.2017.11.004 |
Siirila-Woodburn, E. R., Rhoades, A. M., Hatchett, B. J., Huning, L. S., Szinai, J., Tague, C., et al. (2021). A low-to-no snow future and its impacts on water resources in the western United States. Nat. Rev. Earth Environ. 2, 800–819. doi:10.1038/s43017-021-00219-y |
Sillmann, J., Kharin, V. V., Zwiers, F. W., Zhang, X., and Bronaugh, D. (2013). Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 118, 2473–2493. doi:10.1002/jgrd.50188 |
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Liu, Z., Berner, J., et al. (2019). A description of the advanced research WRF model version 4. National Center for Atmospheric Research. Boulder, CO, United States, 145.
Snauffer, A. M., Hsieh, W. W., and Cannon, A. J. (2016). Comparison of gridded snow water equivalent products with in situ measurements in British Columbia, Canada. J. Hydrology 541, 714–726. doi:10.1016/j.jhydrol.2016.07.027 |
Spero, T. L., Nolte, C. G., Mallard, M. S., and Bowden, J. H. (2018). A maieutic exploration of nudging strategies for regional climate applications using the WRF model. J. Appl. Meteorol. Climatol. 57 (8), 1883–1906. doi:10.1175/Jamc-D-17-0360.1 | |
Spero, T. L., Otte, M. J., Bowden, J. H., and Nolte, C. G. (2014). Improving the representation of clouds, radiation, and precipitation using spectral nudging in the Weather Research and Forecasting model. J. Geophys. Res. Atmos. 119 (20), 11682–11694. doi:10.1002/2014jd022173 |
Stewart, I. T., Cayan, D. R., and Dettinger, M. D. (2004). Changes in snowmelt runoff timing in western North America under a `Business as usual’ climate change scenario. Clim. Change 62, 217–232. doi:10.1023/B:CLIM.0000013702.22656.e8 |
Sturm, M., Goldstien, M. A., and Parr, C. (2017). Water and life from snow: A trillion dollar science question. Water Resour. Res. 53, 3534–3544. doi:10.1002/2017WR020840 |
Sturm, M., Holmgren, J., and Liston, G. E. (1995). A seasonal snow cover classification system for local to global applications. J. Clim. 8, 1261–1283. doi:10.1175/1520-0442(1995)008<1261:ASSCCS>2.0.CO;2 |
Sun, F. P., Hall, A., Schwartz, M., Walton, D. B., and Berg, N. (2016). Twenty-first-century snowfall and snowpack changes over the Southern California Mountains. J. Clim. 29, 91–110. doi:10.1175/Jcli-D-15-0199.1 |
Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498. doi:10.1175/BAMS-D-11-00094.1 |
Thompson, G., Field, P. R., Rasmussen, R. M., and Hall, W. D. (2008). Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 136 (12), 5095–5115. doi:10.1175/2008mwr2387.1 |
Tidwell, V. C., Moreland, B. D., Zemlick, K. M., Roberts, B. L., Passell, H. D., Jensen, D., et al. (2014). Mapping water availability, projected use and cost in the western United States. Environ. Res. Lett. 9 (6), 064009. doi:10.1088/1748-9326/9/6/064009 |
Ullrich, P. A., Xu, Z., Rhoades, A. M., Dettinger, M. D., Mount, J. F., Jones, A. D., et al. (2018). California’s drought of the future: A midcentury recreation of the exceptional conditions of 2012-2017. Earth's. Future 6, 1568–1587. doi:10.1029/2018EF001007 |
van Vuuren, D. P., Edmonds, J., Kainuma, M., Riahi, K., Thomson, A., Hibbard, K., et al. (2011). The representative concentration pathways: An overview. Clim. Change 109 (1), 5–31. doi:10.1007/s10584-011-0148-z |
Vicuna, S., and Dracup, J. A. (2007). The evolution of climate change impact studies on hydrology and water resources in California. Clim. Change 82 (3–4), 327–350. doi:10.1007/s10584-006-9207-2 |
Walton, D. B., Hall, A., Berg, N., Schwartz, M., and Sun, F. (2017). Incorporating snow albedo feedback into downscaled temperature and snow cover projections for California’s Sierra Nevada. J. Clim. 30, 1417–1438. doi:10.1175/JCLI-D-16-0168.1 |
Walton, D. B., Sun, F. P., Hall, A., and Capps, S. (2015). A hybrid dynamical-statistical downscaling technique. Part I: Development and validation of the technique. J. Clim. 28, 4597–4617. doi:10.1175/Jcli-D-14-00196.1 |
Wang, J. L., and Kotamarthi, V. R. (2015). High-resolution dynamically downscaled projections of precipitation in the mid and late 21st century over North America. Earth's. Future 3 (7), 268–288. doi:10.1002/2015ef000304 |
Wang, J., and Zhang, X. (2008). Downscaling and projection of winter extreme daily precipitation over North America. J. Clim. 21, 923–937. doi:10.1175/2007JCLI1671.1 |
Wrzesien, M. L., Durand, M. T., Pavelsky, T. M., Howat, I. M., Margulis, S. A., and Huning, L. S. (2017). Comparison of methods to estimate snow water equivalent at the mountain range scale: A case study of the California Sierra Nevada. J. Hydrometeorol. 18 (4), 1101–1119. doi:10.1175/Jhm-D-16-0246.1 |
Wrzesien, M. L., Durand, M. T., Pavelsky, T. M., Kapnick, S. B., Zhang, Y., Guo, J. Y., et al. (2018). A new estimate of North American mountain snow accumulation from regional climate model simulations. Geophys. Res. Lett. 45 (3), 1423–1432. doi:10.1002/2017gl076664 |
Wrzesien, M. L., Pavelsky, T. M., Durand, M. T., Dozier, J., and Lundquist, J. D. (2019). Characterizing biases in mountain snow accumulation from global data sets. Water Resour. Res. 55 (11), 9873–9891. doi:10.1029/2019wr025350 |
Wrzesien, M. L., and Pavelsky, T. M. (2020). Projected changes to extreme runoff and precipitation events from a downscaled simulation over the western United States. Front. Earth Sci. 7, 355. doi:10.3389/feart.2019.00355 |
Xu, Z., and Yang, Z. L. (2015). A new dynamical downscaling approach with GCM bias corrections and spectral nudging. J. Geophys. Res. Atmos. 120 (8), 3063–3084. doi:10.1002/2014jd022958 |
Yazdandoost, F., Moradian, S., Izadi, A., and Aghakouchak, A. (2021). Evaluation of CMIP6 precipitation simulations across different climatic zones: Uncertainty and model intercomparison. Atmos. Res. 250, 105369. doi:10.1016/j.atmosres.2020.105369 |
Keywords: western US, climate change, precipitation phase, streamflow, reservoir management
Citation: Wrzesien ML, Pavelsky TM, Sobolowski SP, Huning LS, Cohen JS and Herman JD (2022) Tracking the impacts of precipitation phase changes through the hydrologic cycle in snowy regions: From precipitation to reservoir storage. Front. Earth Sci. 10:995874. doi: 10.3389/feart.2022.995874
Received: 16 July 2022; Accepted: 25 August 2022;
Published: 16 September 2022.
Edited by:
Andreas Franz Prein, National Center for Atmospheric Research, United StatesReviewed by:
Mimi Hughes, National Oceanic and Atmospheric Administration (NOAA), United StatesCopyright © 2022 Wrzesien, Pavelsky, Sobolowski, Huning, Cohen and Herman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tamlin M. Pavelsky, cGF2ZWxza3lAdW5jLmVkdS5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.