Simultaneous reconstruction and denoising for DAS-VSP seismic data by RRU-net

Distributed acoustic sensing in vertical seismic profile (DAS-VSP) acquisition plays an important role in reservoir monitoring. But the field data can be noisy and associated with missing traces which affects the seismic imaging and geological interpretation. Therefore, the DAS-VSP seismic data reconstruction with a high signal-to-noise ratio (SNR) is worth studying. There are no exact relationships between signals and noise in the t-x domain DAS-VSP seismic data, which means that reconstructing signals and suppressing noise simultaneously by the deep neural network is difficult. We develop a novel algorithm based on U-net in combination with the Hankel matrix as input/output, rather than t-x domain seismic data. The frequency domain Hankel matrix of the seismic data is proposed to facilitate the reconstruction and denoising of DAS-VSP seismic data as a rank reduction problem of the high-rank matrix. The Hankel matrices of incomplete data with noise are high-rank ones while those of complete data without noise are low-rank ones, which is beneficial to the network learning. In our proposed rank reduction U-net (RRU-net), two-channel input/output layers are designed for the real and the imaginary parts of the Hankel matrix in the frequency domain. Thus, reconstructed data with high precision and high SNR could be obtained using a trained RRU-net. Meanwhile, we tested our RRU-net algorithm on two synthetic data and one field data, and the results show the effectiveness and the feasibility of the method. Our algorithm performs better than both the U-net-based method that uses $t-x$ domain data as input/output and the rank reduction approach.

Introduction

Recently, DAS has been used in vertical seismic profile (VSP) acquisition for permanent reservoir monitoring due to its advantages of full vertical coverage, low cost, repeatability, adaptability to high-temperature and high-pressure environment, and long-term deployment (Miller et al., 2012). However, the quality of DAS seismic data is poor for the following three reasons: first, the low sensitivity of DAS results in the weakly received upward-reflected signal, worsened by a large amount of environmental noise, optical noise, and “ringing” noise. Second, the obstacles in the acquisition area and the pressure of economic costs for long-term monitoring result in low-density shot arrangement and sparsely acquired data. Third, the perforation operation can easily destroy the fiber in the well, making the signals hardly recordable at this point. Additionally, the storage cost for time-lapse DAS-VSP seismic data is usually measured in TB, which is a challenge for data processing. Briefly, the DAS-VSP seismic data have the characteristics of low SNR, sparseness, and big data. Therefore, it is necessary to research the reconstruction and denoising of the DAS-VSP seismic data in high precision and real time.

Thanks to the rapid development of deep learning technology in the field of image processing in recent years (Krizhevsky et al., 2012; Ronneberger et al., 2015; Liu et al., 2018), intelligent processing has been widely used in the field of massive seismic data reconstruction (Jia and Ma, 2017; Jia et al., 2018; Mandelli et al., 2018). Among those methods, the convolutional neural network (CNN) is the most widely used method. The local perception capability of the CNN could extract more detailed intrinsic features of data. At the same time, the number of CNN parameters could be reduced by weight-sharing, which improves the training speed of the network. This kind of method (deep learning methods, including the aforementioned CNN) extracts the inherent high-dimensional features of the data adaptively through massive datasets and does not rely on prior conditions and artificial experience. Moreover, the trained net takes less than a few milliseconds to predict $1024\times 112$ data (Chai et al., 2020). Therefore, deep learning could be a potential method to solve the problem of massive DAS-VSP seismic data reconstruction. Currently, many researchers have applied deep learning methods to seismic data reconstruction and denoising. In these studies, seismic data reconstruction and denoising are always discussed separately. For example, Liu et al. (2018) proposed the use of partial convolution methods to improve the blur problem of reconstructed images. Siahkoohi et al. (2019) accomplished the accurate reconstruction of the common shot records by the CNN, which is trained by the common receiver records in the FK domain based on the reciprocity theorem. Chen and Wang, (2021) proposed a method to enrich the training set by sampling at different scales and image flipping to improve the generalization ability of CNN in seismic data reconstruction. Furthermore, different nets based on CNN, such as residual net (ResNet) (Wang et al., 2019), generative adversarial neural network (GAN) (Oliveira et al., 2018), and U-net (Chai et al., 2020; Fang et al., 2021), were applied to data reconstruction. In the seismic data noise suppression problem, learning data augmentation strategies are also adopted to train the CNN (Wang et al., 2019). Dong et al. (2020) combined the denoising convolutional neural network (DnCNN) with robust principal component analysis to learn the noise characteristics in the noisy desert seismic data and realized the effective suppression of irregular random noise and regular surface waves. Then, based on the CNN, an energy ratio factor is used to adjust the energy ratio of the effective signal patch and noise patch in the training process to improve the generalization ability of the CNN denoising model to different SNRs (Dong et al., 2021). Feng and Li, (2022) designed a denoising neural network based on spectral decomposition analysis (SVDDCNN), and the net extracted DAS-VSP data features from a singular spectrum instead of the time-domain data, which can represent geophysical features more accurately. In addition, cycle generative adversarial networks (Cycle-GANs) and residual encoding–decoding neural networks (RED-Nets) are also used in random noise suppression (Li and Wang, 2021; Zhong et al., 2021). The aforementioned methods achieved high-precision reconstructed data and effective noise suppression data, respectively. However, noise and missing data coexist in the field records, and only a few studies have applied a simultaneous reconstruction and denoising of seismic data by the deep learning method (Wang, 2020; Jiang et al., 2021). In Wang’s research (2020), the CNN-based 3D data reconstruction and denoising method first trained the network for denoising and then trained the network for reconstruction, separately. Jiang et al. (2021) proposed an improved convolutional auto-encoder (CAE) method to achieve simultaneous reconstruction and denoising of seismic data; however, the noise was residual in the field data testing. For noisy incomplete DAS-VSP seismic data, when the neural network is trained to implement one of the tasks (reconstruction/denoising), the other factor (noise/missing data) will adversely affect the neural network. Therefore, it is a difficult problem to realize the simultaneous reconstruction and denoising of DAS-VSP seismic data based on deep learning.

Among the traditional simultaneous reconstruction and denoising methods of seismic data, the rank reduction based on the Hankel matrix is one of the effective methods (Gao et al., 2011; Oropeza and Sacchi, 2011; Chen et al., 2016). The principle is that the seismic data will repeatedly record the information of the same or adjacent underground locations, so that the seismic data have a low-rank structure. The absence of data or the noise will increase the rank; therefore, seismic data reconstruction and noise suppression can be regarded as the rank reduction problem of the high-rank matrix. However, the data in some columns are all zero in the incomplete seismic data gather, which will lead to instability in the rank reduction process. Generally, the incomplete seismic data need to be transformed into a Hankel matrix and then the rank of which will be reduced by singular value decomposition (SVD) (Cadzow, 1988; Trickett, 2008; Gao et al., 2011; Popa et al., 2021). The disadvantage of the rank reduction method is that the SVD of large Hankel matrices requires a huge amount of computational cost, which makes it unsuitable for massive DAS-VSP monitoring data. In addition, it is difficult to determine the number of retained eigenvalues in the SVD process, which will lead to insufficient noise suppression or signal leakage.

In this article, we propose a simultaneous reconstruction and denoising method for DAS-VSP seismic data under the framework of deep learning based on rank reduction. When using a U-net instead of the SVD process of the Hankel matrix, the U-net is trained to learn the mapping relationship between the high-rank Hankel matrix (noisy missing data) and the low-rank Hankel matrix (noise-free complete data) adaptively, which neatly avoids the shortcomings of the rank reduction method. First, the $t-x$-domain training data are transformed into the Hankel matrices in the frequency domain. So, the two different tasks of data reconstruction and noise suppression are unified into a reduced-rank learning task, which could improve the reconstruction accuracy and efficiency. Second, two-channel input/output layers are designed for the real and imaginary parts of the frequency-domain Hankel matrix. Meanwhile, different types of noise and signal data with different missing percentages are added to the training set to improve the generalization ability of the network. In this article, synthetic examples and field data are provided to prove the effectiveness of the proposed method. Furthermore, the results of the rank reduction method, the U-net trained in the $t-x$ domain, and the RRU-net are compared to show the superiority of the RRU-net in simultaneous reconstruction and denoising of DAS-VSP seismic data.

Methodology

Rank reduction method

Fully sampled seismic data can be represented by a low-rank matrix. Missing trace or noise will increase the rank of the data. Therefore, the reconstruction and denoising of DAS-VSP seismic data can be regarded as a rank reduction problem of a high-rank matrix (Sacchi, 2009; Oropeza and Sacchi, 2011). When approximated, seismic data are linear within the $t-x$ window, and then the seismic data $d$ with one event can be expressed as

$d\left(t,x_n\right)=w\left(t_0+p{x}_n\right),(1)$

where $t$ is the time, $t_0$ is the time intercept of the first trace in the time–space window, $x_n$ is the offset of the $n^{th}$ trace, $w$ is the wavelet, and $p$ is the dip of the event. In the frequency domain, Eq. 1 becomes

$D\left(\omega ,x_n\right)=W\left(\omega \right)e^{i\omega p{x}_n}.(2)$

For regularly sampled seismic data, $x_n=\left(n-1\right)\Delta x$, where $n=\mathrm{1,2},...,N$, $N$ is the number of geophones on a receiver line, and $\Delta x$ is the spacing of geophones within lines. The seismic data of adjacent traces have the following recurrence relation in the frequency domain:

$\begin{array}{l}D\left(\omega ,x_{n+1}\right)=W\left(\omega \right)e^{i\omega p{x}_{n+1}},\\ =W\left(\omega \right)e^{i\omega pn\Delta x},\\ =D\left(\omega ,x_n\right)e^{i\omega p\Delta x},\end{array}(3)$

where $e^{i\omega p\Delta x}$ is constant for seismic data with certain frequency $\omega$ and dip $p$. By denoting $e^{i\omega p\Delta x}$ as ${\lambda }_{\omega }$ and $D\left(\omega ,x_n\right)$ as $D_n$, Eq. 3 is simplified to

$D_{n+1}={\lambda }_{\omega }{D}_n.(4)$

The equation for constructing the Hankel matrix with seismic data in the frequency domain is

$H=\left[\begin{array}{cccc}{D}_1& D_2& \cdots & D_k\\ D_2& D_3& \cdots & D_{k+1}\\ ⋮& ⋮& \ddots & ⋮\\ D_l& D_{l+1}& \dots & D_N\end{array}\right],(5)$

where $k+l-1=N$. Based on Eq. 4, the Hankel matrix in Eq. 5 can be further expressed as

$H=\left[\begin{array}{cccc}{D}_1& \lambda D_1& \cdots & {\lambda }^{\left(k-1\right)}{D}_1\\ D_2& \lambda D_2& \cdots & {\lambda }^{\left(k-1\right)}{D}_2\\ ⋮& ⋮& \ddots & ⋮\\ D_l& \lambda D_l& \dots & {\lambda }^{\left(k-1\right)}{D}_l\end{array}\right].(6)$

From Eq. 6, there is a linear relationship among the columns of the Hankel matrix, that is, the rank of the matrix is 1. Similarly, it can be proved that when the seismic data contain multiple dip events, the rank of the Hankel matrix is equal to the number of dips. Therefore, the Hankel matrix constructed with the seismic data in the frequency domain is a low-rank Hankel matrix. When there are missing traces or noise, Eq. 6 becomes non-linear; thus, the rank of $H$ will increase. The signal reconstruction and the noise suppression can be effectively achieved by performing SVD on the Hankel matrix $H$ and reducing its rank. The SVD of the Hankel matrix is

$H=U\Sigma V^T.(7)$

In Eq. 7, $U$ and $V$ are the unitary matrices with sizes $l\times l$ and $k\times k$, respectively, and they are the eigenvector matrices of $H$. $\Sigma$ is a diagonal matrix, and its diagonal elements are the singular values of $H$. $\Sigma$ can be presented as

$\Sigma =\left[\begin{array}{ccc}{\sigma }_{\mathrm{1,1}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_{l\times k}\end{array}\right],(8)$

where ${\sigma }_1\ge {\sigma }_2\ge \cdots {\sigma }_i\ge 0$. We reduce the rank of the Hankel matrix by keeping the first $r$ eigenvalues:

$\Sigma =\left[\begin{array}{cc}{\Sigma }_r& 0\\ 0& 0\end{array}\right],(9)$

where ${\Sigma }_r=diag\left({\sigma }_1,\cdots ,{\sigma }_r\right)$. Then, the rank-reduced Hankel matrix $\stackrel{\sim }{H}$ is calculated as

$\stackrel{\sim }{H}=U_r{\Sigma }_r{V}_r^T.(10)$

Next, the elements along the anti-diagonal of the matrix $\stackrel{\sim }{H}$ are averaged to obtain ${\stackrel{\sim }{D}}_n$, and ${\stackrel{\sim }{D}}_n$ is the reconstructed and denoised seismic data in the frequency domain. There are two shortcomings in the aforementioned process of simultaneous reconstruction and denoising of seismic data based on rank reduction. One, for field seismic data, the rank of seismic data in different time–space windows is different, and it is difficult to determine how many ranks are needed to be retained. The other problem is that both the SVD of the matrix $H$ and the rank-reduced matrices $\stackrel{\sim }{H}$ require huge computations. Therefore, we propose to use a U-net to adaptively learn the mapping relationship between the high-rank Hankel matrix (noisy missing data) and the low-rank Hankel matrix (noise-free complete data), instead of relying on artificial experience to determine the number of the retained rank. Moreover, once the training of one net has been carried out, the prediction will be highly efficient.

The architecture of the rank reduction U-net

The architecture of the RRU-net proposed in this article is shown in Figure 1. The main part of this network is a U-net with 27 layers, which is a symmetric structure based on CNNs (Falk et al., 2019). The input of the RRU-net is the Hankel matrix of seismic data in the frequency domain. Since the elements in the Hankel matrix are complex, the real convolution neural network cannot process the data directly. We design the U-net with two-channel input/output layers, which correspond to the real and imaginary parts of the Hankel matrix, respectively. In this way, the RRU-net can extract signal features from both the real and imaginary parts of the input data. The U-net has three important components. One is the encoder (left side) composed of the repeated operators of two $3\times 3$ convolutions (purple arrow) that are followed by batch normalization (BN), a rectified linear unit (ReLU), and a $2\times 2$ max-pooling (red arrow) for down-sampling. After the down-sampling step, the effective receptive field of the network increases as the size of the feature maps decreases. Meanwhile, the amounts of feature channels are generally doubled. For the simultaneous seismic data reconstruction and denoising task, the encoding process is responsible for extracting features in different scales of the input noisy missing data. The second component is the decoder (right side) with an expansive path, in which the feature maps are first up-sampled by bilinear interpolation (green arrow) to halve the number of feature channels at each step. In the decoding process, the size of the feature maps increases after each up-sampling step, which leads to the reduction of the effective receptive field of the network. The decoding process is used to decode the low-dimensional features to the original size, obtaining the location information. The last layer uses a $1\times 1$ convolution to map the multi-channel features to the desired number of classes. The third component is a skip connection (black dotted arrows) combining the deep feature maps from the decoder network with the shallow feature maps from the encoder network, which is useful to learn the rank reduction theory of the Hankel matrix with noisy missing data and then implement two $3\times 3$ convolutions, each followed by BN and ReLU.

FIGURE 1

FIGURE 1. Architecture of the RRU-net.

In Eq. 11, $L$ is the loss function of the RRU-net, and it is defined as

$L\left(\theta \right)=\frac{1}{M}{\displaystyle \sum }_{j=1}^M(f(\theta ,H_{sample}^j)-H_{label}^j{)}^2,(11)$

where $M$ is the batch size in the training process, $f$ is the U-net described in Figure 1, $\theta$ represents the parameters of the convolution kernel, $H_{sample}^j$ is the Hankel matrix with noisy missing data in the training set, and $H_{label}^j$ is the label (noise-free complete data) in the training set. The RRU-net is trained to minimize the loss function $L$ to obtain the best value of $\theta$ under the framework of 1.7 PyTorch version. The other parameters of the RRU-net such as convolution, max-pooling, and bilinear interpolation are shown in Table 1. In addition, the patch size of the training data, the layers of the net, and the convolution kernel size all have an impact on the result of deep learning as established in other research studies (Wang et al., 2019; Chai et al., 2020; Feng and Li, 2022). Therefore, this article does not repeat the analysis, but we refer to the relevant research in the selection of these parameters.

TABLE 1

TABLE 1. Parameters setting of the RRU-net.

Training datasets

We prepare the training data with the synthetic signals by forward modeling and the noises from the field DAS-VSP seismic data. The synthetic signals are simulated by forward modeling using the finite difference method for a 2D profile of the SEAM model (Figure 2). The model has 70 km width and 5 km depth, and the velocity range is distributed from 1,490 m/s to 4,800 m/s. The well is located at 3 km (the white stripe in Figure 2) and equipped with 401 receivers (the blue triangle in Figure 2) spaced at 10-m intervals and has a depth range from 0 to 4,000 m. There are 176 sources spaced at 40-m intervals (the red circle in Figure 2) at the surface. A 30-Hz Ricker wavelet is used in the simulation. The size of the synthetic data is $1905\times 401\times 176$, that is, the size of the time axis (0.004 s interval), receiver axis, and shot axis, respectively. In the 176 common shot gathers, 150 shot gathers are randomly selected for training and the rest for testing. One of the common shot gathers is shown in Figure 3A. The noise records including the background noise (arrow 1), ringing noise (arrow 2), and horizontal noise (arrow 3) are obtained from the real DAS-VSP data as shown in Figure 3B. Approximately, 40%–70% of the traces are randomly deleted in different gathers. The noise records from the real data are added to the incomplete signal records to obtain the noisy incomplete data as shown in Figure 4A. So, the noisy incomplete data and the noise-free complete data are transformed into the Hankel matrix separately, before all the needed data are normalized to $\left[-\mathrm{1,1}\right]$ and windowed to patches with size $51\times 51$. There are 266400 pairs of samples in the training dataset, each sample with size $26\times 26$, and parts of them are shown in Figures 4B,C.

FIGURE 2

FIGURE 2. Two-dimensional profile of the SEAM model and the acquisition geometry.

FIGURE 3

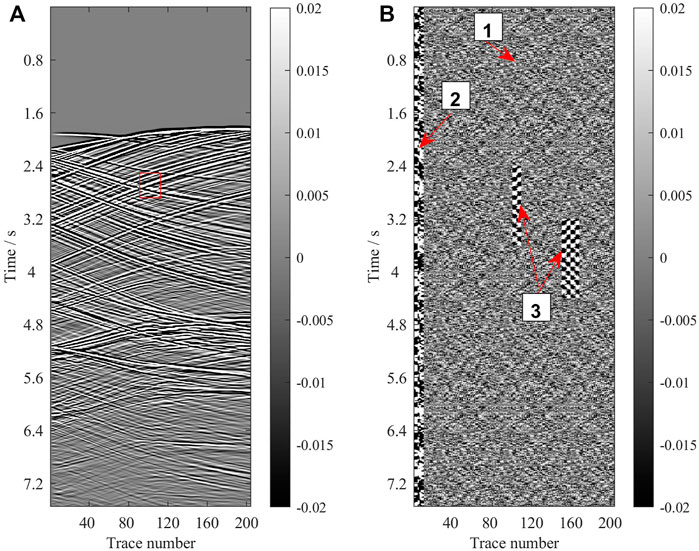
FIGURE 3. (A) Synthetic noise-free complete signal data and the shot is located at $x=0$ m. (B) Noise data from the field DAS-VSP records.

FIGURE 4

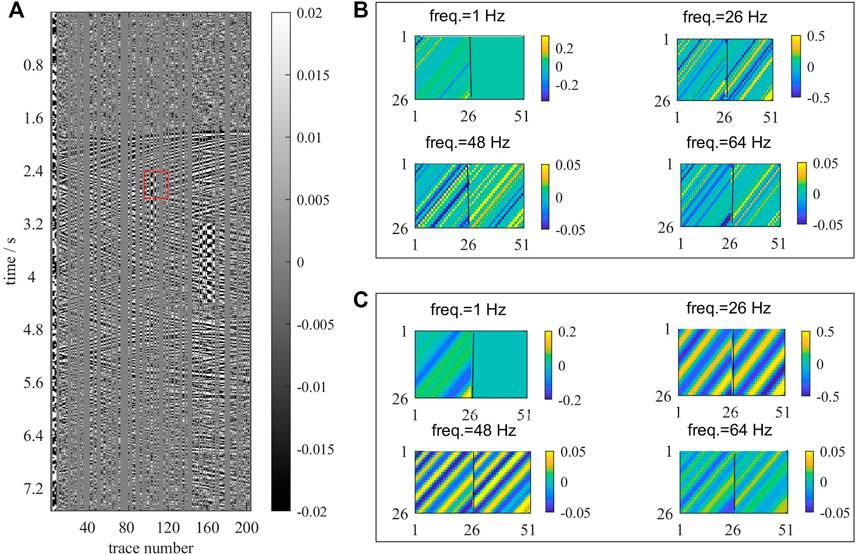
FIGURE 4. (A) Synthetic noisy incomplete data based on Figure 3 and the missing trace percentage is 56.4%. (B) Hankel matrices in different frequencies of the noise incomplete data in the red rectangle of Figure 4A; each Hankel matrix contains a real part (left side) and an imaginary part (right side). (C) Hankel matrices in different frequencies of the noise-free complete data in the red rectangle of Figure 3A; each Hankel matrix contains a real part (left side) and an imaginary part (right side).

The training environment is in the PyTorch framework with GPU (8 cores) in the Linux system. The total training cost is about 25 h, and the loss error in epochs is shown in Figure 5.

FIGURE 5

FIGURE 5. Training loss and validation loss of the RRU-net.

Numerical examples

The reconstruction and denoising effectiveness of the trained RRU-net is validated by two synthetic datasets and one field dataset. One of the synthetic datasets is modeled by the same velocity model as the training dataset (Figure 4) with different source positions. The other is from the Marmousi2 model. The field DAS-VSP records are employed to test the generalization capacity of the RRU-net. Moreover, to prove the superiority of the RRU-net in handling simultaneous reconstruction and denoising of the DAS-VSP data, we compare the results of the RRU-net with those of the rank reduction method and U-net trained with t-x-domain data.

Synthetic records

There are 26 shot gathers in the first synthetic records to be tested. One of the processed gathers by the rank reduction method, U-net, and RRU-net is presented in Figures 6C,D,E, respectively. The original data are shown in Figures 6A,B. These figures show data with 65% missing traces. Figures 6C,D show that the rank reduction method and U-net cannot suppress the strong ringing noise as marked by the red arrows, while the RRU-net is able to suppress it more entirely as seen in Figure 6E. Meanwhile, the signals divided in the window with the strong ringing noise also are suppressed by the rank reduction method (Figure 6C) because in the SVD process for the near traces, ringing noise dominates the eigenvalues. As we can see in Figures 6D,E, the RRU-net suppressed the horizontal noise (red rectangle) more efficiently than the other two methods. In addition, the RRU-net performs the best in suppressing the background noise. For the missing signal reconstruction, the near traces are barely reconstructed by the rank reduction method as shown in Figure 6C, while the U-net method has poor effectiveness for the big gap as marked by the yellow arrow in Figure 6D. Contrary to the rank reduction method and U-net, the reconstructed signal by the RRU-net is complete, and the event continuity is the best as shown in Figure 6E.

FIGURE 6

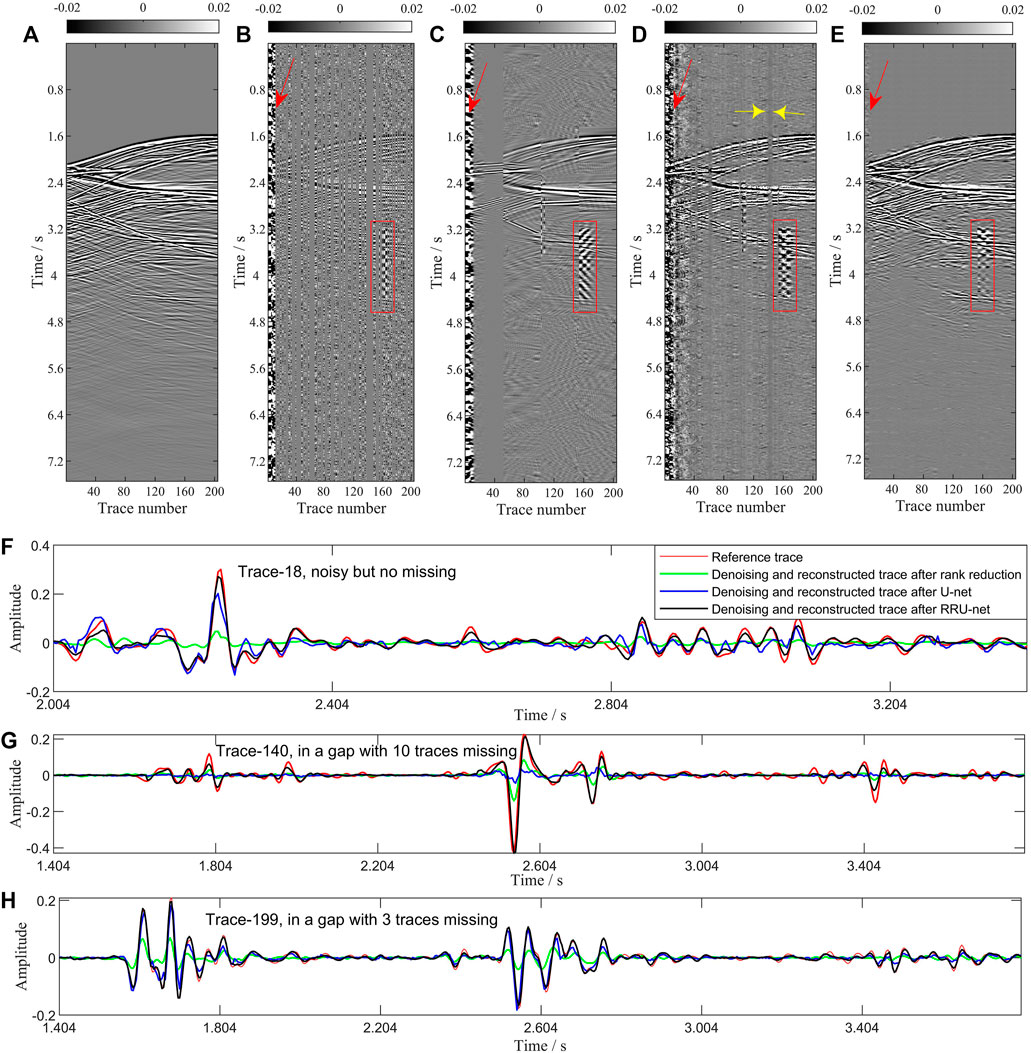
FIGURE 6. Simultaneous reconstruction and denoising results of the three methods on synthetic data generated with the SEAM model. (A) Synthetic noise-free complete signal data and the shot is located at $x=6400$ m. (B) Original gather with noise and the missing trace percentage is 63%. (C) Result by rank reduction. (D) Result by U-net. (E) Result by RRU-net. (F–H) One-dimensional waveform comparison.

To prove the accuracy of the reconstructed signals and to confirm whether the studied method harms the signal in the denoised results, we carry out a detailed 1D waveform comparison. Three traces are shown in Figures 6F–H, respectively. Figure 6F is the denoised results of the 18th trace in Figure 6B. Figures 6G,H are the reconstructed signals of the 140th and 199th trace, respectively, which are in different gaps. The 1D waveform comparison shows that the RRU-net method best fits the single trace and yields fewer reconstruction errors. Additionally, the SNR of the 26 shot gathers processed by the three methods is presented in Figure 7. It is obvious that the SNR of the proposed network is much higher than that of the other two methods. To complete the processing of the 26 shot gathers, the rank reduction method takes 44 s, and the U-net and RRU-net take less than 5s, which demonstrates the efficiency of the deep learning method. All these analyses affirm that the proposed RRU-net can suppress the noise and reconstruct the missing signal effectively. However, for weak signals below 4s, none of these three methods can obtain satisfactory reconstruction results as the weak signal is completely buried in the strong background noise as shown in Figure 6B. In addition, the cross term between the real part and imaginary part of the Hankel matrix in the frequency domain is ignored as we apply the real neural network, which may affect the effectiveness of the proposed method.

FIGURE 7

FIGURE 7. SNRs of the 26 shot gathers processed by three methods.

To test the effect of the trained network on other synthetic data, we use the RRU-net to reconstruct and denoise the DAS-VSP data generated using the Marmousi2 model. The data include a total of 21 shots and 255 receivers per shot, and every trace has 1,000 temporal sampling points. One of the processed gathers by the three methods is presented in Figure 8. As highlighted by the arrows and the boxes (Figures 8B–E), the RRU-net yields the best denoising results, and the 1D waveform comparison of different traces (Figures 8F–H) shows the accuracy of the reconstructed signals by our method. The average SNR value of gathers with noise and 65% missing traces is −17.09 dB, which is increased to 25.69 dB after reconstruction by the RRU-net.

FIGURE 8

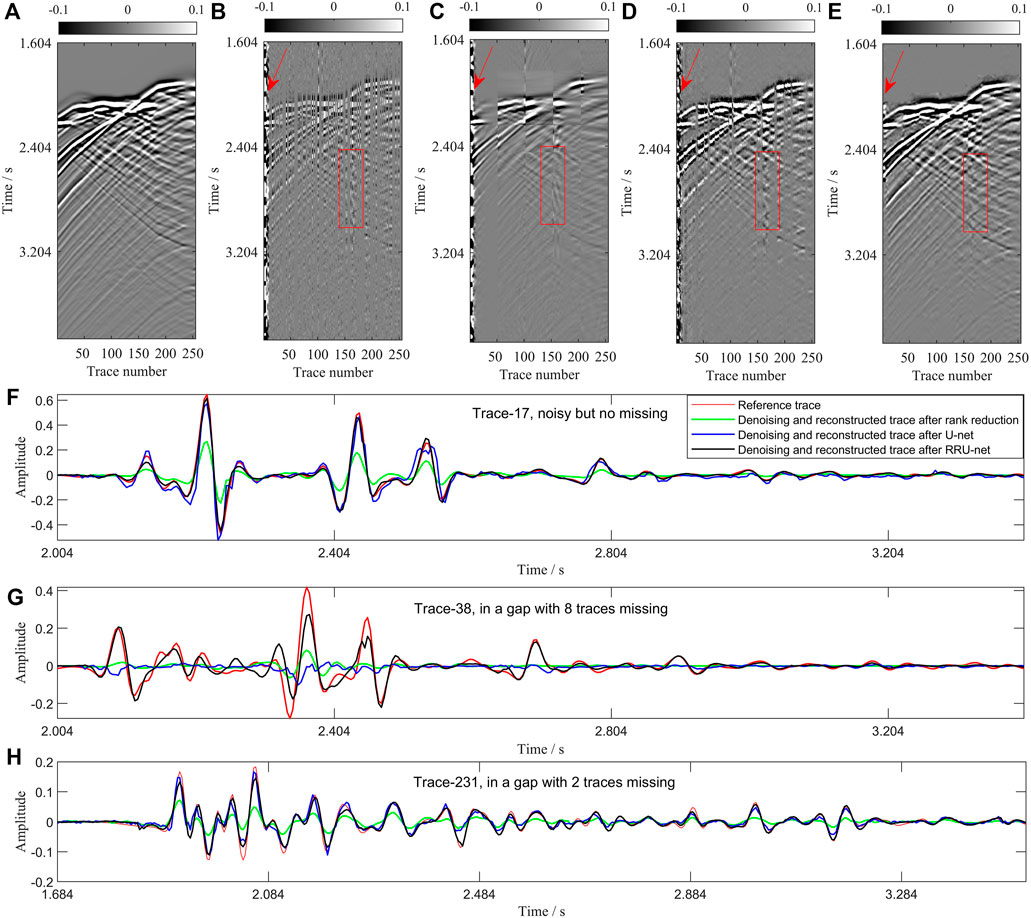
FIGURE 8. Simultaneous reconstruction and denoising results of the three methods on synthetic data generated using the Marmousi2 model. (A) Synthetic noise-free complete signal data. (B) Original gather with noise and the trace missing percentage is 63%. (C) Result by rank reduction. (D) Result by U-net. (E) Result by RRU-net. (F–H) One-dimensional waveform comparison.

Field data application

To further prove the effectiveness of the proposed method, two real DAS-VSP gathers are tested. The data contain 5001 samples along the time axis with a 1-ms time interval and 204 receivers along the well with a 0.1-m space interval as shown in Figures 9Ai,Ei. The signal in Figures 9Ai,Ei is strongly contaminated by several types of noise, and nearly 50% of the traces are missing. The denoised and reconstructed results by rank reduction, U-net, and RRU-net are presented in Figures 9Bi–Di, Fi–Hi, respectively. The rank reduction method in Figures 9Bi,Fi shows the ability to suppress the background noise but fails to preserve the signal events. The RRU-net could suppress the strong ringing noise (red arrows) and the horizontal noise (red rectangles) in Figures 9Di,Hi, while the other two methods could not (Figures 9Bi,Ci,Fi,Gi). At the same time, the RRU-net method also performs very well in recovering the missing signals. The FK spectrum in Figures 9Aii–Dii,Eii–Hii further illustrates the validity of this algorithm.

FIGURE 9

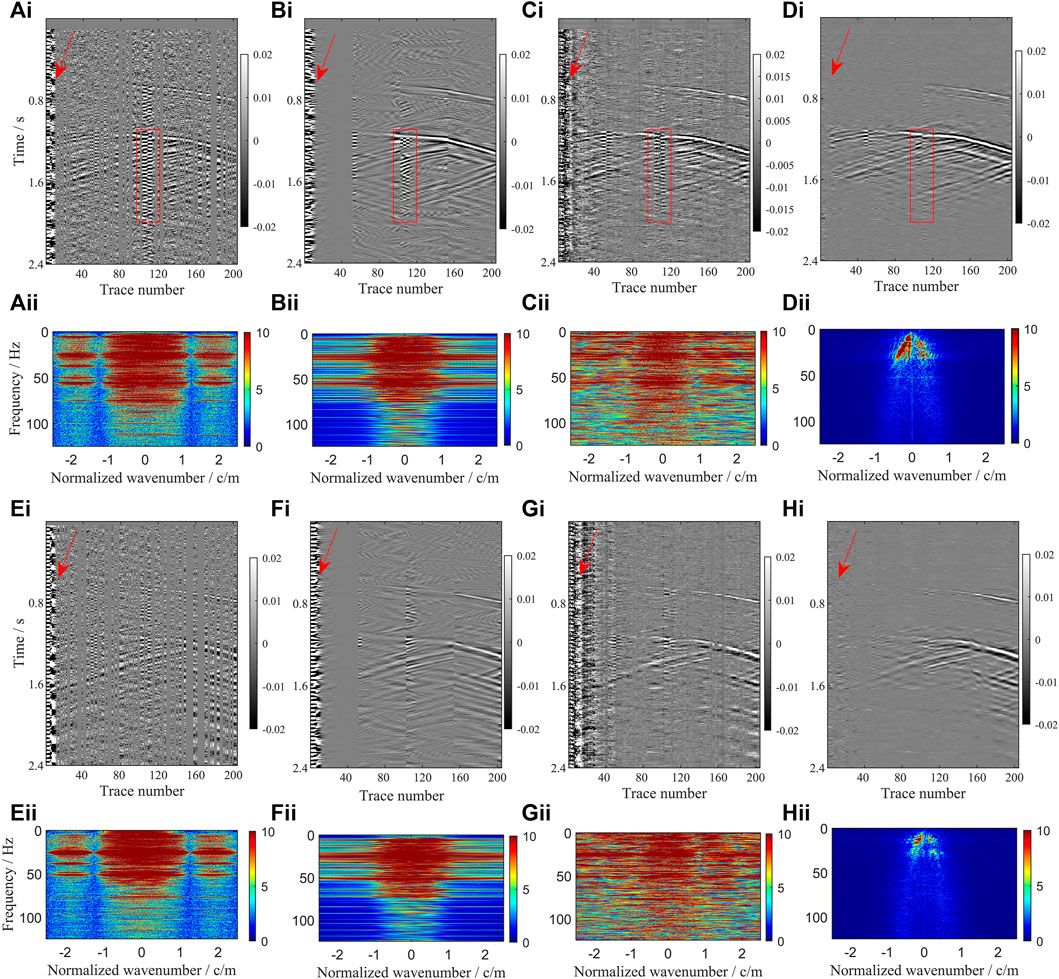
FIGURE 9. Simultaneous reconstruction and denoising results of the three methods in field DAS-VSP data. (Ai) Original field DAS-VSP data, shot1. (Bi) Result of (Ai) by rank reduction. (Ci) Result of (Ai) by U-net. (Di) Result of (Ai) by RRU-net. (Aii–Dii) FK spectrum of (Ai–Di), respectively. (Ei) Original field DAS-VSP data, shot1. (Fi) Result of (Ei) by rank reduction. (Gi) Result of (Ei) by U-net. (Hi) Result of (Ei) by RRU-net. (Eii–Hii) FK spectrum of (Ei–Hi), respectively.

Testing the trained RRU-net on both synthetic and field data indicates its ability to reconstruct randomly missing data with high accuracy on different datasets, which validates the feasibility and generalization capacity of the proposed method.

Conclusion

We proposed the RRU-net to simultaneously pursue the reconstruction and denoising of the massive DAS-VSP seismic data. It is difficult for training the U-net directly with $t-x$-domain data to extract the mapping relationship between noisy incomplete data and noise-free complete data, but the RRU-net proposed in this article can achieve this. Compared with the traditional rank reduction method, the RRU-net avoids the difficulties of selecting the rank parameters and a large amount of computation for SVD. These advantages enable the RRU-net to achieve better results in simultaneous reconstruction and denoising of DAS-VSP seismic data with higher efficiency. Both synthetic data and real DAS-VSP seismic data demonstrate the effectiveness of RRU-net in noise suppression (background noise, ringing noise, and horizontal noise) and signal reconstruction.

There are still issues that require further investigation in the simultaneous reconstruction and denoising of DAS-VSP seismic data. Issues, such as preserving the weak signals, and the application of the neural network with complex convolution for seismic data in the frequency domain also need further investigation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

HT contributed to the original conception, algorithm implementation, and method validation; HT wrote the original draft of the manuscript; WM provided suggestions; and SC and WL assisted with the algorithm. All authors contributed to the study and improved the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China under grant 2021YFA0716802 and the National Natural Science Foundation of China under grants 42130808 and 41974163.

Acknowledgments

The authors appreciate the valuable suggestions and comments from Qianru Xu, Lingli Gao, Huan Song, and E. I. Evinemi. The authors thank the developers of PyTorch on which they implemented this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cadzow, J. (1988). Signal enhancement-A composite property mapping algorithm. IEEE Trans. Acoust. 36 (1), 49–62. doi:10.1109/29.1488

CrossRef Full Text | Google Scholar

Chai, X., Tang, G., Wang, S., Lin, K., and Peng, R. (2020). Deep learning for irregularly and regularly missing 3-D data reconstruction. IEEE Trans. Geosci. Remote Sens. 99, 6244–6265. doi:10.1109/TGRS.2020.3016343

CrossRef Full Text | Google Scholar

Chen, R., and Wang, Q. (2021). Seismic data reconstruction with data augmentation-based convolutional neural network. Chin. J. Eng. Geophys. 18 (4), 471–478. doi:10.3969/j.issn.1672-7940.2021.04.009

CrossRef Full Text | Google Scholar

Chen, Y., Zhang, D., Jin, Z., Chen, X., Zu, S., Huang, W., et al. (2016). Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 206 (3), 1695–1717. doi:10.1093/gji/ggw230

CrossRef Full Text | Google Scholar

Dong, X., Li, Y., Liu, F., Feng, Q., and Zhong, T. (2021). New suppression technology for the random noise in the DAS seismic data based on convolutional neural network. Chin. J. Geophys. 64 (7), 2554–2565. doi:10.6038/cjg2021O0274

CrossRef Full Text | Google Scholar

Dong, X., Zhong, T., and Li, Y. (2020). New suppression technology for low-frequency noise in desert region: The improved robust principal component analysis based on prediction of neural network. IEEE Trans. Geosci. Remote Sens. 58 (7), 4680–4690. doi:10.1109/TGRS.2020.2966054

CrossRef Full Text | Google Scholar

Falk, T., Mai, D., Bensch, R., Cicek, O., Abdulkadir, A., Marrakchi, Y., et al. (2019). U-Net: deep learning for cell counting, detection, and morphometry. Nat. Met. 16, 67–70. doi:10.1038/s41592-018-0261-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, W., Fu, L., Zhang, M., and Li, Z. (2021). Seismic data interpolation based on U-net with texture loss. Geophysics 86 (1), 41–54. doi:10.1190/geo2019-0615.1

CrossRef Full Text | Google Scholar

Feng, Q., and Li, Y. (2022). Denoising deep learning network based on singular spectrum analysis-DAS seismic data denoising with multichannel SVDDCNN. IEEE Trans. Geosci. Remote Sens. 60, 1–11. doi:10.1109/TGRS.2021.3071189

CrossRef Full Text | Google Scholar

Gao, J., Sacchi, M., and Chen, X. (2011). “A fast rank reduction method for the reconstruction of 5D seismic volumes,” in SEG technical Program expanded abstracts 2011 (San Antonio, Texas: Society of Exploration Geophysicists), 3622–3626. doi:10.1190/1.3627953

CrossRef Full Text | Google Scholar

Jia, Y., and Ma, J. (2017). What can machine learning do for seismic data processing? An interpolation application. Geophysics 82 (3), 163–177. doi:10.1190/geo2016-0300.1

CrossRef Full Text | Google Scholar

Jia, Y., Yu, S., and Ma, J. (2018). Intelligent interpolation by Monte Carlo machine learning. Geophysics 83 (2), 83–97. doi:10.1190/geo2017-0294.1

CrossRef Full Text | Google Scholar

Jiang, J., Ren, H., and Zhang, M. (2021). A convolutional autoencoder method for simultaneous seismic data reconstruction and denoising. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2021.3073560 https://ieeexplore.ieee.org/abstract/document/9416991

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). Image Net classification with deep convolutional neural networks. Adv. neural Inf. Process. Syst. 25.

Google Scholar

Li, W., and Wang, J. (2021). Residual learning of cycle-GAN for seismic data denoising. IEEE Access 9, 11585–11597. doi:10.1109/ACCESS.2021.3049479

CrossRef Full Text | Google Scholar

Liu, G., Reda, F., Shih, K., Wang, T., Tao, A., and Catanzaro, B. (2018). “Image inpainting for irregular holes using partial convolutions,” in Proceedings of the European Conference on Computer Vision (ECCV), 85–100.

CrossRef Full Text | Google Scholar

Mandelli, S., Borra, F., Lipari, V., Bestagini, P., Sarti, A., and Tubaro, S. (2018). “Seismic data interpolation through convolutional auto encoder,” in SEG technical Program expanded abstracts 2018 (Anaheim, CA: Society of Exploration Geophysicists), 4101–4105. doi:10.1190/segm2018-2995428.1

CrossRef Full Text | Google Scholar

Miller, D., Parker, T., Kashikar, S., Todorov, M., and Bostick, T. (2012). Vertical seismic profiling using a fibre-optic cable as a distributed acoustic sensor. Copenhagen, Denmark: EAGE publications. doi:10.3997/2214-4609.20148799

CrossRef Full Text | Google Scholar

Oliveira, D., Ferreria, R., Silva, R., and Brazil, E. (2018). Interpolating seismic data with conditional generative adversarial networks. IEEE Geosci. Remote Sens. Lett. 15 (12), 1952–1956. doi:10.1109/LGRS.2018.2866199

CrossRef Full Text | Google Scholar

Oropeza, V., and Sacchi, M. (2011). Simultaneous seismic data de-noising and reconstruction via multichannel singular spectrum analysis. Geophysics 76 (3), 25–32. doi:10.1190/1.3552706

CrossRef Full Text | Google Scholar

Popa, J., Minkoff, S., and Lou, Y. (2021). An improved seismic data completion algorithm using low-rank tensor optimization: Cost reduction and optimal data orientation. Geophysics 86 (3), 219–232. doi:10.1190/geo2020-0539.1

CrossRef Full Text | Google Scholar

Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-Net: Convolutional network for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention (Cham: Springer), 234–241.

CrossRef Full Text | Google Scholar

Sacchi, M. (2009). “FX singular spectrum analysis,” in Cspg cseg cwls convention, 392–395.

Google Scholar

Siahkoohi, A., Kumar, R., and Herrmann, F. (2019). “Deep-learning based ocean bottom seismic wavefield recovery,” in SEG technical Program expanded abstracts 2019 (San Antonio, Texas: Society of Exploration Geophysicists), 2232–2237. doi:10.1190/segm2019-3216632.1

CrossRef Full Text | Google Scholar

Trickett, S. (2008). “F-xy Cadzow noise suppression,” in SEG technical Program expanded abstracts 2008 (Las Vegas, Nevada: Society of Exploration Geophysicists), 2586–2590. doi:10.1190/1.3063880

CrossRef Full Text | Google Scholar

Wang, B., Zhang, N., Lu, W., and Wang, J. (2019). Deep-learning-based seismic data interpolation: A preliminary result. Geophysics 84 (1), 11–20. doi:10.1190/geo2017-0495.1

CrossRef Full Text | Google Scholar

Wang, F. (2020). Research on seismic data denosing and reconstruction using deep learning. Hangzhou: Zhejiang University.

Google Scholar

Wang, Y., Lu, W., Liu, J., Zhang, M., and Miao, Y. (2019). Random seismic noise attenuation based on data augmentation and CNN. Chin. J. Geophys. 62 (1), 421–433. doi:10.6038/cjg2019M0385

CrossRef Full Text | Google Scholar

Zhong, T., Cheng, M., Lu, S., Dong, X., and Li, Y. (2021). Rcen: A deep-learning-based background noise suppression method for DAS-VSP records. IEEE Geosci. Remote Sens. Lett. 19, 1–5. doi:10.1109/LGRS.2021.3127637

CrossRef Full Text | Google Scholar