Study on flow model of multi-stage fracturing horizontal well in stress-denpendent dual medium reservoir

Often with abundant of natural fracture, Carbonate reservoirs are characterized with the stress sensitive and dual media. Mostly, its flow model solved by numerical method. In this paper, the semi-analytical solution for this problem is presented: firstly, the point source function considering stress sensitivity in infinite dual medium reservoir is obtained in Laplace space by Perturbation Transformation and Laplace Transformation; Secondly, the Laplace space solution of multi-stage fracturing horizontal well in infinite plate reservoir is obtained by Image Principle and Superposition Principle; Finally, the spacial solution of multi-stage fracturing horizontal well is obtained by Stehfest numerical inversion and perturbation inverse transformation. The calculation results show that the flow regime of multi-stage fracturing horizontal well can be divided into six stages: Ⅰ- linear flow, Ⅱ-first radial flow, Ⅲ-double radial flow, Ⅳ-radial flow of natural fracture system, Ⅴ-channeling flow regime and Ⅵ-radial flow of the whole system. The impact of stress sensitivity of formation permeability on linear flow is lower, and mainly affecting the last five flow regimes, and the dimensionless pressure drop derivative curve tends to rise in the later stage of development, showing the characteristics of closed boundary. In this paper, when the reservoir stress sensitivity is not considered, the calculation results will produce a large error, and the wrong well test interpretation will be obtained.

1 Introduction

Most carbonate reservoirs are rich in natural fractures, which were first described by Barenblatt et al. (1960) (Barenblatt and Zheltov, 1960). They assume that there are two flow systems in reservoir:matrix and fracture, and matrix provides main storage space; then fracture is main flow channel. The system is evenly distributed in the fracture system, and the flow rate between them is proportionate to pressure difference. Warren and Root (1962) (Warren and Root, 1963) Based on Barenblatt (Barenblatt and Zheltov, 1960) established the double well test model of heavy medium reservoir; It provides a theoretical basis for well test analysis of natural fractured reservoir. Later, scholars (Kazemi, 1969; De Swaan, 1976) established the flow equations of unsteady channeling flow between matrix and fracture system, and these models laid the foundation for the study of dual medium flow. Based on these models, scholars (Ozkan, 1988; Ozkan and Raghavan, 1991; Chen and Raghavan, 1996; El-Banbi and Wattenbarger, 1998; Bello and Wattenbarger, 2010; Brown et al., 2011; Zhao et al., 2014; Chen et al., 2015; Jia et al., 2015; Luo and Tang, 2015) established unsteady pressure models for vertical wells, horizontal wells, staged fracturing horizontal wells and volumetric fracturing horizontal wells. However, these models assume that the permeability of fracture system and matrix system is fixed, and the permeability stress sensitivity effect is not considered.

Stress sensitive effect refers to that compression of rock causes the reduction of porosity, permeability due to the pressure decrease increase confining pressure as production of oil wells. Since the early 1950s, foreign scholars (Fatt and Davis, 1952; Fatt, 1953; Wyble, 1958; Gray et al., 1963) have studied the stress sensitivity effect of single medium through lab experiments; It is found that the influence of rock stress sensitivity on permeability is greater than that on porosity. In 1971, Vairogs (Vairogs et al., 1971) carried out stress sensitivity experiments on rock samples of different initial permeability (0.04md ∼ 191md) and different properties (whether with micro-fractures and shale zones). The experimental results show that the lower the initial permeability is, the greater the stress sensitivity effect is; The existence of micro-fractures and shale zones aggravate the stress sensitivity effect. Stress sensitivity has a great impact on reservoir flow law and oil well productivity, and can reduce the production of oil wells by 50% (Vairogs and Rhoades, 1973). Pedrosa and Petrobras (1986) (Pedrosa, 1986) found that the change of rock sample permeability was exponentially related to the pressure drop based on the stress sensitivity experiment; The permeability modulus is proposed and the quantitative relationship between permeability and pressure to drop is established. Then, an analytical model of unsteady pressure under the fixed production condition of infinite stress sensitive reservoir is established by perturbation transformation. The calculation results show that with the progress of production, the dimensionless bottom hole pressure will rise like the influence of “closed boundary”. After that, scholars (Zhang and Ambastha, 1994; Chin et al., 2000; Franquet et al., 2004; Raghavan and Chin, 2004; Guo et al., 2005; Ali and Sheng, 2015; Wang and Marongiu-Porcu, 2015) conducted a lot of research on the flow law of stress sensitive reservoir. The research results show that in stress sensitive reservoir, if the change of permeability with pressure is not considered, it will cause large errors. However, the above calculation models are based on single heavy medium reservoir.

Vairogs et al, (1971) conducted stress sensitivity experiments on fractured reservoirs, scholars (Jia-Jyun et al., 2010; Cho et al., 2012; Han et al., 2013) also conducted stress sensitivity experiments on dual media reservoirs. The experimental results show that stress sensitivity has a great influence on permeability in dual medium reservoir. Scholars (Tong et al., 1999; Su et al., 2000; Tong et al., 2001; Tong et al., 2002; Tong and Zhang, 2003; MA et al., 2007) established the flow control equation considering the influence of stress sensitivity based on the dual medium flow model, and solved the model by numerical method. So far, no scholar has given a semi analytical solution to the flow model based on Kazemi, (1969) dual medium reservoir considering the influence of stress sensitivity. Based on Kazemi (Kazemi, 1969) dual medium model, this paper applies Pedrosa (Pedrosa, 1986) permeability calculation formula; The flow model of dual media reservoir considering stress sensitivity is established. Then, through perturbation transformation and Laplace transformation, the point source function of infinite dual medium reservoir considering stress sensitivity is obtained in Laplace space. Secondly, the Laplace space solution of staged fracturing horizontal well in infinite plate reservoir is obtained by image principle and superposition principle. Finally, the spatiotemporal solution of staged fractured horizontal wells is obtained through Stehfest (Stehfest, 1970) numerical inversion and perturbation inverse transformation.

2 Physical model description

Dual media reservoir is composed of matrix system and fracture system, which provides main reservoir space; The fracture system provides a channel for fluid flow. Kazemi (Kazemi, 1969) gives a simplified schematic diagram of dual media reservoir, as shown in Figure 1.

FIGURE 1

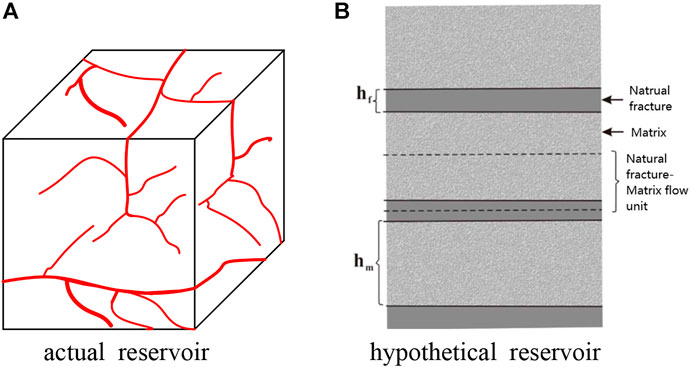
FIGURE 1. Schematic diagram of dual medium reservoir. (A) Actual reservoir; (B) Hypothetical reservoir.

Assume that there is a point source in the infinite dual medium reservoir, which is infinitely small on the reservoir scale; Large enough on the micro scale. When t = 0, the generated production at this point is $\stackrel{\sim }{q}$, and the fluid flow is caused near this point due to the output of liquid.

Assumption of the mode.

a. The reservoir is composed of matrix system and fracture system. The flow between the two systems is unsteady channeling flow, and the matrix system is evenly distributed in the fracture system;

b. Matrix system is the main storage space and fracture system is the main flow channel; All oil well production comes from the inflow of fracture system;

c. Considering the permeability sensitivity of fracture system, the permeability of matrix system is assumed to be constant;

d. There is a point source in the reservoir in production, the initial pressure of the reservoir is, and the temperature is constant during production;

e. The fluid in the reservoir can be either oil or gas. When the gas pressure is expressed by pseudo pressure, the form of flow control equation is consistent with that of oil; Therefore, the model established in this paper is also applicable to gas reservoirs.

The flow model of formation pressure change caused by the output of fluid at the point source is established below.

3 Establishment of point source function for infinite stress sensitive dual media reservoir

3.1 Flow in matrix system

The flow control equation of matrix system is:

$\{\begin{array}{l}\frac{k_m}{\mu }\frac{{\partial }^2{p}_m}{\partial z^2}={\varphi }_m{c}_m\frac{\partial p_m}{\partial t}\\ p_m\left(z,0\right)=p_i\\ {\frac{\partial p_m}{\partial z}|}_{z=0}=0\\ {p_m|}_{z=h_m/2}=p_f\end{array}(1)$

If the dimensionless parameter in Appendix 1 is introduced, Eq. 1 can be dimensionless as:

$\{\begin{array}{l}\frac{{\partial }^2\Delta p_m}{\partial z_D^2}=\frac{3\left(1-\omega \right)}{\lambda }\frac{\partial \Delta p_m}{\partial t_D}\\ \Delta p_m\left(z_D,0\right)=0\\ {\frac{\partial \Delta p_m}{\partial z_D}|}_{z_D=0}=0\\ {\Delta p_m|}_{z_D=1}=\Delta p_f\end{array}(2)$

Laplace transform Eq. 2 to obtain:

$\{\begin{array}{c}\frac{d^2\Delta {\overline{p}}_m}{d{z}_D^2}=\frac{3\left(1-\omega \right)}{\lambda }s\Delta {\overline{p}}_m\\ \begin{array}{l}\frac{d\Delta {\overline{p}}_m}{d{z}_D}\left(z_D=0,s\right)=0\\ \Delta {\overline{p}}_m\left(z_D=1,s\right)=\Delta {\overline{p}}_f\end{array}\end{array}(3)$

The general solution of Eq. 3 is expressed as

$\Delta {\overline{p}}_m=A\cosh \sqrt{\frac{3}{\lambda }\left(1-\omega \right)s}\cdot z_D+B\sinh \sqrt{\frac{3}{\lambda }\left(1-\omega \right)s}\cdot z_D(4)$

Substitute in the boundary conditions and simplify

$\Delta {\overline{p}}_m=\Delta {\overline{p}}_f\frac{\cosh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\cdot z_D}{\cosh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}}(5)$

The derivative of Eq. 5, then the derivation of ${\overline{p}}_m$ is obtained:

${\left(\frac{d\Delta {\overline{p}}_m}{d{z}_D}\right)}_{z_D=1}=\Delta {\overline{p}}_f\sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\tanh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}(6)$

The calculation formula of channeling flow from matrix system to fracture system is (Nanba, 1991):

$Q_m=\frac{2}{h_m}\frac{A{k}_m}{\mu V_m}{\left(\frac{\partial \Delta p_m}{\partial z_D}\right)}_{z_D=1}(7)$

Laplace transform equation (7) to obtain:

${\overline{Q}}_m=\frac{2k_m}{\mu h_m}{\left(\frac{A}{V}\right)}_m{\left(\frac{d{\overline{p}}_m}{d{z}_D}\right)}_{z_D=1}(8)$

Eq. 6 is introduced into Eq. 8 and simplified to:

${\overline{Q}}_m=\Delta {\overline{p}}_f{C}_Q(9)$

The expression of $C_Q$ in Eq. 9 is:

$C_Q=\frac{k_m}{\mu }{\left(\frac{2}{h_m}\right)}^2\sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\tanh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}(10)$

3.2 Flow model of fracture system

The flow control equation of fracture system is

$\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \Delta p_f}{\partial r}\right)-\frac{\mu }{k_f}{Q}_m=\frac{{\left(\varphi c_t\right)}_f\mu }{k_f}\frac{\partial \Delta p_f}{\partial t}(11)$

Considering the stress sensitivity of fracture system, fracture permeability can be expressed as (Pedrosa, 1986):

$k_f=k_{if}{e}^{-\alpha \left(p_i-p_f\right)}(12)$

Substitute equation (12) into equation (11):

$\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial \Delta p_f}{\partial r}\right)-\frac{\mu }{k_{if}{e}^{-\alpha \left(p_i-p_f\right)}}{Q}_m=\frac{{\left(\varphi c_t\right)}_f\mu }{k_{if}{e}^{-\alpha \left(p_i-p_f\right)}}\frac{\partial \Delta p_f}{\partial t}(13)$

If the dimensionless parameter in Annex A is introduced, Eq. 13 is dimensionless as follows:

$e^{-\alpha \Delta p_f}\frac{1}{r_D^2}\frac{\partial }{\partial r_D}\left(r_D^2\frac{\partial \Delta p_f}{\partial r_D}\right)-\frac{\mu L^2}{k_{if}}{Q}_m=\omega \frac{\partial \Delta p_f}{\partial t_D}(14)$

Eq. 14 is a strongly nonlinear partial differential equation, and perturbation transformation is introduced:

$\Delta p_f=-\frac{\ln \left(1-\alpha \eta \right)}{\alpha }(15)$

Eq. 15 is substituted into Eq. 14 and simplified to:

$\frac{1}{r_D^2}\frac{\partial }{\partial r_D}\left(r_D^2\frac{\partial \eta }{\partial r_D}\right)-\frac{\mu L^2}{k_{if}}{Q}_m=\frac{\omega }{\left(1-\alpha \eta \right)}\frac{\partial \eta }{\partial t_D}(16)$

The neutralization $\eta$ and $1/\left(1-\alpha \eta \right)$ in formula (16) is written as a power series in the form of:

$\eta ={\eta }_0+\alpha {\eta }_1+{\alpha }^2{\eta }_2+{\alpha }^3{\eta }_3+\dots (17)$

$\frac{1}{1-\alpha \eta }=1+\alpha \eta +{\alpha }^2{\eta }^2+{\alpha }^3{\eta }^3+\dots (18)$

Due to the low permeability modulus $\alpha$, scholars Yeung et al. (Yeung et al., 1993) believe that the 0-order perturbation solution fully meets the needs of engineering calculation. Take Eq. 17–18 and substitute the 0-order perturbation transformation into Eq. 16 and simplify it to:

$\frac{1}{r_D^2}\frac{\partial }{\partial r_D}\left(r_D^2\frac{\partial {\eta }_0}{\partial r_D}\right)-\frac{\mu L^2}{k_{if}}{Q}_m=\omega \frac{\partial {\eta }_0}{\partial t_D}(19)$

By Laplace transformation of Eq. 19 and combining with the initial condition equation (B-12), it is simplified as follows:

$\frac{1}{r_D^2}\frac{d}{d{r}_D}\left(r_D^2\frac{d{\overline{\eta }}_0}{d{r}_D}\right)-\frac{\mu L^2}{k_{if}}{\overline{p}}_f{C}_Q=\omega s{\overline{\eta }}_0(20)$

Eq. 9 is substituted into Eq. 20 and simplified to:

$\frac{1}{r_D^2}\frac{d}{d{r}_D}\left(r_D^2\frac{d{\overline{\eta }}_0}{d{r}_D}\right)-\left[\omega +\frac{\lambda }{3s}\sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\tanh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\right]s{\overline{\eta }}_0=0(21)$

Then:

$f\left(s\right)=\omega +\frac{\lambda }{3s}\sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}\tanh \sqrt{\frac{3\left(1-\omega \right)s}{\lambda }}$

Then Eq. 21 can be written as:

$\frac{d^2{\overline{\eta }}_0}{d{r}_D^2}+\frac{2}{r_D}\frac{d{\overline{\eta }}_0}{d{r}_D}-sf\left(s\right){\overline{\eta }}_0=0(22)$

Then:

$g=r_D{\overline{\eta }}_0(23)$

Then equation (22) can be transformed into:

$\frac{d^{2}g}{d{r}_D^2}-sf\left(s\right)g=0(24)$

Eq. 24 is a conventional unary differential equation, and it is easy to obtain the general solution. Then, the solution of the equation can be obtained based on the initial conditions and boundary conditions (for specific steps, see reference (Ren et al., 2017)). Through the mirror image principle, the calculation formula of unsteady pressure of vertical fractured wells in plate reservoir is as follows:

${\overline{\eta }}_{D0}={\overline{q}}_D{\int }_{x_{wD}-L_{Df}}^{x_{wD}+L_{Df}}{K}_0\left(\sqrt{{\left(x_D-\xi \right)}^2+{\left(y_D-y_{wD}\right)}^2}\sqrt{sf\left(s\right)}\right)d\xi (25)$

4 Unsteady pressure model of staged fracturing horizontal well in infinite closed plate reservoir

Considering the mutual interference between fractures, according to the superposition principle, the dimensionless pressure drop ${\overline{\eta }}_{D0i}$ of any fracture expressed as:

${\overline{\eta }}_{D0i}={\displaystyle \sum }_{j=1}^N{\overline{q}}_{fDj}{\overline{\eta }}_{D0i,j}(26)$

In formula (26), ${\overline{q}}_{fDj}$ is the dimensionless rate of the j_th fracture; ${\overline{\eta }}_{D0i,j}$ is the dimensionless pressure drop of the j_th fracture at the i_th fracture (this value can be calculated by Eq. 25).

Without considering the flow resistance of fractures, then:

$\begin{array}{cc}{\overline{\eta }}_{D0i}={\overline{\eta }}_{wD}& i\mathrm{1,2},\dots ,N\end{array}(27)$

${\overline{\eta }}_{wD}$ is the dimensionless pressure drop at the bottom of horizontal well in Eq. 27

The sum of dimensionless production of each fracture is 1, which is expressed as:

${\displaystyle \sum }_{j=1}^N{\overline{q}}_{fDj}=1/\mathrm{s}(28)$

Eqs. 26–28 are written in matrix form as follows:

$\left[\begin{array}{ccccc}{{\overline{\eta }}_{D0}}_{\mathrm{1,1}}& {{\overline{\eta }}_{D0}}_{\mathrm{1,2}}& \cdots & {{\overline{\eta }}_{D0}}_{1,N}& -1\\ {{\overline{\eta }}_{D0}}_{\mathrm{2,1}}& {{\overline{\eta }}_{D0}}_{\mathrm{2,2}}& \cdots & {{\overline{\eta }}_{D0}}_{2,N}& -1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ {{\overline{\eta }}_{D0}}_{N,1}& {{\overline{\eta }}_{D0}}_{N,2}& \cdots & {{\overline{\eta }}_{D0}}_{N,N}& -1\\ 1& 1& \cdots & 1& 0\end{array}\right]\left[\begin{array}{c}{\overline{q}}_{fD1}\\ {\overline{q}}_{fD2}\\ ⋮\\ {\overline{q}}_{fD,N}\\ {\overline{\eta }}_{wD}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1/s\end{array}\right](29)$

There are unknowns in Eq. 29, including ${\overline{q}}_{fDj}$ $\left(j=\mathrm{1,2},\dots ,N\right)$ and ${\overline{\eta }}_{wD}$ the number of equations is N+1 as well. Therefore, the equations are solvable, and the solution of the unknown in Laplace space can be obtained by Gauss Jordan elimination method. Using Stehfest (Stehfest, 1970) numerical inversion, Laplace space solution can be transformed into space solution ${\eta }_{wD}$. Then, the dimensionless bottom hole pressure is obtained from the perturbation inverse transformation (15).

5 Analysis of calculation results of pressure model of staged fracturing horizontal well in dual medium reservoir

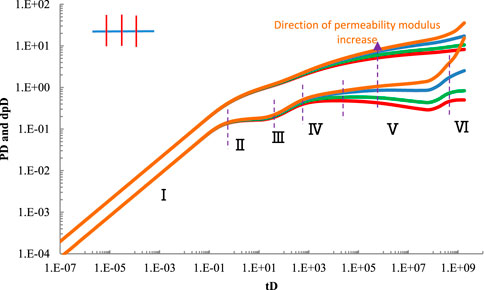
5.1 Flow regime divisions of staged fracturing horizontal wells in stress sensitive reservoirs

There are three vertical fractures with equal spacing and length in the stress sensitive dual medium reservoir. When the fracture half length $L_{fD}=6$, spacing $L_{fD}=6$, storage capacity ratio $\omega =0.1$, cross to flow coefficient $\lambda ={10}^{-8}$ and permeability modulus $\alpha$ are 0, 0.05, 0.1 and 0.12 respectively, the initial pressure of the reservoir is 34.5 MPa and the production is 15.8 m³/d. The relationship curve between dimensionless bottom hole pressure drop, dimensionless pressure drop derivative and dimensionless time in the double logarithmic coordinate system is shown in Figure 2.

FIGURE 2

FIGURE 2. well test curves of three vertical fracture horizontal.

According to the relationship curve between dimensionless pressure drop derivative and time in Figure 2, the flow of staged fracturing horizontal well reservoir in stress sensitive dual medium reservoir can be divided into six flow regimes. I is linear flow. Because the reservoir pressure drop is small, the reservoir stress sensitivity has little effect on this stage. The reservoir fluid flows into the artificial fractures linearly, and the slope of the pressure drop derivative curve in Figure 2 is 0.5. The reservoir only uses the area between the artificial fractures. II. The first radial flow. In this flow process, there is no mutual interference between artificial fractures, and the slope of the corresponding pressure drop derivative is almost 0. It is known from the curve in Figure 2 that the reservoir pressure drop is affected by stress sensitivity. III. double radial flow, mutual interference between artificial fractures has occurred; The reservoir pressure decreases further, and the greater the permeability modulus, the higher the well test curve. Ⅳ radial flow in natural fracture system. V. in the stage of channeling flow, there is channeling flow from bedrock system to fracture system in dual medium reservoir; This stage shows a “groove” on the dimensionless pressure derivative curve. The position and depth of the “groove” are affected by the cross flow coefficient and storage capacity ratio respectively. At this time, the influence of stress sensitivity on bottom hole pressure is very obvious. Ⅵ for the radial flow of the whole system, the well test curve rises significantly with the increase of permeability modulus; It shows the characteristics of closed boundary influence (Huang et al., 2015; Ren et al., 2017; Ren et al., 2019a).

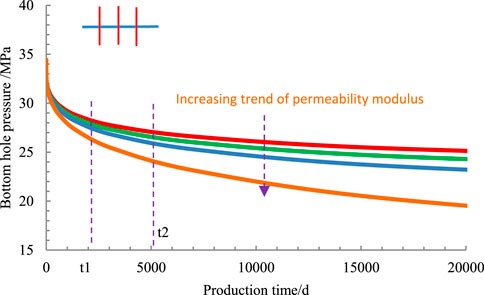
5.2 Effect of permeability modulus on bottom hole pressure and oil well production

Other data are the same as 4.1, when the permeability modulus $\alpha$ is 0, 0.05, 0.1 and 0.2 respectively; The relationship curve between bottom hole flow pressure and production time is shown in Figure 3.

FIGURE 3

FIGURE 3. Sensitivity analysis of permeability modulus to BHP.

It can be seen from Figure 3 that when the production of fractured horizontal wells remains unchanged, the greater the permeability modulus, the greater the bottom hole differential pressure required to produce the same production. At times t1 (2000 days), the maximum bottom hole flow pressure is 28.5 MPa and the minimum bottom hole flow pressure is 26.3MPa; The difference between them is 2.2 MPa. At t2 time (5000 days), the maximum bottom hole flow pressure is 27.3 MPa and the minimum bottom hole flow pressure is 24.2mpa; The difference between them is 3.1Mpa. Through the comparison of bottom hole flow pressure data at two times (it can also be seen from the curve trend in the figure), with the progress of production, the stress sensitivity has a greater and greater impact on bottom hole flow pressure (Ren et al., 2016; Ren et al., 2019b; Ren et al., 2019c).

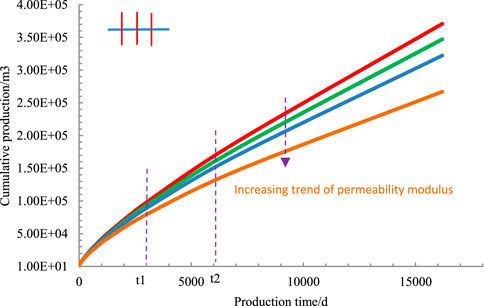
The bottom hole flowing pressure is 24MPa, and other data are consistent with 4.1. When the permeability modulus $\alpha$ is 0, 0.05, 0.1 and 0.2 respectively; The relationship curve between cumulative production and production time of fractured horizontal wells is shown in Figure 4.

FIGURE 4

FIGURE 4. Influence of permeability modulus on cumulative production of fractured horizontal Wells.

It can be seen from Figure 4 that when the production differential pressure on horizontal wells remains unchanged, the greater the permeability modulus, the smaller the cumulative production of horizontal wells. The maximum cumulative production at t1 time (3000 days) is 9.9×10⁴ m³, with a minimum cumulative yield of 8.1×10⁴ m³; The difference is 1.8×10⁴ m³。 The maximum cumulative yield at t2 time (6000 days) is 1.6×10⁵ m³, with a minimum cumulative production of 1.25×10⁵ m^3. The difference between the two is 3.5×10⁴ m³。Through the comparison of the accumulated production data onto two moments, it can be seen that the stress sensitivity has an increasing influence on the accumulated production of horizontal Wells with the progress of production.

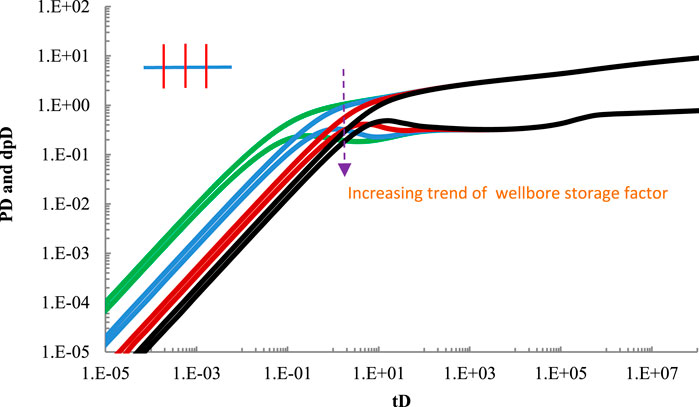
5.3 Sensitivity analysis of wellbore storage factor

Other data are consistent with 4.1. When wellbore storage factor is 0.1, 0.5, 2, 5, respectively, the well test curve of fractured horizontal well is shown in Figure 5. It can be seen from Figure 5 that the larger the wellbore storage factor, the longer the wellbore storage phase lasts. Wellbore storage factor has little influence on other seepage stages.

FIGURE 5

FIGURE 5. Sensitivity analysis of cross-flow coefficient.

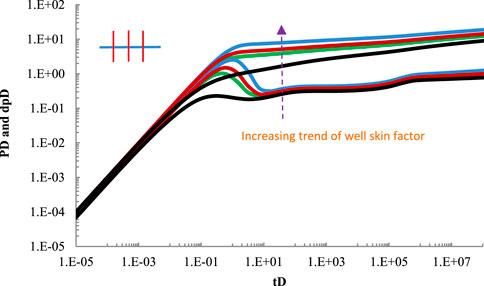
5.4 Sensitivity analysis of well skin factor

Other data are consistent with 4.1. When well skin factor is 0.5,1,3,5, respectively, the well test curve of fractured horizontal well is shown in Figure 6. As can be seen from Figure 6, the larger the skin coefficient of oil well, the longer the duration of transition flow phase and the shorter the duration of radial flow phase, and the larger the dimensionless pressure drop.

FIGURE 6

FIGURE 6. Sensitivity analysis of cross-flow coefficient.

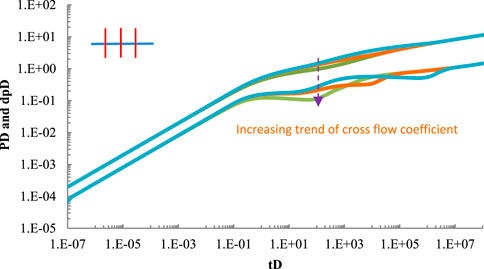
5.5 Sensitivity analysis of cross flow coefficient

Other data are consistent with 4.1. When the cross flow coefficient is ${10}^{-6}$ , ${10}^{-4}$ , ${10}^{-3}$ respectively, the well test curve of fractured horizontal well is shown in Figure 7.

FIGURE 7

FIGURE 7. Sensitivity analysis of cross-flow coefficient.

The larger the cross flow coefficient, the faster the liquid supply speed of matrix to the fracture system, and the earlier the channeling stage appears. The position of “groove” in Figure 7 is closer to the left. However, because the total liquid volume in the matrix system is certain, the dimensionless pressure drop curve tends to be consistent in the later stage of development.

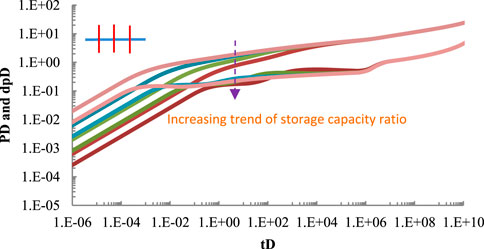
5.6 Sensitivity analysis of storage capacity ratio

Other data are consistent with 4.1. When the storage capacity ratio is 0.0001,0.001,0.01, 0.1, the well test curve of fractured horizontal well is shown in Figure 8.

FIGURE 8

FIGURE 8. Sensitivity analysis of storage ratio.

It can be seen from Figure 8 that the storage capacity ratio has a great impact on most production stages; With the increase of storage capacity ratio, the dimensionless pressure drop decreases and the duration of channeling becomes shorter and shorter; The dimensionless pressure drop derivative curve shifts to the right as a whole. Compared with the reservoir with low reservoir volume ratio, when the pressure of fracture system decreases, the reservoir with high reservoir volume ratio can quickly increase the pressure of fracture system; The pressure drop of fracture system changes little, so the “groove” duration of dimensionless pressure drop derivative is shorter.

6 Conclusion

Based on Kazemi’s dual medium flow model, the flow equation of dual medium reservoir considering stress sensitivity is established in this paper. The equation is a strongly nonlinear partial differential equation, which is linearized by introducing perturbation transformation; Then, a series of processing methods such as Laplace transform and image principle are applied to establish the non-point source function of infinite plate reservoir considering stress sensitivity. In the process of writing, the following conclusions are drawn:

1) Based on area source function and superposition principle; The unsteady pressure model of staged fracturing horizontal well under stress sensitive dual medium reservoir is established. According to the calculation, the flow period of staged fracturing horizontal well can be divided into six regimes: I is linear flow, II is first radial flow, III is double radial flow, IV is radial flow of natural fracture system, V is channeling flow regime, and VI is radial flow of the whole system.

2) With the increase of permeability stress sensitivity, the well test curve moves upward gradually. The stress sensitivity has little effect on the linear flow regime, and the dimensionless pressure drop derivative curve tends to rise in the later stage of development, showing the influence characteristics of closed boundary (see Figure 2); If the influence of permeability stress sensitivity is not considered in well test analysis, wrong well test interpretation results will be obtained. Through the calculation and analysis in part 4.2, it is known that the permeability stress sensitivity has a great impact on the bottom hole flow pressure and oil well production.

3) The sensitivity analysis of cross flow coefficient and storage capacity ratio of dual media reservoir is carried out respectively. The results show that the larger the cross flow coefficient is, the earlier the channeling stage appears. The storage capacity ratio has a great influence on the first five flow regimes. With the increase of storage capacity ratio, the duration of channeling flow becomes shorter and shorter.

The development of carbonate reservoir is greatly affected by stress sensitivity, which can not be ignored in model calculation. The semi analytical model established in this paper provides a very useful method for quickly predicting the productivity of staged fracturing horizontal wells in stress sensitive reservoirs, understanding the flow law of fractured horizontal wells, and evaluating and analyzing the fracturing effect.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZJ---Conceptualization, Methodology, Investigation, Formal Analysis, Writing—Original Draft; RZ----Conceptualization, Funding Acquisition, Resources, Supervision, Writing—Review & Editing. Others---Visualization, Writing—Review & Editing.

Funding

This work is funded by National Natural Science Foundation of China (Grant No. 51804258, 51974255), Natural Science Basic Research Program of Shaanxi Province (Grant No.2019JQ-807, 2020JM-544, 2018JM-5054, 2019JM-141), and the Youth Innovation Team of Shaanxi Universities. Scientific Research Program Funded by Shaanxi Provincial Education Department (Program No.22JS029).

Conflict of interest

Author ZG was employed by Engineering Technology Research Institute Xibu Drilling Engineering Company. Author LE was employed by Research Institute of Oil and Gas Engineering, Tarim Oilfield Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix A Definition of dimensionless variables

The dimensionless variables introduced are:

$\begin{array}{cc}{p}_{Dj}=\frac{2\pi k_{if}h\left(p_i-p_j\right)}{\mu Q}& j=f/m\end{array}$(A-1)

$q_D=\frac{\stackrel{\sim }{q}L}{Q}$(A-2)

$t_D=\frac{k_{if}t}{{\left(\varphi c\right)}_{f+m}\mu L^2}$(A-3)

$z_D=\frac{2z}{h_m}$(A-4)

$\lambda =\frac{12k_m{L}^2}{k_{if}{h}_m^2}$(A-5)

$\omega =\frac{{\left(\varphi c\right)}_f}{{\left(\varphi c\right)}_{f+m}}$(A-6)

References

Ali, T. A., and Sheng, J. J. (2015). Evaluation of the effect of stress-dependent permeability on production performance in shale gas reservoirs. West Virginia USA: Society of Petroleum Engineers. doi:10.2118/177299-MS

CrossRef Full Text | Google Scholar

Barenblatt, G. I., and Zheltov, Yu. P. (1960). Fundamental equations of filtration of homogeneous liquids in fissured rocks, “ soviet physics. Doklady 5, 522. doi:10.1016/0021-8928(60)90107-6

CrossRef Full Text | Google Scholar

Bello, R. O., and Wattenbarger, R. A. (2010). “Multi-stage hydraulically fractured horizontal shale gas well rate transient analysis,” in Paper presented at the North Africa Technical Conference and Exhibition (Cairo Egypt: Society of Petroleum Engineers). doi:10.2118/126754-MS

CrossRef Full Text | Google Scholar

Brown, M., Ozkan, E., Raghavan, R., and Kazemi, H. (2011). Practical solutions for pressure transient responses of fractured horizontal wells in unconventional Shale reservoirs. SPE Reserv. Eval. Eng. 14 (3), 663–676. doi:10.2118/125043-PA

CrossRef Full Text | Google Scholar

Chen, C., and Raghavan, R. (1996). A multiply-fractured horizontal well in a rectangular drainage region. SPE 37072 2 (04), 455–465. doi:10.2118/37072-PA

CrossRef Full Text | Google Scholar

Chen, Z., Liao, X., Zhao, X., Lv, S., and Zhu, L. (2015). A semianalytical approach for obtaining type curves of multiple-fractured horizontal wells with secondary-fracture networks. Soc. Petroleum Eng. 21 (02), 538–549. doi:10.2118/178913-PA

CrossRef Full Text | Google Scholar

Chin, L. Y., Raghavan, R., and Thomas, L. K. (2000). “Fully coupled geomechanics and fluid-flow analysis of wells with stress-dependent permeability,”, 32–45. doi:10.2118/58968-PA

CrossRef Full Text | Google Scholar

Cho, Y., Ozkan, E., and Apaydin, O. G. (2012). Pressure-Dependent natural-fracture permeability in shale and its effect on shale-gas well production. USA: Society of Petroleum Engineers. doi:10.2118/159801-MS

CrossRef Full Text | Google Scholar

De Swaan, O., A. (1976). Analytic solutions for determining naturally fractured reservoir properties by well testing. Soc. Petroleum Eng. 16 (03), 117–122. doi:10.2118/5346-PA

CrossRef Full Text | Google Scholar

El-Banbi, A. H., and Wattenbarger, R. A. (1998). “Analysis of linear flow in gas well production,” in Proceeding Paper presented at the SPE Gas Technology Symposium, (Alberta Canada: Society of Petroleum Engineers). doi:10.2118/39972-MS

CrossRef Full Text | Google Scholar

Fatt, I., and Davis, T. H. (1952). The reduction in permeability with overburden pressure. Trans. AIME 195, 329. doi:10.2118/952329-G

CrossRef Full Text | Google Scholar

Fatt, I. (1953). The effect of overburden pressure permeability on relative permeability. AIME 198, 325. doi:10.2118/953325-G

CrossRef Full Text | Google Scholar

Franquet, M., Ibrahim, M., Wattenbarger, R. A., and Maggard, J. B. (2004). Effect of pressure dependent permeability in tight gas reservoirs, transient radial flow in Proceeding Paper presented at the Canadian International Petroleum Conference (Calgary Alberta: Petroleum Society of Canada). doi:10.2118/2004-089

CrossRef Full Text | Google Scholar

Gray, D. H., Fatt, I., and Bergarnini, G. (1963). The effect of stress on permeability of sandstone cores. Soc. Petroleum Eng. J. 3, 95–100. doi:10.2118/531-pa

CrossRef Full Text | Google Scholar

Guo, X., Li, Y., Du, Z., and Shu, Z. (2005). “Numerical modelling for simulating coupled flow in stess-sensitive gas reservoirs,” in Proceding Petroleum Society of Canada. Petroleum Society of Canada, 2005–2064. doi:10.2118/2005-064

CrossRef Full Text | Google Scholar

Han, G., Gutierrez, M., and Schmitz, P. (2013). Stress-Dependent flow, mechanical, and acoustic properties for an unconventional oil reservoir rock. USA: Society of Petroleum Engineers. doi:10.1190/URTEC2013-177

CrossRef Full Text | Google Scholar

Huang, T., Guo, X., and Chen, F. (2015). Modeling transient flow behavior of a multiscale triple porosity model for shale gas reservoirs. J. Nat. Gas Sci. Eng. 23, 33–46. doi:10.1016/j.jngse.2015.01.022

CrossRef Full Text | Google Scholar

Jia, P., Cheng, L., Huang, S., and Liu, H. (2015). Transient behavior of complex fracture networks. J. Petroleum Sci. Eng. 132, 1–17. ISSN 0920-4105. doi:10.1016/j.petrol.2015.04.041-

CrossRef Full Text | Google Scholar

Jia-Jyun, D., Jui-Yu, H., Wen-Jie, W., Shimamoto, T., Hung, J. H., Yeh, E. C., et al. (2010). Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. Int. J. Rock Mech. Min. Sci. 47 (7), 1141–1157. ISSN 1365-1609. doi:10.1016/j.ijrmms.2010.06.019

CrossRef Full Text | Google Scholar

Kazemi, H. (1969). Pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution. Soc. Petroleum Eng. 9 (04), 451–462. doi:10.2118/2156-A

CrossRef Full Text | Google Scholar

Luo, W., and Tang, C. (2015). Pressure-Transient analysis of multiwing fractures connected to a vertical wellbore. Soc. Petroleum Eng. 20 (02), 360–367. doi:10.2118/171556-PA

CrossRef Full Text | Google Scholar

Ma, X., Tong, D., and Huawei, H. (2007). Non-Darcy flow analysis of fluid in deformed fractal reservoir with double porosity[J]. Chin. J. Comput. Phys. 02, 197–202.

Google Scholar

Nanba, T. (1991). Numerical simulation of pressure transients in naturally fractured reservoirs with unsteady-state matrix-to-fracture flow. Japan: Society of Petroleum Engineers. doi:10.2118/22719-MS

CrossRef Full Text | Google Scholar

Ozkan, E., and Raghavan, R. (1991). New solutions for well test analysis problems : Part1 analytical considerations. SPEFE 6 (03), 359–368. doi:10.2118/18615-PA

CrossRef Full Text | Google Scholar

Ozkan, E. (1988). Performance of horizontal wells. Tulsa. OK: U. of Tulsa. PhD dissertation.

Google Scholar

Pedrosa, O. A. (1986). Pressure transient response in stress-sensitive formations.” in Proceeding Paper presented at the SPE California Regional Meeting (Oakland: SPE California Regional Meeting), 15115 MS. doi:10.2118/15115-MS

CrossRef Full Text | Google Scholar

Raghavan, R., and Chin, L. Y. (2004). Productivity changes in reservoirs with stress-dependent permeability. Soc. Petroleum Eng. 7 (04), 308–315. doi:10.2118/88870-PA

CrossRef Full Text | Google Scholar

Ren, Z., Wu Dandan, L., et al. (2016). Semi-analytical model for transient pressure behavior of complex fracture networks in tight oil reservoirs [J]. J. Nat. Gas Sci. Eng. 33, 497–508.doi:10.1016/j.jngse.2016.09.006

CrossRef Full Text | Google Scholar

Ren, Z., Wu, X., and Han, G. (2017). Transient pressure behavior of multi-stage fractured horizontal wells in stress-sensitive tight oil reservoirs[J]. J. Petroleum Sci. Eng. 157., 1197. doi:10.1016/j.petrol.2017.07.073

CrossRef Full Text | Google Scholar

Ren, Z., Yan, R., Huang, X., Liu, W., Yuan, S., Xu, J., et al. (2019). The transient pressure behavior model of multiple horizontal wells with complex fracture networks in tight oil reservoir. J. Pet. Sci. Eng. 173, 650–665. doi:10.1016/j.petrol.2018.10.029

CrossRef Full Text | Google Scholar

Ren, Z., Du, K., and Shi, J. (2019). Semi-analytical coupled model of transient pressure behavior for horizontal well with complex fracture networks in tight oil reservoirs[J]. Math. Problems Eng. 12, 231–245.doi:10.1155/2019/6524105

CrossRef Full Text | Google Scholar

Ren, Z., Wu, X., and Han, G. (2019). Transient pressure behavior of multi-stage fractured horizontal well in stress-sensitive coal seam[J]. Int. J. Oil Gas CoalTechnology 15, 45–52. doi:10.1016/j.petrol.2017.07.073

CrossRef Full Text | Google Scholar

Stehfest, H. (1970). Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 13 (1), 47–49. doi:10.1145/361953.361969

CrossRef Full Text | Google Scholar

Su, Y., Luan, Z., and Zhang, Y. (2000). A study on development characteristics for deformed reservoir[J]. Acta Pet. Sin. 02, 51. doi:10.7623/syxb200002010

CrossRef Full Text | Google Scholar

Tong, D., and Zhang, H. (2003). Flow analysis of fluid in fractal reservoir with deformed double porosity medium[J]. J. Univ. Petroleum 04, 76China. doi:10.1007/BF02974893

CrossRef Full Text | Google Scholar

Tong, D., Zhou, D., and Chen, Q. (1999). An approximate analytical study of fluids flow in fractal reservoir with pressure-sensitive formation permeability. [J].Petroleum Explor. Dev. 03, 73

Google Scholar

Tong, D., Chen, Q., and Zong, G. (2001). Exact solution and pressure transient analysis for the flow problem of fluids flow in a bounded fractal reservoir with double porosity [J]. Acta Pet. Sin. 03, 58–62. doi:10.7623/syxb200103012

CrossRef Full Text | Google Scholar

Tong, D., Jiang, D., and Wang, R. (2002). Generalized flow analysis of fluid in deformed reservoir with double-porosity media[J]. Chin. J. Appl. Mech. 02, 141

Google Scholar

Vairogs, J., and Rhoades, V. W. (1973). Pressure transient tests in formations having stress-sensitive permeability. Soc. Petroleum Eng. 25 (08), 965–970. doi:10.2118/4050-PA

CrossRef Full Text | Google Scholar

Vairogs, J., Hearn, C. L., Dareing, D. W., and Rhoades, V. W. (1971). Effect of rock stress on gas production from low permeability reservoirs. J. Petroleum Technol. (23), 1161–1167. doi:10.2118/3001-pa

CrossRef Full Text | Google Scholar

Wang, H., and Marongiu-Porcu, M. (2015). Impact of shale-gas apparent permeability on production: Combined effects of non-Darcy flow/gas-slippage, desorption, and geomechanics. Soc. Petroleum Eng. 18 (04), 495–507. doi:10.2118/173196-PA

CrossRef Full Text | Google Scholar

Warren, J. E., and Root, P. J. (1963). The behavior of naturally fractured reservoirs. Sot. Pet. Eng. 3, 245–255. doi:10.2118/426-PA

CrossRef Full Text | Google Scholar

Wyble, D. O. (1958). Effect of applied pressure on conductivity, porosity and permeability of sandstones. Trans. AIME 213, 430. doi:10.2118/1081-G

CrossRef Full Text | Google Scholar

Yeung, K., Chakrabarty, C., and Zhang, X. (1993). An approximate analytical study of aquifers with pressure-sensitive formation permeability. Water Resour. Res. 29 (10), 3495–3501. doi:10.1029/93wr01493

CrossRef Full Text | Google Scholar

Zhang, M. Y., and Ambastha, A. K. (1994). New insights in pressure-transient analysis for stress-sensitive reservoirs.” in ProceedingPaper presented at the SPE Annual Technical Conference and Exhibition. New Orleans, Louisiana: Society of Petroleum Engineers. doi:10.2118/28420-MS

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. H., Luo, J. X., and Zhang, B. N. (2014). Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. X. 512, 447–456. doi:10.1016/j.jhydrol.2014.03.026

CrossRef Full Text | Google Scholar

Glossary

Parameter definition

$\mathit{\alpha }$ _:permeability modulus,MPa⁻¹

$\mathit{c}$ total comprehensibility, MPa⁻¹

$\mathit{g}$ : Conversion function

$\mathit{h}$ : length, m

$\mathit{H}$ : length, m

$\mathit{k}$ : permeability,m²

${\mathit{k}}_{\mathit{i}\mathit{f}}$ :Initial permeability of natural fracture,m²

$\mathit{l}$ :horizontal well length,m

${\mathit{L}}_{\mathit{f}}$ :half length of fracture,m

$\mathit{L}$ :reference length,m

$\mathit{p}$ :pressure,MPa

$\Delta \mathit{p}$ :difference from initial formation pressure,MPa

${\mathit{p}}_{\mathit{i}}$ :initial formation pressure, MPa

$\stackrel{\sim }{\mathit{q}}$ :point source instantaneous rate, m³/s;

$\mathit{Q}$ : production rate, m³/s;

s: Laplace variable

S: conversion function

t: time, s;

$\mathit{V}$ :ratio of each system to total reservoir volume

x, y, z: variables in Cartesian coordinate system,m

${\mathit{z}}_{\mathit{e}}$ :height of oil columu,m

$\mathit{\varphi }$ :porosity

$\mathit{\mu }$ :oil viscosity, Pa·s

$\mathit{\omega }$ _:storage ratio

$\mathit{\lambda }$ :channel flow

$\mathit{\sigma }$ :shape factor

subscript

m represent the matrix system

f represents the fracture system

D is dimensionless

w is location of point source

i j is hydraulic fracture