- 1Engineering Research Center of Eco-Environment in TGR Region, Ministry of Education, College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang, China
- 2State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing, China
- 3Yinshanbeilu National Field Research Station of Steppe Eco-hydrological System, China Institute of Water Resources and Hydropower Research, Hohhot, China
- 4China Fire and Rescue Institute, Beijing, China
- 5College of Resource Environment and Tourism, Capital Normal University, Beijing, China
- 6Department of Hydraulic Engineering, Tsinghua University, Beijing, China
It is essential to quantify the rate of root water uptake (RWU) and characterize the variability of RWU, which benefits understanding the water use of alpine meadows and its response to environmental changes. In addition, model simulation is one of the feasible methods to obtain the RWU characteristics of alpine meadows. However, recent research on RWU models mainly focused on crops and trees, while barely on alpine meadows. Thus, it is of great significance to develop an RWU model applicable to alpine meadows, which can describe local plant water consumption processes. In this paper, we measured the distribution characteristics of root density and soil characteristics of alpine meadows in the Qinghai-Tibet Plateau (QTP) with prototype observation experiments. The root length density (RLD) of the wilting stage decreased by 16.2% on average compared to the re-greening stage, and the ability of root growth was poorer in the high altitude area. Based on the distribution characteristics of root length density (RLD) and the three soil resistance indexes (soil water potential, soil hydraulic diffusivity, and soil hydraulic conductivity), which have obvious impacts on RWU. The improved Feddes model, Selim-Iskandar model, and Molz-Remson model were selected to simulate the RWU in alpine meadows, which fully considered the above impact factors, but the applicability in alpine meadows was not discussed. The results showed that the model performance of the Selim-Iskandar model was better than the improved Feddes model and Molz-Remson model, and its simulation performance was improved by 44.76 and 22.16% compared to the improved Feddes model and Molz-Remson model, respectively. Based on the quantified RWU rate, the RWU characteristics showed that the top 50% of the rhizosphere was responsible for 72.65% of the water uptake of the entire rhizosphere. At the same time, the obvious difference in RWU rate in different phenological stages was obvious, showing that the RWU rate in the re-greening stage increased by 36.52% compared to that in the wilting stage. This study can provide technical support for a more accurate estimation of transpiration and water use efficiency in alpine meadows, and could provide theoretical support for the implementation of vegetation.
1 Introduction
Root water uptake (RWU) is an important process in plant growth and a key link in the SPAC system (Soil-Plant-Atmosphere continuum) (Boanares et al., 2020). The plants extract water from the soil through their roots and release it into the atmosphere in the form of foliar transpiration. In the context of a warming climate, to quantify the root water use capacity on the soil profile is critical to understanding the impact of warming on the water balance of ecosystems and sound water management policies.
The Qinghai-Tibet Plateau (QTP) is one of the regions most significantly affected by climate change globally (Yuke, 2019), and because of its unique climatic characteristics, alpine meadows with more fragile ecosystems grow extensively (Jin et al., 2019). Studies have shown that the increase in temperature will affect the temporal stability of plant biomass (Ma et al., 2017), and under warming conditions, alpine meadows show a clear trend of degradation (Qian et al., 2022), and nowadays, its restoration has become a key concern for scholars (Wang S. R. et al., 2020).
Water is a key factor for plant growth, and the root is an important organ for plant water use. Differences in the morphological characteristics of root distribution will directly affect the ability of water consumed by plants (Zheng et al., 2022), and studies have shown that limited water availability is a major factor in alpine meadow degradation (Cai et al., 2015). Therefore, investigating the efficiency of water use by roots and the key factors affecting water use can help alpine meadow ecosystem restoration projects to be carried out reasonably and efficiently. However, there is a paucity of studies on RWU in alpine meadows, and it is of great significance to develop a more applicable simulation method to quantify the water uptake capacity of roots. At the same time, few studies have paid attention to the impact mechanism of RWU, and a quantitative study of the RWU rate will help to investigate the impact factors and mechanisms of RWU.
The study of RWU rate has been commonly conducted by using RWU model simulations. Although a large number of RWU models have been proposed by a wide range of scholars, most of these models have not been widely used due to the lack of parametric experimental data (Cai et al., 2022b), therefore, it is a great significance to evaluate the applicability of the models under different soil and environmental conditions. The existing RWU models can be classified into macroscopic and microscopic types depending on the scale of study (Peddinti et al., 2020). Microscopic RWU models were proposed by Gardner (Gardner, 1960), and after intensive research and innovative development by scholars, they still exhibit the defects of difficulty in determining various parameters such as water transfer resistance terms, making it more difficult to reflect the water movement patterns of the soil in the whole root zone.
Macroscopic RWU models consider the roots as a whole (Hillel et al., 1975; Hainsworth and Aylmore, 1986), and its prominent feature is to allocate the transpiration rate of the plant according to certain rules. The allocation can be divided into linear and nonlinear, with nonlinear being more widely used and various (Kumar et al., 2015). Macroscopic models have many advantages over microscopic models. Because macroscopic models do not require excessive research on the whole process of RWU and define complex soil parameters, and are more consistent with the real situation, they are more widely used.
Macroscopic nonlinear models have been developed for decades and various model equations such as the Molz-Remson model (Molz and Remson, 1970), Selim-Iskandar model (Selim and Iskandar, 1978), Jervis model (Jarvis, 1989), Hillel model (Hillel and Talpaz, 1976), and Feddes model (Feddes et al., 1974) have been proposed, which can be generally classified into two categories. The first category is similar to the Jervis model, Hillel model, and Feddes model, which consider resistance parameters of soil water movement, although the construction of these models is simpler, the simulation may be less effective in practical application due to the incomplete parameters. The second category considers the root distribution characteristics when considering resistance parameters of soil water movement, and adequate consideration of the parameters will make the physical equations more scientific and accurate. There exists the Feddes model as an example, which is improved by adding root distribution characteristics (Luo et al., 2000), making a significant improvement in simulation performance.
The criteria for the selection and study of the model in this paper are based on whether the resistance parameters of soil water movement selected by the model affect the ability of the RWU. It is shown that soil water potential (Cai et al., 2022a), soil hydraulic conductivity (Lebron et al., 2007; Lima et al., 2008), and soil water diffusivity (Deery et al., 2013) are the key resistance factors that affect RWU capacity. Among the proposed models, the improved Feddes model, Selim-Iskandar model, and Molz-Remson model take these three factors into full consideration and use them as important parameters of the model. Relatively speaking, the rest of the models may have certain shortcomings. Meanwhile, the improved Feddes model is mostly applied to crops and trees and shows good simulation performance (Feng et al., 2008; Nguyen et al., 2022), but some studies show that the lag of water stress and salinity stress may affect the sensitivity of the model parameters, so the model may not apply to the QTP with a variable climate. The Selim-Iskandar model and Molz-Remson model have been less studied (Luo et al., 2000), the acquisition of the studied model parameters is complicated and difficult, and the mode of action on RWU is more difficult to be impacted by natural conditions and more stable, but there is a lack of studies in alpine meadows. Therefore, the above three macroscopic RWU models still need to be evaluated for applicability in the study of alpine meadows.
The flow of the study is shown in Figure 1. In this paper, the root length density (RLD) distribution is characterized by a prototype observation experiment in the field. The RWU rate was simulated by parametric index measurements in combination with the improved Feddes model, Selim-Iskandar model, and Molz-Remson model. The accuracy of the model was tested using the soil water movement equation that included the RWU term. At the same time, the simulated values of soil water content (SWC) were compared with the real values to determine the applicability of the RWU models in the study of alpine meadows. Based on the simulation results, we analyzed the RWU pattern in alpine meadows, and investigate the reasons for the formation of RWU variation characteristics and the impact mechanism of RWU. This study will address the methodological vacancy of quantitative calculation of RWU rate in alpine meadows, and provide a useful reference and theoretical support for plant RWU simulation practice worldwide. The results of the study can also provide theoretical references for the sustainable development of the QTB and suggest feasible suggestions for local ecological restoration.
2 Overview of the study area
The study area is located in the Nagqu watershed (30°54′–32°43′N, 91°12′–92°54′E) in northern Tibet (Figure 2A), with an average altitude above 4,500 m (Figure 2B), and the geographical coordinates and altitude of the experimental sites are shown in Table 1. The climate type belongs to the semi-arid monsoon climate of the plateau subfrigid zone, with an average sunshine duration of 2723 h per year, a large temperature difference between day and night, an average temperature of -0.6°C, and the existence of obvious extremely climate characteristics, with an extremely low temperature of −41.2°C and an extremely high temperature of 23.6°C. The study area exhibited distinctly indistinguishable seasons, with plant growth periods concentrated in the relatively warm period from May to September, and the vegetation was extremely sensitive to the environment and very susceptible to global climate change. The average annual rainfall is 477.8 mm, and the precipitation period is also concentrated from May to September, with the maximum precipitation from June to September, accounting for 81.9% of the annual precipitation.
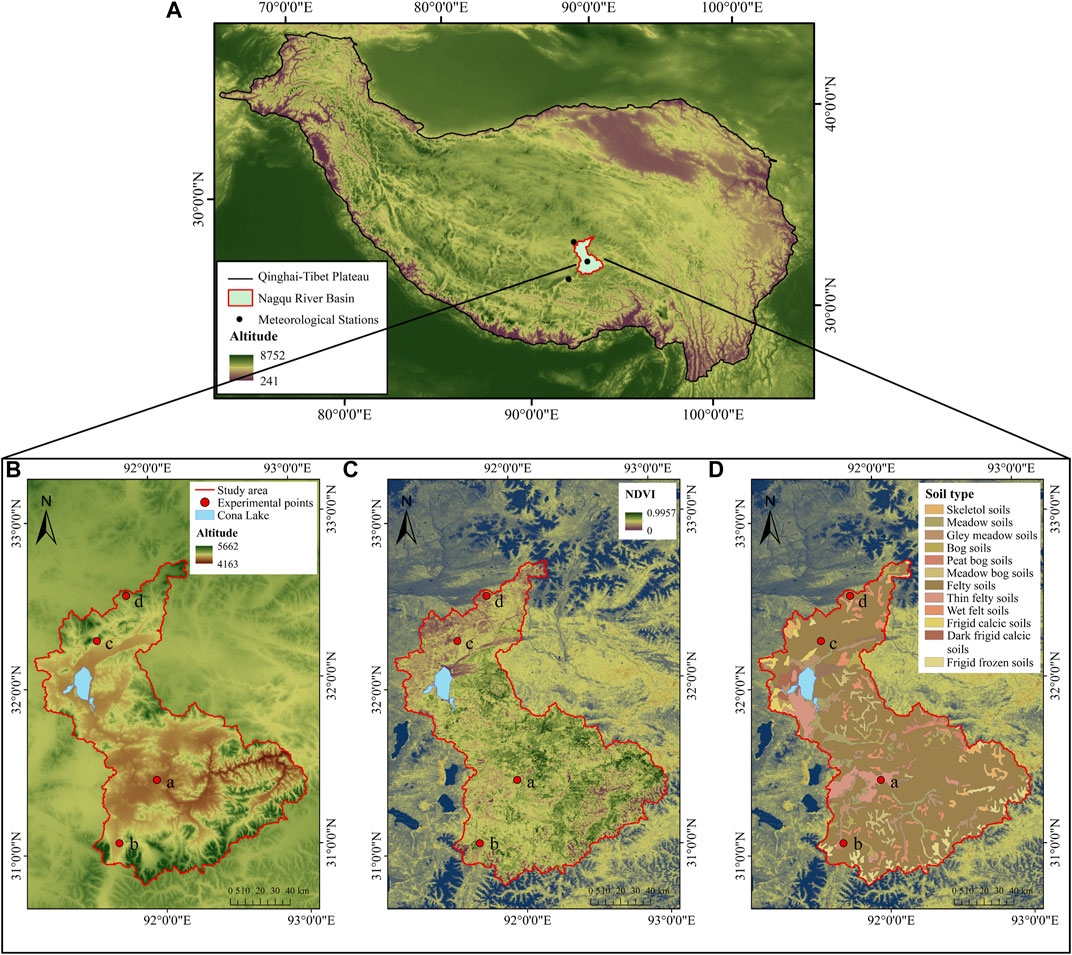
FIGURE 2. Map of the study area. Contains elevation characteristics of the Qinghai-Tibet Plateau (A), elevation characteristics of the study area and location of the prototype experimental site (B), NDVI distribution (C), and soil type distribution (D).
TABLE 1. The longitude, latitude, and altitude of the experimental locations; the mean crop coefficients (
The main geological characteristics of the study area are fragmented bedrock, hills and plains, and a variety of soil types. The felt soils are the most widely distributed, with an area of 11018.3 km3, accounting for 75.29% of the entire watershed, followed by meadow soils, accounting for 7.70% of the entire watershed, and finally other soil types, mainly bog soils (Figure 2D). The alpine meadow is the most dominant vegetation type in the study area, and the most typical one is Kobresia pygmaea, which covers more than 80% of the entire watershed (Figure 2C). The above multiple soil types and alpine meadows together constitute a complex soil vegetation condition in the study area.
3 Materials and methods
3.1 Selection of experimental sites and deployment of experimental equipment
The criteria for selecting the experimental sites in this study were based on the fact that they could fully reflect the overall vegetation root change characteristics of alpine meadows on the QTP, were less impacted by anthropogenic factors, and were conducive to the safe conduct of field experiments. After a long field study, four typical field experiment sites a, b, c, and d (Table 1 and Figure 2B) were established in the Nagqu watershed in August 2018. Four experimental samples with more consistent vegetation habitat conditions were laid out at each experimental site.
In this study, root characteristics were observed using the minirhizotron technique (a non-destructive, fixed-point method for direct observation and study of plant roots. The minirhizotron system consists of a minirhizotron tube, an optical camera, a calibration handle, a controller, and a computer). In each experimental sample, a circular hole with a depth of about 1 m and a vertical direction of 30°was dug by the soil coring method, and a PVC transparent minirhizotron tube (1 m long, 6.4 cm inner diameter, 7 cm outer diameter) was inserted into the hole (Johnson et al., 2001). At the same time, without affecting the minirhizotron tubes, a deep pit of nearly 50 cm was dug in the sample, and soil moisture and water potential sensors (instrument model 5TM, with a measurement accuracy of 0.001 m3 m−3 for SWC and 0.1 kPa for soil water potential) were placed at 5, 10, 20, and 35 cm out of each, and the pit was buried with the original soil to ensure that the soil can be restored to its native state as soon as possible.
As the deployment of minirhizotron tubes will cause some damage to the original habitat of plants (Joslin and Wolfe, 1999), the burial of soil sensors will also destroy the original state of the soil. At the same time, alpine meadows on the QTP are more sensitive and take a longer time to recover to the original habitat state after being damaged by external factors (Li and Song, 2021; Xia et al., 2021). Therefore, the vegetation in the study area was given nearly 2 years to recover the vegetation ecology, and the instruments were regularly maintained without destroying the vegetation in the experimental site. The experiment was started in June 2020, and prototype field observations were conducted for two consecutive years.
3.2 Experimental design
In this study, the two key phenological stages of alpine meadows, the re-greening stage, and the wilting stage were studied. Based on the climatic characteristics of the study area and the research of scholars, it was determined that the re-greening stage of alpine meadows is in June and the wilting stage is in September. Thus, Exp. 1 and Exp. 2 were conducted in 2020, and Exp. 3 and Exp. 4 were conducted in 2021, respectively, with Exp. 1 and Exp. 3 being the re-greening experimental group and Exp. 2 and Exp. 4 being the wilting experimental group. Before the start of the experiments, the 5TM soil moisture and water potential sensors in the sample plots were read numerically by ECH2O Utility software, and the data were recorded at a frequency of 1 h. In this study, data for four experimental periods of whole months were extracted from continuous observation data throughout the year. And it was used as the base data for the subsequent study.
The root index of alpine meadows was obtained by the minirhizotron technique (Taylor et al., 2014) in this paper. The collection method was to move the minirhizotron camera deep into the minirhizotron tube and move down 5.8 cm at a time (the vertical depth was about 5 cm). Since the camera’s shooting range was only 2 cm×2 cm and after each photo was taken, the camera was rotated 45° in the clockwise direction and a total of 8 photos were taken in each layer to ensure the integrity of the photographed roots. After the shooting was completed, the camera was moved down until no roots could be found in the observation window. In Exp. 1∼Exp. 4, it was found that there were almost no roots in the soil layer below 35 cm in the alpine meadow of the study area, so we considered the thickness of the root layer as 35 cm. After that, the pictures were processed by WinRHIZO Tron MF 2018b picture analysis software. The calculation formula for RLD was:
where
In Exp. 3 and Exp. 4, soil water infiltration experiments were conducted in four samples at four experimental sites (a, b, c, and d) by double-ring infiltration (Rönnqvist, 2018) experiments. The soil saturated hydraulic conductivity was obtained for each experimental site at the re-greening and wilting stages (Table 2). The DJ-IN12-W double-ring infiltrator with an inner and outer diameter of 60 and 30 cm, respectively, was chosen to minimize the impact of soil spatial heterogeneity on the experimental errors. The device was equipped with 3 and 10 L Mariotte tubes to supply water to the inner and outer rings, respectively. At the beginning of the experiment, 10 cm of water was injected simultaneously into the inner and outer rings, and the water level in the outer ring was ensured to be the same as that in the inner ring during the experiment periods. The water level in the inner ring was raised to a height of 10 cm every 5 min for the first half hour through a Mariott tube, and data readings were taken. After that, data readings were taken every 10 min by the same method. Until the infiltration rate is the same for 30 min in a row, it is the saturated hydraulic conductivity of the soil.

TABLE 2. Soil water indicators, including soil saturated hydraulic conductivity (
The method of measurement of physiochemical properties of soil. It was done by taking a set of samples in each group of each experimental site without destroying the minirhizotron tubes. A set of 5, 10, 20, and 35 cm soil samples were collected in each group by the cutting ring method. And measuring soil pH, the content of total organic matter, total carbon, total nitrogen, total phosphorus, total salt, and available potassium, the porosity, bulk weight, and agglomerate composition in the laboratory according to international standards.
3.3 RLD distribution function
In this study, the RLD distribution formula in exponential form was used to functionalize the RLD on soil profiles of alpine meadows (Eq 2), which is more commonly used for tree roots (Luo et al., 2000; Feng et al., 2008; Su et al., 2017), but in this study, similar characteristics of meadow RLD distribution were found.
where
3.4 Plant transpiration rate
Plant transpiration is the main mode of water exchange between plants and the atmosphere, and this paper uses an indirect method to obtain plant transpiration characteristics at the study location (Zhu et al., 2009; Cai et al., 2018b). The reference evapotranspiration rate is impacted by meteorological factors and is generally calculated using the FAO Penman-Montieth equation (Allen et al., 1998; Ojha et al., 2009; Chattaraj et al., 2013):
where
The evapotranspiration rate of a plant is determined by the crop coefficient of the plant and the reference evapotranspiration rate impacted by meteorological conditions, and the relationship between them is:
where
In addition, plant evapotranspiration can generally be divided into three aspects: soil evaporation, interception evaporation, and plant transpiration (Ojha et al., 2009).
where
3.5 Introduction of three macroscopic RWU models
3.5.1 Improved feddes model
The Feddes model (Feddes et al., 1974) is a weighting factor type of RWU model, in which the selection of covariates depends on the change of soil water potential, while the change of root density index and SWC has a weak effect on RWU. In the process of applying and studying Feddes, it was found that when the measured root density index was added to the model, the resulting RWU model could more accurately reflect the RWU in the soil profile. Therefore, the improved Feddes model is more widely accepted than the original Feddes and is more widely used in RWU simulation studies (Luo et al., 2000; Feng et al., 2008; Su et al., 2017). The generalized form of the model is:
where
where
3.5.2 Selim-Iskandar model
The Selim-Iskandar model (Selim and Iskandar, 1978; Molz, 1981) is a weighting factor type model with soil hydraulic conductivity as a covariate. The model considers that the main factors affecting plant RWU are the water conductivity of the soil and the root density on the soil profile, while the effect on soil water potential is not considered. The root density index considered is usually the RLD distribution characteristics of the soil profile (Molz and Remson, 1970; Molz and Remson, 1971). The generalized form of the model is:
where
where
3.5.3 Molz-Remson model
Molz-Remson proposed a total of three weighting factor classes of RWU models in 1970 and 1981, and the model cited in this paper, which focuses on soil hydraulic diffusivity as the study parameter (Molz and Remson, 1970), has the following model structure:
where
Thus, after the derivation of the equation, The formula of soil hydraulic diffusivity about soil saturated hydraulic conductivity and soil effective saturation is obtained (van Genuchten, 1980):
It is verified that the formula can reflect the trend of soil hydraulic diffusivity more accurately.
3.6 Validation of the model
Due to the lack of direct measurement of the RWU rate, the usual method to verify the accuracy of the calculated RWU rate is to simulate the water movement in the soil with the Richards equation that incorporates RWU (Liao et al., 2018). The performance of the model to simulate RWU is determined by comparing the distribution characteristics of the measured SWC with the simulated SWC. The general form of the equation is:
where
where
Then, the equations are linearized to obtain a system of linear equations in the shape of
In this paper, the root mean square error (RMSE) is used to assess the agreement between the simulation results of the model and the measured data:
where n is the number of measured data;
4 Results and analysis
4.1 Characteristics and distribution functions of RLD distribution in alpine meadows
The RLD variation in alpine meadows showed a clear pattern in time and space (Figure 3). At the spatial scale, the RLD showed a gradual decrease in the shallow to deep layers of the soil profile, the sum of RLD in the top 43% of the rhizosphere accounted for an average of 63% of the total RLD in alpine meadows. At different altitudes, RLD also differed significantly. At a, b, and c below 5,000 m altitude, RLD size was more similar and all were greater than that at d above 5,000 m altitude. Compared with lower altitudes, the RLD of alpine meadows at higher altitudes decreased by 59.9% on average, indicating that altitude has some impact on the growth of plant roots.
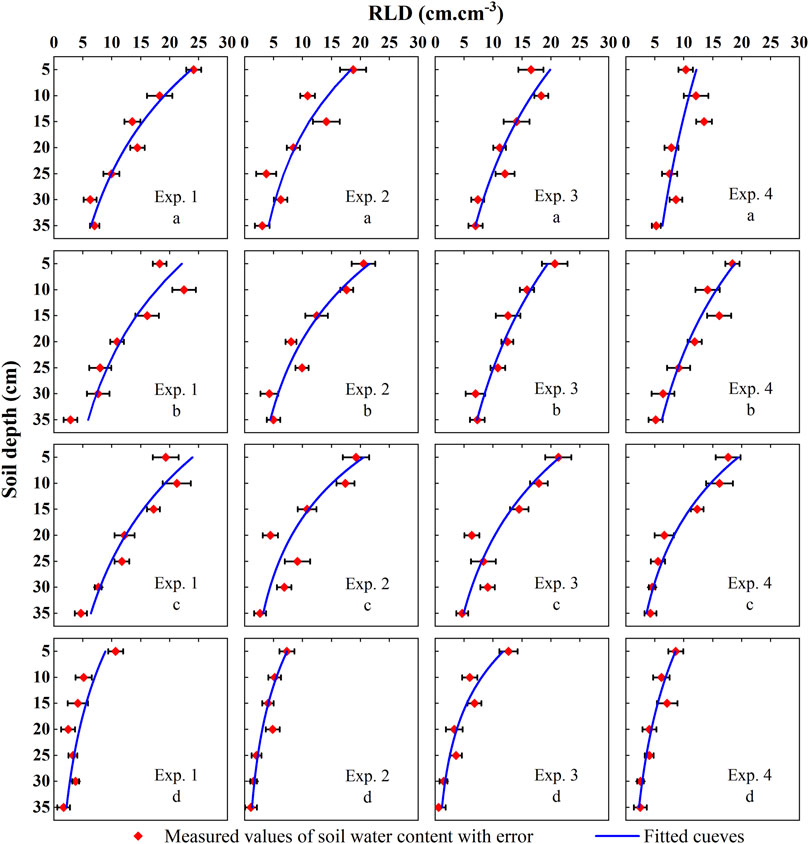
FIGURE 3. Distribution characteristics of root length density on the soil profile and the fitted curve based on Eq. 2.
On the time scale, the RLD in alpine meadows was significantly greater in the re-greening stage than in the wilting stage, and the RLD in the wilting stage decreased by 16.2% on average compared to the re-greening stage. This phenomenon is related to the plant growth process, and there are some differences in the water consumption of plants in different phenological stages, with higher water consumption in the early stage of plant growth and a gradual decrease in the later stage of growth (Yu et al., 2015; Zheng et al., 2022). Roots are important organs for plant water uptake, and when plants consume more water, the corresponding root index tends to be larger.
In this study, the RLD of the four experimental sites was fitted based on Eq 2 (Figure 3), and the regression significance of the coefficient values with this function in the RLD fitting process was obtained (Table 3). The coefficient A of the RLD distribution equation of alpine meadows ranged from 1.02 to 2.62, and B ranged from 0.02 to 0.05, with a small variation. Therefore, it can be considered that the RLD equation has a good simulation performance in reflecting the RLD distribution characteristics of alpine meadows.
4.2 Comparison of the adaptability of three macroscopic RWU models
In this paper, the SWC distribution characteristics of soil profiles, plant root characteristics, and meteorological factors in the wilting and re-greening stages of alpine meadows were used as the initial conditions of the model. And the soil water movement equation Eqs. 16–18, which includes RWU, was combined with the RWU rates simulated by the three macroscopic RWU models to obtain the simulated values of SWC changes for each model. The real and simulated values of SWC in the rhizosphere of alpine meadows at four different locations and four different periods were compared (Figure 4). The 16 sets of measured data were used to eliminate errors due to chance. At the same time, due to the variable climate on the QTP, the model validation time range was taken as four consecutive days with stable climate conditions to minimize the impact of external conditions on the model accuracy.
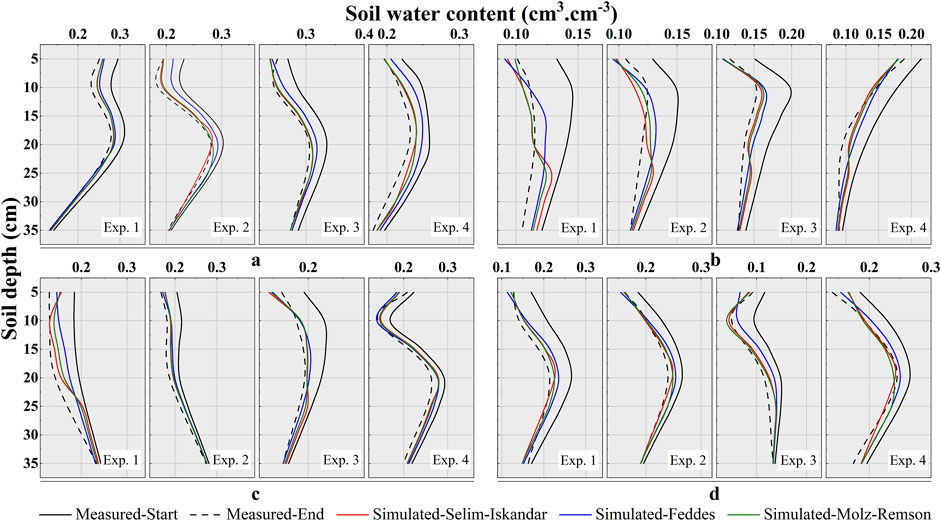
FIGURE 4. Based on the initial soil water content (Measured-Start), combined with the improved Feddes model, Selim-Iskandar model, and Molz-Remson model, the simulated values of soil water content were obtained. Then, it is compared with the measured soil water content (Measured-end), to verify the accuracy and simulation performance of the model. a, b, c and d represent four experimental sites, Exp. 1, Exp. 2, Exp. 3 and exp. 4 represent different experimental periods respectively.
After the RMSE calculation (Figure 5), it was found that the results simulated by the Selim-Iskandar model and the Molz-Remson model were more similar. The RMSE of Selim-Iskandar and Molz-Remson models were reduced by 31.58 and 30.76%, respectively, compared with the improved Feddes model. At the same time, comparing the three simulated SWC with the actual SWC, it was found that all three models underestimated the RWU capacity to some extent, which resulted in the simulated SWC being smaller than the actual SWC. Integrating the measured and simulated values, it was found that the amount of SWC variation simulated by the improved Feddes model, Selim-Iskandar model, and Molz-Remson model was reduced by 38.34, 21.18, and 27.21% on average compared to the measured SWC. Compared with the improved Feddes model and Molz-Remson model, the simulation performance of the Selim-Iskandar model was improved by 44.76 and 22.16%.
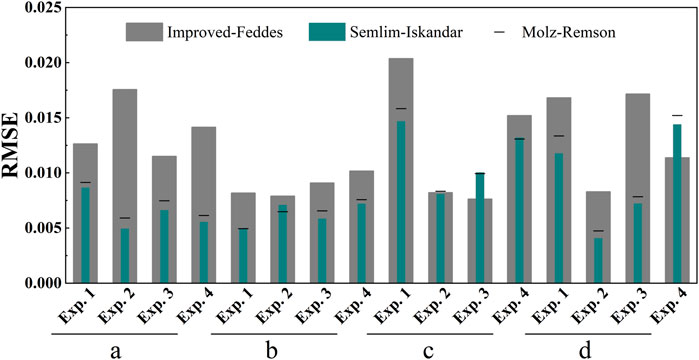
FIGURE 5. EMSE comparison chart. RMSE between the measured values of soil water content at each experimental location at different experimental times, and the simulated values predicted by three macroscopic root water uptake models combined with the soil water equation of motion.
Therefore, by combining the ability to simulate the amount of SWC variation with RMSE to evaluate the applicability of the three macroscopic RWU models in a comprehensive manner. We concluded that the simulations of the more widely used improved Feddes model showed less effectiveness in the simulation of RWU in alpine meadows, and the Selim-Iskandar model was more applicable.
4.3 RWU characteristics of alpine meadow soil profiles based on Selim-Iskandar model
After comparing the applicability of the three macroscopic models in simulating RWU in alpine meadows from Section 3.2, we concluded that the Selim-Iskandar model is more applicable in simulating RWU in alpine meadows. So we used the simulated values of this model as the actual RWU rate in alpine meadows. Based on the calculation results of this model, we have analyzed the RWU characteristics of alpine meadows on the soil profile (Figure 6), and it can be found that the RWU rate of alpine meadows has obvious regularity in time and space.
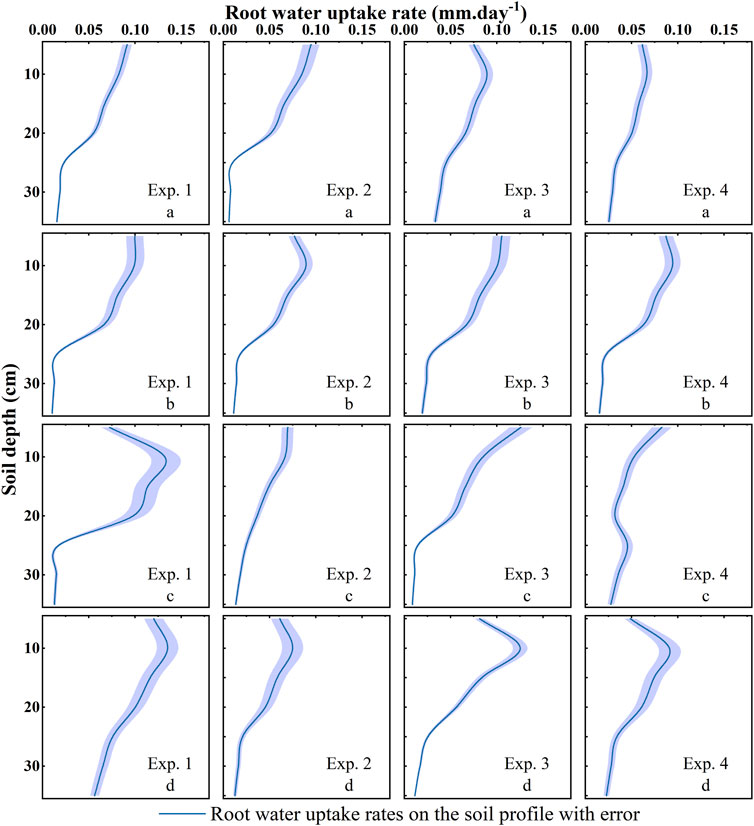
FIGURE 6. Based on the Selim-Iskandar model, the distribution of root water uptake rates at experimental sites a, b, c, and d in alpine meadows on soil profiles in Exp. 1, Exp. 2, Exp. 3, and Exp. 4 were obtained.
Spatially, the RWU capacity of alpine meadows tended to weaken with increasing soil depth, and although some of them showed fluctuating characteristics of first increasing and then decreasing, all of them showed a significantly lower RWU capacity at 25–35 cm of the rhizosphere. After the integral treatment of each soil layer, it can be found that the top 50% of the soil rhizosphere, on average, bears 72.65% of the total rhizosphere water uptake. Temporally, the RWU rate in alpine meadows was greater at the re-greening stage than at the wilting stage. In one growth cycle of the meadow, the RWU rate increased by 36.52% on average at the re-greening stage compared to the wilting stage.
5 Discussion
5.1 Reasons for the formation of RWU variation characteristics and analysis of the mechanism affecting RWU
It was found that the RWU rate in alpine meadows in the re-greening stage was significantly greater than that in the wilting stage, which is more consistent with the results of Wang et al. (2022) and Li and Cao (1996). The reason for this result is that during the pre-growth and vigorous growth periods, the plant has a higher growth rate, and consumes water and nutrients at a faster rate. In the late growth period, the plant tends to wilt and the rate of water consumption tends to slow down.
The top 50% of the rhizosphere in alpine meadows is responsible for an average of 72.65% of the total RWU. Due to the lack of basic soil profile water consumption characteristics studies in alpine meadows. Therefore, this paper is analogous to the variation in water requirements of crops at different soil depths of the roots (Yu et al., 2015; Cai et al., 2018b). Soil layers with higher root density indicators tend to bear most of the water uptake responsibility. Therefore, we believe that the corresponding pattern presented by alpine meadows is correct.
The RWU rate in alpine meadows showed fluctuating changes of increasing and then decreasing in the soil profile of some experimental sites. This is because the RWU rate in this study was determined by a combination of RLD and soil hydraulic conductivity. In the soil profile, the trend of soil hydraulic conductivity is not consistent with the trend of RLD. Under the joint effect of both, the distribution of RWU rate in the soil profile will show corresponding fluctuations.
The analysis of the mechanism influencing RWU can be focused on the influencing factors that determine RWU capacity. Most studies have focused on root factors when exploring the influencing factors (Zheng et al., 2022), however, we believe that roots and soil are inseparable. Thus, the study of two key factors, RLD, and soil hydraulic conductivity, will improve the understanding of the mechanism that impacts RWU. Studies have shown that soil physicochemical properties can have a large effect on soil hydraulic conductivity and root growth (Ren et al., 2016). In this study, the correlation analysis (Figure 7) revealed that the impact of soil physicochemical properties on RWU was mainly manifested in:
1) Effect of soil porosity and macroaggregates on soil hydraulic conductivity. The impact of soil hydraulic conductivity exists mainly in physical properties, and the study showed that both porosity and agglomerate composition of soil can affect the hydraulic conductivity of alpine meadow soils (Lima et al., 2008; Slawinski et al., 2011; Wang Y. K. et al., 2020). The size and number of agglomerates determine the condition of the soil pore space. When the number of large agglomerates is large and stable, the soil porosity tends to be large, and the connectivity of the soil will be enhanced. Thus, the resistance of water movement is weakened, and the soil hydraulic conductivity will be enhanced (Liu et al., 2018). This will also reduce the resistance of the roots in absorbing water, and increase the water absorption capacity of the roots.
2) Effect of soil physicochemical properties on root growth. Soil nutrients are the key elements for plant growth, and their condition has a significant effect on root growth (Marschner et al., 1996). Plants will make adaptive changes in root morphology and distribution with changes in soil nutrient content (Bonser et al., 1996; Bonifas and Lindquist, 2009), and plant root density indicators tend to be larger in soils with more suitable nutrient content to improve water and nutrient uptake (Ericsson, 1995). When the density index of roots increases, the interpenetration in the soil will also be enhanced (Liu et al., 2020), thus improving the water infiltration capacity in the soil, and the hydraulic conductivity is closely related to the water infiltration rate (van Genuchten, 1980). Therefore, plant roots directly affect water uptake while also indirectly affecting RWU rate by changing soil water conductivity.
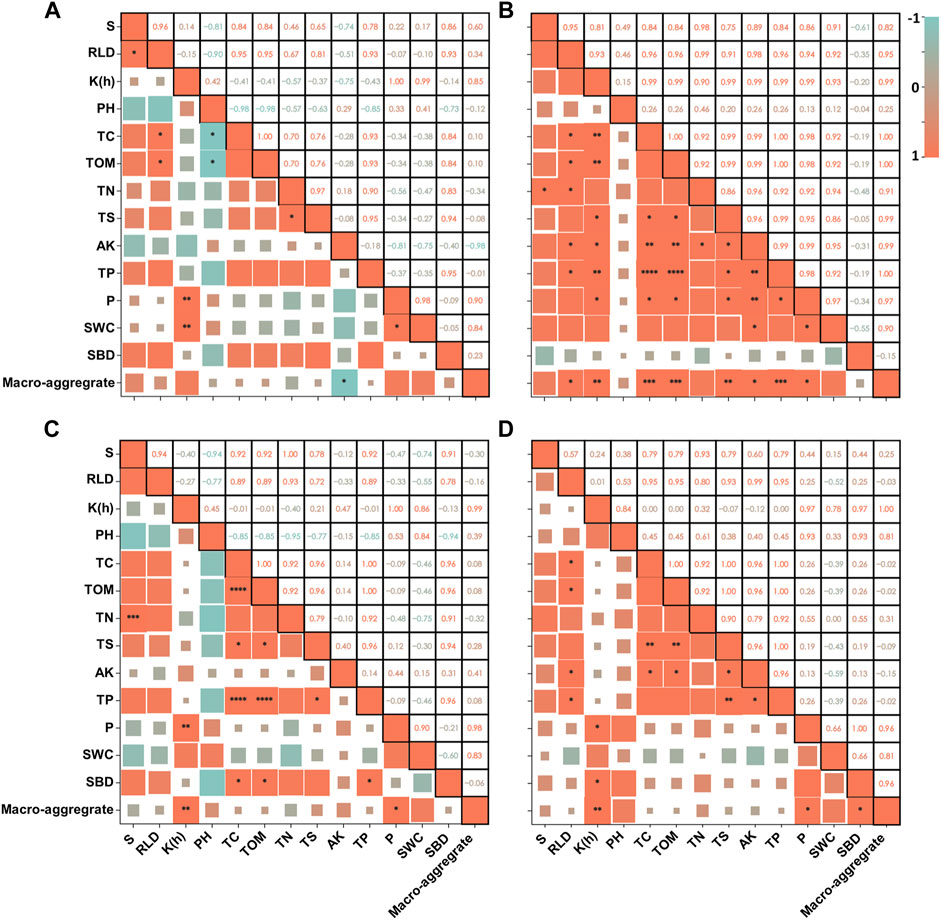
FIGURE 7. Correlation between RLD, water uptake index, soil hydraulic conductivity, and soil physiochemical properties at four experimental sites (a–d). Soil physiochemical properties indicators include soil PH (PH), total carbon (TC), soil hydraulic conductivity [K(θ)], total organic matter (TOM), total nitrogen (TN), total salt (TS), soil available potassium (SAK), total phosphorus (TP), porosity (P), soil water content (SWC), soil bulk density (SBD), and the ratio of the number of macroaggregates (diameter > 0.25 mm) to the total number of aggregates (Macro-aggregate). (Note: * means p < 0.05, ** means p < 0.01, *** means p < 0.001, **** means significant level of p < 0.0001. The figure was drawn on the https://www.chiplot.online/).
5.2 Error analysis of the model and research outlook
This paper discusses the applicability of three macroscopic RWU models that fully consider resistance factors of soil water movement and root factors for alpine meadow studies. The results show that although the models with soil water potential as a parameter have shown excellent performance in a large number of RWU studies (Cai et al., 2018a; Wu et al., 2020), the models developed with soil hydraulic conductivity as a key parameter affecting RWU are more applicable in alpine meadow studies. However, the model still has some errors in the simulation process, and it can be found that more model validation results exhibit significant differences between the model simulated and real values at 5 cm of soil substratum when the model simulates the SWC.
The analysis of the reasons for this may focus on three aspects. First, the plant transpiration rate is calculated by the local meteorological data, the empirical formula of vegetation leaf area index, and crop coefficient (Zhu et al., 2009; Chattaraj et al., 2013; Cai et al., 2018b). The simulated values of plant transpiration rate may be different from the real values. Second, in the simulation of RWU, the model parameters studied only include root indicators, soil water potential, soil hydraulic conductivity, and soil hydraulic diffusivity, while the actual indicators affecting RWU may not be limited to these parameters, and some studies have shown that the root tip density of plants may be the most effective indicator of water uptake (Segal et al., 2008; Huang et al., 2020). Third, the definition of parameters may be less accurate in the process of model validation by the soil water movement equation, and the error between the simulated SWC and the actual SWC was expanded during the infiltration of soil moisture and the recharge of the lower soil moisture to the upper soil moisture. All these aspects are issues that need to be focused on in further studies.
The RWU models have undergone only a few decades of development since they were proposed. Due to the limitations of technical means and the lack of theoretical knowledge, the existing models show obvious deficiencies to some extent. For the accurate construction of the model, it is necessary to fully consider the relevant parameters that contribute most to the simulation. There are some limitations in the definition of resistance parameters such as soil water potential, soil hydraulic conductivity, and soil hydraulic diffusivity that affect the water transfer from the soil to the roots, as well as the measurement of key root indicators that most directly affect the RWU capacity. Meanwhile, all existing models consider RWU statically, however, the RWU capacity changes accordingly during the growth of roots. To achieve a simulation situation that matches the actual situation, it is also necessary to combine the microscopic model with the macroscopic model to investigate the dynamic RWU model. And the development of direct observation techniques for RWU, thus providing direct validation of model accuracy, is also needed to be focused on.
6 Conclusion
The RLD in alpine meadows on the soil profile is one of the key factors affecting RWU, an obvious spatial and temporal distribution pattern was found as well. The RLD distribution showed that in the re-greening stage was significantly larger than that in the wilting stage, the RLD of the wilting stage decreased by 16.2% on average, and the ability of root growth was poorer in the high altitude area.
In the comparison of the models, the model considering soil hydraulic conductivity is better. The results simulated by the Selim-Iskandar model were more accurate than the improved Feddes model and Molz-Remson model. Compared with the improved Feddes model and Molz-Remson model, the simulation performance of the Selim-Iskandar model was improved by 44.76 and 22.16%. Thus, the Selim-Iskandar model is more suitable for alpine meadows.
Based on the distribution characteristics of the RWU rate obtained from the model, it clearly showed that the roots in the shallow layer were responsible for most of the water uptake in the whole rhizosphere. At the same time, the RWU capacity was stronger in the re-greening stage than that in the wilting stage, and the RWU rate in the re-greening stage increased by 36.08% on average.
Both root growth and soil hydraulic conductivity showed significant correlations with soil physicochemical properties. This study was mainly conducted on felty soils, and further refinement studies are needed for other types of soils to expand the evaluation of the applicability of the model in different environments.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
BD, XG, WL, and ML collected basic data, and BD designed the analysis and drafted the manuscript. BW provides the working concept. The manuscript was critically revised by BW, DY, and SX. BW provided a revised version of the manuscript. All authors contributed to this article and approved this version for submission.
Funding
This study was supported by the National Natural Science Foundation of China (No. 52022110, 51879276), the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (No. 2019QZKK0207), and the IWHR Research & Development Support Program (No. MK0145B022021).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56, 300. Rome: Fao, D05109.
Belmans, C., Wesseling, J. G., and Feddes, R. A. (1983). Simulation model of the water balance of a cropped soil: Swatre. J. hydrology 63, 271–286. doi:10.1016/0022-1694(83)90045-8
Boanares, D., Oliveira, R. S., Isaias, R. M. S., Franca, M. G. C., and Penuelas, J. (2020). The neglected reverse water pathway: Atmosphere-Plant-Soil continuum. Trends Plant Sci. 25, 1073–1075. doi:10.1016/j.tplants.2020.07.012
Bonifas, K. D., and Lindquist, J. L. (2009). Effects of nitrogen supply on the root morphology of corn and velvetleaf. J. Plant Nutr. 32, 1371–1382. doi:10.1080/01904160903007893
Bonser, A. M., Lynch, J., and Snapp, S. (1996). Effect of phosphorus deficiency on growth angle of basal roots in Phaseolus vulgaris. New Phytol. 132, 281–288. doi:10.1111/j.1469-8137.1996.tb01847.x
Cai, G. C., Ahmed, M. A., Abdalla, M., and Carminati, A. (2022a). Root hydraulic phenotypes impacting water uptake in drying soils. Plant Cell. Environ. 45, 650–663. doi:10.1111/pce.14259
Cai, G. C., Totzke, C., Kaestner, A., and Ahmed, M. A. (2022b). Quantification of root water uptake and redistribution using neutron imaging: A review and future directions. Plant J. 111, 348–359. doi:10.1111/tpj.15839
Cai, G. C., Vanderborght, J., Couvreur, V., Mboh, C. M., and Vereecken, H. (2018a). Parameterization of root water uptake models considering dynamic root distributions and water uptake compensation. Vadose Zone J. 17, 160125. doi:10.2136/vzj2016.12.0125
Cai, G. C., Vanderborght, J., Langensiepen, M., Schnepf, A., Huging, H., and Vereecken, H. (2018b). Root growth, water uptake, and sap flow of winter wheat in response to different soil water conditions. Hydrol. Earth Syst. Sci. 22, 2449–2470. doi:10.5194/hess-22-2449-2018
Cai, H. Y., Yang, X. H., and Xu, X. L. (2015). Human-induced grassland degradation/restoration in the central tibetan plateau: The effects of ecological protection and restoration projects. Ecol. Eng. 83, 112–119. doi:10.1016/j.ecoleng.2015.06.031
Chattaraj, S., Chakraborty, D., Garg, R., Singh, G., Gupta, V., Singh, S., et al. (2013). Hyperspectral remote sensing for growth-stage-specific water use in wheat. Field Crops Res. 144, 179–191. doi:10.1016/j.fcr.2012.12.009
de Melo, M. L. A., and de Jong van Lier, Q. (2021). Revisiting the Feddes reduction function for modeling root water uptake and crop transpiration. J. Hydrology 603, 126952. doi:10.1016/j.jhydrol.2021.126952
Deery, D. M., Passioura, J. B., Condon, J. R., and Katupitiya, A. (2013). Uptake of water from a kandosol subsoil: I. Determination of soil water diffusivity. Plant Soil 368, 483–492. doi:10.1007/s11104-012-1525-8
Ericsson, T. (1995). “Growth and shoot: Root ratio of seedlings in relation to nutrient availability,” in Nutrient uptake and cycling in forest ecosystems (Springer), 205.
Fan, X. M. (2011). Influence of vegetation coverage on evapotranspiration process of alpine meadow in the head of the Yangtza River, 49-52. Lanzhou (Gansu): LANZHOU UNIVERSITY. Master’s thesis.
Feddes, R. A., Bresler, E., and Neuman, S. P. (1974). Field test of a modified numerical model for water uptake by root systems. Water Resour. Res. 10, 1199–1206. doi:10.1029/WR010i006p01199
Feng, Q., Si, J. H., Li, J. L., and Xi, H. Y. (2008). Feature of root distribution of populus euphratica and its water uptake model in extreme arid region. Adv. Earth Sci. 23, 765–772. doi:10.3321/j.issn:1001-8166.2008.07.016
Gardner, W. R. (1960). Dynamic aspects of water availability to plants. Soil Sci. 89, 63–73. doi:10.1097/00010694-196002000-00001
Genxu, W., Guangsheng, L., and Chunjie, L. (2012). Effects of changes in alpine grassland vegetation cover on hillslope hydrological processes in a permafrost watershed. J. Hydrology 444-445, 22–33. doi:10.1016/j.jhydrol.2012.03.033
Hainsworth, J., and Aylmore, L. (1986). Water extraction by single plant roots. Soil Sci. Soc. Am. J. 50, 841–848. doi:10.2136/sssaj1986.03615995005000040003x
Hillel, D., Beek, V., and Talpaz, H. (1975). A microscopic-scale model of soil water uptake and salt movement to plant roots. Soil Sci. 120, 385–399. doi:10.1097/00010694-197511000-00010
Hillel, D., and Talpaz, H. (1976). Note simulation of root growth and its effect on the pattern of soil water uptake by a nonuniform root system. Soil Sci. 121, 307–312. doi:10.1097/00010694-197605000-00008
Huang, F., Chen, Z., Du, D., Guan, P., Chai, L., Guo, W., et al. (2020). Genome-wide linkage mapping of QTL for root hair length in a Chinese common wheat population. Crop J. 8, 1049–1056. doi:10.1016/j.cj.2020.02.007
Jarvis, N. J. (1989). A simple empirical model of root water uptake. J. Hydrology 107, 57–72. doi:10.1016/0022-1694(89)90050-4
Jin, X., Jin, Y., and Mao, X. (2019). Ecological risk assessment of cities on the tibetan plateau based on land use/land cover changes–Case study of Delingha City. Ecol. Indic. 101, 185–191. doi:10.1016/j.ecolind.2018.12.050
Johnson, M. G., Tingey, D. T., Phillips, D. L., and Storm, M. J. (2001). Advancing fine root research with minirhizotrons. Environ. Exp. Bot. 45, 263–289. doi:10.1016/S0098-8472(01)00077-6
Joslin, J. D., and Wolfe, M. H. (1999). Disturbances during minirhizotron installation can affect root observation data. Soil Sci. Soc. Am. J. 63, 218–221. doi:10.2136/sssaj1999.03615995006300010031x
Kuang, X. X., Jiao, J. J., Shan, J. P., and Yang, Z. L. (2021). A modification to the van Genuchten model for improved prediction of relative hydraulic conductivity of unsaturated soils. Eur. J. Soil Sci. 72, 1354–1372. doi:10.1111/ejss.13034
Kumar, R., Shankar, V., and Jat, M. K. (2015). Evaluation of root water uptake models – A review. ISH J. Hydraulic Eng. 21, 115–124. doi:10.1080/09715010.2014.981955
Lebron, I., Madsen, M., Chandler, D., Robinson, D., Wendroth, O., and Belnap, J. (2007). Ecohydrological controls on soil moisture and hydraulic conductivity within a pinyon‐juniper woodland. Water Resour. Res. 43, 5398. doi:10.1029/2006WR005398
Li, H., and Song, W. (2021). Spatiotemporal distribution and influencing factors of ecosystem vulnerability on Qinghai-Tibet Plateau. Int. J. Environ. Res. Public Health 18, 6508. doi:10.3390/ijerph18126508
Li, Y., N., and Cao, G., M. (1996). Analysis on water consumption and water consumption law of alpine meadow vegetation in growth period. Chin. J. Agrometeorology 017, 41.
Liao, R., Yang, P., Yu, H., Wu, W., and Ren, S. (2018). Establishing and validating a root water uptake model under the effects of superabsorbent polymers. Land Degrad. Dev. 29, 1478–1488. doi:10.1002/ldr.2907
Lima, C. L. R. d., Pillon, C. N., Suzuki, L. E. A. S., and Cruz, L. E. C. d. (2008). Atributos físicos de um planossolo háplico sob sistemas de manejo comparados aos do campo nativo. Rev. Bras. Cienc. Solo 32, 1849–1855. doi:10.1590/s0100-06832008000500006
Liu, J. E., Wang, Z. L., and Li, Y. Y. (2018). Efficacy of natural polymer derivatives on soil physical properties and erosion on an experimental loess hillslope. Int. J. Environ. Res. Public Health 15, 9. doi:10.3390/ijerph15010009
Liu, Y., Guo, L., Huang, Z., Lopez-Vicente, M., and Wu, G. L. (2020). Root morphological characteristics and soil water infiltration capacity in semi-arid artificial grassland soils. Agric. Water Manag. 235, 106153. doi:10.1016/j.agwat.2020.106153
Luo, Y., Yu, Q., OuYang, Z., Tang, D. Y., and Xie, X. Q. (2000). The evaluation of water uptake models by using precise field observation data. J. Hydraulic Eng. 4, 73–81. doi:10.13243/j.cnki.slxb.2000.04.014
Ma, Z. Y., Liu, H. Y., Mi, Z. R., Zhang, Z. H., Wang, Y. H., Xu, W., et al. (2017). Climate warming reduces the temporal stability of plant community biomass production. Nat. Commun. 8, 15378. doi:10.1038/ncomms15378
Marschner, H., Kirkby, E., and Cakmak, I. (1996). Effect of mineral nutritional status on shoot-root partitioning of photoassimilates and cycling of mineral nutrients. J. Exp. Bot. 47, 1255–1263. doi:10.1093/jxb/47.Special_Issue.1255
Molz, F. J. (1981). Models of water transport in the soil-plant system: A review. Water Resour. Res. 17, 1245–1260. doi:10.1029/WR017i005p01245
Molz, F. J., and Remson, I. (1971). Application of an extraction-term model to the study of moisture flow to plant Roots1. Agron. J. 63, 72–77. doi:10.2134/agronj1971.00021962006300010023x
Molz, F. J., and Remson, I. (1970). Extraction term models of soil moisture use by transpiring plants. Water Resour. Res. 6, 1346–1356. doi:10.1029/WR006i005p01346
Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12, 513–522. doi:10.1029/WR012i003p00513
Nguyen, T. H., Langensiepen, M., Hueging, H., Gaiser, T., Seidel, S. J., and Ewert, F. (2022). Expansion and evaluation of two coupled root–shoot models in simulating CO2 and H2O fluxes and growth of maize. Vadose Zone J. 21, e20181. doi:10.1002/vzj2.20181
Ojha, C. S., Prasad, K. S., Shankar, V., and Madramootoo, C. A.(2009). Evaluation of a nonlinear root-water uptake model. J. Irrig. Drain. Eng. 135, 303–312. doi:10.1061/(ASCE)IR.1943-4774.0000067
Peddinti, S. R., Kambhammettu, B., Lad, R. S., Simunek, J., Gade, R. M., and Adinarayana, J. (2020). A macroscopic soil-water transport model to simulate root water uptake in the presence of water and disease stress. J. Hydrology 587, 124940. doi:10.1016/j.jhydrol.2020.124940
Qian, D. W., Du, Y. G., Li, Q., Guo, X. W., Fan, B., and Cao, G. M. (2022). Impacts of alpine shrub-meadow degradation on its ecosystem services and spatial patterns in Qinghai-Tibetan Plateau. Ecol. Indic. 135, 108541. doi:10.1016/j.ecolind.2022.108541
Ren, Z. P., Zhu, L. J., Wang, B., and Cheng, S. D. (2016). Soil hydraulic conductivity as affected by vegetation restoration age on the Loess Plateau, China. J. Arid. Land 8, 546–555. doi:10.1007/s40333-016-0010-2
Rönnqvist, H. (2018). Double-ring infiltrometer for ;in-situ permeability determination of dam material. Engineering. 10, 320–328. doi:10.4236/eng.2018.106022
Segal, E., Kushnir, T., Mualem, Y., and Shani, U. (2008). Water uptake and hydraulics of the root hair rhizosphere. Vadose Zone J. 7, 1027–1034. doi:10.2136/vzj2007.0122
Selim, H., and Iskandar, I. (1978). Nitrogen behavior in land treatment of wastewater: A simplified model. state Knowl. land Treat. wastewater 1, 171.
Slawinski, C., Witkowska-Walczak, B., Lipiec, J., and Nosalewicz, A. (2011). Effect of aggregate size on water movement in soils. Int. Agrophysics 25, 53–58.
Su, L., Gulimire, H., and Liu, Q. (2017). Root water uptake model of Populus euphratica in the lower reaches of Tarim River. Arid. Land Geogr. 40, 102–107. doi:10.13826/j.cnki.cn65-1103/x.2017.01.013
Taylor, B. N., Beidler, K. V., Strand, A. E., and Pritchard, S. G. (2014). Improved scaling of minirhizotron data using an empirically-derived depth of field and correcting for the underestimation of root diameters. Plant Soil 374, 941–948. doi:10.1007/s11104-013-1930-7
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898. doi:10.2136/sssaj1980.03615995004400050002x
Vrugt, J. A., van Wijk, M. T., Hopmans, J. W., and Šimunek, J. (2001). One-two-and three-dimensional root water uptake functions for transient modeling. Water Resour. Res. 37, 2457–2470. doi:10.1029/2000WR000027
Wang, S. R., Guo, L. L., He, B., Lyu, Y. L., and Li, T. W. (2020a). The stability of Qinghai-Tibet Plateau ecosystem to climate change. Phys. Chem. Earth Parts A/B/C 115, 102827. doi:10.1016/j.pce.2019.102827
Wang, X., Zhou, B., Chen, Q., Li, F., and Quan, C. (2022). Study on water consumption law of typical alpine meadow and alpine swamp wetland vegetation in qinghai-xizang plateau. Plateau Meteorol. 41, 338–348. doi:10.7522/j.issn.1000-0534.2021.00079
Wang, Y. K., Ge, L., Chen, S., Wang, H. Y., Han, J. C., Guo, Z., et al. (2020b). Analysis on hydraulic characteristics of improved sandy soil with soft rock. Plos One 15, e0227957. doi:10.1371/journal.pone.0227957
Wu, X., Zuo, Q., Shi, J. C., Wang, L. C., Xue, X. Z., and Ben-Gal, A. (2020). Introducing water stress hysteresis to the Feddes empirical macroscopic root water uptake model. Agric. Water Manag. 240, 106293. doi:10.1016/j.agwat.2020.106293
Wu, Y., Che, R., Ma, S., Deng, Y., Zhu, M., and Cui, X. (2014). Estimation of root production and turnover in an alpine meadow: Comparison of three measurement methods. Acta eco. Sin. 34, 3529–3537. doi:10.5846/stxb201307031831
Xia, M., Jia, K., Zhao, W. W., Liu, S. L., Wei, X. Q., and Wang, B. (2021). Spatio-temporal changes of ecological vulnerability across the Qinghai-Tibetan Plateau. Ecol. Indic. 123, 107274. doi:10.1016/j.ecolind.2020.107274
Yu, W., Ji, R. P., Feng, R., and Zhang, Y. (2015). Estimation of root production and turnover in an apline meadow: Comparison of three measurement methods. Acta eco. Sin. 35, 3529–3537. doi:10.5846/stxb201306101632
Yuke, Z. (2019). Characterizing the spatio-temporal dynamics and variability in climate extremes over the Tibetan plateau during 1960–2012. J. Resour. Ecol. 10, 397–414. doi:10.5814/j.issn.1674-764x.2019.04.007
Zhao, M., and Zhang, (2021). 30m resolution leaf area index products over the Tibetan Plateau (2010-2019). Editor C. National Tibetan Plateau Data (National Tibetan Plateau Data Center).
Zheng, X. J., Yu, Z. W., Shi, Y., and Liang, P. (2022). Differences in water consumption of wheat varieties are affected by root morphology characteristics and post-anthesis root senescence. Front. Plant Sci. 12, 814658. doi:10.3389/fpls.2021.814658
Keywords: alpine meadow, distribution characteristics of root length density, root water uptake model, characteristics of root water uptake, soil physiochemical properties
Citation: Deng B, Weng B, Yan D, Xiao S, Gong X, Li W and Li M (2022) Evaluation of the applicability of the root water uptake model on alpine meadows and analysis of root water uptake characteristics. Front. Earth Sci. 10:987680. doi: 10.3389/feart.2022.987680
Received: 06 July 2022; Accepted: 22 August 2022;
Published: 14 September 2022.
Edited by:
Jun Niu, China Agricultural University, ChinaReviewed by:
Yujiu Xiong, Sun Yat-sen University, ChinaMohd Yawar Ali Khan, King Abdulaziz University, Saudi Arabia
Copyright © 2022 Deng, Weng, Yan, Xiao, Gong, Li and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Baisha Weng, YmFpc2hhd2VuZ0AxNjMuY29t
 Bin Deng
Bin Deng Baisha Weng
Baisha Weng Denghua Yan
Denghua Yan Shangbin Xiao
Shangbin Xiao Xiaoyan Gong
Xiaoyan Gong Wenwen Li
Wenwen Li Meng Li
Meng Li