The inflow performance relationship in fractured, vertical, and dewatered coalbed-methane wells

Although not greatly studied, the inflow performance relationship (IPR) in dewatered and vertical coalbed methane (CBM) wells is essential in the development of a CBM reservoir. The dynamics of the stress sensitivity effect (SSE) and the matrix shrinkage effect (MSE), as well as the hydraulic fracture propagation, have all been neglected, especially for the exterior region, which is larger than the drainage radius. A novel IPR model has now been built that integrates dynamic SSE–MSE and hydraulic fracture propagation into the skin factor, and is validated with real production data from the Qinshui Basin, China. The absolute open flow rate given the SSE–MSE is 60.5% larger than without SSE–MSE. If the positive effect of the SSE–MSE on the permeability in the exterior region is neglected, the absolute open flow rate is reduced by 21%. The MSE has a greater effect on the fracturing skin factor than the SSE and tends to lower the fracturing skin factor, benefitting the production of CBM. Moreover, in light of the SSE or MSE, the non-Darcy flow effect is weaker due to restraints on the velocity of flow or the permeability. Useful and essential theoretical guidance for real CBM production can thus be gleaned from this novel IPR model.

1 Introduction

Given the great energy demand of the modern world, coalbed methane (CBM) has been well developed and studied as an unconventional oil and gas resource offering both challenges and opportunities (Gash, 1991; Freij-Ayoub, 2012; Park and Liang, 2016). The production status of a CBM wellbore and the variations in the behavior of a CBM reservoir should be comprehensively analyzed to ensure the increased development of CBM.

Depending on their reservoir characteristics, vertical and horizontal CBM wells are selected and drilled to drain off water and trigger the desorption of methane. Horizontal wells provide an easier and larger channel for gas and water flowing from the coal to the wellbore, by overcoming the low production and heterogeneity of a CBM reservoir (Osisanya and Schaffitzel, 1996). The drilling of a horizontal well can damage the structure of a fragile CBM reservoir, however, rendering the wellbore unstable (Lau et al., 2017). A vertical well is hence a better choice. In the southern Qinshui Basin in Shanxi, China, vertical wells are widely used because of their production characteristics (Tao et al., 2014; Ni et al., 2020; Yang et al., 2020). For improved development of CBM in China, the internal working mechanism of vertical CBM wells should be investigated along with that of horizontal wells. In the Qinshui Basin, lower water production means higher gas production for CBM wells (Jin et al., 2016): after 4 years of production, there was no water in 58% of CBM test wells. Single-phase (gas) CBM wells, known as “dry” or “dewatered” (Zang and Wang, 2016), are common in some development blocks (Clarkson et al., 2007; Palmer, 2010). A dry CBM well occurs if there is no mobile water in the reservoir (Metcalfe et al., 1991). While much research has focused on CBM wells with water production, less attention has been paid to such dewatered, vertical CBM wells.

As a connection between reservoir and wellbore, analysis of the inflow performance relationship (IPR) can help with investigating gas well production status (Meng et al., 2021). Given the characteristics of CBM reservoirs, there are great differences between the IPRs of CBM wells and conventional wells (King, 1993). Nevertheless, the traditional IPR model can provide a reference for the IPR model of a CBM well (Seidle and Erickson, 1993). To accurately describe the IPR of a CBM well, among other matters, its gas-bearing properties, coal adsorbability, and the mechanical properties of the coal should all be considered. In the nanopores of a coal or shale matrix, the adsorption mechanism is complicated (Wu et al., 2019; Huang et al., 2021; Wu et al., 2022). The interlayer interference needs to be studied in detail for the IPR of a CBM well (Quan et al., 2022). The matrix shrinkage effect (MSE) is also considered in the model (Thungsuntonkhun and Engler, 2001), because of its essential impact on CBM production (Harpalani and Schraufnagel, 1990). The IPR model was then developed taking the MSE and the stress sensitivity effect (SSE) into consideration for the entire production period (Feng et al., 2012). For purposes of simplification, the pressure of a single-well control area was regarded as homogeneous, with the MSE and SSE varying uniformly, and not acting as a pressure-drop funnel. Another IPR model was later developed with production data for a two-phase CBM well (Sugiarto et al., 2015). Previous IPR models considered the MSE and SSE values uniform, and the dynamics of SSE and MSE have not been studied in an IPR model of a dewatered CBM well. The comprehensive joint impact of the SSE and MSE is called the SSE–MSE herein.

The impact of the SSE–MSE on CBM production is reflected by permeability, which is the key parameter of the IPR model (Feng et al., 2012). With reservoir pressure decreasing during the production period, the coal expands and shrinks, controlled by the SSE and MSE, respectively. There are two types of permeability models for the SSE–MSE. The Palmer and Mansoori (P&M) model (Palmer and Mansoori, 1996) is based on the variations in porosity controlled by the SSE–MSE. The Shi and Durucan (S&D) model was later developed with reference to thermal deformation (Shi and Durucan, 2004). The other permeability models are modifications of the P&M and S&D models (Seidle et al., 1992; Mavor and Vaughn, 1998; Wang et al., 2009; Wu et al., 2010; Ma et al., 2011; Pan and Connell, 2011; Karimpouli et al., 2020). A permeability model is necessary for a better consideration of the SSE–MSE and an accurate IPR model.

Along with the SSE–MSE, multi-wing fractures have not been taken into account in the study of IPR either. Hydraulic fracturing is essential in the effective development of CBM, and various forms of fractures can appear (Colmenares and Zoback, 2007; Zhou et al., 2015; Jiang et al., 2016). Such hydraulic fracturing is more important in vertical CBM wells than in horizontal ones (Shi et al., 2019; Sun et al., 2022). The hydraulic fractures of a horizontal well are much more complicated than those of a vertical well and are difficult to depict (Ren et al., 2019). Hydraulic fractures can improve CBM production dramatically (Jiang et al., 2017), and there are multi-wing fractures controlling production in fractured vertical CBM wells (Zhang et al., 2018; Xu et al., 2021; Li et al., 2022). Due to the complications of hydraulic fracturing, two-wing fractures were considered simple solutions in previous productivity models (Xu et al., 2013; Zhang, 2014). A comprehensive model with multi-wing fractures was then constructed for vertical well production using conformal mapping (Chen et al., 2017), and applied to a production model for an accurate simulation (Zhang et al., 2018). Without taking multi-wing fractures into account, the IPR model of a vertical CBM well would not be sufficiently accurate.

To investigate the dewatered vertical CBM well, an IPR model with both dynamic SSE–MSE and multi-wing fractures is necessary. Herein, an appropriate SSE–MSE permeability model was selected. By combining the dynamic pressure in a single-well control region, the dynamic permeability of the inner and exterior regions is obtained. We simplify the multi-wing fractures to major and secondary hydraulic fractures, and integrate them in a fracturing skin factor through a unidirectional productivity equation with pseudo-pressure and conformal transformation. Combining the completion skin factor and the speed sensitivity skin factor, an accurate IPR model resulted, which could be used to investigate the inner mechanisms of the impact of multi-wing fractures and the SSE–MSE on well flow performance. This research may thus provide useful theoretical guidance for real CBM production.

2 Model development

Mathematical models have previously been constructed for the investigation of single-phase (gas) flow in vertical CBM wells (Metcalfe et al., 1991; Nie et al., 2012; Zang and Wang, 2016). Less attention has been paid to the inflow performance of gas affected by SSE, MSE, and multi-wing fractures in the entire reservoir area.

2.1 Productivity model

Seidle applied the single-phase (gas) pseudo-pressure productivity equation to a dewatered coalbed according to its production characteristics (Seidle, 1993). From the definition of pseudo-pressure, the lower limit of the integral is arbitrary and can be set as zero. Then,

$m\left(p\right)=\frac{p^2}{\overline{\mu }\overline{Z}}(1)$

where m(p) is the pseudo pressure, and $\overline{Z}$ and $\overline{\mu }$ are the average deviation factor and viscosity, respectively, which can be calculated by the empirical expressions used for Chinese gas wells by Chen and Dong (2001), and shown in detail in Appendix A. In light of the work of Feng et al. (2012), the radial productivity equation can be expressed as follows:

$q_{\text{gsc}}=\frac{2\text{π}kh{T}_{\text{sc}}\left(m\left(\overline{p}\right)-m\left(p_{\text{wf}}\right)\right)}{p_{\text{sc}}T\left(\ln \frac{r_{\text{d}}}{r_{\text{w}}}+S_{\text{t}}\right)}(2)$

where q_gsc is the production of CBM at surface conditions; p_sc and T_sc are the standard pressure and temperature, which are 0.1 MPa and 293.15 K, respectively; k is the permeability of the CBM reservoir; h is the thickness of the reservoir; S_t is the total skin factor; T is the reservoir temperature; $\overline{p}$ is the average reservoir pressure; p_wf is the bottom-hole pressure; r_d is the drainage radius, which is 0.472 times the physical drainage radius r_e (Al-Hussainy et al., 1966); and r_w is the radius of the wellbore.

In this study, the effects of SSE, MSE, and multi-wing fractures in the entire reservoir area are integrated into a fracturing skin factor. In addition, the SSE–MSE has a significant bearing on the speed sensitivity skin factor. For a more accurate IPR study, the total skin factor is investigated in detail and presented in Section 2.2.

2.2 Skin factors of a fractured vertical well

For CBM wells in the Qinshui Basin, the total skin factor is composed of the speed sensitivity skin factor, the well completion skin factor, and the fracturing skin factor. The well completion skin factor can be obtained directly from in-situ construction, while the other two can be calculated based on the in-situ reservoir parameters. Hence, the total skin factor can be expressed as follows:

$S_{\text{t}}=S_{\text{c}}+S_{\text{f}}+D{q}_{\text{gsc}}(3)$

where S_c is the well completion skin factor, S_f is the fracturing skin factor, and D is the non-Darcy flow constant. In Eq. 3, Dq_gsc refers to the speed sensitivity skin factor. The expressions for the speed sensitivity skin factor and the fracturing skin factor will be discussed in what follows.

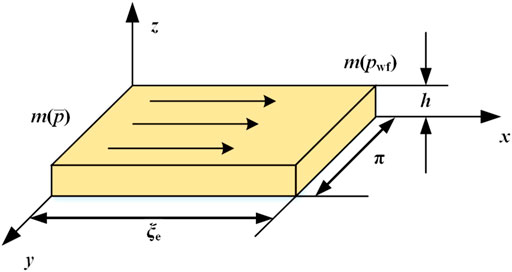
As shown in Figure 1A, the major and secondary hydraulic fractures intersect at the wellbore in a vertical CBM well at a certain angle. Unlike the traditional two-wing fractures, the effect of all hydraulic fractures on production should be considered in multi-wing fracture conditions (Zhang et al., 2018). Based on microseismic data (Runsheng et al., 2016), complicated (or major) hydraulic fractures primarily propagate along the main crack direction, while secondary hydraulic-fractures tend to propagate along the vertical direction. Therefore, the crossing of major and secondary hydraulic fractures represents the primary fracture morphology of complicated hydraulic fractures, which can take the form of multi-wing fractures. To investigate the fracturing skin factor and the speed sensitivity skin factor better, the production area of a single well was divided into an inner region (r ≤ r_d) and an exterior region (r_d < r ≤ r_e), shown in Figure 1B. For the calculation of gas productivity with a closed boundary, the physical drainage radius r_e should be replaced by r_d in Eq. 1. However, given that gas flows in the area with radius r_e instead of r_d in actual wells, ignoring the permeability variation and flow characteristics of the exterior region in Eq. 1 could lead to a critical calculation error. Therefore, the flow characteristics of both the inner and exterior regions should be emphasized. The permeabilities of the inner and exterior regions (i.e., k₁ and k₂) are both dominated by the SSE–MSE and will be discussed in Section 2.3. Due to the fact that the speed sensitivity influences the area near the wellbore, the non-Darcy flow constant should be calculated based on the permeability of the inner region (Jones, 1987).

$D=\frac{2.56\times {10}^{-9}{k}_1\gamma \beta }{\overline{\mu }h{r}_{\text{w}}}(4)$

$\beta =\frac{4.52\times {10}^6}{k_1^{1.55}}(5)$

where γ is the relative density of the gas, and β is the inertial coefficient. In Eq. 4, the constant values are revised to unify the units.

FIGURE 1

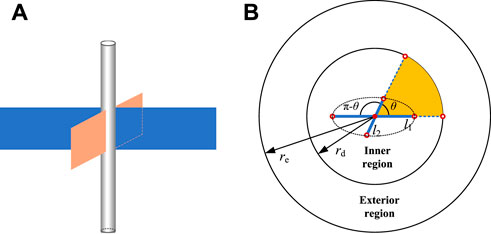
FIGURE 1. Diagrammatic sketch of vertical coalbed methane well with multi-wing fractures (A) and the regional division of the physical drainage area (B).

As shown in Figure 1B, to form a simplified central symmetry fracture model, we take the wellbore as the center and the major and secondary hydraulic fractures as the long and short axes. The lengths of half the long and short axes are l₁ and l₂, and the included angles are θ and π−θ. Furthermore, based on the long and short axes, the multi-wing fractures control area is elliptical. According to related research (Zhiming et al., 2014; Chen et al., 2017), the radial flow between the intersecting fractures (yellow area in Figure 1A) could be transferred to unidirectional flow by conformal transformation, shown in Figure 2. For the transformed unidirectional flow, the width, thickness, and length of the flowing medium are π, h, and ξ_e. The parameter ξ_e refers to the flow length after conformal transformation.

FIGURE 2

FIGURE 2. Unidirectional flow transferred from conformal transformation.

The radial flow model is more consistent with actual production demands and more valuable to production investigations than the unidirectional flow model. Therefore, the radial flow model with its pseudo-pressure has been developed and widely accepted (Al-Hussainy et al., 1966; Sun et al., 2018), while the radial flow model with pseudo-pressure is less studied. The unidirectional flow model with pseudo-pressure is given as follows:

$\{\begin{array}{l}\frac{d^{2}m\left(p\right)}{d{x}^2}=0\\ {m\left(p\right)|}_{x=0}=m\left(\overline{p}\right)\\ {m\left(p\right)|}_{x={\xi }_{\text{e}}}=m\left(p_{\text{wf}}\right)\end{array}(6)$

By solving Eq. 6 and deriving a solution, the unidirectional productivity equation with pseudo-pressure is:

$q_{\text{gsc}}=\frac{\text{π}h{T}_{\text{sc}}\left(m\left(\overline{p}\right)-m\left(p_{\text{wf}}\right)\right)}{2p_{\text{sc}}T{\xi }_{\text{e}}}(7)$

The derivation of Eq. 7 is found in Appendix B. With θ and π−θ included angles, the parameter ξ_e could be presented based on the conformal transformation.

${\xi }_{\text{e}1}=\ln \frac{4r_{\text{d}}^{\text{π}/\theta }}{{\left(l_1+r_{\text{w}}\right)}^{\text{π}/\theta }+{\left(l_2+r_{\text{w}}\right)}^{\text{π}/\theta }}(8)$

${\xi }_{\text{e}2}=\ln \frac{4r_{\text{d}}^{\text{π}/\left(\text{π}-\theta \right)}}{{\left(l_1+r_{\text{w}}\right)}^{\text{π}/\left(\text{π}-\theta \right)}+{\left(l_2+r_{\text{w}}\right)}^{\text{π}/\left(\text{π}-\theta \right)}}(9)$

Equations 8, 9 are for four-wing fractures and were derived from the equations for multi-wing fractures with arbitrary angles and fracture lengths (Chen et al., 2017). By substituting fixed angles and fracture lengths into the multi-wing fracture equations, four-wing fracture equations could be obtained. Combining Eqs 7–9, the productivity equation for the inner region can be written as:

$m\left(\overline{p}\right)-m\left(p_{\text{wf}}\right)=\frac{q_{\text{gsc}}{p}_{\text{sc}}T{\xi }_{\text{e}1}{\xi }_{\text{e}2}}{\text{π}{k}_{1}h{T}_{\text{sc}}\left({\xi }_{\text{e}1}+{\xi }_{\text{e}2}\right)}(10)$

For the exterior region, the productivity equation is:

$m\left(p_e\right)-m\left(\overline{p}\right)=\frac{q_{\text{gsc}}{p}_{\text{sc}}T\ln \frac{r_{\text{e}}}{r_{\text{d}}}}{\text{π}{k}_{2}h{T}_{\text{sc}}}(11)$

Based on Eqs 10, 11, the productivity equation for the whole drainage region, with multi-wing hydraulic fractures, can be expressed as:

$m\left(p_{\text{e}}\right)-m\left(p_{\text{wf}}\right)=\frac{q_{\text{gsc}}{k}_1{p}_{\text{sc}}T{\xi }_{\text{e}1}{\xi }_{\text{e}2}+q_{\text{gsc}}{k}_1{p}_{\text{sc}}T\ln \frac{r_{\text{e}}}{r_{\text{d}}}\left({\xi }_{\text{e}1}+{\xi }_{\text{e}2}\right)}{\text{π}{k}_1{k}_{2}h{T}_{\text{sc}}\left({\xi }_{\text{e}1}+{\xi }_{\text{e}2}\right)}(12)$

Without the effect of skin factors, the productivity equation of an ideal CBM well is:

$m\left(p_{\text{e}}\right)-m\left(p_{\text{wf}}^{\prime }\right)=\frac{q_{\text{gsc}}{p}_{\text{sc}}T\ln \frac{r_{\text{e}}}{r_{\text{w}}}}{\text{π}{k}_{0}h{T}_{\text{sc}}} (13)$

where k₀ is the intrinsic permeability, and p'_wf is the ideal bottom-hole pressure.

Eqs 12, 13 can be combined to obtain the difference between the real and ideal bottom-hole pseudo-pressure.

$m\left(p_{\text{wf}}\right)-m\left(p_{\text{wf}}^{\prime }\right)=\frac{q_{\text{gsc}}{p}_{\text{sc}}T}{\text{π}{k}_{0}h{T}_{\text{sc}}}{S}_{\text{f}}(14)$

where S_f is the fracturing skin factor, expressed as:

$S_{\text{f}}=\frac{k_0{\xi }_{\text{e}1}{\xi }_{\text{e}2}}{k_1\left({\xi }_{\text{e}1}+{\xi }_{\text{e}2}\right)}+\frac{k_0}{k_2}\ln \frac{r_{\text{e}}}{r_{\text{d}}}-\ln \frac{r_{\text{e}}}{r_{\text{w}}}(15)$

From Eqs 4, 15, the speed sensitivity skin factor and fracturing skin factor can be calculated.

2.3 Permeability in the control region of a CBM well

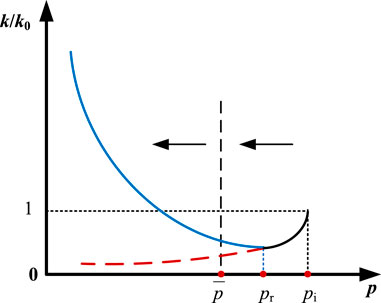
Equations 3, 14, which represent permeability in the inner and exterior regions, as controlled by the SSE–MSE, are discussed here. As shown in Figure 3, the CBM well production triggers the decrease of reservoir pressure from the initial pressure p_i to the critical desorption pressure p_r, and the permeability k declines correspondingly due to the SSE (the black line in Figure 3). With the continued decrease of reservoir pressure (smaller than p_r), permeability is influenced by the combined SSE–MSE. This permeability is reversed and starts to increase (the blue line in Figure 3). Without the MSE, the coal matrix will swell because of the SSE, and permeability will continue to decrease (the red line in Figure 3). The average pressure p is also marked in Figure 3. For reservoir pressures smaller than p, permeability has a negative relationship with pressure.

FIGURE 3

FIGURE 3. Relationship curve of permeability and reservoir pressure.

The permeability model developed by Zhao et al. (2013) was selected for demonstrating the permeability variations. This permeability model is a modification of the S&D model (Shi and Durucan, 2004), requires fewer experimental test parameters, and is given in Eq. 16. The detailed derivation of the model is given in Appendix B.

$\begin{array}{cc}{k}_{\text{d}}=k_0{e}^{-3C_{\text{f}0}\left\{-\frac{\nu }{1-\nu }\left(p-p_{\text{e}}\right)+\frac{\left[\ln \left(1+bp\right)-\ln \left(1+b{p}_r\right)\right]{\rho }_{\text{c}}\text{R}T{V}_{\text{L}}}{3\left(1-\nu \right)V_0}\right\}}& \left(p\le p_{\text{r}}\right)\end{array}(16)$

where k_d is the dynamic permeability; the C_f0 is the compressibility factor of the microfractures; υ is Poisson’s ratio; ρ_c is the density of the coal matrix; R is the universal gas constant; V_L is the Langmuir volume; b is the reciprocal Langmuir pressure; and V₀ is the molar volume.

As shown in Figure 4, the pseudo-pressure is distributed in a funnel shape. The permeability grows with increased proximity to the wellbore. To obtain the permeability of the inner and exterior regions, special treatment should be applied.

$k_1=\frac{1}{m\left(\overline{p}\right)-m\left(p_{\text{wf}}\right)}{\displaystyle {\int }_{m\left(p_{\text{wf}}\right)}^{m\left(\overline{p}\right)}{k}_{\text{d}}}dm\left(p\right)(17)$

$k_2=\frac{1}{m\left(p_{\text{e}}\right)-m\left(\overline{p}\right)}{\displaystyle {\int }_{m\left(\overline{p}\right)}^{m\left(p_{\text{e}}\right)}{k}_{\text{d}}}dm\left(p\right)(18)$

where p_e is the pressure of the closed boundary. At the closed boundary position, the pseudo-pressure distribution curve is perpendicular to the outer boundary (Al-Hussainy et al., 1966), indicating that the variation in pseudo-pressure in the exterior region is less than in the inner region, resulting in similar values of p_e and p. Therefore, to avoid seeking boundary pressure, Eq. 17 could be simplified to,

$k_2=k_{\text{d}}\left(\overline{p}\right)(19)$

FIGURE 4

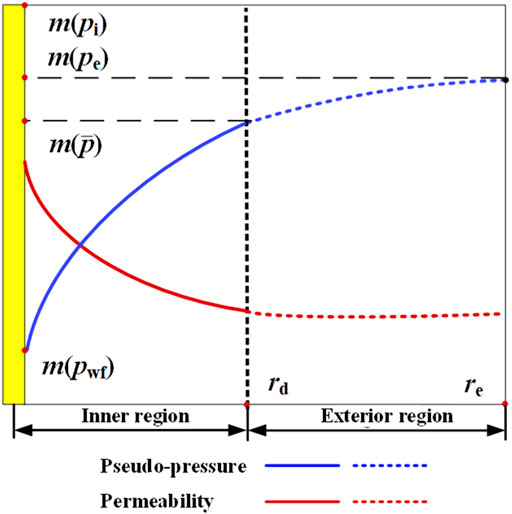
FIGURE 4. Distributions of pseudo-pressure and permeability in the coalbed methane reservoir during exploitation.

3 Validation and discussion

3.1 Validation

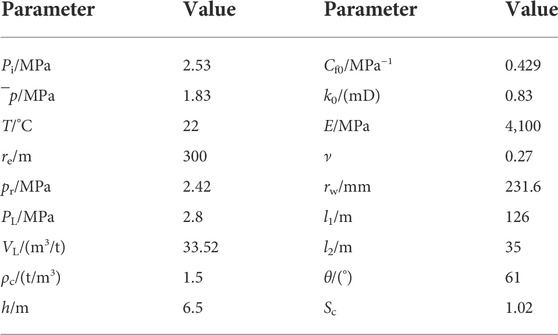
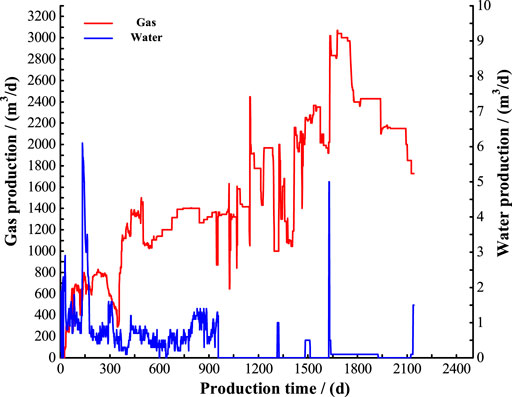
The relative data of CBM Well A from the No. 3 coal seam in the South Shizhuang Block of the Qinshui Basin was used to validate the model (Table 1). Based on the microseismic crack monitoring technique, the lengths of the major and secondary hydraulic fractures and the included angle were all obtained (Table 1). The boundary is closed and the relative gas density is 0.556. The target coal seam has low water content with minimal supply from distant water. Water production, therefore, declined to zero with the increase in gas production (Figure 5). After 3 years of exploitation, Well A is considered a dry or dewatered gas well, due to the scant water production. This may be related to the underground hydrodynamic conditions and well pattern distribution (Ye et al., 2011). The dewatered gas well is a condition of CBM, which is producing gas without water, instead of being a kind of CBM well. A dewatered well, or one in a reservoir with no mobile water in the first place, can both be called a dewatered CBM well. As shown in Figure 6, after 1,000 days of production, there is temporary water production due to the desorption of new coal and the removal of irreducible water. However, compared with gas production, water production is negligible. The relationship data of p_wf and gas production for the well test are presented in Figure 6. The IPR curve with SSE–MSE for the entire region (Curve I in Figure 6), calculated by Eq. 2, is consistent with the well test data, which proves the validity of the production model for a vertical CBM well with multi-wing hydraulic fractures.

TABLE 1

TABLE 1. Parameters of fractured vertical coalbed methane well.

FIGURE 5

FIGURE 5. Gas and water productions of coalbed methane Well A.

FIGURE 6

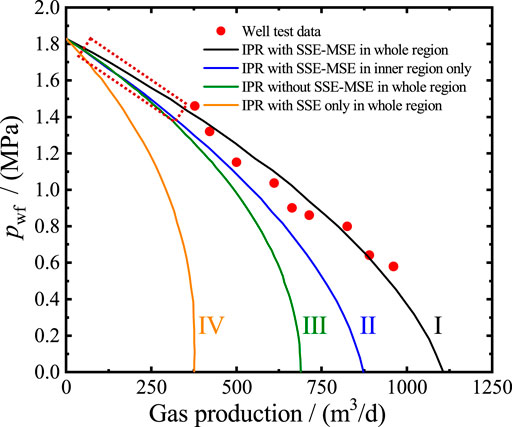
FIGURE 6. Validation of the inflow performance relationship (IPR) curves at different situations of the stress sensitivity effect (SSE) and the matrix shrinkage effect (MSE).

When considering only the SSE in the entire region (Curve IV in Figure 6), the absolute open flow rate is much smaller than the ones with and without SSE–MSE in the entire region (Curves I and III), which are 83.2% and 194.1% larger, respectively. These results reveal that the SSE strongly inhibits CBM productivity due to the positive relationship of permeability with pressure caused by the SSE on its own. However, when considering SSE–MSE together, CBM productivity is stimulated instead of inhibited. Thus, the MSE has a much stronger stimulating impact on productivity than the inhibiting impact of the SSE. As a result, the SSE–MSE benefits CBM productivity. Thus, the absolute open flow rate with the SSE–MSE is 60.5% larger than the ones without (Curves I and III in Figure 6). These results correspond to increasing permeability with decreasing pressure (blue line in Figure 3). When considering the SSE–MSE in the inner region only (Curve II in Figure 6), the absolute open flow rate is reduced by 21%, compared to the SSE–MSE in the whole region. These results indicate that the SSE–MSE in the exterior region has an apparent influence on gas production and should not be neglected. The permeability in the exterior region is larger than the intrinsic permeability due to the SSE–MSE (Figure 3), hence improving gas production.

For bottom-hole pressures close to the average reservoir pressure, Curves II and III are close to each other, while an obvious difference appears between Curves I and II (marked by the dotted rectangle in Figure 6). In this situation, the SSE–MSE of Well A in the exterior region has a considerable impact on productivity, while the one in the inner region does not. Due to the close values of bottom-hole pressure and the average reservoir pressure, the permeability of the inner region, k₁, is close to k_d(p), based on Eq. 17, resulting in the overlap of Curves II and III. When considering the permeability of the exterior region k₂, total permeability is improved as 2k_d(p), bringing larger productivity. This result further proves the importance of the exterior region.

3.2 Variations in fracturing skin factor

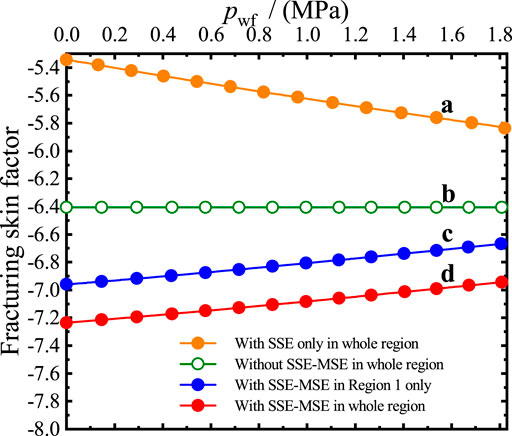
Owing to the influence of the SSE–MSE and consideration of the drainage areas in the inner and exterior regions, the stimulation effect of multi-wing fractures varies with pressure (Figure 7). Curves a, b, c, and d represent the relationships of S_f and p_wf for different situations. Smaller S_f corresponds to a stronger stimulation effect on productivity. Without the SSE–MSE, the fracturing skin factor has no relationship with pressure (Curve b), while the fracturing skin factor with the SSE (Curve a) increases with the decline of p_wf, owing to the positive relationship of permeability controlled by the SSE and the reservoir pressure (the pressure larger than p_r in Figure 3). Greater permeability helps the fluid flow from cleats to the artificial fracture and the stimulation effect of the multi-wing fractures is enhanced.

FIGURE 7

FIGURE 7. Relationships of S_f and p_wf in different situations.

The fracturing skin factor is smaller with the SSE–MSE than without (Curves c and d in Figure 7). These results indicate that the MSE has a greater effect on the fracturing skin factor than the SSE, and tends to lower it, benefitting CBM well production. Unlike the situation with the SSE only, the fracturing skin factor with the SSE–MSE has a positive relationship with p_wf. This is explained by the negative relationship between permeability and reservoir pressure (the pressure is lower than p_r in Figure 3). In addition to the inner region, and comparing Curves c and d, the SSE–MSE in the exterior region also has an important impact on the fracturing skin factor. The fracturing skin factor with the SSE–MSE in the entire region (Curve d), is the smallest among these four situations. This is due to additional consideration of the MSE in the exterior region, compared with Curve c. Therefore, for the gas well production system, reducing p_wf not only enlarges the producing pressure difference but also improves the stimulation effect of multi-wing fractures. When considering the SSE only, or neglecting the SSE–MSE in the exterior region, the stimulation effect of hydraulic fracturing is either overestimated or underestimated, and the optimization of the gas well production system is misdirected.

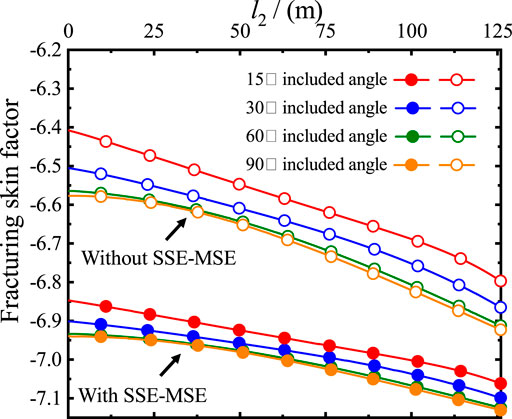
Fixing the p_wf as 1.5 MPa, the variation in fracturing skin factor in light of the included angle and length of fracture can be observed (Figure 8). The fracturing skin factor has a negative relationship with l₂, by a similar variation rate as the arbitrary included angle. With the increase of the included angle, the fracturing skin factor decreases, and the decreasing rate gradually slows. Considering the area of the ellipse, a longer short axis or larger included angle creates a larger multi-wing fracture control area, which promotes the flow of CBM from the cleats to the fractures. Multi-wing fractures of longer length and a larger included angle produce a stronger stimulation effect. The curves with 60° and 90° angles almost overlap in Figure 8, due to the similarity of the elliptical areas with 60° and 90° angles and fixed l₁ and l₂ values. Similar to Figure 7, the fracturing skin factor with SSE–MSE in Figure 8 is smaller than the one without. Observing the curves with SSE–MSE in Figure 8, the variation in the fracturing skin factor with l₂ would be less, and the diversity among these curves would be lower. These results indicate that the SSE–MSE weakens the negative impact of the fracture length and the included angle on the fracturing skin factor. Under the influence of the SSE–MSE, enhanced permeability provides more benefit than fracture length and included angle in making the gas flow more easily to the fractures. In other words, the SSE–MSE contributes more to the relative flow capacity than fracture length and included angle. Overall, a weaker SSE, a stronger MSE, longer fracture length, and a larger included angle, all increase the productivity of a CBM well.

FIGURE 8

FIGURE 8. Relationships of fracturing skin factor with fracture length and included angle.

3.3 Variation of speed sensitivity skin factor

In addition to the fracturing skin factor, the speed sensitivity skin factor also influences the productivity of a CBM well. The relationship of the non-Darcy flow constant with p_wf is similar to that of the fracturing skin factor (Figure 9). Without the SSE–MSE, the non-Darcy flow constant is not related to p_wf, due to the stable permeability (Figure 9A). Due to the positive relationship of permeability with reservoir pressure, the non-Darcy flow constant with the SSE only decreases with the increase of p_wf. However, when considering the SSE–MSE, the negative relationship of permeability and reservoir pressure results in the positive relationship of the non-Darcy flow constant and p_wf. Furthermore, compared to the curve without the SSE–MSE, the SSE increases the non-Darcy flow constant, while additional consideration of the MSE decreases and attenuates the extent of the non-Darcy flow.

FIGURE 9

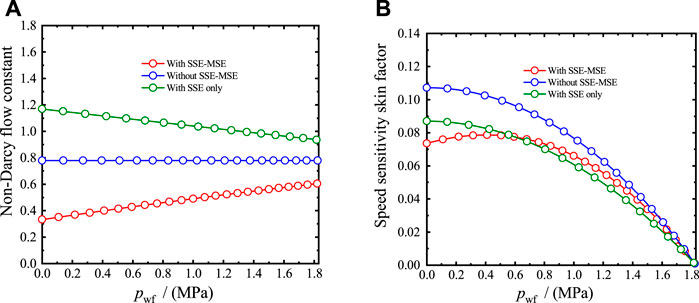
FIGURE 9. Relationships of (A) non-Darcy flow constant and (B) speed sensitivity skin factor with p_wf.

Based on Eq. 3, the speed sensitivity skin factor is the product of the non-Darcy flow constant and gas production. As shown in Figure 9B, the absolute value of the speed sensitivity skin factor is much smaller than that of the fracturing skin factor. These results indicate that the positive effect of artificial fractures is much stronger than the negative effect of the non-Darcy flow with respect to CBM productivity. Nevertheless, the variation in speed sensitivity deserves further investigation for the most accurate evaluation of gas productivity. In Figure 9B, the speed sensitivity skin factor without the SSE–MSE is the largest among the three situations (with SSE–MSE, without SSE–MSE, and with SSE only). Combining Figures 6 and 9B, for the same p_wf, the non-Darcy flow constant is the largest with the SSE only, while the gas production is the smallest. In the situation with the SSE–MSE, the opposite is true. Accordingly, the curves with the SSE only and those with the SSE–MSE are similar. When considering the SSE or MSE, the non-Darcy flow effect would be weaker due to the reduced flow velocity or permeability.

4 Conclusion

The dynamic SSE–MSE and multi-wing fractures were considered with skin factors in the IPR model for an accurate investigation of a dewatered vertical CBM well. Three conclusions were provided as follows:

1) The IPR model with dynamic SSE–MSE and multi-wing fractures is well constructed using the skin factor and validated by real CBM production data. The absolute open flow rate with the SSE–MSE is 60.5% larger than the one without. The permeability in the exterior region is larger than the intrinsic permeability, due to the SSE–MS improving gas production.

2) The MSE has a larger effect on the fracturing skin factor than the SSE and tends to lower the fracturing skin factor, benefitting CBM well production. The reduction of bottom-hole pressure, i.e., pwf, not only enlarges the gas well, producing a pressure difference, but also improves the stimulation effect of multi-wing fractures.

3) The SSE increases the non-Darcy flow constant, while the additional consideration of the MSE lowers it and attenuates the extent of the non-Darcy flow. With the consideration of the SSE or MSE, the non-Darcy flow effect is weaker due to the reduced flow velocity or permeability.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

XD and XW wrote the manuscript and constructed the inflow performance relationship model. JaL and YZ contributed significantly to the analysis and manuscript preparation. XD, JnL, and XW performed the validation and the discussions of skin factors. BW and KQ wrote and edited the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 52004038) and the General Project of Natural Science Research in Colleges and Universities of Jiangsu Province (Grant No. 20KJB440003).

Conflict of interest

JL was employed by PetroChina Coalbed Methane Company Limited. YZ was employed by PetroChina Tuha Oilfield Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Hussainy, R., Ramey, H., and Crawford, P. (1966). The flow of real gases through porous media. J. Petroleum Technol. 18, 624–636. doi:10.2118/1243-a-pa

CrossRef Full Text | Google Scholar

Chen, Y., and Dong, N. (2001). New method of determining turbulence factor and turbulence skin factor. Puyang, China: Fault-Block Oil & Gas Field, 20–23+67.

Google Scholar

Chen, Z., Liao, X., Zhao, X., Lyu, S., and Zhu, L. (2017). A comprehensive productivity equation for multiple fractured vertical wells with non-linear effects under steady-state flow. J. Petroleum Sci. Eng. 149, 9–24. doi:10.1016/j.petrol.2016.09.050

CrossRef Full Text | Google Scholar

Clarkson, C. R., Bustin, R. M., and Seidle, J. P. (2007). Production-data analysis of single-phase (gas) coalbed-methane wells. SPE Reserv. Eval. Eng. 10, 312–331. doi:10.2118/100313-pa

CrossRef Full Text | Google Scholar

Colmenares, L. B., and Zoback, M. D. (2007). Hydraulic fracturing and wellbore completion of coalbed methane wells in the Powder River Basin, Wyoming: Implications for water and gas production. Am. Assoc. Pet. Geol. Bull. 91, 51–67. doi:10.1306/07180605154

CrossRef Full Text | Google Scholar

Feng, Q., Shi, H., Zhang, X., Du, P., and Zhang, J. (2012). “New inflow performance relationship for coalbed methane wells,” in SPE/EAGE European unconventional resources conference and exhibition (Vienna, Austria: Society of Petroleum Engineers).

CrossRef Full Text | Google Scholar

Freij-Ayoub, R. (2012). Opportunities and challenges to coal bed methane production in Australia. J. Petroleum Sci. Eng. 88-89, 1–4.

CrossRef Full Text | Google Scholar

Gash, B. W. (1991). “Measurement of rock properties in coal for coalbed methane production,” in SPE annual technical conference and exhibition (Dallas, Texas: OnePetro).

CrossRef Full Text | Google Scholar

Harpalani, S., and Schraufnagel, R. A. (1990). Shrinkage of coal matrix with release of gas and its impact on permeability of coal. Fuel 69, 551–556. doi:10.1016/0016-2361(90)90137-f

CrossRef Full Text | Google Scholar

Huang, L., Zhou, W., Xu, H., Wang, L., Zou, J., and Zhou, Q. (2021). Dynamic fluid states in organic-inorganic nanocomposite: Implications for shale gas recovery and CO2 sequestration. Chem. Eng. J. 411, 128423. doi:10.1016/j.cej.2021.128423

CrossRef Full Text | Google Scholar

Jiang, T., Zhang, J., and Wu, H. (2016). Experimental and numerical study on hydraulic fracture propagation in coalbed methane reservoir. J. Nat. Gas Sci. Eng. 35, 455–467. doi:10.1016/j.jngse.2016.08.077

CrossRef Full Text | Google Scholar

Jiang, T., Zhang, J., and Wu, H. (2017). Effects of fractures on the well production in a coalbed methane reservoir. Arab. J. Geosci. 10, 1–10. doi:10.1007/s12517-017-3283-7

CrossRef Full Text | Google Scholar

Jin, W., Yongshang, K., Shanyu, J., Shouren, Z., Jianping, Y., and Jian, W. (2016). Reasons for water production difference of CBM wells in Shouyang Block, Qinshui Basin, and prediction on favorable areas. Nat. Gas. Ind. 36, 52–59. doi:10.3787/j.issn.1000-0976.2016.08.007

CrossRef Full Text | Google Scholar

Jones, S. (1987). “Using the inertial coefficient, b, to characterize heterogeneity in reservoir rock,” in SPE annual technical conference and exhibition (Dallas, Texas: Society of Petroleum Engineers).

CrossRef Full Text | Google Scholar

Karimpouli, S., Tahmasebi, P., and Ramandi, H. L. (2020). A review of experimental and numerical modeling of digital coalbed methane: Imaging, segmentation, fracture modeling and permeability prediction. Int. J. Coal Geol. 228, 103552. doi:10.1016/j.coal.2020.103552

CrossRef Full Text | Google Scholar

King, G. (1993). “Measurement of inflow performance parameters for coal seam and Devonian shale gas reservoirs and its implication in numerical reservoir simulation,” in SPE annual technical conference and exhibition (Houston, Texas: OnePetro).

CrossRef Full Text | Google Scholar

Lau, H. C., Li, H., and Huang, S. (2017). Challenges and opportunities of coalbed methane development in China. Energy fuels. 31, 4588–4602. doi:10.1021/acs.energyfuels.7b00656

CrossRef Full Text | Google Scholar

Li, H., Zhang, Q., Li, Z., Pang, Q., Wei, K., Zeng, Y., et al. (2022). Pressure transient analysis for multi-wing fractured vertical well in coalbed methane reservoir based on fractal geometry and fractional calculus. Energy Explor. Exploitation 40, 926–946. doi:10.1177/01445987221090366

CrossRef Full Text | Google Scholar

Ma, Q., Harpalani, S., and Liu, S. (2011). A simplified permeability model for coalbed methane reservoirs based on matchstick strain and constant volume theory. Int. J. Coal Geol. 85, 43–48. doi:10.1016/j.coal.2010.09.007

CrossRef Full Text | Google Scholar

Mavor, M., and Vaughn, J. (1998). Increasing coal absolute permeability in the San Juan Basin fruitland formation. SPE Reserv. Eval. Eng. 1, 201–206. doi:10.2118/39105-pa

CrossRef Full Text | Google Scholar

Meng, F., He, D., Yan, H., Zhao, H., Zhang, H., and Li, C. (2021). Production performance analysis for slanted well in multilayer commingled carbonate gas reservoir. J. Petroleum Sci. Eng. 204, 108769. doi:10.1016/j.petrol.2021.108769

CrossRef Full Text | Google Scholar

Metcalfe, R., Yee, D., Seidle, J., and Puri, R. (1991). “Review of research efforts in coalbed methane recovery,” in SPE asia-pacific conference (Perth. Australia: OnePetro).

CrossRef Full Text | Google Scholar

Ni, X., Zhao, Z., Wang, Y., and Wang, L. (2020). Optimisation and application of well types for ground development of coalbed methane from no. 3 coal seam in shizhuang south block in Qinshui basin, Shanxi province, China. J. Petroleum Sci. Eng. 193, 107453. doi:10.1016/j.petrol.2020.107453

CrossRef Full Text | Google Scholar

Nie, R.-S., Meng, Y.-F., Guo, J.-C., and Jia, Y.-L. (2012). Modeling transient flow behavior of a horizontal well in a coal seam. Int. J. Coal Geol. 92, 54–68. doi:10.1016/j.coal.2011.12.005

CrossRef Full Text | Google Scholar

Osisanya, S. O., and Schaffitzel, R. F. (1996). “A review of horizontal drilling and completion techniques for recovery of coalbed methane,” in International conference on horizontal well technology (Calgary, Alberta: OnePetro).

CrossRef Full Text | Google Scholar

Palmer, I. (2010). Coalbed methane completions: A world view. Int. J. Coal Geol. 82, 184–195. doi:10.1016/j.coal.2009.12.010

CrossRef Full Text | Google Scholar

Palmer, I., and Mansoori, J. (1996). How permeability depends on stress and pore pressure in coalbeds: A new model. Spe Reserv. Eval. Eng. 1, 539–544. doi:10.2118/52607-pa

CrossRef Full Text | Google Scholar

Pan, Z., and Connell, L. D. (2011). Modelling of anisotropic coal swelling and its impact on permeability behaviour for primary and enhanced coalbed methane recovery. Int. J. Coal Geol. 85, 257–267. doi:10.1016/j.coal.2010.12.003

CrossRef Full Text | Google Scholar

Park, S. Y., and Liang, Y. (2016). Biogenic methane production from coal: A review on recent research and development on microbially enhanced coalbed methane (mecbm). Fuel 166, 258–267. doi:10.1016/j.fuel.2015.10.121

CrossRef Full Text | Google Scholar

Quan, F., Wei, C., Ma, J., Hao, S., and Song, Y. (2022). Modeling analysis of coalbed methane co-production interference: A case study in eastern yunnan basin, China. J. Nat. Gas Sci. Eng. 103, 104631. doi:10.1016/j.jngse.2022.104631

CrossRef Full Text | Google Scholar

Ren, Z., Yan, R., Huang, X., Liu, W., Yuan, S., Xu, J., et al. (2019). The transient pressure behavior model of multiple horizontal wells with complex fracture networks in tight oil reservoir. J. Pet. Sci. Eng. 173, 650–665. doi:10.1016/j.petrol.2018.10.029

CrossRef Full Text | Google Scholar

Runsheng, L., Xiaoming, N., Gaofeng, L., and Jiangang, R. (2016). A physical model of outburst elimination boundaryafterhydraulicfracturingin coal⁃ bed methane well. J. China Coal Soc. 41, 2273–2280. doi:10.13225/j.cnki.jccs.2016.0122

CrossRef Full Text | Google Scholar

Seidle, J., and Erickson, D. (1993). “Use of vogel's inflow performance relation for coal wells,” in SPE gas technology symposium (Calgary, Alberta: OnePetro).

CrossRef Full Text | Google Scholar

Seidle, J., Jeansonne, M., and Erickson, D. (1992). “Application of matchstick geometry to stress dependent permeability in coals,” in SPE rocky mountain regional meeting (Casper, Wyoming: Society of Petroleum Engineers).

CrossRef Full Text | Google Scholar

Seidle, J. (1993). Long-term gas deliverability of a dewatered coalbed. J. Petroleum Technol. 45, 564–569. doi:10.2118/21488-pa

CrossRef Full Text | Google Scholar

Shi, J., and Durucan, S. (2004). Drawdown induced changes in permeability of coalbeds: A new interpretation of the reservoir response to primary recovery. Transp. porous media 56, 1–16. doi:10.1023/b:tipm.0000018398.19928.5a

CrossRef Full Text | Google Scholar

Shi, J., Hou, C., Wang, S., Xiong, X., Wu, S., and Liu, C. (2019). The semi-analytical productivity equations for vertically fractured coalbed methane wells considering pressure propagation process, variable mass flow, and fracture conductivity decrease. J. Petroleum Sci. Eng. 178, 528–543. doi:10.1016/j.petrol.2019.03.047

CrossRef Full Text | Google Scholar

Sugiarto, I., Mazumder, S., Wittemeier, R., and Sharma, V. (2015). “Inflow performance relationship correlation of 2 phase CBM reservoir,” in SPE/IATMI Asia pacific oil & gas conference and exhibition (Nusa Dua, Bali, Indonesia: OnePetro).

Google Scholar

Sun, Z., Shi, J., Zhang, T., Wu, K., Miao, Y., Feng, D., et al. (2018). The modified gas-water two phase version flowing material balance equation for low permeability CBM reservoirs. J. Petroleum Sci. Eng. 165, 726–735. doi:10.1016/j.petrol.2018.03.011

CrossRef Full Text | Google Scholar

Sun, Z., Huang, B., Li, Y., Yu, W., and Ji, L. (2022). Production forecast of fractured vertical wells in coalbed methane reservoirs: Coupling dynamic drainage area. Arab. J. Geosci. 15, 7–9. doi:10.1007/s12517-021-09094-9

CrossRef Full Text | Google Scholar

Tao, S., Tang, D., Xu, H., Gao, L., and Fang, Y. (2014). Factors controlling high-yield coalbed methane vertical wells in the Fanzhuang Block, Southern Qinshui Basin. Int. J. Coal Geol. 134, 38–45. doi:10.1016/j.coal.2014.10.002

CrossRef Full Text | Google Scholar

Thungsuntonkhun, W., and Engler, T. W. (2001). “Well deliverability of undersaturated coalbed reservoir,” in SPE rocky mountain petroleum technology conference (Keystone, Colorado: OnePetro).

CrossRef Full Text | Google Scholar

Wang, G., Massarotto, P., and Rudolph, V. (2009). An improved permeability model of coal for coalbed methane recovery and CO2 geosequestration. Int. J. Coal Geol. 77, 127–136. doi:10.1016/j.coal.2008.10.007

CrossRef Full Text | Google Scholar

Wu, Y., Liu, J., Elsworth, D., Miao, X., and Mao, X. (2010). Development of anisotropic permeability during coalbed methane production. J. Nat. Gas Sci. Eng. 2, 197–210. doi:10.1016/j.jngse.2010.06.002

CrossRef Full Text | Google Scholar

Wu, X., Ning, Z., Han, G., Wang, Q., Zhong, Z., Qi, R., et al. (2019). Modified SLD model for coalbed methane adsorption under reservoir conditions. Arab. J. Geosci. 12, 562. doi:10.1007/s12517-019-4763-8

CrossRef Full Text | Google Scholar

Wu, X., He, Y., Ning, Z., Lyu, F., Dou, X., and Wu, B. (2022). Mechanistic insights into confined methane adsorption in carbon nanopores at the molecular level. Chem. Eng. Sci. 250, 117374. doi:10.1016/j.ces.2021.117374

CrossRef Full Text | Google Scholar

Xu, B., Li, X., Haghighi, M., Ren, W., Du, X., Chen, D., et al. (2013). Optimization of hydraulically fractured well configuration in anisotropic coal-bed methane reservoirs. Fuel 107, 859–865. doi:10.1016/j.fuel.2013.01.063

CrossRef Full Text | Google Scholar

Xu, Y., Li, X., Liu, Q., Yang, S., and Tan, X. (2021). A semi-analytical solution of finite-conductivity multi-wing fractured well in naturally fractured reservoirs by boundary element method. J. Petroleum Sci. Eng. 203, 108584. doi:10.1016/j.petrol.2021.108584

CrossRef Full Text | Google Scholar

Yang, G., Tang, S., Hu, W., Song, Z., Zhang, S., Xi, Z., et al. (2020). Analysis of abnormally high water production in coalbed methane vertical wells: A case study of the shizhuangnan block in the southern Qinshui Basin, China. J. Petroleum Sci. Eng. 190, 107100. doi:10.1016/j.petrol.2020.107100

CrossRef Full Text | Google Scholar

Ye, J., Zhang, J., and Wang, Z. (2011). Production performance and its controlling factors in the panhe CMB gas field, southern Qinshui Basin. Nat. Gas. Ind. 31, 28–30. doi:10.3787/j.issn.1000-0976.2011.05.007

CrossRef Full Text | Google Scholar

Zang, J., and Wang, K. (2016). A numerical model for simulating single-phase gas flow in anisotropic coal. J. Nat. Gas Sci. Eng. 28, 153–172. doi:10.1016/j.jngse.2015.11.006

CrossRef Full Text | Google Scholar

Zhang, J. (2014). Numerical simulation of hydraulic fracturing coalbed methane reservoir. Fuel 136, 57–61. doi:10.1016/j.fuel.2014.07.013

CrossRef Full Text | Google Scholar

Zhang, L., Kou, Z., Wang, H., Zhao, Y., Dejam, M., Guo, J., et al. (2018). Performance analysis for a model of a multi-wing hydraulically fractured vertical well in a coalbed methane gas reservoir. J. Petroleum Sci. Eng. 166, 104–120. doi:10.1016/j.petrol.2018.03.038

CrossRef Full Text | Google Scholar

Zhao, M., Yao, Z., Xu, M., Li, J., and Xu, J. (2013). Dynamic permeability model considering self-adjustment effect for coalbed methane. Fault-Block Oil Gas Field 1, 63–66. doi:10.6056/dkyqt201301015

CrossRef Full Text | Google Scholar

Zhiming, C., Xinwei, L., Chenghui, H., Xiaoliang, Z., Langtao, Z., Yizhou, C., et al. (2014). Productivity estimations for vertically fractured wells with asymmetrical multiple fractures. J. Nat. Gas Sci. Eng. 21, 1048–1060. doi:10.1016/j.jngse.2014.10.025

CrossRef Full Text | Google Scholar

Zhou, F., Chen, Z., and Rahman, S. S. (2015). Effect of hydraulic fracture extension into sandstone on coalbed methane production. J. Nat. Gas Sci. Eng. 22, 459–467. doi:10.1016/j.jngse.2014.12.017

CrossRef Full Text | Google Scholar

Appendix A Expressions of average deviation factor and viscosity

The empirical expressions of average deviation factor and viscosity were used by Chen and Dong (2001) and accepted in Chinese gas well production and investigation. The empirical expressions of the average deviation factor are written as,

$\overline{Z}=a+\frac{1-a}{e^b}+c{p}_{\text{pr}}^d(\mathrm{A1})$

where

$a=1.39{\left(T_{\text{pr}}-0.92\right)}^{0.5}-0.36T_{\text{pr}}-0.101(\mathrm{A2})$

$b=\left(0.62-0.23T_{\text{pr}}\right)p_{\text{pr}}+\left(\frac{0.066}{T_{\text{pr}}-0.86}-0.037\right)p_{\text{pr}}^2+\frac{0.32p_{\text{pr}}^6}{\exp \left[20.727\left(T_{\text{pr}}-1\right)\right]}(\mathrm{A3})$

$c=0.132-0.31\lg T_{\text{pr}}(\mathrm{A4})$

$d=\exp \left(0.7153-1.1285T_{\text{pr}}+0.4201T_{\text{pr}}^2\right)(\mathrm{A5})$

$p_{\text{pr}}=p/p_{\text{pc}}(\mathrm{A6})$

$T_{\text{pr}}=T/T_{\text{pc}}(\mathrm{A7})$

$p_{\text{pc}}=4.6677+0.1034{\gamma }_{\text{g}}-0.2585{\gamma }_{\text{g}}^2(\mathrm{A8})$

$T_{\text{pc}}=93.3333+180.5556{\gamma }_{\text{g}}-6.9444{\gamma }_{\text{g}}^2(\mathrm{A9})$

where a, b, c, and d are empirical parameters for calculating average deviation factor; p_pc and T_pc are the critical pressure and temperature of gas; and p_pr and T_pr are the relative pressure and temperature of gas.

The average viscosity could be expressed as below:

${\overline{\mu }}_{\text{g}}={10}^{-4}{k}_{\text{v}}\exp \left(x{\rho }_{\text{g}}^y\right)(\mathrm{A10})$

where

$k_{\text{v}}=\frac{0.777\left(16.22+{\gamma }_{\text{g}}\right)T^{1.5}}{116.1+307.1{\gamma }_{\text{g}}+T}(\mathrm{A11})$

$x=0.29\left(12.08+\frac{1890}{T}+{\gamma }_{\text{g}}\right)(\mathrm{A12})$

$y=0.2\left(12-x\right)(\mathrm{A13})$

${\rho }_{\text{g}}=\frac{3\text{.}4841{\gamma }_{\text{g}}p}{\overline{Z}T}(\mathrm{A14})$

where k_v, x, and y are empirical parameters for calculating average viscosity and ρ_g is the gas density.

Appendix B Derivation for unidirectional productivity equation with pseudo-pressure

By solving Eq. 6, the following equation is obtained:

$\mathrm{\nabla }m\left(p\right)=-\frac{m\left(p_{\text{e}}\right)-m\left(p_{\text{wf}}\right)}{{\xi }_{\text{e}}}(\mathrm{B1})$

In the form of pseudo-pressure, the mass flow of gas is (Al-Hussainy et al., 1966):

$\rho v=-\frac{Mk}{2RT}\mathrm{\nabla }m\left(p\right)(\mathrm{B2})$

Based on the real gas equation of state, Eq. B3 could be rewritten as:

$v=-\frac{Zk}{2p}\mathrm{\nabla }m\left(p\right)(\mathrm{B3})$

The gas velocities on and under the ground have the following relationship:

$v_{\text{sc}}=\frac{T_{\text{sc}}pv}{T{p}_{\text{sc}}Z}(\mathrm{B4})$

Combining Eqs B1, B3, and B4, the unidirectional productivity equation with pseudo-pressure could be attained.

$q_{\text{gsc}}=\frac{\text{π}hK{T}_{\text{sc}}\left(m\left(\overline{p}\right)-m\left(p_{\text{wf}}\right)\right)}{2p_{\text{sc}}T{\xi }_{\text{e}}}(\mathrm{B5})$