Review on risk assessments of dammed lakes

As one type of natural disaster, dammed lakes pose a serious threat to the safety of lives and properties downstream. Scientific risk assessments of dammed lakes are key for pre-disaster prevention and post-disaster rescue. However, due to the lack of basic information and uncertainty surrounding materials and loads, risk assessments of dammed lakes are more complex than those of artificial reservoir dams, and comprehensive assessment methods are lacking. Based on the evolution of dammed lake hazard chains, starting with the concept of a dammed lake risk assessment, this paper focused on six aspects: worldwide dammed lake databases, hazard assessments for landslide dams, breach mechanisms and breach processes, flood routing after landslide dam breaching, loss assessments, and risk mitigation measures. A comprehensive review was conducted on the qualitative and quantitative risk assessment methods around the world, as well as future outlooks.

Highlights

• The hazard chain evolution process of dammed lake was focused.

• A worldwide database was compiled to provide basic information on dammed lakes.

• Hazard assessment methods of landslide dams were reviewed.

• The simulation methods of breach processes and flood routing were reviewed.

• Loss assessment methods and risk mitigation measures were reviewed.

1 Introduction

Triggered by earthquakes or rainfall, dammed lakes are a type of geological hazard in mountainous areas, and are caused by landslides that block rivers (Costa and Schuster, 1988; Korup, 2002; Ermini and Casagli, 2003; Fan et al., 2020). The accumulations blocking the rivers are called landslide dams. A global diagram of the distribution of 350 dammed lakes using topographic data from US Geological Survey from Ermini and Casagli (2003) showed that dammed lakes are widely spread around the world. Shen et al. (2020a) studied 1,393 documented dammed lakes and reported that 50.5% were earthquake-induced and 39.3% were rainfall-induced, which together made up nearly 90% of the total cases. The other causes were snowmelt, human-causes, and volcanic eruptions.

As the water retaining structures of dammed lakes, landslide dams are composed of Earth and stone materials, but there are significant differences between natural dams and artificial embankment dams. The main differences lie in (Zhong et al. 2021): 1) Dam geometry. Landslide dams are generally longer in the longitudinal direction and the crests are uneven. 2) Structure and materials. Most landslide dams have complex structures, strong heterogeneity and wide grain-size distributions. 3) Hydrodynamic conditions. Because there are no flood discharge facilities on landslide dams, overtopping failures are prone to occur when water levels rise in dammed lakes; furthermore, due to the long length in the longitudinal direction, the maximum hydraulic gradient of a landslide dam is generally lower than that of an embankment dam. Hence, overtopping failures are the main failure type and more 90% of documented historical failures have been overtopping-induced (Costa and Schuster, 1988; Zhang et al., 2016).

Out of 73 dammed lakes around the world studied by Costa and Schuster (1988), 85% of the cases lasted less than 1 year, and 27% less than 1 day. Later, Peng and Zhang (2012a) and Shen et al. (2020a) also found similar statistical results based on 204 and 352 cases, respectively. In general, the failure probabilities of dammed lakes are much higher than those of artificial reservoirs. Once a dammed lake breaches, it may cause a serious flood disaster, so a reasonable assessment of the risk of the dammed lake can prepare emergency response, reduce the loss of property and environmental damage, as well as protect people’s lives.

Risk is defined as the probability of injury or loss, which is a measurement of the likelihood and severity of negative effects on life, property, safety, health, or the environment. Although there are different understandings of risk, they are usually described from two perspectives: the first is possibility, as in the probability of occurrence; the second is consequence, as in the loss caused. According to the definition, risk can be quantified by the expected value of the consequences, which can be depicted by the product of the frequency of disasters and the losses. For a dammed lake, risk can be expressed as the product of failure probability and loss in Eq. 1.

$R=P\times C(1)$

where R is the dammed lake risk; P is the failure probability; C is the loss after a dammed lake breach.

Since the 1980s, much research has focused on risk assessments of dammed lakes. After decades of development, great progress has been achieved in theoretical and practical aspects. A number of reviews covered the related topics (i.e., Costa and Schuster, 1988; Korup, 2002; Liu et al., 2019; Fan et al., 2019a; Fan et al., 2020; Fan et al., 2021; Zhong et al., 2021). Based on the information of 225 landslide dams, the publication of a benchmark review by Costa and Schuster (1988) first provided a comprehensive overview on the causes, classification, and grain size distribution of landslide dams, as well as their longevity and failure modes. Fourteen years later, with special attention to New Zealand, Korup (2002) emphasized the importance of high-quality essential data, and reviewed the state of knowledge at that time and elucidated several directions of future research potential on the formation and failure of landslide dams. Later, Liu et al. (2019) reviewed the outburst floods of landslide dams in China in terms of their characteristics, distribution, causes, as well as case studies and future research directions. Fan et al. (2019a), Fan et al. (2020), and Fan et al. (2021) presented a series of overviews on the patterns, mechanisms, and impacts geologic hazard chains, especially technological and methodological advances on landslide dam formation, stability, and impacts. Zhong et al. (2021) focused on the breach mechanisms and numerical modeling of embankment and landslide dam breaches, and illustrated model uncertainties, limitations, and further directions.

Despite these efforts, most of the reviews focused on landslide dam formation, stability, and breach processes; according to the definition of risk, a thorough review of dammed lake risk assessments has not been conducted, particularly with respect to advances in hazard chain evolution due to the damming of rivers by landslides.

This review focuses on hazard chain evolution of dammed lake formation and provides an overview of hazard assessments of landslide dams, breach processes, breach-induced flood routing, loss assessments, and risk mitigation measures.

Section 2 reports on data from landslide dam cases around the world. The cases in these databases are compiled to provide fundamental information on dammed lakes (Section 2.1). Furthermore, in order to unify the understanding, the terminology (Section 2.1) used for characterizing the stability of landslide dams, damming modes, and data classification (Section 2.2) based on the study purpose is also discussed in this section. Landslide dam stability is the prerequisite and foundation for a risk assessment, and Section 3 attempts to summarize hazard assessment methods for landslide dam stability, which includes qualitative (Section 3.1) and quantitative (Section 3.2) assessment methods. Section 4 is devoted to breach mechanisms and numerical simulation methods of landslide dam breach processes. A synopsis of the model tests for landslide dam breach processes and influencing factors is provided and illustrated (Section 4.1). Numeric simulation methods, including parametric, simplified physical, and detailed physical modeling are introduced and compared (Section 4.2). Then, model tests (Section 5.1) and numerical modeling (Section 5.2) to describe breach-induced flood routing are analyzed and summarized in Section 5, in which inundation is a key component of risk assessment. Section 6 reviews loss assessment methods after landslide dam breaching, while associated progresses in loss of life are introduced. Section 7 presents risk mitigation measures for dammed lakes, focusing on engineering measures. Section 8 discusses the uncertainties and limitations in the current study, and suggests several scientific issues for further study in the field of dammed lake risk assessments. Section 9 summarizes the research results based on the review work. The overall architecture of this review is shown in Figure 1. This review is a continuation of a study on breaches of embankment and landslide dams (Zhong et al., 2021). Herein, the advances of risk assessments methodologies for dammed lake geologic hazard chains are presented (Figure 2).

FIGURE 1

FIGURE 1. Overall architecture of the review.

FIGURE 2

FIGURE 2. Geologic hazard chain triggered by dammed lake breaching and risk mitigation.

2 Worldwide dammed lake databases

2.1 Dammed lake inventories and terminology definitions

In recent decades, a high degree of study of dammed lakes has produced a multitude of documented cases. In this review, in order to comprehensively understand the fundamental information on dammed lakes, such as global distribution, geological and hydrological conditions, dam geomorphology, dam material composition, failure modes, and breach characteristics, an extensive collection of dammed lake cases was conducted. The published inventories that were closely related to the review and compiled in our database, are summarized in Table 1.

TABLE 1

TABLE 1. Summary of published dammed lakes inventories.

In Table 1, according to the stability classification, dammed lakes were classified into formed-stable, formed-unstable, and unknown in terms of landslide dam status. Herein, formed-stable refers to a landslide dam in which the blocked a river/valley still exists or has disappeared due to sediment infilling. Over its lifetime, inflow water may overtopped the dam crest, but neither total failure nor destructive flood occurred (Stefanelli et al., 2015; Stefanelli et al., 2016; Shan et al., 2020). Formed-unstable refers to a landslide dam that had disappeared when statistical work was conducted, and the longevity may have been minutes to centuries after its formation. A landslide dam can be classified as formed-unstable if human intervention has strongly influenced the dam morphology and hydrological conditions to prevent potential disasters (Stefanelli et al., 2015; Stefanelli et al., 2016; Shan et al., 2020). Unknown means the current status of a landslide dam could not be verified during the investigation. The unknown dams are not of concern in this review.

Based on the relationship with the stream/valley floor, landslide dams can be classified into six categories (Costa and Schuster, 1988; Hermanns et al., 2011a; Fan et al., 2020): 1) Partial blocking. A landslide did not reach the opposite bank of the stream/valley. 2) Complete blocking. A landslide reached the opposite bank of the stream/valley. 3) Longitudinal blocking. A landslide extended a long distance in the streamwise direction of the stream/valley. 4) Two sides blocking. Simultaneous movement of two landslides detached from opposite sides of the same stream/valley. 5) Multiple blocking. A single landslide sent multiple tongues of debris into a stream/valley and formed two or more landslide dams in the same section of the river. 6) Down-traverse blocking. A landslide involved one or more failure surfaces that extended under the stream/valley and emerged on the opposite side.

Based on the collection methods, theses inventories can be categorized as historical or event-based. The cases in the inventories of Cui et al. (2009), Xu et al. (2009), and Chen et al. (2011) are event-based. Of these, the first two referred to cases that were triggered by the 2008 Wenchuan earthquake in China, and the cases in the third inventory were triggered by the Morakot typhoon in 2009 in Taiwan, China. The other inventories are all historical cases.

In terms of the study purposes, the recorded information within these inventories have been used for geological surveys (i.e., Costa and Schuster, 1991; Chai et al., 1995; Cui et al., 2009; Xu et al., 2009; Chen et al., 2011; Hermanns et al., 2011b; Stefanelli et al., 2015; Stefanelli et al., 2018), landslide dam stability analysis (i.e., Ermini and Casagli, 2003; Casagli et al. 2003; Korup, 2004; Tong, 2008; Dong et al., 2009; Shen et al., 2020a; Shan et al., 2020) or dammed lake breach process simulations (Peng and Zhang, 2012a; Zhang et al., 2016).

In this review, based on the previous inventories and information collection, a database of 1,765 recorded dammed lakes was collected and sorted by the authors. The distribution of the 1,765 dammed lakes around the world is shown in Figure 3. Where cases were repeated across inventories, scientific inspection work was conducted to select the most accurate and complete information. Figure 4 chronologically presents the number of documented dammed lake cases in China. The landslide dam cases prior to the 1860s are listed together according to age, and other cases were organized every two decades until 2020. Because of the vast territory and special geographical conditions of China, the Tibetan Plateau and southwestern China located in a strong seismic activity zone have become high incidence areas of dammed lakes. It is worth mentioning that, the number of documented dammed lakes have increased in China in past decades.

FIGURE 3

FIGURE 3. Worldwide distribution of 1,765 dammed lakes.

FIGURE 4

FIGURE 4. Number of documented dammed lake cases in China.

2.2 Classification of documented information of dammed lakes

As historical recorded dammed lakes have increased, global databases have shown an increasing trend. Depending on the purpose of a study, the documented information for dammed lakes varied from one to another. The information for dammed lakes can be categorized into three types: morphological indexes of landslide dams (i.e., dam height/width/length/volume), hydrodynamic conditions of dammed lakes (i.e., lake surface area/length/volume, catchment area, inflow discharge, dammed river steepness), and material composition of landslide deposits (i.e., lithology, material composition, grain-size distribution). Furthermore, for the formed-unstable dammed lakes, breaching information, such as breach flow discharge, breach size, and failure time, was the main concern. However, due to the scarcity of historical data, there was not complete information for most of the recorded cases. Of the available information, most had morphology indexes and some of the hydrodynamic conditions, such as lake surface area/length/volume or catchment area. In addition, dammed river steepness, lithology, material composition, and grain-size distribution of landslide deposits were available if the relevant field investigations were conducted, as well as the final breach size after dam breaching. In contrast, some information could not be found through retrospective analysis or field investigations, such as inflow discharge, breach flow discharge, and failure time, if the hydrological information was unavailable.

3 Hazard assessments for landslide dams

Dammed lakes are generally formed by the rapid accumulation of collapsible rock, debris, and Earth triggered by earthquake or rainfall. For a dammed lake, its hazard can be transformed into the stability of water-retaining structure, the landslide dam. Investigations have found that landslide dam stability is mainly related to the material composition, structural characteristics, hydrodynamic conditions of dammed lake, as well as local precipitation conditions and secondary disasters. Considering these influencing factors, a series of studies have assessed landslide dam stability, which can be divided into qualitative and quantitative assessment methods.

3.1 Qualitative assessment methods

The qualitative assessment methods for landslide dam stability are mainly based on formation mechanisms, geometry, material composition, catchment area, and inflow rate, to evaluate global stability. These methods do not use mathematical calculations, and the evaluation indexes can be obtained by means of remote sensing (Ermini et al., 2006; Scaioni et al., 2014; Fan et al., 2021) and geophysical methods (McCann and Forster, 1990; Jongmans and Garambois, 2007; Whiteley et al., 2019; Fan et al., 2021).

In recent decades, remote sensing technology has made significant advances in resolution, accuracy, acquisition time, and logistics, making it a powerful tool in landslide dam identification and investigation. It can be used for geometry mapping of landslide dams and dammed lakes, as well as the deformation monitoring of landslide dams. In addition, in regions without data, an alternative method of optical photogrammetry using unmanned aerial vehicles can be employed. Three types of geophysical methods are utilized to investigate landslide dams (Fan et al., 2021): electromagnetic surveys (i.e., active electromagnetics, ground penetrating radar, and magnetotellurics), geoelectric surveys (i.e., electrical resistivity tomography and self-potential), and seismic surveys (i.e., compressional P-waves and transverse S-waves).

Qualitative assessment methods can be divided into engineering analogy methods and historical analysis methods. The engineering analogy methods compare select landslide dams with similar ones in terms of the formation mechanisms and geological conditions, to assess the landslide dam stability. The historical analysis methods assess stability according to the landslide dam formation history and evolution process. Table 2 shows a brief overview of the qualitative hazard assessment methods for landslide dams. With the development of remote sensing and geophysical technologies, significant progress has been made in emergency response for dammed lake events. However, there are few studies that have focused only on qualitative assessments, most of which are used as the basic data support for quantitative assessments. Meanwhile, qualitative assessment is also the first step to judge the erosion resistance of the dam material. Accurate and rapid acquisition of topographic and hydrodynamic information, as well as geotechnical properties of landslide debris, is the basis for outburst flood analysis.

TABLE 2

TABLE 2. A brief overview of qualitative hazard assessment methods for landslide dams.

3.2 Quantitative assessment methods

The quantitative assessment methods for landslide dam stability can be classified into probability-based mathematical statistics methods and computer-based numerical analysis methods.

3.2.1 Probability-based mathematical statistics methods

Mathematical statistics is a branch of mathematics based on probability theory that studies the statistical regularity of a large number of random phenomena. In recent years, using measured data from formed-stable and formed-unstable landslide dams, a series of mathematical expressions and judgement criteria have been developed to rapidly evaluate landslide dam stability. With increased survey data for landslide dams around the world, the input parameters of the mathematical expressions of the assessment methods have gradually increased, and the influencing factors are more comprehensive. In this review, following the definition by Costa and Schuster (1991), landslide dam length is the crest length perpendicular to the valley axis, and landslide dam width is the base width parallel to the valley axis.

Starting from a database of 70 landslide dam cases collected in the northern Apennines, Casagli and Ermini (1999) defined the blockage index (BI) and proposed the first mathematical expression to evaluate landslide dam stability. In the expression, landslide dam volume and catchment area are the input parameters. The state of landslide dam stability can then be categorized into stable, unstable, and uncertain. Later on, based on 84 landslide dam cases, Ermini and Casagli (2003) introduced landslide dam height into the BI method and defined a new dimensionless blockage index (DBI). In 2004, based on 232 landslide dam cases in New Zealand, Korup (2004) proposed three dimensionless indexes, i.e., the backstow index (I_s), basin index (I_a), and relief index (I_r), to describe landslide dam stability. Landslide dam height and dammed lake volume are the input parameters for I_s, landslide dam height and catchment area are the input parameters for I_a, and landslide dam height and upstream relief are the input parameters for I_r. Subsequently, based on 300 cases, combining landslide dam volume, catchment area, and local longitudinal slope of the channel bed, Stefanelli et al. (2016) defined the hydromorphological dam stability index (HDSI) to discriminate between formed-stable and formed-unstable landslide dams.

In order to eliminate uncertainty in landslide dam stability assessments and establish judgement criteria, some mathematical statistics methods based on logistic regression algorithms have been proposed. The value 0 is set as the demarcation point, and a landslide dam is formed-stable if the calculated result is greater than 0. A dam is formed-unstable if the calculated result is less than 0. Based on 43 documented landslide dam cases in Japan, Dong et al. (2011) defined three indexes [i.e., L_s(PHWL), L_s(AHWL), and L_s(AHV)] to judge landslide dam stability. For L_s(PHWL), parameters such as peak inflow rate, landslide dam height/width/length were selected; for L_s(AHWL), catchment area, landslide dam height/width/length were selected; for L_s(AHV), catchment area, landslide dam height and volume were selected as input parameters. Based on 79 landslide dam occurrences, Shi et al. (2020) proposed a three-parameter expression and two five-parameter expressions to evaluate landslide dam stability. Herein, landslide dam height and width, and dammed lake volume, were chosen for the three-parameter expression. In addition, for the five-parameter expressions, dimensional and dimensionless parameters were adopted, such as landslide dam height/width/length, dammed lake volume, and backwater length, as well as combinations of two for dimensionless input parameters.

It is well known that material composition has significant impacts landslide dam stability. Thus, according to the material composition of landslide dam debris, Shan et al. (2020) defined two indexes that can be classified as either detailed [L_s(IVAS)] or simplified [L_s(IVAM)] according to 27 and 150 cases, respectively. For L_s(IVAS), the ratio of landslide dam height and width (to reflect the hydraulic gradient), landslide dam volume, catchment area, and particle composition index (to quantitative describe the grain size distribution) are the input parameters. Instead of a particle composition index, L_s(IVAM) utilizes a particle characteristic parameter (to qualitative describe the material composition), and the other input parameters are the same as L_s(IVAS). Table 3 presents an overview of the hazard assessment methods for landslide dams based on mathematical statistics.

TABLE 3

TABLE 3. Hazard assessment methods of landslide dams based on mathematical statistics.

As far as the current research status is concerned, regression analysis is the most used mathematical statistical method, but it depends on the reliability of samples and the rationality and representativeness of fitting factors. With the continuous accumulation of landslide dam data, the accuracy of landslide dam stability assessments using mathematical statistics methods have gradually improved.

3.2.2 Computer-based numerical analysis methods

Numerical analysis methods are usually used to analyze landslide dam stability according to dam configuration, internal structure, and geotechnical properties of landslide deposits, as well as the hydrodynamic conditions of the dammed lake. Because landslide dams are formed naturally, the upstream and downstream slope ratios (vertical/horizontal) are usually gentle, and numerical analysis is generally focused on landslide dam slope stability under different external loads, such as unsteady seepage flow (Shi et al., 2015a), aftershocks (Hu et al., 2011), and rainfall (Tsai et al., 2013). So far, the commonly used numerical analysis methods for landslide dam stability included the limit equilibrium method, finite element method, finite difference method, and discrete element method.

It is worth mentioning that, due to the longevity of most landslide dams, when the damming events occurred, the available time for hazard assessments was very short. In general, numerical analysis is relatively time-consuming; hence, this type of methods is relatively rare and most studies are retrospective analysis after landslide dam breach. Compared with landslide dam stability analysis, numerical analysis is applied more to evaluate mountain slope stability and simulate landslide damming processes.

4 Breach mechanisms and breach processes of landslide dams

The failure processes of landslide dams involve complex coupling effects of soil and water. Because landslide dams are usually located in mountain valleys with poor transportation, due to the rapid breach process and large peak breach flow, it is difficult to collect prototype data and documented failure processes of landslide dams are relatively scarce. Breach records from Tangjiashan (Liu et al., 2010) and Baige (Cai et al., 2020) in China are important reference values for this study. In order to better understand landslide breach mechanisms, numerous physical model tests have been conducted to investigate failure processes and factors influencing breach morphology and hydrographs. Because most of the landslide dam failure model tests have focused on overtopping-induced dam breaching, this section only reviews the breach mechanisms and processes due to overtopping failure.

4.1 Breach mechanisms of landslide dams

4.1.1 Landslide dam breach model tests

The common physical model tests of the landslide dam breach process can be mainly classified into small-scale flume model tests, large-scale field model tests, and centrifugal model tests. Landslide dam failure is a nonlinear erosion process of dam material during unsteady flow. Researchers have divided the failure process into different stages through different types of model tests. 1) Flume model tests. Based on seven flume model tests with landslide dam heights of 0.3 m, Yang et al. (2015) distinguished five stages of breaching: seepage erosion, formation of the initial breach, backward erosion, expansion and incision of the breach, and re-equilibration of the river channel through the breach. Using four flume model tests with dam heights of 0.7 m, Zhou et al. (2019) divided the whole hydrodynamic breaching process into three stages: headcut erosion process, accelerated erosional process, and attenuating erosional process. Based on 12 flume model tests with a maximum landslide dam height of 0.3 m, Zhu et al. (2021) divided the breaching process into four stages: initiation, head cutting, acceleration, and riverbed rebalancing. 2) Field model tests. Reports on large-scale model tests for landslide dam breaching have been relatively rare and are represented by three field model tests with dam heights of 2.5 m conducted by Li D. Y. et al. (2021). Li L. et al. (2021) divided the breach process into three stages: the initiation stage, the development stage, and the failure stage. Furthermore, in terms of the erosion characteristics during dam breaching, Zhang et al. (2021) found that the dominant erosion pattern is surface progressive erosion, and divided the breach process into three stages: headward erosion, rapid erosion, and attenuated erosion. Using two field model tests with dam heights of 1.0 m and different longitudinal dam shapes, Takayama et al. (2021) divided the overtopping-induced landslide dam breach process into two stages: progressive erosion and overtopping erosion. 3) Centrifugal model tests. Utilizing the “space-time amplification effect” of the centrifuge and a centrifugal model test system for dam breaching developed at the Nanjing Hydraulic Research Institute (NHRI), two centrifugal model tests with a dam height of 0.2 m and centrifugal acceleration of 30 g (the corresponding prototype dam height was 6 m) for breaching were conducted (Zhao et al., 2019). Zhao et al. (2019) divided the breach process into five stages: erosion on downstream slope, notch cutting, notch wall scouring, breach side slope collapse, and downstream slope coarsening.

In addition, based on the documentation of the “11·03” Baige landslide dam breach case, Zhong et al. (2020a) divided the breach process into four stages: uniform erosion, backward erosion, streamwise erosion, and breach rebalance.

Although there are different classification methods for the division of landslide dam breach processes, in terms of the sudden changes of breach hydrograph and morphology, the outburst process of landslide dams can be classified into the initial, accelerated, and stable stages. Further, backward erosion occurs in the initial stage, and the accelerated stage occurs after backward erosion enters an upstream dammed lake. The stable stage occurs when the inflow and outflow rates are balanced.

4.1.2 Factors influencing the landslide dam breach process

In order to further investigate breach mechanisms, a series of model tests have been conducted on landslide dam breach processes considering different influencing factors. There are five main categories of influencing factors: landslide dam morphology [i.e., downstream slope angle (Gregoretti et al., 2010; Jiang and Wei, 2020; Zhu et al., 2021), and dam height (Walder et al., 2015; Zhu et al., 2021)], physical and mechanical indexes of dam material [i.e., grain size distribution (Cao et al., 2011a; Zhu et al., 2020), initial soil moisture (Chen S. C. et al., 2015; Jiang and Wei, 2019), soil hydraulic conductivity (Chen S. C. et al., 2015; Jiang et al., 2018), and soil compactness (Chen S. C. et al., 2015)], hydrodynamic conditions of dammed lake [i.e., river channel bed gradient (Jiang and Wei, 2019; Zhu et al., 2021), and inflow rate (Cao et al., 2011a; Chen S. C. et al., 2015; Jiang et al., 2018; Zhou et al., 2019)], initial spillway [i.e., with or without (Cao et al., 2011a), shape (Zhao et al., 2018), and location (Li D. Y. et al., 2021)], and surge waves [i.e., heights of surge waves above dam crest (Peng et al., 2019; Peng et al., 2021)]. By analyzing breach morphologies and hydrographs, useful information about breach mechanisms has been acquired. A brief introduction to model tests for influencing factors on landslide dam breach processes is shown in Table 4.

TABLE 4

TABLE 4. Model tests of factors influencing landslide dam breach processes.

Based on the model tests in Table 4, a preliminary summary of the influencing factors on the breach process can be presented. The downstream slope angle of landslide dam does not have a simple increasing relationship with erosion rate and breach flow discharge, and there is a given threshold value. However, there is no clear understanding of the factors governing the threshold value. The higher the landslide dam height is, the higher the dammed lake volume would be, and hydrodynamic conditions would be enhanced, which results in an increase of peak breach flow. Whether the time to peak flow is advanced or not depends on the expansion rate of the breach morphology. When the landslide dam material is well graded, the dam is more stable. Peak breach flow is relatively low and the time to peak flow is delayed. The timing of the outburst process is relatively long and the breach hydrograph is relatively smooth. Peak breach flow usually increases as initial soil moisture increases, while the failure time and residual dam height decreases; however, the existing studies are not in agreement and lack model testing under high initial soil moisture conditions. Soil hydraulic conductivity plays an important role in the longevities and failure modes of landslide dams, and when the dam breach occurs, the effect of soil hydraulic conductivity on the outburst process is embodied by the initial soil moisture. As soil compactness increases the peak breach flow declines, and the time to peak flow would also lag behind. The river channel bed slope angle plus the downstream slope angle equals the breach flow gradient; hence, given the stability of the landslide dam slope, the sum of the two has an upper limit. In general, as the river channel bed gradient increases the erosion process intensifies and the time to peak breach flow occurs earlier. When the inflow rate increases, the outburst process is accelerated and the erosion rate increases. The excavation of the initial spillway is a problem to be considered when manual interference is involved. If the spillway is not excavated, the breach flow is significantly increased, aggravating the flood disaster downstream. Under the condition of the same excavation amount, the disposal of a compound spillway can effectively increase the discharge rate and make the breach hydrograph relatively gentle. When the initial spillway is located close to the bank, one-sided erosion occurs, the final breach width is smaller, and the volume of the residual dam is larger. In addition, when subjected to surge waves, landslide dam stability is determined by the difference between the effective water level and dam height, and dam material erosion rate is determined by the wave height and mean grain size.

In recent years, influencing factors, such as morphological indexes of landslide dam, physical and mechanical indexes of landslide deposits, hydrodynamic conditions of dammed lakes, manual intervention measures, and external loads, have been considered in the study of landslide dam breach mechanisms. However, due to the complexity in the grain-size distribution and internal structure, further validation is needed to determine whether the conclusions truly reflect the actual situation. There are two aspects that need more study: First, landslide deposits are generally composed of broadly graded soils and the upper limit of grain size in the scaled model tests is often less than 20 cm; thus, the similarity relation of erosion characteristics of landslide deposits needs further study. Second, triggered by different disaster factors, as well as the variations of slope materials and motion patterns, the internal structures of landslide dams are multifarious; however, the structural characteristics of landslide dam are not considered in traditional model tests.

4.2 Numerical simulation methods for the landslide dam breach process

Numerical simulation methods are widely used to analyze dam breach processes. Based on a report by the ASCE/EWRI (American Society of Civil Engineers/Environmental and Water Resources Institute) Task Committee on Dam/Levee Breaching (ASCE/EWRI Task Committee on Dam/Levee Breach, 2011), dam breach models can be classified as parametric, simplified physically based, or detailed physically based. Based on measured data from historical dam breach cases, regression analysis or machine learning are often utilized to develop empirical formulas to predict breaching parameters (i.e., peak breach flow, final breach size, and failure time) in the parametric models. Assumptions such as a regular shape (inverted triangle or rectangle or inverted trapezoidal) are adopted to confine the breach morphology, and various sediment transport equations and water flow formulas are respectively used to simulate the erosion process and breach flow discharge in simplified physically based models. In addition, some simplified physically based models consider the instability of breach side slopes during the failure processes. Unlike parametric models, the simplified physically based models can output breach flow discharge and breach size for each time step in the simulation period. Furthermore, some detailed physically based dam breach models have been developed to describe the morphology evolution process without the predefinition of breach shape, based on the shallow water hypothesis and sediment transport theory.

Recently, a numerical simulation method that coupled a discrete element method (DEM) and computational fluid dynamics (CFD) was used to simulate the breach process of landslide dams (Li L. et al., 2021). The advantage of the coupled DEM-CFD method is that it models landslide dam deposits through discontinuous particles, and reproduces the breach hydrograph with free water surface evolution, which is conducive to understanding the landslide dam breach mechanism of water and soil coupling. Although the DEM-CFD method can reflect the breach mechanisms more clearly, it distinctly restricted by spatial and temporal scales, and the grain size distribution of landslide dam materials and dam morphology indexes are set in a relatively narrow range. Due to the excessive computational costs, the applications of these models to real field scale cases still have a long way to go.

Nowadays, most of the dam breach models are reserved for embankment dams, while only a few numerical models are used to simulate landslide dam breaching; hence, the models for embankment dam breach are often used as substitutes. Because of obvious differences between the two types of dams, large errors may be produced due to the misapplication of the numerical models. In recent years, frequent events such as earthquakes and extreme rainstorms have directed attention to landslides that block rivers and research on numerical simulation technology for landslide dam breaching is gradually increasing. In this review, parametric, simplified and detailed physically based models are the main concerns.

4.2.1 Parametric models

Due to the simplicity and convenience of parametric models, they are often used in the rapid evaluation of disasters caused by landslide dam breaching. Compared to embankment dams, there are fewer parametric models available to predict the breaching parameters of landslide dams because of the complexity of structures and materials, as well as the uncertainty of parameters. Based on 10 landslide dam breach cases, Costa (1985) proposed three regression equations to predict the peak breach flow of landslide dams. Input parameters were landslide dam height or dammed lake volume, or the combination of both variables. Subsequently, another mathematical expression for the relationship between potential dammed lake energy and peak breach flow was established (Costa and Schuster, 1988). Based on 29 landslide dam breach cases, Evans (1986) developed an empirical relationship between peak breach flow and volume of water released during embankment dam failure that was thought to be applicable to landslide dam breaching. Later, based on 18 landslide dam breach occurrences, Walder and O’Connor (1997) provided the statistical relationships between peak breach flow and released water volume, or drop in dammed lake level, or the combination of both variables. The early parametric models only considered the morphological characteristics of landslide dams and dammed lake hydrodynamic conditions, and the mathematical expressions were single or double parametric. Further, the models only presented the expressions of peak breach flow.

Based on 45 documented landslide dam breach cases around the world, Peng and Zhang (2012a) developed a rapid prediction model of breaching parameters that considers the morphology of landslide dams, the hydrodynamic conditions of dammed lakes, and the erosion characteristics of dam materials (i.e., high, medium, and low erodibility coefficients). The model can be used to predict the peak breach flow during the outburst process, the final breach size (i.e., breach top width, bottom width, and depth), and the elapsed time of the landslide dam breach process. Later, a new regression model for estimating breaching parameters was established based on 41 cases with detailed information by Shi et al. (2014).

Landslide dams often retain a residual dam height after breaching. Based on 31 cases, Liu et al. (2013) proposed an empirical model to calculate the breaching parameters of landslide dams under natural conditions, including the final breach average width and residual dam height. The major factors included landslide dam morphology, hydrodynamic conditions of dammed lake, and physical and mechanical indexes of dam materials.

Table 5 describes the existing parametric models for landslide dam breaching parameters. With their small number of geomorphology parameters, some of which represent soil erosion features, parameter models can offer rapid access to the breaching parameters of landslide dams. However, the models cannot consider breach hydrographs and the evolution process of breach size, so they are generally used for rapid assessments of dam breaching disasters. For areas without hydrological data, parametric models are of great significance for emergency response.

TABLE 5

TABLE 5. Existing parametric models for landslide dam breaching parameters.

4.2.2 Simplified physically based models

Simplified physically based models are the most popular models for dam breach modeling around the world, and are widely used for the numerical simulation of dams composed by soils and rocks (Zhong et al., 2016). In the early days, simplified physically based models describing embankment dam failures were often adopted to simulate landslide dam breach processes, such as the NWS (National Weather Services) BREACH model (Fread, 1988), which is one of the earliest and most used models. However, due to the large discrepancies between embankment and landslide dams, especially the characteristics of grain size distribution and dam structure, landslide dams do not always release all of the stored water. The application of models for embankment dams can introduce large errors by overestimating the breach flow discharge.

In the 21st Century, more attention has been paid to the numerical simulation of landslide dam breach process and simplified physically based models have been developed. For the landslide dam breaching process models, the cross section of the breach channel is often predefined to be an inverted trapezoid and outflow through the breach is simulated using the hydraulics of a broad-crested weir for most of the models. Hence, key points in the landslide dam breaching process modeling are how to reasonably reflect the structure features of landslide dams, the erosion rate of wide graded dam materials, and the evolution process of breach morphology in cross and longitudinal sections.

Field investigation have demonstrated stratification based on soil grain size distribution in the depth direction, and the grain size distribution in each layer varies for landslide dams with different accumulation forms (Fan et al., 2020). Using field test data or empirical formulas, some models can consider the landslide dam structure based on variations in soil erodibility (Chang and Zhang, 2010) or the grain size distribution of dam materials (Zhong et al., 2020b).

Stress-based erosion rate equations have been widely adopted to simulate breach bed erosion. The bed erosion rate can be expressed as the soil erodibility coefficient multiplied by the difference between the flow shear stress and the critical shear stress of the soil. For the flow shear stress, the Manning equation or shear stress equation for uniform flow is often adopted; for critical shear stress of soil and soil erodibility coefficient, empirical equations derived from erosion tests of wide graded dam materials have also been applied (Chang et al., 2011). Once the critical shear stress of soil is larger than the water shear stress, the bed erosion ceases. In addition, based on monitoring data from the Tangjiashan landslide dam breach process, Chen Z. Y. et al. (2015) proposed a hyperbolic model to describe the bed erosion rate. In this work, the maximum possible erosion rate was predefined according to regression on field measurements.

For breach development in the cross section, the lateral erosion rate is often assumed to be equal to the bed erosion rate or multiplied by a coefficient. The lateral enlargement due to the instability of breach side slopes is the main mechanism behind breach widening, and limited equilibrium methods with planar or circular slip surfaces are often utilized. For breach development in the longitudinal section, the main difference between the models is the assumption of downstream slope angle variability. Three assumption are often accepted, such as that the downstream slope angle remains constant, or decreases, or increases to a certain value and then remains constant.

In this section, three typical simplified physically based modes for landslide dam breaching, such as DABA (DAm Breach Analysis) (Chang and Zhang, 2010; Peng et al., 2014; Shi et al., 2015b; Zhang et al., 2019; Chen C. et al., 2020), DB-IWHR (Dam Breach—China Institute of Water Resources and Hydropower Research) (Chen Z. Y. et al., 2015; Wang G. H. et al., 2016; Chen et al., 2018; Chen Z. Y. et al., 2020), and DB-NHRI (Dam Breach—Nanjing Hydraulic Research Institute) (Zhong et al., 2018; Zhong et al., 2020a; Zhong et al., 2020b; Shen et al., 2020b; Mei et al., 2021), are introduced in Table 6. Although the simplified physically based landslide dam breach models have shortcomings, they are computationally efficient and have considered the necessary breach mechanisms.

TABLE 6

TABLE 6. Typical simplified physically based models for the landslide dam breaching process.

Although the simplified physically based models can describe the breach process of landslide dams, they introduce many artificial assumptions in expressions of breach morphology, physical and mechanical properties of dam deposits, breach flow discharge, and breach side slope stability. In addition, because breach flow discharge and breach size evolution are calculated separately, these types of models cannot consider the characteristics of high-velocity flow and broadly graded soils, or the coupling effect of soil and water in the dam breach process, so landslide dam breach mechanisms cannot be fully reflected.

4.2.3 Detailed physically based models

In recent years, with the development of computational fluid dynamics and sediment science, as well as hydrodynamics and sediment transport theory, a series of one-, two-, and three-dimensional numerical models for dam breach processes have been developed under the assumptions of shallow water and hydrostatic pressure distribution. These models are categorized as detailed physically based. They typically contain three modules, such as a hydrodynamic module (i.e., continuity and momentum conservation equations for clean or muddy water), a sediment transport module (i.e., equilibrium or nonequlibrium sediment transport equations), and a morphological evolution module (i.e., bed erosion equation, breach slope collapse equation). According to the types of sediment transport models selected in the dam breach models (Guan et al., 2015), the detailed physically based dam breach models can be divided into four categories: capacity models (i.e., Faeh, 2007; Swartenbroekx et al., 2010; Juez et al., 2014; Abderrezzak et al., 2016; Dazzi et al., 2019; Takayama et al., 2021), noncapacity models (i.e., Wu and Wang, 2007; Cao et al., 2011b; Wu et al., 2012; Guan et al., 2014; Marsooli and Wu, 2015), two-phase flow models (i.e., Rosatti and Begnudelli, 2013; Razavitoosi et al., 2014; Cristo et al., 2016), and two-layer transport models (i.e., Swartenbroekx et al., 2013; Li et al., 2013; Cantero-Chinchilla et al., 2016).

The capacity models are mainly composed of the shallow water equation and the Exner equation. The shallow water equation describes the flow movement of clear water and the Exner equation describes the breach morphology evolution process. In these models, the erosion process is dominated by bedload sediment transport where the velocity of dam material is less than that of the water flow. In addition, various empirical formulas for bedload erosion rate are often adopted.

In the noncapacity model, the flow is assumed to be muddy water and the shallow water equation containing the density of muddy water is used to describe the flow process. It is assumed that the erosion process consists of bedload transport and suspended load transport, and the interaction process between bedload and suspended load is determined by empirical formulas. The actual erosion rate is converted into the volume concentration of muddy water, and the erosion process is calculated by the volume concentration and the flow rate of muddy water.

Two-phase flow models assume that solid particles move in the liquid flow, the volume concentration of the solid particles is relatively low, and the solid particles move under the driving force of the liquid flow, but the interaction between the solid and liquid phases is weak. The solid and liquid phases are modeled based on the continuum hypothesis, and the continuity and momentum conservation equations describe the movement of the two phases, in which the solid phase has characteristics similar to particle flow.

In two-layer transport models, the water flow above the breach bottom bed is assumed to be made up of a upper clear water layer and the under bedload flow layer. Each layer has its own depth and concentration. There is clear water exchange between the clear water layer and the bedload flow layer, while there is soil exchange between the bedload flow layer and the breach bottom bed. The exchange capacity is often determined by empirical formulas. Continuity and momentum conservation equations are developed for the clear water and sand-water layers, respectively.

Mean grain size is commonly adopted to represent the dam material diameter in detailed physically based dam breach models. This is a suitable method for simulating the failure process of non-cohesive dams with relatively uniform particles. Some of the existing detailed physically based dam breach models in each of the four types are listed in Table 7.

TABLE 7

TABLE 7. Existing typical detailed physically based dam breach models.

The four types of detailed physically based models can simulate the breach hydrograph and rapid change in dam morphology during dam breaching under their own assumptions and theoretical frameworks. However, there are still some difficulties in their practical application. One of the key problems is how to select an appropriate erosion model. Most erosion formulas are obtained under the conditions of steady uniform flow, low sediment transport intensity, and slow riverbed deformation, while the theoretical results of breach slope instability are also obtained under many assumptions. These theoretical shortcomings greatly limit the simulation ability of detailed physically based models. Hence, there are few models that can reasonably reflect the erosion characteristics of broadly graded soils under high-velocity breach flow, which depends on the development of sediment theory.

In addition, although detailed physically based models can effectively improve accuracy in numerical simulation, they still have low computational efficiency when dealing with large-scale dam failure simulations. With the enhancement of computer processing capacity, GPU acceleration technology has been introduced into some models (Lacasta et al., 2014; Lacasta et al., 2015; Juez et al., 2016; Dazzi et al., 2019) to improve the calculation efficiency of dam breach flow. In general, future numerical simulation of landslide dam breach processes is moving in the direction of detailed physically based models.

5 Flood routing after landslide dam breaching

Once a landslide dam breaks, it forms a catastrophic outburst flood, then the dam-break flow spreads to the downstream area. Flooding can submerge riverine buildings and traffic facilities, causing direct harm to lives and properties. In addition, flood flow due to the failure of a landslide dam usually has fine to coarse sediment particles, and the characteristics of flood routing are different from those of clear water flow. Erosion or siltation on the riverbed results from the dam-break flood, altering the original river topography. In general, for dam-break flood routing, the inundated area, flow depth and velocity, riverbed elevation variability, and time to peak flood in a certain location are the main concerns.

5.1 Model tests for flood routing after dam breaching

5.1.1 Model tests for dam-break flow propagation

Flood routing after dam breaching is a strong and complex dynamic water-soil-riverbed coupled process with rapid changes in physical quantity; thus, the propagation process of a dam breach flood has its own special features.

Flume tests have been the principle physical model tests to study the characteristics of flood routing. In the model tests, a flood is often generated by the instantaneous dam breach or a prescribed flow curve, and the downstream river channel is generally set as fixed or movable bed. 1) Fixed bed model tests. In terms of the material composition of dam-break flow, fixed bed model tests can be classified as clean and muddy water flows. Regardless of whether the dam-break flow is clean or muddy water, the study main focuses on the propagation characteristics of dam-break waves in man-made river channels with different cross sections, such as a smooth rectangular and horizontal channel (Lauber and Hager, 1998), an initially dry channel with a 90° bend (Soares-Frazão and Zech, 2002), a frictional triangular channel (Wang et al., 2021), or a meandering channel (Itoh et al., 2018). Consequently, the mechanical properties of dam-break waves and water-soil mixture deposition are discussed. 2) Movable bed model tests. Dam-break flows in most of the movable bed model tests are clean water, so the study purpose is to describe the propagation characteristics of dam-break flows on the movable beds, as well as riverbed topography variations (i.e., Capart and Young, 1998; Spinewine and Zech, 2007; Goutiere et al., 2011; Carrivick et al., 2011; IAHR Working Group for Dam-break Flows over Mobile Beds, 2012; Qian et al., 2018). In general, compared with fixed bed model tests, dam-break flood waves on the movable bed propagate slower and attenuate faster.

The landslide dam breach process is not an instantaneous incident, but rather it is a nonlinear gradual process; in addition, natural river channel morphology is quite different from an experimental river channel. However, physical experimental studies of flood routing caused by the gradual collapse of a landslide dam in a natural river channel are still rare. Therefore, in the discussion on the influencing factors of flood routing in the next subsection, in-situ test results are the main basis for evaluation.

Dam-break flow propagation after landslide dam breaching is more complicated than that of clear water due to the high sediment content, which is almost sand-carrying flow or even debris flow. Experiments and in-situ tests have shown that the evolution of a sand-carrying flood caused by dam breaching in the lower reaches of a river involves erosion or deposition, as well as sediment sorting along the river channels.

5.1.2 Factors influencing flood routing

Flood routing after landslide dam breaching is mainly affected by flood rheology, breach flow hydrographs, dry and wet conditions downstream, river branches, river channel roughness, and downstream river topography (Liu et al., 2019). Because of the high sediment concentration in the flood water, the propagation of muddy water is more complicated than that of clear water. In addition, the dammed lake is generally formed in alpine valley areas with complex river terrain conditions; hence, flood routing in a mountainous area is obviously different from a plains area.

Because both sides of river banks are generally controlled by mountains, a dam-break flow propagates without planarization and water loss is relatively limited. Therefore, the flood discharge propagating along the downstream river channel decreases slowly, and its rate of decrease is significantly influenced by the breach hydrograph during the breach. In general, when peak breach flow is high and long in duration, the flood peak attenuates gradually downstream because the downstream river channel has been filled before the peak arrives (O’Connor and Beebee, 2009; Liu et al., 2019). Historical statistics have shown that the peak discharge of an outburst flood observed 60 km downstream of the Tangjiashan landslide dam in China showed no significant decline compared with the peak breach flow at the dam site (Liu et al., 2019). Similarly, at over 200 km and 100 km downstream of the Tanggudong and Dixi landslide dam sites, respectively, over 50% of the initial peak breach flow was maintained after long distance propagation (Chen et al., 1992; Wang et al., 2012).

In addition, after the landslide dam breaching, the outburst flood carries a large amount of sediment, which is deposited in the river channel and on both sides of the beach as flood velocity decreases during flood routing. Taking the 2018 failure event of the “11.03” Baige landslide dam on the Jinsha River, China as an example, on both sides of the river in the Shangri-La Development Zone, which is located about 600 km downstream of the dam site, the mud thickness on the beach was over 0.5 m after flood routing.

The huge amount of sediment carried in a dam-break flow that propagates downstream has serious impacts on downstream water environments in the river. Moderate amounts of sediment can increase nutrients in the water, while high sediment flows can be disastrous for most aquatic life. The formed-stable dammed lake may have positive effects on a mountain river ecosystem, but may be destroyed in 1 day in case the dammed lake fails.

5.2 Numerical simulation for flood routing after dam breaching

The model tests and in-situ tests demonstrated that dam-break flows contain shock and sparse waves, compared to conventional river floods. They also have the following characteristics (Aureli et al., 2000): 1) The peak breach flow of dam-break flood is relatively high; meanwhile, the water level is high, the water surface gradient is large, and the dam-break flow is often discontinuous during the propagation. 2) The topography of the area downstream of a landslide dam is commonly very irregular and it is easy to cause a flow regime transition. Supercritical, critical, and subcritical flows often occur simultaneously. Surge waves and hydraulic jumps often occur during dam-break flow propagation. 3) During flood routing, the dam-break flow often overflows the river channel and moves onto the dry bed, so there are complex dynamic boundary conditions.

The governing equations for dam-break flow routing simulation generally adopt Shallow Water Equations (for two-dimensional simulation) or Saint-Venant Equations (for one-dimensional simulation). The particularity of dam-break flow is mainly reflected in corresponding physical flow field discontinuities. Therefore, accurate simulation must capture this strong discontinuity or large gradient flow. There are two main approaches, such as the Shock Fitting Method and Shock Capture Method (Toro, 2000). With the rapid development of computer technology, the Shock Capture Method has been more widely used. However, the Shock Capture Method for non-conserved Shallow Water Equations may lead to calculation errors (Toro, 2000). Therefore, in order to correctly use the Shock Capture Method to solve the discontinuous problem, conservative variables, equation forms, and numerical solution methods should be used.

There are two main kinds of adaptive numerical solutions to capture discontinuities: 1) Discontinuities can be treated as special cases with large gradients, which can be smoothed by artificially introducing a diffusion term with a viscosity effect when solving differential equations. This is called the artificial viscosity method. Or, when discretizing differential equations, a format with similar viscosity can be selected (i.e., Lax-Wendroff format, or Lax-Friedrichs format) (Anderson, 1995) to produce a smooth transition, called the format viscosity method. However, the first order precision scheme of this method will stretch the discontinuous transition zone too wide. 2) The Godunov Scheme (Godunov, 1959) was based on the idea of solving Riemann’s approximate solution and is not only suitable for smooth classical solutions, but can also adapt to cases with large gradients or/and large deformation solutions, and can accurately and automatically capture the discontinuities. It has become one of the main methods for computing large gradient water surfaces.

As discussed above, dam-break flows have shock and sparse waves, which are usually expressed as the Saint-Venant or Shallow Water Equations, and the breach flow can be clear or muddy water. According to the discrete principle, numerical simulation methods can generally be classified as Method of Characteristics (MOC), the Finite Difference Method (FDM), the Finite Element Method (FEM), and the Finite Volume Method (FVM). The MOC, FDM, and FEM have achieved great success in many subcritical flow problems, but they are not completely suitable for solving the strong discontinuous flow of dam-break floods. The Finite Volume Method does not directly discretize the governing equations numerically, but starts from the integral form of conservative equations, forming the Riemann problem for discontinuous solutions on the boundary of a control body. For any region composed of one or more control bodies, even the whole computational region, physical conservation is strictly satisfied, there is no conservative error, and the discontinuity can be calculated correctly. After input/output flows and momentum fluxes are calculated along the normal direction of the computing element boundary, balance calculations of water volume and momentum are conducted for each element, and then the average water depth and velocity of each element at the end of the time step are obtained.

The Godunov scheme used in the Riemann solution is currently the main scheme for solving large gradient flows. The Roe scheme (Roe, 1981), Osher scheme (Osher and Solomon, 1982), HLL scheme (Harten et al., 1983), and HLLC scheme (Toro et al., 1994) are other widely used schemes. In addition, the high resolution methods of shock capture by the Finite Difference Method and others can be directly used in the Finite Volume Method. It is worth mentioning that there are some common software programs that can simulate dam-break flood propogation, such as FLDWAV (Fread and Lewis, 1988), DHI MIKE FLOOD (Danish Hydraulic Institute, 2021), HEC-RAS (US Army Corps of Engineers, 2021), and so on.

In recent years, numerous calculation methods have been developed to simulate flood routing after dam breaching, and the characteristics of downstream outburst flood (peak discharge, submergence area, average water depth, and average flow velocity) have been considered and discussed in-depth. However, more research is needed on the sensitivity of outburst floods to the dam breach process and the interaction mechanism involving sand-carrying flow and the downstream river channel.

Although many numerical models for flood routing can simulate sediment transport, the simulation of actual dam-break flow is mainly concerned with the propagation of flood flow, while the role of sediment carried by dam-break flow is ignored. The effects of rapidly releasing a huge amount of sediment on variable river topography and river ecology need to be further studied.

6 Loss assessments after dammed lake breaching

In order to effectively reduce life and property safety risks associated with dam-break floods, loss assessments are needed for the following purposes (Bowles et al., 2003): 1) To evaluate existing and residual risks against tolerable risk guidelines. 2) To evaluate the benefits associated with risk-reduction measures, such as more effective emergency plans and evacuation measures. 3) To estimate cost effectiveness and feasibility to aid in prioritizing and justifying expenditures on risk-reduction measures.

Therefore, a better understanding of flood-induced loss dynamics is of great importance for improving the scientific quality and availability of emergency response plans. Since the 1980s, scholars have studied loss assessments due to dam failures. In general, dam-break loss studies are still in the exploratory stage, and have mainly focused on the loss assessment of artificial dam reservoirs rather than dammed lakes. However, dam reservoirs and dammed lakes have common outburst flood propagation characteristics, so loss assessment methods for dam reservoirs can be used for reference in dammed lakes. According to the classification, loss assessments for dammed lake breaching can be classified as loss of life, loss of economy, and loss of ecology. However, compared to assessment methods for loss of life, there are fewer assessment methods for loss of economy and ecology. There are two main reasons for this (Ge et al., 2020): 1) The ability of potential inundation areas to endure losses of economy and ecology caused by dam failure changes over time due to constant economic and social development. 2) Economic and social development levels are distinct across different areas, resulting in significant differences in economic and ecology losses after a dam breach. It is difficult to establish a uniform assessment method for scientifically predicting these losses. Hence, in this review, the assessment methods for loss of life are the focus of attention.

Loss of life refers to the number of people potentially killed by flood disasters in the inundated area by a dam-break flood. It is coupled by qualitative and quantitative factors, and the disaster causing factor system is uncertain, which increases the difficulty of quantitative assessment. The state-of-the-art life loss assessment methods mostly use the main influencing factors as input parameters to develop models. The influencing factors can be classified into four categories, such as hazard factors, exposure factors, population-related factors, and rescue capability factors (Mahmoud et al., 2020), as shown in Figure 5.

FIGURE 5

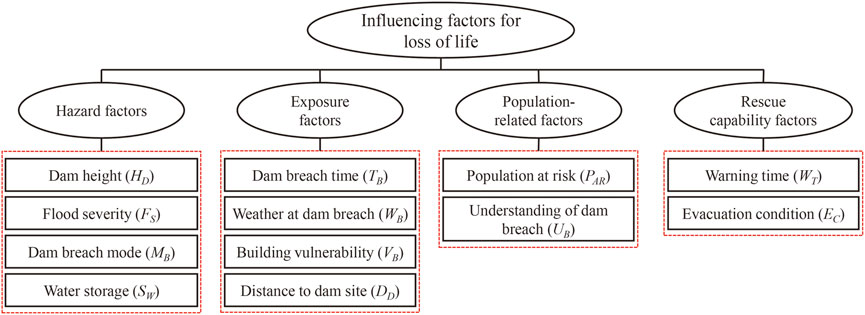
FIGURE 5. Factors influencing loss of life due to a dam breach [modified from Mahmoudet al. (2020)].

A previous study divided the assessment methods for loss of life into three types: empirical models, physical models, and compromised models (Peng and Zhang, 2012b). These three categories are generally deterministic models quantified with a few independent parameters and may not sufficiently clarify the relationship between the input parameters and the calculated results. Therefore, a series of uncertainty models based on intelligent algorithms, fuzzy mathematics, and probability theory have been developed. The assessment methods for loss of life in this review are classified into four types, such as empirical, physical, compromised, and uncertainty models.

Empirical models describe the relationship between loss of life and influencing factors by integrating statistics of historical data and mathematical methods. Brown and Graham (1988) developed three empirical formulas to predict loss of life considering the population at risk and different available warning times based on statistics from historical dam failures of many countries around the world. Subsequently, more influencing factors have been considered to assess the loss of life (Table 8).

TABLE 8

TABLE 8. Existing typical models for loss of life due to flood flow.

Physical models simulate human behavior in dam-break flood, and explore the stability of human beings in flood flow by taking individuals as the research object. Abt et al. (1989) first conducted a study to identify when an adult human could not stand or maneuver in a simulated flood flow. Then, a series of models were developed to measure human instability in flood flows with different combinations of water depth and flow velocity (Table 8).

Compromised models combine the characteristics of both empirical and physical models. A potential inundated area is often separated into several subareas based on physical concepts; simultaneously, flood-caused fatality mechanisms are considered. The relationship between loss of life and influencing factors in each subarea is calibrated with historical data or expert judgment in each subarea, then the assessment model for loss of life is developed (Table 8).

The above three types of models (empirical, physical, and compromised) can be generally defined as deterministic models, and loss of life can be quantified with a few independent input parameters. However, deterministic models may not sufficiently reveal the inter-relationships between the input parameters or include the uncertainties of these parameters, meanwhile, some important parameters cannot be quantified. Hence, uncertainty models came into existence. In these models, uncertainties in the predicted models are identified by performing uncertainty analyses regarding both the influence factors and their inter-relationships (Table 8).

Empirical models for loss of life are generally at a macroscale, developed and calibrated based on documented dam failure information and statistical data from disaster losses, which are easy to follow. However, due to the adoption of statistical approaches, this type of model cannot reflect the causes of flood-induced casualties the inter-relationships between the key influencing factors. In addition, empirical models are often established in terms of documented data from historical flood events, most of which are of low credibility or availability, resulting in relatively low accuracy in most of the applications.

Physical models for loss of life mainly focus on the instability of individual in the flood flow and most are complicated and cannot consider the subjective factors of individuals in danger. Hence, the theoretical analyses for every individual are very complicated and rarely applied in actual cases, while the correlation between human behavior in floods and loss of life needs further study and verification.

Compromised models for loss of life can describe the relationship between loss rate and dam-break flood characteristics by considering the causes of loss of life. This type of model combines the advantages of statistical approaches and theoretical analysis, which can quantitatively predict the loss of life under relevant risk criteria. However, the inter-relationships between the influence parameters are not included in these models.

Given the importance of subjective consciousness in empirical, physical, and compromise models, none of the deterministic models for loss of life can provide an accurate number of fatalities caused by a given dam breach case. Therefore, loss of life predicted by the deterministic models is subjective to uncertainty. Uncertainties in predicted loss of life due to dam-break floods can be identified by performing uncertainty analyses regarding the flood routing analysis results and loss of life estimations. Hence, uncertainty models are the future direction for loss of life assessments.

7 Risk mitigation measures for dammed lakes

Dammed lakes pose tremendous threats to people and properties in the inundation areas caused by landslide dam breaching floods. Due to the lack of flood discharge facilities, most landslide dams are breached naturally by overtopping flow a short time after the formation of dammed lakes. Therefore, quantitative risk assessment is urgently needed as the prerequisite and preliminary requirement to support the decision making in landslide-dam emergency response. Then, risk mitigation measures can be taken according to the dam failure risk assessment results. Risk mitigation measures for dammed lakes can be classified as non-engineering measures and engineering measures (Peng et al., 2014; Shi et al., 2016). Non-engineering measures mitigate risks by means of reducing the people and properties at risk through evacuation or reservoir regulation. In general, there are two kinds of implementation schemes: 1) Warning and evacuating people and movable assets at risk out of the potential inundated areas. 2) Emergency operation of upstream and downstream reservoirs on the river. This could mean reducing discharged water into an upstream reservoir, or emptying water stored in a downstream reservoir. Admittedly, non-engineering measures are low cost and high efficiency in rescuing people and movable assets at flood risk; however, measures of this category cannot reduce the loss of unmovable assets. Engineering measures mitigate risks by moving the people and properties at risk and limiting the dam failure probability, inundation area, flood severity, and vulnerability of population and assets at risk.

Sections 3–6 in this review are the basis for non-engineering measures, hence, engineering measures are the focus in this section.

After the formation of a landslide dam that threatens people and important infrastructure in the potential flooded area, immediate engineering measures must be taken if objective conditions are permitted. The purposes of this category are to prevent the water level in the dammed lake from reaching dangerous heights, or control the erosion rate if a landslide dam breach occurs (Peng et al., 2014). The most common engineering measures include: water level control by pumps or siphons, diversion tunnels through bedrock abutments, and drainage spillways through landslide dams.

For a dammed lake with small storage capacity and upstream inflow, pumps or siphons can be utilized to control the rising speed of water level in the dammed lake. For instance, on 5 June 2009, a landslide occurred in Wulong County, Chongqing City, China, and then blocked the river, resulted in a dammed lake. Pumps were installed to release the inflow water and keep the water level in the dammed lake below the dam crest (Figure 6).

FIGURE 6

FIGURE 6. Draining the Wulong dammed lake using pumps (Photo credit Xinhuanet.com).

Construction of diversion tunnels is a money- and time-consuming measure. This measure can be taken when the following requirements are met. 1) Geological conditions. The mountain slope upstream of the dam site should be made of bedrock for diversion tunnel construction. 2) Road and transport conditions. A temporary road to the dam site for transporting equipment and supplies is indispensable. For example, on 3 August 2014, the Mw 6.5 earthquake in Ludian County, Yunnan Province, China, resulted in the Hongshiyan landslide dam, which had a height of 83 m and a lake volume 260 million m³, threatening more than 10,000 people (Shi et al., 2016). The landslide dam was located between an artificial dam and a hydropower plant; fortunately, there was an existing drainage tunnel that connected the dammed lake and the hydropower plant. Hence, the drainage tunnel was used as a natural diversion and played an important role in risk mitigation (Zhou et al., 2015; Shi et al., 2016).

Building a spillway across a dam is the most common measure for dammed lake risk mitigation. The function of a spillway is to control the breach process of landslide debris, preventing erosion from occurring too fast or slow. For a landslide dam with relatively small volume made of large blocks on the top, blasting can be used to break up the dam materials. The emergency disposal of the Xiaogangjian landslide dam, which was triggered by Wenchuan earthquake, 2008, China, is one example of this approach. The upper part of the Xiaogangjian landslide dam was composed of large blocks, while the lower part was composed of highly fragmented debris (Mei et al., 2021). Due to the traffic jams caused by earthquake, rescuers only accessed the dam site by rubber boats (Chen et al., 2018); thus, they considered various factors, and blasting a spillway was a preferable plan. After blasting, a spillway with 8 m depth and 30 m bottom width was constructed on the left bank of the dam (Figure 7). For landslide dams with large volume made of mixture of soil and stone, building a spillway with excavators is the most common measure. In terms of the workload and traffic conditions, as well as the rising speed of water level in the dammed lake, an emergency plan would be formulated. For example, in the risk mitigation of the Yigong dammed lake in China, a spillway with 30 m depth and 30 m bottom width was excavated before dam breaching (Figure 8), which significantly reduced the storage capacity in the dammed lake (Wang L. et al., 2016).

FIGURE 7

FIGURE 7. Blasting a spillway for the Xiaogangjian dammed lake (Photo credit Xinhuanet.com).

FIGURE 8

FIGURE 8. Constructing a spillway for the Yigong dammed lake using excavators (Photo credit Xinhuanet.com).

One must acknowledge the fact that because dammed lakes are generally trigged by earthquakes or rainfall, which are unforeseen emergencies that commonly result in inaccessible dam sites within the limited available time. Hence, although various measures for dammed lake risk mitigation can be adopted, non-engineering measures such as warning and evacuating people in the potential inundated areas are more prevalent disposal countermeasure than engineering measures.

For the available engineering measures, building a spillway is an effective method for dammed lake risk mitigation. However, for the landslide dams with different material composition, how to design an optimal spillway to minimize dammed lake risks also requires further study. In addition, for a high-risk dammed lake, the combined utilization of engineering and non-engineering measures is usually more applicable in risk mitigation for a dammed lake breach disaster.

8 Discussion

Based on global databases, a comprehensive review on risk assessments of dammed lakes has been conducted considering the hazard chains that they trigger. Five topics have been discussed, such as hazard assessments for landslide dams, breach mechanisms and breach processes, flood routing after landslide dam breaching, loss assessments, and risk mitigation measures. In general, after systematic studies in recent decades, especially in the past 20 years, the basic framework for dammed lake risk assessments has been built, but there are still several scientific issues are encountered and worthy of further study:

1) Acquisition of basic information for dammed lakes. Due to the scarcity of historical documented data, modern technologies for field investigations should be adopted to obtain key information on dammed lakes for risk assessment, such as morphological indexes of landslide dams, hydrodynamic conditions of dammed lakes, and material composition of landslide deposits. Further, more attention is needed when a new dammed lake appears, such as in-situ measurements of breaches—especially breach hydrographs—which are key for validating risk assessment methods.

2) Uncertainty in hazard assessments of landslide dams. For dammed lakes, the occurrence of the breach disaster is a probability event. Therefore, it is necessary to utilize advanced technologies and methodologies to study landslide dams and delineate their internal structure, so that mechanical properties of the landslide deposits can be interpreted to assist assessment of the stability and erodibility of the materials. These measures help to overcome the uncertainty to a certain degree in the hazard assessment of landslide dams. Combining a large amount of basic information of dammed lakes, the near real probability of the landslide dam breach will be achieved through continuous algorithm improvement.

3) Accuracy of dammed lake outburst flood simulation. The simulation of landslide dam breaching involves complex coupling effects of water and soil. Because of the uncertainty of particle distribution in landslide deposits, accurate prediction of landslide dam breaching due to different triggering factors is key to flood routing and disaster consequences. Hence, it is necessary to reveal the damming mechanisms of landslides and obtain the material and structure of the landslide dams by making full use of remote sensing and geophysical prospecting methods. A dam-break flood has sand-carrying fluid, so to improve accuracy, the evolution of riverbed morphology under the action of erosion or deposition by a dam-break flood, as well as sediment sorting along the river channels, should be considered for flood routing simulation.

4) Quantitative methods for loss assessment of dammed lake breaching. Due to the lack of historical loss data, as well as the influence of sustained economic and social development, how to use limited historical data to quantitatively process input parameters in loss assessment models is a major problem that needs to be solved. With the development of big data technology and the rise of multidisciplinary research, integrating survey data and deterministic/uncertainty methods under the proper algorithms may make up for the lack of historical data to a certain extent.

5) Quantitative risk assessments and risk mitigation for dammed lakes. The risk of a dammed lake is a dynamic process, but risk assessments are mostly conducted through static analysis, ignoring the uncertain evolution process of the hazard chain itself. A complete quantitative assessment system has not been established for the risk assessments of dammed lakes, and assessments of hazard chain evolution are independent of each other, while the quantitative degree is relatively low. Subsequent studies can consider the dynamic characteristics of human behavior and social organization evacuation, and combine satellite remote sensing and aerial photography techniques with unmanned aerial vehicles to dynamically assess the risk of dammed lakes. From the point of view of artificial intelligence, a reasonable overall risk assessment platform for dammed lakes should be explored through an intelligent network with forecasting and early warning. In addition, various uncertainties should be considered in engineering measures for risk mitigation, as well as the development of technologies to control the pace of landslide dam erosion progression.

9 Conclusion

The risk assessment of dammed lakes is a very complicated process that involves the geologic hazard chain triggered by dammed lake breaching and risk mitigation. Based on the overview of each aspect of dammed lake risk assessment, the following conclusion can be drawn:

Although a high degree of study of dammed lakes has produced a multitude of documented cases, the historical documented information is often insufficient in the risk assessment of dammed lakes. Great progresses on breach mechanisms and breach processes of landslide dams have been achieved by laboratory and field model tests, as well as by studying actual failure cases. However, the similarity relation of erosion characteristics of landslide deposits and the structural characteristics of landslide dam needs further study. A number of influencing factors (i.e., landslide dam morphology, physical and mechanical indexes of dam material, hydrodynamic conditions of dammed lake, downstream river topography, roughness of underlying surface, and so on) significantly affect the breach flow hydrographs and flood routing. Although a series of empirically and physically based models have been developed for dam-break flood and loss assessment, great uncertainties are still associated with predictions of the key parameters. Thus, it is very important to conduct mechanism investigations to improve the accuracy in the numerical modeling. In addition, for a high-risk dammed lake, the combined utilization of engineering (building a spillway) and non-engineering measures (evacuating people at risk) is usually an effective way in disaster mitigation.

Author contributions

QmZ: Conceptualization, methodology, writing-reviewing and editing. LW: Formal analysis, writing-reviewing and editing. YS: Conceptualization, methodology. SM: Conceptualization, methodology. QaZ: Formal analysis, Data curation. MY: Data curation, validation. LZ: Validation, investigation. ZD: Data curation.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant Nos U2040221, U22A20602, and 51909214), and the National Key Research and Development Program of China (Grant No. 2018YFC1508604).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abderrezzak, K.E.K., Moran, A.D., Tassia, P., Ata, R., and Hervouet, J.M. (2016). Modelling river bank erosion using a 2D depth-averaged numerical model of flow and non-cohesive, non-uniform sediment transport. Advances in Water Resources 93, 75–88.

Google Scholar

Aboelata, M.A., and Bowles, D.S. (2005). LIFESim: a model for estimating dam failure life loss. Logan, USA: Report to Institute for Water Resources, US Army Corps of Engineers and Australian National Committee on Large Dams, Institute for Dam Safety Risk Management, Utah State University.

Google Scholar

Abt, S.R., Wittler, R.J., Taylor, A., and Love, D.J. (1989). Human stability in a high flood hazard zone. Water Resources Bulletin 25 (4), 881–890. doi:10.1111/j.1752-1688.1989.tb05404.x

CrossRef Full Text | Google Scholar

Anderson, J.D. (1995). Computational fluid dynamics: The basics with applications. New York, USA: McGraw-Hill, Inc.

Google Scholar

ASCE/EWRI Task Committee on Dam/Levee Breach (2011). Earthen Embankment Breaching. Journal of Hydraulic Engineering 137 (12), 1549–1564. doi:10.1061/(asce)hy.1943-7900.0000498

CrossRef Full Text | Google Scholar

Aureli, F., Mignosa, P., and Tomorotti, M. (2000). Numerical simulation and experimental verification of dam-break flows with shocks. Journal of Hydraulic Research 38 (3), 197–206. doi:10.1080/00221680009498337

CrossRef Full Text | Google Scholar

Bianchi-Fasani, G., Esposito, C., Petitta, M., Scarascia-Mugnozza, G., Barbieri, M., Cardarelli, E., Cercato, M., and Di Filippo, G. (2011). The importance of geological models in understanding and predicting the life span of rockslide dams: the case of Scanno Lake, Central Italy. Natural and Artificial Rockslide Dams. Springer, 323–345.

CrossRef Full Text | Google Scholar

Bowles, D.S., Anderson, L.R., Glover, T.F., and Chauhan, S.S. (2003). “Dam safety decision-making: Combining engineering assessments with risk information,” in Proceedings of the 2003 US Society on Dams Annual Lecture. USA: Charleston.

Google Scholar

Brazdova, M., and Riha, J. (2014). A simple model for the estimation of the number of fatalities due to floods in Central Europe. Natural Hazards and Earth System Sciences 14 (7), 1663–1676. doi:10.5194/nhess-14-1663-2014

CrossRef Full Text | Google Scholar

Brideau, M.A., Shugar, D.H., Bevington, A.R., Willis, M.J., and Wong, C. (2019). Evolution of the 2014 Vulcan Creek landslide-dammed lake, Yukon, Canada, using field and remote survey techniques. Landslides 19 (6), 1823–1840. doi:10.1007/s10346-019-01199-3

CrossRef Full Text | Google Scholar

Brown, C.A., and Graham, W.J. (1988). Assessing the threat to life from dam failure. Journal of the American Water Resources Association 24 (6), 1303–1309. doi:10.1111/j.1752-1688.1988.tb03051.x

CrossRef Full Text | Google Scholar

Cai, Y.J., Cheng, H.Y., Wu, S.F., Yang, Q.G., Wang, L., Luan, Y.S., and Chen, Z.Y. (2020). Breaches of the Baige barrier lake: Emergency response and dam breach flood. Science China: Technological Sciences 63 (7), 1164–1176. doi:10.1007/s11431-019-1475-y

CrossRef Full Text | Google Scholar

Cantero-Chinchilla, F.N., Castro-Orgaz, O., Dey, S., and Ayuso-Muñoz, J.L. (2016). Nonhydrostatic dam break flows. II: One-dimensional depth-averaged modeling for movable bed flows. Journal of Hydraulic Engineering 142 (12), 04016069. doi:10.1061/(asce)hy.1943-7900.0001206

CrossRef Full Text | Google Scholar

Cao, Z.X., Yue, Z.Y., and Gareth, P. (2011a). Landslide dam failure and flood hydraulics. Part I: experimental investigation. Natural Hazards 59 (2), 1003–1019. doi:10.1007/s11069-011-9814-8

CrossRef Full Text | Google Scholar

Cao, Z.X., Yue, Z.Y., and Pender, G. (2011b). Landslide dam failure and flood hydraulics. Part II: coupled mathematical modelling. Natural Hazards 59 (2), 1021–1045. doi:10.1007/s11069-011-9815-7

CrossRef Full Text | Google Scholar

Capart, H., and Young, D.L. (1998). Formation of a jump by the dam-break wave over a granular bed. Journal of Fluid Mechanics 372, 165–187. doi:10.1017/s0022112098002250

CrossRef Full Text | Google Scholar

Carrivick, J.L., Jones, R., and Keevil, G. (2011). Experimental insights on geomorphological processes within dam break outburst floods. Journal of Hydrology 408, 153–163. doi:10.1016/j.jhydrol.2011.07.037

CrossRef Full Text | Google Scholar

Casagli, N., Ermini, L., and Rosati, G. (2003). Determining grain size distribution of the material composing landslide dams in the Northern Apennines: Sampling and processing methods. Engineering Geology 69, 83–97. doi:10.1016/s0013-7952(02)00249-1

CrossRef Full Text | Google Scholar

Casagli, N., and Ermini, L. (1999). Geomorphic analysis of landslide dams in the Northern Apennine. Transactions of the Japanese Geomorphological Union 20 (3), 219–249.

Google Scholar

Chai, H.J., Liu, H.C., and Zhang, Z.Y. (1995). The catalog of Chinese landslide dam events. Journal of Geological Hazards and Environment Preservation 6 (4), 1–9. (in Chinese).

Google Scholar

Chang, D.S., and Zhang, L.M. (2010). Simulation of the erosion process of landslide dams due to overtopping considering variations in soil erodibility along depth. Natural Hazards and Earth System Sciences 10 (4), 933–946. doi:10.5194/nhess-10-933-2010

CrossRef Full Text | Google Scholar

Chang, D.S., Zhang, L.M., Xu, Y., and Huang, R.Q. (2011). Field testing of erodibility of two landslide dams triggered by the 12 May Wenchuan earthquake. Landslides 8 (3), 321–332. doi:10.1007/s10346-011-0256-x

CrossRef Full Text | Google Scholar

Chen, C., Zhang, L.M., Xiao, T., and He, J. (2020). Barrier lake bursting and flood routing in the Yarlung Tsangpo Grand Canyon in October 2018. Journal of Hydrology 583, 124603. doi:10.1016/j.jhydrol.2020.124603

CrossRef Full Text | Google Scholar

Chen, S.C., Hsu, C.L., Wu, T.Y., Chou, H.T., and Cui, P. (2011). “Landslide dams induced by typhoon Morakot and risk assessment,” in 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics (Padua, Italy: Prediction and Assessment), 653–660.

Google Scholar

Chen, S.C., Lin, T.W., and Chen, C.Y. (2015). Modeling of natural dam failure modes and downstream riverbed morphological changes with different dam materials in a flume test. Engineering Geology 188, 148–158. doi:10.1016/j.enggeo.2015.01.016

CrossRef Full Text | Google Scholar

Chen, S.J., Chen, Z.Y., Tao, R., Yu, S., Xu, W.J., Zhou, X.B., and Zhou, Z.D. (2018). Emergency response and back analysis of the failures of earthquake triggered cascade landslide dams on the Mianyuan River, China. Natural Hazards Review 19 (3), 05018005. doi:10.1061/(asce)nh.1527-6996.0000285

CrossRef Full Text | Google Scholar

Chen, Y.J., Zhou, F., Feng, Y., and Xia, Y.C. (1992). Breach of a naturally embanked dam on Yalong River. Can. J. Civ. Eng. 19 (5), 811–818. (in Chinese). doi:10.1139/l92-092

CrossRef Full Text | Google Scholar

Chen, Z.Y., Ma, L.Q., Yu, S., Chen, S.J., Zhou, X.B., Sun, P., and Li, X. (2015). Back analysis of the draining process of the Tangjiashan barrier lake. Journal of Hydraulic Engineering 141 (4), 05014011. doi:10.1061/(asce)hy.1943-7900.0000965

CrossRef Full Text | Google Scholar

Chen, Z.Y., Zhang, Q., Chen, S.J., Wang, L., and Zhou, X.B. (2020). Evaluation of barrier lake breach floods - insights from recent case studies in China. WIREs Water 7 (2), e1408. doi:10.1002/wat2.1408

CrossRef Full Text | Google Scholar

Costa, J.E., and Schuster, R.L. (1988). The formation and failure of natural dams. Geological Society of America Bulletin 100 (7), 1054–1068. doi:10.1130/0016-7606(1988)100<1054:tfafon>2.3.co;2

CrossRef Full Text | Google Scholar

Costa, J.E., and Schuster, R.L. (1991). Documented historical landslide dams from around the world. Open-File Report 91-239. Washington D C, USA: U.S. Geological Survey.

Google Scholar

Costa, J.E. (1985). Floods from dam failures. Open-File Report 85-560. Washington D C, USA: U.S. Geological Survey.

Google Scholar

Cristo, C.D., Greco, M., Iervolino, M., Leopardi, A., and Vacca, A. (2016). Two-dimensional two-phase depth-integrated model for transients over mobile bed. Journal of Hydraulic Engineering 142 (2), 04015043. doi:10.1061/(asce)hy.1943-7900.0001024

CrossRef Full Text | Google Scholar

Cui, P., Zhu, Y.Y., Han, Y.S., Chen, X.Q., and Zhuang, J.Q. (2009). The 12 May Wenchuan earthquake-induced landslide lakes: distribution and preliminary risk evaluation. Landslides 7 (6), 209–223. doi:10.1007/s10346-009-0160-9

CrossRef Full Text | Google Scholar

Danish Hydraulic Institute (2021). MIKE FLOOD: Modelling of urban flooding. Copenhagen, Denmark: Danish Hydraulic Institute.

Google Scholar

Dazzi, S., Vacondio, R., and Mignosa, P. (2019). Integration of a levee breach erosion model in a GPU-accelerated 2D shallow water equations code. Water resources research 55 (1), 682–702. doi:10.1029/2018wr023826

CrossRef Full Text | Google Scholar

DeKay, M.L., and McClelland, G.H. (1993). Predicting Loss of Life in Cases of Dam Failure and Flash Flood. Risk Analysis 13 (2), 193–205. doi:10.1111/j.1539-6924.1993.tb01069.x

CrossRef Full Text | Google Scholar

Dong, J.J., Tung, Y.H., Chen, C.C., Liao, J.J., and Pan, Y.W. (2009). Discriminant analysis of the geomorphic characteristics and stability of landslide dams. Engineering Geology 110, 162–171. doi:10.1016/j.geomorph.2009.04.004

CrossRef Full Text | Google Scholar

Dong, J.J., Tung, Y.H., Chen, C.C., Liao, J.J., and Pan, Y.W. (2011). Logistic regression model for predicting the failure probability of a landslide dam. Engineering Geology 117, 52–61. doi:10.1016/j.enggeo.2010.10.004

CrossRef Full Text | Google Scholar

Ermini, L., and Casagli, N. (2003). Prediction of the behaviour of landslide dams using a geomorphological dimensionless index. Earth Surface Processes and Landforms 28 (1), 31–47. doi:10.1002/esp.424

CrossRef Full Text | Google Scholar

Ermini, L., Casagli, N., and Farina, P. (2006). Landslide dams: analysis of case histories and new perspectives from the application of remote sensing monitoring techniques to hazard and risk assessment. Italian Journal of Engineering Geology and Environment Special Issue 1, 45–52.

Google Scholar

Evans, S.G. (1986). The maximum discharge of outburst floods caused by the breaching of man-made and natural dams. Canadian Geotechnical Journal 23 (3), 385–387. doi:10.1139/t86-053

CrossRef Full Text | Google Scholar

Faeh, R. (2007). Numerical modeling of breach erosion of river embankments. Journal of Hydraulic Engineering 133 (9), 1000–1009. doi:10.1061/(asce)0733-9429(2007)133:9(1000)

CrossRef Full Text | Google Scholar

Fan, X.M., Dufresne, A., Subramanian, S.S., Strom, A., Hermanns, R., Stefanelli, C.T., Hewitt, K., Yunus, A.P., Dunning, S., Capra, L., Geertsema, M., Miller, B., Casagli, N., Jansen, J.D., and Xu, Q. (2020). The formation and impact of landslide dams – State of the art. Earth-Science Reviews 203, 103116. doi:10.1016/j.earscirev.2020.103116

CrossRef Full Text | Google Scholar

Fan, X.M., Scaringi, G., Korup, O., West, A.J., van Westen, C.J., Tanyas, H., Hovius, N., Hales, T.C., Jibson, R.W., Allstadt, K.E., Zhang, L.M., Evans, S.G., Xu, C., Li, G., Pei, X.J., Xu, Q., and Huang, R.Q. (2019a). Earthquake-induced chains of geologic hazards: Patterns, mechanisms, and impacts. Reviews of Geophysics 57, 421–503. doi:10.1029/2018rg000626

CrossRef Full Text | Google Scholar

Fan, X.M., Dufresne, A., Whiteley, J., Yunus, A.P., Subramanian, S.S., Okeke, C.A.U., Pánek, T., Hermanns, R.L., Peng, M., Strom, A., Havenith, H.B., Dunning, S., Wang, G.H., and Stefanelli, C.T. (2021). Recent technological and methodological advances for the investigation of landslide dams. Earth-Science Reviews 218, 103646. doi:10.1016/j.earscirev.2021.103646

CrossRef Full Text | Google Scholar

Fan, X.M., Xu, Q., Alonso-Rodriguez, A., Siva Subramanian, S., Li, W.L., Zheng, G., Dong, X.J., and Huang, R.Q. (2019b). Successive landsliding and damming of the Jinsha River in eastern Tibet, China: prime investigation, early warning, and emergency response. Landslides 16 (5), 1003–1020. doi:10.1007/s10346-019-01159-x

CrossRef Full Text | Google Scholar

Fread, D.L. (1988). National Oceanic and Atmospheric Administration. USA: National Weather Service, Silver Spring.BREACH: An erosion model for earthen dam failures (Model description and user manual)

Google Scholar

Fread, D.L., and Lewis, J.M. (1988). “FLDWAV: A generalized flood routing model,” in Proceedings of National Conference on Hydraulic Engineering, Colorado Springs, USA.

Google Scholar

Ge, W., Sun, H.Q., Zhang, H.X., Li, Z.K., Guo, X.Y., Wang, X.W., Qin, Y.P., Gao, W.X., and van Gelder, P. (2020). Economic risk criteria for dams considering the relative level of economy and industrial economic contribution. Science of the Total Environment 725, 138139. doi:10.1016/j.scitotenv.2020.138139

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, W., Jiao, Y.T., Sun, H.Q., Li, Z.K., Zhang, H.X., Zheng, Y., Guo, X.Y., Zhang, Z.S., and van Gelder, P. (2019). A method for fast evaluation of potential consequences of dam breach. Water 11 (11), 2224. doi:10.3390/w11112224

CrossRef Full Text | Google Scholar

Ge, W., Wang, X.W., Li, Z.K., Zhang, H.X., Guo, X.Y., Wang, T., Gao, W.X., Lin, C.N., and van Gelder, P. (2021). Interval analysis of the loss of life caused by dam failure. Journal of Water Resources Planning and Management 147 (1), 04020098. doi:10.1061/(asce)wr.1943-5452.0001311

CrossRef Full Text | Google Scholar

Godunov, S.K. (1959). Finite difference method for the computation of discontinuous solutions of the equations of fluid dynamics. Sbornik Mathematics 47, 271–306.

Google Scholar

Goutiere, L., Soares-Frazão, S., and Zech, Y. (2011). Dam-break flow on mobile bed in abruptly widening channel: experimental data. Journal of Hydraulic Research 49 (3), 367–371. doi:10.1080/00221686.2010.548969

CrossRef Full Text | Google Scholar

Graham, W.J. (1999). A procedure for estimating loss of life caused by dam failure. Denver, USA: U.S. Bureau of Reclamation. Dam Safety Office, Report No. DSO-99-06.

Google Scholar

Gregoretti, C., Maltauro, A., and Lanzoni, S. (2010). Laboratory experiments on the failure of coarse homogeneous sediment natural dams on a sloping bed. Journal of Hydraulic Engineering 136 (11), 868–879. doi:10.1061/(asce)hy.1943-7900.0000259

CrossRef Full Text | Google Scholar

Guan, M.F., Wright, N.G., and Sleigh, P.A. (2015). Multimode morphodynamic model for sediment-laden flows and geomorphic impacts. Journal of Hydraulic Engineering 141 (6), 04015006. doi:10.1061/(asce)hy.1943-7900.0000997

CrossRef Full Text | Google Scholar

Guan, M.F., Wright, N.G., and Sleigh, P.A. (2014). 2D process-based morphodynamic model for flooding by noncohesive dyke breach. Journal of Hydraulic Engineering 140 (7), 04014022. doi:10.1061/(asce)hy.1943-7900.0000861

CrossRef Full Text | Google Scholar

Harten, A., Lax, P.D., and van Leer, B. (1983). On upstream differencing and Godunov-Type schemes for hyperbolic conservation laws. SIAM Review 25 (1), 35–61. doi:10.1137/1025002

CrossRef Full Text | Google Scholar

Hermanns, R.L., Hewitt, K., Strom, A., Evans, S.G., Dunning, S.A., and Scarascia-Mugnozza, G. (2011a). The classification of rockslide dams. Natural and Artificial Rockslide Dams. Springer, 581–593.

CrossRef Full Text | Google Scholar

Hermanns, R.L., Folguera, A., Penna, I., Fauqué, L., and Niedermann, S. (2011b). Landslide dams in the central Andes of Argentina (northern Patagonia and the Argentine northwest). Natural and Artificial Rockslide Dams, 147–176. Springer.

CrossRef Full Text | Google Scholar

Hu, X.W., Luo, G., Lv, X.P., Huang, R.Q., and Shi, Y.B. (2011). Analysis on dam-breaking mode of Tangjiashan barrier dam in Beichuan County. Journal of Mountain Science 8 (2), 354–362. doi:10.1007/s11629-011-2097-4

CrossRef Full Text | Google Scholar

Huang, D.J., Yu, Z.B., Li, Y.P., Han, D.W., Zhao, L.L., and Chu, Q. (2017). Calculation method and application of loss of life caused by dam break in China. Natural Hazards 85 (1), 39–57. doi:10.1007/s11069-016-2557-9

CrossRef Full Text | Google Scholar

IAHR Working Group for Dam-break Flows over Mobile Beds Canelas, R., Cao, Z., Cea, L., Chaudhry, H. M., Die Moran, A., et al. (2012). Dam-break flows over mobile beds: experiments and benchmark tests for numerical models. Journal of Hydraulic Research 50 (4), 364–375. doi:10.1080/00221686.2012.689682

CrossRef Full Text | Google Scholar

Ischuk, A.R. (2011). Usoi rockslide dam and lake Sarez, Pamir mountains, Tajikistan. Natural and Artificial Rockslide Dams. Springer, 423–440.

CrossRef Full Text | Google Scholar

Itoh, T., Ikeda, A., Nagayama, T., and Mizuyama, T. (2018). Hydraulic model tests for propagation of flow and sediment in floods due to breaking of a natural landslide dam during a mountainous torrent. International Journal of Sediment Research 33, 107–116. doi:10.1016/j.ijsrc.2017.10.001

CrossRef Full Text | Google Scholar

Jiang, X.G., and Wei, Y.W. (2020). Erosion characteristics of outburst floods on channel beds under the conditions of different natural dam downstream slope angles. Landslides 17 (4), 1823–1834. doi:10.1007/s10346-020-01381-y

CrossRef Full Text | Google Scholar

Jiang, X.G., and Wei, Y.W. (2019). Natural dam breaching due to overtopping: effects of initial soil moisture. Bulletin of Engineering Geology and the Environment 78, 4821–4831. doi:10.1007/s10064-018-01441-7

CrossRef Full Text | Google Scholar

Jiang, X.G., Wei, Y.W., Wu, L., and Lei, Y. (2018). Experimental investigation of failure modes and breaching characteristics of natural dams. Geomatics, Natural Hazards and Risk 9 (1), 33–48. doi:10.1080/19475705.2017.1407367

CrossRef Full Text | Google Scholar

Jongmans, D., and Garambois, S. (2007). Geophysical investigation of landslides: a review. Bulletin de la Soci´et´e g´eologique de France 178 (2), 101–112. doi:10.2113/gssgfbull.178.2.101

CrossRef Full Text | Google Scholar

Jonkman, S.N. (2007). Loss of life estimation in flood risk assessment: theory and applications. Ph.D. Thesis. Delft, Netherlands: Delft University of Technology.

Google Scholar

Jonkman, S.N., and Penning-Rowsell, E. (2008). Human instability in flood flows. Journal of the American Water Resources Association 44 (5), 1208–1218. doi:10.1111/j.1752-1688.2008.00217.x

CrossRef Full Text | Google Scholar

Juez, C., Murillo, J., and García-Navarro, P. (2014). A 2D weakly-coupled and efficient numerical model for transient shallow flow and movable bed. Advances in Water Resources 71, 93–109. doi:10.1016/j.advwatres.2014.05.014

CrossRef Full Text | Google Scholar

Juez, C., Lacasta, A., Murillo, J., and García-Navarro, P. (2016). An efficient GPU implementation for a faster simulation of unsteady bed-load transport. Journal of Hydraulic Research 55 (3), 275–288. doi:10.1080/00221686.2016.1143042

CrossRef Full Text | Google Scholar

Korup, O. (2002). Recent research on landslide dams - a literature review with special attention to New Zealand. Progress in Physical Geography 26 (2), 206–235. doi:10.1191/0309133302pp333ra

CrossRef Full Text | Google Scholar

Korup, O. (2004). Geomorphometric characteristics of New Zealand landslide dams. Engineering Geology 73, 13–35. doi:10.1016/j.enggeo.2003.11.003

CrossRef Full Text | Google Scholar

Lacasta, A., Morales-Hernández, M., Murillo, J., and García-Navarro, P. (2014). An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes. Advances in Engineering Software 78, 1–15. doi:10.1016/j.advengsoft.2014.08.007

CrossRef Full Text | Google Scholar

Lacasta, A., Juez, C., Murillo, J., and García-Navarro, P. (2015). An efficient solution for hazardous geophysical flows simulation using GPUs. Computers and Geosciences 78, 63–72. doi:10.1016/j.cageo.2015.02.010

CrossRef Full Text | Google Scholar

Lauber, G., and Hager, W.H. (1998). Experiments to dambreak wave: Horizontal channel. Journal of Hydraulic Research 36 (3), 291–307. doi:10.1080/00221689809498620

CrossRef Full Text | Google Scholar

Lee, J.S. (2003). Uncertainties in the predicted number of life loss due to the dam breach floods. KSCE Journal of Civil Engineering 7 (1), 81–91. doi:10.1007/bf02841991

CrossRef Full Text | Google Scholar

Li, L., Yang, X.G., Zhou, J.W., Zhang, J.Y., and Fan, G. (2021). Large-scale field test study on failure mechanism of non-cohesive landslide dam by overtopping. Frontiers in Earth Science 9, 660408. doi:10.3389/feart.2021.660408

CrossRef Full Text | Google Scholar

Li, D.Y., Zheng, D.F., Wu, H., Shen, Y.Q., and Nian, T.K. (2021). Numerical simulation on the longitudinal breach process of landslide dams using an improved coupled DEM-CFD method. Frontiers in Earth Science 9, 673249. doi:10.3389/feart.2021.673249

CrossRef Full Text | Google Scholar

Li, J., Cao, Z.X., Pender, G., and Liu, Q.Q. (2013). A double layer-averaged model for dam-break flows over mobile bed. Journal of Hydraulic Research 51 (5), 518–534. doi:10.1080/00221686.2013.812047

CrossRef Full Text | Google Scholar

Lind, N, Hartford, D, and Assaf, H (2004). Hydrodynamic models of human instability in a flood. Journal of the American Water Resources Association 40 (1), 89–96. doi:10.1111/j.1752-1688.2004.tb01012.x

CrossRef Full Text | Google Scholar

Liu, J.K., Cheng, Z.L., and Wu, J.S. (2013). An empirical model calculating the breach parameters of landslide and debris-flow dam. Journal of Sichuan University (Engineering Science Edition) 45 (S2), 84–89. (in Chinese).

Google Scholar

Liu, N., Chen, Z.Y., Zhang, J.X., Lin, W., Chen, W.Y., and Xu, W.J. (2010). Draining the Tangjiashan barrier lake. Journal of Hydraulic Engineering 136 (11), 914–923. doi:10.1061/(asce)hy.1943-7900.0000241

CrossRef Full Text | Google Scholar

Liu, W.M., Carling, P.A., Hu, K.H., Wang, H., Zhou, Z., Zhou, L.Q., Liu, D.Z., Lai, Z.P., and Zhang, X.B. (2019). Outburst floods in China: A review. Earth-Science Review 197, 102895. doi:10.1016/j.earscirev.2019.102895

CrossRef Full Text | Google Scholar

Mahmoud, A.A., Wang, J.T., and Jin, F. (2020). An improved method for estimating life losses from dam failure in China. Stochastic Environmental Research and Risk Assessment 34, 1263–1279. doi:10.1007/s00477-020-01820-1

CrossRef Full Text | Google Scholar

Marsooli, R., and Wu, W.M. (2015). Three-dimensional numerical modeling of dam-break flows with sediment transport over movable beds. Journal of Hydraulic Engineering 141 (1), 04014066. doi:10.1061/(asce)hy.1943-7900.0000947

CrossRef Full Text | Google Scholar

McCann, D., and Forster, A. (1990). Reconnaissance geophysical methods in landslide investigations. Engineering Geology 29 (1), 59–78. doi:10.1016/0013-7952(90)90082-c

CrossRef Full Text | Google Scholar

Mei, S.Y., Chen, S.S., Zhong, Q.M., and Shan, Y.B. (2021). Effects of Grain Size Distribution on Landslide Dam Breaching—Insights From Recent Cases in China. Frontiers in Earth Science 9, 658578. doi:10.3389/feart.2021.658578

CrossRef Full Text | Google Scholar

Niazi, F.S., Habib Ur, R., and Akram, T. (2010). Application of electrical resistivity for subsurface characterization of Hattian Bala landslide dam, GeoFlorida 2010. Adv. Analysis Model. Desig., 480–489.

Google Scholar

O’Connor, J.E., and Beebee, R.A. (2009). Floods from natural rock-material dams. New York: Cambridge University Press.

Google Scholar

Osher, S., and Solomon, F. (1982). Upwind difference schemes for hyperbolic systems of conservation laws. Mathematics of Computation 158, 339–374. doi:10.1090/s0025-5718-1982-0645656-0

CrossRef Full Text | Google Scholar

Peng, M., and Zhang, L.M. (2012a). Breaching parameters of landslide dams. Landslides 9 (1), 13–31. doi:10.1007/s10346-011-0271-y

CrossRef Full Text | Google Scholar

Peng, M., and Zhang, L.M. (2012b). Analysis of human risks due to dam-break floods – part 1: a new model based on Bayesian networks. Natural Hazards 64, 903–933. doi:10.1007/s11069-012-0275-5

CrossRef Full Text | Google Scholar

Peng, M., Jiang, Q.L., Zhang, Q.Z., Hong, Y., Jiang, M.Z., Shi, Z.M., and Zhang, L.M. (2019). Stability analysis of landslide dams under surge action based on large-scale flume experiments. Engineering Geology 259, 105191. doi:10.1016/j.enggeo.2019.105191

CrossRef Full Text | Google Scholar

Peng, M., Ma, C.Y., Chen, H.X., Zhang, P., Zhang, L.M., Jiang, M.Z., Zhang, Q.Z., and Shi, Z.M. (2021). Experimental study on breaching mechanisms of landslide dams composed of different materials under surge waves. Engineering Geology 291, 106242. doi:10.1016/j.enggeo.2021.106242

CrossRef Full Text | Google Scholar

Peng, M., Zhang, L.M., Chang, D.S., and Shi, Z.M. (2014). Engineering risk mitigation measures for the landslide dams induced by the 2008 Wenchuan earthquake. Engineering Geology 180, 68–84. doi:10.1016/j.enggeo.2014.03.016

CrossRef Full Text | Google Scholar

Priest, S., Wilson, T., Tapsell, S., Penning-Rowsell, E., Viavattene, C., and Fernandez-Bilbao, A. (2007). Building a model to estimate Risk to Life for European flood events - final report. Integrated flood risk analysis and management methodologies. Available at: http://www.floodsite.net/html/partner_area/search_results3b.asp?docID=265.

Google Scholar

Qian, H.L, Cao, Z.X., Liu, H.H., and Pender, G. (2018). New experimental dataset for partial dam-break floods over mobile beds. Journal of Hydraulic Research 56 (1), 124–135. doi:10.1080/00221686.2017.1289264

CrossRef Full Text | Google Scholar

Razavitoosi, S.L., Ayyoubzadeh, S.A., and Valizadeh, A. (2014). Two-phase SPH modelling of waves caused by dam break over a movable bed. International Journal of Sediment Research 29 (3), 344–356. doi:10.1016/s1001-6279(14)60049-4

CrossRef Full Text | Google Scholar

Reiter, P. (2001). Loss of life caused by dam failure: the RESCDAM LOL method and its application to Kyrkosjarvi dam in Seinajoki. Helsinki: PR Water Consulting Ltd.

Google Scholar

Roe, P.L. (1981). Approximate Riemann solvers, parameter vectors, and difference schemes. Journal of Computational Physics 43, 357–372. doi:10.1016/0021-9991(81)90128-5

CrossRef Full Text | Google Scholar

Rosatti, G., and Begnudelli, L. (2013). Two-dimensional simulation of debris flows over mobile bed: Enhancing the TRENT2D model by using a well-balanced Generalized Roe-type solver. Computers and Fluids 71, 179–195. doi:10.1016/j.compfluid.2012.10.006

CrossRef Full Text | Google Scholar

Scaioni, M., Longoni, L., Melillo, V., and Papini, M. (2014). Remote sensing for landslide investigations: an overview of recent achievements and perspectives. Remote Sensing 6 (10), 9600–9652. doi:10.3390/rs6109600

CrossRef Full Text | Google Scholar

Shan, Y.B., Chen, S.S., and Zhong, Q.M. (2020). Rapid prediction of landslide dam stability using the logistic regression method. Landslides 17 (12), 2931–2956. doi:10.1007/s10346-020-01414-6

CrossRef Full Text | Google Scholar

Shan, Y.B., Chen, S.S., Zhong, Q.M., Mei, S.Y., and Yang, M. (2022). Development of an empirical model for predicting peak breach flow of landslide dams considering material composition. Landslides 19 (6), 1491–1518. doi:10.1007/s10346-022-01863-1

CrossRef Full Text | Google Scholar

Shen, D.Y., Shi, Z.M., Peng, M., Zhang, L.M., and Jiang, M.Z. (2020a). Longevity analysis of landslide dams. Landslides 17 (8), 1797–1821. doi:10.1007/s10346-020-01386-7

CrossRef Full Text | Google Scholar

Shen, G.Z., Sheng, J.B., Xiang, Y., Zhong, Q.M., and Yang, D.W. (2020b). Numerical modeling of overtopping-induced breach of landslide dams. Natural Hazards Review 21 (2), 04020002. doi:10.1061/(asce)nh.1527-6996.0000362

CrossRef Full Text | Google Scholar

Shi, Z.M., Cheng, S.Y., Zhang, Q.Z., and Xue, D.X. (2020). A fast model for landslide dams stability assessment: a case study of Xiaogangjian (Upper) landslide dam. Journal of Water Resources and Architectural Engineering 18 (2), 95–100+146. (in Chinese).

Google Scholar

Shi, Z.M., Guan, S.G., Peng, M., and Xiong, X. (2015a). “Research on the influence of material permeability to landslide dam seepage stability,” in 10th Asian Region Conference of IAEG, Kyoto, Japan, Sept. 26-27, 2015.

Google Scholar

Shi, Z.M., Ma, X.L., Peng, M., and Zhang, L.M. (2014). Statistical analysis and efficient dam burst modelling of landslide dams based on a large-scale database. Chinese Journal of Rock Mechanics and Engineering 33 (9), 1780–1790. (in Chinese).

Google Scholar

Shi, Z.M., Guan, S.G., Peng, M., Zhang, L.M., Zhu, Y., and Cai, Q.P. (2015b). Cascading breaching of the Tangjiashan landslide dam and two smaller downstream landslide dams. Engineering Geology 193, 445–458. doi:10.1016/j.enggeo.2015.05.021

CrossRef Full Text | Google Scholar

Shi, Z.M., Xiong, X., Peng, M., Zhang, L.M., Xiong, Y.F., Chen, H.X., and Zhu, Y. (2016). Risk assessment and mitigation for the Hongshiyan landslide dam triggered by the 2014 Ludian earthquake in Yunnan, China. Landslides 14 (1), 269–285. doi:10.1007/s10346-016-0699-1

CrossRef Full Text | Google Scholar

Soares-Frazão, S., and Zech, Y. (2002). Dam break in channels with 90° bend. Journal of Hydraulic Engineering 128 (11), 956–968. doi:10.1061/(asce)0733-9429(2002)128:11(956)

CrossRef Full Text | Google Scholar

Spinewine, B., and Zech, Y. (2007). Small-scale laboratory dam-break waves on movable beds. Journal of Hydraulic Research 45 (S1), 73–86. doi:10.1080/00221686.2007.9521834

CrossRef Full Text | Google Scholar

Stefanelli, C. T., Catani, F., and Casagli, N. (2015). Geomorphological investigations on landslide dams. Geoenvironmental Disasters 2 (2), 21. doi:10.1186/s40677-015-0030-9

CrossRef Full Text | Google Scholar

Stefanelli, C.T., Segoni, S., Casagli, N., and Catani, F. (2016). Geomorphic indexing of landslide dams evolution. Engineering Geology 208, 1–10. doi:10.1016/j.enggeo.2016.04.024

CrossRef Full Text | Google Scholar

Stefanelli, C.T., Vilímek, V., Emmer, A., and Catani, F. (2018). Morphological analysis and features of the landslide dams in the Cordillera Blanca, Peru. Landslides 15 (3), 507–521. doi:10.1007/s10346-017-0888-6

CrossRef Full Text | Google Scholar

Swartenbroekx, C., Soares-Frazão, S., Staquet, R., and Zech, Y. (2010). Two-dimensional operator for bank failures induced by water-level rise in dam-break flows. Journal of Hydraulic Research 48 (3), 302–314. doi:10.1080/00221686.2010.481856

CrossRef Full Text | Google Scholar

Swartenbroekx, C., Zech, Y., and Soares-Frazão, S. (2013). Two-dimensional two-layer shallow water model for dam break flows with significant bed load transport. International Journal for Numerical Methods in Fluids 73 (5), 477–508. doi:10.1002/fld.3809

CrossRef Full Text | Google Scholar

Takayama, S., Miyata, S., Fujimoto, M., and Satofuka, Y. (2021). Numerical simulation method for predicting a flood hydrograph due to progressive failure of a landslide dam. Landslides 18, 3655–3670. doi:10.1007/s10346-021-01712-7

CrossRef Full Text | Google Scholar

Tong, Y.X. (2008). Master Thesis. Taoyuan: National Central University. (in Chinese).Quantitative analysis for stability of landslide dams

Google Scholar

Toro, E.F. (2000). Shocking methods for free surface shallow flows. New York, USA: Wiley.

Google Scholar

Toro, E.F., Spruce, M., and Speares, W. (1994). Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4 (4), 25–34. doi:10.1007/bf01414629

CrossRef Full Text | Google Scholar

Tsai, P.H., Feng, Z.Y., Yu, F.C., and Lin, J.H. (2013). “Stability analysis of landslide dam under rainfall,” in IACGE 2013 - Challenges and Recent Advances in Geotechnical and Seismic Research and Practices, Chengdu, China, October 25-27, 2013.

CrossRef Full Text | Google Scholar

US Army Corps of Engineers (2021). HEC-RAS, River analysis system user’s manual. Davis, USA: Hydrologic Engineering Center, US Army Corps of Engineers.

Google Scholar

Walder, J.S., Iverson, R.M., Godt, J.W., Logan, M., and Solovitz, S.A. (2015). Controls on the breach geometry and flood hydrograph during overtopping of noncohesive earthen dams. Water Resources Research 51 (8), 6701–6724. doi:10.1002/2014wr016620

CrossRef Full Text | Google Scholar

Walder, J.S., and O’Connor, J.E. (1997). Methods for predicting peak discharge of floods caused by failure of natural and constructed earthen dams. Water Resources Research 33 (10), 2337–2348. doi:10.1029/97wr01616

CrossRef Full Text | Google Scholar

Wang, B., Zhang, F.J., Liu, X., Guo, Y.K., Zhang, J.M., and Peng, Y. (2021). Approximate analytical solution and laboratory experiments for dam-break wave tip region in triangular channels. Journal of Hydraulic Engineering 147 (9), 06021015. doi:10.1061/(asce)hy.1943-7900.0001928

CrossRef Full Text | Google Scholar

Wang, F.W., Okeke, A.C.U., Kogure, T., Sakai, T., and Hayashi, H. (2018). Assessing the internal structure of landslide dams subject to possible piping erosion by means of microtremor chain array and self-potential surveys. Engineering Geology 234, 11–26. doi:10.1016/j.enggeo.2017.12.023

CrossRef Full Text | Google Scholar

Wang, G.H., Huang, R.Q., Kamai, T., and Zhang, F.Y. (2013). The internal structure of a rockslide dam induced by the 2008 Wenchuan (Mw7.9) earthquake, China. Engineering Geology 156, 28–36. doi:10.1016/j.enggeo.2013.01.004

CrossRef Full Text | Google Scholar

Wang, G.H., Huang, R.Q., Lourenço, S.D., and Kamai, T. (2014). A large landslide triggered by the 2008 Wenchuan (M8.0) earthquake in Donghekou area: Phenomena and mechanisms. Engineering Geology 182, 148–157. doi:10.1016/j.enggeo.2014.07.013

CrossRef Full Text | Google Scholar

Wang, G.H., Furuya, G., Zhang, F.Y., Doi, I., Watanabe, N., Wakai, A., and Marui, H. (2016). Layered internal structure and breaching risk assessment of the Higashi-Takezawa landslide dam in Niigata, Japan. Geomorphology 267, 48–58. doi:10.1016/j.geomorph.2016.05.021

CrossRef Full Text | Google Scholar

Wang, K.W., Deng, C.J., and Zhang, F. (2012). Formation process of Tanggudong landslide and Yuri accumulation body in Yalong River valley in southwest. China. J. Eng. Geol. 20 (6), 955–970. (in Chinese).

Google Scholar

Wang L., L., Chen, Z.Y., Wang, N.X., Sun, P., Yu, S., Li, S.Y., and Du, X.H. (2016). Modeling lateral enlargement in dam breaches using slope stability analysis based on circular slip mode. Engineering Geology 209, 70–81. doi:10.1016/j.enggeo.2016.04.027

CrossRef Full Text | Google Scholar

Weidinger, J.T. (2006). Landslide dams in the high mountains of India, Nepal and China - Stability and life span of their dammed lakes. Italian Journal of Engineering Geology and Environment Special Issue 1, 67–80.

Google Scholar

Whiteley, J., Chambers, J., Uhlemann, S., Wilkinson, P., and Kendall, J. (2019). Geophysical monitoring of moisture-induced landslides: a review. Reviews of Geophysics 57, 106–145. doi:10.1029/2018rg000603

CrossRef Full Text | Google Scholar

Wu, W.M., and Wang, S.S.Y. (2007). One-dimensional modeling of dam-break flow over movable beds. Journal of Hydraulic Engineering 133 (1), 48–58. doi:10.1061/(asce)0733-9429(2007)133:1(48)

CrossRef Full Text | Google Scholar

Wu, W.M., Marsooli, R., and He, Z.G. (2012). Depth-averaged two-dimensional model of unsteady flow and sediment transport due to noncohesive embankment break/breaching. Journal of Hydraulic Engineering 138 (6), 503–516. doi:10.1061/(asce)hy.1943-7900.0000546

CrossRef Full Text | Google Scholar

Xu, Q., Fan, X.M., Huang, R.Q., and Westen, C.V. (2009). Landslide dams triggered by the Wenchuan earthquake, Sichuan Province, south west China. Bulletin of Engineering Geology and the Environment 68, 373–386. doi:10.1007/s10064-009-0214-1

CrossRef Full Text | Google Scholar

Yang, Y., Cao, S.Y., Yang, K.J., and Li, W.P. (2015). Experimental study of breach process of landslide dams by overtopping and its initiation mechanisms. Journal of Hydrodynamics 27 (6), 872–883. doi:10.1016/s1001-6058(15)60550-9

CrossRef Full Text | Google Scholar

Zhai, G.F., Fukuzono, T., and Ikeda, S. (2006). An empirical model of fatailities and injuries due to flood in Japan. Journal of the American Water Resources Association 42 (4), 863–875. doi:10.1111/j.1752-1688.2006.tb04500.x

CrossRef Full Text | Google Scholar

Zhang, J.Y., Fan, G., Li, H.B., Zhou, J.W., and Yang, X.G. (2021). Large-scale field model tests of landslide dam breaching. Engineering Geology 293, 106322. doi:10.1016/j.enggeo.2021.106322

CrossRef Full Text | Google Scholar

Zhang, L.M., Peng, M., Chang, D. S., and Xu, Y. (2016). Dam failure mechanisms and risk assessment. Singapore: John Wiley & Sons Singapore Pte. Ltd.

Google Scholar

Zhang, L.M., Xiao, T., He, J., and Chen, C. (2019). Erosion-based analysis of breaching of Baige landslide dams on the Jinsha River, China, in 2018. Landslides 16 (10), 1965–1979. doi:10.1007/s10346-019-01247-y

CrossRef Full Text | Google Scholar

Zhao, T.L., Chen, S.S., Fu, C.J., and Zhong, Q.M. (2019). Centrifugal model test on the failure mechanism of barrier dam overtopping. KSCE Journal of Civil Engineering 23 (4), 1548–1559. doi:10.1007/s12205-019-0375-9

CrossRef Full Text | Google Scholar

Zhao, T.L., Chen, S.S., Fu, C.J., and Zhong, Q.M. (2018). Influence of diversion channel section type on landslide dam draining effect. Environmental Earth Sciences 77 (2), 54–62. doi:10.1007/s12665-017-7217-1

CrossRef Full Text | Google Scholar

Zhong, Q.M., Wang, L., Chen, S.S., Chen, Z.Y., Shan, Y.B., Zhang, Q., Ren, Q., Mei, S.Y., Jiang, J.D., Hu, L., and Liu, J.X. (2021). Breaches of embankment and landslide dams – State of the art review. Earth-Science Reviews 216, 103597. doi:10.1016/j.earscirev.2021.103597

CrossRef Full Text | Google Scholar

Zhong, Q.M., Chen, S.S., Wang, L., and Shan, Y.B. (2020a). Back analysis of breaching process of Baige landslide dam. Landslides 17 (7), 1681–1692. doi:10.1007/s10346-020-01398-3

CrossRef Full Text | Google Scholar

Zhong, Q.M., Wu, W.M., Chen, S.S., and Wang, M. (2016). Comparison of simplified physically based dam breach models. Natural Hazards 84 (2), 1385–1418. doi:10.1007/s11069-016-2492-9

CrossRef Full Text | Google Scholar

Zhong, Q.M., Chen, S.S., and Shan, Y.B. (2020b). Prediction of the overtopping-induced breach process of the landslide dam. Engineering Geology 274, 105709. doi:10.1016/j.enggeo.2020.105709

CrossRef Full Text | Google Scholar

Zhong, Q.M., Chen, S.S., Mei, S.A., and Cao, W. (2018). Numerical simulation of landslide dam breaching due to overtopping. Landslides 15 (6), 1183–1192. doi:10.1007/s10346-017-0935-3

CrossRef Full Text | Google Scholar

Zhou, G.G.D, Zhou, M.J., Shrestha, M.S., Song, D.R., Choi, C.E., Cui, K.F.E., Peng, M., Shi, Z.M., Zhu, X.H., and Chen, H.Y. (2019). Experimental investigation on the longitudinal evolution of landslide dam breaching and outburst floods. Geomorphology 334, 29–43. doi:10.1016/j.geomorph.2019.02.035

CrossRef Full Text | Google Scholar

Zhou, X.B., Chen, Z.Y., Yu, S., Wang, L., Deng, G., Sha, P.J., and Li, S.Y. (2015). Risk analysis and emergency actions for Hongshiyan barrier lake. Natural Hazards 79 (3), 1933–1959. doi:10.1007/s11069-015-1940-2

CrossRef Full Text | Google Scholar

Zhu, X.H., Liu, B.X., Peng, J.B., Zhang, Z.F., Zhuang, J.Q., Huang, W.L., Leng, Y.Q., and Duan, Z. (2021). Experimental study on the longitudinal evolution of the overtopping breaching of noncohesive landslide dams. Engineering Geology 288, 106137. doi:10.1016/j.enggeo.2021.106137

CrossRef Full Text | Google Scholar

Zhu, X.H., Peng, J.B., Liu, B.X., Jiang, C., and Guo, J. (2020). Influence of textural properties on the failure mode and process of landslide dams. Engineering Geology 271, 105613. doi:10.1016/j.enggeo.2020.105613

CrossRef Full Text | Google Scholar