Strength and seismic anisotropy of textured FeSi at planetary core conditions

Elastic anisotropy of iron-bearing alloys and compounds can lead to a variation of seismic velocities along different directions in planetary cores. Understanding the deformation properties of candidate core-forming materials is thus necessary to reveal the details about the interior of distant planets. Silicon has been considered to be one of the dominant light elements in the cores. Here we investigated the deformation of the ε-FeSi phase up to 49 GPa and 1100 K employing the radial X-ray diffraction technique in diamond anvil cells. Stoichiometric FeSi is a good approximation for the deformation behavior of the Fe-FeSi system and the low-pressure polymorph of FeSi may be the stable phase in the cores of small terrestrial planets such as Mercury. Yield strength in ε-FeSi is higher than in hcp-Fe and hcp-Fe-Si alloys, in the temperature range we investigated here the temperature has little influence on the lattice strain parameters, yield strength, and anisotropy within experimental precision. The azimuthal anisotropy of the longitudinal sound waves in ε-FeSi is below 0.6% at low pressure and decreases further with compression, while the shear wave contrast is below 1.25% in the entire investigated pressure range. Therefore, polycrystalline aggregates of iron silicide are nearly isotropic at extreme conditions. Consequently, any observed anisotropy in planetary cores will be incompatible with silicon being the dominant light element in the core composition.

1 Introduction

The heterogeneous nature of sound wave propagation inside the deepest portions of the Earth’s interior was already discovered 40 years ago (Masters and Gilbert, 1981; Anderson and Dziewonski, 1982; Poupinet et al., 1983; Vinnik et al., 1989; Lay and Young, 1991). One of the first explanations of these effects was the hypothesis of inner core material anisotropy (Morelli et al., 1986; Woodhouse et al., 1986). Later it gained a firm confirmation from other geophysical observations (Creager, 1992; Song and Helmberger, 1993; Tromp, 1993). Evidence for inner core anisotropy comes from two sources—a directional variation of travel times (Poupinet et al., 1983) and an anomalous splitting of the normal modes (Masters and Gilbert, 1981) that cannot be explained by the contributions of the Coriolis effect or the ellipticity of the Earth (Song, 1997). The initial models assumed cylindrical symmetry with the waves travelling 3% faster along the Earth’s north-south spin axis compared to the equatorial plane (Song and Helmberger, 1993; Irving and Deuss, 2011). Later, more complex models were proposed, such as the presence of the innermost inner core (Ishii and Dziewonski, 2002), depth dependence of anisotropic properties (Garcia and Souriau, 2000), and hemispherical variation in anisotropic properties (Creager, 1999; Irving and Deuss, 2011), recently reviewed in Deuss (2014) and Tkalčić (2015).

The anisotropy in the solid inner core originates either from the shape preferred orientation (SPO) or from lattice preferred orientation (LPO) of the core-forming material (Singh et al., 2000; Deuss, 2014). LPO is considered to be more likely due to the anisotropy of iron that most probably crystallizes in the hexagonally close-packed structure at the inner core conditions (Tateno et al., 2010). The anisotropy due to LPO can be induced by (re)crystallization but most likely, it is the result of the deformation-induced lattice rotation of core-forming materials. The deformation may originate from various sources, such as Maxwell stress (Karato, 1999), thermal convection (Wenk et al., 2000), preferential equatorial solidification (Yoshida et al., 1996), or Joule heating (Takehiro, 2011). In the most recent research, Frost et al. (2021) suggested that the structure of the inner core can be well reproduced by the deformation of hcp-Fe-Ni alloy induced by a combination of its preferential growth on one side of the equator followed by a slow translation.

Measurements of the moments of inertia of the terrestrial planets, i.e., Mercury (Genova et al., 2019), Venus (Dumoulin et al., 2017), Mars (Cook, 1977), and the Moon (Toksöz et al., 1974) suggested the existence of dense metallic cores. The presence of the magnetic fields and quite a small mean moment of inertia (Sohl et al., 2002; Breuer et al., 2015) indicate that Jovian moons such as Io, Europa, and Ganymede also have metallic cores (Sohl et al., 2002; Soderlund et al., 2020).

The cores of terrestrial planets are likely comprised of Fe-Ni alloys with some other, lighter elements (Breuer et al., 2015; Trønnes et al., 2019). The amount of light elements can reach up to 25 wt% in the core of Mercury (Chabot et al., 2014), 9 wt% in the core of Venus, 5 wt% in the Moon, and 14 wt% in Mars (Trønnes et al., 2019). Silicon has long been considered as a major light element of the Earth’s core: it has a high cosmic abundance and can be incorporated into Fe-Ni alloy during core formation (Trønnes et al., 2019). Silicon content in planetary cores is heavily dependent on how reducing are the conditions inside the planet. For example, estimations for silicon content in Mercury’s core range from 15 to 25 wt% (Chabot et al., 2014; Knibbe and van Westrenen, 2018; Trønnes et al., 2019), while Venus’s core may contain up to 6 wt% of silicon, (O’Neill, 2021). Pressure conditions in the cores of terrestrial planets span over a huge range, from less than 6 GPa in the Jovian moons and the Moon to 20—40 GPa in Mercury and Mars, over 100 GPa in Venus (Trønnes et al., 2019). This diversity in pressure, temperature, and composition determines the conditions for the study of the physical properties of iron alloys relevant for planetary interiors.

We performed plastic deformation experiments employing diamond anvil cells (DAC) as a deformation apparatus at extreme pressure and temperature conditions coupled with X-ray diffraction in the radial geometry. In view of a potentially high Si content of the core Fe-alloy, we investigated yield strength and anisotropy of stoichiometric ε-FeSi. That provides a good first-order approximation of the deformation behavior of the Fe-FeSi system at the conditions of planetary cores. Our results tell that ε-FeSi is less anisotropic than hcp-Fe and its alloys. This difference can be used for constraining the silicon amount in planetary cores from seismic observations.

2 Materials and methods

2.1 Resistive-heated diamond-anvil cell experiments

We performed all the experiments on commercial iron silicide (FeSi) powders (AlfaAesar, CAS 12022-95-6, 99.9% nominal purity). Upon preliminary X-ray diffraction analysis, we found that the sample powder contained a small amount of SiC impurity (below 3.5 mass%). The initial powder was finely ground in an agate mortar and further loaded into the high-pressure chamber made of an X-ray transparent amorphous boron epoxy gasket (Merkel and Yagi, 2005). Diamond anvils with culet sizes of 300 µm were employed and typical diameters sizes for the sample chamber were 80 µm. The gaskets were held in place by a piece of Kapton. We did not use any pressure transmitting mediums in order to maximize the stress applied to the sample. Mao-Bell piston-cylinder type diamond anvil cells modified for high-temperature studies and equipped with graphite resistive heaters were employed to reach the desired P-T conditions (Liermann et al., 2009; Liermann et al., 2015; Immoor et al., 2020). The temperature was monitored with two type-R thermocouples. One thermocouple was put in contact with the diamond near the compression chamber while the second one was in contact with the heater. A water-cooled vacuum vessel capable to maintain 10^–4 mbar was used to avoid oxidation of the diamonds, seats, and electrical connections. Additional details about the design and operation of the resistive heated DAC for X-ray diffraction in radial geometry can be found elsewhere (Liermann et al., 2015; Immoor et al., 2020).

2.2 Synchrotron radial X-ray diffraction experiments

We performed measurements at the P02.2 extreme conditions beamline of PETRA III synchrotron (DESY). The radial X-ray diffraction data were collected along isotherms at 300 K and 1100 K up to 49 GPa (Supplementary Table S1).

The X-ray beam was focused down to 8(H) × 2(V) µm² by an array of compound refractive lenses. Diffraction experiments were conducted during two separate beamtimes with monochromatic X-rays of 0.4817 Å and 0.4843 Å wavelengths at 300 K and 1100 K, respectively, collected by a Perkin Elmer XRD 1621 flat panel detector. The sample-detector distances were 415.6 mm and 502.3 mm for the experiments at room temperature and high temperature, respectively. The sample-detector distance, tilt, and beam center were calibrated using a CeO₂ standard from NIST (674b) in DIOPTAS software (Prescher and Prakapenka, 2015).

We employed the equation of state (EOS) of the sample (Fischer et al., 2014) to determine the pressure in the experiment conducted at room temperature. In the heated cell, the pressure was determined (Supplementary Table S2) using the EOS of Au pieces placed inside the high-pressure chamber (Fei et al., 2007). The pressure dependence of the unit-cell volumes at both temperatures is on Supplementary Figure S1.

2.3 Data reduction

Collected data were divided into 72 azimuthal sections by 5° and each section was fitted using the MAUD software (Lutterotti et al., 1999). The fitting of lattice strain parameters was performed utilizing a model “radial diffraction in the DAC” as implemented in MAUD that relies on the formalism of Singh et al. (1998).

The stress (${\sigma }_{ij}$) applied to a sample in a diamond anvil cell can be described as (Singh and Balasingh, 1994):

${\sigma }_{ij}=\left[\begin{array}{ccc}{\sigma }_{11}& {\sigma }_{11}& {\sigma }_{33}\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_P& {\sigma }_P& {\sigma }_P\end{array}\right]+\left[\begin{array}{ccc}-t/3& -t/3& 2t/3\end{array}\right]={\sigma }_P+D_{ij}(1)$

where ${\sigma }_{11}$ and ${\sigma }_{33}$ are radial and axial stress components, respectively, ${\sigma }_P$ is the normal mean stress (hydrostatic pressure) applied to a sample and $t$ is the differential stress. The term $D_{ij}$ denotes the deviatoric stress tensor. Deviatoric stress produces lattice strains (${\epsilon }_D\left(hkl,\psi \right)$) that can be calculated as:

${\epsilon }_D\left(hkl,\psi \right)=\frac{\left(d_m\left(hkl\right)-d_P\left(hkl\right)\right)}{d_P\left(hkl\right)}(2)$

where $d_m\left(hkl\right)$ and $d_P\left(hkl\right)$ are the interplanar distances under deviatoric and hydrostatic stresses, respectively. $\psi$ is the angle between the maximum stress direction and the normal to the diffracting plane. The ${\epsilon }_D\left(hkl,\psi \right)$ is described by:

${\epsilon }_D\left(hkl,\psi \right)=\left(1-3{\mathit{cos}}^2\psi \right)\bullet Q\left(hkl\right)(3)$

where coefficient $Q\left(hkl\right)$ is the lattice strain parameter. Deformation of the diffraction planes leads to the deviation of the positions of the diffraction lines and the lattice strain parameter represents the amplitude of this deformation (Merkel, 2010). Under the assumption of the absence of lattice preferred orientations in a polycrystalline sample, $Q\left(hkl\right)$ is linked to the differential stress t and shear modulus $G$ by the relationship:

$t\approx 6G\langle Q\left(hkl\right)\rangle (4)$

We used the Voigt-Reuss-Hill scheme (Hill, 1952) to calculate the shear modulus $G_H$ of a polycrystalline aggregate of FeSi:

$G_H=\frac{G_V+G_R}{2}(5)$

where $G_V$ and $G_R$ are the Voigt and Reuss shear moduli, respectively. For cubic crystals, G_V and $G_R$ can be calculated as:

$G_V=\frac{C_{11}-C_{12}+3C_{44}}{5}(6)$

$G_R=\frac{5\left(C_{11}-C_{12}\right)C_{44}}{4C_{44}+3\left(C_{11}-C_{12}\right)}(7)$

where C_ij are the corresponding stiffness tensor components. The pressure and temperature dependence of the stiffness tensor components of ε-FeSi were derived from the first-principle calculations by Qi et al. (2019) and presented in Supplementary Table S3. Stiffness tensor components at 1100 K were obtained by linear interpolation of data between 300 K and 2000 K.

The texture of crystallites developed due to the plastic deformation was refined with the E-WIMV model implemented in MAUD with the assumed fiber symmetry around the compression axis. The model is based on the WIMV method (Matthies and Vinel, 1982), extended to be used on irregular grids, which includes a build-in smoothing function (Lutterotti et al., 2004). The corresponding pole figures were exported from MAUD and the MTEX software (Bachmann et al., 2010; Mainprice et al., 2015) was used for plotting the inverse pole figures (IPFs) and the anisotropy of the sound velocities derived from the elastic tensor of Qi et al. (2019).

3 Results

We carried out the experiments in the FeSi polycrystalline sample at pressures from 7 GPa to 49 GPa at 300 K and from 13 to 49 GPa at about 1100 K (1080 ± 30 K). Our diffraction data confirms that the sample remains in the ε-FeSi (B20-structure, P2₁3 space group) throughout the studied range.

Representative unrolled diffraction data are presented in Figure 1. The deviations of d-spacings from the straight line are due to the induced lattice strains, Eq. 2. We used the strongest reflections corresponding to (110), (111), (200), (120), (211), and (130) lattice planes. We used them to derive the lattice strain parameters $Q\left(hkl\right)$. These values were then averaged for the calculation of the differential stress according to Eq. 4. The results are presented in Supplementary Table S1. The individual lattice strain parameters at various pressure-temperature conditions are summarized in Supplementary Tables S4, S5.

FIGURE 1

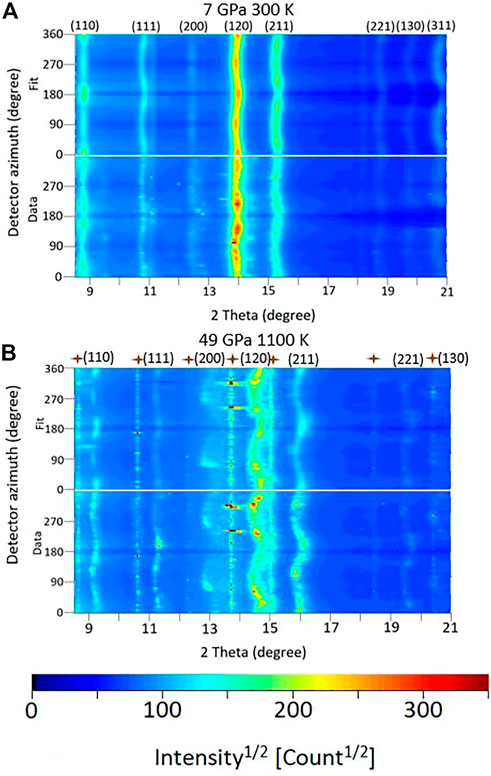
FIGURE 1. Unrolled diffraction patterns (bottom) collected at 7 GPa and 300 K (A) and 49 GPa and 1100 K (B) along with the best-fit models (top). The intensity variations of the diffraction lines are caused by lattice preferred orientation in ε-FeSi, the curvature is a measure of elastic lattice strains. Numbers (e.g., 110) indicate the Laue indices of the Bragg reflections of compressed ε-FeSi, brown crosses are the diffraction lines of ε-FeSi located outside the pressure chamber, as indicated by the absence of strain or change in 2θ upon increasing pressure.

Analysis of the average lattice strain parameters $\langle Q\left(hkl\right)\rangle$ obtained at two temperatures (300 K and 1100 K) is shown in Figure 2 and Supplementary Table S1. At relatively low pressures, $\langle Q\left(hkl\right)\rangle$ increases at both temperatures. At 300 K, $\langle Q\left(hkl\right)\rangle$ increases continuously until around 15 GPa and much more smoothly above this pressure. At 1100 K $\langle Q\left(hkl\right)\rangle$ increases with a slower rate until 20 GPa and reaches approximately the same values as at room temperatures (≈0.005). Upon further compression up to 49 GPa, lattice strain parameters remain scattered around this value, both at 300 K and 1100 K.

FIGURE 2

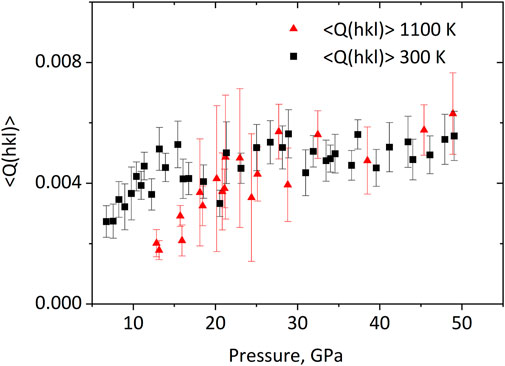
FIGURE 2. Pressure evolution of the average lattice strain parameter $\langle Q\left(hkl\right)\rangle$ in ε-FeSi at 300 (black squares) and 1100 K (red triangles).

The pressure evolution lattice preferred orientations in ε-FeSi at different temperatures is presented in Figure 3 as IPF of the compression direction. The B20-structure is cubic but without the 4-fold rotation axis and therefore directions $\left[\overline{1}01\right]$ and $\left[011\right]$ are not equivalent. At low pressures, the texture is almost absent resulting in almost uniform IPF (Figure 3A). At higher pressures, both at room and high temperature, the maximum intensity on the fitted IPFs does not exceed 1.5 multiples of the random distribution (mrd) indicating low texturing of the polycrystalline aggregate. Upon compression, the intensity on IPFs grows along [111] direction at the expense of [001]. Textures are slightly stronger at 1100 K than at room temperature even at relatively low pressures (Figure 3B).

FIGURE 3

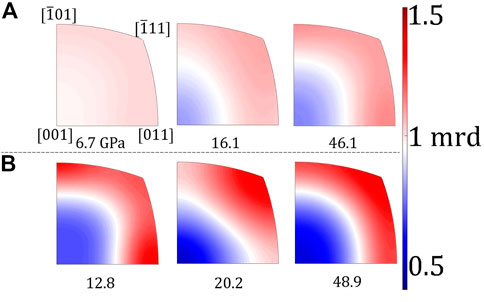
FIGURE 3. Inverse pole figures of the compression direction showing deformation textures in ε-FeSi at 300 K (A) and 1100 K (B) and indicated pressures, in GPa. Texture is expressed in mrd—multiples of a random distribution.

4 Discussion

At all studied pressures we detected only ε-FeSi without evidence for the transition towards the high-pressure FeSi phase (B2-structure, space group $Pm\overline{3}m$). Previous studies (Lord et al., 2010; Fischer et al., 2013; Geballe and Jeanloz, 2014; Edmund et al., 2022) that employed laser-heating in DACs reported on the transformation in the 14–42 GPa pressure range. There is a huge discrepancy in the exact pressure of the B20 to B2 phase transition, which is characterized by a wide two-phase coexistence region, which could be explained by the temperature gradient, common for the laser-heating DAC experiments, and further inhibited by a high kinetic barrier of the transition as shown by recent first-principle studies (Niu et al., 2020). Thus, our study indicates that a temperature as high as 1100 K is not sufficient to overcome the kinetic barrier to form a B2 phase even at 49 GPa.

Analysis of texture evolution of B20 ε-FeSi shows strong intensities on [$11\overline{1}$], and to a lesser degree on [$\overline{1}01$] and [011]. In most face centered cubic metals (such Cu, Al, or Ni alloys or austenitic stainless steel), compression textures develop along [110] as a result of {111}[110] slip (Calnan, 1954; Kestens and Pirgazi, 2016; El-Tahawy et al., 2020). In cubic materials with the B1-structure, e.g., in MgO and low-pressure phase of NaCl, compression textures develop along [100] direction as a result of {110}[$1\overline{1}0$] slip (Kern and Braun, 1973; Mi et al., 2018). Materials with the B2 structure tend to develop either [110] texture due to {112}[$1\overline{1}0$] slip as in the high-pressure phase of NaCl (Mi et al., 2018) or a maximum along [111] with the most active slip system {011} $\left[100\right]$ as in the intermetallic NiAl (Khadkikar et al., 1990; Margevicius and Cotton, 1995). Thus, textures developed in B20 ε-FeSi somewhat resemble the textures of the B2-structured crystals. Note, however, that none of the regular slip systems reported for cubic metals or ionic crystals can result in textures with a minimum at [001] and maxima at both [011], [111], and [101]. Also note that, in the body-centered cubic Fe-Si alloys, texture develops along [111] direction in compression (Brennan et al., 2021) this behavior is similar to the dominant texture in the B20 ε-FeSi phase. However, the Fe-Si alloy does not show the secondary maximum along [110] we observe here. Overall, we have not been able to unambiguously attribute our measured textures to a single dominant slip system. The deformation mechanisms in intermetallic compounds such as ε-FeSi are less studied and understood than those of pure metals hence this point will require additional work in the future.

Our results demonstrate that temperature does not significantly influence the average lattice strain parameter in ε-FeSi, at least within the experimental precision. Brennan et al. (2021) reported a decrease of the $\langle Q\left(hkl\right)\rangle$ with estimated $\frac{d\langle Q\rangle }{dT}$ = -1.6∙10^–6 K⁻¹ in iron with 5 wt% silicon in the 43–46 GPa pressure range. This disagreement with our observations may arise from the difference in plastic behavior of hcp Fe-Si alloy and cubic FeSi, but more likely from differences in the experimental strategy. Brennan et al. (2021) measured the sample stress while increasing temperature between 300 and 1800 K at 43–46 GPa but did not further deform their sample at high temperature. Their measurement is hence more related to stress relaxation induced by laser heating rather than an effect of temperature on plastic strength. Our result demonstrates that $\langle Q\left(hkl\right)\rangle$ is indeed lower at higher temperatures in the low pressure range, where $\langle Q\left(hkl\right)\rangle$ increases, but not in the higher pressure range where $\langle Q\left(hkl\right)\rangle$ values saturate (Figure 2).

We further employed the experimental $\langle Q\left(hkl\right)\rangle$ values to calculate the differential stress applied to the sample as described in Eq. 4. Assuming that the sample undergoes plastic flow, the differential stress deduced from Eq. 4 should equal the material yield strength, with the addition of plastic hardening. Unfortunately, increases in pressure and applied plastic strain are coupled in a diamond anvil cell experiment. Hence, it is not possible to separate the relative effects of pressure strengthening and strain hardening with our data. However, we should note, that at high temperatures most crystalline materials exhibit negligible hardening and can reasonably be considered perfectly plastic solids (Poirier, 1995). Our measurements can hence be seen as a steady state flow stress under the conditions of a diamond anvil cell experiment. A proper extrapolation to planetary cores would require scaling the measurements to planetary strain rates, which is not feasible experimentally for long strain rates and would be better addressed through numerical methods (e.g., Reali et al., 2019). Nevertheless, our data provide critical anchoring points for such calculation to be performed. The results of our calculations are shown in Figure 4 and Supplementary Table S1. We do not observe any significant difference of the yield strength based on temperature. Figure 4 shows a comparison of the strength of ε-FeSi, Fe-Si alloys (Brennan et al., 2021) with the compositions Fe-5 wt% Si (Fe-5Si) and Fe-9 wt% Si (Fe-9Si), and pure iron (Gleason and Mao, 2013) at 300 K. The ε-FeSi investigated here displays a yield strength about 3 times higher than hcp-Fe and about 2 times higher than that of Fe-9Si and Fe-5Si alloy at 30 GPa. In other words, our result suggests that ε-FeSi is a harder material to deform compared to pure iron and iron-silicon alloys.

FIGURE 4

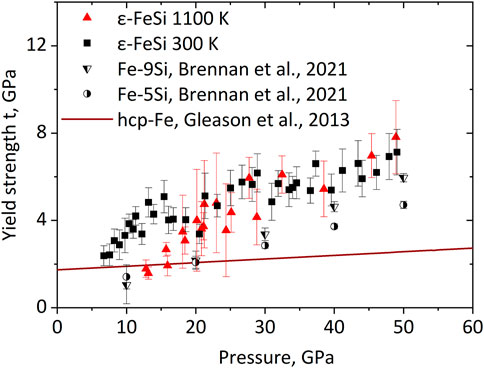
FIGURE 4. Pressure evolution of the yield strength of ε-FeSi at 300 K and 1100 K along with data for hcp-Fe-5Si, hcp-Fe-9Si alloy (Brennan et al., 2021), and hcp-Fe (Gleason and Mao, 2013) for comparison.

Experimental textures combined with elasticity data (Qi et al., 2019) allow calculating the anisotropy of sound velocities in a textured polycrystalline aggregate. The azimuthal anisotropy refers to the relative difference in the velocity of the wave propagation between different propagation directions:

$Anisotropy=\frac{2\left(V_{\mathit{max}}-V_{\mathit{min}}\right)}{\left(V_{\mathit{max}}+V_{\mathit{min}}\right)}\bullet 100\%(8)$

Shear wave splitting could be described by Eq. 9:

$Shearwavesplitting=\mathit{Max}\left(V_{S1}-V_{S2}\right)(9)$

where V_S1 and V_S2 are two perpendicular components of shear waves and their splitting is maximum difference between them. Shear wave contrast is also a measure of difference between the two shear waves given by:

$Shearwavecontrast=\frac{2\left(V_{S1}-V_{S2}\right)}{\left(V_{S1}+V_{S2}\right)}\bullet 100\%(10)$

For a single-crystal, anisotropy of sound velocity depends only on the C_ij elastic constants (Supplementary Table S3). The calculated values for the anisotropy of the longitudinal waves (V_P) in ε-FeSi single-crystal are presented in Figure 5 and for the two transverse waves (V_S1 and V_S2) in Supplementary Figure S2. Numerical data on sound-wave anisotropy is shown in Supplementary Tables S6, S7 for 300 and 1100 K, respectively. At low pressure, the single-crystal anisotropy is higher at high temperatures. However, the single-crystal V_P anisotropy decreases from 4.3% to 0.6% at 300 K and from 4.4% to 0.7% at 1100 K, reaching similar values above 30 GPa.

FIGURE 5

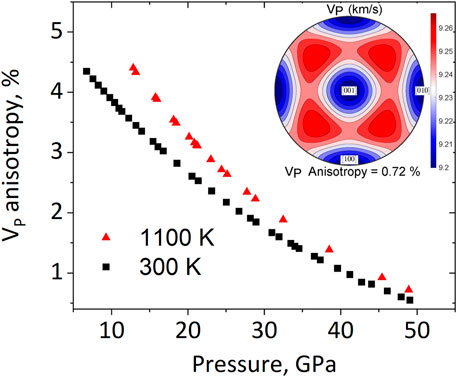
FIGURE 5. Anisotropy of the longitudinal waves (V_P) in ε-FeSi single crystal at 300 K (black squares) and 1100 K (red triangles) (recalculated based on elastic constants from Qi et al. (2019). Insert: pole figure of V_P anisotropy in ε-FeSi single crystal at 48.9 GPa and 1100 K.

Further, we have utilized experimental deformation textures to model sound velocities for a polycrystalline aggregate of ε-FeSi deformed in compression (Figure 6, Supplementary Figure S3 and Supplementary Tables S8, S9). Due to relatively weak textures, the azimuthal anisotropy for longitudinal waves in a polycrystalline aggregate does not exceed 0.2% above 30 GPa (Figure 6) with anisotropy at the high temperature slightly higher than that at 300 K. Compressional waves are fast along the compression direction and reach a minimum at approximately 45° of the compression direction. The measurement of azimuthal anisotropy of shear waves is currently beyond the capabilities of seismological methods for core studies. Shear wave splitting between two shear waves with different polarization (V_S1 and V_S2) is presently not measured for the Earth’s inner core but could potentially be addressed in future studies. Our predictions for the shear wave splitting are presented in Figure 7, Supplementary Tables S6, S7, and demonstrate vanishingly low values (less than 0.05 km/s in all cases and all propagation directions). Thus, the shear wave contrast is below 0.1% for all studied pressure-temperature conditions. This value is well below those of anisotropic regions of the Earth’s mantle with typical shear wave splitting of up to several percent in the D″ layer, for instance (Mainprice, 2015).

FIGURE 6

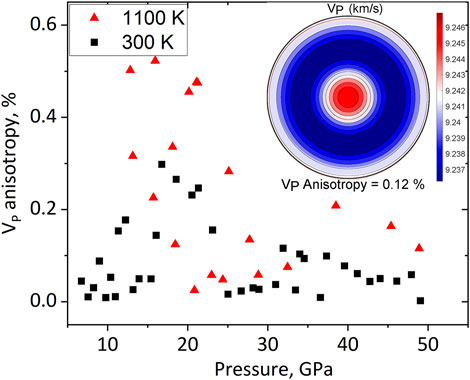
FIGURE 6. Azimuthal anisotropy of the longitudinal waves (V_P) in polycrystalline ε-FeSi at 300 K (black squares) and 1100 K (red triangles) based on single-crystal elastic moduli and the measured experimental textures. Insert: pole figure of V_P velocities in a polycrystalline ε-FeSi assembly along the compression direction at 48.9 GPa and 1100 K.

FIGURE 7

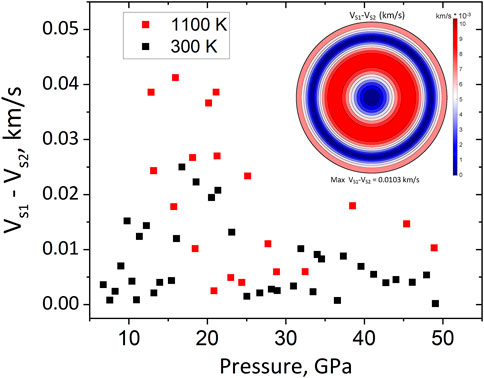
FIGURE 7. Maximum shear wave splitting (V_S1-V_S2) in polycrystalline ε-FeSi at 300 K (black squares) and 1100 K (red squares) based on single-crystal elastic moduli and the measured experimental textures. Insert: pole figure of V_S1-V_S2 shear wave splitting in a polycrystalline ε-FeSi assembly along the compression direction at 48.9 GPa and 1100 K.

Obtained results contribute to a global understanding of the effect of elements other than Fe on the mechanical properties of planetary core Fe alloys. Our observations of weak anisotropy of sound waves in ε-FeSi at high-pressure high-temperature conditions may play an important role in understanding the composition of inner cores of small terrestrial planets. Among such bodies is primarily Mercury, where ε-FeSi can crystalize, due to the compatibility with a sufficient amount of silicon in the composition of its core and suitable pressure-temperature conditions for the stability of the ε-FeSi phase. Solidification of the planetary cores can happen in two ways: either from the center of the planet or at some depth within the liquid outer core (Breuer et al., 2015; Edmund et al., 2022). The depth of solidification depends on the change of the liquidus temperature with pressure in the core-forming mixture and on the nature of the core-forming mixture itself. For the cores with high silicon content, and, hence with ε-FeSi as the liquidus phase, solidification of the FeSi layer on the mantle side may take place (Edmund et al., 2022).

The lowest pressure when B2-FeSi appears is 14 GPa and the full transformation to B2-FeSi occurs within the limit of 42 GPa, according to Fischer et al. (2013) and Geballe and Jeanloz (2014). The estimated pressure at the outer border of the Mercury core does not exceed 6 GPa, below which there is a liquid core (Hauck et al., 2013; Trønnes et al., 2019). With a crystallization on the outer portion of the core, we do not expect any B2 FeSi phase but rather the ε-phase to crystallize in Mercury’s core. Core pressures in the Moon and other planetary satellites are below 10 GPa. Hence, FeSi would also solidify there as ε-FeSi. Venus core-mantle boundary pressure is above 100 GPa (Trønnes et al., 2019), while the Mars core-mantle boundary pressure is about 18–19 GPa at temperatures of 1900–2000 K (Stähler et al., 2021). Thus, FeSi could exist in the B2 form in the cores of Mars or Venus. However, current estimations of the amounts of silicon in the Venusian and Martian cores suggest that there are too low concentrations for stoichiometric FeSi crystallization (Trønnes et al., 2019).

Alloys of hcp-Fe-Ni-Si demonstrate stronger texture (Brennan et al., 2021) compared to ε-FeSi (Figure 3). In addition, inelastic X-Ray scattering measurements by Antonangeli et al., 2004 revealed that V_P anisotropy in polycrystalline hcp-Fe increases from about 1% at 22 GPa to above 4% at 112 GPa. Thus, hcp-Fe and Fe-Si alloys show at least one order of magnitude higher anisotropy compared to that of ε-FeSi. Our data suggest that, contrary to iron and its alloys, intermetallic FeSi should form an isotropic solid layer on the outer side of the planetary core. Consequently, measurement of the anisotropy of the seismic wave propagation by planetary missions could confirm or rule out iron silicide as a dominant component in planetary cores.

5 Conclusions

We have conducted radial X-ray diffraction experiments on stoichiometric FeSi at 300 K and 1100 K. FeSi remained in the B20-phase (ε-FeSi) up to 49 GPa.

Lattice strains in ε-FeSi do not show significant temperature dependence at least up to 1100 K. At both studied temperatures, 300 K and 1100 K, the lattice strains initially increase fast upon pressurization until about 20 GPa and then stagnate. As a result, the yield strength in ε-FeSi demonstrates only a weak increase above 20 GPa, which originates from the increase of the shear modulus. We have not detected the temperature effect on the yield strength of ε-FeSi within experimental precision.

The yield strength of ε-FeSi is higher compared to iron-silicon alloys and pure iron i.e., ε-FeSi is a harder material to deform. Consequently, the polycrystalline aggregate of ε-FeSi shows weak textures at extreme pressure-temperature conditions, resulting in the weak anisotropy of sound velocities. The anisotropy we estimate for ε-FeSi deformed in axial compression does not exceed 1.2% and decreases below 0.5% upon compression.

The plastic properties of ε-FeSi can be used to constrain the amount of silicon in planetary cores. Our research demonstrates that ε-FeSi should form elastically isotropic structures in the interior of small terrestrial planets. Therefore, any anisotropy detected in planetary cores will be incompatible with crystallized ε-FeSi and could rule out silicon as the dominant element in the core composition.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://zenodo.org/record/6672195#.YrC9NWBBzct.

Author contributions

IK, SM, and CS-V designed and organized the project. IK, MA, CP, H-PL, SM, and CS-V conducted the high-pressure high-temperature radial X-ray diffraction experiments. EK analyzed the data. EK and IK interpreted the results and wrote the manuscript with contributions from all authors.

Funding

This research was partially supported by the German Research Foundation (DFG) through the DFG Project AOBJ:662965 GZ.:KU 3832/2-1 and start-up funds of WWU Münster. This study received support from the bilateral PROCOPE-PPP program (PHC 40555PC; DAAD 57390184). The research leading to this result was also supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020.

Acknowledgments

The authors acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of beamtime allocated for proposals I-20170400 and I-20170881.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.974148/full#supplementary-material

References

Anderson, D. L., and Dziewonski, A. M. (1982). Upper mantle anisotropy: evidence from free oscillations. Geophys. J. Int. 69, 383–404. doi:10.1111/j.1365-246X.1982.tb04956.x

CrossRef Full Text | Google Scholar

Antonangeli, D., Occelli, F., Requardt, H., Badro, J., Fiquet, G., and Krisch, M. (2004). Elastic anisotropy in textured hcp-iron to 112 GPa from sound wave propagation measurements. Earth Planet. Sci. Lett. 225, 243–251. doi:10.1016/j.epsl.2004.06.004

CrossRef Full Text | Google Scholar

Bachmann, F., Hielscher, R., and Schaeben, H. (2010). Texture analysis with MTEX – free and open source software toolbox. Solid State Phenom. 160, 63–68. doi:10.4028/www.scientific.net/ssp.160.63

CrossRef Full Text | Google Scholar

Brennan, M. C., Fischer, R. A., Couper, S., Miyagi, L., Antonangeli, D., and Morard, G. (2021). High-pressure deformation of iron – nickel – silicon alloys and implications for earth ’ s inner core journal of geophysical research: Solid earth. J. Geophys. Res. Solid Earth 126, 1–14. doi:10.1029/2020JB021077

CrossRef Full Text | Google Scholar

Breuer, D., Rueckriemen, T., and Spohn, T. (2015). Iron snow, crystal floats, and inner-core growth: modes of core solidification and implications for dynamos in terrestrial planets and moons. Prog. Earth Planet. Sci. 2, 39. doi:10.1186/s40645-015-0069-y

CrossRef Full Text | Google Scholar

Calnan, E. (1954). Deformation textures of face-centred cubic metals. Acta Metall. 2, 865–874. doi:10.1016/0001-6160(54)90041-3

CrossRef Full Text | Google Scholar

Chabot, N. L., Wollack, E. A., Klima, R. L., and Minitti, M. E. (2014). Experimental constraints on Mercury’s core composition. Earth Planet. Sci. Lett. 390, 199–208. doi:10.1016/j.epsl.2014.01.004

CrossRef Full Text | Google Scholar

Cook, A. H. (1977). The moment of inertia of Mars and the existence of a core. Geophys. J. Int. 51, 349–356. doi:10.1111/j.1365-246X.1977.tb06922.x

CrossRef Full Text | Google Scholar

Creager, K. C. (1992). Anisotropy of the inner core from differential travel times of the phases PKP and PKIKP. Nature 356, 309–314. doi:10.1038/356309a0

CrossRef Full Text | Google Scholar

Creager, K. C. (1999). Large-scale variations in inner core anisotropy. J. Geophys. Res. 104, 23127–23139. doi:10.1029/1999JB900162

CrossRef Full Text | Google Scholar

Deuss, A. (2014). Heterogeneity and anisotropy of Earth’s inner core. Annu. Rev. Earth Planet. Sci. 42, 103–126. doi:10.1146/annurev-earth-060313-054658

CrossRef Full Text | Google Scholar

Dumoulin, C., Tobie, G., Verhoeven, O., Rosenblatt, P., and Rambaux, N. (2017). Tidal constraints on the interior of Venus. J. Geophys. Res. Planets 122, 1338–1352. doi:10.1002/2016JE005249

CrossRef Full Text | Google Scholar

Edmund, E., Morard, G., Baron, M. A., Rivoldini, A., Yokoo, S., Boccato, S., et al. (2022). The Fe-FeSi phase diagram at Mercury’s core conditions. Nat. Commun. 13, 387. doi:10.1038/s41467-022-27991-9

PubMed Abstract | CrossRef Full Text | Google Scholar

El-Tahawy, M., Jenei, P., Kolonits, T., Han, G., Park, H., Choe, H., et al. (2020). Different evolutions of the microstructure, texture, and mechanical performance during tension and compression of 316L stainless steel. Metall. Mater. Trans. A 51, 3447–3460. doi:10.1007/s11661-020-05782-5

CrossRef Full Text | Google Scholar

Fei, Y., Ricolleau, A., Frank, M., Mibe, K., Shen, G., and Prakapenka, V. (2007). Toward an internally consistent pressure scale. Proc. Natl. Acad. Sci. U. S. A. 104, 9182–9186. doi:10.1073/pnas.0609013104

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischer, R. A., Campbell, A. J., Reaman, D. M., Miller, N. A., Heinz, D. L., Dera, P., et al. (2013). Phase relations in the Fe – FeSi system at high pressures and temperatures. Earth Planet. Sci. Lett. 373, 54–64. doi:10.1016/j.epsl.2013.04.035

CrossRef Full Text | Google Scholar

Fischer, R. A., Campbell, A. J., Caracas, R., Reaman, D. M., Heinz, D. L., Dera, P., et al. (2014). Equations of state in the Fe‐FeSi system at high pressures and temperatures. J. Geophys. Res. Solid Earth 119, 2810–2827. doi:10.1002/2013JB010898

CrossRef Full Text | Google Scholar

Frost, D. A., Lasbleis, M., Chandler, B., and Romanowicz, B. (2021). Dynamic history of the inner core constrained by seismic anisotropy. Nat. Geosci. 14, 531–535. doi:10.1038/s41561-021-00761-w

CrossRef Full Text | Google Scholar

Garcia, R., and Souriau, A. (2000). Inner core anisotropy and heterogeneity level. Geophys. Res. Lett. 27, 3121–3124. doi:10.1029/2000GL008520

CrossRef Full Text | Google Scholar

Geballe, Z. M., and Jeanloz, R. (2014). Solid phases of FeSi to 47 GPa and 2800 K: New data. Am. Mineral. 99, 720–723. doi:10.2138/am.2014.4612

CrossRef Full Text | Google Scholar

Genova, A., Goossens, S., Mazarico, E., Lemoine, F. G., Neumann, G. A., Kuang, W., et al. (2019). Geodetic evidence that Mercury has A solid inner core. Geophys. Res. Lett. 46, 3625–3633. doi:10.1029/2018GL081135

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleason, A. E., and Mao, W. L. (2013). Strength of iron at core pressures and evidence for a weak Earth’s inner core. Nat. Geosci. 6, 571–574. doi:10.1038/ngeo1808

CrossRef Full Text | Google Scholar

Hauck, S. A., Margot, J.-L., Solomon, S. C., Phillips, R. J., Johnson, C. L., Lemoine, F. G., et al. (2013). The curious case of Mercury’s internal structure. J. Geophys. Res. Planets 118 (6), 1204–1220. doi:10.1002/jgre.20091

CrossRef Full Text | Google Scholar

Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 6, 349–354. doi:10.1088/0370-1298/65/5/307

CrossRef Full Text | Google Scholar

Immoor, J., Marquardt, H., Miyagi, L., Speziale, S., Merkel, S., Schwark, I., et al. (2020). An improved setup for radial diffraction experiments at high pressures and high temperatures in a resistive graphite-heated diamond anvil cell. Rev. Sci. Instrum. 91, 045121. doi:10.1063/1.5143293

PubMed Abstract | CrossRef Full Text | Google Scholar

Irving, J. C. E., and Deuss, A. (2011). Hemispherical structure in inner core velocity anisotropy. J. Geophys. Res. 116, B04307. doi:10.1029/2010JB007942

CrossRef Full Text | Google Scholar

Ishii, M., and Dziewonski, A. M. (2002). The innermost inner core of the Earth: Evidence for a change in anisotropic behavior at the radius of about 300 km. Proc. Natl. Acad. Sci. U. S. A. 99, 14026–14030. doi:10.1073/pnas.172508499

PubMed Abstract | CrossRef Full Text | Google Scholar

Karato, S. (1999). Seismic anisotropy of the Earth’s inner core resulting from flow induced by Maxwell stresses. Nature 402, 871–873. doi:10.1038/47235

CrossRef Full Text | Google Scholar

Kern, H., and Braun, G. (1973). Deformation und Gefügeregelung von Steinsalz im Temperaturbereich 20-200 °C. Contr. Mineral. Pet. 40, 169–181. doi:10.1007/BF00378174

CrossRef Full Text | Google Scholar

Kestens, L. A. I., and Pirgazi, H. (2016). Texture formation in metal alloys with cubic crystal structures. Mater. Sci. Technol. 32, 1303–1315. doi:10.1080/02670836.2016.1231746

CrossRef Full Text | Google Scholar

Khadkikar, P. S., Michal, G. M., and Vedula, K. (1990). Preferred orientations in extruded nickel and iron aluminides. Metall. Trans. A 21, 279–288. doi:10.1007/BF02782408

CrossRef Full Text | Google Scholar

Knibbe, J. S., and van Westrenen, W. (2018). The thermal evolution of Mercury’s Fe–Si core. Earth Planet. Sci. Lett. 482, 147–159. doi:10.1016/j.epsl.2017.11.006

CrossRef Full Text | Google Scholar

Lay, T., and Young, C. J. (1991). Analysis of seismic SV waves in the core’s penumbra. Geophys. Res. Lett. 18, 1373–1376. doi:10.1029/91GL01691

CrossRef Full Text | Google Scholar

Liermann, H.-P., Merkel, S., Miyagi, L., Wenk, H.-R., Shen, G., Cynn, H., et al. (2009). Experimental method for in situ determination of material textures at simultaneous high pressure and high temperature by means of radial diffraction in the diamond anvil cell. Rev. Sci. Instrum. 80, 104501. doi:10.1063/1.3236365

PubMed Abstract | CrossRef Full Text | Google Scholar

Liermann, H.-P., Konôpková, Z., Morgenroth, W., Glazyrin, K., Bednarčik, J., McBride, E. E., et al. (2015). The extreme conditions beamline P02.2 and the extreme conditions science infrastructure at PETRA III. J. Synchrotron Radiat. 22, 908–924. doi:10.1107/S1600577515005937

PubMed Abstract | CrossRef Full Text | Google Scholar

Lord, O. T., Walter, M. J., Dobson, D. P., Armstrong, L., Clark, S. M., and Kleppe, A. (2010). The FeSi phase diagram to 150 GPa. J. Geophys. Res. 115, B06208. doi:10.1029/2009JB006528

CrossRef Full Text | Google Scholar

Lutterotti, L. S., Matthies, S., and Wenk, H.-R. (1999). MAUD: a friendly java program for material analysis using diffraction. IUCr Newsl. CPD 21, 14–15.

Google Scholar

Lutterotti, L., Chateigner, D., Ferrari, S., and Ricote, J. (2004). Texture, residual stress and structural analysis of thin films using a combined X-ray analysis. Thin Solid Films 450, 34–41. doi:10.1016/j.tsf.2003.10.150

CrossRef Full Text | Google Scholar

Mainprice, D., Bachmann, F., Hielscher, R., and Schaeben, H. (2015). Descriptive tools for the analysis of texture projects with large datasets using MTEX : strength, symmetry and components. Geol. Soc. Lond. Spec. Publ. 409, 251–271. doi:10.1144/SP409.8

CrossRef Full Text | Google Scholar

Mainprice, D. (2015). “Seismic anisotropy of the deep earth from a mineral and rock Physics perspective,” in Treatise on geophysics (Elsevier), 487–538. doi:10.1016/B978-0-444-53802-4.00044-0

CrossRef Full Text | Google Scholar

Margevicius, R. W., and Cotton, J. D. (1995). Study of the brittle-to-ductile transition in NiAl by texture analysis. Acta Metall. Mater. 43, 645–655. doi:10.1016/0956-7151(94)00273-K

CrossRef Full Text | Google Scholar

Masters, G., and Gilbert, F. (1981). Structure of the inner core inferred from observations of its spheroidal shear modes. Geophys. Res. Lett. 8, 569–571. doi:10.1029/GL008i006p00569

CrossRef Full Text | Google Scholar

Matthies, S., and Vinel, G. W. (1982). On the reproduction of the orientation distribution function of texturized samples from reduced Pole figures using the conception of a conditional ghost correction. Phys. Stat. Sol. 111, 111–114. doi:10.1002/pssb.2221120254

CrossRef Full Text | Google Scholar

Merkel, S., and Yagi, T. (2005). X-ray transparent gasket for diamond anvil cell high pressure experiments. Rev. Sci. Instrum. 76, 046109. doi:10.1063/1.1884195

CrossRef Full Text | Google Scholar

Merkel, S. (2010). “Radial diffraction in the diamond anvil cell: Methods and applications,” in NATO science for peace and security series B: Physics and biophysics, 111–122. doi:10.1007/978-90-481-9258-8_10

CrossRef Full Text | Google Scholar

Mi, Z., Shieh, S. R., Kavner, A., Kiefer, B., Wenk, H.-R., and Duffy, T. S. (2018). Strength and texture of sodium chloride to 56 GPa. J. Appl. Phys. 123, 135901. doi:10.1063/1.5022273

CrossRef Full Text | Google Scholar

Morelli, A., Dziewonski, A. M., and Woodhouse, J. H. (1986). Anisotropy of the inner core inferred from PKIKP travel times. Geophys. Res. Lett. 13, 1545–1548. doi:10.1029/GL013i013p01545

CrossRef Full Text | Google Scholar

Niu, Z. W., Tang, M., and Cai, L. C. (2020). Mechanism for structure conversion of FeSi under pressures. Phys. Lett. A 384, 126598. doi:10.1016/j.physleta.2020.126598

CrossRef Full Text | Google Scholar

O’Neill, C. (2021). End‐member venusian core scenarios: Does Venus have an inner core? Geophys. Res. Lett. 48, 1–7. doi:10.1029/2021GL095499

CrossRef Full Text | Google Scholar

Poirier, J. P. (1995). “Plastic rheology of crystals,” in Mineral physics and crystallosraphy. Washington: American Geophysical Union.

Google Scholar

Poupinet, G., Pillet, R., and Souriau, A. (1983). Possible heterogeneity of the Earth’s core deduced from PKIKP travel times. Nature 305, 204–206. doi:10.1038/305204a0

CrossRef Full Text | Google Scholar

Prescher, C., and Prakapenka, V. B. (2015). DIOPTAS : a program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res. 35, 223–230. doi:10.1080/08957959.2015.1059835

CrossRef Full Text | Google Scholar

Qi, S., Zhang, X., Niu, Z., Liu, C., and Cai, L. (2019). First-principles investigations on elasticity properties of FeSi under high pressure and temperature. Phys. B Condens. Matter 557, 82–87. doi:10.1016/j.physb.2019.01.009

CrossRef Full Text | Google Scholar

Reali, R., Jackson, J. M., Van Orman, J., Bower, D. J., Carrez, P., and Cordier, P. (2019). Modeling viscosity of (Mg, Fe)O at lowermost mantle conditions. Phys. Earth Planet. Inter. 287, 65–75. doi:10.1016/j.pepi.2018.12.005

CrossRef Full Text | Google Scholar

Singh, A. K., and Balasingh, C. (1994). The lattice strains in a specimen (hexagonal system) compressed nonhydrostatically in an opposed anvil high pressure setup. J. Appl. Phys. 75, 4956–4962. doi:10.1063/1.355786

CrossRef Full Text | Google Scholar

Singh, A. K., Balasingh, C., Mao, H., Hemley, R. J., and Shu, J. (1998). Analysis of lattice strains measured under nonhydrostatic pressure. J. Appl. Phys. 83, 7567–7575. doi:10.1063/1.367872

CrossRef Full Text | Google Scholar

Singh, S. C., Taylor, M. A. J., and Montagner, J. P. (2000). On the presence of liquid in Earth’s inner core. Science 287, 2471–2474. doi:10.1126/science.287.5462.2471

PubMed Abstract | CrossRef Full Text | Google Scholar

Soderlund, K. M., Kalousová, K., Buffo, J. J., Glein, C. R., Goodman, J. C., Mitri, G., et al. (2020). Ice-ocean exchange processes in the jovian and saturnian satellites. Space Sci. Rev. 216, 80–57. doi:10.1007/s11214-020-00706-6

CrossRef Full Text | Google Scholar

Sohl, F., Spohn, T., Breuer, D., and Nagel, K. (2002). Implications from Galileo observations on the interior structure and chemistry of the Galilean satellites. Icarus 157, 104–119. doi:10.1006/icar.2002.6828

CrossRef Full Text | Google Scholar

Song, X., and Helmberger, D. V. (1993). Anisotropy of Earth’s inner core. Geophys. Res. Lett. 20, 2591–2594. doi:10.1029/93GL02812

CrossRef Full Text | Google Scholar

Song, X. (1997). Anisotropy of the Earth’s inner core. Rev. Geophys. 35, 297–313. doi:10.1029/97RG01285

CrossRef Full Text | Google Scholar

Stähler, S. C., Khan, A., Banerdt, W. B., Lognonné, P., Giardini, D., Ceylan, S., et al. (2021). Seismic detection of the martian core. Science 373 (6553), 443–448. doi:10.1126/science.abi7730

PubMed Abstract | CrossRef Full Text | Google Scholar

Takehiro, S.-I. (2011). Fluid motions induced by horizontally heterogeneous Joule heating in the Earth’s inner core. Phys. Earth Planet. Inter. 184, 134–142. doi:10.1016/j.pepi.2010.11.002

CrossRef Full Text | Google Scholar

Tateno, S., Hirose, K., Ohishi, Y., and Tatsumi, Y. (2010). The structure of iron in Earth’s inner core. Science 330, 359–361. doi:10.1126/science.1194662

PubMed Abstract | CrossRef Full Text | Google Scholar

Tkalčić, H. (2015). Complex inner core of the Earth: The last frontier of global seismology. Rev. Geophys. 53, 59–94. doi:10.1002/2014RG000469

CrossRef Full Text | Google Scholar

Toksöz, M. N., Dainty, A. M., Solomon, S. C., and Anderson, K. R. (1974). Structure of the moon. Rev. Geophys. 12, 539. doi:10.1029/RG012i004p00539

CrossRef Full Text | Google Scholar

Tromp, J. (1993). Support for anisotropy of the Earth’s inner core from free oscillations. Nature 366, 678–681. doi:10.1038/366678a0

CrossRef Full Text | Google Scholar

Trønnes, R. G., Baron, M. A., Eigenmann, K. R., Guren, M. G., Heyn, B. H., Løken, A., et al. (2019). Core formation, mantle differentiation and core-mantle interaction within Earth and the terrestrial planets. Tectonophysics 760, 165–198. doi:10.1016/j.tecto.2018.10.021

CrossRef Full Text | Google Scholar

Vinnik, L. P., Farra, V., and Romanowicz, B. (1989). Observational evidence for diffracted SV in the shadow of the Earth’s core. Geophys. Res. Lett. 16, 519–522. doi:10.1029/GL016i006p00519

CrossRef Full Text | Google Scholar

Wenk, H.-R., Baumgardner, J. R., Lebensohn, R. A., and Tomé, C. N. (2000). A convection model to explain anisotropy of the inner core. J. Geophys. Res. 105, 5663–5677. doi:10.1029/1999JB900346

CrossRef Full Text | Google Scholar

Woodhouse, J. H., Giardini, D., and Li, X. (1986). Evidence for inner core anisotropy from free oscillations. Geophys. Res. Lett. 13, 1549–1552. doi:10.1029/GL013i013p01549

CrossRef Full Text | Google Scholar

Yoshida, S., Sumita, I., and Kumazawa, M. (1996). Growth model of the inner core coupled with the outer core dynamics and the resulting elastic anisotropy. J. Geophys. Res. 101, 28085–28103. doi:10.1029/96JB02700

CrossRef Full Text | Google Scholar