An improved method of GB-SAR phase unwrapping for landslide monitoring

The ground-based Synthetic Aperture Radar (GB-SAR) technique can be applied to the safety monitoring and early warning of geo-hazards, especially for monitoring displacement of various types of landslide masses. One of the key techniques of processing GB-SAR monitoring data is phase unwrapping, which can be dramatically affected by atmospheric humidity, atmospheric pressure, sampling interval, etc. In high mountains and valleys where environmental change is drastic, GB-SAR monitoring data is vulnerable to incoherence both spatially and temporally. Therefore, an improved phase unwrapping method of GB-SAR data for landslide monitoring is proposed in this paper, which can realize three-dimensional phase unwrapping in time and space. The method adopts the idea of sparse data processing and realizes phase unwrapping of monitoring data in two steps. Firstly, taking full advantage of the high temporal resolution of GB-SAR monitoring data, the one-dimensional phase unwrapping method in the spatial domain is applied to the time domain, and the interference phases of PS points are unwrapped in the time domain. Then, the PS network is constructed based on the time-phase unwrapping results, the double-difference phases of the network baselines are obtained and the spatial consistency adjustment is applied to them, and the spatial phase unwrapping can be realized by the indirect least square adjustment method. This method successfully solves the problem of path dependence, island isolation and large computation of the common method of space-borne SAR phase unwrapping, which can process GB-SAR data with high accuracy and efficiency.

Introduction

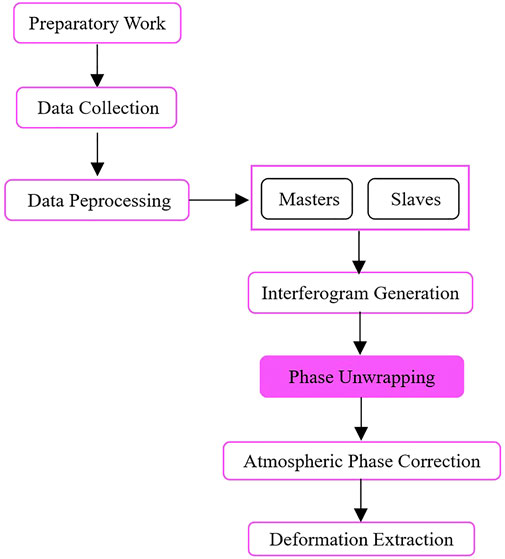
GB-SAR is a new microwave remote sensing monitoring technology that has emerged in the last decade. It has the characteristics of high spatial and temporal resolution, high precision, free orbit, and all-area remote automatic monitoring, etc. It has become an effective supplementary approach for space-borne and airborne SAR in deformation monitoring of natural slopes in mountainous areas (Chen et al., 2006; Li et al., 2021a; Li et al., 2021b; Li et al., 2022). In addition to slope deformation monitoring, GB-SAR is also commonly used in landslide, mass deformation and ground subsidence monitoring caused by various geological disasters. Such as monitoring of ground subsidence and landslides caused by earthquake (Bozzano et al., 2011; Hernández, 2012; Takahashi et al., 2013), volcano activity (Luzi et al., 2010). According to the different deformation rates of monitored objects, GB-SAR can also adopt different monitoring modes, such as discontinuous GB-SAR monitoring mode and continuous monitoring mode, to deal with the hazards more efficiently (Crosetto et al., 2014; Pieraccini et al., 2006., Monserrat et al., 2014). In the GB-SAR deformation monitoring (Cui et al., 2021; Zhou et al., 2021), the data processing and analysis inevitably involve the key technology of phase unwrapping (Figure 1).

FIGURE 1

FIGURE 1. GB-SAR data processing flowchart.

Since the interference phase is in the interval [-π, π], and the InSAR phase is wrapped in the coherence process, making its principal value “blurred”. Phase unwrapping refers to the process of restoring the phase principal value or interference phase difference to the true phase value, which is the most critical and difficult step when processing SAR data. Primarily, the most widely used unwrapping method is path-related, such as the branch cutting method, the mask secant method and the regional growth method (e.g., Goldstein et al., 1988; Flynn, 1996; Xu and Cumming, 1999; Fan, 2010). The objective of these path-related unwrapping methods is to find the residuals to determine the integral paths, which can reduce the occurrence of island isolation and achieve the shortest integral path so as to obtain high precision unwrapping results. However, search for the shortest path is time-consuming, making path-related unwrapping methods inefficient.

In 1994, the path-independent phase unwrapping method was firstly proposed by Pritt et al., they adopted unweighted least square method based on fast Fourier transform to realize the unwrapping process (Pritt and Shipman, 1994). Since then, path-independent phase unwrapping methods emerged in large numbers, including the minimum norm method, the minimum weighted discontinuity method, etc. (e.g., Ghiglia and Romero, 1996; Flynn, 1997). These algorithms smoothed the whole image through global fitting, which improved the whole image unwrapping accuracy but polluted each single point by errors, making the unwrapping results approximate and inaccurate. Costantini, Carballo and Pepe et al. advanced these path-independent method by using network programming and the minimum network flow method, which improved the accuracy of unwrapping results, but the calculation load is heavy (Costantini, 1997; Costantini, 1998; Carballo and Fieguth, 2000; Pepe and Lanari, 2006; Pepe, 2012).

In addition to the path-related and path-independent methods mentioned above, with the continuous research of scholars, many new methods have emerged, such as genetic algorithm (Collaro et al., 1998), knowledge intervention (Abutaleb, 2002), ant colony algorithm (Zhi-qiang and Jin, 2008), greedy algorithm (Peng et al., 2008), support vector machine (He et al., 2008), the least square ambiguity reduction correlation adjustment algorithm (Kampes and Hanssen, 2004), Kalman filtering technology (Loffeld et al., 2008), etc., this kind of algorithms are more complex, still need to further optimize (Cen, 2008).

Comparing with the spaceborne SAR, GB-SAR observation phases is more affected by the environment (He and Kusiak, 2017). Especially in high mountains and valleys, the atmospheric humidity is large, atmospheric pressure changes rapidly, and the spatial correlation of atmosphere is very strong, which has a severe impact on the signal. Therefore, it is necessary to develop a phase unwrapping method of GB-SAR particularly for landslide monitoring, which can improve the efficiency and accuracy of phase unwrapping by taking advantage of the high time resolution and environmental susceptibility of GB-SAR data, thus realizing three-dimensional phase unwrapping.

This paper proposes a method of phase unwrapping for GB-SAR landslide deformation monitoring data. Firstly, preprocessing of the monitoring data should be carried out. The Permanent Scatterer (PS) in the monitoring area is used to achieve the sparse data, the double-difference phases are obtained by sparse PS, and the phase unwrapping of the interference phases and double-difference phases are performed in the time domain and space domain, respectively. Then, the phase unwrapping of the monitoring data can be conducted by sparse data processing in two steps. The first step is to make full use of the high temporal resolution of GB-SAR landslide monitoring data, and to apply the one-dimensional phase unwrapping method in the spatial domain to the time domain to perform the time-phase unwrapping of interference phases. In the second step, the PS network is constructed for the time-phase unwrapping results, and the double-difference phases of each network baseline are obtained. The double-difference phases are treated with spatial consistency adjustment, and the method based on indirect least square adjustment is adopted to realize spatial phase unwrapping. This method solves the problems such as path dependence, island isolation and large computation of common spaceborne SAR phase unwrapping methods. Meanwhile, it also considers the characteristics of GB-SAR monitoring data to ensure the phase unwrapping effect.

The arrangement of this paper is to introduce the phase composition of GB-SAR landslide monitoring data and the characteristics of phase unwrapping at first. Then, the phase unwrapping algorithm and its model are studied and analyzed in detail. Finally, the proposed improved phase unwrapping method is applied to the monitoring data processing of the HS large-scale landslide in the Three Gorges Reservoir Area and the GY arch dam to verify its effectiveness and high accuracy.

Phase unwrapping and characteristics of GB-SAR monitoring

GB-SAR interferometric phase components

If the GB-SAR transmitting signal z is expressed as a complex form by amplitude a and phase $\varphi$, then

$z=a\cdot e^{i\varphi }=a\cdot \left(\cos \varphi -i\sin \varphi \right)(1)$

Thus, the interference signal can be expressed as:

$z_1{z}_2^{\ast }=a_1{a}_2\cdot e^{i({\varphi }_1-{\varphi }_2)}(2)$

Where $z^{\ast }$ stands for complex conjugate of $z$.

The amount of deformation in slope deformation monitoring can be measured by the change of relative distance between the measured object and the sensor. The relation between the amount of deformation and the interference phase ${\phi }_{disp}$ is as follows:

${\phi }_{disp}=\frac{4\pi }{\lambda }\cdot \mathrm{\Delta }r=\frac{4\pi }{\lambda }\cdot \mathbf{\Delta }{\mathbf{r}}_{xyz}\cdot \mathbf{s}(3)$

Where, s is the line-of-sight unit vector; $\mathbf{\Delta }{\mathbf{r}}_{xyz}$ is the three-dimensional displacement vector; $\lambda$ is GB-SAR signal wavelength, 17.4 mm.

According to Eq. 3, the deformation of landslide monitoring is calculated by interference phase. In the actual interference phase, besides the phase generated by displacement changes, there are some other phase components which together constitute the interference phase of each pixel in the interference image. If an interference image is generated by the interference of two images taken at different times but at the same sensor location, then the interference phase is related to the distance change (displacement) between the sensor and the landslide. The time difference between the two images is called the time baseline $B_t$. If an interference image is generated by the interference of two images collected at the same time but at different sensor locations, then the interference phase is related to the topography of the observed area. The distance between the sensors when the two images are acquired is called the spatial baseline $B_s$. For different baseline cases, the interference phase $\phi$ consists of the following components:

$\phi ={\phi }_{topo}+{\phi }_{disp}+{\phi }_{atm}+{\phi }_{noise}-2\pi n(4)$

Where, ${\phi }_{topo}$ is the space phase part caused by terrain difference; ${\phi }_{disp}$ and ${\phi }_{atm}$ are the phase parts related to the time baseline due to displacement and atmospheric influence; ${\phi }_{noise}$ is noise; n is the whole cycle fuzzy number of the phase.

The left side of Eq. 4 is the interference phase $\phi$, while the right side contains unknown parameters to be solved. In the application of GB-SAR in landslide deformation monitoring, the observation slide is generally fixed on a very stable monitoring platform to ensure that its spatial baseline is zero. The landslide is monitored at different times, so the time baseline is not zero. In Eq. 4, the component ${\phi }_{topo}$ related to the spatial baseline is zero, so ${\phi }_{disp}$ can be determined by the following formula:

${\phi }_{disp}=\phi -{\phi }_{atm}-{\phi }_{noise}+2\pi n(5)$

It can be seen from Eq. 5 that in order to obtain the displacement of the measured object, only the real interference phase $\phi$ can be solved, and ${\phi }_{atm}$ and ${\phi }_{noise}$ can be obtained respectively. The determination of the real interference phase is essentially phase unwrapping, that is, the fuzzy number N value of the whole cycle in Eqs 4, 5 is determined. Therefore, phase unwrapping has become a key problem in GB-SAR data processing. It is a mathematical problem with nonlinear and non-unique solution, and it is difficult to find the solution without other assumptions. If the sampling interval is $\mathrm{\Delta }t$, then the linear displacement rate $v$ of the target in the measured object is

$v<\frac{\lambda }{4\mathrm{\Delta }t}(6)$

Where, $v$ is the linear displacement rate; $\mathrm{\Delta }t$ is the sampling interval; $\lambda$ is the wavelength.

If Eq. 6 is true, then the observed phase is continuous in the time domain and the whole phase fuzzy number n can be avoided.

GB-SAR monitoring phase unwrapping characteristics

When GB-SAR is used for landslide deformation monitoring, the data sampling time interval is short, which can reach once every 5 min or even shorter. The phase change collected at such a sampling frequency is far less than one phase period of GB-SAR in the absence of sudden disasters. That is to say, for deformation monitoring of dams or landslides, at a normal sampling interval, the whole fuzzy number n of the interference phases at two adjacent moments in Eq. 5 is zero, which just meets the requirements of one-dimensional phase unwrapping Itoh method.

Itoh proposed the one-dimensional phase unwrapping method in 1982 (Itoh, 1982), This method is used to unwrap the one-dimensional phase under the assumption of “phase continuity”. It is mainly used in the phase unwrapping of continuous space. However, as for GB-SAR phase, it is a two-dimensional problem in space, which is not applicable to the assumptions of this method. In terms of time series, the sampling interval of images is short. When the observation process is uninterrupted, the images acquired at adjacent moments fully meet the condition of “phase continuity” (Yu et al., 2019). Therefore, Itoh method in spatial domain can be applied to the time domain unwrapping, so as to realize the time phase unwrapping. This is unique to the GB - SAR monitoring data, In space-borne and airborne SAR, the satellite or aircraft revisit cycle is long, often sampling interval in days or longer for a cycle, The time resolution of the phase observations is low, which cannot meet the condition of “phase continuity” in the time domain, and the use of Itoh for phase unwrapping will produce large errors, or even fail to obtain the correct results.

Based on this, the paper proposes to decompose GB-SAR phase unwrapping into two parts: time phase unwrapping and space phase unwrapping. The Itoh method was used for time phase unwrapping. Obtained the unwrapped interference phase of the PS. Then, each PS is constructed into a triangulation network to obtain the double difference phase on the edge of each triangle. According to the spatial consistency condition of the triangle, the double difference phases are unwrapped spatially. In order to eliminate the spatial consistency problem after the time phase is unwrapped, the spatial phase unwrapping problem can be transformed into an adjustment problem, and the spatial phase unwrapping can be realized by using the indirect least square adjustment.

Construction of phase unwrapping algorithm

According to the acquisition of GB-SAR interferometric images in slope deformation monitoring, the image can be unwrapped in one-dimensional phase in time, and then in two-dimensional phase in space. The three-dimensional unwrapping problem can be transformed into one-dimensional and two-dimensional problems, and the processing method can be simplified.

Time phase unwrapping

The basic principle of the one-dimensional phase unwrapping method proposed by Itoh is as follows: For m discrete wrapping phase sequences $[{\varphi }_1^w,{\varphi }_2^w,\cdots ,{\varphi }_m^w]$, the unwrapped interference phase ${\phi }_{1,k}={\varphi }_1-{\varphi }_k$ can be obtained by the sum of the interference after the single view plural image obtained at different times as follows:

$\begin{array}{l}{\phi }_{1,k}={\varphi }_1^w-{\varphi }_2^w-2\pi n_{12}+{\varphi }_2^w-{\varphi }_3^w-2\pi n_{23}+\cdots +{\varphi }_{k-1}^w-{\varphi }_k^w-2\pi n_{k-1,k}\\ ={\varphi }_1^w-{\varphi }_k^w-2\pi \left(n_{12}+n_{23}+\cdots +n_{k-1,k}\right),\left(k=\mathrm{1,2},\cdots ,m\right)\end{array}(7)$

It can be seen from the above formula that as long as the phase blur number $n_{k-1,k}$ between two mono-visual images in time continuity is guaranteed to be zero. The unwrapped phase ${\phi }_k$ of the interference can be calculated at any time. In fact, in radar signal acquisition, as long as the sampling rate of radar signal is high enough to detect phase cycle slip, it can be guaranteed $n_{k-1,k}$ to be zero, so as to obtain the correct unwinding result. In other words, as long as the sampling rate satisfies Nyquist criterion, the cycle slip can be detected and the interference phase between continuous images can be calculated as

${\phi }_{k-1,k}={\varphi }_{k-1}^w-{\varphi }_k^w-2\pi n_{k-1,k}={\varphi }_{k-1}^w-{\varphi }_k^w(8)$

Since the sampling rate of GB-SAR data satisfies Nyquist criterion, one-dimensional time phase unwrapping of the interference phase can be performed preliminarily.

Space phase unwrapping

After the time phase unwrapping, the interference phase of each PS point may be inconsistent in the spatial relationship. Therefore, it is necessary to further unwrap the result in space, and finally obtain the space-time consistent value of unwrapped phase. The method of spatial phase unwrapping belongs to two-dimensional phase unwrapping, and there are many methods, but each method has certain limitation in concrete operation. In order to get strict results of spatial phase unwrapping from theory, this paper adopts indirect least square adjustment to do spatial phase unwrapping.

The phase unwrapping of the indirect least square adjustment space has a strict mathematical description, high precision and reliable quality. The basic principle is to minimize the difference between the phase difference of wrapping at adjacent PS and the phase difference after unwrapping, and to solve the unwrapped phase at each PS by using the indirect least square adjustment. The following is the mathematical model derivation of GB-SAR data space phase unwrapping algorithm in slope deformation monitoring, and the theoretical analysis and evaluation of unwrapping accuracy.

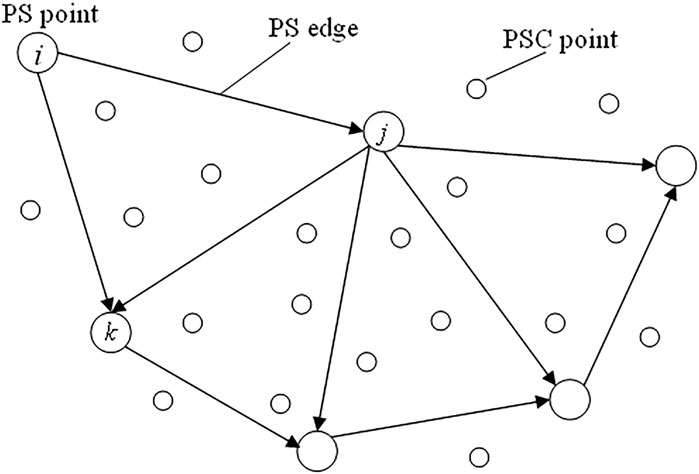
After obtaining the PS in the monitoring area according to the PS selection method (Xiang et al., 2019), the Delaunay triangle network construction principle can be adopted to establish PS triangle network. As shown in Figure 2, if there are N PS points in an image, M PS edges are formed according to the Delaunay triangle network construction principle, then M double-difference phases can be obtained (i.e. the interference phase difference between two PS on the PS edge). The corresponding error equation and normal equation can be established by using the basic principle of least square phase unwrapping, and its stochastic model is obtained (Group of Survey Adjustment, Institute of surveying and mapping, 2014).

FIGURE 2

FIGURE 2. Schematic diagram of PS triangulation network.

Let the interference phase of each PS obtained after the time phase unwrapping be ${\phi }_1^w,{\phi }_2^w,\cdots ,{\phi }_N^w$, and the time phase unwrapping value of each edge in the PS triangulation network be M double-difference phases ${\varphi }_{ij}^w(i,j=\mathrm{1,2},\cdots ,M)$, then

${\phi }_{ij}^w={\phi }_j^w-{\phi }_i^w(9)$

According to the observation conditions, the indirect least square adjustment is used to construct the error equation. The unwrapping interference phase at each PS is selected as the parameter, and the mathematical model of the phase unwrapping could be determined exclusively through the N independent parameters:

$v_{i,j}=({\phi }_j-{\phi }_i)-({\phi }_j^w-{\phi }_i^w)(10)$

Namely

$v_{i,j}=({\phi }_j-{\phi }_i)-{\phi }_{ij}^w(11)$

For M PS edges, M error equations in the form of Eq. 11 can be obtained, and the error equations are denoted in matrix form:

$\underset{M\times 1}{\mathbf{V}}=\underset{M\times N}{\mathbf{A}}\underset{N\times 1}{\text{Φ}}-\underset{M\times 1}{\mathbf{L}}(12)$

Eq. 12 is the mathematical model of space phase unwrapping in the least square adjustment of the indirect method. Where $\mathbf{V}$ is the error matrix of row 1 column M; A is the coefficient matrix of M rows and N columns, which is determined by the composition of triangulation network. $\text{Φ}$ is a parametric matrix with N rows and 1 column, corresponding to the unwrapped phases of N PS points; $\mathbf{L}$ is the double-difference phase observation value of row M and column 1, corresponding to the observation results of PS edge of M.

The phase unwrapping of each PS was calculated in x direction and y direction respectively, and then A in Eq. 12 is changed into the coefficient matrix of $\left[2N(N-1)(N\times N)\right]$:

$\mathbf{A}={\left[\begin{array}{cccccccccccc}-1& 0& 0& \cdots & 0& 1& 0& 0& \cdots & 0& 0& 0\\ 0& -1& 0& \cdots & 0& 0& 1& 0& \cdots & 0& 0& 0\\ & & & ⋮& & & & & ⋮& & & \\ 0& 0& 0& \cdots & 0& -1& 0& 0& \cdots & 0& 1& 0\\ 0& 0& 0& \cdots & 0& 0& -1& 0& \cdots & 0& 0& 1\\ -1& 1& 0& \cdots & 0& 0& 0& 0& \cdots & 0& 0& 0\\ 0& -1& 1& \cdots & 0& 0& 0& 0& \cdots & 0& 0& 0\\ & & & ⋮& & & & & ⋮& & & \\ 0& 0& 0& \cdots & 0& 0& 0& 0& \cdots & -1& 1& 0\\ 0& 0& 0& \cdots & 0& 0& 0& 0& \cdots & 0& -1& 1\end{array}\right]}_{2N(N-1),NN}(13)$

Set:

$\mathrm{\Phi }={\left[\begin{array}{c}{\phi }_{\mathrm{0,0}}\\ {\phi }_{\mathrm{0,1}}\\ ⋮\\ {\phi }_{0,N-1}\\ {\phi }_{\mathrm{1,0}}\\ ⋮\\ {\phi }_{N-1,N-2}\\ {\phi }_{N-1,N-1}\end{array}\right]}_{NN}L={\left[\begin{array}{c}{\mathrm{\Delta }}_{\mathrm{0,0}}^x\\ {\mathrm{\Delta }}_{\mathrm{0,1}}^x\\ ⋮\\ \begin{array}{l}{\mathrm{\Delta }}_{0,N-1}^x\\ {\mathrm{\Delta }}_{\mathrm{1,0}}^x\\ ⋮\\ {\mathrm{\Delta }}_{N-2,N-1}^x\\ {\mathrm{\Delta }}_{\mathrm{0,0}}^y\\ ⋮\\ {\mathrm{\Delta }}_{N-1,N-3}^y\\ {\mathrm{\Delta }}_{N-1,N-2}^y\end{array}\end{array}\right]}_{2N(N-1)}(14)$

According to the basic principle of least square method, $\Phi$ in Eq. 12 must meet the requirements of ${\mathbf{V}}^T\mathbf{PV}=\min$, and the corresponding normal equation can be established as follows:

${\mathbf{A}}^{\mathit{T}}\mathbf{PA}-\mathbf{A}{\mathbf{P}}^{\mathit{T}}\mathbf{L}=0(15)$

Where $\mathbf{P}$ is a weight matrix of M rows and M columns, the value $p_{ij}$ of each element in the matrix can be determined by the size of the side length in the triangulation network, and the elements $p_{ij}$ on the main diagonal are the reciprocal of the corresponding side length value $D_{ij}$, i.e

$p_{ij}=\frac{1}{D_{ij}}(16)$

At the same time, since the phase values of each end point in the triangulation network are independent of each other, each element on the non-main diagonal of the weight matrix is 0 respectively, so the weight matrix is determined. According to the normal Eq. 15, the real interference phase value of each PS point can be obtained:

$\text{Φ}={\left({\mathbf{A}}^T\mathbf{PA}\right)}^{-1}\mathbf{A}{\mathbf{P}}^T\mathbf{L}(17)$

Precision evaluation

On the basis of the mathematical model, the accuracy of phase unwrapping of least square method can be studied theoretically by using the covariance matrix of each observation vector and the law of error propagation. According to the error theory, in order to evaluate the observation accuracy, it is necessary to calculate the estimation ${\widehat{\sigma }}_0^2$ of unit weight variance, then calculate the covariance matrix of each observation value, and finally calculate the precision of the parameter matrix $\mathbf{\Phi }$ according to the cofactor propagation law and error propagation law.

The unit weight variance can be calculated from the error value v of the difference phase at the edge of the triangle network as follows:

${\widehat{\sigma }}_0^2=\frac{V^{T}PV}{M-N}(18)$

The variance of each differential phase can be calculated according to the weighting method of the differential phases:

${\widehat{\sigma }}_{ij}^2=\frac{{\widehat{\sigma }}_0^2}{p_{ij}}(19)$

Or it can be expressed by the length of the side as:

${\widehat{\sigma }}_{ij}^2=D_{ij}{\widehat{\sigma }}_0^2(20)$

Thus, the median error of thedifferential phase on each edge can be obtained:

${\sigma }_{ij}={\widehat{\sigma }}_0\sqrt{D_{ij}}(21)$

In order to determine the covariance matrix $\mathbf{\Phi }$ of the parameters and obtain the median error of the unwrapped phase of the PSs, the cofactor matrix ${\mathbf{Q}}_{\text{Φ}\text{Φ}}$ of the parameters can be obtained according to the cofactor propagation law.

${\mathbf{Q}}_{\mathbf{\Phi \Phi }}={\left({\mathbf{A}}^{\mathbf{T}}\mathbf{PL}\right)}^{-1}(22)$

Then the covariance matrix ${\mathbf{D}}_{\mathrm{\Phi }\mathrm{\Phi }}$ of parameters is obtained by the relation between the cofactor matrix and the covariance matrix

${\mathbf{D}}_{\mathbf{\Phi \Phi }}={\widehat{\sigma }}_0^2{\mathbf{Q}}_{\mathbf{\Phi \Phi }}(23)$

The element on the main diagonal of the covariance matrix is the variance of the space unwrapped phase corresponding to each PS, and the accuracy of the unwrapping can be obtained.

Experiment and result analysis

In order to verify the effectiveness of the indirect least square adjustment spatial phase unwrapping algorithm, GB-SAR images of GY arch dam and HS large-scale landslide deformation monitoring were used for spatial phase unwrapping and accuracy analysis.

Phase unwrapping of GY arch dam monitoring data

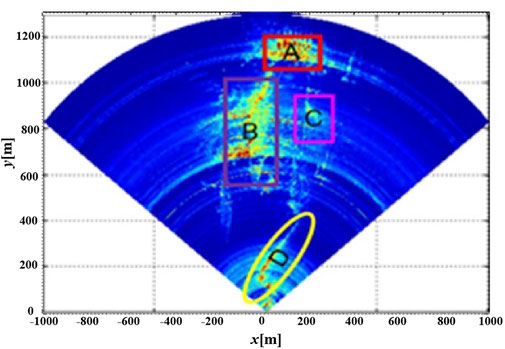
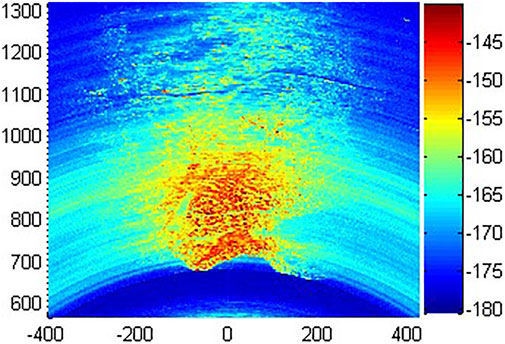
In this paper, the deformation monitoring of gravity arch dam of GY Hydropower Station in Hubei Province, China, was taken as an example. The monitoring process lasted for 7 days and 147 h. Figure 3 is the image intensity map, where A, B, C and D correspond to each building in Figure 4. The data acquisition interval is set to 5 min, and the dam is in stable operation period. The phase change during the 5 min sampling interval is far less than 2π radian, which meets the requirement of Nyquist sampling rate.

FIGURE 3

FIGURE 3. GB-SAR image corresponds to the physical relationship.

FIGURE 4

FIGURE 4. GB-SAR monitoring equipment layout schematic.

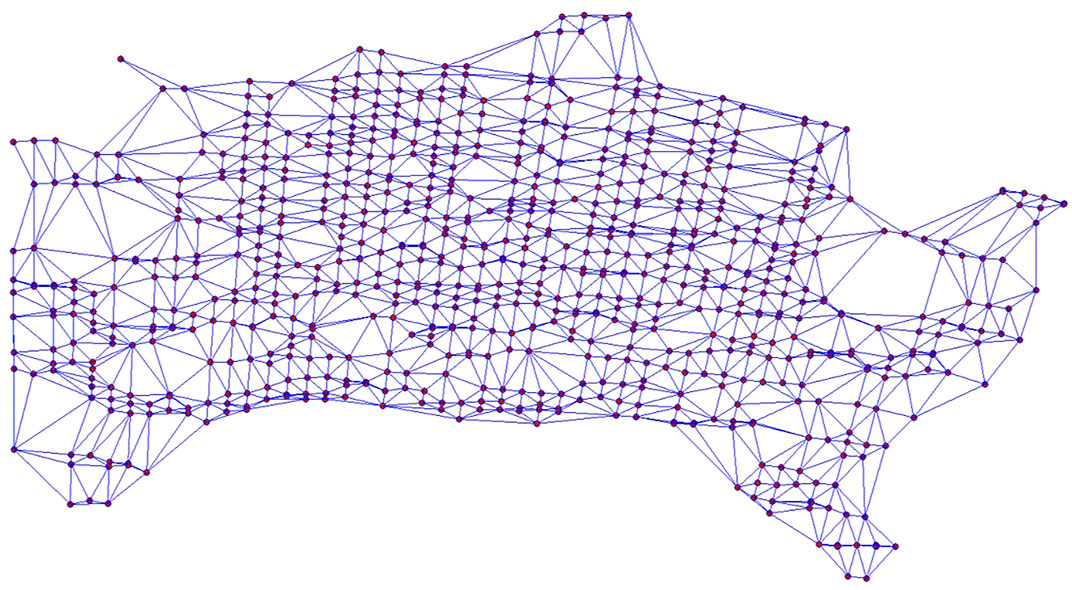
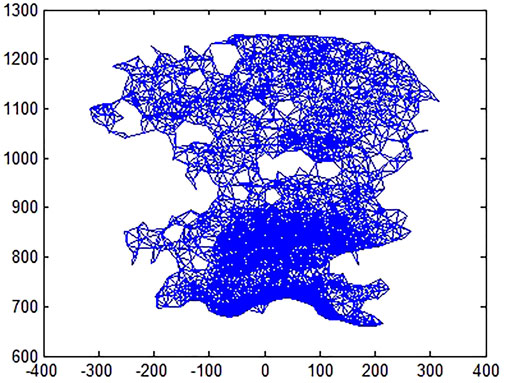
After interference image generation, using the PS combination method to extract 4289 PSs, Then use the Itoh method for time phase unwrapping, and build the PS triangle as shown in Figure 5, with 14,433 baseline and 9617 triangles.

FIGURE 5

FIGURE 5. Delaunay triangulation network of PS points in GY arch dam body.

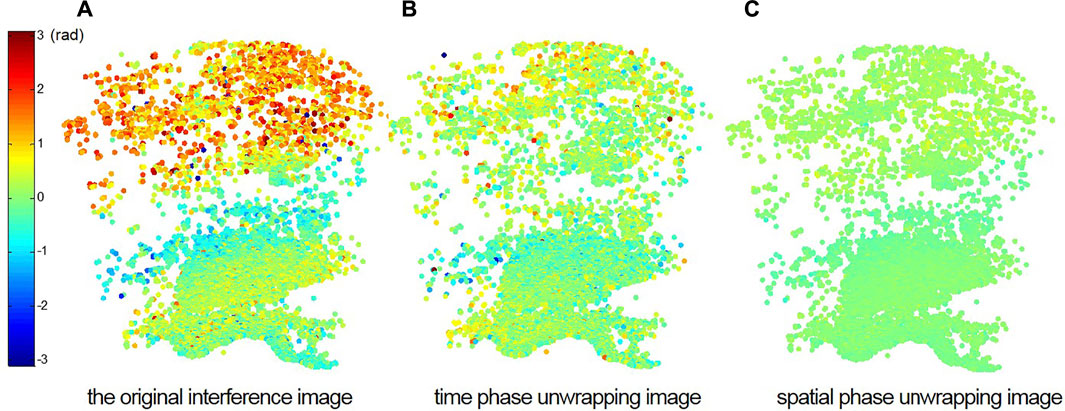
In the case of the difference phase observation of the 37 images of the dam body, according to the spatial phase unwrapping model of the indirect least square adjustment method, the error equation is established and the unwrapping solution is obtained. The mean median error of the spatial phase unwrapping of the 37 images is ±0.004 mrad, the maximum is ±0.027 mrad, and the minimum is ±0.001 mrad. Figure 6 shows the situation before and after the temporal and spatial phase unwrapping of the first image and the ninth image.

FIGURE 6

FIGURE 6. Comparison of the first image and the ninth image before and after phase unwrapping.

Figure 6A is the first interference image of phase wrapping, which is more serious. This is because at the beginning of the experiment, the data collection is still in the debugging state, so the phase continuity between the two adjacent moments is poor. The interference phase value of some pixels exceeds 2π radian, and the whole cycle fuzzy number is not 0. As can be seen from Figure 6B, before and after the time phase unwrapping with Itoh, the phase values at many points still have a large discontinuity.

With a large jump, indicating that the unwrapping of these points is incomplete and further unwrapping is needed. On the basis of time phase unwrapping, the spatial phase unwrapping based on indirect least square adjustment is performed, the unwrapping image as shown in Figure 6C is obtained. It can be seen from the figure that the spatial continuity of each PS is very good and all of them are in the interval of $[-\pi ,\pi )$. Figure 6D shows the ninth interference image of phase wrapping, which is in the stable monitoring period and has good time continuity of phase. After using Itoh time phase unwrapping, the results of Figure 6E are obtained, the unwrapping effect is good, and the whole fuzzy number contained in the interference phase of each PS is almost 0, only the phase at a few points don’t meet the requirements of consistency in space. The spatial phase unwrapping method in this paper is continued to be used for unwrapping, and the final unwrapping result is obtained as shown in Figure 6F. At this time the consistency of all PS points in space is better, get better results.

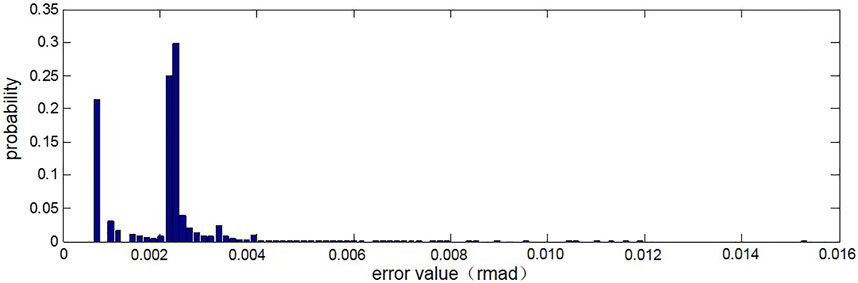
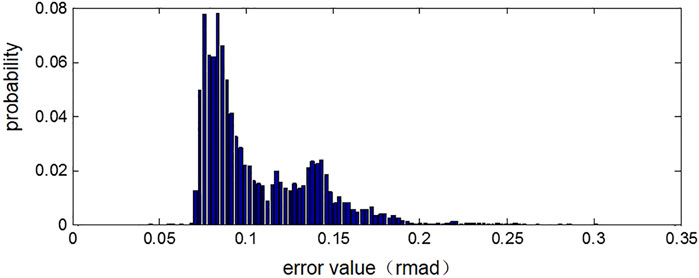
The phase unwrapping errors of each PS point in the first and ninth interference images are respectively calculated and their distribution is counted, as shown in Figures 7, 8. As can be seen from the statistical histogram of error, most of the unwrapping errors of PSs in the first interference image are between 0.002 and 0.004 mrad, while most of the unwrapping errors in the ninth interference image are between 0.001 and 0.003 mrad. There is no gross error in the unwrapping results, and the error distribution is in line with the distribution characteristics of accidental errors. The unwrapping results have strong robustness and high unwrapping accuracy. As the phase observed value of the first interference image fluctuates greatly during data acquisition, the data is not stable enough, so the error is slightly larger than the unwrapping accuracy of the ninth interference image, which also indicates that the unwrapping method adopted in this paper can fully reflect the quality of the data itself, so as to carry out effective unwrapping.

FIGURE 7

FIGURE 7. Statistical histogram of error in the first image phase unwrapping.

FIGURE 8

FIGURE 8. Statistical histogram of error in phase unwrapping of the 9th image.

Phase unwrapping of HS landslide monitoring data

The landslide body is one of the largest landslide bodies in the Three Gorges Reservoir Area. With a leading edge elevation of about 65.0 m and a trailing edge elevation of about 840.0 m, with a total volume of about 18 million m³. Topographic surface and bedrock surface basically parallel, steep slope. In order to prevent the sliding body from sliding into the river at high speed on a large scale, causing disasters such as navigation obstruction and serious obstruction to navigation and the safety of the county on the other side of the river affected by surges, GB-SAR was adopted for deformation monitoring from April 20, 2019 to June 20, 2019, and the SAR image data of the whole landslide for two months are obtained, as shown in Figure 9.

FIGURE 9

FIGURE 9. The original image of the slope.

PSs are selected for interference images and PS triangulation network is constructed, as shown in Figure 10. First, the itoh method is used for time phase unwrapping, and then indirect least square adjustment is used for spatial phase unwrapping. The mean median error of phase unwrapping during the whole monitoring period is obtained as ±0.031 mrad, the maximum is ±0.301 mrad, and the minimum is ±0.001 mrad. Figure 11 shows the image before and after phase unwrapping at 18:39 on April 30, 2019. As can be seen from Figure 11A, the phase of each point is discontinuous before unwrapping, which is in the interval of $[-\pi ,\pi )$. Firstly, Itoh method is used for time phase unwrapping, as shown in Figure 11B. Due to the long monitoring time, many weather changes such as rainfall occurred during this process, and the PS points changed somewhat in space, so the spatial consistency condition can not be strictly met. Therefore, after time phase unwrapping, the phase of some PSs are still spatially discontinuous. After the spatial phase unwrapping, the result as shown in Figure 11C is obtained. The spatial continuity of each PS point is very good.

FIGURE 10

FIGURE 10. PS triangulation of the landslide.

FIGURE 11

FIGURE 11. Comparison before and after phase unwrapping of an image of HS landslide.

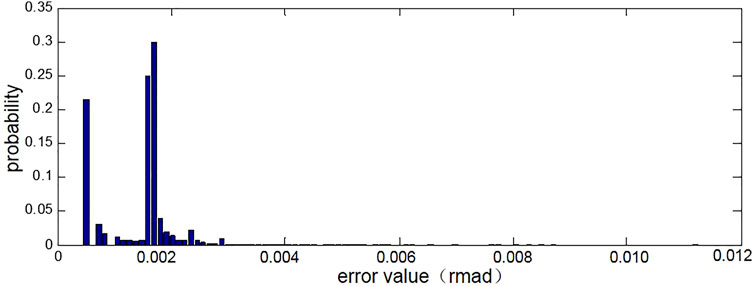
The phase unwrapping error of each PS point in this image is calculated and its distribution is counted, as shown in Figure 12, the unwrapping errors of most PSs are concentrated between 0.06 and 0.18 mrad. Compared with the deformation monitoring of GY arch dam, the monitoring time of the landslide body is longer, the phase observation value is more obviously affected by atmospheric disturbance, and the unwrapping accuracy is greatly affected by it. However, from the analysis of the overall unwrapping accuracy, it can be seen that the unwrapping result has no gross error and conforms to the distribution characteristics of accidental error, and the unwrapping accuracy is still high. The results show that the indirect least square adjustment spatial phase unwrapping algorithm has good applicability in the spatial phase unwrapping of continuous monitoring data for a long time.

FIGURE 12

FIGURE 12. Statistical histogram of error in phase unwrapping of an image of HS landslide.

Conclusions and suggestions

In this paper, the key step of GB-SAR dam and landslide safety monitoring data processing-phase unwrapping is studied. Based on the idea of sparse data, a phase unwrapping method for GB-SAR landslide monitoring data is proposed. In this method, the phase unwrapping of PSs is decomposed into time domain and space domain, and the real phase value of each PS is obtained through two-step unwrapping. The validity of the method is verified by the phase unwrapping of GY dam and HS landslide monitoring experimental data. The specific research work and conclusions of this paper are as follows:

1) The characteristics of phase unwrapping of GB-SAR landslide monitoring data are analyzed. According to the short sampling interval of GB-SAR data, phase unwrapping is decomposed into two steps: time domain and space domain.

2) Firstly, the time phase unwrapping is carried out, and the continuity conditions of GB-SAR landslide monitoring data in time are analyzed. The Itoh method, which is used in the spatial domain, is applied to the time dimension, and the preliminary unwrapping results are obtained.

3) According to the spatial relationship between PSs, the triangulation network was constructed to obtain the double-difference phase observation values. The spatial phase unwrapping is further carried out based on the spatial consistency requirements. Here, the indirect least square method is introduced to realize the spatial phase unwrapping.

4) According to the situation of GB-SAR data, the adjustment model is built, the specific content of each matrix is determined, and the error equation is established. The weight matrix P is constructed according to the spatial distribution characteristics of GB-SAR data, and the normal equation is obtained.

5) According to the spatial phase unwrapping model, the indirect least square adjustment method is used to conduct the spatial phase unwrapping, and the mathematical rigor and error estimation ability of least square method are fully used to conduct the unwrapping and accuracy evaluation.

6) Through the dam and the landslide monitoring experiment validates the effectiveness of the wrapped the solution method, the experimental results show that the algorithm has good applicability in phase unwrapping of both short-term monitoring and continuous long-term monitoring data, it can effectively solve the problems such as path dependence, island isolation and large amount of calculation in common space-borne SAR phase unwrapping methods. Meanwhile, it also takes into account the characteristics of GB-SAR landslide monitoring data to ensure the effect of phase unwrapping.

The phase unwrapping method proposed in this paper provides a new solution for the application of GB-SAR monitoring technology in slope or landslide monitoring. It has a wide application prospect in the high-precision, non-contact, all-weather and automatic safety monitoring of large volume targets, such as dams, slopes, bridges, landslides, etc. However, this paper mainly studies the principle and thought of the method and verifies the effectiveness of the method through experiments. The specific effect comparison between this method and other traditional methods is worth further study, which will be the content of our next paper.

Data availability statement

The datasets presented in this article are not readily available because the original data is classified and cannot be provided publicly. Requests to access the datasets should be directed to xiangxia@scu.edu.cn.

Author contributions

XX: method proposal and model establishment, CC: data analysis and paper writing, HW: data collection and data analysis, CX: experimental design and data collection, JC: model establishment and data analysis, HZ: writing–reviewing and editing.

Funding

This research was substantially supported by the State Key Program of National Nature Science Foundation of China (Grant No.52130904), the National Key R&D Program of China (2019YFC1510700), the National Natural Science Foundation of China (Grant No. 51909181), the Sichuan Science and Technology Program (2022YFS0539).

Conflict of interest

HZ was employed by the company AECOM Asia Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abutaleb, A. S. (2002). Number theory and bootstrapping for phase unwrapping. IEEE Trans. Circuits Syst. I. 49 (5), 632–638. doi:10.1109/tcsi.2002.1001952

CrossRef Full Text | Google Scholar

Bozzano, F., Cipriani, I., Mazzanti, P., and Prestininzi, A. (2011). Displacement patterns of a landslide affected by human activities: Insights from ground-based InSAR monitoring. Nat. Hazards (Dordr). 59 (3), 1377–1396. doi:10.1007/s11069-011-9840-6

CrossRef Full Text | Google Scholar

Carballo, G. F., and Fieguth, P. W. (2000). Probabilistic cost functions for network flow phase unwrapping. IEEE Trans. Geosci. Remote Sens. 38 (5), 2192–2201. doi:10.1109/36.868877

CrossRef Full Text | Google Scholar

Cen, X. (2008). Research on InSAR phase unwrapping algorithm. Changsha: Hunan University. (In Chinese).

Google Scholar

Chen, Y., Jia, Y., and Dang, Y. (2006). Research on deformation monitoring using InSAR technology. Sci. Surv. Mapp. 31 (3), 56–58. (In Chinese).

Google Scholar

Collaro, A., Franceschetti, G., Palmieri, F., and Ferreiro, M. S. (1998). Phase unwrapping by means of genetic algorithms. J. Opt. Soc. Am. A 15 (2), 407–418. doi:10.1364/josaa.15.000407

CrossRef Full Text | Google Scholar

Costantini, M. (1998). A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 36 (3), 813–821. doi:10.1109/36.673674

CrossRef Full Text | Google Scholar

Costantini, M. (1997). A phase unwrapping method based on network programming. ERS SAR Interferometry. 406, 261.

Google Scholar

Crosetto, M., Monserrat, O., Luzi, G., Cuevas-Gonzalez, M., and Devanthery, N. (2014). Discontinuous GBSAR deformation monitoring. ISPRS J. photogrammetry remote Sens. 93, 136–141. doi:10.1016/j.isprsjprs.2014.04.002

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a bedding fault: Understanding the initiation and movement of the Daguangbao landslide triggered by the 2008 Wenchuan Earthquake (Ms = 8.0) fault, bedding fault: Understanding the initiation and movement of the Daguangbao landslide triggeredby the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455. doi:10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

Fan, H-d. (2010). Study on several key algorithms of InSAR technique and its application in land subsidence monitoring. Beijing: China University of Mining and Technology. (In Chinese).

Google Scholar

Flynn, T. J. (1996). Consistent 2-D phase unwrapping guided by a quality map. Geoscience Remote Sens. Symposium 4, 2057–2059.

Google Scholar

Flynn, T. J. (1997). Two-dimensional phase unwrapping with minimum weighted discontinuity. J. Opt. Soc. Am. A 14 (10), 2692–2701. doi:10.1364/josaa.14.002692

CrossRef Full Text | Google Scholar

Ghiglia, D. C., and Romero, L. A. (1996). Minimum Lp-norm two-dimensional phase unwrapping. J. Opt. Soc. Am. A 13 (10), 1999–2013. doi:10.1364/josaa.13.001999

CrossRef Full Text | Google Scholar

Goldstein, R. M., Zebker, H. A., and Werner, C. L. (1988). Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 23 (4), 713–720. doi:10.1029/rs023i004p00713

CrossRef Full Text | Google Scholar

Group of Survey Adjustment, Institute of surveying and mapping (2014). Error theory and basis of measurement adjustment. 3rd Edition. Wuhan: Wuhan Universitywuhan university press, 5. (In Chinese).

Google Scholar

He, R., Wang, Y., and Mao, J. (2008). Region-cutting InSAR phase unwrapping algorithm based on support vector machine. J. Syst. Simul. 20 (6), 1493–1496. (In Chinese).

Google Scholar

He, Y., and Kusiak, A. (2017). Performance assessment of wind turbines: Data-derived quantitative metrics metrics. IEEE Trans. Sustain. Energy 9 (1), 65–73. doi:10.1109/tste.2017.2715061

CrossRef Full Text | Google Scholar

Hernández, O. M. (2012). Deformation measurement and monitoring with ground-based SAR. Catalonia: Universitat Politècnica de Catalunya UPC.

Google Scholar

Itoh, K. (1982). Analysis of the phase unwrapping algorithm. Appl. Opt. 21 (14), 2470. doi:10.1364/ao.21.002470

PubMed Abstract | CrossRef Full Text | Google Scholar

Kampes, B. M., and Hanssen, R. F. (2004). Ambiguity resolution for permanent scatterer interferometry. IEEE Trans. Geosci. Remote Sens. 42 (11), 2446–2453. doi:10.1109/tgrs.2004.835222

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D., and Cheng, Q. (2021a). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021b). Monitoring and identifying wind turbine generator bearing faults using deep belief network and EWMA control charts turbine generator bearing faults using deep belief network and EWMA control charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, H., He, Y., Xu, Q., Deng, j., Li, W., and Wei, Y. (2022). Detection and segmentation of loess landslides via satellite images: A two-phase framework landslides via satellite images: A two-phase framework. Landslides 19, 673–686. doi:10.1007/s10346-021-01789-0

CrossRef Full Text | Google Scholar

Loffeld, O., Nies, H., Knedlik, S., and Yu, W. (2008). Phase unwrapping for SAR interferometry—a data fusion approach by kalman filtering. IEEE Trans. Geosci. Remote Sens. 46 (1), 47–58. doi:10.1109/tgrs.2007.909081

CrossRef Full Text | Google Scholar

Luzi, G., Imperatore, P., and Riccio, D. (2010). Ground based SAR interferometry: A novel tool for geoscience. Geoscience Remote Sens. New Achiev., 508.

CrossRef Full Text | Google Scholar

Peng, S., Yuan, J., and Xiang, J. (2008). An improved InSAR phase unwrapping method based on iterative-weighted greedy algorithm. J. Electron. Inf. Technol. 6, 014. (In Chinese).

Google Scholar

Pepe, A. (2012). Advanced multitemporal phase unwrapping techniques for DInSAR analyses recent interferometry applications in topography and astronomy. Italy: InTech.

Google Scholar

Pepe, A., and Lanari, R. (2006). On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 44 (9), 2374–2383. doi:10.1109/tgrs.2006.873207

CrossRef Full Text | Google Scholar

Pieraccini, M., Luzi, G., and Mecatti, D. (2006). Ground–Based Radar Interferometry for Monitoring Unstable Slopes. 3rd IAG/12 FIG Symposium, Baden

Google Scholar

Pritt, M. D., and Shipman, J. S. (1994). Least-squares two-dimensional phase unwrapping using FFT's. IEEE Trans. Geosci. Remote Sens. 32 (3), 706–708. doi:10.1109/36.297989

CrossRef Full Text | Google Scholar

Takahashi, K., Matsumoto, M., and Sato, M. (2013). Continuous observation of natural-disaster-affected areas using ground-based SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 6 (3), 1286–1294. doi:10.1109/jstars.2013.2249497

CrossRef Full Text | Google Scholar

Xiang, X., Chen, J., Wang, H., Pei, L., and Wu, Z. (2019). PS selection method for and application to GB-SAR monitoring of dam deformation. Adv. Civ. Eng., 1–15. doi:10.1155/2019/8320351

CrossRef Full Text | Google Scholar

Xu, W., and Cumming, I. (1999). A region-growing algorithm for InSAR phase unwrapping [J]. IEEE Trans. Geoscience Remote Sens. 37 (1), 124–134.

Google Scholar

Yu, H., Yang, L., Yuan, Z., Xu, J., and Lee, H. (2019). Phase unwrapping in InSAR: A review. IEEE Geosci. Remote Sens. Mag. 7 (1), 40–58. doi:10.1109/mgrs.2018.2873644

CrossRef Full Text | Google Scholar

Zhi-qiang, W., and Jin, Y. (2008). InSAR phase unwrapping algorithm based on ant colony algorithm. J. Electron. Inf. Technol. 3, 004. (In Chinese).

Google Scholar

Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021). Seepage channel development in the crown pillar: Insights from induced microseismicity. Int. J. Rock Mech. Min. Sci. 145, 104851. doi:10.1016/j.ijrmms.2021.104851

CrossRef Full Text | Google Scholar