Influence of soil mechanical and hydraulic parameters on the definition of rainfall intensity and duration thresholds based on Transient rainfall infiltration and grid-based regional slope-stability model (TRIGRS)

As a supplement to empirical-statistical methods, physically based methods can be employed to define rainfall thresholds for triggering landslides in areas lacking records of landslides. The transient rainfall infiltration and grid-based regional slope-stability model (TRIGRS), as a physically based model, has been applied to define rainfall thresholds at the basin, slope unit, and grid cell scales. However, as far as we know to date, the influence of soil mechanical and hydraulic parameters on defining rainfall thresholds at various scales has not been comprehensively evaluated. In this study, TRIGRS was used to define rainfall intensity (I) and duration (D) thresholds at various scales for Buzhe village, Pu’an county, Guizhou province, China, under the conditions of different soil physical parameters. The results show that the number of rainfall thresholds decreased with cohesion ($c$) and internal friction angle ($\phi$) and increased with soil unit weight (${\gamma }_s$), excluding the basin scale. Threshold position varied positively with $c$ and $\phi$ and negatively with ${\gamma }_s$. Soil mechanical parameters have a greater influence on the definition of rainfall thresholds based on TRIGRS than hydraulic parameters.

Introduction

Rainfall-induced shallow landslides mainly occur on slopes covered by a layer of colluvium or residual soil (Salciarini et al., 2006; Montrasio and Valentino, 2007; Montrasio and Valentino, 2008). Rainfall infiltration in slopes increases the pore-water pressure and decreases the shear strength, thereby triggering landslides (Lim et al., 1996; Vanapalli et al., 1996). Thus, rainfall is recognized as the primary trigger of shallow landslides (Campbell, 1975; Keefer et al., 1987; Wilson, 2005), and rainfall thresholds are the most used tools to forecast landslides (Caine, 1980; Aleotti, 2004; Guzzetti et al., 2007; Guzzetti et al., 2008; Li et al., 2017; He et al., 2020). Guizhou province is located in the mountainous area of southwest China. As one of the landslide-prone provinces in China, shallow landslides frequently occur in Guizhou province (Yu et al., 2016; Zhang et al., 2017; Lin and Wang, 2018; Ma et al., 2020). However, only few defined rainfall thresholds or landslide early warning systems (LEWSs) exist in this area to address the risk of shallow landslides.

Empirical-statistical and physically based methods can be used to define rainfall thresholds (Aleotti, 2004; Guzzetti et al., 2007; Park et al., 2019). Empirical-statistical rainfall methods define rainfall thresholds through the statistical analysis of rainfall conditions that have triggered landslides (Brunetti et al., 2010; Peruccacci et al., 2012; Melillo et al., 2018). Currently, empirical-statistical rainfall thresholds have become the most common landslide model (i.e., the functional relationship between weather conditions and landslide events) in LEWSs (Calvello, 2017; Piciullo et al., 2018; Guzzetti et al., 2020). However, empirical-statistical methods mainly rely on the availability and quality of landslide records (Peres and Cancelliere, 2014). They are severely limited for the areas with incomplete or unavailable landslide records. In this case, physically based methods are the ideal alternative.

Physically based methods define rainfall thresholds by simulating the hydrological process of soil and slope stability during rainfall infiltration (Salciarini et al., 2008; Salciarini et al., 2012). TRIGRS is a physically based model for shallow landslide prediction (Baum et al., 2002; Baum et al., 2008; Baum et al., 2010; Alvioli and Baum, 2016). Thus, TRIGRS is widely used in modeling the timing and distribution of shallow landslides (Vieira et al., 2010; Lee et al., 2017; Tran et al., 2018; He et al., 2021; Ip et al., 2021) and landslide susceptibility mapping (Baum et al., 2005; Park et al., 2013; Marin and Mattos, 2020). In addition to these widespread applications, TRIGRS is applied in defining physically based rainfall thresholds given its ability to describe the scaling behavior of rainfall thresholds (Alvioli et al., 2014).

The Sendai Framework for Disaster Risk Reduction proposes the goal of substantially increasing the availability and access to multi-hazard early warning systems and disaster risk information and assessments to people by 2030 (UNISDR, 2015). Guzzetti et al. (2020) proposed that LEWSs can be deployed and operated worldwide, and suggested increasing the rate of LEWS deployment for landslide-prone areas. In some landslide-prone areas of China, the quality of records of landslides is poor. Although this situation has improved in recent years, the time span and quality of existing landslide records are insufficient to support the definition of empirical-statistical rainfall thresholds. For these areas, physically based methods can extend the application scenarios of LEWS based on rainfall thresholds, which is important for LEWS deployment.

TRIGRS can be employed to define rainfall thresholds at three scales, namely, basin, slope unit, and grid cell scales. At the basin scale, the rainfall threshold is defined for the whole area. Rainfall conditions exceeding the defined rainfall threshold can trigger several landslides in the entire area. Alvioli et al. (2018) used TRIGRS to define the rainfall event-duration (E-D) threshold for Upper Tiber River Basin in Italy. Bordoni et al. (2019) used TRIGRS to define the E-D threshold for an area of Oltrepò Pavese in Italy. Marin and Velásquez (2020) used TRIGRS to define the I-D thresholds for the Envigado Basin of Colombia under the conditions of different soil hydraulic properties. Marin et al. (2020) used TRIGRS to define the I-D thresholds for 93 small basins in Colombian Andes and analyzed the effect of basin morphometric parameters on defined I-D thresholds. Marin et al. (2021) used TRIGRS to define the I-D thresholds for La Arenosa and La Liboriana Basins in Colombian Andes. At the slope unit scale, rainfall thresholds are defined for slope units with critical rainfall. Rainfall conditions exceeding the defined rainfall thresholds can trigger landslides in the corresponding slope units. Alvioli et al. (2014) used TRIGRS to define the I-D thresholds for several sub-basins of the Upper Tiber River Basin. Zhang et al. (2022) divided Dabang village, Pu’an County, Guizhou Province, China, into several slope units and used TRIGRS to define the I-D thresholds for the slope units with critical rainfall. At the grid cell scale, rainfall thresholds are defined for grid cells with critical rainfall. Rainfall conditions exceeding the defined rainfall thresholds can trigger landslides in the area of the corresponding grid cells. Marin (2020) used TRIGRS to define the I-D thresholds for grid cells with critical rainfall in the Envigado Basin. Marin et al. (2021) used TRIGRS to define the I-D thresholds for grid cells with critical rainfall of La Arenosa and La Liboriana Basins.

Detailed and accurate soil parameters (e.g., soil depth, soil mechanical, and hydraulic parameters) are required to properly apply TRIGRS. However, obtaining substantial information on distributed soil properties at a large scale is a challenge, especially regarding soil physical properties (i.e., mechanical and hydraulic parameters) (Gariano and Guzzetti, 2016; Zhang et al., 2018). Uncertainties in soil parameters are caused by complex geological conditions, spatial variability, and laboratory measurement (Catani et al., 2010; Ho et al., 2012; Corominas et al., 2014; Bicocchi et al., 2015), which make it impossible to eliminate all uncertainties. In terms of using TRIGRS to predict the spatiotemporal information of shallow landslides and landslide susceptibility mapping, the influence of soil mechanical and hydraulic parameters on the prediction and mapping results has been extensively explored (Salciarini et al., 2006; Montrasio et al., 2011; Bordoni et al., 2015; Gioia et al., 2016; He et al., 2016; Ciurleo et al., 2017; de Lima Neves Seefelder et al., 2017; Weidner et al., 2018; Ciurleo et al., 2019). Some probabilistic approaches have been adopted with TRIGRS to quantitatively account for soil parameter uncertainties (Raia et al., 2014; Salciarini et al., 2017). In these probabilistic approaches, the input parameters are considered random variables, and the output is the probability of failure.

However, few studies have explored the influence of soil mechanical and hydraulic parameters on the definition of rainfall thresholds based on TRIGRS. Only Marin and Velásquez (2020) explored the effect of soil hydraulic parameters on the position of rainfall thresholds defined at the basin scale. The performance of the rainfall threshold requires evaluation before applying it in LEWSs (Piciullo et al., 2017; Segoni et al., 2018). Exploring the influence of soil physical parameters on the rainfall thresholds defined by using TRIGRS can facilitate the evaluation of the physically based rainfall thresholds.

In this study, Buzhe village, Pu’an county, Guizhou province of China was taken as the study area. The soil mechanical and hydraulic parameters measured by field sampling were taken as standard values. In each TRIGRS simulation, a parameter was varied by the given proportion and the rest remained constant. Then, the I-D thresholds at various scales were defined under the conditions of given physical parameters. Finally, the influence of soil physical parameters on the number and position of rainfall thresholds was explored by comparing the simulated $F_s$ maps and defined thresholds.

Study area

Pu’an county, which is located in southwest Guizhou province of China (Figure 1), has tremendous undulating terrains, and the dissolution and erosion of landforms are staggered. Moreover, soft rocks such as siltstone and sandstone are widespread. These soft rocks are easily weathered into the eluvium and slope wash. As for rainfall, the average annual precipitation of Pu’an county is 1,443 mm. Owing to the complex geological setting and rainy environment, Pu’an county is one of the landslide-prone counties in Guizhou province.

FIGURE 1

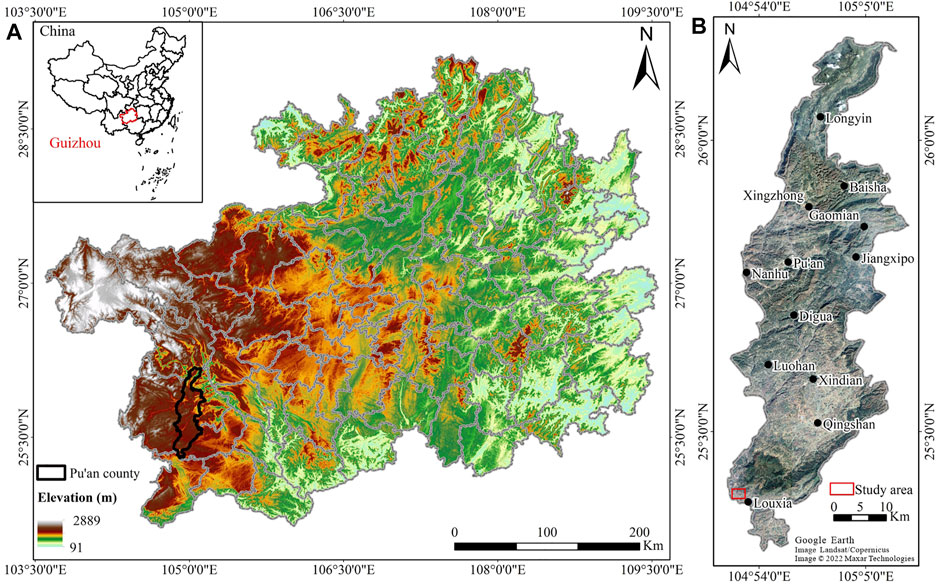
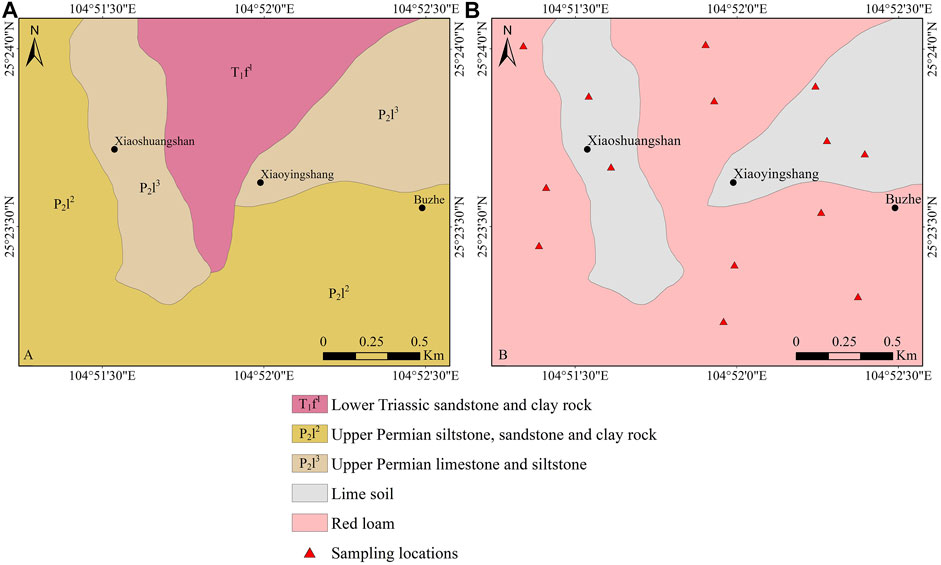
FIGURE 1. (A) Location of Pu’an county (image source: SRTM data) and (B) location of the study area.

Lower Triassic sandstone and clay rock, Upper Permian siltstone, sandstone, and clay rock, and Upper Permian limestone and siltstone are distributed in the study area (Figure 2A). The soil types in the study area are red loam and lime soil (Figure 2B). The distribution of each soil type is consistent with the corresponding soil parent material. Red loam is distributed on sandstone, siltstone, and clay rock. Lime soil is distributed on limestone.

FIGURE 2

FIGURE 2. (A) Geology map of the study area and (B) spatial distribution of soil types.

Data

Digital elevation model

The input data for TRIGRS are topographic factors, soil parameters, soil thickness, and initial conditions for surface flux and groundwater table. As for topographic factors, the 10-m resolution DEM was taken as input. Other required input slopes and flow direction maps were generated using ArcGIS software based on the DEM data.

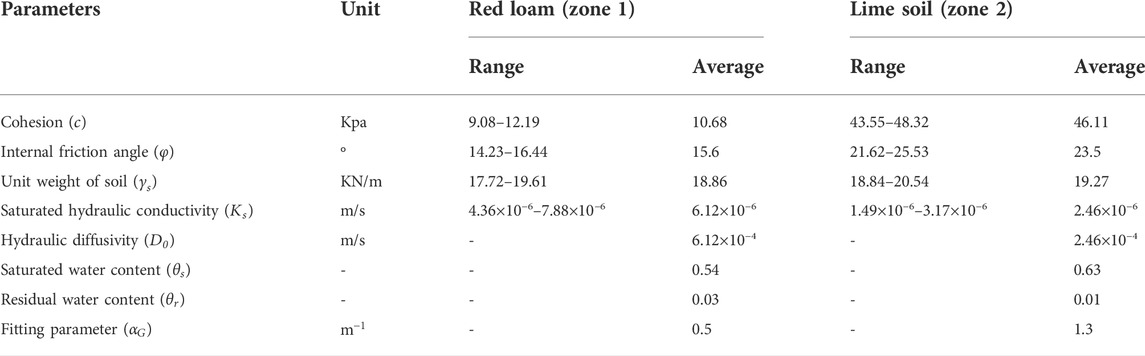
Soil parameters

The input soil mechanical parameters include ${\gamma }_s$, $\phi$, and $c$. The input hydraulic parameters include saturated hydraulic conductivity ($K_s$), hydraulic diffusivity ($D_0$), saturated water content (${\theta }_s$), residual water content (${\theta }_r$), and fitting parameter (${\alpha }_G$) of Gardner’s model for the soil water characteristic curve (SWCC) (Gardner, 1958). A total of 18 samples of red loam and 10 samples of lime soil were collected at the 14 sampling locations (Figure 2B). The mechanical parameters were measured through laboratory static triaxial experiments. The hydraulic parameters were measured through laboratory variable tap penetration experiments. For each parameter, the average of the measurements was taken as the standard value (Table 1). Regarding ${\theta }_s$, ${\theta }_r$, and ${\alpha }_G$, this study determined the parameters for the Gardner model (used in TRIGRS) based on the Van Genuchten model (Van Genuchten, 1980) for SWCC of typical soil types in Guizhou province (Zhao, 2021). The volumetric water contents were the same in the two models for each soil type, and ${\alpha }_G$ was fitted to be within the limits of the Van Genuchten curves, as suggested by Marin (2020).

TABLE 1

TABLE 1. The range and average of soil samples measurements in the study area.

$c$, $\phi$, and ${\gamma }_s$ were taken 0.8, 0.9, 1.1, and 1.2 times the standard values as input. $K_s$ and $D_0$ were taken 0.7, 0.8, 1.2, and 1.3 times standard values as input. The input mechanical and hydraulic parameters were assigned to each grid cell according to the spatial distribution of soil types in the study area (Figure 2B). One parameter was changed, and the remaining parameters were kept constant for each simulation. A total of 20 simulations were performed.

Soil thickness significantly influences the simulation results of TRIGRS (Tran et al., 2018). Many studies have shown that the linear relation of slope angle and soil thickness to characterize the soil thickness map can obtain suitable simulation results of TRIGRS (Viet et al., 2017; Tran et al., 2018; He et al., 2021). The relationship assumes that soil thickness ($y$) is in inverse proportion to slope angle ($x$), that is, the minimum soil thickness (0.1 m) corresponds to the maximum slope (69.41°) and the maximum soil thickness (3.3 m) corresponds to the minimum slope (0.1°). From the relationship, the soil thickness map was generated by the linear equation (Eq. 1). The units of $y$ and $x$ are meter and degree, respectively.

$y=-0.04617x+3.3.(1)$

The input initial conditions include initial surface flux ($I_z$) and initial groundwater table. Given the complex properties of soil (e.g., void and uniformity), $I_z$ is difficult to measure using laboratory tests. Thus, the empirical relationship between $I_z$ and $K_s$ was used to determine $I_z$. This study set $I_z$ to be 0.01 of $K_s$ and set the initial groundwater table to be the same as the soil thickness, as suggested by Kim et al. (2010), Park et al. (2013), Lee et al. (2017), and Viet et al. (2017).

Methods

TRIGRS model

The TRIGRS model is designed for simulating the timing and distribution of shallow landslides by computing the transient pore-pressure changes and attendant changes in the factor of safety of slope caused by rainfall infiltration (Baum et al., 2002; Baum et al., 2008; Baum et al., 2010; Alvioli and Baum, 2016). Infiltration models include the models for saturated initial and unsaturated initial conditions. For saturated initial conditions, infiltration models in TRIGRS adopt Iverson’s linearized solution (Iverson, 2000) of the Richards equation (Richards, 1931). For unsaturated initial conditions, infiltration models in TRIGRS adopt the analytical solution of the Richards equation for unsaturated soil proposed by Srivastava and Yeh (1991) to approximate the infiltration process and the Gardner model to describe SWCC (Gardner, 1958). TRIGRS simulates the slope stability based on the infinite-slope model (Taylor, 1948). The slope stability is represented by $F_s$, which is calculated as follows:

$F_s\left(Z,t\right)=\frac{\mathit{tan}{\varphi }^{\prime }}{\mathit{tan}\delta }+\frac{c^{\prime }-\psi \left(Z,t\right){\gamma }_w\mathit{tan}{\varphi }^{\prime }}{{\gamma }_{S}Zsin\delta \mathit{cos}\delta },(2)$

where ${\gamma }_w$ and ${\gamma }_S$ represent the unit weights of water and soil, respectively; $c^{\prime }$ is the effective soil cohesion; ${\varphi }^{\prime }$ is the effective soil internal friction angle; $\delta$ is the slope angle; and $\psi \left(Z,t\right)$ is the pressure head as a function of depth $Z$ and time $t$. Failure is predicted when $F_s<1$, and stability holds when $F_s\ge 1$. The simulation results of $F_s$ are visualized on GIS software. The latest version (v2.1) of TRIGRS was used in this study (Alvioli and Baum, 2016).

Definition of I-D thresholds at the basin scale

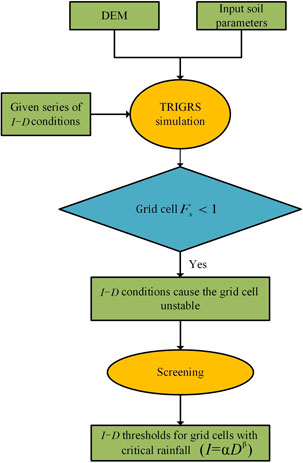
In this study, the method proposed by Marin and Velásquez (2020), Marin et al. (2020), and Marin et al. (2021) was used to define the I-D thresholds at the basin scale. This method proposed two ratios, namely, the critical failure area ratio ($a_c$) and failing area ratio ($a_f$), where $a_c$ is the ratio that excludes unconditionally unstable grid cells (i.e., $F_s<1$ without rainfall). At the basin scale, $a_f$ is calculated as the ratio of the area of grid cells with $F_s<1$ to the area of study area.

Figure 3A shows the flowchart of the definition of I-D thresholds at the basin scale. TRIGRS was run with a set of I-D conditions to simulate. In the simulation, I was increased from 2 mm/h to 30 mm/h, with an increment step of 2 mm/h. D was increased from 2 to 60 h, ranging from 2 to 20 h with an increment step of 2 h and ranging from 20 to 60 h with an increment step of 4 h. For each I-D condition, $a_f$ was calculated and compared with $a_c$. If $a_f\ge a_c$, the I-D condition was regarded to cause instability. This study defined rainfall thresholds using the $a_c$ of 1%.

FIGURE 3

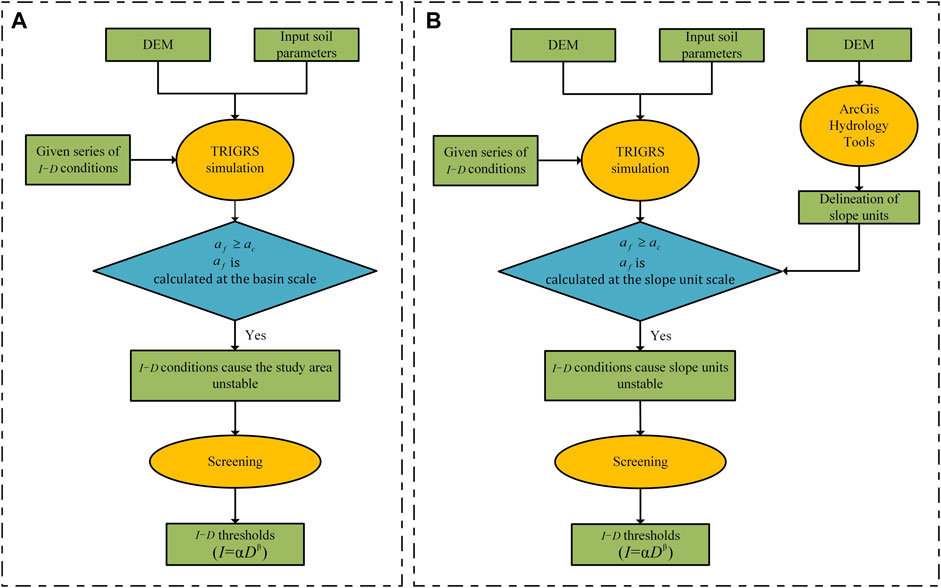
FIGURE 3. The flowchart of the definition of I-D thresholds based on TRIGRS (A) at the basin scale and (B) at the slope unit scale.

Before fitting, the I-D conditions that cause instability were screened to exclude the I-D conditions with the same I or D values (Zhang et al., 2022). Then, the screened I-D conditions were plotted in a log–log plot (log$I$ vs log$D$). Also, the distribution of I-D conditions was fit to be the linear equation of Eq. 3.

$\log I=\beta \log D+\log \alpha ,(3)$

where $I$ is the rainfall intensity (mm/h), $D$ is the rainfall duration (h), $\beta$ is the slope, and log$\alpha$ is the intercept. After getting the $\alpha$ and $\beta$, Eq. 3 was transferred into the power law equation (Eq. 4).

$I=\alpha D^{\beta },(4)$

Definition of I-D thresholds at the slope unit scale.

In this study, the method proposed by Zhang et al. (2022) was used to define I-D thresholds at the slope unit scale. The slope units were delineated based on ridge and valley lines obtained by using hydrology analysis tools in ArcGIS. (Xie et al., 2004; Wei et al., 2018).

The flowchart of the definition of I-D thresholds at the slope unit scale is shown in Figure 3B. The definition of rainfall thresholds at the slope unit scale involves defining rainfall thresholds for slope units with critical rainfall (i.e., under the given rainfall conditions, the slope units can reach instability). For each slope unit, $a_f$ was calculated as the area of unstable grid cells within its range to the area of the slope unit. The remaining steps were the same as those for the basin scale.

Definition of I-D thresholds at the grid cell scale.

In this study, the method proposed by Marin (2020) was used to define I-D thresholds at the grid cell scale. Defining rainfall thresholds at the grid cell scale involves defining rainfall thresholds for grid cells with critical rainfall, that is, under the given rainfall conditions, the grid cells can reach instability. At the grid cell scale, the rule for determining I-D conditions causing instability was $Fs$<1. The remaining steps were the same as the abovementioned methods (Figure 4).

FIGURE 4

FIGURE 4. The flowchart of the definition of I-D thresholds based on TRIGRS at the grid cell scale.

Rainfall thresholds defined at any scale are not applicable to rainfall events of any rainfall duration. The defined rainfall thresholds are valid for a range of duration with initial and final durations. The initial duration is the duration that causes the whole study area or each slope unit unstable for the first time. The final duration is the maximum duration at which the increase in duration no longer affects the stability for the given range of intensities.

Results

Factor of safety maps

When I and D are at the maximum, that is, $I$ = 30 mm/h and $D$ = 60 h, the $F_s$ maps under different soil mechanical and hydraulic parameters conditions can reflect the number of slope units and grid cells with critical rainfall and whether the whole study area has critical rainfall.

Supplementary Video 1 (in the supplementary material) shows the distribution variation of grid cells with $F_s<1$ under the maximum I-D condition when $c$, $\phi$, and ${\gamma }_s$ were 0.8, 0.9, 1.1, and 1.2 times the standard values. The whole study area had critical rainfall under given soil mechanical parameters. Figure 5 shows the number of slope units and grid cells with critical rainfall under given soil physical parameters. When $c$ was 0.8, 0.9, 1.1, and 1.2 times the standard value, the number of slope units with critical rainfall was 46, 45, 39, and 36, respectively. The number of grid cells with critical rainfall was 13,518, 11,585, 7,613, and 3,414, respectively. The number of slope units and grid cells with critical rainfall decreased when $c$ increased. When $\phi$ was 0.8, 0.9, 1.1, and 1.2 times the standard value, the number of slope units with critical rainfall was 45, 44, 40, and 40, respectively. The number of slope units with critical rainfall was 10,930, 10,201, 8,800, and 8,122, respectively. The number of slope units and grid cells with critical rainfall decreased when $\phi$ increased. When ${\gamma }_s$ was 0.8, 0.9, 1.1, and 1.2 times the standard value, the number of slope units with critical rainfall was 37, 40, 45, and 45, respectively. The number of grid cells with critical rainfall was 4,324, 7,789, 10,680, and 11,639, respectively. The number of slope units and grid cells with critical rainfall increased when ${\gamma }_s$ increased.

FIGURE 5

FIGURE 5. The number of objects with critical rainfall (A) slope units and (B) grid cells.

Supplementary Video 2 (in the supplementary material) shows the distribution variation of grid cells with $F_s<1$ under the maximum I-D condition when $K_s$ and $D_0$ were 0.7, 0.8, 1.2, and 1.3 times the standard values. In these cases, the whole study area had critical rainfall. The number of slope units and grid cells with critical rainfall was 41 and 9,502. The number of slope units and grid cells with critical rainfall did not vary with $K_s$ or $D_0$.

I-D thresholds at the basin scale

Supplementary Video 3 (in the supplementary material) show the variation of I-D thresholds defined at the basin scale when $c$, $\phi$, and ${\gamma }_s$ were 0.8, 0.9, 1.1, and 1.2 times the standard values. Figures 6A–C show the comparison of thresholds defined at the basin scale under given $c$, $\phi$, and ${\gamma }_s$ values, respectively. The results showed that the threshold with higher $c$ or $\phi$ was located on the higher part of the graph. The threshold with higher ${\gamma }_s$ was located on the lower part of the graph.

FIGURE 6

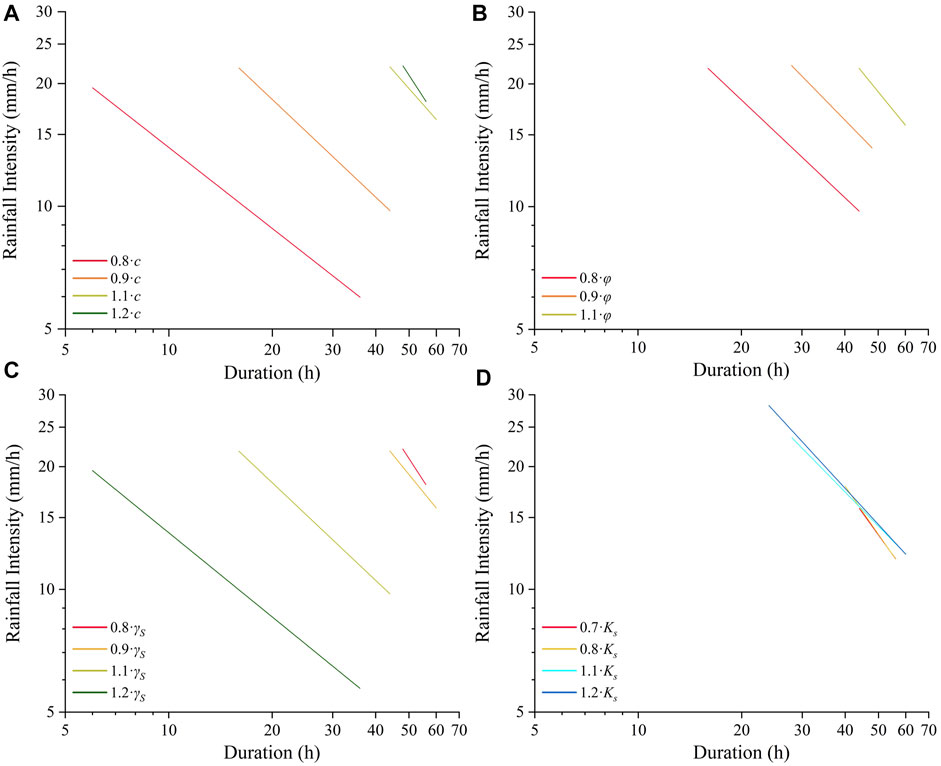
FIGURE 6. I-D thresholds defined at the basin scale under given soil mechanical and hydraulic parameters: (A) $c$, (B) $\phi$ (the thresholds were the same under the condition of 1.1$\bullet \phi$ and 1.2$\bullet \phi$), (C) ${\gamma }_s$, and (D) $K_s$.

Supplementary Video 4 (in the supplementary material) and Figure 7 show the variation of thresholds defined at the basin scale when $K_s$ and $D_0$ were 0.7, 0.8, 1.2, and 1.3 times the standard values. Figure 6D shows the comparison of thresholds defined at the basin scale under given $K_s$ values. The results showed that the variation in $K_s$ did not significantly influence the position of thresholds defined at the basin scale. The threshold with higher $K_s$ had a larger applicable duration range. Meanwhile, under the condition evaluated, $D_0$ did not influence the position of thresholds defined at the basin scale.

FIGURE 7

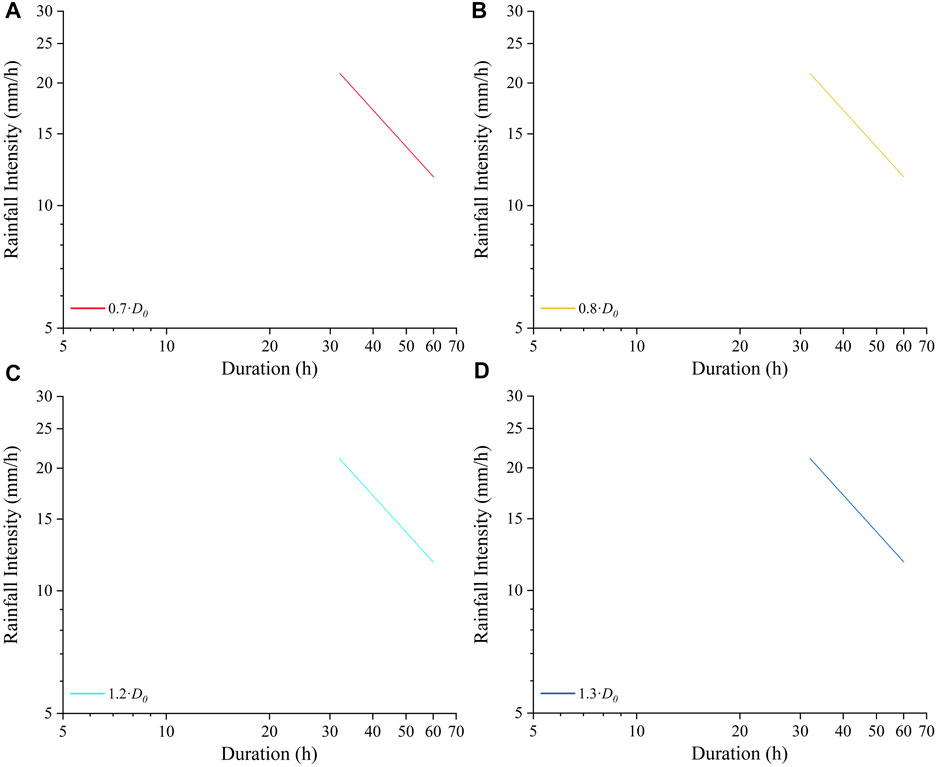
FIGURE 7. I-D thresholds defined at the basin scale under the conditions: (A) 0.8$\bullet D_0$, (B) 0.9$\bullet D_0$, (C) 1.1$\bullet D_0$, and (D) 1.2$\bullet D_0$.

I-D thresholds at the slope unit scale

Supplementary Video 5 (in the supplementary material) show the variation of I-D thresholds defined at the slope unit scale when$c$, $\phi$, and ${\gamma }_s$ were 0.8, 0.9, 1.1, and 1.2 times the standard values. Figures 8A–C show the comparison of thresholds defined at the slope unit scale under given $c$, $\phi$, and ${\gamma }_s$ values, respectively. The results showed that the thresholds with higher $c$ or $\phi$ tended to be the higher part of the graph. The thresholds with higher ${\gamma }_s$ tended to be the lower part of the graph.

FIGURE 8

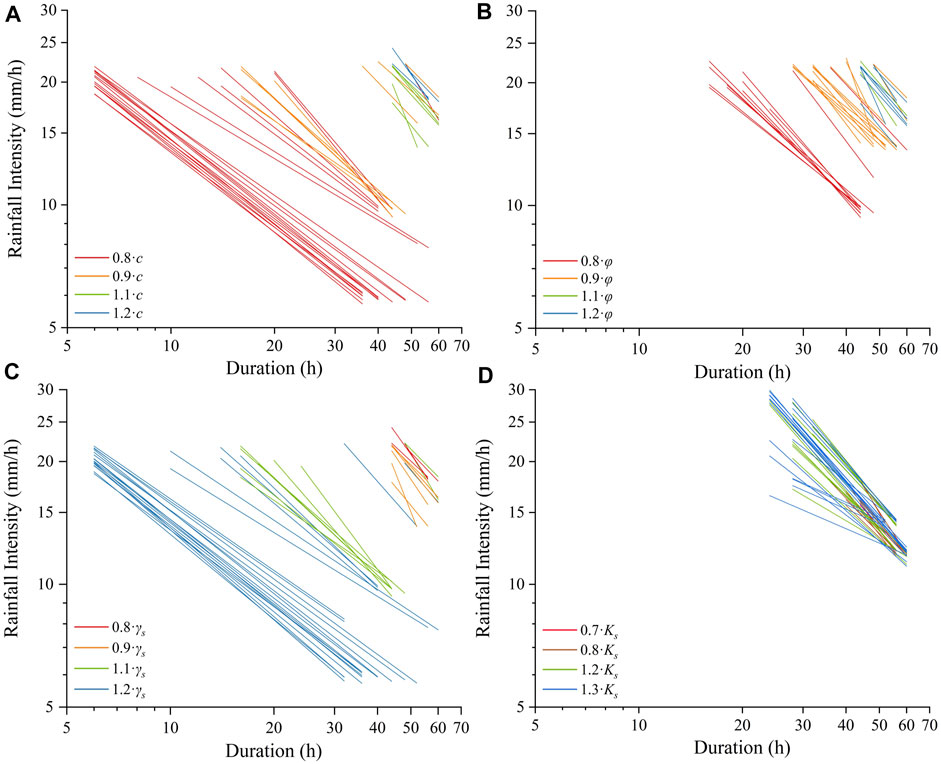
FIGURE 8. I-D thresholds defined at the slope unit scale under given soil mechanical and hydraulic parameters: (A) $c$, (B) $\phi$, (C) ${\gamma }_s$, and (D) $K_s$.

Supplementary Video 6 (in the supplementary material) and Figure 9 show the variation of thresholds defined at the slope unit scale when $K_s$ and $D_0$ were 0.7, 0.9, 1.1, and 1.2 times the standard values. Figure 8D shows the comparison of thresholds defined at the slope unit scale under given $K_s$ values. The results showed that the variation in $K_s$ did significantly influence the position of thresholds defined at the slope unit scale. The thresholds with higher $K_s$ tended to be applicable to large duration ranges. $D_0$ did not influence the position of thresholds defined at the slope unit scale under the condition evaluated.

FIGURE 9

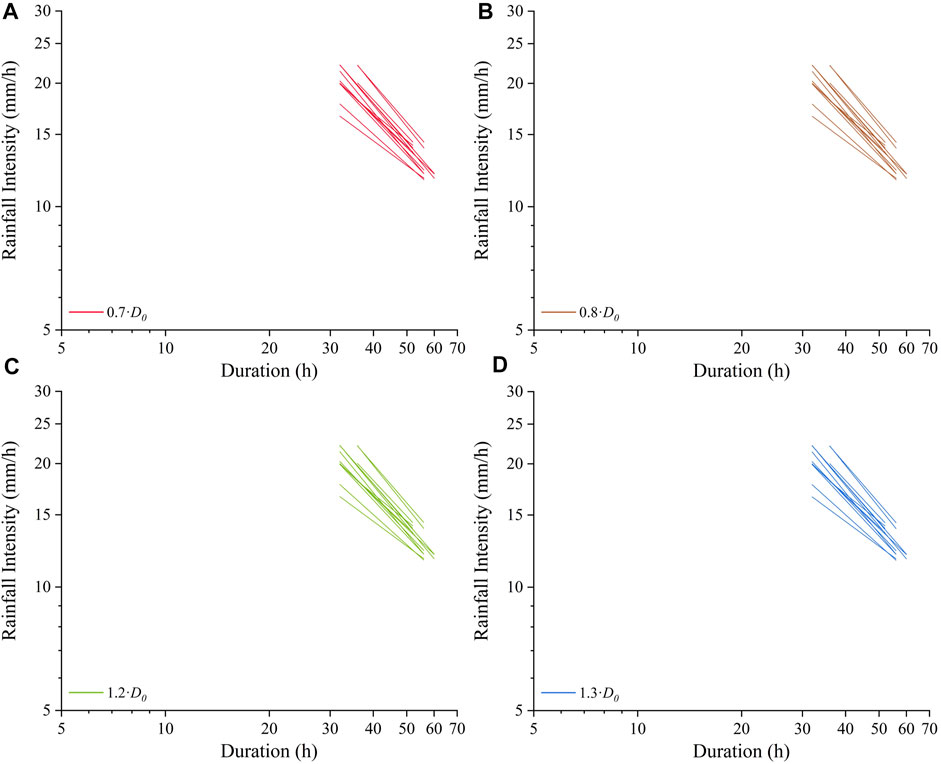
FIGURE 9. I-D thresholds defined at the slope unit scale under the conditions: (A) 0.8$\bullet D_0$, (B) 0.9$\bullet D_0$, (C) 1.1$\bullet D_0$, and (D) 1.2$\bullet D_0$.

I-D thresholds at the grid cell scale

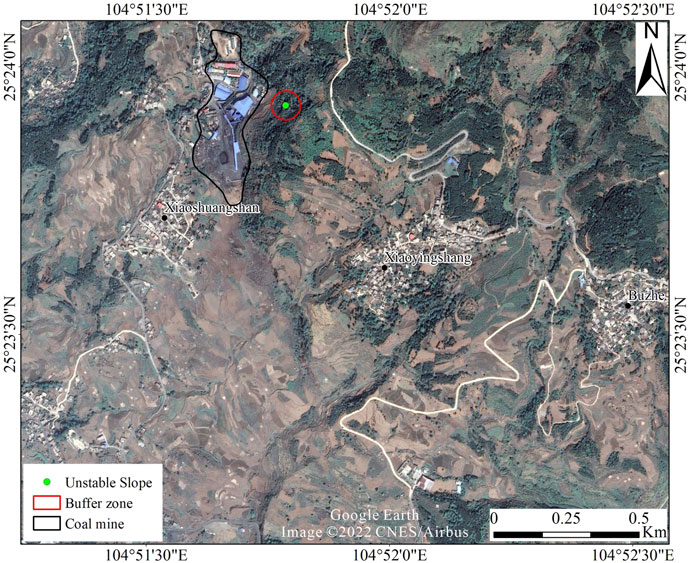
A monitored unstable slope is located near a coal mine in the study area. A buffer zone was built with a radius of 50 m around the unstable slope (Figure 10). I-D thresholds were defined for the grid cells with critical rainfall in the buffer zone.

FIGURE 10

FIGURE 10. Location of the monitored unstable slope, coal mine, and built buffer zone.

Supplementary Video 7 (in the supplementary material) show the variation of I-D thresholds defined at the grid cell scale when $c$, $\phi$, and ${\gamma }_s$ were 0.8, 0.9, 1.1, and 1.2 times the standard values. Figures 11A–C show the comparison of thresholds defined at the grid cell scale under given $c$, $\phi$, and ${\gamma }_s$ values, respectively. The results showed that the thresholds with higher $c$ or $\phi$ tended to be the higher part of the graph. The thresholds with higher ${\gamma }_s$ tended to be the lower part of the graph.

FIGURE 11

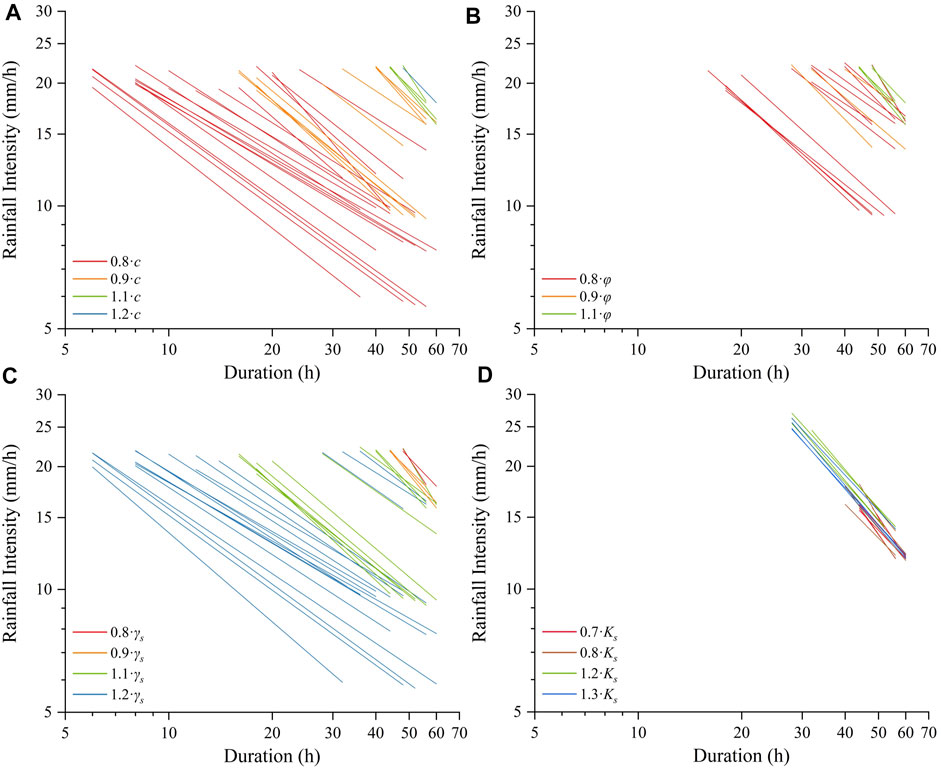
FIGURE 11. I-D thresholds defined at the grid cell scale under different soil mechanical and hydraulic parameters: (A) $c$, (B) $\phi$ (the thresholds were the same under the condition of 1.1$\bullet \phi$ and 1.2$\bullet \phi$), (C) ${\gamma }_s$, and (D) $K_s$.

Supplementary Video 8 (in the supplementary material) and Figure 12 show the variation of I-D thresholds defined at the grid cell scale when $K_s$ and $D_0$ were 0.7, 0.9, 1.1, and 1.2 times the standard values. Figure 11D shows the comparison of thresholds defined at the gird cell scale under given $K_s$ values. The results showed that the variation in $K_s$ did significantly influence the position of thresholds defined at the grid cell scale. The thresholds with higher $K_s$ tended to be applicable to large duration ranges. $D_0$ did not influence the position of thresholds defined at the grid cell scale under the condition evaluated.

FIGURE 12

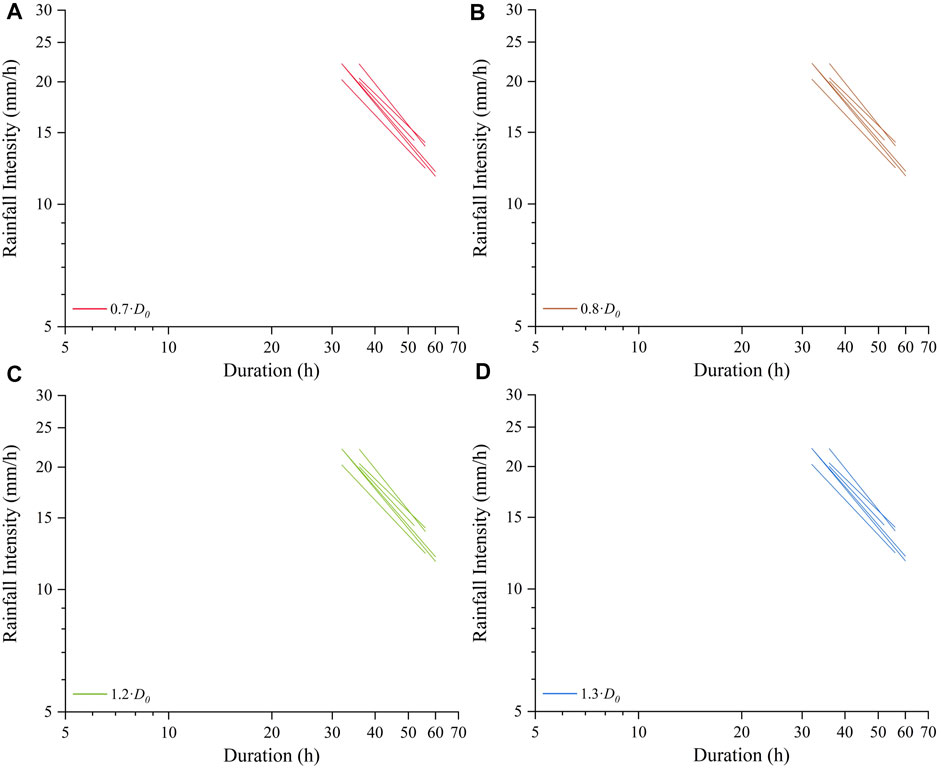
FIGURE 12. I-D thresholds defined at the grid cell scale under the conditions: (A) 0.8$\bullet D_0$, (B) 0.9$\bullet D_0$, (C) 1.1$\bullet D_0$, and (D) 1.2$\bullet D_0$.

Discussion

The methods of defining rainfall thresholds at different scales have their own characteristics. At the basin scale, given that the threshold is defined for the entire area, the process is the simplest. However, the defined threshold can only judge the occurrence of landslides and cannot provide detailed spatial information for landslide prediction. At the slope unit scale, given that the thresholds are defined for slope units with critical rainfall, the process is relatively complicated. The defined thresholds can provide spatial information specific to the range of slope units for prediction. At the grid cell scale, given that the thresholds are defined for grid cells with critical rainfall, the process is the most complicated. The defined thresholds can provide the most spatial information (i.e., specific to the range of grid cells) for prediction. When defining rainfall thresholds at the basin and slope unit scales, an additional condition is used to determine whether I-D conditions cause instability ($a_f>a_c$). When defining rainfall thresholds at the grid cell scale, the rule for determining whether I-D conditions cause instability is simply $F_s<1$ without additional conditions.

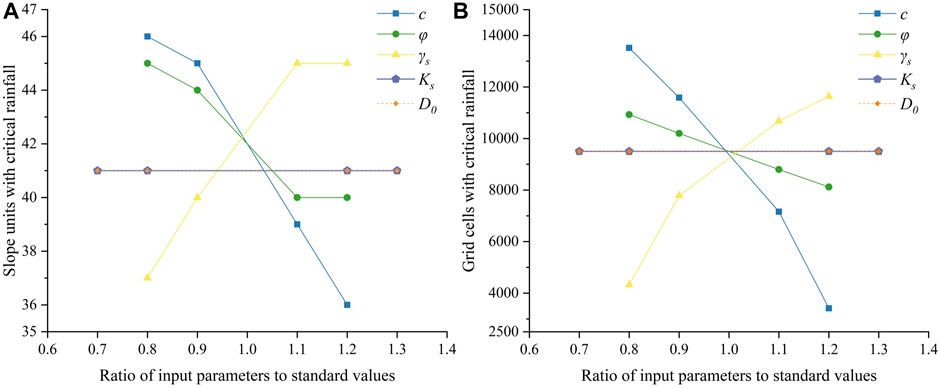
Soil physical parameters influence the number and position of rainfall thresholds defined at various scales. The number of rainfall thresholds is the number of objects warned by thresholds (i.e., the objects with critical rainfall). At the basin scale, the rainfall threshold was defined for the entire study area, and the entire study area had critical rainfall under the considered conditions in this study. At the slope unit and grid cell scales, the number of rainfall thresholds was positively correlated with ${\gamma }_s$ and negatively correlated with $c$ and $\phi$. $K_s$ and $D_0$ did not cause any variation (Figure 5).

For threshold position, the position of thresholds varied positively with $c$ and $\phi$ and varied negatively with ${\gamma }_s$. Under the considered conditions, $K_s$ did not significantly influence the threshold position. The thresholds with higher $K_s$ were applicable to larger duration ranges. $D_0$ did not influence the threshold position. Marin and Velásquez (2020) discovered that $K_s$ did not produce a noticeable variation on the position of the I-D threshold defined at the basin scale, and $D_0$ did not affect the position of threshold, which are in line with the results of this study. Wu et al. (2017) conducted a sensitivity analysis of soil physical parameters to evaluate the rainfall threshold determined by using TRIGRS. In the literature (Wu et al., 2017), rainfall threshold is defined as the critical rainfall condition causing the simulated $F_s$ to be less than a specific critical value under a specific warning duration. Actually, this study conducted the sensitivity analysis of soil physical parameters to $F_s$. Wu et al. (2017) proposed that $F_s$ varied positively with $c$ and $\phi$, negatively with ${\gamma }_s$. $c$, and $\phi$, and ${\gamma }_s$ affected $F_s$ more significantly than $K_s$ and $D_0$. Thus, the influence of soil physical parameters on the position of rainfall thresholds is the same as the influence on $F_s$.

TRIGRS does not have a function for defining rainfall thresholds. Rainfall thresholds are defined by analyzing the relationship between the output $F_s$ grid and the input rainfall conditions of TRIGRS. The conditions for determining landslide occurrence differ in defining rainfall thresholds at various scales. The methods at the basin and slope unit scales take the condition that serval grid cells with $F_s<\mathit{1}$ exist for given rainfall conditions to determine landslide occurrence, which is to analyze the overall behavior of unstable grid cells. The method at the grid cell scale analyzes the individual behavior of a single unstable grid cell by treating a single grid cell with $F_s<\mathit{1}$ as a landslide. The variation of $F_s$ of a random single grid cell directly influences the definition of rainfall thresholds at the grid cell scale. For example, under the conditions of $c$ was 0.8 and 1.2 times the standard value, the variation in the number of grid cells with $F_s<1$ is 10,104. The variation directly caused the variation of 10,104 for the number of rainfall thresholds defined at the grid cell scale. However, the variation only caused the variation of 10 for the number of rainfall thresholds defined at the slope unit scale. Thus, the method at the grid cell scale is easier affected by the uncertainty and spatial variability of soil physical parameters.

Conclusion

The influence of soil mechanical and hydraulic parameters on the definition of I-D thresholds based on TRIGRS can be divided into the influence on the number of rainfall thresholds and threshold position.

The number of rainfall thresholds defined at the slope unit and grid cell scale decreased with $c$ and $\phi$, increased with ${\gamma }_s$, and did not vary with $K_s$ and $D_0$. Under the considered conditions, the number of thresholds defined at the basin scale was not affected by soil physical parameters.

The position of rainfall thresholds varied positively with $c$ and $\phi$ and negatively with ${\gamma }_s$. $K_s$ did not produce a noticeable variation in the threshold position. $D_0$ did not influence the threshold position. The thresholds with greater $K_s$ were applicable to larger duration ranges.

Soil mechanical and hydraulic parameters have less effect on rainfall thresholds defined by analyzing the overall behavior of unstable grid cells (i.e., basin and slope unit scales) than the thresholds defined by analyzing the individual behavior of unstable grid cells (i.e., grid cell scale).

Data availability statement

The data analyzed in this study are subject to the following licenses/restrictions: The data presented in this research are available from the corresponding author by reasonable request. Requests to access these datasets should be directed to Qigang Jiang, jiangqigang@jlu.edu.cn.

Author contributions

SZ collected the soil samples, designed the analysis, performed the analysis, and wrote the original draft. XX developed a Python program for the definition of rainfall thresholds. The other authors helped to draft the manuscript.

Funding

This study was supported by The First Surveying and Mapping Institute of Guizhou Province under Grant number GZWH-2021-4536Y.

Acknowledgments

We thank The First Surveying and Mapping Institute of Guizhou Province for the assistance in the field sampling.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.971655/full#supplementary-material

References

Aleotti, P. (2004). A warning system for rainfall-induced shallow failures. Eng. Geol. 73, 247–265. doi:10.1016/j.enggeo.2004.01.007

CrossRef Full Text | Google Scholar

Alvioli, M., and Baum, R. L. (2016). Parallelization of the TRIGRS model for rainfall-induced landslides using the message passing interface. Environ. Model. Softw. 81, 122–135. doi:10.1016/j.envsoft.2016.04.002

CrossRef Full Text | Google Scholar

Alvioli, M., Guzzetti, F., and Rossi, M. (2014). Scaling properties of rainfall induced landslides predicted by a physically based model. Geomorphology 213, 38–47. doi:10.1016/j.geomorph.2013.12.039

CrossRef Full Text | Google Scholar

Alvioli, M., Melillo, M., Guzzetti, F., Rossi, M., Palazzi, E., von Hardenberg, J., et al. (2018). Implications of climate change on landslide hazard in Central Italy. Sci. Total Environ. 630, 1528–1543. doi:10.1016/j.scitotenv.2018.02.315

PubMed Abstract | CrossRef Full Text | Google Scholar

Baum, R. L., Coe, J. A., Godt, J. W., Harp, E. L., Reid, M. E., Savage, W. Z., et al. (2005)., Regional landslide-hazard assessment for Seattle, Washington, USA. Landslides 2, 266–279. doi:10.1007/s10346-005-0023-y

CrossRef Full Text | Google Scholar

Baum, R. L., Godt, J. W., and Savage, W. Z. (2010). Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. 115, F03013. doi:10.1029/2009JF001321

CrossRef Full Text | Google Scholar

Baum, R. L., Savage, W. Z., and Godt, J. W. (2002). TRIGRS—a fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. Golden, Colorado: U. S. Geol. Surv. Open-File Rep. 424, 38.

Google Scholar

Baum, R. L., Savage, W. Z., and Godt, J. W. (2008). Trigrs — a fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis, version 2.0. Denver, Colorado, USA: US Geological Survey Open-File. Report 2008-1159.

Google Scholar

Bicocchi, G., D’Ambrosio, M., Vannocci, P., Nocentini, M., Tacconi-Stefanelli, C., Masi, E., et al. (2015). “Preliminary assessment of the factors controlling the geotechnical and hydrological properties in the hillslope deposits of eastern Tuscany (Central Italy),” in IAMG 2015 proceedings, 867–874.

Google Scholar

Bordoni, M., Corradini, B., Lucchelli, L., Valentino, R., Bittelli, M., Vivaldi, V., et al. (2019). Empirical and physically based thresholds for the occurrence of shallow landslides in a prone area of Northern Italian Apennines. WaterSwitzerl. 11, 2653. doi:10.3390/W11122653

CrossRef Full Text | Google Scholar

Bordoni, M., Meisina, C., Valentino, R., Bittelli, M., and Chersich, S. (2015). Site-specific to local-scale shallow landslides triggering zones assessment using TRIGRS. Nat. Hazards Earth Syst. Sci. 15, 1025–1050. doi:10.5194/nhess-15-1025-2015

CrossRef Full Text | Google Scholar

Brunetti, M. T., Peruccacci, S., Rossi, M., Luciani, S., Valigi, D., and Guzzetti, F. (2010). Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 10, 447–458. doi:10.5194/nhess-10-447-2010

CrossRef Full Text | Google Scholar

Caine, N. (1980). The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. Geogr. 62, 23–27. doi:10.1080/04353676.1980.11879996

CrossRef Full Text | Google Scholar

Calvello, M. (2017). Early warning strategies to cope with landslide risk. Riv. Ital. Geotec. 2017, 63–91. doi:10.19199/2017.2.0557-1405.063

CrossRef Full Text | Google Scholar

Campbell, R. H. (1975). Soil slips, debris flows, and rainstorms in the Santa Monica Mountains and vicinity, southern California. Washington, DC, USA: US Geological Survey Professional Paper, 851.

Google Scholar

Catani, F., Segoni, S., and Falorni, G. (2010). An empirical geomorphology‐based approach to the spatial prediction of soil thickness at catchment scale. Water Resour. Res. 46, W05508. doi:10.1029/2008WR007450

CrossRef Full Text | Google Scholar

Ciurleo, M., Cascini, L., and Calvello, M. (2017). A comparison of statistical and deterministic methods for shallow landslide susceptibility zoning in clayey soils. Eng. Geol. 223, 71–81. doi:10.1016/j.enggeo.2017.04.023

CrossRef Full Text | Google Scholar

Ciurleo, M., Mandaglio, M. C., and Moraci, N. (2019). Landslide susceptibility assessment by TRIGRS in a frequently affected shallow instability area. Landslides 16, 175–188. doi:10.1007/s10346-018-1072-3

CrossRef Full Text | Google Scholar

Corominas, J., van Westen, C., Frattini, P., Cascini, L., Malet, J. P., Fotopoulou, S., et al. (2014). Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 73, 209–263. doi:10.1007/s10064-013-0538-8

CrossRef Full Text | Google Scholar

de Lima Neves Seefelder, C., Koide, S., and Mergili, M. (2017). Does parameterization influence the performance of slope stability model results? A case study in rio de Janeiro, Brazil. Landslides 14, 1389–1401. doi:10.1007/s10346-016-0783-6

CrossRef Full Text | Google Scholar

Gardner, W. R. (1958). Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 85, 228–232. doi:10.1097/00010694-195804000-00006

CrossRef Full Text | Google Scholar

Gariano, S. L., and Guzzetti, F. (2016). Landslides in a changing climate. Earth. Sci. Rev. 162, 227–252. doi:10.1016/j.earscirev.2016.08.011

CrossRef Full Text | Google Scholar

Gioia, E., Speranza, G., Ferretti, M., Godt, J. W., Baum, R. L., and Marincioni, F. (2016). Application of a process-based shallow landslide hazard model over a broad area in Central Italy. Landslides 13, 1197–1214. doi:10.1007/s10346-015-0670-6

CrossRef Full Text | Google Scholar

Guzzetti, F., Gariano, S. L., Peruccacci, S., Brunetti, M. T., Marchesini, I., Rossi, M., et al. (2020). Geographical landslide early warning systems. Earth. Sci. Rev. 200, 102973. doi:10.1016/j.earscirev.2019.102973

CrossRef Full Text | Google Scholar

Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2007). Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 98, 239–267. doi:10.1007/s00703-007-0262-7

CrossRef Full Text | Google Scholar

Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P. (2008). The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 5, 3–17. doi:10.1007/s10346-007-0112-1

CrossRef Full Text | Google Scholar

He, J., Qiu, H., Qu, F., Hu, S., Yang, D., Shen, Y., et al. (2021). Prediction of spatiotemporal stability and rainfall threshold of shallow landslides using the TRIGRS and Scoops3D models. Catena 197, 104999. doi:10.1016/j.catena.2020.104999

CrossRef Full Text | Google Scholar

He, S., Wang, J., and Liu, S. (2020). Rainfall event-duration thresholds for landslide occurrences in China. Water 12, 494. doi:10.3390/w12020494

CrossRef Full Text | Google Scholar

He, X., Hong, Y., Vergara, H., Zhang, K., Kirstetter, P. E., Gourley, J. J., et al. (2016). Development of a coupled hydrological-geotechnical framework for rainfall-induced landslides prediction. J. Hydrol. X. 543, 395–405. doi:10.1016/j.jhydrol.2016.10.016

CrossRef Full Text | Google Scholar

Ho, J.-Y., Lee, K. T., Chang, T.-C., Wang, Z.-Y., and Liao, Y.-H. (2012). Influences of spatial distribution of soil thickness on shallow landslide prediction. Eng. Geol. 124, 38–46. doi:10.1016/j.enggeo.2011.09.013

CrossRef Full Text | Google Scholar

Ip, S. C. Y., Rahardjo, H., and Satyanaga, A. (2021). Three-dimensional slope stability analysis incorporating unsaturated soil properties in Singapore. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 15, 98–112. doi:10.1080/17499518.2020.1737880

CrossRef Full Text | Google Scholar

Iverson, R. M. (2000). Landslide triggering by rain infiltration. Water Resour. Res. 36, 1897–1910. doi:10.1029/2000WR900090

CrossRef Full Text | Google Scholar

Keefer, D. K., Wilson, R. C., Mark, R. K., Brabb, E. E., Brown, W. M., Ellen, S. D., et al. (1987). Real-time landslide warning during heavy rainfall. Science 238, 921–925. doi:10.1126/science.238.4829.921

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, D., Im, S., Lee, S. H., Hong, Y., and Cha, K.-S. (2010). Predicting the rainfall-triggered landslides in a forested mountain region using TRIGRS model. J. Mt. Sci. 7, 83–91. doi:10.1007/s11629-010-1072-9

CrossRef Full Text | Google Scholar

Lee, G., An, H., and Kim, M. (2017). Comparing the performance of TRIGRS and TiVaSS in spatial and temporal prediction of rainfall-induced shallow landslides. Environ. Earth Sci. 76, 315. doi:10.1007/s12665-017-6635-4

CrossRef Full Text | Google Scholar

Li, W. Y., Liu, C., Scaioni, M., Sun, W. W., Chen, Y., Yao, D. J., et al. (2017). Spatio-temporal analysis and simulation on shallow rainfall-induced landslides in China using landslide susceptibility dynamics and rainfall I-D thresholds. Sci. China Earth Sci. 60, 720–732. doi:10.1007/s11430-016-9008-4

CrossRef Full Text | Google Scholar

Lim, T. T., Rahardjo, H., Chang, M. F., and Fredlund, D. G. (1996). Effect of rainfall on matric suctions in a residual soil slope. Can. Geotech. J. 33, 618–628. doi:10.1139/t96-087

CrossRef Full Text | Google Scholar

Lin, Q., and Wang, Y. (2018). Spatial and temporal analysis of a fatal landslide inventory in China from 1950 to 2016. Landslides 15, 2357–2372. doi:10.1007/s10346-018-1037-6

CrossRef Full Text | Google Scholar

Ma, S., Xu, C., Xu, X., He, X., Qian, H., Jiao, Q., et al. (2020). Characteristics and causes of the landslide on july 23, 2019 in shuicheng, Guizhou province, China. Landslides 17, 1441–1452. doi:10.1007/s10346-020-01374-x

CrossRef Full Text | Google Scholar

Marin, R. J., García, E. F., and Aristizábal, E. (2020). Effect of basin morphometric parameters on physically-based rainfall thresholds for shallow landslides. Eng. Geol. 278, 105855. doi:10.1016/j.enggeo.2020.105855

CrossRef Full Text | Google Scholar

Marin, R. J., and Mattos, Á. J. (2020). Physically-based landslide susceptibility analysis using Monte Carlo simulation in a tropical mountain basin. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 14, 192–205. doi:10.1080/17499518.2019.1633582

CrossRef Full Text | Google Scholar

Marin, R. J. (2020). Physically based and distributed rainfall intensity and duration thresholds for shallow landslides. Landslides 17, 2907–2917. doi:10.1007/s10346-020-01481-9

CrossRef Full Text | Google Scholar

Marin, R. J., Velásquez, M. F., García, E. F., Alvioli, M., and Aristizábal, E. (2021). Assessing two methods of defining rainfall intensity and duration thresholds for shallow landslides in data-scarce catchments of the Colombian Andean Mountains. Catena 206, 105563. doi:10.1016/j.catena.2021.105563

CrossRef Full Text | Google Scholar

Marin, R. J., and Velásquez, M. F. (2020). Influence of hydraulic properties on physically modelling slope stability and the definition of rainfall thresholds for shallow landslides. Geomorphology 351, 106976. doi:10.1016/j.geomorph.2019.106976

CrossRef Full Text | Google Scholar

Melillo, M., Brunetti, M. T., Peruccacci, S., Gariano, S. L., Roccati, A., and Guzzetti, F. (2018). A tool for the automatic calculation of rainfall thresholds for landslide occurrence. Environ. Model. Softw. 105, 230–243. doi:10.1016/j.envsoft.2018.03.024

CrossRef Full Text | Google Scholar

Montrasio, L., and Valentino, R. (2008). A model for triggering mechanisms of shallow landslides. Nat. Hazards Earth Syst. Sci. 8, 1149–1159. doi:10.5194/nhess-8-1149-2008

CrossRef Full Text | Google Scholar

Montrasio, L., and Valentino, R. (2007). Experimental analysis and modelling of shallow landslides. Landslides 4, 291–296. doi:10.1007/s10346-007-0082-3

CrossRef Full Text | Google Scholar

Montrasio, L., Valentino, R., and Losi, G. L. (2011). Towards a real-time susceptibility assessment of rainfall-induced shallow landslides on a regional scale. Nat. Hazards Earth Syst. Sci. 11, 1927. doi:10.5194/nhess-11-1927-2011

CrossRef Full Text | Google Scholar

Park, D. W., Nikhil, N. V., and Lee, S. R. (2013). Landslide and debris flow susceptibility zonation using TRIGRS for the 2011 Seoul landslide event. Nat. Hazards Earth Syst. Sci. 13, 2833–2849. doi:10.5194/nhess-13-2833-2013

CrossRef Full Text | Google Scholar

Park, J. Y., Lee, S. R., Lee, D. H., Kim, Y. T., and Lee, J. S. (2019). A regional-scale landslide early warning methodology applying statistical and physically based approaches in sequence. Eng. Geol. 260, 105193. doi:10.1016/j.enggeo.2019.105193

CrossRef Full Text | Google Scholar

Peres, D. J., and Cancelliere, A. (2014). Derivation and evaluation of landslide-triggering thresholds by a Monte Carlo approach. Hydrol. Earth Syst. Sci. 18, 4913–4931. doi:10.5194/hess-18-4913-2014

CrossRef Full Text | Google Scholar

Peruccacci, S., Brunetti, M. T., Luciani, S., Vennari, C., and Guzzetti, F. (2012). Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 139–140, 79–90. doi:10.1016/j.geomorph.2011.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Piciullo, L., Calvello, M., and Cepeda, J. M. (2018). Territorial early warning systems for rainfall-induced landslides. Earth. Sci. Rev. 179, 228–247. doi:10.1016/j.earscirev.2018.02.013

CrossRef Full Text | Google Scholar

Piciullo, L., Gariano, S. L., Melillo, M., Brunetti, M. T., Peruccacci, S., Guzzetti, F., et al. (2017). Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 14, 995–1008. doi:10.1007/s10346-016-0750-2

CrossRef Full Text | Google Scholar

Raia, S., Alvioli, M., Rossi, M., Baum, R. L., Godt, J. W., and Guzzetti, F. (2014). Improving predictive power of physically based rainfall-induced shallow landslide models: A probabilistic approach. Geosci. Model Dev. 7, 495–514. doi:10.5194/gmd-7-495-2014

CrossRef Full Text | Google Scholar

Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Physics 1, 318–333. doi:10.1063/1.1745010

CrossRef Full Text | Google Scholar

Salciarini, D., Fanelli, G., and Tamagnini, C. (2017). A probabilistic model for rainfall—Induced shallow landslide prediction at the regional scale. Landslides 14, 1731–1746. doi:10.1007/s10346-017-0812-0

CrossRef Full Text | Google Scholar

Salciarini, D., Godt, J. W., Savage, W. Z., Baum, R. L., and Conversini, P. (2008). Modeling landslide recurrence in Seattle, Washington, USA. Eng. Geol. 102, 227–237. doi:10.1016/j.enggeo.2008.03.013

CrossRef Full Text | Google Scholar

Salciarini, D., Godt, J. W., Savage, W. Z., Conversini, P., Baum, R. L., and Michael, J. A. (2006). Modeling regional initiation of rainfall-induced shallow landslides in the eastern Umbria Region of central Italy. Landslides 3, 181–194. doi:10.1007/s10346-006-0037-0

CrossRef Full Text | Google Scholar

Salciarini, D., Tamagnini, C., Conversini, P., and Rapinesi, S. (2012). Spatially distributed rainfall thresholds for the initiation of shallow landslides. Nat. Hazards 61, 229–245. doi:10.1007/s11069-011-9739-2

CrossRef Full Text | Google Scholar

Segoni, S., Piciullo, L., and Gariano, S. L. (2018). A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 15, 1483–1501. doi:10.1007/s10346-018-0966-4

CrossRef Full Text | Google Scholar

Srivastava, R., and Yeh, T. J. (1991). Analytical solutions for one‐dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 27, 753–762. doi:10.1029/90WR02772

CrossRef Full Text | Google Scholar

Taylor, D. W. (1948). Fundamentals of soil mechanics. New York: Wiley.

Google Scholar

Tran, T. V., Alvioli, M., Lee, G., and An, H. U. (2018). Three-dimensional, time-dependent modeling of rainfall-induced landslides over a digital landscape: A case study. Landslides 15, 1071–1084. doi:10.1007/s10346-017-0931-7

CrossRef Full Text | Google Scholar

United Nations International Strategy for Disaster Reduction (UNISDR) (2015). Sendai framework for disaster risk reduction 2015–2030. Available at: http://www.wcdrr.org/uploads/Sendai_Framework_for_Disaster_Risk_Reduction_2015-2030.pdf (Access June 6, 2015).

Google Scholar

Van Genuchten, M. T. (1980). A closed‐form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Vanapalli, S. K., Fredlund, D. G., Pufahl, D. E., and Clifton, A. W. (1996). Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 33, 379–392. doi:10.1139/t96-060

CrossRef Full Text | Google Scholar

Vieira, B. C., Fernandes, N. F., and Filho, O. A. (2010). Shallow landslide prediction in the serra do mar, são paulo, Brazil. Nat. Hazards Earth Syst. Sci. 10, 1829–1837. doi:10.5194/nhess-10-1829-2010

CrossRef Full Text | Google Scholar

Viet, T. T., Lee, G., Thu, T. M., and An, H. U. (2017). Effect of digital elevation model resolution on shallow landslide modeling using TRIGRS. Nat. Hazards Rev. 18, 04016011. doi:10.1061/(asce)nh.1527-6996.0000233

CrossRef Full Text | Google Scholar

Wei, L. W., Huang, C. M., Chen, H., Lee, C. T., Chi, C. C., and Chiu, C. L. (2018). Adopting the &lt;i&gt;I&lt;/i&gt;&lt;sub&gt;3&lt;/sub&gt;–&lt;i&gt;R&lt;/i&gt;&lt;sub&gt;24&lt;/sub&gt; rainfall index and landslide susceptibility for the establishment of an early warning model for rainfall-induced shallow landslides. Nat. Hazards Earth Syst. Sci. 18, 1717–1733. doi:10.5194/nhess-18-1717-2018

CrossRef Full Text | Google Scholar

Weidner, L., Oommen, T., Escobar-Wolf, R., Sajinkumar, K. S., and Samuel, R. A. (2018). Regional-scale back-analysis using TRIGRS: An approach to advance landslide hazard modeling and prediction in sparse data regions. Landslides 15, 2343–2356. doi:10.1007/s10346-018-1044-7

CrossRef Full Text | Google Scholar

Wilson, R. C. (2005). The rise and fall of a debris‐flow warning system for the San Francisco Bay region, California. Chichester, England: Landslide hazard risk, 493–516. doi:10.1002/9780470012659.ch17

CrossRef Full Text | Google Scholar

Wu, S. J., Hsiao, Y. H., Yeh, K. C., and Yang, S. H. (2017). A probabilistic model for evaluating the reliability of rainfall thresholds for shallow landslides based on uncertainties in rainfall characteristics and soil properties. Nat. Hazards 87, 469–513. doi:10.1007/s11069-017-2773-y

CrossRef Full Text | Google Scholar

Xie, M., Esaki, T., and Zhou, G. (2004). GIS-based probabilistic mapping of landslide hazard using a three-dimensional deterministic model. Nat. Hazards (Dordr). 33, 265–282. doi:10.1023/B:NHAZ.0000037036.01850.0d

CrossRef Full Text | Google Scholar

Yu, B., Wang, T., Zhu, Y., and Zhu, Y. (2016). Topographical and rainfall factors determining the formation of gully-type debris flows caused by shallow landslides in the Dayi area, Guizhou Province, China. Environ. Earth Sci. 75, 551–618. doi:10.1007/s12665-016-5243-z

CrossRef Full Text | Google Scholar

Zhang, N., et al. (2017). A study of the instability mechanism and investigation methods of shallow bedrock landslides in karst mountain areas: Taking the jinxing landslide in dafang county as an example. Hydrogeol. Eng. Geol. 44, 142–146. (In Chinese).

Google Scholar

Zhang, S., Jiang, Q., Wu, D., Xu, X., Tan, Y., and Shi, P. (2022). Improved method of defining rainfall intensity and duration thresholds for shallow landslides based on TRIGRS. Water 14, 524. doi:10.3390/w14040524

CrossRef Full Text | Google Scholar

Zhang, S., Zhao, L., Delgado-Tellez, R., and Bao, H. (2018). A physics-based probabilistic forecasting model for rainfall-induced shallow landslides at regional scale. Nat. Hazards Earth Syst. Sci. 18, 969–982. doi:10.5194/nhess-18-969-2018

CrossRef Full Text | Google Scholar

Zhao, G. (2021). Soil physical characteristics of calcareous soil and yellow soil in a small catchment of typical karst area and their water regulation techniques. Guiyang, Guizhou Province, China: Guizhou Minzu University (Guiyang). [master’s thesis]. (In Chinese).

Google Scholar