Advances in seismic imaging of magma and crystal mush

Seismic imaging methods have provided detailed three-dimensional constraints on the physical properties of magmatic systems leading to invaluable insight into the storage, differentiation and dynamics of magma. These constraints have been crucial to the development of our modern understanding of magmatic systems. However, there are still outstanding knowledge gaps resulting from the challenges inherent in seismic imaging of volcanoes. These challenges stem from the complex physics of wave propagation across highly heterogeneous low-velocity anomalies associated with magma reservoirs. Ray-based seismic imaging methods such as travel-time and surface-wave tomography lead to under-recovery of such velocity anomalies and to under-estimation of melt fractions. This review aims to help the volcanologist to fully utilize the insights gained from seismic imaging and account for the resolution limits. We summarize the advantages and limitations of the most common imaging methods and propose best practices for their implementation and the quantitative interpretation of low-velocity anomalies. We constructed and analysed a database of 277 seismic imaging studies at 78 arc, hotspot and continental rift volcanoes. Each study is accompanied by information about the seismic source, part of the wavefield used, imaging method, any detected low-velocity zones, and estimated melt fraction. Thirty nine studies attempted to estimate melt fractions at 22 different volcanoes. Only five studies have found evidence of melt storage at melt fractions above the critical porosity that separates crystal mush from mobile magma. The median reported melt fraction is 13% suggesting that magma storage is dominated by low-melt fraction crystal mush. However, due to the limits of seismic resolution, the seismological evidence does not rule out the presence of small (<10 km³) and medium-sized (<100 km³) high-melt fraction magma chambers at many of the studied volcanoes. The combination of multiple tomographic imaging methods and the wider adoption of methods that use more of the seismic wavefield than the first arriving travel-times, promise to overcome some of the limitations of seismic tomography and provide more reliable constraints on melt fractions. Wider adoption of these new methods and advances in data collection are needed to enable a revolution in imaging magma reservoirs.

1 Introduction

Our understanding of magma differentiation and storage in the crust at arc and hotspot volcanoes is undergoing a paradigm shift. An increasing number of observations are at odds with the classical magma chamber model, which postulates that evolved magma is brewed by fractional crystallization, assimilation of host-rock, and crystal settling in high melt fraction magma chambers that are several cubic kilometres in volume (DePaolo, 1981; Marsh, 1989). According to the magma chamber model, the separation of crystals from melt in the magma chamber is responsible for the diversity in the chemical characteristics of magmas and, to some extent, the eruptive behaviour of volcanoes. However, seismic tomography studies have been unable to detect large melt-rich magma chambers and are generally consistent with low melt fractions (Lees, 2007). In addition, petrological studies of crystal residence and differentiation timescales indicate that most magma chambers are ephemeral (Turner and Costa, 2007; Druitt et al., 2012) and that magmatic systems are likely dominated volumetrically and over long time periods by crystal mush reservoirs (Cooper, 2017).

A similar paradigm shift occurred a few decades ago for mid-ocean ridge magmatic systems following the collection of detailed geophysical images (Solomon and Toomey, 1992; Sinton and Detrick, 1992; Hussenoeder et al., 1996). Those results showed that crustal magma systems at fast-spreading ridges are complex, layered, and mush-dominated and do not conform to predictions for a steady-state, melt-filled axial magma chamber that, based on thermal models and geological observations in ophiolites, were envisioned to be up to 10-km-wide and several kilometres in thickness (Cann 1974; Casey & Karson 1981; Pallister & Hopson 1981).

At fast-spreading ridges such as the East Pacific Rise, the melt distribution inferred from seismic refraction and reflection studies indicates that magma accumulates at several levels in the magmatic system. A narrow (∼1-km-wide), axially discontinuous, and by inference ephemeral, magma lens is imaged 1–2 km beneath the seabed (Detrick et al., 1987; Kent et al., 1990; Hooft et al., 1997; Singh et al., 1998). The axial magma lens overlies a wider (5–7 km) lower-crustal region dominated by crystal mush (e.g., Vera et al., 1990) that broadens significantly at, and below, the Moho transition zone (Dunn et al., 2000; Toomey et al., 2007). The melt fraction in the axial magma lens is spatially variable (Xu et al., 2014) and partially molten magma lenses may also exist off-axis (e.g., Aghaei et al., 2017). Seismic studies at the intermediate-spreading Juan de Fuca Ridge reinforced the general view of a composite magmatic system comprised of small, ephemeral melt lenses (Canales et al., 2006; Carbotte et al., 2006; Van Ark et al., 2007) that caps a crystal mush zone of variable width in the crust (Arnoux et al., 2019) and topmost mantle (VanderBeek et al., 2016). Similar studies at slow-spreading ridges revealed a much more discontinuous and temporally variable magmatic system. Seismic results from the Mid-Atlantic ridge indicate that mantle melts are focused toward the segment centre at mantle depths (e.g., Tolstoy et al., 1993; Hooft et al., 2000; Dunn et al., 2005). In the shallow crust, low-velocity bodies of limited size indicate that melt is redistributed along axis by lateral dike injection to supply seafloor eruptions along the ridge segment (Magde et al., 2000).

The new paradigm at arc and hotspot volcanoes, the mush model, is described in detail by Sparks et al. (2019). The mush model does not entirely eliminate the concept of a magma chamber. Instead, it recognizes that magmatic systems may include both regions of mush and magma chambers. Magma differentiation is inferred to happen primarily in the middle and lower crust in mushy hot zones, but magma chambers can play an essential role in the final stages of magma evolution leading up to eruption (Sparks and Cashman, 2017). A range of melt storage conditions, spanning from low to high melt fraction storage, may exist in systems of different geological settings and maturity (Giordano and Caricchi, 2022).

Seismological and other geophysical studies are often cited as a key body of evidence supporting mush-dominated systems (Cashman and Giordano, 2014; Sparks et al., 2019) but the primary literature is usually cautious about interpreting the presence of melt. A seminal review paper on seismic imaging of magmatic systems by Lees (2007) concluded that “there is a general lack of strong evidence for large regions of pure melt below most volcanoes”. We show that Lees’ conclusions are still valid in 2022 and that more recent experiments have not uncovered large magma chambers.

A lack of evidence does not necessarily equate to evidence of absence. Lees’ review emphasized that the evidence for low melt fraction storage is not entirely conclusive because seismic tomography models come with two important caveats. Firstly, the limited sensitivity of seismic waves and inherent smoothing of many inversion methods lead almost universally to the under-recovery of low-velocity anomalies (Malcolm and Trampert, 2011). Secondly, rock physics models that tie seismic velocities to melt fraction are fraught with large uncertainties and trade-offs, meaning that most published melt fraction estimates are “speculative at best” (quote from Lees, 2007). These caveats are still extremely relevant today, despite the increased quality of seismological data and the development of advanced inversion methods. We discuss seismic resolution and sensitivity in Seismic tomography in brief and the rock physics of partially molten rocks in Seismological signatures of mush and magma.

The mush model has far-reaching implications for a wide range of phenomena, from volcanic hazards to the search for precious metal deposits. Therefore, it is of great importance that its foundations are established on robust observations. To fully understand the seismological evidence for the mush model one needs an understanding of the different imaging methods, seismic wavefield sensitivity and model resolution, and the rock physics of partially molten rocks. There are several barriers which make the results of seismic tomography inaccessible to the non-specialist: i) The last couple of decades have seen a proliferation of tomography methods using different parts of the seismic signal, each with its advantages and drawbacks; ii) There is no standard tomography code used by the community; codes are often proprietary and are used by small groups; iii) The results of seismic tomography depend as much on the inversion method as on accurately predicting the travel-times and on the quality of the input data; iv) Resolution limits and uncertainties are often unclear and/or not properly accounted for.

The principal aims of this review are twofold: 1) to help the volcanologist and other non-specialists to understand and interpret seismic tomography, including its limitations; and 2) to provide a template for the volcano tomography practitioner to enhance the impact of their results and make them more accessible to the volcanological community. We focus in particular on one aspect that previous reviews have only touched on briefly: how can melt fractions be estimated from seismological data? We also summarize the main contributions of volcano tomography to the field of volcanology, particularly concerning the development of the mush model. Our review is accompanied by an online database of volcano tomography studies, which will be updated with new results as they become available.

2 Seismic tomography in brief

Seismic tomography is a family of subsurface imaging techniques that have the objective to determine the seismic properties and structure of a geological target. The key feature of seismic tomography is the reconstruction of the seismic properties of the subsurface (such as the P-wave velocity, $V_P$ and the S-wave velocity, $V_S$) by solving a geophysical inverse problem using recordings of seismic waves propagating in the subsurface. Excellent reviews of the theory and methods behind it can be found e.g., in Iyer and Hirahara (1993) and Nolet (2008), while the methodological limitations are highlighted by Foulger et al. (2013). Earlier reviews that specifically focus on seismic tomography of magmatic systems can be found in Lees (2007) and Koulakov and Shapiro (2015).

The most common type of seismic tomography is arrival-time tomography, and it can be used to illustrate the general underlying principles. The starting point is to identify known seismic phases and measure their time of arrival at the recording station. If one knows the origin time, the average speed of the seismic waves along the assumed propagation path can be determined by dividing the distance by the travel-time. If enough measurements are available to cover the target from multiple angles and azimuths, one can in principle reconstruct the three-dimensional distribution of seismic velocity using one of the well-established algorithms such as the regularized least-squares method or back projection (e.g., Toomey et al., 1994; Zelt and Barton, 1998). In practice, seismic tomography must be carried out iteratively due to the linear approximation that has to be applied to tackle real-world seismic problems that are almost always non-linear, particularly for volcanoes. The main source of non-linearity is the fact that the ray trajectories are dependent on the unknown velocity distribution. If earthquakes are being used, the source parameters are also unknown and must be determined; this results in additional tradeoffs between hypocentral parameters and velocity structure.

The well-established workflow of geophysical inversion starts with an initial guess of the distribution of seismic velocities (the starting model). Synthetic travel-times are calculated for the starting model. This is called solving the forward problem. For volcanoes, where multipathing, diffraction, and attenuation are common, a critical step in forward modelling is correctly identifying if a phase is primary or secondary and then solving the forward problem for the correct ray geometry. The synthetic travel-times are then compared to the observed travel-times (the data). The differences between the data and synthetics are called residuals. A correction to the starting model (called the model update) that minimizes, or at least reduces, the residuals are then calculated. This is the inversion or optimization step. New synthetic data are then computed and compared again to the observed data to find a new model update. The inversion continues until the residuals are reduced to a level comparable to the measurement uncertainty or until the model update becomes too small to be meaningful, i.e., convergence is achieved. The residuals have two sources of error, one is observational (uncertainty in the time assigned to an arrival) and one is numerical (error in time predicted by forward modelling) and it is not uncommon that the latter rivals the former. In practice, many tomographic methods are incapable of fitting data to the measurement uncertainty due to these inaccuracies and to trade-offs between model parameters (e.g., seismic velocity and hypocentral parameters).

Although the basic principle of seismic tomography is relatively straightforward for simple velocity structures, its application to field data from volcanoes is nothing but. For volcanoes, the primary challenge is the physics of wave propagation around and through pronounced low-velocity anomalies, a topic discussed below. Additionally, one common misconception is that one can find the “true” solution to the seismic inverse problem. Because the solution to the seismic inversion of real data is always non-unique, there are an infinite number of models that can fit the data equally well. The goal is to constrain a family or families of models that reduce the residuals. The tomographic method can also be used in a hypothesis-testing mode (e.g., Hammond and Toomey, 2003) to both find classes of models that are consistent with the data and to eliminate classes of models that are inconsistent with observations. Ideally, we should assign an uncertainty to each of these models; however, the inherent non-linearity makes this a challenging task. Because of nonuniqueness, additional constraints are introduced to stabilize the inversion, reduce the range of possible models, or test null hypotheses (e.g., Hammond and Toomey, 2003). These constraints fall under two main categories: i) a priori constraints i.e. any independent information about the velocity distribution, e.g., information about the possible range of seismic velocities expected; ii) regularization constraints that prevent the output model from being too complex. Regularization effectively limits the impact of ill-constrained perturbations that are both large and uncertain on the output model.

The main challenges in seismic tomography are:

1. Designing field strategies that best illuminate the chosen target

2. Finding accurate and computationally efficient ways to solve the forward problem and calculate synthetic data

3. Finding efficient strategies to solve the inverse problem and minimize the residuals

4. Limiting the effect of noisy data on the results

5. Estimating the uncertainties and resolution

The development of different solutions to these challenges has led to an array of different seismic tomography algorithms. Many seismic imaging methods have been applied to volcanic targets. The main differentiating features are the type of seismic source and the part of the seismic wavefield used. Above we have described travel-time tomography, which uses the travel-times of body waves. Other popular methods use surface waves, and more advanced methods use the full wavefield. Below we briefly review some of the most popular seismic tomography approaches. This list will be used to categorize the recent literature presented in Overview of recent volcano tomography results.

2.1 Active source travel-time tomography

One of the most reliable methods for seismic imaging relies on generating artificial seismic signals at known times and locations and recording their arrival times at an array of seismic receivers. Offshore experiments typically use air guns (Figure 1A) while experiments on land use controlled explosions (Figure 1B). The recorded time series are analyzed to identify P-wave and sometimes the S-wave arrivals and measure their travel-times. The advantage of active source tomography is that the origin times and locations of the sources are known. The geometry of the experiment can be tightly controlled to provide the best possible target illumination and achieve the desired resolution. Field campaigns can be relatively short and typically last a few weeks or months. The main disadvantages are high costs and the limitation of having all sources and receivers at or close to the surface. Active source tomography can provide high resolution isotropic and anisotropic $V_P$ models, particularly for submarine volcanoes or island volcanoes where dense marine seismic acquisition can be employed; the method can also constrain compressional wave attenuation. Offshore experiments have the advantage of being able to use airguns, with many closely spaced and nearly identical sources, but they have difficulties in constraining $V_S$ since sources in the water column do not directly generate S-waves. ASTT has been applied to imaging Montserrat (Shalev et al., 2010; Paulatto et al., 2012), Santorini (McVey et al., 2020; Heath et al., 2021), Mount St. Helens (Kiser et al., 2018) and many other volcanoes (Table 1). Popular algorithms for ASTT include the FAST code by Zelt and Barton (1998); Jive3D by Hobro et al. (2003), TomoLab by Toomey et al. (1994), Tomo2D by Korenaga et al. (2000), Tomo3D by Meléndez et al. (2015), and the code of Van Avendonk et al. (2001).

FIGURE 1

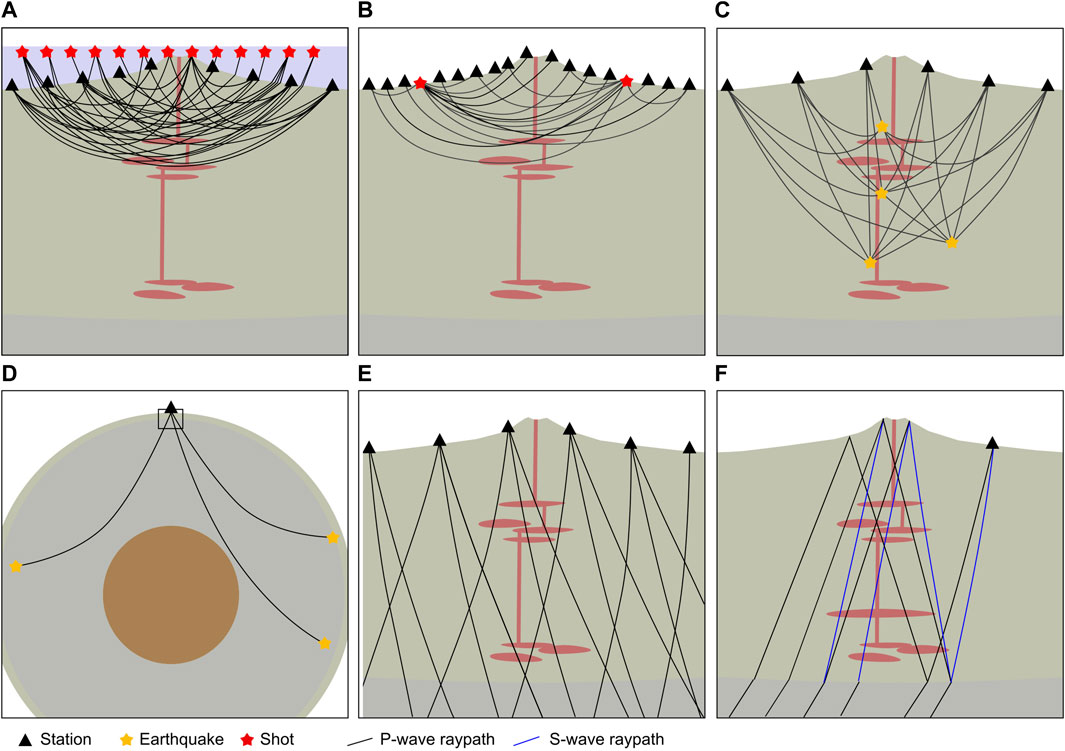
FIGURE 1. Schematic representation of the most common seismic imaging methods. (A) Marine active source travel-time tomography (marine ASTT). (B) Land active source travel-time tomography (land ASTT). (C) Local earthquake tomography (LET). (D and E) Teleseismic tomography (TST). (D) illustrates the far field propagation from the source to the boundary of the local domain. (E) Illustrates the ray-paths within the local domain. (F) Teleseismic receiver functions imaging (TRFI).

TABLE 1

TABLE 1. List of seismic imaging studies reporting melt fractions.

2.2 Local earthquake tomography

Local earthquake tomography uses a similar principle to active source tomography but employs earthquakes as sources (Figure 1C). The earthquakes must be located within the target region, meaning that this technique is only suitable for tectonically active regions. Active volcanoes are very often seismically active, and many are monitored with continuously-recording seismometer arrays. Therefore, volcanoes are prime targets for the application of LET and indeed there are many published LET studies in the last 2 decades (as evidenced in our database). Since the origin time and location of the sources are unknown, LET suffers from greater non-linearity than ASTT. This limitation usually result in lower resolution and a greater incidence of artifacts in the output models compared to ASTT.

In addition to the issue of non-linearity, the main disadvantage of LET compared to ASTT is that the location and timing of the sources cannot be controlled. Illumination of the target may not be optimal. Moreover, if the seismicity rate is low, instruments may need to be deployed in the field for long periods of time to achieve sufficient coverage. On the other hand, the main advantages of LET are that it is cheaper to carry out, it can more easily provide joint constraints on $V_P$ and $V_S$ or $V_P$/$V_S$, and it can provide deeper constraints if deep earthquakes are present. LET is the most widely adopted volcano imaging technique and has been applied to Aso caldera (Sudo and Kong, 2001), Merapi (Luehr et al., 2013), Askja (Greenfield et al., 2016) and Sinabung (Indrastuti et al., 2019) among many others. Popular LET codes include the SimulPS family of algorithms (Thurber, 1983) and the LOTHOS code by Koulakov (2009).

2.3 Teleseismic tomography

Teleseismic (literally “far earthquake”) body wave tomography relies on recording the body waves from distant earthquakes on a local or regional network of seismic stations to image the structure beneath the network (Figures 1D,E). This technique can be applied almost anywhere in the world with the deployment of a dense network of seismometers. TST usually requires broad-band instruments (that are sensitive to low-frequency signals) to achieve a good signal-to-noise ratio because high-frequency seismic waves are more rapidly attenuated when propagating over long distances and are more easily swamped by noise in teleseismic data.

TST can image deeper than most other methods but provides lower resolution because of the low-frequency content and long propagation paths of teleseismic signals (which result in broad Fresnel zones, see Wavefront healing). For this reason, it is most successful in imaging large magmatic systems associated with large calderas (e.g., Steck et al., 1998; Bai et al., 2020) or continental rifts (e.g. Kounoudis et al., 2021). For a more complete comparison of LET and TST see Thurber (2003). A detailed discussion of TST applications to imaging volcanoes can be found in Iyer and Hirahara (1993). Popular algorithms for TST include the algorithm of VanDecar et al. (1995), the FMTT code by Rawlinson et al. (2006), and TomoLab (Hammond and Toomey, 2003).

2.4 Surface wave tomography and ambient noise surface wave tomography

Surface wave tomography uses a different part of the wavefield to image the subsurface. Surface waves are seismic waves that propagate close to the Earth’s surface. Most often SWT relies on Rayleigh waves, a type of surface wave that causes ground oscillations along a vertical plane parallel to the direction of propagation. They arrive later than P and S waves in seismic recordings, but their amplitude is typically stronger. The velocity of surface waves is related to $V_S$ but is slower than both $V_P$ and $V_S$. Lower frequency surface waves sample deeper, therefore deeper targets require lower frequency data. $V_S$ near the Earth’s surface typically increases with depth therefore low-frequency surface waves, which are sensitive to deeper structure, propagate faster than high-frequency surface waves. This principle is at the core of SWT. SWT starts with determining surface wave dispersion curves (the frequency dependence of the surface wave phase velocity). These are used to construct horizontal 2D phase velocity maps at different frequencies. The phase velocity maps are then inverted to obtain a 3D model of $V_S$.

SWT can be carried out using local earthquakes (earthquakes with hypocenter inside the area of the recording network) or distant earthquakes. Surface wave dispersion curves can also be generated by cross-correlation of ambient noise signals (Shapiro et al., 2005). Ambient noise surface wave tomography (ANSWT) has the advantage of not requiring any sources at all and it can therefore be applied at locations where there are few or no earthquake sources.

The resolution of SWT depends on the frequency range considered. Higher frequencies lead to better resolution but cannot sample deep targets. The characteristic depth of penetration is proportional to the wavelength of the signal. It follows that SWT resolution decays with increasing depth and the resolution length is about half of the depth.

SWT and ANSWT have been applied to several magmatic targets including Aso (Huang et al., 2018), Yellowstone (Jiang et al., 2018) and Campi Flegrei (Guidarelli et al., 2002). Popular SWT algorithms include the algorithm of Barmin et al. (2001), the FMST code by Rawlinson (Bodin et al., 2012a), the ASWMS code by Jin and Gaherty (2015), and the two-plane wave approximation technique (Forsyth and Li, 2005; Yang and Forsyth, 2006).

2.5 Full waveform inversion

Full waveform inversion is based on modelling and matching the seismic recordings wiggle for wiggle instead of just measuring and fitting travel-times (e.g., Pratt, 1999). FWI relies on the ability to accurately model the wavefield to generate synthetic data. As in travel-time tomography, data and synthetics are compared and the residuals are minimized. In this case, however, the residuals are the difference between the recorded and modelled waveforms within a pre-determined time window. The main advantages of FWI are improved resolution and in some cases the ability to constrain multiple physical parameters including seismic attenuation and anisotropy. The main disadvantages are high computational costs and tight requirements on the survey parameters. The recording network or the source distribution needs to be closely spaced (of the order of the dominant wavelength), therefore FWI has seen the widest adoption in active source studies (ASFWI). Typically, FWI starts by inverting low-frequency data to determine the long-wavelength velocity distribution and then proceeds by gradually introducing higher frequencies. The resolution of FWI depends on the frequency range considered and the resolution length can be as low as half the wavelength (Virieux and Operto, 2009). However, inverting higher and higher frequencies requires finer modelling grids and denser survey geometry leading to rapidly increasing compute times.

Monetary and computational costs have in the past limited the wide adoption of FWI, but several recent successful applications have shown that FWI is feasible today for a wide range of problems (Morgan et al., 2013). In magma imaging, FWI has been applied to active source data (Arnulf et al., 2014; Morgan et al., 2016) and to surface wave Green’s functions derived from ambient noise cross-correlation (Flinders and Shen, 2017). Finite-frequency tomography which may be thought of as an intermediate step between travel-time and full-waveform inversion (Tape et al., 2007), has not yet been widely applied to volcanic targets (e. g., Koulakov & Shapiro, 2015) and will not be discussed here.

2.6 Other imaging methods

Several other seismic imaging methods that do not technically fall within the category of seismic tomography have been applied to magmatic systems. All these methods seek to identify sharp boundaries at magma/rock interfaces and are complementary to the information obtained from tomography.

Multi-channel seismic (MCS) reflection imaging is an active source seismic imaging technique that uses reflected seismic waves to build an image of the subsurface. It is best known for its widespread application in hydrocarbon exploration. MCS can provide the highest resolution constrain of any of the listed techniques but struggles to image deep targets and does not on its own provide reliable constraints on the seismic velocities. It is best suited for imaging shallow sub-horizontal targets. It has been successfully applied to image axial magma lenses and other magmatic sills beneath mid-ocean ridges (e.g., Hooft et al., 2000; Carbotte et al., 2020) and to image a melt layer at Campi Flegrei caldera (Zollo et al., 2008). Reflection imaging is best carried out with man-made seismic sources but can also be attempted using earthquake sources and a dense recording array (Byerly et al., 2010).

MCS data offer one of the most robust ways of determining the seismic properties of a low-velocity layer. The analysis of amplitudes vs. offset (AVO analysis) or amplitude vs. angle of incidence (AVA analysis) of the seismic waves reflected at the interface at the top of the layer can be used to accurately determine the seismic velocities of the layer (e.g., Castagna and Backus, 1993). This method has been used to distinguish between fully molten and mushy layers at mid-ocean ridges (Singh et al., 1998; Canales et al., 2006; Xu et al., 2014).

Teleseismic receiver function imaging (TRFI) uses signals from distant earthquakes and their reflections and conversions created by interfaces beneath the recording array (Figures 1D,F) (e.g., Burdick and Langston, 1977; Zhu and Kanamori, 2000). It is conceptually similar to MCS (Ryberg and Weber, 2000) but is better suited to imaging larger scale and deeper targets. It is most sensitive to horizontal layering and is widely used to determine Moho depth variations and the shape of subducting slabs (e.g., MacKenzie et al., 2010). Receiver functions are most often used to generate a direct image of subsurface discontinuities (e.g., Cornwell et al., 2010), but can also be inverted to obtain a velocity model (Lodge and Helffrich, 2009). When applied to volcano imaging TRFI can provide robust constraints on the deeper parts of magmatic systems (e.g., Hammond et al., 2020). In addition, reflection Green’s functions can be obtained from autocorrelations of seismic signals and/or of ambient noise to identify sharp boundaries associated with the top of magma systems (Heath et al., 2018).

An alternative approach for imaging volcanoes is attenuation tomography (AT). Attenuation tomography uses information contained in the Fourier amplitude spectrum of seismic phases to reconstruct a model of the spatial distribution of the attenuation parameter Q (e.g., Lees and Lindley, 1994). AT can use body waves from active source or earthquake sources, earthquake coda waves or ambient seismic noise. Magmatically active areas are typically strongly attenuative because high temperatures and melting can greatly increase viscous dissipation (e.g., Mavko, 1980; Hammond and Humphreys, 2000). Different AT approaches have been developed and have been applied to active volcanoes, including at Newberry caldera (Zucca and Evans, 1992), Mount St. Helens (De Siena et al., 2014) and Tenerife (Prudencio et al., 2015). We do not discuss attenuation tomography in detail in this paper as we think that it would be best treated in a dedicated stand-alone manuscript.

Some of the methods discussed above can be used in tandem to achieve better imaging than would be possible with one single method. For example, surface waves are often used in conjunction with receiver functions, taking advantage of their complementary sensitivity which leads to more robust images (Bodin et al., 2012b). When performed separately, SWT and TRFI suffer from low resolution and a trade-off between the depth of the discontinuity and the velocity of the overburden (Ammon et al., 1990), respectively. Joint inversion, unlike TRFI, constrains absolute shear velocities, and provides better vertical resolution than SWT (e.g., Chrapkiewicz et al., 2020). LET, ASTT and TST are also often used together to achieve better target illumination and more robust convergence (e.g., Battaglia et al., 2008; Heath et al., 2015; Díaz-Moreno et al., 2018). Seismic methods can also be coupled with other geophysical data, e. g gravity (Paulatto et al., 2019). Joint inversion can help reduce the null space of the solution (narrow the range of acceptable models).

2.7 Understanding seismic resolution

Seismic tomography studies should be accompanied by comprehensive resolution and uncertainty analysis so that the output model can be interpreted with confidence. In addition, since volcanoes are strongly heterogenous, extensive forward-inverse modeling should be conducted to understand the sensitivity of the results to starting models and to pronounced low-velocity anomalies. Estimating seismic resolution and model sensitivity is not straightforward and can be even more time consuming than carrying out the inversion in the first place.

Seismic resolution is a matrix that describes the linear averaging of the model parameters that results from the distribution of data coverage (e.g., Tarantola, 2005; Rawlinson and Spakman, 2016). For a model defined by N parameters, the resolution matrix is an NxN square, symmetric matrix. Each row of the resolution matrix corresponds to the linear averaging kernel for one model parameter. For example, if we estimate $V_P$ by measuring P-wave travel-times using rays travelling only in the z-direction, the resulting model will be smeared, and the resolution matrix will represent that smearing or vertical averaging of information.

For small inverse problems, e.g., 2D travel-time inversions, the resolution matrix can be directly calculated. However, for most modern large and/or 3D problems this is impractical. This is the case particularly for FWI, which has a much higher computational cost than travel-time tomography (Fichtner and Trampert, 2011). Therefore, in most cases, the calculation of the full resolution matrix is replaced with a sensitivity analysis.

Checkerboard recovery tests are the most common type of sensitivity analysis. These consist of carrying out a simulated inversion experiment using synthetic data to test the recovery of an alternating pattern of positive and negative anomalies given the geometry of sources and receivers of the experiment (Zelt, 1998; Rawlinson et al., 2014). By performing multiple tests with anomalies of different wavelengths and observing where the anomalies can be recovered and how they are smoothed and smeared it is possible to estimate how the resolution varies throughout the model. Checkerboard tests for volcanoes, however, can be misleading since the amplitude of the anomalies tested (nominally ± a few percent) is much smaller than the heterogeneity typical of volcanoes. As a result, the non-linearity for the checkerboard test is much less than for a geologically plausible model.

Less common, but often more informative are spike tests, which use isolated anomalies rather than a pattern of alternating anomalies and test the recovery of a single model parameter. In practice, they are a way of estimating one row of the resolution matrix in isolation. Rawlinson and Spakman (2016) argue that spike tests should be preferred to checkerboard tests, because the ray coverage of the checkerboard test may be significantly different from the ray coverage of the experiment. Checkerboard tests lead to the overlap of recovered patterns, and they can give a false impression of the resolving power (Rawlinson and Spakman, 2016).

Another important concept, closely related to the resolution matrix, is the resolution length, i.e., the minimum separation between two real features that can be distinguished as separate in the output model. From a checkerboard test, one can estimate the resolution length as the smallest anomaly that can be correctly distinguished and recovered, under the assumption that the magnitude of anomalies in the checkerboard and the actual medium are similar.

Particularly useful for volcanoes are forward-inverse tests to study the recovery of low-velocity anomalies. Typically these are geologically or thermodynamically informed models that test the melt fraction and spatial geometry of the magmatic system (e.g., Beachly et al., 2012; Paulatto et al., 2012; McVey et al., 2020). Such tests probe the family of models that fit a given data set and are crucial for expanding our understanding beyond a discussion of the minimal tomographically recovered structure. These studies also allow authors to estimate the amount of under-recovery in their studies, a typical problem with wavefront healing around low-velocity bodies (discussed below). A sensitivity analysis that tests a suite of hypotheses can be more informative than either checkerboards or spike tests.

For the purpose of discussing the reliability of tomographic images, we define several terms (Figure 2).

•Image fidelity is defined by the size of the image pixels (voxels in the case of a 3D model) or the spacing of grid nodes (Figure 2B). The image fidelity or grid resolution is specified by the user and it affects both the forward and inverse problems. Image fidelity is sometimes determined by stability and accuracy requirements of the forward problem or considerations of computational cost. For example, stable wave propagation modelling requires a grid spacing that is fine enough so that the wavefront does not travel more than about half of the length of a model cell over each timestep (Press et al., 1990). Similarly, finite difference Eikonal solvers or shortest path methods require a relatively fine grid to produce accurate travel-times. Image fidelity also trades off with model resolution such that improvements in image fidelity decrease the resolution of individual model parameters as measured by the resolution matrix. Jackson (1979) argues that low image fidelity can give rise to non-random errors, or bias in the output model.

•Physical sensitivity describes the sensitivity of the seismic waves to the velocity structure that they travel through or in other words the extent to which the waves “feel” any velocity anomalies (Figure 2C). The sensitivity of seismic waves can be described by a sensitivity kernel and is sometimes included in the inversion regularization. Different parts of the wavefield have different sensitivity to certain structures. For example, transmitted waves are sensitive to the seismic velocity along the travel path while reflected waves are sensitive to discontinuities. Higher-frequency waves have better sensitivity to small scale structures. In principle, one could increase the frequency of investigation to improve the physical resolution, but in practice, this can only go so far. The main reason is that higher frequency signals are attenuated more strongly than low-frequency signals and are therefore swamped by noise at longer offsets.

•Data coverage describes the ability of the data to sample the target (Figure 2D). This includes the effect of the acquisition geometry, source distribution, density of sampling and azimuthal coverage of the target. Even within regions of good data coverage, the model resolution can vary spatially.

•Inversion regularization describes the model damping, smoothing, or other pre-defined relations that are introduced during inversion. Most seismic tomography studies use some form of smoothing or damping of the solution and some incorporate physical sensitivity via kernels. Spatial smoothing constraints or sensitivity kernels give rise to similar effects by imposing relations on volumetric averaging of the velocity model (Tape et al., 2007). Some form of regularization is always necessary to stabilize the inversion and rule out models that have large and poorly constrained perturbations.

•Model resolution is the combined effects of the image fidelity, data coverage, and inversion regularization (Figure 2E). Since many tomographic algorithms do not include sensitivity kernels in their inversions, the effects of physical sensitivity may not be explicitly part of model resolution. In these cases, one must use prior understanding of the physical sensitivity to interpret the results. In parts of the model with excellent data coverage, the model resolution can theoretically approach the physical sensitivity. However, as discussed below, the physics of seismic wave propagation around and through pronounced low-velocity anomalies means that excellent data coverage is not often attainable in a volcanic setting.

FIGURE 2

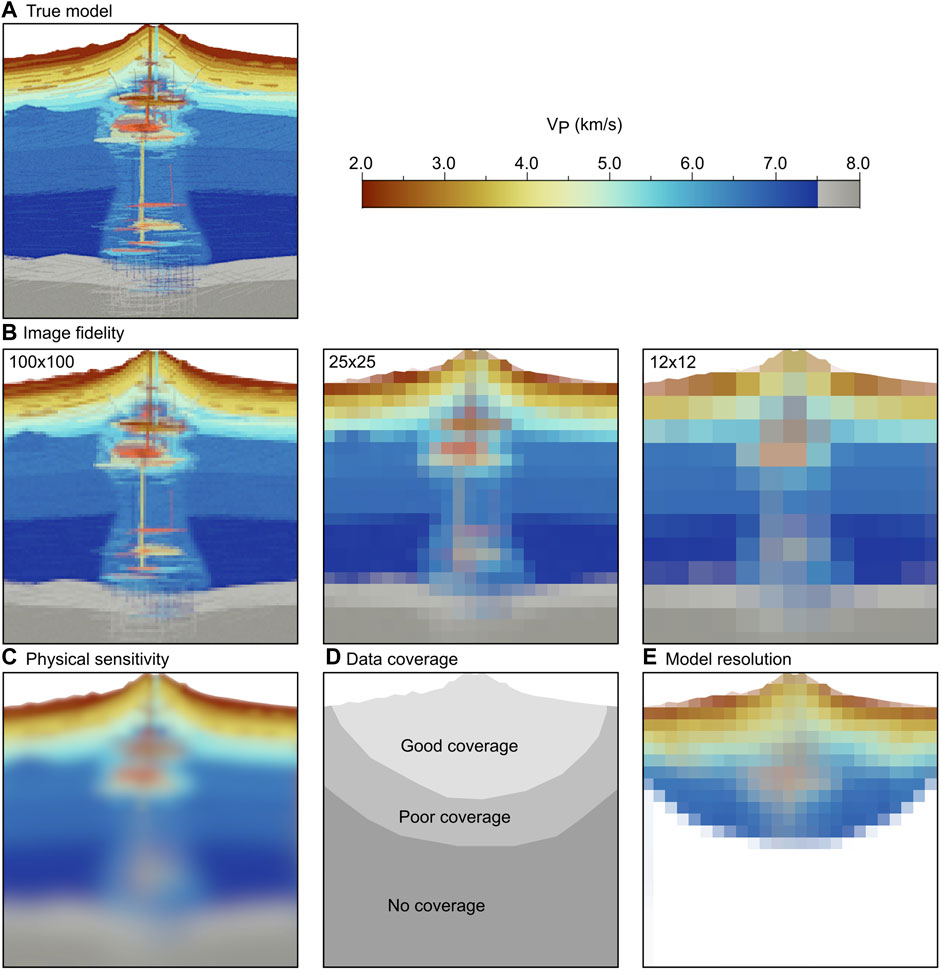
FIGURE 2. The effect of different quantities on model recovery. (A) Idealized true velocity model of an active volcano. (B) Representations of the true model with different image fidelities. The numbers on the top left corners indicate number of pixels on each side of the image. (C) The true model as “felt” by the seismic waves due to the limits of the physical sensitivity. (D) The data coverage. (E) The model resolution is affected by image fidelity, the data coverage, and the inversion regularization.

2.8 Resolution of travel-time tomography and surface wave tomography

To better understand seismic resolution, we use travel-time tomography as an example once again. Most travel-time tomography studies rely on the ray approximation i.e., on the assumption that the travel-time depends only on the seismic velocities along a ray. This is equivalent to an infinite frequency approximation. In practice, field data contain a limited range of frequencies and travel-times are picked on band-pass filtered data. In this case, scattering and diffraction effects become important, leading to inaccuracies in the reconstructed model (Williamson, 1991; Williamson and Worthington, 1993). The ray approximation leads to incorrect travel-times and wrong model updates when the size of the velocity anomaly is comparable to or smaller than the seismic wavelength. Scattering can be particularly pronounced in volcanic settings, where the Earth’s structure is highly heterogeneous (e.g., De Siena et al., 2014).

The physical sensitivity of travel-time tomography is approximated by the Fresnel radius or the radius of the first Fresnel zone. The first Fresnel zone is the area from which energy arriving at the receiver has a phase differing no more than half a period, and so interferes constructively with the direct arrival. For refracted ray paths the Fresnel radius can be approximated as $r=\sqrt{L\lambda }$, where $L$ is the length of the propagation path and $\lambda$ is the wavelength (Williamson, 1991). For a typical crustal-scale LET study like the one by Greenfield et al. (2016), where the path length is 10 km–20 km and the dominant frequency is 5 Hz–10 Hz, the Fresnel radius is estimated to be 2.5 km–5 km. This range matches the resolution length determined using checkerboard tests.

The resolution of traditional SWT methods is also limited by the Fresnel radius since ray theory is used to invert the phase velocity maps for the 3D $V_S$ structure (e.g., Godey et al., 2003). SWT is often carried out using relatively low frequencies and therefore typically has relatively low resolution. For example, Huang et al. (2018) use Rayleigh wave phase velocity measurements at a maximum frequency of 1 Hz and 5–50 km long ray paths, leading to a resolution length of 3.5 km–11 km.

The overall effect of the physical sensitivity and model resolution is that the recovered image is blurred, and anomalies are diminished in amplitude compared to the true model (Dahlen, 2004). Anomalies with a size comparable to the physical sensitivity cannot be fully recovered. The sensitivity and resolution typically worsen with depth since longer offsets or lower frequencies are needed to sample deeper. The resolution length is not a clear-cut limit and smaller features can still be detectable, although the anomaly amplitude will be adversely affected (Sheriff and Geldart, 1995; Spetzler and Snieder, 2004).

2.9 Wavefront healing

A more intuitive way to understand why anomalies comparable to or smaller than the seismic wavelength cannot be recovered is to look at wavefront healing, which is the result of scattering (Malcolm and Trampert, 2011). Seismic waves crossing a low-velocity anomaly are slowed down creating a delay in the wavefront behind the anomaly (Figure 3). As the wavefront propagates further, scattering of the waves around the anomaly causes the shadow of the anomaly to “heal”. If the anomaly is similar in size to the wavelength of the signal and the propagation distance is significantly larger than the wavelength, wavefront healing can effectively hide the anomaly, i.e., the anomaly results in a negligible observed travel-time delay (Figure 3H). However, even when an anomaly is fully hidden from travel-times by wavefront healing, it affects the amplitude of arrivals and generates secondary waves (Figure 3) which can be exploited by forward waveform modelling (e.g., Beachly et al., 2012), explicit ray tracing of secondary arrivals, or more advanced methods like full-waveform inversion. There is an asymmetry in the evolution of the wavefield around positive vs. negative travel-time anomalies. Negative delays will initially grow, or ‘unheal’, but then heal at a rate faster than positive delays (Nolet and Dahlen, 2000). This means that slow anomalies are less resolvable than fast anomalies of the same size using travel-times.

FIGURE 3

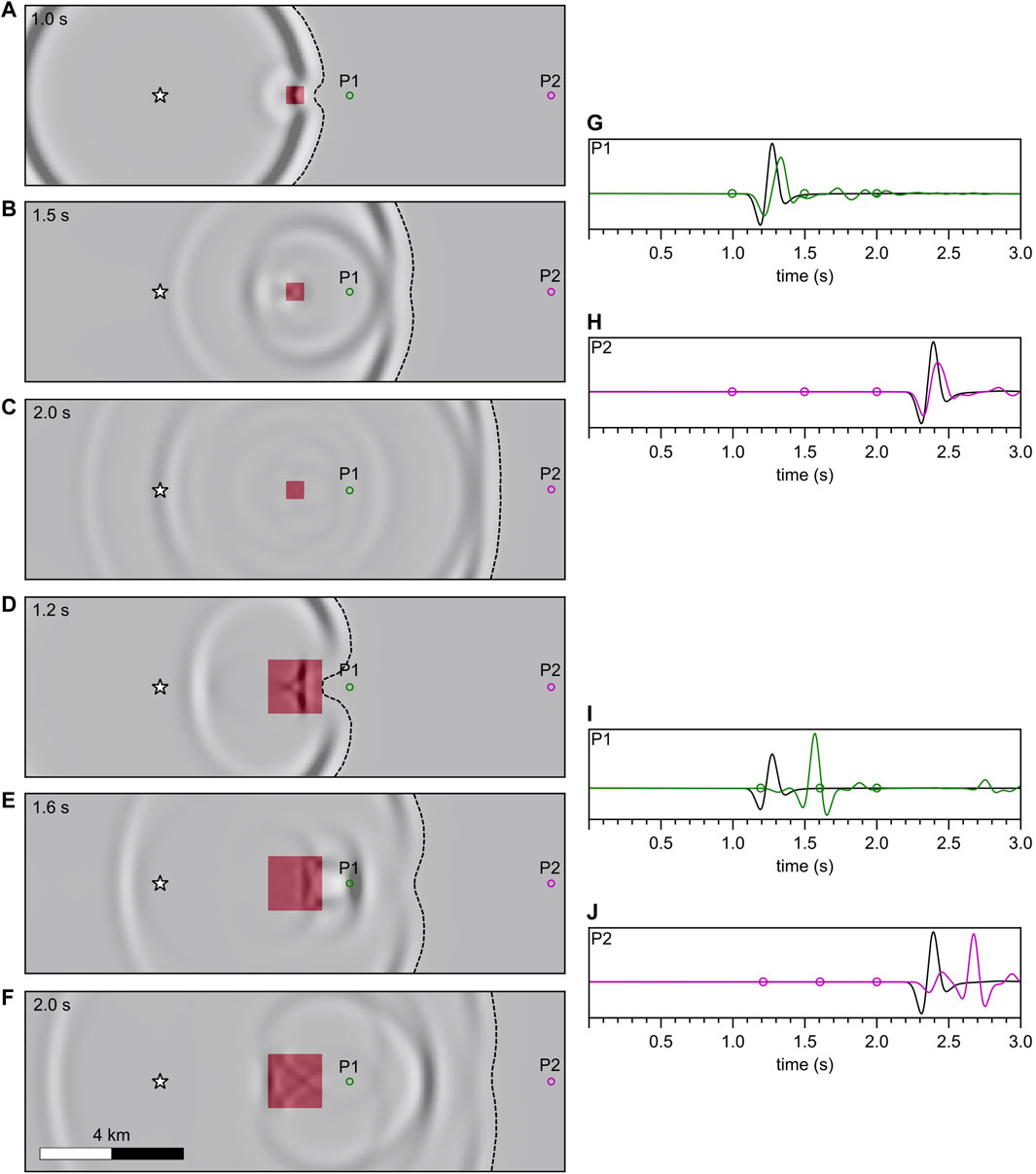
FIGURE 3. Illustration of the wavefront healing effect. (A–C) Wavefield snapshots at 1.0 s, 1.5 s, and 2.0 s after the source origin time. A square low-velocity anomaly with side equal to 0.5 times the wavelength is located between the source (star) and the receivers (P1, and P2). The strength of the anomaly is −50% of the background velocity. (D–F) Wavefield snapshots at 1.2 s, 1.6 s, and 2.0 s after the source origin time with a square low-velocity anomaly with side equal to 1.5 times the wavelength. The first arrival wavefront is highlighted with a dashed line. (G) Time-series recorded at points P1 with the ×0.5 wavelength anomaly (green) and without the anomaly (black). (H) Same as (G) at point P2. (I) Same as (G) but for the ×1.5 wavelength anomaly. (J) Same as (I) at point P2. Wavefields were calculated using an acoustic finite difference method (Warner et al., 2013).

FWI resolution is not limited by the Fresnel radius and can recover anomalies as small as half the wavelength (Virieux and Operto, 2009). This is because FWI uses not only the travel-time but also the amplitude of the waves and can use secondary phases like the diffractions and converted phases generated by velocity perturbations. The resolution length of FWI is controlled by the seismic frequency and by the geometry of the data acquisition (via the scattering angle). It increases with the frequency of the wavefield and decreases with the scattering angle (Eq. 30 of Virieux and Operto, 2009). For the scattering angle approaching zero (normal-incidence reflection), the resolution length approaches half of the seismic wavelength.

In the FWI study of Chrapkiewicz et al. (2022) the frequencies used are up to 6 Hz leading to a physical resolution limit of ∼0.4 km. In practice, the model regularization introduced to stabilize the inversion due to data sparsity means that the model resolution is about 1 km. The resolution length for seismic imaging of magma reservoirs in the upper crust is typically 2 km–10 km for travel-time tomography (ASTT and LET), 4 km–20 km for SWT, and 0.4 km–2 km for ASFWI. We will discuss the implication of resolution limits on melt estimates in Melt fractions in the crust.

3 Seismological signatures of mush and magma

Using an analogy from hydrocarbon exploration, we can think of composition, temperature, and melt fraction within a magma reservoir as reservoir parameters. These are the parameters of interest to the volcanologist to understand the dynamics of the system and interpret unrest. However, the primary outputs of seismic tomography are constraints on the elastic properties, like seismic velocities and anisotropy. Determining the reservoir parameters requires an understanding of the physical relationships that tie them to the measured elastic properties. These relationships are sometimes called constitutive relationships and can be derived either theoretically or experimentally. In this section, we focus on the constitutive relationships that tie melt fraction to the elastic moduli and seismic velocities. Before we tackle this topic, we need to introduce a few rock physics concepts.

3.1 Elastic moduli and seismic velocities

The elastic moduli are the parameters that describe how a material reacts to stress under the assumption of linear elasticity. The most intuitive to understand is the bulk modulus ($K$), which is defined as the pressure increase resulting from a decrease in volume (compression). A material with a high bulk modulus will strongly resist compression (it has a low compressibility). Similarly, the shear modulus ($G$) describes the material’s response to shear deformation. More generally, the response of a material to an external force is described by an elastic modulus:

$M=\frac{stress}{strain}$

Stress is defined as force per unit area, while strain describes the deformation.

For a general anisotropic material, 81 elastic moduli can be defined. The elasticity tensor or stiffness tensor C is a matrix containing the 81 elastic moduli. Of the 81 components only 21 are independent because of the symmetry properties of the stress tensor, therefore 21 constants are needed to fully describe the elastic response of a general anisotropic material. For isotropic materials, the number of independent constants is reduced to two. Popular choices are the Lamé parameters $\lambda$ and $\mu$ or the bulk and shear modulus. For a detailed description of the stiffness tensor see e.g. Mavko et al. (2020).

The seismic velocities are related to the components of the stiffness tensor and to density. In a solid isotropic material two types of seismic body waves can propagate, P-waves and S-waves, and these are characterized by the P-wave velocity ($V_P$) and the S-wave velocity ($V_S$):

$V_P=\sqrt{\frac{K+4/3G}{\rho }}$

$V_S=\sqrt{\frac{G}{\rho }}$

The seismic waves used in crustal-scale seismic tomography have wavelengths ranging from a few hundred meters to several kilometres. As seen in Seismic tomography in brief, the sensitivity of the seismic waves in the best-case scenario is about half of the signal wavelength. The Earth contains heterogeneity at all length scales, and magma reservoirs are no exception. Seismic waves passing through a partially molten region are insensitive to small-scale heterogeneities and will “feel” or react to the average or effective seismic velocities and the related effective elastic moduli.

3.2 Effective elastic properties of partially molten rocks

The effective elastic moduli of partially molten rocks depend on the elastic moduli of the components (crystals/melt/gases), their respective abundances, and on their geometric arrangement and connectivity (Figure 4A). In general, the effective elastic moduli will be frequency-dependent as the flow of fluid phases causes viscous energy dissipation and frequency dispersion. The response may also be anisotropic if any of the constituents are anisotropic (as are most minerals) and/or if the microstructure has a preferential alignment. In this paper, we focus on isotropic elastic properties. For a discussion of the effect of magma on seismic anisotropy see e.g. Hammond et al. (2014).

FIGURE 4

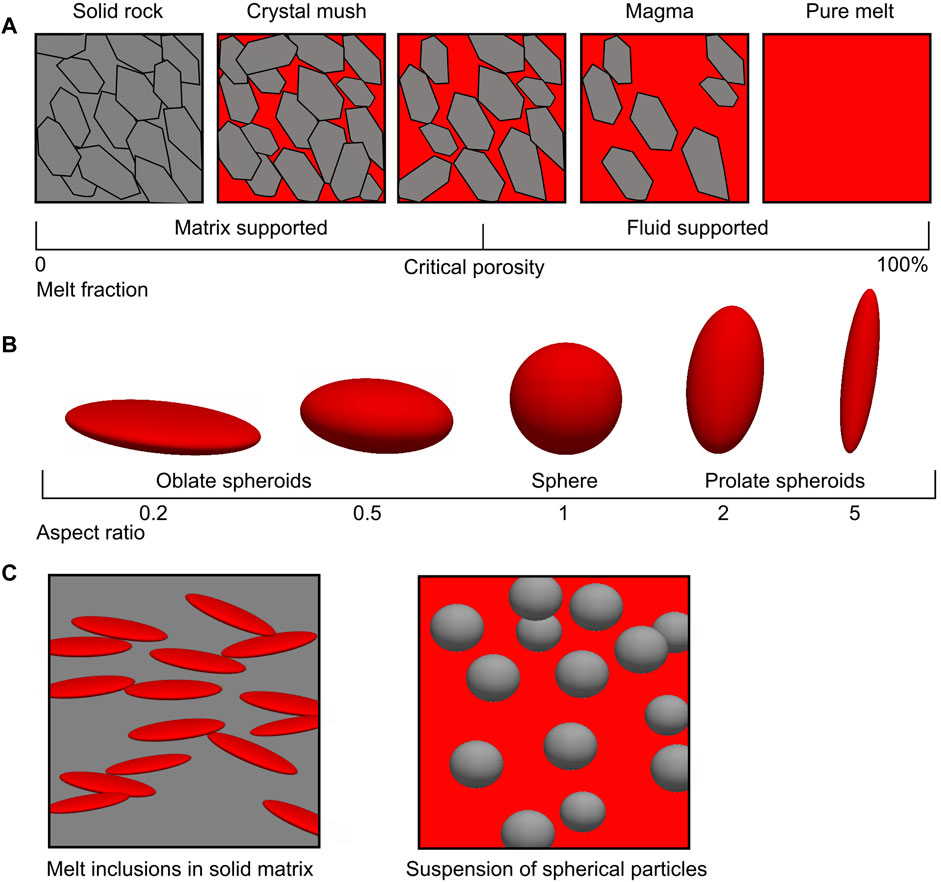
FIGURE 4. (A) Classification of partially molten rocks on a scale from solid rock to pure melt adapted from Nur et al. (1998). The critical porosity is the melt fraction where the mechanical behavior transitions from matrix supported mush to fluid supported suspension. (B) Spheroidal shapes used to model the effect of melting on elastic properties. (C) Crystal mush can be represented as a distribution of spheroidal melt pockets embedded in a solid matrix. Magma can be represented as a suspension of solid particles in melt.

3.2.1 Bounds and averages

The simplest approach to estimating the physical properties of composite materials is to take the volumetric average of the properties of the components and ignore any geometric effects. The arithmetic mean of the elastic moduli is also called the Voigt bound (Voigt, 1928), while the geometric mean (mean of the reciprocals) is called the Reuss bound (Reuss, 1929). It can be proved that the Voigt and Reuss bounds are maximum and minimum bounds on the possible elastic properties of an isotropic mixture (Hill, 1952). The Reuss bound is particularly useful as it is exactly valid for an idealized dilute suspension of solid particles in a fluid. The Reuss bound is therefore a good approximation for calculating the elastic moduli of magma with suspended crystals. For solid rocks and solid/fluid composites, the mean of the Voigt and Reuss bounds, known as the Voigt-Reuss-Hill (VRH) average (Chung et al., 1963) is sometimes used as a first approximation in the absence of any information on the microstructure. The Hashin-Shtrikman (HS) bounds [Hashin & Shtrikman, 1963, eqs (4.1–4.4)] are a bit more complex than the Voigt and Reuss bounds and are the tightest bounds that can be derived for the elastic moduli of an isotropic random mixture (Figure 5). The upper HS bound is exactly valid for an idealized distribution of fluid spheres within a solid. The lower HS bound is equivalent to the Reuss bound.

FIGURE 5

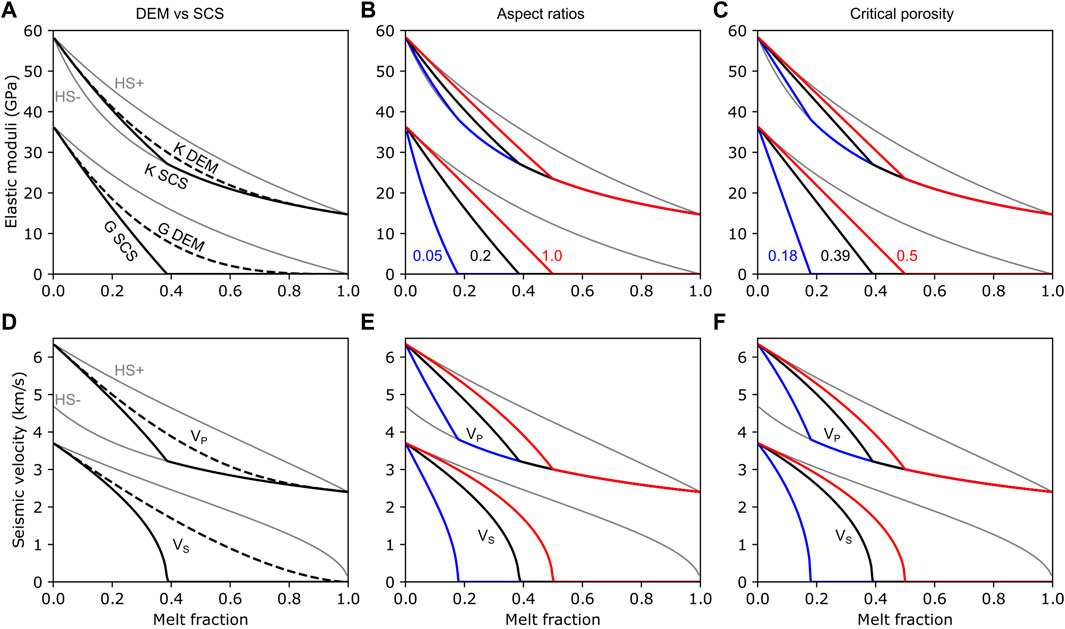
FIGURE 5. Example constitutive relationships for partially molten rocks. (A) Bulk modulus (K) and shear modulus (G) as a function of melt fraction for a two-phase composite with spheroidal melt inclusions (aspect ratio = 0.2) calculate with the SCS (solid line) and the DEM (dashed line). (B) Elastic moduli as a function of melt fraction calculated with the SCS for different values of the inclusion aspect ratio; blue: 0.05, black: 0.2, red: 1.0. (C) Elastic moduli as a function of melt fraction calculated with the critical porosity approach of Nur et al. (1998). (D–F) Same as (A–C) but showing Vp and Vs. instead of the K and G. The grey lines mark the upper and lower Hashin-Shtrikman bounds (HS+ and HS-).

3.2.2 Effective medium theories

Progressing beyond the simple bounds approach requires some information on the geometrical shape and arrangement of the components. A popular approach is to assume that the material is composed of a matrix made of one material with one or more additional phases embedded in the matrix in the form of inclusions with a defined simple geometrical shape. For example, a magma can be represented by a melt “matrix” with suspended crystal grains represented as sub-spherical solid inclusions. Similarly, a crystal mush can be represented as a solid matrix with interconnected melt inclusions (Figure 4C). This approach was pioneered by Eshelby (1957), who calculated the effect on the elastic properties of an ellipsoidal inclusion (Figure 4B). Based on his work, a wide range of effective medium theories have been developed to calculate the properties of materials containing inclusions with different shapes including spheroids (Wu, 1966; Kuster and Toksöz, 1974), films (Walsh and Grosenbaugh, 1979), and cuspate tubes (Mavko, 1980). For more in-depth information on the elastic properties of composite materials see e.g. Watt et al. (1976) and Mavko et al. (2020).

The two most widely used effective medium approaches are the differential effective medium (DEM) approach and the self-consistent scheme (SCS). These are both implicit semi-analytical schemes that require integration or iteration to reach a solution. The DEM approach (Norris, 1985; Avellaneda, 1987) simulates a composite material and calculates the effective elastic moduli by gradually adding inclusions to a matrix. The method is solved by numerical integration and is suitable when the inclusions are sparse enough and do not form an interconnected network (Berge et al., 1993). The SCS approach (Budiansky, 1965; O’Connell and Budiansky, 1974; Berryman, 1980; Mavko, 1980; Schmeling, 1985) considers inclusions embedded in an effective matrix with properties to be determined. The properties of the medium are calculated by iteration, starting with an approximate initial guess (e.g the VRH average). Its advantage is that it implicitly accounts for interaction between inclusions and predicts the existence of a critical porosity (see discussion below).

3.2.3 Inclusion aspect ratios

Figures 5A,D shows the melt-velocity relationships calculated with the DEM and SCS approaches for spheroidal inclusions using typical solid and melt properties for a granite. The velocity reduction for a given melt fraction can be vastly different depending on the chosen inclusion geometry, described by the aspect ratio $\alpha$ of the spheroids (Figures 5B,E). It is impossible to recommend one simplified geometry that is optimal for all applications. In real rock samples, the geometry of the melt is related to the melt fraction, the composition of the melt and crystals, and the temperature of the reservoir. Garapić et al. (2013) used nano-scale imaging to show that low percentages of melt in the upper mantle are best described by a combination of cuspate tubes and low aspect ratio films ($\alpha ={10}^{-3}-{10}^{-4}$). Takei (1998) derived a set of theoretical constitutive relationships tying melt fraction and the dihedral angle to the elastic properties assuming thermodynamic equilibrium between the melt and crystal grains. These relationships were then compared to the SCS approach to derive equivalent aspect ratios for a wide range of dihedral angles (Takei, 2002). These results provide a rationale for selecting a particular aspect ratio when the approximate range of dihedral angles is known. Typical dihedral angle values of 20° to 40° correspond to equivalent aspect ratios of 0.1–0.15. The link to dihedral angles is extremely useful to narrow down the range of plausible aspect ratios. However, it relies on two important assumptions that are rarely valid in crustal systems. Firstly, the melt is rarely in thermal equilibrium with the surrounding crystals; mush reservoir models predict that the melt and crystals are efficiently segregated by porous flow (Jackson et al., 2018). Secondly, a significant proportion of melt is likely stored in mesoscopic pockets, lenses, or channels that have no relation to the grain-scale equilibrium geometry. For these reasons, even when the microgeometry of the melt is well constrained, it is necessary to consider a range of aspect ratios.

3.2.4 Critical porosity

An alternative approach that avoids the problem of choosing an aspect ratio altogether relies on the observation that the mechanical behaviour of partially molten rocks is bimodal. At low melt fractions, below a critical porosity ${\varphi }_c$, the medium behaves like a solid, with stresses supported by the solid matrix. Above the critical porosity, the solid matrix loses its cohesion and the medium behaves like a fluid suspension (Costa et al., 2009). The elastic properties above the critical porosity can be described by the Reuss bound (fluid suspension), while below the critical porosity they can be approximated by a modified Voigt bound (Figures 5C,F) (Nur et al., 1998). The advantage of this approach is that it does not require knowledge of the microgeometry of the melt and instead relies on estimating the critical porosity, which can be achieved by fitting experimental data (Chu et al., 2010). This approach results in constitutive curves that contain a kink at the critical porosity and are similar to those obtained with the SCS approach (Figure 5). By using a modified Voigt bound there is a risk of overestimating the seismic velocities at low melt fractions compared to the SCS (Figure 5F), so this approach is best suited to systems where the melt fraction is expected to be higher than about 10%.

3.3 Estimating melt fraction from seismic velocities

If the seismic velocities of the magma reservoir can be measured with sufficient accuracy one may attempt to estimate melt fraction. This is not as simple as converting the velocity with a simple scaling constant. Multiple inter-related factors need to be carefully considered. First, one needs to have an approximate idea of the bulk composition of the melt and of the host rock. The composition of the components will dictate their elastic moduli, densities, melting temperatures, and likely micro-geometry or critical porosity.

Estimating these parameters requires some geological knowledge of the volcanic system under study. The seismic properties of the host rock can be estimated by analyzing plutonic xenoliths found in the erupted lavas (Kiddle et al., 2010). Plutonic xenoliths are fragments of crystalline rocks carried to the surface during an eruption. The assumption is that they represent an approximation of the solid component of the magmatic system. Their seismic velocity can be determined by laboratory measurements or as the VRH average of the properties of the constitutive minerals. This type of analysis is only available for a few of the most well-studied volcanoes. More often, the average composition of the host rock is estimated based on the bulk composition of the eruptive products and any available general information about the tectonic setting. This might lead to a broad classification in terms of silica content (e.g., granitic or gabbroic). The seismic velocities of the host rock can then be determined from tabulated laboratory measurements (e.g., Christensen and Stanley, 2003) and then corrected for temperature and pressure. The composition of the melt component is easier to determine. For example, one may assume that the bulk composition of the melt in the magmatic system is similar to the composition of the quenched glass and groundmass in the eruptive products. From the major element composition of the melt, one can then estimate the elastic properties and density using for example the model of Ueki and Iwamori (2016), which was developed by fitting an extensive suite of experimental measurements.

With the composition of the components constrained, one may then make an educated guess of the melt geometry. The different approaches described in Effective elastic properties of partially molten rocks require different parameters and will require different strategies:

1. Critical porosity - Yu and Lee (2016) estimate that the critical porosity at a dacite volcano is ∼30%. This value can be used to tune a critical porosity curve or the SCS approach for volcanoes with similar composition. Van der Molen and Paterson (1979) obtain a value between 30% and 35% for granite. The latter value is used by Chu et al. (2010) to estimate melt fractions beneath Yellowstone caldera.

2. Dihedral angles and spheroidal models - If the mineral composition of the solid component is known at least approximately, dihedral angles can be estimated based for example on the compilation of Holness (2006). One can then use the model of Takei (2002) to relate the dihedral angles to an equivalent aspect ratio (or a range of aspect ratios) and then use a spheroidal model e.g. the SCS to calculate a constitutive relationship.

Having chosen and tuned an appropriate constitutive relationship, it can then be inverted, for example with a line search method. This is equivalent to finding the melt fraction where the constitutive curve matches the observed value of the elastic property considered. The predicted melt fraction should be accompanied by an uncertainty estimate. The largest uncertainty contribution typically arises from uncertainties in the measured seismic properties and in the melt geometry. As mentioned above, the microscopic melt geometry constrained from exhumed samples may not be entirely meaningful if a significant amount of melt is stored in macroscopic melt layers or dikes. More work is needed to determine the best way to deal with multi-scale melt distribution. In the meantime, the safest approach is to consider a range of melt geometries and propagate the resulting uncertainties (e.g., McVey et al., 2020). Other significant uncertainties may arise from the choice of host rock and melt seismic properties and from temperature effects.

4 Overview of recent volcano tomography results

Lees (2007) covered in some detail the most significant volcano tomography results published from 1993 to 2007. Since then, the number of published volcano tomography studies has more than doubled (Figure 6). We have collated over 270 volcano tomography studies published between 1975 and 2022. At least 78 volcanoes have been imaged with seismic methods (Figure 7). We have chosen not to include mid-ocean ridge magmatic systems in our database; for context we briefly summarize the mid-ocean ridge results in Introduction.

FIGURE 6

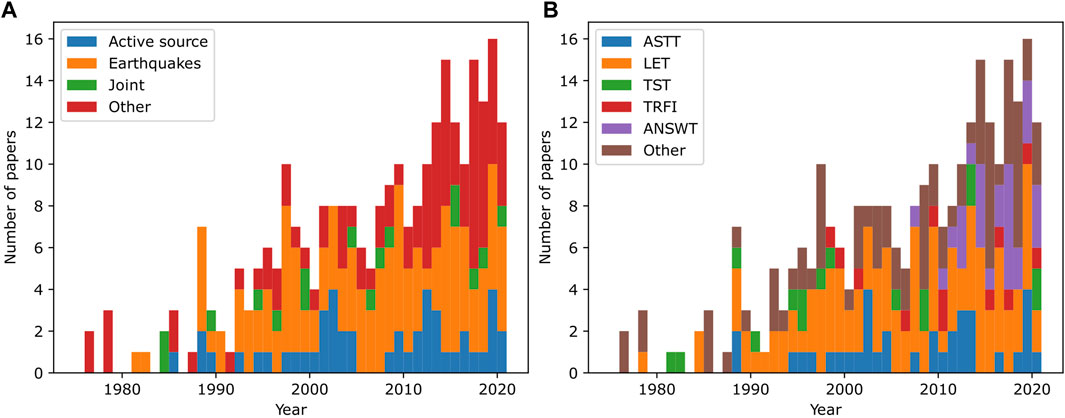
FIGURE 6. (A) Volcano imaging studies listed by publication year and grouped based on type of seismic source used. “Joint” means joint inversion of active source and earthquake data. “Other” includes mostly ambient noise studies. (B) Same as (A) but grouped based on imaging method used. ASTT, Active Source Travel-time Tomography; LET, Local Earthquake Tomography; TST, Teleseismic Tomography; TRFI, Teleseismic Receiver Function Inversion; ANSWT, Ambient Noise Surface Wave Tomography.

FIGURE 7

FIGURE 7. Location of volcanoes imaged with seismic methods during the period 1975–2022.

From each paper, we have extracted information about the recording array, sources, part of the wavefield used, imaging method, quantitative data about any observed low-velocity anomalies, and reported melt estimates. We have strived to be as complete as possible in our literature search, but a few studies may have been missed. The data are collected in an online database (https://github.com/kmch/VolcanoTomo) which is open to new submissions from authors and will be kept up to date with new results. We encourage readers to report any inaccurate or missing information in the database. We particularly welcome input from the authors of the cited studies.

Below we summarize some of the most significant volcano imaging results published before 2022. We focus particularly on those studies that reported clear evidence of melt and provided quantitative and well documented estimates of melt fraction (Table 1).

4.1 Santorini and Kolumbo

Santorini (Hellenic arc, Greece) was first imaged using LET by Dimitriadis et al. (2010). This study found low velocities beneath the northern part of the island extending in the direction of known tectonic lineaments, but the resolution afforded by the sparse dataset was not sufficient to estimate melt fractions. In 2015, a large, dense amphibious active source seismic study (the PROTEUS experiment) recorded ∼14,300 controlled sound sources from a large airgun array on 90 ocean-bottom bottom and 65 land seismometers covering an area of 120 × 60 km² (Heath et al., 2019). Hooft et al. (2019) used ASTT to generate a model of the shallow subsurface, revealing evidence for a strong low-$V_P$ anomaly at 2 km depth. They interpreted this anomaly as fractured caldera fill saturated with hydrothermal fluids. McVey et al. (2020) used the same ASTT approach to extend the $V_P$ model to greater depth and found evidence for a deeper low-velocity volume at 2.8 km–5 km depth. The anomaly can be explained by a 4%–13% melt fraction, but higher melt fractions cannot be ruled out because of the effect of wavefront healing.

Kolumbo is a small submarine volcanic cone, a part of the Santorini volcanic system. Dimitriadis et al. (2010) found evidence for a −3% $V_P$ anomaly and a −5% $V_S$ anomaly at 5 km–9 km depth using LET. McVey et al. (2020) confirmed the presence of a small $V_P$ anomaly at 3 km–4 km depth using ASTT. They estimated the melt fraction required to explain the data as <1%. The PROTEUS dataset was the first volcano study specifically designed for active source FWI and Chrapkiewicz et al. (2022) used this method to process the same dataset as McVey et al., 2020. The resulting high-resolution model revealed the presence of a strong but small low $V_P$ volume at 2.2 km–4.0 km depth beneath Kolumbo (Figure 8A). The value of $V_P$ at the centre of the −40% anomaly is 3 km/s. The inferred melt fraction is 44 $\pm$ 4% based on detailed calculations using the SCS approach. This result is particularly significant for two reasons: i) it is the clearest and most robust image of a high-melt fraction reservoir or melt lens obtained with seismic tomography, ii) it starkly highlights the limits of travel-time tomography. These results are best explained by a multi-level melt reservoir topped by a melt lens.

FIGURE 8

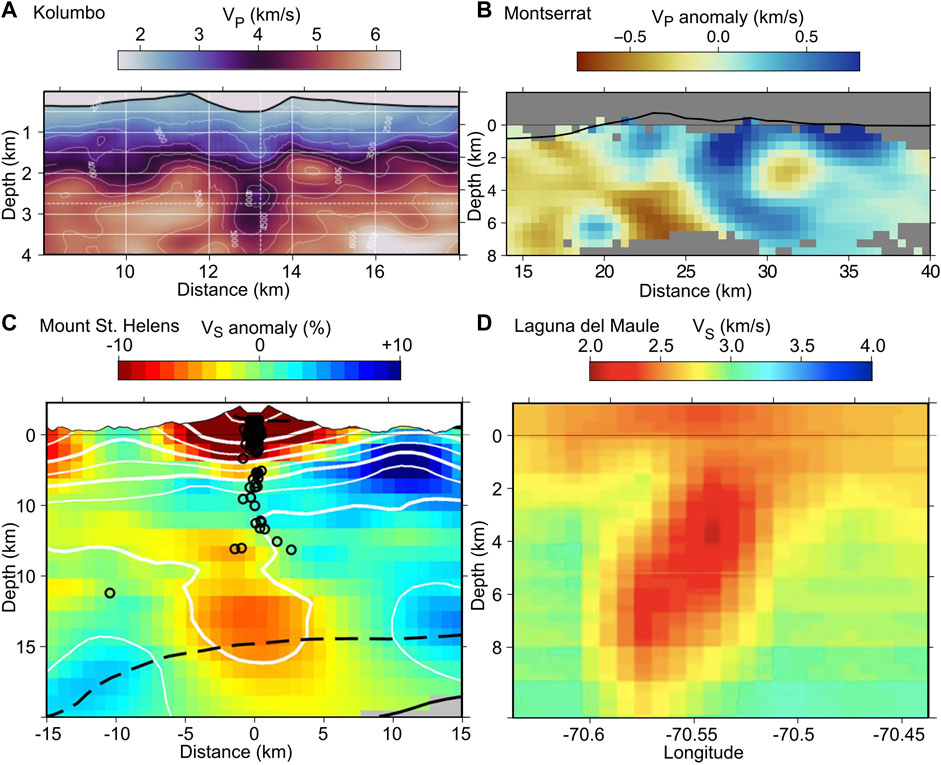
FIGURE 8. Examples of seismic tomography results. (A) P-wave velocity model of Kolumbo from active source FWI (adapted from Chrapkiewicz et al., 2022). (B) P-wave velocity model of Montserrat from joint inversion of active source P-wave travel-times and gravity data (Paulatto et al., 2019). (C) S-wave velocity model of Mount St. Helens from joint LET and ASTT (adapted from Ulberg et al., 2020). (D) S-wave velocity model of Laguna del Maule from SWT (adapted from Wespestad et al., 2019).

FWI has yet to be applied to the larger magmatic system directly beneath Santorini (McVey et al., 2020). For this target, the spatial extent, heterogeneity, and attenuation of the magmatic system significantly impact data quality. As such, it remains to be seen whether active-source FWI can image the larger magma bodies expected beneath volcanoes that are associated with significantly reduced signal-to-noise ratio data.

4.2 Montserrat

The Soufriere Hills Volcano (SHV) on Montserrat (Lesser Antilles) was surveyed in 2007 and imaged with ASTT. Shalev et al. (2010), published a $V_P$ model based on travel-times from offshore airgun shots to land stations. The model extends to 6 km depth and revealed the shallow structure of the island. SHV and the two neighbouring and extinct volcanoes Centre Hills and Silver Hills all have high $V_P$ cores in the top 4 km. High-velocity cores are observed at many volcanoes worldwide (e.g., Lees, 1992) and are attributed to the presence of intrusive igneous rocks contrasting with the surrounding volcaniclastic apron. Paulatto et al. (2012) complemented the land station data of Shalev et al. (2010) with OBS data. Thanks to the longer offset OBS data that undershot the island, their model was able to constrain the deeper structure at up to 8 km depth. This deeper model revealed a large low-$V_P$ volume beneath SHV. The anomaly has a volume of at least 20 km³ and a maximum anomaly amplitude of −12%. They used the SCS method to estimate a melt fraction of 3%–10%, but acknowledged that this represents a minimum melt fraction, due to wavefront healing and smoothing. They attempted to better constrain the melt fraction by integrating the tomography results with thermal modelling and concluded that the observed seismic data could be explained by a magma reservoir with a 35% melt fraction and a total volume of 13 km³. Annen et al. (2014) further expanded the thermal modelling to constrain the long-term magmatic flux. Paulatto et al. (2019) reprocessed the seismic dataset and jointly inverted the seismic travel-times together with land and marine gravity data (Figure 8B). They used $V_P$/density cross-plots and rock physics calculations to re-estimate the melt fraction. They conclude that the melt fraction in the shallow reservoir is at least 3% but could be 28% or higher depending on the severity of the wavefront healing effect. Their best estimate for the melt fraction is 17%.

4.3 Mount St. Helens

Mount St. Helens (Washington, United States) was first imaged in detail using LET by Lees and Crosson (1989) and Lees (1992) who found a possible shallow magma reservoir, a high-velocity core, and a deeper low-velocity volume at 9 km depth. The shallow reservoir at 2 km–5 km depth is more evident in Lees (2007) who republished the model of Lees (1992) using higher quality colour figures. Waite and Moran (2009) carried out a LET study with a more extensive earthquake database and imaged two low-$V_P$ volumes at 2 km–3.5 km and 5.5 km–8 km depth. They estimate the melt fraction in the shallow melt reservoir to be at least 5%. In 2014 Mount St. Helens was the subject of the most complex field campaign ever conducted on a continental arc volcano (the iMush experiment). The deployment involved a total of about 6000 recording stations and the firing of 23 explosive shots. Several studies were published using the data from this experiment. Kiser et al. (2016) processed the active source data along two perpendicular 2D profiles and found generally higher-than-average $V_P$ beneath the volcano. They also found high $V_P$/$V_S$ at 4 km–13 km depth and interpreted it to correspond to a magma reservoir. Kiser et al. (2018) used 3D ASTT and confirmed the presence of a low-$V_P$ anomaly at 3.4 km–14 km depth. The low-$V_P$ volume shows a complex structure with multiple lobes and layers and probably encompasses the two reservoirs postulated by Lees (1992) and Waite and Moran (2009). The melt fraction is estimated to be 10%–12% using the critical porosity method of Chu et al. (2010). Flinders and Shen (2017) imaged the crust at Mount St. Helens as part of a larger-scale surface wave waveform inversion. They confirmed the presence of a low $V_S$ anomaly of at least -15% corresponding to ∼5% melt fraction. They also found low-velocity volumes beneath the neighbouring Mount Rainer and Mount Adams. The most complete model of the Mount St. Helens magmatic system comes from joint ASTT and LET by Ulberg et al. (2020), providing constraints on both $V_P$ and $V_S$ (Figure 8C). They interpret the observed low-$V_P$/low-$V_S$ as due to 3% melt fraction. An independent constraint on melt fraction was obtained by Bedrosian et al. (2018) using MT inversion. The overall picture at Mount St. Helens is of a complex multi-level magmatic system dominated by low melt fractions.

4.4 Newberry

Newberry volcano (Oregon, United States) was the subject of one of the earliest 3D volcano tomography studies (Achauer et al., 1988). They used ASTT and imaged a low-$V_P$ anomaly of −10% at depth of 2 km–5 km but could not confidently attribute it to partial melt. At the same time, Stauber et al. (1988) used TST to image the same target to a greater depth. Their model extends deeper and resolves a high-velocity core beneath the volcano but does not have the resolution to detect any robust low-velocity anomalies. The seismic attenuation study of Zucca and Evans (1992) seemed to contradict the findings of Achauer et al. (1988) and concluded that no magma was present. More recently, Beachly et al. (2012) combined the 1980s data with a new active source 2D dataset and inverted them together using a more modern tomography code (Toomey et al., 1994) to obtain a better resolved 3D $V_P$ model. Their tomography model finds a weak low-$V_P$ anomaly, in agreement with Achauer et al. (1988). More importantly, they conducted a detailed analysis of wavefront healing, using two-dimensional finite-difference wave propagation modelling. Their work showed that the travel-time results and even waveform modelling results are non-unique, and that the data could be explained equally well by a low melt fraction mush or a melt sill, with possible melt fractions ranging from 11% to 100%. Heath et al. (2015) combined the active source data from Beachly et al. (2012) with teleseismic earthquake data. Their $V_P$ model once again confirms the presence of a low velocity volume at 3 km–5 km depth, requiring a minimum of about 10% partial melt. A sharp boundary at the top of this magmatic system was mapped with a coherent P-wave reflections at ∼2.5 km depth using auto-correlations of the ambient and seismic wavefields (Heath et al., 2018).

4.5 Campi Flegrei

The Campi Flegrei caldera (Italy) has been imaged with LET (Aster & Meyer, 1988; Vanorio et al., 2005; Calò and Tramelli, 2018), ASTT (Zollo et al., 2003; Chiarabba and Moretti, 2006; Battaglia et al., 2008) and SWT (Guidarelli et al., 2002). At shallow depth, the system is characterized by low-velocity caldera fill surrounded by a high-velocity ring (e.g., Chiarabba and Moretti, 2006). At 4 km depth, there is evidence for a low-$V_P$/$V_S$ ratio volume, interpreted as a volatile-rich fractured rock (e.g Vanorio et al., 2005). These studies did not find evidence for significant amounts of magma in the top 5 km of the crust. The breakthrough in terms of magma imaging came from Zollo et al. (2008), who used Amplitude vs. Offset analysis (AVO), a method commonly used in the oil industry to determine hydrocarbon saturation. They identified seismic reflections in marine active source data collected in the Bay of Naples. The reflections are generated by a discontinuity at 7.5 km depth, and the AVO analysis indicates that the underlying layer has a $V_P$ of about 2,800 m/s and a $V_P$/$V_S$ of 2.35. They then used the Hashin-Shtrikman bounds to calculate a melt fraction of 80–90%. This low-$V_P$ layer might represent a large tabular magma body at the top of the magma reservoir, perhaps similar to the high melt fraction layers predicted by Jackson et al. (2018) based on modelling of reactive melt flow in mush reservoirs.

4.6 Toba

The Toba caldera (Sumatra, Indonesia) was first imaged by Mastruyono et al. (2001) using LET. They imaged a low $V_P$ anomaly in the upper crust with a magnitude of up to −37%. They concluded that melt must be present but did not attempt to quantify the melt fraction. The TRFI study of Sakaguchi et al. (2006) supported this conclusion and placed the magma reservoir at 8 km–14 km depth. They also found increased $V_P$/$V_S$ but again did not attempt to estimate melt fraction. Koulakov et al. (2009) generated a regional $V_P$ and $V_S$ model using LET and confirmed the presence of an extensive region of low velocities beneath Toba. Stankiewicz et al. (2010) and Jaxybulatov et al. (2014) came to the same conclusion using SWT. Jaxybulatov et al. (2014) found evidence for strong positive $V_S$ radial anisotropy in the lower crust, indicative of horizontal layering, similar to observations at Yellowstone and Long Valley caldera (Jiang et al., 2018). Koulakov et al. (2016) revisited LET at Toba and found evidence for a multi-level magmatic system comprising at least two separate large reservoirs located in the crust and in the upper mantle.

4.7 Aso caldera

Aso caldera (Japan) was first imaged by Sudo and Kong (2001). Their study is an exemplary application of LET, containing detailed quality control and a quantitative estimate of melt fraction. They found evidence for a −26% $V_P$ anomaly and a −31% $V_S$ anomaly at 6 km depth. They attempted to estimate melt fraction using the SCS method of Mavko (1980) and inferred a minimum melt fraction of 10%. Abe et al. (2017) imaged the deeper structure of the system using TRFI and found evidence for two connected low-$V_S$ volumes, one at 8 km–15 km depth and one at 15 km–23 km depth. They estimate melt fraction to be about 10%–14%. An ANSWT study by Huang et al. (2018) found more evidence for a low-velocity volume at about 6 km depth and also detected an additional low-velocity volume at 2 km depth. The evidence at Aso is of a large trans-crustal magmatic system comprising multiple levels of magma storage.

4.8 Uturuncu/Altiplano Puna

Uturuncu (Bolivia) is the location of some of the most spectacular volcano tomography images worldwide. An early TSRFI study found evidence for a low-$V_S$ (<0.5 km/s) layer at ∼19 km depth (Chmielowski et al., 1999), which they interpret as a sill-like magma body, and they named it the Altiplano-Puna magma body (APMB). Ward et al. (2013) carried out ambient noise SWT and confirmed the presence of a large low-$V_S$ layer. Ward et al. (2014) combined SWT with receiver functions to better define the extent and properties of the APMB. They concluded that the APMB extends from 4 to 25 km depth and has a radius of ∼100 km, corresponding to a colossal volume of ∼500.000 km³. They use a critical porosity approach (Chu et al., 2010) to estimate the melt fraction to be 4%–25% and interpret it as a region of layered crystal mush. Independent evidence from inversion of magnetotelluric (MT) data (Comeau et al., 2016) puts the depth of the APMB at 13 km–17 km and indicates that the melt fraction is above 15%. A shallow magma reservoir may also be present. Kukarina et al. (2017) found high $V_P$/$V_S$ values at 6 km–80 km depth using LET. The evidence at Uturuncu clearly points to the presence of a vast magmatic system, likely dominated by low-melt fractions, but sizable high-melt-fraction bodies may also be present within the mush region.

4.9 Colima

Volcán de Colima (Mexico) and the surrounding Colima Volcanic Complex were imaged using both LET (Ochoa-Chávez et al., 2016; Watkins et al., 2018; Sychev et al., 2019) and SWT (Spica et al., 2014; Escudero and Bandy, 2017; Spica et al., 2017). All these studies found evidence for low seismic velocities in the crust beneath Colima at depth of about 10 km–25 km, although depth ranges from each study differ. Particularly notable are the results of Spica et al. (2017), who imaged a low-velocity volume at 10 km–20 km depth. $V_S$ at the centre of the anomaly is <2.3 km/s, a velocity decrease of at least 12%. This low-$V_S$ anomaly and the region below it are characterized by negative radial anisotropy, suggesting vertically aligned heterogeneity likely related to vertical faults or dikes associated with the extensional tectonic environment. This result is unusual compared to other volcanically active regions discussed in this paper (e.g., Yellowstone and Toba), where seismic studies have found positive radial anisotropy caused by horizontal layering. Negative radial anisotropy, however, has been observed in other rift settings and is thought to be associated with vertically aligned melt or cracks (e.g., Bastow et al., 2010; Hammond et al., 2014; Hammond and Kendall, 2016; Chambers et al., 2021).

4.10 Long Valley

Long Valley caldera (California, United States) has been the subject of many seismic studies already summarized in Lees (2007). Early studies found evidence for large, small-amplitude low-velocity anomalies. Dawson et al. (1990), Steck and Prothero (1994), and Weiland et al. (1995) used TST and found low $V_P$ anomalies at about 7 km–20 km depth with magnitude as high as -30%. Melt estimates range from 8% to 25%. Almost every conceivable imaging method has been applied to Long Valley since those early experiments. Perhaps the most successful results came from combined LET and TRFI by Seccia et al. (2011). Their LET study found a weak low-$V_P$ anomaly at 6 km–7 km depth, indicating 2%–3% melt. More significantly, their receiver function analysis suggests the presence of a much stronger low-$V_S$ anomaly at 7 km–11 km depth, requiring melt fractions of 30–60%. Further evidence came from a regional surface wave waveform inversion by Flinders et al. (2018). Their $V_S$ model includes a low-$V_S$ anomaly of at least −20% at 5 km–20 km depth, requiring a melt fraction of 23% $\pm$ 4%. The evidence at Long Valley is suggestive of a large magmatic system including both regions of crystal mush and some high-melt fraction layers.

4.11 Katla

Katla (Iceland) was first imaged in 1994 by Gudmundsson et al. (1994). They collected active source data along a 2D profile crossing the caldera and the glacier that covers it. They used iterative forward modelling of P-waves to build a model of $V_P$ and found evidence for a shallow (1 km–2 km depth) low-$V_P$ volume with $V_P$ of 3 km/s. They estimate a melt fraction of 50% using the lower Hashin-Shtrikman bound and a melt volume of 5 km³. This result should be taken with a grain of salt because the forward modelling approach used by Gudmundsson et al. (1994) can be highly non-unique. A more recent experiment using LET did not have good enough resolution to confirm these results (Jonsdottir et al., 2007). Jeddi et al. (2016) used a denser earthquake dataset and combined it with the active source data from Gudmundsson et al. (1994) to perform joint ASTT/LET. They found velocities of 3.5 km/s–4.0 km/s beneath the caldera, suggesting a smaller but still significant amount of melt. A SWT study (Jeddi et al., 2017) could not find evidence of melt.

4.12 Mt. Paektu/Changbaishan

Mt. Paektu (North Korea), also known as Changbaishan has been imaged by Kyong-Song et al. (2016) using receiver functions. Their study revealed a negative polarity arrival and high $V_P$/$V_S$ in the crust indicating the presence of melt. The model was extended and refined by Hammond et al. (2020) who carried out TRFI and detected a low $V_S$ layer at 4 km–8 km depth with a $V_P$/$V_S$ as high as 2.1. Independent evidence from 3D MT inversion revealed a multi-level system with 7%–30% melt (Yang et al., 2021).

4.13 Yellowstone

The first attempts at imaging Yellowstone caldera (Wyoming, United States) were carried out in the 1970s and early 1980s by Iyer and others (e.g. Iyer, 1979; Iyer et al., 1981). By analysing teleseismic travel-times using one of the earliest applications of TST they found evidence for low-velocity bodies within the crust and upper mantle beneath the caldera. A subsequent LET study by Benz and Smith (1984) also found a substantial low-velocity body with $V_P$ as low as 4.9 km/s, a 21% reduction compared to a solidified granite. Several additional LET studies were carried out in the following decades including notably by Kissling (1988), Miller and Smith (1999), Husen et al. (2004), Farrell et al. (2014), and Huang et al. (2015). They all found evidence for low-$V_P$ anomalies of various magnitudes and volumes at depths of 5 km–15 km. Huang et al. (2015) combined TST and LET to extend the velocity model to the upper mantle, providing a complete view of the magmatic system. The emerging picture at Yellowstone is of a system comprising two large reservoirs: a rhyolitic reservoir in the upper crust and a basaltic reservoir in the lower crust. Stachnik et al. (2008) and Schutt et al. (2008) used SWT to image the system down to depths of 150 km and came to similar conclusions. In addition, they imaged low velocities in the upper mantle attributed to the mantle plume. Chu et al. (2010) used a joint inversion of surface waves and teleseismic receiver functions to better constrain the melt fractions in the crust. They concluded that the upper crustal reservoir has a melt fraction of about 32%. Jiang et al. (2018) analyzed vertically polarized and horizontally polarized surface waves to determine seismic anisotropy beneath the caldera. They found positive radial anisotropy at 5 km–18 km depth indicative of horizontal layering as would be expected in the presence of a large sill complex or a layered mush reservoir.

4.14 Canary Islands

Several of the Canary Islands volcanoes (Spain) have been imaged with seismic methods. Their large volumes, long histories and complex geological structure make it hard to distinguish melt bodies. Krastel and Schmincke (2002) imaged Gran Canaria using ASTT but found no evidence for significant melt regions. García-Yeguas et al. (2012) used ASTT to image Tenerife. Their $V_P$ model is highly heterogeneous but no clear evidence for magma storage was found. Tenerife’s complex structure was also imaged with attenuation tomography by Prudencio et al. (2015). Several high-attenuation bodies stand out in their model, but no clear magma body can be identified. El Hierro was imaged using LET by García-Yeguas et al. (2014) and later by Martí et al. (2017). Both studies found evidence for a low velocity volume at the base of the crust or in the upper mantle at depth of about 12 km–22 km, but neither attempted to estimate melt fraction. More recently, D’Auria et al. (2022) used LET to image the source of the recent eruption on La Palma. They imaged a low-velocity volume at 7 km–25 km depth an interpreted it as the active magma reservoir.

4.15 Hawaii volcanoes

The active volcanoes on Hawaii’s Big Island (United States) have been the subject of many seismic investigations starting with the TST study of Ellsworth and Koyanagi (1977). Early studies found a high-velocity core beneath Mauna Loa (Okubo et al., 1997) and both low and high velocity regions beneath Kilauea (Thurber, 1984). Haslinger et al. (2001) used LET to image Kilauea and found evidence for low velocities beneath the East Rift Zone, interpreted as a possible magma reservoir with 10% melt fraction. Park et al. (2007, 2009) found evidence for low velocities in the upper mantle beneath Lohi Seamount. Lin et al. (2014) used LET to generate joint $V_P$ and $V_P$/$V_S$ models. They discuss several low and high velocity anomalies but do not find evidence for large magma accumulations. Kilauea has erupted multiple times in recent decades; therefore, the lack of significant magma bodies is surprising. It is likely that shallow magma reservoirs exist but are too small to be detected with the methods used so far. Larger magma bodies may exist in the deeper crust or upper mantle.

5 Melt fractions in the crust

We found 39 studies that reported quantitative melt fraction estimates associated with 22 different volcanoes (Table 1). The median and mean reported melt fractions are 13% and 18% respectively. The distribution is highly skewed, with the majority of studies reporting melt fractions between 0% and 20% (Figure 9). This result seems to unequivocally support a model where melt storage is dominated by low-melt-fraction processes; however, the story is not so simple.

FIGURE 9

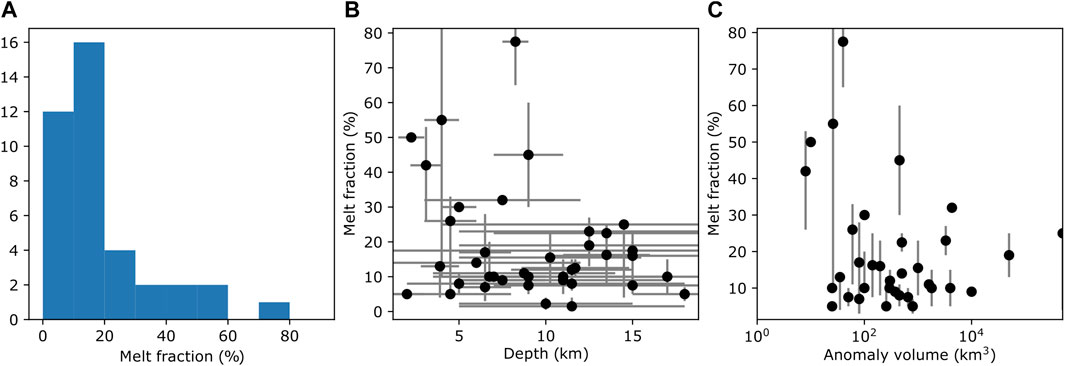
FIGURE 9. (A) Histogram of reported melt fraction. (B) Reported melt fraction versus depth of low velocity anomalies. (C) Reported melt fraction vs estimated anomaly volume.

Recalling the discussion of seismic resolution in Seismic tomography in brief, we note that at any of the studied volcanoes low-velocity anomalies smaller than the seismic resolution length may have gone undetected. Given that the resolution length is typically 2 km–10 km (Table 1), anomalies as large as several tens of cubic kilometres may have been missed by geophysical imaging even at some of the best-studied volcanoes. In addition, any anomaly comparable to the seismic resolution length would be strongly affected by blurring and amplitude reduction. Many of the reported low-velocity volumes are 4 km–10 km in diameter, a size comparable to the resolution length.

Most studies only take into account some of the sources of error and typically do not account for the under-recovery of low-velocity anomalies. This issue is often glossed over because the under-recovery cannot be easily corrected with a multiplicative constant. Beachly et al. (2012) showed how a −15% $V_P$ anomaly and a −55% $V_P$ anomaly can produce the same observed travel-time delay and are therefore indistinguishable with travel-time tomography. A regularized least-squares travel-time inversion that has been carefully tuned aims for the simplest model and thus would recover the smallest anomaly that is compatible with the data. Consequently, any derived melt fraction should be interpreted as a lower bound. Therefore, we can expect a skew towards low melt fractions. This conclusion is further complicated when the uncertainties in melt fraction calculations are considered. It follows that reported melt estimates are often highly inaccurate.

Only five studies reported melt fractions above 35%. These are listed below, together with the estimated melt fractions and imaging methods.

1. Chrapkiewicz et al. (2022), Kolumbo volcano (Hellenic arc), full waveform inversion, 26%–53%

2. Seccia et al. (2011), Long Valley caldera, teleseismic receiver function imaging, 30%–60%

3. Gudmundsson et al. (1994), Katla, active source P-wave forward modelling, 50%

4. Beachly et al. (2012), Newberry volcano, waveform forward modelling, 10%–100%

5. Zollo et al. (2008), Campi Flegrei, amplitude-vs-offset analysis, 65%–90%

It is worth noting that none of these five studies used travel-time tomography and only Chrapkiewicz et al. (2022) used a true inverse method. Beachly et al. (2012) used waveform forward modelling of secondary arrivals, Gudmundsson et al. (1994) used travel-time forward modelling, and the other studies used reflected or converted phases that are particularly sensitive to velocity contrasts across a solid-liquid interface. At all the five above locations, traveltime tomography (either LET or ASTT) was applied by the same or other authors and found small or negligible amounts of melt. Higher melt fractions were detected only when alternative methods, that are more sensitive to low-velocity anomalies, were applied.

There are some unequivocal cases where large anomalies have been observed that are clearly significantly larger than the resolution limit. At Uturuncu, Ward et al. (2014) imaged the 500,000 km³ Altiplano Puna magma body. The seismic velocities within this low-velocity anomaly are consistent with melt fractions below 25%. The diameter of the body is about 200 km, about 4–5 times larger than the horizontal resolution length which is about 30 km–50 km. When this evidence is combined with electrical resistivity data from magneto-telluric inversion (Comeau et al., 2016), it points to the existence of a large and heterogeneous region of crystal mush with melt fraction >15%. Little is known about the internal structure of this crystal mush reservoir. The 15%–25% melt fraction estimate is an average over the scale of the resolution length. Future investigation should focus on determining the multi-scale distribution of melt within mush reservoirs. The distribution of melt fraction is tightly tied to permeability and therefore can have a large effect on the dynamics of melt transport and on the rheology of the mush.

The seismic tomography evidence collected so far does not rule out the presence of small (<10 km³) and medium-sized (<100 km³) magma chambers. These may be present either as isolated bodies or embedded within regions of mush. The only study that reports the presence of a large (>100 km³) reservoir with a melt fraction possibly above the critical porosity is the teleseismic receiver function study of Long Valley Caldera by Seccia et al. (2011). None of the other studies analyzed has uncovered large magma chambers and all are generally in line with the results summarized by Lees (2007). There is an absence of seismological evidence for the existence of large magma chambers, but is this the same as stating that large magma chambers do not exist? Proving the non-existence of something is a notoriously difficult ontological problem since the lack of evidence does not necessarily equate to evidence of absence. However, we can conclude that large magma chambers are at least geologically rare since none have been imaged beyond doubt and we have no reason to believe that the present day is special in any way.

Many authors have argued that large magma chambers must form quickly before an eruption (e.g., Parks et al., 2012; Cashman et al., 2017; Tavazzani et al., 2020). Different mechanisms have been proposed for how low crystallinity magma may be extracted from mush zones. Transfer of heat and volatiles from fresh magma injections may rapidly bring the crystallinity below the lock-up threshold and prime a reservoir for eruption (Weber et al., 2020; Zou and Ma, 2020). Mush remobilization initiated by injection of mafic magma has been suggested as the trigger of eruptions at Volcan de Colima (Hughes et al., 2021) and Lassen Volcanic field (Klemetti and Clynne, 2014). Unrest and eruptions have been linked to the destabilization of the mush at Montserrat (Christopher et al., 2015; Didonna et al., 2022). More work is needed to understand the structure and dynamics of mushy magmatic systems to more confidently interpret geophysical signals that may be associated with the destabilization of the mush.

Outstanding knowledge gaps that are crucial to understanding eruption precursors and magma dynamics and can be addressed by advances in geophysical imaging include. (Figure 10C):

1. The prevalence of volatile-rich and high melt fraction lenses (Rooyakkers et al., 2021)

2. The geometry of eruptive conduits (Cassidy et al., 2018)

3. The melt fraction, internal structure, and eruptive potential of magma reservoirs (Rosi et al., 2022)

4. The melt fraction of deep crustal magma storage regions and the nature of deep melt ascent pathways (Giordano and Caricchi, 2022)

FIGURE 10

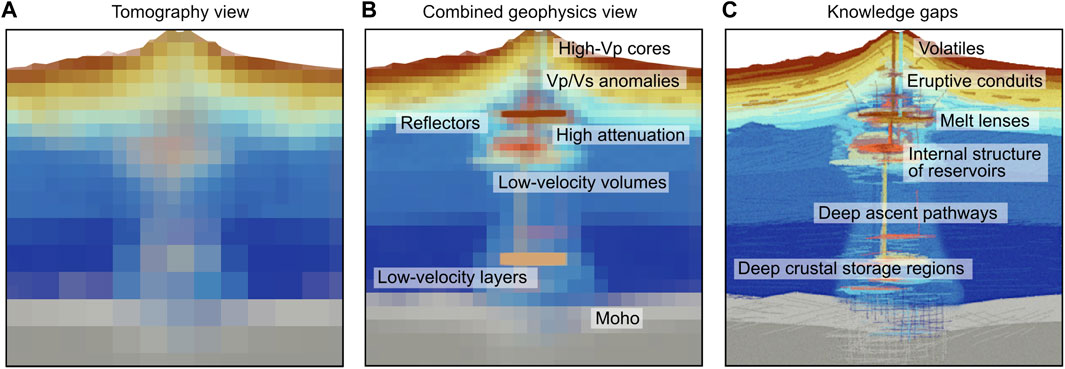
FIGURE 10. (A) Schematic representation of the typical level of detail provided by traditional travel-time tomography. (B) Level of detail that can be achieved by combining the best seismic imaging methods currently available. (C) Modern conceptual model of magmatic systems. Deeper and higher resolution constraints are needed to address outstanding knowledge gaps including: the distribution of magmatic volatiles, the geometry of eruptive conduits, the presence of melt lenses, the internal structure of mush reservoirs, the nature of deep ascent pathways, the properties of deep crustal storage regions.

6 Recommendations for best practice

Our extensive literature review uncovered an impressive body of work on volcano imaging. We identified a few desirable features that in our opinion make a volcano tomography paper particularly useful for the volcanological community. We have distilled these features into a set of recommendations for best practice. These are intended to allow the non-expert reader to extract the most important information, like the depth, size, and strength of low-velocity anomalies, with relative ease. We recommend that authors:

1. Provide a complete description of the dataset used, including the number and type of stations and sources and the frequency bandwidth of the data. Include a map displaying the geometry of the sources and receivers.

2. Describe the inversion method and procedure in sufficient detail to allow replication of the study or at least to allow the expert reader to confidently assess the robustness of the results in comparison to other studies.

3. Carry out and clearly describe a resolution and sensitivity analysis. Provide a quantitative estimate of the resolution length, preferably using spike tests instead of or in addition to checkerboard tests. Provide synthetic studies that specifically test hypotheses about the ability to recover the spatial extent and magnitude of velocity anomalies that are interpreted.

4. Describe any significant and interesting velocity anomaly in the text, listing its depth, size, and amplitude. Provide a rationale to justify the reference velocity used to calculate the anomaly. List both the absolute velocity and the velocity perturbation at the centre of the anomaly. Discuss how the resolution limits and physical sensitivity affect the recovery of the observed anomaly. Refrain from interpreting anomalies that are not robustly constrained.

5. If a low-velocity anomaly is detected and the resolution is sufficient to warrant further investigation, attempt a quantitative estimate of the melt fraction. Report the method used, and all the assumptions made, including the thermal structure, the assumed composition and elastic properties of the melt and of the host rock, and the melt geometries considered. Report the estimated ranges of melt fraction and melt volume with associated uncertainties.

7 Final remarks

Volcano tomography has contributed greatly to the development of the modern paradigm for magma storage and differentiation. An increasing number of active volcanoes have been imaged with seismic methods and many studies have found evidence of clear low-velocity anomalies that can only be explained by the presence of partial melt. The observation of low-velocity anomalies at multiple levels in the crust supports the emerging concept of transcrustal magmatic systems (Sparks and Cashman, 2017). Most seismological observations seem to be consistent with magma storage dominated by crystal-rich mush; however, estimates of melt fraction are still highly speculative.

We argue that traditional travel-time tomography and surface wave tomography provide weak constraints on melt fractions, with a potential bias toward underestimating. They remain powerful and useful tools for understanding the three-dimensional structure of volcanoes and they can inform the location of magma storage. When applied with care and interpreted within the bounds imposed by resolution and sensitivity limits, they can provide broad constraints on possible magma volumes. To recover robust constraints on melt fractions and answer the many important outstanding questions concerning the nature of magma reservoirs other methods must be employed that use more information derived from the full seismic wavefield.

Determining melt fraction from seismic properties is conceptually very similar to estimating porosity and hydrocarbon saturation in hydrocarbon reservoirs. Therefore, the volcano seismologist has the opportunity to borrow from the array of methods developed by the geophysical exploration industry. In traditional hydrocarbon exploration, tomography is used routinely to recover the long-wavelength structure and multi-channel seismic imaging is used to determine the high-resolution tectonic structure. The most common approach to determine reservoir porosity and hydrocarbon saturation is AVO analysis (Smith and Gidlow, 1987; Castagna and Backus, 1993; Fawad et al., 2020). This method has been used successfully to constrain melt fractions beneath mid-ocean ridges (e.g., Singh et al., 1998). More recently, the exploration industry has embraced full-waveform inversion, which can simultaneously provide high-resolution structural constraints and robust reservoir parameters (Prieux et al., 2013; Warner et al., 2013; Zhang and Alkhalifah, 2020). Where these methods have been applied to magma imaging, they have been successful in revealing small melt bodies and constraining melt fractions more robustly than possible with traditional methods. (e.g., Xu et al., 2014; Chrapkiewicz et al., 2022).

Wider adoption of these techniques is needed to shed new light on magma reservoir properties. Achieving this objective will also require new strategies for collecting dense broad-band seismic data on active volcanoes. Higher-resolution seismic imaging and robust melt fraction constraints have the potential to transform seismic imaging into a diagnostic tool for volcanic hazards. Deeper and higher resolution imaging should be integrated into a multi-disciplinary strategy including information from geophysical monitoring, the geological record, petrology, and numerical modelling to determine the potential for future eruptions and the likely eruption style and size (Giordano and Caricchi, 2022).

Author contributions

MP assembled and analysed the database, generated the figures and wrote the manuscript. KC produced the wavefront healing analysis and created the first version of the GitHub repository and the included Jupyter notebooks. EH, BH, DT, and JM helped interpret the result and write the manuscript.

Funding

MP was supported by a NERC Independent Research Fellowship (grant number NE/R015708/1) and EH by the National Science Foundation (grant number OCE-2023338).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abe, Y., Ohkura, T., Shibutani, T., Hirahara, K., and Kato, M. (2010). Crustal structure beneath Aso Caldera, Southwest Japan, as derived from receiver function analysis. J. Volcanol. Geotherm. Res. 195 (1), 1–12. doi:10.1016/j.jvolgeores.2010.05.011

CrossRef Full Text | Google Scholar

Abe, Y., Ohkura, T., Shibutani, T., Hirahara, K., Yoshikawa, S., and Inoue, H. (2017). Low‐velocity zones in the crust beneath Aso caldera, Kyushu, Japan, derived from receiver function analyses. J. Geophys. Res. Solid Earth 122 (3), 2013–2033. doi:10.1002/2016jb013686

CrossRef Full Text | Google Scholar

Achauer, U., Evans, J. R., and Stauber, D. A. (1988). High‐resolution seismic tomography of compressional wave velocity structure at Newberry Volcano, Oregon Cascade Range. J. Geophys. Res. 93 (B9), 10135–10147. doi:10.1029/jb093ib09p10135

CrossRef Full Text | Google Scholar

Aghaei, O., Nedimović, M. R., Marjanović, M., Carbotte, S. M., Canales, J. P., Carton, H., et al. (2017). Constraints on melt content of off‐axis magma lenses at the East Pacific Rise from analysis of 3‐D seismic amplitude variation with angle of incidence. J. Geophys. Res. Solid Earth 122 (6), 4123–4142. doi:10.1002/2016jb013785

CrossRef Full Text | Google Scholar

Ammon, C. J., Randall, G. E., and Zandt, G. (1990). On the nonuniqueness of receiver function inversions. J. Geophys. Res. 95, 15303–15318. doi:10.1029/jb095ib10p15303

CrossRef Full Text | Google Scholar

Annen, C., Paulatto, M., Sparks, R. S. J., Minshull, T. A., and Kiddle, E. J. (2014). Quantification of the intrusive magma fluxes during magma chamber growth at Soufrière Hills Volcano (Montserrat, Lesser Antilles). J. Petrology 55 (3), 529–548. doi:10.1093/petrology/egt075

CrossRef Full Text | Google Scholar

Arnoux, G. M., Toomey, D. R., Hooft, E. E. E., and Wilcock, W. S. D. (2019). Seismic imaging and physical properties of the Endeavour segment: Evidence that skew between mantle and crustal magmatic systems governs spreading center processes. Geochem. Geophys. Geosyst. 20 (3), 1319–1339. doi:10.1029/2018GC007978

CrossRef Full Text | Google Scholar

Arnulf, A. F., Harding, A. J., Singh, S. C., Kent, G. M., and Crawford, W. C. (2014). Nature of upper crust beneath the Lucky Strike volcano using elastic full waveform inversion of streamer data. Geophys. J. Int. 196 (3), 1471–1491. doi:10.1093/gji/ggt461

CrossRef Full Text | Google Scholar

Aster, R. C., and Meyer, R. P. (1988). Three-dimensional velocity structure and hypocenter distribution in the Campi Flegrei caldera, Italy. Tectonophysics 149 (3-4), 195–218. doi:10.1016/0040-1951(88)90173-4

CrossRef Full Text | Google Scholar

Avellaneda, M. (1987). Iterated homogenization, differential effective medium theory and applications. Commun. Pure Appl. Math. 40 (5), 527–554. doi:10.1002/cpa.3160400502

CrossRef Full Text | Google Scholar

Bai, T., Thurber, C., Lanza, F., Singer, B. S., Bennington, N., Keranen, K., et al. (2020). Teleseismic tomography of the Laguna del Maule volcanic field in Chile. JGR. Solid Earth 125 (8), e2020JB019449. doi:10.1029/2020jb019449

CrossRef Full Text | Google Scholar

Barmin, M. P., Ritzwoller, M. H., and Levshin, A. L. (2001). “A fast and reliable method for surface wave tomography,” in Monitoring the comprehensive nuclear-test-ban treaty: Surface waves (Basel: Birkhäuser), 1351–1375.

CrossRef Full Text | Google Scholar

Bastow, I. D., Pilidou, S., Kendall, J. M., and Stuart, G. W. (2010). Melt‐induced seismic anisotropy and magma assisted rifting in Ethiopia: Evidence from surface waves. Geochem. Geophys. Geosyst. 11 (6). doi:10.1029/2010gc003036

CrossRef Full Text | Google Scholar

Battaglia, J., Zollo, A., Virieux, J., and Iacono, D. D. (2008). Merging active and passive data sets in traveltime tomography: The case study of Campi Flegrei caldera (southern Italy). Geophys. Prospect. 56 (4), 555–573. doi:10.1111/j.1365-2478.2007.00687.x

CrossRef Full Text | Google Scholar

Beachly, M. W., Hooft, E. E., Toomey, D. R., and Waite, G. P. (2012). Upper crustal structure of Newberry volcano from P‐wave tomography and finite difference waveform modeling. J. Geophys. Res. 117 (B10). doi:10.1029/2012jb009458

CrossRef Full Text | Google Scholar

Bedrosian, P. A., Peacock, J. R., Bowles-Martinez, E., Schultz, A., and Hill, G. J. (2018). Crustal inheritance and a top-down control on arc magmatism at Mount St Helens. Nat. Geosci. 11 (11), 865–870. doi:10.1038/s41561-018-0217-2

CrossRef Full Text | Google Scholar

Behr, Y., Townend, J., Bannister, S., and Savage, M. K. (2011). Crustal shear wave tomography of the Taupo Volcanic Zone, New Zealand, via ambient noise correlation between multiple three‐component networks. Geochem. Geophys. Geosyst. 12 (3). doi:10.1029/2010gc003385

CrossRef Full Text | Google Scholar

Benz, H. M., and Smith, R. B. (1984). Simultaneous inversion for lateral velocity variations and hypocenters in the Yellowstone region using earthquake and refraction data. J. Geophys. Res. 89 (B2), 1208–1220. doi:10.1029/jb089ib02p01208

CrossRef Full Text | Google Scholar

Berge, P. A., Berryman, J. G., and Bonner, B. P. (1993). Influence of microstructure on rock elastic properties. Geophys. Res. Lett. 20 (23), 2619–2622. doi:10.1029/93gl03131

CrossRef Full Text | Google Scholar

Berryman, J. G. (1980). Long‐wavelength propagation in composite elastic media II. Ellipsoidal inclusions. J. Acoust. Soc. Am. 68 (6), 1820–1831. doi:10.1121/1.385172

CrossRef Full Text | Google Scholar

Bodin, T., Sambridge, M., Rawlinson, N., and Arroucau, P. (2012a). Transdimensional tomography with unknown data noise. Geophys. J. Int. 189 (3), 1536–1556. doi:10.1111/j.1365-246x.2012.05414.x

CrossRef Full Text | Google Scholar

Bodin, T., Sambridge, M., Tkalčić, H., Arroucau, P., Gallagher, K., and Rawlinson, N. (2012b). Transdimensional inversion of receiver functions and surface wave dispersion. J. Geophys. Res. 117 (B2). doi:10.1029/2011jb008560

CrossRef Full Text | Google Scholar

Bottinga, Y., and Steinmetz, L. (1979). A geophysical, geochemical, petrological model of the sub-marine lithosphere. Tectonophysics 55 (3-4), 311–347. doi:10.1016/0040-1951(79)90182-3

CrossRef Full Text | Google Scholar

Budiansky, B. (1965). On the elastic moduli of some heterogeneous materials. J. Mech. Phys. Solids 13 (4), 223–227. doi:10.1016/0022-5096(65)90011-6

CrossRef Full Text | Google Scholar

Burdick, L. J., and Langston, C. A. (1977). Modeling crustal structure through the use of converted phases in teleseismic body-wave forms. Bull. Seismol. Soc. Am. 67 (3), 677–691. doi:10.1785/bssa0670030677

CrossRef Full Text | Google Scholar

Byerly, K., Brown, L., Voight, B., and Miller, V. (2010). Reflection imaging of deep structure beneath Montserrat using microearthquake sources. Geophys. Res. Lett. 37 (19). doi:10.1029/2009gl041995

CrossRef Full Text | Google Scholar

Calò, M., and Tramelli, A. (2018). Anatomy of the Campi Flegrei caldera using enhanced seismic tomography models. Sci. Rep. 8 (1). doi:10.1038/s41598-018-34456-x

CrossRef Full Text | Google Scholar

Canales, J. P., Singh, S. C., Detrick, R. S., Carbotte, S. M., Harding, A., Kent, G. M., et al. (2006). Seismic evidence for variations in axial magma chamber properties along the southern Juan de Fuca Ridge. Earth Planet. Sci. Lett. 246 (3-4), 353–366. doi:10.1016/j.epsl.2006.04.032

CrossRef Full Text | Google Scholar

Cann, J. R. (1974). A model for oceanic crystal structure developed. Geophys. J. Int. 39 (1), 169–187. doi:10.1111/j.1365-246x.1974.tb05446.x

CrossRef Full Text | Google Scholar

Carbotte, S. M., Detrick, R. S., Harding, A., Canales, J. P., Babcock, J., Kent, G., et al. (2006). Rift topography linked to magmatism at the intermediate spreading Juan de Fuca Ridge. Geol. 34 (3), 209–212. doi:10.1130/G21969.1

CrossRef Full Text | Google Scholar

Carbotte, S. M., Arnulf, A., Spiegelman, M., Lee, M., Harding, A., Kent, G., et al. (2020). Stacked sills forming a deep melt-mush feeder conduit beneath Axial Seamount. Geology 48 (7), 693–697. doi:10.1130/g47223.1

CrossRef Full Text | Google Scholar

Caricchi, L., Burlini, L., and Ulmer, P. (2008). Propagation of P and S-waves in magmas with different crystal contents: Insights into the crystallinity of magmatic reservoirs. J. Volcanol. Geotherm. Res. 178 (4), 740–750. doi:10.1016/j.jvolgeores.2008.09.006

CrossRef Full Text | Google Scholar

Casey, J. F., and Karson, J. A. (1981). Magma chamber profiles from the Bay of Islands ophiolite complex. Nature 292 (5821), 295–301. doi:10.1038/292295a0

CrossRef Full Text | Google Scholar

Cashman, K. V., and Giordano, G. (2014). Calderas and magma reservoirs. J. Volcanol. Geotherm. Res. 288, 28–45. doi:10.1016/j.jvolgeores.2014.09.007

CrossRef Full Text | Google Scholar

Cashman, K. V., Sparks, R. S. J., and Blundy, J. D. (2017). Vertically extensive and unstable magmatic systems: A unified view of igneous processes. Science 355 (6331), eaag3055. doi:10.1126/science.aag3055

PubMed Abstract | CrossRef Full Text | Google Scholar

Cassidy, M., Manga, M., Cashman, K., and Bachmann, O. (2018). Controls on explosive-effusive volcanic eruption styles. Nat. Commun. 9 (1). doi:10.1038/s41467-018-05293-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Castagna, J. P., and Backus, M. M. (1993). AVO analysis—tutorial and review. Offset-dependent reflectivity—Theory Pract. AVO analysis SEG Investigations Geophys. 8, 3–36. doi:10.5724/gcs.96.17.0059

CrossRef Full Text | Google Scholar

Chambers, E. L., Harmon, N., Rychert, C. A., and Keir, D. (2021). Variations in melt emplacement beneath the northern East African Rift from radial anisotropy. Earth Planet. Sci. Lett. 573, 117150. doi:10.1016/j.epsl.2021.117150

CrossRef Full Text | Google Scholar

Chiarabba, C., and Moretti, M. (2006). An insight into the unrest phenomena at the Campi Flegrei caldera from Vp and Vp/Vs tomography. Terra nova. 18 (6), 373–379. doi:10.1111/j.1365-3121.2006.00701.x

CrossRef Full Text | Google Scholar

Chmielowski, J., Zandt, G., and Haberland, C. (1999). The central Andean Altiplano‐Puna magma body. Geophys. Res. Lett. 26 (6), 783–786. doi:10.1029/1999gl900078

CrossRef Full Text | Google Scholar

Chrapkiewicz, K., Wilde-Piórko, M., Polkowski, M., and Grad, M. (2020). Reliable workflow for inversion of seismic receiver function and surface wave dispersion data: A “13 BB star” case study. J. Seismol. 24, 101–120. doi:10.1007/s10950-019-09888-1

CrossRef Full Text | Google Scholar

Chrapkiewicz, K., Paulatto, M., Heath, B., Hooft, E. E. E., Nomikou, P., Papazachos, C. B., et al. (2022). Magma chamber detected beneath an active arc volcano with high-resolution velocity images. pre-print. doi:10.31223/X5934R

CrossRef Full Text | Google Scholar

Christensen, N. I., and Stanley, D. (2003). “Seismic velocities and densities of rocks,”. International Geophysics (Academic Press), 81, 1587–1594.

CrossRef Full Text | Google Scholar

Christopher, T. E., Blundy, J., Cashman, K., Cole, P., Edmonds, M., Smith, P. J., et al. (2015). Crustal‐scale degassing due to magma system destabilization and magma‐gas decoupling at S oufrière H ills V olcano, M ontserrat. Geochem. Geophys. Geosyst. 16 (9), 2797–2811. doi:10.1002/2015gc005791

CrossRef Full Text | Google Scholar

Chu, R., Helmberger, D. V., Sun, D., Jackson, J. M., and Zhu, L. (2010). Mushy magma beneath Yellowstone. Geophys. Res. Lett. 37 (1), 41656. doi:10.1029/2009gl041656

CrossRef Full Text | Google Scholar

Chung, D. H., Swica, J. J., and Crandall, W. B. (1963). Relation of single‐crystal elastic Constants to polycrystalline isotropic elastic moduli of MgO. J. Am. Ceram. Soc. 46 (9), 452–457. doi:10.1111/j.1151-2916.1963.tb11775.x

CrossRef Full Text | Google Scholar

Comeau, M. J., Unsworth, M. J., and Cordell, D. (2016). New constraints on the magma distribution and composition beneath Volcán Uturuncu and the southern Bolivian Altiplano from magnetotelluric data. Geosphere 12 (5), 1391–1421. doi:10.1130/ges01277.1

CrossRef Full Text | Google Scholar

Cooper, K. M. (2017). What does a magma reservoir look like? The “crystal's-eye” view. Elements 13 (1), 23–28. doi:10.2113/gselements.13.1.23

CrossRef Full Text | Google Scholar

Cornwell, D. G., Maguire, P. K. H., England, R. W., and Stuart, G. W. (2010). Imaging detailed crustal structure and magmatic intrusion across the Ethiopian Rift using a dense linear broadband array. Geochem. Geophys. Geosyst. 11 (1). doi:10.1029/2009gc002637

CrossRef Full Text | Google Scholar

Costa, A., Caricchi, L., and Bagdassarov, N. (2009). A model for the rheology of particle‐bearing suspensions and partially molten rocks. Geochem. Geophys. Geosyst. 10 (3), 2138. doi:10.1029/2008gc002138

CrossRef Full Text | Google Scholar

D'Auria, L., Koulakov, I., Prudencio, J., Cabrera-Perez, I., Ibanez, J., Martinez, J. B., et al. (2022). Voluminous storage and rapid magma ascent beneath La palma revealed by seismic tomography.

Google Scholar

Dahlen, F. A. (2004). Resolution limit of traveltime tomography. Geophys. J. Int. 157 (1), 315–331. doi:10.1111/j.1365-246x.2004.02214.x

CrossRef Full Text | Google Scholar

Dawson, P. B., Evans, J. R., and Iyer, H. M. (1990). Teleseismic tomography of the compressional wave velocity structure beneath the Long Valley region, California. J. Geophys. Res. 95 (B7), 11021–11050. doi:10.1029/jb095ib07p11021

CrossRef Full Text | Google Scholar

De Siena, L., Thomas, C., Waite, G. P., Moran, S. C., and Klemme, S. (2014). Attenuation and scattering tomography of the deep plumbing system of Mount St. Helens. J. Geophys. Res. Solid Earth 119 (11), 8223–8238. doi:10.1002/2014JB011372

CrossRef Full Text | Google Scholar

DePaolo, D. J. (1981). Trace element and isotopic effects of combined wallrock assimilation and fractional crystallization. Earth Planet. Sci. Lett. 53 (2), 189–202. doi:10.1016/0012-821x(81)90153-9

CrossRef Full Text | Google Scholar

Detrick, R. S., Buhl, P., Vera, E., Mutter, J., Orcutt, J., Madsen, J., et al. (1987). Multi-channel seismic imaging of a crustal magma chamber along the East Pacific Rise. Nature 326 (6108), 35–41. doi:10.1038/326035a0

CrossRef Full Text | Google Scholar

Díaz-Moreno, A., Barberi, G., Cocina, O., Koulakov, I., Scarfì, L., Zuccarello, L., et al. (2018). New insights on Mt. Etna’s crust and relationship with the regional tectonic framework from joint active and passive P-wave seismic tomography. Surv. Geophys. 39 (1), 57–97. doi:10.1007/s10712-017-9425-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Didonna, R., Costa, F., Handley, H., Turner, S., and Barclay, J. (2022). Dynamics and timescales of mafic–silicic magma interactions at Soufrière Hills Volcano, Montserrat. Contrib. Mineral. Pet.177 (2), 28–17. doi:10.1007/s00410-022-01891-z

CrossRef Full Text | Google Scholar

Dimitriadis, I., Papazachos, C., Panagiotopoulos, D., Hatzidimitriou, P., Bohnhoff, M., Rische, M., et al. (2010). P and S velocity structures of the Santorini–Coloumbo volcanic system (Aegean Sea, Greece) obtained by non-linear inversion of travel times and its tectonic implications. J. Volcanol. Geotherm. Res. 195 (1), 13–30. doi:10.1016/j.jvolgeores.2010.05.013

CrossRef Full Text | Google Scholar

Druitt, T. H., Costa, F., Deloule, E., Dungan, M., and Scaillet, B. (2012). Decadal to monthly timescales of magma transfer and reservoir growth at a caldera volcano. Nature 482 (7383), 77–80. doi:10.1038/nature10706

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunn, R. A., Toomey, D. R., and Solomon, S. C. (2000). Three‐dimensional seismic structure and physical properties of the crust and shallow mantle beneath the East Pacific Rise at 9° 30'N. J. Geophys. Res. 105 (B10), 23537–23555. doi:10.1029/2000jb900210

CrossRef Full Text | Google Scholar

Dunn, R. A., Lekić, V., Detrick, R. S., and Toomey, D. R. (2005). Three‐dimensional seismic structure of the Mid‐Atlantic Ridge (35 N): Evidence for focused melt supply and lower crustal dike injection. J. Geophys. Res. 110 (B9). doi:10.1029/2004jb003473

CrossRef Full Text | Google Scholar

Ellsworth, W. L., and Koyanagi, R. Y. (1977). Three‐dimensional crust and mantle structure of Kilauea Volcano, Hawaii. J. Geophys. Res. 82 (33), 5379–5394. doi:10.1029/jb082i033p05379

CrossRef Full Text | Google Scholar

Escudero, C. R., and Bandy, W. L. (2017). Ambient seismic noise tomography of the Colima volcano complex. Bull. Volcanol. 79 (2), 13–19. doi:10.1007/s00445-016-1096-2

CrossRef Full Text | Google Scholar

Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 241 (1226), 376–396. doi:10.1098/rspa.1958.0133

CrossRef Full Text | Google Scholar

Farrell, J., Smith, R. B., Husen, S., and Diehl, T. (2014). Tomography from 26 years of seismicity revealing that the spatial extent of the Yellowstone crustal magma reservoir extends well beyond the Yellowstone caldera. Geophys. Res. Lett. 41 (9), 3068–3073. doi:10.1002/2014gl059588

CrossRef Full Text | Google Scholar

Fawad, M., Hansen, J. A., and Mondol, N. H. (2020). Seismic-fluid detection-a review. Earth-Science Rev. 210, 103347. doi:10.1016/j.earscirev.2020.103347

CrossRef Full Text | Google Scholar

Fichtner, A., and Trampert, J. (2011). Resolution analysis in full waveform inversion. Geophys. J. Int. 187 (3), 1604–1624. doi:10.1111/j.1365-246x.2011.05218.x

CrossRef Full Text | Google Scholar

Flinders, A. F., Shelly, D. R., Dawson, P. B., Hill, D. P., Tripoli, B., and Shen, Y. (2018). Seismic evidence for significant melt beneath the Long Valley caldera, California, USA. Geology 46 (9), 799–802. doi:10.1130/g45094.1

CrossRef Full Text | Google Scholar

Flinders, A. F., and Shen, Y. (2017). Seismic evidence for a possible deep crustal hot zone beneath Southwest Washington. Sci. Rep. 7 (1), 7400–7410. doi:10.1038/s41598-017-07123-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Forsyth, D. W., and Li, A. (2005). “Array analysis of two-dimensional variations in surface wave phase velocity and azimuthal anisotropy in the presence of multipathing interference,” in Seismic Earth: Array analysis of broadband seismograms. Geophysical monograph. Editors A. Levander, and G. Nolet (Washington, D.C: AGU), 157, 81–97. doi:10.1029/157GM0

CrossRef Full Text | Google Scholar

Foulger, G. R., Panza, G. F., Artemieva, I. M., Bastow, I. D., Cammarano, F., Evans, J. R., et al. (2013). Caveats on tomographic images. Terra nova. 25 (4), 259–281. doi:10.1111/ter.12041

CrossRef Full Text | Google Scholar

Garapić, G., Faul, U. H., and Brisson, E. (2013). High‐resolution imaging of the melt distribution in partially molten upper mantle rocks: Evidence for wetted two‐grain boundaries. Geochem. Geophys. Geosyst. 14 (3), 556–566. doi:10.1029/2012gc004547

CrossRef Full Text | Google Scholar

García‐Yeguas, A., Koulakov, I., Ibáñez, J. M., and Rietbrock, A. (2012). High resolution 3D P wave velocity structure beneath Tenerife Island (Canary Islands, Spain) based on tomographic inversion of active‐source data. J. Geophys. Res. 117 (B9), 8970. doi:10.1029/2011jb008970

CrossRef Full Text | Google Scholar

García-Yeguas, A., Ibánez, J. M., Koulakov, I., Jakovlev, A., Romero-Ruiz, M. C., and Prudencio, J. (2014). Seismic tomography model reveals mantle magma sources of recent volcanic activity at El Hierro Island (Canary Islands, Spain). Geophys. J. Int. 199 (3), 1739–1750. doi:10.1093/gji/ggu339

CrossRef Full Text | Google Scholar

Giordano, G., and Caricchi, L. (2022). Determining the state of activity of transcrustal magmatic systems and their volcanoes. Annu. Rev. Earth Planet. Sci. 50, 231–259. doi:10.1146/annurev-earth-032320-084733

CrossRef Full Text | Google Scholar

Godey, S., Snieder, R., Villaseñor, A., and Benz, H. M. (2003). Surface wave tomography of north America and the caribbean using global and regional broad-band networks: Phase velocity maps and limitations of ray theory. Geophys. J. Int. 152 (3), 620–632. doi:10.1046/j.1365-246x.2003.01866.x

CrossRef Full Text | Google Scholar

Greenfield, T., White, R. S., and Roecker, S. (2016). The magmatic plumbing system of the Askja central volcano, Iceland, as imaged by seismic tomography. J. Geophys. Res. Solid Earth 121 (10), 7211–7229. doi:10.1002/2016jb013163

CrossRef Full Text | Google Scholar

Gudmundsson, O., Brandsdóttir, B., Menke, W., and Sigvaldason, G. E. (1994). The crustal magma chamber of the Katla volcano in south Iceland revealed by 2-D seismic undershooting. Geophys. J. Int. 119 (1), 277–296. doi:10.1111/j.1365-246x.1994.tb00928.x

CrossRef Full Text | Google Scholar

Guidarelli, M., Sarao, A., and Panza, G. F. (2002). Surface wave tomography and seismic source studies at Campi Flegrei (Italy). Phys. Earth Planet. Interiors 134 (3-4), 157–173. doi:10.1016/s0031-9201(02)00154-1

CrossRef Full Text | Google Scholar

Hammond, J. O., Kendall, J. M., Wookey, J., Stuart, G. W., Keir, D., and Ayele, A. (2014). Differentiating flow, melt, or fossil seismic anisotropy beneath Ethiopia. Geochem. Geophys. Geosyst. 15 (5), 1878–1894. doi:10.1002/2013gc005185

CrossRef Full Text | Google Scholar

Hammond, J. O., Wu, J. P., Ri, K. S., Wei, W., Yu, J. N., and Oppenheimer, C. (2020). Distribution of partial melt beneath Changbaishan/Paektu Volcano, China/democratic people's Republic of Korea. Geochem. Geophys. Geosyst. 21 (1), e2019GC008461. doi:10.1029/2019gc008461

CrossRef Full Text | Google Scholar

Hammond, J. O., and Kendall, J. M. (2016). Constraints on melt distribution from seismology: A case study in Ethiopia. Geol. Soc. Lond. Spec. Publ. 420 (1), 127–147. doi:10.1144/SP420.14

CrossRef Full Text | Google Scholar

Hammond, W. C., and Humphreys, E. D. (2000). Upper mantle seismic wave attenuation: Effects of realistic partial melt distribution. J. Geophys. Res. 105 (B5), 10987–10999. doi:10.1029/2000JB900042

CrossRef Full Text | Google Scholar

Hammond, W. C., and Toomey, D. R. (2003). Seismic velocity anisotropy and heterogeneity beneath the mantle electromagnetic and tomography experiment (MELT) region of the East pacific rise from analysis of P and S body waves. J. Geophys. Res. 108 (B4), 1789. doi:10.1029/2002jb001789

CrossRef Full Text | Google Scholar

Hashin, Z., and Shtrikman, S. (1963). A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 11 (2), 127–140. doi:10.1016/0022-5096(63)90060-7

CrossRef Full Text | Google Scholar

Haslinger, F., Thurber, C., Mandernach, M., and Okubo, P. (2001). Tomographic image of P‐velocity structure beneath Kilauea's East Rift Zone and South Flank: Seismic evidence for a deep magma body. Geophys. Res. Lett. 28 (2), 375–378. doi:10.1029/2000gl012018

CrossRef Full Text | Google Scholar

Heath, B. A., Hooft, E. E., Toomey, D. R., and Bezada, M. J. (2015). Imaging the magmatic system of Newberry Volcano using joint active source and teleseismic tomography. Geochem. Geophys. Geosyst. 16 (12), 4433–4448. doi:10.1002/2015GC006129

CrossRef Full Text | Google Scholar

Heath, B. A., Hooft, E. E., and Toomey, D. R. (2018). Autocorrelation of the seismic wavefield at Newberry Volcano: Reflections from the magmatic and geothermal systems. Geophys. Res. Lett. 45 (5), 2311–2318. doi:10.1002/2017GL076706

CrossRef Full Text | Google Scholar

Heath, B. A., Hooft, E. E. E., Toomey, D. R., Papazachos, C. B., Nomikou, P., Paulatto, M., et al. (2019). Tectonism and its relation to magmatism around Santorini Volcano from upper crustal P wave velocity. J. Geophys. Res. Solid Earth 124 (10), 10610–10629. doi:10.1029/2019jb017699

CrossRef Full Text | Google Scholar

Heath, B. A., Hooft, E. E. E., Toomey, D. R., Paulatto, M., Papazachos, C. B., Nomikou, P., et al. (2021). Relationship between active faulting/fracturing and magmatism around Santorini: Seismic anisotropy from an active source tomography experiment. JGR. Solid Earth 126 (8), e2021JB021898. doi:10.1029/2021jb021898

CrossRef Full Text | Google Scholar

Hill, R. (1952). The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 65 (5), 349–354. doi:10.1088/0370-1298/65/5/307

CrossRef Full Text | Google Scholar

Hobro, J. W., Singh, S. C., and Minshull, T. A. (2003). Three-dimensional tomographic inversion of combined reflection and refraction seismic traveltime data. Geophys. J. Int. 152 (1), 79–93. doi:10.1046/j.1365-246x.2003.01822.x

CrossRef Full Text | Google Scholar

Holness, M. B. (2006). Melt–solid dihedral angles of common minerals in natural rocks. J. Petrology 47 (4), 791–800. doi:10.1093/petrology/egi094

CrossRef Full Text | Google Scholar

Hooft, E. E., Detrick, R. S., and Kent, G. M. (1997). Seismic structure and indicators of magma budget along the southern East Pacific Rise. J. Geophys. Res. 102 (B12), 27319–27340. doi:10.1029/97jb02349

CrossRef Full Text | Google Scholar

Hooft, E. E. E., Detrick, R. S., Toomey, D. R., Collins, J. A., and Lin, J. (2000). Crustal thickness and structure along three contrasting spreading segments of the Mid‐Atlantic Ridge, 33.5–35 N. J. Geophys. Res. 105 (B4), 8205–8226. doi:10.1029/1999jb900442

CrossRef Full Text | Google Scholar

Hooft, E. E. E., Heath, B. A., Toomey, D. R., Paulatto, M., Papazachos, C. B., Nomikou, P., et al. (2019). Seismic imaging of Santorini: Subsurface constraints on caldera collapse and present-day magma recharge. Earth Planet. Sci. Lett. 514, 48–61. doi:10.1016/j.epsl.2019.02.033

CrossRef Full Text | Google Scholar

Huang, H. H., Lin, F. C., Schmandt, B., Farrell, J., Smith, R. B., and Tsai, V. C. (2015). The Yellowstone magmatic system from the mantle plume to the upper crust. Science 348 (6236), 773–776. doi:10.1126/science.aaa5648

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y. C., Ohkura, T., Kagiyama, T., Yoshikawa, S., and Inoue, H. (2018). Shallow volcanic reservoirs and pathways beneath Aso caldera revealed using ambient seismic noise tomography. Earth Planets Space 70 (1), 169–221. doi:10.1186/s40623-018-0941-2

CrossRef Full Text | Google Scholar

Hughes, G. E., Petrone, C. M., Downes, H., Varley, N. R., and Hammond, S. J. (2021). Mush remobilisation and mafic recharge: A study of the crystal cargo of the 2013–17 eruption at volcán de Colima, Mexico. J. Volcanol. Geotherm. Res. 416, 107296. doi:10.1016/j.jvolgeores.2021.107296

CrossRef Full Text | Google Scholar

Husen, S., Smith, R. B., and Waite, G. P. (2004). Evidence for gas and magmatic sources beneath the Yellowstone volcanic field from seismic tomographic imaging. J. Volcanol. Geotherm. Res. 131 (3-4), 397–410. doi:10.1016/s0377-0273(03)00416-5

CrossRef Full Text | Google Scholar

Hussenoeder, S. A., Collins, J. A., Kent, G. M., and Detrick, R. S. (1996). Seismic analysis of the axial magma chamber reflector along the southern East Pacific Rise from conventional reflection profiling. J. Geophy. Res.: Solid Earth 101 (B10), 22087–22105.

CrossRef Full Text | Google Scholar

Indrastuti, N., Nugraha, A. D., McCausland, W. A., Hendrasto, M., Gunawan, H., Kusnandar, R., et al. (2019). 3-D seismic tomographic study of Sinabung volcano, northern sumatra, Indonesia, during the inter-eruptive period october 2010–july 2013. J. Volcanol. Geotherm. Res. 382, 197–209. doi:10.1016/j.jvolgeores.2019.03.001

CrossRef Full Text | Google Scholar

Iyer, H. M. (1979). Deep structure under Yellowstone national park USA: A continental “hot spot”. Tectonophysics 56 (1-2), 165–197. doi:10.1016/0040-1951(79)90030-1

CrossRef Full Text | Google Scholar

Iyer, H. M., Evans, J. R., Zandt, G., Stewart, R. M., Coakley, J. M., and Roloff, J. N. (1981). A deep low-velocity body under the Yellowstone caldera, Wyoming: Delineation using teleseismic P-wave residuals and tectonic interpretation. GSA Bull. 92, 1471–1646. doi:10.1130/gsab-p2-92-1471

CrossRef Full Text | Google Scholar

H. M. Iyer, and K. Hirahara (Editors) (1993). Seismic tomography: Theory and practice (Springer Science & Business Media).

Google Scholar

Jackson, D. D. (1979). The use of a priori data to resolve non-uniqueness in linear inversion. Geophys. J. Int. 57 (1), 137–157. doi:10.1111/j.1365-246X.1979.tb03777.x

CrossRef Full Text | Google Scholar

Jackson, M. D., Blundy, J., and Sparks, R. S. J. (2018). Chemical differentiation, cold storage and remobilization of magma in the Earth’s crust. Nature 564 (7736), 405–409. doi:10.1038/s41586-018-0746-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Janiszewski, H. A., Wagner, L. S., and Roman, D. C. (2020). Aseismic mid-crustal magma reservoir at Cleveland Volcano imaged through novel receiver function analyses. Sci. Rep. 10 (1), 1780–1789. doi:10.1038/s41598-020-58589-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaxybulatov, K., Shapiro, N. M., Koulakov, I., Mordret, A., Landès, M., and Sens-Schönfelder, C. (2014). A large magmatic sill complex beneath the Toba caldera. science 346 (6209), 617–619. doi:10.1126/science.1258582

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeddi, Z., Tryggvason, A., and Gudmundsson, Ó. (2016). The Katla volcanic system imaged using local earthquakes recorded with a temporary seismic network. J. Geophys. Res. Solid Earth 121 (10), 7230–7251. doi:10.1002/2016jb013044

CrossRef Full Text | Google Scholar

Jeddi, Z., Gudmundsson, O., and Tryggvason, A. (2017). Ambient-noise tomography of Katla volcano, south Iceland. J. Volcanol. Geotherm. Res. 347, 264–277. doi:10.1016/j.jvolgeores.2017.09.019

CrossRef Full Text | Google Scholar

Jiang, C., Schmandt, B., Farrell, J., Lin, F. C., and Ward, K. M. (2018). Seismically anisotropic magma reservoirs underlying silicic calderas. Geology 46 (8), 727–730. doi:10.1130/g45104.1

CrossRef Full Text | Google Scholar

Jin, G., and Gaherty, J. B. (2015). Surface wave phase-velocity tomography based on multichannel cross-correlation. Geophys. J. Int. 201, 1383–1398. doi:10.1093/gji/ggv079

CrossRef Full Text | Google Scholar

Jónsdóttir, K., Tryggvason, A., Roberts, R., Lund, B., Soosalu, H., and Böðvarsson, R. (2007). Habits of a glacier-covered volcano: Seismicity patterns and velocity structure of Katla volcano, Iceland. Ann. Glaciol. 45, 169–177. doi:10.3189/172756407782282499

CrossRef Full Text | Google Scholar

Kent, G. M., Harding, A. J., and Orcutt, J. A. (1990). Evidence for a smaller magma chamber beneath the East pacific rise at 9 30′ N. Nature 344 (6267), 650–653. doi:10.1038/344650a0

CrossRef Full Text | Google Scholar

Kiddle, E. J., Edwards, B. R., Loughlin, S. C., Petterson, M., Sparks, R. S. J., and Voight, B. (2010). Crustal structure beneath Montserrat, Lesser Antilles, constrained by xenoliths, seismic velocity structure and petrology. Geophys. Res. Lett. 37 (19), 42145. doi:10.1029/2009gl042145

CrossRef Full Text | Google Scholar

Kiser, E., Palomeras, I., Levander, A., Zelt, C., Harder, S., Schmandt, B., et al. (2016). Magma reservoirs from the upper crust to the Moho inferred from high-resolution Vp and vs models beneath Mount St. Helens, Washington State, USA. Geology 44 (6), 411–414. doi:10.1130/g37591.1

CrossRef Full Text | Google Scholar

Kiser, E., Levander, A., Zelt, C., Schmandt, B., and Hansen, S. (2018). Focusing of melt near the top of the Mount St. Helens (USA) magma reservoir and its relationship to major volcanic eruptions. Geology 46 (9), 775–778. doi:10.1130/G45140.1

CrossRef Full Text | Google Scholar

Kissling, E. (1988). Geotomography with local earthquake data. Rev. Geophys. 26 (4), 659–698. doi:10.1029/rg026i004p00659

CrossRef Full Text | Google Scholar

Klemetti, E. W., and Clynne, M. A. (2014). Localized rejuvenation of a crystal mush recorded in zircon temporal and compositional variation at the Lassen Volcanic Center, Northern California. PloS one 9 (12), e113157. doi:10.1371/journal.pone.0113157

PubMed Abstract | CrossRef Full Text | Google Scholar

Korenaga, J., Holbrook, W. S., Kent, G. M., Kelemen, P. B., Detrick, R. S., Larsen, H. C., et al. (2000). Crustal structure of the southeast Greenland margin from joint refraction and reflection seismic tomography. J. Geophys. Res. 105 (B9), 21591–21614. doi:10.1029/2000jb900188

CrossRef Full Text | Google Scholar

Koulakov, I., Kasatkina, E., Shapiro, N. M., Jaupart, C., Vasilevsky, A., El Khrepy, S., et al. (2016). The feeder system of the Toba supervolcano from the slab to the shallow reservoir. Nat. Commun. 7 (1). doi:10.1038/ncomms12228

PubMed Abstract | CrossRef Full Text | Google Scholar

Koulakov, I. (2009). LOTOS code for local earthquake tomographic inversion: Benchmarks for testing tomographic algorithms. Bull. Seismol. Soc. Am. 99 (1), 194–214. doi:10.1785/0120080013

CrossRef Full Text | Google Scholar

Koulakov, I., and Shapiro, N. (2015). Seismic tomography of volcanoes. Encycl. Earthq. Eng. 15 (1), 3117–3134. doi:10.1007/978-3-642-35344-4_51

CrossRef Full Text | Google Scholar

Koulakov, I., Yudistira, T., Luehr, B. G., and Wandono, (2009). P, S velocity and V_P/V_S ratio beneath the Toba caldera complex (Northern Sumatra) from local earthquake tomography. Geophys. J. Int. 177 (3), 1121–1139. doi:10.1111/j.1365-246x.2009.04114.x

CrossRef Full Text | Google Scholar

Kounoudis, R., Bastow, I. D., Ebinger, C. J., Ogden, C. S., Ayele, A., Bendick, R., et al. (2021). Body-wave tomographic imaging of the Turkana Depression: Implications for rift development and plume–lithosphere interactions. Geochem. Geophys. Geosyst. 22 (8), e2021GC009782. doi:10.1029/2021gc009782

CrossRef Full Text | Google Scholar

Krastel, S., and Schmincke, H. U. (2002). Crustal structure of northern Gran Canaria, Canary Islands, deduced from active seismic tomography. J. Volcanol. Geotherm. Res. 115 (1-2), 153–177. doi:10.1016/s0377-0273(01)00313-4

CrossRef Full Text | Google Scholar

Kukarina, E., West, M., Keyson, L. H., Koulakov, I., Tsibizov, L., and Smirnov, S. (2017). Focused magmatism beneath Uturuncu volcano, Bolivia: Insights from seismic tomography and deformation modeling. Geosphere 13 (6), 1855–1866. doi:10.1130/ges01403.1

CrossRef Full Text | Google Scholar

Kuster, G. T., and Toksöz, M. N. (1974). Velocity and attenuation of seismic waves in two-phase media: Part I. Theoretical formulations. Geophysics 39 (5), 587–606. doi:10.1190/1.1440450

CrossRef Full Text | Google Scholar

Kyong-Song, R., Hammond, J. O., Chol-Nam, K., Hyok, K., Yong-Gun, Y., Gil-Jong, P., et al. (2016). Evidence for partial melt in the crust beneath Mt. Paektu (changbaishan), democratic people’s republic of Korea and China. Sci. Adv. 2 (4), e1501513. doi:10.1126/sciadv.1501513

PubMed Abstract | CrossRef Full Text | Google Scholar

Lees, J. M., and Crosson, R. S. (1989). Tomographic inversion for three‐dimensional velocity structure at Mount St. Helens using earthquake data. J. Geophys. Res. 94 (B5), 5716–5728. doi:10.1029/jb094ib05p05716

CrossRef Full Text | Google Scholar

Lees, J. M., and Lindley, G. T. (1994). Three‐dimensional attenuation tomography at Loma Prieta: Inversion of t* for Q. J. Geophys. Res. 99 (B4), 6843–6863. doi:10.1029/93JB03460

CrossRef Full Text | Google Scholar

Lees, J. M. (1992). The magma system of Mount St. Helens: Non-linear high-resolution P-wave tomography. J. Volcanol. Geotherm. Res. 53 (1-4), 103–116. doi:10.1016/0377-0273(92)90077-q

CrossRef Full Text | Google Scholar

Lees, J. M. (2007). Seismic tomography of magmatic systems. J. Volcanol. Geotherm. Res. 167 (1-4), 37–56. doi:10.1016/j.jvolgeores.2007.06.008

CrossRef Full Text | Google Scholar

Lin, G., Shearer, P. M., Matoza, R. S., Okubo, P. G., and Amelung, F. (2014). Three‐dimensional seismic velocity structure of Mauna Loa and Kilauea volcanoes in Hawaii from local seismic tomography. J. Geophys. Res. Solid Earth 119 (5), 4377–4392. doi:10.1002/2013jb010820

CrossRef Full Text | Google Scholar

Lodge, A., and Helffrich, G. (2009). Grid search inversion of teleseismic receiver functions. Geophys. J. Int. 178 (1), 513–523. doi:10.1111/j.1365-246x.2009.04176.x

CrossRef Full Text | Google Scholar

Luehr, B. G., Koulakov, I., Rabbel, W., Zschau, J., Ratdomopurbo, A., Brotopuspito, K. S., et al. (2013). Fluid ascent and magma storage beneath Gunung Merapi revealed by multi-scale seismic imaging. J. Volcanol. Geotherm. Res. 261, 7–19. doi:10.1016/j.jvolgeores.2013.03.015

CrossRef Full Text | Google Scholar

MacKenzie, L. S., Abers, G. A., Rondenay, S., and Fischer, K. M. (2010). Imaging a steeply dipping subducting slab in Southern Central America. Earth Planet. Sci. Lett. 296 (3-4), 459–468. doi:10.1016/j.epsl.2010.05.033

CrossRef Full Text | Google Scholar

Magde, L. S., Barclay, A. H., Toomey, D. R., Detrick, R. S., and Collins, J. A. (2000). Crustal magma plumbing within a segment of the Mid-Atlantic Ridge, 35 N. Earth Planet. Sci. Lett. 175 (1-2), 55–67. doi:10.1016/s0012-821x(99)00281-2

CrossRef Full Text | Google Scholar

Malcolm, A. E., and Trampert, J. (2011). Tomographic errors from wave front healing: More than just a fast bias. Geophys. J. Int. 185 (1), 385–402. doi:10.1111/j.1365-246x.2011.04945.x

CrossRef Full Text | Google Scholar

Marsh, B. D. (1989). Magma chambers. Annu. Rev. Earth Planet. Sci. 17 (1), 439–472. doi:10.1146/annurev.ea.17.050189.002255

CrossRef Full Text | Google Scholar

Martí, J., Villaseñor, A., Geyer, A., López, C., and Tryggvason, A. (2017). Stress barriers controlling lateral migration of magma revealed by seismic tomography. Sci. Rep. 7 (1). doi:10.1038/srep40757

CrossRef Full Text | Google Scholar

Martinez‐Arevalo, C., Musumeci, C., and Patane, D. (2009). Evidence of a partial melt zone beneath Stromboli volcano (Italy) from inversion of teleseismic receiver functions. Terra nova.21 (5), 386–392. doi:10.1111/j.1365-3121.2009.00894.x

CrossRef Full Text | Google Scholar

Mastruyono, M., McCaffrey, R., Wark, D. A., Roecker, S. W., Ibrahim, G., Fauzi, , et al. (2001). Distribution of magma beneath the Toba caldera complex, north Sumatra, Indonesia, constrained by three‐dimensional P wave velocities, seismicity, and gravity data. Geochem. Geophys. Geosyst. 2 (4). doi:10.1029/2000gc000096

CrossRef Full Text | Google Scholar

Mavko, G., Mukerji, T., and Dvorkin, J. (2020). The rock physics handbook. Cambridge University Press.

Google Scholar

Mavko, G. M. (1980). Velocity and attenuation in partially molten rocks. J. Geophys. Res. 85 (B10), 5173–5189. doi:10.1029/jb085ib10p05173

CrossRef Full Text | Google Scholar

McVey, B. G., Hooft, E. E. E., Heath, B. A., Toomey, D. R., Paulatto, M., Morgan, J. V., et al. (2020). Magma accumulation beneath Santorini volcano, Greece, from P-wave tomography. Geology 48 (3), 231–235. doi:10.1130/g47127.1

CrossRef Full Text | Google Scholar

Meléndez, A., Korenaga, J., Sallarès, V., Miniussi, A., and Ranero, C. R. (2015). TOMO3D: 3-D joint refraction and reflection traveltime tomography parallel code for active-source seismic data—synthetic test. Geophys. J. Int. 203 (1), 158–174. doi:10.1093/gji/ggv292

CrossRef Full Text | Google Scholar

Miller, D. S., and Smith, R. B. (1999). P and S velocity structure of the Yellowstone volcanic field from local earthquake and controlled‐source tomography. J. Geophys. Res. 104 (B7), 15105–15121. doi:10.1029/1998jb900095

CrossRef Full Text | Google Scholar

Morgan, J., Warner, M., Bell, R., Ashley, J., Barnes, D., Little, R., et al. (2013). Next-generation seismic experiments: Wide-angle, multi-azimuth, three-dimensional, full-waveform inversion. Geophys. J. Int. 195 (3), 1657–1678. doi:10.1093/gji/ggt345

CrossRef Full Text | Google Scholar

Morgan, J., Warner, M., Arnoux, G., Hooft, E., Toomey, D., VanderBeek, B., et al. (2016). Next-generation seismic experiments–II: Wide-angle, multi-azimuth, 3-D, full-waveform inversion of sparse field data. Geophys. J. Int. 204 (2), 1342–1363. doi:10.1093/gji/ggv513

CrossRef Full Text | Google Scholar

Natale, M., Nunziata, C., and Panza, G. F. (2005). verage shear wave velocity models of the crustal structure at Mt. Vesuvius. Phys. Earth Planet. Inter. 152 (1–2), 7–21. doi:10.1016/j.pepi.2005.03.011

CrossRef Full Text | Google Scholar

Nolet, G. (2008). A breviary of seismic tomography. New Jersey: Cambridge University Press.

Google Scholar

Nolet, G., and Dahlen, F. A. (2000). Wave front healing and the evolution of seismic delay times. J. Geophys. Res. 105 (B8), 19043–19054. doi:10.1029/2000jb900161

CrossRef Full Text | Google Scholar

Norris, A. N. (1985). A differential scheme for the effective moduli of composites. Mech. Mater. 4 (1), 1–16. doi:10.1016/0167-6636(85)90002-x

CrossRef Full Text | Google Scholar

Nur, A., Mavko, G., Dvorkin, J., and Galmudi, D. (1998). Critical porosity: A key to relating physical properties to porosity in rocks. Lead. Edge 17 (3), 357–362. doi:10.1190/1.1437977

CrossRef Full Text | Google Scholar

Nurfiani, D., Wang, X., Gunawan, H., Triastuty, H., Hidayat, D., Wei, S. J., et al. (2021). Combining petrology and seismology to unravel the plumbing system of a typical arc volcano: An example from Marapi, West Sumatra, Indonesia. Geochem. Geophys. Geosyst. 22 (4), e2020GC009524. doi:10.1029/2020gc009524

CrossRef Full Text | Google Scholar

O'Connell, R. J., and Budiansky, B. (1974). Seismic velocities in dry and saturated cracked solids. J. Geophys. Res. 79 (35), 5412–5426. doi:10.1029/jb079i035p05412

CrossRef Full Text | Google Scholar

O'Connell, R. J., and Budiansky, B. (1977). Viscoelastic properties of fluid‐saturated cracked solids. J. Geophys. Res. 82 (36), 5719–5735. doi:10.1029/jb082i036p05719

CrossRef Full Text | Google Scholar

Ochoa-Chávez, J. A., Escudero, C. R., Núñez-Cornú, F. J., and Bandy, W. L. (2016). P-wave velocity tomography from local earthquakes in Western Mexico. Pure Appl. Geophys. 173 (10), 3487–3511. doi:10.1007/s00024-015-1183-x

CrossRef Full Text | Google Scholar

Ohlendorf, S. J., Thurber, C. H., Pesicek, J. D., and Prejean, S. G. (2014). Seismicity and seismic structure at okmok volcano, Alaska. J. Volcanol. Geotherm. Res. 278, 103–119. doi:10.1016/j.jvolgeores.2014.04.002

CrossRef Full Text | Google Scholar

Okubo, P. G., Benz, H. M., and Chouet, B. A. (1997). Imaging the crustal magma sources beneath Mauna Loa and Kilauea volcanoes, Hawaii. Geol. 25 (10), 867–870. doi:10.1130/0091-7613(1997)025<0867:itcmsb>2.3.co;2

CrossRef Full Text | Google Scholar

Pallister, J. S., and Hopson, C. A. (1981). Samail ophiolite plutonic suite: Field relations, phase variation, cryptic variation and layering, and a model of a spreading ridge magma chamber. J. Geophys. Res. 86 (B4), 2593–2644. doi:10.1029/jb086ib04p02593

CrossRef Full Text | Google Scholar

Park, J., Morgan, J. K., Zelt, C. A., Okubo, P. G., Peters, L., and Benesh, N. (2007). Comparative velocity structure of active Hawaiian volcanoes from 3-D onshore–offshore seismic tomography. Earth Planet. Sci. Lett. 259 (3-4), 500–516. doi:10.1016/j.epsl.2007.05.008

CrossRef Full Text | Google Scholar

Park, J., Morgan, J. K., Zelt, C. A., and Okubo, P. G. (2009). Volcano‐tectonic implications of 3‐D velocity structures derived from joint active and passive source tomography of the island of Hawaii. J. Geophys. Res. 114 (B9), B09301. doi:10.1029/2008jb005929

CrossRef Full Text | Google Scholar

Parks, M. M., Biggs, J., England, P., Mather, T. A., Nomikou, P., Palamartchouk, K., et al. (2012). Evolution of Santorini Volcano dominated by episodic and rapid fluxes of melt from depth. Nat. Geosci. 5 (10), 749–754. doi:10.1038/ngeo1562

CrossRef Full Text | Google Scholar

Paulatto, M., Annen, C., Henstock, T. J., Kiddle, E., Minshull, T. A., Sparks, R. S. J., et al. (2012). Magma chamber properties from integrated seismic tomography and thermal modeling at Montserrat. Geochem. Geophys. Geosyst. 13 (1). doi:10.1029/2011gc003892

CrossRef Full Text | Google Scholar

Paulatto, M., Moorkamp, M., Hautmann, S., Hooft, E., Morgan, J. V., and Sparks, R. S. J. (2019). Vertically extensive magma reservoir revealed from joint inversion and quantitative interpretation of seismic and gravity data. J. Geophys. Res. Solid Earth 124 (11), 11170–11191. doi:10.1029/2019jb018476

CrossRef Full Text | Google Scholar

Pratt, R. G. (1999). Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model. Geophysics 64 (3), 888–901. doi:10.1190/1.1444597

CrossRef Full Text | Google Scholar

Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterline, W. T. (1990). Numerical recipes: The art of scientific computing. 4th edition.

Google Scholar

Prieux, V., Brossier, R., Operto, S., and Virieux, J. (2013). Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the valhall field. Part 2: Imaging compressive-wave and shear-wave velocities. Geophys. J. Int. 194 (3), 1665–1681. doi:10.1093/gji/ggt178

CrossRef Full Text | Google Scholar

Prudencio, J., Ibáñez, J. M., Del Pezzo, E., Martí, J., García-Yeguas, A., and De Siena, L. (2015). 3D attenuation tomography of the volcanic island of Tenerife (Canary Islands). Surv. Geophys. 36 (5), 693–716. doi:10.1007/s10712-015-9333-3

CrossRef Full Text | Google Scholar

Rawlinson, N., Reading, A. M., and Kennett, B. L. (2006). Lithospheric structure of Tasmania from a novel form of teleseismic tomography. J. Geophys. Res. 111 (B2). doi:10.1029/2005jb003803

CrossRef Full Text | Google Scholar

Rawlinson, N., Fichtner, A., Sambridge, M., and Young, M. K. (2014). Seismic tomography and the assessment of uncertainty. Adv. Geophys. 55, 1–76. doi:10.1016/bs.agph.2014.08.001

CrossRef Full Text | Google Scholar

Rawlinson, N., and Spakman, W. (2016). On the use of sensitivity tests in seismic tomography. Geophys. J. Int. 205 (2), 1221–1243. doi:10.1093/gji/ggw084

CrossRef Full Text | Google Scholar

Reuss, A. (1929). Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. Z. Angew. Math. Mech. 9 (1), 49–58. doi:10.1002/zamm.19290090104

CrossRef Full Text | Google Scholar

Rooyakkers, S. M., Stix, J., Berlo, K., Petrelli, M., and Sigmundsson, F. (2021). Eruption risks from covert silicic magma bodies. Geology 49 (8), 921–925. doi:10.1130/G48697.1

CrossRef Full Text | Google Scholar

Rosi, M., Acocella, V., Cioni, R., Bianco, F., Costa, A., De Martino, P., et al. (2022). Defining the pre-eruptive states of active volcanoes for improving eruption forecasting. Front. Earth Sci. (Lausanne). 10, 795700. doi:10.3389/feart.2022.795700

CrossRef Full Text | Google Scholar

Ryberg, T., and Weber, M. (2000). Receiver function arrays: A reflection seismic approach. Geophys. J. Int. 141 (1), 1–11. doi:10.1046/j.1365-246x.2000.00077.x

CrossRef Full Text | Google Scholar

Sakaguchi, K., Gilbert, H., and Zandt, G. (2006). Converted wave imaging of the Toba caldera, Indonesia. Geophys. Res. Lett. 33 (20), L20305. doi:10.1029/2006gl027397

CrossRef Full Text | Google Scholar

Schmeling, H. (1985). Numerical models on the influence of partial melt on elastic, anelastic and electric properties of rocks. Part I: Elasticity and anelasticity. Phys. earth Planet. interiors 41 (1), 34–57. doi:10.1016/0031-9201(85)90100-1

CrossRef Full Text | Google Scholar

Schmitz, M., Heinsohn, W. D., and Schilling, F. R. (1997). Seismic, gravity and petrological evidence for partial melt beneath the thickened central Andean crust (21–23 S). Tectonophysics 270 (3-4), 313–326. doi:10.1016/s0040-1951(96)00217-x

CrossRef Full Text | Google Scholar

Schutt, D. L., Dueker, K., and Yuan, H. (2008). Crust and upper mantle velocity structure of the Yellowstone hot spot and surroundings. J. Geophys. Res. 113 (B3), B03310. doi:10.1029/2007jb005109

CrossRef Full Text | Google Scholar

Seccia, D., Chiarabba, C., De Gori, P., Bianchi, I., and Hill, D. P. (2011). Evidence for the contemporary magmatic system beneath Long Valley Caldera from local earthquake tomography and receiver function analysis. J. Geophys. Res. 116 (B12), B12314. doi:10.1029/2011jb008471

CrossRef Full Text | Google Scholar

Shalev, E., Kenedi, C. L., Malin, P., Voight, V., Miller, V., Hidayat, D., et al. (2010). Three‐dimensional seismic velocity tomography of Montserrat from the SEA‐CALIPSO offshore/onshore experiment. Geophys. Res. Lett. 37 (19). doi:10.1029/2010gl042498

CrossRef Full Text | Google Scholar

Shapiro, N. M., Campillo, M., Stehly, L., and Ritzwoller, M. H. (2005). High-resolution surface-wave tomography from ambient seismic noise. Science 307 (5715), 1615–1618. doi:10.1126/science.1108339

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheriff, R. E., and Geldart, L. P. (1995). Exploration seismology. Cambridge University Press.

Google Scholar

Singh, S. C., Kent, G. M., Collier, J. S., Harding, A. J., and Orcutt, J. A. (1998). Melt to mush variations in crustal magma properties along the ridge crest at the southern East Pacific Rise. Nature 394 (6696), 874–878. doi:10.1038/29740

CrossRef Full Text | Google Scholar

Sinton, J. M., and Detrick, R. S. (1992). Mid‐ocean ridge magma chambers. J. Geophys. Res. 97 (B1), 197–216. doi:10.1029/91jb02508

CrossRef Full Text | Google Scholar

Smith, G. C., and Gidlow, P. M. (1987). Weighted stacking for rock property estimation and detection of gas. Geophys. Prospect. 35 (9), 993–1014. doi:10.1111/j.1365-2478.1987.tb00856.x

CrossRef Full Text | Google Scholar

Solomon, S. C., and Toomey, D. R. (1992). The structure of mid-ocean ridges. Annu. Rev. Earth Planet. Sci. 20 (1), 329–366. doi:10.1146/annurev.ea.20.050192.001553

CrossRef Full Text | Google Scholar

Sparks, R. S. J., Annen, C., Blundy, J. D., Cashman, K. V., Rust, A. C., and Jackson, M. D. (2019). Formation and dynamics of magma reservoirs. Phil. Trans. R. Soc. A 377 (2139), 20180019. doi:10.1098/rsta.2018.0019

PubMed Abstract | CrossRef Full Text | Google Scholar

Sparks, R. S. J., and Cashman, K. V. (2017). Dynamic magma systems: Implications for forecasting volcanic activity. Elements 13 (1), 35–40. doi:10.2113/gselements.13.1.35

CrossRef Full Text | Google Scholar

Spetzler, J., and Snieder, R. (2004). The Fresnel volume and transmitted waves. Geophysics 69 (3), 653–663. doi:10.1190/1.1759451

CrossRef Full Text | Google Scholar

Spica, Z., Cruz-Atienza, V. M., Reyes-Alfaro, G., Legrand, D., and Iglesias, A. (2014). Crustal imaging of Western Michoacán and the Jalisco Block, Mexico, from ambient seismic noise. J. Volcanol. Geotherm. Res. 289, 193–201. doi:10.1016/j.jvolgeores.2014.11.005

CrossRef Full Text | Google Scholar

Spica, Z., Perton, M., and Legrand, D. (2017). Anatomy of the Colima volcano magmatic system, Mexico. Earth Planet. Sci. Lett. 459, 1–13. doi:10.1016/j.epsl.2016.11.010

CrossRef Full Text | Google Scholar

Stachnik, J. C., Dueker, K., Schutt, D. L., and Yuan, H. (2008). Imaging Yellowstone plume‐lithosphere interactions from inversion of ballistic and diffusive Rayleigh wave dispersion and crustal thickness data. Geochem. Geophys. Geosyst. 9 (6). doi:10.1029/2008gc001992

CrossRef Full Text | Google Scholar

Stankiewicz, J., Ryberg, T., Haberland, C., and Natawidjaja, D. (2010). Lake Toba volcano magma chamber imaged by ambient seismic noise tomography. Geophys. Res. Lett. 37 (17). doi:10.1029/2010gl044211

CrossRef Full Text | Google Scholar

Stauber, D. A., Green, S. M., and Iyer, H. M. (1988). Three‐dimensional P velocity structure of the crust below Newberry Volcano, Oregon. J. Geophys. Res. 93 (B9), 10095–10107. doi:10.1029/jb093ib09p10095

CrossRef Full Text | Google Scholar

Steck, L. K., and Prothero, W. A. (1994). Crustal structure beneath Long Valley caldera from modeling of teleseismic P wave polarizations and Ps converted waves. J. Geophys. Res. 99 (B4), 6881–6898. doi:10.1029/93jb03284

CrossRef Full Text | Google Scholar

Steck, L. K., Thurber, C. H., Fehler, M. C., Lutter, W. J., Roberts, P. M., Baldridge, W. S., et al. (1998). Crust and upper mantle P wave velocity structure beneath valles caldera, new Mexico: Results from the jemez teleseismic tomography experiment. J. Geophys. Res. 103 (B10), 24301–24320. doi:10.1029/98jb00750

CrossRef Full Text | Google Scholar

Sudo, Y., and Kong, L. (2001). Three-dimensional seismic velocity structure beneath Aso volcano, kyushu, Japan. Bull. Volcanol. 63 (5), 326–344. doi:10.1007/s004450100145

CrossRef Full Text | Google Scholar

Sychev, I. V., Koulakov, I., Egorushkin, I., Zhuravlev, S., West, M., El Khrepy, S., et al. (2019). Fault‐associated magma conduits beneath Volcán de Colima revealed by seismic velocity and attenuation tomography studies. J. Geophys. Res. Solid Earth 124 (8), 8908–8923. doi:10.1029/2019jb017449

CrossRef Full Text | Google Scholar

Takei, Y. (1998). Constitutive mechanical relations of solid‐liquid composites in terms of grain‐boundary contiguity. J. Geophys. Res. 103 (B8), 18183–18203. doi:10.1029/98jb01489

CrossRef Full Text | Google Scholar

Takei, Y. (2002). Effect of pore geometry on VP/VS: From equilibrium geometry to crack. J. Geophys. Res. Solid Earth 107 (B2), ECV–6.

CrossRef Full Text | Google Scholar

Tape, C., Liu, Q., and Tromp, J. (2007). Finite‐frequency tomography using adjoint methods—methodology and examples using membrane surface waves. Geophys. J. Int. 168 (3), 1105–1129. doi:10.1111/j.1365-246X.2006.03191.x

CrossRef Full Text | Google Scholar

Tarantola, A. (2005). Inverse problem theory and methods for model parameter estimation. Philadelphia, PA, United States: Society for Industrial and Applied Mathematics.

Google Scholar

Tavazzani, L., Peres, S., Sinigoi, S., Demarchi, G., Economos, R. C., and Quick, J. E. (2020). Timescales and mechanisms of crystal-mush rejuvenation and melt extraction recorded in Permian plutonic and volcanic rocks of the Sesia magmatic system (Southern Alps, Italy). J. Petrology 61 (5), egaa049. doi:10.1093/petrology/egaa049

CrossRef Full Text | Google Scholar

Taylor, M. A. J., and Singh, S. C. (2002). Composition and microstructure of magma bodies from effective medium theory. Geophys. J. Int. 149 (1), 15–21. doi:10.1046/j.1365-246x.2002.01577.x

CrossRef Full Text | Google Scholar

Thurber, C. H. (1983). Earthquake locations and three‐dimensional crustal structure in the Coyote Lake area, central California. J. Geophys. Res. 88 (B10), 8226–8236. doi:10.1029/jb088ib10p08226

CrossRef Full Text | Google Scholar

Thurber, C. H. (1984). Seismic detection of the summit magma complex of Kilauea volcano, Hawaii. Science 223 (4632), 165–167. doi:10.1126/science.223.4632.165

PubMed Abstract | CrossRef Full Text | Google Scholar

Thurber, C. H. (2003). Seismic tomography of the lithosphere with body waves. Pure Appl. Geophys. 160 (3), 717–737. doi:10.1007/pl00012555

CrossRef Full Text | Google Scholar

Tolstoy, M., Harding, A. J., and Orcutt, J. A. (1993). Crustal thickness on the Mid-Atlantic Ridge: Bull's-eye gravity anomalies and focused accretion. Science 262 (5134), 726–729. doi:10.1126/science.262.5134.726

PubMed Abstract | CrossRef Full Text | Google Scholar

Toomey, D. R., Solomon, S. C., and Purdy, G. M. (1994). Tomographic imaging of the shallow crustal structure of the East Pacific Rise at 9° 30′ N. J. Geophys. Res. 99 (B12), 24135–24157. doi:10.1029/94jb01942

CrossRef Full Text | Google Scholar

Toomey, D. R., Jousselin, D., Dunn, R. A., Wilcock, W. S., and Detrick, R. S. (2007). Skew of mantle upwelling beneath the East Pacific Rise governs segmentation. Nature 446 (7134), 409–414. doi:10.1038/nature05679

PubMed Abstract | CrossRef Full Text | Google Scholar

Turner, S., and Costa, F. (2007). Measuring timescales of magmatic evolution. Elements 3 (4), 267–272. doi:10.2113/gselements.3.4.267

CrossRef Full Text | Google Scholar

Ueki, K., and Iwamori, H. (2016). Density and seismic velocity of hydrous melts under crustal and upper mantle conditions. Geochem. Geophys. Geosyst. 17 (5), 1799–1814. doi:10.1002/2015gc006242

CrossRef Full Text | Google Scholar

Ulberg, C. W., Creager, K. C., Moran, S. C., Abers, G. A., Thelen, W. A., Levander, A., et al. (2020). Local source Vp and vs tomography in the Mount St. Helens region with the iMUSH broadband array. Geochem. Geophys. Geosyst. 21 (3), e2019GC008888. doi:10.1029/2019gc008888

CrossRef Full Text | Google Scholar

Van Ark, E. M., Detrick, R. S., Canales, J. P., Carbotte, S. M., Harding, A. J., Kent, G. M., et al. (2007). Seismic structure of the endeavour segment, juan de Fuca ridge: Correlations with seismicity and hydrothermal activity. J. Geophys. Res. 112 (B2), B02401. doi:10.1029/2005JB004210

CrossRef Full Text | Google Scholar

Van Avendonk, H. J., Harding, A. J., Orcutt, J. A., and Holbrook, W. S. (2001). Hybrid shortest path and ray bending method for traveltime and raypath calculations. Geophysics 66 (2), 648–653. doi:10.1190/1.1444955

CrossRef Full Text | Google Scholar

Van der Molen, I., and Paterson, M. S. (1979). Experimental deformation of partially-melted granite. Contr. Mineral. Pet. 70 (3), 299–318. doi:10.1007/bf00375359

CrossRef Full Text | Google Scholar

VanDecar, J. C., James, D. E., and Assumpção, M. (1995). Seismic evidence for a fossil mantle plume beneath South America and implications for plate driving forces. Nature 378 (6552), 25–31. doi:10.1038/378025a0

CrossRef Full Text | Google Scholar

VanderBeek, B. P., Toomey, D. R., Hooft, E., and Wilcock, W. (2016). Segmentation of mid-ocean ridges attributed to oblique mantle divergence. Nature Geosci. 9, 636–642. doi:10.1038/ngeo2745

CrossRef Full Text | Google Scholar

Vanorio, T., Virieux, J., Capuano, P., and Russo, G. (2005). Three‐dimensional seismic tomography from P wave and S wave microearthquake travel times and rock physics characterization of the Campi Flegrei Caldera. J. Geophys. Res. 110 (B3), B03201. doi:10.1029/2004jb003102

CrossRef Full Text | Google Scholar

Vera, E. E., Mutter, J. C., Buhl, P., Orcutt, J. A., Harding, A. J., Kappus, M. E., et al. (1990). The structure of 0‐to 0.2‐my‐old oceanic crust at 9° N on the East Pacific Rise from expanded spread profiles. J. Geophys. Res. 95 (B10), 15529–15556. doi:10.1029/jb095ib10p15529

CrossRef Full Text | Google Scholar

Virieux, J., and Operto, S. (2009). An overview of full-waveform inversion in exploration geophysics. Geophysics 74 (6), WCC1–WCC26. doi:10.1190/1.3238367

CrossRef Full Text | Google Scholar

Voigt, W. (1928). Lehrbuch der Kristallphysik. Teubner-Leipzig.

Google Scholar

Waite, G. P., and Moran, S. C. (2009). VP Structure of Mount St. Helens, Washington, USA, imaged with local earthquake tomography. J. Volcanol. Geotherm. Res. 182 (1-2), 113–122. doi:10.1016/j.jvolgeores.2009.02.009

CrossRef Full Text | Google Scholar

Walsh, J. B., and Grosenbaugh, M. A. (1979). A new model for analyzing the effect of fractures on compressibility. J. Geophys. Res. 84 (B7), 3532–3536. doi:10.1029/jb084ib07p03532

CrossRef Full Text | Google Scholar

Ward, K. M., Porter, R. C., Zandt, G., Beck, S. L., Wagner, L. S., Minaya, E., et al. (2013). Ambient noise tomography across the central andes. Geophys. J. Int. 194 (3), 1559–1573. doi:10.1093/gji/ggt166

CrossRef Full Text | Google Scholar

Ward, K. M., Zandt, G., Beck, S. L., Christensen, D. H., and McFarlin, H. (2014). Seismic imaging of the magmatic underpinnings beneath the Altiplano-Puna volcanic complex from the joint inversion of surface wave dispersion and receiver functions. Earth Planet. Sci. Lett. 404, 43–53. doi:10.1016/j.epsl.2014.07.022

CrossRef Full Text | Google Scholar

Warner, M., Ratcliffe, A., Nangoo, T., Morgan, J., Umpleby, A., Shah, N., et al. (2013). Anisotropic 3D full-waveform inversion. Geophysics 78 (2), R59–R80. doi:10.1190/geo2012-0338.1

CrossRef Full Text | Google Scholar

Watkins, W. D., Thurber, C. H., Abbott, E. R., and Brudzinski, M. R. (2018). Local earthquake tomography of the Jalisco, Mexico region. Tectonophysics 724, 51–64. doi:10.1016/j.tecto.2018.01.002

CrossRef Full Text | Google Scholar

Watt, J. P., Davies, G. F., and O'Connell, R. J. (1976). The elastic properties of composite materials. Rev. Geophys. 14 (4), 541–563. doi:10.1029/rg014i004p00541

CrossRef Full Text | Google Scholar

Weber, G., Caricchi, L., Arce, J. L., and Schmitt, A. K. (2020). Determining the current size and state of subvolcanic magma reservoirs. Nat. Commun. 11 (1), 5477–5514. doi:10.1038/s41467-020-19084-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiland, C. M., Steck, L. K., Dawson, P. B., and Korneev, V. A. (1995). Nonlinear teleseismic tomography at Long Valley Caldera, using three‐dimensional minimum travel time ray tracing. J. Geophys. Res. 100 (B10), 20379–20390. doi:10.1029/95jb01147

CrossRef Full Text | Google Scholar

Wespestad, C. E., Thurber, C. H., Andersen, N. L., Singer, B. S., Cardona, C., Zeng, X., et al. (2019). Magma reservoir below Laguna del Maule volcanic field, Chile, imaged with surface‐wave tomography. J. Geophys. Res. Solid Earth 124 (3), 2858–2872. doi:10.1029/2018jb016485

CrossRef Full Text | Google Scholar

Williamson, P. R. (1991). A guide to the limits of resolution imposed by scattering in ray tomography. Geophysics 56 (2), 202–207. doi:10.1190/1.1443032

CrossRef Full Text | Google Scholar

Williamson, P. R., and Worthington, M. H. (1993). Resolution limits in ray tomography due to wave behavior: Numerical experiments. Geophysics 58 (5), 727–735. doi:10.1190/1.1443457

CrossRef Full Text | Google Scholar

Wu, T. (1966). The effect of inclusion shape on the elastic moduli of a two-phase material. Int. J. solids Struct. 2 (1), 1–8. doi:10.1016/0020-7683(66)90002-3

CrossRef Full Text | Google Scholar

Xu, M., Pablo Canales, J., Carbotte, S. M., Carton, H., Nedimović, M. R., and Mutter, J. C. (2014). Variations in axial magma lens properties along the East Pacific Rise (9° 30′ N–10° 00′ N) from swath 3‐D seismic imaging and 1‐D waveform inversion. J. Geophys. Res. Solid Earth 119 (4), 2721–2744. doi:10.1002/2013jb010730

CrossRef Full Text | Google Scholar

Yang, B., Lin, W., Hu, X., Fang, H., Qiu, G., and Wang, G. (2021). The magma system beneath Changbaishan-Tianchi Volcano, China/North Korea: Constraints from three-dimensional magnetotelluric imaging. J. Volcanol. Geotherm. Res. 419, 107385. doi:10.1016/j.jvolgeores.2021.107385

CrossRef Full Text | Google Scholar

Yang, Y., and Forsyth, D. W. (2006). Regional tomographic inversion of the amplitude and phase of Rayleigh waves with 2-D sensitivity kernels. Geophys. J. Int. 166, 1148–1160. doi:10.1111/j.1365-246X.2006.02972.x

CrossRef Full Text | Google Scholar

Yu, X., and Lee, C. T. A. (2016). Critical porosity of melt segregation during crustal melting: Constraints from zonation of peritectic garnets in a dacite volcano. Earth Planet. Sci. Lett. 449, 127–134. doi:10.1016/j.epsl.2016.05.025

CrossRef Full Text | Google Scholar

Zelt, C. A., and Barton, P. J. (1998). Three‐dimensional seismic refraction tomography: A comparison of two methods applied to data from the faeroe basin. J. Geophys. Res. 103 (B4), 7187–7210. doi:10.1029/97jb03536

CrossRef Full Text | Google Scholar

Zelt, C. A. (1998). Lateral velocity resolution from three-dimensional seismic refraction data. Geophys. J. Int. 135 (3), 1101–1112. doi:10.1046/j.1365-246x.1998.00695.x

CrossRef Full Text | Google Scholar

Zhang, Z. D., and Alkhalifah, T. (2020). High-resolution reservoir characterization using deep learning-aided elastic full-waveform inversion: The North Sea field data example. Geophysics 85 (4), WA137–WA146. doi:10.1190/geo2019-0340.1

CrossRef Full Text | Google Scholar

Zhu, L., and Kanamori, H. (2000). Moho depth variation in southern California from teleseismic receiver functions. J. Geophys. Res. 105 (B2), 2969–2980. doi:10.1029/1999jb900322

CrossRef Full Text | Google Scholar

Zollo, A., Judenherc, S., Auger, E., D'Auria, L., Virieux, J., Capuano, P., et al. (2003). Evidence for the buried rim of Campi Flegrei caldera from 3‐d active seismic imaging. Geophys. Res. Lett. 30 (19), 2002. doi:10.1029/2003gl018173

CrossRef Full Text | Google Scholar

Zollo, A., Maercklin, N., Vassallo, M., Dello Iacono, D., Virieux, J., and Gasparini, P. (2008). Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. 35 (12). doi:10.1029/2008gl034242

CrossRef Full Text | Google Scholar

Zou, B., and Ma, C. (2020). Crystal mush rejuvenation induced by heat and water transfer: Evidence from amphibole analyses in the jialuhe composite pluton, East kunlun orogen, northern tibet plateau. Lithos 376, 105722. doi:10.1016/j.lithos.2020.105722

CrossRef Full Text | Google Scholar

Zucca, J. J., and Evans, J. R. (1992). Active high‐resolution compressional wave attenuation tomography at Newberry volcano, central Cascade Range. J. Geophys. Res. 97 (B7), 11047–11055. doi:10.1029/92jb00492

CrossRef Full Text | Google Scholar