Research of the broken roof structure and supporting capacity of a shield in a deep and thick coal seam

We determine the key issues of the reasonable supporting capacity of a shield and the shield selection in the panel face in a deep and thick coal seam. The No.232204 panel face of the Meihuajing mine in the Yuanyanghu mining area is taken as the research background. Using theoretical analysis, numerical simulation, and field measurement, the fracture characteristics and instability forms of roof structure of the panel face were studied. A mechanical model of roof fracture structure was established to calculate the reasonable supporting capacity of the shield, which guided the shield selection for the panel face. Also, a calculation and analysis system of the supporting capacity of the shield in a deep and thick coal seam was developed to realize the dynamic calculation and analysis of the supporting capacity of the shield. The results are as follows. 1) when the first weighting of the main roof appears, the broken rock block is hinged to form a “three-hinged arch” balanced structure. When the periodic weighting of the main roof appears, the broken rock block forms a “voussoir beam” balance structure. Also, the supporting capacity of the shield is stable between 8,900 and 9,600 kN. 2) The theoretical calculation showed that the supporting capacity of the shield in the No.232204 panel face was 9,581.04 kN, and the ZY10000/28/62D shield with supporting capacity of 10,000 kN is selected in the No.232204 panel face. 3) Through self-developed calculation software, the thickness and bulk density of the immediate roof had little influence on the supporting capacity of the shield, and the main roof thickness and bulk density have considerable influence on the supporting capacity of the shield. 4) The field measurement showed that the maximum supporting capacity of the shield in the panel face was distributed between 9,000 and 10,000 kN, which accounted for 77.58%. The loading utilization rate was more than 90%, and therefore the selected shield was reasonable. The research results provide a theoretical basis for the selection of shield supports for a deep buried and thick coal seam in the Yuanyanghu mining area.

1 Introduction

The base reserves of China’s coal resources amount to 279.58 billion tons, of which the reserves of thick coal seams account for 44%, and annual underground mining of thick coal seams accounts for more than 45% of total coal production (Xie et al., 2011; Wang, 2013). In recent years, with the continuous mining of shallow coal resources, these reserves are gradually decreasing. Consequently, the deep mining of coal resources has become a research hotspot. However, the ground pressure behavior is violent when mining deep buried and thick coal seams due to the large space for coal excavation and large extent of overburden damage. Therefore, the reasonable selection of shields plays an important role in safe and efficient production on the panel face (Qian and Xu, 2019; Xie, 2019; Xu, 2019; Zhang et al., 2020a; Li et al., 2020; Rajwa et al., 2020; Klemetti et al., 2021).

In recent years, the broken roof structure of coal seam mining has been widely studied by domestic and foreign scholars, and numerous research results have been achieved. Some scholars have based their research on the mechanical analysis of a masonry beam structure, and the S-R stability theory of surrounding rock structure in stope is established. This theory provides a quantitative analysis of the influence of overlying rock layers in the panel face, pressure changes, and the extent of rock layers to be controlled during mining (Qian et al., 1994). On this basis, the surrounding rock of stope as an organic whole is proposed, structures that play a skeletal role in the movement of the surrounding rock can be considered voussoir beams, and the stress of the voussoir beamstructure and the stability of key blocks have been analyzed (Miao, 1989; Miao and Qian, 1995). To understand the main mode of roof fracturing movement of thin bedrock, the roof fracturing movement and the control of movement after fracturing are discussed. The influence of bedrock thickness, mining height, and advancing speed on roof fracture is further analyzed (Shi and Hou, 1996). For the structural characteristics of the roof in longwall mining, mechanical analysis and simulation experiment have been used to explore the particularity of a broken roof structure in longwall mining. A simplified model of a broken roof structure has been built, and the fracture mechanism and formation mechanism of the roof have been revealed (Shen et al., 2011; Pang et al., 2020; Lu et al., 2021a). In thick coal seam mining with large mining height, it is easy to form a cantilever beam structure. Consequently, scholars have established a cantilever beam-voussoir beam structure model of a hard roof fracture in a large cutting height panel face and have explained the structural characteristics and fracture mechanism of this type of roof (Ju and Xu, 2013; Tan and Guo, 2015; Osouli and Bajestani, 2016; Liu et al., 2017; Zhao et al., 2020).

At present, the main methods for determining the supporting capacity of a shield in a panel face include voussoir beam theory, transfer rock beam theory, the estimation method, the experience method, the dynamic load method, and so on (Zhao, 1988; Kou, 1996). Some scholars have proposed a dynamic load calculation method for determining the supporting capacity of a shield in view of the impact of main roof instability on the shield (Wang, 2009; Wang et al., 2015). Scholars have addressed the problem of calculating and predicting the supporting capacity of a shield in a longwall mining panel face. Early prediction of severe roof weighting can be achieved by establishing a prediction model based on a decision tree algorithm, which provides a reference for roof weighting prediction and shield selection for a longwall mining panel face (Cheng et al., 2018; Lu et al., 2021b; Zhu et al., 2022). Also, the adaptability of a shield in a deep buried and super long longwall mining panel face has been studied, and analysis and research on the supporting capacity of a shield by have been carried out by calculation of ground pressure theory, field dynamic real-time monitoring and numerical modeling , and a calculation formula of supporting capacity of the fully mechanized shield with large mining height (Yan et al., 2011; Peng et al., 2019; Ding et al., 2021; Li et al., 2021).

In summary, many experts and scholars have conducted a lot of research on the roof fracturing characteristics and movement mechanism of the panel face. Many research results have been achieved in roof instability and fracturing, deformation and movement mechanism, judging criterion of roof weighting, and a calculation method for the supporting capacity of the shield. However, there is still lack of relevant research on the fracturing characteristics of a hard roof in the panel face, and a method for determining the reasonable supporting capacity of the shield in a deep buried and thick coal seam is required. Therefore, in this study, the No.232204 panel face of the Meihuajing mine in the Yuanyanghu mining area was used as the background of the study. Numerical simulation, theoretical analysis, field measurements, and system development were used. The fracturing characteristics of the roof of the panel face, the calculation method of reasonable supporting capacity of the shield, and the influencing factors of the supporting capacity of shield in a deep buried and thick coal seam were studied. The reasonable supporting capacity of the shield of the No.232204 panel face was determined. The shield selection was reasonable, as verified by field measurement.

2 Engineering overview

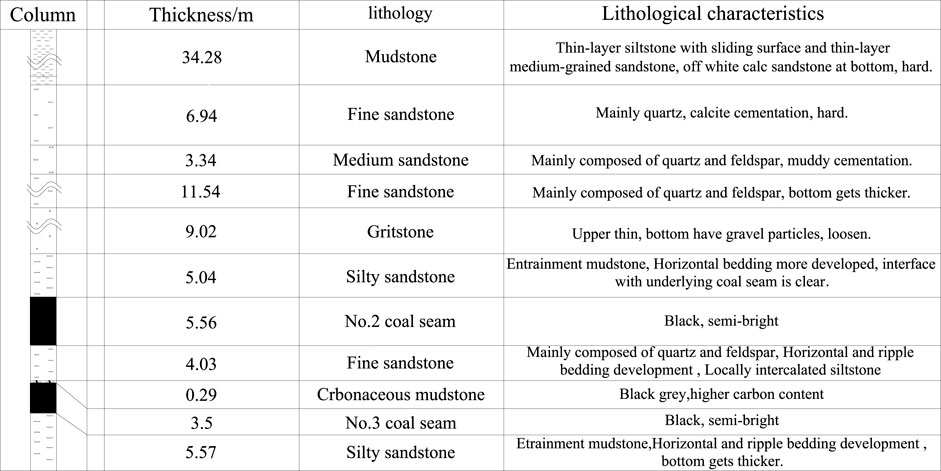
The No. 232204 longwall mining panel face is the second panel face in 23^# mining district of the Meihuajing coal mine in the Yuanyanghu mining area. The north and the south of the No.232204 panel face are the No.232201 panel face, which has been extracted, and the DF3 fault, respectively. The east and west of the No.232204 panel face are the solid coal and the main entries of 23^# mining district, respectively. The panel length is 1,616 m, and panel width is 302.7 m. The average depth of the No.232204 panel face is 600 m, The in-suit stress test has been measured in the No.2 coal seam in the Meihuajing coal mine. The measured results show that the three-dimensional stress is basically equal when the coal seam mining depth is greater than 600 m. The No.232204 panel face mainly extracts the No.2 coal seam with good stability. The average thickness and the dip angle are 5.5 m and 5.6°, respectively.

The immediate roof of the coal seam is silty sandstone, with a thickness of 5.04 m; the main roof is gritstone, with a thickness of 9.02 m; and the immediate floor is fine sandstone, with a thickness of 5.03 m. The longwall coal mining method is used in the No.232204 panel face. Also, the generalized stratigraphic column of the No.232204 panel face is shown in Figure 1.

FIGURE 1

FIGURE 1. Generalized stratigraphic column of the No.232204 panel face.

3 Evolution characteristics of a broken roof structure and loading variation of supporting capacity

Based on the occurrence characteristics of coal and rock in the No.232204 panel face, UDEC7.0 numerical simulation software was selected to analyze the fracture characteristics of a broken roof structure and loading variation of supporting capacity after a thick, deeply buried coal seam has been mined.

3.1 Model development

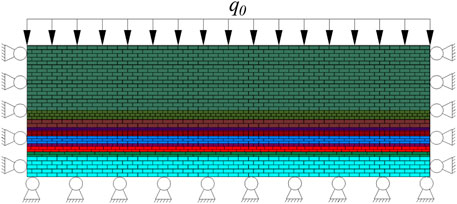
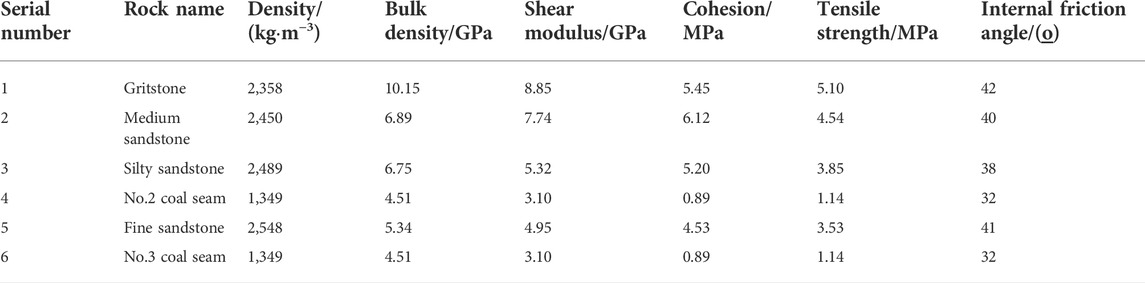
A UDEC numerical model was established, whose length and height are 400 and 130 m, respectively, as shown in Figure 2. Because the dip angle of No.2 coal seam is a horizontal coal seam, the dip angle of rock strata was simplified as 0° in the numerical model. The Mohr–Coulomb criterion was used in the whole model, and the model parameters are shown in Table1. The left and right boundary of the model denoted limited horizontal displacement (Gao et al., 2014; Zhang et al., 2020b; Vergara et al., 2020; Wu et al., 2021; Kim and Larson, 2022). The lower boundary was limited to vertical displacement. To the upper boundary was applied a uniform load with q₀ = 500 × 0.027 MN/m³ = 13.5 MPa. Also, a 100-m coal pillar was left on the two sides to eliminate the boundary effect. The model advances 10 m each time.

FIGURE 2

FIGURE 2. Numerical model.

TABLE 1

TABLE 1. Physical and mechanical parameters of rock strata.

3.2 Simulation results

The evolution of the broken roof structure and supporting pressure of the shield are shown in Figure 3.

FIGURE 3

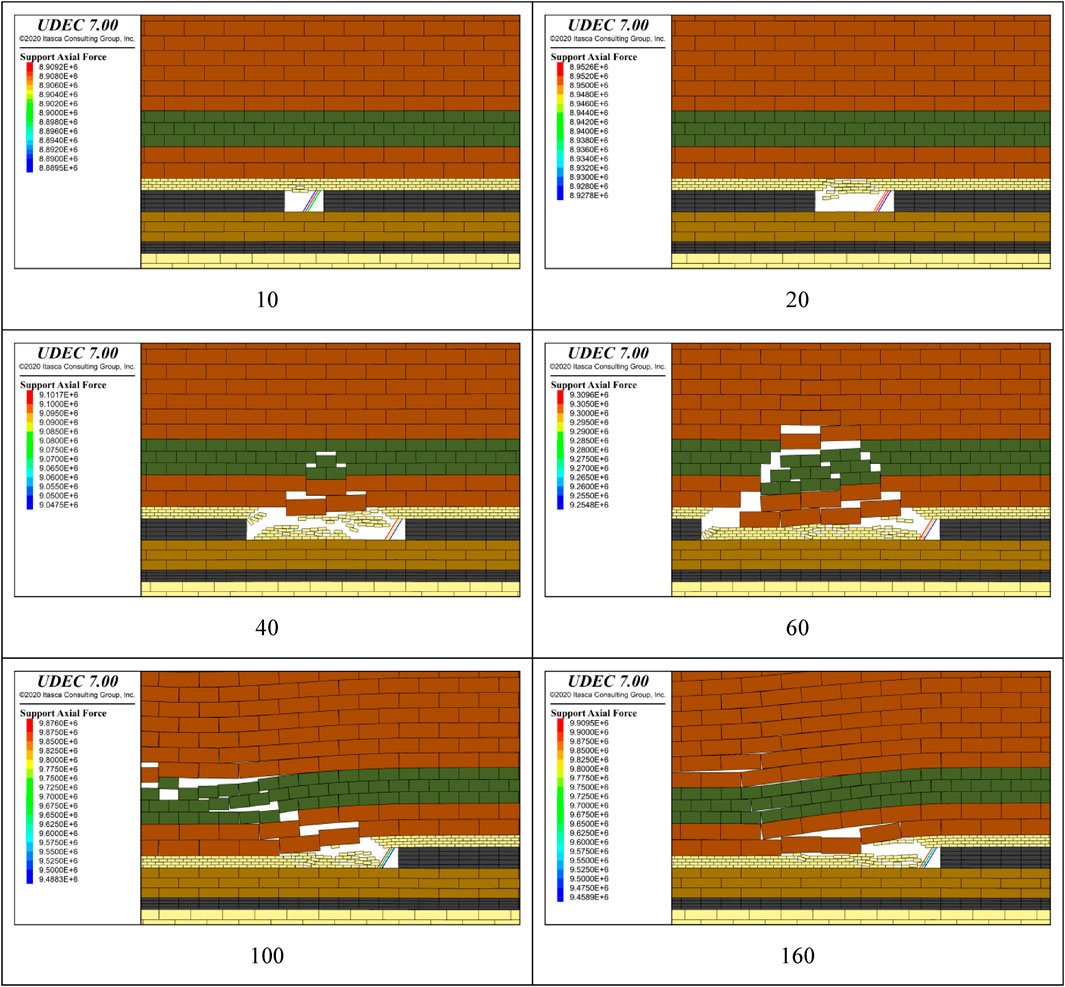
FIGURE 3. Broken roof structure and supporting capacity of the shield at different advancing distances in the panel face.

When the panel face advances to 10 m, the roof remains intact without collapsing, and the supporting pressure of the shield is about 8,900 kN at this time, as shown in Figure 3A.

When the panel face advances to 20 m, the immediate roof reaches the limit span, and the whole fracturing and collapsing at both ends of the stope are observed, as shown in Figure 3B. However, the gob is not filled up with the collapsing immediate roof. The supporting pressure of the shield is still maintained at 8,900 kN, as in the previous step.

When the panel face advances to 40 m, the immediate roof collapses in the gob with coal seam mining. At the same time, the main roof reaches the limit span and fractures, with the first weighting appearing, as shown in Figure 3C. Therefore, the first weighting interval of the main roof is 40 m. The broken rock of the main roof is hinged to form a three-hinged arch balanced structure. The supporting pressure of the shield increases to 9,000 kN. When the broken rock of the main roof bite point shear force is greater than the friction force, the structure experiences sliding instability, which will cause the roof of the panel face to sink in steps and increase the supporting pressure of the shield.

When the panel face advances to 60 m, the main roof is separated from the overburden, and the main roof fractures and rotates with periodic weighting observed, and the periodic weighting interval is 20 m. At this time, the shield of the panel face should balance the load imposed on the shield by the main roof rotation to prevent it from falling off along the coal wall. The supporting capacity of the shield continues to increase to 9,200 kN. The main roof forms a voussoir beam balanced structure at this moment, as shown in Figure 3D.

When the panel face advances to 100 m, the main roof will still form a stable voussoir beam balanced structure, with the third periodic weighting appearing. The supporting capacity of the shield continues to increase to 9,600 kN, as shown in Figure 3E.

When the panel face advances to 160 m, the main roof continues to be a voussoir beam balanced structure, with the sixth periodic weighting observed, as shown in Figure 3F. The supporting capacity of the shield no longer increases and is maintained at 9,600 kN. During the periodic weighting, the shield has no deformation or crushing, with good roof support effect.

4 Calculation and analysis of a shield’s reasonable supporting capacity

Through the previously mentioned numerical simulation analysis, it can be seen that the broken rock blocks are hinged to form a voussoir beam structure during periodic weighting of the main roof. The load on the shield is generated when the voussoir beam structure of the main roof is instable. Therefore, it is necessary to analyze the instability form of the structure and then determine the supporting capacity of the shield through theoretical calculation.

4.1 Instability form of a broken roof structure

The stability of the voussoir beam structure formed by the main roof is mainly controlled by the hinged blocks. When the rotation angle (θ) of hinged blocks is small, the structure may be subjected to sliding instability. When the rotation angle is large, the structure may be subjected to rotation instability (Qian et al., 2010), as shown in Figure 4.

FIGURE 4

FIGURE 4. Movement forms and force of broken roof rock.

The rotation angle (θ) can be expressed as follows:

$\sin \mathit{\theta }=\frac{1}{L}\left[\mathrm{m}-h_1\left({\mathit{K}}_P-1\right)\right](1)$

where L is the length of broken rock, m; m is the thickness of coal seam, m; h₁ is the thickness of immediate roof, m; and K_p is the bulking coefficient of immediate roof collapsing rock, 1.4–1.7.

The main roof experiences periodic weighting, and therefore, the length of the broken rock block is the periodic weighting interval of the main roof (L):

$L=h_2\sqrt{\frac{2R_T}{q}}(2)$

where R_T is tensile strength of the main roof, MPa and q is the load of the main roof, MPa.

In Formula 2, q can be expressed as follows:

${\left(q_n\right)}_2=\frac{E_2{h}_2^3\left({\mathit{\gamma }}_2{h}_2+{\gamma }_3{h}_3+\cdots +{\mathit{\gamma }}_{\mathrm{n}}{h}_n\right)}{E_2{h}_2^3+E_3{h}_3^3+\cdots +E_n{h}_n^3}(3)$

where γ_n is the bulk density of each rock stratum, kN/m³ and E_n is the elastic modulus of each rock stratum, MPa.

According to the S-R stability theory of a voussoir beam structure, the formation conditions of structural sliding instability are as follows:

$\frac{h_2}{L}-\frac{3}{4}\sin \mathit{\theta }>\tan \mathit{\alpha }(4)$

where h₂ is the main roof thickness, m and tanα is friction coefficient between rock blocks, 0.3.

The formation conditions of structural rotation instability are as follows:

$\frac{\mathrm{2q}}{\left(\frac{h_2^2}{L}+\frac{1}{2}L{\sin }^2\theta -\frac{3}{2}{h}_2\sin \theta \right){\mathit{\sigma }}_c}>\eta (5)$

where η is the extrusion coefficient of the broken rock blocks at the corner, 0.3 and σ_c is the compressive strength of the broken rock blocks, MPa.

Through calculation, the results of the broken rock blocks of the deep buried and thick coal seam is in line with Formula 3, and the voussoir beam structure will undergo sliding instability.

4.2 Calculating a shield’s reasonable supporting capacity

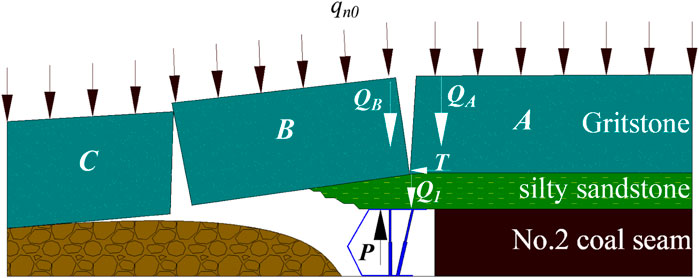
The previously mentioned analysis shows that in the mining process of the No.232204 panel face, the immediate roof collapses in the gob with coal seam mining, and the main roof will form a voussoir beam balanced structure, as shown in Figure 5.

FIGURE 5

FIGURE 5. Mechanical model of a roof fracture structure.

Therefore, during the deep buried and thick coal seam mining, the interaction system between the shield and surrounding rock of the panel face is composed of the shield, immediate roof cantilever beam structure, and main roof voussoir beam balanced structure(Qian et al., 2010). Also, the supporting capacity of shield (P) can be expressed as follows:

$\mathit{P}={\mathit{Q}}_1+\mathit{F}(6)$

In Formula 5, Q₁ can be expressed as follows:

$Q_1={\gamma }_1\times h_1\times l_1(7)$

where γ₁ is the bulk density of immediate roof, 23 kN/m³; h₁ is the thickness of immediate roof, 5.04 m; and l₁ is control distance of immediate roof, 9 m.

Combining knowledge of ground pressure and rock stratum control, the load applied on the shield due to sliding instability of the main roof (F) can be expressed as follows:

$F=Q_{A+B}-\frac{l_0{Q}_{i0}}{2\left(h_2-\mathit{\delta }\right)}\tan \left(\mathit{\phi }-\theta \right)(8)$

where Q_A+B is the weight and load of rock blocks A and B, kN; l₀ is the length of rock block B, m; Q_i0 is the weight and load of rock B, kN; h₂ is the thickness of main roof, 9.02 m; δ is the subsidence of rock block B, m; φ is the internal friction angle,38°; and θ is the break angle of the rock block.

The weight and load of rock blocks A and B (Q_A+B) are calculated as follows:

$\{\begin{array}{l}{Q}_{A+B}=Q_A+Q_B+q_{n0}\\ Q_A={\gamma }_2\times h_2\times l_A\\ Q_B={\gamma }_2\times h_2\times l_B\end{array}(9)$

where Q_A is the weight of rock block A, kN/m³; Q_B is the weight of rock block B, kN/m³; q_n0 is the load on rock blocks A and B, kN; γ₂ is the bulk density of main roof, 25 kN/m³; l_A is the length of rock block A, m; and l_B is the length of rock block B, m.

The subsidence of rock block B (δ) and the fracture angle of rock block (θ) are calculated as follows:

$\{\begin{array}{l}\delta =h_1+m-K_p{h}_1\\ \mathit{\theta }=\arctan \frac{\delta }{l_B}\end{array}(10)$

where m is the thickness of No.2 coal seam, 5.5 m and K_p is the bulking coefficient of immediate roof collapsing rock, 1.5.

According to the calculation, the supporting capacity of shield P is 9,581.04 kN. Combined with mine production experience, a ZY10000/28/62D shield is selected to support the roof. The rate supporting capacity of the ZY10000/28/62D shield is 10,000 kN, which can meet the requirements of support.

4.3 Analysis of the factors that influence the supporting capacity of a shield

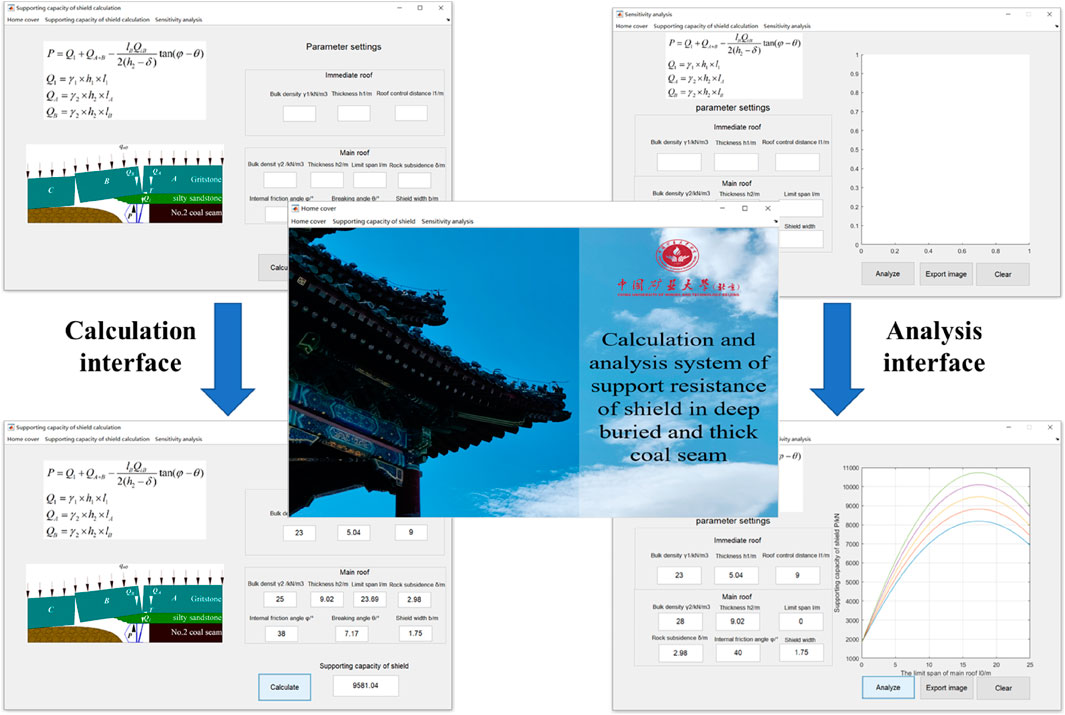
Combining the results of numerical simulation and theoretical analysis of the supporting capacity of the shield, it shield mainly bears the load of the immediate roof and the load applied on the shield due to sliding instability of the main roof within the roof control range of the shield. Among them, the load of the main roof slide instability acting on the shield is mainly related to the horizontal thrust formed by the rotation of the main broken roof rock blocks and the weight and load of the rock blocks. Based on the previously mentioned analysis, using the GUI module in MATLAB software, a calculation and analysis system of the supporting capacity of shield in a deep buried and thick coal seam is developed. The influence of bulk density, thickness, and control distance of immediate roof and bulk density, thickness, and length of the rock block generated by the main roof on the supporting capacity of a shield are studied.

4.3.1 Development of calculation and analysis software system

The calculation and analysis software system of the supporting capacity of the shield in a deep buried and thick coal seam has been developed. The intelligent calculation and real-time analysis of the supporting capacity of the shield are realized. The system mainly includes three interfaces: home cover, supporting capacity of shield calculation cover, and sensitivity analysis cover (as shown in Figure 6). The system includes two functions: supporting capacity of shield calculation and sensitivity analysis. Using the system, the calculation process of the supporting capacity of the shield is simplified, and the calculation efficiency of the supporting capacity of the shield is improved. Moreover, the sensitivity analysis of the supporting capacity of the shield is realized.

FIGURE 6

FIGURE 6. Interface of the calculation and analysis system.

4.3.2 Sensitivity analysis

1) The influence of the immediate roof

Figures 7A,B shows the influence of bulk density, thickness, and control distance of the immediate roof on the supporting capacity of the shield. As can be seen from Figure 7, when the control distance remains constant, the supporting capacity of the shield increases as the bulk density and thickness increase. In detail, when the bulk density increased from 20 to 28 kN/m³, the supporting capacity of the shield increased from 8,456.14 to 9,091.18 kN, which is an increase of 7.5%. When the thickness increased from 8 to 10 m, the supporting capacity of the shield increased from 9,766.54 to 10,491 kN, which is an increase of 7.4%. Otherwise, with the increase of the control distance of the immediate roof, the supporting capacity of the shield increases accordingly. Therefore, it can be considered that the influence of the bulk density and the thickness of the immediate roof changes on the supporting capacity of the shield are not obvious.

2) The influence of the main roof

FIGURE 7

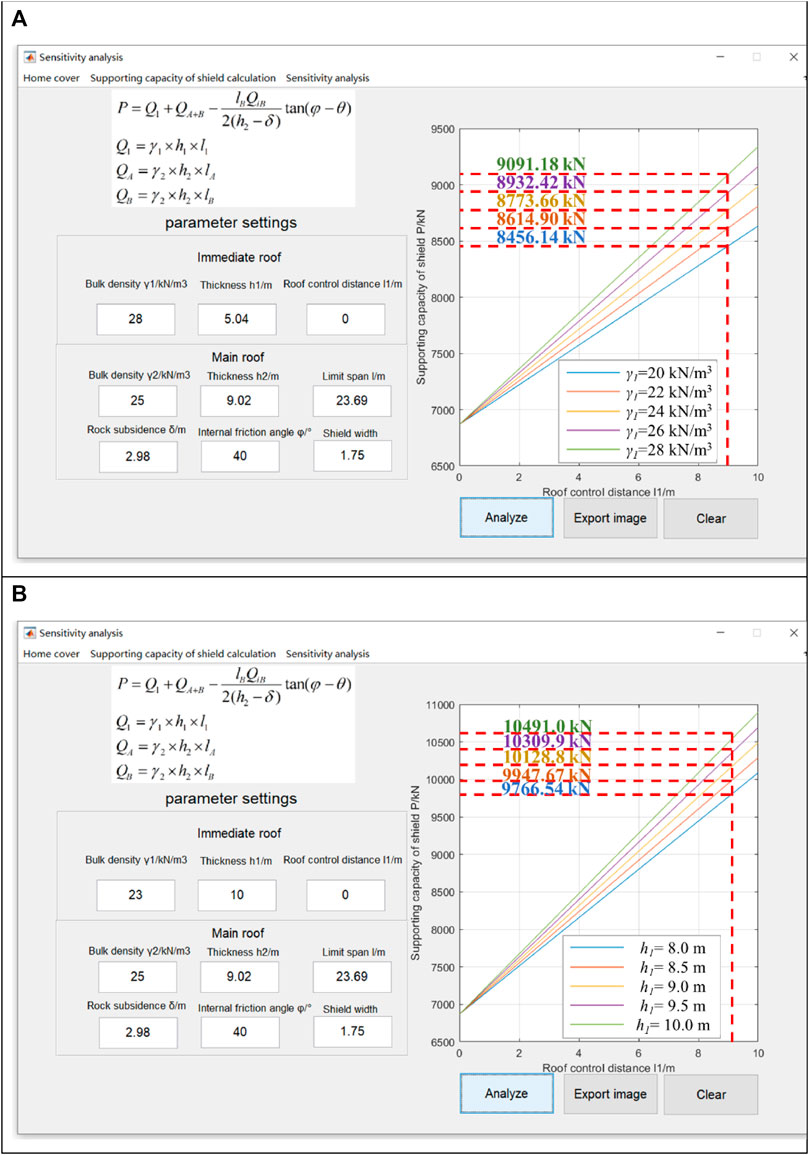
FIGURE 7. Influence of related parameters of the immediate roof on the shield’s supporting capacity. (A) Influence of bulk density and roof control distance on the shield’s supporting capacity. (B) Influence of thickness and roof control distance on the shield’s supporting capacity.

Figures 8A,B shows the influence of bulk density, thickness, and length of the rock block generated by the main roof on the supporting capacity of a shield. As can be seen from Figure 8, when the length remains constant, the supporting capacity of the shield increases with the bulk density and thickness increases. In detail, when the bulk density increased from 20 to 28 kN/m³, the supporting capacity of the shield increased from 7,320.57 to 9,518.51 kN, which is an increase of 30%. When the thickness increased from 8 to 10 m, the supporting capacity of the shield increased from 5,785.90 to 11,271.30 kN, which is an increase of 94.8%. Therefore, it can be considered that the influence of the thickness of the main roof change on the supporting capacity of a shield is much greater than the bulk density of main roof change.

FIGURE 8

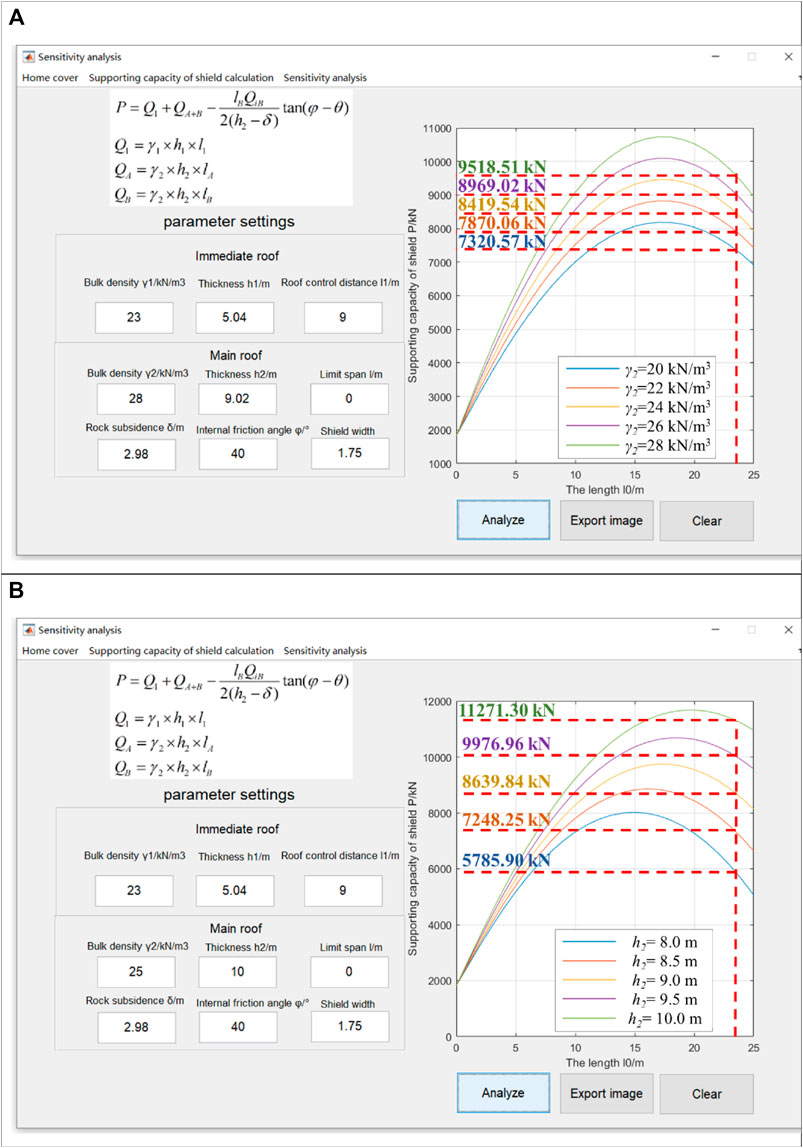
FIGURE 8. Influence of related parameters of the main roof on the shield’s supporting capacity. (A) Influence of bulk density and length on the shield’s supporting capacity. (B) Influence of thickness and length on the shield’s supporting capacity.

In addition, when the bulk density and thickness are 26 kN/m³ and 9 m, the length increases from 0 to 25 m and the supporting capacity of the shield first increases from 1825.74 to 9,464.88 kN and then decreases to 8,585.61 kN with the length of the rock block, showing a trend of first increasing and then decreasing. This happens because the rock block is generated by the main broken roof, so the length of the rock block is approximately the period weighting interval. When the length of the rock block is short, its weight is small. In other words, the load applied on the shield due to the sliding instability of the main roof is small. As the length of the rock block increases, the load also increases, and this causes the support capacity of the shield to increase. However, the load does not increase indefinitely. When the length of the rock block exceeds a certain limit length, the support capacity of the shield does not increase. This happens because the horizontal thrust formed by rock block rotation increases, which causes the friction between two adjacent rock blocks to also increase. As the length of the rock block continues to increase, the friction increase is greater than self-weight increase.

3) Influence comparison of related parameters

It can be seen from Figures 9, 10 that bulk density and thickness of the immediate roof and main roof are positively correlated with supporting capacity of the shield. When the bulk density of the immediate roof and main roof increases from 20 to 28 kN/m³, the supporting capacity of the shield increases by 9.0% and 31.0%, respectively, with the same other parameters and change of bulk density. Compared to the growth rates, it can be seen that the influence of the bulk density of the main roof on the supporting capacity of the shield is much greater than that of the bulk density of the immediate roof. Similarly, when the thickness of the immediate roof and main roof increases from 8 to 10 m, the supporting capacity of the shield increases by 10.6% and 80.0%, respectively, with the same other parameters and change of thickness. Compared to the growth rates, it can be seen that the influence of the thickness of the main roof on the supporting capacity of the shield is much greater than that of the thickness of the immediate roof.

FIGURE 9

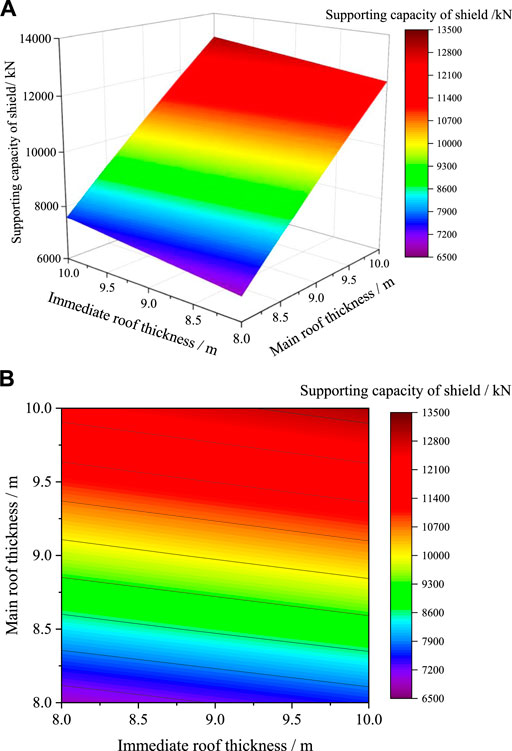
FIGURE 9. Three-dimensional surface diagram of the influence of thickness change on the shield’s supporting capacity.(A) Comparison chart of a change in the shield’s supporting capacity. (B) Isoline chart of the shield’s supporting capacity.

FIGURE 10

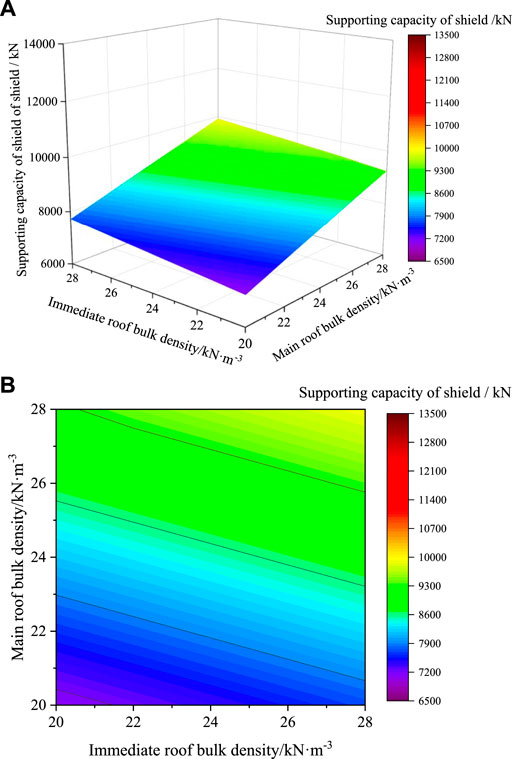
FIGURE 10. Three-dimensional surface diagram of the influence of bulk density change on the shield’s supporting capacity.(A) Comparison chart of a change in the shield’s supporting capacity. (B) Isoline chart of the shield’s supporting capacity.

In addition, the parameters of the immediate roof have little influence on the supporting capacity of the shield, while the parameters of the main roof have a considerable influence on the supporting capacity of the shield. Among these parameters for the immediate roof and main roof, the thickness of the main roof has the greatest influence.

To reduce the influence of thickness of the main roof, the horizontal pre-splitting roof technical method was proposed and employed in the same coal mine. Namely, horizontal directional pre-splitting drilling is arranged in the main roof, which leads to stratification of the thick roof by means of external force and reduces the thickness and integrity of the main roof. At the same time, it can reduce the period weighting interval of the panel face, thus reducing the supporting capacity of the shield (Liu et al., 2015; Zhang et al., 2017; Zhang et al., 2018).

5 Field measurement of the supporting capacity of the shield

To verify the reasonable of support selection, the field measurement results of the supporting capacity of the shield are analyzed during coal seam mining. The ZY10000/28/62D shield was selected to support the roof in the No.232204 panel face. The supporting capacity of the shield is 10,000 kN with 8,000 kN setting load. Also, the ZY10000/28/62D shield is shown in Figure 11.

FIGURE 11

FIGURE 11. ZY10000/28/62D shield.

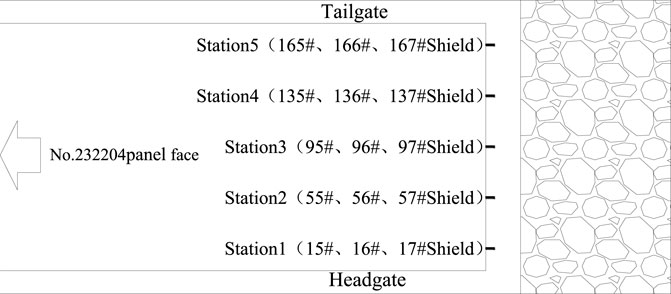
5.1 Measurement scheme for the supporting capacity of a shield in the panel face

Five groups of stations are arranged in the panel face from headgate to tailgate, as seen in Figure 12. The first group measurements are 15#, 16#, and 17# shields. The second group measurements are 55#, 56#, and 57# shields. The third group measurements are 95#, 96#, and 97# shields. The fourth group measurements are 135#, 136#, and 137# shields. The fifth group measurements are 165#, 166#, and 167# shields. The supporting capacity of the shields was measured and recorded using a shield pressure meter in each station in the panel face. Also, the data were then summarized and analyzed.

FIGURE 12

FIGURE 12. Station arrangements of the supporting capacity of a shield in the panel face.

5.2 Analysis of the measurement results of the supporting capacity of the shield

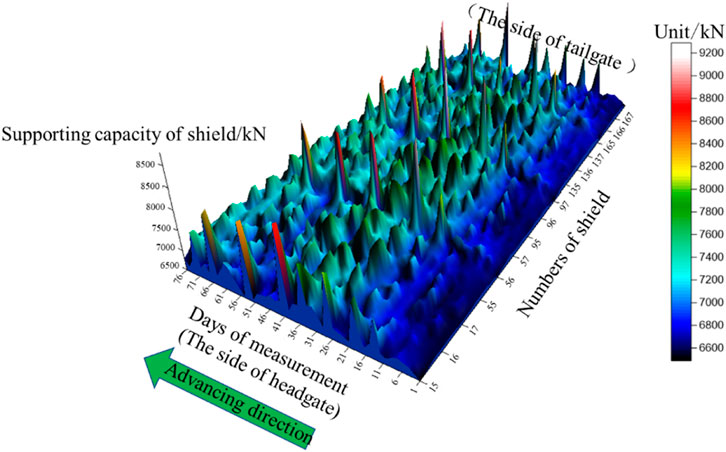
The supporting capacity of shield in No.232204 panel face has been measured since 15 February 2020. Figures 13, 14 show the measurement results from February 15 to April 31. During the measurement period, the first weighting interval of the immediate roof and main roof is 17.2 and 40 m, respectively. The panel face has experienced periodic weighting six times, and the period weighting interval of the main roof is 16 m.

FIGURE 13

FIGURE 13. Measurement results of the shield’s supporting capacity.

FIGURE 14

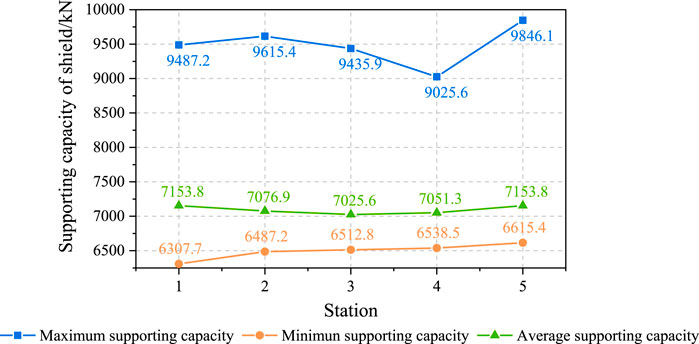
FIGURE 14. Measurement results of the supporting capacity of a shield station in the No.232204 panel face.

The supporting capacity of the shield has been measured since the setup-entry was prepared. The total days and the distance of measurement are 77 and 161.3 m, respectively. It can be seen from Figures 13, 14 that the maximum supporting capacity of the shield during the weighting of the panel face is 8,000–9,846 kN during the measurement period. Also, the supporting capacity of the shield in the station 1 is between 6,538 and 9,846 kN. During the periodic weighting of the main roof, the supporting capacity of the shields in the stations increases with a maximum dynamic load factor of 1.4. At the same time, the maximum supporting capacity of the shield can reach 9,846 kN, and the rib spalling in the area near the headgate is serious. The main reason for this is the influence of the DF3 fault and the strong ground pressure behavior of roof weighting. In addition, the measurement results show that the load utilization rate of the shield is more than 90% during the periodic weighting. There is no shield crushing in the mining process of the No.232204 panel face, which shows that the shield has enough setting load and excellent adaptability.

5.3 Analysis of the maximum supporting capacity of a shield in the panel face

The total advance of the No.232204 panel face is 678.6 m in 2020. So, the distribution of the maximum supporting capacity of the shield in the five stations is summarized for analysis, as shown in Figure 15.

FIGURE 15

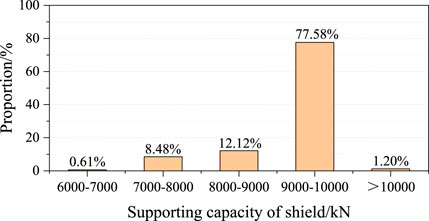
FIGURE 15. Frequency histogram of maximum supporting capacity of shield distribution in the panel face.

From the analysis, the maximum supporting pressure of the shield is mainly distributed between 9,000 and 10,000 kN, with a proportion of 77.58%. There are only 9.09% shields whose load utilization rate does not reach 80% and 1.2% shields whose supporting pressure exceeds the supporting capacity (10,000 kN). Therefore, it shows that the shield selected in the No.232204 panel face is reasonable with sufficient setting load and high load utilization rate, which can meet the requirements of support. In addition, no shield crushing phenomenon is observed.

6 Conclusion

1) The immediate roof and the main roof both reach the limit span with fracturing and collapsing. When the first weighting of the main roof is observed, the broken rock block is hinged to form a three-hinged arch balanced structure. When the periodic weighting of the main roof is observed, the broken rock block forms a voussoir beam balance structure. The supporting capacity of the shield increases with the sliding instability of the two adjacent broken rock blocks. Also, the supporting capacity of the shield is stable between 8,900 and 9,600 kN.

2) Based on voussoir beam theory, combined with the numerical simulation results, the mechanical model of roof fracture structure is established. The calculation formula of the supporting capacity of the shield is proposed, and the reasonable supporting capacity of the shield is obtained as 9,581.04 kN, which is consistent with the numerical simulation result. The ZY10000/28/62D shield with supporting capacity of 10,000 kN is selected in the No.232204 panel face.

3) Based on theoretical analysis, the calculation and analysis software system of supporting capacity of the shield in deep buried and thick coal seam is developed using MATLAB. The bulk density, thickness, and control distance of the immediate roof and the bulk density and thickness of the main roof are positively correlated with the supporting capacity of the shield. The supporting capacity of the shield first increases and then decreases with the length of the rock block generated by the main roof. Also, the parameters of the immediate roof have little influence on the supporting capacity of the shield, while the parameters of the main roof have great influence on the supporting capacity of the shield. The thickness of the main roof has the greatest influence among the parameters studied.

4) The field measurement results show that the periodic weighting interval of the immediate roof and main roof is 17.2 and 40 m, respectively. The load utilization rate of the ZY10000/28/62D shield generally reaches more than 90%.The maximum supporting pressure of the shield is mainly distributed between 9,000 kN and 10,000 kN, with a proportion of 77.58%. The shield selected in the No.232204 panel face is reasonable with a sufficient setting load and high load utilization rate.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. The author’s contributions are project design, paper manuscript, numerical simulation, data analysis, field measurement, and correction paper.

Acknowledgments

We acknowledge the financial support from the National Natural Science Foundation of China (No. 52074293) and the Natural Science Foundation of Hebei Province, China (E2020402041).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cheng, J. Y., Wan, Z. J., and Ji, Y. L. (2018). Shield-roof interaction in longwall panels: Insights from field data and their application to ground control. Adv. Civ. Eng.2018, 1–18. doi:10.1155/2018/3031714

CrossRef Full Text | Google Scholar

Ding, G. L., Lu, X. H., Wu, S. G., and Liu, Y. Q.(2021). Sturdy on ground pressure law and support adaptability of deep-buried and ultra-long fully-mechanized longwall mining face. Coal Sci. Technol.49 (3), 43–48. doi:10.13199/j.cnki.cst.2021.03.004

CrossRef Full Text | Google Scholar

Gao, F., Stead, D., and Kang, H. (2014). Simulation of roof shear failure in coal mine roadways using an innovative UDEC Trigon approach. Comput. Geotechnics61, 33–41. doi:10.1016/j.compgeo.2014.04.009

CrossRef Full Text | Google Scholar

Ju, J., and Xu, J. (2013). Structural characteristics of key strata and strata behaviour of a fully mechanized longwall face with 7.0m height chocks. Int. J. Rock Mech. Min. Sci.58, 46–54. doi:10.1016/j.ijrmms.2012.09.006

CrossRef Full Text | Google Scholar

Kim, B., and Larson, M. (2022). Assessment of floor heave associated with bumps in a longwall mine using the discrete element method. Min. MetallurgyExplor, 1–9. doi:10.1007/s42461-022-00596-y

CrossRef Full Text | Google Scholar

Klemetti, T. M., Van, D. K., Evanek, N., Compton, C. C., and Tulu, I. B. (2021). Insights into the relationships among the roof, rib, floor, and pillars of underground coal mines. Min. Metall. Explor.38 (1), 531–538. doi:10.1007/s42461-020-00313-7

CrossRef Full Text | Google Scholar

Kou, Z. M. (1996). Analysis and detection of dynamic characteristics of hydraulic support. Beijing: Metallurgical Industry Press.

Google Scholar

Li, Y., Chen, H. Z., Ren, Y. Q., Yang, K. P., and Lu, J. B. (2020). Research on economic evaluation of mining mode of close distance coal seam group. Coal Econ. Res.40 (9), 24–28. doi:10.13202/j.cnki.cer.2020.09.005

CrossRef Full Text | Google Scholar

Li, Y., Ren, Y. Q., Wang, N., Luo, J., Li, N., Liu, Y., et al. (2021). A novel mining method for longwall panel face passing through parallel abandoned roadways. Shock Vib., 20211–10. doi:10.1155/2021/9998561

CrossRef Full Text | Google Scholar

Liu, C., Li, H. M., Mitri, H., Jiang, D., and Feng, J. (2017). Voussoir beam model for lower strong roof strata movement in longwall mining – case study. J. Rock Mech. Geotechnical Eng.9 (6), 1171–1176. doi:10.1016/j.jrmge.2017.07.002

CrossRef Full Text | Google Scholar

Liu, J., Liu, Z. G., Xue, J. H., Gao, K., and Zhou, W. (2015). Application of deep borehole blasting on fully mechanized hard top-coal pre-splitting and gas extraction in the special thick seam. Int. J. Min. Sci. Technol.25 (5), 755–760. doi:10.1016/j.ijmst.2015.07.009

CrossRef Full Text | Google Scholar

Lu, J., Jiang, C., Jin, Z., Wang, W., Zhuang, W., and Yu, H. (2021). Three-dimensional physical model experiment of mining-induced deformation and failure characteristics of roof and floor in deep underground coal seams. Process Saf. Environ. Prot.150, 400–415. doi:10.1016/j.psep.2021.04.029

CrossRef Full Text | Google Scholar

Lu, W. Y., Ding, K., Wu, Y. P., Du, X. F., Hu, X., and Luo, X. Y. (2021). PCA-SVR prediction model of support working resistance in fully mechanized mining face. J. Xi'an Univ. Sci. Technol.41 (6), 973–978. doi:10.13800/j.cnki.xakjdxxb.2021.0603

CrossRef Full Text | Google Scholar

Miao, X. X., and Qian, M. G. (1995). Solid structure and model of voussoir beam of face surrounding rock. Mine Press. Roof Manag. (3), 3–12.

Google Scholar

Miao, X. X. (1989). Stability analysis of the main roof during first weighting in longwall face. J. China Univ. Min. Technol.18 (3), 88–92.

Google Scholar

Osouli, A., and Bajestani, B. M. (2016). The interplay between moisture sensitive roof rocks and roof falls in an Illinois underground coal mine. Comput. Geotechnics80, 152–166. doi:10.1016/j.compgeo.2016.07.004

CrossRef Full Text | Google Scholar

Pang, Y. H., Wang, G. F., and Li, B. B. (2020). Stress path effect and instability process analysis of overlying strata in deep stopes. Chin. J. Rock Mech. Eng.39 (4), 682–694. doi:10.13722/j.cnki.jrme.2019.0622

CrossRef Full Text | Google Scholar

Peng, S. S., Cheng, J. Y., Du, F., and Xue, Y. T. (2019). Underground ground control monitoring and interpretation, and numerical modeling, and shield capacity design. Int. J. Min. Sci. Technol.29 (1), 79–85. doi:10.1016/j.ijmst.2018.11.026

CrossRef Full Text | Google Scholar

Qian, M. G., Miao, X. X., and He, H. L. (1994). Analysis of key block in the structure of voussoir beam in longwall mining. J. China Coal Soc.19 (6), 557–563.

Google Scholar

Qian, M. G., Shi, P. W., and Xu, J. L. (2010). Mining pressure and strata control. Xuzhou: China University of Mining and Technology Press.

Google Scholar

Qian, M. G., and Xu, J. L. (2019). Behaviors of strata movement in coal mining. J. China Coal Soc.44 (4), 973–984. doi:10.13225/j.cnki.jccs.2019.0337

CrossRef Full Text | Google Scholar

Rajwa, S., Janoszek, T., and Prusek, S. (2020). Model tests of the effect of active roof support on the working stability of a longwall. Comput. Geotechnics 118, 103302. doi:10.1016/j.compgeo.2019.103302

CrossRef Full Text | Google Scholar

Shen, J., Meng, D., and Wei, L. (2011). Study on the structural system of roof in fully mechanized top coal caving. Appl. Mech. Mater.90-93, 2041–2044. doi:10.4028/www.scientific.net/amm.90-93.2041

CrossRef Full Text | Google Scholar

Shi, P. W., and Hou, Z. J. (1996). Law of roof breaking movement of shallow seams in shenfu CMA. J. Xi'an Univ. Sci. Technol.16 (3), 203–207.

Google Scholar

Tan, Y., and Guo, W. B. (2015). Underground pressure behavior of large-mining-height mining field under hard roof in Quantou colliery. Coal Min.20 (5), 66–69. doi:10.13532/j.cnki.cn11-3677/td.2015.05.018

CrossRef Full Text | Google Scholar

Vergara, M. R., Arismendy, A., Libreros, A., and Brzovic, A. (2020). Numerical investigation into strength and deformability of veined rock mass. Int. J. Rock Mech. Min. Sci.135, 1365–1609.

CrossRef Full Text | Google Scholar

Wang, J. C. (2009). Thick coal seam mining theory and technology. Beijing: Metallurgical Industry Press.

Google Scholar

Wang, J. C., Yang, S. L., Li, Y., and Wang, Z. (2015). A dynamic method to determine the supports capacity in longwall coal mining. Int. J. Min. Reclam. Environ.29 (4), 277–288. doi:10.1080/17480930.2014.891694

CrossRef Full Text | Google Scholar

Wang, J. H. (2013). Key technology for fully-mechanized top coal caving with large mining height in extra-thick coal seam. J. China Coal Soc.38 (12), 2089–2098. doi:10.13225/j.cnki.jccs.2013.12.013

CrossRef Full Text | Google Scholar

Wu, W., Bai, J., Feng, G., and Wang, X. Y. (2021). Investigation on the mechanism and control methods for roof collapse caused by cable bolt shear rupture. Eng. Fail. Anal.30, 1350–6307. doi:10.1016/j.engfailanal.2021.105724

CrossRef Full Text | Google Scholar

Xie, H. P., Qian, M. G., Peng, S. P., Hu, X. S., Cheng, Y. Q., and Zhou, H. W. (2011). Sustainable capacity of coal mining and its strategic plan. Strategic Study CAE13 (6), 44–50.

Google Scholar

Xie, H. P. (2019). Research review of the state key research development program of China: Deep rock mechanics and mining theory. J. China Coal Soc.44 (5), 1283–1305. doi:10.13225/j.cnki.jccs.2019.6038

CrossRef Full Text | Google Scholar

Xu, J. L. (2019). Strata control and scientific coal mining—a celebration of the academic thoughts and achievements of academician minggao qian. J. Min. Saf. Eng.36 (1), 1–6. doi:10.13545/j.cnki.jmse.2019.01.001

CrossRef Full Text | Google Scholar

Yan, S. H., Yin, X. W., Xu, H. J., Xu, G., Liu, Q. M., and Yu, L. (2011). Roof structure of short cantilever-articulated rock beam and calculation of supporting capacity in full-mechanized face with large mining height. J. China Coal Soc.36 (11), 1816–1820. doi:10.13225/j.cnki.jccs.2011.11.022

CrossRef Full Text | Google Scholar

Zhang, C. L., Guo, L., and Zhang, M. P. (2020). Measurements of working resistance and adaptability analysis of shield in fully mechanized coal face with large mining height and medium buried depth. Coal Mine Mach.41 (6), 68–71. doi:10.13436/j.mkjx.202006022

CrossRef Full Text | Google Scholar

Zhang, H., Tu, M., Cheng, H., and Tang, Y. (2020). Breaking mechanism and control technology of sandstone straight roof in thin bedrock stope. Int. J. Min. Sci. Technol.30 (2), 259–263. doi:10.1016/j.ijmst.2018.10.006

CrossRef Full Text | Google Scholar

Zhang, S. J., Yang, S. L., Wang, Z. H., Lv, H. Y., and Xie, F. (2018). Study on pre-splitting blasting technology of thick and hard roof in fully mechanized face. Coal Eng.50 (2), 10–15.

Google Scholar

Zhang, Z. Y., Zhang, N., Shimada, H., Sasaoka, T., and Wahyudi, S. (2017). Optimization of hard roof structure over retained goaf-side gateroad by pre-split blasting technology. Int. J. Rock Mech. Min. Sci.100, 330–337. doi:10.1016/j.ijrmms.2017.04.007

CrossRef Full Text | Google Scholar

Zhao, H. Z. (1988). Working resistance of hydraulic support. Xuzhou: China University of Mining and Technology Press.

Google Scholar

Zhao, Z., Sun, W., Zhang, M., Gao, X., and Chen, S. (2020). Fracture mechanical behavior of cracked cantilever roof with large cutting height mining. Shock Vib.2020, 1–10. doi:10.1155/2020/1641382

CrossRef Full Text | Google Scholar

Zhu, Z. J., Wu, Y. L., and Han, J. (2022). A prediction method of coal burst based on analytic hierarchy process and fuzzy comprehensive evaluation. Front. Earth Sci. (Lausanne).9,834958. doi:10.3389/feart.2021.834958

CrossRef Full Text | Google Scholar