Wind Gusts Associated with Tornado-Scale Vortices in the Tropical Cyclone Boundary Layer: A Numerical Simulation

Introduction

The landing of tropical cyclones (TCs) are often accompanied by strong gusts and heavy rainfall, and can even cause mudslides, landslides, and many other disasters, posing a great threat to the lives and property near the coastlines (Pielke and Landsea, 1998; Pielke et al., 2008; Zhang et al., 2009; Liang et al., 2021; Wang et al., 2021; Zhao et al., 2022). Significant variability in damage patterns has been found after the passing of intense TCs, which indicates that the damage caused by TC is not only related to the sustained strong wind but also the localized strong gusts (Wakimoto and Black, 1994; Wurman and Kosiba, 2018). Since the mechanisms on the generation and evolution of strong wind gusts are complicated and have not been fully understood, wind gust forecast is a major challenge for disaster prevention and mitigation in coastlines affected by TCs (Krayer and Marshall, 1992; Black et al., 1999; Harper et al., 2010; Wurman and Kosiba, 2018).

The peak 3-s average wind within a period is typically defined as a “gust”. The “gust factor” is a conversion between an estimate of the mean wind speed and the expected highest gust wind speed of a given duration (e.g. 10-min, 5-min, 2-min, 1-min, etc.). The gust factor is an important parameter to describe the characteristics of turbulence (Harper et al., 2010). Wind loads that determine the capability of wind resistances require consideration of gusts and gust factors (American Society of Civil Engineers, 2013). The characteristics of gust and gust factors with the impacts of TCs have been studied in observational studies (Paulsen and Schroeder, 2005; Vickery and Skerlj, 2005; Schroeder et al., 2009). It is found that the gust factor tends to decrease as the mean wind speed increases (Vickery and Skerlj, 2005; Schroeder et al., 2009). The influence of topography on the gust factor during TC landfall has been well studied and the gust tends to be higher due to the effect of topography (Paulsen and Schroeder, 2005; Vickery and Skerlj, 2005; Schroeder et al., 2009). In addition, extreme gusts and gust factors within the TC boundary layer (TCBL) are found in many observational studies (Black et al., 1999; Haper et al., 2010; Wurman and Kosiba 2018). A station at Barrow Island in Western Australia recorded the time series of winds when Hurricane Olivia (1996) passed through the island (Black et al., 1999). The results show that the 3-s average gusts were up to 113 m s⁻¹ at 10 m height, with a 5-min gust factor of 2.75 (Black et al., 1999). Extreme gusts were also recorded at the station during the landfall of Hurricane Orson (1989), with extreme gusts reaching more than twice the value of the average wind speed (Harper et al., 2010). They believed that the extreme gusts and gust factors near the eyewall are caused by the small-scale vortices that are associated with extreme downdrafts (Powell et al., 1991; Powell et al., 1996; Black et al., 1999; Harper et al., 2010). Recently, Wurman and Kosiba (2018) found that the surface wind oscillations near the eyewall of Hurricance Harvey (2017) can reach about 30 m s⁻¹ compared with the sustained wind speed based on the winds recorded in the weather station. In addition, the 1-min gust factor is larger than 1.5, which is much larger than that (1.11) suggested by the WMO (World Meteorological Organization, Harper et al., 2010). Wurman and Kosiba (2018) analyzed the fine-scale structures on the radar imagery and they believed that the extreme gusts and gust factors can be caused by tornado-scale vortices (TSVs). The TSV is one of the typical fine-scale structures in the TCBL observed by aircraft observations, dropsondes, and doppler radars (Aberson et al., 2006; Marks et al., 2008; Stern et al., 2016; Wurman and Kosiba, 2018). TSVs are usually located inside the TC eyewall and are associated with extreme updrafts and downdrafts, and strong vertical vorticity.

Our understanding of the TCBL process in TC intensity change and structure evolution has been improved with the advances in observational technology, computational power, and numerical models (Willoughby, 1990; Smith, 2003; Bell and Montgomery, 2008; Smith and Montgomery, 2010; Zhang and Montgomery, 2012; Ma and Fei, 2022; Li et al., 2022). The fine-scale (less than 1000 m) features have been explicitly simulated over the past decade (Zhu, 2008; Rotunno et al., 2009; Zhu et al., 2013; Green and Zhang, 2015; Qin and Zhang, 2018; Stern and Bryan, 2018; Wu et al., 2018; Wu et al., 2019; Zheng et al., 2020; Feng et al., 2021; Liu et al., 2021; Qin et al., 2021; Xu et al., 2021; Xu and Wang, 2021). The TSVs occurring inside the TC eyewall can be resolved with the grid spacing of 37 m in the Weather Research and Forecast (WRF) model with the LES (Wu et al., 2018; Wu et al., 2019; Feng et al., 2021; Liu et al., 2021). The three-dimensional structures of TSVs can also be represented in their numerical studies. The simulated TSVs often contain strong updraft/downdraft couplets and may cause strong localized surface winds. However, the characteristics of TSV-induced gusts and gust factors are still unclear since the model output is stored at one-hour intervals in previous numerical experiments (Wu et al., 2018; Wu et al., 2019; Feng et al., 2021; Liu et al., 2021). In this study, a numerical experiment with a horizontal grid spacing of 37 m is conducted using the WRF-LES framework. It should be noted that surface winds during a 22-min period are stored at 1-s intervals to calculate the surface gusts and gust factors. The objective of this study is to analyze the characteristics of surface gusts and gust factors in the TC inner core and examine wind gusts and gust factors associated with TSVs in the TCBL.

Numerical Experiment and Methods

Following, Wu and Chen, (2018), Wu and Chen, (2019), a semi-idealized numerical experiment is conducted with the WRF-LES framework. Here we briefly describe the settings of the numerical experiment. In this experiment, a TC evolved in a realistic low-frequency large-scale background in the western North Pacific and on an open ocean with a spatially uniform sea surface temperature (29°C). Seven domains are used in this experiment, including six interactive nesting domains with the horizontal grid spacing of 9 km, 3 km, 1 km, 333 m, 111 m, and 37 m. Five domains move with the TC center. The innermost domain covers the TC inner core with an area of 90 × 90 km². The model consists of 75 vertical levels (12 levels below 1 km) with a top of 50 hPa. The vertical grid spacing is about 70–100 m below 1 km and increases to ∼400 m at 4 km. The model output is regularly stored at 1-h intervals. To investigate the characteristics of the surface gusts, surface winds at 10 m height during a 22-min period from the 30th hour of the simulation are stored at 1-s intervals, while the three-dimensional winds are outputted at 3-s intervals to identify the TSVs.

The TC center is determined with the algorithm from previous studies (Wu et al., 2006; Yang et al., 2020), in which the TC center is located until the maximum azimuthally-averaged tangential wind is found. The identification algorithm of TSVs in the numerical experiment is based on the specific threshold of vertical velocity and vorticity similar to that used in the previous studies (Wu et al., 2018; Wu et al., 2019; Feng et al., 2021; Liu et al., 2021). Since the innermost domain moves with the TC, the variables are all projected into a fixed reference framework (overlapped domains within the 22-min) during the 22-min period.

Results

TC Intensity in Terms of Surface Winds

Due to the β effect and the large-scale environmental steering flow (Holland, 1983; Wang and Holland, 1996), the TC moves north-northwestward during the 22-min period. The zonal component of moving speed is ∼ −1 m s⁻¹ and the meridional component of moving speed is ∼4 m s⁻¹.

Figure 1 shows the instantaneous, 1-min, 5-min, and 10-min mean wind fields at 10-m height at 9min 30s during the 22-min period. Significant variability in the wind field at 10-m height can be seen in Figure 1A. The variabilities in the surface winds are caused by the fine-scale coherent structures, which have been studied in many observational and numerical studies (Wurman and Winslow, 1998; Morrison et al., 2005; Marks et al., 2008; Rotunno et al., 2009; Lorsolo et al., 2010; Foster, 2013; Gao and Ginis, 2014; Green and Zhang, 2015; Wu et al., 2018; Wurman and Kosiba, 2018; Wu et al., 2019; Liu et al., 2021). 1-min mean wind fields at 10-m height are shown in Figure 1B. We can see the variabilities are greatly smoothed in the 1-min mean wind field, although there are still some isolated regions with large values on the northern side of the TC eyewall. The 5-min and 10-min mean wind fields are further shown in Figure 1C and Figure 1D, respectively. It seems the variabilities have been fully removed in the 5-min and 10-min wind fields and there is no significant difference between them. The maximum wind speed in terms of instantaneous, 1-min, 5-min, and 10-min at this time is 73.7, 54.8, 51.5, and 51.4 m s⁻¹, respectively.

FIGURE 1

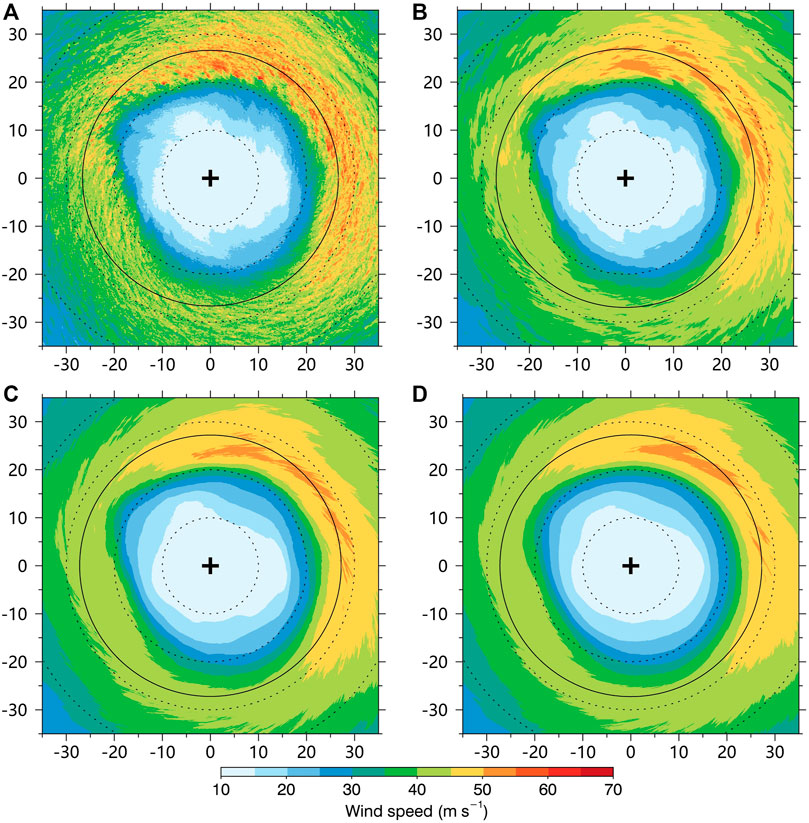
FIGURE 1. (A) Instantaneous 10-m wind speed (m s⁻¹) at 9 min 30 s during the 22-min period. (B) 1-min mean 10-m wind speed (m s⁻¹) at 9min 30 s. (C) 5-min mean 10-m wind speed (m s⁻¹) at 9 min 30 s. (D) 5-min mean 10-m wind speed (m s⁻¹) at 9 min 30 s. The small cross in the figure is the TC center, the solid circle indicates the RMW. The vertical and horizontal axes indicate the relative distances (kilometers) from the TC center.

The TC intensities in terms of the instantaneous, 3-s mean, 1-min mean, 5-min mean, 10-min mean, and azimuthal-mean maximum wind speed are examined at the 10-m height (Figure 2). TC intensities in terms of the maximum instantaneous and 3-s mean wind speed are significantly larger than those of time-averaged intensities and azimuthal-mean intensity, which may be attributed to the coherent structures in the TCBL (Liu et al., 2021). In addition, the TC intensity in terms of azimuthal mean winds is only about 45 m s⁻¹, which is much smaller than the time-averaged intensities of the TC. This is mainly due to the significant asymmetric structure with the strong convection located on the northern side of the simulated TC (Wu et al., 2018; Wu et al., 2019). TC intensities in terms of 5-min and 10-min are very close to each other, ranging from 51 to 54 m s⁻¹. Although the 1-min mean intensity is slightly larger, the deviations from those of 5-min and 10-min during 22-min are less than 5 m s⁻¹. Harper et al. (2010) gave the ratio of intensity based on 10-min mean wind speed to 1-min mean wind speed as 0.93 from the observations. We calculate the ratio of 10-min intensity to 1-min intensity in the 22 min period, which is also exactly 0.93 and is in good agreement with observational studies. The mean intensity in terms of the maximum instantaneous and 3-s mean wind speed is 71 m s⁻¹ and 68 m s⁻¹. The 3-s intensity is about 20% larger than the 1-min intensity and 30% larger than the 5-min intensity, indicating the extreme gust factors exist in the TC inner core at the surface.

FIGURE 2

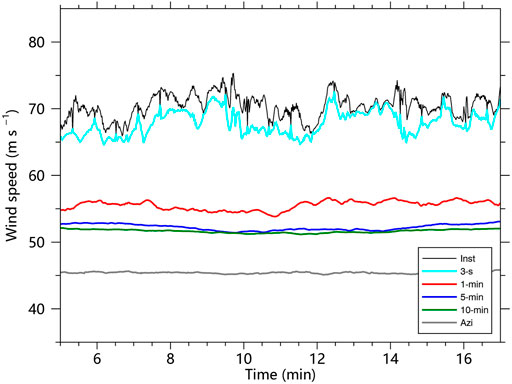
FIGURE 2. TC intensities (m s⁻¹) in terms of instantaneous (black), 3-s mean (cyan), 1-min mean (red), 5-min mean (blue), 10-min mean (green), and azimuthally-averaged maximum wind speed at 10-m height.

Characteristics of the Surface Wind Gust Factors

The mean and maximum 1-min gust factors at 10-m height during the 22-min period are shown in Figures 3A,B. It should be noted that all gust factors are firstly calculated in the fixed coordinate, then mean and maximum factors are calculated at every single grid in the TC inner core during the 22-min period. Additionally, the gust factors are calculated when the mean wind speed is no less than 17 m s⁻¹. The surface wind speed larger than 17 m s⁻¹ is usually called gale-force wind and the radius of gale-force wind has been widely used to define TC size due to its importance in determining TC potential impacts (Knaff et al., 2007; Wu et al., 2015). The gusts and gust factors corresponding to the mean gale-force wind are closely associated with the TC damages, while the gust factors corresponding to small mean winds are largely random and not very representative. So gust factors corresponding to mean winds less than 17 m s⁻¹ are not included in our study. The horizontal distributions of the mean and maximum gust factors are asymmetric as shown in Figure 3, with large values in the northern part of the TC eyewall. From Figure 3A, we can see that the mean 1-min gust factor is 1.1 at a height of 10 m near the TC eyewall, but it can reach 1.15 on the northern side of the TC eyewall. We further calculate the mean and maximum 5-min and 10-min gust factors in the TC inner core and find that the gust factors increase as the time scale increases. The mean 1-min, 5-min, and 10-min gust factors in the TC inner core during the 22-min period are 1.10, 1.17, and 1.21, respectively. Harper et al. (2010) indicated that 1-min mean gust factor recommended by WMO is 1.11 and the 10-min gust factor is 1.23 for the TC at 10-m height over the ocean. Our experiment not only simulated the fine-scale structures in the TCBL (Wu et al., 2018, 2019; Liu et al., 2021), but also the mean values of the gust factors at 10 m height are generally consistent with the observations.

FIGURE 3

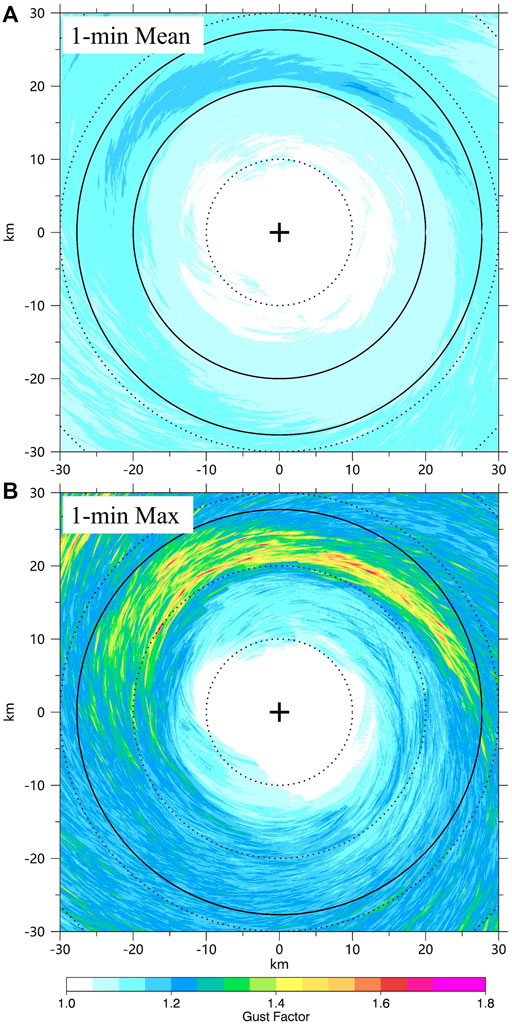
FIGURE 3. Horizontal distributions of the mean 1-min gust factors (A) and maximum 1-min gust factors (B) during the 22-min period. The small cross in the figure is the TC center at the 11th minute, the solid circle indicates the RMW. The vertical and horizontal axes indicate the relative distances (kilometers) from the TC center.

Although extreme gusts and gust factors exist in the TCBL, these extreme values only account for a very small proportion (Black et al., 1999; Harper et al., 2010). The fine-scale structures associated with the extreme gusts and gusts factors have not been detailly discussed (Worsnop et al., 2017; Kapoor et al., 2020). Our simulation indicates that the extreme gust factors prevail inside the TC eyewall. The mean 1-min and 10-min gust factors are only 1.10 and 1.21, but the maximum gust factors can reach 1.79 and 2.23. Furthermore, the mean standard deviation of the 1-min gust factors for the whole field is 0.035, indicating that these extreme gust factors only account for a small percentage of the surface gusts in the TC inner core. The extreme gust factors are checked through the survival functions of the 1-min gust factors and 5-min gust factors averaged in a 60x60 km box centered on the TC center over the 22-min period. The survival function is a function that gives the probability that gust factors will survive past a certain value. The top 1% of the 1-min gust factors and 5-min gust factors are ∼1.25 and 1.4, respectively. Based on the simplified statistical approach, the 1-min gust factors larger than 1.25 and 5-min gust factors larger than 1.4 can be treated as extreme gust factors in our study. According to the extreme gust factors recorded in Barrow Island in Western Australia during the passage of Hurricane Olivia (1996), Black et al. (1999) found that it was only 2% of the gusts reached a 5-min gust factor of 1.6, which caused the extreme gusts and damage. Based on our numerical results, the extreme gust and gust factors are smaller than those in their studies. This might be due to the weaker TC intensity in our simulations or the extreme gusts and gust factors are sensitive to the TC-scale structures since the extreme gust factors tend to be prevalent in the inner edge of the enhanced eyewall convection. Figure 4B shows the horizontal distribution of the frequency of gust factors that is not less than 1.25 during the 22-min period. It should be noted that most of the points (65%) in the domain (Figure 4B) do not have gust factors large than 1.25 during the 22-min period. However, the extreme gust factors tend to occur in the northern side of the TC eyewall with a maximum frequency of 0.4.

FIGURE 4

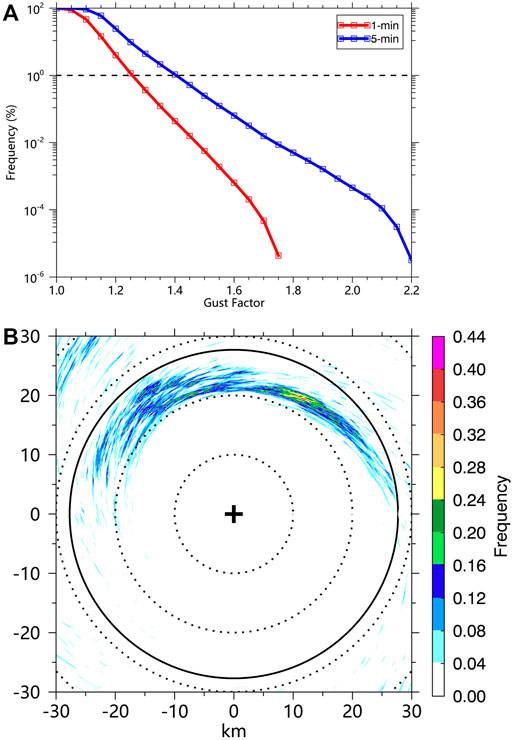
FIGURE 4. (A) Empirical survival function of 1-min gust factors (red) and 5-min gust factors (blue) averaged in a 60 × 60 km box centered on the TC center over the 22-min period. (B) Horizontal distributions of frequencies of 1-min gust factors at every point that are not less than 1.25 during the 22-min period.

Relationships Between TSVs and Surface Wind Gusts

Previous observational and numerical studies show that the TSVs are one of the fine-scale coherent structures in the TCBL which may cause strong localized winds (Wurman and Winslow, 1998; Wu et al., 2018; Wurman and Kosiba 2018; Wu et al., 2019; Liu et al., 2021). Following Wu et al. (2018), the tornado-scale vortex is defined as a small-scale cyclonic circulation with the maximum updraft not less than 15 m s⁻¹ or 20 m s⁻¹ and maximum relative vorticity not less than 0.2 s⁻¹ below the altitude of 3 km. The grid points that satisfy the thresholds of vertical motion (15 m s⁻¹ or 20 m s⁻¹) and relative vorticity (0.2 s⁻¹) belong to the same vortex if they are within a distance of 1 km in the horizontal and vertical direction. There are 3618 (vertical velocity larger than 15 m s⁻¹) and 493 (vertical velocity larger than 20 m s⁻¹) TSVs found in our experiment during the 22-min period. The locations of TSVs with the horizontal distribution of the maximum 1-min gust factors are shown in Figure 5A. The extreme gust factors (the maximum 1-min gust factors are generally larger than 1.25) usually occur along the tracks of identified TSVs. There seem to be some connections between TSVs and the extreme gust factors.

FIGURE 5

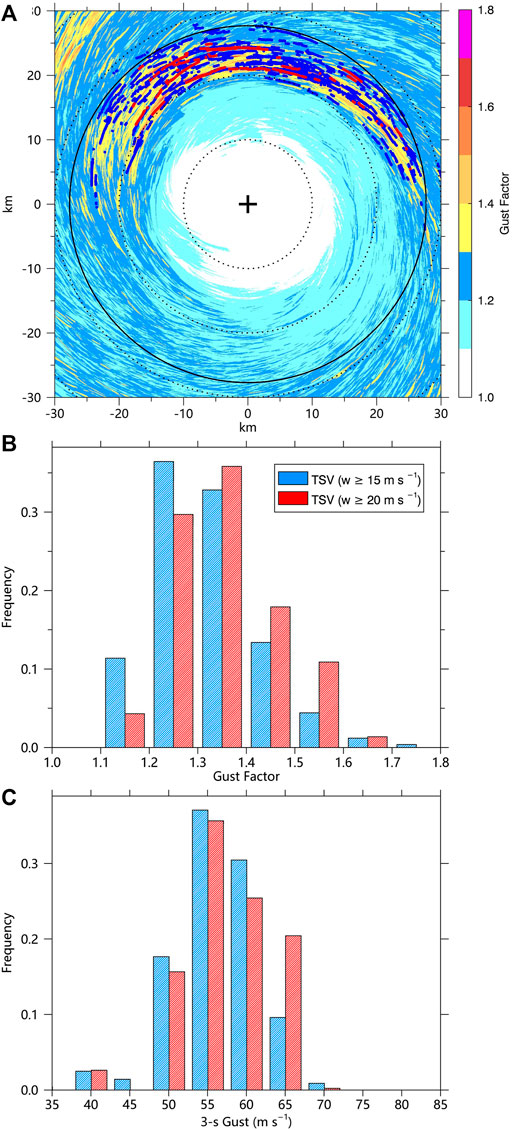
FIGURE 5. (A) Distributions of the maximum 1-min gust factors and TSV locations during the 22-min period. The small cross in the figure is the TC center, the solid circle indicates the RMW. The vertical and horizontal axes indicate the relative distances (kilometers) from the TC center. (B) Frequency of the maximum 1-min gust factors associated with TSVs. (C) Frequency of the maximum 3-s gusts associated with TSVs. The red (blue) dots indicate TSVs with a vertical velocity larger than 20 (15) m s⁻¹. The maximum 3-s gust associated with a TSV is the maximum 3-s gust within a 1-km radius around the TSV center. The maximum 1-min gust factor associated with a TSV is the maximum 1-min gust factor at the location where the maximum 3-s gust occurs.

To further analyze the relations between TSVs and the near-surface extreme gust factors, we calculate the maximum 3-s gusts within a 1-km radius around the TSV centers and the associated maximum 1-min gust factors. The frequency of gust factors and 3-s gusts associated with TSVs are shown in Figures 5B,C. According to the statistical results, the mean maximum 1-min gust factor of TSVs with vertical velocity larger than 20 (15) m s⁻¹ is 1.36 (1.32), and the mean maximum 3-s gust of TSVs with vertical velocity larger than 20 (15) m s⁻¹ is 59.7 (58.7) m s⁻¹. According to the previous analysis, the mean frequency of gust factors larger than 1.25 for the whole field is only 1% during the 22 min period, and such a small percentage of the gust factors can be treated as extreme gust factors. Based on our results, the percentage of maximum gust factors associated with the TSVs (vertical velocity larger than 15 m s⁻¹) larger than 1.25 is 73%, and 88% of maximum gust factors associated with TSVs (vertical velocity larger than 20 m s⁻¹) are larger than 1.25. From the statistical results, TSVs are significantly associated with extreme gust factors. The extreme 1-min gust factor can reach about 1.8. Figure 6 shows the scatter plot of the TSV tracks and associated 1-min gust factors during the 22-min. It can be seen that extreme gust factors caused by TSVs are mostly found in the inner edge of the TC eyewall. We carefully check the gust factors larger than 1.7 (10 cases) and find that they are all associated with typical TSV structures. We choose one of the TSVs in the red box in Figure 6 to show the detailed TSV structures and the associated time series of gusts and gust factors.

FIGURE 6

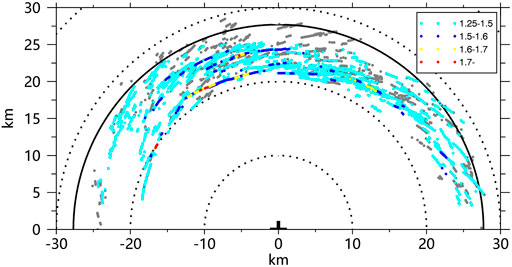
FIGURE 6. Distributions of TSV locations during the 22-min period. The cyan, blue, yellow, and red points represent the maximum 1-min gust factors with a range of 1.25–1.5, 1.5–1.6, 1.6–1.7, and 1.7–1.8, respectively. The small cross in the figure is the TC center, the solid circle indicates the RMW. The vertical and horizontal axes indicate the relative distances (kilometers) from the TC center.

The instantaneous and 1-min mean wind speed at 10-m height during the 22-min are shown in Figure 7A. The maximum instantaneous and 3-s gusts are 73 and 69 m s⁻¹, respectively, although the mean 1-min wind speed during the 22-min is only 39 m s⁻¹. We also present the time series of the 1-min gust factor in Figure 7B, which shows that it is the instantaneous wind of 73 m s⁻¹ associated with the TSV that causes the extreme gust factor at this location. The wind fluctuations can reach 30 m s⁻¹, which is similar to gusts associated with TSV found in observations (Wurman and Kosiba 2018). We further examine the structure of the TSV in Figure 8. It can be seen that the extreme gust (maximum instantaneous wind speed is ∼73 m/s) is associated with coupled strong updrafts and downdrafts, with maximum updraft (downdraft) up to ∼15 (10) m s⁻¹ at 200-m height. Figure 8B shows the perturbation wind field at 200-m height. The perturbation winds are obtained by subtracting an 8-km moving mean. We can see a small-scale horizontal circulation with a scale of ∼1 km in the perturbation wind field, accompanied by strong vertical vorticity up to 0.3 s⁻¹. This structure is consistent with the typical structure of TSVs found in observational and numerical studies (Marks et al., 2008; Wu et al., 2018, 2019; Wurman and Kosiba et al., 2018; Liu et al., 2021). The extreme gust and gust factor at this location is apparently related to a typical TSV.

FIGURE 7

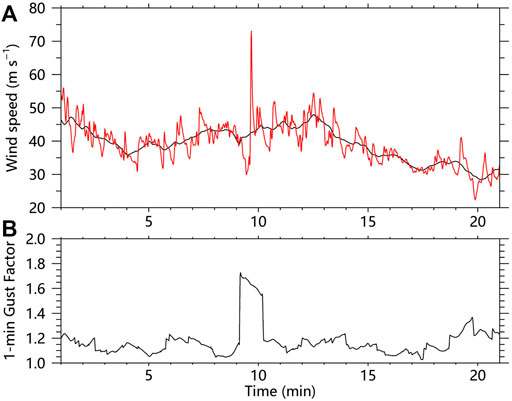
FIGURE 7. (A) Time sequence of the instantaneous wind speed (red) and 1-min mean wind speed (black). (B) Time sequence of the 1-min gust factor.

FIGURE 8

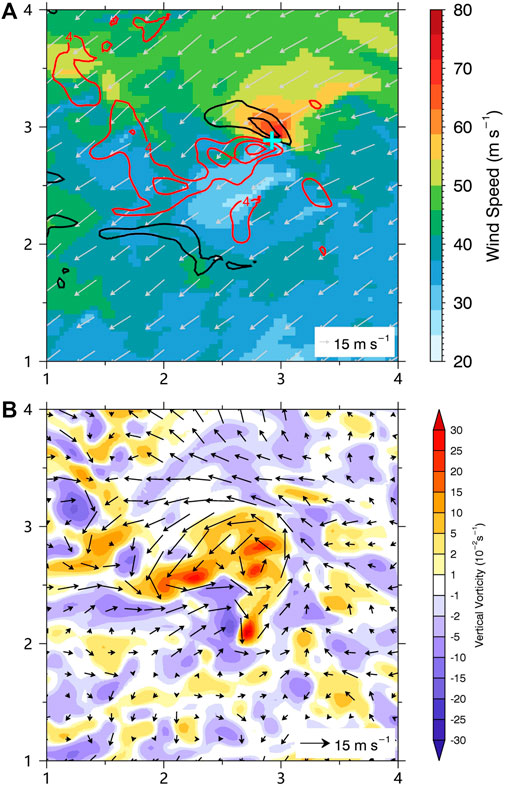
FIGURE 8. (A) 10-m wind speed (shading), 10-m wind vectors, and vertical motions (contour: 4 m s⁻¹) at 200-m height in the area shown in Figure 6. (B) the perturbated winds and vertical component of relative vorticity (shading) at 200-m height in the area shown in Figure 6. The red (black) contours denote the updrafts (downdrafts) in Figure 8A. The cyan cross in Figure 8A is the location of maximum wind speed at 10-m height. The vertical and horizontal axes are in kilometers.

Summary

Previous studies demonstrated that the strong surface gusts may pose a great threat to the lives and property near the coastlines during TC landfall (Black et al., 1999; Harper 2010; Wurman and Kosiba 2018). Recent observational studies suggest that the TC surface strong gusts may be related to the TSVs in the TCBL (Wurman and Kosiba 2018). In this study, a semi-idealized numerical simulation of TC that evolves in a realistic large-scale environment with the WRF-LES framework is conducted with the finest grid spacing of 37 m and time resolution of 1 s to investigate the characteristics of surface gusts and gust factors in the TC inner core and possible relations between the extreme gust factors and TSVs.

The mean 1-min and 10-min gust factors recommended by WMO are 1.11 and 1.23 for TCs at 10-m height (Harper et al., 2010). Based on the 22-min outputs from the numerical experiment, the mean 1-min and 10-min gust factors are 1.10 and 1.21, which are generally in agreement with those recommended by the WMO. Although the mean 1-min gust factor in the TC inner core is 1.1, the maximum gust factor can reach ∼1.8. However, extreme gust factors only account for a small percentage of the surface gusts in the TC inner core and the top 1% of 1-min and 5-min gust factors are 1.25 and 1.4. In addition, there is a strong asymmetry in the horizontal distribution of the mean and maximum gust factors in our experiment, for the extreme gust factors are prevalent in the northern side of the TC eyewall with strong convection. In addition, the TSVs are prevalent on the northern side inside the eyewall, where extreme gust factors tend to occur.

Further analysis shows that the percentage of maximum gust factors associated with the TSVs (vertical velocity larger than 15 m s⁻¹) larger than 1.25 is 73%, and 88% of maximum gust factors associated with TSVs (vertical velocity larger than 20 m s⁻¹) are larger than 1.25. In addition, the stronger the vertical velocity in the TSV, the larger the maximum gust factor. The mean maximum 1-min gust factor associated with a TSV is larger than 1.3, while the mean 1-min gust factor of the TC inner-core is only 1.1. Since the extreme gust factor (top 1% of the 1-min gust factors in the TC inner core) is 1.25, it indicates that most TSVs are associated with localized gusts and extreme gust factors, which can cause severe surface wind hazards, especially near the eyewall region. The surface gust factors associated with TSVs in tropical cyclone eyewall can reach about 1.8, which can cause severe surface wind hazards. Our results suggest that potential risk will increase in the regions where TSVs are prevalent because of the extreme gust factors. Further understanding of the mechanisms on the development and evolution of TSVs is of great significance for gust forecast and resilience against related hazards under the influence of TC.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LW designed research. QL conceptualized the analysis and wrote the manuscript. All authors were involved in helpful discussions and contributions to the manuscript.

Funding

This work was jointly supported by the National Natural Science Foundation of China (41905001, U2142203, 42075072, 42175007, 42192552, 41730961), the Postdoctoral Science Foundation of China (2019M661342), the National Key R&D Program of China (2021YFC3000901), and the Open Grants of the State Key Laboratory of Severe Weather (2022LASW-B14, 2021LASW-B11). The numerical simulation was carried out on the Shuguang Supercomputer, Nanjing, China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aberson, S. D., Montgomery, M. T., Bell, M., and Black, M. (2006). Hurricane Isabel (2003): New Insights into the Physics of Intense Storms. Part II: Extreme Localized Wind. Bull. Amer. Meteor. Soc. 87, 1349–1354. doi:10.1175/BAMS-87-10-1349

CrossRef Full Text | Google Scholar

American Society of Civil Engineers (2013). Minimum Design Loads for Buildings and Other Structures. ASCE/SEI 7-10. American Society of Civil Engineers, 593. doi:10.1061/9780784408094

CrossRef Full Text | Google Scholar

Bell, M. M., and Montgomery, M. T. (2008). Observed Structure, Evolution, and Potential Intensity of Category 5 Hurricane Isabel (2003) from 12-14 September. Mon. Wea. Rev. 136, 2023–2046. doi:10.1175/2007MWR1858.1

CrossRef Full Text | Google Scholar

Black, P. G., Buchan, S. J., and Cohen, R. L. (1999). “The Tropical Cyclone Eyewall Mesovortex: a Physical Mechanism Explaining Extreme Peak Gust Occurrence in TC Olivia, 4 April 1996 on Barrow Island, Australia,” in Paper presented at the Offshore Technology Conference, Houston, Texas, May 1999. doi:10.4043/10792-MS

CrossRef Full Text | Google Scholar

Feng, Y., Wu, L., Liu, Q., and Zhou, W. (2021). Negative Pressure Perturbations Associated with Tornado‐Scale Vortices in the Tropical Cyclone Boundary Layer. Geophys Res. Lett. 48, e2020GL091339. doi:10.1029/2020GL091339

CrossRef Full Text | Google Scholar

Foster, R. (2013). Signature of Large Aspect Ratio Roll Vortices in Synthetic Aperture Radar Images of Tropical Cyclones. oceanog 26, 58–67. doi:10.5670/oceanog.2013.31

CrossRef Full Text | Google Scholar

Gao, K., and Ginis, I. (2014). On the Generation of Roll Vortices Due to the Inflection Point Instability of the Hurricane Boundary Layer Flow. J. Atmos. Sci. 71, 4292–4307. doi:10.1175/JAS-D-13-0362.1

CrossRef Full Text | Google Scholar

Green, B. W., and Zhang, F. (2015). Numerical Simulations of Hurricane Katrina (2005) in the Turbulent Gray Zone. J. Adv. Model. Earth Syst. 7, 142–161. doi:10.1002/2014MS000399

CrossRef Full Text | Google Scholar

Harper, B. A., Kepert, J. D., and Ginger, J. D. (2010). Guidelines for Converting between Various Wind Averaging Periods in Tropical Cyclone Conditions. World Meteorol. Organ. WMO/TD 1555, 54.

Google Scholar

Holland, G. J. (1983). Tropical Cyclone Motion: Environmental Interaction Plus a Beta Effect. J. Atmos. Sci. 40, 328–342. doi:10.1175/1520-0469(1983)040<0328:TCMEIP>2.0.CO

CrossRef Full Text | Google Scholar

Kapoor, A., Ouakka, S., Arwade, S. R., Lundquist, J. K., Lackner, M. A., Myers, A. T., et al. (2020). Hurricane Eyewall Winds and Structural Response of Wind Turbines. Wind Energy Sci. 5, 89–104. doi:10.5194/wes-2019-1410.5194/wes-5-89-2020

CrossRef Full Text | Google Scholar

Knaff, J. A., Sampson, C. R., DeMaria, M., Marchok, T. P., Gross, J. M., and McAdie, C. J. (2007). Statistical Tropical Cyclone Wind Radii Prediction Using Climatology and Persistence. Wea. Forecast. 22, 781–791. doi:10.1175/WAF1026.1

CrossRef Full Text | Google Scholar

Krayer, W. R., and Marshall, R. D. (1992). Gust Factors Applied to Hurricane Winds. Bull. Amer. Meteor. Soc. 73, 613–618. doi:10.1175/1520-0477(1992)073<0613:GFATHW>2.0.CO;2

CrossRef Full Text | Google Scholar

Li, X., Cheng, X., Fei, J., Huang, X., and Ding, J. (2022). The Modulation Effect of Sea Surface Cooling on the Eyewall Replacement Cycle in Typhoon Trami (2018). Mon. Wea. Rev. doi:10.1175/MWR-D-21-0177.1

CrossRef Full Text | Google Scholar

Liang, Z., Ding, J., Fei, J., Cheng, X., and Huang, X. (2021). Direct/indirect Effects of Aerosols and Their Separate Contributions to Typhoon Lupit (2009): Eyewall versus Peripheral Rainbands. Sci. China Earth Sci. 64, 2113–2128. doi:10.1007/s11430-020-9816-7

CrossRef Full Text | Google Scholar

Liu, Q., Wu, L., Qin, N., and Li, Y. (2021). Storm‐Scale and Fine‐Scale Boundary Layer Structures of Tropical Cyclones Simulated with the WRF‐LES Framework. JGR Atmos. 126, e2021JD035511. doi:10.1029/2021JD035511

CrossRef Full Text | Google Scholar

Lorsolo, S., Zhang, J. A., Marks, F., and Gamache, J. (2010). Estimation and Mapping of Hurricane Turbulent Energy Using Airborne Doppler Measurements. Mon. Weather Rev. 138, 3656–3670. doi:10.1175/2010MWR3183.1

CrossRef Full Text | Google Scholar

Ma, Z., and Fei, J. (2022). A Comparison between Moist and Dry Tropical Cyclones: The Low Effectiveness of Surface Sensible Heat Flux in Storm Intensification. J. Atmos. Sci. 79, 31–49. doi:10.1175/JAS-D-21-0014.1

CrossRef Full Text | Google Scholar

Marks, F. D., Black, P. G., Montgomery, M. T., and Burpee, R. W. (2008). Structure of the Eye and Eyewall of Hurricane Hugo (1989). Mon. Wea. Rev. 136, 1237–1259. doi:10.1175/2007MWR2073.1

CrossRef Full Text | Google Scholar

Morrison, I., Businger, S., Marks, F., Dodge, P., and Businger, J. A. (2005). An Observational Case for the Prevalence of Roll Vortices in the Hurricane Boundary Layer*. J. Atmos. Sci. 62, 2662–2673. doi:10.1175/JAS3508.1

CrossRef Full Text | Google Scholar

Paulsen, B. M., and Schroeder, J. L. (2005). An Examination of Tropical and Extratropical Gust Factors and the Associated Wind Speed Histograms. J. Appl. Meteor. 44, 270–280. doi:10.1175/JAM2199.1

CrossRef Full Text | Google Scholar

Pielke, R. A., Gratz, J., Landsea, C. W., Collins, D., Saunders, M. A., and Musulin, R. (2008). Normalized Hurricane Damage in the United States: 1900-2005. Nat. Hazards Rev. 9, 29–42. doi:10.1061/(ASCE)1527-6988

CrossRef Full Text | Google Scholar

Pielke, R. A., and Landsea, C. W. (1998). Normalized Hurricane Damages in the United States: 1925-95. Wea. Forecast. 13, 621–631. doi:10.1175/1520-0434(1998)013<0621:NHDITU>2.0.CO;2

CrossRef Full Text | Google Scholar

Powell, M. D., Dodge, P. P., and Black, M. L. (1991). The Landfall of Hurricane Hugo in the Carolinas: Surface Wind Distribution. Wea. Forecast. 6, 379–399. doi:10.1175/1520-0434(1991)006<0379:TLOHHI>2.0.CO;2

CrossRef Full Text | Google Scholar

Powell, M. D., Houston, S. H., and Reinhold, T. A. (1996). Hurricane Andrew's Landfall in South Florida. Part I: Standardizing Measurements for Documentation of Surface Wind Fields. Wea. Forecast. 11, 304–328. doi:10.1175/1520-0434(1996)011<0304:HALISF>2.0.CO;2

CrossRef Full Text | Google Scholar

Qin, N., Wu, L., and Liu, Q. (2021). Evolution of the Moat Associated with the Secondary Eyewall Formation in a Simulated Tropical Cyclone. J. Atmos. Sci. 78, 4021–4035. doi:10.1175/JAS-D-20-0375.1

CrossRef Full Text | Google Scholar

Qin, N., and Zhang, D.-L. (2018). On the Extraordinary Intensification of Hurricane Patricia (2015). Part I: Numerical Experiments. Weather Forecast. 33, 1205–1224. doi:10.1175/WAF-D-18-0045.1

CrossRef Full Text | Google Scholar

Rotunno, R., Chen, Y., Wang, W., Davis, C., Dudhia, J., and Holland, G. J. (2009). Large-eddy Simulation of an Idealized Tropical Cyclone. Bull. Amer. Meteor. Soc. 90, 1783–1788. doi:10.1175/2009BAMS2884.1

CrossRef Full Text | Google Scholar

Schroeder, J. L., Edwards, B. P., and Giammanco, I. M. (2009). Observed Tropical Cyclone Wind Flow Characteristics. Wind Struct. Int. J. 12, 349–381. doi:10.12989/was.2009.12.4.349

CrossRef Full Text | Google Scholar

Smith, R. K. (2003). A Simple Model of the Hurricane Boundary Layer. Q.J.R. Meteorol. Soc. 129, 1007–1027. doi:10.1256/qj.01.197

CrossRef Full Text | Google Scholar

Smith, R. K., and Montgomery, M. T. (2010). Hurricane Boundary-Layer Theory. Q.J.R. Meteorol. Soc. 136, 1665–1670. doi:10.1002/qj.679

CrossRef Full Text | Google Scholar

Stern, D. P., Bryan, G. H., and Aberson, S. D. (2016). Extreme Low-Level Updrafts and Wind Speeds Measured by Dropsondes in Tropical Cyclones. Mon. Wea. Rev. 144, 2177–2204. doi:10.1175/MWR-D-15-0313.1

CrossRef Full Text | Google Scholar

Stern, D. P., and Bryan, G. H. (2018). Using Simulated Dropsondes to Understand Extreme Updrafts and Wind Speeds in Tropical Cyclones. Mon. Weather Rev. 146, 3901–3925. doi:10.1175/MWR-D-18-0041.1

CrossRef Full Text | Google Scholar

Vickery, P. J., and Skerlj, P. F. (2005). Hurricane Gust Factors Revisited. J. Struct. Eng. 131, 825–832. doi:10.1061/(asce)0733-9445

CrossRef Full Text | Google Scholar

Wakimoto, R. M., and Black, P. G. (1994). Damage Survey of Hurricane Andrew and its Relationship to the Eyewall. Bull. Amer. Meteor. Soc. 75, 189–200. doi:10.1175/1520-0477(1994)075<0189:DSOHAA>2.0.CO;2

CrossRef Full Text | Google Scholar

Wang, C., Wu, K., Wu, L., Zhao, H., and Cao, J. (2021). What Caused the Unprecedented Absence of Western North Pacific Tropical Cyclones in July 2020? Geophys. Res. Lett. 48, 1–9. doi:10.1029/2020GL092282

CrossRef Full Text | Google Scholar

Wang, Y., and Holland, G. J. (1996). The Beta Drift of Baroclinic Vortices. Part II: Diabatic Vortices. J. Atmos. Sci. 53, 3737–3756. doi:10.1175/1520-0469(1996)053<0411:TBDOBV>2.0.CO;2

CrossRef Full Text | Google Scholar

Willoughby, H. E. (1990). Gradient Balance in Tropical Cyclones. J. Atmos. Sci. 47, 265–274. doi:10.1175/1520-0469(1990)047<0265:GBITC>2.0.CO;2

CrossRef Full Text | Google Scholar

Worsnop, R. P., Lundquist, J. K., Bryan, G. H., Damiani, R., and Musial, W. (2017). Gusts and Shear within Hurricane Eyewalls Can Exceed Offshore Wind Turbine Design Standards. Geophys. Res. Lett. 44, 6413–6420. doi:10.1002/2017GL073537

CrossRef Full Text | Google Scholar

Wu, L., Braun, S. A., Halverson, J., and Heymsfield, G. (2006). A Numerical Study of Hurricane Erin (2001). Part I: Model Verification and Storm Evolution. J. Atmos. Sci. 63, 65–86. doi:10.1175/JAS3597.1

CrossRef Full Text | Google Scholar

Wu, L., and Chen, X. (2016). Revisiting the Steering Principal of Tropical Cyclone Motion in a Numerical Experiment. Atmos. Chem. Phys. 16, 14925–14936. doi:10.5194/acp-2016-369

CrossRef Full Text | Google Scholar

Wu, L., Liu, Q., and Li, Y. (2018). Prevalence of Tornado-Scale Vortices in the Tropical Cyclone Eyewall. Proc. Natl. Acad. Sci. U.S.A. 115, 8307–8310. doi:10.1073/pnas.1807217115

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, L., Liu, Q., and Li, Y. (2019). Tornado-scale Vortices in the Tropical Cyclone Boundary Layer: Numerical Simulation with the WRF-LES Framework. Atmos. Chem. Phys. 19, 2477–2487. doi:10.5194/acp-2018-787

CrossRef Full Text | Google Scholar

Wurman, J., and Kosiba, K. (2018). The Role of Small-Scale Vortices in Enhancing Surface Winds and Damage in Hurricane Harvey (2017). Mon. Wea. Rev. 146, 713–722. doi:10.1175/MWR-D-17-0327.1

CrossRef Full Text | Google Scholar

Wurman, J., and Winslow, J. (1998). Intense Sub-kilometer-scale Boundary Layer Rolls Observed in Hurricane Fran. Science 280, 555–557. doi:10.1126/science.280.5363.555

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, H., Wang, H., and Duan, Y. (2021). An Investigation of the Impact of Different Turbulence Schemes on the Tropical Cyclone Boundary Layer at Turbulent Gray‐Zone Resolution. JGR Atmos. 126, e2021JD035327. doi:10.1029/2021JD035327

CrossRef Full Text | Google Scholar

Xu, H., and Wang, Y. (2021). Sensitivity of Fine-Scale Structure in Tropical Cyclone Boundary Layer to Model Horizontal Resolution at Sub-kilometer Grid Spacing. Front. Earth Sci. 9, 707274. doi:10.3389/feart.2021.707274

CrossRef Full Text | Google Scholar

Yang, H., Wu, L., and Xie, T. (2020). Comparisons of Four Methods for Tropical Cyclone Center Detection in a High-Resolution Simulation. J. Meteorological Soc. Jpn. 98, 379–393. doi:10.2151/jmsj.2020-020

CrossRef Full Text | Google Scholar

Zhang, J. A., and Montgomery, M. T. (2012). Observational Estimates of the Horizontal Eddy Diffusivity and Mixing Length in the Low-Level Region of Intense Hurricanes. J. Atmos. Sci. 69, 1306–1316. doi:10.1175/JAS-D-11-0180.1

CrossRef Full Text | Google Scholar

Zhang, Q., Wu, L., and Liu, Q. (2009). Tropical Cyclone Damages in China 1983-2006. Bull. Amer. Meteor. Soc. 90, 489–496. doi:10.1175/2008BAMS2631.1

CrossRef Full Text | Google Scholar

Zhao, H., Zhao, K., Klotzbach, P. J., Wu, L., and Wang, C. (2022). Interannual and Interdecadal Drivers of Meridional Migration of Western North Pacific Tropical Cyclone Lifetime Maximum Intensity Location. J. Clim. 35, 2709–2722. doi:10.1175/JCLI-D-21-0797.1

CrossRef Full Text | Google Scholar

Zheng, Y., Wu, L., Zhao, H., Zhou, X., and Liu, Q. (2020). Simulation of Extreme Updrafts in the Tropical Cyclone Eyewall. Adv. Atmos. Sci. 37, 781–792. doi:10.1007/s00376-020-9197-4

CrossRef Full Text | Google Scholar

Zhu, P., Menelaou, K., and Zhu, Z. (2013). Impact of Subgrid-Scale Vertical Turbulent Mixing on Eyewall Asymmetric Structures and Mesovortices of Hurricanes. Q.J.R. Meteorol. Soc. 140, 416–438. doi:10.1002/qj.2147

CrossRef Full Text | Google Scholar

Zhu, P. (2008). Simulation and Parameterization of the Turbulent Transport in the Hurricane Boundary Layer by Large Eddies. J. Geophys. Res. 113, D17104. doi:10.1029/2007JD009643

CrossRef Full Text | Google Scholar