The Effective Thermal Conductivity of Unsaturated Porous Media Deduced by Pore-Scale SPH Simulation

The smoothed particle hydrodynamics (SPH) method was employed to simulate the heat transfer process in porous media at the pore scale. The effective thermal conductivity of a porous medium can be predicted through a simulation experiment of SPH. The accuracy of the SPH simulation experiment was verified by comparing the predicted values with reference values for ideal homogeneous media and multiphase layered media. 3D simulation experiments were implemented in granular media generated by the PFC method. Based on the SPH framework, a concise method was proposed to produce unsaturated media by simulating the wetting process in dry media. This approach approximates the formation of liquid bridges and water films on granules. Through simulation experiments, the empirical formula of the variation in thermal conductivity with the degree of saturation was tested. The results showed that the reciprocal of the normalized thermal conductivity and the reciprocal of the saturation are linearly related, which is in line with the empirical formula proposed by Cote and Konrad.

1 Introduction

Heat transfer in porous media is a common phenomenon during agricultural and industrial production (Moradi et al., 2016; Varnosfaderani et al., 2016; Cui et al., 2020). The effective thermal conductivity is a key problem for the heat-conducting properties of porous media (Jahangir et al., 2018a; Bai et al., 2021a; Fu et al., 2020), which involves the coupling effects of multi-physical fields. Changes in the thermal field result in changes in the moisture and stress fields of porous media (Das and Cleary, 2016; Jahangir et al., 2018b; Meng et al., 2020; Nishad and AI-Raoush, 2021; Yuan et al., 2021a). Therefore, it is important to determine the effective thermal conductivities of porous media and clarify how they relate to the influencing factors.

As a mixture, a porous medium is composed of solid components that form a solid framework and pore space that is filled by other components (Cheng et al., 2020; Hu et al., 2021; Yuan et al., 2021b). The random and disordered natures of these structures make it difficult to accurately quantify the effective thermal conductivities of porous media in theory. The effective thermal conductivity is a general parameter for characterizing porous media and is mainly affected by the components of the medium, more specifically, the distributions, proportions and properties of the components. When the solid, liquid and gas phases have a layered distribution and are connected in series, the thermal conductivity reaches its minimum; in contrast, when the layers are connected in parallel, the thermal conductivity reaches its maximum. When the layers are connected in series (superscript L) or in parallel (superscript U), the theoretical values of the effective thermal conductivity for a multiphase medium are

$\{\begin{array}{l}{\lambda }^L={\left({\displaystyle \sum {\varphi }_{\text{n}}/{\lambda }_{\text{n}}}\right)}^{-1}\\ {\lambda }^U={\displaystyle \sum {\varphi }_{\text{n}}{\lambda }_{\text{n}}}\end{array}(1)$

where λ is the thermal conductivity of the porous medium, the subscript n refers to different components, and $\varphi$ denotes the volume proportion of each component.

A disordered multiphase mixture can ideally be modeled as some components in series and some components in parallel. Based on this theory, the thermal conductivity values for multiphase media are within the abovementioned limits. For unsaturated porous media, the upper and lower limits of the effective thermal conductivity can be further refined. Since the thermal conductivity of water is much greater than that of air, the thermal conductivity of a porous medium increases with increasing water content. When in a saturated state, the thermal conductivity value of porous media reaches its upper limit; while for a completely dry state, the thermal conductivity reaches the lower limit.

Johansen (1975) proposed the concept of the normalized thermal conductivity λ_r, which is defined as

${\lambda }_{\text{r}}=\frac{\lambda -{\lambda }_{\text{dry}}}{{\lambda }_{\text{sat}}-{\lambda }_{\text{dry}}}(2)$

where λ_dry and λ_sat indicate dry and saturated conditions, respectively.

The value of λ_r varies between 0 and 1. By fitting experimental data from the literature, Johansen (1975) proposed a logarithmic relationship between λ_r and the degree of saturation S_r for several types of soil. By analyzing a large amount of literature data, Cote and Konrad (2005) developed the following empirical equation:

${\lambda }_{\text{r}}=\frac{\alpha S_{\text{r}}}{1+\left(\alpha -1\right)S_{\text{r}}}(3)$

This equation can be transformed into

$\frac{1}{{\lambda }_{\text{r}}}=\frac{1}{\alpha }\cdot \frac{1}{S_{\text{r}}}+\left(1-\frac{1}{\alpha }\right)(4)$

where α is an influence coefficient.

Through laboratory tests on quartz sand, Chen (2008) found that the logarithm of thermal conductivity for sand has a good linear relationship with porosity, and the slope is affected by the degree of saturation. This empirical model is

$\lambda ={\lambda }_{\text{s}}^{1-\phi }{\lambda }_{\text{w}}^{\phi }{\left[\left(1-b\right)S_{\text{r}}+b\right]}^{c\phi }(5)$

where $\phi$ is the porosity, b and c are both empirical parameters.

At present, studies on the thermal conductivity of soil have been mainly conducted at the macroscopic scale (Sass et al., 1971; Vincent and Paul., 2005; Bai et al., 2018). To achieve a deeper understanding of the laws governing the effective thermal conductivity, it is necessary to advance research to the pore scale (Cui et al., 2019; Zhou et al., 2022). This study employs a smoothed particle hydrodynamics (SPH) method due to its flexibility in pore-scale simulations and good computational accuracy in heat conduction calculations.

SPH is a kind of meshless particle algorithm of Lagrangian form. Initially proposed in 1977 to solve a problem in astrophysics, SPH has since been used in heat conduction. Cleary and Monaghan (1999) proposed an improved form of the standard SPH formula that ensures a heat flow balance on material interfaces, and the results showed that the formula is highly accurate. Jeong et al. (2003) improved the SPH method for solving second-order differential equations by decomposing the second-order partial differential equation into two first-order partial differential equations and then checked the accuracy by performing 1D and 2D heat conduction simulations. Jiang and Sousa (2007) employed the SPH method to predict the effective thermal conductivity in heterogeneous materials containing two or three different components. By combining the advantages of SPH and the finite difference method (FDM), Bai et al. (2018) proposed a well-established SPH-FDM method and analyzed the thermal processes of homogeneous media containing discontinuous interfaces and showed that this method can be successfully employed in parabolic problems.

The present work utilizes a pore-scale simulation approach to predict the thermal conductivities of unsaturated porous media using the SPH method and examines the relationship between the normalized thermal conductivity and saturation by using an empirical model. The manuscript is structured as follows: Section 2 introduces the reconstruction process of an unsaturated granular soil at the pore scale and the procedure for the simulation experiment; Section 3 verifies the accuracy of the simulation experiment through ideal media; and Section 4 presents simulation experiments in 3D granular media and discusses the variation in the normalized thermal conductivity with saturation. The conclusions drawn from the work are presented in Section 5.

2 Pore-Scale Simulation on Effective Thermal Conductivity

2.1 Smoothed Particle Hydrodynamics Method

The SPH method is a kind of meshless particle algorithm of Lagrangian form. The computational domain is discretized by separate sets of particles. The discretization of the field function consists of two main steps. First, the field function f at point x can be expressed in integral form:

$f\left(\mathbf{x}\right)\approx \tilde{f}\left(\mathbf{x}\right)={\displaystyle {\int }_{\Omega }f\left({\mathbf{x}}^{\prime }\right)W\left(\left|\mathbf{x}-{\mathrm{x}}^{\prime }\right|,h\right)\text{d}{\mathbf{x}}^{\prime }},(6)$

where Ω, W, and h denote the integral domain, the kernel function and the smoothing length of the kernel function, respectively.

A frequently used kernel function, the cubic B-spline function, is adopted herein (Huang and Liu, 2020):

$W\left(R,h\right)={\alpha }_{\text{d}}\times \{\begin{array}{l}2/3-R^2+R^3/20\le R<1\\ {\left(2-R\right)}^3/61\le R<2\\ 0R\ge 2\end{array}(7)$

where R is the relative distance and is equal to r/h, where r is the particle distance. In 1D, 2D, and 3D spaces, the normalized values of the constant α_d are 1/h, 15/7πh², and 3/2πh³, respectively.

Next, the integral form of the field function is discretized into a series summation. The field function at particle i is approximated as

$f\left({\mathbf{x}}_i\right)\approx {\displaystyle \sum _{j=1}^N\frac{m_j}{{\rho }_j}f\left({\mathbf{x}}_j\right)W\left(\left|{\mathbf{x}}_i-{\mathbf{x}}_j\right|,h\right)},(8)$

where x is the distance vector, m and ρ are the mass and density of particle j, respectively, the subscript j denotes a particle within the influence area of particle i, and N is the total number of particles.

However, the traditional SPH algorithm has several drawbacks when applied to complex engineering problems. To address these defects, many researchers have proposed improved calculation methods, which is a driving force for the further development of the SPH method (Huang et al., 2019; Rao and Bai, 2020). At the same time, this method is also being used in an increasingly broad range of applications, such as heat conduction problems at the pore scale and thermal consolidation problems in geotechnical materials (Bai et al., 2021b; Xue et al., 2021).

The differential equation for unsteady heat conduction within a three-dimensional isotropic medium without an internal heat source is (Carslaw and Jaeger, 1959).

$\frac{\partial T}{\partial t}=\frac{\lambda }{\rho c}\cdot {\nabla }^{2}T(9)$

where c is the specific heat.

The SPH approximation of Eq. 9 at point i can be written as (Sass et al., 1971; Bai et al., 2018).

${\left(\frac{\partial T}{\partial t}\right)}_i=\frac{1}{{\rho }_i{c}_i}{\displaystyle \sum _{j=1}^N\frac{m_j}{{\rho }_j}\cdot \frac{4{\lambda }_i{\lambda }_j}{ \left({\lambda }_i+{\lambda }_j\right) }\left(T_i-T_j\right)\cdot \frac{{\mathbf{x}}_i-{\mathbf{x}}_j}{r_{ij}^2}{\nabla }_i{W}_{ij}}(10)$

where r_ij =|x_ij |.

The size of each time interval is suggested to be (Bai et al., 2018).

$\mathrm{\Delta }t\le \min \left(\frac{0.15h^2}{\kappa }\right)(11)$

where κ is the thermal diffusion coefficient equal to λ/ρc.

The explicit Euler method is employed for the integration step, $\tilde{f}\left(t+\mathrm{\Delta }t\right)=f\left(t\right)+\mathrm{\Delta }t{\frac{df}{dt}|}_t$. SPH has different discretization schemes for different derivation processes (Price, 2012). Among these schemes, Eq. 10 is the most suitable for modeling thermal conduction. Its accuracy in 1D, 2D, and 3D spaces has been verified by extensive numerical tests (Cleary and Monaghan, 1999).

2.2 Generation of 3D Porous Media

The particle flow code (PFC) method is employed to produce a 3D granular medium. Cundall and Strack (1979) developed the PFC method from the discrete element method by defining the discrete element as a rigid sphere. Based on PFC3D 3.10 software (developed by ITASCA Inc., United States), there are five steps involved in generating a 3D dry granular medium: first, the software sets rigid walls that represent the boundaries of the sample; second, the software sets the number and size range of the spheres and randomly generates them in the calculation domain; then, gravity is applied to the spheres, which are allowed to fall freely; fourth, when the spheres have naturally accumulated, the software applies a plate with slow downward movement over the accumulated body to compact it to the predefined porosity; finally, the software outputs the radii of all the spheres and the coordinates of the centers of mass and then discretizes the medium into solid and gas particles (Figure 1A).

FIGURE 1

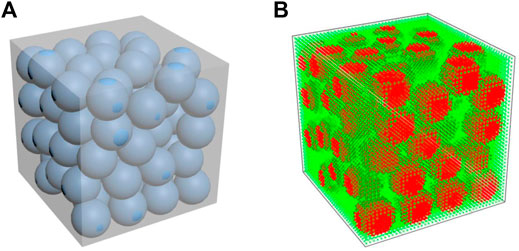
FIGURE 1. Solid and gas particles: (A) Restructured 3D porous medium (named SAP1); (B) discretization of SAP1 in the dry state (the green particles are gas particles, while the red particles are solid particles).

In Figure 1A, the length L of the cubic medium (named SAP1) is 0.008 m. It contains 70 spherical granules with identical radii of a = 1 mm. After spatial discretization, the medium (Figure 1B) contains a total of 64,000 particles with a particle spacing of 0.0002 m. The particles are divided into gas and solid particles. The porosity is set at 0.43. The calculation time is about 3 h.

2.3 Simulation of the Humidifying Process

When a porous medium gradually humidifies from a completely dry state, the evolution of the distributions of pore water and air can be approximately described as follows: First, water forms liquid bridges over the narrow spaces between pores and fills some of the dead-end pores in the medium. Pore water forms films on the surfaces of the granules. As the degree of water saturation increases, the liquid bridges widen, and the thickness of the water films increases. Then, the liquid bridges gradually connect to each other. When the proportion of air is further reduced, the connections between the bubbles are blocked, and eventually only isolated bubbles exist in the pores.

Figure 2 shows a 2D-CT (computed tomography) scanning image as an example. As shown in Figure 2, the humidifying process is achieved approximately in accordance with the description. This process can be simply divided into two steps: first, the gas particles are sorted according to degree of influence from the solid surface; second, these gas particles are converted into water particles in a certain order. The first step adopts the particle pairing algorithm of the SPH method. For the dry state, there are both solid particles and gas particles in the identification zone of a gas particle located near the surface of the granules (Figure 3). The parameter p is defined as the proportion of solid particles in the identification zone. In Figure 3, the p value for point A is greater than that for point B, and the p value for point B is greater than that for point C. According to their evolution, these particles located in dead-end pores (such as particle A) or near the surface of the solid phase (such as particle B) are wetted before those located in the centers of the pore channels (such as particle C). Moreover, the p values of the former are higher than those of the latter. Hence, the wetting order of the gas particles is basically in agreement with the order of the p values.

FIGURE 2

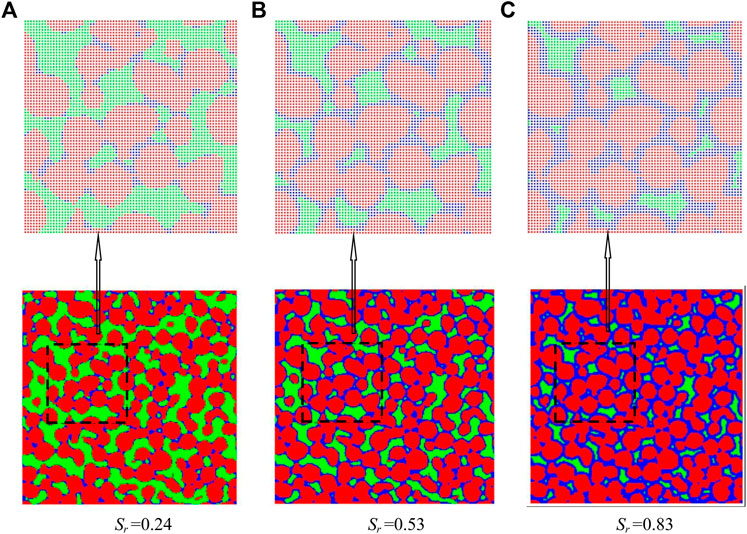
FIGURE 2. Simulation of the humidifying process for a 2D porous medium obtained by processing a 2D-CT scanning image (The blue particles denote water particles). (A) S_r =0.24 (B) S_r =0.53 (C) Sr =0.83.

FIGURE 3

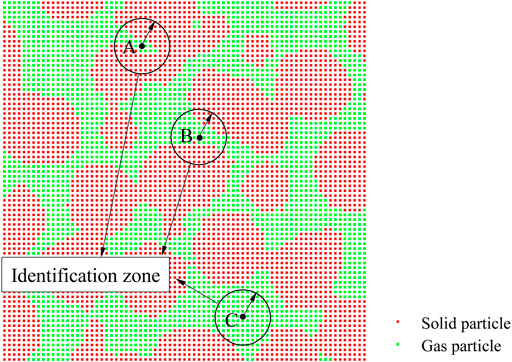
FIGURE 3. The identification zone is similar to the influence domain of a particle, and the radius is defined as a multiple of the smoothing length.

Similarly, the humidifying process of SAP1 can also be obtained by the algorithm, as shown in Figure 4.

FIGURE 4

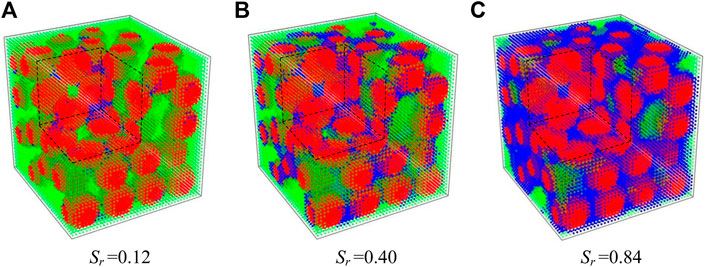
FIGURE 4. Simulation of the humidifying process for a 3D granular medium (Note: the corner is removed to reveal the internal details). (A) S_r =0.12 (B) S_r =0.40 (C) Sr =0.84.

2.4 Simulation Scheme

The steady-state method is a conventional laboratory measurement method for modeling the thermal conductivity. When the system reaches equilibrium, the heat transfer rate is equal to the heat dissipation rate in a stable thermal conduction process. According to Fourier’s law, the heat flux q of an ideal infinite plate satisfies (Cundall and Strack, 1979; Bai et al., 2019).

$q=\lambda \frac{\mathrm{\Delta }T}{L}(12)$

where ΔT is the temperature difference between the two sides of the plate, and L is the thickness of the plate.

In this calculation, an infinite plate is simulated by applying periodic boundary conditions to a square or cubic medium. The boundary conditions for the 2D simulation experiment are applied as shown in Figure 5. The upper and lower edges of the square medium are set as periodic boundaries so that the square medium can be periodically extended into an infinite plate with a certain thickness L. The left and right boundaries of the medium are set at different temperature values acting as the initial boundary conditions. For SPH particle sets, if the temperature difference is T₀, the average heat flux is calculated as

$\overline{q}=\frac{1}{\mathit{{\rm N}}}{\displaystyle \sum _{i=1}^{\mathit{{\rm N}}}{\mathit{\lambda }}_i}{\left(\frac{\mathrm{d}T}{\mathrm{d}x}\right)}_i(13)$

FIGURE 5

FIGURE 5. Diagram showing the boundary conditions of the steady-state simulation experiment.

When the temperature field reaches a steady state, the thermal conductivity of the medium can be determined by Eq. 12 ($\lambda =\raisebox{1ex}{$\overline{q}L$}\!\left/ \!\raisebox{-1ex}{$T_{\text{0}}$}\right.$).

The application of the finite difference method in SPH has been proposed in Bai’s work (Bai et al., 2018). In this work, the differential equations are applied in the post processing step of the SPH simulation experiments to output the temperature gradient. For some complex fluid-structure coupling boundary problems, some scholars (Huang et al., 2016; Liu and Zhang, 2019; Ye et al., 2019) have also proposed many improved calculation methods that can further improve the calculation accuracy (Liu and Liu, 2010).

3 Verification Using Typical Cases

3.1 Case 1: Homogeneous Medium

For this case, we assume that the infinite plate is a homogeneous medium with density ρ = 1000 kg/m³, specific heat capacity c = 1000 J/(kg°C), and default thermal conductivity λ₀ = 1 W/(m°C) (Bai et al., 2020; Bai et al., 2021a). The initial temperature of the particles is set to 0. In this calculation, the boundary conditions are applied as shown in Figure 5. The thickness of the square medium is L = 0.012 m. The other calculation parameters are listed in Table 1.

TABLE 1

TABLE 1. Calculation parameters for the 2D case.

Figure 6A shows that the temperature distribution in the medium gradually becomes more linear. The dimensionless time factor is defined as t_d = κt/L² (Bai et al., 2020). Figure 6B shows that the calculated values of the thermal conductivity rapidly approach the baseline value during the dimensionless time t_d.

FIGURE 6

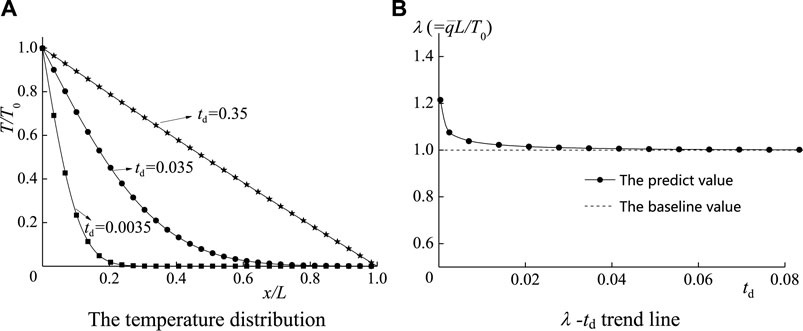
FIGURE 6. Calculation results of the homogeneous medium. (A) The temperature distribution (B) $\lambda$ -td trend line

3.2 Case 2: Three-Phase Layered Medium

As shown in Figure 7A, it is assumed that the solid, liquid, and gas components are arranged in layers, and each component occupies the same volume in the medium. The physical parameters of the materials are listed in Table 2. If boundaries 1 and 2 are treated as periodic boundaries and boundaries 3 and 4 are treated as the temperature boundaries, the three layers are connected in series. In contrast, if boundaries 3 and 4 are treated as periodic boundaries while boundaries 1 and 2 are treated as the temperature boundaries, the three layers are connected in parallel. In this simulation, the parameters are the same as those in Case 1 (Table 1) and are in agreement with the parameters in the existing literature (Alrtimi et al., 2014; Yang, 2019).

FIGURE 7

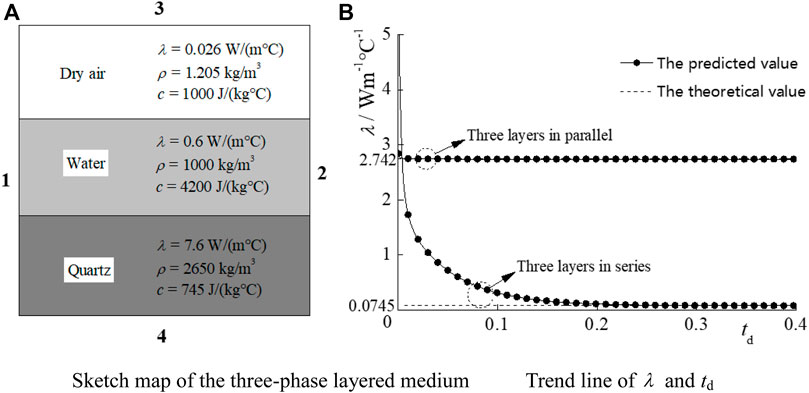
FIGURE 7. Three-phase layered medium and the calculation results. (A) Sketch map of the three-phase layered medium (B) Trend line of $\lambda$ and t_d.

TABLE 2

TABLE 2. Thermal parameters of the materials involved in the calculation.

According to Eq. 1, the theoretical value of effective thermal conductivity for the three-phase series medium is 0.0745 W/(m°C), while that for the three-phase parallel medium is 2.742 W/(m°C).

Figure 7B shows that for both connection modes, the predicted values of the effective thermal conductivity precisely converge to the theoretical values over the chosen calculation time. The dimensionless time factor for the three-phase medium is defined as t_d = κt/L², with κ being the thermal diffusion coefficient of water (Bai et al., 2021c). The results show that the proposed simulation experiment is suitable for predicting the effective thermal conductivities of multiphase media.

4 The Relationship Between the Normalized Thermal Conductivity and Saturation Degree

In the SAP1 calculation, the temperature boundary is set to T₀ at the upper boundary (plate z = L) and set to 0 at the lower boundary (plate z = 0), while the other boundaries are set as periodic boundaries. The granular medium is simulated as an infinite porous layer with a thickness equal to L. The physical parameters for the components are assigned according to Table 2. The time step Δt is set to 0.0001 s. The simulated steady-state dimensionless temperature distribution of the sample in Figure 4 is predicted (Figure 8A).

FIGURE 8

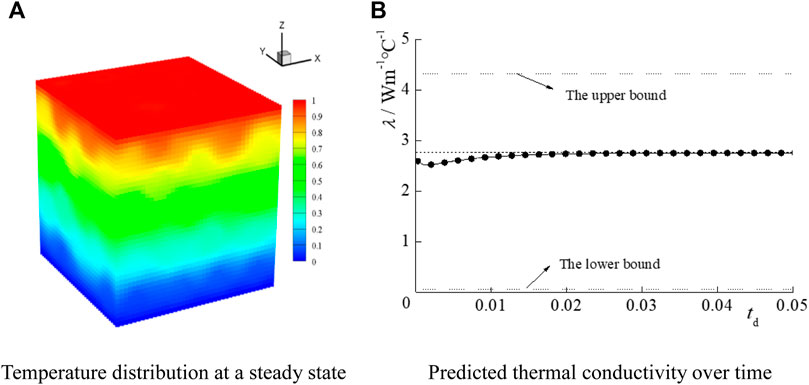
FIGURE 8. 3D stacked media and calculation results. (A)Temperature distribution at a steady state (B) Predicted thermal conductivity over time.

Figure 8B shows that the effective thermal conductivity value gradually stabilizes over time. To ensure the precision of the three significant figures in the predicted λ value, the calculation process continues until the fourth significant digit stops changing in the time interval of Δt_d = 0.01. As shown in Figure 8B, the final result for the effective thermal conductivity for the medium reaches 2.75 W/(m°C), in agreement with the Wiener limits [the upper bound being 4.32 W/(m°C) and the lower bound being 0.06 W/(m°C), as calculated by Eq. 1].

A sample named SAP2 (Figure 9), with a granule radius of a = 0.8 mm, is generated as the control sample. SAP2 has the same porosity as SAP1. By applying the humidifying algorithm to both SAP1 and SAP2, two sets of samples with incremental degrees of saturation are obtained. In the simulation, the solid component for each group of soil samples is assigned first as quartz and then as feldspar. Thus, four sets of simulation experimental results are obtained. For feldspar, the values of λ, ρ and c are 2.3 W/(m°C), 2650 kg m⁻³ and 710 J/(kg°C), respectively. The trend line for λ_r versus S_r is plotted in Figure 10.

FIGURE 9

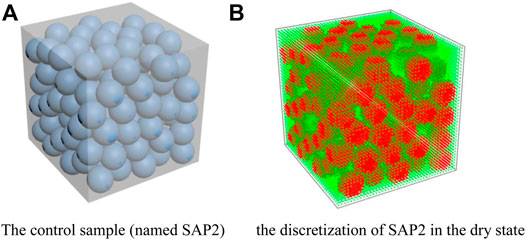
FIGURE 9. Particle distribution. (A) The control sample (named SAP2); (B) the discretization of SAP2 in the dry state.

FIGURE 10

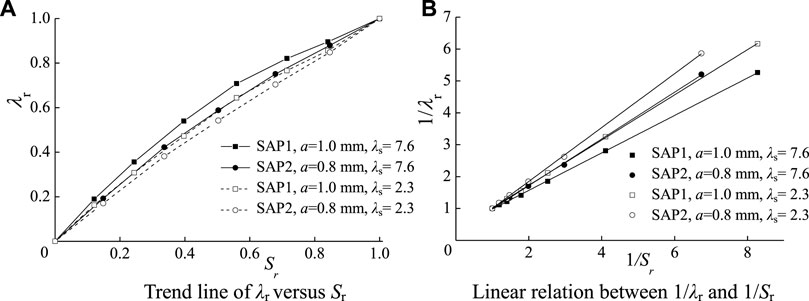
FIGURE 10. The relationship between λ_r and S_r. (A) Trend line of λ_r versus S_r (B) Linear relation between 1/λ_r and 1/S_r.

The results show that the slope of the λ_r-S_r curve reaches a maximum when the degree of saturation is 0 and then decreases gradually. This curve indicates that the formation of a liquid bridge in the early stage of the humidifying process can improve the thermal conductivity of porous media. This phenomenon is consistent with the conclusions from other reference (Bai et al., 2019). Figure 10B shows that 1/λ_r has a good linear relationship with 1/S_r, which agrees with the empirical rule in Eq. 4. In addition, a comparison of the solid and hollow data points in Figure 10 shows that the slope of the linear fit for the 1/λ_r−1/S_r graph varies for different materials and granule sizes. Thus, the influence coefficient α from Eq. 4 is related to the thermal conductivity value of the solid phase and the granularity of the medium.

5 Conclusion

This research deduces a pore-scale simulation method to predict the effective thermal conductivities of unsaturated porous media using the SPH method. This study also discusses the relationship between the thermal conductivity and the degree of saturation in porous media. A concise method to simulate the wetting process of porous media is proposed based on pore-scale SPH simulation.

Based on a dry medium, the humidifying process can be modeled by sorting the gas particles according to the influence degree of the solid surface and then converting these gas particles into water particles in a certain order. This approach models the formation of liquid bridges and water films on granules. For three-phase layered media, the thermal conductivity values predicted by the simulation experiments agree with the theoretical values. This shows that the simulation experimental method is accurate for multiphase media. The particle fluid code is employed to generate the granular samples on which the simulation experiments are implemented.

The simulation experiments enable an investigation into the laws governing the relationship between the thermal conductivity and degree of saturation. The results show that the reciprocal of the normalized thermal conductivity and the reciprocal of the degree of saturation are linearly related. This result is consistent with the empirical formula proposed by Cote and Konrad. This verification of the law provides another way to demonstrate the usefulness and credibility of the humidifying process.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

The main contribution of BB in this paper is methodology, and the other authors (YW, DR, and FB) contributed in investigation and analysis.

Funding

This research was funded by the Beijing Natural Science Foundation (822023) and National Natural Science Foundation of China (52079003).

Conflict of Interest

YW was employed by the company Beijing Uni.-Construction Group Co., Ltd. DR was employed by the company Guangzhou Expressway Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

a, granule radius; c, specific heat capacity; f, field function; h, smoothing length of the kernel function; i, serial number of objective particles; j, serial number of particle i’s adjacent particles; L, thickness of the medium; m, mass of a particle; N, total number of particles within the influence area of particle i; p, the proportion of the solid particles in the identification zone; r, particle distance; R, relative distance; Sr, degree of saturation; t, time; t_d, dimensionless time, t_d = D₀t/L²; T, temperature; x, x’, x_i, x_j, distance vector of particle; W, kernel function; α, influence coefficient; α_d, normalized constant in the kernel function; $\nabla$, vector gradient operator; κ, thermal diffusion coefficient, equal to λ/ρc; λ, thermal conductivity; λ_r, normalized thermal conductivity; Δx, particle spacing; ρ, density of particle; $\phi$, porosity; $\varphi$, volume proportion of each component; Ω, integral domain.

References

Alrtimi, A., Rouainia, M., and Manning, D. A. C. (2014). An Improved Steady-State Apparatus for Measuring Thermal Conductivity of Soils. Int. J. Heat Mass Transf. 72, 630–636. doi:10.1016/j.ijheatmasstransfer.2014.01.034

CrossRef Full Text | Google Scholar

Bai, B., Jiang, S., Liu, L., Li, X., and Wu, H. (2021a). The Transport of Silica Powders and Lead Ions under Unsteady Flow and Variable Injection Concentrations. Powder Technol. 387, 22–30. doi:10.1016/j.powtec.2021.04.014

CrossRef Full Text | Google Scholar

Bai, B., Nie, Q., Zhang, Y., Wang, X., and Hu, W. (2021b). Cotransport of Heavy Metals and SiO2 Particles at Different Temperatures by Seepage. J. Hydrology 597, 125771. doi:10.1016/j.jhydrol.2020.125771

CrossRef Full Text | Google Scholar

Bai, B., Rao, D., Xu, T., and Chen, P. (2018). SPH-FDM Boundary for the Analysis of Thermal Process in Homogeneous Media with a Discontinuous Interface. Int. J. Heat Mass Transf. 117, 517–526. doi:10.1016/j.ijheatmasstransfer.2017.10.004

CrossRef Full Text | Google Scholar

Bai, B., Xu, T., Nie, Q., and Li, P. (2020). Temperature-driven Migration of Heavy Metal Pb2+ along with Moisture Movement in Unsaturated Soils. Int. J. Heat Mass Transf. 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Bai, B., Yang, G.-c., Li, T., and Yang, G.-s. (2019). A Thermodynamic Constitutive Model with Temperature Effect Based on Particle Rearrangement for Geomaterials. Mech. Mater. 139, 103180. doi:10.1016/j.mechmat.2019.103180

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Cai, G., Hu, W., and Yang, G. (2021c). Coupled Thermo-Hydro-Mechanical Mechanism in View of the Soil Particle Rearrangement of Granular Thermodynamics. Comput. Geotechnics 137 (8), 104272. doi:10.1016/j.compgeo.2021.104272

CrossRef Full Text | Google Scholar

Carslaw, H., and Jaeger, J. (1959). Conduction of Heat in Solids. Oxford: Oxford University Press.

Google Scholar

Chen, S. X. (2008). Thermal Conductivity of Sands. Heat. Mass Transf. 44 (10), 1241–1246. doi:10.1007/s00231-007-0357-1

CrossRef Full Text | Google Scholar

Cheng, W.-C., Bai, X.-D., Sheil, B. B., Li, G., and Wang, F. (2020). Identifying Characteristics of Pipejacking Parameters to Assess Geological Conditions Using Optimisation Algorithm-Based Support Vector Machines. Tunn. Undergr. Space Technol. 106, 103592. doi:10.1016/j.tust.2020.103592

CrossRef Full Text | Google Scholar

Cleary, P. W., and Monaghan, J. J. (1999). Conduction Modelling Using Smoothed Particle Hydrodynamics. J. Comput. Phys. 148, 227–264. doi:10.1006/jcph.1998.6118

CrossRef Full Text | Google Scholar

Côté, J., and Konrad, J.-M. (2005). A Generalized Thermal Conductivity Model for Soils and Construction Materials. Can. Geotech. J. 42 (2), 443–458. doi:10.1139/t04-106

CrossRef Full Text | Google Scholar

Cui, X., Fan, Y., Wang, H., and Huang, S. (2019). Experimental Investigation of Suspended Particles Transport in Porous Medium under Variable Temperatures. Hydrol. Process. 33 (7), 1117–1126. doi:10.1002/hyp.13390

CrossRef Full Text | Google Scholar

Cui, X., Fan, Y., Wang, H., and Huang, S. (2020). Ground Environment Characteristics during the Operation of GWHP Considering the Particle Deposition Effect. Energy Build. 206, 109593. doi:10.1016/j.enbuild.2019.109593

CrossRef Full Text | Google Scholar

Cundall, P. A., and Strack, O. D. L. (1979). A Discrete Numerical Model for Granular Assemblies. Géotechnique 29, 47–65. doi:10.1680/geot.1979.29.1.47

CrossRef Full Text | Google Scholar

Das, R., and Cleary, P. W. (2016). Three-dimensional Modelling of Coupled Flow Dynamics, Heat Transfer and Residual Stress Generation in Arc Welding Processes Using the Mesh-free SPH Method. J. Comput. Sci. 16, 200–216. doi:10.1016/j.jocs.2016.03.006

CrossRef Full Text | Google Scholar

Fu, X., Sheng, Q., Li, G., Zhang, Z., Zhou, Y., and Du, Y. (2020). Analysis of Landslide Stability under Seismic Action and Subsequent Rainfall: a Case Study on the Ganjiazhai Giant Landslide along the Zhaotong-Qiaojia Road during the 2014 Ludian Earthquake, Yunnan, China. Bull. Eng. Geol. Environ. 79, 5229–5248. doi:10.1007/s10064-020-01890-z

CrossRef Full Text | Google Scholar

Hu, W., Cheng, W.-C., Wen, S., and Mizanur Rahman, M. (2021). Effects of Chemical Contamination on Microscale Structural Characteristics of Intact Loess and Resultant Macroscale Mechanical Properties. Catena 203, 105361. doi:10.1016/j.catena.2021.105361

CrossRef Full Text | Google Scholar

Huang, C., and Liu, M. B. (2020). Modeling Hydrate-Bearing Sediment with a Mixed Smoothed Particle Hydrodynamics. Comput. Mech. 66, 77–891. doi:10.1007/s00466-020-01895-1

CrossRef Full Text | Google Scholar

Huang, C., Lei, J. M., Liu, M. B., and Peng, X. Y. (2016). An Improved KGF-SPH with a Novel Discrete Scheme of Laplacian Operator for Viscous Incompressible Fluid Flows. Int. J. Numer. Meth. Fluids 81, 377–396. doi:10.1002/fld.4191

CrossRef Full Text | Google Scholar

Huang, C., Long, T., Li, S. M., and Liu, M. B. (2019). A Kernel Gradient-free SPH Method with Iterative Particle Shifting Technology for Modeling Low-Reynolds Flows Around Airfoils. Eng. Analysis Bound. Elem. 106, 571–587. doi:10.1016/j.enganabound.2019.06.010

CrossRef Full Text | Google Scholar

Jahangir, M. H., Ghazvini, M., Pourfayaz, F., Ahmadi, M. H., Sharifpur, M., and Meyer, J. P. (2018a). Numerical Investigation into Mutual Effects of Soil Thermal and Isothermal Properties on Heat and Moisture Transfer in Unsaturated Soil Applied as Thermal Storage System. Numer. Heat. Transf. Part A Appl. 73 (7), 466–481. doi:10.1080/10407782.2018.1449518

CrossRef Full Text | Google Scholar

Jahangir, M. H., Sarrafha, H., and Kasaeian, A. (2018b). Numerical Modeling of Energy Transfer in Underground Borehole Heat Exchanger within Unsaturated Soil. Appl. Therm. Eng. 132, 697–707. doi:10.1016/j.applthermaleng.2018.01.020

CrossRef Full Text | Google Scholar

Jeong, J. H., Jhon, M. S., Halow, J. S., and Osdol, J. V. (2003). Smoothed Particle Hydrodynamics: Applications to Heat Conduction. Comput. Phys. Commun. 153 (1), 71–84. doi:10.1016/S0010-4655(03)00155-3

CrossRef Full Text | Google Scholar

Jiang, F., and Sousa, A. C. M. (2007). Effective Thermal Conductivity of Heterogeneous Multi-Component Materials: an SPH Implementation. Heat. Mass Transf. 43 (5), 479–491. doi:10.1007/s00231-006-0131-9

CrossRef Full Text | Google Scholar

Johansen, O. (1975). Thermal Conductivity of Soils. Norway: TrondheimUniversity of Trondheim.

Google Scholar

Liu, M. B., and Liu, G. R. (2010). Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 17, 25–76. doi:10.1007/s11831-010-9040-7

CrossRef Full Text | Google Scholar

Liu, M., and Zhang, Z. (2019). Smoothed Particle Hydrodynamics (SPH) for Modeling Fluid-Structure Interactions. Sci. China Phys. Mech. Astron. 62, 984701. doi:10.1007/s11433-018-9357-0

CrossRef Full Text | Google Scholar

Meng, K., Cui, C., Liang, Z., Li, H., and Pei, H. (2020). A New Approach for Longitudinal Vibration of a Large-Diameter Floating Pipe Pile in Visco-Elastic Soil Considering the Three-Dimensional Wave Effects. Comput. Geotechnics 128, 103840. doi:10.1016/j.compgeo.2020.103840

CrossRef Full Text | Google Scholar

Moradi, A., Smits, K. M., Lu, N., and McCartney, J. S. (2016). Heat Transfer in Unsaturated Soil with Application to Borehole Thermal Energy Storage. Vadose zone J. 15 (10), 1–17. doi:10.2136/vzj2016.03.0027

CrossRef Full Text | Google Scholar

Nishad, S., and Al-Raoush, R. I. (2021). Colloid Retention and Mobilization Mechanisms under Different Physicochemical Conditions in Porous Media: a Micromodel Study. Powder Technol. 377, 163–173. doi:10.1016/j.powtec.2020.08.086

CrossRef Full Text | Google Scholar

Price, D. J. (2012). Smoothed Particle Hydrodynamics and Magnetohydrodynamics. J. Comput. Phys. 231, 759–794. doi:10.1016/j.jcp.2010.12.011

CrossRef Full Text | Google Scholar

Rao, D., and Bai, B. (2020). Study of the Factors Influencing Diffusive Tortuosity Based on Pore-Scale SPH Simulation of Granular Soil. Transp. Porous Med. 132 (2), 333–353. doi:10.1007/s11242-020-01394-0

CrossRef Full Text | Google Scholar

Sass, J. H., Lachenbruch, A. H., and Munroe, R. J. (1971). Thermal Conductivity of Rocks from Measurements on Fragments and its Application to Heat-Flow Determinations. J. Geophys. Res. 76 (14), 3391–3401. doi:10.1029/jb076i014p03391

CrossRef Full Text | Google Scholar

Varnosfaderani, A. M., Gatmiri, B., and Haghighi, E. M. (2016). A Model for Moisture and Heat Flow in Fractured Unsaturated Porous Media. Int. J. Numer. Anal. Meth. Geomech. 41, 828–858. doi:10.1002/nag.2577

CrossRef Full Text | Google Scholar

Vincent, B., and Paul, A. A. (2005). Modeling Soil Thermal Conductivities over a Wide Range of Conditions. J. Environ. Eng. Sci. 4 (6), 549–558.

Google Scholar

Xue, Z. F., Cheng, W. C., Wang, L., and Hu, W. (2022). Effects of Bacterial Inoculation and Calcium Source on Microbial-Induced Carbonate Precipitation for Lead Remediation. J. Hazard Mater 426, 128090. doi:10.1016/j.jhazmat.2021.128090

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, G., and Bai, B. (2019). Thermo-hydro-mechanical Model for Unsaturated Clay Soils Based on Granular Solid Hydrodynamics Theory. Int. J. Geomech. 19 (10), 04019115. doi:10.1061/(asce)gm.1943-5622.0001498

CrossRef Full Text | Google Scholar

Ye, T., Pan, D., Huang, C., and Liu, M. B. (2019). Smoothed Particle Hydrodynamics (SPH) for Complex Fluid Flows: Recent Developments in Methodology and Applications. Phys. fluids 31, 011301.

Google Scholar

Yuan, B. X., Li, Z. H., Chen, Y., Ni, H., Zhao, Z. Q., Chen, W. J., et al. (2021a). Mechanical and Microstructural Properties of Recycling Granite Residual Soil Reinforced with Glass Fiber and Liquid-Modified Polyvinyl Alcohol Polymer. Chemosphere 268, 131652.

Google Scholar

Yuan, B., Li, Z., Zhao, Z., Ni, H., Su, Z., and Li, Z. (2021b). Experimental Study of Displacement Field of Layered Soils Surrounding Laterally Loaded Pile Based on Transparent Soil. J. Soils Sediments 21, 3072–3083. doi:10.1007/s11368-021-03004-y

CrossRef Full Text | Google Scholar

Zhou, Y., Sheng, Q., Li, N., and Fu, X. (2022). The Dynamic Mechanical Properties of a Hard Rock under True Triaxial Damage-Controlled Dynamic Cyclic Loading with Different Loading Rates: a Case Study. Rock Mech. Rock Eng. 55, 2471–2492. doi:10.1007/s00603-021-02756-w

CrossRef Full Text | Google Scholar