Experimental research on damage identification of topping dangerous rock structural surface based on dynamic characteristic parameters

Rock block tilting is one of the most common types of dangerous rock block failures with no clear indicator of displacement prior to failure. Existing stability evaluation methods remain limited in their ability to constrain the non-penetrating section area, which is closely related to rock stability, and stability evaluations are therefore associated with large uncertainties. The dynamic characteristic parameters of toppling dangerous rock are closely related to structural plane strength. Under vibration loading, rainfall, and/or excavation unloading conditions, the structural plane becomes damaged and the dynamic characteristic parameters change. In this study, we present a dynamic characteristic model of rock tilting and identify the quantitative and qualitative relationship between dynamic characteristic parameters and the bonded area of the structural plane. The model accuracy is verified by experiments. The experimental results show that the damping ratio decreases linearly with structural plane damage, whereas the maximum vibration speed and particle trajectory increases nonlinearly and the natural vibration frequency decreases nonlinearly. The dynamic characteristic model and experimental results can be used to evaluate the degree of structural surface damage of toppling dangerous rock.

Introduction

The collapse of toppling dangerous rock is characterized by a sudden burst and spatial dispersion. Rock block stability is related to many external factors (e.g., rainfall, seismic activity, blasting, excavation unloading) whereas internal factors (e.g., rock strength, mechanical properties and conditions) control the structural plane. A combination of internal and external factors may ultimately lead to cracking of the structural plane and bond area reduction, which reduce the structural plane strength and anti-tipping torque. Rock falls occur when the anti-falling torque is smaller than the tilting moment. Selection of appropriate bonding condition analysis indicators is therefore a key factor for evaluating the stability of toppling dangerous rock. Previous studies have shown that dynamic characteristic parameters change regularly during gradual separation and structural plane damage processes. Damage evaluation modeling based on dynamic characteristic parameters is therefore of great theoretical significance and can help engineering applications to identify, evaluate and monitor the stability of toppling dangerous rock, and predict rock failure (Jia, 2018).

Structural damage identification and stability evaluation based on dynamic characteristics are widely used in the field (Han and Shi, 2011). Proposed damage identification of a derrick steel structure based on the frequency and equivalent damage coefficient. Damage location has been identified using the second-order frequency change ratio and frequency squared change ratio, and the rate of frequency change has been used to identify the degree of damage. This approach is simple, easy, and efficien. Chen et al. (2010) assessed structural damage according to formation and perturbation changes before and after the damage, and checked the evaluation accuracy based on the natural vibration frequency change. The feasibility of the method was verified by numerical simulation. Zhang and He (2014) expressed a structure’s mass matrix and stiffness matrix as a function of unit damage parameters according to the matrix perturbation theory and proposed a method to identify the structural damage based on frequency and mode perturbation.

Structural damage identification techniques have been developed in the field of rock damage identification but currently remain in the basic experimental stage (Liao et al., 2016; Li et al., 2022; Zhang et al., 2022). Studied the vibration characteristics during fan blade fatigue loading, analyzed the vibration frequency variation, and established a dynamic characteristic model. The experimental results showed that the difference between the driving and natural frequency is closely related to the vibration amplitude and frequency fluctuation in the forced vibration. Ma et al. (2012) and Ma et al. (2011) measured the vibration frequencies of concrete blocks with different bonding conditions. The experimental results showed that the natural vibration frequency was closely related to adhesion conditions. Du et al. (2022), Du et al. (2020) and Du et al. (2016) determined the relationship between the natural vibration frequency and cohesive force of rock blocks through stress analysis and reported a stability evaluation based on the natural vibration frequency. Yao (2016) and Ye et al. (2015) studied falling rock qualitatively and established a stability evaluation model based on dynamic characteristic parameters. Jia et al. (2017) established a dynamic characteristic model of crash-damaged and slip-damaged rock blocks. The relationship between the safety factor and natural vibration frequency was identified on the basis of the dynamic characteristic model and limit equilibrium method, and safety evaluation and early warning monitoring plans for rock blocks were established based on the natural vibration frequency (Du and Xie, 2022). Du et al. (2022), Du et al. (2021) and Du et al. (2017) studied the collapse mechanism and early warning index of dangerous rock through experiments. Fukata et al. (2013) assessed the soil burial depth of rock blocks according to the natural vibration frequency in three directions, the size of the rock block, and the soil mechanical properties.

The damage identification method of rock structures based on dynamic characteristic parameters can rapidly assess rock block stability. (Jia et al., 2021). However, the existing dynamic characteristic model is narrow in focus and does not accurately reflect the variation law of the dynamic characteristic parameters of rock masses in all failure modes. In this paper we present a theoretical study of the dynamic characteristics model and dynamic characteristic parameter behavior of collapsing rock blocks. We perform experiments to verify the model results.

Dynamic characteristic model

Toppling dangerous rock

The back edge of a toppling dangerous rock has a large angle along the main control structure plane, and the bottom has a concave cavity formed by differential weathering. Under internal and external forces, the rock block forms a destructive torque that rotates outwards and forms a vandal-resistant moment that turns inwards When the breaking torque that turns outwards is greater than the outward turning moment, the rock block collapses. The rock block swing is shown in Figure 1.

FIGURE 1

FIGURE 1. Force diagram of toppling dangerous rock.

The stability of a rock block is closely related to the load it bears. In the natural state, the load of the block is caused mostly by gravity, vibrational load, and internal and external cavity water pressure.

1) Gravity

The rock block volume can be obtained through site surveys. In the stability calculation, gravity is generally applied to the center of gravity and the direction of gravity is vertically downward:

$\mathit{W=abh\gamma }(1)$

Where W and γ represent rock weight (kN) and bulk density (kN/m³), respectively.

2) Vibration load

The vibration load acting on a rock block is usually obtained using the pseudo-static calculation method where the vibration load acts on the weight of the rock block:

$\mathit{P=\lambda W}(2)$

Where P is the vibration load (kN) and λ is the dimensionless vibration load coefficient. When the horizontal vibration load coefficient is selected, the calculated vibration load is the horizontal vibration load (i.e., the direction horizontal to the free surface) and when the vertical vibration load coefficient is selected, the vibration load can be calculated as a vertical vibration load in the vertically downward direction.

3) Fissure water pressure

In the existing stability analysis of slope rocks, the fissure water pressure is calculated based on the linear distribution of the static water pressure, which is perpendicular to the main control structure plane and acts as a filling height of 1/3 above the tip of the main control structure plane.

$\mathit{V}=1/3{\mathit{\gamma }}_{\mathit{w}}{\mathit{h}}_{\mathit{w}}^2(3)$

Where V represents the fissure water produced by the static pressure (kN/m), γ_w is the fissure water bulk density (kN/m³), and h_w is the water filling height (m).

Dynamic characteristics

The damage to a rock block structure is directly reflected in its dynamic characteristic parameters (e.g., natural vibration frequency, vibration mode, damping ratio, changes in amplitude and particle trajectory), which are easy to obtain and can produce high-precision results without parameter analysis using a complicated mathematical model. These parameters are therefore important for assessing the structural plane damage of a dangerous rock block.

When an object is free to vibrate, it reciprocates periodically over a given time period. Once a rock block is disturbed by natural or artificial external forces, the structural plane becomes damaged and the bond strength of the slope rock body decreases continuously. These features are reflected in the particle trajectory and amplitude. A dangerous rock block is not only the particle track of a stable rock block, but also enhances the waveform amplitude. Damage of the structural plane generally leads to a reduction of the structural plane area or bond strength. The friction between the blocks increases, resulting in a change in the system’s damping. The damage degree of the structural plane can be judged to some extent using the damping variation. The study of vibration resistance of dangerous rock blocks is therefore of great significance for understanding slope stability. In addition to the natural vibration frequency, the particle trajectory, amplitude, and damping ratio can be used for structural damage identification. Using these methods, laboratory experiments have identified the damage degree of rock block structures.

Modeling procedure

Toppling dangerous rock are typically relatively isolated single rocks with good block integrity and high overall stiffness. Forces are mainly transmitted by a relatively weak structural plane and the physical properties of the main control structural plane significantly influence the dynamic characteristics of the block.

In terms of vibrational characteristics, the rock block pivots on the edge of the concave cavity, forms a rotational force distance outside the inclined slope, and swings up and down when subjected to external forces. The simplified model of the pendulum vibration rock block, without damping, is shown in Figure 2.

FIGURE 2

FIGURE 2. Simplified mechanical model of toppling dangerous rock.

Rock block tilting is caused by gravity, vibrational load, and fissure water pressure. When the shear strength of the structural plane is insufficient to resist the gravitational load, vibrational load, and fissure water pressure, the rock body falls. The parent rock can be regarded as an infinite block relative to the rock block. The overall stiffness of the pedestal and rock block is high. The strength of the structural face of the rock block is weak relative to the strength of the rock block and parent rock. When subjected to external forces, the rock block can be regarded as a ball, the structural plane is regarded as a spring, and the parent rock transmits power to the rock block through the structural plane. The block body swings along the pivot because the parent rock is regarded as an infinite block body which does not affect the system swing. Pendulum vibration can be used to model the dynamic characteristics of toppling dangerous rock failure. The theoretical model of pendulum vibration in a rock block is shown in Figure 3.

FIGURE 3

FIGURE 3. Vibration model of toppling dangerous rock.

The parent rock is assumed to be large relative to the rock block, and the latter is represented by a ball. The main controlling structural plane is isotropic and the system damping ratio is less than 1. Deformation in the amplitude range is linear elastic, and the vibration model of the rock block can be simplified into a pendulum dynamic characteristic model, with the constitutive equation given by Eqs. 4, 5 (Jia et al., 2021):

$\mathit{MgL}+\mathit{EIl}=0(4)$

$\mathit{I}=\mathit{A}{\mathit{B}}^3/12(5)$

Then the vibration frequency can be derived as Eqn. 6:

$\mathit{f}=\frac{1}{\mathit{\pi }}\sqrt{\frac{\mathit{ElA}{\mathit{B}}^3}{48\mathit{ML}}}(6)$

Where $f$ is the natural frequency of undamped system ($\text{Hz}$); $E$ is the elastic modulus ($\text{Pa}$); M is the mass of toppling dangerous rock ($\text{kg}$); $I$ is moment of inertia of structural section; $L$ is the distance between the centroid of toppling dangerous rock and $\text{O}$ ($\text{m}$); $l$ is the distance between $\text{O}$ and the centroid of bounding surface ($\text{m}$); $A$ is the bonding surface width of toppling dangerous rock ($\text{m}$); B is the bonding surface length of toppling dangerous rock ($\text{m}$).

In the above theory, the system damping effect is neglected. When the system damping ratio is equal to 1 (critical damping) or is greater than 1 (overdamped), the motion of the system is rapidly attenuated, there is no vibration characteristic, and the vibration frequency of the rock block does not exist. The model therefore does not apply to the critical damping and over-damping rock block system. When the damping ratio of the rock block is less than 1 (weak damping system), the natural vibration frequency of the damped pendulum vibration of the rock block can be obtained.

${\mathit{f}}_{\mathit{d}}=\frac{\sqrt{1-{\mathit{\xi }}^2}}{\mathit{\pi }}\sqrt{\frac{\mathit{El}{\mathit{S}}^3}{48\mathit{ML}{\mathit{A}}^2}}(7)$

Where $f_d$ is the natural frequency of damped system ($\text{Hz}$); $\xi$ is the damping ratio of the system (unitless); $S$ is the bonding surface area (${\text{m}}^2$);

It can be seen from Eqn. 7 that the rock block bonding area is positively correlated with the natural vibration frequency, and the pendulum length and mass are negatively correlated with the natural vibration frequency.

Experimental study

An orthogonal experiment was carried out by selecting two factors: rock block mass and bonding area. The natural vibration frequency of the experimental block was monitored and compared with the theoretically calculated natural vibration frequency. The experimental design was also used to monitor the dynamic characteristics of the experimental model, and the variation of the dynamic characteristic parameters with the bonding area was further analyzed.

Experimental design

1) Model verification experiment design

In the experiments, a block of marble with side lengths of 10 cm, 15 cm and 20 cm was selected and each block was measured for its dynamic characteristics under different bonding areas. The bonding surface was made of a 2.5-cm-thick Elastic plastic plate that was not corroded by glue. The elastic modulus of the structural plane is 2.0 GPa. The rock mass and bonding surface were bonded with non-corrosive epoxy resin. In the experiment the earth was used as the pedestal to ensure that the pedestal was infinite relative to the experimental rock block and that the pedestal has no effect on the vibration of the block during the experiment (Figure 4).

FIGURE 4

FIGURE 4. Experimental model of rock blocks.

The marble block, bonding surface, and vertical wall surface were bonded by glue to change the contact area between the foam board and rock block. The natural vibration frequency of the rock block under different bonding areas was measured for nine sets of experiments.

2) Additional dynamic characteristics experiment

The experiment uses Doppler laser vibrometer to monitor the damping ratio, particle trajectory, and the maximum vibration speed of the experimental blocks under different bonding areas. We then studied the relationship between structural damage and the dynamic characteristic parameters.

The Doppler laser vibrometer is a high-precision vibration measuring device based on the principle of optical interference. It can accurately measure vibration signals, including displacement and velocity. The maximum frequency can reach 10000 Hz and the measurement resolution can reach 2.5 nm/s and 2 pm. Doppler laser vibrometer is shown in Figure 5.

FIGURE 5

FIGURE 5. Doppler laser vibrometer.

Experimental results

The experimental results are listed in Table 1. Under different bonding area conditions, the difference between the theoretical and measured natural vibration frequencies is less than 6.90% with an average error of 3.34%, indicating good agreement between the theoretical value and the measured value. The theoretical value is consistent with the measured value, indicating the accuracy of the theoretical model.

TABLE 1

TABLE 1. Experimental results.

Discussion

Relationship between vibration frequency and bonding area

In the experiment, the block was struck for excitation and the vibration time-domain curve of the marble block was recorded using a laser vibrometer. The vibration time-domain curve obtained from the experiments was Fourier transformed and filtered to obtain the experimental blocks of the experimental block frequency-domain diagram. The measured vibration frequency of different sized experimental rock masses under different bonding areas and the theoretical values calculated by the model are plotted in Figure 6.

FIGURE 6

FIGURE 6. Natural vibration frequency of different size blocks with different bonding areas.

For the 10-cm blocks with bonded areas of 20, 40, 60, 80, and 100 cm², the natural vibration frequencies were1.08, 3.27, 5.85, 9.57, and 12.12 Hz, respectively (Table 1 and Figure 6). For the 15-cm blocks with bonded areas of 45, 90, 135, 180 and 225 cm², the natural vibration frequencies were 1.42, 3.79, 7.13, 10.32, and 15.96 Hz, respectively (Table 1 and Figure 6). For the 20-cm blocks with bonded areas of 80,160, 240, 320 and 400 cm², the natural vibration frequencies were 1.48, 4.58, 8.65, 12.69, and 18.13 Hz, respectively, (Table 1 and Figure 6).

For the blocks, the natural vibration frequency increased with bonding area when other conditions were held constant, that is, the natural vibration frequency of the rock block gradually decreased with damage of the structural plane. The natural vibration frequency can quantitatively identify the bonding area of the structural surface, and then realize the stability evaluation of the toppling dangerous rock.

Relationship between particle trajectory and bonded area

Analysis of the five groups of experiments show a relationship between the particle trajectory and bonded area, as shown in Table 1. Figure 7 shows that the maximum value of the particle trajectory of the experimental block decreases linearly with increasing bonded area.

FIGURE 7

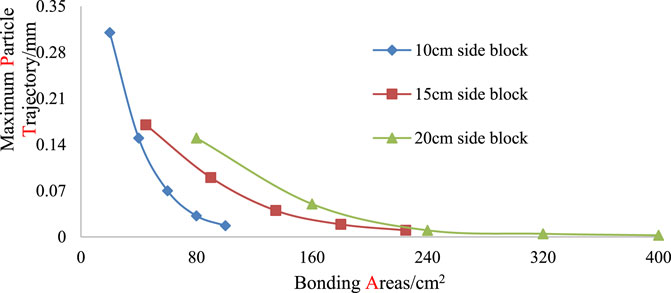
FIGURE 7. Relationship between maximum particle trajectory and bonded area under the same excitation.

In summary, for the 10-cm blocks, the particle trajectory of the experimental block decreases with increasing bonding area under the same excitation conditions. When the bonding area was 20 cm², the particle trajectory range does not exceed 0.31 mm, and the bonding area is 40 cm². The particle trajectory range of motion does not exceed 0.15 mm. When the bonded area is 60 cm², the particle trajectory range does not exceed 0.07 mm. When the bonded area is 80 cm², the particle trajectory range does not exceed 0.032 mm. When the bonded area is 100 cm², the particle trajectory range does not exceed 0.017 mm. For 15-cm blocks, the particle trajectory of the experimental block decreases with increasing bonding area under the same excitation conditions. When the bonding area was 45 cm², the particle trajectory range does not exceed 0.17 mm, and the bonding area is 90 cm². The particle trajectory range of motion does not exceed 0.09 mm. When the bonded area is 135 cm², the particle trajectory range does not exceed 0.04 mm. When the bonded area is 180 cm², the particle trajectory range does not exceed 0.019 mm. When the bonded area is 225 cm², the particle trajectory range does not exceed 0.01 mm. For 20-cm blocks, the particle trajectory of the experimental block decreases with increasing bonding area under the same excitation conditions. When the bonding area was 80 cm², the particle trajectory range does not exceed 0.15 mm, and the bonding area is 160 cm². The particle trajectory range of motion does not exceed 0.05 mm. When the bonded area is 240 cm², the particle trajectory range does not exceed 0.01 mm. When the bonded area is 320 cm², the particle trajectory range does not exceed 0.005 mm. When the bonded area is 400 cm², the particle trajectory range does not exceed 0.003 mm.

After being disturbed by external force, the structural surface is damaged, and the bond strength of the toppling dangerous rock decreases continuously. The active area of the particle trajectory is significantly expanded, so the particle trajectory can quantitatively identify the damage and stability of the structural plane of the toppling dangerous rock.

Relationship between damping ratio and bonding area

For the same experimental block, the damping ratio decreases as the bonded area between the experimental block and ground increases (Figure 8).

FIGURE 8

FIGURE 8. Relationship between damping ratio and bonded area.

Based on the damping and experimental data of the bonded area, the relationship between the damping ratio and bonded area of the block is shown in table and Figure 7. For the experimental block with a side length of 10 cm under the same excitation, the damping ratio of the experimental block decreases with increasing bonded area. The damping ratio is 0.178, 0.151, 0.119, 0.089 and 0.051 when the bonded area is 20, 40, 60, 80 and 100 cm², respectively. For the experimental block with a side length of 15 cm under the same excitation, the damping ratio of the experimental block decreases with increasing bonded area. The damping ratio is 0.12, 0.085, 0.06, 0.04 and 0.011 when the bonded area is 45, 90, 135, 180 and 225 cm², respectively. In summary, the damping ratio of the experimental block decreases with increasing bonding area under the same excitation conditions. For the experimental block with a side length of 20 cm under the same excitation, the damping ratio of the experimental block decreases with increasing bonded area. The damping ratio is 0.081, 0.050, 0.036, 0.014 and 0.008 when the bonded area is 80, 160, 240, 320 and 400 cm², respectively. In summary, the damping ratio of the experimental block decreases with increasing bonding area under the same excitation conditions.

The damping is mainly determined by the properties of the structural surface. When the structural surface is damaged, the area of the structural surface decreases or the bond strength decreases, the frictional force changes and the damping changes. Therefore, the damage degree of the structural surface can be judged to a certain extent through the damping change. According to the variation law of the structural plane damping, when the structural plane is damaged, the damping of the toppling dangerous rock decreases linearly, and the stability of the dangerous rock becomes worse.

Relationship between bonding areas and maximum vibration speed

The relationship between natural vibration frequency and maximum velocity and bonding area is shown in Table 1. According to the measured value, the maximum vibration speed and the bonded area is plotted in Figure 9.

FIGURE 9

FIGURE 9. Relationship between maximum vibration speed and bonded area.

It can be seen from Figure 9 that the maximum vibration velocity increases nonlinearly as the bonding area decreases under the same excitation conditions. When the bonding rate is greater than 50%, the maximum vibration velocity changes little with the structural surface damage. When the bonding rate is less than 50%, the maximum velocity change can qualitatively identify the damage degree of the structural surface.

Conclusion

1) Based on the theory of rock block dynamics, we established the relationship between the natural vibration frequency of toppling dangerous rock, the bonding area of the rock block and bedrock, the elastic modulus, and rock block quality. The dynamic characteristic model was verified through laboratory experiments.

2) The dynamic characteristic model and experimental results show that the dynamic characteristics of toppling dangerous rock change regularly with structural plane damage. The maximum vibration speed and maximum particle trajectory increases nonlinearly, while natural vibration frequency of the structural plane damage decreases nonlinearly and the damping ratio decreases linearly.

3) The stability evaluation of toppling dangerous rock based on dynamic characteristic parameters can be realized by combining the variation law of the dynamic characteristic parameters with the limit equilibrium model. The research results can be applied to the stability evaluation of hydropower slope or road slope toppling dangerous rock.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YJ and TJ were responsible for the work concept or design. YJ and GY were responsible for data collection. YY were responsible for drafting the manuscript. LW were responsible for making important revisions to the manuscript. YJ and YY were responsible for approving the final version of the manuscript for publication.

Funding

This research was supported by the National Natural Science Foundation of China (No. U1704243) and Natural Science Foundation granted by Department of Education, Anhui Province (No. KJ 2020A0235).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, H., He, W., Wang, B., and Li, J. B. (2010). Study on structure damage detection based on perturbations of frequency and mode shapes. Chin. J. Eng. Mech. 27 (12), 244–249.

Google Scholar

Du, Y., Li, H., Chicas, S. D., and Huo, L. (2022). Progress and perspectives of geotechnical anchor bolts on slope engineering in China. Front. Environ. Sci. 10, 928064. doi:10.3389/fenvs.2022.928064

CrossRef Full Text | Google Scholar

Du, Y., Xie, M., and Jia, J. L. (2020). Stepped settlement: a possible mechanism for translational landslides. Catena 187, 104365. doi:10.1016/j.catena.2019.104365

CrossRef Full Text | Google Scholar

Du, Y., and Xie, M. W. (2022). Indirect method for the quantitative identification of unstable rock. Nat. Hazards (Dordr). 112 (1), 1005–1012. doi:10.1007/s11069-021-05197-4

CrossRef Full Text | Google Scholar

Du, Y., Xie, M. W., Jiang, Y. J., Chen, C., Jia, B. N., and Huo, L. C. (2021). Review on the formation mechanism and early warning of rock collapse. Chin. J. Metal Mine 50 (1), 106–119. doi:10.19614/j.cnki.jsks.202101008

CrossRef Full Text | Google Scholar

Du, Y., Xie, M. W., Jiang, Y. J., Li, B., and Chicas, S. (2017). Experimental rock stability assessment using the frozen-thawing test. Rock Mech. Rock Eng. 50 (4), 1049–1053. doi:10.1007/s00603-016-1138-2

CrossRef Full Text | Google Scholar

Du, Y., Xie, M. W., Jiang, Y. J., Li, B., Gao, Y., and Liu, Q. Q. (2016). Safety monitoring experiment of unstable rock based on natural vibration frequency. Chin. J. Rock Soil Mech. 37 (10), 3035–3040. doi:10.16285/j.rsm.2016.10.039

CrossRef Full Text | Google Scholar

Fukata, T., Taniguchi, T., and Shibuya, S. (2013). A proposal of estimation method for rockfall risk degree based on vibration measurement of the boulder. J. Jpn. Soc. Civ. Eng. Ser C Geosph. Eng. 69 (1), 140–151. doi:10.2208/jscejge.69.140

CrossRef Full Text | Google Scholar

Han, D. Y., and Shi, P. M. (2011). Damage identification of derrick steel structures based on frequency and equivalent damage coefficient. Chin. J. Eng. Mech. 28 (9), 109–114. doi:10.6052/j.issn.1000-4750.2010.01.0037

CrossRef Full Text | Google Scholar

Jia, Y. C., Jiang, T., and Liu, H. D. (2021). Stability evaluation model of toppling unstable rock based on natural vibration frequency. J. Appl. Sci. Eng. 24 (2), 177–184. doi:10.6180/jase.202104_24(2).0007

CrossRef Full Text | Google Scholar

Jia, Y. C. (2018). Study on stability model of slope dangerous rock block based on dynamic characteristics. Beijing: University of Science and Technology of Beijing.

Google Scholar

Jia, Y. C., Xie, M. W., Chang, S. X., and Lyu, F. X. (2017). A model for evaluation of stability of sliding-and falling-type dangerous rock blocks based on natural vibration frequency. Chin. J. Rock Soil Mech. 38 (7), 2149–2156. doi:10.19614/j.cnki.jsks.202101008

CrossRef Full Text | Google Scholar

Li, B., Zhang, G., Wang, G., and Qiao, J. (2022). Damage evolution of frozen-thawed granite based on high-resolution computed tomographic scanning. Front. Earth Sci. (Lausanne) 760, 912356. doi:10.3389/feart.2022.912356

CrossRef Full Text | Google Scholar

Liao, G. H., Wu, J. Z., and Zhang, L. A. (2016). Analysis on coupling vibration frequency characteristics of wind turbine blade rotating fatigue loading system. Chin. J. Vib. Meas. Diagnosis 36 (6), 1085–1090+1235. doi:10.16450/j.cnki.issn.1004-6801.2016.06.008

CrossRef Full Text | Google Scholar

Ma, G. C., Sawada, K., Saito, H., Uehan, F., and Yashima, A. (2012). Study on evaluating rock block stability by using a remotely positioned laser Doppler vibrometer. Geomate 2 (4), 247–252. doi:10.21660/2012.4.3j

CrossRef Full Text | Google Scholar

Ma, G. C., Sawada, K., Yashima, A., Uehan, F., Murata, O., and Saito, H. (2011). “Study of scale effect in rock block stability by remote vibration measurements and numerical experiments,” in Proceedings of the 40th Symposium on Rock Mechanics, Committee on Rock Mechanics, Anchorage, AK, June 25–29, 2005, 339–344.

Google Scholar

Yao, G. Z. (2016). Vibration characteristics of falling unstable rock under different stability states. Guizhou: Guizhou University.

Google Scholar

Ye, Y. S., Cai, D. G., Yan, H. Y., Yao, G. Z., and Yao, J. P. (2015). Experiment study on vibration characteristics of falling unstable rock under excitation. China Railw. Sci. 36 (6), 16–21. doi:10.3969/j.issn.1001-4632.2015.06.03

CrossRef Full Text | Google Scholar

Zhang, F. H., and He, R. (2014). Natural frequency analysis of wind turbines based on flexible multi-body dynamics. Proc. CSEE 34 (11), 1807–1814. doi:10.13334/j.0258-8013.pcsee.2014.11.012

CrossRef Full Text | Google Scholar

Zhang, L., Niu, F. J., Liu, M. H., Ju, X., Wang, Z. W., Wang, J. C., et al. (2022). Fracture characteristics and anisotropic strength criterion of bedded sandstone. Front. Earth Sci. (Lausanne). 451, 879332. doi:10.3389/feart.2022.879332

CrossRef Full Text | Google Scholar