Review of the Deformation Mechanism and Earth Pressure Research on the Double-Row Pile Support Structure

As a new support structure system, the double-row pile is widely used in foundations in pit engineering, slope engineering, water conservancy engineering, and other fields. It has a big horizontal stiffness and strong anti-overturning ability and has less impact on the surrounding neighboring existing buildings (structures) when it is applied. It must be mentioned that the design experience of the double-row pile is ahead of the theory, and some research has been carried out on double-row pile support structures. This work reviews and evaluates the force deformation and earth pressure on piles of double-row piles, including pile deformation damage mechanism, soil pressure distribution law, and double-row pile structure form. In addition, the problems and shortcomings of the current double-row pile research are concluded. These results have enriched the study of the mechanism of double-row piles, provided the theoretical guidance for double-row pile support structures, and laid the foundation for further theoretical research.

Introduction

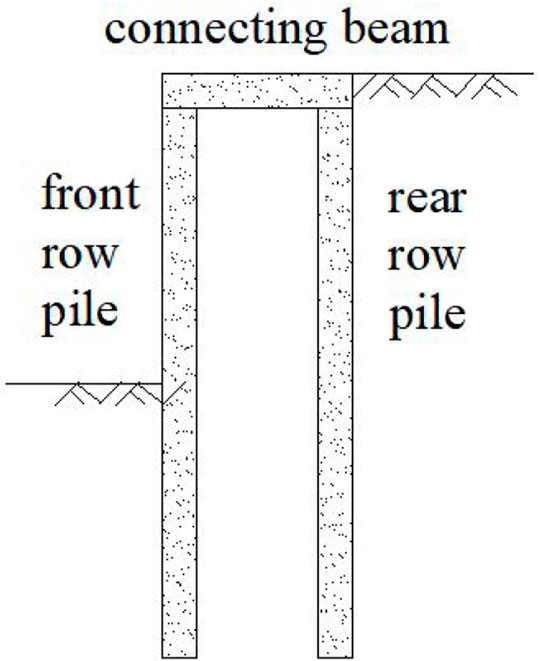
The double-row pile support structure is evolved from the single-row pile support structure, and this support structure has good force performance; its stability and stiffness of lateral displacement resistance are more excellent than a single row of piles. The double-row pile support structure mainly consists of a front pile, back pile, crown beam, and connecting beam (Gong, 1998; Technical specification, 2021), which can be regarded as a space structure system that connects the tops of two parallel rows of anti-slip piles with the rigid connecting beam. The double-row pile support structure is shown in Figure 1.

FIGURE 1

FIGURE 1. Double-row pile support structure.

The double-row pile support structure is a spatial support structure system formed by adjusting the pile position so that part of the pile is retracted to form a rectangle or plum shape and connected at the top of the pile with connecting beams and crown beams (Wang and Liu, 2001; Yang and Wang, 2010; Li, 2013). This support structure can ensure a better support effect without increasing or adding a small number of piles. There are various ways of laying piles for double-row pile support structures: zigzag, plum, double triangle, single triangle, rectangular lattice, continuous arch, single arch, and T-shape (Fan, 2009; Zhu, 2013). Among them, rectangular lattice and plum are more common in actual projects. The forms of double-row piles are shown in Figure 2.

FIGURE 2

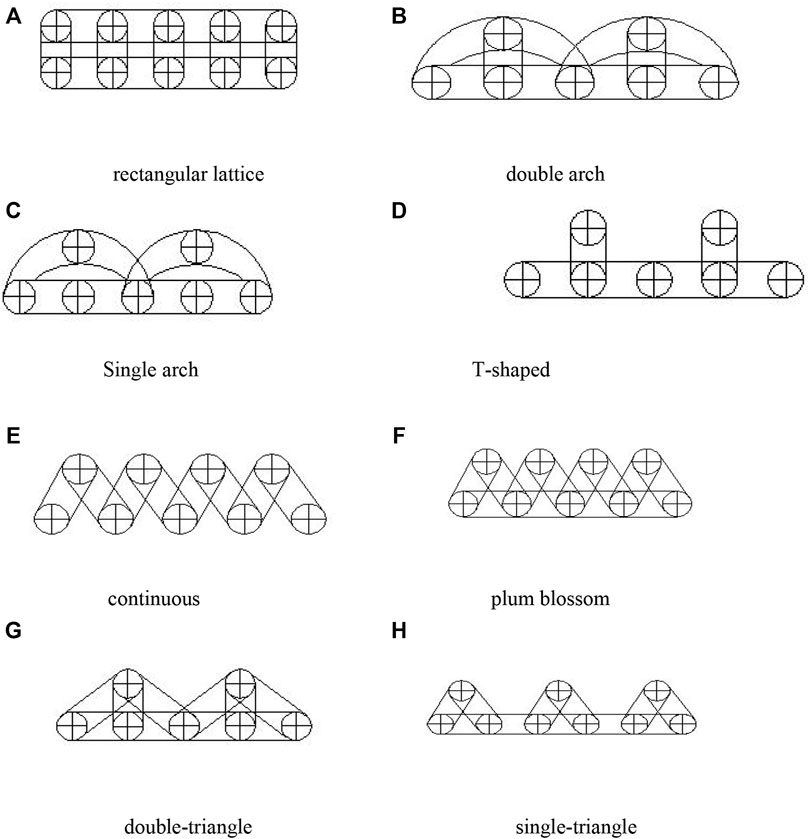
FIGURE 2. Forms of double-row piles: (A) rectangular lattice, (B) double-arch, (C) single-arch, (D) T-shaped, (E) continuous arch, (F) plum blossom, (G) double-triangle, and (H) single-triangle.

These are the advantages of double-row pile support structures compared to single-row piles:

1) When pipelines, subways, foundations of adjacent buildings, basements, or other obstacles around the foundation pit make it impossible to apply anchors, a double-row pile support structure can be used.

2) When the water table around the foundation pit is high, it is difficult to make holes with anchor rods and a double-row pile support structure can be used.

3) When the geological conditions around the pit are complex and cannot provide sufficient anchorage, a double-row pile support structure can be used.

4) According to local laws and regulations, when the anchors cannot exceed the red line of the site, a double-row pile support structure can be used.

5) When a single row of anchor piles cannot meet the requirements of horizontal displacement control, an anchor-pulling double-row pile support structure can be used.

Study of the Mechanical Model of Double-Row Pile and Soil Pressure

Some foreign scholars have explored the mechanical model of the double-row pile and soil pressure. Franx and Boonstra (1948), HeymanBoersma (1961), and Wenz (1973) studied the internal force and deformation of piles under lateral soil pressure and found that the deformation damage of piles is strongly related to the amount of soil displacement. Oteo (1974) and Nicu et al. (1971) derived the formula for the quantitative relationship between soil displacement and pile internal force based on the summary of previous studies. Marche and Lacroix (1972) derived the conversion equation of the modulus of elasticity of the pile with the horizontal displacement of the pile and the vertical displacement of the pile top. Begemann and DeLeeuw, (1972) approximated the distribution of the pile as a continuous wall and calculated the distribution of the pile displacement field and stress field by considering the pile as a rigid body. Tschebotariof (1973) applied the Rankine soil pressure theory, assuming a triangular distribution of soil pressure along the pile body, and calculated the internal forces and displacements of the pile body by the soil pressure acting on it. Springman (1989) and Stewart et al. (1994) established a formula for the interaction between the soil and pile of a double-row pile and calculated the distribution of soil pressure and the distribution of bending moment and displacement of the pile.

In China, the most representative is the volume ratio coefficient method proposed by He et al. (1996) based on the classical soil pressure theory.

The soil pressure of the front and rear piles is calculated according to the volume of the sliding soil between piles that accounts for the total volume of the whole sliding soil. The calculation formula of the proportional coefficient $a$ is expressed as:

$a=L\times \left(2L_0-L\right)/L_0^2,(1)$

$L_0=H\tan \left({45}^0-\varphi /2\right),(2)$

where $a$ is the coefficient of volume ratio, $L$ is the row spacing of double-row piles, $L_0$ is the distance from the intersection of the slip surface and top of the foundation pit to the edge of the foundation pit, $H$ is the depth of the foundation pit, and $\varphi$ is the angle of internal friction of soil.

The volume ratio coefficient method proposed a calculation model of the double-row pile and the coupling beam at the top of the pile as the rigid frame structure. The pile body and the coupling beam are rigid connections and are only translational without rotation. The disadvantage of the volumetric proportional coefficient method is that the distribution of soil pressure in front- and back-row piles is artificially distributed, and the actual stress of pile and soil is not considered.

According to the classical Rankine earth pressure theory, the rigid-plastic analysis method proposed by Huang (1995) takes the land studied as a rigid-plastic body analysis. The shear failure surface of the soil is changed due to the existence of rear piles, and the distribution of soil pressure is different with or without rear piles.

The total weight of soil per unit length $W$ is expressed as:

$W=\gamma b\left[z-\frac{b}{2}\tan \left(\eta \right)\right].(3)$

The resultant force of soil active earth pressure is expressed as:

$W=\gamma b\left[z-\frac{b}{2}\tan \left(\eta \right)\right]\tan \left(\eta -\phi \right).(4)$

Considering that the existence of the back-row pile changes the shear fracture surface of the back-row pile, according to the limit equilibrium principle $d{E}_a/d\eta =0$, the equation is given as follows:

$z/b=0.5\left[\tan \eta +\tan \left(\eta -\phi \right){\cos }^2\left(\eta -\phi \right)/{\cos }^2\eta \right].(5)$

Assuming that the sum of lateral earth pressure acting on the front and rear piles is Rankine active earth pressure, the influence of spacing between the front and rear piles is approximately considered.

On the basis of previous studies, a new calculation method for the soil behind piles is proposed by Cheng and Zhang (2001). It is considered that the soil pressure between piles can be neglected compared with the soil behind piles. Double-row piles can be regarded as a statically indeterminate structure of a steel frame inserted into the soil. Due to the existence of the back-row piles, the soil sliding surface is no longer a fixed value ${45}^0+\varphi /2$, but with the change of depth–width ratio, $\xi =z/b$.The calculation formula of active earth pressure of front- and back-row piles is derived.

The active earth pressure formula of front-row piles is:

$e_{af}=\left(1+a\right)e_a\left(\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\right),(6)$

$e_{af}=\left(1-a\right)e_a\left(\mathrm{r}\mathrm{e}\mathrm{c}\tan \mathrm{g}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\right).(7)$

The active earth pressure formula of back-row piles is:

$e_{ab}=\left(1-a\right)e_a,(8)$

where $a$ is the area ratio of the front soil to the back soil of the rear pile, $a=\left(2bz\cot \eta -b^2\right)/\left(z\cot \eta -b^2\right).$

Although the theoretical calculation method proposed by Cheng Zhiyan considers the influence of the existence of the back-row piles on the sliding surface, the double-row piles as statically indeterminate structures do not consider the deformation coordination effect of the front- and back-row piles.

Xiong (1999) takes the different row spacing of double-row piles as the study’s starting point. When the row spacing is greater than 8 times the pile diameter, the double-row pile support structure can be regarded as an anchor pull structure. When the row spacing is between 4 and 8 times the pile diameter, the double-row pile supporting structure can be regarded as the portal frame structure inserted into the soil. The front and rear piles are rigidly connected with the connecting beam, and the internal force is calculated using the knowledge of structural mechanics. When the row spacing is less than 4 times the pile diameter, the calculation method of equivalent bending stiffness is proposed so that it can be calculated by the elastic fulcrum method and applied to engineering examples. The feasibility of this method is proved. The basic principle of equivalent bending stiffness is to represent the front-row pile, the back-row pile, and the soil between piles to the stiffness and convert it into an equivalent continuous wall through the formula, with the thickness of h1, h2, and h3, respectively.

Zhang (1993) proposed the modified ultimate earth pressure method to calculate the earth pressure on the pile body. He regarded the soil between piles as an infinite elastic body subject to lateral constraints. Considering the constraint effect of the crown beam on the top of the pile, it is taken that the transverse strain at a certain depth is 0, and the earth pressure acting on the back of the front-row pile is expressed as:

${\sigma }_1=\mu \gamma z/\left(1-\mu \right),(9)$

where $\mu$ is the Poisson’s ratio of the soil behind the wall, $\gamma$ is the gravity of soil behind the wall, and $z$ is the vertical distance from the ground to the calculation point.

The lateral earth pressure acting on the front row of piles $e_{pf}^{\prime }$ is calculated according to the reduced passive earth pressure, and the formula is expressed as:

$e_{pf}^{\prime }=k_1{e}_p=k_1\left(\gamma z{k}_p+2c\sqrt{k_p}\right),(10)$

where $k_1$ is the reduction coefficient of passive earth pressure, 0.5–0.7 based on experience, and $k_p$ is the coefficient of passive earth pressure.

The calculation of earth pressure acting on the back-row pile is ${\sigma }_1=\mu \gamma z/\left(1-\mu \right)$.

The earth pressure acting on the rear pile is between the active earth pressure and the static earth pressure, and the formula is:

$e_{ab}=k_2{e}_a=k_2\left(\gamma z{k}_a-2c\sqrt{k_a}\right),(11)$

where $k_2$ is the reduction coefficient of active earth pressure, 1.1–1.2 based on experience, and $k_a$ is the coefficient of active earth pressure.

At present, the elastic foundation beam method based on the Winkler theory is widely used in the research of the double-row pile theory. Its advantage is to consider the interaction between pile and soil, set the lateral soil spring on the pile–soil interface, and replace the coefficient of the horizontal subgrade reaction of soil between piles with spring stiffness. The soil pressure acting on each part of the pile is calculated by method “m” below the excavation surface of the foundation pit, and then the internal force of each part of the pile is obtained according to the calculation of the rigid bent frame in structural mechanics.

Liu (1992) believed that the soil between piles above the excavation face is disturbed by the lateral movement of the pile, so it is regarded as an infinite soil with lateral constraints. According to the physical equation of the plane strain problem, the distribution formula of soil pressure between piles along depth is obtained. It is considered that the back-row piles above the excavation face bear active earth pressure and the piles below the excavation face are calculated by the foundation beam method. Then, the differential equations of the front- and rear-piles and coupling beams are established and solved under certain boundary conditions.

After the double-row piles enter the working state, the soil between piles is disturbed by the translation of the pile body. The soil above the bottom of the foundation pit can be approximately regarded as semi-infinite soil subjected to lateral constraints, which can be simplified as a plane strain problem. According to the corresponding physical equation, assuming that the soil between piles does not have a transverse strain, the lateral pressure of soil between piles can be expressed as Chen et al. (2021) and Chen et al. (2021):

$\begin{array}{l}{p}_1=\mu \gamma y/\left(1-\mu \right),\\ p_x=b_0{k}_{h}x,\end{array}(12)$

where b0 is the calculated width of the pile, Kh is the coefficient of the horizontal foundation, and X is the lateral displacement.

Zheng and Liu (2004) proposed a new finite element model of a plane rod system considering pile–soil interaction based on the Winkler elastic foundation beam theory. By setting soil springs between double-row piles, the soil between piles is regarded as a thin compression layer to simulate the deformation coordination between piles and soil. The soil pressure under the excavation face is also replaced by the soil spring to simulate the passive soil pressure in front of the front-row pile in foundation pit excavation. Setting soil spring is advantageous in avoiding the artificial distribution of soil pressure distribution of the front- and rear-piles. When the row spacing of double-row piles is reasonable, the horizontal foundation reaction coefficient of soil between piles is used to replace the spring stiffness. The horizontal foundation reaction coefficient $k$ can be calculated by the following simplified formula:

$K=E_S/H,(13)$

where $E_s$ is the horizontal compressive modulus of soil between piles and $H$ is the thickness of the soil between piles.

Summary

In summary, previous studies on double-row pile support structures have made some achievements. However, as a more complex system, there are still some problems to be solved:

1) The deformation mechanism of the double-row pile supporting structure is still unclear, especially the deformation laws of the front-and rear-piles in the excavation process need to be further studied.

2) The distribution of soil pressure on the front- and rear-piles is still unclear. At present, most of the calculation methods are based on the Rankine semi-infinite soil theory to calculate the soil pressure between the front- and rear-piles, resulting in the calculation results of soil pressure being too great. The soil around the pile is regarded as a rigid-plastic body without considering the pile–soil interaction.

3) At present, the design of a double-row pile supporting structure in practical engineering mainly relies on the existing norms and engineering experience. The structure is relatively traditional, and it is necessary to further optimize and innovate under special construction conditions.

Therefore, it is necessary to further study the change of soil pressure and deformation mechanism of the double-row pile supporting structure to achieve a better engineering application effect.

Author Contributions

YZ: investigation and writing—original draft. LL: supervision and writing—review and editing. LZ: translation and checking the draft.

Funding

This study was supported by the Hebei Provincial Universities’ Basic Scientific Research Operating Expenses (No. JQN2020027), the doctoral Research Initiation Fund of North China University of Science and Technology (No. 28418599), and the Construction Cultural Research Project of “National Cultural Relics Protection and Utilization Demonstration Area” of Qing Dong Ling (QDLWHYJ0007). Fujian Provincial Transportation Technology Project (No.201911).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Begemann, H-K. S., and DeLeeuw, E. H. (1972). Horizontal Earth Pressures on Piles as a Result of Nearby Soil Fills. Proc. 5th ECSMFE. Madr. 1, 3–9.

Google Scholar

Chen, J. H., Zhao, H. B., He, F. L., and Zhang, J. W. (2021). Studying the Performance of Fully Encapsulated Rock Boltswith Modified Structural Elements. Int. J. Coal Sci. Technol. 8 (01), 64–76. doi:10.1007/s40789-020-00388-z

CrossRef Full Text | Google Scholar

Chen, Y. L., Zuo, J. P., and Liu, D. J. (2021). Experimental and Numerical Study of Coal-Rock Bimaterialcomposite Bodies Under Triaxial Compression. Int. J. Coal Sci. Technol. 8 (5), 908–924. doi:10.1007/s40789-021-00409-5

CrossRef Full Text | Google Scholar

Cheng, Z. Y., and Zhang, K. N. (2001). Discussion on Design and Calculation Method of Double Row Pile Retaining Structure. Geol. Explor. 37 (2), 88–93.

Google Scholar

Fan, S. J. (2009). Three-dimensional Analysis of Spatial Stress Model and Influencing Factors of Double Row Pile Foundation Pit Retaining Structure and Engineering Application. Qingdao, China: Qingdao University of Technology.

Google Scholar

Franx, C., and Boonstra, G. C. (1948). Horizontal Pressures on Pile Foundations. Proc.2nd ICSMFE.Rorrerdam. 4, 131–135.

Google Scholar

Gong, X. N. (1998). Deep Foundation Pit Engineering Design and Construction Manual. Beijing: China Architecture and Architecture Press.

Google Scholar

He, Y. H., Yang, B., and Jin, B. S. (1996). Study on Test and Calculation of Double Row Slope Protection Piles. J. Build. Struct. 17 (02), 58–66.

Google Scholar

HeymanBoersma, L. F. (1961). Bending Moments in Piles Due to Lateral Earth Pressure. Proe. 5th ICSMFE. Paris. (2), 425–429.

Google Scholar

Huang, Q. (1995). Deep Foundation Pit Supporting Engineering Design Technology. Beijing: China Architecture and Architecture Press.

Google Scholar

Li, L. J. (2013). Numerical Analysis and Field Test of Double Row Pile Retaining Structure. Taiyuan, China: Taiyuan University of Technology.

Google Scholar

Liu, Z. (1992). Analysis and Experimental Study of Double Row Retaining Pile Structure. J. Geotechnical Eng. 05, 76–80.

Google Scholar

Marche, R., and Lacroix, Y. (1972). Stabilité des culées de ponts établies sur des pieux traversant une couche molle. Can. Geotech. J. 9 (1), 1–24. doi:10.1139/t72-001

CrossRef Full Text | Google Scholar

Nicu, N. D., Antes, D. R., and Kessler, R. S. (1971). Field Measurements on Instrumented Piles under an Overpass Aburraent. Highw. Res. Rec. (354), 90–99.

Google Scholar

Oteo, C. S. (1974). Discussion to Poulos. JSMFD. ASCE 100 (GT4), 464–467. doi:10.1061/ajgeb6.0000039

CrossRef Full Text | Google Scholar

Springman, S. M. (1989). Lateral Loading on Piles Due to Simulated Embankment constructionPhD Thesis. City of Cambridge: University of Cambridge.

Google Scholar

Stewart, D. P., Jewell, R. J., and Randolph, M. F. (1994). Design of Piled Bridge Abutments on Soft Clay for Loading from Lateral Soil Movements. Géotechnique 44 (2), 277–296. doi:10.1680/geot.1994.44.2.277

CrossRef Full Text | Google Scholar

Technical specification(2021). Technical Specification for Building Foundation Pit Support, JGJ 120-2012 Industrial Standard of the People's Republic of China, 24–52.

Google Scholar

Tschebotariof, G. P. (1973). Foundations, Retaining,and Earth Structures. New York: McGraw-Hill.

Google Scholar

Wang, Z., and Liu, B. H. (2001). Discussion on Calculation Method of Double Row Pile. Northeast Seismol. study 17 (02), 64–68.

Google Scholar

Wenz, K. P. (1973). “Large Scale Tests for Determination of Lateral Loads on Piles in Soft Cohesive Soils,” in 8th International Conference on Soil Mechanics and Foundation Engineering (Moscow), 2, 2.

Google Scholar

Xiong, J. H. (1999). A Simplified Calculation Method for a Class of Double Row Pile Retaining Structures. Investigation Sci. Technol. 02, 32–34.

Google Scholar

Yang, D. J., and Wang, T. C. (2010). Research on Optimal Design and Engineering Application of Double Row Pile Retaining Structure. Eng. Mech. 27 (S2), 284–288.

Google Scholar

Zhang, M. (1993). Application and Discussion of Double Row Pile Supporting Structure in Deep Foundation Pit Excavation. Found. Treat. 4 (3), 42–47.

Google Scholar

Zheng, G., and Liu, C. (2004). Double Row Pile Analysis Considering Pile-Soil Interaction. J. Build. Struct. 25 (01), 99–106.

Google Scholar

Zhu, Q. K. (2013). Analysis and Research on Some Problems of Deep Foundation Pit Double Row Pile Supporting Structure System. Guangzhou, China: South China University of Technology.

Google Scholar