A new method for estimating multi-source water supply considering joint probability distributions under uncertainty

A new method integrating techniques of copula and interval estimation to estimate multi-source water supply was proposed. Using the copula theory, joint probability distributions of multiple water sources were constructed for the estimation of water supply. In addition, the interval estimation was used to obtain the interval of water supply under uncertainty for the formulation of water-diversion strategies and the efficient allocation of water resources. This method can give an in-depth investigation on correlations and synchronous–asynchronous characteristics of runoff variations for multiple water sources, thus solving the uncertainty problem of water supply. To demonstrate its applicability, the method was applied to a case study in the Xiong’an New Area, a future metropolis in North China. The results showed that log-normal distributions for the marginal distributions of source 2 (i.e., the Water Diversion Project from the Yellow River to Baiyangdian Lake) and source 3 (i.e., the South-to-North Water Diversion Project) were feasible. The combined channel source, composed of source 2 and source 3, provided [5.20, 12.10] × 10⁸ m³, and reservoir source provided [0.76, 3.60] × 10⁸ m³ of water resources to the Xiong’an New Area per year. Furthermore, without the implementation of multi-source combined water supply pattern in the Xiong’an New Area, there would be a large water supply deficit. This research can provide effective practical suggestions and guidance on water-resource planning and management.

1 Introduction

Due to the boom of population and the acceleration of urbanization progress worldwide, the contradiction between water supply and demand has become increasingly prominent (Song et al., 2020), especially in arid and semi-arid areas. Accordingly, many inter-basin water diversion projects have been constructed as the main means to alleviate water shortage (Yu et al., 2017; Zhang et al., 2019; Song et al., 2020), and examples include but are not limited to the South-to-North Water Diversion Project (Zhang et al., 2021). The required amount of water relocated through the water diversion projects can be calculated with two constraints, i.e., the amount of water demand of receiving regions and economic benefits from water relocation. Therefore, the estimation of water supply is of great significance for optimal allocations of regional water resources and improvements of water-use efficiency (Huang et al., 2021).

According to different estimation principles, water-supply estimation models fall into two categories: process-simulation models based on runoff generation and data-driven phenomenological models (Fleming et al., 2021). Using the two types of models, point estimation can be obtained; that is, the estimated water supply amount is a fixed value for a certain time and space. However, most hydrological runoff series are usually non-stationary with seasonal fluctuations (Ghasempour et al., 2021) leading to corresponding fluctuations in the water supply within a certain range when river runoff is used as a water source. In addition, urban areas are always in a dynamic state of development, so the point estimation of water supply is neither operable nor practical for water management in the real world. By contrast, interval estimation can not only effectively cover the range of water supply (Mykhailovych and Fryz 2020; Shimakawa and Murakami 2003), but also bring convenience to decision-makers of water resource management. With regard to the uncertainty of water supply and practical water planning and management, the interval estimation is desired.

In recent years, water supply systems have rapidly developed from a single water source to multiple water sources due to their obvious advantage of ensuring the reliability of urban water supply (Puleo et al., 2014; Zhang et al., 2019; An et al., 2021). This multi-source water supply faces new challenges in water resource management (Gao et al., 2018; Yu et al., 2017). On the one hand, available water supply along with spatial and temporal distributions of multiple water resources are different (Zhang et al., 2018; Song et al., 2020), resulting in the increased complexity of water supply management. On the other hand, the indefinite competition and complementarity of multiple water sources, as well as special water supply rules may cause conflicts in water supply calculations (Song et al., 2020). Therefore, it is necessary to conduct the multivariate joint probability analysis of multiple water sources, which is of great significance for reducing the water shortage risk through maintaining the water supply safety.

Copula is a powerful tool for constructing multivariate joint probability distributions and exploring dependency structures between random variables (Hao and Singh, 2016; Wang et al., 2017). As copula can analyze the interactions and interconnections between multiple variables quantitatively, it has been widely used to construct joint probability distributions of multiple variables. One of the main characteristics of copula is that the construction of joint probability distributions and marginal distributions is separated (Hao and Singh, 2016). To date, besides numerous investigations of multivariate flood frequency (Han et al., 2018; Naz et al., 2020), the frequency of rainfall (Zhang and Singh, 2007b; Kuhn et al., 2007), and multivariate drought events (Ayantobo et al., 2019; Li et al., 2020), some studies have reported successful applications of copula in the field of water resource allocation, e.g., the confirmation of compensative operating feasibility of the South-to-North Water Diversion Project (Huang and Niu, 2015). It has been proved that copula can offer technical and decision-making support for the smooth implementation of multi-source water supply.

Taking the Xiong’an New Area, a future metropolis in North China, as an example, this study attempted to propose a water supply estimation method based on joint probability distributions of multiple water sources. The specific objectives were: 1) to generate appropriate marginal distributions of single water source and further construct joint probability distributions of multiple water sources with copula; 2) to determine the interval estimation of water supply according to joint probability distributions of multiple water sources; and 3) to calculate the interval of water supply and guarantee the rate of water use, laying a necessary basis for water resource allocation. The proposed method considering joint probability distributions of multiple water sources for water supply estimation proved to be a reliable and reasonable method, which can provide scientific support for ensuring water supply safety through the optimal allocation of water resources.

2 Materials and methods

2.1 Study area

The Xiong’an New Area (115°37′E–116°20′E, 38°41′N–39°10′N) sits at the heart of the triangular area formed by the cities of Beijing, Tianjin, and Baoding. It is an important area of China’s strategic planning of the Coordinated Development of the Beijing–Tianjin–Hebei Region (Figure 1). It covers Xiong County, Rongcheng County, Anxin County, and other surrounding areas with an initial development zone covering 100 km². Currently, its economic development level and urbanization rate are far lower than the average level of the Hebei Province and China, still having much room for improvement. Consequently, the rapid development of the Xiong’an New Area has great demand for water resources.

FIGURE 1

FIGURE 1. The location of the Xiong’an New Area, North China.

Located in the mid-latitude zone, the Xiong’an New Area has a semi-arid temperate monsoon continental climate with four distinct seasons. The annual average precipitation and evaporation are 551.5 mm and 1,369 mm, respectively (Li et al., 2021; Yang et al., 2021). Eighty percent of the precipitation occurs from June to September during the flood season (Liu et al., 2020b). The average annual temperature is 11.7°C and the lowest average monthly temperature is −4.9°C (Yang et al., 2021). The study area used to be rich in wetland resources, including the Baiyangdian Lake and several rivers (Yang et al., 2021). However, in the past five decades, due to the dual effects of climate change and human activity interference, the input water from upstream rivers and reservoirs to the Baiyangdian Lake has gradually decreased with only a few rivers running all year round at present. Water shortage has become a major problem in the region (Zhao et al., 2021).

In general, the water resource conditions in the Xiong’an New Area are poor at this stage. The development of this area is limited due to the grim water resource situation and the contradiction between water supply and demand. In view of the current situation of water resources in the Xiong’an New Area, a large number of water diversion projects, mainly including the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir, the Water Diversion Project from the Yellow River to Baiyangdian Lake and the South-to-North Water Diversion Project, have been implemented with joint water supply patterns to alleviate regional water shortage (Zhang et al., 2019; Song et al., 2020; An et al., 2021).

2.2 Data collection

The runoff data of the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir (1956–2000), the Water Diversion Project from the Yellow River to Baiyangdian Lake (1919–2013) and the South-to-North Water Diversion Project (1980–2005) were obtained from the Hydrological Yearbook of the People’s Republic of China. The economic and social data of the Xiong’an New Area were obtained from the Baoding City Economic Statistics Yearbook, Hebei Province Economic Statistical Yearbook, Hebei Province National Economic and Social Development Statistical Bulletin, Anxin County Chronicles, and relevant data released by the local statistical bureau.

2.3 Methods

2.3.1 Framework for water-supply estimation based on joint probability distributions of multiple water sources

A new method considering the joint probability distributions of multiple water sources was proposed for water supply estimation. The amount of water supply was calculated under different scenarios by setting various frequency combinations of multiple water sources, so as to provide a quantitative basis for the optimal deployment of regional water resources. The technical roadmap of the study is shown in Figure 2. The main steps are as follows: 1) calculate the correlation coefficients of the runoff series for paired water sources; 2) generate and identify the optimal marginal distribution type of single water sources; 3) construct joint probability distributions of water sources with strong correlation by copula and plot the annual runoff frequency curves of water sources with weak correlation by using the Pearson-III distribution curve; 4) determine the amount of water supply of multiple water sources; and 5) calculate the guarantee rate of water use in sixteen schemes.

FIGURE 2

FIGURE 2. Framework for estimating the water supply for multiple water sources.

2.3.2 Measurement of runoff correlations between paired water sources

The Pearson, Spearman, and Kendall correlation coefficients have been widely used to measure the correlation of variables (Wang et al., 2017). Among them, the Pearson correlation coefficient is often used to measure the correlation between two variables that are linearly related (Hao and Singh, 2016; Wang et al., 2017). In cases where the normal assumption is not true or non-linear correlation exists between variables, the Pearson correlation coefficient is not applicable while the Spearman correlation coefficient and Kendall correlation coefficient can be used instead (Hao and Singh, 2016). More details can be found in the published literature by Wang et al. (2017). We used the Pearson, Spearman, and Kendall correlation coefficients to measure the correlation of random variables.

2.3.3 Construction of marginal distributions and evaluation of fitting degree

The kernel density estimation (KDE) was used for obtaining the probability density function to define univariate marginals. Five distributions including normal distribution, log-normal distribution, Gamma distribution, Weibull distribution, and exponential distribution were selected as candidates to fit the marginal distributions of multiple water sources, with their parameters being estimated by the maximum likelihood method (MLE). According to the Akaike information criterion (AIC), Bayesian information criterion (BIC), and Kolmogorov–Smirnov test (K–S test), appropriate marginal distributions and parameters were determined (Tu et al., 2016). In addition, the fitting of theoretical frequency and empirical frequency was compared. The empirical frequency was calculated by using Gringorten formula (Gringorten, 1963; Zhang and Singh, 2007a).

2.3.4 Construction of joint probability distributions of multiple water sources

Copula can be used to construct multivariate joint probability distributions by linking univariate marginal distributions which can characterize dependence structures among variables (Yu and Zhang, 2021). The main advantage of copula is that it can connect any form of marginal distribution. Moreover, the construction of joint probability distributions is independent of the marginal distributions (Hao and Singh, 2016; Wang et al., 2017). Copula has great flexibility to characterize the dependency between variables (Yu and Zhang, 2021), and thus has become a powerful tool for constructing multivariate joint probability distributions and exploring the correlation among random variables (Wang et al., 2017). Based on Sklar’s theorem (Nelsen, 2006), $\mathrm{H}\left({\mathrm{x}}_1,{\mathrm{x}}_2,\cdots ,{\mathrm{x}}_{\mathrm{n}}\right)$ is the joint distribution with marginal distributions of ${\mathrm{H}}_1\left({\mathrm{x}}_1\right),{\mathrm{H}}_2\left({\mathrm{x}}_2\right)\dots {\mathrm{H}}_{\mathrm{n}}\left({\mathrm{x}}_{\mathrm{n}}\right)$. For any $\mathrm{x}\in {\mathrm{R}}_{\mathrm{n}}$, the distribution function is shown in Eq. 1. If ${\mathrm{H}}_1\left({\mathrm{x}}_1\right),{\mathrm{H}}_2\left({\mathrm{x}}_2\right)\dots {\mathrm{H}}_{\mathrm{n}}\left({\mathrm{x}}_{\mathrm{n}}\right)$ are all continuous, then ${\mathrm{C}}_{\theta }$ serving as a connection operator is unique.

$\mathrm{H}({\mathrm{x}}_1,{\mathrm{x}}_2,\cdots ,{\mathrm{x}}_{\mathrm{n}})={\mathrm{C}}_{\theta }(({\mathrm{H}}_1\left({\mathrm{x}}_1\right),{\mathrm{H}}_2\left({\mathrm{x}}_2\right),\cdots ,{\mathrm{H}}_{\mathrm{n}}\left({\mathrm{x}}_{\mathrm{n}}\right))(1)$

where $\theta$ is the parameter of copula; ${\mathrm{C}}_{\theta }$ is a copula function; and ${\mathrm{H}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{i}}\right)$ is the marginal distribution for the i-th random variable ${\mathrm{x}}_{\mathrm{i}}$.

There are many types of copulas with different dependency characteristics (Yu and Zhang, 2021). A variety of copulas can be used for the construction of multivariate joint probability distributions, e.g., Archimedean copulas and Elliptical copulas. Archimedean copulas contain only one parameter and are easy to generate (Salvadori and Michele, 2010; Serinaldi and Grimaldi, 2007), thus having a high utilization frequency in hydrology (Song and Singh, 2010). In this study, Clayton copula, Frank copula, Gaussian copula, Gumbel copula, and BB5 copula were selected as the candidate copulas to construct joint probability distributions of multiple water sources. Frank copula and Gaussian copula exhibited symmetric dependence behavior. Both Clayton copula and Gumbel copula permitted asymmetric dependence (Hao and Singh, 2016); however, in contrast to Gumbel copula, which exhibits strong right tail dependence, Clayton copula exhibits strong left tail dependence. Joe’s BB5 copula belongs to extreme-value copulas (Genest and Favre, 2007; Joe, 1997; Sadegh et al., 2017) which can be used to model the dependence structure of rare events or extreme values (Hao and Singh, 2016). The maximum likelihood estimation (MLE) method was used to obtain the parameters of these five candidate copulas. The goodness-of-fit test was performed by using the square Euclidean distance to test the fitting degree to select an optimal copula.

The three-dimensional and contour figures of joint cumulative distributions of multiple water sources were used to calculate the amount of water supply in the multi-source combined water supply system. Each curve in the contour figures represented a joint probability value. The projection of the points on this curve on x-axis and y-axis represented the water supply from each of the two water sources. The joint water supply at a certain joint probability was equal to the sum of projections of this point on the x-axis and y-axis. Since there were an infinite number of points on this curve, the amount of water supply fluctuated within a certain range.

2.3.5 Guarantee rate of water use for multiple water sources

With the implementation of water diversion projects including the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir, the Water Diversion Project from the Yellow River to Biayangdian Lake, and the South-to-North Water Diversion Project, a multi-source combined water supply pattern was formed in the Xiong’an New Area. The guarantee rate of water use under various encounter situations can be calculated based on the different occurrence frequency combinations for the aforementioned three projects which reflect the synchronous–asynchronous characteristics of runoff for these water sources. Based on the runoff correlation results shown in Table 1, water sources can be divided into two groups, which were, a combined channel source with strong correlation and a reservoir source with weak correlation. Among them, the combined channel source here contained the Water Diversion Project from the Yellow River to Baiyangdian Lake and the South-to-North Water Diversion Project; the reservoir source was the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir. Since the combined channel source and reservoir source were independent of each other, the concept of mutually independent events from the probability theory was used (Michael Steele, 2015; Zhang et al., 2018; Zhang et al., 2019). Assuming that the combined channel source was event A and the reservoir source was event B, the probability that the combined channel source and reservoir source would occur simultaneously at different encounter probabilities was:

$\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}{\mathrm{B}}_{\mathrm{j}}\right)=\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\right)\times \mathrm{P}\left({\mathrm{B}}_{\mathrm{j}}\right)(2)$

where $\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}\right)$ is the joint probability i of combined channel source A; $\mathrm{P}\left({\mathrm{B}}_{\mathrm{j}}\right)$ is the runoff frequency j of reservoir source B; and $\mathrm{P}\left({\mathrm{A}}_{\mathrm{i}}{\mathrm{B}}_{\mathrm{j}}\right)$ is the encounter probability of the combined channel source A with the joint probability i and reservoir source B with the runoff frequency j.

TABLE 1

TABLE 1. The results of runoff correlation measurements for multiple water sources by various correlation coefficients.

The water shortages are usually derived from the contradiction between water supply and water demand. The guarantee rate of water use, defined as the degree to which water demand is met, was mainly based on the comparison between the actual water supply and water demand of the water resource system (Zhang et al., 2019). The guarantee rate of water use ranges from 0 to 1; in the case that the actual water supply was greater than water demand, the guarantee rate of water use was 1.

$\mathrm{G}={\mathrm{Q}}_{\mathrm{s}}/{\mathrm{Q}}_{\mathrm{d}}(3)$

where $\mathrm{G}$ is the guarantee rate of water use; ${\mathrm{Q}}_{\mathrm{s}}$ is the amount of water supply (10⁸ m³); and ${\mathrm{Q}}_{\mathrm{d}}$ is the amount of water demand (10⁸ m³).

3 Results

3.1 Measurement of runoff correlations between multiple water sources

The Xiong’an New Area has three external water sources, namely, the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir (source 1), the Water Diversion Project from the Yellow River to Baiyangdian Lake (source 2), and the South-to-North Water Diversion Project (source 3). The results of runoff correlation measurements for the three water sources by various correlation coefficients are shown in Table 1. It can be seen that, three correlation coefficients between source 2 and source 3 were high (specifically, the Pearson correlation coefficient was 0.82, the Spearman correlation coefficient was 0.73, and the Kendall correlation coefficient was 0.60), indicating a strong correlation between source 2 and source 3. Therefore, copula can be used to construct joint probability distributions of source 2 and source 3. The values of the aforementioned three correlation coefficients of source 1 and source 2 were small, indicating a weak correlation between them. Correlation coefficients of source 1 and source 3 were also small. Therefore, copulas were not suitable for constructing joint probability distributions of source 1 and source 2/source 3 due to their weak correlations. The Pearson type III (P-III) distribution was used to fit the distribution of source 1 for hydrological frequency analysis.

3.2 Water supply estimation based on joint probability distributions of multiple water sources

3.2.1 Marginal distribution analysis of water sources

The Cullen and Frey map is a good summary of the properties of marginal distributions. Two Cullen and Frey maps were plotted to preliminarily identify the marginal distribution types of source 2 and source 3 (Figure 3). As Figure 3 shows, compared to other types of marginal distributions, log-normal distribution was more suitable for marginal distributions of both source 2 and source 3. The results of the fitting degree evaluation for source 2 and source 3 with candidate marginal distributions are summarized in Table 2. The smaller the values of AIC and BIC, the better the fitting effects of candidate marginal distributions (Zang et al., 2022). For source 2, log-normal distribution presented the lowest AIC and BIC (243.28 and 245.30, respectively) among the five candidate marginal distributions and passed the K–S test. For source 3, log-normal distribution also presented the lowest AIC and BIC (267.87 and 269.96, respectively) among the five candidate marginal distributions and passed the K–S test. In addition, the results of fitting degree between theoretical frequency and empirical frequency show that the log-normal distribution presented low values of SSE and RMSE, indicating a good performance in fitting the marginal distributions of source 2 and source 3 (Supplementary Table S1). Therefore, log-normal distribution was employed to describe the marginal distributions of source 2 and source 3. Parameter estimation results of the marginal distribution for runoff volume of source 2 and source 3 can be found in Supplementary Table S2. Figure 4 shows the fitting distribution results of source 2 with log-normal distribution. Figure 5 shows the fitting distribution results of source 3 with log-normal distribution. The results further confirmed that it was satisfactory to fit marginal distributions with log-normal distribution for source 2 and source 3.

FIGURE 3

FIGURE 3. Cullen and Frey maps of (A) source 2 and (B) source 3.

TABLE 2

TABLE 2. AIC and BIC results of five candidate marginal distributions.

FIGURE 4

FIGURE 4. Fitting distribution results of source 2 with log-normal distribution.

FIGURE 5

FIGURE 5. Fitting distribution results of source 3 with log-normal distribution.

3.2.2 Joint probability distribution analysis of water sources

Among the five candidate copulas (i.e., Clayton copula, Frank copula, Gaussian copula, Gumbel copula, and BB5 copula), Clayton copula exhibited the smallest square Euclidean distance, suggesting the highest fitting effect. Therefore, Clayton copula was selected to construct joint probability distributions of source 2 and source 3. Figure 6 shows the three-dimensional contour figures of joint probability density distributions of the runoff volume for source 2 and source 3. According to Figure 6, joint probability distributions and dependency characteristics of the runoff volume for various combinations of water sources at specific probability levels were estimated. On the whole, joint probability density distributions of the runoff volume fitted by Clayton copula were bell-shaped with no symmetry on both sides. The overall upper-left trend indicated that variations of joint probability densities of the runoff volume were greatly affected by source 3. Therefore, it was inferred that the high joint probability of the runoff volume would not easily occur in the low-value interval of source 3 (less than 400 million m³). As shown in Figure 6B, runoff volume contours were dense in the low-value interval (less than 400 million m³) and sparse in the high-value interval, indicating that the variation of joint probability was much significant in the low-value interval.

FIGURE 6

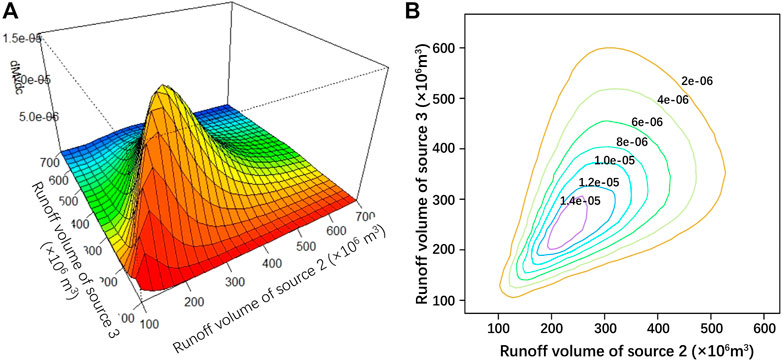
FIGURE 6. (A) Three-dimensional and (B) contour figures of joint probability density distributions of source 2 and source 3.

Figure 7 shows the three-dimensional joint cumulative distributions and their contour figures of runoff volume for source 2 and source 3. As can be seen, the joint cumulative probability increased with the increase of runoff volume of a single water source. When the joint cumulative probability was larger than 0.6, the contour spacing became sparse and the isosurface spacing became larger. In other words, variations of joint cumulative probabilities became less significant in high-value intervals (greater than 0.6) when compared to low-value interval. Through an in-depth analysis of joint cumulative distributions in Figure 7, the encounter situations when the joint probability was equal to or less than a certain probability were obtained. Then, the interval estimations of water supply under different encounter situations were obtained. Figure 7 also shows that when joint cumulative probabilities were 12.5%, 37.5%, 62.5%, and 87.5%, the corresponding interval estimations of water supply were [5.20, 8.90] × 10⁸ m³, [6.80, 9.70] × 10⁸ m³, [8.30,10.40] × 10⁸ m³, [11.40, 12.10] × 10⁸ m³, respectively. Therefore, source 2 and source 3 provided [5.20, 12.10] × 10⁸ m³ of water resources to the Xiong’an New Area per year.

FIGURE 7

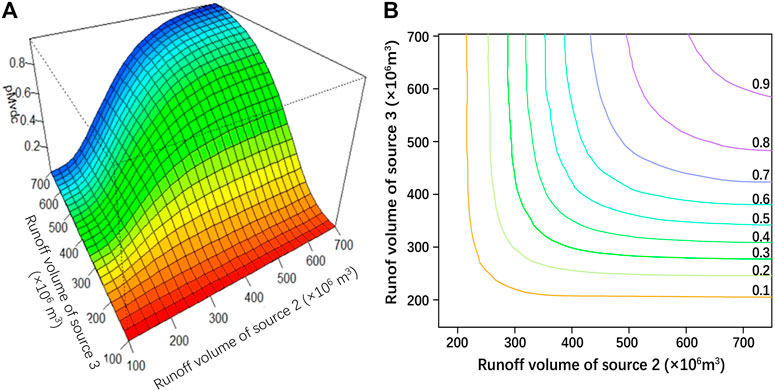
FIGURE 7. (A) Three-dimensional and (B) contour figures of joint cumulative distributions of source 2 and source 3.

3.3 Water supply estimation based on the runoff frequency analysis of reservoirs

The Pearson-III distribution was used to fit the marginal distribution of the runoff volume of the Xidayang Reservoir and the Wangkuai Reservoir. The Pearson-III distribution is asymmetrically unimodal with a finite boundary on one side but infinite on the other. It is one of the most popular distributions for hydrological frequency analysis (Liu et al., 2015; Wang et al., 2017). The parameters of Pearson-III distribution were determined by using the curve-fitting method and the results of the statistical parameters are shown in Table 3. The runoff frequency curves were drawn by using MATLAB software and the fitting lines were optimized by the non-linear least-square method (Figures 8, 9). According to Figure 8, when the frequencies were 12.5%, 37.5%, 62.5%, and 87.5%, the runoff volume of the Wangkuai Reservoir were 11.80 × 10⁸ m³, 5.60 × 10⁸ m³, 3.90 × 10⁸ m³, and 2.40 × 10⁸ m³, respectively. According to Figure 9, when the frequencies were 12.5%, 37.5%, 62.5%, and 87.5%, the runoff volume of the Xidayang Reservoir were 8.70 × 10⁸ m³, 4.70 × 10⁸ m³, 2.60 × 10⁸ m³, and 2.10 × 10⁸ m³, respectively. Considering water storage requirements as well as basic ecological base flow requirements of the Wangkuai Reservoir and the Xidayang Reservoir, 3.60 × 10⁸ m³, 2.25 × 10⁸ m³, 1.22 × 10⁸ m³, and 0.76 × 10⁸ m³ of water resources were provided to the Xiong’an New Area when the frequencies were 12.5%, 37.5%, 62.5%, and 87.5%, respectively.

TABLE 3

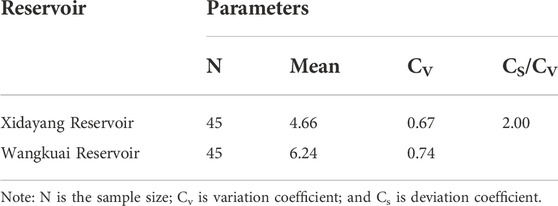
TABLE 3. The statistical parameters of the runoff frequency curves for the Xidayang Reservoir and the Wangkuai Reservoir (Unit: 10⁸ m³).

FIGURE 8

FIGURE 8. Annual runoff frequency curve of Wangkuai Reservoir.

FIGURE 9

FIGURE 9. Annual runoff frequency curve of Xidayang Reservoir.

3.4 Calculation of the guarantee rate of water use

Figure 10 shows the variations of the guarantee rate of water use in the Xiong’an New Area when combined channel source or reservoir source was used as the only water source. As seen from Figure 10A, when a reservoir source was the only water source, the guarantee rate of water use for the four schemes (i.e., frequencies = 12.5%, 37.5%, 62.5%, and 87.5%, respectively) was generally low (less than 0.1), indicating a large water supply deficit in the region. As can be seen in Figure 10B, when a combined channel source was the only water source, the guarantee rate of water use increased with the increase of joint probabilities ranging from 0.07 to 1 for the four schemes (i.e., joint probabilities = 12.5%, 37.5%, 62.5%, and 87.5%, respectively). It was worth noting that the guarantee rate of water use reached 1 when the joint probability increased to 87.5%. Therefore, the combined channel source was an indispensable water source for the Xiong’an New Area. By comparing Figures 10A, B, it can be found that only the multi-source combined water supply system (namely, both combined channel source and reservoir source) can ensure a high guarantee rate of water use for improving water supply safety.

FIGURE 10

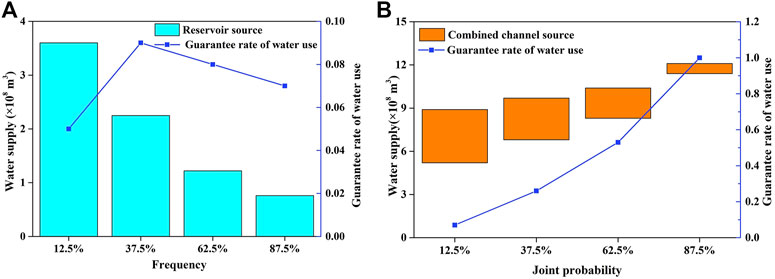
FIGURE 10. The amount of water supply and guarantee rate of water use for four schemes when (A) the reservoir source; and (B) the combined channel source was the only water source.

To analyze variations of the guarantee rate of water use under different encounter situations, sixteen schemes were set up (Table 4), and the results are shown in Figure 11. It can be seen that the Xiong’an New Area had a low guarantee rate of water use (less than 0.6) in most cases, showing that there existed a certain risk of water shortages. With the increase of water supply (from 1.10 × 10⁸ m³ to 10.82 × 10⁸ m³), the guarantee rate of water use gradually increased (from 0.11 to 1), which was consistent with the trend shown in Figure 10. In addition, under the same frequency, the guarantee rate of water use increased significantly with the increase of the joint probability. Without the combined channel source, there would be a large gap between water supply and demand. These illustrated that the combined channel source had a great impact on the mitigation of the water shortage risk. Therefore, the implementation of multi-source combined water supply pattern was a necessary way to improve regional water security.

TABLE 4

TABLE 4. Water supply scheme settings under different encounter situations.

FIGURE 11

FIGURE 11. Sixteen schemes when both the combined channel source and reservoir source were used.

4 Discussion

4.1 Analysis of correlations and variation pace differences of runoff in multi-source system using copula

The estimation of water supply of the multi-source combined water supply system is essentially a stochastic sequential decision-making process with uncertainty (Song et al., 2020). Water sources located in different hydrological zones usually have complex correlations and synchronous–asynchronous characteristics of runoff variations in the multi-source system. However, the commonly used methods have limitations in characterizing the correlation and dependence structure between water sources. The proposed copula-based method conducted a joint probability analysis of three water sources and comprehensively assessed the overall characteristics of water diversion events, overcoming the shortcomings of conventional methods. Hou et al. (2022) predicted that the water supply from upstream reservoirs in 2025 were 0.29 × 10⁸–3.71 × 10⁸ m³, which were basically consistent with our results of interval estimations of water supply. However, their results about the total available water supply were based on the simple linear composition for multiple water sources, without considering their correlations and synchronous–asynchronous characteristics of runoff variations in actual situations. The proposed method made up this deficit by using copulas to take account of various encounter probabilities in a multi-source water supply system, improving the reliability of the estimation results. The results demonstrated the feasibility of the copula-based method considering joint probability distributions of water sources for estimating the water supply in a multi-source combined water supply system. Successful applications of this method have also been reported in the research on the Yellow River Basin, Yangtze River Basin, Yalong River Basin, and Indus River Basin (Huang and Niu, 2015; Gao et al., 2018; Lei et al., 2018; Nazir et al., 2020; Wu et al., 2020; An et al., 2021), demonstrating that the copula-based method is both reliable and generalizable in different regions or basins.

4.2 Treatment of interrelationship between hydrological variables considering their distribution characteristics using copula

In a previous analysis of multivariate hydrological events, some models were built based on the assumption of linear correlation between variables, but this was not in accordance with the fact of complex dependencies usually existing among variables (Hao and Singh, 2016). Another frequently used assumption was that random variables conformed to the same marginal distribution. However, the marginal distributions of different random variables in hydrological events tend to be inconsistent. As a result, these assumptions reduce the accuracy and reliability of the models. As an important connection tool, copula has the following two prominent advantages. First, it can completely describe the correlation structure between random variables with arbitrary marginal distributions by analyzing their joint probability distributions (Cai et al., 2021; Hao and Singh, 2016; Wang et al., 2017). Second, unlike other multivariate parametric distribution models, copula-based methods allow us to separate the univariate margins from the dependence structure for the construction of joint probability distributions with the characteristics of flexibility and diversity (Czado and Nagler, 2022; Hao and Singh, 2016). Based on this advantage, the selection of the copula function becomes more flexible; for example, the tail dependency can be captured and expressed using certain copula functions which is essential in assessing risks such as water scarcity in hydrological process analysis (Ayantobo et al., 2019; Hao and Singh, 2016; Liu X. et al., 2020). Interestingly, we found that different copulas were used for solving the same hydrological-related problem. The reason is that copulas lack a physical basis in hydrology; thus, they cannot determine the theoretical joint distribution models of each random variable in a physical sense (Hou et al., 2021). Therefore, the selection of a suitable copula instead of a complex one is particularly critical (Zhang et al., 2021).

4.3 Applicability of interval estimations using copula in water supply management

From Figure 7, the water supply from source 2 and source 3 to the Xiong’an New Area per year was obtained in the form of intervals using copulas. According to Zhang (2017), the corresponding amount of water supply by these two sources were 2 × 10⁸ m³ and 4 × 10⁸ m³; that is, a total of approximately 6 × 10⁸ m³, which was consistent with our interval estimations of water supply. According to Lv et al. (2021), the water consumption should be controlled at 9.8 × 10⁸ m³ per year in the context of focusing on the socioeconomic development and eco-environmental protection, and was generally consistent with our interval estimation results of water supply. In addition, the interval estimation of water supply of source 2 and source 3 was almost the same as the amount of water supply of the actual planning and management (Zhang, 2017). These results confirmed the reliability of our relationship analysis between water supply and water consumption when compared with deterministic results.

Actually, as the results from copula-based methods are displayed correspondingly in the form of intervals under some certain probabilities, it overcomes the defect of point estimation results that cannot take advantage of error estimations when conventional deterministic models are applied (Mykhailovych and Fryz, 2020; Shimakawa and Murakami, 2003). Obviously, interval estimations are more reasonable than point estimations and thus more appropriate for real-world decision-making. For example, as the water supply is determined by the water demand of the receiving area for water diversion projects (Zhang et al., 2021), the water supply amount fluctuates over time without keeping a deterministic value. Considering that the joint probability reflects the occurrence of stochastic events, the multi-source water supply under uncertainty can be modeled by bivariate joint probability distribution functions using copula-based methods (Gao et al., 2018). For bivariate joint probability distributions of variables A and B, there are infinite combinations satisfying the solution conditions under a given occurrence probability characterizing their coexistence status (Dodangeh et al., 2020). For example, the joint probabilities of water supply were set based on the local situations, acquiring various combinations of water supply scenarios. These combinations can be selected for formulating alternative schemes of water resource planning and management with a comprehensive consideration of actual situations, e.g., water supply objectives, social and economic benefits, and so on. In summary, owing to its flexibility and adaptability, copula-based methods can be used to solve joint probability distribution problems of water sources for estimating the water supply in multi-source combined water supply system, expanding its application scopes in the field of water resource research.

5 Conclusions

Taking the Xiong’an New Area in northern China as a typical area, we proposed a new method for the estimation of water supply that considered the joint probability distributions of multiple water sources under uncertainty. Considering runoff correlations between water sources and synchronous–asynchronous characteristics of the water supply capacity related to runoff variations for water sources in different hydrological regions, the copula was used to construct joint probability distributions for describing the dependence structure of a multi-source water supply system and estimating water supply under different encounter situations. It was an innovative application of copulas into the field of water supply estimation. Interval estimation was used in this research to represent the estimation results, which can effectively predict the fluctuation ranges of water supply amount for the convenience of the practical operation of optimal regional water resource allocation. Considering different encounter probabilities of runoff variations, the Water Diversion Project from the Yellow River to Baiyangdian Lake and the South-to-North Water Diversion Project can provide [5.20, 12.10] × 10⁸ m³ of water resources, and the Water Diversion Project from Xidayang Reservoir and Wangkuai Reservoir can provide [0.76, 3.60] × 10⁸ m³ of water resources to the Xiong’an New Area per year with the multi-source water supply pattern. The water demand of the Xiong’an New Area can be met through the joint operation of these three water sources.

Due to the limitation of the data availability, this research did not take water quality into consideration. Water quality and water quantity are equally important properties for the water supply. If there was not enough water that met the water quality requirements of regional production and domestic water, a risk of available water shortage would occur (Song et al., 2020). Therefore, the influence of water quality constraints should be highlighted in the estimation of water supply. In addition, besides surface water that accounted for a large proportion of regional water supply, groundwater and reclaimed water should also be considered in subsequent studies.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CW: conceptualization, methodology, validation and writing—original draft preparation. XW: writing—review and editing, supervision. JF: software, resources, and visualization. ZW: software, data curation, and visualization. CL: supervision. QL: supervision. JY: editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by the National Natural Science Foundation of China (Grant Nos. 52070024, 52270194 and 51679008).

Acknowledgments

The authors would like to extend their special thanks to the editor from the AJE team for editing the English text of a draft of this manuscript. The authors would also like to extend their special thanks to the editor and the reviewers for their valuable comments and suggestions in greatly improving the quality of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.929613/full#supplementary-material

References

An, C., Dou, M., Zhang, J., and Li, G. (2021). Method for analyzing copula-based water shortage risk in multisource water supply cities. Water Resour. manage. 35 (14), 4877–4894. doi:10.1007/s11269-021-02975-4

CrossRef Full Text | Google Scholar

Ayantobo, O. O., Li, Y., and Song, S. (2019). Copula-based trivariate drought frequency analysis approach in seven climatic sub-regions of mainland China over 1961-2013. Theor. Appl. Climatol. 137 (3-4), 2217–2237. doi:10.1007/s00704-018-2724-x

CrossRef Full Text | Google Scholar

Cai, Y., Cai, J., Chen, D., Xie, Y., and Feng, J. (2021). Development of an integrated prediction-optimization modeling approach for coupled risk management of water and energy nexus systems. Sci. Total Environ. 781, 146744. doi:10.1016/j.scitotenv.2021.146744

CrossRef Full Text | Google Scholar

Czado, C., and Nagler, T. (2022). Vine copula based modeling. Annu. Rev. Stat. Appl. 9 (1), 453–477. doi:10.1146/annurev-statistics-040220-101153

CrossRef Full Text | Google Scholar

Dodangeh, E., Singh, V. P., Binh Thai, P., Yin, J., Yang, G., and Mosavi, A. (2020). Flood frequency analysis of interconnected rivers by copulas. Water Resour. manage. 34 (11), 3533–3549. doi:10.1007/s11269-020-02634-0

CrossRef Full Text | Google Scholar

Fleming, S. W., Vesselinov, V. V., and Goodbody, A. G. (2021). Augmenting geophysical interpretation of data-driven operational water supply forecast modeling for a Western US river using a hybrid machine learning approach. J. Hydrology 597, 126327. doi:10.1016/j.jhydrol.2021.126327

CrossRef Full Text | Google Scholar

Gao, X., Liu, Y., and Sun, B. (2018). Water shortage risk assessment considering large-scale regional transfers: A copula-based uncertainty case study in lunan, China. Environ. Sci. Pollut. Res. 25 (23), 23328–23341. doi:10.1007/s11356-018-2408-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Genest, C., and Favre, A. C. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 12, 347–368. doi:10.1061/(ASCE)1084-0699(2007)12:4(347)

CrossRef Full Text | Google Scholar

Ghasempour, R., Azamathulla, H. M., and Roushangar, K. (2021). EEMD and VMD based hybrid GPR models for river streamflow point and interval predictions. Water Supply 21 (7), 3960–3975. doi:10.2166/ws.2021.151

CrossRef Full Text | Google Scholar

Gringorten, I. I. (1963). A plotting rule for extreme probability paper. J. Geophys. Res. 68, 813–814. doi:10.1029/JZ068i003p00813

CrossRef Full Text | Google Scholar

Han, C., Liu, S., Guo, Y., Lin, H., Liang, Y., and Zhang, H. (2018). Copula-based analysis of flood peak level and duration: Two case studies in taihu basin, China. J. Hydrol. Eng. 23 (6), 05018009. doi:10.1061/(ASCE)HE.1943-5584.0001661

CrossRef Full Text | Google Scholar

Hao, Z., and Singh, V. P. (2016). Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. Earth Environ. 40 (4), 549–578. doi:10.1177/0309133316632460

CrossRef Full Text | Google Scholar

Hou, E., Zhang, S., Wang, R., Zhang, C., Yang, H., Duan, J., et al. (2021). Change in water quality and its relationship to water quantity in tai’an section of the dawen River Basin. J. Irrigation Drainage 40, 137–144. in Chinese with English abstract. doi:10.13522/j.cnki.ggps.2021141

CrossRef Full Text | Google Scholar

Hou, X., Yang, R., Hou, B., Lu, F., Zhao, Y., Zhou, Y. Y., et al. (2022). Joint allocation of multiple water sources in Xiongan New Area under complex and uncertain environment. Water Resour. Hydropower Eng. 53 (1), 45–54. in Chinese with English abstract. doi:10.13928/j.cnki.wrahe.2022.01.005

CrossRef Full Text | Google Scholar

Huang, H., and Niu, J. (2015). Compensative operating feasibility analysis of the west route of South-to-North Water transfer project dased on M-copula function. Water Resour. manage. 29 (11), 3919–3927. doi:10.1007/s11269-015-1036-5

CrossRef Full Text | Google Scholar

Huang, H., Zhang, Z., and Song, F. (2021). An Ensemble-Learning-Based method for short-term water demand forecasting. Water Resour. manage. 35 (6), 1757–1773. doi:10.1007/s11269-021-02808-4

CrossRef Full Text | Google Scholar

Joe, H. (1997). “Multivariate models and dependence concepts,” in Monographs in Statistics and probability (London: Chapman & Hall).

Google Scholar

Kuhn, G., Khan, S., Ganguly, A., and Branstetter, M. (2007). Geospatial–temporal dependence among weekly precipitation extremes with applications to observations and climate model simulations in South America. Adv. Water Resour. 30, 2401–2423. doi:10.1016/j.advwatres.2007.05.006

CrossRef Full Text | Google Scholar

Lei, X., Tan, Q., Wang, X., Wang, H., Wen, X., Wang, C., et al. (2018). Stochastic optimal operation of reservoirs based on copula functions. J. Hydrology 557, 265–275. doi:10.1016/j.jhydrol.2017.12.038

CrossRef Full Text | Google Scholar

Li, Z., Shao, Q., Tian, Q., and Zhang, L. (2020). Copula-based drought severity-area-frequency curve and its uncertainty, a case study of Heihe River basin, China. Hydrology Res. 51 (5), 867–881. doi:10.2166/nh.2020.173

CrossRef Full Text | Google Scholar

Li, Z., Sun, W., Chen, H., Xue, B., Yu, J., and Tian, Z. (2021). Interannual and seasonal variations of hydrological connectivity in a large shallow wetland of north China estimated from Landsat 8 Images. Remote Sens. 13 (6), 1214. doi:10.3390/rs13061214

CrossRef Full Text | Google Scholar

Liu, D., Guo, S., Lian, Y., Xiong, L., and Chen, X. (2015). Climate-informed low-flow frequency analysis using nonstationary modelling. Hydrol. Process. 29 (9), 2112–2124. doi:10.1002/hyp.10360

CrossRef Full Text | Google Scholar

Liu, X., Pan, F., Cai, W., and Peng, R. (2020a). Correlation and risk measurement modeling: A markov-switching mixed Clayton copula approach. Reliab. Eng. Syst. Saf. 197, 106808. doi:10.1016/j.ress.2020.106808

CrossRef Full Text | Google Scholar

Liu, Y., Cui, B., Du, J., Wang, Q., Yu, S., and Yang, W. (2020b). A method for evaluating the longitudinal functional connectivity of a river-lake-marsh system and its application in China. Hydrol. Process. 34 (26), 5278–5297. doi:10.1002/hyp.13946

CrossRef Full Text | Google Scholar

Lv, L., Jiang, B., Geng, L., Zhang, H., and Yu, X. (2021). Water use intensity and water demand prediction of Xiongan New Area under different development scenarios. Hydro-science Eng. 1, 18–25. in Chinese with English abstract. doi:10.12170/2020040100

CrossRef Full Text | Google Scholar

Michael Steele, J. (2015). Probability theory: Formal international encyclopedia of the social & behavioral sciences. UK: Cambridge University Press.

Google Scholar

Mykhailovych, T., and Fryz, M. (2020). “Model and information technology for hourly water consumption interval forecasting,” in Proceedings of the 2020 IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 25-29 Feb. 2020, 341–345.

CrossRef Full Text | Google Scholar

Naz, S., Jamil, S. S., and Iqbal, M. J. (2020). Archimedean copula-based bivariate flood-frequency analysis on Sukkur, Pakistan. Arab. J. Geosci. 13 (7), 282. doi:10.1007/s12517-020-5223-1

CrossRef Full Text | Google Scholar

Nazir, H. M., Hussain, I., Faisal, M., Shoukry, A. M., Sharkawy, M. A. W., Al-Deek, F. F., et al. (2020). Dependence structure analysis of multisite river inflow data using vine copula-CEEMDAN based hybrid model. Peerj 8, e10285. doi:10.7717/peerj.10285

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelsen, R. B. (2006). An introduction to copulas. New York: Springer.

Google Scholar

Puleo, V., Fontanazza, C. M., Notaro, V., and Freni, G. (2014). Multi sources water supply system optimal control: A case study. Procedia Eng. 89, 247–254. doi:10.1016/j.proeng.2014.11.184

CrossRef Full Text | Google Scholar

Sadegh, M., Ragno, E., and Aghakouchak, A. (2017). Multivariate copula analysis toolbox (MvCAT): Describing dependence and underlying uncertainty using a bayesian framework. Water Resour. Res. 53, 5166–5183. doi:10.1002/2016WR020242

CrossRef Full Text | Google Scholar

Salvadori, G., and Michele, C. D. (2010). Multivariate multiparameter extreme value models and return periods: A copula approach. Water Resour. Res. 46, 2009WR009040. doi:10.1029/2009WR009040

CrossRef Full Text | Google Scholar

Serinaldi, F., and Grimaldi, S. (2007). Fully nested 3-copula: Procedure and application on hydrological data. J. Hydrol. Eng. 12 (4), 420–430. doi:10.1061/(asce)1084-0699(2007)12:4(420)(2007)12:4(420)

CrossRef Full Text | Google Scholar

Shimakawa, M., and Murakami, S. (2003). Fuzzy prediction model for water demand prediction using an interpolative fuzzy reasoning method. Int. J. Syst. Sci. 34 (14-15), 775–785. doi:10.1080/00207720310001640250

CrossRef Full Text | Google Scholar

Song, P., Wang, C., Zhang, W., Liu, W., Sun, J., Wang, X., et al. (2020). Urban multi-source water supply in China: Variation tendency, modeling methods and challenges. Water 12 (4), 1199. doi:10.3390/w12041199

CrossRef Full Text | Google Scholar

Song, S., and Singh, V. P. (2010). Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk Assess. 24 (3), 425–444. doi:10.1007/s00477-009-0331-1

CrossRef Full Text | Google Scholar

Tu, X., Singh, V. P., Chen, X., Ma, M., Zhang, Q., and Zhao, Y. (2016). Uncertainty and variability in bivariate modeling of hydrological droughts. Stoch. Environ. Res. Risk Assess. 30 (5), 1317–1334. doi:10.1007/s00477-015-1185-3

CrossRef Full Text | Google Scholar

Wang, X., Zang, N., Liang, P., Cai, Y., Li, C., and Yang, Z. (2017). Identifying priority management intervals of discharge and TN/TP concentration with copula analysis for Miyun Reservoir inflows, North China. Sci. Total Environ. 609, 1258–1269. doi:10.1016/j.scitotenv.2017.07.135

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Z., Chentao, H., Wang, H., and Zhang, Q. (2020). Reservoir inflow synchronization analysis for four reservoirs on a mainstream and its tributaries in flood season based on a multivariate copula model. Water Resour. manage. 34 (9), 2753–2770. doi:10.1007/s11269-020-02572-x

CrossRef Full Text | Google Scholar

Yang, M., Gong, J., Zhao, Y., Wang, H., Zhao, C., Yang, Q., et al. (2021). Landscape pattern evolution processes of wetlands and their driving factors in the xiong’an new area of China. Int. J. Environ. Res. Public Health 18 (9), 4403. doi:10.3390/ijerph18094403

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, B., Zhang, C., Jiang, Y., Li, Y., and Zhou, H. (2017). Conjunctive use of inter-basin transferred and desalinated Water in a multi-source water supply system based on cost-benefit analysis. Water Resour. manage. 31 (11), 3313–3328. doi:10.1007/s11269-017-1669-7

CrossRef Full Text | Google Scholar

Yu, R., and Zhang, C. (2021). Early warning of water quality degradation: A copula-based bayesian network model for highly efficient water quality risk assessment. J. Environ. Manag. 292, 112749. doi:10.1016/j.jenvman.2021.112749

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, N., Zhu, J., Wang, X., Liao, Y., Cao, G., Li, C., et al. (2022). Eutrophication risk assessment considering joint effects of water quality and water quantity for a receiving reservoir in the South-to-North Water Transfer Project, China. J. Clean. Prod. 331, 129966. doi:10.1016/j.jclepro.2021.129966

CrossRef Full Text | Google Scholar

Zhang, C., Nong, X., Shao, D., Zhong, H., Shang, Y., and Liang, J. (2021). Multivariate water environmental risk analysis in long-distance water supply project: A case study in China. Ecol. Indic. 125, 107577–107582. doi:10.1016/j.ecolind.2021.107577

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2007a). Bivariate rainfall frequency distributions using Archimedean copulas. J. Hydrology 332 (1), 93–109. doi:10.1016/j.jhydrol.2006.06.033

CrossRef Full Text | Google Scholar

Zhang, L., and Singh, V. P. (2007b). Gumbel-Hougaard copula for trivariate rainfall frequency analysis. J. Hydrol. Eng. 12 (4), 409–419. doi:10.1061/(asce)1084-0699(2007)12:4(409)(200712:4(409)

CrossRef Full Text | Google Scholar

Zhang, S., Yang, J., Wan, Z., and Yi, Y. (2018). Multi-water source joint scheduling model using a refined water supply network: Case study of Tianjin. Water 10 (11), 1580. doi:10.3390/w10111580

CrossRef Full Text | Google Scholar

Zhang, S., Yang, J., Xu, Z., and Zhang, C. (2019). Effect of frequency of multi-source water supply on regional guarantee rate of water use. Water 11 (7), 1356. doi:10.3390/w11071356

CrossRef Full Text | Google Scholar

Zhang, Y. (2017). Yellow River water diversion to ensure the supply of water resources in Xiong’an New Area. Water Resour. Plan. Des. 10, 5–9. in Chinese with English abstract. doi:10.3969/j.issn.1672-2469.2017.10.002

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, S., Zhang, F., Shen, Q., Li, J., and Yang, F. (2021). Remote sensing-based analysis of spatial and temporal water colour variations in Baiyangdian Lake after the establishment of the Xiong'an New Area. Remote Sens. 13 (9), 1729. doi:10.3390/rs13091729

CrossRef Full Text | Google Scholar