- 1Sichuan Communication Surveying and Design Institute Co., Ltd, Chengdu, China
- 2Sichuan Transportation Construction Group Co., Ltd, Chengdu, China
- 3State Key Laboratory of Geohazard Prevention and Environment Protection, Chengdu University of Technology, Chengdu, China
- 4PowerChina Huadong Engineering Corporation Limited, Hangzhou, China
- 5Badong National Observation and Research Station of Geohazards, China University of Geosciences, Wuhan, China
- 6School of Emergency Science, Xihua University, Chengdu, China
- 7Key Laboratory of Geohazard Prevention of Hilly Mountains, Ministry of Natural Resources, Fuzhou, China
- 8Sichuan Highway Planning, Survey, Design and Research Institute Ltd, Chengdu, China
The study on the failure difference of deep hard rock based on the comparison between conventional and true triaxial tests can help us better understand the fracture processes and failure characteristics of the deep rock mass. Therefore, this article carries out a comparative analysis of the failure of hard rock under conventional and true triaxial stress states. Within the scope of this study, it is found that the brittle–ductile transformation properties can be intuitively reflected in the rock stress–strain curve and failure mode. The brittle–ductile transition point of rock can also be determined by the difference between peak and residual strengths. The rock failure strength increases with the increase of σ2, the peak strain decreases with the increase of σ2, the stress drop of the post-peak curve becomes more obvious with the increase of σ2, and the rock tends toward Class II brittle failure after the peak with the increase of σ2. When σ3 is relatively high, the rock fracture angle increases with the increase of σ2 with obvious regularity. Compared with conventional triaxial stress conditions, the differential stress-induced anisotropy failure is the biggest difference in rock fracture characteristics between true and conventional triaxial stress states. This study can supply useful references to the study of failure properties of hard rock under complex stress states.
Introduction
The continuous demand for resources makes human activities continue to expand to “deep space, deep sea, deep earth.” Among them, due to the complexity of the earth’s internal system and the uniqueness of the geological medium, the research of “deep earth” is in a “black box” state. The difficulty of scientific research on “deep earth” is no less than that of “deep space and deep sea.” The excavation depth of underground works in international and domestic industries such as transportation, water conservation, hydropower, mineral resource development, oil and gas reservoir development, geological storage, and military protection engineering is still increasing (Martin and Chandler 1994; Malan 2002; Hajiabdolmajid and Kaiser 2003; Diederichs 2007; Zhao et al., 2014; Zhuang et al., 2017; Bai et al., 2019; Feng et al., 2022). For example, the deepest oil well in the world is drilled by the Orlan platform of Chaivo oilfield, and its depth has reached 15,000 m. At present, there are more than 120 metal mines with a mining depth of more than 1,000 m in the world, and the mining depth of the Mponeng gold mine in South Africa is as deep as 4,350 m (Zhang 2020). Besides, there are many underground projects with a depth of more than kilometers in China. For example, the diversion tunnel in Jinping II hydropower station has a maximum buried depth of 2,525 m. The Jinping underground laboratory in China built on this diversion tunnel is also the laboratory with the largest rock coverage depth in the world with a buried depth of 2,400 m (Feng et al., 2018; Zhang 2020).
Different from shallow-rock mechanical engineering, in the deep tunnel construction process, it is inevitable to face the challenges of high ground stress, complex geological conditions, strong excavation unloading, and mechanical and blasting disturbance (Wang et al., 2004; Qiu et al., 2012; Feng et al., 2015; Gao et al., 2018; Feng et al., 2019; Do et al., 2020). Generally, the surrounding rock of the cavern is mostly high-strength hard rock. For example, the maximum ground stress of Jinping I Hydropower Station is 40 MPa, and the surrounding rock is mainly marble. The uniaxial compressive strength is 50–80 MPa (Gong et al., 2010). The Paoma mountain No. 1 tunnel is located in the northeast of Kangding City. The maximum buried depth of the Paoma mountain No. 1 tunnel is 1,250 m, more than 85% of the whole tunnel section is hard granite, and the saturated uniaxial compressive strength is 48.82–49.74 MPa.
Generally, there is a high possibility of stress-induced failure in deep buried hard rock tunnels, such as cracking, wall splitting, and rockburst, which will seriously threaten the lives of workers and the safety of construction equipment and will also affect the construction cycle and the final completion of the tunnel, resulting in huge economic losses. As shown in Figure 1, rockburst disasters occurred at different locations during the construction of the Paoma mountain No. 1 tunnel.
The site selection of deep underground engineering, such as deeply buried tunnels and underground powerhouses of hydropower stations, tends to be the hard rock area with relatively complete lithology, so as to ensure the stability of deep engineering. Many scholars have carried out a great number of in-depth studies on the mechanical characteristics of deep buried hard rock and its influence from many angles such as theory, experiment, and numerical calculation. In this study, the mechanical properties and failure differences of hard rock based on a comparison between conventional and true triaxial tests are analyzed. The research of this article is helpful to deeply understand the fracture and failure characteristics of deep hard rock mass and can provide a useful reference for disaster prevention and reduction of deep rock mass engineering.
Failure Analysis of Marble Sample Based on Conventional Triaxial Test
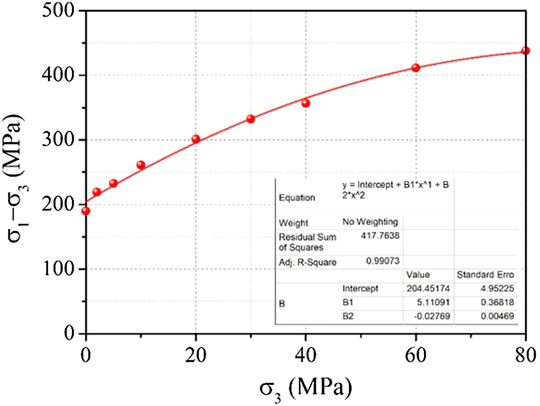
Figure 2 and Figure 3 are the stress–strain curve and failure–strength diagrams of a group of Jinping marble samples in a conventional triaxial compression test (Gao 2020). Figure 4 shows the corresponding peak axial and radial strains (ε1 and ε3) diagram in Figure 2 and Figure 3.
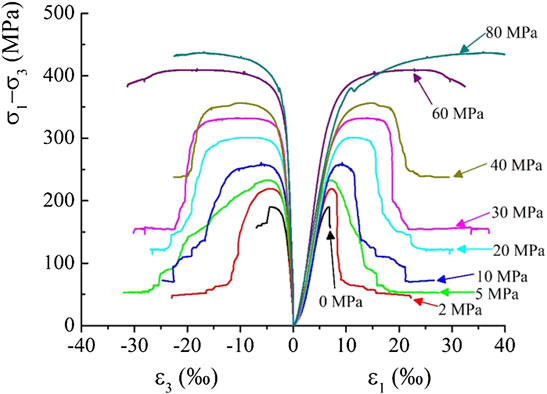
FIGURE 2. Stress–strain curves of the tested samples under conventional triaxial compression state (revised form Gao 2020).
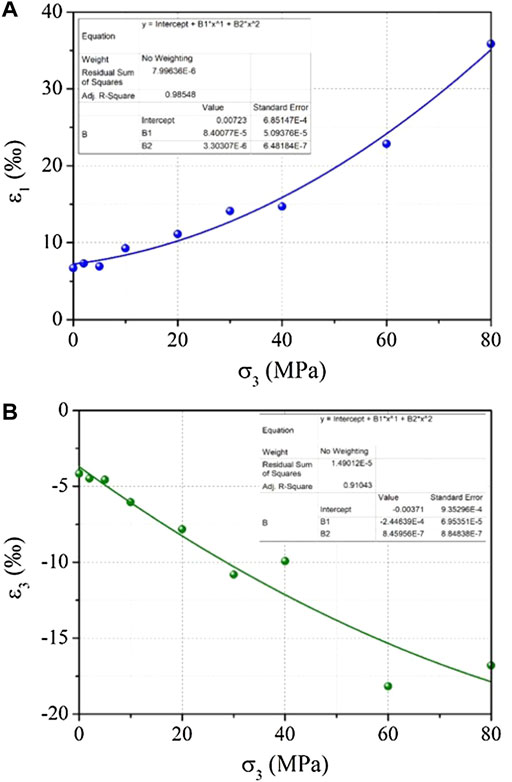
FIGURE 4. Strain characteristics of the tested samples under conventional triaxial compression state.
It can be found from the Figures 2–4 that when confining pressure is 0 MPa, 2 MPa, 5 MPa, 10 MPa, 20 MPa, 30 MPa, 40 MPa, 60 MPa, and 80 MPa, respectively, the corresponding peak strength is 190 MPa, 219 MPa, 233 MPa, 261 MPa, 301 MPa, 332 MPa, 356 MPa, 411 MPa, and 438 MPa, respectively, the corresponding peak ε1 is 0.0067, 0.0073, 0.0069, 0.0111, 0.0141, 0.0147, 0.0229, and 0.0359, respectively, and the corresponding peak ε3 is −0.0042, −0.0045, −0.0046, −0.0061, −0.0078, −0.0108, −0.0099, −0.0182, and −0.0168, respectively. It could be concluded that peak strength increases with the increasing confining pressure, the ε1 and ε3 also increase with the increasing confining pressure, but the difference is that the ε1 is the compression deformation and ε3 is the expansion deformation. The variations of peak strength, axial strain ε1, and radial strain ε3 with confining pressure are shown in formula as below:
As shown in Figure 2 and Figure 5, the brittle–ductile transformation properties of rock could be reflected in the sample stress–strain curve and failure mode (Lajtai 1974; Tarasov and Potvin 2013; Ai et al., 2016; Tarasov and Stacey 2017; Kanaya and Hirth 2018; Ning et al., 2018; Zhao et al., 2018; Gao 2020). When confining pressure is small (confining pressure is less than 10 MPa), there is no platform section at the peak section of stress–strain curve for the marble sample, and the stress-drop phenomenon after the peak is obvious. The rock failure surface shows splitting failure characteristics, and the failure surface is basically parallel to the maximum principal stress direction (axial direction), indicating that the rock brittleness under this stress condition is obvious.

FIGURE 5. Failure modes of the tested samples under conventional triaxial compression state (revised form Gao 2020).
With increasing confining pressure, the rock ductile deformation increases, that is, the rock peak platform section on the stress–strain curve is gradually significant, the stress drop after the peak decreases, and the failure of the sample gradually transitions from complete splitting to single shear plane, indicating that the brittleness of the rock decreases and the ductility increases. After the confining pressure reaches 60 MPa, the ductile deformation characteristics of the sample are particularly obvious, the post-peak stress-drop phenomenon of the sample basically disappears, and the failure of the sample is obviously bulking in the middle; when the confining pressure reaches 80 MPa, there is no macro fracture surface, and only weak bulking exists in the middle of the sample. Therefore, it can be considered that the confining pressure of 60 MPa is the brittle–ductile transformation point of marble samples.
In addition, the brittle–ductile transition point of rock can also be determined by the difference between peak and residual strength. With increasing confining pressure, the difference between peak and residual strength gradually decreases. Even in an ideal ductile state, the difference is 0, that is, the rock peak strength is equal to residual strength.
Failure Analysis of Granite Sample Based on True Triaxial Test
Figure 6 shows the granite sample used in the true triaxial test (Zhang 2020). The rock thin-section micrograph obtained shows the microstructure and mineral composition of the granite. It can be seen from Figure 6 that the granite is a medium-grain coarse-grain structure with strong isotropy in structure and mineral composition. The density of the granite is 2.61 g/cm3, and the tested granite has the characteristics of high density, dense lithology, and high rock strength. The tested granite is mainly composed of about 40% plagioclase, 33% quartz, 17% potassium feldspar, and 10% other materials.

FIGURE 6. Schematic diagram of granite samples used in the true triaxial experiment. (A) Sample physical drawing, (B) sample SEM image, (C) plane polarized light micrograph of sample, and (D) crossed polars micrograph of sample (quartz = Qtz, K-feldspar = Kfs, plagioclase = Pl, biotite = Bt).
To simulate the stress path of rock mass failure in deep underground engineering, the typical stress path (Zhang et al., 2019) finally adopted in this study is shown as follows: (a) Hydrostatic loading stage: loading simultaneously in three principal stress directions (σ1 = σ2 = σ3) at a loading rate of 0.5 MPa/s to the minimum principal stress level. (b) Intermediate principal stress loading stage: keeping σ3 unchanged and loading σ1 and σ2 simultaneously (σ1 = σ2) at a loading rate of 0.5 MPa/s to set the σ2 level. (c) Maximum principal stress loading stage: keeping σ2 and σ3 unchanged and loading σ1 at loading rate of 0.5 MPa/s. When σ1 reached the crack damage stress of the sample, the control mode was changed from stress control to strain control ε1 with the rate of 0.015 mm/min.
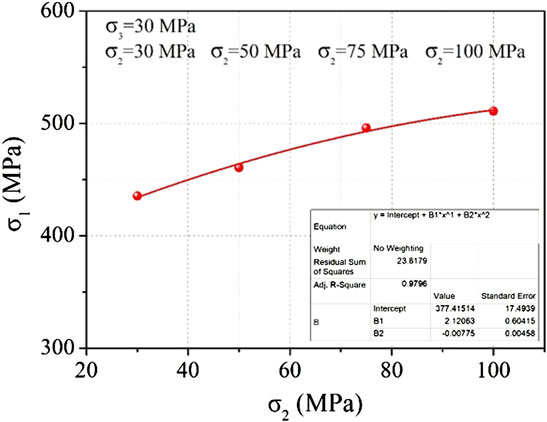
Figure 7 and Figure 8 show the variation of stress–strain relationship and strength characteristic of granite with different σ2 under true triaxial compression stress state (Zhang 2020). It can be found from Figure 7 and Figure 8 that within the scope of this study, when σ3 is 30 MP and σ2 is 30 MPa, 50 MPa, 75 MPa, and 100 MPa, respectively, the peak failure strength σ1peak of granite shows an increasing rule with increasing of σ2. Meanwhile, for the stress–strain curve shape, the rock tends toward Class II failure with the increase of σ2, and the post-peak stress drop of the curve is more obvious, indicating that the increase of σ2 makes the rock failure more prone to brittle failure. In addition, with the increase of σ2, the degree of differentiation of the σ1–ε2 curve and the σ1–ε3 curve of rock is increasing, which indicates that under true triaxial stress conditions, the differential stress makes the deformation of rock appear anisotropic, and the greater the differential stress between σ2 and σ3, the more obvious the deformation anisotropy of ε2 and ε3.
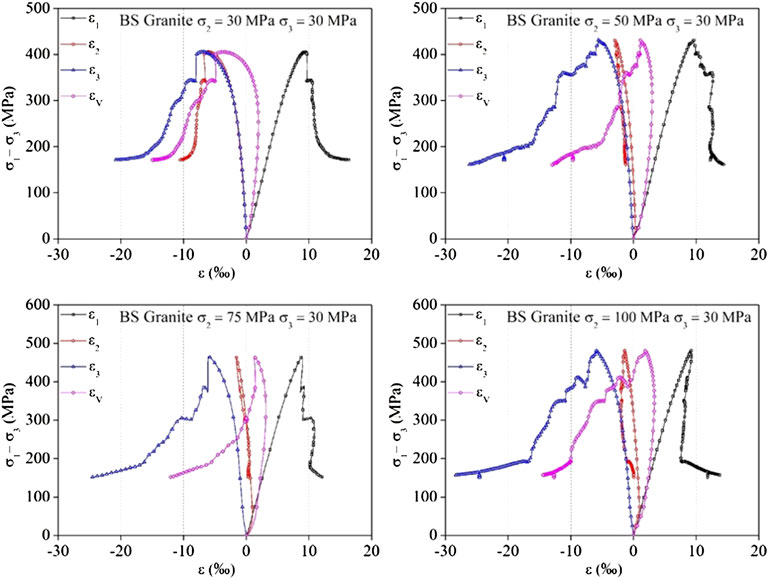
FIGURE 7. Stress–strain curves of granite samples adopted in the true triaxial experiment (revised form Zhang 2020).
Nadaia used octahedral shear stress τoct and octahedral normal stress σoct to describe rock materials’ three-dimensional failure strength criterion, namely, τoct = f (σoct) (Nadaia 1950). Subsequently, based on a large number of tests and the analysis of the true triaxial compression failure mode of hard rock, Mogi revised the three-dimensional failure strength criterion proposed by Nadaia and replaced σoct with σm,2 (Mogi 1971). The obtained three-dimensional failure strength criterion is shown as follows:
The peak strength characteristics of granite under true triaxial stress conditions obtained in this article are shown in Figure 8. Using the aforementioned two three-dimensional failure strength criteria, the strength data obtained in Figure 8 are fitted by power law form. The relationship between τoct and σoct in Nadaia’s domain (Figure 9A) and between τoct and σm,2 in the Mogi domain (Figure 9B) are obtained. The following formulas are obtained:
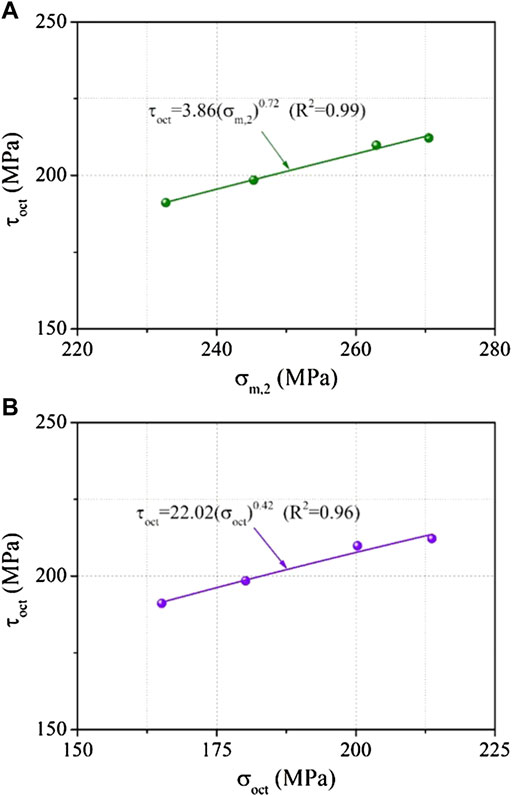
FIGURE 9. True triaxial compression strength for tested granite in terms of (A) τoct versus σoct and (B) τoct versus σm,2.
It can be found from Figure 9 that τoct monotonically increases with increasing σoct or σm,2, and the fitting goodness of the modified strength criterion proposed by Mogi is R2 = 0.99, which is better than that proposed by Nadai (R2 = 0.96).
Figure 10 shows the variation of principal strain ε1, ε2, and ε3 of granite samples with intermediate principal stress σ2. Within the research scope of this article, it can be seen from Figure 10 that when σ3 is 30 MP and σ2 is 30 MPa, 50 MPa, 75 MPa, and 100 MPa, respectively, the principal strain ε2 increases with increasing σ2, and its variation law is good (Figure 10B), while the variation law of principal strain ε1 and ε3 with intermediate principal stress σ2 is not obvious (Figures 10A,C).
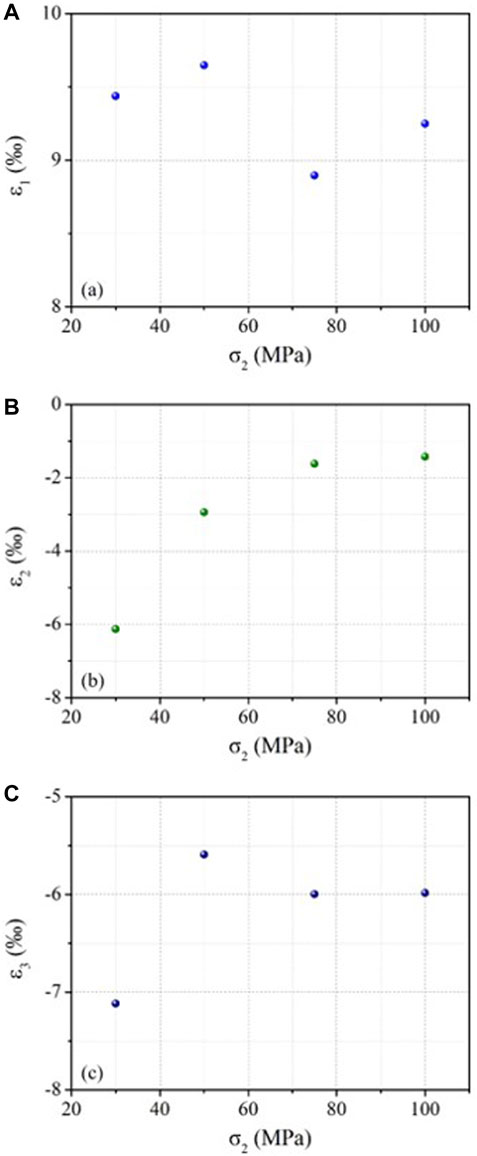
FIGURE 10. Strain characteristics of granite samples adopted in the true triaxial experiment. (A) ε1 versus σ2, (B) ε2 versus σ2, and (C) ε3 versus σ2.
Figure 11 shows the variation of failure mode and fracture angle of granite under true triaxial compression with σ2 (Zhang 2020). In practical tests, the macroscopic main crack morphology perpendicular to the σ2 sample surface is not a straight line, but an irregular broken line, which makes it difficult to determine the fracture angle (θ). In this article, the fracture angle (θ) is determined by the angle between the overall direction of a macroscopic main crack and the σ3 loading direction. It can be seen from Figure 11 that within the scope of this study, when σ3 = 30 MPa and when σ3 is 30 MPa, 50 MPa, 75 MPa, and 100 MPa, the fracture angles of granite are 72°, 74°, 75°, and 80°, respectively. It can be found that the fracture angle of granite increases with the increase of σ2 and the regularity is obvious.
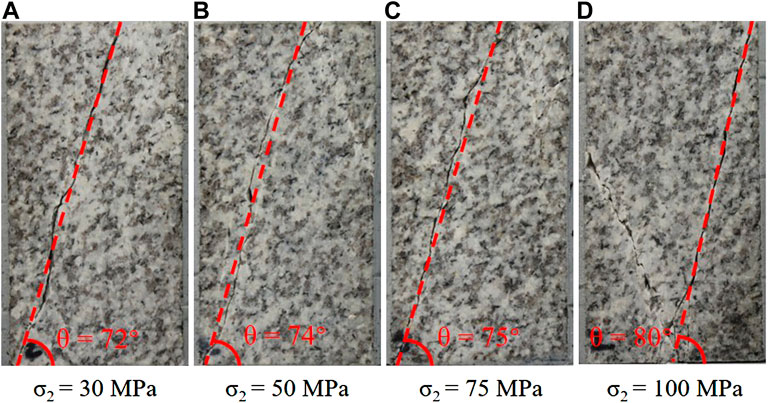
FIGURE 11. Fracture angle and failure mode of granite samples adopted in the true triaxial experiment (revised form Zhang 2020).
Discussion
Figure 12 shows the comparison of the failure of the sandstone samples under conventional triaxial (σ2 = σ3) and true triaxial (σ2 > σ3) stress conditions. The first pictures in Figure 12A and Figure 12B are the actual failure situations of the samples, the second pictures are the computed tomography (CT) scan results corresponding to the first picture, and the third pictures are CT scan of the I-I cross-section of the samples corresponding to the second picture (Lu et al., 2018).
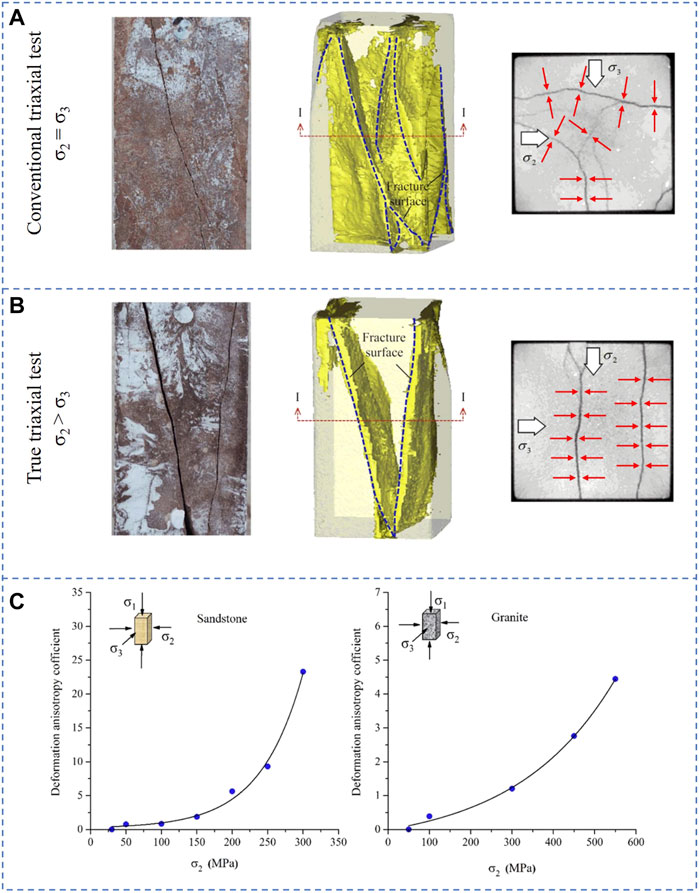
FIGURE 12. Failure difference of hard rock based on comparison between the conventional triaxial test and true triaxial test (revised form Lu et al., 2018 and Feng et al., 2019). (A) Conventional triaxial stress state, (B) true triaxial stress state, and (C) differential stress-induced anisotropy failure analysis.
It can be clearly concluded from Figure 12A that the sample failure under the condition of conventional triaxial stress (σ2 = σ3) is random, and its crack presents irregular propagation and evolution. This is due to the fact that the σ2 is equal to σ3 so the cracks of the sample randomly propagate and evolve on the σ2-σ3 plane. The failure of the sample under true triaxial stress (σ2 > σ3) is different, and it can be clearly found from Figure 12B that the sample main crack growth is obviously parallel to the σ2 action direction and perpendicular to the σ3 action direction. It can be concluded that under the condition of true triaxial stress (σ2 > σ3), the cracks of the sample cannot propagate randomly, but they have a certain directional arrangement and distribution characteristics.
Obviously, compared with the uniaxial and conventional triaxial stress conditions (σ2 = σ3) (Ingraham et al., 2013; Frash et al., 2014; Li et al., 2015; Ma and Haimson 2016; Meng et al., 2016; Shi et al., 2017; Yu et al., 2022), this is due to the particular point that σ2 is greater than σ3 under true triaxial stress conditions (σ2 > σ3), and the anisotropic fracture characteristics of sample under true triaxial stress conditions (σ2 > σ3) are different from the failure anisotropy of the layered rock mass due to the layered structure, which is caused by the difference of stress, also called the differential stress-induced anisotropy under true triaxial stress (σ2 > σ3) condition. This differential stress-induced anisotropy failure characteristic is the biggest difference between the fracture characteristics of samples under true triaxial stress conditions (σ2 > σ3) and those under conventional triaxial stress conditions (σ2 = σ3), this also makes a series of hard rock failure and disaster problems under deep true triaxial stress (σ2 > σ3) very complex.
For the differential stress-induced anisotropy failure of the rock, Feng et al. (2019) have made a systematic quantitative study on it. They used the following Eqn. 9 as an index to quantitatively study the differential stress-induced anisotropy failure of the rock:
where K12 and K13 are the deformation moduli of the stress–strain curve corresponding to σ2 and σ3.
It can be found from the definition of Eqn. 9 that when the differential stress of σ2 and σ3 is larger, the value of A in Eqn. 9 is larger, indicating that the anisotropic failure of rock induced by differential stress is more obvious. Figure 12C shows the variation of differential stress-induced anisotropy failure index of sandstone and granite with intermediate principal stress σ2. It can also be found that when the intermediate principal stress σ2 is larger, the anisotropy index A is larger, which indicates that the anisotropic failure of rock is more obvious.
It should be noted that this differential stress-induced anisotropy failure of the rock is essentially different from the initial anisotropic failure of layered rock. Layered rock is a typical complex geological body, which widely exists in the engineering surrounding rock. The layered rock is distributed with a group of dominant primary bedding structural planes (bedding planes), and usually has a relatively determined occurrence and good spatial continuity, which makes the mechanical properties of layered hard rocks differ greatly in the direction parallel to and perpendicular to the bedding plane, showing significant initial anisotropy and heterogeneity.
Under deep complex geological conditions, engineering excavation and other activities lead to stress transfer and stress concentration of surrounding rock, which not only enhances the intermediate principal stress effect in surrounding rocks but also makes the phenomenon of true triaxial high stress and high-stress difference of deep hard rock remarkable. The typical stress characteristics in the deep rock make the energy storage and release threshold of rock mass increase, and the energy release intensity increases, leading to the deep rock mass becoming a high-energy environmental field. Under the condition of true triaxial stress, the process and mechanism of energy storage, distribution, driving, and release in the failure process of layered rock will be more complex. Deep-layered hard rock shows the characteristics of complex stress, prone to a variety of disaster phenomena and complex disaster causing mechanisms. The failure and instability of deep-layered hard rock are significantly greater than those of shallow rock engineering in terms of type, quantity, frequency, scale, and strength.
When the layered rock mass is in the deep true triaxial stress state, its failure problem becomes very complex. Under the coupling action of true triaxial stress and layered rock dip angle, the layered hard rock has obvious mixed anisotropy. This complex mixed action between differential stress-induced anisotropy failure and initial anisotropy failure of the rock makes the mechanical properties, fracture mechanism, and energy evolution process of deep layered hard rock very complex. Therefore, the research on the true triaxial mechanical properties of deep layered hard rock is a very important research topic that needs to be further explored.
Conclusion
In this article, the conventional triaxial test and true triaxial test of hard rock are carried out respectively to explore the influence and mechanism of stress state on the failure characteristics of hard rock. The following conclusions within the research scope have been obtained:
1) Brittle–ductile transformation properties of rock can be reflected from the stress–strain curve and failure mode. With increasing confining pressure, the ductile deformation of the sample increases, the peak platform section of the sample stress–strain curve is gradually significant, the post-peak stress drop decreases, and the failure of the sample gradually transitions from complete splitting to a single shear plane.
2) The brittle–ductile transition point of rock can also be determined by the difference between peak and residual strength. With increasing confining pressure, the difference between peak, and residual strength gradually decreases.
3) Within the scope of this study, the rock failure strength under true triaxial stress conditions increases with increasing σ2, the peak strain decreases with the increase of σ2, the stress drop of the post-peak curve becomes more obvious with the increase of σ2, and the rock tends to Class II brittle failure after the peak with the increase of σ2.
4) When σ3 is relatively high, most rock samples have only one macroscopic main crack under true triaxial stress condition, and the fracture angle of granite samples increases with the increase of σ2 with obvious regularity.
5) Compared with the conventional triaxial stress, due to the stress difference of rock under true triaxial stress (σ2 is greater than σ3), the differential stress-induced anisotropy failure is the biggest difference between the fracture characteristics of rock under true triaxial stress and the conventional triaxial stress state.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study is supported by the National Natural Science Foundation of China (Grant No. 42107211) and China Postdoctoral Science Foundation (Grant No. 2021M691000). This study is also supported by the Opening Foundation of Key Laboratory of Geohazard Prevention of Hilly Mountains, Ministry of Natural Resources (Fujian Key Laboratory of Geohazard Prevention) (Grant No. FJKLGH 2022K005).
Conflict of Interest
Authors GZ and KC were employed by the Sichuan Communication Surveying & Design Institute Co., Ltd. Authors YT and JS were employed by the Sichuan Transportation Construction Group CO., LTD. Author YG is employed by the PowerChina Huadong Engineering Corporation Limited. Author JR is employed by the Sichuan Highway Planning, Survey, Design and Research Institute Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors sincerely acknowledge the research support from Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University.
References
Ai, C., Zhang, J., Li, Y.-w., Zeng, J., Yang, X.-l., and Wang, J.-g. (2016). Estimation Criteria for Rock Brittleness Based on Energy Analysis during the Rupturing Process. Rock Mech. Rock Eng. 49 (12), 4681–4698. doi:10.1007/s00603-016-1078-x
Bai, Q., Tibbo, M., Nasseri, M. H. B., and Young, R. P. (2019). True Triaxial Experimental Investigation of Rock Response Around the Mine-By Tunnel under an In Situ 3D Stress Path. Rock Mech. Rock Eng. 52 (10), 3971–3986. doi:10.1007/s00603-019-01824-6
Diederichs, M. S. (2007). The 2003 Canadian Geotechnical Colloquium: Mechanistic Interpretation and Practical Application of Damage and Spalling Prediction Criteria for Deep Tunnelling. Can. Geotech. J. 44 (9), 1082–1116. doi:10.1139/t07-033
Do, D.-P., Tran, N.-T., Mai, V.-T., Hoxha, D., and Vu, M.-N. (2020). Time-dependent Reliability Analysis of Deep Tunnel in the Viscoelastic Burger Rock with Sequential Installation of Liners. Rock Mech. Rock Eng. 53, 1259–1285. doi:10.1007/s00603-019-01975-6
Feng, G.-L., Chen, B.-R., Xiao, Y.-X., Jiang, Q., Li, P.-X., Zheng, H., et al. (2022). Microseismic Characteristics of Rockburst Development in Deep TBM Tunnels with Alternating Soft-Hard Strata and Application to Rockburst Warning: A Case Study of the Neelum-Jhelum Hydropower Project. Tunn. Undergr. Space Technol. 122, 104398. doi:10.1016/j.tust.2022.104398
Feng, G.-L., Feng, X.-T., Chen, B.-r., Xiao, Y.-X., and Yu, Y. (2015). A Microseismic Method for Dynamic Warning of Rockburst Development Processes in Tunnels. Rock Mech. Rock Eng. 48 (5), 2061–2076. doi:10.1007/s00603-014-0689-3
Feng, X.-T., Kong, R., Zhang, X., and Yang, C. (2019). Experimental Study of Failure Differences in Hard Rock under True Triaxial Compression. Rock Mech. Rock Eng. 52, 2109–2122. doi:10.1007/s00603-018-1700-1
Feng, X.-T., Xu, H., Qiu, S.-L., Li, S.-J., Yang, C.-X., Guo, H.-S., et al. (2018). In Situ observation of Rock Spalling in the Deep Tunnels of the China Jinping Underground Laboratory (2400 M Depth). Rock Mech. Rock Eng. 51, 1193–1213. doi:10.1007/s00603-017-1387-8
Frash, L. P., Gutierrez, M., and Hampton, J. (2014). True-triaxial Apparatus for Simulation of Hydraulically Fractured Multi-Borehole Hot Dry Rock Reservoirs. Int. J. Rock Mech. Min. Sci. 70 (9), 496–506. doi:10.1016/j.ijrmms.2014.05.017
Gao, Y.-H., Feng, X.-T., Zhang, X.-W., Feng, G.-L., Jiang, Q., and Qiu, S.-L. (2018). Characteristic Stress Levels and Brittle Fracturing of Hard Rocks Subjected to True Triaxial Compression with Low Minimum Principal Stress. Rock Mech. Rock Eng. 51 (12), 3681–3697. doi:10.1007/s00603-018-1548-4
Gao, Y. H. (2020). Study on Failure Mechanism of Deep-Buried Marble Tunnel with Calcium-Cemented Stiff Discontinuity. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.
Gong, M., Qi, S., and Liu, J. (2010). Engineering Geological Problems Related to High Geo-Stresses at the Jinping I Hydropower Station, Southwest China. Bull. Eng. Geol. Environ. 69 (3), 373–380. doi:10.1007/s10064-010-0267-1
Hajiabdolmajid, V., and Kaiser, P. (2003). Brittleness of Rock and Stability Assessment in Hard Rock Tunneling. Tunn. Undergr. Space Technol. 18 (1), 35–48. doi:10.1016/s0886-7798(02)00100-1
Ingraham, M. D., Issen, K. A., and Holcomb, D. J. (2013). Response of Castlegate Sandstone to True Triaxial States of Stress. J. Geophys. Res. Solid Earth 118 (2), 536–552. doi:10.1002/jgrb.50084
Kanaya, T., and Hirth, G. (2018). Brittle to Semibrittle Transition in Quartz Sandstone: Energetics. J. Geophys. Res. Solid Earth 123, 84–106. doi:10.1002/2017jb014682
Lajtai, E. Z. (1974). Brittle Fracture in Compression. Int. J. Fract. 10 (4), 525–536. doi:10.1007/bf00155255
Li, X., Du, K., and Li, D. (2015). True Triaxial Strength and Failure Modes of Cubic Rock Specimens with Unloading the Minor Principal Stress. Rock Mech. Rock Eng. 48 (6), 2185–2196. doi:10.1007/s00603-014-0701-y
Lu, Y., Li, W., Wang, L., Li, Z., Meng, X., Wang, B., et al. (2018). Damage Evolution and Failure Behavior of Sandstone under True Triaxial Compression. Geotech. Test. J. 42 (3), 20170295. doi:10.1520/gtj20170295
Ma, X., and Haimson, B. C. (2016). Failure Characteristics of Two Porous Sandstones Subjected to True Triaxial Stresses. J. Geophys. Res. Solid Earth 121 (9), 6477–6498. doi:10.1002/2016jb012979
Malan, D. F. (2002). Manuel Rocha Medal Recipient Simulating the Time-dependent Behaviour of Excavations in Hard Rock. Rock Mech. Rock Eng. 35 (4), 225–254. doi:10.1007/s00603-002-0026-0
Martin, C. D., and Chandler, N. A. (1994). The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 31 (6), 643–659. doi:10.1016/0148-9062(94)90005-1
Meng, Q., Zhang, M., Han, L., Pu, H., and Nie, T. (2016). Effects of Acoustic Emission and Energy Evolution of Rock Specimens under the Uniaxial Cyclic Loading and Unloading Compression. Rock Mech. Rock Eng. 49, 3873–3886. doi:10.1007/s00603-016-1077-y
Mogi, K. (1971). Fracture and Flow of Rocks under High Triaxial Compression. J. Geophys. Res. 76, 1255–1269. doi:10.1029/jb076i005p01255
Ning, J., Wang, J., Jiang, J., Hu, S., Jiang, L., and Liu, X. (2018). Estimation of Crack Initiation and Propagation Thresholds of Confined Brittle Coal Specimens Based on Energy Dissipation Theory. Rock Mech. Rock Eng. 51, 119–134. doi:10.1007/s00603-017-1317-9
Qiu, S. L., Feng, X. T., Zhang, C. Q., and Yang, J. B. (2012). Experimental Research on Mechanical Properties of Deep Marble under Different Initial Damage Levels and Unloading Paths[J]. Chin. J. Rock Mech. Eng. 31 (8), 1686–1697. doi:10.3969/j.issn.1000-6915.2012.08.024
Shi, L., Li, X., Bing, B., Wang, A., Zeng, Z., and He, H. (2017). A Mogi-type True Triaxial Testing Apparatus for Rocks with Two Moveable Frames in Horizontal Layout for Providing Orthogonal Loads. Geotech. Test. J. 40 (4), 20160242. doi:10.1520/gtj20160242
Tarasov, B. G., and Stacey, T. R. (2017). Features of the Energy Balance and Fragmentation Mechanisms at Spontaneous Failure of Class I and Class II Rocks. Rock Mech. Rock Eng. 50 (10), 2563–2584. doi:10.1007/s00603-017-1251-x
Tarasov, B., and Potvin, Y. (2013). Universal Criteria for Rock Brittleness Estimation under Triaxial Compression. Int. J. Rock Mech. Min. Sci. 59, 57–69. doi:10.1016/j.ijrmms.2012.12.011
Wang, S. H., Liu, J. X., Tang, C. A., Li, L. C., and Zhao, X. D. (2004). Stability Analysis of a Large-Span and Deep Tunnel. Int. J. Rock Mech. Min. Sci. 41 (3), 870–875. doi:10.1016/j.ijrmms.2004.03.150
Yu, Y., Zhao, D.-C., Feng, G.-L., Geng, D.-X., and Guo, H.-S. (2022). Energy Evolution and Acoustic Emission Characteristics of Uniaxial Compression Failure of Anchored Layered Sandstone. Front. Earth Sci. 10, 841598. doi:10.3389/feart.2022.841598
Zhang, Y. (2020). Energy Evolution Mechanism of Failure Process of Deep Hard Rock and Discrimination of Typical Hazard Types of Deep Tunnel. Shengyang: Northeastern University.
Zhang, Y., Feng, X.-T., Yang, C., Zhang, X., Sharifzadeh, M., and Wang, Z. (2019). Fracturing Evolution Analysis of Beishan Granite under True Triaxial Compression Based on Acoustic Emission and Strain Energy. Int. J. Rock Mech. Min. Sci. 117, 150–161. doi:10.1016/j.ijrmms.2019.03.029
Zhao, J., Feng, X.-T., Zhang, X.-W., Zhang, Y., Zhou, Y.-Y., and Yang, C.-X. (2018). Brittle-ductile Transition and Failure Mechanism of Jinping Marble under True Triaxial Compression. Eng. Geol. 232, 160–170. doi:10.1016/j.enggeo.2017.11.008
Zhao, X. G., Wang, J., Cai, M., Cheng, C., Ma, L. K., Su, R., et al. (2014). Influence of Unloading Rate on the Strainburst Characteristics of Beishan Granite under True-Triaxial Unloading Conditions. Rock Mech. Rock Eng. 47 (2), 467–483. doi:10.1007/s00603-013-0443-2
Keywords: failure, deep hard rock, conventional triaxial, true triaxial, mechanical properties
Citation: Zheng G, Tang Y, Zhang Y, Gao Y, Zhu G, Gao M, Ren J, Chen K and Sun J (2022) Study on Failure Difference of Hard Rock Based on a Comparison Between the Conventional Triaxial Test and True Triaxial Test. Front. Earth Sci. 10:923611. doi: 10.3389/feart.2022.923611
Received: 19 April 2022; Accepted: 18 May 2022;
Published: 28 June 2022.
Edited by:
Guang-Liang Feng, Institute of Rock and Soil Mechanics (CAS), ChinaReviewed by:
Chang'An Qin, Beijing University of Civil Engineering and Architecture, ChinaZhongyuan Xu, Southwest Jiaotong University, China
Copyright © 2022 Zheng, Tang, Zhang, Gao, Zhu, Gao, Ren, Chen and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yonghui Tang, NzkwMjc5NDQyQHFxLmNvbQ==; Yan Zhang, emhhbmd5YW4yMDIwQGNkdXQuZWR1LmNu, emh5bHIxOTg4QDEyNi5jb20=
 Guoqiang Zheng1
Guoqiang Zheng1 Yan Zhang
Yan Zhang Yaohui Gao
Yaohui Gao Meiben Gao
Meiben Gao