Bottom Drag Variations Under Waves and Currents: A Case Study on a Muddy Deposit off the Shandong Peninsula

Bottom drag coefficient is one of the key parameters in quantifying shelf hydrodynamics and sediment transport processes. It varies markedly due to dynamic forcing and bed type differences, so a set of empirical values have been used for beds of coarse material where bedforms are often present. In comparison, dramatically fewer such rule-of-thumb values are available for muddy beds. Here, we present results of variations in bottom drag as calculated from in situ measurements by bottom-mounted tripods that were placed across the top of a muddy deposit during two different deployments, one in summer and another in winter. A tidal asymmetry of bottom drag was observed, most likely caused by variations of local bed roughness. For hydrodynamically smooth ($Re<2.3\times {10}^5$) flows, computed values of bottom drag coefficient were fairly scattered but still showed an overall decreasing trend with an increase in Reynolds number. The bottom drag coefficient for hydrodynamically rough or transitional flow was typically constant, while the averaged drag coefficient over all observation periods was $1.7\times {10}^{-3}$. Smaller waves (bottom orbital velocity $u_b$ <0.1 m/s) had a very limited impact on the bottom drag coefficient. However, with an increase in $u_b$, the wave–current interactions can decrease the time-averaged near-bed velocity and enhance turbulent kinetic energy, thus leading to an increase in the drag coefficient.

Introduction

Within the bottom boundary layer (BBL) on an oceanic shelf, bottom friction changes the velocity profile of the flow and the production/dissipation of turbulence, thus affecting the processes of physical, biological, chemical, and sediment transport (Trowbridge and Lentz, 2018). Among the numerous hydrodynamic and sediment dynamic models (Fringer et al., 2019), the current-related bed shear stress, ${\tau }_c$, is commonly parameterized with the quadratic drag-law:

${\tau }_c=\rho C_D\overline{u}\left|\overline{u}\right|,(1)$

where $\rho$ is the water density, $\overline{u}$ is the near-bed burst mean current velocity, and $C_D$ is the bottom drag coefficient. In a current BBL (without waves and unstratified), the near-bed current velocity is usually represented by the logarithmic law of the wall (log-law):

$\overline{u}\left(z\right)=\frac{u_{\text{∗}c}}{\kappa }ln\left(\frac{z}{z_0}\right),(2)$

where $u_{\ast c}$ ($\sqrt{{\tau }_c/\rho }$) is current-related frictional velocity, $\text{κ}=0.40$ is the von Kármán constant, and $z_0$ is hydrodynamic roughness length, which is commonly a function of grain size, bedforms, and sediment motion (Xu and Wright, 1995; Trembanis et al., 2004). Combining Eqs. 1, 2, we can deduce that the value $C_D$ depends upon $z_0$ (e.g., Soulsby, 1997; Feddersen et al., 2003). Regions of sandy deposits with ripples or sand waves $C_D$ could be well estimated by $z_0$ assuming the anisotropy of bedforms is appropriately quantified with sufficient spatiotemporal resolution (Scully et al., 2018). Unlike sandy deposits, sediments in muddy deposits usually exhibit cohesive properties that hinder the development of bedforms such as ripples (Baas et al., 2019). In the research practice of hydrodynamics, $C_D$ is usually assumed to be a constant or a tuning parameter in the muddy areas (e.g., Harris and Wiberg, 2001; Magaldi et al., 2009). However, numerous observational studies have shown that $C_D$ varies with waves, currents, biological conditions, and stratifications (e.g., Herrmann and Madsen, 2007; Safak, 2016; Xu et al., 2017; Egan et al., 2020a).

In the shallow water of continental shelves, the presence of surface waves (therefore wave-current interaction) impacts the hydrodynamics of the centimeter-scale wave BBL as well as the entire water column (Grant and Madsen, 1986). Wave actions change the velocity structure within the BBL and cause the flow to experience stronger drag (Grant and Madsen, 1979; Signell and List, 1997; Styles and Glenn, 2000; Nayak et al., 2015; Egan et al., 2019), but a recent study by Nelson and Fringer (2018) has shown that waves may lead to a decrease in drag on a smooth bed. Enhanced shear stress by energetic waves often leads to the resuspension of bed sediments (Brand et al., 2010; Egan et al., 2020b), which can further lead to stratification of suspended sediment and the drag-reduction effect on the flow (e.g., Wright et al., 1999; Peng et al., 2020). Therefore, the use of in situ data to obtain $C_D$ a certain spatial and temporal resolution is of great importance for hydrodynamic and sediment dynamic studies.

Recent studies on sediment transport processes in the muddy areas of the East China Shelf Seas (ECSS) have often deployed numerical models such as the Regional Ocean Modeling System (e.g., Bian et al., 2013; Liu et al., 2015; Wang et al., 2019; Wang et al., 2020). The Regional Ocean Modeling System implements the simple quadratic drag-law approach for calculating BBL processes that require user input of the drag coefficient (Warner et al., 2008). This is often not an easy task because direct measurements of a drag coefficient are extremely scarce in the muddy areas of the ECSS due to a lack of in situ observations. Fan et al. (2019) derived the empirical relationship between $C_D$ both currents and waves based on BBL observations at eight stations scattered over the ECSS, many of which are composed of the sandy sea bottom. To our knowledge, however, there has been no report on whether this empirical relationship also applies to coastal muddy areas of the ECSS.

In this study, a field campaign was conducted to measure the BBL dynamics across the top of a mud deposit off the Shandong Peninsula in the Yellow Sea of China. Reynolds stress, therefore $C_D$, can be estimated from those direct measurements of flows and turbulences. Our goal is to quantify the temporal and spatial variation $C_D$ across the mud deposit, which is essential to interpreting the sediment transport and deposition patterns that shape the unique, elongated mud deposit. This paper is arranged as follows: This paper is arranged as follows: this “Introduction” is followed by “Study Area”. “Materials and Methods” describes the data and methods used in this study. The time series and tidally averages C_D are presented in “Results”. Detailed analyses on flood–ebb asymmetry C_D and the effect of waves are discussed in “Discussion”. “Conclusion” summarizes the findings in this research.

Study Area

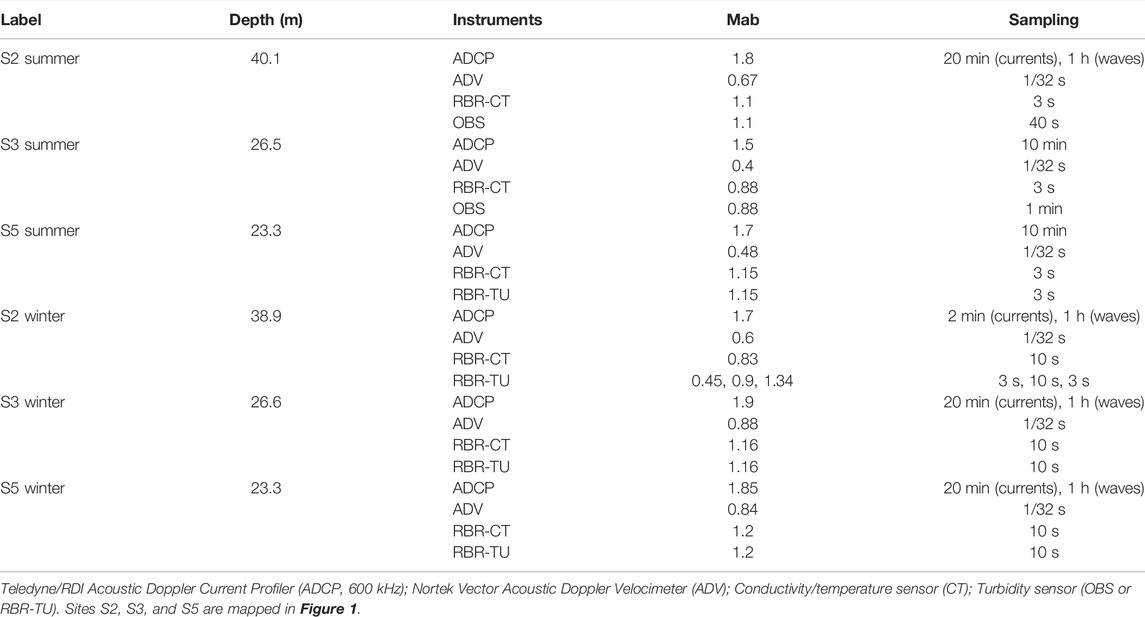
The scene of this study is around the depocenter of a muddy deposit in the coastal seas to the east of the Shandong Peninsula, China (Figure 1A). The water depths at the study stations are basically within 40 m, and their specific values are shown in Table 1. Previous sedimentary studies suggested that this muddy deposit was formed by sediments sourced from the Yellow River and transported by the Shandong Coastal Currents (SDCC), which flow out of the Bohai Sea to the Yellow Sea around the Shandong Peninsula (Figure 1A) (Alexander et al., 1991; Yang and Liu, 2007). Followed the Shepard scheme (Shepard, 1954), the surface sediment in the study area belongs to sandy silt with a mean grain size ranging from 5 to 6 $\varphi$ (Yuan et al., 2020). Moreover, because the mud fraction is more than 10% (Yuan et al., 2020; Qi et al., 2022), the bed sediment may have significant cohesive properties (Bass et al., 2002; Van Rijn, 2007). In the Yellow Sea, the principal tidal constituent is M₂, followed by S₂ and K₁ (Teague et al., 1998). The hydrography of the Yellow Sea is also influenced by the seasonally varied East Asian Monsoon (Naimie et al., 2001). In summer, the southerly winds dominate the wind field, and in winter, strong northerly winds generally prevail over the Yellow Sea (Bian et al., 2013; Mo et al., 2016; Wang et al., 2020).

FIGURE 1

FIGURE 1. (A) Topography and currents of the Bohai and Yellow seas. The isopaches of the muddy area were from Yang and Liu (2007), and the currents were based on Bian et al. (2013). These currents are the Shandong Coastal Current (SDCC), the Yellow Sea Warm Current (YSWC), and the Korea Coastal Current (KCC) (B) The location of the observation sites.

TABLE 1

TABLE 1. Mean water depth and settings of six observations.

Materials and Methods

Data Collection

Tripods were deployed at three stations on the Inner Shelf of the Shandong Peninsula during two 10-day field campaigns, one in summer (August 18–27, 2017), and another in winter (February 23–March 2, 2018) (Figure 1B). One more winter deployment (January 6–26, 2020) was conducted to make up for a fallen instrument at S2 during a previous deployment. Each tripod was equipped with an upward-looking Teledyne/RDI 600 kHz Acoustic Doppler Current Profiler (ADCP), a Nortek Vector Acoustic Doppler Velocimeter (ADV), a conductivity/temperature (CT) sensor, and a turbidity sensor (OBS or RBR-TU) (Table 1). The sampling period of each instrument is shown in Table 1. In addition, for winter observations at S2, turbidity sensors were placed at 0.45, 0.9, and 1.34 m above the bottom (mab) to record sediment concentrations within the bottom boundary layer (Table 1). CTD (SeaBird 19) packaged with Niskin bottles and a turbidity sensor was cast to collect water samples and profiles of temperature, salinity, and turbidity periodically from the watching boats that guarded each instrument against being damaged by trawling nets of passing fishing boats. These water samples were used to calibrate and convert the observed turbidities into suspended sediment concentrations (SSCs). Detailed processes of data quality assurance/quality control and calibration can be found in Qi et al. (2022).

Most ADCPs are equipped with a waving module that enables wave measurements (Table 1). In addition, hourly significant wave height and wave period data from the WaveWatch III Global Wave Model (WW3) at approximately 0.5° (∼50 km) resolution (Tolman et al., 2014), is widely used in coastal studies (e.g., Duan et al., 2020; Silva et al., 2018), were downloaded. We compared the modeled and observed significant wave height ($H_s$) and peak wave period ($T_p$) at Site 3 (S3) in winter to verify the validity of the model, and the results showed that both of them have a strong relationship, with a correlation coefficient R = 0.95 and 0.91, respectively (Supplementary Figure S1). Wind data were downloaded from the National Enters for Environmental Prediction Climate Forecast System Version 2 (NCEP/CFSv2) with a horizontal resolution of 0.205 ° × 0.204 ° (Saha et al., 2014).

Tidal Analysis and Wave Parameter Estimates

We used T_TIDE, a package of routines in MATLAB for harmonic analysis, to make a tidal prediction (Pawlowicz et al., 2002). In agreement with previous studies, the dominant tidal constituent was M₂, flowing southwest during flood tide and northeast during ebb tide.

The bottom wave orbital velocity, $u_b$, was estimated following Van Rijn (1993):

$u_b=\frac{\pi H_s}{T_{p}shih\left(k\cdot h\right)},(3)$

where $H_s$ is the significant wave height, $T_p$ is the peak wave period. $k$ ($=2\pi /L,$ where $L$ is wavelength) is the wavenumber. Soulsby (2006) Newton–Raphson method was used to calculate wavenumbers, and the MATLAB function for this method could be found in Wiberg and Sherwood (2008). $h$ is water depth.

Wave–Turbulence Decomposition and Turbulence Quantities

In a wavy aquatic environment, the ADV measured velocity components ($u$, v, and $w$) can be decomposed into the mean, wave, and turbulent fluctuation components. Before analysis, the horizontal velocities were rotated into a streamwise orthogonal coordinate system with $u$ v components aligned with and orthogonal to the direction of the mean flow. Take $u$ as an example, $u=\overline{u}+\tilde{u}+u^{\prime }$, where $\overline{u}$ the burst mean velocity averaged per 10 min, $\tilde{u}$ is the wave component and $u_t^{\prime }$ is the turbulent fluctuation. Assuming that waves and turbulence are uncorrelated (i.e., terms such as $\overline{u^{\prime }\tilde{w}}$ vanish), the shear stress can be decomposed into turbulent and wave components:

$\text{Total shear stress}=-\overline{u^{\prime }{w}^{\prime }}-\overline{\tilde{u}\tilde{w}},(4)$

where $-\overline{u^{\prime }{w}^{\prime }}$ is the turbulent Reynolds stress and $-\overline{\tilde{u}\tilde{w}}$ is the wave momentum flux (wave stress). To obtain an accurate estimate of Reynolds stress, here we used the “Phase method” of Bricker and Monismith (2007) for the wave-turbulence decomposition (WTD). As shown in Figure 2, the Phase method can effectively remove the wave motions.

FIGURE 2

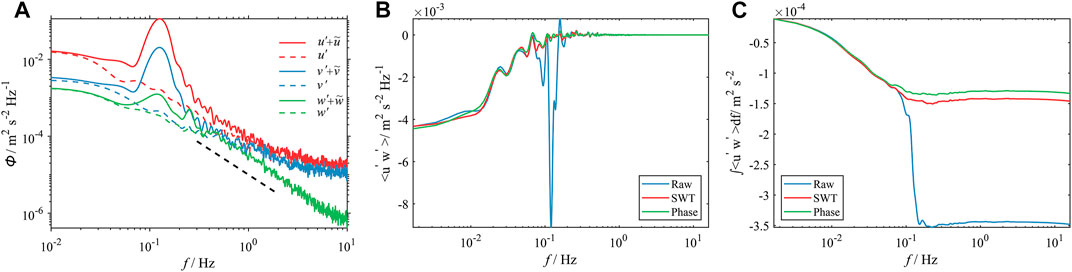
FIGURE 2. (A) Power spectra of velocity fluctuation and turbulent fluctuation ($u^{\prime }$, $v^{\prime }$ and $w^{\prime }$) estimated by Phase method for burst 41 of S3 winter observation. (B) Cospectra and (C) accumulative cospectra of raw velocity fluctuation and turbulent fluctuations estimated by these two methods.

Following Feddersen and Williams (2007), we used the nondimensional integrated cospectrum (ogive) for controlling the quality of WTD and the Reynolds stress estimates. The ogive for $\overline{u^{\prime }{w}^{\prime }}$ is defined as

$O{g}_{u^{\prime }{w}^{\prime }}\left(f\right)=\frac{{\mathrm{\int }}^{f}C{o}_{u^{\prime }{w}^{\prime }}\left(\widehat{f}\right)d\widehat{f}}{\langle u^{\prime }{w}^{\prime }\rangle },(5)$

where $C{o}_{u^{\prime }{w}^{\prime }}$ is the $u^{\prime }{w}^{\prime }$ cospectrum. After removing the wave bias, the $Og\left(f\right)$ curves are expected to increase smoothly from 0 to 1 in the range ${10}^{-1}<2\pi fzu<10$ (Feddersen and Williams, 2007), similar to empirical curves proposed by Kaimal et al. (1972). Following Ruessink (2010), we applied the ogive acceptance range as: $-0.3<Og\left(f\right)<1.3$, where estimates outside of this range were eliminated. In addition, referring to Tu et al. (2021), we compared the observed ogive curves $\overline{u^{\prime }{w}^{\prime }}$ in the empirical form and rejected those that were not well fitted. The ogive test excluded 8.5–29.7% of the bursts from each deployment (Supplementary Table S1).

After obtaining the turbulent fluctuation in three directions, we calculated the Reynolds stress, turbulent kinetic energy (TKE), and turbulent energy dissipation rates ($\epsilon$). The TKE was estimated as: $1/2\rho \left(\overline{u^{\prime 2}}+\overline{v^{\prime 2}}+\overline{w^{\prime 2}}\right)$. The inertial dissipation method was used to calculate the turbulent energy dissipation rates (Liu and Wei, 2007):

$\epsilon =2\pi U^{-1}{\alpha }_3^{-3/2}\overline{\left[f^{5/2}{\varphi }_{w^{\prime }}^{3/2}\left(f\right)\right]},(6)$

where $U$ is the mean velocity of each burst, ${\alpha }_3\approx 0.71$ is the Kolmogorov constant (Sreenivasan and Katepalli, 1995), $f$ is the frequency of the inertial subrange, which is approximately 1–3 Hz here (Figure 2), and ${\varphi }_{w_t^{\prime }}$ is the frequency spectrum density of the $w$ component over the inertial subrange.

Calculation of the Bottom Drag Coefficient

The Bottom drag coefficient was estimated following Egan et al. (2020a). As ${\tau }_c=-\rho \overline{u^{\prime }{w}^{\prime }}$, we rearranged Eq. 1 and obtained

$C_D=\frac{-\overline{u^{\prime }{w}^{\prime }}}{\overline{u}\left|\overline{u}\right|}.(7)$

The instantaneous $C_D$ can be directly calculated by Eq. 7, and the $C_D$ in a certain range of conditions (e.g., flood and ebb tide) can be estimated as the best-fit slope from a least-squares regression of the two terms on the right-hand side of Eq. 7. For the convenience of comparing $C_D$ at different sites, we applied the log-law to deduce mean velocity at 1 mab (${\overline{u}}_{100}$) during weak waves and unstratified periods. Based on Eq. 2, the mean current velocity at the reference height (1 mab) can be expressed as ${\overline{u}}_{100}=u\left(z\right)+\left(u_{\ast c}/\kappa \right)ln\left(1/z\right)$. $C_{100}$ represents the drag coefficient calculated at 1 mab. As the calculation $C_D$ is based on the assumption that the measuring volume is within the constant stress layer which is ∼10–30% of the BBL thickness ($\delta$) (Soulsby, 1997), we calculated $\delta$ using the equation (Soulsby, 1983): $\delta =0.44u_{\text{*}c}/f$, where $f$ is the Coriolis parameter, and retained data for $\delta$ greater than 10 m. The calculation results show that more than 99.8% of the bursts satisfy this condition.

Combining Eqs. 1, 2, we can deduce the dependence of $C_D$ on $z_0$:

$C_D={\left[\frac{1}{\kappa }ln\left(\frac{z}{z_0}\right)\right]}^{-2}.(8)$

Results

Tides, Currents, Waves, and Winds

Figure 3 shows the tidal ellipses of M₂ tidal components in summer and winter for each of the three stations. According to the rotation rate of the tidal ellipse, tide currents in sites S2 and S3 were reversing currents, while the tide in Site 5 (S5) was rotary currents (Figure 3). The maximum tidal velocity had a certain difference for each site, and was generally satisfied: S2>S3>S5, where the maximum tidal velocity of S2 was approximately 0.5 m/s (Figure 3).

FIGURE 3

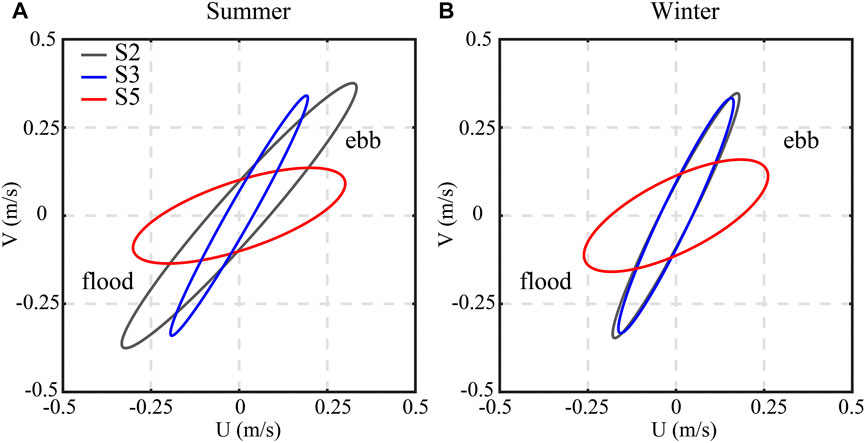
FIGURE 3. Tidal ellipses of M₂ tidal components were calculated from the mean velocity at 1 mab in (A) summer and (B) winter for each of the three stations. The mean velocity was translated from ADV data by log law.

Figure 4 shows the magnitude of wave orbital velocities and wave directions. The maximum value of wave orbital velocity in summer was about 0.12 m/s (Figure 4A), and the average values were 0.01 m/s, 0.03 m/s, and 0.04 m/s at S2, S3, and S5, respectively. The wave propagation was mainly in the northwesterly direction in summer. It was not exactly matching with the direction of the instantaneous winds (Figure 5A) but was consistent with the trend of the prevailing southerly winds (Wu et al., 2019), indicating that the swell waves and background flow dominated the wave propagation.

FIGURE 4

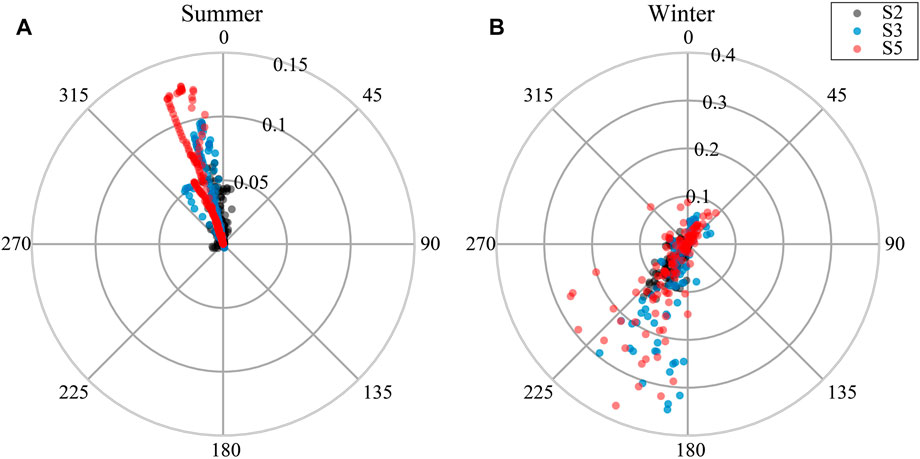
FIGURE 4. Wave magnitude and direction for three stations (S2, S3, and S5) in (A) summer and (B) winter, with 0° corresponding to the northward propagating wave, and the radial axis representing the bottom wave-orbital velocity, $u_b$, in m/s.

FIGURE 5

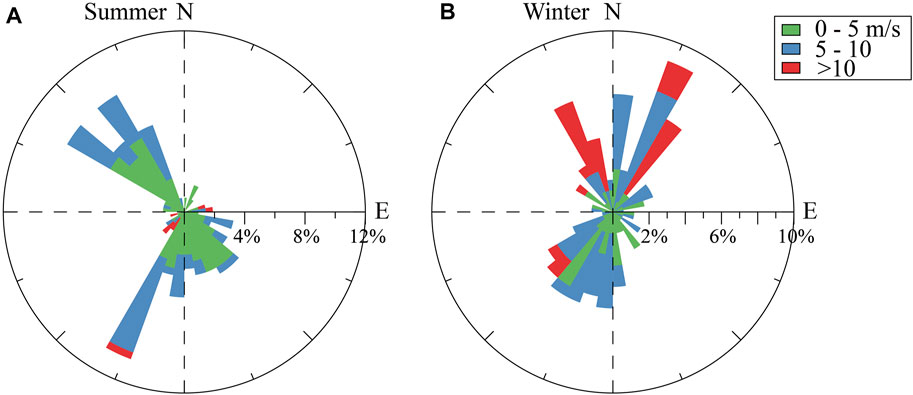
FIGURE 5. Rose diagrams of hourly averaged wind frequencies during (A) summer and (B) winter observations at S3. The greyscale indicates the categories of wind speed (m/s).

The overall intensity of waves was significantly higher in winter than that in summer (Figure 4). The maximum value of wave orbital velocity in winter was about 0.37 m/s, and the average values at S2, S3, and S5 were 0.01 m/s, 0.05 m/s, and 0.06 m/s, respectively. The wave direction was modulated by the local wind field. During periods of weak wind (wind speed less than 10 m/s), the wind direction was not fixed and was dominated alternately by southwesterly and northeasterly winds (Figure 5B). Therefore, when the orbital velocity was smaller than 0.1 m/s, the wave propagation direction was mainly southwestward or northeastward (Figure 4B). However, the stronger wind events (wind speed greater than 10 m/s) that occurred during the observation period were dominated by northerly winds (Figure 5B). Therefore, the wave propagation direction was mainly southwesterly when the orbital velocity was greater than 0.1 m/s (Figure 4B). Wave orbital velocities were higher at S3 and S5 than that at S2 because of the shallower water depth (Table 1). We used data in winter to discuss wave-current interactions in the rest of the article.

Bottom Drag Coefficient

First, we estimated time-series $C_D$ values at the three stations during both summer and winter deployments. In summer, $C_D$ varied from $5\times {10}^{-4}$ to ${10}^{-2}$ at all stations, with most of it between ${10}^{-3}$ and $2\times {10}^{-3}$ (Figure 6). In winter, $C_D$ varied from ${10}^{-3}$ to ${10}^{-2}$ at S3 and S5, with most of it between ${10}^{-3}$ and $3\times {10}^{-3}$ (Figure 7). At S2 in winter, the range $C_D$ was the same as S3 and S5 before January 18. However, after 18 the maximum $C_D$ extent to ${10}^{-1}$ (Figure 8B). From the time series data, we found that a sudden increase of the near-bottom SSC occurred around 08:00 on January 18 of the winter observation at S2 (Figure 8C). Thus, we divided the data into two periods: calm and event periods (Figure 8). The probable reason for this event will be discussed in the following part. Moreover, we found that $C_D$ showed varying degrees of flood–ebb tidal asymmetry during the different observation periods. For example, at S3 in summer, the $C_D$ values during ebb tides were larger than those during flood tides (Figure 6D). However, this relationship was not fixed between observations at different stations or even at the same station in different seasons. For example, station S2 had a larger $C_D$ ebb tide in summer (Figure 6B) and a larger $C_D$ flood tide in winter (Figure 8B). Moreover, after the event, $C_D$ increased significantly during flood tides, while the change $C_D$ during ebb tides was relatively small (Figure 8B). In addition, the fluctuation $C_D$ in summer followed the tidal cycle variation of flow velocity while the effect of waves was weak (Figure 6). But in winter, affected by stronger waves, $C_D$ during the wind events were relatively larger than that during calm periods at all three stations (Figures 7,8A,8B).

FIGURE 6

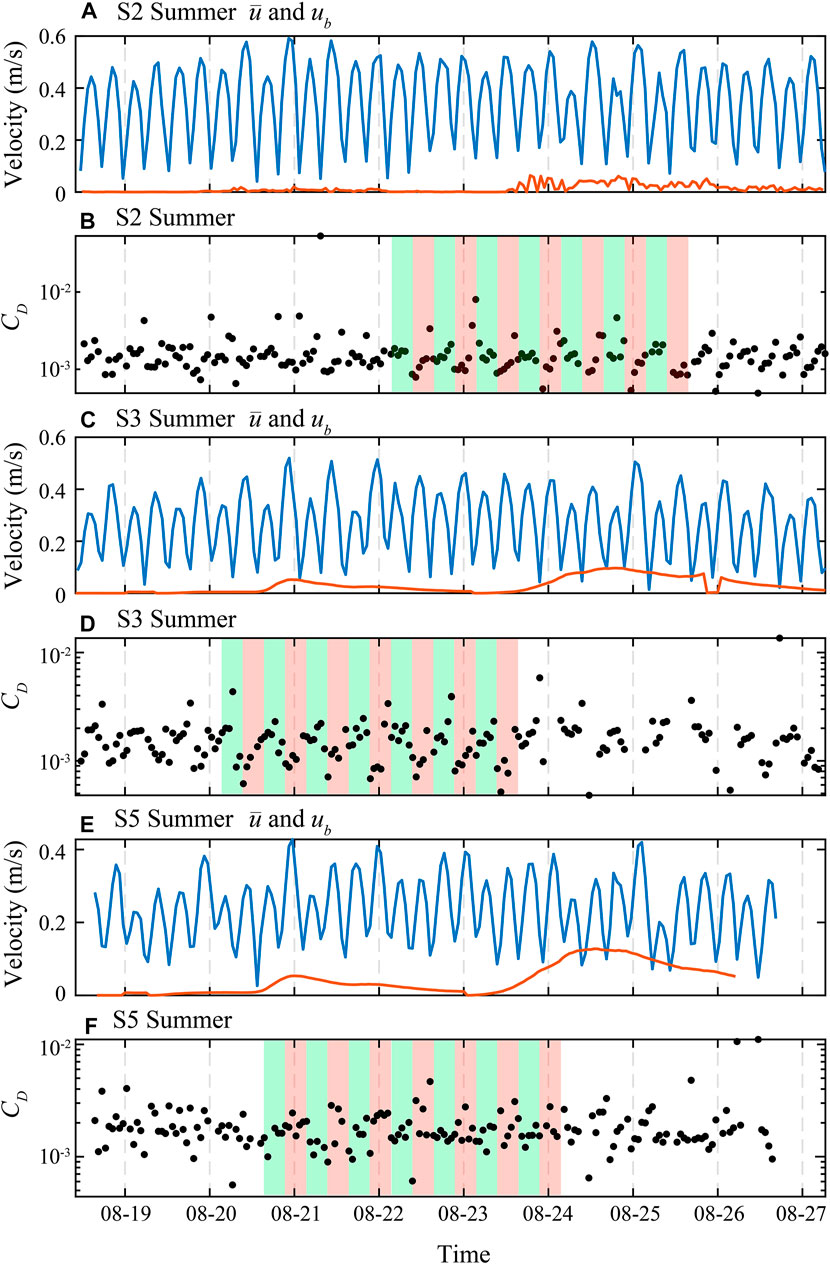
FIGURE 6. Time series of (A,C,E) ADV’s burst mean velocity ($\overline{u}$, blue line) and bottom wave orbital velocity ($u_b$, orange line) and (B,D,F) drag coefficient, $C_D$, estimated using ADV’s burst mean velocity at S2, S3, and S5 in summer. Green and red shaded areas denote periods of ebb and flood tides, respectively.

FIGURE 7

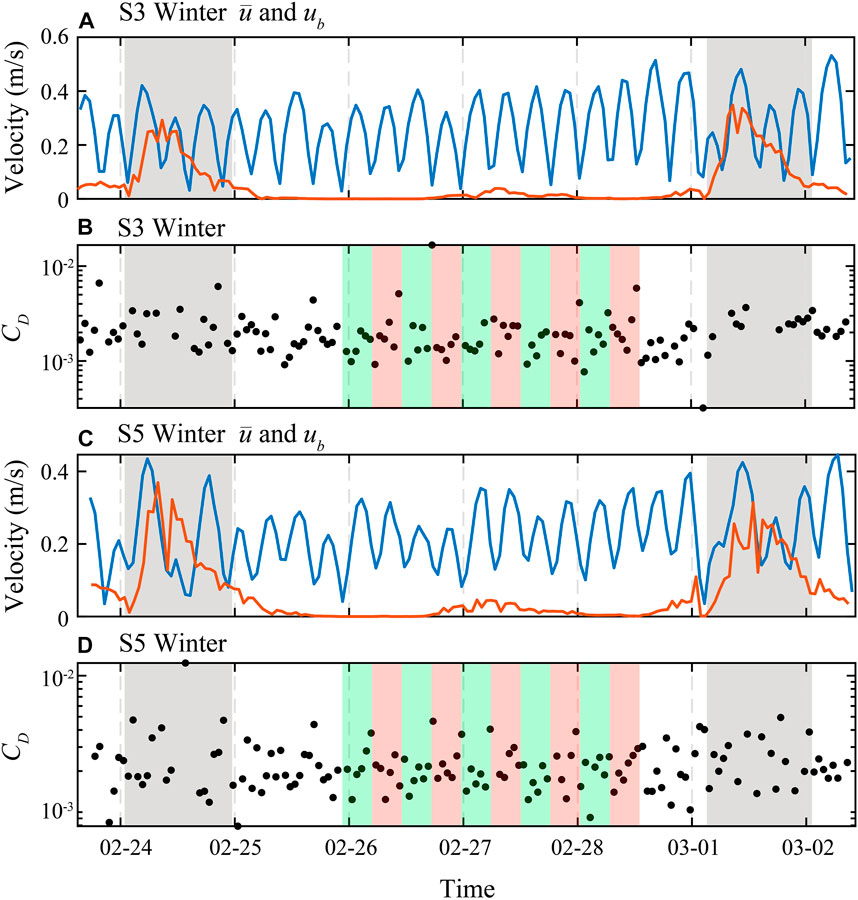
FIGURE 7. Time series of (A,C) ADV’s burst mean velocity ($\overline{u}$, blue line) and bottom wave orbital velocity ($u_b$, orange line) and (B,D) drag coefficient, $C_D$, estimated using ADV’s burst mean velocity at S3 and S5 in winter. Green and red shaded areas denote periods of ebb and flood tides, respectively, and gray shaded areas denote periods of strong winds.

FIGURE 8

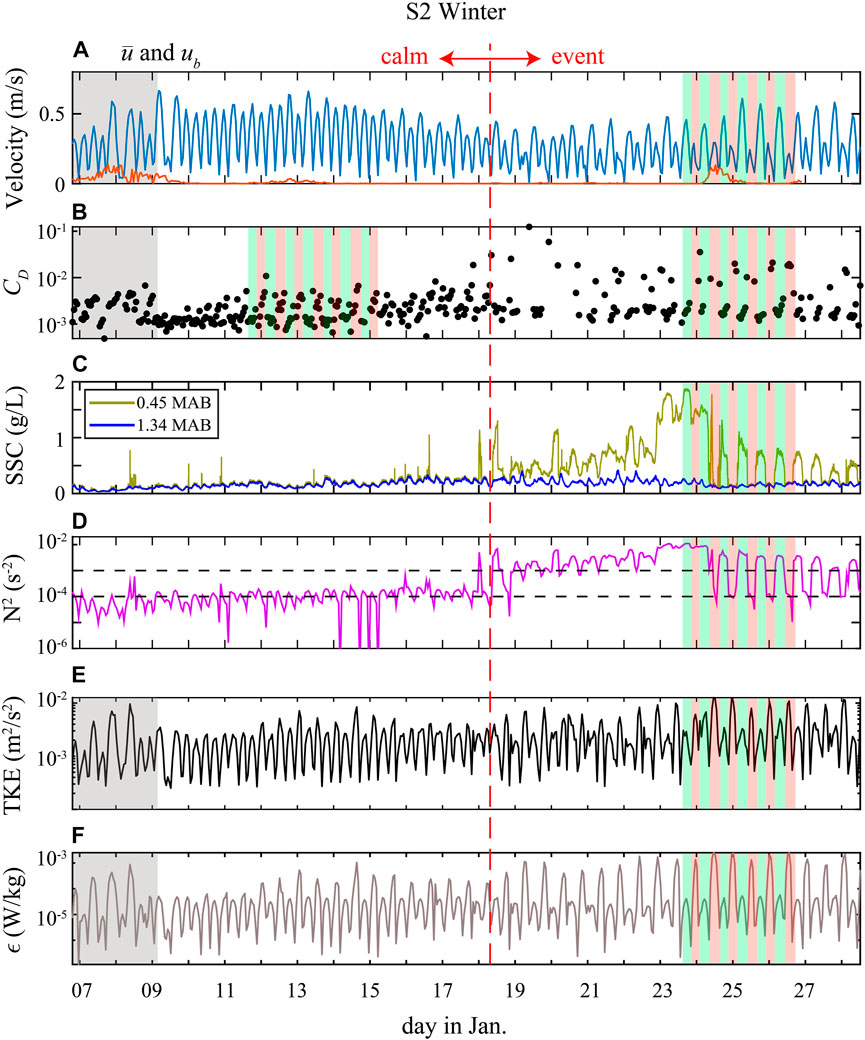
FIGURE 8. Twenty-day time series during the winter deployment at S2 showing measurements of (A) ADV’s burst mean velocity ($\overline{u}$, blue line) and bottom wave orbital velocity ($u_b$, orange line), (B) drag coefficient, $C_D$, estimated using ADV’s burst mean velocity, (C) suspended sediment concentration (SSC) at 0.45 mab (yellow line) and 1.34 mab (blue line), (D) buoyancy frequency ($N^2$) and the black dashed line indicates $N^2$ is equal to ${10}^{-3} {\text{s}}^{-2}$, and ${10}^{-4} {\text{s}}^{-2}$, (E) turbulent kinetic energy (TKE) and (F) turbulence dissipation rates ($\epsilon$). Green and red shaded areas denote periods of ebb and flood tides, respectively, and gray shaded areas denote periods of strong winds. The vertical red dashed line is the demarcation between the calm and event periods.

To recognize the flood–ebb tidal asymmetry $C_D$ and compare $C_D$ at different sites, $C_{100}$ flood or ebb tides at each station were estimated using least-squares regression (Figure 9). Note that only data during calm periods (with weak waves and no sediment stratification) are shown in Figure 9 to ensure the feasibility of log law. Generally, $C_{100}$ ranged from 0.0010 to 0.0020 (average, 0.0015 $\pm$ 0.0004) in summer and from 0.0013 to 0.0026 (average, 0.0019 $\pm$ 0.0005) in winter. There was little difference estimated $C_D$ between summer and winter at S5. However, at S2 and S3, the $C_D$ in winter was twice that in summer during the flood tide, while the estimated $C_D$ did not show extensive differences during the ebbing tide in summer and winter. The R² of the fitted curves for each observation was above 0.71 except for the $C_D$ S2 in winter. At S3 in summer and at S2 in winter, $C_D$ a significant flood–ebb tidal asymmetry, and its controlling factors are discussed in Section 5.

FIGURE 9

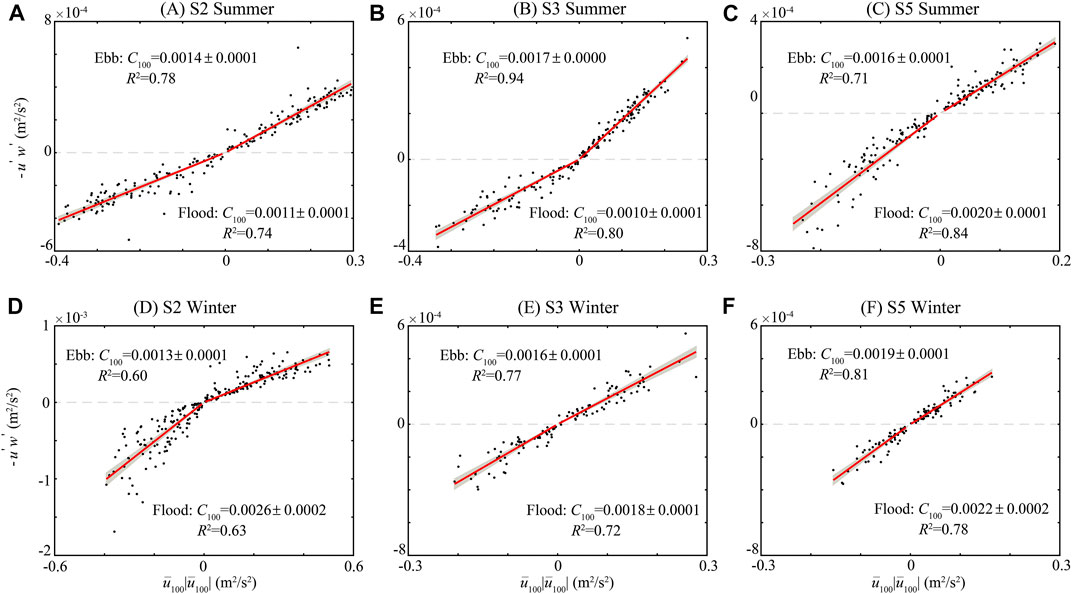
FIGURE 9. Correlation between measured turbulent Reynolds stress, $-\overline{u^{\prime }{w}^{\prime }}$, and the sign-preserving squared mean velocity at 1 mab, ${\overline{u}}_{100}\left|{\overline{u}}_{100}\right|$, for the (A,B,C) summer and (D,E,F) winter. Note that only data during calm periods (with weak waves and no sediment stratification) are shown to ensure the feasibility of log law. The best fit lines are shown in red, with the slopes indicating the drag coefficient, $C_{100}$, for ebb tides (top) and flood tides (bottom). The 95% confidence intervals (gray shaded areas) and R² are shown for each regression.

Discussion

Variation of ${\mathit{C}}_{\mathit{D}}$ During an S2 Winter Event

During event periods, the SSC at 0.45 mab was significantly higher than that of 1.34 mab, which caused significant suspended sediment stratification (Figure 8C). We used the buoyancy frequency squared, $N^2=-\frac{g}{{\rho }_0}\frac{\partial \overline{\rho }}{\partial z}$, to quantify the magnitude of density stratification (Figure 8D). Jones and Monismith (2008) and MacVean and Lacy (2014) took $N^2={10}^{-4} {\text{s}}^{-2}$ it as the threshold for sediment stratification. Also by comparing gradient Richardson numbers, Peters (1999) showed the critical $N^2$ of stratification probably be ${10}^{-3} {\text{s}}^{-2}$. In our study, $N^2$ fluctuated mainly around two typical values, i.e. about ${10}^{-4}$ during the calm period and exceeding ${10}^{-3}$ during a significant portion of the event period (Figure 8D). To facilitate the discussion of stratification, we took $N^2={10}^{-3} {\text{s}}^{-2}$ it as the threshold for sediment stratification. The results showed that sediment stratification mainly occurred during the ebb tides, especially after January 24, and SSC showed significant tidal asymmetry, i.e., the concentration was not stratified during the flood tides but stratified during the ebb tides. At the same time, the current velocity also showed asymmetry (Figure 8A). During the calm period (except for January 9 when S2 was affected by strong winds), the current velocities of flood and ebb tides were similar. In contrast, during the event period, the velocity of the flood tides was significantly smaller than that of the ebb tides (Figure 8A).

Figure 10 shows the estimated $C_D$ for two periods. Possibly due to enhanced noise contamination in the water column (Ruessink, 2010; Tu et al., 2021), there were few valid Reynolds stress estimates at the beginning of the event period and we only plotted data after 12:00 on January 24 (Figure 10B). For ebb tides, stronger stratification was observed during the event period. Previous studies have shown that sediment stratification could suppress turbulence and reduce the bottom drag (Adams and Weatherly, 1981; Tu et al., 2019; Wu et al., 2022). However, when comparing data from before and after the event, estimations $C_D$ were generally the same during ebb tides (Figure 10). In addition, TKE and turbulent dissipation rates were also not controlled by stratification even from January 23 to 24, when sediment stratification was more significant and continuous (Figures 8E,F), but followed the asymmetry of the flood and ebb tides (Figure 8A). For flood tides, the $C_D$ value during the event period was generally seven times larger than that during the calm period. These results suggest that the effect of stratification on $C_D$ was relatively small and the variation of bed configurations, which increased upstream during flood tides, could be the main reason for the variation $C_D$. Because the study area was located in a shipping channel with shipping vessels moored for shelter and fishing vessels actively trawling, the actual cause of the bed roughness change remains difficult to determine.

FIGURE 10

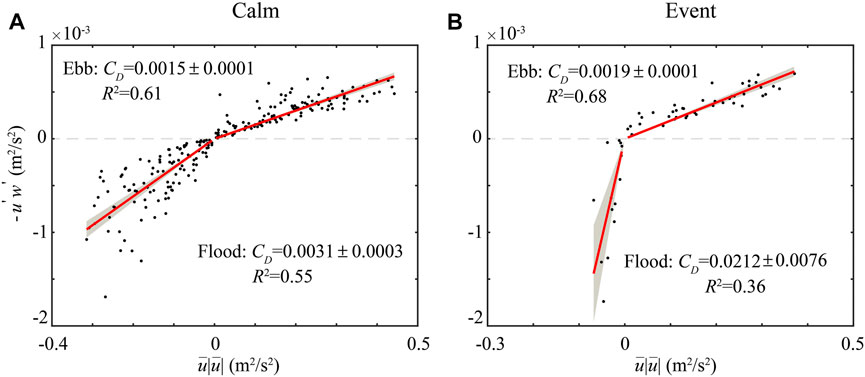
FIGURE 10. Correlation between measured turbulent Reynolds stress, $-\overline{u^{\prime }{w}^{\prime }}$, and the sign-preserving squared ADV’s burst mean velocity, $\overline{u}\left|\overline{u}\right|$ at S2 during winter observation. (A) Calm period with time before January 18, (B) event period after 12:00 on January 24.

Flood–Ebb Asymmetry of ${\mathit{C}}_{\mathit{D}}$

The variation of $C_D$ could be affected by different factors, such as tidal currents (Wright, 1989; Xu et al., 2017), accelerating/decelerating flow (Soulsby and Dyer, 1981; Wright, 1989), waves (Safak, 2016), stratification (Peng et al., 2020), local bathymetry (Fong et al., 2009), upstream/downstream roughness (Scully et al., 2018), benthic biology (Egan et al., 2020a), and water depth (Wang et al., 2014). These factors can lead to asymmetry $C_D$ by influencing mean current velocity or turbulence. First, changes in water depth between flood and ebb tides were relatively small and not sufficient to alter $C_D$, and we did not find sufficient substrate organisms to alter drag in several box samples. In addition, we did not observe near-bottom density stratification including temperature, salinity, and SSC in either CTD casts or bottom observations, except for the S2 winter (Figure 8C), for which there is still asymmetry $C_D$ in the calm period without sediment stratification (Figure 10A). Moreover, it is difficult to explain the asymmetry with seasonal variation based on the wind and wave data. For example, the mean wavelength (L) at S5 during strong wind periods was estimated as 65 m; therefore, the wave base (L/2) was significantly larger than the water depth. However, $C_D$ had no significant flood–ebb asymmetry at S5. For S2 and S3, the direction of flood tide coincided with the prevailing winter wind direction and was opposed to the prevailing summer wind, but the current experienced stronger drag during flood tides in winter than in summer, which is contrary to our general understanding. Furthermore, the acceleration/deceleration scale of the flow could be characterized by the time derivative of shear velocity (Soulsby and Dyer, 1981; Wilkinson, 1986). As each flood or ebb tide contains an accelerating and decelerating stage, acceleration and deceleration will only affect the fluctuations within a flood or ebb tide and cannot explain the flood–ebb asymmetry. By comparing phase-averaged tidal height (data not shown), we observed no significant seasonal differences, which indicates the variation in tidal forcing is small between winter and summer (Egan et al., 2020a).

Combined with the above analysis, variation in the tidal asymmetry $C_D$ was most likely caused by the difference between upstream and downstream roughness. In order to estimate upstream and downstream roughness, we should first determine the hydrodynamic roughness regimes. Generally, the flow regime in the boundary layer can be classified into smooth, transitional, and rough conditions. Hydrodynamically smooth flow, $z_0$ reflects only the thickness of the laminar sublayer and is not determined by bed configurations (Chriss and Caldwell, 1982; 1984). Meanwhile, experimental and observational evidence has shown that hydrodynamically rough flow, $z_0$ and $C_D$ are no longer dependent on flow conditions but are related to bed configurations (Sternberg, 1970; Green and Mccave, 1995). Here, we used the Reynolds number ($Re$) as a criterion for distinguishing the flow conditions:

$Re=\frac{u_r{z}_r}{\upsilon },(9)$

where $u_r$ is the velocity at the reference height $z_r$ ($=1$ m), and $\upsilon$ is the molecular kinematic viscosity taken as 0.01 cm²/s in summer (20°C, 32 ‰) and 0.016 cm²/s in winter (4°C, 32 ‰) (Soulsby, 1997). Figure 11 shows the estimates $C_D$ as a function of $Re$. Generally, the dispersion $C_D$ decreased with increase $Re$. Following Sternberg (1968), using the criterion that $C_D$ is generally a constant, we visually estimated the threshold of hydrodynamically smooth flow (vertical dashed lines in Figure 11). The mean value of critical $Re$ was about $2.3\times {10}^5$. Unsurprisingly, as $Re$ was less than the threshold (i.e., smooth flow), $C_D$ decreased with increase $Re$, which is consistent with previous findings (Sherwood et al., 2006; Safak, 2016). We substituted the empirical formula $z_0$ for smooth flow ($z_0=0.11\upsilon /u_{\ast }$) (Sternberg, 1968, 1970; Chriss and Caldwell, 1984; Soulsby, 1997) into the log-law and plotted this relationship in Figure 11 (yellow lines) for comparison. When $Re$ was slightly larger than the threshold, $C_D$ fluctuated around the empirical relationship but did not follow the empirical relationship exactly, which may reflect the characteristics of transitional flow. Because $z_0$ is a constant for rough flow, we found the estimation $z_0$ by substituting the mean values of $C_D$ Eq. 8 (Table 2). This shows that the larger the tidal asymmetry $C_D$, the greater the difference in upstream and downstream roughness, which suggests that varying upstream and downstream roughness is the main reason for the flood–ebb asymmetry of $C_D$.

FIGURE 11

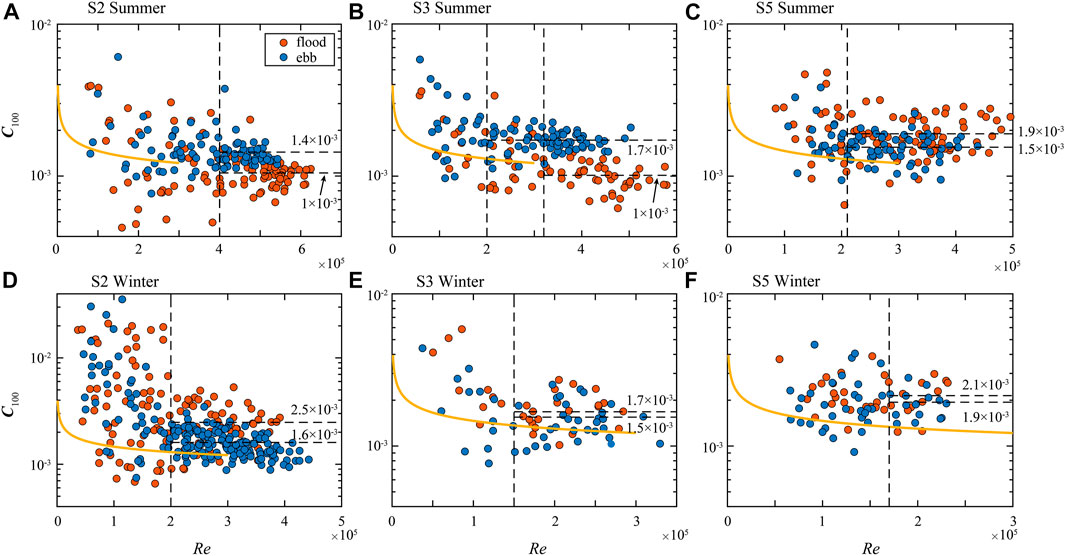
FIGURE 11. Scatter plots of drag coefficient estimated at 1 mab, $C_{100}$, versus the Reynolds number ($Re$) for the (A,B,C) summer and (D,E,F) winter. The orange scatters represent the flood tide, and the blue scatters represent the ebb tide. The vertical dashed lines are the boundary between regions of relatively large and small dispersion. The horizontal dashed lines are the mean value of $C_D$ the right-hand side of the boundary. The yellow lines are the empirical relationship under the assumptions for smooth flow.

TABLE 2

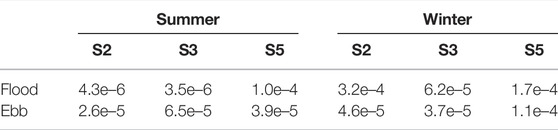
TABLE 2. The mean value of $z_0$ for hydrodynamic rough flow for flood and ebb tides in summer and winter.

Bottom Drag Enhanced by Waves

In addition to the change in roughness, the bottom drag experienced by currents could be enhanced by waves, which do affect the flood–ebb asymmetry $C_D$. We removed the data during strong waves ($u_b>0.1$ m/s) in winter (red dots in Figure 12) and refitted the data to obtain $C_D$. After refitting the data of S3, the tidal asymmetry was reduced and the difference $C_D$ between the flood and ebb tides changed from 5 $\times {10}^{-4}$ to 2 $\times {10}^{-4}$ (Figure 12B). After refitting the data of S5, the fitted R² during flood tides changed from 0.66 to 0.76 (Figure 12C). These findings indicated that stronger waves can have a significant effect on bottom drag at S3 and S5, leading to a bias in the $C_D$ estimates. Because relatively few data are available for strong waves, the re-estimated $C_D$ did not change significantly at S2 (Figure 12A).

FIGURE 12

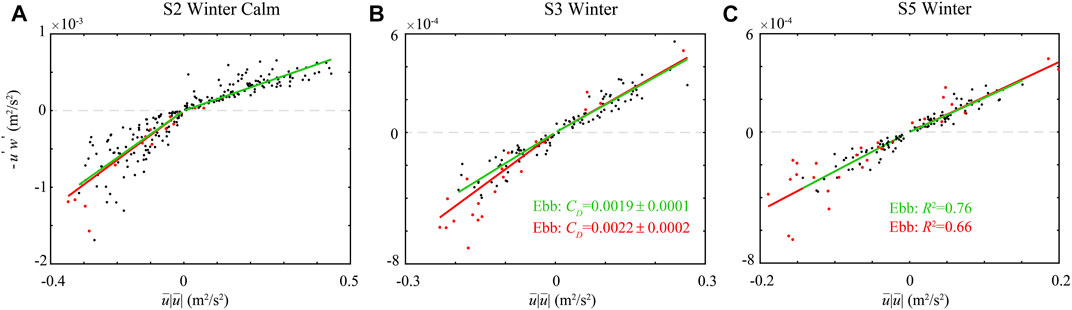
FIGURE 12. Correlation between measured turbulent Reynolds stress, $-\overline{u^{\prime }{w}^{\prime }}$, and the sign-preserving squared ADV’s burst mean velocity, $\overline{u}\left|\overline{u}\right|$, for the (A) S2 calm period, (B) S3, and (C) S5 in winter without the strong wave observations (red dots). The best fit lines without the strong wave observations (red dots) are shown in green and the best fit lines of all data are shown in red, with the slopes indicating the drag coefficients, $C_D$, for ebb tide (top) and flood tide (bottom).

To quantify the effect of waves, we used a one-dimensional time-dependent model, referred to as the Grant-Madsen (GM) model, that incorporates the combined effects of a steady current in the presence of oscillatory waves (Grant and Madsen, 1979). In the GM model, the friction velocity combined waves and currents ($u_{\ast cw}$) is given by

$u_{\text{∗}cw}=u_{\text{∗}w}{\left[1+2{\left(u_{\text{∗}c}/u_{\text{∗}w}\right)}^2\mathit{cos}\varphi +{\left(u_{\text{∗}c}/u_{\text{∗}w}\right)}^4\right]}^{1/4},(10)$

where $\varphi$ is the angle between currents and the direction of wave propagation. In addition, $u_{\ast w}$ is the friction velocity associated with the wave-related bed shear stress (${\tau }_w$) given as

$u_{\text{∗}w}^2=\frac{{\tau }_w}{{\rho }_0}=\frac{\kappa u_{\text{∗}cw}{u}_b}{\sqrt{{\left[\log \left(\frac{\kappa u_{\text{∗}cw}}{z_0\omega }\right)-1.15\right]}^2+{\left(\frac{\pi }{2}\right)}^2}},(11)$

where $\omega$ ($=2\text{π}/T_p$) is the wave frequency. Here, we assumed $z_0=2\times {10}^{-5}$ m, which is generally consistent with the value reported for other sites dominated by silt (Soulsby, 1983; Brand et al., 2010) and is in general agreement with our estimate in Table 2. In the region aforementionedthe wave-current boundary layer ($z>{\delta }_{cw}=\kappa u_{\ast cw}/\omega$), the effect of the wave-current interaction is to increase the roughness experienced by the current so that the log-law becomes

$U\left(z\right)=\frac{u_{\text{∗}c}}{\kappa }\left(\frac{u_{\text{∗}c}}{u_{\text{∗}cw}}\log \frac{{\delta }_{cw}}{z_0}+\log \frac{z}{{\delta }_{cw}}\right).(12)$

Based on the observed data, we calculated the $u_{\ast c-\text{GM}}$ by solving Eqs. 10–12 iteratively. By comparison, we found that $u_{\ast c-\text{GM}}$ was in good agreement with the results calculated by observed data ($u_{\ast c-\text{ADV}}$) (Supplementary Figure S2).

Figure 13A shows the estimates $C_D$ as a function of the ratio of bottom wave orbital velocity to mean current velocity ($u_b/\overline{u}$) during strong waves, which is a common parameter used to quantify the effect of waves (Safak, 2016). The results show that $C_D$ increased with the increase $u_b/\overline{u}$, which is similar to the findings of Safak (2016) and Fan et al. (2019) in muddy environments. In our study, the fitted equation between $C_D$ and $u_b/\overline{u}$ was $C_D=0.00087\frac{u_b}{\overline{u}}+0.00194$, $R^2=0.61$ (orange line in Figure 13A). Although bin average $C_D$ is somewhat scattered, the $R^2$ is pretty good. The constant term in the fitted equation was approximately equal to the average $C_D$ during the winter S3 and S5 observations (Figures 11E,F). Moreover, GM-model results (red dots in Figure 13A) are in good agreement with the trend of the fitted curve of observed values (orange line in Figure 13A). However, when we used the log-law, which does not consider wave-current interactions, the calculation $C_D$ remained almost unchanged (black dots in Figure 13A). It indicates that although our observations are not within the wave's bottom boundary layer, the effect of the wave is still significant. On the one hand, waves can modify the current structure within the bottom boundary layer. We obtained the difference $\overline{u}$ calculated by log-law (${\overline{u}}_{log}$) and GM-model (${\overline{u}}_{GM}$) (Figure 13B) and found that when $u_b$ > 0.1 $\pm$ 0.03 m/s, ${\overline{u}}_{log}-{\overline{u}}_{GM}$ tended to gradually increase. On the other hand, the wave effect could lead to an enhancement of the TKE (Perlin and Kit, 2002; Bricker et al., 2005). Figure 13C shows the variation of TKE, which is also bounded by $u_b=$ 0.1 $\pm$ 0.03 m/s. Therefore, we infer that in the study area, $u_b\approx$ 0.1 m/s can be defined as an important threshold for determining whether the wave effect is significant in the bottom boundary layer. Note that although GM-model results have the right trend, there is no good agreement between it and the observed data, especially when $u_b/\overline{u}$ is large. It indicates that under wave-current conditions similar to those in this article, the fitted equation between $C_D$ and $u_b/\overline{u}$ could give a more accurate estimate $C_D$.

FIGURE 13

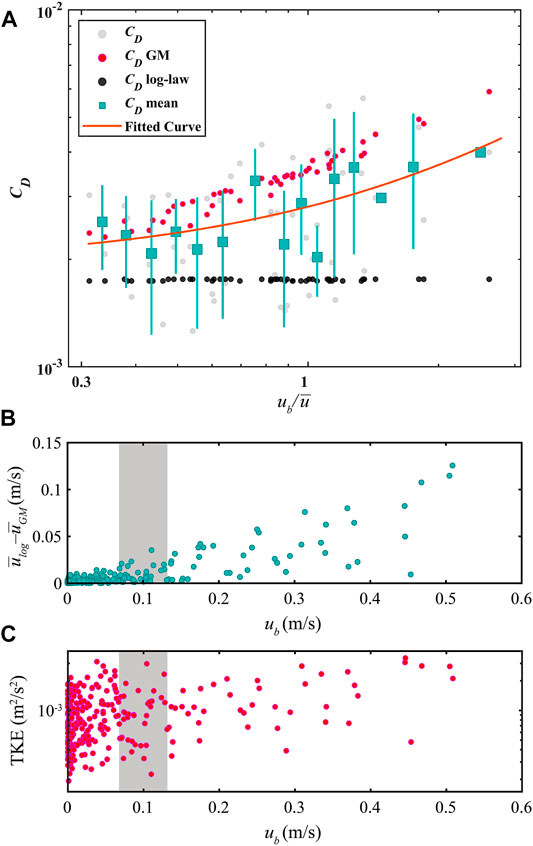
FIGURE 13. (A) Scatter plots of $C_D$ verses $u_b$ / $\overline{u}$ when $u_b>0.1$ m/s for S3 and S5 in winter. Gray dots indicate directly observed $C_D$, red dots indicate $C_D$ calculated by the Grant-Madsen model, black dots indicate $C_D$ calculated by log-law, blue squares are the bin averages of observed $C_D$, and vertical lines indicate standard deviation. The best fine line observed $C_D$ is shown in orange. (B) The difference $\overline{u}$ calculated by the log-law velocity profile (${\overline{u}}_{law}$) and the Grant-Madsen model (${\overline{u}}_{GM}$) and (C) turbulent kinetic energy (TKE) as a function of $u_b$.

Conclusion

In situ observations of currents, waves, and suspended sediment concentration at three stations on the muddy deposits off the Shandong Peninsula was conducted to investigate the variation of the bottom drag coefficient. Data collected in both summer and winter highlight the tidal variations and the effect of winter storm events. The results show that the estimated $C_D$ was around 0.0015 in summer and 0.0019 in winter. A significant tidal asymmetry $C_D$ was observed in both summer and winter. By analyzing the different influencing factors one by one, we conclude that this flood–ebb asymmetry was mainly caused by the variation of local roughness; the drag reduction caused by the suspended sediment stratification was limited. Variations $C_D$ could be affected by different hydrodynamic flow regimes. For hydrodynamically smooth flow, the bottom drag coefficient was relatively dispersed and showed an overall decrease with increase $Re$. For hydrodynamically rough or transitional flow, the bottom drag coefficient typically was a constant that varied from $1\times {10}^{-3}$ to $2.5\times {10}^{-3}$ over the different observation periods. On average, hydrodynamically smooth flow occurred when $Re$ was less than $2.3\times {10}^5$. In addition, strong waves, during which the bottom drag generally increases with increasing wave forcing, can lead to bias in the $C_D$ estimates. When $u_b$ > 0.1 $\pm$ 0.03 m/s, the current-only log-law is not valid in BBL while the GMmodel performs well in terms of trends. As the waves strengthen, TKE is also significantly enhanced. In general, we believe that $u_b\approx$ 0.1 m/s is the critical value to determine whether the wave effect is important in the bottom boundary layer.

In this work, we provide an accurate estimate of $C_D$ the study area, which would be useful to improve the hydrodynamic and sediment transport models in the muddy deposits of the East China Shelf Seas. Moreover, the threshold of $u_b$ ($\approx$ 0.1 m/s) has guiding significance for the study of sediment transport and erosion dynamics in the bottom boundary layer. These relationships between $C_D$ waves or currents, though based on observations off the Shandong Peninsula, could provide a reference to related research in other muddy deposits over the continental shelf.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

JX and ZL: conceptualization, methodology, and reviewing. FQ: conceptualization, methodology, data curation, analyses, and original draft preparation.

Funding

The authors gratefully acknowledge the financial support of the Key Special Project for Introduced Talents Team of the Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou) (GML2019ZD0210), Guangdong Basic and Applied Basic Research Foundation (2021B1515120080) and the National Natural Science Foundation of China (NSFC, Grant No. 41530966).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Special thanks go to Baoduo Wang, Meng Liu, Zhiwen Wang, and Xiaohang Liu for their support in fieldwork.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.921995/full#supplementary-material

References

Adams, C. E., and Weatherly, G. L. (1981). Some Effects of Suspended Sediment Stratification on an Oceanic Bottom Boundary Layer. J. Geophys. Res. 86 (C5), 4161–4172. doi:10.1029/JC086iC05p04161

CrossRef Full Text | Google Scholar

Alexander, C. R., DeMaster, D. J., and Nittrouer, C. A. (1991). Sediment Accumulation in a Modern Epicontinental-Shelf Setting: The Yellow Sea. Mar. Geol. 98 (1), 51–72. doi:10.1016/0025-3227(91)90035-3

CrossRef Full Text | Google Scholar

Baas, J. H., Baker, M. L., Malarkey, J., Bass, S. J., Manning, A. J., Hope, J. A., et al. (2019). Integrating Field and Laboratory Approaches for Ripple Development in Mixed Sand-Clay-EPS. Sedimentology 66 (7), 2749–2768. doi:10.1111/sed.12611

PubMed Abstract | CrossRef Full Text | Google Scholar

Bass, S. J., Aldridge, J. N., McCave, I. N., and Vincent, C. E. (2002). Phase Relationships between Fine Sediment Suspensions and Tidal Currents in Coastal Seas. J. Geophys. Res. 107 (C10), 3146. doi:10.1029/2001jc001269

CrossRef Full Text | Google Scholar

Bian, C., Jiang, W., and Greatbatch, R. J. (2013). An Exploratory Model Study of Sediment Transport Sources and Deposits in the Bohai Sea, Yellow Sea, and East China Sea. J. Geophys. Res. Oceans 118 (11), 5908–5923. doi:10.1002/2013JC009116

CrossRef Full Text | Google Scholar

Brand, A., Lacy, J. R., Hsu, K., Hoover, D., Gladding, S., and Stacey, M. T. (2010). Wind-enhanced Resuspension in the Shallow Waters of South San Francisco Bay: Mechanisms and Potential Implications for Cohesive Sediment Transport. J. Geophys. Res. 115. doi:10.1029/2010JC006172

CrossRef Full Text | Google Scholar

Bricker, J. D., Inagaki, S., and Monismith, S. G. (2005). Bed Drag Coefficient Variability under Wind Waves in a Tidal Estuary. J. Hydraul. Eng. 131 (6), 497–508. doi:10.1061/(asce)0733-9429(2005)131:6(497)

CrossRef Full Text | Google Scholar

Bricker, J. D., and Monismith, S. G. (2007). Spectral Wave-Turbulence Decomposition. J. Atmos. Ocean. Technol. 24 (8), 1479–1487. doi:10.1175/JTECH2066.1

CrossRef Full Text | Google Scholar

Chriss, T. M., and Caldwell, D. R. (1982). Evidence for the Influence of Form Drag on Bottom Boundary Layer Flow. J. Geophys. Res. 87 (C6), 4148. doi:10.1029/JC087iC06p04148

CrossRef Full Text | Google Scholar

Chriss, T. M., and Caldwell, D. R. (1984). Universal Similarity and the Thickness of the Viscous Sublayer at the Ocean Floor. J. Geophys. Res. 89 (C4), 6403–6414. doi:10.1029/JC089iC04p06403

CrossRef Full Text | Google Scholar

Duan, H., Xu, J., Wu, X., Wang, H., Liu, Z., and Wang, C. (2020). Periodic Oscillation of Sediment Transport Influenced by Winter Synoptic Events, Bohai Strait, China. Water 12 (4), 986. doi:10.3390/w12040986

CrossRef Full Text | Google Scholar

Egan, G., Chang, G., Revelas, G., Monismith, S., and Fringer, O. (2020a). Bottom Drag Varies Seasonally with Biological Roughness. Geophys. Res. Lett. 47 (15). doi:10.1029/2020GL088425

CrossRef Full Text | Google Scholar

Egan, G., Cowherd, M., Fringer, O., and Monismith, S. (2019). Observations of Near‐Bed Shear Stress in a Shallow, Wave‐ and Current‐Driven Flow. J. Geophys. Res. Oceans 124 (8), 6323–6344. doi:10.1029/2019JC015165

CrossRef Full Text | Google Scholar

Egan, G., Manning, A. J., Chang, G., Fringer, O., and Monismith, S. (2020b). Sediment‐Induced Stratification in an Estuarine Bottom Boundary Layer. J. Geophys. Res. Oceans 125 (8). doi:10.1029/2019JC016022

CrossRef Full Text | Google Scholar

Fan, R., Zhao, L., Lu, Y., Nie, H., and Wei, H. (2019). Impacts of Currents and Waves on Bottom Drag Coefficient in the East China Shelf Seas. J. Geophys. Res. Oceans 124 (11), 7344–7354. doi:10.1029/2019JC015097

CrossRef Full Text | Google Scholar

Feddersen, F., Gallagher, E. L., Guza, R. T., and Elgar, S. (2003). The Drag Coefficient, Bottom Roughness, and Wave-Breaking in the Nearshore. Coast. Eng. 48 (3), 189–195. doi:10.1016/s0378-3839(03)00026-7

CrossRef Full Text | Google Scholar

Feddersen, F., and Williams, A. J. (2007). Direct Estimation of the Reynolds Stress Vertical Structure in the Nearshore. J. Atmos. Ocean. Technol. 24 (1), 102–116. doi:10.1175/JTECH1953.1

CrossRef Full Text | Google Scholar

Fong, D. A., Monismith, S. G., Stacey, M. T., and Burau, J. R. (2009). Turbulent Stresses and Secondary Currents in a Tidal-Forced Channel with Significant Curvature and Asymmetric Bed Forms. J. Hydraul. Eng. 135 (3), 198–208. doi:10.1061/(asce)0733-9429(2009)135:3(198)

CrossRef Full Text | Google Scholar

Francis P. Shepard, F. P. (1954). Nomenclature Based on Sand-Silt-Clay Ratios. Sepm Jsr Vol. 24 (3), 151–158. doi:10.1306/d4269774-2b26-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Fringer, O. B., Dawson, C. N., He, R., Ralston, D. K., and Zhang, Y. J. (2019). The Future of Coastal and Estuarine Modeling: Findings from a Workshop. Ocean. Model. 143, 101458. doi:10.1016/j.ocemod.2019.101458

CrossRef Full Text | Google Scholar

Grant, W. D., and Madsen, O. S. (1979). Combined Wave and Current Interaction with a Rough Bottom. J. Geophys. Res. 84 (C4), 1797–1808. doi:10.1029/JC084iC04p01797

CrossRef Full Text | Google Scholar

Grant, W. D., and Madsen, O. S. (1986). The Continental-Shelf Bottom Boundary Layer. Annu. Rev. Fluid Mech. 18 (1), 265–305. doi:10.1146/ANNUREV.FL.18.010186.001405

CrossRef Full Text | Google Scholar

Green, M. O., and Mccave, I. N. (1995). Seabed Drag Coefficient under Tidal Currents in the Eastern Irish Sea. J. Geophys. Res. 100 (C8), 16057–16069. doi:10.1029/95JC01381

CrossRef Full Text | Google Scholar

Harris, C. K., and Wiberg, P. L. (2001). A Two-Dimensional, Time-dependent Model of Suspended Sediment Transport and Bed Reworking for Continental Shelves. Comput. Geosciences 27 (6), 675–690. doi:10.1016/S0098-3004(00)00122-9

CrossRef Full Text | Google Scholar

Herrmann, M. J., and Madsen, O. S. (2007). Effect of Stratification Due to Suspended Sand on Velocity and Concentration Distribution in Unidirectional Flows. J. Geophys. Res. 112 (C2). doi:10.1029/2006jc003569

CrossRef Full Text | Google Scholar

Jones, N. L., and Monismith, S. G. (2008). Modeling the Influence of Wave-Enhanced Turbulence in a Shallow Tide- and Wind-Driven Water Column. J. Geophys. Res. 113, 1–13. doi:10.1029/2007JC004246

CrossRef Full Text | Google Scholar

Kaimal, J. C., Wyngaard, J. C., Izumi, Y., and Coté, O. R. (1972). Spectral Characteristics of Surface-Layer Turbulence. Q.J R. Met. Soc. 98 (417), 563–589. doi:10.1002/QJ.49709841707

CrossRef Full Text | Google Scholar

Liu, S., Qiao, L., Li, G., Li, J., Wang, N., and Yang, J. (2015). Distribution and Cross-Front Transport of Suspended Particulate Matter over the Inner Shelf of the East China Sea. Cont. Shelf Res. 107, 92–102. doi:10.1016/j.csr.2015.07.013

CrossRef Full Text | Google Scholar

Liu, Z., and Wei, H. (2007). Estimation to the Turbulent Kinetic Energy Dissipation Rate and Bottom Shear Stress in the Tidal Bottom Boundary Layer of the Yellow Sea. Progress in Natural Science 17, 289–297. doi:10.1080/10020070612331343260

CrossRef Full Text | Google Scholar

MacVean, L. J., and Lacy, J. R. (2014). Interactions between Waves, Sediment, and Turbulence on a Shallow Estuarine Mudflat. J. Geophys. Res. Oceans 119 (3), 1534–1553. doi:10.1002/2013JC009477

CrossRef Full Text | Google Scholar

Magaldi, M. G., Özgökmen, T. M., Griffa, A., and Rixen, M. (2009). On the Response of a Turbulent Coastal Buoyant Current to Wind Events: the Case of the Western Adriatic Current. Ocean. Dyn. 60 (1), 93–122. doi:10.1007/s10236-009-0247-9

CrossRef Full Text | Google Scholar

Mo, D., Hou, Y., Li, J., and Liu, Y. (2016). Study on the Storm Surges Induced by Cold Waves in the Northern East China Sea. J. Mar. Syst. 160, 26–39. doi:10.1016/j.jmarsys.2016.04.002

CrossRef Full Text | Google Scholar

Naimie, C. E., Blain, C. A., and Lynch, D. R. (2001). Seasonal Mean Circulation in the Yellow Sea } a Model-Generated Climatology. Cont. Shelf Res. 21 (6), 667–695. doi:10.1016/S0278-4343(00)00102-3

CrossRef Full Text | Google Scholar

Nayak, A. R., Li, C., Kiani, B. T., and Katz, J. (2015). On the Wave and Current Interaction with a Rippled Seabed in the Coastal Ocean Bottom Boundary Layer. J. Geophys. Res. Oceans 120 (7), 4595–4624. doi:10.1002/2014jc010606

CrossRef Full Text | Google Scholar

Nelson, K. S., and Fringer, O. B. (2018). Sediment Dynamics in Wind Wave‐Dominated Shallow‐Water Environments. J. Geophys. Res. Oceans 123 (10), 6996–7015. doi:10.1029/2018jc013894

CrossRef Full Text | Google Scholar

Pawlowicz, R., Beardsley, B., and Lentz, S. (2002). Classical Tidal Harmonic Analysis Including Error Estimates in MATLAB Using T_TIDE. Comput. Geosciences 28 (8), 929–937. doi:10.1016/S0098-3004(02)00013-4

CrossRef Full Text | Google Scholar

Peng, Y., Yu, Q., Yang, Y., Wang, Y., Wang, Y. P., and Gao, S. (2020). Flow Structure Modification and Drag Reduction Induced by Sediment Stratification in Coastal Tidal Bottom Boundary Layers. Estuar. Coast. Shelf Sci. 241, 106829. doi:10.1016/j.ecss.2020.106829

CrossRef Full Text | Google Scholar

Perlin, A., and Kit, E. (2002). Apparent Roughness in Wave-Current Flow: Implication for Coastal Studies. J. Hydraul. Eng. 128 (8), 729–741. doi:10.1061/(asce)0733-9429(2002)128:8(729)

CrossRef Full Text | Google Scholar

Peters, H. (1999). Spatial and Temporal Variability of Turbulent Mixing in an Estuary. J. Mar. Res. 57 (6), 805–845. doi:10.1357/002224099321514060

CrossRef Full Text | Google Scholar

Qi, F., Wu, X., Wang, Z., Wang, C., Duan, H., Liu, M., et al. (2022). Transport and Deposition Processes of the Sediment Depocenter off the Shandong Peninsula: An Observational Study. Cont. Shelf Res. 244, 104763. doi:10.1016/j.csr.2022.104763

CrossRef Full Text | Google Scholar

Ruessink, B. G. (2010). Observations of Turbulence within a Natural Surf Zone. J. Phys. Oceanogr. 40 (12), 2696–2712. doi:10.1175/2010jpo4466.1

CrossRef Full Text | Google Scholar

Safak, I. (2016). Variability of Bed Drag on Cohesive Beds under Wave Action. Water 8 (4), 131. doi:10.3390/w8040131

CrossRef Full Text | Google Scholar

Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., et al. (2014). The NCEP Climate Forecast System Version 2. J. Clim. 27 (6), 2185–2208. doi:10.1175/JCLI-D-12-00823.1

CrossRef Full Text | Google Scholar

Scully, M. E., Trowbridge, J. H., Sherwood, C. R., Jones, K. R., and Traykovski, P. (2018). Direct Measurements of Mean Reynolds Stress and Ripple Roughness in the Presence of Energetic Forcing by Surface Waves. J. Geophys. Res. Oceans 123 (4), 2494–2512. doi:10.1002/2017jc013252

CrossRef Full Text | Google Scholar

Sherwood, C. R., Lacy, J. R., and Voulgaris, G. (2006). Shear Velocity Estimates on the Inner Shelf off Grays Harbor, Washington, USA. Cont. Shelf Res. 26 (17-18), 1995–2018. doi:10.1016/j.csr.2006.07.025

CrossRef Full Text | Google Scholar

Signell, R. P., and List, J. H. (1997). Effect of Wave-Enhanced Bottom Friction on Storm-Driven Circulation in Massachusetts Bay. J. Waterw. Port Coast. Ocean Eng. 123 (5), 233–239. doi:10.1061/(asce)0733-950x(1997)123:5(233)

CrossRef Full Text | Google Scholar

Soulsby, R. L. (1983). Chapter 5 the Bottom Boundary Layer of Shelf Seas. Elsevier Oceanogr. 35, 189–266. doi:10.1016/S0422-9894(08)70503-8

CrossRef Full Text | Google Scholar

Soulsby, R. L., and Dyer, K. R. (1981). The Form of the Near-Bed Velocity Profile in a Tidally Accelerating Flow. J. Geophys. Res. 86 (C9), 8067–8074. doi:10.1029/JC086iC09p08067

CrossRef Full Text | Google Scholar

Soulsby, R. L. (2006). Simplified Calculation of Wave Orbital Velocities. Wallingford: HR Wallingford Ltd.

Google Scholar

Soulsby, R. L. (1997). The Dynamics of Marine Sands: A Manual for Practical Applications. London: Thomas Thelford.

Google Scholar

Sreenivasan, K. R., and Katepalli, R. (1995). On the Universality of the Kolmogorov Constant. Phys. Fluids 7 (11), 2778–2784. doi:10.1063/1.868656

CrossRef Full Text | Google Scholar

Sternberg, R. W. (1970). Field Measurements of the Hydrodynamic Roughness of the Deep-Sea Boundary. Deep Sea Res. Oceanogr. Abstr. 17 (3), 413–420. doi:10.1016/0011-7471(70)90056-2

CrossRef Full Text | Google Scholar

Sternberg, R. W. (1968). Friction Factors in Tidal Channels with Differing Bed Roughness. Mar. Geol. 6 (3), 243–260. doi:10.1016/0025-3227(68)90033-9

CrossRef Full Text | Google Scholar

Styles, R., and Glenn, S. M. (2000). Modeling Stratified Wave and Current Bottom Boundary Layers on the Continental Shelf. J. Geophys. Res. 105 (C10), 24119–24139. doi:10.1029/2000jc900115

CrossRef Full Text | Google Scholar

Teague, W. J., Perkins, H. T., Hallock, Z. R., and Jacobs, G. A. (1998). Current and Tide Observations in the Southern Yellow Sea. J. Geophys. Res. 103 (C12), 27783–27793. doi:10.1029/98jc02672

CrossRef Full Text | Google Scholar

Tolman, H. L., Accensi, M., Alves, H., Ardhuin, F., Bidlot, J., Booij, N., et al. (2014). User Manual and System Documentation of WAVEWATCH III R Version 4.18.

Google Scholar

Trembanis, A. C., Wright, L. D., Friedrichs, C. T., Green, M. O., and Hume, T. (2004). The Effects of Spatially Complex Inner Shelf Roughness on Boundary Layer Turbulence and Current and Wave Friction: Tairua Embayment, New Zealand. Cont. Shelf Res. 24 (13-14), 1549–1571. doi:10.1016/j.csr.2004.04.006

CrossRef Full Text | Google Scholar

Trowbridge, J. H., and Lentz, S. J. (2018). The Bottom Boundary Layer. Annu. Rev. Mar. Sci. 10, 397–420. doi:10.1146/annurev-marine-121916-063351

PubMed Abstract | CrossRef Full Text | Google Scholar

Tu, J., Fan, D., and Voulgaris, G. (2021). Field Observations of Turbulence, Sediment Suspension, and Transport under Breaking Tidal Bores. Mar. Geol. 437, 106498. doi:10.1016/j.margeo.2021.106498

CrossRef Full Text | Google Scholar

Tu, J., Fan, D., Zhang, Y., and Voulgaris, G. (2019). Turbulence, Sediment‐Induced Stratification, and Mixing under Macrotidal Estuarine Conditions (Qiantang Estuary, China). J. Geophys. Res. Oceans 124 (6), 4058–4077. doi:10.1029/2018jc014281

CrossRef Full Text | Google Scholar

Van Rijn, L. C. (1993). Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas Part 1. Amsterdam: Aqua Publications.

Google Scholar

Van Rijn, L. C. (2007). Unified View of Sediment Transport by Currents and Waves. I: Initiation of Motion, Bed Roughness, and Bed-Load Transport. J. Hydraul. Eng. 133 (6), 649–667. doi:10.1061/(asce)0733-9429(2007)133:6(649)

CrossRef Full Text | Google Scholar

Vieira da Silva, G., Toldo Jr., E. E., Klein, A. H. d. F., and Short, A. D. (2018). The Influence of Wave-, Wind- and Tide-Forced Currents on Headland Sand Bypassing - Study Case: Santa Catarina Island North Shore, Brazil. Geomorphology 312, 1–11. doi:10.1016/J.GEOMORPH.2018.03.026

CrossRef Full Text | Google Scholar

Wang, A., Ralston, D. K., Bi, N., Cheng, Z., Wu, X., and Wang, H. (2019). Seasonal Variation in Sediment Transport and Deposition on a Muddy Clinoform in the Yellow Sea. Cont. Shelf Res. 179, 37–51. doi:10.1016/j.csr.2019.04.009

CrossRef Full Text | Google Scholar

Wang, C., Liu, Z., Harris, C. K., Wu, X., Wang, H., Bian, C., et al. (2020). The Impact of Winter Storms on Sediment Transport through a Narrow Strait, Bohai, China. J. Geophys. Res. Oceans 125 (6), e2020JC016069. doi:10.1029/2020jc016069

CrossRef Full Text | Google Scholar

Wang, D., Liu, Q., and Lv, X. (2014). A Study on Bottom Friction Coefficient in the Bohai, Yellow, and East China Sea. Math. Problems Eng. 2014, 1–7. doi:10.1155/2014/432529

CrossRef Full Text | Google Scholar

Warner, J. C., Sherwood, C. R., Signell, R. P., Harris, C. K., and Arango, H. G. (2008). Development of a Three-Dimensional, Regional, Coupled Wave, Current, and Sediment-Transport Model. Comput. Geosciences 34 (10), 1284–1306. doi:10.1016/j.cageo.2008.02.012

CrossRef Full Text | Google Scholar

Wiberg, P. L., and Sherwood, C. R. (2008). Calculating Wave-Generated Bottom Orbital Velocities from Surface-Wave Parameters. Comput. Geosciences 34 (10), 1243–1262. doi:10.1016/j.cageo.2008.02.010

CrossRef Full Text | Google Scholar

Wilkinson, R. H. (1985). Variation of Roughness Length of a Mobile Sand Bed in a Tidal Flow. Geo-Marine Lett. 5 (4), 231–239. doi:10.1007/BF02233808

CrossRef Full Text | Google Scholar

Wright, L. D. (1989). Benthic Boundary Layers of Estuarine and Coastal Environments. Rev. Aquatic Sci. 1, 75–95.

Google Scholar

Wright, L. D., Kim, S. C., and Friedrichs, C. T. (1999). Across-shelf Variations in Bed Roughness, Bed Stress and Sediment Suspension on the Northern California Shelf. Mar. Geol. 154 (1), 99–115. doi:10.1016/S0025-3227(98)00106-6

CrossRef Full Text | Google Scholar

Wu, H., Wang, Y. P., Gao, S., Xing, F., Tang, J., and Chen, D. (2022). Fluid Mud Dynamics in a Tide-Dominated Estuary: A Case Study from the Yangtze River. Cont. Shelf Res. 232, 104623. doi:10.1016/j.csr.2021.104623

CrossRef Full Text | Google Scholar

Wu, X., Xu, J., Wu, H., Bi, N., Bian, C., Li, P., et al. (2019). Synoptic Variations of Residual Currents in the Huanghe (Yellow River)-Derived Distal Mud Patch off the Shandong Peninsula: Implications for Long-Term Sediment Transport. Mar. Geol. 417, 106014. doi:10.1016/j.margeo.2019.106014

CrossRef Full Text | Google Scholar

Xu, J. P., and Wright, L. D. (1995). Tests of Bed Roughness Models Using Field Data from the Middle Atlantic Bight. Cont. Shelf Res. 15, 1409–1434. doi:10.1016/0278-4343(94)00083-Y

CrossRef Full Text | Google Scholar

Xu, P., Mao, X., and Jiang, W. (2017). Estimation of the Bottom Stress and Bottom Drag Coefficient in a Highly Asymmetric Tidal Bay Using Three Independent Methods. Cont. Shelf Res. 140, 37–46. doi:10.1016/j.csr.2017.04.004

CrossRef Full Text | Google Scholar

Yang, Z. S., and Liu, J. P. (2007). A Unique Yellow River-Derived Distal Subaqueous Delta in the Yellow Sea. Mar. Geol. 240 (1-4), 169–176. doi:10.1016/j.margeo.2007.02.008

CrossRef Full Text | Google Scholar

Yuan, P., Wang, H., Wu, X., and Bi, N. (2020). Grain-Size Distribution of Surface Sediments in the Bohai Sea and the Northern Yellow Sea: Sediment Supply and Hydrodynamics. J. Ocean. Univ. China 19 (3), 589–600. doi:10.1007/s11802-020-4221-y

CrossRef Full Text | Google Scholar