Study on Parameter Influence of New Composite Lining of Water Conveyance Tunnel Under High Internal Water Pressure

A new type of composite lining structure consisting of segments, steel pipes, and concrete lining can be adopted in the water conveyance tunnel to bear large internal water pressure. However, there is still no effective analysis model and calculation method for the parameter influence effect of this new composite lining. In this paper, the load structure method and the elasticity theory are adopted, the stress analysis model and theoretical calculation method of a new type of composite lining of water conveyance tunnel are given, and the influence law of lining structure parameters is studied. Each part of the shield assembled lining is regarded as a stressed spring, and a formula for calculating the equivalent elastic modulus of the overall structure at the joint of the lining under partial tension and partial compression is given. The stress and deformation of each layer of lining are deduced based on the theory of thick-walled cylinders. According to the actual project, the rationality of the calculation method is verified by comparing the results of finite element analysis, and the influence of the thickness of intermediate concrete lining and inner lining parameters on the distribution of force transmission among lining layers is further analyzed. The results show that the radial displacement and circumferential stress of each layer of lining structure decrease with increasing the thickness of the concrete lining. The larger the elastic modulus of the inner lining material is, the smaller the radial displacement of each lining structure will be, but the circumferential stress of the inner lining will increase. In addition, when the thickness of the steel pipe lining is reduced or the internal water pressure is increased, the circumferential stress and radial displacement generated by the inner lining will increase. This analysis model and method considering the deformation coordination relationship solves the problem of setting the parameters of the lining structure and has obvious advantages in the calculation of the stress and deformation of the new composite lining water conveyance tunnel structure, which can provide a theoretical basis for related engineering design.

1 Introduction

With the development of regional economy and the difference of population distribution, the problem of water resources distribution is becoming more and more serious. In order to solve the problem of regional water use, a number of representative shield water conveyance tunnels have been built in China, such as the Pearl River Delta Water Resources Allocation Project (Yang et al., 2018; Cao, 2020), the Xijiang Water Diversion Project in Guangxi (Cao, 2020), the South-to-North Water Diversion Project through the Yellow River Tunnel Project (Chen et al., 2014; Yang et al., 2018a,b) and so on. The water conveyance tunnel structure is not only subjected to external water and soil loads, but also bears large internal water pressure. Therefore, multi-layer lining structures are usually used in engineering to joint force to improve the overall load-bearing capacity of the structure (Vogel et al., 2017; Wang et al., 2019; Ding et al., 2020). Facing the construction requirements of large sections, high internal pressure, and complex internal and external loads, part of the project began to try to use the new composite lining structure of “steel lining—self-compacting concrete (SCC)—segment” (Cao, 2020). Part of the water delivery project with this structure is shown in Figure 1. Compared with single-layer lining and double-layer lining structures, the new composite lining structure has higher designed internal water pressure, and under the protection of self-compacting concrete lining in the middle layer, the internal steel pipe is not prone to buckling failure (Gavriilidis and Karamanos, 2019; Yuan and Kyriakides, 2021). At present, there are few water conveyance tunnels with the new composite lining structure of “steel lining—SCC—segment”, and there is a lack of corresponding engineering experience and theoretical research, especially the stress and deformation of each layer lining are still unclear (Nabipour et al., 2020). In addition, the unreasonable setting of structural parameters makes the material stress distribution unreasonable, reduces the bearing capacity of the lining structure, and leads to a series of problems such as concrete cracking and excessive deformation of segments (Guan et al., 2015). Therefore, it is necessary to conduct in-depth research on the theoretical calculation and parameter analysis of the new composite lining structure of the water conveyance tunnel.

FIGURE 1

FIGURE 1. New composite lining water conveyance project.

At present, many scholars have conducted relevant theoretical research on the lining structure of water conveyance tunnel. At first, most of the water conveyance tunnels adopt single-layer lining structure. Yuan et al. (2017) established an elastoplastic damage constitutive model of stress-seepage coupling of surrounding rock, and analyzed the unfavorable situation of grouting cycle failure for a water conveyance tunnel. Yang et al. (2020) put forward an innovative analysis method to evaluate the safety of muddy sandstone pressure water conveyance tunnel under weak water conditions based on the test results and numerical analysis method. Based on the shear test results, Li et al. (2019) put forward the bond zone model of bolt connection in the lining structure of water conveyance tunnel. With the continuous improvement of design load and single-layer lining is prone to a series of problems such as insufficient bearing capacity, pipe wall cracking, water leakage and so on, the double-layer lining structure has gradually become the mainstream form of lining structure of water conveyance tunnel. Zhu et al. (2022) put forward the stress analysis model and method of double-layer lining structure of shield water conveyance tunnel considering the influence of transition layer and revealed the influence law of transition layer parameters on the internal force and deformation of lining structure. Based on the elastic theory, Li et al. (2021) put forward a simplified calculation method that can accurately calculate the stress distribution of composite lining structure, considering the influence of internal water pressure and surrounding rock. Yan et al. (2016) studied the dynamic response of double-layer lining shield tunnel with different thicknesses by using the plastic damage model of concrete.

Facing the complex design requirements and application environment, some special forms of composite lining structures are used in water conveyance projects, such as prestressed composite lining and steel fiber reinforced concrete lining. By applying to prestress to the lining structure, initial compressive stress can prevent the concrete from cracking and improve the capacity of the structure to bear the internal water pressure (Andjelkovic et al., 2013). Yang et al. (2018) analyzed the mechanical properties of each component of prestressed composite lining of a water conveyance tunnel and the interaction between inner and outer linings through numerical simulation. Wang et al. (2020) revealed the change in the tension of the ring anchor and the characteristics of the redistribution of prestress in the lining in the process of tensioning the prestressed tendons and applying the internal water pressure through field tests. Adding steel fiber to concrete can effectively improve the strength and crack resistance of the lining structure (Liu X et al., 2020). Gong et al. (2017) studied the ultimate bearing capacity and cracking process of steel fiber reinforced concrete segment joints under different load conditions through full-scale tests. Nehdi et al. (2015) conducted a model test on the mechanical behavior of concrete tunnel lining segments with different lengths and contents of steel fibers. The above research mainly focuses on single-layer lining and double-layer lining structure. Compared with single-layer lining and double-layer lining, the materials of the new composite lining structure are more diverse and the force transmission forms are more complex. There is a still lack of relevant research on force transmission among different layers of lining and the mechanism of load sharing (Mezger et al., 2017; Dong et al., 2021; Huang et al., 2021; Zhang et al., 2021; Zhou et al., 2021). In the past, it was seldom used to analyze the influence of structural parameters of “steel lining -SCC- segment” new composite lining by establishing an analytical model and analytical calculation method. The reasonable setting of structural parameters in the process of engineering design and construction can not only improve the bearing capacity and safety of the structure but also reduce the engineering cost (Salemi et al., 2018).

To solve the joint force problem of the new composite lining structure and consider the influence of structural parameters, a stress analysis model of the lining structure under the action of uniformly distributed pressure is established in this paper. Segments, bolts, and joint gaskets of shield lining are regarded as stressed springs, and a formula for calculating the equivalent elastic modulus of the whole structure at the joint of lining under partial tension and partial compression is given. Based on the load structure method and the theory of thick-walled cylinders, a calculation method for solving the stress and coordinated deformation of lining structures in different layers is proposed. According to an engineering example, the rationality of the calculation method is verified by finite element analysis. On this basis, the influence of concrete lining thickness and inner lining parameters on structure stress and deformation is further analyzed. This method, which combines the load structure method with the elasticity theory, can effectively calculate the stress and deformation of the new lining structure, solve the problem of setting the parameters of the lining structure and provide a theoretical basis for related engineering design.

2 Analysis Model and Methods

In this section, based on simplifying the stress of lining structure of water conveyance tunnel, a force analysis model of new composite lining is given. Using the spring series formula, the equivalent elastic modulus of shield assembled lining is calculated. Then, the force analysis of the lining structure is carried out independently, and the calculation formulas of radial displacement and circumferential stress of each layer lining are obtained. Through the deformation compatibility conditions, the relationship between the radial displacement of each layer of the lining is established, to obtain the magnitude of the interaction force between the lining structures.

2.1 Establish Analysis Model

The lining structure of the water conveyance tunnel in the project is in a complex stress environment. The outside is affected by the gravity of water and soil loads, the inside by the gravity and pressure of water, the dead weight of each structure, and the external resistance caused by structural deformation. To simplify the calculation, the pressure on the outer surface of the lining is taken as uniform pressure equal to the minimum water and soil pressure value, regardless of the influence of the lining structure weight, water weight, and external resistance. Establish the stress calculation model of the new composite lining structure of shield water conveyance tunnel under the action of uniformly distributed internal water pressure and uniformly distributed external water and soil load, considering the deformation coordination relationship, as shown in Figure 2.

FIGURE 2

FIGURE 2. Force analysis model of new composite lining.

The whole lining structure consists of external assembled segments, internal steel pipe lining, and middle self-compacting concrete lining. The three layers of linings are tightly connected, and it is considered that only radial pressure is transmitted on the contact surfaces of each layer of linings. As shown in Figure 2, taking the isolated body from the overall structure and the lining structure of each layer is analyzed separately. It is known that the uniformly distributed internal pressure is P and the uniformly distributed external pressure is P₃. Assume that the reaction force of the concrete lining to the steel pipe lining is P₁, and the reaction force of the shield lining to the concrete lining is P₂.

To calculate the internal force and deformation of the lining structure, the magnitude of the unknown interaction force is required. The equivalent elastic modulus of shield assembling lining structure will be obtained by using the series equivalent formula of springs. Then, through the coordinated relation of deformation between each layer of lining. The calculation formula of radius increment obtained by independent analysis of lining structure is used to solve the values of the unknown forces P₁ and P₂.

2.2 Equivalent Elastic Modulus

The outer lining of the shield water conveyance tunnel is composed of assembled segments, which are mainly used to bear the external water and soil pressure. The stress and deformation of the segment joints are complex, and the connecting bolts and joint gaskets are the weak links of the whole shield assembling lining structure. According to the force analysis model established in Figure 2, the force analysis of the shield assembling lining is carried out alone, and the structure is affected by the uniformly distributed internal pressure P₂ transmitted by the concrete lining and the uniformly distributed external water and soil pressure P₃. The analysis model is shown in Figure 3.

FIGURE 3

FIGURE 3. Analysis model of shield assembling lining.

Under the action of external force, the circumferential direction of the shield assembling lining is in a tension or compression state. The connecting bolt, joint gasket, and shield tunnel segment can be regarded as the force spring, and the whole can form a spring ring, and then the stiffness of the spring ring can be calculated like a steel pipe.

According to the relationship between the elastic modulus of the material and the spring stiffness (Yang et al., 2018), the equivalent spring stiffness of each assembled segment can be obtained as follows:

$K_F=\frac{E_C\cdot A_C}{L_F};K_L=\frac{E_C\cdot A_C}{L_L};K_B=\frac{E_C\cdot A_C}{L_B}(1)$

Where: K_F, K_L, and K_B are the spring stiffness of cap block, connecting block, and standard block respectively. E_C is the elastic modulus of the segment. A_C is the sectional area of the segment. L_F, L_L, and L_B are neutral axis arc lengths of cap block, connecting block, and standard block respectively.

In previous studies, the segment joints were in tension, and only the bolts played a role in the joints (Yang et al., 2018). In practice, the shield lining structure is mostly in a state of partial tension and partial compression. When the external assembled segment joint is under tension, the connecting bolt works, but the joint gasket does not work. When the external assembled segment joint is under pressure, the joint gasket works, but the connecting bolt does not work. The equivalent spring stiffness of the joint under the corresponding two cases is:

$K_S=n_S\cdot \frac{E_S\cdot A_S}{L_S};K_{S1}=n_{S1}\cdot \frac{E_{S1}\cdot A_{S1}}{L_{S1}}(2)$

Where: K_S and K_S1 are the total stiffness of bolts at a tensile joint and gaskets at a compressive joint respectively. n_S is the number of bolts at a single tensile joint. n_S1 is the number of joint gaskets at a single compression joint. E_S and E_S1 are elastic moduli of the connecting bolt and joint gasket respectively. A_S and A_S1 are the cross-sectional areas of a single connecting bolt and joint gasket respectively. L_S and L_S1 are the effective lengths of connecting bolt and joint gasket respectively.

From the series equivalent formula of springs (Yang et al., 2018), we can get:

$\frac{1}{K}=\frac{n_J}{K_S}+\frac{n_{J1}}{K_{S1}}+\frac{n_F}{K_F}+\frac{n_L}{K_L}+\frac{n_B}{K_B}(3)$

Where: K is the total equivalent stiffness of shield assembling lining. n_J, n_J1, n_F, n_L, n_B are the number of tensile joints, compressive joints, cap blocks, connecting blocks, and standard blocks respectively.

Therefore, the equivalent elastic modulus of shield lining ring can be obtained from the relationship between elastic modulus of material and spring stiffness as follows:

$E=\frac{K\cdot L}{A_C}(4)$

Where: E is the equivalent elastic modulus of the shield assembling lining. L is the neutral axis length of the shield assembling lining.

2.3 Force Analysis of Lining

According to the theory of thick-walled cylinder in elasticity (Xu, 2002), the general solution formula of axisymmetric stress is as follows:

$\{\begin{array}{c}{\sigma }_{\rho }=\frac{A}{{\rho }^2}+B\left(1+2ln\rho \right)+2C\\ {\sigma }_{\phi }=-\frac{A}{{\rho }^2}+B\left(3+2ln\rho \right)+2C\end{array}(5)$

Where: σ_ρ is radial stress; σ_φ is circumferential stress; ρ is the polar diameter at the calculated position; A, B, and C are all undetermined constants.

The calculation formula of the corresponding displacement component in the axisymmetric stress state is as follows:

$\{\begin{array}{c}{u}_{\rho }=\frac{1}{E^{\prime }}\left[-\left(1+\mu \right)\frac{A}{\rho }+2\left(1-\mu \right)B\rho \left(ln\rho -1\right)+\left(1-3\mu \right)B\rho +2\left(1-\mu \right)C\rho \right]\\ +I\cos \phi +K\sin \phi \\ u_{\phi }=\frac{4B\rho \phi }{E^{\prime }}+H\rho -I\sin \phi +K\cos \phi \end{array}(6)$

Where: u_ρ is radial displacement; u_φ is circumferential displacement; φ is the angular coordinate at the calculated position; μ is Poisson’s ratio; E′ is the elastic modulus of the material; H, I, and K are all undetermined constants.

According to the force analysis model of the new composite lining established in Figure 2, the shield lining, concrete lining, and steel pipe lining are all under the action of uniformly distributed internal and external pressures, so the independent analysis model of each lining is shown in Figure 4.

FIGURE 4

FIGURE 4. Lining force analysis model.

In the ring, the points (ρ₁,φ₁) and (ρ₁,φ₁+2π) represent the same point, so the corresponding circumferential displacements are equal. There are:

$u_{{\phi }_1+2\pi }-u_{{\phi }_1}=\frac{8B{\rho }_1\pi }{E}=0(7)$

Where: ρ₁ and φ₁ are the polar diameter and angular coordinates of a point in the ring, respectively.

Therefore, according to the single-value condition of displacement, it must be B = 0.

As can be seen from Figure 4, the stress boundary conditions of the inner and outer surfaces are:

$\{\begin{array}{c}{\left({\sigma }_{\rho }\right)}_{\rho =r}=-P_4\\ {\left({\sigma }_{\rho }\right)}_{\rho =R}=-P_5\end{array}(8)$

Where: r and R are the inner radius and outer radius of the lining ring, respectively; P₄ and P₅ are the uniformly distributed pressures acting on the inner and outer surfaces of the lining, respectively.

Substituting Eq. 5 and B = 0 Into Eq. 8 can Give:

$\{\begin{array}{c}A=\frac{r^2{R}^2}{R^2-r^2}\left(P_5-P_4\right)\\ 2C=\frac{1}{R^2-r^2}\left(r^2{P}_4-R^2{P}_5\right)\end{array}(9)$

According to the force analysis model shown in Figure 4, the external force and the structure are symmetrical about any straight line passing through the centroid. Therefore, the radial displacement at any position with the same polar diameter is equal. Therefore, u_ρ is not a function about φ, so we can get:

$I\cos \phi +K\sin \phi =0(10)$

Substituting A, B, C, and Eq. 10 into the corresponding expressions, the calculation expressions of radial displacement u_ρ and circumferential stress σ_φ at any position of the lining can be obtained as follows:

$u_{\rho }=(\frac{1-\mu }{E^{\prime }}\frac{r^2\rho }{R^2-r^2}+\frac{1+\mu }{E^{\prime }\rho }\frac{r^2{R}^2}{R^2-r^2})P_4-(\frac{1-\mu }{E^{\prime }}\frac{R^2\rho }{R^2-r^2}+\frac{1+\mu }{E^{\prime }\rho }\frac{r^2{R}^2}{R^2-r^2})P_5(11)$

${\sigma }_{\phi }=\frac{r^2{P}_4-R^2{P}_5}{R^2-r^2}-\frac{r^2{R}^2}{R^2-r^2}\frac{P_5-P_4}{{\rho }^2}(12)$

2.4 Unknown Force Solution

Based on the new force analysis model of composite lining established as shown in Figure 2, the lining structures of each layer are analyzed independently. From this, the expressions of radial displacement and circumferential stress of lining structure under uniform internal and external pressure are obtained. Next, through the deformation coordination relation, the formula for calculating the increment of the lining radius of each layer will be established simultaneously, to find out the magnitude of unknown interaction forces P₁ and P₂.

From the calculation formula of the radial displacement u_ρ obtained in the previous section, the calculation expressions of the increase of the outer radius of the inner lining Δr₂, the increase of the inner radius of the shield lining Δr₅, and the increase of the inner and outer radii of the concrete lining Δr₃ and Δr₄ can be obtained respectively as follows:

$\mathrm{\Delta }{r}_2=(\frac{1-{\mu }_1}{E_1}\frac{r_1^2{r}_2}{r_2^2-r_1^2}+\frac{1+{\mu }_1}{E_1{r}_2}\frac{r_1^2{r}_2^2}{r_2^2-r_1^2})\cdot P-(\frac{1-{\mu }_1}{E_1}\frac{r_2^3}{r_2^2-r_1^2}+\frac{1+{\mu }_1}{E_1{r}_2}\frac{r_1^2{r}_2^2}{r_2^2-r_1^2})\cdot P_1=k_1\cdot P-k_2\cdot P_1(13)$

$\mathrm{\Delta }{r}_3=(\frac{1-{\mu }_2}{E_2}\frac{r_3^3}{r_4^2-r_3^2}+\frac{1+{\mu }_2}{E_2{r}_3}\frac{r_3^2{r}_4^2}{r_4^2-r_3^2})\cdot P_1-(\frac{1-{\mu }_2}{E_2}\frac{r_4^2{r}_3}{r_4^2-r_3^2}+\frac{1+{\mu }_2}{E_2{r}_3}\frac{r_3^2{r}_4^2}{r_4^2-r_3^2})\cdot P_2=k_3\cdot P_1-k_4\cdot P_2(14)$

$\mathrm{\Delta }{r}_4=(\frac{1-{\mu }_2}{E_2}\frac{r_3^2{r}_4}{r_4^2-r_3^2}+\frac{1+{\mu }_2}{E_2{r}_4}\frac{r_3^2{r}_4^2}{r_4^2-r_3^2})\cdot P_1-(\frac{1-{\mu }_2}{E_2}\frac{r_4^3}{r_4^2-r_3^2}+\frac{1+{\mu }_2}{E_2{r}_4}\frac{r_3^2{r}_4^2}{r_4^2-r_3^2})\cdot P_2=k_5\cdot P_1-k_6\cdot P_2(15)$

$\mathrm{\Delta }{r}_5=(\frac{1-{\mu }_3}{E_3}\frac{r_5^3}{r_6^2-r_5^2}+\frac{1+{\mu }_3}{E_3{r}_5}\frac{r_5^2{r}_6^2}{r_6^2-r_5^2})\cdot P_2-(\frac{1-{\mu }_3}{E_3}\frac{r_6^2{r}_5}{r_6^2-r_5^2}+\frac{1+{\mu }_3}{E_3{r}_5}\frac{r_5^2{r}_6^2}{r_6^2-r_5^2})\cdot P_3=k_7\cdot P_2-k_8\cdot P_3(16)$

Where: E₁, E₂, and E₃ are the elastic moduli of inner lining, concrete lining, and shield lining respectively. μ₁, μ₂, and μ₃ are Poisson’s ratios of inner lining, concrete lining, and shield lining respectively. r₁ and r₂ are the inner and outer radii of the inner lining respectively. r₃ and r₄ are the inner and outer radii of the concrete lining respectively. r₅ and r₆ are the inner and outer radii of the shield lining respectively. k₁, k₂, k₃, k₄, k₅, k₆, k₇, and k₈ are all coefficients.

The lining of each layer of the water conveyance tunnel structure is regarded as a tight connection, so the increase of radius at adjacent positions is equal. Therefore, the following deformation coordination relation can be obtained:

$\{\begin{array}{c}\mathrm{\Delta }{r}_2=\mathrm{\Delta }{r}_3\\ \mathrm{\Delta }{r}_4=\mathrm{\Delta }{r}_5\end{array}(17)$

Substituting Eqs. 13–15, and Eq. 16 into Eq. 17, we can get the computational expressions of unknown interaction forces P₁ and P₂ as follows:

$\{\begin{array}{c}{P}_1=\frac{k_1\left(k_6+k_7\right)P+k_4{k}_8{P}_3}{\left(k_2+k_3\right)\left(k_6+k_7\right)-k_4{k}_5}\\ P_2=\frac{k_1{k}_{5}P+k_8\left(k_2+k_3\right)P_3}{\left(k_2+k_3\right)\left(k_6+k_7\right)-k_4{k}_5}\end{array}(18)$

To sum up, the calculation formulas of unknown forces P₁ and P₂ have been obtained. And the corresponding parameter values can be obtained by substituting them into the computational expressions of radius increment Δr and circumferential stress σ_φ of lining structures in each layer.

3 Analytical Solution Verification

3.1 Equivalent Elastic Modulus Calculation

The designed internal water pressure of the Guangxi Xijiang River Diversion Project reaches 0.6 MPa. To ensure the effective operation of the water conveyance tunnel, a new composite lining structure of “steel lining—SCC—segment” is adopted in some pipe sections. A schematic diagram of shield lining structure size and segment segmentation is shown in Figure 5. Using the calculation method of equivalent elastic modulus introduced in Section 2.2, and relying on the engineering design data, the equivalent elastic modulus of the shield lining of the Xijiang Water Diversion Project is calculated.

FIGURE 5

FIGURE 5. Schematic diagram of shield lining structure.

The shield lining of this project is divided into six segments per ring, 3 standard blocks (central angle 67.5°), two connecting blocks (central angle 68.75°), and one cap block (central angle 20°). Two adjacent segments are connected by bent bolts, with 12 bolts in each ring. The segment is made of C50 concrete, with an inner diameter of 5.4 m, an outer diameter of 6 m, a thickness of 30 cm, and a width of 1.5 m per ring. The elastic modulus E_C of the segment is 34.5 GPa, and the cross-sectional area A_C is 0.45 m². The elastic modulus E_S of the bolt is 200 GPa, the cross-sectional area A_S is 573 mm², and the effective length L_S is 0.43 m (Cao, 2020). Because the inner water pressure borne by the water conveyance tunnel structure is relatively high, so the shield lining is in tension in the circumferential direction, only the role of bolts is considered at the joint.

From this, the total equivalent stiffness and equivalent elastic modulus of shield assembled lining can be obtained:

$K=1/\left(\frac{n_J}{K_S}+\frac{n_F}{K_F}+\frac{n_L}{K_L}+\frac{n_B}{K_B}\right)=1/\left(\frac{6}{5.33\times {10}^8}+\frac{1}{1.57\times {10}^{10}}+\frac{2}{4.54\times {10}^9}+\frac{3}{4.62\times {10}^9}\right)=8.06\times {10}^{7}N/m(19)$

$E=\frac{K\cdot L}{A_C}=\frac{17.91\times 8.06\times {10}^7}{0.45}=3.21\times {10}^{9}Pa(20)$

3.2 Computational Model Verification

To verify the correctness of the calculation model and method in this paper, numerical analysis, and analytical solution are used to calculate the deformation and stress values of lining structure, and a comparative analysis is made.

The water conveyance tunnel of the Xiaotang interchange section of the Guangzhou Xijiang Water Diversion Project is about 2.4 km long, and the designed internal water pressure is 0.6 MPa. The external lining is a precast reinforced concrete segment poured with C50 concrete, with an outer diameter of 6 m and an inner diameter of 5.4 m. The thickness of the steel pipe lining is 20 mm C20 self-compacting concrete with a thickness of 30 cm is filled between the shield lining and the steel pipe (Cao, 2020).

According to the design data of the water conveyance tunnel of the Xiaotang interchange section of the Guangzhou Xijiang Water Diversion Project (Cao, 2020), the finite element analysis software, ABAQUS is used to establish a new composite lining water conveyance tunnel model. The tunnel parameters required for simulation are the same as the analytical calculation, as shown in Table 1. Some parameters are commonly used values, and the shield lining considers the influence of the joint, and the corresponding equivalent elastic modulus is calculated according to the calculation results in Section 3.1.

TABLE 1

TABLE 1. Model calculation material parameter table.

The finite element calculation model bears the uniformly distributed internal water pressure of 0.6 MPa and the uniformly distributed external water and soil pressure of 0.3 MPa, and the components are connected by Tie. The horizontal displacement of the top and bottom cross-sections of the structure and the vertical displacement of the leftmost and rightmost cross-sections of the structure are constrained. All structural components adopt the CPE4I plane strain four-node nonconforming element. External shield lining has an outer radius of 3 m and an inner radius of 2.7 m. The outer radius of the intermediate concrete lining is 2.7 m and the inner radius is 2.4 m. The internal steel pipe lining has an outer radius of 2.4 m and an inner radius of 2.38 m. The finite element model is shown in Figure 6, and some calculation results are shown in Figure 7, Figure 8, Figure 9.

FIGURE 6

FIGURE 6. Finite element calculation model.

FIGURE 7

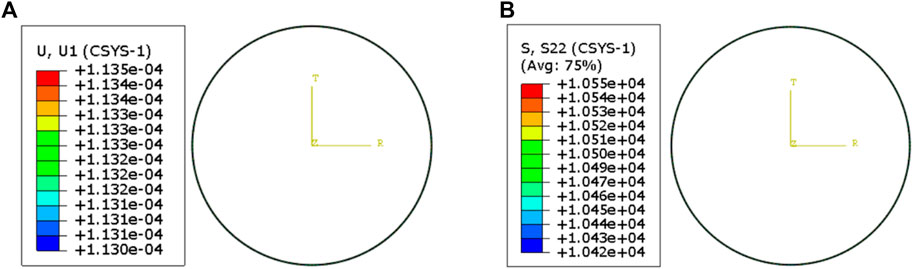
FIGURE 7. Radial deformation and circumferential stress of steel pipe lining. (A) Radial deformation of steel pipe lining. (B) Circumferential stress of steel pipe lining.

FIGURE 8

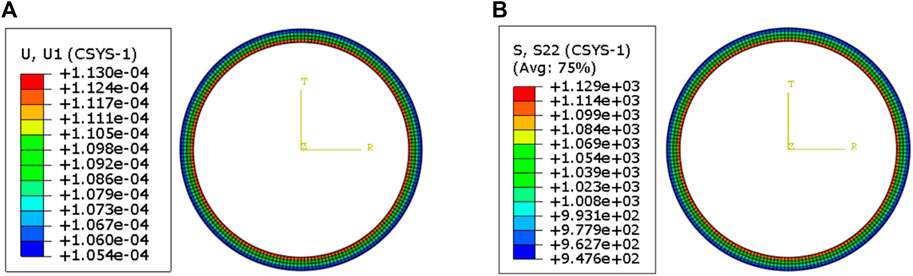
FIGURE 8. Radial deformation and circumferential stress of concrete lining. (A) Radial deformation of concrete lining. (B) Circumferential stress of concrete lining.

FIGURE 9

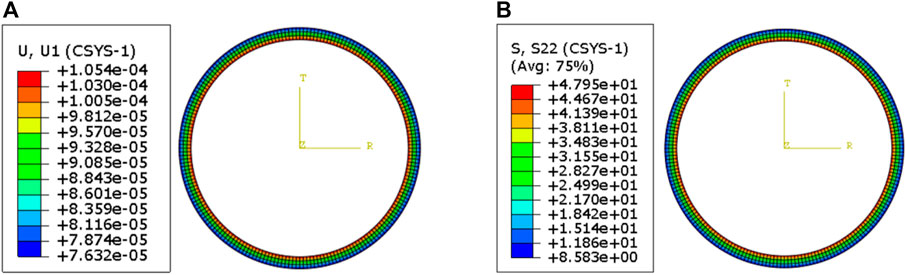
FIGURE 9. Radial deformation and circumferential stress of shield lining. (A) Radial deformation of shield lining. (B) Circumferential stress of shield lining.

As shown in Figure 7, due to the thin thickness of the internal steel pipe lining, the radial deformation and stress variation of the lining are very small. In addition, the circumferential stress value of the internal steel pipe lining is relatively large, about 10 MPa. As shown in Figure 8, the radial deformation and circumferential stress of the middle concrete lining gradually decrease from inside to outside under the reaction of the steel pipe lining and the shield lining. The circumferential stress value of concrete lining is much smaller than that of steel pipe lining. As shown in Figure 9, under the action of external water and soil load and the reaction force of concrete lining, the radial deformation of the shield lining gradually decreases from inside to outside, and the circumferential stress value of the shield lining at the steel pipe radius is significantly smaller than that at the outer radius.

Summarize the results of numerical analysis and analytical calculation as shown in Table 2.

TABLE 2

TABLE 2. Model calculation results.

From the data in Table 2, it can be seen that the numerical simulation results are consistent with the calculation results. Except for the error of the circumferential stress at the inner radius of the shield lining is 23.9%, the errors of other results are all within 6%, so the rationality of the calculation model and method in this paper can be verified. In the analytical solution, it is considered that only radial pressure is transmitted between the linings, which leads to some errors in the results of deformation and stress calculated by the two methods (Chen et al., 2020). It needs to be further improved.

4 Influence Analysis of Lining Structure Parameters

Compared with the concrete lining and internal steel pipe lining, the setting of the shield assembling lining structure type of the “segment—SCC—steel lining” new composite lining water conveyance tunnel is relatively fixed, so it is not taken as the analysis object. The following is based on the water conveyance tunnel of the Xiaotang interchange section of the Guangzhou Xijiang Water Diversion Project (Cao, 2020). Through the analytical method given in this paper, the influence of concrete lining thickness and inner lining material parameters on the stress and deformation of lining structure is analyzed.

4.1 Influence Analysis of Concrete Lining Thickness

The setting of the middle self-compacting concrete lining is flexible, and different thicknesses of concrete lining will affect the deformation and stress of the overall structure. To make the stress distribution and deformation control among the structures more reasonable, the influence law of concrete lining thickness on the stress and deformation of the lining structure will be explored according to the model parameters in Table 3. Some parameters are commonly used values, and the shield lining considers the influence of the joint, and the corresponding equivalent elastic modulus is calculated according to the calculation results in Section 3.1.

TABLE 3

TABLE 3. Calculation parameter table.

The inner radius of the concrete lining is 2.3, 2.35, 2.4, 2.45, 2.5, and 2.55 m respectively. The lining structure bears the uniformly distributed internal water pressure of 0.6 MPa and the external uniformly distributed water and soil pressure of 0.3 MPa. Analytical calculation and numerical analysis are used to calculate the inner radius increment and circumferential stress value of lining in each layer respectively, as shown in Figure 10.

FIGURE 10

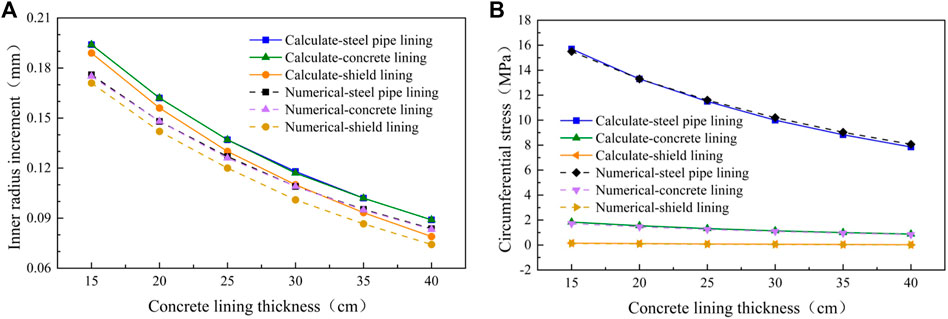
FIGURE 10. Influence of concrete lining thickness on structural stress and deformation. (A) Inner radius increment. (B) Circumferential stress at the inner radius.

Figure 10A shows that with the increase of the thickness of the concrete lining, the deformation amount of the inner radius of each layer of lining decreases, and the reduction range is very large. Figure 10B shows that with the increase of the thickness of the concrete lining, the circumferential stress at the inner radius of each layer of lining decreases continuously. Among them, the circumferential stress at the inner radius of the steel pipe lining decreases greatly, while the circumferential stress at the inner radius of the shield lining is almost negligible compared with the other two linings. It shows that increasing the thickness of the middle self-compacting concrete lining can reduce the radial displacement and circumferential stress of the lining structure and improve the bearing capacity of the structure. However, the thickness should not be too large. According to relevant codes, the thickness of non-structural secondary lining should generally not exceed 30 cm (Takano, 2000).

4.2 Influence Analysis of Inner Lining Materials

The use of different materials for the inner lining will affect the deformation and stress of the overall structure. To make the stress distribution and deformation control among the structures more reasonable, the influence law of elastic modulus of inner lining materials on the stress and deformation of composite lining structures will be explored according to the design data of the Xijiang water diversion project. Some parameters are commonly used values, and the shield lining considers the influence of the joint, and the corresponding equivalent elastic modulus is calculated according to the calculation results in Section 3.1.

Using the data in Table 3, the inner radius of the concrete lining is 2.4 m, and other parameters only change the elastic modulus of the inner lining. The elastic modulus of inner lining materials is 5e7, 8e7, 1.1e8, 1.4e8, 1.7e8, and 2e8 kPa, respectively. The lining structure bears the uniformly distributed internal water pressure of 0.6 MPa and the external uniformly distributed water and soil pressure of 0.3 MPa. Analytical calculation and numerical analysis are used to calculate the inner radius increment and circumferential stress value of lining in each layer respectively, as shown in Figure 11.

FIGURE 11

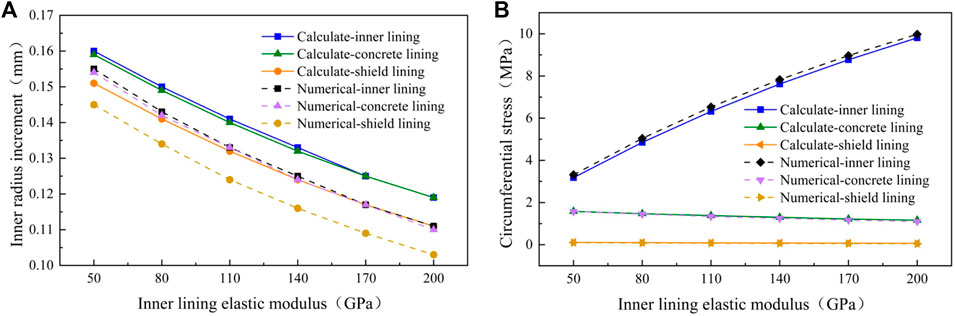
FIGURE 11. Influence of inner lining elastic modulus on structural stress and deformation. (A) Inner radius increment. (B) Circumferential stress at the inner radius.

Figure 11A shows that with the increase of elastic modulus of the inner lining, the deformation of the inner radius of the lining structure in each layer decreases. It shows that the inner lining is made of materials with large elastic modulus, which is beneficial to reduce the overall deformation of the composite lining structure. Figure 11B shows that with the increase of the elastic modulus of the inner lining, the circumferential stress at the inner radius of the inner lining increases significantly, while the circumferential stress of the concrete lining and the shield lining decreases to some extent. The potential mechanism of this phenomenon is that under the same internal water pressure, the deformation of the inner lining decreases with the increase of the elastic modulus of the inner lining. At this time, the internal water pressure shared by the coordinated deformation to other lining structures decreases, and the internal water pressure borne by the inner lining increases. Which makes the circumferential stress of the inner lining increase while that of the other lining decreases.

To sum up, increasing the thickness of intermediate concrete lining can effectively reduce the radius increment and circumferential stress value of lining structure in each layer, but increasing the thickness of concrete lining will also significantly increase the project cost. Increasing the elastic modulus of the inner lining can effectively reduce the increase of the overall structure radius, but the circumferential stress of the inner lining will increase significantly. Compared with concrete lining and outer lining, the circumferential stress of the inner lining is much larger. Therefore, the lining should be made of materials with high tensile strength, and it is not advisable to use the assembled structure similar to the outer lining. In addition, it can be seen from the figure that the results calculated by analytical calculation and numerical analysis are very close, which further verifies the correctness of the calculation model and method in this paper.

4.3 Influence Analysis of Steel Pipe Lining Thickness

Different thicknesses of steel pipe lining will affect the deformation and stress of the overall structure. To make the stress distribution and deformation control among structures more reasonable, the following will explore the influence law of inner lining steel pipes with different thicknesses on inner lining stress and deformation under different internal water pressures according to the design data of the Xijiang water diversion project. Some parameters are commonly used values, and the shield lining considers the influence of the joint, and the corresponding equivalent elastic modulus is calculated according to the calculation results in Section 3.1.

Using the data in Table 3, the inner radius of the concrete lining is 2.4 m, and other parameters only change the inner radius of the inner lining. The thickness of steel pipe lining is 15, 20, 25, 30, and 35 mm respectively. The internal water pressure in the lining structure is 0.4, 0.6, 0.8, 1.0, 1.2, and 1.4 MPa, respectively, and the external uniform water and soil pressure is 0.3 MPa. Using the calculation method provided in this paper, the inner radius increase and circumferential stress of the steel pipe lining are calculated respectively, as shown in Figure 12.

FIGURE 12

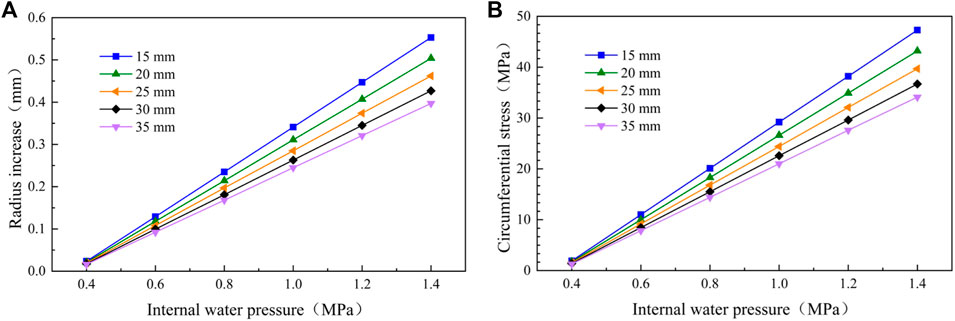
FIGURE 12. Influence of thickness of steel pipe lining on structure under different internal water pressure. (A) Inner radius increment. (B) Circumferential stress at the inner radius.

Figure 12A shows that the radial deformation at the inner radius of the inner lining decreases with the increase of the thickness of the steel pipe lining. The greater the internal water pressure, the greater the radial displacement of the inner lining. Figure 12B shows that the circumferential stress at the inner radius of the inner lining decreases with the increase of the thickness of the steel pipe lining. The greater the internal water pressure, the greater the circumferential stress of the inner lining. It shows that increasing the thickness of steel pipe lining properly can improve the bearing capacity of the lining structure. Especially under the action of high internal water pressure, increasing the thickness of steel pipe lining is an effective measure to reduce the stress and deformation of the lining structure.

5 Conclusion

The stress and deformation of the new composite lining structure of “steel lining—SCC—segment” are affected by many factors, among which the size and material parameters of the lining structure are the common control factors. A theoretical method for calculating the stress and deformation of the new composite lining structure is given by establishing the stress analysis model of the new composite lining structure of the water conveyance tunnel. Based on verifying the correctness of the calculation method by finite element numerical simulation, the influence law of the thickness of the intermediate concrete lining and the parameters of the inner lining is deeply analyzed. Through the above analysis, the main conclusions are as follows:

1) With the increase of the thickness of the intermediate concrete lining, the radial displacement and circumferential stress of each layer lining structure decrease continuously, and the bearing capacity of the structure increase significantly. However, according to relevant specifications, the thickness of the lining should generally not exceed 30 cm. In addition, the circumferential stress value of the inner lining is large, so the inner lining should be made of materials with high tensile strength.

2) The deformation of the inner lining will decrease with the increase of the elastic modulus of the inner lining. At this time, the internal water pressure shared by the coordinated deformation to other lining structures decreases, resulting in the internal water pressure borne by the inner lining increasing. It increases the circumferential stress of the inner lining and decreases the circumferential stress of other linings. Therefore, the elastic modulus of the inner lining should not be too large in the design of the lining structure.

3) With the increase in internal water pressure, the stress and deformation of steel pipe lining will increase linearly. However, increasing the thickness of steel pipe lining can reduce the stress and deformation of steel pipe lining. Therefore, increasing the thickness of steel pipe lining is an effective measure to reduce the stress and deformation of the lining structure in a high-pressure water conveyance tunnel.

With the increasing internal water pressure and cross-section size of the water conveyance tunnel, there will be more and more application scenarios of “steel lining—SCC—segment” as a new lining structure. Based on the above-mentioned load structure method and elastic theory, considering the deformation coordination relationship, the analysis model and calculation method gave provided a theoretical basis for the mechanical analysis and structural parameter design of the new composite lining of the water conveyance tunnel.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YZ: Theoretical analysis, numerical verification, and wrote this paper. CL: Provide guidance and revision for research ideas and thesis writing.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 51508278).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andjelkovic, V., Lazarevic, Z., Nedovic, V., and Stojanovic, Z. (2013). Application of the Pressure Grouting in the Hydraulic Tunnels. Tunn. Undergr. Space Technol. 37, 165–179. doi:10.1016/j.tust.2012.08.012

CrossRef Full Text | Google Scholar

Cao, W. Q. (2020). Finite Element Analysis of Stress and Deformation of Composite Structure of Water Shield Tunnel. Dissertation: Zhejiang University. (in Chinese).

Google Scholar

Chen, Q. J., Wang, J. C., Huang, W. M., Yang, Z. X., and Xu, R. Q. (2020). Analytical Solution for a Jointed Shield Tunnel Lining Reinforced by Secondary Linings. Int. J. Mech. Sci. 185, 105813. doi:10.1016/j.ijmecsci.2020.105813

CrossRef Full Text | Google Scholar

Chen, Y., Wang, Y., and Zhang, Q. Y. (2014). Coupled Seepage-Elastoplastic-Damage Analysis of Saturated Porous Media and its Application to Water Conveyance Tunnel. Tunn. Undergr. Space Technol. 44, 80–87. doi:10.1016/j.tust.2014.07.007

CrossRef Full Text | Google Scholar

Ding, H., Tong, L. H., Xu, C., and Hu, W. (2020). Aseismic Performance Analysis of Composite Lining Embedded in Saturated Poroelastic Half Space. Int. J. Geomech. 20 (9), 04020156. doi:10.1061/(asce)gm.1943-5622.0001787

CrossRef Full Text | Google Scholar

Dong, Z., Kuo, C., Yin, J., Wen, S., Liu, G., and Gou, Y. (2021). Examination of Longitudinal Seismic Vulnerability of Shield Tunnels Utilizing Incremental Dynamic Analysis. Front. Earth Sci. 9, 779879. doi:10.3389/feart.2021.779879

CrossRef Full Text | Google Scholar

Gavriilidis, I., and Karamanos, S. A. (2019). Bending and Buckling of Internally-Pressurized Steel Lined Pipes. Ocean. Eng. 171, 540–553. doi:10.1016/j.oceaneng.2018.11.052

CrossRef Full Text | Google Scholar

Gong, C., Ding, W., Mosalam, K. M., Günay, S., and Soga, K. (2017). Comparison of the Structural Behavior of Reinforced Concrete and Steel Fiber Reinforced Concrete Tunnel Segmental Joints. Tunn. Undergr. Space Technol. 68, 38–57. doi:10.1016/j.tust.2017.05.010

CrossRef Full Text | Google Scholar

Guan, Z., Deng, T., Wang, G., and Jiang, Y. (2015). Studies on the Key Parameters in Segmental Lining Design. J. Rock Mech. Geotechnical Eng. 7 (6), 674–683. doi:10.1016/j.jrmge.2015.08.008

CrossRef Full Text | Google Scholar

Huang, X., Li, L., Zhang, C., Liu, B., Li, K., Shi, H., et al. (2021). Multi-step Combined Control Technology for Karst and Fissure Water Inrush Disaster during Shield Tunneling in Spring Areas. Front. Earth Sci. 9, 795457. doi:10.3389/feart.2021.795457

CrossRef Full Text | Google Scholar

Li, B., Zhang, Z., Wang, X., and Liu, X. (2019). Investigation on Cohesive Zone Model of Bolted Joint for Water Conveyance Tunnel Lining. Ec 36 (5), 1449–1468. doi:10.1108/EC-07-2018-0310

CrossRef Full Text | Google Scholar

Li, F., Chang, N., Wang, J., Feng, T., and Li, C. (2021). Research on the Algorithm for Composite Lining of Deep Buried Water Conveyance Tunnel. Adv. Civ. Eng. 2021 (12), 1–14. doi:10.1155/2021/6686360

CrossRef Full Text | Google Scholar

Liu, X., Sun, Q., Yuan, Y., and Taerwe, L. (2020). Comparison of the Structural Behavior of Reinforced Concrete Tunnel Segments with Steel Fiber and Synthetic Fiber Addition. Tunn. Undergr. Space Technol. 103, 103506. doi:10.1016/j.tust.2020.103506

CrossRef Full Text | Google Scholar

Mezger, F., Ramoni, M., Anagnostou, G., Dimitrakopoulos, A., and Meystre, N. (2017). Evaluation of Higher Capacity Segmental Lining Systems when Tunnelling in Squeezing Rock. Tunn. Undergr. Space Technol. 65, 200–214. doi:10.1016/j.tust.2017.02.012

CrossRef Full Text | Google Scholar

Nabipour, M., Rezapour, S., and Mohajeri, S. H. (2020). A Parametric Study on Friction-Loss in Water Conveyance Tunnels Considering Misalignment of Precast Concrete Segments. Tunn. Undergr. Space Technol. 96, 103221. doi:10.1016/j.tust.2019.103221

CrossRef Full Text | Google Scholar

Nehdi, M. L., Abbas, S., and Soliman, A. M. (2015). Exploratory Study of Ultra-high Performance Fiber Reinforced Concrete Tunnel Lining Segments with Varying Steel Fiber Lengths and Dosages. Eng. Struct. 101, 733–742. doi:10.1016/j.engstruct.2015.07.012

CrossRef Full Text | Google Scholar

Salemi, N., Abtahi, S. M., Rowshanzamir, M., and Hejazi, S. M. (2018). Geosynthetic Clay Liners: Effect of Structural Properties and Additives on Hydraulic Performance and Durability. Environ. Earth Sci. 77 (5), 1–13. doi:10.1007/s12665-018-7364-z

CrossRef Full Text | Google Scholar

Takano, Y. H. (2000). Guidelines for the Design of Shield Tunnel Lining. Tunn. Undergr. Space Technol. 15 (3), 303–331. doi:10.1016/S0886-7798(00)00058-4

CrossRef Full Text | Google Scholar

Vogel, F., Sovják, R., and Pešková, Š. (2017). Static Response of Double Shell Concrete Lining with a Spray-Applied Waterproofing Membrane. Tunn. Undergr. Space Technol. 68, 106–112. doi:10.1016/j.tust.2017.05.022

CrossRef Full Text | Google Scholar

Wang, S., Jian, Y., Lu, X., Ruan, L., Dong, W., and Feng, K. (2019). Study on Load Distribution Characteristics of Secondary Lining of Shield under Different Construction Time. Tunn. Undergr. Space Technol. 89, 25–37. doi:10.1016/j.tust.2019.03.010

CrossRef Full Text | Google Scholar

Wang, Y., Cao, R., Pi, J., Jiang, L., and Zhao, Y. (2020). Mechanical Properties and Analytic Solutions of Prestressed Linings with Un-bonded Annular Anchors under Internal Water Loading. Tunn. Undergr. Space Technol. 97, 103244. doi:10.1016/j.tust.2019.103244

CrossRef Full Text | Google Scholar

Xu, Z. L. (2002). Elastic Mechanics Concise Tutorial. Beijing: Higher Education Press. (in Chinese).

Google Scholar

Yan, Q., Li, B., Geng, P., Chen, C., He, C., and Yang, W. (2016). Dynamic Response of a Double-Lined Shield Tunnel to Train Impact Loads. Tunn. Undergr. Space Technol. 53, 33–45. doi:10.1016/j.tust.2015.12.004

CrossRef Full Text | Google Scholar

Yang, F., Cao, S. R., and Qin, G. (2018b). Mechanical Behavior of Two Kinds of Prestressed Composite Linings: A Case Study of the Yellow River Crossing Tunnel in China. Tunn. Undergr. Space Technol. 79, 96–109. doi:10.1016/j.tust.2018.04.036

CrossRef Full Text | Google Scholar

Yang, F., Cao, S., and Qin, G. (2018a). Performance of the Prestressed Composite Lining of a Tunnel: Case Study of the Yellow River Crossing Tunnel. Int. J. Civ. Eng. 16 (2), 229–241. doi:10.1007/s40999-016-0124-0

CrossRef Full Text | Google Scholar

Yang, F., Zhou, H., Zhang, C., Lu, J., Lu, X., and Geng, Y. (2020). An Analysis Method for Evaluating the Safety of Pressure Water Conveyance Tunnel in Argillaceous Sandstone under Water-Weakening Conditions. Tunn. Undergr. Space Technol. 97, 103264. doi:10.1016/j.tust.2019.103264

CrossRef Full Text | Google Scholar

Yang, G. H., Li, Z. Y., Xu, C. B., Jia, K., and Jiang, Y. (2018). Load-structure Interaction Model of Shield Tunnel Composite Lining. J. Hydroelectr. Eng. 37 (10), 20–30. (in Chinese). doi:10.11660/slfdxb.20181003

CrossRef Full Text | Google Scholar

Yuan, L., and Kyriakides, S. (2021). Hydraulic Expansion of Lined Pipe for Offshore Pipeline Applications. Appl. Ocean Res. 108, 102523. doi:10.1016/j.apor.2020.102523

CrossRef Full Text | Google Scholar

Yuan, Q., Wang, Y., You, W., and Xu, G. (2017). Structure Analysis of a Large Water Conveyance Tunnel with Consideration of Grouting Circle Failure. MMC_B 86 (1), 155–168. doi:10.18280/mmc_b.860112

CrossRef Full Text | Google Scholar

Zhang, N., Zhang, Y., Gao, Y., Dai, D., and Huang, C. (2021). Effect of Imperfect Interfaces on Dynamic Response of a Composite Lining Tunnel with an Isolation Layer under Plane P and SV Waves. Soil Dyn. Earthq. Eng. 142, 106586. doi:10.1016/j.soildyn.2021.106586

CrossRef Full Text | Google Scholar

Zhou, J., Yang, X.-A., Ma, M.-J., and Li, L.-H. (2021). The Support Load Analysis of Deep-Buried Composite Lining Tunnel in Rheological Rock Mass. Comput. Geotechnics 130, 103934. doi:10.1016/j.compgeo.2020.103934

CrossRef Full Text | Google Scholar

Zhu, Y. Y., Liu, C. C., Yin, X. T., and Zhang, J. Y. (2022). Analysis of the Internal Force and Deformation Characteristics of Double-Layer Lining Structure of Water Conveyance Tunnel. Geofluids 2022, 1–12. doi:10.1155/2022/9159632

CrossRef Full Text | Google Scholar