- 1Southwest Institute of Geological Survey, Non-Ferrous Metal Minerals Geological Survey, Kunming University of Science and Technology, Kunming, China
- 2Chengdu University of Technology, Chengdu, China
Considering the needs of current deep mineral exploration and development, the tunnel gravity exploration method is advantageous, as it is unaffected by electromagnetic interference, is hardly affected by terrain, has a high detection accuracy, and overcomes the multi-solution problem of geophysical anomalies. Herein, to systematically explain the distribution law and principle of the tunnel gravity method in spatial position prediction, a systematic study was performed on upright orebodies, and 18 types of positive and negative combination rules of spatial distribution anomalies are proposed. The method is used for the detection of concealed ore in the deep part of the Huangshaping skarn-type deposit in southern Hunan, China, and accurate results are obtained. The results indicate that tunnel gravity exploration solves the problem of orebodies located in the deep parts of a high-density vertical orebody when a single tunnel or multiple tunnels are detected. This study not only extends the theory and method of tunnel gravity exploration but also provides an important basis for the layout of deep exploration projects.
Introduction
In China’s 14th Five-Year Plan for the geological prospecting industry, deepening prospecting prediction and resource exploitation are key directions of future development (Huang et al., 2021). In both theory and practice, the exploration and discovery of large and super-large polymetallic deposits in the second deep space in the crust is the only route for future exploration and development. Today, one-third of the metal mines in China have been explored at a depth of 1,000 m and approximately 2,000–3,000 m underground (Cai et al., 2019). Geophysical exploration work for such deposits is typically conducted in the half-space domain using geophysical exploration methods, such as electrical prospecting and magnetic prospecting, from the surface to depths below the surface. However, these methods experience strong electromagnetic interference in the detection of deep concealed orebodies during the implementation process, thereby resulting in a series of abnormal multi-solution issues, which often lead to poor detection results and exploration difficulty (Wang, 2021). Thus, traditional geological prospecting technology is unable to satisfy the current requirements, and new geophysical prospecting methods must be developed (Lv et al., 2019). Developing new methods for detecting deep concealed orebodies through spatial positioning is fundamental to prospecting prediction.
Studies on tunnel gravity detection methods have been conducted in China and globally. Smith and Hammer investigated underground gravity measurement methods (Hammer, 1950; Smith, 1950). Among Chinese scholars, Gongda and Guofan examined gravity measurement in wells (Xu and Zhou, 1989). Compared with the traditional method, the tunnel gravity detection method innovatively uses the four parameters Vz, Vxz, Vyz, and Vzz from the entire space domain to detect deep concealed orebodies. Herein, Vz represents the gravity anomaly, Vxz represents the second derivative of gravity with respect to x, Vyz represents the second derivative of gravity with respect to y, and Vzz represents the second derivative of gravity with respect to z. These four parameters are used because the detection depth is closer to the orebody. The tunnel gravity detection method has substantially enriched and extended new geophysical methods (Han et al., 2014; Li and Han, 2014). In particular, Han et al. (2014) reported the successful application of deep ore prospecting in Maoping and Huize lead–zinc mines, thereby elucidating the spatial positioning of high-density inclined concealed orebodies (Han et al., 2014; Zhang, 2017; Han et al., 2020a; Han et al., 2021).However, the scales and trends of deep orebodies vary widely, and there has been no qualitative or quantitative research on vertical concealed orebodies. Considering the principles of full-space positioning and tunnel gravity detection methods, this study proposed the principles of spatial positioning of vertical high-density concealed orebodies. These principles were applied to deep prospecting in the Huangshaping skarn-type copper-tin polymetallic deposit in southern Hunan (Wang, 2019), and satisfactory results were obtained. This study enriches and extends the tunnel gravity exploration theory and provides an important basis for the layout of deep exploration projects.
Principles of spatial positioning for high-density vertical orebodies
In the three-dimensional (3D) coordinate system, the positive and negative conditions of abnormal parameter values (Vz, Vxz, Vyz, and Vzz) produced by different parts of high-density vertical orebodies differ. Therefore, in this study, by establishing a 3D coordinate system in space, a forward modeling simulation of the upright cuboid at the center of the orebodies was conducted to locate them in space.
Gravity anomaly formula for vertical cuboids
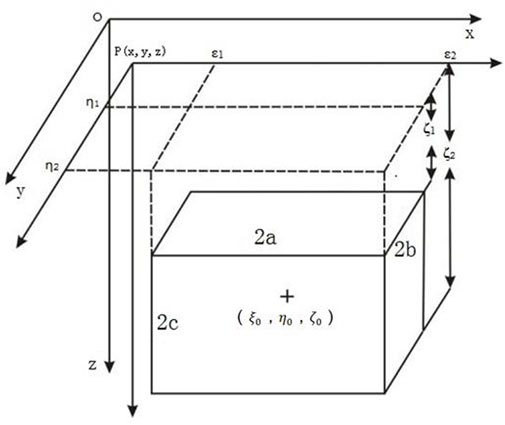
Assuming that an orebody is a homogeneous cuboid with residual density σ, half-length a, half-width b, and half-height c and that the length, width, and height of the orebody are parallel to the x-, y-, and z-axes, respectively, the coordinates of the center point of the orebody are
According to Newton’s law of universal gravitation, the gravity anomaly formula for the geological body modeled as a cuboid with uniform residual density σ is (Zeng, 2008)
where the partial derivatives of Vz (the gravity anomaly) along the x-, y-, and z-axes are Vxz, Vyz, and Vzz, respectively, as follows:
where G is the Newtonian gravitational constant and x, y, and z are the coordinates of the observation point.
The distance from the center of the cuboid to the measurement point can be expressed as follows:
Equation 1 is a general formula for calculating the gravity anomaly for the cuboids.
After taking the integral, eq. 1 can be transformed into the following formula for vertical mean cuboids:
where
Equations 1–5 are the gravity anomaly formulas for vertical cuboids.
Distribution pattern of anomaly sections of vertical high-density orebodies
The gravity anomalies of vertical high-density orebodies can be calculated using Eqs 2–5. Through further calculation, the vertical high-density cuboid orebody xoz section is found to have a gravity anomaly. Figure 2 shows the four-parameter section anomaly pattern. The following observations are drawn from the figure.
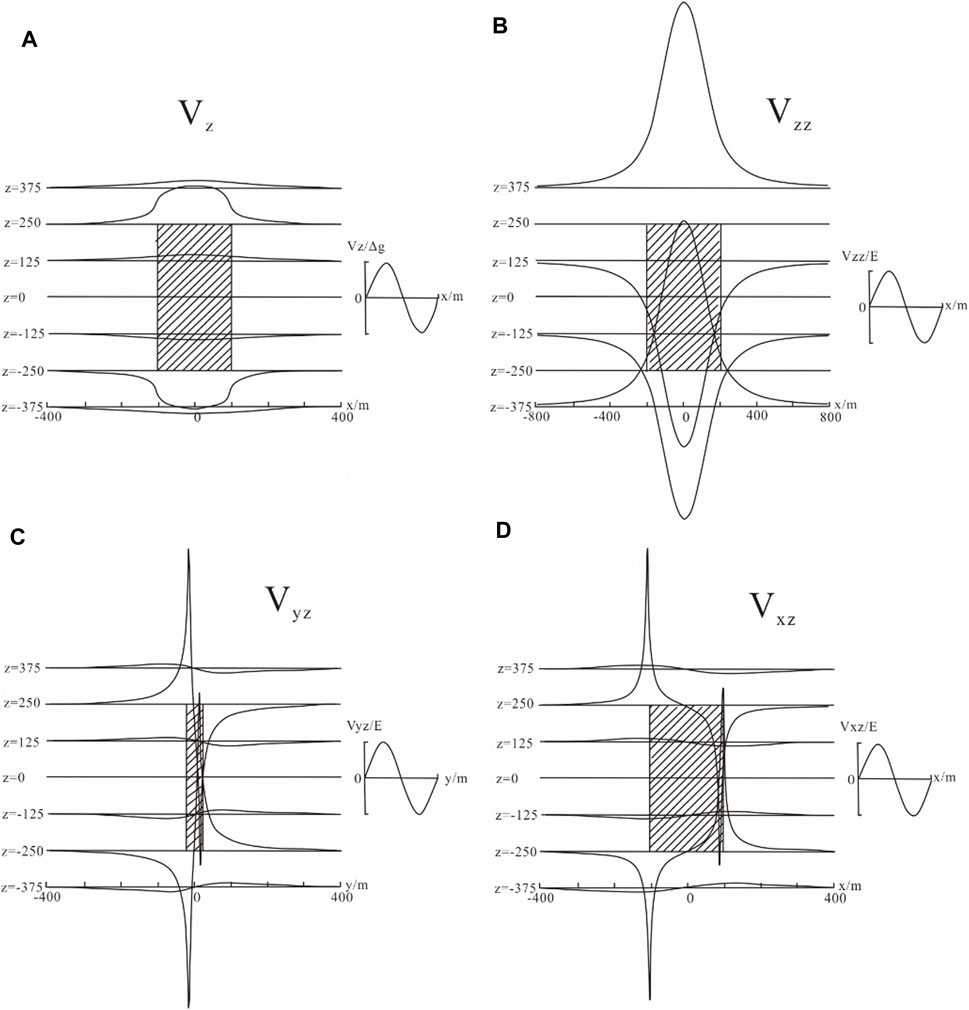
FIGURE 2. Model parameters: length 200 m, width 40 m, height 500 m, density difference 1.0 × 103 kg/m3(A) xoz section (B) xoz section (C) xoz section (D) yoz section.
Model parameters: length = 200 m, width = 40 m, and height = 500 m with a density difference of 1.0 × 103 kg/m3.
a: cross section xoz; b: cross section xoy; c: cross section xoz; d: cross section yoz.
(1) The value of Vz is symmetric about the axes x = 0 and z = 0 and has a maximum (minimum) at x = 0. Subsequently, it decreases (increases) along the x-axis in both directions; that is, x approaches ±∞, and the gravity anomaly approaches 0.
(2) The value of Vzz is symmetric about the axis x = 0, where it has a maximum (minimum) value. It decreases (increases) along the x-axis in both directions; that is, as x approaches ±∞, the anomaly approaches 0.
When the section line is in the upper (lower) part of the orebody (z = −375 and z = 375), there is a positive maximum at x = 0, and the values decrease symmetrically on both sides.
When the section line is at the top (bottom) of the orebody (z = −250 and z = 250), Vzz = 0.
When the section line is in the upper middle (lower middle) part of the orebody (z = −125 and z = 125), the small negative value at x = 0 increases symmetrically on both sides; furthermore, Vzz = 0 at the section line is in the middle of the orebody.
(3) The value of Vyz is symmetric about the z = 0 axis and centrally symmetric about the y = 0 axis. Thus, y = 0 and Vyz = 0, whereas when y approaches ±∞, Vyz infinitely approaches 0 g.u.
When the section line is at the top of the orebody, Vyz follows an increasing → decreasing → increasing trend, with maximum and minimum values at y = −b and y = b, respectively.
When the section line is at the top of and in the upper middle part of the orebody, Vyz follows an increasing → decreasing → increasing trend.
When the section line is at the bottom of the orebody, Vyz follows a decreasing → increasing → decreasing trend, with maximum and minimum values at y = b and y = −b, respectively.
When the section line is in the lower or lower middle part of the orebody, Vyz follows an increasing → decreasing → increasing trend.
When the section line is in the middle of the orebody, Vyz = 0.
(4) The value of Vxz is symmetric about the z = 0 axis and centrally symmetric about the x = 0 axis. Thus, x = 0 and Vxz = 0, whereas when x approaches ±∞, Vxz infinitely approaches 0.
When the section line is above the middle of the orebody, Vyz follows an increasing → decreasing → increasing trend, with maximum and minimum values at x = –a and x = a, respectively.
When the section line is below the middle of the orebody, Vyz follows a decreasing → increasing → decreasing trend, with maximum and minimum values at x = a and x = −a, respectively. When the section line is in the middle of the orebody, Vyz = 0.
Spatial distribution pattern of gravity anomalies in vertical high-density orebodies
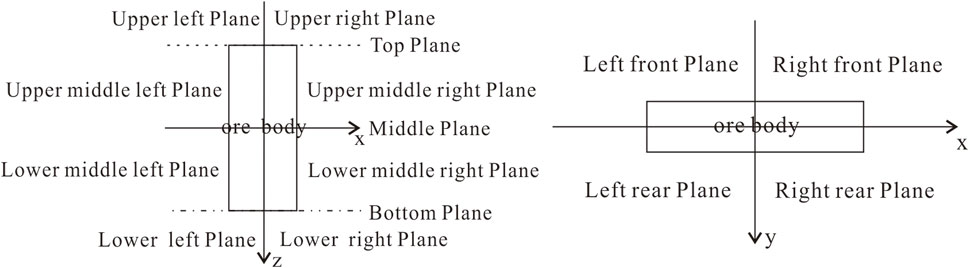
To more intuitively examine the patterns of positive and negative combinations of the four parameters when the gravity anomaly is in different parts of the orebody, the xoz section of the orebody was divided into eight areas, and the xoy plane was divided into four areas, as shown in Figure 3.
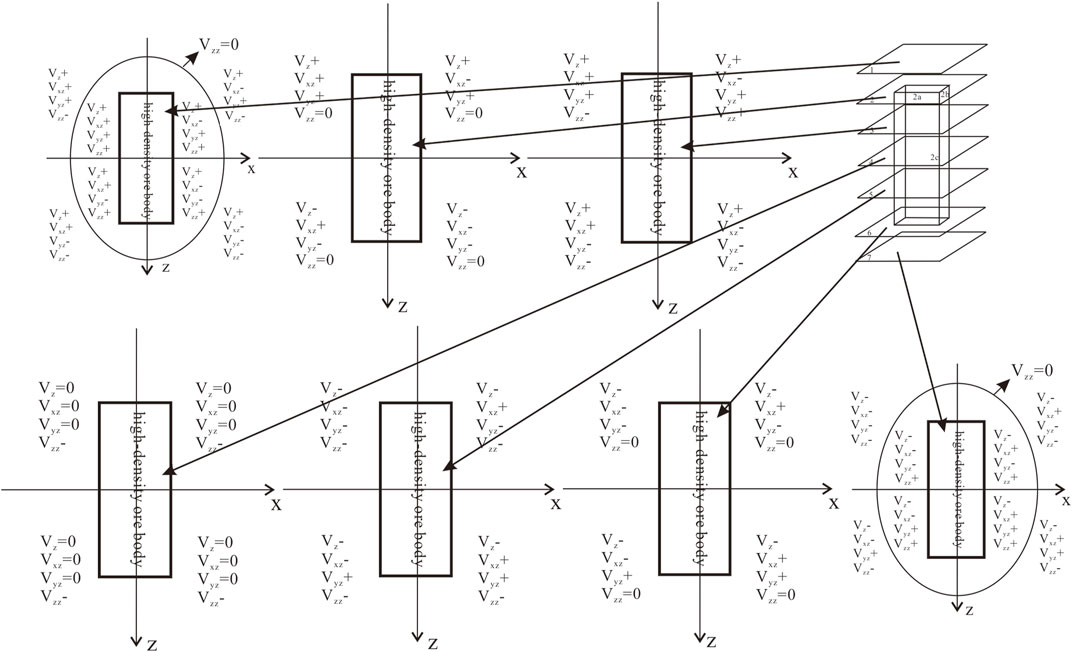
Taking the length, width, and height of the vertical cuboid as 2a = 200 m, 2b = 40 m, and 2c = 500 m, respectively, and the residual density as σ = 1.0 × 103 kg/m3, the coordinates of the center point were (0, 0, 0). The patterns of positive and negative combinations of the four parameters of the gravity anomaly on each plane and the gravity gradient anomaly in three directions were obtained through the gravity forward modeling of the vertical cuboid, as shown in Figures 4A–G.

FIGURE 4. (Continued). (A) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the upper plane (z = −300 m) of the vertical cuboid. (B) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the top plane (z = −250 m) of the vertical cuboid. (C) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the upper middle plane (z = −125 m) of the vertical cuboid. (D) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the middle plane (z = 0 m) of the vertical cuboid. (E) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the lower middle plane (z = 125 m) of the vertical cuboid. (F) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the bottom plane (z = 250 m) of the vertical cuboid. (G) Positive and negative combination patterns of the gravity anomaly and gravity gradient anomaly on the lower plane (z = 300 m) of the vertical cuboid.
In Figures 4A–G, the positive and negative combination distributions of the four parameters, the vertical cuboid, and the gravity anomaly in different planes are observed, as summarized in Table 1.
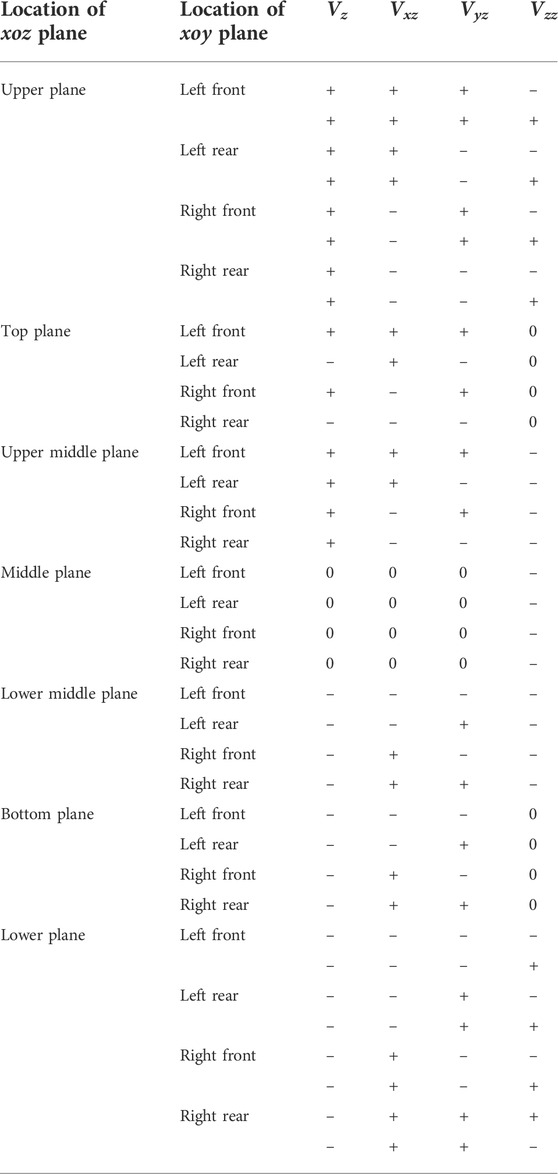
TABLE 1. Correspondence between plane positions and the four parameters of vertical high-density cuboid orebodies.
Figure 2 presents the calculation results of Eqs 2–5. According to Figure 2, the positive and negative values of the gravity anomaly (Vz), vertical gravity gradient anomaly (Vzz), and horizontal gravity gradient anomaly (Vxz and Vyz) of the high-density cuboid ore can be obtained using the combined spatial variation law (Figure 5). According to Figure 5, in any spatial plane of the orebody, the curve obtained by setting the vertical gravity gradient anomaly (Vzz) equal to 0 is an ellipse, Vzz is positive inside the ellipse, and Vzz is negative outside the ellipse. To facilitate the description of the spatial location, the deep orebody is called “external” when Vzz is negative and “internal” when Vzz is positive. Figure 5 shows the results for the positive and negative combinations of the four parameters (Vz, Vxz, Vyz, and Vzz) of upright high-density cuboid concealed orebodies.
With further analysis, a total of 26 relative positions between the measurement points and orebody were obtained, as summarized in Table 2. These 26 cases include all the combinations of the four parameters and the corresponding spatial locations of the orebodies; thus, they can be used to accurately locate orebodies.
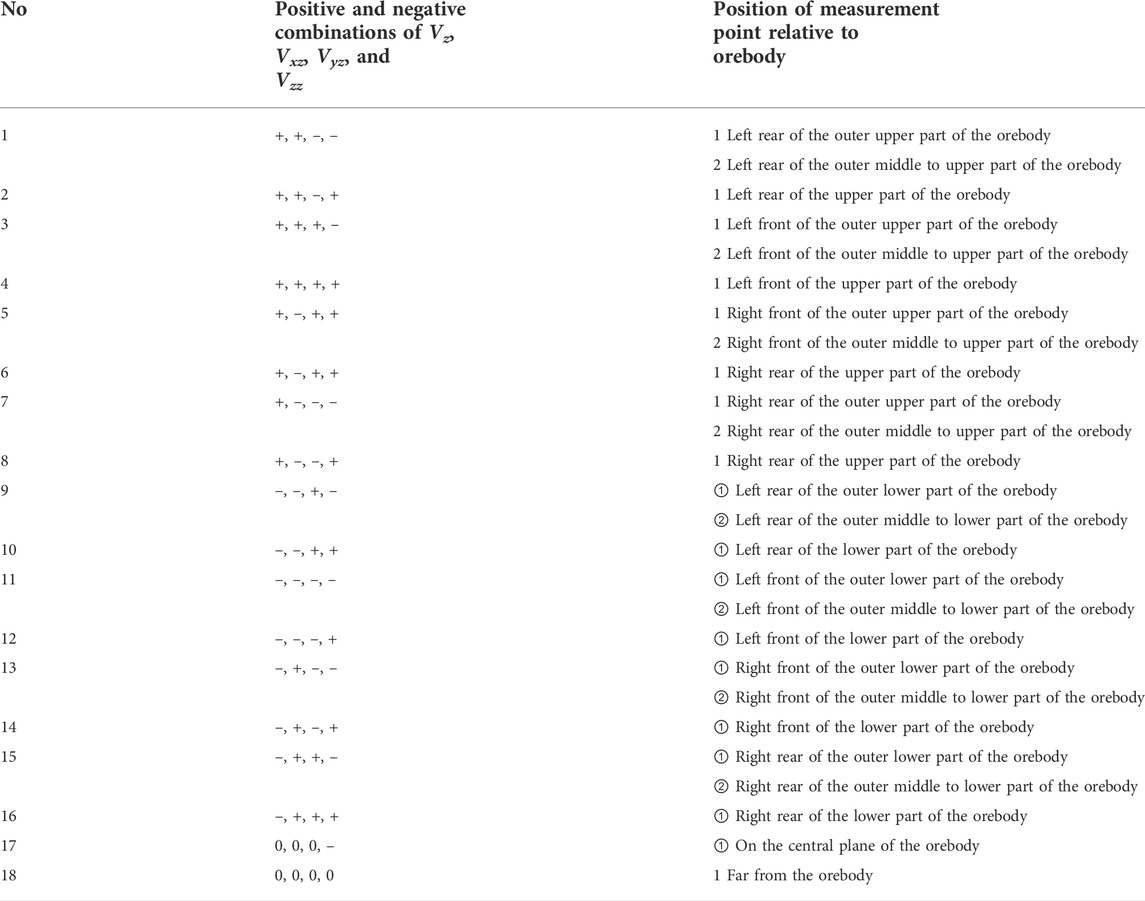
TABLE 2. Correspondence between the four parameters of the vertical high-density cuboid orebodies and the relative positions of the orebodies.
Case study
The tunnel gravity method exhibited a clear prospecting effect during the exploration of deep parts of the Huangshaping skarn deposit. This deposit is representative of copper-tin polymetallic deposits in the southern Hunan Province. Furthermore, its formation is closely related to the skarn in the contact zone between early to middle Yanshan quartz porphyries and wall rocks in the area (Zhao et al., 2016). The deposit is controlled by the contact zone, where the main body takes the shape of large veins and irregularities and occurs on both sides of the contact zone between the quartz porphyry body and crystalline limestone in the area (Han et al., 2020b). After decades of deposit development and utilization, the resources in the deep parts are in crisis; thus, the deep orebodies must be explored to prepare for tunnel gravity exploration.
Gravity measurements were performed using a high-precision gravimeter (CG-5, Scintrex, Canada). The precision of the instrument was 0.01 g.u, the standard error was < 0.05 g.u, and the direct reading range was 80,000 g.u.
Before the gravimeter was employed for tunnel gravimetric measurements, it passed the static test; dynamic test; stability time test, which was conducted after adjusting the range; and grid value calibration test. The overall basepoint of tunnel gravity was set near the tunnel entrance, where the ground was stable and free of interference, thereby rendering observation at the basepoint convenient in the morning and evening. Observations at the basepoint in the morning and evening were conducted via the “basepoint–auxiliary reference point–basepoint” method. The measurement points were observed using the “basepoint–measurement point 1, measurement point 2, .., measurement point n–basepoint” method. The tunnel gravity measurement point was positioned using the layout of the middle section of the tunnel, with a tape measure and laser rangefinder. The point distance was 25 m.
Temperature correction, inclination correction, solid tide correction, zero drift correction, terrain correction, Bouguer correction, and latitude correction were performed on the tunnel gravity observation results. Additionally, field separation of the corrected Bouguer gravity anomaly was performed. Subsequently, the obtained residual gravity anomaly was analyzed and interpreted to conduct deep extension prediction of orebodies.
The ore-hosting surrounding rocks in the study area were quartz porphyry and crystalline limestone with an average density of 2.62 × 103 kg/m3, and the average density of the skarn-type orebodies (eight pieces) was 3.45 × 103 kg/m3, that is, 0.83 × 103 kg/m3 higher than that of the surrounding rocks. Therefore, the orebodies in the study area had high densities and vein-like structures, which satisfy the density-difference requirement for the application of this method.
Through the measurement of the gravity profile of the tunnel in the middle section of −136 and the middle section of −256 in the Huangshaping mining area, as shown in Figure 6, Δg−2, Δg−4, Δg−6, Δg−7, and Δg−12 mineralized anomalies were detected. According to the measurement data and the results presented in Table 2 along with the observed ore condition in the tunnel, the positions of the four measurement points relative to the orebody were determined, as summarized in Table 3.
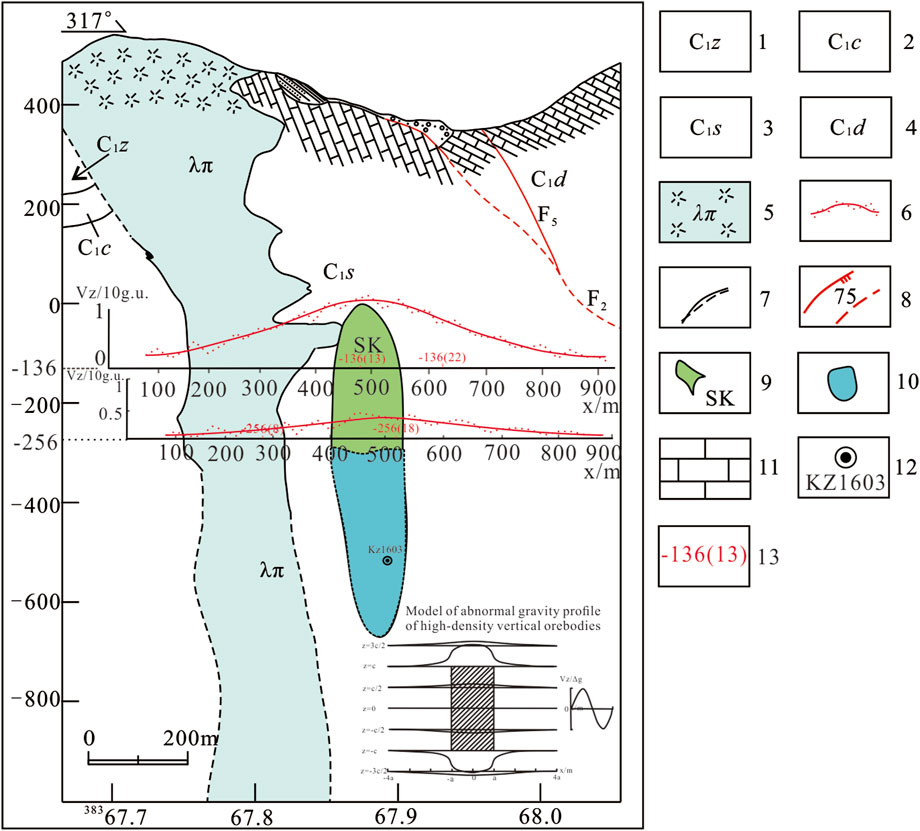
FIGURE 6. Tunnel gravity prediction target area and engineering verification diagram for the Huangshaping mining area.
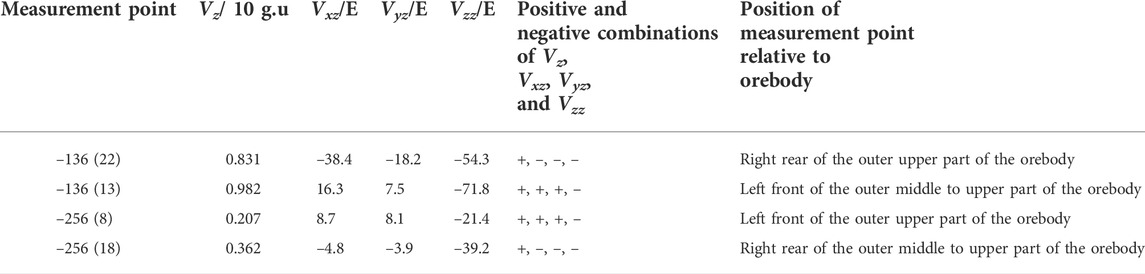
TABLE 3. Positive and negative combinations of Vz, Vxz, Vyz, and Vzz and the relative positions of the orebody in the middle section of the Huangshaping mining area (−136 and −256 m).
Through the application of the tunnel gravity method to the Huangshaping skarn-type deposit, drilling verification was performed, which not only confirmed the existence of deep concealed deposits but also validated the scientific nature of the principles of the method.
Discussion
The collection and analysis of the abnormal data of the two middle sections of the Huangshaping deposit (−136 and −256) indicate that the overall law of the abnormality is consistent with the basic principles proposed in this study. The tunnel gravity method exhibited the following characteristics in this application:
(1) It has a high detection accuracy and can be applied to the deep detection and accurate positioning of high-density vertical orebodies in the entire space at a scale of 1:500–1:10,000.
(2) It is suitable for the positioning and detection of deep vertical orebodies where the density difference between the ore and the ore-hosting rock is obvious, and the anomaly is significantly greater than the detection accuracy of the gravimeter.
(3) It can accurately detect ores, including lead-zinc ore, iron-rich ore, copper-rich ore, and uranium-rich ore. Additionally, it is suitable for determining the locations of low-density geological bodies (such as underground caves and low-density orebodies).
(4) It overcomes the multi-solution problem of spatial positioning of deep vertical orebodies.
(5) It is unaffected by electromagnetism and is hardly affected by terrain.
(6) The observation surface does not need to be curved or leveled; thus, the method is facile.
The limitations of the method are reflected primarily in the limitation of the tunnel height. The abnormal changes of the effective vertical gradient in a tunnel cannot be detected, owing to the insufficient accuracy of the existing high-precision gravimeter. This problem can be solved by collecting data in tunnels with different elevations; however, this increases the workload.
Conclusion
The gravity gradient tensor has the advantages of high precision, high resolution, and multiple parameters. The successful application of the tunnel gravity detection method using the gravity anomaly (Vz) and its three-direction gravity gradient tensors (Vxz, Vyz, and Vzz) combined forward and inversion to the Huangshaping copper-tin polymetallic deposit indicated that this method can accurately locate deep orebodies. Additionally, the method is unaffected by electromagnetic interference and has high detection accuracy. It overcomes the multi-solution problem of geophysical anomalies in deep spatial positioning and the detection of orebodies. Therefore, this new method of practical geophysical exploration has broad research and application prospects.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research project was jointly funded by the National Key Research and Development Program of China (SQ2018YFC06017102), Projects of YMLab (2010), and Innovation Team of Yunnan province (2012).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cai, M. F., Xue, D. L., and Ren, F. H. (2019). Current status and development strategy of metal mines. Chin. J. Eng. 41, 417–426. doi:10.13374/j.issn2095-9389.2019.04.001
Hammer, S. (1950). Density determinations by underground gravity measurements. Geophysics 15, 637–652. doi:10.1190/1.1437625
Han, R., Li, W., Cheng, R., Wang, F., and Zhang, Y. (2020a). 3D high-precision tunnel gravity exploration theory and its application for concealed inclined high-density ore deposits. J. Appl. Geophys. 180, 104119. doi:10.1016/j.jappgeo.2020.104119
Han, R., Li, W., Cheng, R., and Wang, J. (2021). 3D high-precision tunnel gravity exploration method for locating and detecting deeply concealed inclined high-density orebodies. Report.
Han, R., Wang, F., Hu, Y., Wang, X., Ren, T., Qiu, W., et al. (2014). Study on metallogenic tectonic dynamics and chronological constraints of Huize type (HZT) germanium-rich lead-zinc deposit. Tect. Metallogenesis 38, 758–771. doi:10.16539/j.ddgzyckx.2014.04.003
Han, R., Zhao, R., Wu, P., Wang, L., Qiu, W., Long, Y., et al. (2020b). Structural rock-controlling and ore-controlling mechanism of the Huangshaping copper-tin polymetallic deposit in southern Hunan and enlightenment from deep prospecting and exploration. Lead. Edge 27, 199–218. doi:10.13745/j.esf.sf.2020.6.33
Huang, X., Zhang, X., and Ma, S. (2021). A new path for the development of my country's mineral exploration economy during the “14th Five-Year Plan” period. China Land Resour. Econ. 34, 64–68. doi:10.19676/j.cnki.1672-6995.000573
Li, W., and Han, R. (2014). A method for detecting low-density concealed orebodies in the whole space of tunnel gravity. Report, 11.
Lv, Q., Zhang, X., Tang, J., Jin, S., Liang, L., Niu, J., et al. (2019). Geophysical exploration technology and equipment for metal deposits: Review and progress. Chin. J. Geophys. 62, 3629–3664. doi:10.6038/cjg2019N0056
Smith, N. J. (1950). The case for gravity data from boreholes. Geophysics 15, 605–636. doi:10.1190/1.1437623
Wang, C. (2021). Development status and practical application of geophysical exploration technology. China Metal. Bull. 2021 (10), 3–4. doi:10.3969/j.issn.1672-1667.2021.19.002
Wang, J. (2019). Influencing factors of high-precision tunnel gravity exploration in the Huangshaping W-Sn-Cu-Pb-Zn polymetallic mining area, Southern Hunan. Acta Geol. sin.-engl. 93 (2), 418. doi:10.26914/c.cnkihy.2019.028519
Xu, G., and Zhou, G. (1989). Gravity measurement in wells and tunnels. Beijing: Beijing Geological Publishing House.
Zhang, D. (2017). Application of high-precision gravity in prospecting in Xiaozhuqing survey area of Huize lead-zinc mining area. Kunming, China: [D] Kunming University of Science and Technology.
Keywords: tunnel gravity exploration, full spatial domain, deep spatial positioning prediction, high-density vertical ore body, Huangshaping skarn-type deposit
Citation: Wang J, Han R, Li W and Cheng R (2022) Principles and application of tunnel gravity full-space positioning and detection method for deep high-density vertical orebodies. Front. Earth Sci. 10:919673. doi: 10.3389/feart.2022.919673
Received: 13 April 2022; Accepted: 27 July 2022;
Published: 02 September 2022.
Edited by:
Mehdi Eshagh, University West, SwedenReviewed by:
Andenet Gedamu, Addis Ababa University, EthiopiaFarzam Fatolazadeh, Université de Sherbrooke, Canada
Copyright © 2022 Wang, Han, Li and Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Runsheng Han, NTU0NjcwMDQyQHFxLmNvbQ==
 Jiyu Wang
Jiyu Wang Runsheng Han1*
Runsheng Han1*