The Tension-Shear and Compression-Shear Joint Strength Model for Unsaturated Clay and Its Application to Slopes

The capillary component and adsorptive component of matric suction differently impact the soil strength. Due to the cavitation effects of pore water, the adsorption effect dominates the behavior of soil when matric suction exceeds the cavitation tension. Based on the binary medium theory, a compression-shear strength model for unsaturated soils considering both capillary effect and adsorption effect is established. Compared with test data, the proposed compression-shear strength model has better prediction performance on the compression-shear strength of soil over a range of wide suction. The soil failure depends both on tension-shear stress and compression-shear stress. The tension-shear coupling mechanism in the soil is first investigated. A concept of closed stress point is introduced to divide the two zones of tension-shear coupling stress and compression-shear stress. According to the compression-shear strength model and tension-shear failure mechanism, the tension-shear and compression-shear joint strength model applicable to plane stress conditions is then established. Compared with test data, the proposed model in this article can better predict the nonlinear strength characteristics of clays and has better applicability. Finally, using the user material subroutine (UMAT), the secondary development of the joint strength model is conducted in ABAQUS and then applied to the slope stability analysis. The calculation results show that the established strength model presents a reasonable description of the development of the tension-shear coupling plastic zone in slope and gives an accurate safety factor.

Introduction

Due to the existence of suction, unsaturated soils have more complicated properties than saturated soils. Thus, considering the influence of suction or degree of saturation on shear strength in a reasonable way is the key to studying the shear strength of unsaturated soils. Many scholars have proposed formulas that can directly or indirectly predict the shear strength of unsaturated soils by means of the soil–water characteristic curve (SWCC) and shear strength parameters of saturated soil in recent years, such as Khalili and Khabbaz (1998), Tarantino and Tombolato (2005), Garven and Vanapalli (2006), Lu et al. (2010), and Sheng et al. (2011). It is worth noting that, however, most existing strength formulas have no difference in essence and can all be expressed in the forms of Bishop-type (Bishop and Blight, 1963) or Fredlund-type (Fredlund et al., 1978) strength formulas. The different mathematical forms and parameters involved in these strength formulas determine their ability to predict the strength characteristics of different soils. In general, strength formulas with more parameters have better fitting performance.

The matric suction is directly defined as $s=u_a-u_w$ in major research on unsaturated soils, where $u_a$ is the pore gas pressure and $u_w$ is the pore water pressure. By this definition, the matric suction depends only on the negative pore-water pressure generated by capillarity. In fact, however, besides the capillarity, the other factors such as adsorption, osmosis, temperature, and gravity can also contribute to the change of total suction. Tuller et al. (1999), Baker and Frydman (2009), and Zhao et al. (2016) pointed out that the matric suction in soil generally comprises capillary components and adsorptive components when ignoring the effects of osmosis, temperature, gravity, and other factors. The two components of matric suction have different mechanisms and differently influence the mechanical behavior of soils. Ignoring the effect of the adsorptive component of matric suction, the existing strength theories fail to accurately describe the strength characteristics under high suction (or the low degree of saturation). Very few shear strength formulas consider the effects of both components of matric suction.

The mutual changes between the states of tensile stress and compressive stress occur during the failure process of soil under natural conditions. Accordingly, the soil failure is affected both by tension-shear coupling stress and compression-shear stress, especially in clay slopes, embankments, and impervious layers of landfills. It has always been a key issue in the strength theory of soil, that is, how to comprehensively consider the tension-shear and compression-shear characteristics and establish a joint strength model considering both coupling stresses. This is mainly because the issue is seemingly simple but actually complex in the intrinsic mechanism. After years of research, some beneficial results of the joint strength theory have been obtained, such as the Griffith strength criterion (Margolin, 1984; Singh and Zimmerman, 2014), the hyperbolic joint strength criterion (Abbo and Sloan, 1995; Li R. J. et al., 2014; Li et al., 2016) and the Griffith–Mohr strength criterion (Vesga, 2009; Zhang et al., 2010). However, most existing research adopts some simplified methods to describe the tension-shear coupling strength owing to the unclear strength mechanism of soil under tension-shear coupling stress. Presently, it has not yet established a unified coupling strength theory of soil. Therefore, establishing a tension-shear and compression-shear joint strength model that reasonably considers the tension-shear coupling mechanism is of great significance to accurately describe the tension-shear coupling failure and compression-shear failure of soils and the relationship between them.

Aiming at the problems in current theory, this article first establishes a compression-shear strength model that comprehensively considers the effects of the capillary component and adsorptive component of matric suction. Taking the tension-shear coupling mechanism into account, a tension-shear and compression-shear joint strength model is then proposed. Finally, the established joint strength model is numerically implemented in ABAQUS, which is then applied to the stability analysis of unsaturated slopes, and its validity and accuracy are discussed.

The Compression-Shear Strength Model Considering Adsorption Effect

The capillary component of matric suction in the soil is capillary suction with its value of $u_a-u_w$, which results from the surface tension at the gas–liquid interface and is related to the free water in pore water. The adsorptive component of matric suction is generated by the physicochemical actions between liquid water and soil particles, including long-range electrostatic force (such as electric double-layer force), van der Waals force, cementation force, and other forces, which are related to the bound water in pore water (Gens, 2010). The action mechanisms of these two components on soil strength are significantly different and their action effects depend on soil type and water content. Capillarity tends to dominate in non-cohesive soils or in soils with a higher degree of saturation, while the adsorption effect tends to dominate in clays with higher plasticity indices or in soils with a low degree of saturation (Zhao et al., 2016).

To consider capillarity and adsorption effect in soil, the method of binary medium theory (Liu and Zhang, 2013; Li R. J. et al., 2014) is introduced. The soil is abstracted as a medium consisting of two ideal elements that can be quantitatively described (that is, capillary element and adsorption element). The ideal capillary strength and ideal adsorption strength for capillary element and adsorption element are formulated, respectively. Then, these two ideal strength formulas are rationally combined, and a compression-shear strength model involving the adsorption effect is thus proposed.

Ideal Capillary Strength

In the capillary element, the soil strength is assumed to be independent of physicochemical action and only related to capillarity. Accordingly, the ideal capillary strength conforms to the strength theory established on account of the macroscopic capillary phenomenon, and can be expressed as follows:

${\tau }_f^c=c^{\prime }+(\sigma -u_a)\tan {\phi }^{\prime }+(u_a-u_w)S_r\tan {\phi }^{″},(1)$

where ${\tau }_f^c$ is the ideal capillary strength, $\sigma$ is the normal stress, $c^{\prime }$ is the effective cohesion, ${\phi }^{\prime }$ is the effective angle of internal friction, $S_r$ is the degree of saturation, and ${\phi }^{″}$ is the friction angle corresponding to capillarity and can be simplified as $\tan {\phi }^{″}=\tan {\phi }^{\prime }$ (Fredlund et al., 1996; Chaney et al., 1997).

Ideal Adsorption Strength

Because of the cavitation effects of pore water in practical soil, tensile stress in pore water cannot be larger than a limiting value $s_m$ (i.e., cavitation tension), typically in the range of 100∼400 kPa, at which the water is transformed from liquid to vapor (Baker and Frydman, 2009; Lu, 2016). When matric suction exceeds $s_m$, the cavitation of pore water occurs, and the capillarity fails. Thus, the adsorption effect controls the mechanical behavior of soil under this situation, whose influence on strength can be reflected by the degree of saturation.

In the adsorption element, the soil strength is assumed to be dependent only on physicochemical interaction between liquid water and soil particles and independent of capillarity. Accordingly, the ideal adsorption strength can be expressed as follows:

${\tau }_f^{ad}=c^{\prime }+\left(\sigma -u_a\right)\tan {\phi }^{\prime }+{\tau }_{ad},(2)$

where ${\tau }_f^{ad}$ is the ideal adsorption strength and ${\tau }_{ad}$ is the additional strength due to the adsorption effect, which relates to $s_m$ and $S_r$ (Zhao et al., 2016), and can be expressed as follows:

${\tau }_{ad}=s_m\zeta \left(S_r\right),(3)$

where $\zeta \left(S_r\right)$ is a function dependent on $S_r$.

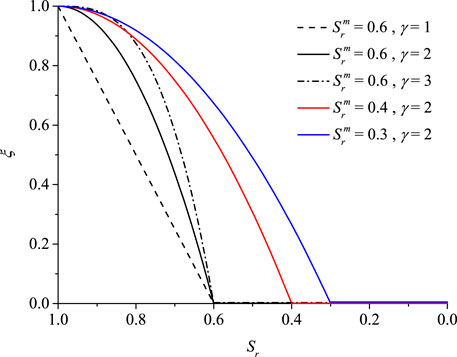
Based on the strength test results of different types of clay with low degrees of saturation (Escario and Saez, 1986; Tarantino and Tombolato, 2005; Shen et al., 2007), the evolution law of the additional strength due to the adsorption effect with the degree of saturation was fitted and analyzed, as illustrated in Figure 1. It can be found from Figure 1 that with the decrease in the degree of saturation, the additional strength due to the adsorption effect increases nonlinearly and its growth rate decreases continuously, which approaches a constant at a very low degree of saturation. According to the data fitting of the tests, $\zeta \left(S_r\right)$ can be obtained as follows:

$\zeta \left(S_r\right)=a\left(1-S_r^b\right),(4)$

where a and b are the fitting parameters. $\zeta \left(S_r\right)$ has a tendency toward a with the decrease of degree of saturation.

FIGURE 1

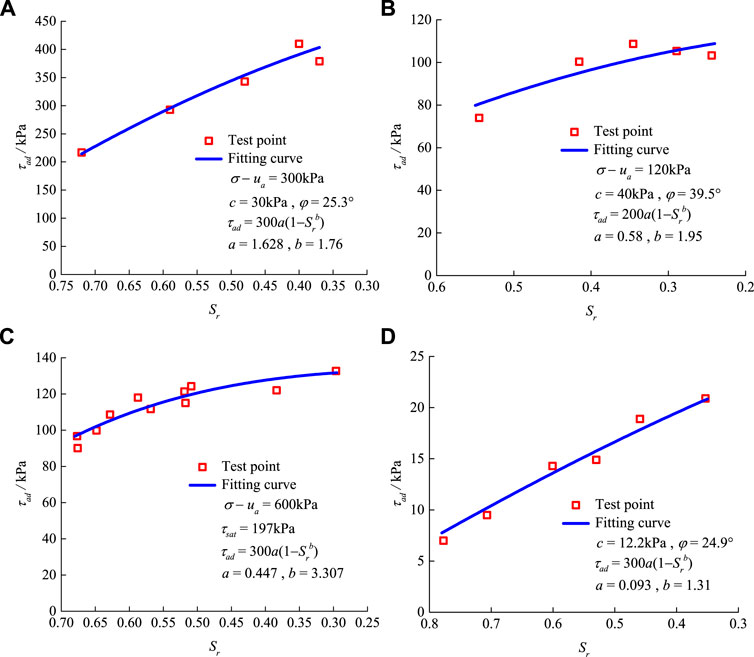
FIGURE 1. Data fitting of different clays: (A) Madrid clay (Escario and Saez, 1986), (B) Madrid sandy clay (Escario and Saez, 1986), (C) kaolin clay (Tarantino and Tombolato, 2005), and (D) silty clay (Shen et al., 2007).

Therefore, the formula of ideal adsorption strength can be written as follows:

${\tau }_f^{ad}=c^{\prime }+\left(\sigma -u_a\right)\tan {\phi }^{\prime }+s_{m}a\left(1-S_r^b\right),(5)$

The Binary-Medium Compression-Shear Strength Model

According to the binary medium theory, the practical unsaturated soil is idealized as a medium composed of the capillary element and the absorption element. The compression-shear strength of soil can be expressed as follows:

${\tau }_f=\xi {\tau }_f^c+\left(1-\xi \right){\tau }_f^{ad},(6)$

where $\xi$ is the participation function and represents the proportion of the capillary element in the practical soil.

Experimental studies have shown that the degree of saturation impacts the mechanics and hydraulic behavior of unsaturated soils, in turn affecting their behavioral characteristics (Li J. et al., 2014). Therefore, $\xi$ is related to the degree of saturation and can be expressed as follows:

$\xi =\langle 1-{\left(\frac{1-S_r}{1-S_r^m}\right)}^{\gamma }\rangle ,(7)$

where $\langle \cdot \rangle$ is the McCauley bracket, $\langle x\rangle =x$ when $x>0$ and $\langle x\rangle =0$ when $x\le 0$; $S_r^m$ is the degree of saturation corresponding to the cavitation tension $s_m$ and can be called cavitation saturation; and $\gamma$ is the fitting parameter, reflecting the degree of influence of the degree of saturation change on the participation function. The characteristic curve of the participation function $\xi$ is shown in Figure 2. $\xi$ gradually decreases with the degree of saturation and decreases to 0 at the cavitation saturation. As the parameter $\gamma$ increases, the characteristic curve of the participation function presents an upward convex, and the degree of curvature increases gradually. The range of the descending section of the characteristic curve increases with the cavitation saturation $S_r^m$ decreasing.

FIGURE 2

FIGURE 2. Participation function characteristic curve.

Combining Eqs. 1,5–7 with Eq. 6, the formula of binary-medium compression-shear strength can be expressed as follows:

${\tau }_f=c^{\prime }+\left(\sigma -u_a\right)\tan {\phi }^{\prime }+\left[\xi \left(u_a-u_w\right)S_r\tan {\phi }^{″}+\left(1-\xi \right)s_{m}a\left(1-S_r^b\right)\right],(8)$

Parameters in the Compression-Shear Strength Model

The compression-shear strength model contains eight material parameters, $c^{\prime }$, ${\phi }^{\prime }$, ${\phi }^{″}$, $s_m$, $S_r^m$, a, b, and $\gamma$, which can be determined by the following methods.

(1) Shear strength parameters of saturated soil: effective cohesion $c^{\prime }$ and effective internal friction angle ${\phi }^{\prime }$. They can be determined by the triaxial shear test of saturated soil.

(2) Friction angle corresponding to capillarity, ${\phi }^{″}$. It can be determined by the shear strength test under the condition of a high degree of saturation (near-saturation state). ${\phi }^{″}$ is simplified as ${\phi }^{″}={\phi }^{\prime }$ in this article.

(3) Cavitation tension $s_m$ and cavitation saturation $S_r^m$. The existing research on the cavitation tension is too insufficient to directly obtain its value. Based on the existing research results (Baker and Frydman, 2009; Lu, 2016), we compared the SWCC of types of soil and obtained corresponding cavitation tension $s_m$ by analogy. The cavitation saturation $S_r^m$ is then determined by SWCC.

(4) Parameters in the ideal adsorption strength formula: a and b. They can be determined according to the shear strength test at low degrees of saturation or high suctions.

(5) Parameter in participation function: $\gamma$. The parameter $\gamma$ is the prediction parameter of the compression-shear strength model, through which the prediction effect of the model is controlled.

The Tension-Shear and Compression-Shear Joint Strength Model for Unsaturated Clay

The strength theory that can describe both tensile failure and shear failure is generally called joint strength theory. The theoretical research on the joint strength of soil mainly focuses on plane stress conditions and clay and can be roughly divided into two categories. One category is that the joint strength formula is established by using an empirical curve from strength test data (Abbo and Sloan, 1995; Li et al., 2016); the other category is that the joint strength formula is derived by using soil strength index ($c$, $\mathit{\phi }$, and ${\sigma }_t$) based on some assumptions (Vesga, 2009; Zhang et al., 2010). $c$ is the cohesion of unsaturated soil, $\mathit{\phi }$ is the compression-shear internal friction angle of unsaturated soil, and ${\sigma }_{\text{t}}$ is the uniaxial tensile strength. However, none of these studies have revealed the tension-shear failure mechanism of soil properly. This section first analyzes the failure mechanism of soil under tension-shear coupling stress and then investigates the establishment of tension-shear and compression-shear joint strength models under plane stress conditions.

Mechanism of Tension-Shear Coupling Strength

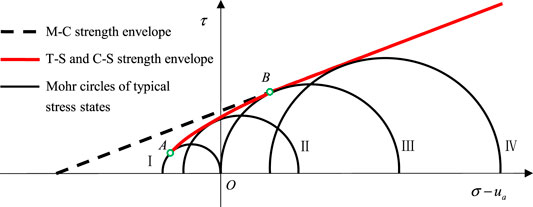
Under compression-shear stress, the traditional M-C strength theory gives an accurate description of soil strength. Under tension-shear coupling stress, however, the linear M-C strength theory tends to significantly overestimate the soil strength exhibiting typical nonlinearity. Several typical failure stress states of soil are shown in Figure 3. Stress state I is the Mohr circle of uniaxial tensile failure, stress state II is the Mohr circle of tension-shear coupling failure, stress state III is the Mohr circle of uniaxial compressive failure, and stress state IV is the Mohr circle of triaxial shear failure. Point A and point B in Figure 3 are the uniaxial tensile failure point and uniaxial compressive failure point, respectively. It should be noted that the practical soil is in a three-dimensional stress space and is under three-dimensional stress. Only under the equal tensile stress in three directions is the soil without shear stress completely controlled by the tensile stress. Under the uniaxial tensile stress, however, the soil bears both tensile stress and shear stress and the tension-shear coupling failure occurs. Therefore, the strength envelope under plane stress conditions has the following characteristics: 1) the multidirectional tensile strength of soil cannot be described, which needs to be discussed in the three-dimensional stress space; 2) the strength envelope is tangential to the Mohr circle of uniaxial tensile failure at the failure point instead of simply intersecting with the effective stress axis at the uniaxial tensile strength point; and 3) the strength envelope is not closed.

FIGURE 3

FIGURE 3. The illustration of typical stress states at soil failure (plane stress problem).

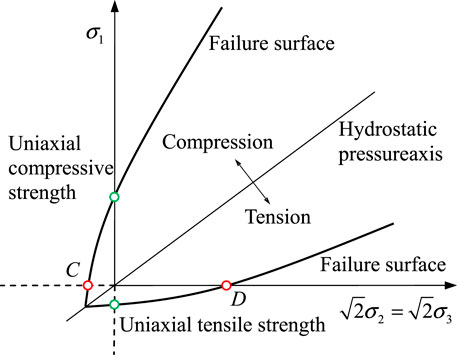
The mechanism of tension-shear coupling failure applies not only to the traditional triaxial tensile test (or triaxial extension test) with constant confining pressure and reduced axial compression, but also to the triaxial compression-shear test associated with tension-shear coupling strength. That is, the mechanism of tension-shear coupling failure can be used for both triaxial tension conditions and triaxial compression conditions. The following points need special attention: 1) Under triaxial compression, the stress state on Mohr circle I is that the confining pressure is negative and the failure axial pressure is zero (as shown by point C in Figure 4). This stress state is difficult to achieve experimentally, but it differs little from the uniaxial tensile stress state under plane stress, which thus can be simply viewed as the stress state at uniaxial tensile failure. Mohr circle III represents the stress state at uniaxial compression failure. 2) Under triaxial tension, Mohr circle I represents the stress state at uniaxial tensile failure, and the stress state on Mohr circle III is characterized by confining pressure being positive and failure axial pressure being zero (as shown by point D in Figure 4).

FIGURE 4

FIGURE 4. Schematic diagram of failure states in the triaxial plane.

Tension-Shear and Compression-Shear Joint Strength

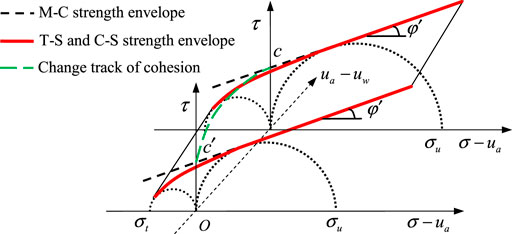
Based on the tension-shear coupling failure mechanism, we used for reference the concept of a closed stress point (Murrell and Digby, 1970) and define it as the dividing point between the zones of the tension-shear and compression-shear stresses. The failure functions within the two zones smoothly connected at the closed stress points are then established, respectively. The uniaxial compression failure point is by definition selected as the closed stress point, which gives this point specific physical meaning. Figure 5 illustrates the failure envelopes of unsaturated clay under tension-shear coupling stress and compression-shear stress at a certain suction.

FIGURE 5

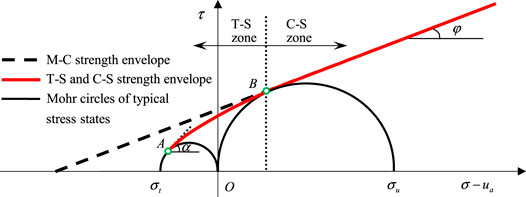
FIGURE 5. Failure envelopes of unsaturated clay under tension-shear and compression-shear stresses (note: the T-S zone and C-S zone mean the compression-shear action zone and tension-shear coupling action zone, respectively).

The shear stress of soil in the compression-shear action zone satisfies the M-C strength criterion, but the shear stress in the tension-shear coupling action zone exhibits characteristics of typical nonlinear strength. Therefore, the soil strength can be described by the quadratic curve function, and be expressed as follows:

$\sigma -u_a=A^{\prime }{\tau }^2+B^{\prime }\tau +C^{\prime },(9)$

where $A^{\prime }$, $B^{\prime }$, and $C^{\prime }$ are the coefficients, which can be deduced by using three characteristic parameters ($A({\sigma }_{\text{t}}^{\prime },{\tau }_{\text{t}}^{\prime })$, $B({\sigma }_{\text{b}},{\tau }_{\text{b}})$, and $\phi$) and the geometric continuity requirements:

$\{\begin{array}{c}\tau {|}_{\sigma -u_a={\sigma }_{\mathrm{t}}^{\prime }}={\tau }_{\mathrm{t}}^{\prime }\\ \tau {|}_{\sigma -u_a={\sigma }_{\text{b}}}={\tau }_{\mathrm{b}}\\ {\tau }^{\prime }{|}_{\sigma -u_{\mathrm{a}}={\sigma }_{\mathrm{b}}}=\tan \phi \end{array}\Rightarrow \{\begin{array}{l}{A}^{\prime }=-m\\ B^{\prime }=\cot \phi +2{\tau }_{\text{b}}m\\ C^{\prime }={\sigma }_{\text{b}}-{\tau }_{\text{b}}\cot \phi -{\tau }_{\mathrm{b}}^{2}m\end{array},(10)$

where:

$\{\begin{array}{l}m=\left[{\sigma }_{\text{b}}-{\sigma }_{\mathrm{t}}^{\prime }-\cot \phi \left({\tau }_{\text{b}}-{\tau }_{\mathrm{t}}^{\prime }\right)\right]/{({\tau }_{\text{b}}-{\tau }_{\mathrm{t}}^{\prime })}^2\\ {\sigma }_{\text{b}}={\sigma }_{\text{u}}\left(1-\sin \phi \right)/2\\ {\tau }_{\text{b}}={\sigma }_{\text{u}}\cos \phi /2\\ {\sigma }_{\mathrm{t}}^{\prime }=-{\sigma }_{\text{t}}\left(1+\sin \alpha \right)/2\\ {\tau }_{\mathrm{t}}^{\prime }={\sigma }_{\text{t}}\cos \alpha /2\end{array},(11)$

Where ${\sigma }_{\text{u}}$ is the uniaxial compressive strength, and $\alpha =\chi \phi$ is the tension-shear internal friction angle (Mitachi and Kitago, 1976; Mayne, 1985) with $\chi$ ($=1\sim 1.5$) being the physical parameter related to the tension-shear coupling stress action. The compression-shear internal friction angle $\phi$ can be taken as the effective internal friction angle ${\phi }^{\prime }$. In simplifying calculation, ${\sigma }_t$ and ${\sigma }_u$ can be expressed as ${\sigma }_t=2c\cos \phi /(1+\sin \phi )$ and ${\sigma }_u=2c\cos \phi /(1-\sin \phi )$.

Combining Eqs. 8, 9, the complete tension-shear and compression-shear joint strength formulas can be obtained as:

$\{\begin{array}{cc}{A}^{\prime }{\tau }^2+B^{\prime }\tau =\left(\sigma -u_a\right)-C^{\prime }& \left(\sigma -u_a\right)<{\sigma }_{\text{u}}(1-\sin {\phi }^{\prime })/2\\ \tau =c+\left(\sigma -u_a\right)\tan {\phi }^{\prime }& \left(\sigma -u_a\right)\mathrm{\ge }{\sigma }_{\text{u}}(1-\sin {\phi }^{\prime })/2\end{array},(12)$

The failure surfaces of unsaturated clay under tension-shear and compression-shear stress are shown in Figure 6, which consists of a series of failure envelopes at different suctions.

FIGURE 6

FIGURE 6. Failure surfaces of unsaturated clay under tension-shear and compression-shear stresses.

Prediction and Verification

Prediction and Verification of the Compression-Shear Strength Model

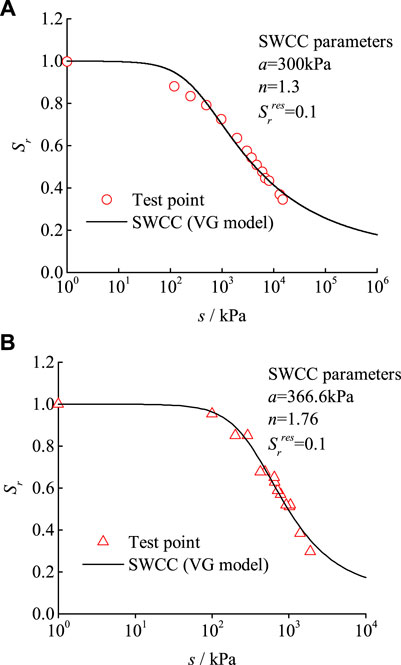
The compression-shear strength model considering the adsorption effect was first verified using the strength test results of kaolin clay (Tarantino and Tombolato, 2005) and Madrid clay (Escario and Saez, 1986). Model parameters can be determined by test data, which are shown in Table 1. In this article, the Van Genuehten (VG) model (Genuchten, 1980) is used to convert the degree of saturation of unsaturated soil into the corresponding suction. The variation of suction with the degree of saturation is illustrated in Figure 7.

TABLE 1

TABLE 1. Model parameters of clays.

FIGURE 7

FIGURE 7. SWCC of clays: (A) Madrid clay and (B) kaolin clay.

The predictions of the compression-shear strength model are shown in Figure 8. Through comparison, it can be found from Figure 8 that the proposed model has accurate prediction performances on the compression-shear strength of soil over a range of wide suction. The strength increases nonlinearly with matric suction, whose growth rate decreases continuously (this law is not directly reflected in logarithmic coordinate), and almost remains unchanged with large enough matric suction. The influences of the parameter $\gamma$ being 0.5, 1.0, and 2.0 in turn on soil strength are also analyzed. The strength increases gradually $\gamma$, but its variation only focuses on a relatively small zone where capillarity coexists with the adsorption effect. This is mainly because the contribution of capillarity to soil strength increases with $\gamma$, and the interaction zone of capillarity and adsorption effect is relatively small due to the cavitation effect.

FIGURE 8

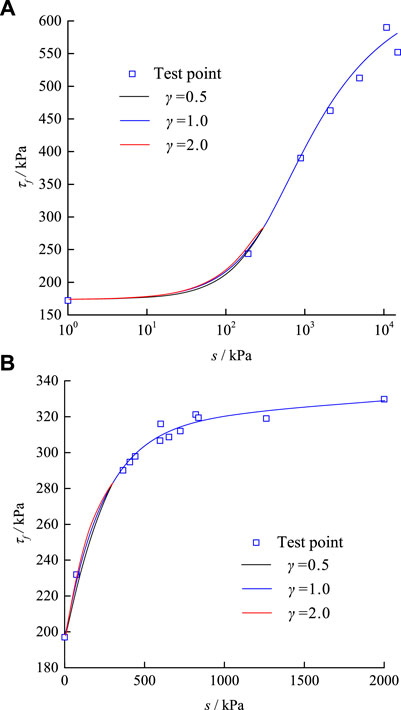
FIGURE 8. The predictions of the compression-shear strength model: (A) Madrid clay and (B) kaolin clay.

Prediction and Verification of the Tension-Shear and Compression-Shear Joint Strength Model

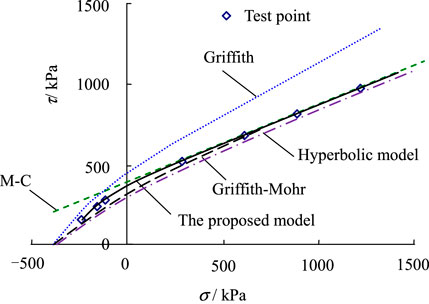
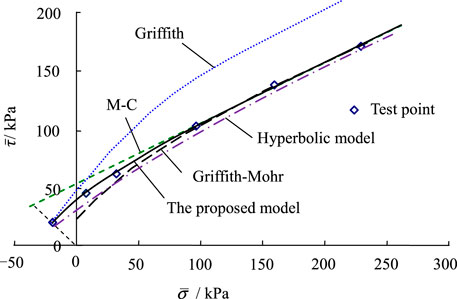
The triaxial tension-shear tests from Vesga (2009) and Zhang et al. (2010) are used to verify the tension-shear and compression-shear joint strength model. The soil samples selected by Vesga and Zhang et al. are kaolin clay and dam clay, respectively, with their specific gravity being 2.59 and 2.71, water content being 15 and 15%, the liquid limit being 44, and 33.4%, and plastic limit being 26 and 19.6%. The model parameters of the two clays are shown in Table 2. Figures 9,10 show the predictions of our strength model and other models for the two clays. Through comparison and analysis, it can be found that the prediction of the M-C strength criterion is significantly larger than the test data in the tension-shear coupling zone. In addition, the Griffith strength criterion (Singh and Zimmerman, 2014) markedly overestimates the soil strength in all zones and thus is inapplicable to clay materials. Meanwhile, the hyperbolic strength criterion (Li R. J. et al., 2014) and the Griffith–Mohr strength criterion (Zhang et al., 2010) underestimate the strength of soil under tension-shear stress. These happen mainly because the above models fail to well describe the tension-shear failure mechanism. The tension-shear and compression-shear joint strength model established in this article gives good predictions for both unsaturated clays and makes accurate descriptions of the nonlinear strength of clay.

TABLE 2

TABLE 2. Model parameters of unsaturated soil sample.

FIGURE 9

FIGURE 9. Predictions by different strength models for kaolin clay.

FIGURE 10

FIGURE 10. Predictions by different strength models for dam clay.

Application of the Model to Slope Stability Analysis

The tension-shear and compression-shear joint strength model is numerically implemented by using ABAQUS which provides a secondary developmental user material subroutine (UMAT). A UMAT subroutine is programmed by means of the implicit integral algorithm (Sutharsan et al., 2017; Sabetamal et al., 2021; Singh et al., 2021) in this article and is then applied to the slope stability analysis. The instability and failure of the slope are finally discussed by adopting the finite element strength reduction method.

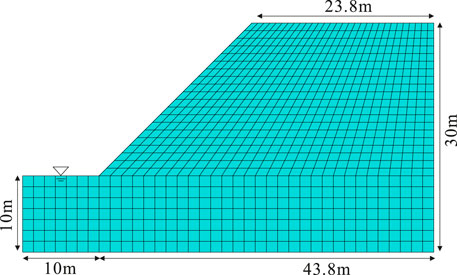
A general soil slope (Jiang et al., 2018) is selected to analyze the stability of the unsaturated slope. The calculation model and grid partition are illustrated in Figure11. As shown in Figure11, the grid cell CPE4P is used in the finite element model of the slope and the water table is located at the toe. The boundary conditions of the left and right sides below the water table are the pressure conditions with the hydrostatic pore water pressure increasing linearly with the depth. In the calculation, the soil is regarded as an ideal elastic-plastic material and the associated flow law is adopted. In addition to the tension-shear and compression-shear joint model yielding the criterion established in this article, the M-C yield criterion is also taken as the yield criterion. The material parameters of soil are shown in Table 3.

FIGURE 11

FIGURE 11. Finite element model of the slope.

TABLE 3

TABLE 3. Geotechnical properties of soil.

The role of the static water table is first analyzed. Some initial conditions (pore water pressure, effective degree of saturation, and stress distribution ) of the slope can be obtained as the initial states of the subsequent slope stability analysis. The initial distributions of pore water pressure and effective degree of saturation are illustrated in Figure 12. It can be seen from Figure 12A that the initial pore water pressure presents a linear distribution with its value at slope bottom being 100kPa, its value at slope top being −200kPa, and its value at the water table being 0. As shown in Figure 12B, the initial effective degree of saturation below the water table remains one and the initial effective degree of saturation above the water table decreases with height.

FIGURE 12

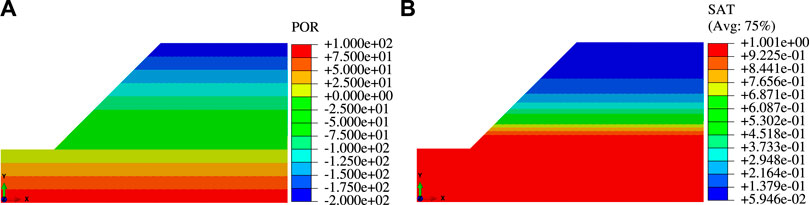
FIGURE 12. Nephogram of pore pressure and effective degree of saturation at the initial state: (A) Pore pressure and (B) effective degree of saturation.

Based on the initial states of the slope, the stability of the unsaturated slope is then analyzed by using the finite element strength reduction method. The developments of the equivalent plastic strain zone of a progressively unstable slope are shown in Figure 13 (three calculation steps are selected during slope instability from the near instability to the final instability). When the M-C yield criterion is used, the equivalent plastic zone develops upward from the toe and extends to the slope top, resulting in the generation of a plastic penetration zone. When the tension-shear and compression-shear joint yield criterion is used, an obvious tension-shear coupling plastic zone generates from the top of the slope, which gradually develops downward, and finally connects with the equivalent plastic zone that develops upward from the slope toe. Taking the penetration of the plastic zone as the standard, the slope safety factors calculated based on the two yield criteria are 1.516 and 1.504, respectively. Figure 14 shows the maximum principal stress nephograms of the unstable slope. It can be seen from Figure 14 that the ranges of the tensile stress region are essentially the same in cases of different yield criteria, but the maximum value of the tensile stress region in the case of the tension-shear and compression-shear joint yield criterion (3.220 kPa) is smaller than that in the case of the M-C yield criterion (4.148 kPa).

FIGURE 13

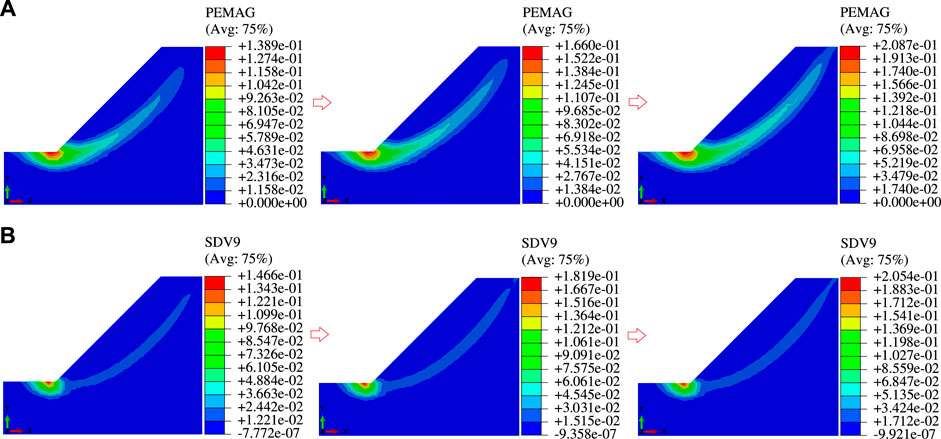
FIGURE 13. Development of the equivalent plastic strain zone of a progressively unstable slope: (A) M-C yield criterion and (B) tension-shear and compression-shear joint yield criterion.

FIGURE 14

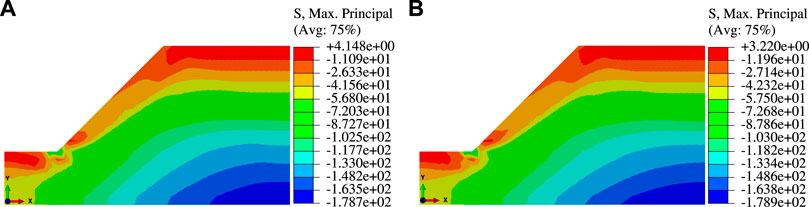
FIGURE 14. Maximum principal stress nephograms of unstable slopes: (A) M-C yield criterion and (B) tension-shear and compression-shear joint yield criterion.

The calculation results in the cases of the two yield criteria indicate that the M-C yield criterion overestimates the tension-shear coupling strength of soil and gives a larger safety factor (dangerous result), but the tension-shear and compression-shear joint yield criterion presents a reasonable description of the strength characteristics of soil under tension-shear coupling stress and gives a smaller safety factor. Therefore, the influence of tension-shear coupling stress should be included in the stability analysis of unsaturated slopes. The use of the tension-shear and compression-shear joint yield criterion can avoid some dangerous results.

Conclusion

(1) The existing strength theories on unsaturated soils almost focus only on the macroscopic capillarity and ignore the effect of the adsorptive component of matric suction, which fails to well describe the soil strength. The unsaturated soil is idealized as a medium consisting of two elements that can be quantitatively described, that is, the capillary element and the adsorption element. The strength formulas for each element are first proposed successively and then a compression-shear strength model considering the adsorption effect is established based on the binary medium theory.

(2) The action mechanism of tension-shear strength not revealed in current research on joint strength theory is systematically analyzed. The multi-directional tensile strength of soil cannot be described by the failure envelope under plane stress conditions and thus needs to be investigated in three-dimensional stress space. Under the uniaxial tensile stress, the soil bears both tensile stress and shear stress and the tension-shear coupling failure occurs.

(3) Based on the established compression-shear strength model for unsaturated clays and the tension-shear coupling mechanism, the closed point is introduced to properly divide the zones affected by tension-shear stress and compression-shear stress. A tension-shear and compression-shear joint strength model applicable to plane stress conditions is established.

(4) According to the test data from types of clays, the compression-shear strength model considering the adsorption effect can well describe the compression-shear strength of soils with different suctions. Compared with several existing joint strength models, the tension-shear and compression-shear joint strength models established in this article can better predict the strength characteristics of soil and have better applicability.

(5) The tension-shear and compression-shear joint strength model is numerically implemented by programming a UMAT subroutine in ABAQUS, which is then applied to the slope stability analysis. The calculation results show that the established strength model presents a reasonable description of the development of the tension-shear coupling plastic zone in slope and gives an accurate safety factor.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XK contributed to the conception and investigation of the study and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was funded by the National Key Research and Development (R&D) Program of China, grant number 2018YFC0809400.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbo, A. J., and Sloan, S. W. (1995). A Smooth Hyperbolic Approximation to the Mohr-Coulomb Yield Criterion. Comput. Struct. 54 (3), 427–441. doi:10.1016/0045-7949(94)00339-5

CrossRef Full Text | Google Scholar

Baker, R., and Frydman, S. (2009). Unsaturated Soil Mechanics. Eng. Geol. 106 (1-2), 26–39. doi:10.1016/j.enggeo.2009.02.010

CrossRef Full Text | Google Scholar

Bishop, A. W., and Blight, G. E. (1963). Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Géotechnique 13 (3), 177–197. doi:10.1680/geot.1963.13.3.177

CrossRef Full Text | Google Scholar

Chaney, R., Demars, K., Öberg, A., and Sällfors, G. (1997). Determination of Shear Strength Parameters of Unsaturated Silts and Sands Based on the Water Retention Curve. Geotech. Test. J. 20 (1), 40–48. doi:10.1520/gtj11419j

CrossRef Full Text | Google Scholar

Escario, V., and Sáez, J. (1986). The Shear Strength of Partly Saturated Soils. Géotechnique 36 (3), 453–456. doi:10.1680/geot.1986.36.3.453

CrossRef Full Text | Google Scholar

Fredlund, D. G., Morgenstern, N. R., and Widger, R. A. (1978). The Shear Strength of Unsaturated Soils. Can. Geotech. J. 15 (3), 313–321. doi:10.1139/t78-029

CrossRef Full Text | Google Scholar

Fredlund, D. G., Xing, A., Fredlund, M. D., and Barbour, S. L. (1996). The Relationship of the Unsaturated Soil Shear Strength to the Soil-Water Characteristic Curve. Can. Geotech. J. 33 (3), 440–448. doi:10.1139/t96-065

CrossRef Full Text | Google Scholar

Garven, E. A., and Vanapalli, S. K. (2006). “Evaluation of Empirical Procedures for Predicting the Shear Strength of Unsaturated Soils”, in: Fourth International Conference on Unsaturated Soils, Portugal, Lisbon. 19-10-2020 - 21-10-2020. 2570–2592. doi:10.1061/40802(189)219

CrossRef Full Text | Google Scholar

Gens, A. (2010). Soil-environment Interactions in Geotechnical Engineering. Géotechnique 60 (1), 3–74. doi:10.1680/geot.9.P.109

CrossRef Full Text | Google Scholar

Jiang, M., Liu, J., and Shen, Z. (2018). Investigating the Shear Band of Methane Hydrate-Bearing Sediments by FEM with an Elasto-Plastic Constitutive Model. Bull. Eng. Geol. Environ. 77 (3), 1015–1025. doi:10.1007/s10064-017-1109-1

CrossRef Full Text | Google Scholar

Khalili, N., and Khabbaz, M. H. (1998). A Unique Relationship for χ for the Determination of the Shear Strength of Unsaturated Soils. Géotechnique 48 (5), 681–687. doi:10.1680/geot.1998.48.5.681

CrossRef Full Text | Google Scholar

Li, J., Zhao, C., Cai, G., and Guo, Y. (2014a). A Model Considering Solid-Fluid Interactions Stemming from Capillarity and Adsorption Mechanisms in Unsaturated Expansive Clays. Chin. Sci. Bull. 59 (26), 3314–3324. doi:10.1007/s11434-014-0411-6

CrossRef Full Text | Google Scholar

Li, R. J., Liu, J. D., Yan, R., Zheng, W., and Shao, S. J. (2014b). Characteristics of Structural Loess Strength and Preliminary Framework for Joint Strength Formula. Water Sci. and Eng. 7 (3), 319–330. doi:10.3882/j.issn.1674-2370.2014.03.007

CrossRef Full Text | Google Scholar

Li, R., Liu, J., Wang, Z., Luo, J., and Mu, H. (2016). Modifying Algorithm for the Failure Stress According to the Joint Strength Formula. J. Comput. Theor. Nanosci. 13 (2), 1153–1157. doi:10.1166/jctn.2016.5026

CrossRef Full Text | Google Scholar

Liu, E., and Zhang, J. (2013). “Binary Medium Model for Rock Sample,” in Constitutive Modeling of Geomaterials (Berlin, Heidelberg: Springer), 341–347. doi:10.1007/978-3-642-32814-5_47

CrossRef Full Text | Google Scholar

Lu, N. (2016). Generalized Soil Water Retention Equation for Adsorption and Capillarity. J. Geotech. Geoenviron. Eng. 142 (10), 04016051. doi:10.1061/(ASCE)GT.1943-5606.0001524

CrossRef Full Text | Google Scholar

Lu, N., Godt, J. W., and Wu, D. T. (2010). A Closed-form Equation for Effective Stress in Unsaturated Soil. Water Resour. Res. 46 (5), 567–573. doi:10.1029/2009WR008646

CrossRef Full Text | Google Scholar

Margolin, L. G. (1984). A Generalized Griffith Criterion for Crack Propagation. Eng. Fract. Mech. 19 (3), 539–543. doi:10.1016/0013-7944(84)90010-9

CrossRef Full Text | Google Scholar

Mayne, P. W. (1985). Stress Anisotropy Effects on Clay Strength. J. Geotechnical Eng. 111 (3), 356–366. doi:10.1061/(asce)0733-9410(1985)111:3(356)

CrossRef Full Text | Google Scholar

Mitachi, T., and Kitago, S. (1976). Change in Undrained Shear Strength Characteristics of Saturated Remolded Clay Due to Swelling. Soils and Found. 16 (1), 45–58. doi:10.3208/sandf1972.16.45

CrossRef Full Text | Google Scholar

Murrell, S. A. F., and Digby, P. J. (1970). The Theory of Brittle Fracture Initiation under Triaxial Stress Conditions--II. Geophys. J. Int. 19 (5), 499–512. doi:10.1111/j.1365-246X.1970.tb00155.x

CrossRef Full Text | Google Scholar

Sabetamal, H., Salgado, R., Carter, J. P., and Sheng, D. (2021). A Two-Surface Plasticity Model for Clay; Numerical Implementation and Applications to Large Deformation Coupled Problems of Geomechanics. Comput. and Geotechnics 139, 104405. doi:10.1016/j.compgeo.2021.104405

CrossRef Full Text | Google Scholar

Shen, X. Z., Guan, X. J., and Lan, Y. (2007). Calculation of Effective Strength Indexes of Unsaturated Low Liquid Limit Clay. Rock and Soil Mech. 28, 207–210.

Google Scholar

Sheng, D., Zhou, A., and Fredlund, D. G. (2011). Shear Strength Criteria for Unsaturated Soils. Geotech. Geol. Eng. 29 (2), 145–159. doi:10.1007/s10706-009-9276-x

CrossRef Full Text | Google Scholar

Singh, G., and Zimmerman, R. W. (2014). Modification of Griffith-McClintock-Walsh Model for Crack Growth under Compression to Incorporate Stick-Slip along the Crack Faces. Int. J. Rock Mech. and Min. Sci. 72, 311–318. doi:10.1016/j.ijrmms.2014.09.020

CrossRef Full Text | Google Scholar

Singh, V., Stanier, S., Bienen, B., and Randolph, M. F. (2021). Modelling the Behaviour of Sensitive Clays Experiencing Large Deformations Using Non-local Regularisation Techniques. Comput. and Geotechnics 133, 104025. doi:10.1016/j.compgeo.2021.104025

CrossRef Full Text | Google Scholar

Suits, L. D., Sheahan, T. C., and Vesga, L. F. (2009). Direct Tensile-Shear Test (DTS) on Unsaturated Kaolinite Clay. Geotech. Test. J. 32 (5), 101563–102409. doi:10.1520/GTJ101563

CrossRef Full Text | Google Scholar

Sutharsan, T., Muhunthan, B., and Liu, Y. (2017). Development and Implementation of a Constitutive Model for Unsaturated Sands. Int. J. Geomechanics 17 (11), 4017103. doi:10.1061/(ASCE)GM.1943-5622.0001004

CrossRef Full Text | Google Scholar

Tarantino, A., and Tombolato, S. (2005). Coupling of Hydraulic and Mechanical Behaviour in Unsaturated Compacted Clay. Géotechnique 55 (4), 307–317. doi:10.1680/geot.2005.55.4.307

CrossRef Full Text | Google Scholar

Tuller, M., Or, D., and Dudley, L. M. (1999). Adsorption and Capillary Condensation in Porous Media: Liquid Retention and Interfacial Configurations in Angular Pores. Water Resour. Res. 35 (7), 1949–1964. doi:10.1029/1999wr900098

CrossRef Full Text | Google Scholar

van Genuchten, M. T. (1980). A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, B., Sun, X., and Li, G. (2010). Experimental Study on Triaxial Tensile Property of Compacted Clay. J. Hydroelectr. Eng. 29 (6), 172–177. CNKI:SUN:SFXB.0.2010-06-030.

Google Scholar

Zhao, C. G., Liu, Z. Z., Shi, P. X., Li, J., Cai, G. Q., and Wei, C. F. (2016). Average Soil Skeleton Stress for Unsaturated Soils and Discussion on Effective Stress. Int. J. Geomechanics 16 (6), D4015006. doi:10.1061/(asce)gm.1943-5622.0000610

CrossRef Full Text | Google Scholar