Triple-Porosity and Dual-Permeability Productivity Prediction Model of CBM Wells Considering Complex Flow Regimes

The productivity evaluation of CBM wells can yield significant insights into exploring the patterns of CBM production, predicting the effectiveness of the CBM well and reservoir stimulation, optimizing the gas reservoir development program, and developing a reasonable production system, for the purpose of facilitating efficient development of CBM. In particular, to accurately evaluate CBM productivity, we should establish the corresponding mathematical model of fluid flow through porous media and productivity evaluation model based on a clear understanding of CBM occurrence states and mechanisms of its flow through porous media. After considering the effects of slip flow, Knudsen diffusion, surface diffusion, stress sensitivity, and matrix shrinkage on fluid mass transfer, we have put forward a triple-porosity and dual-permeability mathematical model to predict CBM productivity that incorporates matrix gas desorption, complex flow in matrix pores, and gas–water two-phase flow in a cleat system. In combination with reservoir characteristic parameters, a case study of Ma-26 well in the Mabidong block in the south of the Qinshui Basin, we carried out a numerical simulation of the productivity of a fractured CBM well and analyzed the effects (on production performance) of occurrence states, cleat system permeability, complex flow regimes in the matrix, Langmuir pressure, and Langmuir volume on production are provided. The results show that 1) in the initial drainage and production stage of CBM wells, both free gas and adsorbed gas are produced simultaneously, while adsorbed gas dominates the production in later stages; 2) the peak output and cumulative output of CBM wells increase significantly with the rise in cleat system permeability; 3) the increase of Langmuir pressure, volume, and matrix porosity are conducive to the increase of CBM production. The research has considerable reference value for work on mechanisms of CBM flow in porous media and post fracturing productivity evaluation of CBM and also provides a theoretical basis for fieldwork in CBM development.

Introduction

As an unconventional natural gas, CBM has entered the stage of commercial exploitation in China. At present, the prevalent view among both Chinese and foreign researchers is that CBM is mainly adsorbed on the surface of coal matrix blocks. In the process of depressurized production, the gas desorbs from the matrix surface and then diffuses to the cleat-fracture system, before flowing into the wellbore through the cleat-fracture system, in a process that satisfies Darcy’s law regarding fluid flow through porous media. There are three processes of desorption, diffusion, and porous flow in the process of CBM recovery (Dong et al., 2017), and the reservoir porosity and permeability vary continuously with changes in reservoir stress. During the production of CBM wells, an increase in effective stress reduces the permeability of the fracture system, while the gas is desorbed from the matrix surface, and the shrinkage of the matrix increases the permeability of coalbed fractures (Palmer and Mansoori, 1996; Clarkson et al., 2010).The net effect of the two will have an important impact on the production of CBM wells. Researchers around the world have put forward many mathematical models considering the abovementioned mechanisms (Seidle and Huitt, 1995; Moore and Higgs, 2015; Ye et al., 2021). Based on the S&D permeability change model, Meng et al. (2018) established a dynamic prediction model of coal seam permeability considering effective stress, coal matrix shrinkage, and gas slip effect, revealing the dynamic change law of permeability during coalbed methane development. Luo et al. (2021) proposed a fractal permeability model for dual-porosity media with curved natural fractures based on the analysis of pore-fracture structure characteristics of real coal samples. Compared with the traditional dual porous media model with embedded parallel planar fractures, Both the characteristics of pore and fracture curvatures are considered in the model. The results show that the permeability prediction value of this model is 1–2 orders of magnitude lower than that of the traditional model, which indicates that the permeability of coal seam is overestimated in the conventional model. Wei et al. (2022) adopted a strain rate-based permeability model to characterize the effect of matrix expansion on permeability during gas adsorption and evaluate the competing effects of pressure depletion and desorption contraction on permeability changes. Shaw et al. (2019), used an indoor test method to study the effects of stress sensitivity and coal seam matrix shrinkage on the relative permeabilities of gas and water in coalbed fractures. Currently, CBM productivity evaluation mostly involves mathematical models for numerical simulation considering coalbed gas desorption, diffusion, and gas–water two-phase flow in fractures (Wei and Zhang, 2013). In this process, fluid–solid coupling flow mathematical models were developed in consideration of the changes of reservoir parameters, including porosity and permeability (Jiang et al., 2011; Moore et al., 2015; Kong et al., 2017). By introducing the S&D permeability change model, (Yan et al. (2012). established a three-dimensional gas–water two-phase dual-porosity single-permeability mathematical model of coal reservoir considering permeability variation, and a software is developed to study the effects of coal reservoir, adsorption and characteristic parameters on production performance. The research shows that the production of CBM is directly proportional to initial gas content, effective thickness, fracture permeability, and Langmuir pressure. On the basis of comprehensive consideration of the gas desorption, diffusion and flow mechanisms through porous media, a dynamic two-dimensional gas-water two-phase dual-porosity and single-permeability mathematical model was proposed by Zhang et al. (2015), to simulate production performance of fractured CBM wells, and the impacts of relative parameters incorporating Langmuir volume, Langmuir pressure, desorption time, coalbed pressure, cleat permeability and porosity on production of fractured CBM wells are analyzed. With consideration of effective stress, matrix shrinkage, and Klinkenberg effect, Yang (2016) established a permeability model and a three-dimensional dual-medium gas-water two-phase CBM porous flow production model to carry out production simulation research of fractured CBM wells. In addition, He also designed a dynamic simulation program to study self-stimulation effect on CBM production and predict the development performance of fractured CBM wells. Ma et al. (2017) put forward a dual-porosity, single-permeability, fluid-solid fully-coupled production simulation model of CBM wells. The effects of coal seam porosity, permeability, water phase retention and relative permeability change on productivity are investigated in the model. The results indicate that the desorption and matrix shrinkage effect will lead to an increase in permeability near the wellbore and a decrease in permeability at places far away from the wellbore. A large desorption strain and elastic modulus but a small Poisson’s ratio is conducive to increasing the permeability and production of gas wells. Chen et al. (2013) proposed a dual-porosity, dual-permeability, and fluid-solid coupled model to investigate the effects of different reservoir parameters on productivity. The gas transport process of desorbed gas moving into the macroscopic pores of matrix, and then to fractures are took into consideration, and an analysis of the effects of desorption time, fracture permeability, fracture spacing, matrix shrinkage effect, bottom-hole pressure, Langmuir volume, matrix and fracture porosity on production performance are performed in the paper. Wei and Zhang (2010) developed a set of triple-porosity, and dual-permeability flow model of CBM coupled with solid deformation. It is believed that after gas desorption, CBM does not directly enter the fractures, but first moves into the macropores and then transport from these pores into the natural fractures and that there are gas-water two-phase flow in both the matrix pores and fractures. On the basis of the characteristics of gas–water two-phase flow in the early stage of CBM reservoir production Qiao et al. (2018) treated the critical desorption pressure of the reservoir as the supply pressure, and developed the productivity formula suitable for CBM reservoir by combining numerical simulation and mathematical derivation.

For CBM flow through porous media and its production models, previous models created by the research community take only of the adsorbed gas into account, considering that the adsorbed gas in the matrix desorbs directly into the cleat system during CBM production, without considering the free gas in the micropores of the matrix. Xiao et al. (2021) studied the micro-occurrence and mass transfer patterns of CBM by using NMR online detection. The research shows that about 90% of CBM exists in adsorbed manner. Adsorbed gas is the main source of CBM production, followed by free gas. About 70% of the gas produced from dry coal samples comes from adsorbed gas. The contribution of gas in different occurrence states to production varies greatly. In the early stage, it is chiefly the free gas and pore-confined gas that are produced, and in the later stage, it is mainly the adsorbed gas (Xiao et al., 2021). In addition, the model mainly focuses on the effects of fracture system stress sensitivity and matrix shrinkage on fracture permeability and does not account for the flow of gas desorbed from the matrix surface into micropores and the complex flow states of gas in them (Duan et al., 2017; Huang et al., 2018; Liu et al., 2018). In the present study, we take into consideration the gas slip flow, Knudsen diffusion, and surface diffusion in the micropores of the coal seam matrix, the stress sensitivity of the coal seam, and the matrix shrinkage effect, and then develop a triple-porosity, double permeability productivity evaluation mathematical model that incorporates the desorption of the gas from coal seam matrix, the transport of gas in micropores and the gas-water two-phase flow in the fracture system. Then, we proceed to derive the numerical solution equations of the model by the finite difference method and design the corresponding calculation program. In combination with reservoir characteristic parameters, the effects of different reservoir parameters on the production of CBM wells are simulated and analyzed.

Mathematical Model for Productivity Prediction of Fractured CBM Wells

As shown in Figure 1A, coal bed matrix includes matrix bulk and matrix micropores. CBM exists on the surface of matrix grains as adsorbed gas and then enters matrix micropores through desorption and diffusion. The free gas in the matrix micropores flows into the natural cleat system together with the desorbed gas. Under the original reservoir conditions, the coal seam natural cleat system is saturated with water. With the progress of production, due to the pressure difference between the cleat system and matrix, the methane in the matrix will flow into the natural cleat system, resulting in gas-water two-phase flow in the natural cleat system, as shown in Figure 1B.

FIGURE 1

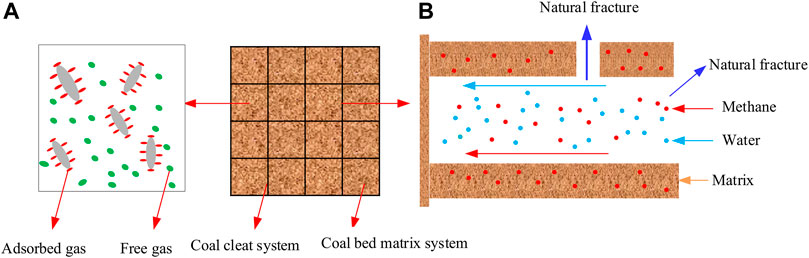
FIGURE 1. (A) Schematic diagram of occurrence state of CBM (B) Schematic diagram of the physical model of gas-water two-phase flow in a natural cleat system.

Mathematical Model of Porous Flow in the Coal Seam Matrix System

The gas flow equation in the matrix should incorporate gas adsorption, desorption, and diffusion on the surface of matrix grains, and gas flow in the macro-pores of the matrix.

1) Gas adsorption and diffusion:

The mechanism of desorption from the micropores of the coal seam matrix is shown that with the decrease of pore pressure in production, the gas desorbs from the surface of the coal seam matrix. This process is described by Langmuir isothermal adsorption equation:

$C\left(P_{\text{gm}}\right)=V_L\frac{P_{\text{gm}}}{P_{\text{gm}}+P_L},(1)$

where C(P_gm) is the amount of gas adsorbed in unit mass coal seam(m³/kg), V_L is the Langmuir volume, (m³/kg), P_gm is the pressure of matrix system (MPa), and P_L is the Langmuir pressure (MPa).

Based on the pseudo steady non-equilibrium adsorption model, the diffusion of gas in micropores is described by Fick’s first law as follows:

$-\frac{\partial C}{\partial t}=\frac{1}{\tau }\left(C-C\left(P_{\text{gm}}\right)\right),(2)$

where t is desorption time (day). The amount of gas desorbed in micropores is finally expressed as:

$q_{\mathrm{gms}}=\rho s\left(1-{\varphi }_t\right)\frac{1}{\tau }\left(C-C\left(P_{\mathrm{gm}}\right)\right),(3)$

where ρ_s is coal density (kg/s), and φ_t is total porosity (dimensionless quantity).

2) Gas flow in matrix pores

The pores of the coal matrix include micropores with adsorbed gas and macropores with the free gas phase. The gas desorbed from the micropores is transported into the macropores that in turn provide the gas source to natural fractures, which is similar to the triple porosity model.

Considering the viscous flow and slippage flow in the macropores of the matrix, the adsorption and desorption of gas in the micropores of the matrix, and the interporosity flow between the matrix and natural fractures, the flow equation in the coal seam matrix is obtained on the basis of the continuous medium theory as follows:

$\frac{\partial }{\partial x}\left(\frac{{\rho }_{\text{g}}{K}_{\text{mapp}}}{{\mu }_{\text{g}}}\frac{\partial P_{\text{m}}}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{{\rho }_{\text{g}}{K}_{\text{mapp}}}{{\mu }_{\text{g}}}\frac{\partial P_{\text{m}}}{\partial y}\right)+q_{\text{gms}}-q_{\text{gmf}}=\frac{\partial \left({\varphi }_{\text{m}}{\rho }_{\text{g}}\right)}{\partial t},(4)$

where q_gmf is the amount of interporosity flow between natural fractures and matrix kg/(m³ · d⁻¹), K_mapp is the apparent permeability (mD) of the matrix; ρ_g is gas density (kg/m³), φ_m is matrix porosity (dimensionless), μ_g is gas viscosity (mPa·s), and t is the time (d).

The coal seam with developed natural fractures can be treated as a dual-porosity medium containing matrix and fractures. When there is a pressure difference between matrix and fractures, the fluid will exchange mass between the two media.

The mass interporosity flow between fractures and matrix per unit grid volume is:

$q_{\text{gmf}}=\frac{\sigma {\rho }_{\text{g}}{K}_{\text{mapp}}\left(P_{\text{m}}-P_{\text{f}}\right)}{{\mu }_{\text{g}}},(5)$

where P_f is the pore pressure in natural fractures (MPa) and σ is the shape factor (1/m²), defined as:

$\sigma =4\left(\frac{1}{L_{\text{x}}^2}+\frac{1}{L_{\text{y}}^2}\right),(6)$

where L_X is the length of the matrix block in the x direction (m); L_y is the length of the matrix block in the y direction (m).

3) Matrix apparent permeability

The diffusion flux of mass transfer in the micropores of coal seam matrix is the sum of surface diffusion flux and free gas diffusion flux, and the gas transport in the micropores includes viscous slip flow and Knudsen diffusion (Wu et al., 2016a; Wu et al., 2016b). Combined with the Darcy equation, the apparent permeability model of the coal seam matrix is proposed as follows:

$K_{map}=-\frac{{\varphi }_m}{\tau }\left[\begin{array}{l}{f}_s\frac{r_{ef}^2}{8}\left(1+{\alpha }_{r}K{n}_r\right)\left(1+\frac{4K{n}_r}{1-bK{n}_r}\right)+f_k\left(\frac{2r_{ef}{\delta }^{D_{\text{f}}-2}}{3}\right){\left(\frac{8ZRT}{\pi M_{\text{g}}}\right)}^{1/2}{\mu }_g{C}_g\\ +\frac{D_{\text{s}}{\mu }_{g}ZRT{\rho }_s{V}_L}{V_{std}p}\frac{p_L}{{\left(p_L+p\right)}^2}\end{array}\right],(7)$

$f_s=\frac{1}{\left(1+K{n}_r\right)},(8)$

$f_{\text{k}}=\frac{1}{\left(1+1/K{n}_r\right)},(9)$

where Kn_r represents the Knudsen number of real gas, a dimensionless quantity, r_ef is the effective pore radius(nm), D_s is the surface diffusion coefficient(m²/s), b is the gas slip constant(dimensionless), M_g is the molecular weight of gas(kg/mol), R is the general gas constant, Pa/mol/K. δ Represents the dimensionless ratio of molecular diameter to local pore diameter, D_f represents the fractal dimension of pore wall (dimensionless); C_g is the gas compression factor(MPa⁻¹), V_std represents the molar volume of gas in standard state, m³/mol, α_r is the rare effect coefficient of the ideal gas, dimensionless, ρ_s is the density of coal (kg/m³), and τ indicates pore tortuosity, a dimensionless quantity.

When both the shrinkage and stress sensitivity of organic matrix is considered (Sheng et al., 2019), the nanopore radius can be expressed as:

$r_{ef}=\left(r_o{\left(p_e/p_o\right)}^{0.5\left(q-s\right)}\right)\left(\sqrt{1+\frac{\left(1-{\varphi }_{\text{m}}\right)}{{\varphi }_{\text{m}}}\frac{{\epsilon }_L{p}_L\left(p_{in}-p\right)}{\left(p_L+p\right)\left(p_{in}+p_L\right)}}\right),(10)$

where P_in is the initial pore pressure(MPa), r_o is the initial pore radius (m), s is the permeability coefficient of coal obtained by fitting experimental data (dimensionless), q is the porosity coefficient of coal obtained by fitting experimental data (dimensionless), P_e is the effective overlying stress (MPa), P_o is atmospheric pressure(MPa), ε_L is Langmuir strain (dimensionless).

Mathematical Model of Flow Through the Natural Cleat System of Coal Seam

Darcy flow is assumed in the natural cleat system, and the mathematical model of gas-water dual-phase two-dimensional plane flow in coal reservoir can be obtained from Darcy’s law and continuity equation. The expression is as follows.

Water-phase flow differential equation:

$\frac{\partial }{\partial x}\left(\frac{K_{fx}{K}_{rw}{\rho }_w}{{\mu }_w}\frac{\partial P_{fw}}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{fy}{K}_{rw}{\rho }_w}{{\mu }_w}\frac{\partial P_{fw}}{\partial y}\right)-q_{w\left(f-F\right)}=\frac{\partial \left({\rho }_w{S}_{fw}{\varphi }_f\right)}{\partial t}.(11)$

Gas flow differential equation:

$\frac{\partial }{\partial x}\left(\frac{K_{fx}{K}_{rg}{\rho }_g}{{\mu }_g}\frac{\partial P_{fg}}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{K_{fy}{K}_{rg}{\rho }_g}{{\mu }_g}\frac{\partial P_{fg}}{\partial y}\right)+q_{gmf}-q_{g\left(f-F\right)}=\frac{\partial \left({\rho }_g{S}_{fg}{\varphi }_f\right)}{\partial t}.(12)$

Auxiliary equations:

$S_{fg}+S_{fw}=1,(13)$

$p_{\mathit{fcgw}}\left(S_w\right)=p_{\mathit{fg}}-p_{\mathit{fw}},(14)$

where K_f is the absolute permeability of cleat (mD), K_frg is the relative permeability of gas phase in cleats (dimensionless quantity), K_frw is the relative permeability of water phase in cleats (dimensionless quantity), μ_w is the viscosity of water phase (mPa·s), ρ_w is water phase density(kg/m³), φ_f is the porosity of cleat system (dimensionless quantity), P_fg is the pressure of gas in cleat system (MPa), P_fw is water phase pressure of cleat system (MPa), S_fw is water saturation in natural fractures(dimensionless quantity), S_fg is gas saturation in natural fractures (dimensionless quantity), q_{w (f-F)} is interporosity gas flow between natural fractures and artificial fractures p_er unit volume of reservoir in unit time (kg/m³ · d⁻¹); q_{g (f-F)} is interporosity water flow between natural fractures and artificial fractures per unit volume of reservoir in unit time (kg/m³ · d⁻¹) and P_fcgw is capillary pressure (MPa).

Mathematical Model of Porous Flow Through the Artificial Fracture System in Coal Seam

After hydraulic fracturing of vertical wells in a coal reservoir, the productivity is actually controlled by discrete large-scale artificial fractures, which are relatively independent systems of flow through porous media. In line with the law of mass conservation, the differential equations of gas–water two-phase flow due to artificial fractures are obtained as follows:

$\frac{\partial }{\partial x}\left(\frac{K_F{K}_{Frg}{\rho }_g}{{\mu }_g}\frac{\partial P_F}{\partial x}\right)+q_{g\left(f-F\right)}-q_{gwell}=\frac{\partial \left({\rho }_g{S}_{Fg}{\varphi }_F\right)}{\partial t},(15)$

$\frac{\partial }{\partial x}\left(\frac{K_F{K}_{Frw}{\rho }_w}{{\mu }_w}\frac{\partial P_F}{\partial x}\right)+q_{w\left(f-F\right)}-q_{wwell}=\frac{\partial \left({\rho }_w{S}_{Fw}{\varphi }_F\right)}{\partial t},(16)$

where K_F is the absolute permeability of artificial fractures (mD), K_Frg is the relative permeability of the gas phase in artificial fractures (dimensionless quantity), K_Frw is the relative permeability of the water phase in artificial fractures (dimensionless quantity), φ_F is the porosity of artificial fracture system (dimensionless), P_F is pore pressure in artificial fracture system (MPa), S_Fw is water saturation in artificial fractures (dimensionless quantity), S_Fg is gas saturation in artificial fractures (dimensionless quantity), q_wwell is water production per unit volume of reservoir in unit time (kg/m³ .d⁻¹), q_gwell is gas production per unit volume of reservoir in unit time (kg/m³ .d⁻¹).

During coalbed methane well production, the conductivity of hydraulic fracture decreases with the increase of effective stress, showing strong stress sensitivity. Based on relevant experimental results, the relationship between permeability and effective stress of artificial fracture system is (Li et al., 2019; Li et al., 2020)

${{\displaystyle \mathit{K}}}_F={{\displaystyle \mathit{K}}}_{F\text{i}}\exp \left(-d_f{\delta }_{me}\right),(17)$

where K_F is the absolute permeability of artificial fractures (mD), K_Fi is the initial fracture permeability (mD), d_f is the stress sensitivity coefficient of the fracture system (MPa⁻¹), and ${\delta }_{me}$ represents the mean effective stress (MPa).

It is assumed that, after the hydraulic fracturing of the coal reservoir and during the production of the gas well, the gas will vertically flow from the natural fractures into the main artificial fractures in the form of linear flow.

By approximating the artificial fractures by the well sources in the natural fracture grid unit, we can obtain the interporosity flow of gas and water between the natural fractures and the artificial fractures:

$q_{l\left(f-F\right)}=\frac{4\cdot h_f\cdot \text{Δ}x}{\text{Δ}y}\frac{{\rho }_l{K}_F{K}_{Frl}\left(P_f-P_F\right)}{{\mu }_l}.(18)$

For a hydraulically fractured vertical well, the well production mainly comes from the vertical fractures on both flanks, and the fluid near the wellbore changes from radial flow to linear flow in artificial fractures.

According to Darcy’s law, the well production can be expressed as

$q_{lwell}=\frac{4{\rho }_l{K}_F{K}_{Frl}{h}_F{W}_F}{{\mu }_l}\frac{P_F-P_{wf}}{\text{Δ}x},(19)$

where subscript l is either w or g, representing water or gas, P_wf is bottom-hole flow pressure (MPa), Δx and Δy represent the size of the grid (where the artificial fracture is located) along with the X and Y directions (m), h_F is hydraulic fracture height (m) and W_F is the width of artificial fracture (m).

Productivity Prediction of the Fractured CBM Well

Historical fitting and Projection of well Ma 26 in the Mabidong block.

For the historical fitting, we selected the actual production data of well Ma 26, a vertical well. Through relevant tests, the reservoir parameters of well Ma 26 in No. 15 coal seam of the Mabidong block are obtained and shown in Table 1. The bottom-hole flow pressure is calculated based on the initial drainage and production data (for both water and gas) of well Ma 26, and the actual bottom-hole flow pressure is fitted by adjusting the artificial fracture parameters (uncertain parameters) in the model. The fitting fracture length and fracture conductivity are 100 m and 2 D˙cm, respectively. Based on the historical fitting method, the projection of gas production of well Ma 26 is obtained and the results are shown in Figure 2. In the stage of production allocation, if the production is assumed at 500 m³/day, the gas well can produce stably for about 600 days, then the cumulative figure of well Ma 26 in five years is predicted to be about 75 × 10⁴ m³.

TABLE 1

TABLE 1. Reservoir parameters of well Ma 26 in No. 15 coal seam of the Mabidong block.

FIGURE 2

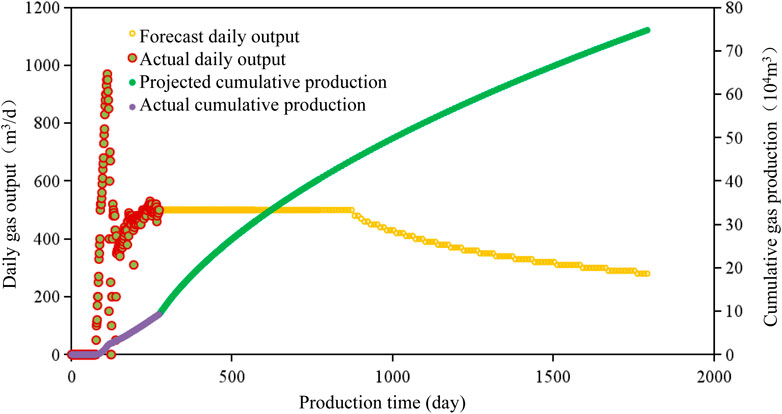
FIGURE 2. Historical fitting and production prediction of well Ma 26 in No. 15 coal seam of the Mabidong block.

Next, a systematic research on the productivity prediction and influencing factors of CBM wells after fracturing are carried out, focusing on the variation of coalbed free gas and adsorbed gas with production time, and the effects of permeability of coal cleat system, adsorption and desorption characterization parameters, matrix porosity and complex flow regimes on production performance. For this purpose, the reservoir parameters of Ma Bidong block in the south of Qinshui Basin are shown in Table 2, the reservoir parameters of the Mabidong block in the south of the Qinshui Basin, which is a typical CBM development block of PetroChina.

TABLE 2

TABLE 2. Main parameters of the coal seam.

Production Change of Free Gas and Adsorbed Gas

Figure 3 shows the production performance curves of adsorbed gas and free gas during the production of CBM wells. Figure 4 shows the variation of free gas and adsorbed gas in the production process. It can be seen from the figures that the output of a CBM well mainly comes from adsorbed gas. At the initial stage of production, it mainly produces free gas and adsorbed gas in pores. With the progress of production, the proportion of free gas output decreases rapidly, while that of adsorbed gas increases rapidly, accounting for more than 80%. This research result is consistent with the occurrence and production law of CBM in the Mabidong block tested by Xiao et al. (2021) using low field NMR online detection.

FIGURE 3

FIGURE 3. Variation of free gas and adsorbed gas with production time.

FIGURE 4

FIGURE 4. Proportion of free gas and adsorbed gas with production time.

Effect of Cleat System Permeability on Production

Figure 5 and Table 3 show the influence of cleat system permeability on CBM production. It can be seen from the figures that when the permeability of the cleat system increases from 10 mD to 20 mD, and then from 20 mD to 30 mD, the cumulative output of CBM wells increases from 2.08 million m³ to 3.07 million m³, and then from 3.07 million m³ to 3.64 million m³, representing a rise of 47.3% and 74% respectively. Meanwhile, peak output increases from 768m³/d to 1493 m³/d and then to 2225 m³/d and the peaking time of daily CBM output is also advanced. Therefore, the permeability of the cleat system has a great influence on the gas production, peak daily output, and peaking time of CBM wells.

FIGURE 5

FIGURE 5. Effect of permeability of coal seam cleat system on production.

TABLE 3

TABLE 3. Effect of the permeability of the coal seam cleat system on CBM production.

Effect of Complex Flow Regimes in the Matrix on Production

In the process of CBM production, a decrease in pore pressure results in an increase in effective stress and a decrease in coal seam permeability. However, the gas desorption causes matrix shrinkage with the progress of production. In addition, the decrease of pore pressure leads to a rise in slip flow, Knudsen diffusion, and surface diffusion in the micropores of the matrix, resulting in an increase in the permeability of the coal seam matrix. The combined effects cause the dynamic change in the permeability of the coal seam matrix in the production process of CBM wells. Figure 6 shows the production curve of CBM wells with and without consideration of complex flow regimes. It can be seen that when complex flow regimes in the matrix are taken into account, both peak output and cumulative output of CBM are higher than those without complex flow regimes. As shown in Table 4, the cumulative output considering only the slippage effect is 6.2% higher than that of without considering any flow regime, and the output difference is 17% according to whether complex flow regimes are considered or not.

FIGURE 6

FIGURE 6. Effects on gas production when whether complex flow regimes are considered or not.

TABLE 4

TABLE 4. Effects on gas production when complex flow regimes are and are not considered.

The above results show that during the production of CBM wells, the matrix shrinkage, diffusion, and slippage effects cause an increase in matrix permeability, offsetting the negative impact of stress sensitivity on permeability, which causes a higher CBM production under dynamic permeability than constant permeability. Pore pressure is the key factor affecting the complex transport mechanisms in the matrix. With the progress of production, the apparent permeability of the matrix increases as the pore pressure declines. The apparent permeability distribution of the coal seam matrix is shown in Figure 7.

FIGURE 7

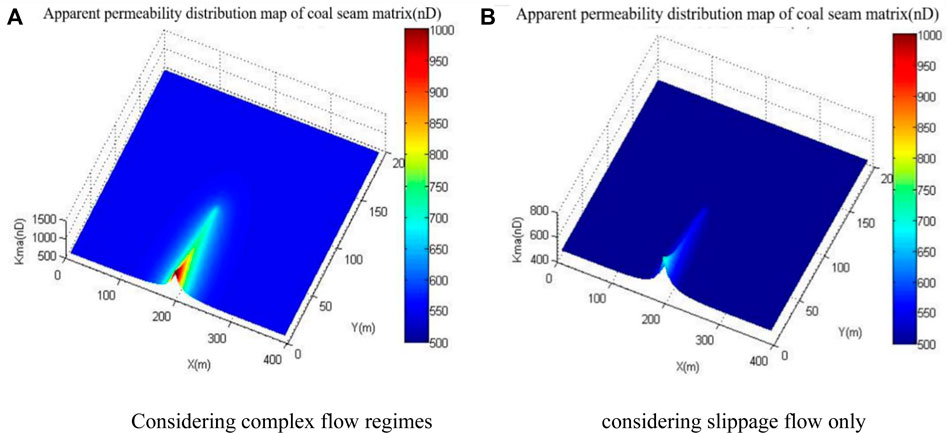
FIGURE 7. Apparent permeability distribution of CBM reservoir matrix. (A) Considering complex flow regimes (B) considering slippage flow only.

Impact of Langmuir Pressure on Production

Figure 8 illustrates the effect of Langmuir pressure on CBM production performance. It can be seen that when the Langmuir pressure rises from 2 MPa to 4 MPa and then to 6MPa, the peak CBM output increases from 1316 m³/d to 1496 m³/d and then to 1561 m³/d. Meanwhile, the cumulative output rises from 2.62 million m³ to 3.07 million m³ and then to 3.19 million m³, representing a gain of 17.2% and 21.8% respectively, as shown in Table 5. The peak output and cumulative output of CBM increase with rises in Langmuir pressure, but the margin of growth slows. This is because a rise in Langmuir pressure causes an increase in the desorption pressure of CBM, which means it is then easier for CBM to desorb, and more adsorbed gas will desorb into free gas.

FIGURE 8

FIGURE 8. Effect of Langmuir pressure on CBM production.

TABLE 5

TABLE 5. Effect of Langmuir pressure on CBM production.

Effect of Langmuir Volume on Production

The influence of Langmuir volume (gas adsorption capacity of coal) on the daily production and cumulative production of gas wells are illustrated in Figure 9. It can be seen that Langmuir volume has an important effect on the daily output and cumulative output of CBM. A rise in (Figure 9). Langmuir volume will bring a significant increase in CBM peak output, daily output, and cumulative output. When the Langmuir volume increases from 10 m³/t to 15 m³/t and then to 20 m³/t, the peak output increases from 1295 m³/d to 1496 m³/d and then to 1661 m³/d, and the cumulative output increases from 241 × 10⁴ m³ to 307 × 10⁴ m³ and then to 363 × 10⁴ m³. As provided in Table 6, the cumulative output increases by 27.3% and 50.7% respectively. The time required for CBM to reach the peak daily output also increases slightly with the rise in Langmuir volume. This is because when the reservoir pressure is constant, the total gas content of the coal reservoir rises with the increase of the Langmuir volume, which is equivalent to increasing the geological reserves of CBM. It can also be seen from the daily gas output in Figure 9 that the Langmuir volume has no effect on the initial daily output. This is because the free gas phase in the matrix micropores is mainly produced in the initial stage of production, while the contribution of adsorbed gas to the output becomes gradually apparent with the passage of production time.

FIGURE 9

FIGURE 9. Influence of Langmuir volume on CBM production.

TABLE 6

TABLE 6. Effect of Langmuir volume on output.

Conclusion

Taking into consideration the comprehensive effects of coalbed matrix shrinkage effect, gas slippage, Knudsen diffusion, surface diffusion, and fracture stress sensitivity on CBM flow, a mathematical model of production performance that incorporates coalbed matrix gas desorption, complex flow regimes in micropore gas, fracture stress sensitivity and gas-water two-phase flow is developed. We selected the reservoir parameters of the Mabidong block in the south of the Qinshui Basin to carry out the numerical simulation and projection of CBM well output and focused on the impact of some key parameters on CBM well production performance. The following conclusions are drawn:

1) The productivity simulation shows that free gas and adsorbed gas are produced simultaneously in the stage of coalbed methane drainage and production, but the free gas is the main gas, and the percentage of free gas production decreases rapidly with production time, while the percentage of adsorbed gas production increases rapidly. By the late production stage,70–80% of daily gas comes from adsorbed gas.

2) The complex flow regimes in the coal seam matrix has some effect on the output of CBM. Considering the complex flow regimes, the output is increased by about 17% compared with output where these regimes are not considered, and the output is increased by 6.2% if only the slip effect is considered. In the later stage of production, the gas transport in the micropores of the coal seam matrix is mainly surface diffusion and Knudsen diffusion.

3) The permeability of the coalbed cleat system has a great impact on CBM production. The peak output and cumulative output of CBM increase significantly with a rise in cleat system permeability. The greater the permeability of the cleat system, the earlier the CBM production reaches the peak output.

4) The cumulative output and peak output of CBM wells are directly proportional to Langmuir volume and pressure. When Langmuir volume increases from 10 m³/t to 20 m³/t, the cumulative production of CBM wells will increase by about 50%. When the Langmuir pressure increases from 2 MPa to 6 MPa, the cumulative output of CBM will increase by about 21.8%.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Drafting of the article: QX and BJ; analysis and interpretation of data: HW, YY, and ZL; numerical modeling: ZL and ZX; and revision of the manuscript: QX, HW, and JL.

Funding

This research was financially supported by the National Science and Technology Major Special Support Program (Grant No. 2017ZX05064); Major Science and Technology Special Support Program of CNPC (Grant No. 2017E-1404); Chongqing Natural Science Foundation (cstc20jcyj-msxmx0216); and Bayu Scholars Program, College-Level Fund of Guilin Institute of Aerospace Technology (Grant No. XJ20KT04). These sources of funding are all gratefully acknowledged.

Conflict of Interest

YY was employed by the company Pilot Test Base for CBM Production of the China National Petroleum Corporation and PetroChina Huabei Oilfield Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, Z., Liu, J., Kabir, A., Wang, J., and Pan, Z. (2013). Impact of Various Parameters on the Production of Coalbed Methane. SPE J. 18 (05), 910–923. doi:10.2118/162722-pa

CrossRef Full Text | Google Scholar

Clarkson, C. R. R., Pan, Z., Palmer, I., and Harpalani, S. (2010). Predicting Sorption-Induced Strain and Permeability Increase with Depletion for Coalbed-Methane Reservoirs. Spe J. 15 (01), 152–159. doi:10.2118/114778-pa

CrossRef Full Text | Google Scholar

Dong, J., Cheng, Y., Jin, K., Zhang, H., Liu, Q., and Jiang, J., (2017). Effects of Diffusion and Suction Negative Pressure on Coalbed Methane Extraction and a New Measure to Increase the Methane Utilization Rate. Fuel 197, 70–81. doi:10.1016/j.fuel.2017.02.006

CrossRef Full Text | Google Scholar

Duan, X., Gao, S., Hu, Z., and Jin, C. (2017). Research Progress in Multi-Scale Percolation Theory in Shale Micro-nano Pores. Special Oil & Gas Reservoirs.

Google Scholar

Huang, S., Wu, Y., Cheng, L., Liu, H., Xue, Y., and Ding, G. (2018 2018). Apparent Permeability Model for Shale Gas Reservoirs Considering Multiple Transport Mechanisms. Geofluids,2186194 1–18. doi:10.1155/2018/2186194

CrossRef Full Text | Google Scholar

Jiang, Y., Yang, X., Xiong, L., and Zheng, Q. (2011). Multi-field Coupling Effect on Coalbed Methane Seepage Characteristics and Numerical Simulation. Journal of Chongqing University 34 (4), 30–35.

Google Scholar

Kong, X., Wang, E., Liu, Q., Li, Z., Li, D., Cao, Z., et al. (2017). Dynamic Permeability and Porosity Evolution of Coal Seam Rich in CBM Based on the Flow-Solid Coupling Theory. J. Nat. Gas Sci. Eng. 40, 61–71. doi:10.1016/j.jngse.2017.02.011

CrossRef Full Text | Google Scholar

Li, Z., Qi, Z., Yan, W., Xiang, Z., Ao, X., Huang, X., et al. (2020). Prediction of Production Performance of Refractured Shale Gas Well Considering Coupled Multiscale Gas Flow and Geomechanics.Geofluids 2020 (4) 1–21 doi:10.1155/2020/9160346

CrossRef Full Text | Google Scholar

Li, Z., Yan, W., Qi, Z., Dong, D., Huang, X., and Yu, R. (2019). Production Performance Model Based on Quadruple-Porosity Medium in Shale Gas Reservoirs Considering Multi-Transport Mechanisms. Energy Sources, Part A Recovery, Util. Environ. Eff., 1–19. doi:10.1080/15567036.2019.1662520

CrossRef Full Text | Google Scholar

Liu, J., Zhang, Y., Hu, Z., Li, Y., and Yang, X. (2018). An Experimental Study on the Mass Transfer Mechanism and the Flow Regime of Gas in Nano-Scale Pores of Shale Gas Reservoirs. Nat. Gas. Ind. 38 (12), 87–95.

Google Scholar

Luo, Y., Xia, B., Li, H., Hu, H., Wu, M., and Ji, K. (2021). Fractal Permeability Model for Dual-Porosity Media Embedded with Natural Tortuous Fractures. Fuel 295, 120610. doi:10.1016/j.fuel.2021.120610

CrossRef Full Text | Google Scholar

Ma, T., Rutqvist, J., Oldenburg, C. M., Liu, W., and Chen, J. (2017). Fully Coupled Two-phase Flow and Poromechanics Modeling of Coalbed Methane Recovery: Impact of Geomechanics on Production Rate. J. Nat. Gas Sci. Eng. 45, 474–486. doi:10.1016/j.jngse.2017.05.024

CrossRef Full Text | Google Scholar

Meng, Y., Wang, J. Y., Li, Z., and Zhang, J. (2018). An Improved Productivity Model in Coal Reservoir and its Application during Coalbed Methane Production. J. Nat. Gas Sci. Eng. 49, 342–351. doi:10.1016/j.jngse.2017.11.030

CrossRef Full Text | Google Scholar

Moore, R., and Higgs, N. (2015). Anisotropic Model for Permeability Change in Coalbed-Methane Wells. SPE Reserv. Eval. Eng. 18 (04), 456–462. doi:10.2118/169592-pa

CrossRef Full Text | Google Scholar

Palmer, I., and Mansoori, J. (1996). “How Permeability Depends on Stress and Pore Pressure in Coalbeds: a New Model,” in SPE Annual Technical Conference and Exhibition: SPE-30010-MS). doi:10.2118/36737-ms

CrossRef Full Text | Google Scholar

Qiao, Y., Peng, X., Zhu, S., and Sun, H. (2018). Coalbed Methane Productivity Model Considering Desorption and Phase Permeability. China Coalbed methane 15 (1), 19–22.

Google Scholar

Seidle, J. R., and Huitt, L. (1995). “Experimental Measurement of Coal Matrix Shrinkage Due to Gas Desorption and Implications for Cleat Permeability Increases,” in International Meeting on Petroleum Engineering: SPE-30010-MS). doi:10.2118/30010-ms

CrossRef Full Text | Google Scholar

Shaw, D., Mostaghimi, P., and Armstrong, R. T. (2019). The Dynamic Behaviour of Coal Relative Permeability Curves. Fuel 253, 293–304. doi:10.1016/j.fuel.2019.04.107

CrossRef Full Text | Google Scholar

Sheng, G., Javadpour, F., and Su, Y. (2019). Dynamic Porosity and Apparent Permeability in Porous Organic Matter of Shale Gas Reservoirs. Fuel 251, 341–351. doi:10.1016/j.fuel.2019.04.044

CrossRef Full Text | Google Scholar

Wei, M., Liu, C., Liu, Y., Liu, J., Elsworth, D., Tivane, O. A., et al. (2022). Long-term Effect of Desorption-Induced Matrix Shrinkage on the Evolution of Coal Permeability during Coalbed Methane Production. J. Petroleum Sci. Eng. 208, 109378. doi:10.1016/j.petrol.2021.109378

CrossRef Full Text | Google Scholar

Wei, Z., and Zhang, D. (2013). A Fully Coupled Multiphase Multicomponent Flow and Geomechanics Model for Enhanced Coalbed-Methane Recovery and CO2 Storage. SPE J. 18 (03), 448–467. doi:10.2118/163078-pa

CrossRef Full Text | Google Scholar

Wei, Z., and Zhang, D. (2010). Coupled Fluid-Flow and Geomechanics for Triple-Porosity/dual-Permeability Modeling of Coalbed Methane Recovery. Int. J. Rock Mech. Min. Sci. 47 (8), 1242–1253. doi:10.1016/j.ijrmms.2010.08.020

CrossRef Full Text | Google Scholar

Wu, K., Chen, Z., Li, X., Guo, C., and Wei, M. (2016a). A Model for Multiple Transport Mechanisms through Nanopores of Shale Gas Reservoirs with Real Gas Effect–Adsorption-Mechanic Coupling. Int. J. Heat Mass Transf. 93, 408–426. doi:10.1016/j.ijheatmasstransfer.2015.10.003

CrossRef Full Text | Google Scholar

Wu, K., Li, X., Guo, C., Wang, C., and Chen, Z. (2016b). A Unified Model for Gas Transfer in Nanopores of Shale-Gas Reservoirs: Coupling Pore Diffusion and Surface Diffusion SPE Journal 21 (1), 1583–1611. doi:10.2118/2014-1921039-pa

CrossRef Full Text | Google Scholar

Xiao, Q., Yang, Y., Jiang, B., Zhao, X., Yu, R., Liu, Z., et al. (2021). Evaluation Method of the Micro-occurrence and Utilization Patterns of Gas via a Novel Method Based on Nuclear Magnetic Resonance. J. Nat. Gas Sci. Eng. 86, 103721. doi:10.1016/j.jngse.2020.103721

CrossRef Full Text | Google Scholar

Yang, Z. (2016). Dynamic Simulation of Self-Modification of Fractured Wells in Coalbed Methane Reservoirmaster's Degree. Southwest Petroleum University.

Google Scholar

Zhang, Y., Shang, F., Sun, X., Li, S., and Sun, R. (2012). Research on Coalbed Methane Numerical Simulation Considering Permeability Changes and Parameter Sensitivity Analysis. Coal Geol. Chi⁃ na 24 (4), 18–23.

Google Scholar

Ye, D., Liu, G., Gao, F., Xu, R., and Yue, F. (2021). A Multi-Field Coupling Model of Gas Flow in Fractured Coal Seam. Adv. Geo-Energy Res. 5 (1), 104–118. doi:10.46690/ager.2021.01.10

CrossRef Full Text | Google Scholar

Zhang, L., Hu, Y., Zhang, P., Zhao, J., Wu, J., and Sun, H. (2015). Influencing Factors Of The Production Performances For The Fractured CBM Wells In QinShui Basin. Petroleum Geology anf Oilfield Development in Daqing 34 (5), 170–174.

Google Scholar