- School of Civil Engineering, Qingdao University of Technology, Qingdao, China
Collapse is one of the most frequent geological disasters in mountain tunnel engineering, posing major safety concerns for underground structures and construction crews. According to a catastrophic collapse in the shallow buried area of the Huangjiakuang tunnel in Weihai City, Shandong Province, the contributing factors, that is, the surrounding rock property, influence of neighboring tunnel construction, and tunnel over-excavation are systematically investigated. The tunnel collapse, breaks through the ground surface, is inverted using MIDAS GTS NX. A tunnel deformation analysis model is created using the quantitative methods of grey relation analysis and entropy weight methods based on crown settlement and lateral wall horizontal contraction during tunnel excavation. The surrounding rock property, the distance between the left and right tunnel faces, and the over-excavation height have a significant effect on tunnel deformation, which are quantitatively interpreted using the tunnel deformation analysis model. This study is valuable for the multi-factor analysis of tunnel deformation and determining the main contributing factors to the collapse quantitatively.
1 Introduction
The continual development of China’s transportation industry has resulted in more flawless infrastructure construction. Tunnels are becoming an increasingly important component of transportation networks, both in terms of number and total length. According to data from the People’s Republic of China’s Ministry of Transport, China added 14,032 new motorway tunnels between 2010 and 2020, totaling more than 169,000 km. Meanwhile, tunnel accidents are becoming more frequent. There were 97 tunnel accidents between 2002 and 2018, with tunnel collapse accounting for 62.89 percent of mountain tunnel geological disasters, and 150 workers or management losing their lives (Wang et al., 2020). The collapse accident prompted the project’s extension, resulting in countless property losses and casualties, making it one of the most damaging disasters in tunnel engineering history.
Consequently, many scholars have studied the failure mechanism of the tunnel surrounding rock in detail, and the main research directions are theoretical analysis, model experiment, and numerical simulation. Among the theoretical methods, the classical pressure theory was the first to be used in the research on the surrounding rock’s stability. Based on the Hoek–Brown failure criterion, Fraldi and Guarracino, (2009); Fraldi and Guarracino (2010) obtained the exact solution of tunnel collapse prediction in the field of plastic theory by using the classical tools of the variational method. Yang and Huang (2011) used the nonlinear Hoek–Brown failure criterion to carry out limit analysis on the collapse of the shallow circular tunnel under support pressure; obtained the collapse mechanism of the shallow circular tunnel. By utilizing the nonlinear Hoek–Brown failure criterion, Zhang et al. (2014) deduced the analytical solution of the collapse block shape curve by replacing the elementary function with the total potential energy in the form of functional and introduced the criterion to judge whether the roof collapse occurred in the deep tunnel. Li and Yang (2017) modified Fraldi and Guarracino (2009); Fraldi and Guarracino (2010) tunnel collapse solution by introducing a simplified method based on the variable separation velocity of the yield surface. Ding et al. (2019) proposed a new three-dimensional collapse mechanism, which shows that the working face stability of a circular tunnel in pure clay soil is related to the cover diameter ratio and provides a scheme for soft soil tunnel collapsing stability. By utilizing the upper bound theorem of limit analysis and the nonlinear Hoek–Brown yield criterion, Lyu and Zeng (2019) obtained the range of potential collapse blocks and the total gravity equations of rectangular and circular tunnels in shallow tunnels under the inclined strata using the variational principle. These theoretical investigations serve as a theoretical foundation for the application of other research approaches.
Concurrently, many articles studied tunnel collapse by applying the modeling experiment (Barla, 2008; Yang et al., 2019; Liu et al., 2020; Hao et al., 2021; Wang et al., 2021; Lan et al., 2022; Li et al., 2022). The simulation experiment allows for a more intuitive understanding of the structure’s failure process and a detailed investigation of its failure mechanism. Li et al. (2014) developed an artificial speckle to monitor the change in the strain field of the specimen, and based on the developed degradation constitutive model, the failure mechanism and deformation law of tunnel surrounding rock are studied. Cui et al. (2021) applied monotonic and cyclic loading tests in the laboratory and determined that the carbonate fault breccia on the sliding layer has a high liquefaction potential. Lei et al. (2015) systematically studied the variation and distribution of structural stress and surrounding the rock stress and the failure mechanism of the lining. Zhang et al. (2016) utilized a variety of methods to measure the convergence of the large deformation, the displacement, and damage mode of the critical points of the sidewall and obtained the change process and regular curve of the displacement of the surrounding rock and the critical issues of the sidewall in the excavation stage. Xiao et al. (2016) conducted a geomechanical model test to investigate the deformation, stress, and potential damage of the Baihetan hydropower tunnel. After the triaxial compression test, Xia et al. (2022) established standard specimens by 3D printing technology and obtained the microscopic failure mechanism of the columnar jointed rock mass. Zhang et al. (2020) quantitatively analyzed the peak strength, effective elastic modulus, and related failure characteristics of fractured marble using the discrete element method and numerical experiments. Liu et al. (2019), Liu et al. (2022) studied the progressive failure process of surrounding rock using field microseismic (MS) monitoring technology and provided a method for predicting collapse. Zhou et al. (2021a) studied the stability of the crown pillar from induced microseismicity and that it is helpful for the characterization of seepage channel development. Sx et al. (2020) established the tunnel model of gully terrain, analyzed the relationship between tunnel construction collapse and longitudinal terrain, and provided theoretical support for constructing shallow tunnels under gully terrain. However, model testing takes a significant amount of time and money. This strategy frequently involves a significant amount of time and effort to achieve the desired results. It is hard to conclude universally applicable conclusions.
Over the past few decades, global technological levels have multiplied. Numerical simulation methods, such as the discrete element method (DEM), finite element method (FEM), and DEM–FEM, are widely used to study the failure of the tunnel surrounding rock. The variation laws of stress and strain for these structures are obtained during the entire process of inversion construction (Jia and Tang, 2008; Kong et al., 2016; Li et al., 2020a). Zhang et al. (2011) calibrated and predicted the excavation damage zone of the tunnel section using continuous fast Lagrangian analysis (FLAC) and particle flow code (PFC). Huang et al. (2013) applied experiments and numerical simulations to study the influence of weak interlayers on the failure mode of the tunnel surrounding rock. Zampieri et al. (2018) used ABAQUS software to conduct quantitative analysis combined with construction conditions, obtained the deformation law of the tunnel without support, and confirmed the causes of motorway tunnel collapse. Li et al. (2019) used finite element software to study the stress, strain, and potential damage area of tunnel construction in hilly terrain with slope stratification. Yan et al. (2021) used FLUNT software to study the collapse accident caused by water inrush in the Qingdao subway and proposed remedial measures using advanced pipe roof grouting reinforcement. These studies help to understand the mechanism of tunnel collapse and improve the stability of tunnel construction. Nonetheless, it is impossible to evaluate the causes of tunnel collapse caused by multiple factors. The influence of different factors on tunnel collapse must be accurately interpreted, and the leading causes of tunnel collapse cannot be established.
Meanwhile, various statistical methods or others have been used (Ma et al., 2020; He and Kusiak, 2017; Li et al., 2021a; Li et al., 2021b). In these tools, statistical methods account for the majority. In disaster prevention and mitigation of geotechnical engineering, grey relation analysis can determine the relation degree between disaster factors according to the similarity of change curves, so this method has been widely used (Deng, 2014). It can quantitatively analyze the development of dynamic processes, complete the comparison of geometric relations of time series in the system, and attain the grey relation degree between the reference sequence and the comparison sequence. Zhang et al. (2019) used this method to evaluate the relationship between soil elastic modulus, stress release rate, and ground settlement during tunnel construction and established an equation for predicting ground settlement. Qiu et al. (2021) modified this theory and determined the relation degree of the water inrush risk level by taking fault zone properties, fault structure characteristics, and other factors as criteria. Based on 24 collapse accidents, Kim et al. (2022) proposed a tunnel collapse assessment model based on a quantitative classification system and significant influencing factors of tunnel collapse risk. These research studies give the impact of different factors on accidents from a statistical perspective but do not consider the weight of various factors on landslides. Alternatively, judging weights by an expert review is not objective enough.
The entropy weight method is an objective weighting method. The information entropy is used to estimate the entropy weight of each index according to the variation degree. Then, the weight of each index is corrected by entropy weight. The entropy weight method overcomes the intense subjectivity of the expert evaluation method and equal distribution method and determines the index weight according to the measured data. A more reasonable and reliable index weight can be attained (Zhou et al., 2021b). Thus, the combination of grey relation analysis and the entropy weight method can more effectively determine influencing factors. Currently, multiple pieces of literature have studied this problem (Zhang and Yang, 2018; Li et al., 2020b; Zheng et al., 2021). There are many studies on tunnel collapse. Nonetheless, in many studies, some scholars attribute the cause of tunnel collapse to a particular factor. Alternatively, many factors have been considered but there are fewer related studies (Wang, 2021). The method to determine the leading cause of the collapse was not introduced in the multi-factor accident. The research system to analyze the failure under multi-factor was not established. Therefore, it is essential to establish an effective collapse analysis method for engineering accident investigation.
This article studied the collapse accident which occurred at a large section of the mountain neighborhood tunnel’s shallow buried area in Weihai City, Shandong Province. The properties of the surrounding rock, the distance between the left and right tunnel faces, and the over-excavation height are analyzed in detail, and the collapse accident was inversed with the MIDAS GTS NX. On this basis, the three factors are analyzed by controlling variables. Based on the crown deformation and horizontal convergence, the grey relation analysis–entropy weight method is used to calculate the relation degree. The main factors influencing tunnel deformation among the three factors are determined. This research proposes a new analysis approach for the investigation of multi-factor collapse events by performing a quantitative analysis of numerous components impacting tunnel deformation. This study is valuable for the multi-factor analysis of tunnel deformation and for determining the main contributing factors to the collapse quantitatively.
2 Brief Description of the Project and Tunnel Collapse
2.1 Project Overview
As illustrated in Figure 1A, the engineering location is the Huangjiakuang tunnels in Weihai City, Shandong Province, China. The tunnels are located southwest of the village of Huangjiakuang. These tunnels are twin-lined six-lane roadways with a design speed of 60 km per hour, divided into left and right tunnels. The left line tunnel has an import and export mileage of ZK5 + 540 and ZK6 + 000, whereas the right line tunnel has an import and export mileage of YK5 + 533.5 and YK6 + 113.5. The tunnels span 580 m in length and reach a maximum depth of 47 m. The project is a large section neighborhood tunnel in the mountain region, measuring 134.89 m2 in the section area. The tunnels have a maximum width of 15.5 m, while the middle rock pillar has a width of 10.09 m. The whole tunnels’ terrain is steep in the north and flat in the south, with a slope of 20°–45°. YK5 + 540 to YK6 + 120 is depicted in Figure 1B. According to the survey study, gneiss covers the tunnels in large part. The buried depth varies significantly, from 4 to 45 m. The foundation soil of the Huangjiakuang tunnels is separated into three strata from top to bottom: plain fill soil, strongly weathered granitic gneiss, and weakly weathered granitic gneiss. China divides the strength of the surrounding rock of the highway tunnel into six grades according to the rock mass basic quality (BQ). It is a comprehensive indicator which includes three aspects. The surrounding rock classification basis is obtained according to Eq. 1. The strength of the surrounding rock decreases from Ⅰ to Ⅵ.
where
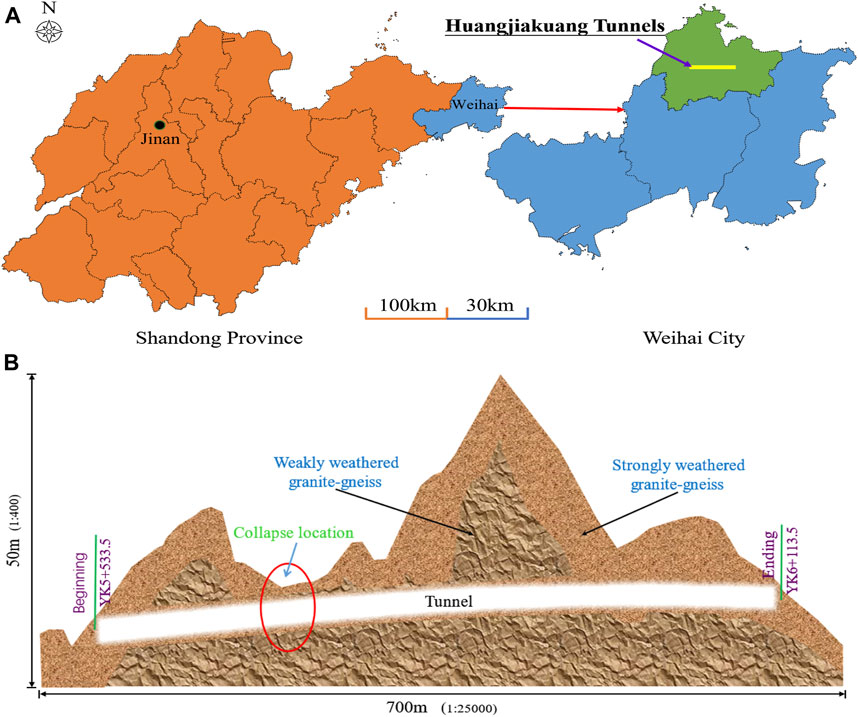
FIGURE 1. Specific information of Huangjiakuang tunnels. (A) Geographic location of Huangjiakuang tunnels in Weihai City, Shandong Province, China. (B) Collapse location longitudinal section of the Huangjiakuang right tunnel.
According to the geological description, the tunnel ground is primarily composed of three types of soil. At the shallow buried section of the tunnel, the rock mass basic quality is 207 and its uniaxial compression strength is 20 MPa. On the basis of the classification standard of the surrounding rock in China, this kind of geology is judged as grade Ⅴ surrounding rock.
2.2 Tunnel Collapse
On 2 October 2018, the right tunnel to the area denoted in Figure 1B was constructed. The working face (YK5 + 680) was abnormal. Soil and stones began to fall above the left area of the tunnel. Many soils and fragmentary rocks started to fall, ultimately becoming a collapse accident directly to the surface. A ground settlement area of 7 m long and 5 m in depth was formed after the collapse, and both tunnels were compelled to halt. Figure 2 shows the photograph of the collapsed roof fall wreck. It can be seen from the pictures that the soil in the collapse area is predominantly soil. After investigation, the engineering data show that the collapsed roof area is grade V surrounding rock. The tunnel construction method is the bench-cut method, and the cyclic footage is 4 m. Only the upper step which is 16 m in length was carried out. The soil above the tunnel face collapsed after constructing the YK5 + 678 area. So, the size of the excavation section expanded. The highest collapsed soil was 1.8 m above the tunnel vault contour.
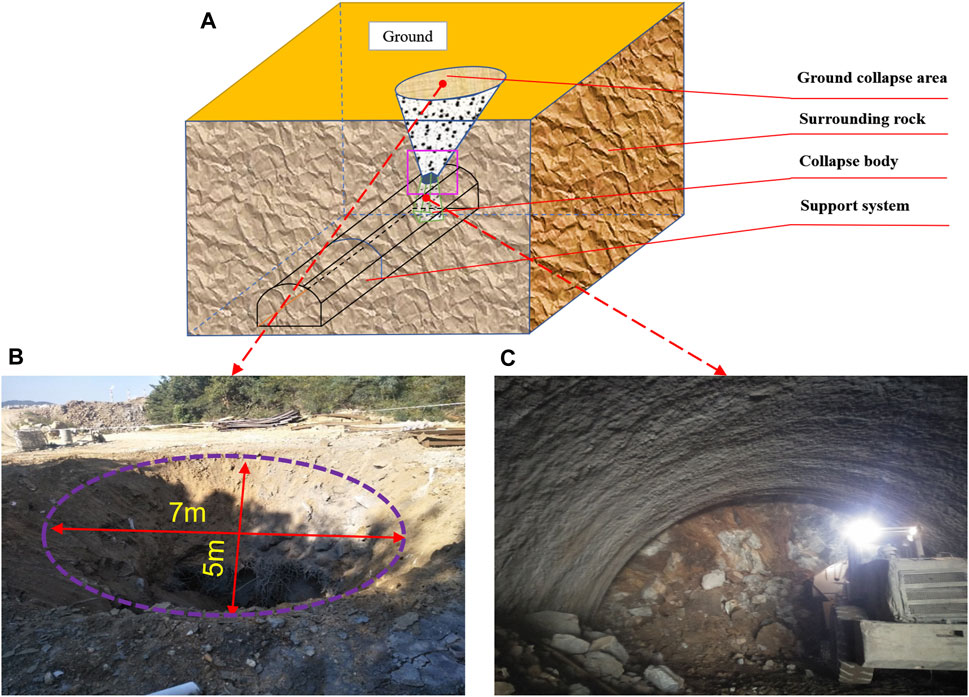
FIGURE 2. Collapse of Huangjiakuang tunnels: (A) Schematic diagram of tunnel-shaped collapse at the Huangjiakuang right tunnel (Li et al., 2020b), (B) Influence range of collapse on the surface reaches 27.5 m2 and (C) after the collapse, the construction machinery is dealing with the soil falling inside the tunnel.
3 Analysis of the Collapse Mechanism
3.1 Analysis of the Disaster Causes
After the collapse accident, the tunnel construction was compelled to stop, resulting in delays in the construction period and economic and property losses. The construction conditions and the mechanical parameters of the soil at the collapse position are collected. The collapse occurred on October 2nd, and there was no substantial rainfall at the Huangjiakuang tunnels before the disaster. In September, the rainfall at this site is 36.0 mm, while the annual rainfall is 596.8 mm. It only makes up a small fraction of the total. According to the survey report, the shallow buried section has minimal groundwater resources. The water outlet formed during the excavation process is primarily linear and drip seepage. As a result, the reasons for hydrological and climatic conditions are not thoroughly investigated. It primarily investigates the nature of the surrounding rock, excavation events, and structural aspects of tunnel building.
3.1.1 Surrounding Rock Characteristics
The collapse location of tunnels pertains to the shallow buried section (YK5 + 648.5–703.5). The surrounding rock of grade V covers this part of the right tunnel. The geological exploration report shows that tunnels are mainly composed of broken soil and gravel containing sand and gravel. Tunnel collapse (YK5 + 680) is strongly weathered by granitic gneiss, rock fragmentation, and joint development. The rock mass basic quality (BQ) is 207 and its uniaxial compression strength (Rc) is 20 MPa. The tunnel face condition is shown in Figure 3A.
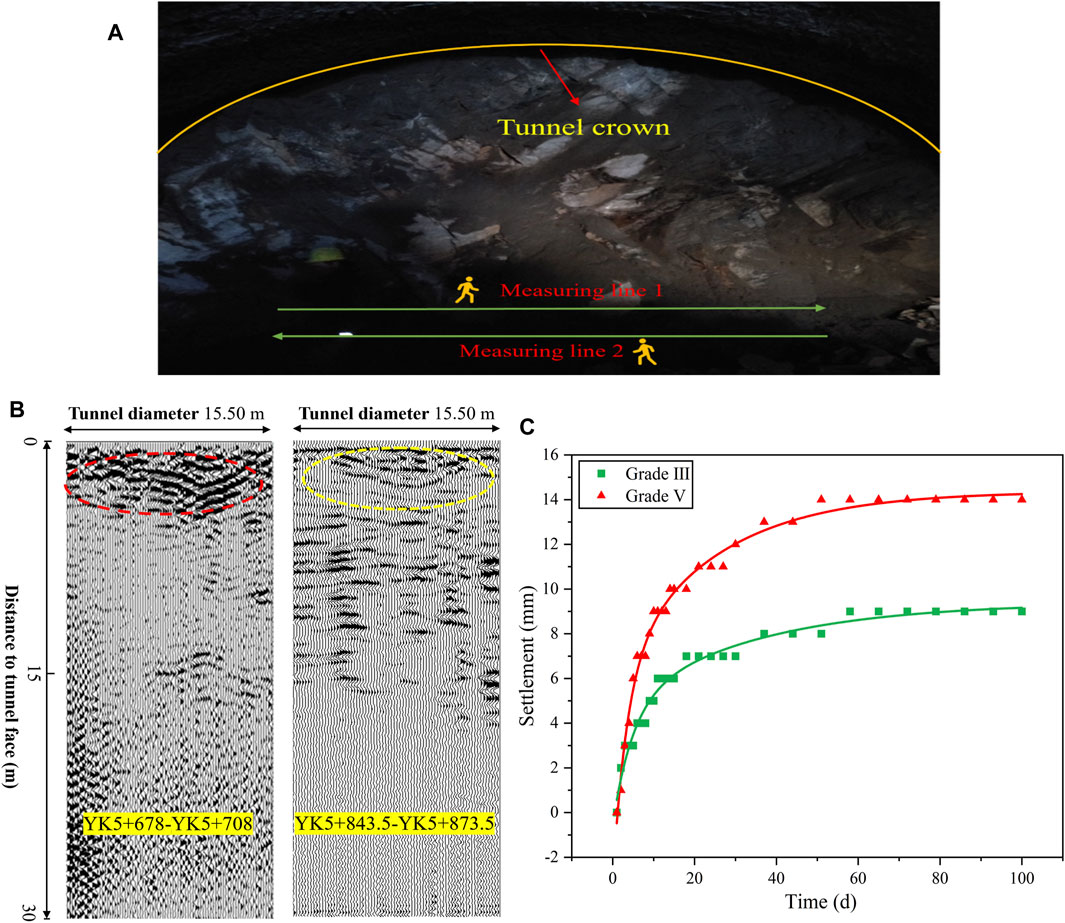
FIGURE 3. Monitoring data of ground penetrating radar and tunnel crown settlement. (A) Tunnel face and monitoring program of ground penetrating radar at YK5+678. (B) Radar reflection images of the tunnel faces and (C) the tunnel crown settlement of grade Ⅲ and Ⅴ surrounding rocks for 100 days.
Ground-penetrating radar (GPR) is one of the most popular electromagnetic methods in tunnel ahead prospecting, which can propose information about the subsurface with high resolution (Li et al., 2017). Before the collapse, the ground-penetrating radar was used to detect the excavation face. The use frequency of ground penetrating radar is 100 MHz, and the maximum depth that can be identified is 30 m. Two lines are laid on the working face, line 1 from left to right and line 2 from right to left. Radar image processing is shown in Figure 3B. YK5 + 678–YK5 + 708 regional geological radar image is shown as Figure 3B. The geological report shows this place is grade V surrounding rock. The starting point of the radar image is 2 m before the collapse position, and the ending point is 28 m after the accident location. The collapsed position is in the red area and is shown in Figure 3B. It can be seen that the pulse signal in the red region is predominantly medium–low frequency from Figure 3B. The waveform is disordered and discontinuous, and the phase axis is cracked. The amplitude has multiple oscillations, and the pulse frequency is different and irregular. The reflection pulse of the broken rock is distributed in a band, and the reflection intensity of medium- and low-frequency signals is high. The geological radar image of YK5 + 843.5–YK5 + 873.5 area is also illustrated in Figure 3B. The geological report demonstrates that grade III surrounding rock covered this area. Figure 3B shows that the blue area 2 m in front of the radar is grade III surrounding rock. The reflected pulse signal in this area is predominantly medium and high frequency, which changes slightly. The in-phase axis is steady and uniform, and the signal amplitude is small. The properties of the surrounding rock are better than those shown in Figure 3B.
To see more intuitively the influence of different surrounding rocks on tunnel deformation, the crown settlement monitoring data of grade III (BQ = 371) and V (BQ = 207) surrounding rocks are collected, as shown in Figure 3C. The tunnel crown settlement can be divided into three stages according to the settlement curve (Gao et al., 2018). In the first stage, the crown settlement of the grade V surrounding rock is faster than that of the grade III surrounding rock. The settlement of the grade V surrounding rock rises swiftly to 10 mm, and the grade III surrounding rock is just 6 mm. The second stage takes 40 days for the third-level surrounding rock to enter a stable state and 60 days for the grade Ⅴ surrounding rock to reach a steady condition. Currently, the settlements are 13 and 7 mm, respectively. In the third stage, the crown settlement of the three-level surrounding rock and five-level surrounding rock attained a stable state. Currently, the settlement of grade V surrounding rock was steady at 8 mm, and that for grade V surrounding rock was 14 mm. The maximum settlement and times to reach a stable state for grade V surrounding rock are greater than those of the grade III.
3.1.2 Excavation Disturbance of the Left Tunnel
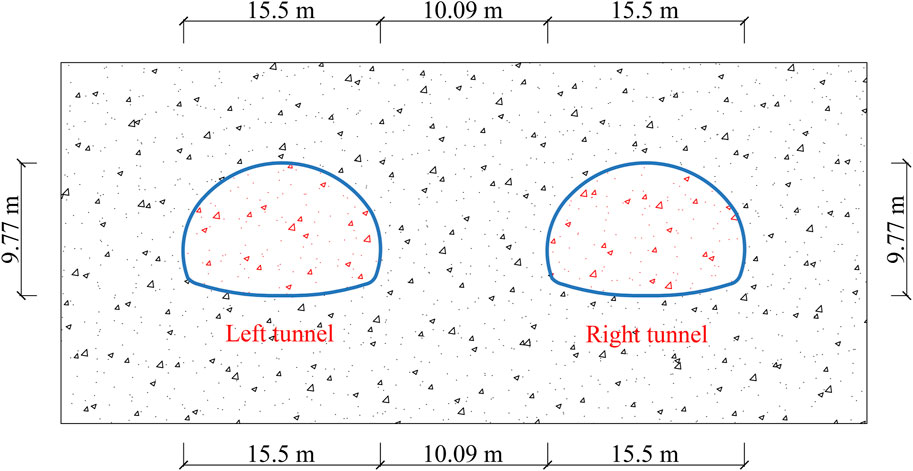
The tunnels’ section area is 134.89 m2, and the distance between the left and right tunnels is 10.09 m. The clear distance between the left and right tunnel is less than the tunnel’s diameter. The distance between the two tunnels is shown in Figure 4. The construction process involves excavating the left tunnel first; then, the right tunnel is excavated. The two tunnels are constructed using the bench-cut method. The original equilibrium state in the soil is lost as a result of excavation disturbance. The stress in the rock mass is redistributed until a new equilibrium is found. The excavation disturbance has induced a change in the size, direction, and character of the original stress in the rock. The tunnel is excavated by blasting, which causes damage accumulation to the shared rock in the neighborhood tunnel (Cao et al., 2020). Therefore, the disturbance to the right tunnel after constructing the other tunnel is considered in this study. The underground cavern excavation will lead to the redistribution of soil stress in the range of 6R0. The R0 is the diameter of a single circular tunnel excavation. (Han et al., 2020). In ‘Technical Guidelines for Construction of Highway Tunnels’ (U.S. Department of Transportation Federal Highway Administration, 2009), the mutual influence degree of two neighborhood tunnels is divided, as summarized in Table 1.
In the Table, the parameter b is the width of the excavation section of a single tunnel. Under the condition of grade V surrounding rock, the thickness of middle rock pillar ≤0.75 b is seriously affected. The rock width in the Huangjiakuang tunnel is 10.09 m, and the tunnel span is 15.5 m. The tunnel’s height is 9.77 m. So, the tunnels belong to the category of serious impact. The location of the right tunnel is in the excavation influence area of the left tunnel. Considering that the tunnel section is a non-circular tunnel, the equivalent radius of the tunnel section is calculated using the equivalent method (Peng et al., 2010). The equation of the equivalent method is.
where
where
where
Only the variation of the maximum principal stress is discussed here. Thus, the influence area of the right tunnel is 1.10–1.20
3.1.3 Tunnel Over-Excavation
The tunnel collapse occurs in the shallow buried area with the surrounding rocks of grade V. The upper and lower steps method is used for excavation in these areas. After excavation, the soil is hauled out of the tunnel by machinery, and then the anchor rod and shotcrete are set up. The primary support is C25 concrete. The C25 concrete is defined as concrete with a compressive strength of at least 25 MPa after 28 days of curing in laboratory settings. The thickness of the primary support is 30 mm. Figure 5A shows the construction diagram of the tunnel bench-cut method, and only the upper bench excavation is carried out during the collapse.

FIGURE 5. Construction scheme at the collapse area and over-excavation event. (A) Schematic diagram of the bench-cut method, and the pictures of construction site inside the tunnel. (B) Schematic diagram of over-excavation area inside the tunnel.
The right line of the tunnel was constructed to the YK5 + 677 area after the workers carried out the blasting operation, the rock fell over the right side of the tunnel, and the maximum rock particle size was 0.5 m, forming an over-excavation accident. The over-excavation position is located at the top right of the tunnel contour line vault, and the maximum height of over-excavation is about 1.8 m from the tunnel contour line. After over-excavation, the cross-section area of the tunnel expanded, and the cavity was formed above the right of the tunnel. The over-excavation area diagram is shown in Figure 5B. The over-excavation will change the stresses around the tunnel face and affect the deformation of the ground surface (Xu et al., 2021).
The aforementioned three factors are obtained from the investigation of construction conditions and the search of relevant geological survey reports. Whether it is related to the collapse requires further verification. Consequently, the FEM is used to verify our conjecture.
3.2 Inversion of the Tunnel Collapse
In this study, based on the FEM, the construction simulation of tunnel excavation is used to explain the deformation of the tunnels. Based on Figures 2, 4, a three-dimensional finite element simulation model of the tunnels in the collapse section is established, as shown in Figure 6. The tunnel size in the model is identified as the actual tunnel measurement. The model’s dimensions in X and Y directions are 100 and 210 m, respectively, and the distance from the roof to the bottom is 50 m. The width of the tunnel is 15.5 m, and the height is 9.77 m. The clear distance between the two tunnels is 10.09 m. In the model, the left and right boundary constraints X and Y direction displacement, the bottom constraints X-, Y-, and Z-direction displacement. The building approach of tunnels is the bench-cut method, divided into two steps. First, 16 m long upper steps were excavated, and the primary support construction was implemented next. The surrounding rock adopts a three-dimensional solid element, and the effect of steel arch and steel mesh is converted into primary support using the equivalent stiffness method. The primary support adopts a two-dimensional plate element with a 0.30 m thickness. In actual tunnel construction, the secondary lining support was not carried out when the right tunnel collapsed. So, the secondary lining support was not considered in the tunnel simulation process, just the primary support was analyzed. The specific parameters in the model are summarized in Table 2.
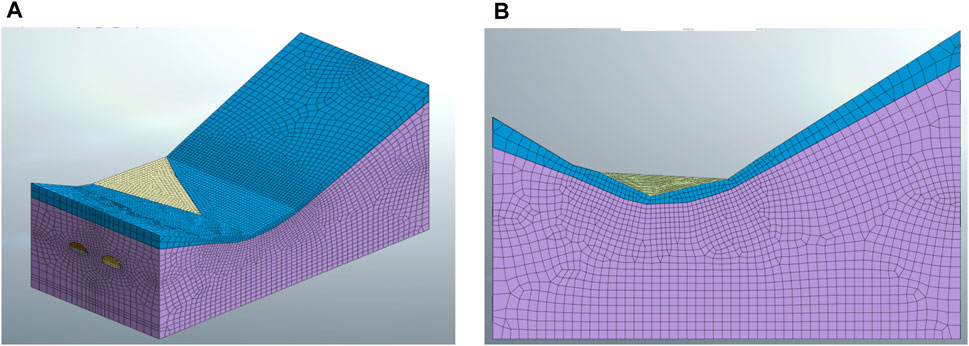
FIGURE 6. Finite element model of Huangjiakuang tunnels: (A) Side view of the model and (B) the right view of the model.
The Z-direction displacement diagrams of the right tunnel are extracted before and after the collapse, which are shown in Figure 7. At the collapse position, the displacement diagram is different before and after the failure. In Figure 7A, the largest displacement occurs at the tunnel portal, with a maximum displacement of 11mm; in Figure 7B, it occurs at the collapse location, with a maximum displacement of 117 mm. As shown in Figure 7, the settlement at the arch crown of the right tunnel far exceeds the specified value, so it can be determined that the collapse accident has occurred.
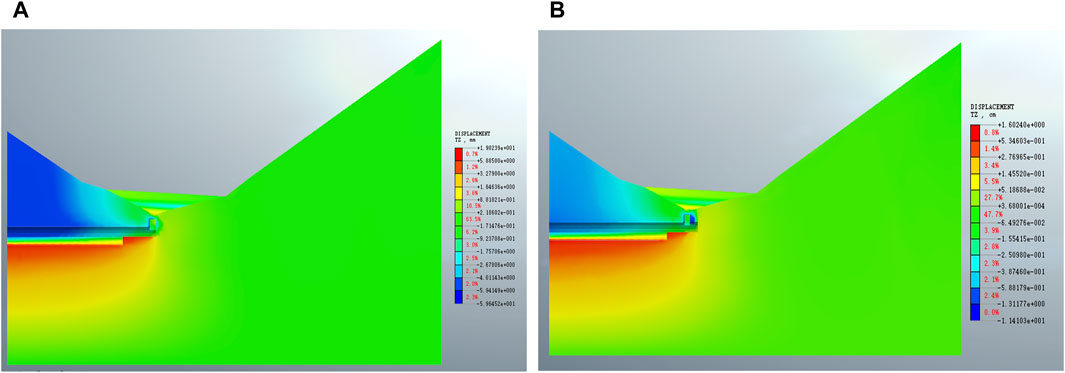
FIGURE 7. Progressive process of collapse accident. (A) Displacement field after excavating YK5+678 and (B) the displacement field after excavating YK5+680.
Considering the major principal stress variation calculated in Equation 3 earlier, the major principal stress from the finite element simulation model is extracted after excavating the left tunnel. All results are shown in Figure 8A. The collapsed section of the tunnel is at the foot of the slope connecting two peaks. There is a topographic feature of left high and right low in the direction of the tunnel section, so the overall curve is left high and right low. The purple area is the right tunnel place. The maximum major principal stress in the right tunnel area is 0.33MPa, and the minimum is 0.25 MPa when the left tunnel is unexcavated. After the excavation of the left tunnel, the major principal stress of the right tunnel increased. The major principal stress of the right tunnel increases by 0.06 MPa which accounts for 20% of field stress, and the stress increase in the right edge was small, which was 0.023 MPa which accounts for 10% of the field stress. The calculation results are 1.1–1.2
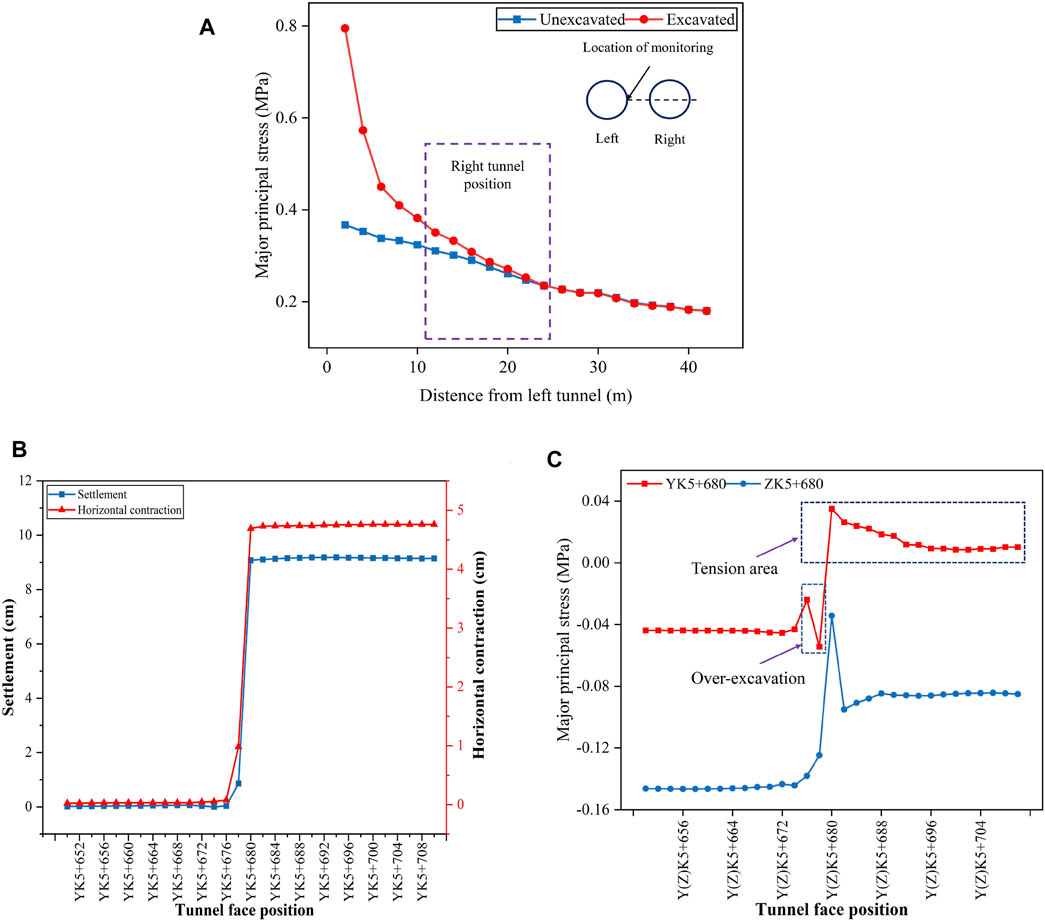
FIGURE 8. Results of numerical simulation. (A) Differences of major principal stress between un-excavation and excavation. (B) Tunnel crown settlement and horizontal contraction at YK5+680. (C) Change of major principal stress at YK5+680 and ZK5+680.
The crown settlement and tunnel horizontal convergence results are extracted from YK5 + 680 monitoring points, as shown in Figure 8B. When the working face is excavated before YK5 + 676, the deformation at the collapse position is slight. The small-scale deformation occurs in the monitoring point area when the working face is excavated to YK5 + 678. When the working face is excavated to YK5 + 680, a large settlement occurs, and the settlement abruptly changes by 8.2 cm, far surpassing the required 3 cm. At the same time, the tunnel diameter convergence has tremendous changes, which also exceeds the prescribed limit value.
Most existing displacement monitoring is based on single-dimensional displacement parameters as instability criteria. Still, the apparent prediction parameters and criterion system of one-dimensional displacement cannot fully and accurately describe the mechanism and law of evolution of deformation in the process of tunnel excavation. Therefore, the major principal stress variation curve of the left and right tunnels extracted from the landslide location mileage is shown in Figure 8C. With the excavation of the tunnel, the major principal stress increases. When the right tunnel is excavated to YK5 + 678, the construction of workers leads to over-excavation. The curve in the diagram also shows that the stress has a downward mutation, and the stress release occurs (Xu et al., 2021). The stress is changed from −0.02 MPa to -0.06 MPa. When excavated to YK5 + 680, the crown settlement and horizontal convergence caused mutation, and the mutation value is 9 cm and 8 cm. Also, the major principal stress changed from −0.06 to 0.04 MPa, and the tunnel surrounding rock stress changed from compression to tension. When the displacement increases from 2 to 11 mm, the surrounding rock of the tunnel produces large deformation. The left tunnel is still under pressure compared with the YK5 + 680 position. After excavation, the maximum principal stress decrease of ZK5 + 680 is from −0.04 to 0.1 Mpa and reaches a stable state after the excavation of ZK5 + 688.
In the essence, the whole process of collapse is caused by the coupling of three factors. When the tunnel is constructed to the collapse area, the soil property of the collapse location is poor. The previous excavation of the left tunnel impacts the collapse area, making the right tunnel’s stress increase. After the workers’ construction of over-excavation, the collapse accident is induced. The accident is directly connected to the ground surface, resulting in surface collapse. Nevertheless, the influence of the three factors on the collapse has not been confirmed, and further analysis is required to find out the main reason for the collapse accident.
4 Analysis of the Relation Degree of Tunnel Deformation
4.1 Analytical Method
The experimental scheme was designed with the distance of two tunnel faces, the surrounding rock strength of the collapse section, and different over-excavation heights. To gain a better understanding of the critical factors influencing the deformation of the surrounding rock, the impact of three parameters on the collapse accident is assessed. This section will quantify the variables that contributed to the collapse accident. In this study, the influence of overburden thickness is excluded. The main factors affecting the stability of the surrounding rock are determined by combining the grey relation analysis and the entropy weight method. Considering the different judgment bases of surrounding rock properties, this study only changes the elastic modulus of soil according to the requirements in the specification. Grey relation analysis has low requirements for working conditions, so nine schemes are set up, and the test scheme is shown in Table 3. The key factors affecting the stability of tunnel surrounding rock are determined by the tunnel crown settlement and horizontal convergence as grey relation analysis evaluation indexes.
4.1.1 Grey Relation Analysis Method
The grey relation analysis method is applied to determine the effect of multiple factors to the collapse. By determining the geometric shape similarity between the reference data column and several comparison data columns, the tightness of their connection is judged. Also, the relation degree between their comparison sequence and the reference sequence is calculated. Then, the results are sorted according to size. The specific steps of the method are as follows.
First, the grey relation analysis method is used to calculate the relation coefficient. Classify the sorted data and divide the corresponding matrix. The reference matrix is shown in Eq. 4:
where
Then, list the data of the reference matrix. The comparison matrix is shown in Eq. 5:
where
Because the comparison data matrix and the reference data matrix units are different, to determine the relation coefficient, the relation coefficient between the data is usually used to unify the data, so that each sequence is dimensionless. The normalization method is as follows:
Therefore, considering the influence of the comparison sequence on
where
As indicated in Equation 8, the relation coefficients of each parameter are averaged to yield the relation degree of each parameter.
4.1.2 Entropy Weight Method
The entropy weighting method is a form of objective weighting. It calculates the index’s entropy weight based on the change in each index. After that, the index is corrected using the entropy weight method. In comparison to the original grey relation analysis, the entropy weight approach can confirm the weighting effect of many indices and improve the relation coefficient’s accuracy. As a result, the matrix is further processed using the entropy weight method.
Since the measuring units for various indicators are not standardized, the data must first be normalized. That is, transform the index’s absolute value to its relative value. The standardizing equation is as follows:
where the
Then, using the standardized data, calculate the index’s entropy. The Entropy value is critical for the subsequent weight calculation.
where
Next, the weight of each parameter is determined using the entropy calculated previously.
where
Finally, the grey relation analysis and entropy methods are combined to yield the final modified grey relation coefficient matrix.
where
The main factors affecting the tunnel deformation are calculated by comparing the grey relation degrees of over-excavation height, surrounding rock property, and the distance between the left and right tunnel faces.
4.2 Result Analysis
Taking the over-excavation height, the distance of the left and right tunnel faces, and the elastic modulus of the surrounding rock as control variables, the tunnel constructions are simulated using the finite element method. Extract the tunnel crown settlement and convergence results, and the roof deformation is positive upward, negative downward, horizontal convergence using the absolute value judgment. All the results of tunnel deformation under different variables are shown in Figure 9.
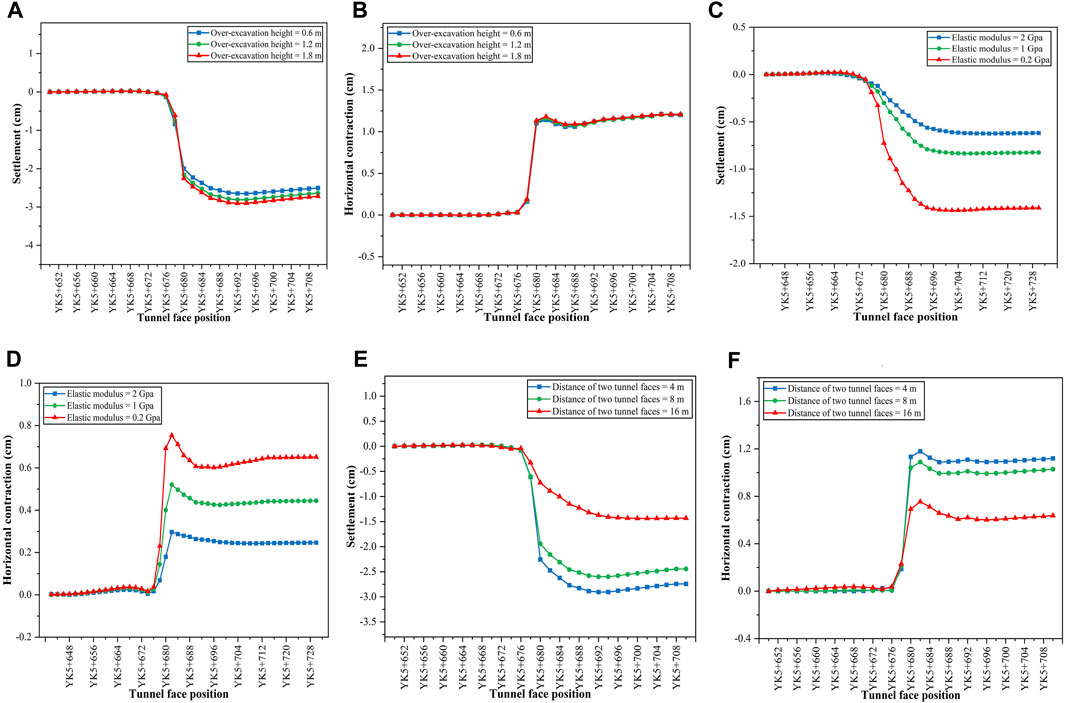
FIGURE 9. Tunnel deformation at YK5+680 under different variables. (A) Crown settlement for three over-excavation heights and (B) Horizontal contraction at YK5+680 for three over-excavation heights. (C) Crown settlement for three surrounding rock strength and (D) horizontal contraction for three surrounding rock strength. (E) Crown settlement for three distances between two tunnel faces and (F) horizontal contraction for three distances between two tunnel faces.
Taking the surrounding rock strength as the control variable, the specific curve is shown in Figures 9A,B. When the tunnel face is progressively advanced, the crown settlement and convergence at YK5 + 680 is increasing, ultimately attaining a stable state in these cases. The maximum crown settlement increases from 0 to 3.0 cm, and the horizontal convergence rises from 0 to 1.25 cm. Before the tunnel is excavated to YK5 + 676, the deformation at YK5 + 680 is almost 0 cm. The crown settlement increases by 2.5 cm after excavating the soils of YK5+680. The horizontal convergence occurs the most significant deformation after YK5 + 680 excavation. The deformation amplitude reaches 1.5 cm in three cases. It can be seen that when the over-excavation height is 1.8 m, the crown settlement and convergence reach the maximum, and the maximum obtained is 3.0 and 1.2 cm. The deformation gap is not evident under the three conditions. The settlement of 1.8 m over-excavation height increases by 0.4 cm, and the convergence increases by 0.2 cm compared with 0.6 m. Therefore, the over-excavation height affects the tunnel deformation, but the tunnel deformation is not apparent with the rise of over-excavation height.
Taking the surrounding rock as the control variable, the specific curve is shown in Figures 9C,D. The settlement of the tunnel crown under different conditions is from 0.6 to 1.5 cm, and the convergence is from 0.3 to 0.75 cm. The deformation of the surrounding rock under 0.2 GPa strength is the greatest when compared to 2 and 1 GPa surrounding rock. The crown settlement reaches 1.5 cm, and the tunnel convergence is 0.75 cm when the tunnel face is excavated to YK5 + 680. When the elastic modulus of the surrounding rock changes from 2 to 1 GPa, the maximum settlement of the roof increases by 0.23 cm, from 0.6 to 0.83 cm. When the elastic modulus of the surrounding rock changed to 0.2 GPa, tunnel deformation increased by 0.67 cm, from 0.83 to 1.5 cm. Then, the tunnel deformation is slowly deformed under the excavation disturbance of the tunnel face. The tunnel deformation is more sensitive to different surrounding rock properties than different over-excavation heights.
While the distance between the left and right tunnel faces are taken as control variables, the tunnel deformation is shown in Figures 9E,F. In the three cases, the maximum deformation of the tunnel crown is 3.0 cm, the convergence is 1. cm, the minimum is 1.48 cm, and the convergence is 0.6 cm. When the distance between the left and right tunnel faces changes from 4–8 m, the tunnel deformation decreases, the crown settlement decreases from 3.0 to 2.5 cm, and the maximum convergence decreases from 1.2 to 1.1 cm. However, when the tunnel face distance changes from 8 to 16 m, the tunnel deformation amplitude is more significant than 4–8 m. The crown settlement decreases from 2.5 to 1.4 cm, and the maximum convergence decreases to 0.75 cm. Compared with the deformation under different surrounding rock strength, the difference of tunnel deformation is not apparent, but it is higher than that of tunnels with different over-excavation heights.
Analyzing all the figures, the distance between the left and right tunnel faces, surrounding rock strength, and over-excavation height all affect the crown settlement and horizontal convergence. The image results show that the variation range of tunnel deformation is small when the over-excavation height is changed. When the surrounding rock properties and the distance between the left and right tunnel faces are altered, the deformation amplitude of the tunnel rises. Nonetheless, the factor which has the most significant impact requires careful identification. Statistics of the results under different conditions are shown in Table 4, using grey relation analysis and entropy weight method to judge.
According to the equations of the chapters earlier, the relation degree between the reference sequence and the comparison sequence is gained. The relation degree value is sorted after calculating which factors are the main influencing factors and relative secondary factors of collapse risk. If
The entropy method is used to calculate the weight of crown settlement and horizontal convergence. According to the calculation results, the information entropy of crown settlement is 0.88 and the horizontal convergence is 0.906. Hence, the proportion of crown settlement is 0.56 and the proportion of horizontal convergence is 0.44。According to equation 12, the grey correlation coefficients of the aforementioned factors are combined to obtain the final grey correlation coefficient. All of these calculation results are shown in Figure 10.
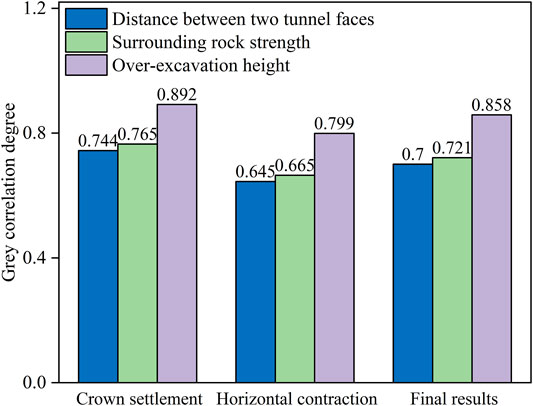
FIGURE 10. Relation degrees of three factors for crown settlement and horizontal contraction and final results.
The relation degree corrected using the entropy method is more objective and accurate. It can be observed that tunnel deformation is influenced by three factors, and their combined influence on tunnel deformation is greater than 0.6. Over-excavation height is the most important element impacting tunnel deformation, with a relation degree of 0.858. This suggests that tunnel collapse is mostly caused by an over-excavation incident. The tunnel’s deformation amplitude under various over-excavation heights is, likewise, the greatest. The surrounding rock is the second, with a relation degree of 0.721. The tunnel deformation is also influenced by the distance between the left and right tunnel faces, and the relation degree is 0.7. The other two elements, as can be seen, are also involved in the collapse disaster.
5 Conclusion
A severe collapse occurred at Huangjiakuang tunnels in Weihai City, Shandong Province, which led to a 27.5 m2 subsidence area on the ground, resulting in delays and economic losses. In this study, the main influencing factors to collapse were studied by combining the advanced geological prediction of working face, excavation characteristics, and construction disturbance. The entire process of collapse to the surface is inversed using numerical simulation software. Based on the data obtained by simulation, the three factors are further analyzed using grey relation analysis and entropy weight method. Some conclusions and numerical insights are summarized as follows:
1. Combined with the advanced geological prediction, geological survey data, and construction records, the whole process of tunnel collapse is inversed by numerical simulation. Before the collapse, the stress in the collapse area is increased to 1.1–1.2 times the initial value. When the collapse happened, the maximum crown settlement in the collapse area is 11 cm, and the surrounding rock bears a tensile stress. Finally, the soil is damaged by tension and evolves into collapse. As a result, it is determined that the collapse is caused by a combination of excavation disturbance and an over-excavation accident in a weak surrounding rock condition.
2. The control variables of surrounding rock property, over-excavation height, and the distance between the left and right tunnel faces are studied, and the corresponding tunnel deformation charts are obtained. It is demonstrated that the three factors quantitatively affect the tunnel deformation. The three factors are quantitatively analyzed using grey relation analysis and entropy weight method and their grey correlation degree exceeds 0.6. The relation degree of over-excavation height to deformation is 0.858. The relation degree of the surrounding rock is 0.721, and the left and right tunnel distance is 0.700. Consequently, the main reason for judging the collapse accident is the tunnel over-excavation.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary Materials; further inquiries can be directed to the corresponding author.
Author Contributions
YZ: resources, data curation, and project; JW: software and writing–original draft preparation; FL: validation and investigation; HX: editing.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Barla, M. (2008). Numerical Simulation of the Swelling Behaviour Around Tunnels Based on Special Triaxial Tests. Tunn. Undergr. Space Technol. 23, 508–521. doi:10.1016/j.tust.2007.09.002
Cao, F., Zhang, S., and Ling, T. (2020). Analysis of Cumulative Damage for Shared Rock in a Neighborhood Tunnel under Cyclic Blasting Loading Using the Ultrasonic Test. Shock Vib. 2020, 1–12. doi:10.1155/2020/8810089
Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a Bedding Fault: Understanding the Initiation and Movement of the Daguangbao Landslide Triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geol. 295, 106455. doi:10.1016/j.enggeo.2021.106455
Ding, W., Liu, K., Shi, P., Li, M., and Hou, M. (2019). Face Stability Analysis of Shallow Circular Tunnels Driven by a Pressurized Shield in Purely Cohesive Soils under Undrained Conditions. Comput. Geotechnics 107, 110–127. doi:10.1016/j.compgeo.2018.11.025
Fraldi, M., and Guarracino, F. (2010). Analytical Solutions for Collapse Mechanisms in Tunnels with Arbitrary Cross Sections. Int. J. Solids Struct. 47, 216–223. doi:10.1016/j.ijsolstr.2009.09.028
Fraldi, M., and Guarracino, F. (2009). Limit Analysis of Collapse Mechanisms in Cavities and Tunnels According to the Hoek-Brown Failure Criterion. Int. J. Rock Mech. Min. Sci. 46, 665–673. doi:10.1016/j.ijrmms.2008.09.014
Gao, Y., Xu, F., Zhang, Q., He, P., and Qin, Z. (2018). Geotechnical Monitoring and Analyses on the Stability and Health of a Large Cross-Section Railway Tunnel Constructed in a Seismic Area. Measurement 122, 620–629. doi:10.1016/j.measurement.2017.10.039
Han, H., Fukuda, D., Liu, H., Fathi Salmi, E., Sellers, E., Liu, T., et al. (2020). FDEM Simulation of Rock Damage Evolution Induced by Contour Blasting in the Bench of Tunnel at Deep Depth. Tunn. Undergr. Space Technol. 103, 103495. doi:10.1016/j.tust.2020.103495
Hao, X., Zhang, Q., Sun, Z., Wang, S., Yang, K., Ren, B., et al. (2021). Effects of the Major Principal Stress Direction Respect to the Long axis of a Tunnel on the Tunnel Stability: Physical Model Tests and Numerical Simulation. Tunn. Undergr. Space Technol. 114 (7), 103993. doi:10.1016/j.tust.2021.103993
He, Y., and Kusiak, A. (2017). “Performance Assessment of Wind Turbines: Data-Derived Quantitative Metrics,” in IEEE Transactions on Sustainable Energy (IEEE), 65–73. doi:10.1109/TSTE.2017.2715061
Huang, F., Zhu, H., Xu, Q., Cai, Y., and Zhuang, X. (2013). The Effect of Weak Interlayer on the Failure Pattern of Rock Mass Around Tunnel - Scaled Model Tests and Numerical Analysis. Tunn. Undergr. Space Technol. 35, 207–218. doi:10.1016/j.tust.2012.06.014
Jia, P., and Tang, C. A. (2008). Numerical Study on Failure Mechanism of Tunnel in Jointed Rock Mass. Tunn. Undergr. Space Technol. 23, 500–507. doi:10.1016/j.tust.2007.09.001
Kim, J., Kim, C., Kim, G., Kim, I., Abbas, Q., and Lee, J. (2022). Probabilistic Tunnel Collapse Risk Evaluation Model Using Analytical Hierarchy Process (AHP) and Delphi Survey Technique. Tunn. Undergr. Space Technol. 120, 104262. doi:10.1016/j.tust.2021.104262
Kong, C., Gao, X., Cao, L., and Liu, K. (2016). Analysis of the Failure of Primary Support of a Deep-Buried Railway Tunnel in Silty Clay. Eng. Fail. Anal. 66, 259–273. doi:10.1016/j.engfailanal.2016.04.008
Lan, X. D., Zhang, X., Li, X. H., Li, Z., Liu, Y. S., and Xia, M. R. (2022). Model Experiment on Surface Subsidence Induced by Excavation of Shallow Small-Spacing Tunnels. Environ. Earth Sci. 133, 4. doi:10.1007/s12665-022-10226-x
Lei, M., Peng, L., and Shi, C. (2015). Model Test to Investigate the Failure Mechanisms and Lining Stress Characteristics of Shallow Buried Tunnels under Unsymmetrical Loading. Tunn. Undergr. Space Technol. 46, 64–75. doi:10.1016/j.tust.2014.11.003
Li, C., Hou, S., Liu, Y., Qin, P., Jin, F., and Yang, Q. (2020). Analysis on the Crown Convergence Deformation of Surrounding Rock for Double-Shield TBM Tunnel Based on Advance Borehole Monitoring and Inversion Analysis. Tunn. Undergr. Space Technol. 103, 103513. doi:10.1016/j.tust.2020.103513
Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D., and Cheng, Q. (2021). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 697, 780928. doi:10.3389/fenrg.2021.780928
Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. (2021). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 770, 799039. doi:10.3389/fenrg.2021.799039
Li, H., He, Y., Xu, Q., Deng, J., Li, W., and Wei, Y. (2022). Detection and Segmentation of Loess Landslides via Satellite Images: a Two-phase Framework. Landslides 19 (3), 673–686. doi:10.1007/s10346-021-01789-0
Li, P., Liu, C., Zhang, Y., Zhang, J., Yang, J., and Feng, T. (2019). Construction Practice of Landslide during Tunneling in Hilly Topography. Eng. Fail. Anal. 104, 1234–1241. doi:10.1016/j.engfailanal.2019.07.064
Li, S., Liu, B., Xu, X., Nie, L., Liu, Z., Song, J., et al. (2017). An Overview of Ahead Geological Prospecting in Tunneling. Tunn. Undergr. Space Technol. 63, 69–94. doi:10.1016/j.tust.2016.12.011
Li, T., and Yang, X. (2017). Limit Analysis of Failure Mechanism of Tunnel Roof Collapse Considering Variable Detaching Velocity along Yield Surface. Int. J. Rock Mech. Min. Sci. 100, 229–237. doi:10.1016/j.ijrmms.2017.10.028
Li, Y., Zhang, D., Fang, Q., Yu, Q., and Xia, L. (2014). A Physical and Numerical Investigation of the Failure Mechanism of Weak Rocks Surrounding Tunnels. Comput. Geotechnics 61, 292–307. doi:10.1016/j.compgeo.2014.05.017
Li, Z., Wang, L., Feng, B., Xiao, J., Zhang, Q., Li, L., et al. (2020). Comprehensive Collapse Investigation and Treatment: An Engineering Case from Qingdao Expressway Tunnel. J. Clean. Prod. 270, 121879. doi:10.1016/j.jclepro.2020.121879
Liu, C., Peng, Z., Pan, L., Liu, H., Yang, Y., Chen, W., et al. (2020). Influence of Tunnel Boring Machine (TBM) Advance on Adjacent Tunnel during Ultra-rapid Underground Pass (URUP) Tunneling: A Case Study and Numerical Investigation. Appl. Sci. 10, 3746. doi:10.3390/app10113746
Liu, F., Ma, T., Tang, C., Liu, X., and Chen, F. (2019). A Case Study of Collapses at the Yangshan Tunnel of the Coal Transportation Channel from the Western Inner Mongolia to the Central China. Tunn. Undergr. space Technol. 92, 1030631–10306313. doi:10.1016/j.tust.2019.103063
Liu, F., Zhang, Y., Ma, T., and Tang, C. A. (2022). Observed Performance of a Deep Excavation of Qingdao Metro Line 4 in China. Tunn. Undergr. Space Technol. 123, 104445. doi:10.1016/j.tust.2022.104445
Lyu, C., and Zeng, Z. (2019). Upper Bound Limit Analysis of Unsymmetrical Progressive Collapse of Shallow Tunnels in Inclined Rock Stratum. Comput. Geotechnics 116, 1031991–10319912. doi:10.1016/j.compgeo.2019.103199
Ma, X., Xue, Y., Bai, C., Liu, H., and Yu, Y. (2020). Prediction Model for Deformation Risk Grade of the Soft Rock Tunnel Based on GRA-Extension. Earth Environ. Sci. 440, 052057. doi:10.1088/1755-1315/440/5/052057
Peng, N. A., Zhang, Y. X., and Wang, C. (2010). Study on Mechanical Properties of Surrounding Rock during Tunnel Construction with In-Situ Expansion Step Excavation Method. Disaster Adv. 570 (4), 194–199. doi:10.1088/1755-1315/570/2/022068
Qiu, D., Chen, Q., Xue, Y., Su, M., Liu, Y., Cui, J., et al. (2021). A New Method for Risk Assessment of Water Inrush in a Subsea Tunnel Crossing Faults. Mar. Georesources Geotechnol. 6, 1–11. doi:10.1080/1064119x.2021.1929594
Sx, A., Hao, L., Chong, L. A., Hl, C., Jl, A., and Tong, L. D. (2020). Model Test on Mechanical Characteristics of Shallow Tunnel Excavation Failure in Gully Topography. Eng. Fail. Anal. 119, 104978. doi:10.1016/j.engfailanal.2020.104978
U.S. Department of Transportation Federal Highway Administration (2009). Technical Guidelines for Construction of Highway Tunnels Standard. JTG/T F60-2009.
Wang, L. (2021). Analysis of the Causes of the Collapse of a Deep-Buried Large Cross-Section of Loess Tunnel and Evaluation of Treatment Measures. Appl. Sci. 12, 161. doi:10.3390/app12010161
Wang, X., Lai, J., Qiu, J., Xu, W., Wang, L., and Luo, Y. (2020). Geohazards, Reflection and Challenges in Mountain Tunnel Construction of China: a Data Collection from 2002 to 2018. Geomatics, Nat. Hazards Risk 11 (1), 766–785. doi:10.1080/19475705.2020.1747554
Wang, Y., Zheng, S., Li, Y., Wang, Y., and Huang, Y. (2021). The Failure Characteristics Around Shallow Buried Tunnels under Rainfall Conditions. Geomatics, Nat. Hazards Risk 12 (1), 363–380. doi:10.1080/19475705.2021.1875058
Xia, Y., Liu, B., Zhang, C., Liu, N., Zhou, H., Chen, J., et al. (2022). Investigations of Mechanical and Failure Properties of 3D Printed Columnar Jointed Rock Mass under True Triaxial Compression with One Free Face. Geomechanics Geophys. Geo-Energy Geo-Resources 1, 1–24. doi:10.1007/s40948-021-00331-9
Xiao, Y.-X., Feng, X.-T., Feng, G.-L., Liu, H.-J., Jiang, Q., and Qiu, S.-L. (2016). Mechanism of Evolution of Stress-Structure Controlled Collapse of Surrounding Rock in Caverns: A Case Study from the Baihetan Hydropower Station in China. Tunn. Undergr. Space Technol. 51, 56–67. doi:10.1016/j.tust.2015.10.020
Xu, C., Xia, C. C., and Han, C. L. (2021). Modified Ground Response Curve (GRC) in Strain-Softening Rock Mass Based on the Generalized Zhang-Zhu Strength Criterion Considering Over-excavation. Undergr. Space 6, 585–602. doi:10.1016/j.undsp.2021.07.002
Yan, F., Qiu, W., Sun, K., Jiang, S., Huang, H., Hong, Y., et al. (2021). Investigation of a Large Ground Collapse, Water Inrush and Mud Outburst, and Countermeasures during Subway Excavation in Qingdao: A Case Study. Tunn. Undergr. Space Technol. 117, 104127. doi:10.1016/j.tust.2021.104127
Yang, S. Q., Tao, Y., Xu, P., and Chen, M. (2019). Large-scale Model Experiment and Numerical Simulation on Convergence Deformation of Tunnel Excavating in Composite Strata. Tunn. Undergr. space Technol. 94, 1031331–10313318. doi:10.1016/j.tust.2019.103133
Yang, X. L., and Huang, F. (2011). Collapse Mechanism of Shallow Tunnel Based on Nonlinear Hoek-Brown Failure Criterion. Tunn. Undergr. Space Technol. 26, 686–691. doi:10.1016/j.tust.2011.05.008
Zampieri, P., Faleschini, F., Zanini, M. A., and Simoncello, N. (2018). Collapse Mechanisms of Masonry Arches with Settled Springing. Eng. Struct. 156, 363–374. doi:10.1016/j.engstruct.2017.11.048
Zhang, C.-p., Han, K.-h., Fang, Q., and Zhang, D.-l. (2014). Functional Catastrophe Analysis of Collapse Mechanisms for Deep Tunnels Based on the Hoek-Brown Failure Criterion. J. Zhejiang Univ. Sci. A 15, 723–731. doi:10.1631/jzus.a1400014
Zhang, C., Chu, W., Liu, N., Zhu, Y., and Hou, J. (2011). Laboratory Tests and Numerical Simulations of Brittle Marble and Squeezing Schist at Jinping II Hydropower Station, China. J. Rock Mech. Geotechnical Eng. 3, 30–38. doi:10.3724/sp.j.1235.2011.00030
Zhang, J., and Yang, T. (2018). Study of a Roof Water Inrush Prediction Model in Shallow Seam Mining Based on an Analytic Hierarchy Process Using a Grey Relational Analysis Method. Arab. J. Geosci. 11, 153. doi:10.1007/s12517-018-3498-2
Zhang, K., Chavez Torres, J. L., and Zang, Z. (2019). Numerical Analysis of Pipelines Settlement Induced by Tunneling. Adv. Civ. Eng. 2019, 1–10. doi:10.1155/2019/4761904
Zhang, Q. B., He, L., and Zhu, W. S. (2016). Displacement Measurement Techniques and Numerical Verification in 3D Geomechanical Model Tests of an Underground Cavern Group. Tunn. Undergr. Space Technol. 56, 54–64. doi:10.1016/j.tust.2016.01.029
Zhang, Y., Liu, S., Kou, M., and Wang, Z. (2020). Mechanical and Failure Characteristics of Fissured Marble Specimens under True Triaxial Compression: Insights from 3-D Numerical Simulations. Comput. Geotechnics 127 (7), 103785. doi:10.1016/j.compgeo.2020.103785
Zheng, C., Gu, Y., Shen, J., Du, M., Ma, G., and Sun, K. (2021). Comprehensive Evaluation of Urban Integrated Transportation Network with Multivariate Statistical Analysis: A Case Study of Haimen. IEEE Access 9, 165034–165048. doi:10.1109/access.2021.3132169
Zhou, H., Chen, S., Li, H., Liu, T., and Wang, H. (2021). Rockburst Prediction for Hard Rock and Deep-Lying Long Tunnels Based on the Entropy Weight Ideal Point Method and Geostress Field Inversion: a Case Study of the Sangzhuling Tunnel. Bull. Eng. Geol. Environ. 80, 3885–3902. doi:10.1007/s10064-021-02175-9
Keywords: mountain tunnels, collapse, grey relation analysis, multi-factor analysis, surrounding rock
Citation: Zhang Y, Wang J, Liu F and Xia H (2022) Mechanism and Sensitivity Analysis of Collapse in Large Section Mountain Neighborhood Tunnels. Front. Earth Sci. 10:904655. doi: 10.3389/feart.2022.904655
Received: 25 March 2022; Accepted: 05 May 2022;
Published: 23 June 2022.
Edited by:
Shenghua Cui, Chengdu University of Technology, ChinaReviewed by:
Bin Zeng, Chongqing Jiaotong University, ChinaYin Zhang, Chengdu University of Technology, China
Jiahao Deng, DePaul University, United States
Copyright © 2022 Zhang, Wang, Liu and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fei Liu, bGl1ZmVpQHF1dC5lZHUuY24=
 Yongjun Zhang
Yongjun Zhang Junyi Wang
Junyi Wang Fei Liu*
Fei Liu*