
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 17 January 2023
Sec. Sedimentology, Stratigraphy and Diagenesis
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.898312
This article is part of the Research Topic Cohesive Sedimentary Systems: Dynamics and Deposits View all 21 articles
The evolution and stability of fracturing in the cyclothymic deposition of phosphate rocks are strongly affected by the viscoelasticity and structural form of the rock-forming minerals. Presently, there is no standardized method that has been widely accepted to accurately quantify the elastic-plastic deformation and fracturing of such striped structural rock nor reflect the role of the different lithogenous minerals in phosphate rocks when subjected to viscoelastic strain loading. In this study, integrated mathematical equations were formulated for modelling the mechanical and fracture behaviour of cyclothymic deposition in structured phosphate rocks. These constitutive equations were developed based on Maxwell’s Theory after the elastic modulus and damping coefficient of the rock-forming mineral from the mechanical testing were substituted into the derived-equations. In these new models, the apatite stripes and dolomite stripes were incorporated into the transverse isotropic model through the analysis of structural characteristics of the phosphate rock. Through experimental validation, the response curves of the creep and stress relaxation tests were found to be consistent with the deformation curves generated by modelling using the mathematical equations. Overall, the formulated model along with the corresponding equations was found to exhibit good applicability properties to describe phosphate’s mechanical and fracture behaviour under low horizontal compressive stresses. In the study, the creep mechanism in phosphate rocks were satisfactorily analysed from the angles of microscopic morphology, cracks evolution, and inter-crystalline strength. The hard brittle apatite was found to be surrounded and separated by high creep variant dolomite. Furthermore, the analysis showed that dolomite crystals possessing high creep properties dominated the distribution and evolution of secondary structures in the phosphate rock, under the condition of long-term low-stress loading.
Due to the widespread usage of phosphate rocks in industrial and agricultural applications, numerous studies have been conducted on the correlation-ship between the mechanical behaviour of the phosphate rock mass and its petrologic properties. Some studies have shown that the thermal and physical stresses in granites, quite often, lead to the initiation and propagation of the cracks (Homand-Etienne and Houpert, 1989; Chen et al., 2010; Li et al., 2015; Zhao et al., 2022). Through the analysis of microcrack anisotropy evolution in deep mining phosphate rocks, it has been confirmed that intergranular fracture is the main grain boundary damage type, and, that the weak grain boundary surface is the contact boundary between dolomite and colloidal phosphate (Zhao et al., 2015; Tu et al., 2017; Bond and Zikry, 2018; Hurai et al., 2022; Zhang et al., 2022).
Regional differences in the petrographic type and the effective mineral quality of the phosphate rock has also inherently led to studies focusing on the formation conditions and mechanical properties of phosphate (Nguidi et al., 2021). Specifically, focus has been on the influence of the ancient geographical environment on the formation of inter-crystalline strength of the rocks (Priyank et al., 2015; Qin et al., 2015; Zhang et al., 2015; Han et al., 2016; Pan et al., 2017; Orlov et al.,2020). These studies have shown that the basic mechanical behaviour of rocks is influenced by the mineral composition, structure type, and formation conditions. But other literature suggests otherwise, the viscoelastic and rheological properties of ribbon structured rocks under low-stress levels have resulted in a series of safety accidents and property losses including instability of roadways and drill pipe sticking (Kounadis, 2014; Zhang et al., 2014). Although, in addition to providing a mathematical model to link the elastoplasticity of rocks to their mechanical behaviour, Maxwell’s Theory also provides a model for relating the rate of damping to the elastic modulus of cracks (Shen and Chen, 2006). However, this is only applicable to homogeneous rocks.
So based on the above background, more research is needed to build a more comprehensive mechanical model to accommodate non-homogeneous rocks, which not only considers characterizing and quantifying the response behaviour of sedimentary rocks with a horizontal bedding structure, but also reflects the viscoelastic and rheological properties of dolomite and apatite. In particular, this has a practical significance when it comes to selecting appropriate cost-effective and safe mining techniques for phosphate rocks.
As presented in this paper, strip-type phosphorus block rocks were used as the test subject of the study. By using a rock triaxial apparatus, the constative modelling of phosphate rock’s elastic and rheological properties under external loading can be accomplished based on Maxwell’s Theory (Maxwell, 1881) through the triaxial test.
The experimental research plan for the study comprised of a six-step work schemes. These steps are described in the subsequent text.
The first step of the work scheme involved identifying the banding phosphate rock type, which was sourced from Yichang Xingfa Group Co., Ltd. in China. The composition and tectonic characteristics of phosphate rock were analysed using an electron microscopy.
The second step of the work scheme involved quantifying the mechanical characteristics of the phosphate rock, the mining roadway wall, and identifying the boundary conditions. Constitutive equations for modelling the mechanical properties of phosphate rock ribbon structure was conceptualized based on the Maxwell Theory of rheology and viscoelastic media.
The third step of the work scheme. The chemical components and micro-morphology were analysed using an X-ray fluorescence ADVANT’XP and a Scanning Electron Microscope, all acquired from Japan.
The fourth step of the work scheme. Preliminary testing was conducted in accordance with the American GCTS rock mechanics test specification (GCTS, 2020) to measure and quantify the mechanical properties of the phosphate rock including the elastic modulus, Poisson’s ratio, and the viscous-damping coefficient. The tested phosphate rocks comprised of carbon-fluorine apatite and dolomite, respectively. Thereafter, the measured laboratory test data were used as input parameters in the preliminary conceptual model for formulating and developing the final constitutive model for the depositional-belt type phosphatic rock.
The fifth step of the work scheme. The mineral phosphate rock’s mechanical test response-curve was verified and compared with the phosphate rock’s deformation that was estimated using the constitutive model. The model prediction accuracy was accordingly judged and ascertained from a comparison of the test response-curves and model deformation predictions, respectively.
The sixth step of the work scheme. The loaded-deformation mechanism of the belt type phosphatic rock was analysed lastly, essentially from the angle of a lattice constant and fracture evolution.
Geologically, the banded phosphate rock found in central China has a high degree of crystallization, hard texture, and a horizontal bedding structure. As can be seen in Figure 1, it has the typical horizontal bedding structure of a sedimentary rock. Geological survey data have shown that the phosphate rock mineral is predominantly composed of sedimentary and metasomatism phosphate on the edge of the craton that was formed during the sinian period, after a series of mineralization processes such as deposition, transformation, and enrichment (Andrieux and Aminot, 2001; Cao et al., 2011). In phosphate, rock apatite usually occurs with siliceous shale and/or carbonate interlayer. The thickness of a single-layer ranges from 1 cm to several meters—see Figure 1. The average burial depth of the ore beds is 800 m. The seam dip angle is less than 5°. The stress level is usually low and equivalent to 10%–20% of the peak stress from the rock strength test because the tectonic stress is mainly controlled by the overburdened rock mass. Furthermore, the rock mass did not show any signs of accelerated creep destruction, which corresponds to the stable creep state expressed by the Maxwell model (Maxwell, 1881).
Apatite’s grain aggregate presents dense clumps and is colourlessly transparent. However, the apatite in the sedimentary rock is dark grey because of silicon. The hardness and relative density are 5.0 and 3.2, respectively (Ma, 2011; Levasseur et al., 2015). Although the dolomite crystal lattice belongs to the hexagonal system just like apatite, its hardness and relative density are 3.7 and 2.75, respectively. From the SEM (scanning electron microscope) test results, it is clear that the crystal lattices of the dolomite are small and orderly arranged, and that the apatite’s lattices are presently bulkier and mutually interlocked—see Figure 2. To set up the perspective for the mathematical model, the phosphate rock band structure was simplified by superimposing it with dolomite and apatite.
Combined with the physical and structural characteristics of the aforementioned banded phosphate rock (Yang and Xiao, 2019), phosphate rock specimens were modelled as an axial superposition of different thickness mineral belts. The thickness of each mineral belt was assumed to be a constant value in the horizontal direction as exemplified in Figure 3. Since each mineral belt was kept in a series condition, the axial stresses were correspondingly equal in each mineral belt. Therefore, the model’s total strain produced by stress loading was considered to be comprised of every mineral belt’s strain when the axial compression load is acting on both ends of the model. Furthermore, the longitudinal deformation of the rock mass was determined as a function of the deviatoric stress, which is essentially the difference in the value of the maximum and minimum principal stresses as expressed in Eq. 1:
On the other hand, every mineral belt’s strain is comprised of the summation of the elastic strains εe and plastic strains εv, respectively (Shen and Chen, 2006). The strain summation as derived based on Maxwell’s Theory is illustrated in Eq. 2:
Where ε is the total strain, and εe and εv are elastic and plastic strains, respectively. The differential equation for the phosphate rock strain rate after differentiating Eq. 2 is shown in Eq. 3 as follows:
The change rate to the time of elastic strains was derived as expressed in Eq. 4 below:
In Eqs 5a–ca–cEqs 5a–c, the symbols
In the study, it was assumed that the plastic deformation-rate of the ribbon structured model is comprised of the plastic deformation rate of the dolomite and apatite ribbon, respectively. The plastic deformation of the ribbon structure is basically a function of the thickness of the dolomite and apatite ribbons. Similar to elastic deformation, plastic deformation was modelled and computed as illustrated in Eq. 6:
Substituting Eqs 4–6 into Eq. 3 yields Eq. 7 as demonstrated below:
In Eq. 7, the phosphate rock specimen’s stress is the same in the axial direction and is characterized as follows: σ0=σe=σv=σ1-σ3. The stress remains unchanged and is characterized by a differential function dσ0/dt=0. Integrating both sides of Eq. 7 with respect to time, yields Eq. 8 as expressed below:
When the load first acts on the specimen, only the elastic deformation emerged with no plastic deformation. Therefore, the constant term C is characterized by ε0=σ0/E, after t=0 has been substituted into Eq. 8. Then, a mathematical model such as Eq. 9 was derived, which represents the relationship of the phosphate rock deformation with loading time under constant-stress conditions. At the same temperature, parameters such as
By contrast, the phosphate rock strain was held constant in the other tests, in which the strain rate is zero and can be characterized as ε′=0. With this consideration, the ε′ model was derived as shown in Eq. 10. After differentiating Eq. 10 with respect to time, t, Eqs 11, 12 were derived as expressed below:
Integrating both sides of Eq. 12, with respect to time, t, yields the exponential function illustrated in Eq. 13:
At 0 h of the test, t = 0s and
Preliminary mechanical tests were carried out to measure the mechanical properties of each rock-forming mineral. One set of specimens for apatite and dolomite were analysed according to the international rock mechanics experiment standard (Ref), with letters “A” used to represent apatite and “D” for dolomite. The specific parameters associated with each rock-forming mineral are listed in Table 1 and includes the dimensions and thickness.
Three axial ultimate bearing capacity tests were performed on the first three blocks of each group, using the dynamic rock triaxial apparatus RTX-1000 American GCTS—see Figure 4. In consideration of the burial conditions of the phosphate rock deposits, the test control conditions in this study were selected as follows: the direction of the specimen axial direction was assumed to be consistent with the gravitational direction, the confining pressure was constant at 5 MPa, and the test temperature was maintained at 15°C in a strain-controlled loading mode. The strain rate was 0.006%/min, which is equivalent to one microstrain per second. The mechanical parameters/properties including the elastic modulus are shown in Table 2.
As shown in Table 2, the mean value of the ultimate compressive strength reached 317.8 MPa, which is 2.59 times than that of dolomites. Although the average density of apatite is 1.09 times that of dolomite, its poisson’s ratio is only half that of dolomite in the elastic deformation stage. The test results of Table 2 indicates that dolomite has obvious deformation susceptibility under the effects of equal confining pressure and loading rate—see Figure 5.
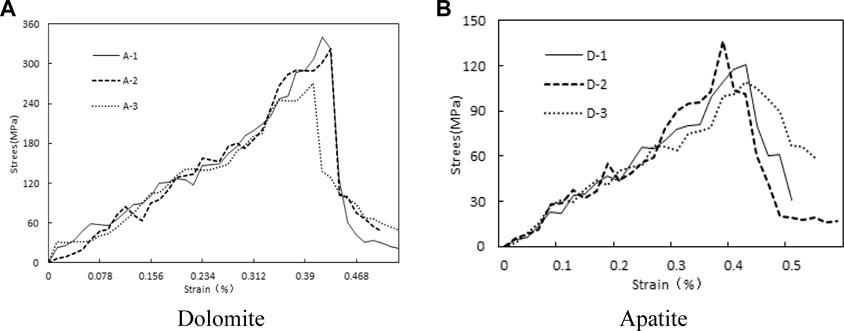
FIGURE 5. The response curves of the rock-forming minerals from mechanical testing. (A) Dolomite (B) Apatite.
The last fourth set of specimens, denoted as D-4 (dolomite) and A-4 (apatite) were used for creep coefficient determination. However, the creep coefficient of a rock is restricted by the load combination, temperature, and stress state. In consideration of the actual geological conditions and brittle characteristics of the phosphate rock, the ribbon structured model in this study was assumed to be under typical low stress loading conditions at a constant temperature. For apatite and dolomite, the creep tests were conducted in stress-controlled loading mode. The axial principal stress was 25 MPa and was held constant over a test time of 300 h under a confinement pressure of 5 MPa (Jiang et al., 2016; Zhou et al., 2016). The creep test results are shown in Figure 6.
From Figure 6, the strain value of apatite increased from 0.38 × 10−3 to 0.61 × 10−3 whilst that of dolomite increased from 0.53 × 10−3 to 2.92 × 10−3. As shown in Figure 6, the total strain magnitude of dolomite is equivalent to about 4.8 times that of apatite. From these data, the sticking factor of apatite and dolomite were determined to be 25,862 GPa•h and 3,968 GPa•h, respectively.
During the verification-test phase, creep and stress relaxation tests of the phosphate rock specimens were conducted to verify and validity the models in Eqs 9, 13. Similar to Table 1, the external dimensions of the phosphate rock test specimens were measured as shown in Table 3.
The creep and stress-relaxation response curves from the verification-tests are plotted in Figure 7. The test conditions were similar to the previous test for the creep coefficient determination, namely stress-controlled loading mode, 25 MPa axial principal stress, and 5 MP confinement pressure. In Figure 7, the solid lines represent test results whilst the dotted lines represents the simulation results.
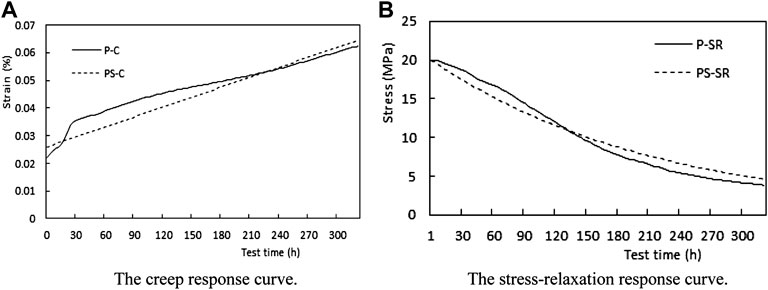
FIGURE 7. Graphical plot of the verification-test results (test versus simulation). (A) The creep response curve. (B) The stress-relaxation response curve.
With respect to the creep properties, it is evident from the “P- C” response curve in Figure 7A that the initial strain of the phosphate rock specimen was about 0.26 × 10−3 under the effects of a deviatoric stress of 20 MPa. Thereafter, the strains increased to 0.36 × 10−3 after 84 h and then, maintained a constant rate of 0.65 x 10−3 after 320 h. In general, Figure 7A indicates that the strain increased linearly as a function of loading test-time.
The stress response curve, “P-SR,” of the phosphate rock specimen from the stress-relaxation verification-test is shown in Figure 7B. In the first phase of the test plan, the specimen’s deviatoric stress increased steadily to 20 MPa within 15 min. In the second phase of testing, the control strain was maintained at a principal strain of 0.28×10−3. Based on the “P-SR” response curve in Figure 7B, the stress of the phosphate rock specimen decreased steadily from 20 MPa to 3.84 MPa over a period of 12 days.
For analytical modelling, the creep and stress-relaxation simulation equations were derived under low-stress loading conditions after the known parameters were substituted into Eqs 9, 14, respectively. These parameters, including the mechanical properties such as the elastic modulus, sticking factor, and the weighted thicknesses of each rock-forming mineral, were obtained from the previous test results contained in Figure 1 through to Figure 6 and Table 1 through to Table 3, respectively.
The simulation response curves “PS- C” and “PS- SR” are shown in Figure 7 with dotted lines. The simulation response curves generally reflect the instantaneous elastic deformation and subsequent steady creep process of the phosphate rock mass when subjected to loading (Walubita et al., 2011). Additionally, the elastic recovery and permanent residual deformation of the phosphate rock mass during unloading are also reflected by similar simulation equations.
Comparing the experimentally measured (solid-curve plots in Figure 7) response curve of the phosphate rock specimen with the predicted values (dotted-curve plots in Figure 7) obtained from the modified models, it was confirmed that the developed approach successfully captures the effect of creep and stress-relaxation of ribbon types of the phosphate rock under low-stress level environment.
(a) The slip and diffusion resistance to mineral crystals have a close relationship with the lattice constant and its spatial structure (Li, 2009; Wang et al., 2015; Sassoni et al., 2021). It was pointed out in the literature that dolomite crystals belong to the trigonal system and its molecular formula is CaMg[CO3]2 and a0 = 0.601 nm. On the other hand, apatite crystal belongs to hexagonal crystal system and its molecular formula is Ca5 [PO4]3(F,OH) and a0 = 0.943–0.938 nm (Ma, 2011). The crystal constant of dolomite is significantly less than apatite. In other words, the crystal size of apatite is greater than that of dolomite crystals.
The SEM of the preliminary microstructure observation tests showed needle-shaped apatite crystal balls presenting an interpenetrating-interlocking typical space architecture like that of a silicate water rigid cementing material. By and large, this type of lattice arrangement improves the integrity of apatite. On the other hand, the total strains of a ribbon type phosphate rock is comprised of the elastic strain εe, and plastic strain εv, that is represented by Eq. 9. The elastic strain of phosphate rock were determined to be 0.26 × 10−3 based on the initial point of the creep response curve, namely the “P-C” plot in Figure 7. However, the elastic strains increased to 0.65 × 10−3 after 320 h.
The plastic deformation in the latter part of the experiment was found to be about three times the elastic deformation. This means that the creep is one of the key factors controlling the mechanical response-behaviour of the phosphate rock. The sticking factor of dolomite was determined to be 3,968 GPa•h, which is significantly smaller than the 25,862 GPa•h of apatite—see Figure 6. Overall, it was concluded that the intergranular creep rupture of dolomite is the leading cause of the mechanical deformation of phosphate rock when subjected to long loading times under low-stress environments.
(b) The creep property of mineral crystals is generally reflected by the distribution and evolution of rock fractures (Reiko and Richard, 2002; Xin, et al., 2017). Based on careful observation of the cylindrical specimen surfaces, the black apatite ribbon has relatively larger crack density of about 2-4 strip/cm2, which is 3.5 times that of dolomite—see Figure 8. Most of the cracks were observed to be in line with the cylindrical axis and perpendicular to horizontal bedding. As indicated by arrow A in Figure 8, the cracks ran through several groups to dozens of bands. These cracks, which exceed all the mineral crystals in the direction of the fracture, were possibly formed by accidental loading forces, such as earthquakes. However, most of these cracks also have a common feature that the same cracks in the dolomite stripe are significantly narrower with some of them even going to the point where it disappears.
The literature shows that dolomite’s critical transformation pressure from brittleness to plasticity is 9.6 MPa, which is less than half of the loading in the Triaxial creep test. This means that the vertically fractured stress of the dolomite crack tip is large enough to make the crack close. Thus, the dolomite crystals were moved from a high-stress place to a lower stress region after overcoming the intercellular sliding resistance. Similarly, some of the apatite-stripe cracks may have been creep-filled with smaller particle size crystals at this stage. This creep-filling behaviour increases the width of the cracks and makes the individual apatite slime slivers to spin at an angle, as indicated by arrow B in Figure 8. With the occurrence of this phenomenon, the end result is that the apatite stripe becomes surrounded by dolomite stripes.
In the laboratory, the creep crystals and their surrounding dolomite stripes were confirmed to possess the same elements and content using the Energy Dispersive Spectrometer test. This again illustrates that the dolomite creep ability is much higher than that of apatite, which indicated that creep was critical factor in characterizing and quantifying the mechanical behaviour of phosphate rocks.
The creep property of the minerals is controlled by the intergranular bonding force (Roufail and Klein, 2013; Li et al., 2020). After experiencing the same grinding energy, the rock-forming mineral produced the corresponding dissociation effect with different intermolecular forces. In this paper, the inter-crystalline strength of different mineral crystals was analysed using the crushability test of minerals. Grinding is the first process of the phosphate ore dressing. The energy efficiency of the process is directly related to the inter-crystalline bonding force of the ore minerals.
For the crushability test, approximately 300 g of the mixed phosphate rock specimens were obtained. These specimens were first broken into a median diameter of 10 mm and put into a ball-mill for 15 min regular grinding. The phosphate rock powder before and after sieve analysis was used to determine the fractional composition and quality of the constituent compounds, which were screened with an 0.08 mm diameter sieve. The test results are shown in Table 4.
From Table 4, the fractional composition of P2O5, as an important component of apatite, went up 1.6 times after screening. However, the content of Silicon dolomite is represented by 65% of CO2 and SiO2 before screening. During the crushability test, it was observed that phosphate minerals are more difficult to break than silicate minerals under the same grinding energy conditions. Furthermore, it was found that the inter-crystalline strength of apatite was even greater than that of dolomite. In other words, apatite needs more external force to do work for relative motion among the crystals and that its creep performance is relatively low.
In this study, integrated mathematical equations were formulated for modelling the mechanical and fracture behaviour of phosphate rocks. The scope of work incorporated model formulation based on Maxwell’s Theory and laboratory testing that included creep, stress-relaxation, crushability, and SEM morphological evaluation. Comparisons with the test data provided a verification and validation platform for the proposed models. From the study results and findings, the following conclusions and recommendations were drawn:
(1) Modelling the relationship between the stress and strain responses of phosphate rocks is an important undertaking for engineering applications tailored towards solving rock related problems. Maxwell Theory has been successful in modelling the rheological behaviour of the rock, however its capacity is restricted in effectively simulating the rheological properties of ribbon structured rock such as phosphate rocks. Constitutive equations reflecting the creep properties and stress-relaxation of phosphate rock were deduced, which are based on the ribbon structural model representing the paragenetic replacement of dolomite and apatite.
The constitutive equations were successfully used to model and characterize the rock-forming mineral’s effects on the elastic-plastic deformation mechanism of the phosphate rock. The equations were able to accurately simulate the deformation of the ribbon structure in the phosphate rock, which is composed of different thickness mineral belts in all the stress stages. The correctness of these constitutive equations were successfully validated by comparing the simulation results with the measured creep response curve of the ribbon structured phosphate rock.
(2) The horizontal tensile strength of the apatite stripe is greatly weakened because there are high density of vertical fractures in them. To avoid the risk of vault collapse, it is suggested to use a relatively complete thick layer of dolomite as the direct roof of the tunnel or alley.
(3) Based on the mechanical test results, it was clear that dolomite’s compressive strength was lower than apatite’s, and its creep ability was about three times greater than apatite’s. And based on the SEM tests, the mechanism of mechanical response-behaviour about the high-intensity apatite crystals been separated by the low-intensity dolomite crystal was analysed from the mesoscopic perspective. The analysis showed that the dolomite crystals possessing high creep properties dominated the distribution and evolution of the banded structure in the phosphate rock under the condition of long-term low-stress loading.
The constitutive equations were developed and enhanced by studying and modelling the elastic-plastic mechanical response-behaviour to cyclothymic deposition structure rock. However, the effects of the small angle for the strip interface was not considered and wants further research in future follow-up studies.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The National Natural Science Foundation of China supported the internships of DP during the progress of this work. DZ and YX provided helpful insights to improve the derivation of the constitutive models. The phosphate rock was graciously supplied by Yichang Xingfa Group Co., Ltd., whilst the specimens were processed in the Rock Mechanics Laboratory of Wuhan Institute of Technology, Wuhan (China). This work was supported by the [National Natural Science Foundation of China Nos. 51474159, 42077228].
JP is thanked for the critical reading of an earlier version of the manuscript. Comments from the editors and the reviewer helped to improve the quality of the paper. The raw test data related to the study are available upon request to the first author.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Andrieux, L. F., and Aminot, A . (2001). Phosphorus forms related to sediment grain size and geochemical characteristics in French coastal areas. Estuar. Coast. Shelf Sci. 52, 617–629. doi:10.1006/ecss.2001.0766
Bond, D. M., and Zikry, M. A. (2018). Differentiating between intergranular and transgranular fracture in polycrystalline aggregates. J. Mat. Sci. 53, 5786–5798. doi:10.1007/s10853-017-1847-2
Cao, Z. J., Zhang, X. B., and Ai, N. S. (2011). Effect of sediment on concentration of dissolved phosphorus in the Three Gorges Reservoir. Int. J. Sediment Res. 26, 87–95. doi:10.1016/S1001-6279(11)60078-4
Chen, J., Chen, F., and Zhang, T. (2010). Technological mineralogical characteristics of Low grade phosphorus containing tombarthite in Guizhou. Tombarthite 31 (2), 70–74.
GCTS (2020). Advanced rock testing systems. Available at: https://www.gcts.com/pdf/catalogs/gcts_catalog_systems_rock.pdf (Accessed October 2020).
Han, C., Zheng, B., Qin, Y., Ma, Y., Cao, W., Yang, C., et al. (2016). Analysis of phosphorus import characteristics of the upstream input rivers of Three Gorges Reservoir. Environ. Earth Sci. 75, 1024. doi:10.1007/s12665-016-5832-x
Homand-Etienne, F., and Houpert, R. (1989). Thermally induced microcracking in granites characterization and analysis. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 26, 125–134. doi:10.1016/0148-9062(89)90001-6
Hurai, V., Huraiová, M., Habler, G., Horschinegg, M., Milovsky, R., Milovska, S., et al. (2022). Carbonatite-melilitite-phosphate immiscible melts from the aragonite stability field entrained from the mantle by a Pliocene basalt. Mineral. Pet. doi:10.1007/s00710-022-00783-1
Jiang, Q., Zhong, S., Cui, J., Feng, X. T., and Song, L. (2016). Statistical characterization of the mechanical parameters of intact rock under triaxial compression: An experimental proof of the jinping marble. Rock Mech. Rock Eng. 49, 4631–4646. doi:10.1007/s00603-016-1054-5
Kounadis, A. (2014). Rocking instability of free-standing statues atop slender viscoelastic columns under ground motion. Soil Dyn. Earthq. Eng. 63, 83–91. doi:10.1016/j.soildyn.2014.01.021
Levasseur, S., Welemane, H., and Kondo, D. (2015). A microcracks-induced damage model for initially anisotropic rocks accounting for microcracks closure. Int. J. Rock Mech. Min. Sci. 77 (7), 122–132. doi:10.1016/j.ijrmms.2015.03.011
Li, X., Yuan, Y., Liu, L., Leung, Y. S., Chen, Y., Guo, Y., et al. (2020). 3D printing of hydroxyapatite/tricalcium phosphate scaffold with hierarchical porous structure for bone regeneration. Bio-des. Manuf. 3, 15–29. doi:10.1007/s42242-019-00056-5
Li, Z., Zhang, G., Yu, X., Liu, Q., and Zhang, X. C. (2015). Phosphorus loss and its estimation in a small watershed of the Yimeng mountainous area, China. Environ. Earth Sci. 73 (3), 1205–1216. doi:10.1007/s12665-014-3475-3
Maxwell, J. C. (1881). Treatise on EIecrriciry and magnetism. 2nd edition, I. Oxford: Clarendon Press, 400.
Nguidi, M. A., Mouflih, M., Abdelmajid, B., László, K., Salem, E. O., Hanane, E. B., et al. (2021). Lithofacies analysis, sedimentary dynamics and Genesis of Maastrichtian-Eocene phosphorites of BouCraa deposit (Southern Morocco). J. Afr. Earth Sci. 177 (1). doi:10.1016/j.jafrearsci.2021.104161
Orlov, N. K., Kiseleva, A. K., Milkin, P. A., Evdokimov, P. V., Putlayev, V. I., and Gunster, J. (2020). Potentialities of reaction sintering in the fabrication of high-strength macroporous ceramics based on substituted calcium phosphate. Inorg. Mat. 56, 1298–1306. doi:10.1134/S0020168520120146
Pan, D., Xia, Y. Y., and Zhang, D. J. (2017). Comparative study on geological structure and mechanical feature of phosphorite in south China. J. Wuhan Inst. Technol. 39 (06), 622–628. doi:10.3969/j.issn.1674?2869.2017.06.017
Priyank, U., Padhyaya, S., and Kumar, (2015). Micromechanics of stress transfer through the interphase in fiber-reinforced composites:Original Research Article. Mech. Mater. 89 (10), 190–201. doi:10.1016/j.mechmat.2015.06.012
Qin, J., An, K., Sheng, L. M., Yu, L. M., and Zhao, X. L. (2015). Scanning tunneling microscope study of graphite grain boundaries. Chin. J. Vac. Sci. Technol. 35 (3), 372–376. doi:10.13922/j.cnki.cjovst.2015.03.23
Reiko, K., and Richard, J. (2002). On measuring creep behaviour in granular materials through triaxial testing. Can. Geotech. J. 39 (5), 1061–1074. doi:10.1139/t02-059
Roufail, R., and Klein, B. (2013). Mineral liberation and particle breakage in stirred mills. Can. Metall. Q. 49 (4), 419–428. doi:10.1179/cmq.2010.49.4.419
Sassoni, E., Delhomme, C., Forst, S., Graziani, G., Henin, J., Masi, G., et al. (2021). Phosphate treatments for stone conservation: 3-year field study in the royal palace of versailles (France). Mat. Struct. 54, 140. doi:10.1617/s11527-021-01717-7
Tu, L., Zhang, D. J*., and Pan, D. (2017). Failure characteristics and laws of acoustic emission for phosphorite under triaxial loading. J. Wuhan Inst. Technol. 39 (06), 616–621. doi:10.13969/j.issn.1674?2869.2017.06.016
Walubita, L. F., Alvarez, A. E., and Simate, G. S. (2011). Evaluating and comparing different methods and models for generating relaxation modulus master-curves for asphalt mixes. Constr. Build. Mater. 25 (5), 2619–2626. doi:10.1016/j.conbuildmat.2010.12.010
Wang, L. L., Bornert, M., Héripré, E., Chanchole, S., Pouya, A., and Halphen, B. (2015). The mechanisms of deformation and damage of mudstones: A micro-scale study combining esem and dic. Rock Mech. Rock Eng. 48, 1913–1926. doi:10.1007/s00603-014-0670-1
Xin, Y., Li, M., An, D., Ji, H., and Kang, J. (2017). Experimental study on the instability mechanism of the major-defect fractured rock. Arab. J. Geosci. 10, 311–320. doi:10.1007/s12517-017-3095-9
Yang, H. Y ., Xiao, J. F., Xie, Z., Tan, Q., Xu, J., et al. (2019). Origin of the ediacaran weng'an and kaiyang phosphorite deposits in the nanhua basin, SW China. J. Asian Earth Sci. 182 (182), 103931–104208. doi:10.1016/j.jseaes.2019.103931
Zhang, C., Xie, R. C., Yao, Y., Lv, J., and Cao, Q. (2014). Micro-mechanical behavior characteristics of rock structure surface for deep tight sandstone reservoir :Fault-Block. Oil Gas Field 21 (5), 560–563. doi:10.6056/dkyqt201405004
Zhang, S., An, W., and Li, X. (2015). Research on phosphorus loads and characteristics of adsorption and release in surface sediments of Nanyang Lake and Weishan Lake in China. Environ. Monit. Assess. 187, 4103–4111. doi:10.1007/s10661-014-4103-0
Zhang, Y., Cui, S., Yu, Z., and Cheng, J. (2022). Fracture characteristics of sliding crack in brittle rock: Analysis based on an improved equivalent crack model. Front. Earth Sci. 10, 893549. doi:10.3389/feart.2022.893549
Zhao, H., Li, W., Wang, L., Fu, J., Xue, Y. L., Zhu, J. J., et al. (2022). The influence of the distribution characteristics of complex natural fracture on the hydraulic fracture propagation morphology. Front. Earth Sci. 9, 784931. doi:10.3389/feart.2021.784931
Zhao, S. L., Zhang, G., Li, M. X., Yue, X. G., and Wang, D. D. (2015). Rock Microcrack′s dominant direction and the anisotropy. J. Wuhan Univ. Technol. 37 (5), 57–65.
Keywords: cyclothymic deposition structure, elastic-plastic deformation, creep coefficient, elastic modulus, fracture, cracking, apatite stripe, dolomite stripe
Citation: Pan D, Xia Y, Zhang D, Chen X, Wu Q, Lin M, Wang Z and Pan J (2023) Using Maxwell’s Theory to model and quantify the fracture evolution of cyclothymic deposition phosphate rock. Front. Earth Sci. 10:898312. doi: 10.3389/feart.2022.898312
Received: 13 April 2022; Accepted: 31 October 2022;
Published: 17 January 2023.
Edited by:
Andrew James Manning, HR Wallingford, United KingdomReviewed by:
Hongjian Zhu, Yanshan University, ChinaCopyright © 2023 Pan, Xia, Zhang, Chen, Wu, Lin, Wang and Pan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuanyou Xia, eGlheXkxOTY1QHdodXQuZWR1LmNu; Dianji Zhang, ZGlhbmppemhhbmdAd2l0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.