Numerical Simulation of Long-Term Deterioration of Rock Mass Supported by Shotcrete Lining

The deterioration of rock mass and shotcrete lining has major consequences on the long-term performance of tunnels in the weak rock mass. In this study, the long-term behavior of rock mass and shotcrete in tunnels was simulated by using the three-dimensional finite difference method, considering the nonlinear deterioration mechanism. The degradation of rock mass was simulated by weakening the mechanical parameters, while the deterioration of shotcrete was modeled by decreasing the thickness. The support pressure, internal force, and displacement of the secondary lining were monitored with the gradual degradation of rock mass and shotcrete. As a consequence, the factor of safety (FoS) evolution with time was discussed. The results indicated that 1) the deterioration of both rock mass and shotcrete would significantly increase the rock pressure on the secondary lining, leading to an increase in the displacement (0–14 mm). The FoS of the secondary lining was reduced by 85%. 2) The influence of shotcrete’s deterioration on the secondary lining was relatively less, and the rock pressure on the secondary lining increased from 0 kPa to 13.8 kPa. The long-term safety of the tunnel is remarkably affected by the deterioration of rock mass, depending on the deterioration characteristics of the rock mass. Therefore, the deterioration characteristics of rock mass should be fully considered in tunnel maintenance.

1 Introduction

In most countries, the life span of a tunnel is generally expected to be 100 years or even more. Many unfavorable factors would decrease its serviceability and safety during tunnel operations, among which the time-dependent deterioration of rock mass and the lining is a key one (Yoshida et al., 1997; Sandrone and Labiouse, 2010; Tating et al., 2013; Mert, 2014). The time-dependent deterioration of rock mass has a great influence on the physical and mechanical parameters of rock mass, which can break the balanced state of the tunnel and produce additional load on the lining in the long term (Usman and Galler, 2013; Aghchai et al., 2020).

Under the influence of external factors, the weathering of rock mass results in a decrease in particle size, change in mineral composition, and decrease in cohesional strength (Lyu et al., 2020). The mechanisms of damage degradation of different rocks under water–rock interaction, wet and dry cycling, or considering the action of corrosive ions were studied (Gullà et al., 2006; Wong et al., 2016; Momeni et al., 2017; Liu et al., 2018; Castellanza et al., 2018). The deterioration of rock mass is a time-dependent phenomenon, which may lead to a reduction of the mechanical parameters due to weathering (Ladanyi, 1980; Graham and Au, 1985; Chandler and Apted, 1988; Khanlari et al., 2012; Undul and Tugrul, 2012), aging (Panet, 1979; Boidy et al., 2002) and some other factors. Extensive studies have been carried out on the deterioration mechanisms of rock mass. Tertiary mudstone tends to soften due to water absorption upon unloading, moisture/humidity changes, weathering, and deterioration with time (Yoshida et al., 1997); viscoplastic properties of the rock mass and shotcrete have been studied using the finite element method (Swoboda et al., 1987). Pore water pressure redistribution (Garber, 2003) and other special geological disasters could contribute to the deterioration of rock mass.

Concrete is the structural material of tunnel support, and its long-term mechanical properties have been studied by many researchers in tunnel engineering. Some concrete deterioration models have been proposed by considering service conditions (Lei et al., 2013; Jiang and Niu, 2016; Alexander and Beushausen, 2019). The deterioration of steel bars has been studied (Ahmad, 2003; Sola et al., 2019). In order to simplify the simulation, reinforcement deterioration is neglected in the present study. The deterioration of the lining is mainly induced by weathering and corrosion in the underground environment. The lining generally consists of shotcrete and the secondary lining. As a temporary support structure, no measures are taken to improve the durability of shotcrete. Simultaneously, shotcrete is tightly attached to rock mass and exposed to underground water. Behind the secondary lining, there is no way to get the shotcrete repaired. As a permanent support structure, the durability of the secondary lining could be maintained during operation. Therefore, the deterioration of the secondary lining could be neglected, and the deterioration of the lining mainly depends on shotcrete.

This study intends to improve the understanding of the mechanisms of long-term deterioration of rock mass and lining and the influence of the deterioration on tunnel performance. The FLAC^3D three-dimensional finite difference method was used in the study, complying with deterioration criteria of rock mass and lining, to simulate the long-term deterioration procedure of rock mass and shotcrete.

2 Deterioration Mechanisms of Rock Mass and Lining

The deterioration of rock mass is a time-dependent phenomenon, which could decrease its shear strength and expansion, and the decrement could be presented by moving down the failure envelop accompanied by a reduction in its nonlinearity at low stress levels. With the evolution of deterioration, the failure mechanisms of point A near the unsupported tunnel are shown in Figure 1. In the initial state, the stress circle of point A kept off the failure envelop at a long distance. With the advancement of deterioration, the envelop moves down gradually. The envelop crosses the stress circle eventually, and point A is in a state of failure. The pressure from the rock mass also increases gradually with the advancement of deterioration.

FIGURE 1

FIGURE 1. Stressed mechanisms under deterioration.

According to the various compositions of rock mass and the hydrogeological conditions around tunnels, the deterioration could be classified into the following three types:

1. Rock mass deteriorates quickly in a short time.

2. Rock mass deteriorates slowly over a long time.

3. Rock mass hardly deteriorates.

The main phases of the progressive transfer of the rock mass pressure from the primary support to the final lining system are described below. During excavation, the primary support ($K_{\text{s}}$) undertakes the main pressure from rock mass; when the secondary lining is completed, the secondary lining and the primary support function together ($K_{\text{s}}+K_{\text{i}}$). During operation, the support pressure of the primary support is gradually shifted to the secondary lining due to the deterioration of the primary support ($K_{\text{s}\left(\text{t}\right)}+K_{\text{i}}$), and the secondary lining is affected by a much slower degradation, which can be neglected during this phase. When the primary support deteriorated completely, the support pressure of the secondary lining includes two parts: shifted pressure from the primary lining and increased pressure from rock mass due to its deterioration.

The rock mass and lining deteriorated together according to different laws, and their deteriorations affect the long-term mechanical behavior of the tunnel. The deterioration mechanisms of the rock mass and lining are shown in Figure 2. The deterioration of both the rock mass and lining can significantly affect the serviceability and safety of tunnels during operation. The deterioration of rock mass will gradually increase the support pressure, and simultaneously, the deterioration of the lining will gradually decrease its own support capacity. When the lining is unable to support the rock mass, deformations such as crack and even collapse occurs resulting in the termination of tunnel operation time ahead of schedule.

$K_{\text{s}}$–stiffness of the primary support;

$P_{\text{s}}$–the maximum support pressure that the primary support could undertake;

$K_{\text{s}\left(\text{t}\right)}$–stiffness of the primary support during deterioration;

$K_{\text{i}}$–stiffness of the secondary lining;

$P_{\text{i}}$–the maximum support pressure that the secondary lining could undertake;

$P_{\text{ri}\left(t\right)}$ ($i$ = 1,2,3)-pressure from rock mass.

FIGURE 2

FIGURE 2. Deterioration mechanisms of the rock mass and lining.

3 Numerical Simulation

3.1 Numerical Model

In order to balance the model efficiency and accuracy, numerical models of different sizes were established, and the calculation results were analyzed and compared. The numerical model was determined as shown in Figure 3, with a dimension of 40 m in longitudinal length, 160 m in width, and 110 m in height. The tunnel is of a polycentric cross section and is 9.7 m in height, 50 m in width, and 50 m in buried depth. The thickness of the shotcrete and secondary lining is 20 and 35 cm, respectively. The model contains 294,400 elements and 613,848 nodes. In terms of boundary conditions, no vertical displacements were allowed along the base of the model, no lateral displacements were allowed along the vertical surface of the model, and the top surface of the model was allowed to be deformed freely.

FIGURE 3

FIGURE 3. Tridimensional finite difference model.

The solid element is applied to simulate shotcrete, complying with the Mohr–Coulomb failure criterion that follows the elastic perfectly plastic stress–strain relationship (Usman and Galler, 2013), and a liner element is applied to simulate the secondary lining. The liner element is a build-in structural element in FLAC3D (as shown in Figure 4), which is usually applied to simulate the lining and geo-textile structure in geotechnical engineering. Liner structural elements are three-node, flat finite elements. In addition to providing the structural behavior of a shell, a shear-directed (in the tangent plane to the liner surface) frictional interaction occurs between the liner and the FLAC3D grid. In addition, in the normal direction, both compressive and tensile forces can be carried, and the liner may break free from (and subsequently come back into contact with) the grid (FLAC3D 2005). Interface elements can be used to model the effect of joints, faults, and frictional interfaces between bodies. Interfaces operating in a small-strain mode derive their forces from a comparison of “virtual positions” of the two interacting faces, where a “virtual position” of a point is the original coordinate of the point combined with the accumulated displacement to date. If one contacting object is removed (for example, backfill within a tunnel) and another substituted (for example, a liner is installed) using the same interface, then large initial stresses may appear because the two sides of the interface appear to interpenetrate (Zhao et al., 2022). The mechanical parameters of the shotcrete and secondary lining are shown in Tables 1, 2, respectively.

FIGURE 4

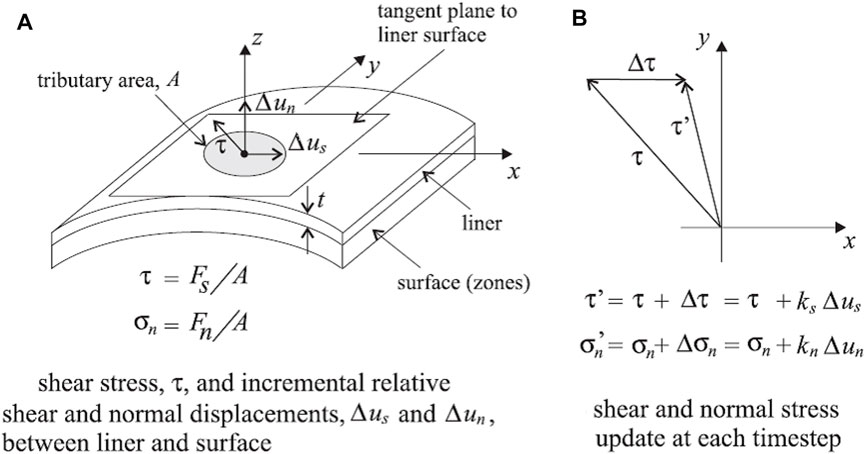
FIGURE 4. Idealization of interface behavior at a liner node. (A) Liner and surface. (B) Shear and normal stress (Itasca, 2005).

TABLE 1

TABLE 1. Mechanical parameters of the shotcrete.

TABLE 2

TABLE 2. Mechanical parameters of the secondary lining (FLAC^3D 2005).

3.2 Simulation of the Deterioration of Rock Mass

According to abundant studies on various rock masses, the failure criterion was put forward by Yoshida et al. (1990), which could describe the time-dependent deterioration of rock mass.

${\sigma }_1={\sigma }_3+A{\sigma }_{\text{c}}{\left(\frac{{\sigma }_3}{{\sigma }_{\text{c}}}-S\right)}^{1/B},(1)$

where A, B, and S are the strength parameters. Strength during deterioration is represented by interpolating the strength parameters (A, B, and S) from the initial to the fully deteriorated values using the following inverse-hyperbolic function of time (Yoshida et al., 1990; Yoshida and Adachi, 2010).

$X=X_0\left[1-\frac{t}{xt+t_{fs}\left\{X_0/\left(X_0-X_{fs}\right)-x\right\}}\right],(2)$

where X is the strength parameter (A, B, and S); x is the strength reduction-rate parameter (a, b and c); t is time. The subscripts o and fs denote the initial and fully deteriorated values, respectively.

The deterioration of rock mass generally complies with Mohr–Coulomb and Hoek–Brown failure criteria that follow the elastic perfectly plastic stress–strain relationship or elastic perfectly plastic soften stress–strain (Sandrone and Labiouse, 2010; Sulem et al., 1987; Ladanyi,1974). In the numerical simulation of this study, a solid element is applied to simulate the rock mass, complying with Mohr–Coulomb failure criterion that follows the elastic perfectly plastic stress–strain relationship. Eq. 1 describes the Mohr–Coulomb criterion when B = 1, and at this time, parameters A and S influence the deterioration of rock mass, where $A=\frac{2\sin \varphi }{1-\sin \varphi }$ and $S=-\frac{c\times \sqrt{4+2A}}{A{\sigma }_{\text{c}}}$.

The mechanical properties of rock mass are indirectly determined (through RMR) from the Q system by means of commonly used empirical equations and correlations as described in the following equations. Initial Q is assumed to be 2 in the numerical simulation, and relative physical and mechanical parameters are computed and shown in Table 3.

TABLE 3

TABLE 3. Initial mechanical parameters of rock mass (before deterioration).

As summative and quantifiable formulas for the characteristic of the rock mass, RMR and Q systems are based on studies on considerable rock mass in the natural state, including rock mass in various conditions of deterioration. So, RMR and Q systems are considered applicable to rock mass during deterioration (Tugrul, 1998; Serafim and Pereira, 1983; Bieniawski, 1989; Palmstrom, 2000).

$RMR=7\ln Q+36.(3)$

$E_{\text{m}}\left(GPa\right)={10}^{\left(RMR-10\right)/40}\left(RMR\le 50\right).(4)$

$c\left(MPa\right)=0.005\left(RMR-1.0\right).(5)$

$\varphi (°)=0.5RMR+\mathrm{4.5.}(6)$

${\sigma }_{\text{cm}}\left(MPa\right)=RMR.(7)$

${\sigma }_{\text{t}}\left(MPa\right)={\sigma }_{\text{cm}}/10.(8)$

The deterioration of rock mass in the numerical simulation is classified into three types:

3.2.1 Case 1

It is assumed that the mechanical parameters of rock mass decreased to a quarter of its original value in 10 years due to its deterioration ($t_{fs}=10$), namely, $A_{fs}/A_0=1/4$, $S_{fs}/S_0=1/4$. a and s are taken as 1.0 and 0.8, respectively (the influence of a and s on A and S is shown in the study by Yoshida et al., 1990). The time-dependent parameters of rock mass during deterioration are shown in Table 4, where $RM{R}_{\text{c}}$ and $RM{R}_{\phi }$ are computed according to Eqs 4, 5, respectively, and $RM{R}_{\text{m}}$ is the median of $RM{R}_{\text{c}}$ and $RM{R}_{\phi }$.

TABLE 4

TABLE 4. Time-dependent parameters of rock mass during deterioration.

As shown in Table 4, $RM{R}_{\text{c}}$ is basically equal to $RM{R}_{\phi }$, and the other parameters of rock mass in various conditions of deterioration could be computed according to Eqs 3–8. The computed results are shown in Table 5, where quality per unit volume is 2100 kg/m³, and Poisson’s ratio assumes an empirical value.

TABLE 5

TABLE 5. Time-dependent mechanical parameters of rock mass during deterioration.

3.2.2 Case 2

It is assumed that the mechanical parameters of rock mass decreased to a quarter of its original value in 100 years due to its deterioration ($t_{fs}=100$), namely, $A_{fs}/A_0=1/4$, $S_{fs}/S_0=1/4$, where a and s are taken as 1.0 and 0.8, respectively. The time-dependent mechanical parameters of rock mass during deterioration are shown in Table 6, where quality per unit volume is 2100 kg/m3 and Poisson’s ratio assumes an empirical value.

TABLE 6

TABLE 6. Time-dependent mechanical parameters of rock mass during deterioration.

3.2.3 Case 3

It is assumed that rock mass rarely deteriorated in 100 years ($t_{fs}=100$), namely, its parameters are equal to the original ones all the time (Table 7).

TABLE 7

TABLE 7. Time-dependent mechanical parameters of rock mass during deterioration.

3.3 Simulating the Deterioration of the Lining

In the lining system, shotcrete alone deteriorated in the numerical simulation. According to Nguyen (2005), the thicknesses of the deterioration zone $xd$ (cm) is considered proportional to the squarer root of time t (year):

$xd=\alpha \sqrt{t}.(9)$

Yokozeki et al. (2004) investigated the tunnels in which the operation time is between 34 and 100 years, and the deterioration thickness of the concrete in 100 years could go up to 100 mm. Due to measures not taken to improve the shotcrete’s durability and corrosion and deterioration of other factors, $\alpha$ was assumed to be 2 in the numerical simulation.

The deterioration thickness of shotcrete in 100 years would go up to 200 mm. The deterioration thicknesses of the shotcrete in various years are shown in Figure 5.

FIGURE 5

FIGURE 5. Variations in deterioration thickness of the shotcrete with time.

The shotcrete after deterioration lost the bearing capacity, so the deterioration of the shotcrete was simulated by decreasing its thickness in the numerical simulation. Shotcrete and rock mass deteriorated together in the numerical simulation.

3.4 The Process of Numerical Simulation

The excavation procedure was as follows:

(1) In the first step, the geostatic analysis was carried out to apply the gravity of the rock mass, without the lining structure. The in situ stress state was achieved as the initial stress condition for the following simulation.

(2) In the second step, the first slice in the tunnel core was excavated, and the shotcrete was activated. The benching tunneling method is applied and the corresponding footage is 2 m. The longitudinal distance between the up and down bench is 6 m. The shotcrete follows the excavation of the bench.

(3) When excavation is totally completed, the secondary lining starts to be installed. As a safety margin, the secondary lining does not sustain the load of the surrounding rock during tunnel construction.

(4) According to the calculation condition, the rock mass parameters and shotcrete are adjusted as mentioned above.

4 Results and Discussion

The support pressure of the secondary lining and its displacement are shown in Figures 6, 7 respectively. In case 1, the rock mass deteriorated rapidly over the period of 10 years and simultaneously, shotcrete deteriorated gradually. In case 2, the rock mass deteriorated slowly over the period of 100 years and simultaneously, shotcrete deteriorated gradually. In case 3, the rock mass did not deteriorate in the period of 100 years and simultaneously, shotcrete deteriorated gradually.

FIGURE 6

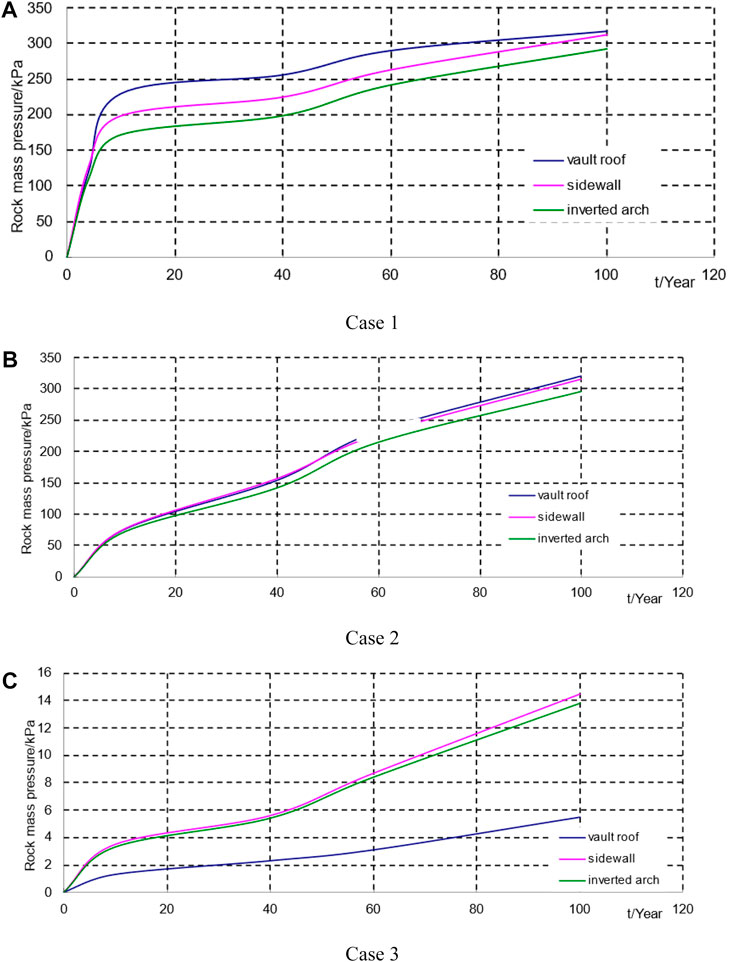
FIGURE 6. Variations in the pressure the secondary lining undertakes with time. (A) Case 1. (B) Case 2. (C) Case 3.

FIGURE 7

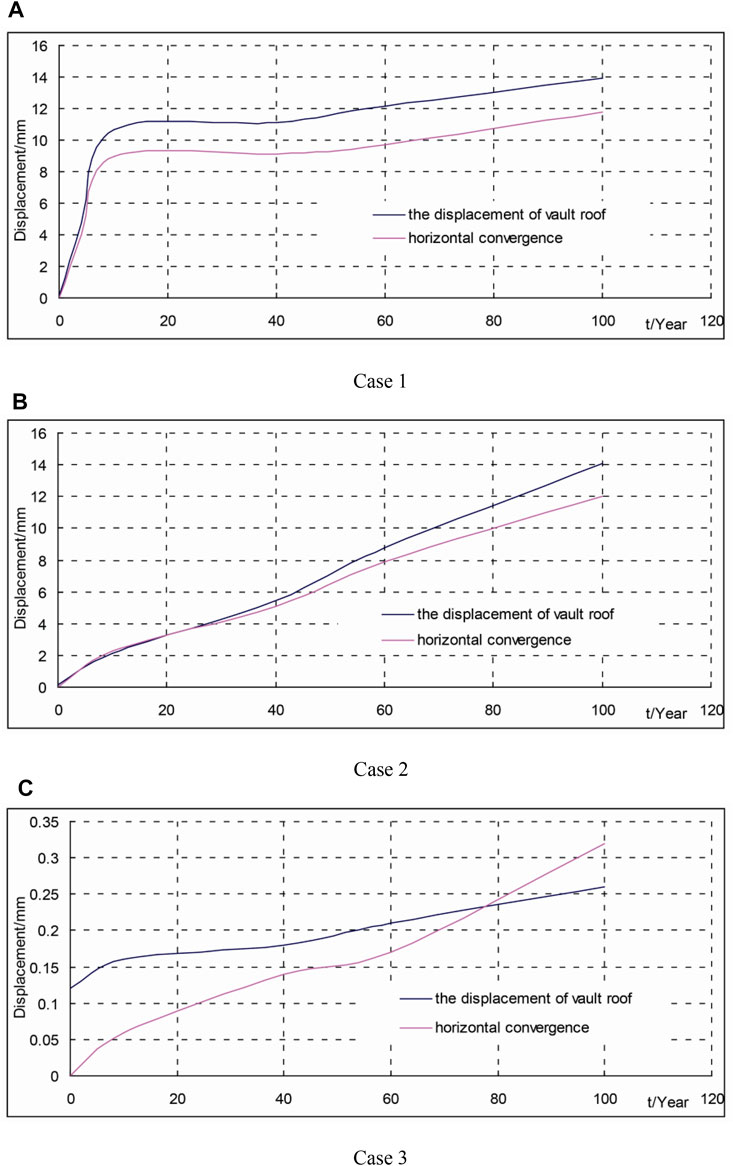
FIGURE 7. Variations in the displacement of the secondary lining with time. (A) Case 1. (B) Case 2. (C) Case 3.

Both the support pressure and displacement of the secondary lining increased gradually during the deterioration of the rock mass and shotcrete. Basically, they shared a common trend, but their increase trends differed during deterioration.

For case 1, the rock mass fully deteriorated in a relatively short time (10 years), and the support pressure of the secondary lining and its displacement increased quickly during deterioration. The rock mass fully deteriorated after 10 years, and shotcrete alone continued to deteriorate gradually. The support pressure of the shotcrete gradually transferred to the secondary lining, and the support pressure and displacement of the secondary lining increased slowly during deterioration. In the 100th year, the maximum support pressure of the secondary lining was 317.7 kPa; the displacement of the vault roof was 13.96 mm, and the horizontal convergence was 11.76 mm.

For case 2, both the rock mass and shotcrete fully deteriorated in a relatively long time (100 years). In the former 60 years, the rock mass deteriorated relatively quickly, increasing the support pressure of the lining, and simultaneously, shotcrete which gradually deteriorated was unable to undertake increased pressure from the rock mass; thus, the support pressure of the secondary lining and its displacement increased in a relatively quick level. In the later 40 years, the rock mass and shotcrete deteriorated at a slower level, while the support pressure of the secondary lining and its displacement increased more slowly. In the 100th year, the maximum support pressure of the secondary lining was 321.2 kPa, the displacement of the vault roof was 14.11 mm, and horizontal convergence was 12.00 mm.

Even though the deterioration processes of case 1 and case 2 given above differed, they reached the same deterioration level eventually (100 years), and the support pressure of the secondary lining and its displacement was basically equal.

For case 3, the rock mass did not deteriorate and shotcrete alone deteriorated with time. The support pressure of the secondary lining mainly came from the support pressure of the shotcrete during construction. In comparison with case 1 and case 2, its pressure and displacement were relatively small and approximated to a linear increase. In the 100th year, the maximum support pressure of the secondary lining was 14.5 kPa; the displacement of the vault roof was 0.26 mm, and the horizontal convergence was 0.32 mm.

The moment and axial force of the secondary lining during deterioration are shown in Figure 8. The axial force gradually increased, and the maximum moment occurred in the spring line. In addition, the vault roof, sidewall, and inverted arch were in tension. The axial force of case 1 and case 2 shared a common distribution, with the bigger ones in the vault roof and inverted arch, and with the smaller ones in the sidewall. In case 3, the smaller one occurred in the vault roof and inverted arch and the bigger one occurred in the sidewall by contrast. Bending moments at the sidewall and inverted arch were much higher, to which attention should be paid. The inner sides of the secondary lining in the two areas were under tension but still within the limit of concrete capacity. Other areas were also within the limit of concrete capacity.

FIGURE 8

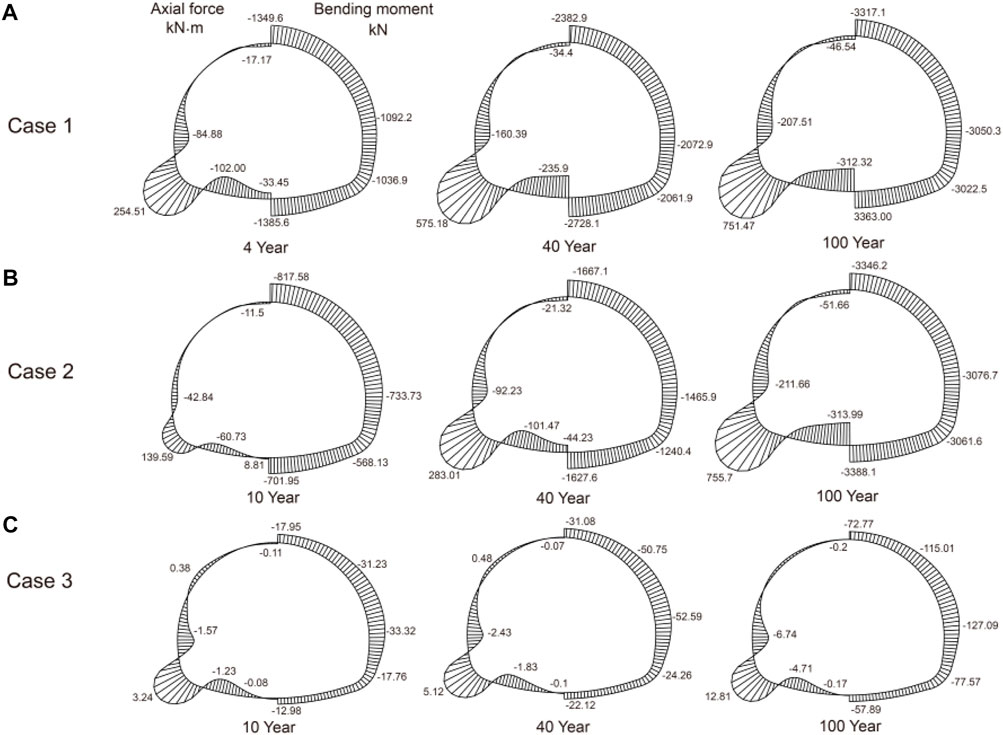
FIGURE 8. Variations in internal force of the secondary lining with time. (A) Case 1. (B) Case 2. (C) Case 3.

The support pressure of the secondary lining would increase significantly since rock mass had deteriorated. The deterioration of the shotcrete would shift pressure from itself to the secondary lining, and shotcrete itself was unable to undertake the left pressure. The deterioration of both the rock mass and shotcrete would significantly increase the support pressure of the secondary lining, leading to an increase in its displacement and internal force and a decrease in the tunnel’s serviceability and safety.

The ratio of the maximum pressure that the supporting structure could bear ($P_{\max }$) to the actual equilibrium pressure ($P_{\text{eq}}$) could be defined as a safety factor, by which the serviceability and safety level of the tunnel could be evaluated (Sandrone and Labiouse, 2010):

$FoS=\frac{p_{\max }}{P_{eq}},(10)$

where $P_{\max }$ could be computed as the following formula (Guang, 1993):

$P_{\max }=\frac{1}{2}{\sigma }_{\text{c}}\left[1-\frac{a^2}{{\left(a+t_c\right)}^2}\right],(11)$

where ${\sigma }_{\text{c}}$ is the uniaxial compressive strength; $a$ is the radius of lining; $t_c$ is the thickness of the concrete (in this study; and ${\sigma }_{\text{c}}$ = 35 MPa; a = 12 m; $t_{\text{c}}$ = 0.35 m). It is notable that Eq. 11 is deduced from the round-pipe theory under external pressure. For the tunnel with a polycentric cross section, its bearing capacity is less than that of a circular tunnel, and therefore the computed $P_{\max }$ may be bigger than the actual one. Accordingly, this study takes half of the computed value as the maximum pressure the secondary lining could bear, namely, $P_{\max }$ = 488.9 kPa and the FoS evolution (in vault roof) with time is shown in Figure 9.

FIGURE 9

FIGURE 9. FoS evolution (in vault roof) with time.

Being relatively big, the safety factor of case 3 (bigger than 10) was not shown in Figure 9. The initial safety factor is assumed to be 10. As shown in Figure 9, the FoS of case 2 was bigger than that of case 1 in the former time, and the two were basically equal at the end. In case 1, the FoS of the secondary lining decreased significantly because the rock mass deteriorated rapidly in the first 10 years. If special disasters, such as earthquakes and fire accidents, took place during operation time, its safety factor would decrease again, posing a threat to the tunnel’s safe operation.

By comparing the three cases comprehensively, the influence of the shotcrete’s deterioration on the secondary lining was relatively small, and the deterioration of the rock mass was the main influencing factor.

5 Conclusion

Based on numerical simulation, this study carries out a contrastive analysis of the three cases discussed earlier. The following conclusions can be drawn:

(1) The deterioration of both the rock mass and shotcrete would significantly increase the rock pressure on the secondary lining (0–321.2 kPa) and the displacement (0–14 mm). The FoS of the secondary lining was reduced by 85%. In the design of the secondary lining, the influence of the rock pressure increased by the deterioration of the rock mass should be properly considered.

(2) The influence of the shotcrete’s deterioration on the secondary lining was relatively small and the rock pressure the secondary lining undertakes was increased from 0 to 13.8 kPa. The secondary lining only undertakes the support pressure of the shotcrete during construction.

(3) When the rock mass deteriorated rapidly (case 1), the support pressure of the secondary lining would increase rapidly in a relatively short time (10 years) and then incline toward stability; When the rock mass deteriorated slowly (case 2), the support pressure of the secondary lining would gradually increase in a long time (60 years). Also, the two cases were basically equal at the end. Different deterioration characteristics of rock mass have different effects on the secondary lining, and the deterioration characteristics of rock mass should be fully considered in the tunnel maintenance.

It is to be noted that the applicable scope of the conclusion is limited due to the fact that only several conditions are considered in the simulation. Furthermore, no field or laboratory tests have been conducted to verify the numerical simulation. These are the focus of future research.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

Funding acquisition and formal writing of the work, CK; investigation and data analysis of the work, HW and KZ; review of the work, XG. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science of China (Grant number 52108385) and the Open Project of State Key Laboratory for structural mechanical behavior and system safety of Traffic Engineering jointly constructed by the Ministry and province (KF2021-08).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aghchai, M. H., Salari, H., and Showkati, A. (2020). Predicting Long-Term Stability of Tunnels Considering Rock Mass Weathering and Deterioration of Primary Support. Tunn. Undergr. Space Technol. 107, 103670.

Google Scholar

Ahmad, S. (2003). Reinforcement Corrosion in Concrete Structures, its Monitoring and Service Life Prediction-A Review. Cem. Concr. Compos. 25 (4), 459–471. doi:10.1016/s0958-9465(02)00086-0

CrossRef Full Text | Google Scholar

Alexander, M., and Beushausen, H. (2019). Durability, Service Life Prediction, and Modelling for Reinforced Concrete Structures - Review and Critique. Cem. Concr. Res. 122, 17–29. doi:10.1016/j.cemconres.2019.04.018

CrossRef Full Text | Google Scholar

Bieniawski, Z. T. (1989). Engineering Rock Mass Classifications. New York: John Wiley and Sons.

Google Scholar

Boidy, E., Bouvard, A., and Pellet, F. (2002). Back Analysis of Time-dependent Behaviour of a Test Gallery in Claystone. Tunn. Undergr. Space Technol. 17 (4), 415–424. doi:10.1016/s0886-7798(02)00066-4

CrossRef Full Text | Google Scholar

Castellanza, R., Lollino, P., and Ciantia, M. (2018). A Methodological Approach to Assess the Hazard of Underground Cavities Subjected to Environmental Weathering. Tunn. Undergr. Space Technol. 82, 278–292. doi:10.1016/j.tust.2018.08.041

CrossRef Full Text | Google Scholar

Chandler, R. J., and Apted, J. P. (1988). The Effect of Weathering on the Strength of London Clay. Q. J. Eng. Geol. Hydrogeology 21 (1), 59–68. doi:10.1144/gsl.qjeg.1988.021.01.04

CrossRef Full Text | Google Scholar

Garber, R. (2003). Design of Deep Galleries in Low Permeable Saturated Porous Media. Thesis EPFL no. 2721. Lausanne: Ecole Polytechnique Federale de Lausanne.

Google Scholar

Graham, J., and Au, V. C. S. (1985). Effects of Freeze-Thaw and Softening on a Natural Clay at Low Stresses. Can. Geotech. J. 22 (1), 69–78. doi:10.1139/t85-007

CrossRef Full Text | Google Scholar

Guang, B. S. (1993). Tunnel Mechanics. Southwest Jiaotong University Press. (in Chinese).

Google Scholar

Gullà, G., Mandaglio, M. C., and Moraci, N. (2006). Effect of Weathering on the Compressibility and Shear Strength of a Natural Clay. Can. Geotechnical J. 43 (6), 618–625.

Google Scholar

Itasca (2005). User’s Guide for FLAC3D.Version 3.0.

Google Scholar

Jiang, L., and Niu, D. (2016). Study of Deterioration of Concrete Exposed to Different Types of Sulfate Solutions under Drying-Wetting Cycles. Constr. Build. Mater. 117, 88–98. doi:10.1016/j.conbuildmat.2016.04.094

CrossRef Full Text | Google Scholar

Khanlari, G. R., Heidari, M., and Momeni, A. A. (2012). Assessment of Weathering Processes Effect on Engineering Properties of Alvand Granitic Rocks (West of Iran), Based on Weathering Indices. Environ. Earth Sci. 67, 713–725. doi:10.1007/s12665-011-1518-6

CrossRef Full Text | Google Scholar

Ladanyi, B. (1980). “Direct Determination of Ground Pressure on Tunnel Lining in a Non-linear Viscoelastic Rock,” in Proceedings of the 13th Canadian rock mechanics symposium, Montreal (CIM), 126–132.

Google Scholar

Ladanyi, B. (1974). “Use of the Long-Term Strength Concept in the Determination of Ground Pressure on Tunnel Linings,” in Advances in rock mechanics: reports of current research, Proceedings of the 3rd international congress on rock mechanics, Denver (National Academy of Sciences), 1150–1156.

Google Scholar

Lei, M., Peng, L., Shi, C., and Wang, S. (2013). Experimental Study on the Damage Mechanism of Tunnel Structure Suffering from Sulfate Attack. Tunn. Undergr. Space Technol. 36, 5–13. doi:10.1016/j.tust.2013.01.007

CrossRef Full Text | Google Scholar

Liu, X., Jin, M., Li, D., and Zhang, L. (2018). Strength Deterioration of a Shaly Sandstone under Dry-Wet Cycles: a Case Study from the Three Gorges Reservoir in China. Bull. Eng. Geol. Environ. 77 (4), 1607–1621. doi:10.1007/s10064-017-1107-3

CrossRef Full Text | Google Scholar

Lyu, H., Gu, J., Li, W., and Liu, F. (2020). Analysis of Compressibility and Mechanical Behavior of Red Clay Considering Structural Strength. Arabian J. Geosciences 13 (11), 1–11. doi:10.1007/s12517-020-05352-4

CrossRef Full Text | Google Scholar

Mert, E. (2014). An Artificial Neural Network Approach to Assess the Weathering Properties of Sancaktepe Granite. Geotech. Geol. Eng. 32 (4), 1109–1121. doi:10.1007/s10706-014-9785-0

CrossRef Full Text | Google Scholar

Momeni, A., Hashemi, S. S., Khanlari, G. R., and Heidari, M. (2017). The Effect of Weathering on Durability and Deformability Properties of Granitoid Rocks. Bull. Eng. Geol. Environ. 76 (3), 1037–1049. doi:10.1007/s10064-016-0999-7

CrossRef Full Text | Google Scholar

Nguyen, V. H. (2005). Couplage degradation chimique-comportement en compression du be´ton. Thesis dedoctorat. Paris: Ecole Nationale des Ponts et Chaussees.

Google Scholar

Palmstrom, A. (2000). On Classification Systems. Melbourne: Proceedings GeoEng.

Google Scholar

Panet, M. (1979). “Time-dependent Deformations in Underground Works,” in Proceedings of the 4th international congress on rock mechanics, Montreux, Balkema, Rotterdam, 2-8 Sept 1979, 279–290.

Google Scholar

Sandrone, F., and Labiouse, V. (2010). Analysis of the Evolution of Road Tunnels Equilibrium Conditions with a Convergence-Confinement Approach. Rock Mech. Rock Eng. 43 (2), 201–218. doi:10.1007/s00603-009-0056-y

CrossRef Full Text | Google Scholar

Serafim, J. L., and Pereira, J. P. (1983). “Considerations of the Geomechanics Classification of Bieniawski,” in Proc. of the International Symposium on Engineering Geology and Underground Construction, Lisbon, A.A. Balkema, Rotterdam, the Netherlands, 1133–1142.

Google Scholar

Sola, E., Ožbolt, J., Balabanić, G., and Mir, Z. M. (2019). Experimental and Numerical Study of Accelerated Corrosion of Steel Reinforcement in Concrete: Transport of Corrosion Products. Cem. Concr. Res. 120, 119–131. doi:10.1016/j.cemconres.2019.03.018

CrossRef Full Text | Google Scholar

Sulem, J., Panet, M., and Guenot, A. (1987). An Analytical Solution for Time-dependent Displacements in a Circular Tunnel. Int. J. Rock Mech. Min. Sci. Geomechanics 24 (87), 155–164. doi:10.1016/0148-9062(87)90523-7

CrossRef Full Text | Google Scholar

Swoboda, G., Mertz, W., and Beer, G. (1987). Rheological Analysis of Tunnel Excavations by Means of Coupled Finite Element (Fem)–boundary Element (BEM) Analysis. Int. J. Numer. Anal. Methods Geomechanics 11. doi:10.1002/nag.1610110202

CrossRef Full Text | Google Scholar

Tating, F., Hack, R., and Jetten, V. (2013). Engineering Aspects and Time Effects of Rapid Deterioration of Sandstone in the Tropical Environment of Sabah, Malaysia. Eng. Geol. 159, 20–30. doi:10.1016/j.enggeo.2013.03.009

CrossRef Full Text | Google Scholar

Tugrul, A. (1998). The Application of Rock Mass Classification Systems to Underground Excavation in Weak Limestone, Atatürk Dam, turkey. Eng. Geol. 50, 337–345.

Google Scholar

Ündül, Ö., and Tuğrul, A. (2012). The Influence of Weathering on the Engineering Properties of Dunites. Rock Mech. Rock Eng. 45, 225–239. doi:10.1007/s00603-011-0174-1

CrossRef Full Text | Google Scholar

Usman, M., and Galler, R. (2013). Long-term Deterioration of Lining in Tunnels. Int. J. Rock Mech. Min. Sci. 64 (6), 84–89. doi:10.1016/j.ijrmms.2013.08.028

CrossRef Full Text | Google Scholar

Wong, L. N. Y., Maruvanchery, V., and Liu, G. (2016). Water Effects on Rock Strength and Stiffness Degradation. Acta Geotech. 11 (4), 713–737. doi:10.1007/s11440-015-0407-7

CrossRef Full Text | Google Scholar

Yokozeki, K., Watanabe, K., Sakata, N., and Otsuki, N. (2004). Modeling of Leaching from Cementitious Materials Used in Underground Environment. Appl. Clayence 26 (1), 293–308. doi:10.1016/j.clay.2003.12.027

CrossRef Full Text | Google Scholar

Yoshida, N., and Adachi, T. (2010). Fe Analysis of Time-dependent Instability of Cut Slopes in Clay Shale. American Society of Civil Engineers.

Google Scholar

Yoshida, N., Morgenstern, N. R., and Chan, D. H. (1990). A Failure Criterion for Stiff Soils and Rocks Exhibiting Softening. Can. Geotech. J. 27 (2), 195–202. doi:10.1139/t90-023

CrossRef Full Text | Google Scholar

Yoshida, N., Nishi, M., Kitamura, M., and Adachi, T. (1997). Analysis of Mudstone Deterioration and its Effect on Tunnel Performance. Int. J. Rock Mech. Min. Sci. 34 (3), 353. e1–353.e19. doi:10.1016/s1365-1609(97)00289-x

CrossRef Full Text | Google Scholar

Zhao, K., Wang, Q., Zhuang, H., Li, Z., and Chen, G. (2022). A Fully Coupled Flow Deformation Model for Seismic Site Response Analyses of Liquefiable Marine Sediments. Ocean. Eng. 251 (4), 111144. doi:10.1016/j.oceaneng.2022.111144

CrossRef Full Text | Google Scholar