Expansion of Blast Vibration Attenuation Equations for Deeply Buried Small Clearance Tunnels Based on Dimensional Analysis

The conventional empirical Sadowski formula has low prediction accuracy for the vibration velocity of the mass point in the near zone of the blast source, which makes it challenging to evaluate the damage of the building structures accurately. Considering the main influencing factors of blast vibration, the blast vibration attenuation law of deeply buried small clearance tunnels is investigated using dimensional analysis, and the Sadowski expansion formula is established considering the resistance line and free face. The regression analysis and fitting results were evaluated by combining the actual blast vibration data measured at the excavation site of the three separated tunnels at Badaling Great Wall Station with the post-expansion formula and the Sadowski formula, respectively. The results show that the correlation coefficients of the blast vibration expansion formulae based on the gauge theory for the fitted predictions of blast vibration isotropic velocities in a practical engineering context (0.92, 0.81, and 0.88, respectively) are higher than those of the conventional attenuation formulae, by 12, 10.5, and 6.3%, respectively, indicating that the expanded Sadowski formulae can better predict the blast vibration attenuation generated by the described deeply buried small clearance tunneling project.

Introduction

With the continuous development of tunnel excavation technology, it has been found that, from the aspects of construction efficiency and economy, etc., the drilling–blasting method has unparalleled advantages and will still play an essential role in the construction of various new types of tunnels in the future. With the development and upgrading of China’s transport facilities, new tunnel projects such as continuous arch tunnels, deeply buried small clearance tunnels, and overlapping cross tunnels have been launched. These projects are more susceptible to topography, geological conditions, and route alignment during construction, and the mutual spatial and positional relationships with existing tunnels are becoming more complex (Hong, 2017). In terms of efficiency and economy of construction, the drilling–blasting method has unparalleled advantages and will continue to play an essential role in the construction of new types of tunnels in the future (Guo, 2018). However, when using the drilling–blasting method for practical blasting engineering, the energy released is used in addition to rock fragmentation, part of which will also cause damage to the surrounding buildings (structures) in the form of waves (Tan et al., 2003). To accurately evaluate the extent of damage caused by seismic blast vibration to adjacent buildings and structures and control blast vibration within safe limits by appropriate means, it is essential to carry out a study of blast vibration propagation attenuation laws.

The Sadowski formula can describe blast vibration decay laws, which has been a great convenience in previous blast engineering studies (Sadowski and Chen, 1986). However, with the application of this formula in practical engineering, scholars have found that Sadowski’s formula is more suitable for predicting the decay of vibration velocities in the far zone of the blast source, while blast vibration in the near zone of the blast source is difficult to predict with the required accuracy (Fu et al., 2011). Due to the special construction environment of deeply buried small clearance tunnels, there is a great need for a more accurate prediction of blast vibration in the near zone of the source to ensure the safety of existing tunnels.

Based on the above practical situation, this paper combines the actual engineering blasting vibration data with the theory of dimensional analysis and proposes an expanded blasting vibration formula that considers the resistance line based on the traditional Sadowski formula. The expanded formula is further demonstrated by comparing the results of the expanded formula with those of the Sadowski formula.

Research Status

At present, the Sadowski formula is a semi-empirical formula widely used in practical blasting engineering in the world, by characterizing the relationship between the peak velocity of mass point vibration, the charge weight of blasting, and the blasting center distance to calculate the decay law of blast vibration velocity (Xiong and Gu, 2002):

$\mathrm{V=}\mathit{k}{\left(\frac{\sqrt[\mathit{3}]{\mathit{Q}}}{\mathit{D}}\right)}^{\alpha },$

where $\mathit{V}$is the peak velocity of blasting vibration, $cm/s$; $k$ is the site coefficient; $Q$ is the charge weight of blasting, $kg$; $D$ is the burst distance, $m$; and $\alpha$ is the attenuation coefficient.

The traditional formula for calculating blasting vibration velocity is the relationship between the peak vibration velocity and the proportional blasting charge. It can be seen from the Sadowski formula that when the blast source distance is certain, the vibration velocity increases with the increase in charge. However, Xin-kuan Zou (Zou et al., 2016) pointed out that, in a tunnel underground boring, blasting often shows a different situation from this, that is, when the free face and the minimum resistance line of influence are large enough, they will also have a certain impact on the blasting vibration velocity.

For the study of blasting vibration, relevant experts have used various research methods such as theoretical analysis, numerical simulation, and field examples. According to Ming-ya Bi (Mingya et al., 2009), the prediction of blasting vibration intensity is affected by various factors including geological and topographical conditions, material quantity, packet shape, and loading form, which are prone to significant errors. Tang et al. (2007) analyzed the influence of concave and convex geomorphology on the propagation of blasting vibration waves by taking geomorphological factors into account in the Guangdong Ling’ao nuclear power plant project. Wang et al. (2017) investigated the propagation of blasting vibration waves within a specific range of the adjacent surface based on investigating the reflection superposition law and the attenuation law of surface vibration velocity of blasting seismic waves in a specific range of the adjacent surface in tunnels with different burial depths based on numerical simulation, verification of measured data, and dimensional analysis and proposed that the calculation formula of surface vibration velocity attenuation considering the influence of burial depth can better reflect the attenuation law of surface vibration velocity. Zhang (2019) considered the influence of elevation and rock damage on the propagation pattern of blast vibration and, combined with actual engineering, concluded that rock damage has a significant weakening effect on the peak velocity of blast vibration.

Equation Expansion and Result Discussion

Calculation Model of Blast Vibration Velocity Based on Dimensional Analysis

In the deeply buried small clear distance tunnel projects, the distance between the excavated tunnel and the existing tunnel will be less than the buried depth of the tunnel. The length of the resistance line is the distance from the center of the blasting charge to the outer surface of the side wall lining of the existing tunnel. (In practical deeply buried small clearance tunneling projects, where the distance between the excavated tunnel and the existing tunnel is less than the tunnel depth, the length of the resistance line usually corresponds to the distance from the package to the lining of the existing tunnel sidewall.) To prevent damage to the existing tunnel lining caused by blasting vibrations during tunnel excavation, it is essential that the influence of the resistance line is considered in the actual predictions. The physical quantities associated with tunnel blasting and excavation are presented below. And through theoretical analysis of the magnitudes, a formula is derived for calculating the vibration velocity of tunnel blasting excavation, considering the effects of free face and resistance lines (Yang et al., 1994; Song et al., 2013).

In tunnel excavation blasting vibration velocity analysis, there are two main variables: one is the dependent variable, that is, the variable brought about by the different blasting design, mainly including the peak vibration velocity, single section blasting charge, and blast source distance, and the second is the independent variable, which includes the characteristics of the rock itself, rock density, and wave velocity. The main variables involved in the calculation of the model for studying the decay of vibration velocity in deeply buried small clearance tunnel blasting excavation are summarized in Table 1.

TABLE 1

TABLE 1. Main variables involved in the analytical calculation of blast vibration velocity.

The above influencing factors were selected as the main physical quantities affecting the peak velocity of blast vibration to be studied. It can be seen that the seven physical quantities affecting the propagation law of blast vibration velocity are all related to time $T$, length $L$, and mass $M$. Therefore, the expression of the basic gauge system is the following equation:

$\left[X\right]=L^{\alpha }{M}^{\beta }{T}^y.$

Here, $\left[X\right]$ represents the dimension of the variable $X$; $L$, $M$, and $T$ represent the dimension of length, mass, and time, respectively; and $\alpha$, $\beta$, and $\gamma$ are real-type indices.

The scale matrix $\theta$, based on the scale of each physical quantity listed in Table 1, is given by the following equation:

$\begin{array}{l}\left[\mathit{V}\mathit{Q}\mathit{D}{\rho }_{\mathrm{c}}c\frac{w}{d_b}A\right]\\ \downarrow \\ \theta =\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ -1& 0& 0\end{array}\begin{array}{ccc}-3& 1& 0\\ 1& 0& 0\\ 0& -1& 0\end{array}\begin{array}{c}2\\ 0\\ 0\end{array}\right]\to \left[\begin{array}{c}L\\ M\\ T\end{array}\right].\end{array}$

In order to determine the rank of the dimensional matrix $\theta$, the maximum charge of one section $D$, distance to the explosive’s center $D$, and rock wave velocity $c$ were selected as independent dimensions, and the following determinant was formed from them:

$\mathrm{\Delta }=\left|\begin{array}{ccc}0& 1& 1\\ 1& 0& 0\\ 0& 0& -1\end{array}\right|=1.$

Calculate the determinant △≠0, so the rank of the dimensional matrix $r\left(\theta \right)=3$, which indicates that the dimensional matrix is a non-linear correlation matrix. The number of dimensionless matrices is $k=n-r\left(\theta \right)=7-3=4$, and the expression of each dimensionless matrix is as follows:

$\begin{array}{l}\{\begin{array}{cccc}{\pi }_1={\left[M\right]}^{{\alpha }_1}& {\left[L\right]}^{{\beta }_1}& {\left[L{T}^{-1}\right]}^{y_1}& \left[L{T}^{-1}\right],\\ {\pi }_2={\left[M\right]}^{{\alpha }_2}& {\left[L\right]}^{{\beta }_2}& {\left[L{T}^{-1}\right]}^{y_2}& \left[M{L}^{-3}\right],\\ {\pi }_3={\left[M\right]}^{{\alpha }_3}& {\left[L\right]}^{{\beta }_3}& {\left[L{T}^{-1}\right]}^{y_3}& \left[L^2\right],& \end{array}{\pi }_4=\frac{w}{d_b}.\end{array}$

It is known that, in the above equation, ${\pi }_1\sim {\pi }_4$ are all dimensionless. And it follows from the volley principle of dimension that the power of any parameter in the fundamental system of magnitudes should be 0 (Li, 1992). Therefore, the parameters $M,L$, and $T$ of ${\pi }_1$ in the above equation have the following relationship:

$\{\begin{array}{c}{\alpha }_1=0,\\ {\beta }_1+{\gamma }_1+1=0\\ -{\gamma }_1-1=0.\end{array},$

The above equation corresponds to the sum of powers of $M,L$, and $T$, respectively, to 0. Solving the above equation gives ${\alpha }_1=0$, ${\beta }_1=0$, and ${\gamma }_1=-1$. Similarly, the values of ${\alpha }_2,{\beta }_2,{\gamma }_2,{\alpha }_3,{\beta }_3$, and ${\gamma }_3$ are $-\mathrm{1,3,0}$ and $0,-\mathrm{2,0}$ for ${\pi }_2$ and ${\pi }_3$, respectively. By bringing the calculated indices back to the expressions ${\pi }_1\sim {\pi }_4$, the dimensionless expressions can also be expressed as follows:

$\{\begin{array}{c}{\pi }_1=\frac{V}{c},\\ {\pi }_2=\frac{{\rho }_c}{Q{D}^{-3}},\\ {\pi }_3=\frac{A}{D^2},\\ {\pi }_4=\frac{w}{d_b}.\end{array}$

According to the theory of dimensional analysis (π theorem), the physical relations can be transformed into dimensionless form and the number of independent variables in the function is reduced. So, the relationship between the vibration velocity and the physical quantities in the tunnel when blasting excavation is carried out can be expressed as follows:

$\frac{V}{c}=\Phi \left(\frac{{\rho }_c}{Q{D}^{-3}},\frac{A}{D^2},\frac{w}{d_b}\right).$

In practical engineering, the density of the rock mass ${\rho }_c$ and the propagation velocity of the rock mass for vibration waves $c$ can be viewed as constants (Cai, 2013). Therefore, the following expression is derived for the function between the vibration velocity of tunnel blasting excavation and other physical quantities:

$\mathrm{In}\mathit{V=}{\alpha }_{\mathrm{0}}+{\alpha }_1\mathrm{In}\frac{\mathrm{1}}{\mathit{Q}{\mathit{D}}^{\mathrm{-3}}}+{\alpha }_2\mathrm{In}\frac{\mathit{A}}{{\mathit{D}}^{\mathrm{2}}}+{\alpha }_2\mathrm{In}\frac{\mathit{w}}{{\mathit{d}}_{\mathit{b}}}.$

Simplifying the equation above, we get

$V={\beta }_0\left(\frac{1}{Q{D}^{-3}}\right){\beta }_1\left(\frac{A}{D^3}\right){\beta }_2{\left(\frac{w}{d_b}\right)}^{{\beta }_3}.$

Observe that the first term of the above equation is found to be consistent with the proportional charge quantity of Sadowski formula $\rho$, so collating the above equation leads to the following equation:

$V={\gamma }_0{\left(\sqrt[3]{\frac{Q}{D}}\right)}^{{\gamma }_1}{\left(\frac{A}{D^2}\right)}^{{\gamma }_2}{\left(\frac{w}{d_b}\right)}^{{\gamma }_3}.$

The corresponding relationships between the coefficients in the above equations are as follows:

$\{\begin{array}{cc}{\beta }_0={\gamma }_0=e^{{\alpha }_0}& \\ {\alpha }_1={\beta }_1=-1\mathrm{/}3{\gamma }_1& \\ {\alpha }_2={\beta }_2={\gamma }_2& \\ {\alpha }_3={\beta }_3={\gamma }_3& \end{array}$

Analyzing the final expression, the first term on the right-hand side of the equation, ${\gamma }_0{\left(\raisebox{1ex}{$\sqrt[3]{Q}$}\!\left/ \!\raisebox{-1ex}{$D$}\right.\right)}^{{\gamma }_1}$, is identical to the traditional Sadowski formula and shows the relationship between the blast vibration velocity and the proportional charge; the second term, ${\left(\raisebox{1ex}{$A$}\!\left/ \!\raisebox{-1ex}{$D^2$}\right.\right)}^{{\gamma }_2}$, integrates the effect of the area of the free face of the blasting excavation on the blast vibration intensity; the last term, ${\left(\raisebox{1ex}{$w$}\!\left/ \!\raisebox{-1ex}{$d_b$}\right.\right)}^{{\gamma }_3}$, considers the effect of the length of the minimal resistance line on the blast intensity and is more applicable to the prediction of blasting vibration velocity for deeply buried small clearance tunnel projects.

Application of the Expansion Formula to the Great Wall Station Tunnel at Badaling

A sample of actual blasting data from Badaling Great Wall Station was used for analysis. The station has many levels, many cavities, and complex cavity types, making it the most complex concealed cavity group station in China. There are multiple spatial relationships in the construction of sections and areas affected by close blasting construction.

Mountain tunnels with a burial depth $H$ exceeding 50 m (conservatively estimated at 100 m) can be classified as deeply buried tunnels (Rao and Wang, 2013). In contrast, a small clear distance tunnel is a special form of tunnel arrangement where the thickness of the intermediate rock column between the tunnels is less than the recommended value in Table 2 (Specification for Design of Highway Route JTG D70). The Badaling tunnel project is a mountainous tunnel with a burial depth of over 100 m and a maximum tunnel spacing of 6 m<2.0 × 7 m (excavated section of Grade III surrounding rock), so it is a deeply buried small clearance tunnel project.

TABLE 2

TABLE 2. Minimum clearances for separate independent double holes.

The three separate cavern sections are part of a three-line parallel tunnel group, with the right line 2 months behind the mainline and the mainline 3 months behind the left line. Their actual excavation dimensions and chamber spacing are shown in Figure 1. As the net distance between the rock columns of the three parallel tunnels is only 2.27–6 m, blasting in the mainline will cause vibration effects or even damage to the left and right line tunnel structures on both sides where the initial support or secondary lining has been completed. Blasting vibration control is required to ensure that the support effect of the existing support is not affected.

FIGURE 1

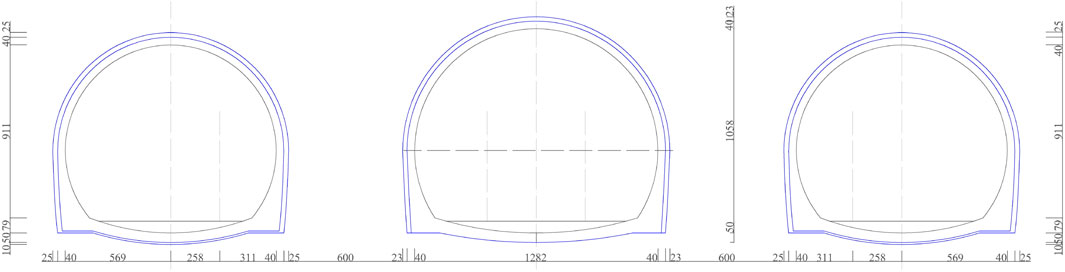
FIGURE 1. Schematic diagram of the cross-sectional dimensions and spacing of the three-hole separation section.

The section of the Great Wall Station at Badaling is 398 m in length, and the surrounding rock level is mainly Grade III. In the actual blasting construction, the section of Grade III surrounding rock is constructed by the step method, with a step length of 5∼8 m, in the order of up- and down-blasting construction. The holes were drilled by hand-held wind drill with a diameter of 42 mm, and the blasting explosive was Φ32 mm rock emulsion explosive. The layered explosive loading structure and uncoupled explosive loading structure are adopted.

Physical measures of blast vibration intensity include the mass vibration velocity, displacement, acceleration, and energy ratio. Following the Safety Regulations for Blasting, this paper uses mass point vibration velocity as the basis for measurement. TC-4850 blasting vibration meter is shown in Figure 2. By importing the vibration data into the software and analyzing the analysis, the vibration velocity of the mass at each monitoring point can be directly obtained as $X$ (horizontal radial), $Y$ (horizontal tangential), and $Z$ (vertical ground direction), and the combined velocity can be analyzed by vector operation of the three velocity values.

FIGURE 2

FIGURE 2. Site layout of the TC-4850 blast vibrometer.

The vibration test was used to monitor the changes in blast vibration velocity and acceleration at the foot and waist of the left-hand side of the excavated chamber and at various points in the same plane as the palm face during the blasting construction of the cavern. The actual measurement points are shown in Figure 3 and Figure 4, with a total of seven measurement points, of which measurement point 2 is facing the blast charging section of the tunnel palm face; measurement point 1 is placed in the excavated section and measurement point 2 is 5 m away; measurement points 3, 4, and 5 are placed in the unexplored area and the distance from measurement point 2 is 5, 13, and 23 m; and measurement points 6 and 7 are in the same plane as measurement point 2 but 0.8 m lower than measurement point 2. The blast vibration velocities at different locations were analyzed by monitoring the vibration velocities of one line and the same plane of measurement points.

FIGURE 3

FIGURE 3. Schematic layout of vibration measurement points.

FIGURE 4

FIGURE 4. Schematic diagram of the lateral arrangement of vibration measurement points.

The measured vibration sensors were recorded in all three directions at the same time, and the measured vibration data are listed in Table 3.

TABLE 3

TABLE 3. Measured vibration velocity data for different blast sources from the measurement point.

Result Evaluation

In examining the accuracy of the predictions, the correlation coefficient $R{ }^2$ is introduced for evaluation. This indicator is used in statistics to evaluate how closely the regression model approximates the sample. As $R{ }^2$ gets closer to 1, it indicates a better fit between the original and sample data, and its mathematical expression is given as

$R^2=1-\frac{SSR}{SST}=1\frac{{\displaystyle \sum {\left(y_i-{\stackrel{⌢}{y}}_i\right)}^2}}{{\displaystyle \sum {\left(y_i-{\overline{y}}_i\right)}^2}},$

where $y^i$ is the ith measured value; $\widehat{y{ }^i}$ is the $A th$ predicted value according to the fitted model; $SST={\displaystyle \sum {\left(y_i-{\overline{y}}_i\right)}^2}$ is the sum of squared total deviations; $SSR={\displaystyle \sum {\left(y_i-{\widehat{y}}_i\right)}^2}$ is the sum of squared residual regressions; and $\overline{y}=1/n{\displaystyle \sum }_{i=1}^n{y}_i$ is the mean of the measured results.

In practical engineering based on the traditional empirical formula to regress the blast vibration peak velocity and proportional charge into a linear relationship and to obtain the decay law of the blast vibration peak velocity, based on the monitoring data in Table 3, the peak vibration velocities of tangential, radial, and vectorial synthesis in measurement points 1 to 5 were calculated to obtain the fitted curves and the corresponding Sadowski empirical decay formulae, as listed in Table 4 for each direction of the fitted results.

TABLE 4

TABLE 4. Results of the fitting of the Sadowski empirical formula.

The predictions of the above two equations were evaluated through correlation coefficients, and the comparison shown in Figure 5 shows that the correlation coefficient R^2 of the attenuation indices calculated using the gauge calculation model has improved, regardless of radial, tangential, or combined velocities.

FIGURE 5

FIGURE 5. Comparison of results before and after formula expansion.

The above data show that the tunnel blasting vibration velocity calculation model based on this method can better reflect the existing tunnel lining vibration attenuation pattern when blasting deeply buried small clearance tunnels. In comparison with the traditional blasting vibration velocity calculation formula, it is found that the traditional empirical formula mainly considers the influence of the proportional dose, although the proportional dose is the main factor of blasting vibration velocity, but in actual engineering, it is found that the peak mass vibration velocity is inversely related to the free surface area $A$. With the increase of the free surface area, the peak blasting vibration velocity decreases but is positively related to the resistance line length $w$. This law accurately reflects the influence of the free face and the resistance line on blast vibration. The effect of the free surface and resistance line on blast vibration velocity cannot be ignored, and both need to be considered as correction factors in the vibration velocity calculation equation to provide a more comprehensive response to the actual vibration characteristics caused by blasting excavation in the tunnel.

Conclusion

This paper combines measured blast vibration monitoring data from the tunnel excavation at Badaling Great Wall Station, systematically analyzes the propagation and attenuation laws of blast seismic waves in deeply buried small clearance tunnels, and draws the following conclusions:

1. By analyzing the relevant factors affecting the vibration velocity of the actual engineering blasting mass, including the length of the resistance line and the area of the free surface, combined with the exhaustive derivation of the dimensional analysis, the expanded blasting vibration velocity decay formula is$\mathrm{V=}{\gamma }_{\mathrm{0}}{\left(\frac{\sqrt[3]{Q}}{D}\right)}^{{\gamma }_1}{\left(\frac{A}{D^2}\right)}^{{\gamma }_2}{\left(\frac{w}{d_b}\right)}^{{\gamma }_3}$.

2. Based on the results of fitting the measured vibration data, it can be concluded that compared to the traditional Sadowski empirical formula, the correlation coefficient of the extended formula proposed in this paper has been improved, and the correlation of the fit is better, which can better reflect the impact of blasting vibration on the existing tunnel lining when blasting a deeply buried tunnel with small clearances.

When blasting other deeply buried small clearance tunneling projects, the expanded vibration velocity decay formula derived in this paper can be used for calculations in the near zone of the blast, and the explosive unit consumption can be adjusted in a timely manner according to the gun hole diameter, free surface area, and other factors.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author Contributions

J-JS conceptualized the research idea, supervised the work, and reviewed and edited the paper. S-CG and J-JS performed the methodology. S-CG and WZ wrote the original draft. All authors have read and agreed to the published version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, M. (2013). Rock Mechanics Rock Engineering. Beijing, China: Science Press.

Google Scholar

Fu, H-X., Zhao, Y., and Jin, S. X. (2011). Study of Blasting Vibration Test of Area Near Tunnel Blasting Source. Chin. J. Rock Mech. Eng. 30 (2), 335–340.

Google Scholar

Guo, S-Y. (2018). Technical Development and Outlook of the Tunnels and Underground Works in China. Mod. Tunn. Technol. 55 (S2), 1.

Google Scholar

Hong, K-R. (2017). Development and Prospects of Tunnels and Underground Works in China in Recent Two Years. Tunn. Constr. 37 (2), 123.

Google Scholar

Li, Y. (1992). Mechanics of Explosion. Beijing, China: Science Press.

Google Scholar

Mingya, B., Li, M., and Liu, C. (2009). Analysis of Forecasting Error for Blasting Vibration. Blasting 26 (2), 96–98.

Google Scholar

Rao, Y., and Wang, H. (2013). Multiple Linear Regression Analysis of Blasting Vibration Velocity Attenuation. Metal. Mine (12), 46–47.

Google Scholar

Sadowski, M. A., and Chen, Y-F. (1986). Earthquake Prediction. translated. Beijing, China: Seismological Press.

Google Scholar

Song, Y., Zhang, Z., and He, H. (2013). Wavelet Packet Energy Analysis of the Vibration and Vibration of the Chamber. Eng. Blasting 19 (4), 14–20.

Google Scholar

Tan, Z-S., Yang, X-L., and Wang, M-S. (2003). Effect of Blast in Double Line Tunnel on Existing Tunnel. Chin. J. Rock Mech. Eng. 22 (2), 281–285.

Google Scholar

Tang, H., Li, H. B., Jiang, P. C., and Wang, X. (2007). Experimental Study on Effect of Topography on Propagation of Blasting Waves. Chin. J. Rock Mech. Eng. 26 (9), 1817–1823.

Google Scholar

Wang, C., Zhou, C., and Lu, S. (2017). Propagation Pattern of Blasting Vibration in the Surrounding Rock of Metro Tunnel. Sci. Technol. Eng. 17 (6), 158–162.

Google Scholar

Xiong, D-Y., and Gu, Y-C. (2002). New Progress in Rock Blasting Theory and Technology. Beijing, China: Metallurgical Industry Press.

Google Scholar

Yang, G. L., Rocque, P., and Bawden, W. F. (1994). Measyrement and Analysis of Near-Field Blast Vibration and Damage. Geotechnical Geol. Eng. 12 (2), 169–182.

CrossRef Full Text | Google Scholar

Zhang, Q. B. (2019). Research on Blasting Vibration Propagation Law and its Control Technology Considering Elevation and Rock Mass Damage. Nanning Guangxi Univ.

Google Scholar

Zou, X-K., Zhang, Ji-C., Pan, Q., and Shi, H-C. (2016). Numerical Simulation and Analysis of Construction Behavior for Dual-Arch Tunnel Tunneling Overlapped to Existing Tunnel. J. Jiangsu Univ. Nat. Sci. Ed. 2016 (2), 225–230.

Google Scholar