Study on Optimization of Stope Structural Parameters and Filling Scheme of Wawu Phosphate Mine in Yichang City, China

Reasonable stope structural parameters are very important to ensure the safety and efficiency of mining. In this paper, based on the elastic-plastic constitutive model of Mohr-Coulomb strength criterion, the reasonable span and critical span are calculated by using simply supported beam theory and mine room width calculation formula. PLAXIS2D finite element analysis software was used to conduct numerical simulation research on 7 m × 9 m, 5 m × 12 m stope structure parameter schemes and 7 m × 9m, 5 m × 12 m waste rock filling schemes. The optimal structure parameters of the stope were determined based on the calculation and analysis of displacement variation rule, surrounding rock stress distribution and plastic zone. The analysis and simulation results show that Case 1 one-time mining 7 m × 9 m and Case 3 one-time mining 5 m × 12 m, the plastic zone is connected, the simulation calculation is not convergent, and the stope is unstable. Case 2 waste rock filling 7 m × 9 m and Case 4 waste rock filling 5 m × 12 m, the distribution and change of stress, displacement and plastic zone in the goaf under the two cases are compared, and finally the waste rock filling 7 m × 9 m is obtained can improve the economy and safety of mining in the mining area, and verify the feasibility of implementing stope structural parameters and waste rock filling mining system is verified.

1 Introduction

In terms of mining design and actual mining conditions, on the one hand, stope structure parameters affect the stability of continuous mining of underground stope, on the other hand, they also affect the economic benefits of mining (Dong et al., 2017; Xu et al., 2021). Thus, it is certainly need to select reasonable stope structure parameters from the aspects of safety and economy (Qiao 2001; Yang and Ore, 2015; Fu et al., 2017; Wojtecki et al., 2021). When the span of the mine room is small and the size of the ore pillar is too large, although the safety is improved, the ore recovery rate will be low, when the pillar size is too small and the room span is large, it will reduce the stope stability and increase the probability of large-scale ground pressure activities (Cao et al., 2019; Huang et al., 2021a; Huang et al., 2021b; Guo et al., 2021; Liu et al., 2021; Wang et al., 2021), which will bring great danger to safety production (Castro-Caicedo, 2019; Hu et al., 2019; Almoataz et al., 2020; Mikhail et al., 2020). Therefore, it is necessary to optimize the stope structural parameters to ensure the safety and efficiency of stope mining (Xiang and Ke, 2014; Tang et al., 2017; Liu et al., 2018; Zhu et al., 2021a; Sun et al., 2021).

The traditional optimization methods of stope structural parameters mainly include field test Zhang (2009) and model test Zhang (2010). These methods are difficult to accurately realize the optimization selection of various structural parameters with the integration of computer technology and numerical analysis method, the stability analysis of stope, pillar and mine room under different stope structural parameters can be carried out by using computer simulation software (Du et al., 2016; Tang et al., 2016; Wang et al., 2016; Barnewold and Lottermoser, 2020).

In recent years, many scholars have used numerical simulation software to study the optimization of stope structural parameters (Wagner 2009; Falaknaz et al., 2015a; Falaknaz et al., 2015b; Kamash et al., 2021). Lin (2021) designed the numerical simulation of different schemes of the stope structure of the metal mine based on the orthogonal test method, so as to analyzed and selected the best parameter optimization results. Qiu et al. (2013) used ANSYS numerical simulation software, the stope structural parameters of room height, length, width and pillar width are optimized. Through comparative analysis, the optimal stope structure parameters are obtained. Zhao et al. (2019) used Mathews stability diagram method, and Yang et al. (2017) used FLAC3D numerical simulation and theoretical calculation, the stability of stope roof and pillar is comprehensively studied to determine the reasonable stope structure parameters. Ge (2017) used MIDAS-GTS technology to obtain the optimization scheme of stope structural parameters. Yi and Liao (2017) optimized the stope structural parameters based on ANSYS and fuzzy evaluation, and obtained the optimal combination scheme of room and pillar width. Li et al. (2019) used the principle of orthogonal test to optimize the parameters of a thick and large iron mine stope and realized efficient and economic mining. Idris and Nordlund (2019) used FLAC3D to study the deformation magnitudes of various stope geometries to determine the optimal stope geometry with a minimum ground control problem. Jing et al. (2020)used FLAC3D numerical software to support scheme of the excavated roadway was then designed, and the effectiveness of this support scheme was further verified by the displacement measurement of the roadway.

The above scholars analyzed the stability of surrounding rock and the optimization of structural parameters in underground mining in the mining area through the change law of ore and rock mechanics in the mining process. However, at present, the scale of the underground goaf of the mine is large, which increases the difficulty of recovering the remaining ore resources. In the process of phosphate rock mining, the joint influence of structural parameters and waste rock filling is still lack of optimization research.

Therefore, this study uses the finite element analysis software PLAXIS 2D, which can simulate the complex geotechnical structure, carry out the simulation calculation of step-by-step construction, activate and suppress various unit components, and simulate the optimization of structural parameters of underground phosphate rock mining by using load and other functions. Through the comparative analysis of stope space width, pillar width and other parameters, combined with simply supported beam theory and reasonable stope width theory, the synergistic effect of the best stope structure parameters and filling scheme is finally obtained. It provides guidance for efficient and safe mining of phosphate rock and reference for mining of similar mines.

2 Study Area and Materials

2.1 Stratigraphic Conditions

Wawu IV ore block belongs to medium and high mountain area. After denudation and strong erosion, it forms the geomorphic characteristics of vertical and horizontal gullies and overlapping mountains. The highest altitude in the area is 1710 m, which is located in Gaobaling in the east of the mining area, and the lowest is 574 m, which is located in Zhuyuan River in the southwest corner of the mining section. The maximum relative elevation difference is 1136 m, generally about 400∼800 m. Most of the peaks are round, a few isolated peaks are bamboo shoots, and most of them are cliffs. The valley is a “V” shaped valley with narrow valley bottom and valley slope of 40°∼80°. The whole mining area is covered with lush forests, and the steep terrain is conducive to drainage.

Phosphate rock is located in the northeast of Huangling anticline. The exposed strata in the area include Mesoproterozoic Shennongjia group (Ptsh) and Kongling group (Ptkn). Neoproterozoic upper Nanhua NANTUO formation (Nh₂n), Sinian Doushantuo Formation (Z₁d), Dengying Formation (Z₂dn), Paleozoic Cambrian (∈), Ordovician (O), Silurian (S) and Cenozoic Quaternary. The phosphorous rock series in this ore block is mainly composed of phosphorous mudstone and dolomite. The main ore bed in the ore section is Ph₁³ ore bed, which is stably distributed in the north of the ore section and occurs in layers. It is monoclinic structure as a whole with slight wavy fluctuation. The ore bed is inclined to the southeast as a whole, with a dip of 130°∼175°, and the dip angle is generally 18°∼35°. Affected by faults, the ore bed becomes steeper or even upright locally.

2.2 Hydrometeorological Conditions

The mining area belongs to subtropical monsoon climate with four distinct seasons and abundant rainfall, with typical mountain climate characteristics. The annual maximum precipitation (83 years) is 1552.42 mm, the annual minimum precipitation (88 years) is 913.7 mm, the annual average rainfall day is 155 days, and the maximum daily precipitation (September 9, 83 years) is 109.7 mm. The precipitation is concentrated. The precipitation in rainy season (may October) accounts for 80.9% of the annual precipitation, the precipitation in dry season (November February of the next year) accounts for 9.4% of the annual precipitation, and the freezing period is from December to march of the next year.

The phosphate rock layers in ore block IV of Wawu mine are concealed underground, and more than two-thirds of the phosphate rock layers occur above the local erosion base level. The hydrogeological conditions of ore block IV belong to the karst water filled deposit of “the water filled rock stratum is mainly composed of dissolution fractures, the roof has direct and indirect water inflow, and the hydrogeological conditions are medium to complex.”

2.3 Lithology of Surrounding Rock at the Top and Bottom of Phosphate Rock Layer

2.3.1 Surrounding Rock of Phosphate Rock Roof

The lithology of the surrounding rock of the phosphate rock roof is siliceous, porous and fine-grained dolomite, with good continuity and integrity of the rock stratum. The thickness of rock stratum is 57.98 ∼ 107.56 m, the average thickness is 93.13 m, the content of P₂O₅ is 0.12% ∼ 6.80%, and the average content is 1.67%. The compressive strength of roof dolomite is 117 mpa, the rock is hard and has high strength. The joint fissures in the dolomite layer of the roof are not very developed, and the fissures are mostly filled with calcite veins. Generally, a tensile fissure can be seen only at a distance of 20 ∼ 40 m, and the tunnel needs support only at the large structural fracture zone.

2.3.2 Phosphate Rock Layer

Ph₁³ phosphate rock layer is produced in layers and blocks with good integrity. The thickness of the ore bed is 1.47 ∼ 10.66 m, the average thickness is 5.46 M, the content of P₂O₅ is 18.06% ∼ 29.86%, and the average content is 22.12%.The compressive strength of phosphate rock layer is 116 mpa, dense, hard and high strength. The joint fissures of phosphate rock layer are basically closed and have good stability. No large fracture zone and water leakage are found in drilling or tunnel excavation.

2.3.3 Floor Surrounding Rock

The lithology of the surrounding rock of the floor of the phosphate rock layer is the same as that of the surrounding rock of the roof. The thickness of the rock stratum is 12.95 ∼ 86.26 m, with an average thickness of 32.30 m. The content of P₂O₅ (phosphorous mudstone in the direct floor) is 0.86% ∼ 9.9%, with an average content of 1.93%. The compressive strength of floor dolomite is 138 mpa, the rock is hard and has high strength.

2.4 Selection of Mechanical Parameters of Rock Mass

The surrounding rock of phosphorus ore bed roof in Wawu IV ore block is dolomite, with hard rock, high strength and good integrity. Ph₁³ phosphorene bed is dense, hard and complete. The engineering geological conditions of Wawu IV ore block belong to medium type. Because there are some differences between the mechanical parameters of rock and rock mass, it is necessary to weaken the mechanical parameters of rock to obtain the mechanical parameters of rock mass. Firstly, the mechanical parameters of rock are obtained through indoor experiments (Wu et al., 2020; Dong et al., 2021; Gao et al., 2021; Wang and Liu 2021), and then weakened by using empirical reduction method and Hoek-Brown strength criterion (Serrano et al., 2016; Shi 2016) according to the on-site geological conditions.

The selection of rock mass parameters in this paper is based on the analysis of the existing data of the mine, and referring to the above relevant literature and field mechanical tests, to comprehensively obtain the physical and mechanical parameters of roof dolomite, floor dolomite, filling body and ore deposit. The obtained physical and mechanical parameters of rock mass are shown in the Table 1.

TABLE 1

TABLE 1. Physical and mechanical parameters of rock mass in ore section.

2.5 Other Geological Conditions

According to records, earthquakes in Yichang City in history are mainly weak earthquakes, and there has been no destructive earthquake. According to the seismic ground motion parameter zoning map of China (GB18036-2001), the mining area belongs to the seismic basic intensity VI area, and the seismic basic acceleration is 0.05 g. According to the crustal stability grade and seismic index, the mining area belongs to the stable area. No magmatism has been found in the ore section. The metamorphism in the ore block only shows the shallow metamorphism of the basement strata of the Middle Proterozoic Shennongjia group.

3 Model Establishment

3.1 Basic Assumptions and Premises

In view of the complexity of stope mining technology, in order to facilitate modeling and calculation analysis, the following simplifications and assumptions are made:

(1) It is assumed that the rocks and fillings in the model are homogeneous and isotropic continuous media.

(2) Because there are few faults and structural planes in the buried area of phosphate rock, the influence of factors such as interruption layer, fracture and structural plane on the stability of the mining area is ignored in the modeling process.

(3) Because the geological structure of the buried area of phosphate rock is also relatively simple, the structural stress is ignored and only the influence of gravity on the calculation model is considered.

(4) In order to improve the calculation efficiency, it is assumed that the processes such as mine room excavation and filling goaf are completed at one time.

(5) The simulated stope height is 68 m, the horizontal thickness of the excavated ore body is 8 m, and the ore body dip angle is 30°. Pillar sizes are 5 m × 5 m and 7 m × 7 m respectively.

3.2 Simulation Area Selection

Select the drift of ore Section 4 of Wawu phosphate mine, take 32 m thick rock mass above and below the phosphate rock layer, and select the section passing through exploration line 23 for numerical analysis. The phosphate rock layer is subjected to the self-weight load of the overlying rock mass. The self-weight load is estimated by multiplying the thickness of the phosphate rock layer from the surface by the unit weight of the soil. The thickness from the surface is taken as 400 m, and the unit weight of the rock mass is taken as 27 KN/m³, equivalent to 400 m × 27 KN/m³ = 12420 KPa, applied to the upper part of phosphate rock layer, p = 12420 KPa. The selected simulation area is shown in Figure 1 and Figure 2.

FIGURE 1

FIGURE 1. Plan of roadway in section IV of Wawu Phosphate Mine.

FIGURE 2

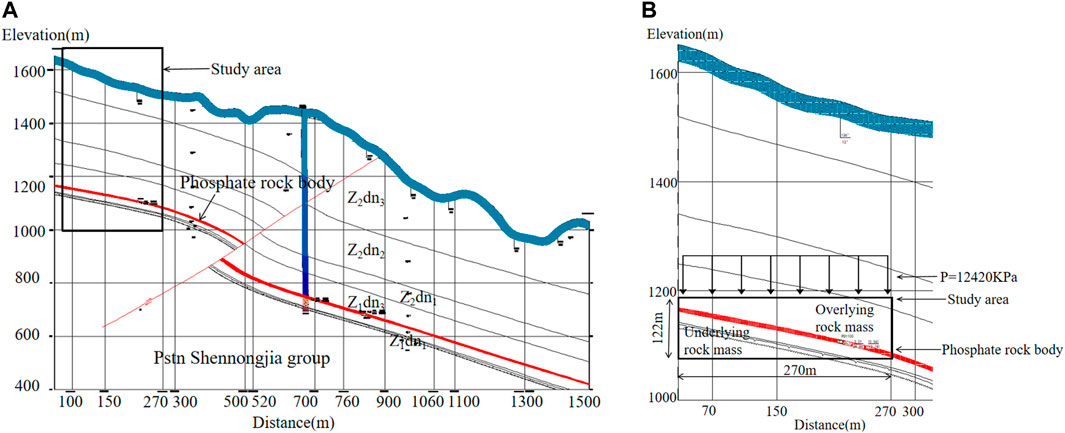
FIGURE 2. (A) Area diagram of numerical simulation of Wawu phosphate ore section IV (Pressure p = 12.42 MPa). (B) Area diagram of numerical simulation of Wawu phosphate ore section IV (Pressure p = 12.42 MPa)

3.3 Simply Supported Beam Theory and Calculation of Reasonable Room

The stope roof can be assumed to be simply supported beams at both ends Yang et al. (2015). According to the material mechanics, the stress at any point on the upper and lower surfaces of the neutral axis of the rock beam is:

$\sigma \left(x\right)=\frac{\gamma \left(2x-l\right)\sin \alpha }{2}\pm \frac{\gamma x\left(x-l\right)\cos \alpha }{h}(1)$

Where, ɑ is the dip angle of ore body, (°). l is the span of rock beam, m. h is the height of rock beam, m. $\gamma$ is the unit weight of rock mass, 10⁴ N/m³. The maximum tensile stress occurs on the lower surface of the neutral axis of the rock beam a $\text{x}=\text{L}/2+\text{h}\tan \text{α}/6$ and the maximum tensile stress is:

${\sigma }_{\max }=\frac{3\gamma L^2\cos \alpha }{4h}-\frac{h\gamma {\tan }^2\alpha \cos \alpha }{12}(2)$

The maximum allowable span of roof inclination is:

$L_{\text{qy}}={\left[\frac{4h{\sigma }_t}{3\gamma \cos \alpha }-\frac{h^2{\tan }^2\alpha }{9}\right]}^{1\text{/}2}(3)$

The maximum allowable span of the vertical strike of the roof is:

$L_{sp}={L_{qy}|}_{\left(\alpha =0^0\right)}={\left[\frac{4h{\sigma }_t}{3\gamma }\right]}^{1/2}(4)$

The stress analysis of simply supported beam is shown in Figure 3.

FIGURE 3

FIGURE 3. Stress analysis of simply supported rock beam.

For the stope mined by stage open stope and subsequent filling method, the width of the stope can be determined according to the safety guarantee and production capacity of stope mining Zhang et al. (2021). When the stope safety is guaranteed, the greater the width and height of the stope, the greater the production capacity of the stope Zhang et al. (2014). The calculation formula of room width is as follows:

$L=\frac{4.5\left(\beta \gamma {\rm H}+{\sigma }_t\right)}{\gamma {\rm H}\left(1-0.8\beta \right)-0.8\sigma {\mathrm{\prime }}_t}(5)$

Where, H is the mining depth of the ore body, m. β Is the lateral pressure coefficient, generally taken as 0.65. σ_t T is the tensile strength of top pillar rock stratum (reduced according to the tensile strength of rock mass, generally 0.4), MPa. Taking H = 400 m, γ = 29 kN/m³, σ_t = 2.1 MPa is substituted into Eq. 5, It can be obtained that the room width of the filling yard of phosphate rock in Ore Section 4 of Wawu phosphate rock area is about L = 9 m. Therefore, we have obtained the empty yard span of each scheme, as shown in Table 2.

TABLE 2

TABLE 2. Allowable empty field span of each scheme.

The calculation result of simply supported beam theory is the maximum allowable span under corresponding ore and rock conditions, so the result is too large. In practical application, the calculation result of reasonable room width should be taken as reference, and the maximum cannot exceed the calculation result of simply supported beam theory. Therefore, the width of the simulated ore room is 12 and 9 m respectively.

3.4 Failure Criterion

PLAXIS program has strong application and can simulate complex engineering geological conditions, especially suitable for deformation and stability analysis. PLAXIS program can calculate two kinds of engineering problems: plane strain problem and axisymmetric problem. It can simulate soil, wall, slab, beam structure, contact surface between various elements and soil, anchor bolt, geotextile, tunnel, pile foundation and other elements. Analyze 2D and 3D deformation, consolidation, graded loading, stability analysis and seepage calculation in geotechnical engineering. PLAXIS uses the finite element strength reduction method to calculate the safety factor in the sense of soil mechanics.

The values of displacement, stress, strain and member internal force can be output to the table. The constitutive model of soil, linear elasticity, Mohr Coulomb, soft soil model, hardening model and soft soil rheological model can simulate the construction steps, and the post-processing of multi-step calculation is simple and convenient (Huang et al., 2017; Zhu et al., 2021b).

The lithology of the phosphate rock is mainly composed of dolomite and mudstone, which are elastic-plastic bodies. Therefore, it is applicable to the strength failure criterion of Mohr Coulomb. The mechanical model is shown in Figure 4. Based on Mohr-Coulomb strength criterion, the shear failure envelope ƒ^s = 0 on segment AB is defined as:

$f^s={\sigma }_1-{\sigma }_3\frac{1+\sin \varphi }{1-\sin \varphi }+2c\sqrt{\frac{1+\sin \varphi }{1-\sin \varphi }}(6)$

FIGURE 4

FIGURE 4. Mohr-Coulomb strength criterion in PLAXIS2D.

Based on the tensile failure criterion, the tensile failure envelope ƒ^t = 0 on segment BC is defined as:

$f^t={\sigma }^t-{\sigma }_3(7)$

Where, σ₁ is the maximum principal stress, MPa. σ₃ is the minimum principal stress, MPa. φ is the internal friction angle, (°). c is cohesion, MPa. σ_t is tensile strength, MPa. In Figure 4, the points on line AB or line BC are in critical failure state. The lower left half (area I) of the area surrounded by three line segments AB, BC and σ₃-σ₁ = 0 is in an undamaged state, the upper right half (area II) is in a damaged state.

3.5 Preliminary Scheme Selection of Stope Structure

This study mainly focuses on the numerical simulation and optimization of stope structural parameters Zhang and Chen (2016). According to 3.3 simply supported beam theory and reasonable chamber width calculation results, the maximum allowable span and reasonable span of each case are determined. Combined with the existing mining technical conditions and actual production conditions, the following four cases are put forward, and the stope stability under the four cases is compared. There are two options. The first scheme is to change the stope structural parameters (Case 1 and Case 3), and the second scheme is to increase waste rock filling (Case 2 and Case 4).

Case 1: The stope structural parameters are the pillar width of 5 m, the room width of 12 m and the ore body thickness of 8 m. No filling is carried out after one-time excavation.

Case 2: The stope structural parameters are pillar width of 5 m, room width of 12 m and ore body thickness of 8 m. For waste rock filling, three ore chambers are filled horizontally and longitudinally to form a large point column with the ore pillar. Two ore chambers are left at the periphery without filling, and then filled all the time according to the same method, as shown in Figure 5.

FIGURE 5

FIGURE 5. Schematic diagram of filling scheme.

Case 3: The stope structural parameters are pillar width of 7 m, room width of 9 m and ore body thickness of 8 m. No filling is carried out after one-time excavation.

Case 4: The stope structural parameters are pillar width 7 m, room width 9 m and ore body thickness 8 m. The waste rock filling method is the same as Case 2. The schematic diagram of mining scheme is shown in Figure 6.

FIGURE 6

FIGURE 6. Schematic diagram of mining scheme.

3.6 Boundary Condition

The finite difference software PLAXIS 2D is used for modeling. According to the elastic-plastic theory, the mining influence range after stope excavation is usually within 5 times of the roadway radius. In this paper, the model is established based on 3–5 times of the analysis area. The model is 270 m long, 122 m high and 8 m thick, with 42,763 nodes and 5,275 units. The horizontal displacement constraint in the X direction is adopted on the left and right sides of the model, the horizontal and vertical constraints are applied on the bottom of the model, the model surface is free constraint, show in Figure 7.

FIGURE 7

FIGURE 7. PLAXIS2D modeling diagram.

4 Simulation Results and Analysis

Under the same mining method, change the stope structural parameters and waste rock filling scheme. According to the numerical simulation results, analyze the displacement, maximum principal stress and plastic zone range of each stope top, floor and point column, so as to judge the stope stability. The displacement, stress and plastic zone parameters of each scheme are shown in Table 3.

TABLE 3

TABLE 3. Displacement, stress and plastic zone parameters of each project.

4.1 Analysis of Displacement Distribution Law

Because the original stress balance state is broken, the roof and floor of the stope are affected by horizontal stress, so they squeeze towards the goaf, resulting in displacement towards the goaf. Among them, the vertical displacement generated in the middle of the roof of the goaf is the largest. It can be seen from Figure 8 that the maximum displacement generated by the roof in Case 1 is 2.8 cm, in Case 2 is 2.0 cm, in Case 3 is 1.8 cm and the maximum displacement of the top plate in Case 4 is 1.0 cm. Therefore, the maximum displacement generated by the roof in Case 4 is the minimum. After filling the goaf, it can be seen from the Figure 8 that the overall displacement of the rock mass in the mining area decreases to a certain extent. The addition of filling body reduces the settlement displacement of surrounding rock in the mining area and the affected area of surrounding rock settlement, so that the influence of mining disturbance on the overlying strata of goaf roof and surface becomes smaller. This shows that filling the goaf after room mining effectively enhances the stability of the seam and reduces the possibility of geological disasters such as surface subsidence and mine collapse.

FIGURE 8

FIGURE 8. Vertical displacement of stope roof in four case.

4.2 Analysis of Distribution Law of Maximum Principal Stress

Due to the mining of stope, the stress of stope and surrounding rock is released, breaking the original stress state and redistributing the stress of surrounding rock. Stress concentration occurs at the top and bottom corners of the stope, and the compressive stress is mainly concentrated on the room and pillar. It can be seen from Figure 9 that the maximum principal stress of the whole goaf roof in Case 1 is about 36.84 MPa, in Case 2 is about 32.51 MPa, in Case 3 is about 28.98 MPa and in Case 4 is about 24.71 MPa. Therefore, the maximum principal stress of goaf roof in Case 4 is the minimum. After filling the goaf, the distribution of stress concentration area becomes less, and part of the tensile area is transformed into compression area; the maximum compressive stress of ore body and the maximum tensile stress of ore pillar are obviously reduced. This shows that the filling body bears part of the vertical compressive stress instead of the roof, floor and pillar, so as to release the concentrated stress in the goaf, effectively prevent the vertical deformation of the roof and floor of the goaf, reduce the possibility of pillar failure and collapse, and strengthen the stability of the surrounding rock of the seam.

FIGURE 9

FIGURE 9. Maximum principal stress diagram of stope roof in four case.

4.3 Analysis of Distribution Law of Plastic Zone

From Figure 10, in Case 1, the plastic zone of the surrounding rock around the stope is asymmetric, mainly because the shear stress generated by the surrounding rock is greater than the shear strength of the rock mass, resulting in the plastic state of the surrounding rock. In Case 3, the plastic area of the stope is basically concentrated at the pillar. And the plastic area generated by Case 1 is larger than that generated by Case 3, and the stress of surrounding rock changes sharply. This is because the two ends of the stope have exceeded the mechanical strength of the rock mass itself, resulting in stress release. To sum up, the stope under the two working conditions are unstable. The plastic zone ratios for Case 1 and Case 3 are shown in Table 4.

FIGURE 10

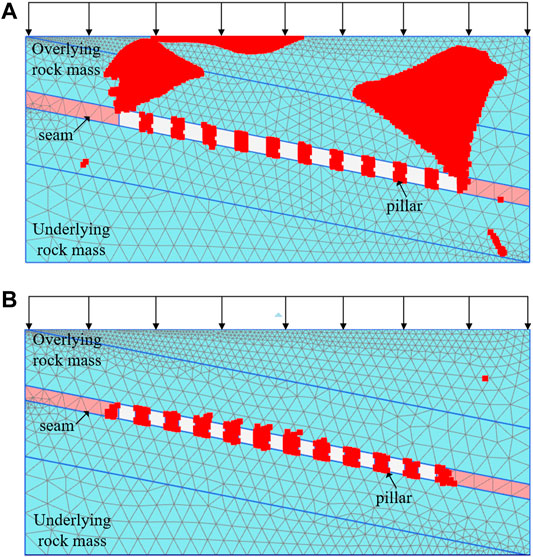
FIGURE 10. | (A) Distribution of stope plastic area in Case 1 and 3. (B) Distribution of stope plastic area in Case 1 and 3.

TABLE 4

TABLE 4. Area ratio of plastic zone under case 1 and case 3.

4.4 Analysis of Plastic Zone Distribution After Filling

In Case 2 and 4, the plastic area of the stope is basically concentrated at the top and bottom of the pillar, and the plastic area is small. Compared with the working condition of unfilled goaf, the range of plastic zone of phosphate rock layer is reduced to a certain extent, and the rock mass stress around the plastic zone is in the state of elastic stress, and the overall stability of phosphate rock layer is strengthened. It can be seen from Figure 11 that the plastic area generated by Case 2 is larger than that generated by Case 4. Compared with Case 1 and 3, the plastic area of Case 2 and 4 is smaller and the stope stability is higher. The plastic zone ratios for Case 2 and Case 4 are shown in Table 5.

FIGURE 11

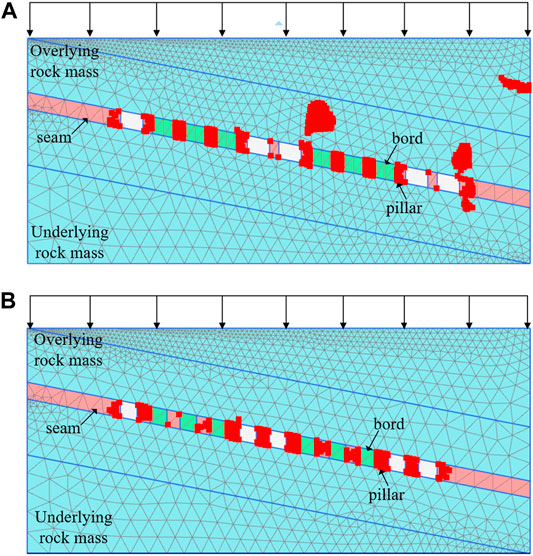
FIGURE 11. | (A) Distribution of stope plastic area in Case 2 and 4. (B) Distribution of stope plastic area in Case 2 and 4.

TABLE 5

TABLE 5. Area ratio of plastic zone under case 2 and case 4.

5 Discussion

5.1 The Best Scheme of the Cases

The results of numerical simulation show that the maximum values of tensile stress and final displacement of each scheme usually appear in the middle of the area, and the increase of mine room span is very easy to cause the rapid increase of the maximum settlement in the mining area. It can be seen from the plastic zone that with the increase of mine room span, the plastic zone is also increasing. In Case 1 and Case 3, the failure area in the pillar appears the failure state of plastic zone penetration, so it is not suitable to use. Considering several factors such as roof stability and plastic area, Case 2 and Case 4 can ensure the safety of stope mining. The data of Case 2 and Case 4 show little difference. Considering the efficient production and stope stability, Case 4 is the most suitable, that is, the stope structure scheme of 7 m pillar and 9 m room waste rock filling.

The optimized stope structure parameters are applied to the stope with a buried depth of about 400 m. The edge pillar, stope pillar, roof and floor can remain stable, and only a small amount of ore caving occurs at the place with relatively developed joint fissures. Compared with the original stope design scheme, the optimized scheme increases the width of pillar and reduces the number of pillars, The stability of the stope has been greatly improved, and the recovery rate of the mine has been increased to about 79%, which has created good economic benefits for the mine.

5.2 Optimal Stope Structure Parameters

Stope structure parameter design is a multi-factor and multi-objective optimization problem. The more factors and objectives, the more advantages of this method can be fully reflected. Therefore, it can be regarded as a general method to solve this kind of problem. The evaluation indexes set in this paper only include stability indexes and economic indexes, while other indexes in the actual production of the mine (mining and cutting ratio, stope production capacity, geological conditions, etc.) can also be taken into account; At the same time, the comprehensive evaluation method used in this paper is only the objective weighting method. If the objective weighting method is combined with the subjective weighting method, a more accurate comprehensive evaluation value can be obtained, and the stope structure parameters most in line with the current situation of mine production can be obtained accordingly.

Mine geological conditions are generally complex, and the simulation process of finite element analysis software fully reflects the complex and changeable geological conditions of the mine. The determination of ore body parameters should adopt the combination of numerical simulation and theoretical calculation. Therefore, based on the elastic-plastic constitutive model of Mohr Coulomb strength criterion, the reasonable span and critical span are calculated by using the simply supported beam theory and the calculation formula of room width. By improving the reliability of the calculation results, the data are closer to the engineering practice, so as to ensure the safety and efficiency of mining operation.

5.3 Research Limitations

The generalization of geometric model involves complex geological bodies. This paper only studies and analyzes the two-dimensional model of phosphate rock mining without three-dimensional numerical simulation, which is slightly different from the actual situation. The model itself has experienced a generalization, so various assumptions are put forward in the simulation calculation to facilitate the simulation calculation. For example, the horizontal displacement constraints in the X direction are adopted on the left and right sides of the model boundary conditions, the horizontal and vertical constraints are applied on the bottom of the model, and the model surface is free constraints, which will be different from the actual situation of the mine; In the actual engineering filling, the filling body can not completely fill the ore chamber, and this factor is not considered in the simulation calculation. The above deficiencies need to be further discussed in the follow-up study.

6 Conclusion

The maximum allowable span and reasonable span of each scheme are determined by comprehensively using the simply supported beam theory and the calculation formula of room width. 7 m × 9 m, 5 m × 12 m two stope structure parameter schemes and 7 m × 9 m, 5 m × 12 m two waste rock filling schemes of are studied by numerical simulation. The analysis and simulation results show that the simulation calculation of Case 1 and Case 3 does not converge, the maximum principal stress exceeds the rock mass strength, the plastic area is too large and there is a penetration phenomenon, resulting in a great reduction in the stability of the phosphate mine stope, the stope is prone to collapse, the mining area is too large, and the stope stability is greatly reduced. Under Case 2 and Case 4, the maximum principal stress does not exceed the rock mass strength, and the plastic area is small, so the stope is relatively safe. When the stope span is 9 m and the waste rock is filled, the maximum vertical displacement, maximum principal stress and the volume of plastic zone change little, the plastic zone is not connected, and the stope is in a stable state; When the stope span is 12 m and the gangue is filled, the vertical displacement and maximum principal stress of the stope roof and floor are the largest, the equivalent safety factor of the upper part of the roof is at the limit value, the plastic area in the study area is connected, the volume of the plastic area increases greatly, and the stope is in the limit stable state. Comprehensively considering the calculation results of the model and the comprehensive comparative analysis of stress, displacement and plastic zone, when the stope span is 9 m and the gangue is filled, the stope production capacity can be brought into full play on the premise of ensuring the Stope Safety and maximizing the interests of the mine.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

GP, DG, CJ, CZ, LM, designed the study, and GP wrote the initial draft of the manuscript. DG, CJ, CZ, and LM, contributed to analysis and interpretation of data, and assisted in the preparation of the manuscript. All other authors have contributed to data collection and interpretation, and critically reviewed the manuscript. All authors approved the final version of the manuscript, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Funding

This study is supported by the National Natural Science Foundation of China (No. 52174085, No.52174086) And the postgraduate education innovation fund project of Wuhan Institute of Technology (CX2021135). The sponsor is Zhou Chunmei, with a subsidy of US $2950.

Conflict of Interest

GP, DG, CJ, CZ, LM were employed by the company Hubei Xingfa Chemical Group Co., Ltd.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would also like to thank Tutor CZ, Dean Zhang Dianji and Teacher LM for their valuable comments and suggestions for improvement of the manuscript.

References

Almoataz, B. M. K., Mohamed, A. G., and Mohamed, A. Y. (2020). Studying the Appropriate Underground Mining Methods in Sukari Gold Mine. J. Eng. Res. Rep., 41–50. doi:10.9734/jerr/2020/v14i117117

CrossRef Full Text | Google Scholar

Barnewold, L., and Lottermoser, B. G. (2020). Identification of Digital Technologies and Digitalisation Trends in the Mining Industry. Int. J. Mining Sci. Technology. 30, 747–757. doi:10.1016/j.ijmst.2020.07.003

CrossRef Full Text | Google Scholar

Cao, W., Shi, J.-Q., Durucan, S., Korre, A., and Jamnikar, S. (2019). Numerical Modelling of Anomalous Microseismicity Influenced by Lithological Heterogeneity in Longwall Top Coal Caving Mining. Int. J. Coal Geology. 216, 103305. doi:10.1016/j.coal.2019.103305

CrossRef Full Text | Google Scholar

Castro-Caicedo, A. J. (2019). Geotechnical design of pillars in underground mines of gold veins in cases of Colombia. DYNA: revista de la Facultad de Minas. Universidad Nacional de Colombia. Sede Medellín. 86, 337–346. doi:10.15446/dyna.v86n209.74041

CrossRef Full Text | Google Scholar

Dong, L., Chen, Y., Sun, D., and Zhang, Y. (2021). Implications for Rock Instability Precursors and Principal Stress Direction from Rock Acoustic Experiments. Int. J. Mining Sci. Technology. 31, 789–798. doi:10.1016/j.ijmst.2021.06.006

CrossRef Full Text | Google Scholar

Dong, L., Shu, W., Li, X., Zhou, Z., Gong, F., and Liu, X. (2017). Quantitative Evaluation and Case Study of Risk Degree for Underground Goafs with Multiple Indexes Considering Uncertain Factors in Mines. Geofluids. 2017, 1–15. doi:10.1155/2017/3271246

CrossRef Full Text | Google Scholar

Du, Z., Qin, B., and Tian, F. (2016). Numerical Analysis of the Effects of Rock Bolts on Stress Redistribution Around a Roadway. Int. J. Mining Sci. Technology. 26, 975–980. doi:10.1016/j.ijmst.2016.09.003

CrossRef Full Text | Google Scholar

Falaknaz, N., Aubertin, M., and Li, L. (2015a). Evaluation of the Stress State in Two Adjacent Backfilled Stopes within an Elasto-Plastic Rock Mass. Geotechnical & Geological Engineering, 1–24.

Google Scholar

Falaknaz, N., Aubertin, M., and Li, L. (2015b). Numerical Analyses of the Stress State in Two Neighboring Stopes Excavated and Backfilled in Sequence. Int. J. Geomech. 15, 04015005. doi:10.1061/(asce)gm.1943-5622.0000466

CrossRef Full Text | Google Scholar

Fu, Y., Zhan, F., and Li, Y. (2017). Study on Structural Parameter Optimization in the Stope Combination of Open Pit and Underground Mining. China Mining Mag. 26, 83–87. doi:10.3969/j.issn.1004-4051.2017.01.019

CrossRef Full Text | Google Scholar

Gao, M., Xie, J., Gao, Y., Wang, W., Li, C., Yang, B., et al. (2021). Mechanical Behavior of Coal under Different Mining Rates: A Case Study from Laboratory Experiments to Field Testing. Int. J. Mining Sci. Technology. 31, 825–841. doi:10.1016/j.ijmst.2021.06.007

CrossRef Full Text | Google Scholar

Ge, W. (2017). Optimization of Stope Structure Parameters Based on MIDAS-GTS. Mining Res. Development. 37, 1–5. doi:10.13827/j.cnki.kyyk.2017.06.001

CrossRef Full Text | Google Scholar

Guo, Z. Z., Shi, Y., Huang, F., and Fan, X. M. (2021). Landslide Susceptibility Zonation Method Based on C5.0 Decision Tree and K-Means Cluster Algorithms to Improve the Efficiency of Risk Management - ScienceDirect. Geosci. Front. 12, 243–261. doi:10.1016/j.gsf.2021.101249

CrossRef Full Text | Google Scholar

Hu, Y., Ren, F., Ding, H., Fu, Y., and Tan, B. (2019). Study on the Process and Mechanism of Slope Failure Induced by Mining under Open Pit Slope: A Case Study from Yanqianshan Iron Mine, China. Adv. Civil Eng. 2019, 1–26. doi:10.1155/2019/6862936

CrossRef Full Text | Google Scholar

Huang, F., Tao, S., Chang, Z., Huang, J., Fan, X., Jiang, S.-H., et al. (2021a). Efficient and Automatic Extraction of Slope Units Based on Multi-Scale Segmentation Method for Landslide Assessments. Landslides. 18, 3715–3731. doi:10.1007/s10346-021-01756-9

CrossRef Full Text | Google Scholar

Huang, F., Yan, J., Fan, X., Yao, C., Huang, J., Chen, W., et al. (2022b). Uncertainty Pattern in Landslide Susceptibility Prediction Modelling: Effects of Different Landslide Boundaries and Spatial Shape Expressions. Geosci. Front. 13, 101317. doi:10.1016/j.gsf.2021.101317

CrossRef Full Text | Google Scholar

Huang, F., Yin, K., Huang, J., Gui, L., and Wang, P. (2017). Landslide Susceptibility Mapping Based on Self-Organizing-Map Network and Extreme Learning Machine. Eng. Geology. 223, 11–22. doi:10.1016/j.enggeo.2017.04.013

CrossRef Full Text | Google Scholar

Idris, M. A., and Nordlund, E. (2019). Probabilistic-Based Stope Design Methodology for Complex Ore Body with Rock Mass Property Variability. J. Min Sci. 55, 743–750. doi:10.1134/s1062739119056112

CrossRef Full Text | Google Scholar

Jing, H., Wu, J., Yin, Q., and Wang, K. (2020). Deformation and Failure Characteristics of anchorage Structure of Surrounding Rock in Deep Roadway. Int. J. Mining Sci. Technology. 30, 593–604. doi:10.1016/j.ijmst.2020.06.003

CrossRef Full Text | Google Scholar

Kamash, W. E., Naggar, H. E., and Nagaratnam, S. (2021). Numerical Analysis of Lateral Earth Pressure Coefficient in Inclined Mine Stopes. Geomechanics Geophys. Geo-Energy Geo-Resources. 7, 61. doi:10.1007/s40948-021-00255-4

CrossRef Full Text | Google Scholar

Li, N., Wang, W., Xiao, Y., and Li, H. (2019). Optimization of Stope Parameters for an Iron Ore Deposit Based on Orthogonal Experiment Theory. Mining Res. Development. 39, 51–55. doi:10.13827/j.cnki.kyyk.2019.07.012

CrossRef Full Text | Google Scholar

Lin, Y. (2021). Optimization of Structural Parameters of Stope without Sill Pillar in Metal Mine by Computer Numerical Simulation. J. Phys. Conf. Ser. 1744, 022095. doi:10.1088/1742-6596/1744/2/022095

CrossRef Full Text | Google Scholar

Liu, J., Xie, L., and Cao, H. (2018). Study on Structural Parameters Optimization and Stability of Stope for Large-Scale Backfill Mining. Metal Mine, 10–13. doi:10.19614/j.cnki.jsks.201812002

CrossRef Full Text | Google Scholar

Liu, X., Song, S., Tan, Y., Fan, D., Ning, J., Li, X., et al. (2021). Similar Simulation Study on the Deformation and Failure of Surrounding Rock of a Large Section Chamber Group under Dynamic Loading. Int. J. Mining Sci. Technology. 31, 495–505. doi:10.1016/j.ijmst.2021.03.009

CrossRef Full Text | Google Scholar

Mikhail, E., Gabriel, E., and Igor, S. (2020). Numerical Simulation of Roof Cavings in Several Kuzbass Mines Using Finite-Difference Continuum Damage Mechanics Approach. Int. J. Mining Sci. Technology. 30 (2), 157–166. doi:10.3969/j.issn.2095-2686.2020.02.003

CrossRef Full Text | Google Scholar

Qiao, L. (2001). Study on the Optimization of Deep Stope Structure Parameters and Mining Sequence of Xincheng Gold Mine, Metal Mine, 11–15. doi:10.3321/j.issn:1001-1250.2001.06.004

CrossRef Full Text | Google Scholar

Qiu, J., Xin, G., Zhang, S., Liu, X., and Sun, X. (2013). Research on Structural Parameters Optimization of Cementing Filling Stope for Super Large Underground Mine. Metal Mine, 1–3+28. doi:10.3969/j.issn.1001-1250.2013.04.001

CrossRef Full Text | Google Scholar

Serrano, A., Olalla, C., and Galindo, R. A. (2016). Ultimate Bearing Capacity of an Anisotropic Discontinuous Rock Mass Based on the Modified Hoek-Brown Criterion. Int. J. Rock Mech. Mining Sci. 83, 24–40. doi:10.1016/j.ijrmms.2015.12.014

CrossRef Full Text | Google Scholar

Shi, X. (2016). Experimental and Modeling Studies on Installation of Arc Sprayed Zn Anodes for protection of Reinforced concrete Structures. Front. Struct. Civ. Eng. 10, 1–11. doi:10.1007/s11709-016-0312-7

CrossRef Full Text | Google Scholar

Sun, M., Ren, F., and Ding, H. (2021). Optimization of Stope Structure Parameters Based on the Mined Orebody at the Meishan Iron Mine. Adv. Civil Eng. 2021, 1–14. doi:10.1155/2021/8052827

CrossRef Full Text | Google Scholar

Tang, L., Deng, L., and Jian, Y. (2016). Study on the Optimization of Structural Parameters of Sublevel Open Stopping with Subsequent Backfilling Mining. Gold Sci. Technology. 24, 8–13. doi:10.11872/j.issn.1005-2518.2016.02.008

CrossRef Full Text | Google Scholar

Tang, X., Huang, G., Shi, L., Wang, M., and Yang, K. (2017). Optimization of the Stope Structure Parameters in a Iron Mine. Mod. Mining. 33, 77–79. doi:10.3969/j.issn.1674-6082.2017.09.016

CrossRef Full Text | Google Scholar

Wagner, H. (2009). Die Rolle von Versatz im Bergbau. Berg Huettenmaenn Monatsh 154, 52–59. doi:10.1007/s00501-009-0439-0

CrossRef Full Text | Google Scholar

Wang, Q., He, M., Li, S., Jiang, Z., Wang, Y., Qin, Q., et al. (2021). Comparative Study of Model Tests on Automatically Formed Roadway and Gob-Side Entry Driving in Deep Coal Mines. Int. J. Mining Sci. Technology. 31, 591–601. doi:10.1016/j.ijmst.2021.04.004

CrossRef Full Text | Google Scholar

Wang, T., Zhao, X., Hu, W., Chen, J., Cheng, L., Zhao, L., et al. (2016). Investigation of Mine Pressure and Deformation Due to Phosphate Ore Body Excavation Based on Hoek-Brown Model. J. Unconventional Oil Gas Resour. 15, 158–164. doi:10.1016/j.juogr.2016.08.001

CrossRef Full Text | Google Scholar

Wang, Z., and Liu, Q. (2021). Failure Criterion for Soft Rocks Considering Intermediate Principal Stress. Int. J. Mining Sci. Technology. 31, 565–575. doi:10.3969/j.issn.2095-2686.2021.04.003

CrossRef Full Text | Google Scholar

Wojtecki, Ł., Kurzeja, J., and Knopik, M. (2021). The Influence of Mining Factors on Seismic Activity during Longwall Mining of a Coal Seam. Int. J. Mining Sci. Technology. 31, 429–437. doi:10.3969/j.issn.2095-2686.2021.03.009

CrossRef Full Text | Google Scholar

Wu, G., Yu, W., Zuo, J., and Du, S. (2020). Experimental and Theoretical Investigation on Mechanisms Performance of the Rock-Coal-Bolt (RCB) Composite System. Int. J. Mining Sci. Technology. 30, 759–768. doi:10.1016/j.ijmst.2020.08.002

CrossRef Full Text | Google Scholar

Xiang, X., and Ke, G. (2014). Optimization of Stope Structural Parameters in Phosphorite Mine and its Stability Analysis. Appl. Mech. Mater. 3307, 1268–1272. doi:10.4028/www.scientific.net/AMM.580-583.1268

CrossRef Full Text | Google Scholar

Xu, S., Liang, R., Suorineni, F. T., and Li, Y. (2021). Evaluation of the Use of Sublevel Open Stoping in the Mining of Moderately Dipping Medium-Thick Orebodies. Int. J. Mining Sci. Technology. 31, 333–346. doi:10.1016/j.ijmst.2020.12.002

CrossRef Full Text | Google Scholar

Yang, Y., Fu, J., and Song, W. (2015). Stope Structural Parameter Optimization under Different Geological Conditions. Metal Mine. 10, 29–32. doi:10.3969/j.issn.1001-1250.2015.10.007

CrossRef Full Text | Google Scholar

Yang, Y., Xu, G., He, S., Zhou, D., and Tian, Y. (2017). Numerical Simulation on Structural Parameters Optimization of Upward Horizontal Slicing Filling Method in Xiadian Gold Mine. Metal Mine., 42–46.

Google Scholar

Yang, Z., and Ore, D. T. (2015). The Study on Stope Structure Parameter Optimization of Steep Thin Veins. Yunnan Metall. 44, 5–10. doi:10.3969/j.issn.1006-0308.2015.06.002

CrossRef Full Text | Google Scholar

Yi, S., and Liao, J. (2017). Optimization Research on Stope Structure Parameters in a Gold Mine Based on Fuzzy Evaluation. Mining Res. Development 37, 73–78. doi:10.13827/j.cnki.kyyk.2017.12.016

CrossRef Full Text | Google Scholar

Zhang, H., Song, W., and Fu, J. (2014). Analysis of Large-Span Goaf Roof Instability Critical Parameters and Stability. Caikuang Yu Anquan Gongcheng Xuebao/Journal Mining Saf. Eng. 31, 66–71. doi:10.13545/j.issn1673-3363.2014.01.011

CrossRef Full Text | Google Scholar

Zhang, J., and Chen, S. (2016). Optimization of Structural Parameters for Deep Stope in a Copper Mine Based on Numerical Simulation. Ind. Minerals Process. 45, 47–51. doi:10.16283/j.cnki.hgkwyjg.2016.12.014

CrossRef Full Text | Google Scholar

Zhang, T. (2009). Optimization of Stope Structure Parameter in Xitieshan Lead-zinc Mine. China Mine Eng. 38, 9–13. doi:10.3969/j.issn.1672-609X.2009.03.003

CrossRef Full Text | Google Scholar

Zhang, L. (2010). Study on Optimization of Stope Structural Parameter of MSG Iron Mine. China Mine Eng. 39, 16–18. doi:10.3969/j.issn.1672-609X.2010.04.006

CrossRef Full Text | Google Scholar

Zhang, Z., Deng, M., Bai, J., Yan, S., and Yu, X. (2021). Stability Control of Gob-Side Entry Retained under the Gob with Close Distance Coal Seams. Int. J. Mining Sci. Technology 31, 321–332. doi:10.1016/j.ijmst.2020.11.002

CrossRef Full Text | Google Scholar

Zhao, K., Wang, Q., Li, Q., Yan, Y., and Cao, S. (2019). Optimization Calculation of Stope Structure Parameters Based on Mathews Stabilization Graph Method. J. Vibroengineering 21, 1227–1239. doi:10.21595/jve.2019.20634

CrossRef Full Text | Google Scholar

Zhu, C., Yuan, Y., Wang, W., Chen, Z., Wang, S., and Zhong, H. (2021). Research on the "three Shells" Cooperative Support Technology of Large-Section chambers in Deep Mines. Int. J. Mining Sci. Technology. 31, 665–680. doi:10.1016/j.ijmst.2021.05.002

CrossRef Full Text | Google Scholar

Zhu, L., Wang, G., Huang, F., Li, Y., and Hong, H. (2021). Landslide Susceptibility Prediction Using Sparse Feature Extraction and Machine Learning Models Based on GIS and Remote Sensing. IEEE Geosci. Remote Sensing Lett., 1–5. doi:10.1109/LGRS.2021.3054029

CrossRef Full Text | Google Scholar