Thermodynamic Properties of Fe-Bearing Wadsleyite and Determination of the Olivine-Wadsleyite Phase Transition Boundary in (Mg,Fe)2SiO4 System

The self-consistent molar volumes, elastic properties and thermodynamic properties of β-(Mg_0.87,Fe_0.13)₂SiO₄ wadsleyite have been determined over a wide temperature and pressure range based on an iterative numerical approach and experimental data from the literature. The obtained molar volumes, adiabatic bulk modulus, and shear modulus generally agree with the available experimental and theoretical results. The thermodynamic properties of α-(Mg_0.9,Fe_0.1)₂SiO₄ were also reinvestigated. Comparisons on thermodynamic properties show that the thermal expansions, heat capacities, and entropies of both β-(Mg_0.87,Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄ exhibit negative and nonlinear behavior with increasing pressure. Besides, the pressure plays a more important role in thermodynamic properties of the α-(Mg_0.9,Fe_0.1)₂SiO₄ than that of the β-(Mg_0.87,Fe_0.13)₂SiO₄. Using the Clausius-Clapeyron equation combined with molar volumes and entropies of both compositions, the phase transition boundary of Fe-bearing olivine and wadsleyite is estimated. The calculated transition pressure shows a nonlinear relationship with increasing temperature, and the value is generally lower than the previous studies on Fe-free olivine and wadsleyite at the same temperature. On the basis of our phase relation, the temperature at the 410 km discontinuity is estimated as 1795 ± 70 K under anhydrous conditions. The results not only confirm the feasibility of the Clausius-Clapeyron equation in obtaining the solid-solid phase transition, but also suggest that the existence of Fe might decrease the transition pressure of olivine-wadsleyite, which would consequently cause a higher temperature at the 410 km discontinuity.

Introduction

Olivine (α-phase) and its high-pressure polymorphs (i.e., wadsleyite and ringwoodite) dominate the Earth’s upper mantle and mantle transition zone (Ringwood, 1962). Since it has been widely accepted that the Earth’s mantle is peridotitic, the seismic wave discontinuities in the Earth’s mantle are usually considered to be related to the high-pressure transformations of olivine (Ringwood and Major, 1970). Furthermore, the existence of the 410 and 520 km discontinuities are attributed to the olivine-wadsleyite (β-phase) and wadsleyite-ringwoodite (γ-phase) transformations, respectively. Previous studies reported that temperatures at these seismic wave discontinuities can be estimated by comparing the depth of the seismic wave discontinuities with the phase transition pressures of mantle minerals (Ito and Katsura, 1989). In turn, it indicates that an accurate phase transition boundary of olivine-wadsleyite is necessary to constrain the temperature at the 410 km discontinuity.

Although it has been demonstrated that there is non-negligible Fe (∼10 mol%) in natural olivine (Bina and Wood, 1987), most studies on the phase transition boundary of olivine-wadsleyite are still limited in Mg₂SiO₄ system (Morishima et al., 1994; Jacobs et al., 2006; Akaogi et al., 2007; Ottonello et al., 2008; Holland and Powell, 2011; Dorogokupets et al., 2015). To date, the transition pressures in (Mg,Fe)₂SiO₄ system have been only determined at several temperatures (Katsura and Ito, 1989; Chen et al., 2002; Katsura et al., 2004), and the effect of Fe on the olivine-wadsleyite phase transition boundary in a continuous P-T range remains unclear.

The determination of the phase transition boundary is usually based on the phase equilibrium, which requires the volumes and thermodynamic properties of coexisting phases at high-temperatures and high-pressures (HT-HP). The molar volume and thermodynamic properties, including thermal expansion and heat capacity, of San Carlos olivine (α-(Mg_0.9,Fe_0.1)₂SiO₄) at HT-HP were reported via an iterative numerical approach in Su et al. (2018). Pioneering investigations on Fe-bearing wadsleyite (β-(Mg,Fe)₂SiO₄) has shown the effect of Fe on the elastic properties (Li and Liebermann, 2000; Liu et al., 2009) and electrical conductivities (Dai and Karato, 2009; Yoshino et al., 2012). At the same time, few works have been devoted to the thermodynamic properties of Fe-bearing wadsleyite at HT-HP.

This study aims to determine the thermodynamic properties of Fe-bearing wadsleyite at HT-HP, and apply them to investigate the effect of Fe on the olivine-wadsleyite phase transition boundary. We refined our calculation procedure and derived the self-consistent molar volume, elastic moduli, thermal expansion, heat capacity, and entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ based on existing experimental measurements. We also reanalyzed our early investigations on α-(Mg_0.9,Fe_0.1)₂SiO₄, and compared the effect of pressure on the thermodynamic properties of β-(Mg_0.87Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄. Then, we determined the phase transition boundary of olivine-wadsleyite in (Mg,Fe)₂SiO₄ system using the obtained molar volumes and entropies of two compositions at HT-HP combined with Clausius-Clapeyron equation. Finally, by comparing the depth of the discontinuity with the transition pressure, we estimated the temperature at the 410 km discontinuity.

Methods

Calculation Procedure

The approach used in this study is described in our recent studies (Su et al., 2018; Su et al., 2022), and the fundamental procedure is described below. The uncertainties of the derived parameters at different P-T conditions are estimated from the experimental measuring error propagations using Taylor series expansion.

The thermal expansion (α) at constant pressure is related to volume (V) as:

$\alpha \left(T\right)=\frac{1}{V}\left(\frac{\partial V}{\partial T}\right)(1)$

And the integration of Eq. 1 yields:

$V\left(T\right)=V_{0}exp\left[{\displaystyle \underset{T_0}{\overset{T}{\int }}\alpha }\left(T\right)dT\right](2)$

where V₀ represents the volume at ambient condition. The isothermal derivative of volume with respect to pressure can be written as:

${\left(\frac{\partial V}{\partial P}\right)}_T=-V^2\left(\frac{1}{v_{\Phi }^2}+\frac{T{\alpha }^2}{C_P}\right)(3)$

where C_P stands for the heat capacity, v_Φ refers to the bulk sound velocity (Bina and Silver, 1990). The bulk sound velocity is related to the specific volume and adiabatic bulk modulus (K_S) by v_Φ = (VK_S)^1/2, which can be calculated from the P- wave velocity (v_P) and S- wave velocity (v_S) by Eq. 4.

$v_{\Phi }={\left(v_p^2-\frac{4}{3}{v}_s^2\right)}^{\frac{1}{2}}(4)$

Meanwhile, the isothermal derivative of the heat capacity with respect to pressure can be evaluated by Eq. 5.

${\left(\frac{\partial C_P}{\partial P}\right)}_T=-VT\left[{\alpha }^2+{\left(\frac{\partial \alpha }{\partial T}\right)}_P\right](5)$

To start the calculation, first, we use the experimental determined volume at high-temperature and ambient pressure conditions to obtain the thermal expansion at ambient pressure. With the obtained thermal expansion and heat capacity as a function of temperature at ambient pressure, the approximate volume at an arbitrary reference pressure could be estimated using Eq. 3. Then resulting volume at this reference pressure can be used to update the value of thermal expansion and heat capacity at the same pressure with Eqs 1, 5, respectively. Hence, iteration of this loop leads to converged volume, thermal expansion, and heat capacity as a function of temperature and pressure based on the experimental elastic wave velocity at HT-HP.

With the determined volume as well as the elastic wave velocity at HT-HP, the adiabatic bulk modulus (K_S) and shear modulus (G) can be obtained using Eqs 6, 7, respectively.

$K_S=\frac{1}{V}\left(v_p^2-\frac{4}{3}{v}_s^2\right)(6)$

$G=\frac{1}{V}{v}_S^2(7)$

Furthermore, since the temperature and pressure dependences of entropy (S) are related to the heat capacity and thermal expansion via Eqs 8, 9, respectively (Johari, 2021), the entropy at HTHP can be also derived with the entropy measured at ambient conditions.

$S\left(P_0,T\right)=S\left(P_0,T_0\right)-{\displaystyle \underset{T_0}{\overset{T}{\int }}\left(\frac{C_P}{T}\right)}dT(8)$

$S\left(P,T_0\right)=S\left(P_0,T_0\right)-{\displaystyle \underset{P_0}{\overset{P}{\int }}\alpha }VdP(9)$

Thermoelastic Data of Fe-Bearing Wadsleyite

Elastic Wave Velocity at High-Temperature and High-Pressure Conditions

Previous studies have measured the elastic wave velocity of Fe-bearing wadsleyite at high-pressure conditions (Li and Liebermann, 2000; Wang et al., 2014). Besides, by using ultrasonic interferometry in conjunction with synchrotron X-ray diffraction measurements, Liu et al. (2009) presented the elastic wave velocity and unit-cell volume of β-(Mg_0.87Fe_0.13)₂SiO₄ to 12 GPa and 1073 K. Here, we fit the P- and S- wave velocities by Liu at al. (2009) with Eq. 10, and the fitting coefficients and their uncertainties are listed in Table 1.

$v\left(P,T\right)=v_0+v_{1}P+v_2\left(T-273\right)+v_3{P}^2+v_4{\left(T-273\right)}^2+v_{5}P\left(T-273\right)(10)$

where pressure is expressed in GPa, temperature is expressed in K, P- and S- wave velocity are expressed in m/s. The differences are less than 0.5% and 1.5% compared with the results reported by Li and Liebermann (2000) and Wang et al. (2014), respectively.

TABLE 1

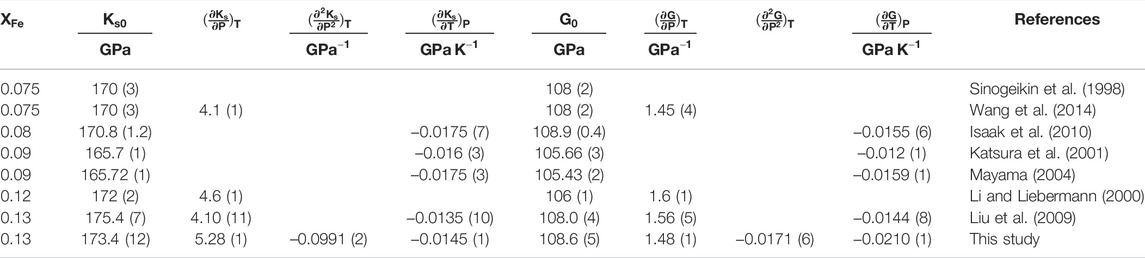
TABLE 1. Fitting coefficients and their uncertainties of Eq. 10 to calculate the P- and S- wave velocities of β-(Mg_0.87Fe_0.13)₂SiO₄ at HT-HPs.

Thermodynamic Properties at High-Temperature and Ambient Pressure Conditions

At present, there is no experimental or theoretical data for the thermal expansion, heat capacity, or entropy of Fe-bearing wadsleyite yet. Since it is suggested that the volume and heat capacity are linearly proportional to the Fe/(Mg + Fe) ratio ($X_{\text{Fe}}$) (Xu et al., 2004), the thermal expansion and heat capacity of Fe-bearing wadsleyite as a function of temperature can be estimated from the data of Mg end-member wadsleyite (β-Mg₂SiO₄) and Fe end-member (β-Fe₂SiO₄) wadsleyite.

However, β-Fe₂SiO₄ is a virtual mineral since fayalite (α-Fe₂SiO₄) is transformed directly to Fe end-member ringwoodite (γ-Fe₂SiO₄) with increasing pressure (Akimoto et al., 1967). According to the studies on α-Fe₂SiO₄ and γ-Fe₂SiO₄ (Fei and Saxena, 1986), Saxena (1996) published the molar volume and heat capacity of β-Fe₂SiO₄ at ambient conditions. Besides, Saxena (1996) also concluded the results from previous studies on β-Mg₂SiO₄ (Akimoto et al., 1978; Watanabe, 1982), and provided the thermodynamic data. Here, we use the database presented by Saxena (1996). For the Fe-bearing wadsleyite with a $X_{\text{Fe}}$ as 0.13, the temperature dependence of heat capacity is represented by a polynomial equation as shown in Eq. 11. The molar volume data is analyzed using the EoSfit software (Gonzalez-Platas et al., 2016), and the equation for the thermal expansion as a function of temperature is defined as Eq. 12. Additionally, the standard entropy is determined as 99.3 J/mol K.

$C_P\left(T\right)=179.59\left(21\right)+1.10\left(1\right)\times {10}^{-2}T-19171\left(297\right)T^{-1}+1.05\left(149\right)\times {10}^6{T}^{-2}-4.34\left(24\right)\times {10}^8{T}^{-3}(11)$

$\alpha \left(T\right)=2.520\left(112\right)\times {10}^{-5}+0.902\left(55\right)\times {10}^{-8}T-0.755\left(269\right)T^{-2}(12)$

Results

Based on the calculation procedure and experimental data discussed in Methods, the molar volume, adiabatic bulk modulus, shear modulus, thermal expansion, heat capacity, and entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ are derived. All the calculated parameters are provided in Supplementary Tables S1–S3, together with their uncertainties approximated using the error propagation calculations.

Molar Volume at High-Temperature and High-Pressure Conditions

The calculated molar volume of β-(Mg_0.87Fe_0.13)₂SiO₄ as a function of pressure at various temperatures is shown in Figure 1. The unit-cell volumes of β-(Mg_0.84Fe_0.16)₂SiO₄ and β-(Mg_0.87Fe_0.13)₂SiO₄ were measured by Fei et al. (1992) and Liu et al. (2009) using X-ray diffraction, respectively. Also, the densities of β-(Mg_0.88Fe_0.12)₂SiO₄ and β-(Mg_0.925Fe_0.075)₂SiO₄ were presented by Li and Liebermann (2000) and Wang et al. (2014) based on ultrasonic and Brillouin scattering measurements, respectively. Based on the molar mass of the Fe-bearing wadsleyite from those previous studies mentioned above, we convert the units of the unit-cell volume (ų) and density (g/cm³) to molar volume (cm³/mol), and the results are also illustrated in Figure 1.

FIGURE 1

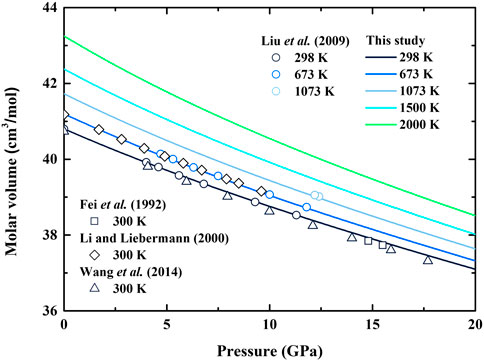
FIGURE 1. Molar volume of Fe-bearing wadsleyite as a function of pressure at various temperatures. Solid lines: calculated result of β-(Mg_0.87Fe_0.13)₂SiO₄ from this study; Circles: X-ray diffraction measurement of β-(Mg_0.87Fe_0.13)₂SiO₄ at various temperatures by Liu et al. (2009); Squares: X-ray diffraction measurement of β-(Mg_0.84Fe_0.16)₂SiO₄ at 300 K by Fei et al. (1992); Diamonds: result of β-(Mg_0.88Fe_0.12)₂SiO₄ obtained from ultrasonic experiment at 300 K by Li and Liebermann (2000); Triangles: result of β-(Mg_0.925Fe_0.075)₂SiO₄ obtained from Brillouin scattering experiment by Wang et al. (2014).

Our result shows good consistency with the X-ray diffraction measurement by Liu et al. (2009), and the difference is less than 0.1% at room temperature. The excellent agreement also holds at high-temperature conditions, and the largest difference is 0.1% at 1073 K compared with that by Liu et al. (2009). In the meantime, our obtained molar volume is ∼0.3% higher than the result by Wang et al. (2014), ∼0.12% higher than that by Fei et al. (1992), and ∼1.9% lower than that by Li and Liebermann (2000). Overall, except for the result by Li and Liebermann (2000), the molar volume of Fe-bearing wadsleyite seems to increase with the value of $X_{\text{Fe}}$.

Elastic Properties at High-Temperature and High-Pressure Conditions

Based on the molar volume, the calculated elastic moduli of β-(Mg_0.87Fe_0.13)₂SiO₄ are shown in Table 2; Figure 2, along with the previous results of Fe-bearing wadsleyite with different values of $X_{\text{Fe}}$ (Sinogeikin et al., 1998; Li and Liebermann, 2000; Katsura et al., 2001; Mayama, 2004; Liu et al., 2009; Isaak et al., 2010; Wang et al., 2014).

TABLE 2

TABLE 2. Elastic moduli of β-(Mg_0.87Fe_0.13)₂SiO₄ and their pressure and temperature derivatives.

FIGURE 2

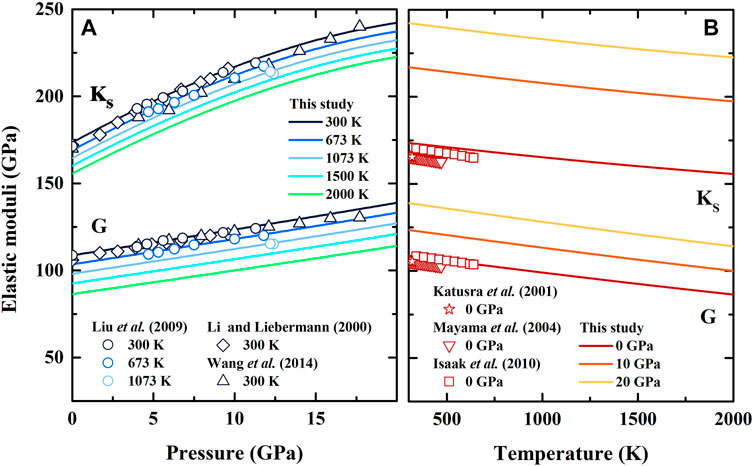
FIGURE 2. Adiabatic bulk modulus (K_S) and shear modulus (G) of Fe-bearing wadsleyite as a function of (A) pressure and (B) temperature. Solid lines: result of β-(Mg_0.87Fe_0.13)₂SiO₄ from this study; Diamonds: result of β-(Mg_0.88Fe_0.12)₂SiO₄ obtained from ultrasonic measurement by Li and Liebermann (2000); Circles: result of β-(Mg_0.87Fe_0.13)₂SiO₄ obtained from ultrasonic measurement by Liu et al. (2009); Triangles: result of β-(Mg_0.925Fe_0.075)₂SiO₄ obtained from Brillouin scattering measurement by Wang et al. (2014); Stars, inverted triangles and squares: results of β-(Mg_0.91Fe_0.09)₂SiO₄ obtained from resonant ultrasound spectroscopy measurements by Katsura et al. (2001), Mayama, (2004) and Isaak et al. (2010), respectively.

In this study, the adiabatic bulk modulus and shear modulus at ambient conditions are determined as K_S0 = 173.4 (12) GPa and G₀ = 108.6 (5) GPa, respectively. In Table 2, our K_S0 is consistent within the uncertainties of Liu et al. (2009), in which $X_{\text{Fe}}$ = 0.13, and generally larger than those with less Fe contents (Isaak et al., 2010; Katsura et al., 2001; Li and Liebermann, 2000; Mayama, 2004; Sinogeikin et al., 1998; Wang et al., 2014). On the other hand, the values of G₀ listed in Table 2 do not show apparent $X_{\text{Fe}}$ dependence. Our G₀ also agrees well with the result by Liu et al. (2009). Although our G₀ is larger than those with $X_{\text{Fe}}$ = 0.12 (Li and Liebermann, 2000) and $X_{\text{Fe}}$ = 0.09 (Katsura et al., 2001; Mayama, 2004), it is nearly the same as those with $X_{\text{Fe}}$ = 0.08 (Isaak et al., 2010) and $X_{\text{Fe}}$ = 0.075 (Sinogeikin et al., 1998; Wang et al., 2014).

In Figure 2A, our adiabatic bulk modulus exhibits significant nonlinear variation with the increasing pressure, whereas shear modulus shows the opposite trend. Both of the derived adiabatic bulk modulus and shear modulus are generally comparable with the data obtained from ultrasonic measurements (Li and Liebermann, 2000; Liu et al., 2009), and the largest separation is 1%. Though our adiabatic bulk modulus is ∼2.5% larger than that by Wang et al. (2014) in the pressure range of 5–12 GPa, it agrees well with the result by Wang et al. (2014) with the differences less than 1%. Also, the first and second pressure derivatives of adiabatic bulk modulus and shear modulus are obtained as ∂K_S/∂P = 5.28(1), ∂²K_S/∂P² = −0.0991(2) GPa⁻¹, ∂G/∂P = 1.48(1) and ∂²G/∂P² = −0.0171(6) GPa⁻¹, respectively.

The temperature dependences of adiabatic bulk modulus and shear modulus are shown in Figure 2B. Our adiabatic bulk modulus is ∼2% larger than that of Isaak et al. (2010), while shear modulus is consistent with Isaak’s result, and the differences are within 0.6%. The obtained adiabatic bulk modulus and shear modulus are 5.4% and 3.5% larger than that of Katsura et al. (2001) and Mayama (2004), respectively. The temperature derivatives of adiabatic bulk modulus and shear modulus are determined as ∂K_S/∂T = −0.0145(1) GPa/K and ∂G/∂T = −0.0210(1) GPa/K, respectively, which are comparable with those obtained by resonant ultrasound spectroscopy (Katsura et al., 2001; Mayama, 2004; Isaak et al., 2010) (Table 2).

Thermodynamic Properties at High-Temperature and High-Pressure Conditions

The thermal expansion, heat capacity, and entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ as a function of temperature at various pressures are illustrated in Figures 3–5, respectively. Since there is no thermodynamic data of Fe-bearing wadsleyite at present, here we only show the available thermal expansion, heat capacity, and entropy of β-Mg₂SiO₄ for comparisons (Suzuki et al., 1980; Akaogi et al., 1984; Ashida et al., 1987; Chopelas, 1991; Wu and Wentzcovitch, 2007; Jahn et al., 2013).

FIGURE 3

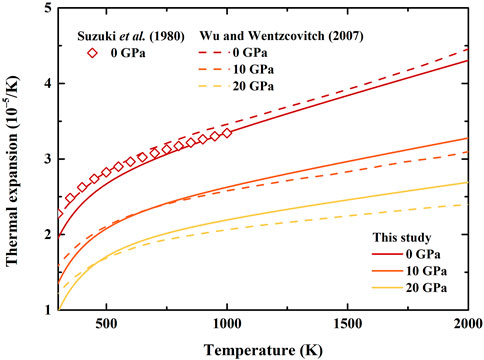
FIGURE 3. Temperature dependence of thermal expansion of β-(Mg_0.87Fe_0.13)₂SiO₄ and β-Mg₂SiO₄ at various pressures. Solid lines: result of β-(Mg_0.87Fe_0.13)₂SiO₄ from this study; Dash lines: first principle calculation result of β-Mg₂SiO₄ by Wu and Wentzcovitch (2007); Diamonds: result modified by Fei et al. (1992) based on X-ray diffraction data of Suzuki et al. (1980).

In Figure 3, our calculated thermal expansion of β-(Mg_0.87Fe_0.13)₂SiO₄ at ambient condition is determined as α₀ = 1.952 (428)×10^–5 K⁻¹, which is lower than the results by Suzuki et al. (1980) (2.27 × 10^–5 K⁻¹) and Wu and Wentzcovitch (2007) (2.21 × 10^–5 K⁻¹). With increasing temperature, the difference between our and Suzuki’s result becomes smaller, and decreases to 0.12% at 1000 K. Also, our thermal expansion shows a similar trend with that of Wu and Wentzcovitch (2007) at ambient pressure conditions over ∼700 K, with an average difference of ∼3%. For high-pressure conditions, our result becomes larger than the result by Wu and Wentzcovitch (2007) over ∼700 and ∼450 K at 10 and 20 GPa, respectively, and causes a difference of 5% and 11% at 2000 K at 10 and 20 GPa, respectively.

The calculated heat capacity of β-(Mg_0.87Fe_0.13)₂SiO₄ as a function of temperature at various pressures is shown in Figure 4, together with the ambient pressure results of β-Mg₂SiO₄ measured using differential scanning calorimetry (Akaogi et al., 1984; Ashida et al., 1987; Jahn et al., 2013), as well as high-pressure results determined using first principle calculation (Wu and Wentzcovitch, 2007). At ambient pressure conditions, the separations between these previous results of β-Mg₂SiO₄ are quite large. Our heat capacity is close to that by Akaogi et al. (1984) with a difference of ∼0.5%, while larger than that by Ashida et al. (1987), and smaller than those by Wu and Wentzcovitch (2007) and Jahn et al. (2013). Moreover, our obtained heat capacity is smaller than the result by Wu and Wentzcovitch (2007) at high-pressure conditions as well.

FIGURE 4

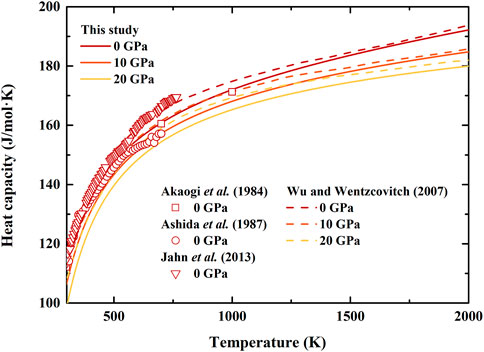
FIGURE 4. Temperature dependence of heat capacity of β-(Mg_0.87Fe_0.13)₂SiO₄ and β-Mg₂SiO₄ at various pressures. Solid lines: result of β-(Mg_0.87Fe_0.13)₂SiO₄ from this study; Dash lines: first principle calculation result of β-Mg₂SiO₄ by Wu and Wentzcovitch (2007); Squares, circles, and inverted triangles: differential scanning calorimetry measurements of β-Mg₂SiO₄ by Akaogi et al. (1984), Ashida et al. (1987), and Jahn et al. (2013), respectively.

Furthermore, the determined entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ is illustrated in Figure 5, which is generally larger than previous experimental (Akaogi et al., 1984; Chopelas, 1991) and theoretical (Wu and Wentzcovitch, 2007) results. Though at ambient conditions, the differences between our and previous results are pretty significant, which is ∼13%, ∼15%, and ∼10% compared to that by Akaogi et al. (1984), Chopelas (1991), and Wu and Wentzcovitch (2007), respectively. Nevertheless, the separations decrease with increasing temperature, and the average differences are ∼5%, ∼8%, and ∼4% compared to the results by Akaogi et al. (1984), Chopelas (1991), and Wu and Wentzcovitch (2007), respectively. In addition, our calculated entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ is ∼5% larger than that of β-Mg₂SiO₄ by Wu and Wentzcovitch (2007) at 10 and 20 GPa.

FIGURE 5

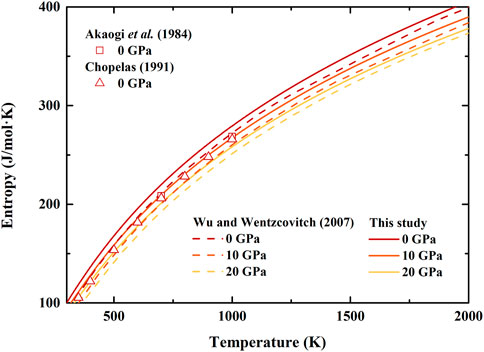
FIGURE 5. Temperature dependence of entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ and β-Mg₂SiO₄ at various pressures. Solid lines: result of β-(Mg_0.87Fe_0.13)₂SiO₄ from this study; Dash lines: first principle calculation result of β-Mg₂SiO₄ by Wu and Wentzcovitch (2007); Squares and Triangles: results of β-Mg₂SiO₄ obtained from differential scanning calorimetry measurement by Akaogi et al. (1984) and Chopelas (1991), respectively.

Based on the database by Saxena (1996), the values of thermal expansion, heat capacity, and entropy of β-Fe₂SiO₄ are larger than those of β-Mg₂SiO₄. Theoretically the thermal expansion, heat capacity, and entropy of the Fe-bearing wadsleyite should be slightly larger than those of β-Mg₂SiO₄. But according to the results, only entropy shows a noticeable increase with the Fe content. Since the differences of the thermal expansions and heat capacities between the available results for β-Mg₂SiO₄ are pretty large (Figures 3, 4), it is difficult to identify the effect of Fe on thermal expansion and heat capacity of wadsleyite based on existing results. More experimental and theoretical investigations are needed to clarify the Fe effects on the thermodynamic properties of wadsleyite.

Discussion and Implications

Comparisons on Thermodynamic Properties of β-(Mg_0.87Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄

The thermoelastic properties, including molar volume, thermal expansion, and heat capacity of α-(Mg_0.9,Fe_0.1)₂SiO₄ at HT-HP have been determined in our previous work (Su et al., 2018). The standard entropy of forsterite (α-Mg₂SiO₄) and fayalite at 298 K were defined by Robie et al. (1982a; 1982b), from which the entropy of α-(Mg_0.9,Fe_0.1)₂SiO₄ can be derived as 99.8 (1) J/mol K. Here, we re-analysis the data and present the entropy of α-(Mg_0.9,Fe_0.1)₂SiO₄ at HT-HP, as well as the uncertainties of the determined parameters. The obtained data is shown in Supplementary Tables S4–S6.

To investigate the pressure effects on the thermodynamic properties of β-(Mg_0.87Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄, we fit the thermodynamic parameters, including thermal expansions, heat capacities, and entropies to an equation of N = N₀ + ∂N/∂P × P + ∂²N/∂P² × P² at different temperatures, where N refers to the thermodynamic properties, N₀ refers to N at ambient pressure, ∂N/∂P and ∂²N/∂P² refer to the first and second pressure derivatives of N, respectively. The fitting coefficients are listed in Table 3.

TABLE 3

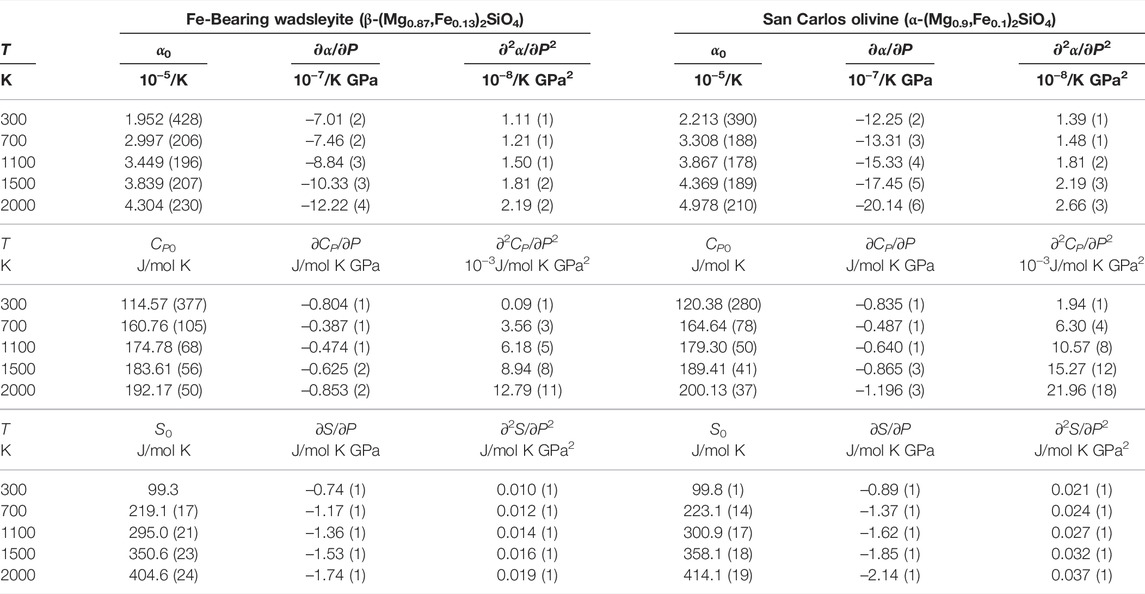
TABLE 3. The thermal expansions, heat capacities, and entropies of β-(Mg_0.87,Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄, and their pressure derivatives at various temperatures.

In Table 3, all the thermodynamic parameters, including thermal expansions, heat capacities, and entropies of β-(Mg_0.87Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄ show negative and nonlinear relationships with the pressure. The thermal expansion of β-(Mg_0.87Fe_0.13)₂SiO₄ is generally smaller than that of α-(Mg_0.9,Fe_0.1)₂SiO₄ at the same temperature, which coincides with the principle that wadsleyite has a more densely packed structure than olivine. Also, the pressure effects on the thermal expansions of both β-(Mg_0.87Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄ increase with the temperature. Also, the pressure derivative of β-(Mg_0.87Fe_0.13)₂SiO₄ is larger than that of α-(Mg_0.9,Fe_0.1)₂SiO₄ at the same temperature. In the temperature range of 300–2000 K, the ∂α/∂P of β-(Mg_0.87Fe_0.13)₂SiO₄ decreases from –7.01 (2) 10⁻⁷/K GPa to –12.22 (4) 10⁻⁷/K GPa, and the ∂α/∂P of α-(Mg_0.9,Fe_0.1)₂SiO₄ decreases from –12.25 (2) 10⁻⁷/K GPa to –20.14 (6) 10⁻⁷/K GPa.

For the heat capacity, the ∂C_P/∂P of β-(Mg_0.87Fe_0.13)₂SiO₄ at 300 K (∂C_P/∂P = –0.804 (1) J/mol K GPa) is smaller than that at 700 K (∂C_P/∂P = –0.387 (1) J/mol K GPa). Then, with the temperature increasing to 2000 K, the ∂C_P/∂P of β-(Mg_0.87Fe_0.13)₂SiO₄ decreases to –0.853 (2) J/mol K GPa. The pressure effect on the heat capacity of α-(Mg_0.9,Fe_0.1)₂SiO₄ shows the same pattern with the temperature, but generally, the ∂C_P/∂P of α-(Mg_0.9,Fe_0.1)₂SiO₄ is smaller than that of β-(Mg_0.87Fe_0.13)₂SiO₄.

Similar to thermal expansion, the entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ is generally lower than that of α-(Mg_0.9,Fe_0.1)₂SiO₄ at the same condition. The pressure effect on the entropy of β-(Mg_0.87Fe_0.13)₂SiO₄ is also smaller than that of α-(Mg_0.9,Fe_0.1)₂SiO₄. The ∂S/∂P of β-(Mg_0.87Fe_0.13)₂SiO₄ decreases from –0.74 (1) J/mol GPa to –1.74 (1) J/mol GPa with the temperature increases from 300 to 2000 K. Besides, the ∂S/∂P of α-(Mg_0.9,Fe_0.1)₂SiO₄ decreases from –0.89 (1) J/mol GPa to –2.14 (1) J/mol GPa in the temperature range of 300–2000 K.

Phase Transition Boundary of Olivine-Wadsleyite in (Mg,Fe)₂SiO₄ System

The global seismic discontinuity at the depth of 410 km, which separates the upper mantle from the transition zone, is most likely caused by the olivine-wadsleyite transition at ∼13–14 GPa (Zhang and Bass, 2016). Therefore, the phase transition boundary of olivine-wadsleyite has been widely studied to infer the composition and temperature at the 410 km discontinuity. By normal and reverse runs using in-situ X-ray diffraction in a cubic anvil apparatus, the olivine-wadsleyite transition pressures in Mg₂SiO₄ system from 1073 to 1873 K were proposed by Morishima et al. (1994). Also, the transition pressures of olivine-wadsleyite with different Fe contents were experimentally determined at various temperatures by Katsura and Ito (1989) (1473 and 1873 K), Chen et al. (2002) (1473 K), and Katsura et al. (2004) (1600 and 1900 K). Then, based on the transition pressures determined in Mg₂SiO₄ system, as well as the thermodynamic properties of α-Mg₂SiO₄ and β-Mg₂SiO₄, the phase transition boundary was calculated using Eq. 13 (Jacobs et al., 2006; Akaogi et al., 2007; Ottonello et al., 2008; Holland and Powell, 2011; Dorogokupets et al., 2015).

$\mathrm{\Delta }G\left(P,T\right)=\mathrm{\Delta }H\left(P_0,T\right)-T\mathrm{\Delta }S\left(P_0,T\right)+{\displaystyle \underset{1atm}{\overset{P}{\int }}\mathrm{\Delta }V}\left(P,T\right)dP=0(13)$

Eq.13 is derived based on the Gibbs free energy equation, in which ΔH(P₀,T) and ΔS(P₀,T) are enthalpy and entropy changes between the low and high-pressure phases at high-temperature and ambient pressure conditions, respectively, ΔG (P,T) and ΔV(P,T) are the Gibbs free energy and volume changes at HT-HP, respectively. In previous studies, the volumes of olivine and wadsleyite as a function of temperature and pressure were obtained from either theoretical calculations (Jacobs et al., 2006; Ottonello et al., 2008; Dorogokupets et al., 2015), or X-ray diffraction experiments with the combination of the third-order Birch–Murnaghan equation of state (3BM EoS) (Akaogi et al., 2007; Holland and Powell, 2011). The empirical EoS such as 3BM EoS and Mie-Grüneisen-Debye EoS undoubtedly provide convenient ways for determining volumes at specific P-T conditions, but the assumptions in the derivation processes of these empirical EoS might cause uncertainties at high P-T range (Anderson, 1995; Angel et al., 2021).

Meanwhile, the Clausius-Clapeyron equation (Eq. 14) is also one of the classic equations for estimating the phase transition boundaries:

$\frac{dP}{dT}=\frac{\mathrm{\Delta }S\left(P,T\right)}{\mathrm{\Delta }V\left(P,T\right)}(14)$

where dP/dT is the Clapeyron slope, ΔS(P,T) and ΔV(P,T) are, respectively, the entropy and volume changes between the two coexisting phases at HT-HP. Since previous measurements on the transition pressures in (Mg,Fe)₂SiO₄ system were usually conducted at high-temperature conditions (Katsura and Ito, 1989; Chen et al., 2002; Katsura et al., 2004), once the transition pressure at an arbitrary temperature is determined, the transition boundary can be simply derived with the entropy and volume changes between olivine and wadsleyite at HT-HP. The Clausius-Clapeyron equation was barely applied to the solid-solid phase transitions because the entropy variations with pressure in solids were often ignored in early studies (Ovrutsky et al., 2014). Here, with our obtained molar volumes and entropies of α-(Mg_0.9,Fe_0.1)₂SiO₄ and β-(Mg_0.87Fe_0.13)₂SiO₄ at HT-HP, we try to determine the phase transition boundary of olivine-wadsleyite in (Mg,Fe)₂SiO₄ system using the Clausius-Clapeyron equation. Note that the uncertainties of the transition pressure and Clapeyron slope are estimated using a Taylor series expansion.

In this study, the $X_{\text{Fe}}$ are 0.13 and 0.1, respectively, for our wadsleyite and olivine, and the partition coefficients of Fe and Mg between α and β phases ($K_{\text{Fe}-\text{Mg}}^{\text{α}-\text{β}}=\left(X_{\text{Fe}}^{\text{α}}/X_{\text{Fe}}^{\text{β}}\right)/\left[\left(1-X_{\text{Fe}}^{\text{α}}\right)/\left(1-X_{\text{Fe}}^{\text{β}}\right)\right]$) is calculated as 0.74. The $X_{\text{Fe}}$ of our wadsleyite and olivine are close to one of the experimental results proposed by Katsura et al. (2004) that the $X_{\text{Fe}}$ increased from 0.094 (5) to 0.148 (7) during the olivine-wadsleyite transition, and the transition temperature and pressure were determined as 1900 K and 14.26 (15) GPa. Since our $K_{\text{Fe}-\text{Mg}}^{\text{α}-\text{β}}$ is slightly higher than that by Katsura et al. (2004) [0.60 (5)], the start P-T point for our calculation is placed at 1900 K and 14.11 GPa, which is the lower limit of the transition pressure determined by Katsura et al. (2004).

Figure 6 illustrates our determined phase transition boundary, along with previous results determined in Mg₂SiO₄ system (Morishima et al., 1994; Jacobs et al., 2006; Akaogi et al., 2007; Ottonello et al., 2008; Holland and Powell, 2011; Dorogokupets et al., 2015). Generally, the transition pressures obtained in Mg₂SiO₄ system are higher than ours over ∼850 K (Ottonello et al., 2008). Also, the transition pressures of most previous studies tend to be linear with increasing temperature (Morishima et al., 1994; Jacobs et al., 2006; Akaogi et al., 2007; Ottonello et al., 2008; Dorogokupets et al., 2015). In contrast, our obtained transition pressure shows obvious nonlinear temperature dependence, which is caused by the nonlinear relationship between determined dP/dT and temperature. At room temperature, the transition pressure is estimated as 10.85 (1) GPa, with the dP/dT as 0.0005 (2) GPa/K. Then, the dP/dT increases with the temperature and reaches 0.0036 (3) GPa/K at 2000 K, where the transition pressure is estimated as 14.47 (18) GPa. The obtained transition pressure can be approximated modeled by a polynomial function of p = 10.78 (1) + 6.73 (2) × 10⁻⁴ (T—273) + 8.49 (1) × 10⁻⁷ (T—273)², where P in GPa and T in K. Detailed data of the calculated transition pressure, dP/dT, and their uncertainties is provided in Supplementary Table S7.

FIGURE 6

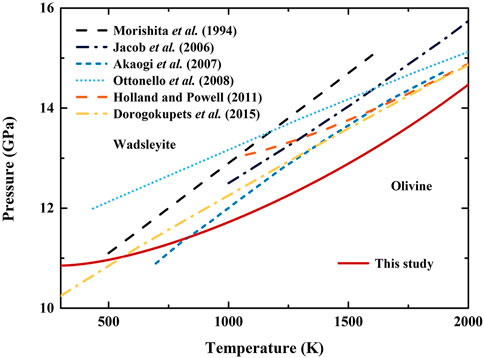
FIGURE 6. phase transition boundary of olivine-wadsleyite in (Mg,Fe)₂SiO₄ system from this study, and previous results in Mg₂SiO₄ system. Red solid line: this study; Blue dash line: Morishima et al. (1994); Blue dash-dot line: Jacobs et al. (2006); Blue short dash line: Akaogi et al. (2007); Blue dot line: Ottonello et al. (2008); Orange dash line: Holland and Powell (2011); Yellow dash-dot line: Dorogokupets et al. (2015).

Furthermore, to investigate the effect of Fe content on the phase transition boundary of olivine-wadsleyite, we collect the variations of $X_{\text{Fe}}$ during the transition from previous work (Katsura and Ito, 1989; Chen et al., 2002; Katsura et al., 2004), and the data is summarized in Figure 7. We find that the transition pressures with the $X_{\text{Fe}}^{\text{α}}$ < 0.1 from previous work are generally higher than our estimation. Also, except for the two data points (1873 K and 14.4 GPa; 1873 K and 14.0 GPa) by Katsura and Ito (1989), the transition pressure decreases with the increasing $X_{\text{Fe}}^{\text{α}}$ at the same temperature condition.

FIGURE 7

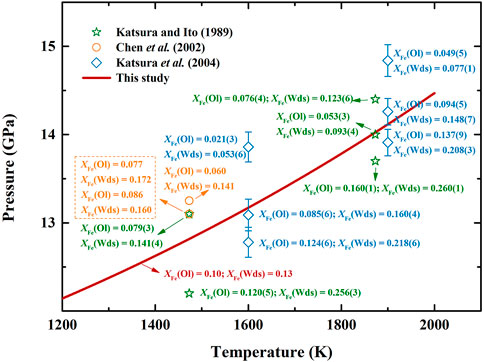
FIGURE 7. Summaries of the variations of $X_{\text{Fe}}$ during the olivine-wadsleyite phase transition in (Mg,Fe)₂SiO₄ system. Ol refers to olivine, and Wds refers to wadsleyite. Red solid line: this study; Green stars: Katsura and Ito (1989); Orange circles: Chen et al. (2002); Blue diamonds: Katsura et al. (2004).

Implication for the Temperature at the 410 km Discontinuity

Temperature is one of the essential parameters for modeling the dynamics of the Earth’s interior. Nearly 4 decades ago, the mantle temperature profiles were presented with the constructions of Earth models (Stacey, 1977; Brown and Shankland, 1981), in which the temperature at the 410 km discontinuity was estimated in a wide range of ∼1700–2000 K. Then, by comparing the depth of the 410 km discontinuity with the pressures of the olivine-wadsleyite transition, Katsura et al. (2004) proposed the temperature as 1760 ± 45 K for a pyrolite model assuming a bulk composition of $X_{\text{Fe}}$ = 0.11. And later, the value was re-evaluated as 1830 ± 48 K (Katsura et al., 2010).

In this study, we regard the globally averaged depth of the 410 km discontinuity as 411 ± 2 km following the results of seismic investigations (Gu et al., 1998; Chambers et al., 2005), and the pressure can be estimated as 13.76 ± 0.05 GPa according to the depth-pressure conversion (Stacey and Davis, 2008). Therefore, the temperature at the 410 km discontinuity is obtained as 1795 ± 70 K on the basis of our phase relations.

It is worth noting that our temperature at the 410 km discontinuity is determined under anhydrous conditions. It has been confirmed that there is water existing in both olivine and wadsleyite in their crystal structure, which would not only reduce their bulk sound velocity (Jacobsen et al., 2008; Mao et al., 2008), but also enlarge their thermal expansion (Ye et al., 2009) and the heat capacity of wadsleyite (Jahn et al., 2013). Evidence has shown that the presence of water would reduce the pressure interval of olivine-wadsleyite phase transformation by 0.3–0.6 GPa (Chen et al., 2002), which leads to an increase of ∼90–176 K in temperature.

Additionally, in this study, we regard $K_{\text{Fe}-\text{Mg}}^{\text{α}-\text{β}}$ as a constant and only present the olivine-wadsleyite phase transition boundary of a simple model in (Mg,Fe)₂SiO₄ system. Previous studies concluded that the values of $K_{\text{Mg}-\text{Fe}}^{\text{α}-\text{β}}$ are in the ranges of 0.38–0.57, 0.52–0.69, and 0.60–0.62 at 1473, 1873, and 1900 K, respectively, which indicates that $K_{\text{Fe}-\text{Mg}}^{\text{α}-\text{β}}$ may decrease with the increasing temperature during the phase transition (Katsura and Ito, 1989; Katsura et al., 2004). Therefore, more complicated systems need to be taken into account in future studies.

Conclusion

In the present study, the self-consistent molar volume, elastic moduli, thermal expansion, heat capacity, and entropy of β-(Mg_0.87,Fe_0.13)₂SiO₄ have been determined up to 2000 K and 20 GPa based on existing experimental data and thermodynamic relations. The calculated parameters were generally consistent with available results. The thermodynamic properties, including entropy of α-(Mg_0.9,Fe_0.1)₂SiO₄ were also reanalyzed on account of our recent work. The thermal expansions, heat capacities, and entropies of both β-(Mg_0.87,Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄ show negative and nonlinear relationships with the pressure. Also, the pressure effects on the thermodynamic properties of α-(Mg_0.9,Fe_0.1)₂SiO₄ are larger than that of β-(Mg_0.87,Fe_0.13)₂SiO₄.

Using the Clausius-Clapeyron equation, the olivine-wadsleyite phase transition boundary with the $K_{\text{Fe}-\text{Mg}}^{\text{α}-\text{β}}$ as 0.74 was estimated with the combination of the obtained molar volumes and entropies of β-(Mg_0.87,Fe_0.13)₂SiO₄ and α-(Mg_0.9,Fe_0.1)₂SiO₄. The transition pressure can be approximately expressed by a polynomial equation of P (GPa) = 10.78 (1) + 6.73 (2) × 10⁻⁴ (T(K)—273) + 8.49 (1) × 10⁻⁷ (T(K)—273)², which is generally lower than the previous studies on Mg₂SiO₄ system at the same temperature condition. For instance, the temperature at the 410 km discontinuity is obtained as 1795 ± 70 K based on our obtained olivine-wadsleyite phase transition boundary under anhydrous conditions, and it would increase by ∼90–176 K if the water effect was considered. The results indicate that both Fe and water contents would influence the transition pressure of olivine-wadsleyite phase transition, which probably leads to a higher temperature at the 410 km discontinuity.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

Conceptualization, CS, YL, and WS; methodology, CS, YL, and DF; software, GY; resources, JJ. and ZS; data curation, WS; writing-original draft preparation, CS; writing-review and editing, YL, WS, and DF; supervision, YL and WS; project administration, YL; funding acquisition, YL. All authors have read and agreed to the published version of the manuscript.

Funding

This project was supported by the National Natural Science Foundation of China (Grant Nos. 41873075 and 42174225), and the Key Research Program of Frontier Sciences of CAS (Grant No. ZDBS-LY-DQC015).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Prof. Wenge Zhou at the Institute of Geochemistry, Chinese Academy of Sciences for helpful discussions and suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.879678/full#supplementary-material

References

Akaogi, M., Ross, N., McMillan, P., and Navrotsky, A. (1984). The Mg₂SiO₄ Polymorphs (Olivine, Modified Spinel and Spinel)-Thermodynamic Properties from Oxide Melt Solution Calorimetry, Phase Relations, and Models of Lattice Vibrations. Am. Mineral. 69, 499–512.

Google Scholar

Akaogi, M., Takayama, H., Kojitani, H., Kawaji, H., and Atake, T. (2007). Low-temperature Heat Capacities, Entropies and Enthalpies of Mg2SiO4 Polymorphs, and α−β−γ and post-spinel Phase Relations at High Pressure. Phys. Chem. Minerals 34, 169–183. doi:10.1007/s00269-006-0137-3

CrossRef Full Text | Google Scholar

Akimoto, S.-i., Komada, E., and Kushiro, I. (1967). Effect of Pressure on the Melting of Olivine and Spinel Polymorph of Fe2SiO4. J. Geophys. Res. 72, 679–686. doi:10.1029/JZ072i002p00679

CrossRef Full Text | Google Scholar

Akimoto, S., Matsui, Y., and Syono, Y. (1978). “High-pressure crystal Chemistry of Orthosilicates and the Formation of the Mantle Transition Zone,” in The Physics and Chemistry of Minerals and Rocks. Editor R. G. J. Strens (New York: John Wiley & Sons).

Google Scholar

Anderson, D. (1995). Equations of State of Solids for Geophysics and Ceramic Science. Oxford University Press.

Google Scholar

Angel, R., Mazzucchelli, M., Gonzalez-Platas, J., and Alvaro, M. (2021). A Self-Consistent Approach to Describe Unit-Cell-Parameter and Volume Variations with Pressure and Temperature. J. Appl. Cryst. 54, 1621–1630. doi:10.1107/S1600576721009092

CrossRef Full Text | Google Scholar

Ashida, T, Kume, S., and Ito, E. (1987), Thermodynamic Aspects of Phase Boundary Among α-, β-, and γ-Mg2SiO4. High‐Pressure Research in Mineral Physics: A Volume in Honor of Syun‐iti Akimoto, 269–274. doi:10.1029/gm039p0269

CrossRef Full Text | Google Scholar

Bina, C. R., and Silver, P. G. (1990). Constraints on Lower Mantle Composition and Temperature from Density and Bulk Sound Velocity Profiles. Geophys. Res. Lett. 17, 1153–1156. doi:10.1029/GL017i008p01153

CrossRef Full Text | Google Scholar

Bina, C. R., and Wood, B. J. (1987). Olivine-spinel Transitions: Experimental and Thermodynamic Constraints and Implications for the Nature of the 400-km Seismic Discontinuity. J. Geophys. Res. 92, 4853–4866. doi:10.1029/JB092iB06p04853

CrossRef Full Text | Google Scholar

Brown, J. M., and Shankland, T. J. (1981). Thermodynamic Parameters in the Earth as Determined from Seismic Profiles. Geophys. J. Int. 66, 579–596. doi:10.1111/j.1365-246X.1981.tb04891.x

CrossRef Full Text | Google Scholar

Chambers, K., Woodhouse, J. H., and Deuss, A. (2005). Topography of the 410-km Discontinuity from PP and SS Precursors. Earth Planet. Sci. Lett. 235, 610–622. doi:10.1016/j.epsl.2005.05.014

CrossRef Full Text | Google Scholar

Chen, J., Inoue, T., Yurimoto, H., and Weidner, D. J. (2002). Effect of Water on Olivine-Wadsleyite Phase Boundary in the (Mg, Fe)2SiO4system. Geophys. Res. Lett. 29, 22–24. 1-22. doi:10.1029/2001gl014429

CrossRef Full Text | Google Scholar

Chopelas, A. (1991). Thermal Properties of β-Mg2SiO4at Mantle Pressures Derived from Vibrational Spectroscopy: Implications for the Mantle at 400 Km Depth. J. Geophys. Res. 96, 11817–11829. doi:10.1029/91jb00898

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2009). Electrical Conductivity of Wadsleyite at High Temperatures and High Pressures. Earth Planet. Sci. Lett. 287, 277–283. doi:10.1016/j.epsl.2009.08.012

CrossRef Full Text | Google Scholar

Dorogokupets, P. I., Dymshits, A. M., Sokolova, T. S., Danilov, B. S., and Litasov, K. D. (2015). The Equations of State of Forsterite, Wadsleyite, Ringwoodite, Akimotoite, MgSiO3-Perovskite, and Postperovskite and Phase Diagram for the Mg2SiO4 System at Pressures of up to 130 GPa. Russ. Geology. Geophys. 56, 172–189. doi:10.1016/j.rgg.2015.01.011

CrossRef Full Text | Google Scholar

Fei, Y., Mao, H.-k., Shu, J., Parthasarathy, G., Bassett, W. A., and Ko, J. (1992). Simultaneous High-P, High-TX ray Diffraction Study of β-(Mg,Fe)2SiO4to 26 GPa and 900 K. J. Geophys. Res. 97, 4489–4495. doi:10.1029/92jb00076

CrossRef Full Text | Google Scholar

Fei, Y., and Saxena, S. K. (1986). A Thermochemical Data Base for Phase Equilibria in the System Fe-Mg-Si-O at High Pressure and Temperature. Phys. Chem. Minerals 13, 311–324. doi:10.1007/bf00308348

CrossRef Full Text | Google Scholar

Gonzalez-Platas, J., Alvaro, M., Nestola, F., and Angel, R. (2016). EosFit7-GUI: a New Graphical User Interface for Equation of State Calculations, Analyses and Teaching. J. Appl. Cryst. 49, 1377–1382. doi:10.1107/s1600576716008050

CrossRef Full Text | Google Scholar

Gu, Y., Dziewonski, A. M., and Agee, C. B. (1998). Global De-correlation of the Topography of Transition Zone Discontinuities. Earth Planet. Sci. Lett. 157, 57–67. doi:10.1016/s0012-821x(98)00027-2

CrossRef Full Text | Google Scholar

Holland, T. J. B., and Powell, R. (2011). An Improved and Extended Internally Consistent Thermodynamic Dataset for Phases of Petrological Interest, Involving a New Equation of State for Solids. J. Metamorphic Geology. 29, 333–383. doi:10.1111/j.1525-1314.2010.00923.x

CrossRef Full Text | Google Scholar

Isaak, D. G., Gwanmesia, G. D., Davis, M. G., Stafford, S. C., Stafford, A. M., and Triplett, R. S. (2010). The Temperature Dependence of the Elasticity of Fe-Bearing Wadsleyite. Phys. Earth Planet. Interiors 182, 107–112. doi:10.1016/j.pepi.2010.06.014

CrossRef Full Text | Google Scholar

Ito, E., and Katsura, T. (1989). A Temperature Profile of the Mantle Transition Zone. Geophys. Res. Lett. 16, 425–428. doi:10.1029/GL016i005p00425

CrossRef Full Text | Google Scholar

Jacobs, M. H. G., van den Berg, A. P., and de Jong, B. H. W. S. (2006). The Derivation of Thermo-Physical Properties and Phase Equilibria of Silicate Materials from Lattice Vibrations: Application to Convection in the Earth's Mantle. Calphad 30, 131–146. doi:10.1016/j.calphad.2005.10.001

CrossRef Full Text | Google Scholar

Jacobsen, S. D., Jiang, F., Mao, Z., Duffy, T. S., Smyth, J. R., Holl, C. M., et al. (2008). Effects of Hydration on the Elastic Properties of Olivine. Geophys. Res. Lett. 35, L14303. doi:10.1029/2008gl034398

CrossRef Full Text | Google Scholar

Jahn, S., Rahner, R., Dachs, E., Mrosko, M., and Koch-Müller, M. (2013). Thermodynamic Properties of Anhydrous and Hydrous Wadsleyite, β−Mg2SiO4. High Press. Res. 33, 584–594. doi:10.1080/08957959.2013.806498

CrossRef Full Text | Google Scholar

Johari, G. P. (2021). Entropy, Enthalpy and Volume of Perfect Crystals at Limiting High Pressure and the Third Law of Thermodynamics. Thermochim. Acta 698, 178891. doi:10.1016/j.tca.2021.178891

CrossRef Full Text | Google Scholar

Katsura, T., and Ito, E. (1989). The System Mg2SiO4-Fe2SiO4at High Pressures and Temperatures: Precise Determination of Stabilities of Olivine, Modified Spinel, and Spinel. J. Geophys. Res. 94, 15663–15670. doi:10.1029/JB094iB11p15663

CrossRef Full Text | Google Scholar

Katsura, T., Mayama, N., Shouno, K., Sakai, M., Yoneda, A., and Suzuki, I. (2001). Temperature Derivatives of Elastic Moduli of (Mg0.91Fe0.09)2SiO4 Modified Spinel. Phys. Earth Planet. Interiors 124, 163–166. doi:10.1016/s0031-9201(01)00189-3

CrossRef Full Text | Google Scholar

Katsura, T., Yamada, H., Nishikawa, O., Song, M., Kubo, A., Shinmei, T., et al. (2004). Olivine-wadsleyite Transition in the System (Mg,Fe)2SiO4. J. Geophys. Res. 109, 2438. doi:10.1029/2003jb002438

CrossRef Full Text | Google Scholar

Katsura, T., Yoneda, A., Yamazaki, D., Yoshino, T., and Ito, E. (2010). Adiabatic Temperature Profile in the Mantle. Phys. Earth Planet. Interiors 183, 212–218. doi:10.1016/j.pepi.2010.07.001

CrossRef Full Text | Google Scholar

Li, B., and Liebermann, R. C. (2000). Sound Velocities of Wadsleyite β-(Mg0.88Fe0.12)2SiO4to 10 GPa. Am. Mineral. 85, 292–295. doi:10.2138/am-2000-2-305

CrossRef Full Text | Google Scholar

Liu, W., Kung, J., Li, B., Nishiyama, N., and Wang, Y. (2009). Elasticity of (Mg0.87Fe0.13)2SiO4 Wadsleyite to 12GPa and 1073K. Phys. Earth Planet. Interiors 174, 98–104. doi:10.1016/j.pepi.2008.10.020

CrossRef Full Text | Google Scholar

Mao, Z., Jacobsen, S. D., Jiang, F., Smyth, J. R., Holl, C. M., Frost, D. J., et al. (2008). Single-crystal Elasticity of Wadsleyites, β-Mg₂SiO₄, Containing 0.37-1.66 wt.% H₂O. Earth Planet. Sci. Lett. 266, 78–89. doi:10.1016/j.epsl.2007.10.045

CrossRef Full Text | Google Scholar

Mayama, N. (2004). Temperature Dependence of Elastic Moduli of β-(Mg, Fe)2SiO4. Geophys. Res. Lett. 31. doi:10.1029/2003gl019247

CrossRef Full Text | Google Scholar

Morishima, H., Kato, T., Suto, M., Ohtani, E., Urakawa, S., Utsumi, W., et al. (1994). The Phase Boundary between α- and β-Mg 2 SiO 4 Determined by In Situ X-ray Observation. Science 265, 1202–1203. doi:10.1126/science.265.5176.1202

PubMed Abstract | CrossRef Full Text | Google Scholar

Ottonello, G., Civalleri, B., Ganguly, J., Vetuschi Zuccolini, M., and Noel, Y. (2008). Thermophysical Properties of the α-β-γ Polymorphs of Mg2SiO4: a Computational Study. Phys. Chem. Minerals 36, 87–106. doi:10.1007/s00269-008-0260-4

CrossRef Full Text | Google Scholar

Ovrutsky, A. M., Prokhoda, A. S., and Rasshchupkyna, M. S. (2014). “Basic Concepts of Theory of Phase Transformations,” in Computational Materials Science. Editors A. M. Ovrutsky, A. S. Prokhoda, and M. S. Rasshchupkyna (Oxford: Elsevier), 35–69. doi:10.1016/b978-0-12-420143-9.00002-8

CrossRef Full Text | Google Scholar

Ringwood, A. E. (1962). A Model for the Upper Mantle: 2. J. Geophys. Res. 67, 4473–4478. doi:10.1029/JZ067i011p04473

CrossRef Full Text | Google Scholar

Ringwood, A. E., and Major, A. (1970). The System Mg2SiO4-Fe2SiO4 at High Pressures and Temperatures. Phys. Earth Planet. Interiors 3, 89–108. doi:10.1016/0031-9201(70)90046-4

CrossRef Full Text | Google Scholar

Robie, R. A., Finch, C. B., and Hemingway, B. S. (1982a). Heat Capacity and Entropy of Fayalite (Fe₂SiO₄) between 5.1 and 383 K: Comparison of Calorimetric and Equilibrium Values for the QFM Buffer Reaction. Am. Mineral. 67, 463–469.

Google Scholar

Robie, R. A., Hemingway, B. S., and Takei, H. (1982b). Heat Capacities and Entropies of Mg₂SiO₄, Mn₂SiO₄, and Co₂SiO₄ between 5 and 380 K. Am. Mineral. 67, 470–482.

Google Scholar

Saxena, S. K. (1996). Earth Mineralogical Model: Gibbs Free Energy Minimization Computation in the System MgOFeOSiO2. Geochimica et Cosmochimica Acta 60, 2379–2395. doi:10.1016/0016-7037(96)00096-8

CrossRef Full Text | Google Scholar

Sinogeikin, S. V., Katsura, T., and Bass, J. D. (1998). Sound Velocities and Elastic Properties of Fe-Bearing Wadsleyite and Ringwoodite. J. Geophys. Res. 103, 20819–20825. doi:10.1029/98jb01819

CrossRef Full Text | Google Scholar

Stacey, F. D. (1977). A thermal Model of the Earth. Phys. Earth Planet. Interiors 15, 341–348. doi:10.1016/0031-9201(77)90096-6

CrossRef Full Text | Google Scholar

Stacey, F., and Davis, P. (2008). Physics of the Earth. Cambridge: Cambridge Univ. Press.

Google Scholar

Su, C., Liu, Y., Fan, D., Song, W., and Yang, G. (2022). Self-consistent Thermodynamic Parameters of Pyrope and Almandine at High-Temperature and High-Pressure Conditions: Implication on the Adiabatic Temperature Gradient. Phys. Earth Planet. Interiors 322, 106789. doi:10.1016/j.pepi.2021.106789

CrossRef Full Text | Google Scholar

Su, C., Liu, Y., Song, W., Fan, D., Wang, Z., and Tang, H. (2018). Thermodynamic Properties of San Carlos Olivine at High Temperature and High Pressure. Acta Geochim 37, 171–179. doi:10.1007/s11631-018-0261-z

CrossRef Full Text | Google Scholar

Suzuki, I., Ohtani, E., and Kumazawa, M. (1980). Thermal Expansion of Modified Spinel, .BETA.-Mg2SiO4. J,Phys,Earth 28, 273–280. doi:10.4294/jpe1952.28.273

CrossRef Full Text | Google Scholar

Wang, J., Bass, J. D., and Kastura, T. (2014). Elastic Properties of Iron-Bearing Wadsleyite to 17.7GPa: Implications for Mantle mineral Models. Phys. Earth Planet. Interiors 228, 92–96. doi:10.1016/j.pepi.2014.01.015

CrossRef Full Text | Google Scholar

Watanabe, H. (1982). “Thermochemical Properties of Synthetic High Pressure Compounds Relevant to the Earth’s Mantle,” in High Pressure Research in Geophysics. Editor H. A. a. M. H. Manghnani (Tokyo: Center for Academic Publishing of Japan).

Google Scholar

Wu, Z., and Wentzcovitch, R. M. (2007). Vibrational and Thermodynamic Properties of Wadsleyite: A Density Functional Study. J. Geophys. Res. 112. doi:10.1029/2007jb005036

CrossRef Full Text | Google Scholar

Xu, Y., Shankland, T. J., Linhardt, S., Rubie, D. C., Langenhorst, F., and Klasinski, K. (2004). Thermal Diffusivity and Conductivity of Olivine, Wadsleyite and Ringwoodite to 20 GPa and 1373 K. Phys. Earth Planet. Interiors 143-144, 321–336. doi:10.1016/j.pepi.2004.03.005

CrossRef Full Text | Google Scholar

Ye, Y., Schwering, R. A., and Smyth, J. R. (2009). Effects of Hydration on thermal Expansion of Forsterite, Wadsleyite, and Ringwoodite at Ambient Pressure. Am. Mineral. 94, 899–904. doi:10.2138/am.2009.3122

CrossRef Full Text | Google Scholar

Yoshino, T., Shimojuku, A., Shan, S., Guo, X., Yamazaki, D., Ito, E., et al. (2012). Effect of Temperature, Pressure and Iron Content on the Electrical Conductivity of Olivine and its High-Pressure Polymorphs. J. Geophys. Res. 117, a–n. doi:10.1029/2011jb008774

CrossRef Full Text | Google Scholar