Applicability of the landscape evolution model in the absence of rills

Cheraghi, Mohsen; Rinaldo, Andrea; Sander, Graham C.; Perona, Paolo; Cimatoribus, Andrea; Jomaa, Seifeddine; Barry, D. A.

doi:10.3389/feart.2022.872711

ORIGINAL RESEARCH article

Front. Earth Sci., 07 July 2022

Sec. Quaternary Science, Geomorphology and Paleoenvironment

Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.872711

This article is part of the Research Topic Modern Geomorphic Processes: From Source to Sink and From Survey to Models View all 8 articles

Applicability of the landscape evolution model in the absence of rills

Mohsen Cheraghi¹*

Andrea Rinaldo^2,3

Graham C. Sander⁴

Paolo Perona^5,6

Andrea Cimatoribus¹

Seifeddine Jomaa⁷

D. A. Barry¹

¹Ecological Engineering Laboratory (ECOL), Institute of Environmental Engineering (IIE), School of Architecture, Civil and Environmental Engineering (ENAC), École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
²Ecohydrology Laboratory (ECHO), Institute of Environmental Engineering (IIE), School of Architecture, Civil and Environmental Engineering (ENAC), École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
³Dipartimento di Ingegneria Civile Edile e Ambientale, Universitá di Padova, Padua, Italy
⁴School of Architecture, Building and Civil Engineering, Loughborough University, Loughborough, United Kingdom
⁵Hydraulic Platform-LCH, Civil Engineering Institute (IIC), School of Architecture, Civil and Environmental Engineering (ENAC), École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
⁶School of Engineering, Institute for Infrastructure and Environment, The University of Edinburgh, Edinburgh, United Kingdom
⁷Department of Aquatic Ecosystem Analysis and Management, Helmholtz Centre for Environmental Research—UFZ, Magdeburg, Germany

Despite numerous applications of physically-based models for incised landscapes, their applicability for overland flow on unchanneled surfaces is not known. This work challenges a widely used landscape evolution model for the case of non-uniform rainfall and absence of rills using laboratory flume experiment. Rainfall with an average intensity of 85 mm h⁻¹ was applied for 16 h during which high resolution laser scans of the morphology were captured. The overland flow was modeled as a network that preserves the water flux for each cell in the discretized domain. This network represented the gravity-driven surface flow and determined the evolution direction. The model was calibrated using the first 8 h of the experiment and was then used to predict the second 8 h. The calibrated model predicted, as expected, a smoother surface morphology (and less detailed overland flow network) than that measured. This difference resulted from quenched randomness (e.g., small pebbles) within the experimental soil that emerged during erosion and that were captured by the laser scans. To investigate the quality of the prediction, a low-pass filter was applied to remove the small-scale variability of the surface morphology. This step confirmed that the model simulations captured the main characteristics of the measured morphology. The experimental results were found to satisfy a scaling relation for the exceedance probability of discharge even in absence of rills. However, the model did not reproduce the experimental scaling relation as the detailed surface micro-roughness was not accounted for by the model. A lower cutoff on the scale of applicability of the general landscape evolution equation is thus suggested, complementing other work on the upper cutoff underpinned by runoff-producing areas.

Introduction

The complexity of natural landscapes reflects the numerous factors involved in their formation such as climate (Francipane et al., 2015; Han et al., 2015; Hooshyar et al., 2019; van der Meij et al., 2020), chemical and physical properties of the sediments (Massong and Montgomery, 2000; Sklar and Dietrich, 2001; Park and Latrubesse, 2015), episodic gully erosion (Pazzaglia et al., 2015), different vegetation types (Istanbulluoglu and Bras, 2005; Jeffery et al., 2014; Corenblit et al., 2015), tectonic effects (Pedrazzini et al., 2016) and the rate of sediment production (Reusser et al., 2015; Rodriguez-Lloveras et al., 2015; Forte et al., 2016). Landscape formation and evolution are not directly measurable in the field due to the time scales involved. Consequently, suitably designed laboratory experiments are of considerable value in that they provide empirical data that are amenable to testing hypotheses of mechanisms underlying observed geomorphological changes (Paola et al., 2009).

Physically-based landscape evolution models (LEMs) (Willgoose, 1989; Willgoose et al., 1991, 1992; Howard, 1994; Whipple and Tucker, 1999, 2002) are useful tools to explain the surface geometry in landscapes and laboratory experiments (Mudd, 2016; Whipple et al., 2016, 2017; Sinclair, 2017). In LEMs, the complex fluid-particle interactions within landscapes are described by a governing equation for the surface elevation, with an additional model for surface flow (Chen et al., 2014). For catchments, the focus of surface flow is the stream/river drainage network, rather than the overland flow. Typically, flow is modeled in a simplified manner that conserves the volume flux at each cell in the landscape (O’Callaghan and Mark, 1984; Freeman, 1991; Quinn et al., 1991; Costa-Cabral and Burges, 1994; Tarboton, 1997). Broadly speaking, the relative importance of the advective and diffusive processes described by the LEM controls the landscape geometry produced. That is, considering an initially non-incised morphology, localized (channel-forming) landscape incision is favored when advection (or surface shear stress) dominates, whereas more gradually varying landscapes will result when (effective) diffusion dominates.

There are numerous applications of LEMs to understand different features of the surface morphology of natural landscapes (Yang et al., 2015; Mudd, 2016; Whipple et al., 2016, 2017; Sinclair, 2017; Bonetti et al., 2020; Hooshyar and Porporato, 2021; Hu et al., 2021; Kwang et al., 2021; Shelef and Goren, 2021; Litwin et al., 2022). For example, Perron et al. (2008) derived an expression for the distance between first-order valleys and validated the formula via measurements from five different natural landscapes (Perron et al., 2009). Willett et al. (2014) showed that in disequilibrium conditions, the drainage divides between basins and migrates towards a steady-state condition and thereby reorganize their structure. The criteria defining the reorganization direction were found by using the steady-state solution of an LEM (Perron and Royden, 2013). It is noteworthy that the LEM equation in its original formulation (where the local landscape-forming fluxes are surrogated by total contributing area thus postulating uniform precipitation) corresponds to the leading term of the small-gradient approximation of the general mass-balance equation under general reprametrization invariance (Banavar et al., 2001). This has consequences, because at steady state optimal channel networks (OCNs) are exact constructions and each local, dynamically accessible minimum proves to be a tree (Rodriguez-Iturbe and Rinaldo, 2001; Rinaldo et al., 2014).

Similar to their application to natural landscapes, LEMs were also used in the analyses of laboratory experiments. Such experiments permit exploration of different initial conditions, e.g., a land surface composed of uniform and non-cohesive sediment grains, with surface morphology changes induced by rainfall. Advection-dominated setups focus on the evolution of the network structure (i.e., surface incisions) (Hancock and Willgoose, 2002; Bonnet and Crave, 2003; Hasbargen and Paola, 2003; Lague et al., 2003; Bonnet and Crave, 2006; Bonnet, 2009; Paola et al., 2009; Graveleau et al., 2012; Rohais et al., 2012; Reinhardt and Ellis, 2015; Singh et al., 2015; Cheraghi et al., 2018). Small raindrop sizes minimize the kinetic energy of raindrop impact, leading to surface morphologies that evolve almost exclusively through shear stress of surface flows. For instance, Hasbargen and Paola (2000) set up an experiment in an elliptical plot (98 cm × 87 cm) subjected to a constant uplift rate. They pointed out that the oscillation of the erosion rate at steady-state was the result of knickpoint migration in the domain. The spatial patterns of landslides and knickpoints in a steady-state landscape were measured by Bigi et al. (2006), who found a power-law relation between the number of landslides and drainage area. The power-law relation was consistent with the gamma-distribution probability density function of landslides in the field (Malamud et al., 2004). Sweeney et al. (2015) analyzed landscapes subjected to rainfall events with different droplet sizes considering the same initial condition. For the different landscape patterns so-created, they showed that the drainage density decreases with increasing droplet size (i.e., relative increase in diffusion).

There are numerous similar studies that examined rill formation on hillslopes (Parker, 1977; Bryan and Poesen, 1989; Gomez and Mullen, 1992; Brunton and Bryan, 2000; Römkens et al., 2002; Pelletier, 2003; Raff et al., 2004; Rieke-Zapp and Nearing, 2005; Tatard et al., 2008; Yao et al., 2008; Oliveto et al., 2010; Gordon et al., 2011, 2012; Stefanon et al., 2012; Shit et al., 2013; He et al., 2014; Bennett et al., 2015; Bennett and Liu, 2016; Wu and Chen, 2020; Ren et al., 2021). In these experiments, droplet sizes are large enough to induce splash-impact erosion, which is manifested in changes in surface morphology. For instance, Gómez et al. (2003) and Berger et al. (2010) tested the minimal energy expenditure theory (Rinaldo et al., 1992) for rill networks considering different slopes, rainfall intensities and initial conditions. They found that, when the land was effectively incised, the total energy dissipation decreased as the rills evolved. McGuire et al. (2013) calibrated experimental data with the shallow water flow equations coupled with a process-based erosion model (Hairsine and Rose, 1991, 1992a,b; Simpson and Schlunegger, 2003; Simpson and Castelltort, 2006). They found that the entrainment term differences between the models have a greater effect on morphology predictions of the models than the diffusive term.

In this work, we report a laboratory experiment with two significant differences to those described above. First, by design rainfall was highly non-uniform in space; and second, the surface morphology did not become incised at all in the experiment (i.e., rills did not form), but still exhibiting self-organized aggregation. Cheraghi et al. (2018) showed that the morphology measured in the laboratory flume exhibits the same scale-invariant power laws during its evolution as found for catchments. In other words, the statistical features of catchment channel networks were found in the unchanneled area when the morphology was captured and analyzed at high resolution. That finding motivated this investigation based on a widely-used catchment-scale LEM (Howard, 1994; Perron et al., 2008) as a tool to predict the evolution of its unchanneled morphology, i.e., for the situation where diffusive processes dominate such that channels do not form. Previous applications of this LEM considered an incised landscape in which discharge occurs either as overland flow (to channels/rivers), or as flow within the channels. In our experiment, only overland flow occurs, and the surface is never incised. Nevertheless, we model the overland flow as a discharge network, as done in other applications of the LEM. Additionally, we test the ability of the model to simulate directly the measured surface morphology, a test that is not possible at the landscape scale, and was hitherto not attempted at the laboratory experiment scale.

Materials and methods

Experiment

The same experimental data set was used previously (Cheraghi et al., 2018), and only essential details are presented here. We applied a nonuniform rainfall with an average intensity of 85 mm h⁻¹ on a 2-m × 1-m erosion flume with 5% slope (Figure 1). There was no infiltration at the flume’s bottom. Sandy sediment was added to the flume to a depth of 15 cm (Table 1). Digital Elevation Models (DEMs) at 0.25, 0.5, 1, 2, 4, 8 and 16 h were captured by a 3D laser scanner with about 4-mm resolution. The rainfall stopped while the morphology was measured and then restarted.

FIGURE 1

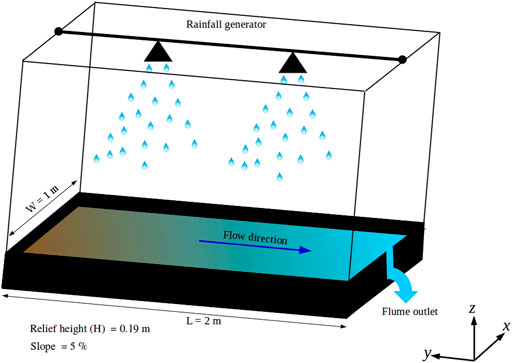
FIGURE 1. Schematic of the flume experiment. The sediment elevation was measured from the outlet (z = 0) and with respect to the horizon. The relief height (the maximum elevation) was 0.19 m. Details on the experimental setup are given in the Supplementary materials of Cheraghi et al. (2018).

TABLE 1

TABLE 1. Characteristics of the sand used in the experiment.

Landscape evolution model

We critically assess the applicability of Fokker–Planck form of landscape evolution model at a scale which is less than a computational cell of catchments. Due to large spatial scales, the model is derived based on simplification of turbulent flows and erosion mechanisms. In this work, the idea is to consider the large-scale model at the plot scale and assess how well the simple LEM can represent the complex fluid-particle interactions during heterogeneous rainfall and in absence of incision. The LEM used here is a modification of Howard’s model (Howard, 1994) and is derived similarly to the approach of Perron et al. (2008) with two differences: 1) it is based on the critical stream power rather than critical shear stress, and 2) instead of the drainage area at large scales, the discharge (Q) is used in the nonlinear part of the advection term. In absence of tectonic effects the model is:

\frac{\partial z}{\partial t} = D \nabla^{2} z - K f (Q^{m} S - Ω_{c r}) (1)

where Cartesian coordinates are used. In this equation, z(x, y, t), t, S, are elevation from the horizontal, time and slope, respectively, and f(ζ) = ζ H(ζ) where H(ζ) is the Heaviside step function. The parameter Ω_cr is proportional to the critical stream power by which fluvial sediment transport is initiated. The two parameters D and K are functions of rainfall intensity, droplet size, sediment properties (e.g., density, particle size, cohesion) and surface roughness (Furbish et al., 2007; Dunne et al., 2010; Mahmoodabadi and Sajjadi, 2016; Sadeghi et al., 2017). The exponent m takes values in the range 0.41–0.857 (Willgoose, 1989; Rodriguez-Iturbe and Rinaldo, 2001). We took m = 1/2 as this value was also used in studies on optimal channel networks based on the theory of minimum energy expenditure for river network evolution (Rinaldo et al., 1992, 1993). At catchment scales, the first term on the right side of Eq. 1 is dominant for hillslopes and includes different processes such as weathering (Perron, 2017), soil creep and rain splash (Culling, 1960, 1963, 1965). The second term on the right is usually assumed to model sediment transport within the river network (since elsewhere this term vanishes). However, in our flume-scale experiment, there were no surface incisions, and the overland flow is at all times continuous across the entire flume. Thus, the overland flow in the experiment is modeled as a network, although there is no river network as found in previous applications of the LEM (Tucker and Hancock, 2010; Benaïchouche et al., 2016; Whipple et al., 2016; Hancock et al., 2017; Perron, 2017).

Numerical simulation and calibration

During the initial stage of the experiment, the surface morphology at the flume exit changed rapidly due to the location of the flume drain. Such behavior is not captured by the model. Therefore, the scanned morphology at t = 15 min was used as the initial condition for the numerical simulations. In applying the LEM, at each time step, the pit points were removed using the algorithm of Planchon and Darboux (2002). After determining the flow direction via the d8 algorithm (O’Callaghan and Mark, 1984), the discharge at the ith cell, Q_i, was calculated using:

Q_{i} = \sum_{j = 1}^{8} w_{j i} Q_{j} + R_{i} Δ x Δ y (2)

where the summation over j refers to the eight cells surrounding the ith cell. The value of the element of the connectivity matrix, w_ji (−) is unit if the cell j flows into cell i, and zero otherwise. R_i (mm h⁻¹) is rainfall intensity on the cell i (Figure 2) and Δx (mm) and Δy (mm) are the grid sizes in x and y directions, respectively. Numerical results presented here used cell sizes of 8 mm × 8 mm.

FIGURE 2

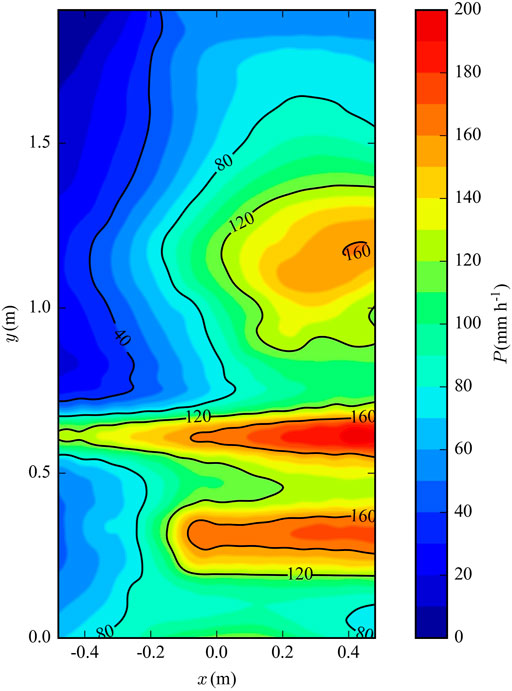
FIGURE 2. Rainfall distribution on the flume. The average precipitation and the uniformity coefficient were 85 mm h⁻¹ and 26%, respectively.

The numerical solution was obtained by two fractional time steps (Press et al., 2007). The first step used the second-order Runge-Kutta scheme to solve the advection term (Eq. 1), while the second used the Alternating-Direction Implicit (ADI) method for the diffusion part. This approach was used previously by Perron et al. (2008), who explain it in detail. At the side wall, a conditional boundary condition was used as shown in Figure 3. At each time step, after the matrix operations (Runge-Kutta + ADI), the gradient normal to the boundary ( $\frac{\partial z}{\partial n} |_{w}^{t}$ , where w refers to the wall) was calculated using the experimental data $(\frac{\partial z^{e}}{\partial n} |_{w}^{t})$ , which were linearly interpolated between scans. Afterwards, the sediment elevations adjacent to the walls $(z_{w}^{t})$ were calculated based on the gradients. In the decision block, the value of $(z_{w}^{t})$ was checked; the condition was that the elevation had to decrease at each time step $(z_{w}^{t} < z_{w}^{t - Δ t})$ . If the condition was not met, the slope remained unchanged (equal to the last time step (t − Δt)) and, based on that, the new elevation at the boundary was calculated.

FIGURE 3

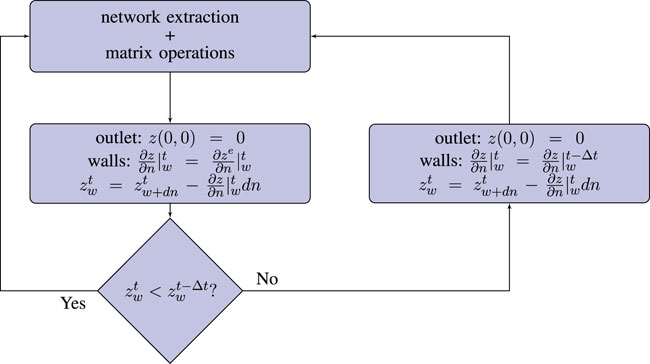
FIGURE 3. The wall boundary condition assuming $\vec{n}$ as the outward unit vector normal to the wall. The term $\frac{\partial z^{e}}{\partial n} |_{w}^{t}$ was calculated by linear interpolation between the two consecutive scans before and after the time t.

An evolutionary algorithm, Borg MOEA (Hadka and Reed, 2013), was used to find the optimal parameters. The initial condition of the numerical modeling was the experimental data at t = 0.25 h (results in Figure 4). The model was calibrated using the root-mean-square error of the morphology (z) at t = 8:

f = \sqrt{\frac{\sum_{i = 1}^{N} {(z_{i, m o d e l} - z_{i, \exp})}^{2}}{N}} |_{t = 8 h} (3)

where z_i,model and z_i, exp are the modeled and measured elevations for cell i.

FIGURE 4

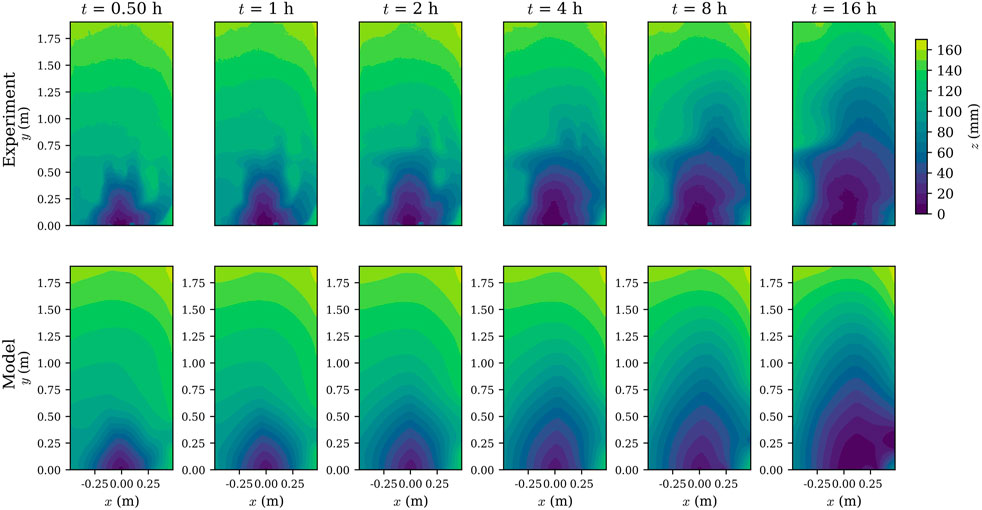
FIGURE 4. Numerical simulation of the LEM and the experimental data. In both experiment and simulation, the morphology evolves toward the high precipitation area.

Results and discussion

Here, we critically examine the LEM’s ability to reproduce the experimental observations of Cheraghi et al. (2018).

Morphological evolution and the corresponding discharge network

The calibrated parameters are presented in Table 2. The average diffusion coefficient (D) is also higher than those reported for the field scale (0.16–222.4 mm² h⁻¹) (Martin, 2000; Benaïchouche et al., 2016). This is consistent with the lack of rilling in our experiments, as rill formation is favored for lower diffusivities (Sweeney et al., 2015). In contrast to the present experimental setup, previous laboratory experiments analyzed with the LEM used fine particles, low rainfall intensities and small droplets, i.e., they were designed to produce rills (Hancock and Willgoose, 2002; Bonnet and Crave, 2003; Hasbargen and Paola, 2003; Lague et al., 2003; Bonnet and Crave, 2006; Bonnet, 2009; Paola et al., 2009; Graveleau et al., 2012; Rohais et al., 2012; Reinhardt and Ellis, 2015; Singh et al., 2015; Sweeney et al., 2015).

TABLE 2

TABLE 2. Calibrated parameters (±95% confidence interval) for the LEM.

The numerical results are compared with the experimental data in Figure 4. The model is able to capture the main characteristics of the morphology, i.e., the downstream area (z < 60 mm) has a symmetric shape while the upstream (z ≥ 60 mm) area is being eroded. In agreement with the experiment, the model shows a noticeable erosion and growth of downstream region (z < 60 mm) at t = 4 and 8 h. Recall that the model was calibrated using measurements at 8 h, and then used to predict the morphology at t = 16 h, where the agreement is satisfactory. The evolution of the surface elevation change in both experiment and model is more evident in the high precipitation area (right hand side of the flume).

Despite simulating the main characteristics of the morphology evolution, some differences are seen between the model and the experiment. These differences are likely due to the local scale fluid-particle and particle-particle interactions that are not accounted for in the model. One of these processes is the armoring effect (Polyakov and Nearing, 2003; Wang et al., 2014; Cheraghi et al., 2016; Lisle et al., 2017). Due to shorter erosion time scales, the fine sediment particles are rapidly removed while the larger particles are deposited on the surface or are not moved at all, resulting in a surface covered by pebbles (Figure 5). Nonetheless, the calibrated LEM can reproduce the main features of the morphology.

FIGURE 5

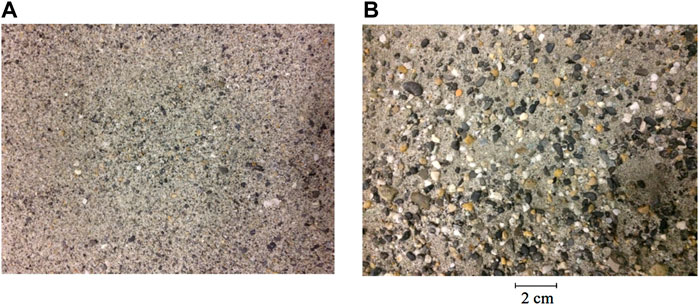
FIGURE 5. Flume surface at t = 0 (A) and t = 16 h (B). This figure is from Cheraghi et al. (2018).

In the LEM (Eq. 1), the advective term is involved in the computation when the value of Q^1/2S exceeds the critical value of Ω_cr. At the catchment scale, the advection-dominated area are observed as rivers networks (Howard, 1994; Perron et al., 2008). However, in this experiment, there is no visual geomorphological criterion to identify the advective regions as there is no incision.

Spectral analysis

The differences in the modeled and measured morphologies were quantified by taking 2D Fourier transforms of each. We present the resulting power spectral densities (PSD) for the morphologies at t = 8 h (plots for other times are similar) in Figure 6, where we show results as a function of the horizontal wave number (azimuthally averaged). The results show that measured and modeled PSD agree up to a wave number of 5–9 m⁻¹. To check the effect of the differences in the spectra, we applied a low-pass filter (Blackman window, Blackman and Tukey (1958)) to both measurements and modeled morphologies, with a cutoff wave number of about 7 m⁻¹. In Figure 7, the original morphologies of the model and experiment are compared with the filtered ones. Filtering removes the small scale roughness (the large deposited stones shown in Figure 5B) of the experiment while the model results are much less sensitive to the low-pass filtering. In Figure 8, the discharge was calculated via Eq. 2 using the original and filtered morphologies. For the experiment, the complex flow patterns of the measured surfaces (due to microtopography, small scale roughness and armoring) are removed by filtering. On the other hand, there is little change to the discharge network of the model. In short, after filtering, the flow networks for both the experimental measurements and model results are in good agreement. Note that the cutoff wave number and the difference between drainage network before and after filtering are a function of many factors such as sediment particle distribution, microtopography, grain size, cohesion (which does not exist in this experiment) and precipitation rate.

FIGURE 6

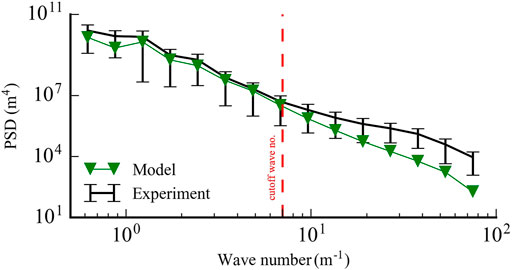
FIGURE 6. Power spectral density of the morphology at t = 8 h. The error bars of the experimental data are based on the standard deviation from the azimuthally averaged PSD in the wave number domain.

FIGURE 7

FIGURE 7. The original morphology of and the low-pass filtered morphology at t = 8 h.

FIGURE 8

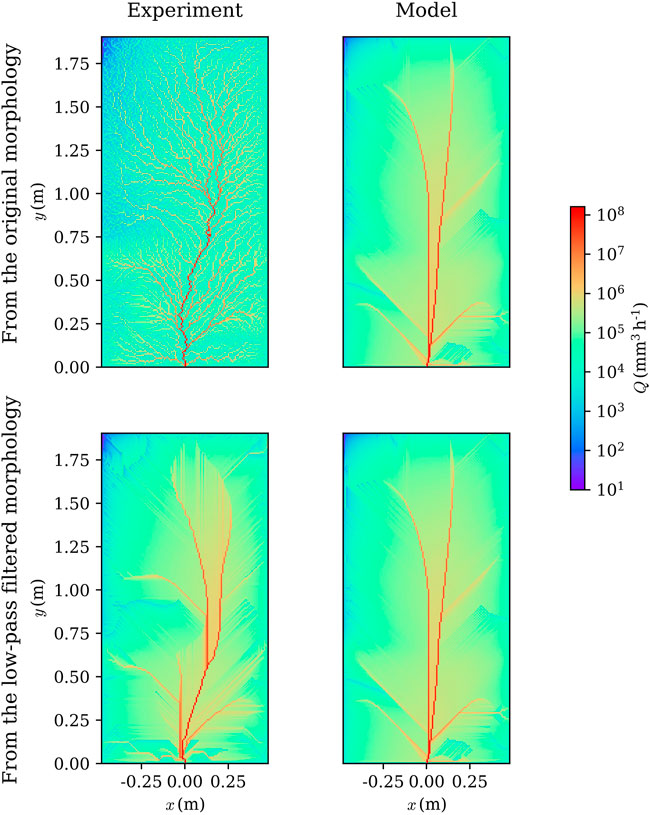
FIGURE 8. The original discharge network and the network extracted from the low-pass filtered morphology at t = 8 h.

The discharge network of the filtered experimental results are compared with the model network in Figure 9. In both experiment and model, the network has a dendritic form at t = 0.5 h. Afterwards, the network becomes more concentrated and the flow from the upstream is directed to two main streams. The two streams migrate from the left to the right of the flume as the precipitation proceeds. This migration is responsible for the dynamic change in the erosion pattern of the upstream (Figure 4). The model is able to reproduce the migration of the concentrated flow to the right hand side, which induces the downstream morphological evolution.

FIGURE 9

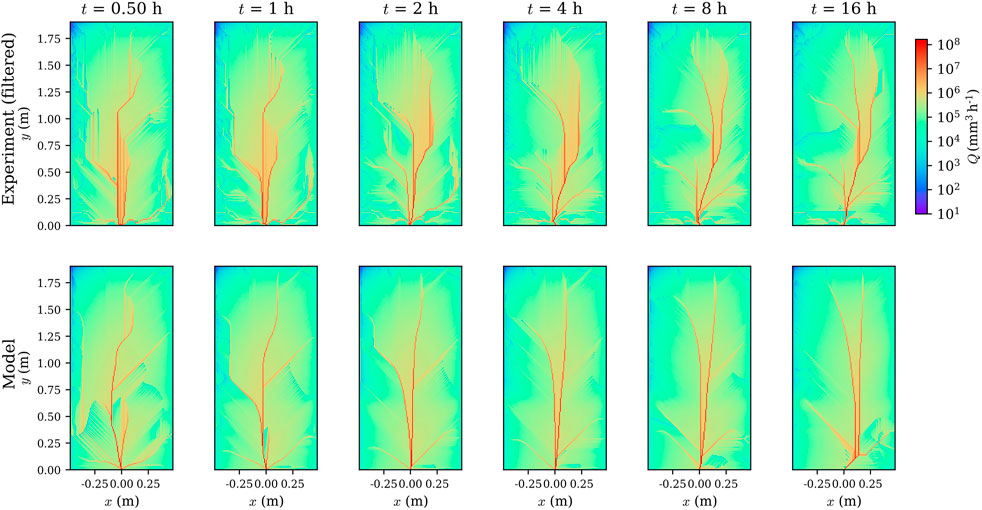
FIGURE 9. Discharge distribution at different times (logarithmic scale). The experimental network was calculated based on the filtered morphology.

An important factor to be investigated in future research would be the scanning resolution. At the catchment-scale, the effect of resolution on the hydrological features such as landslide susceptibility mapping (Meena and Gudiyangada Nachappa, 2019), stream network position (McMaster, 2002), and flood modeling (Muthusamy et al., 2021) is studied. Muthusamy et al. (2021) concluded that the resolution has to be finer than the considered river width for modeling. In the absence of rills, it is highly possible to have similar limitation for the LEM simulation based on the grain sizes and the inter-particle distance after armoring.

Drainage area network statistical analysis

Here we examine the ability of the model to reproduce experimental scaling laws derived from the drainage area network. The drainage area at the ith cell, A_i, was calculated using:

A_{i} = \sum_{j = 1}^{8} w_{j i} A_{j} + Δ x Δ y (4)

where the summation over j and w_ji has the same definition as in Eq. 2.

In the analysis of Cheraghi et al. (2018), the experimental data followed a time-invariant power-law relation (Hack’s law, A = l^h) between upstream length (l) and drainage area (A) with the scaling exponent h in the range [0.54–0.6] during the network evolution. Furthermore, even though no rills were observed, the exceedance probability of drainage area (P(A > a) = a^−β) and the exceedance probability of length (P(L > l) = l^−ψ) had time-invariant exponent values of β = 0.47 and ψ = 0.75. These findings show that, at the flume-scale and in absence of incision, the surface morphology is statistically similar to catchments (Rinaldo et al., 1992; Rodriguez-Iturbe and Rinaldo, 2001) in that the same scalings are observed in each case.

The relation between the upstream length (l) and drainage area (A) and the exceedance probabilities for the LEM, original experiment and its low-pass filtered morphology are presented in Figure 10, Figure 11, Figure 12. The results show that the LEM deviates from the original experimental data for the metrics shown in each plot. However, the results each plot show that the model agrees with the low-pass filtered experimental data. These comparisons further confirm the ability of the model to capture the low-pass filtered experimental morphology, but not the micro roughness. On the other hand, the results for the unfiltered experimental data produce scaling laws that agree with previous results for catchments (Rinaldo et al., 1992; Rodriguez-Iturbe and Rinaldo, 2001). Higher order streams of the network (higher drainage area, A > 2 × 10⁴ mm²) are not affected by the low-pass filtering. As a result, both model and filtered experimental results are in agreement with the original experiment in this range.

FIGURE 10

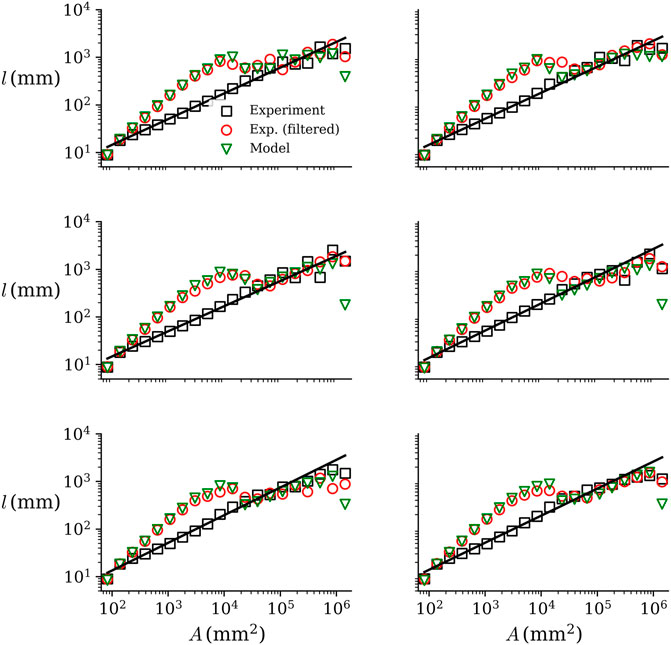
FIGURE 10. Relation between the upstream length and drainage area (Hack’s law) for the model and experiment. The model results differ from the (unfiltered) experimental data, but agrees with the experimental data subjected to the low-pass filter.

FIGURE 11

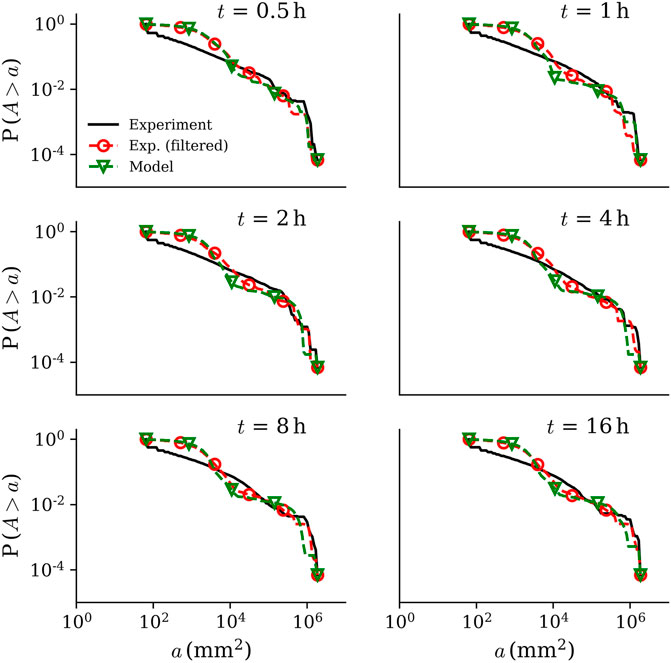
FIGURE 11. Exceedance probability of drainage area for the model, original experiment and its low-pass filtered morphology. The model results and filtered experimental results agree at all times.

FIGURE 12

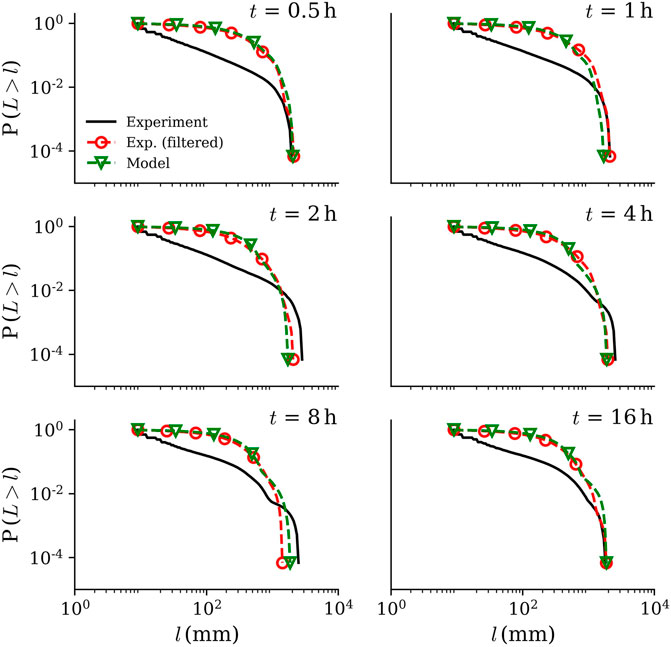
FIGURE 12. Exceedance probability of upstream length the model, original experiment and its low-pass filtered morphology. There is good agreement between the filtered data and the model.

Conclusion

This study introduced the large scale landscape evolution model (LEM), coupled with the d8 algorithm for shallow overland flow, as a robust simulation tool for describing land surface morphology changes in the absence of rills. By calibrating only three model parameters, the LEM was able to capture morphological changes that evolved under a heterogeneous rainfall. This is a manifestation of a simple and efficient model as highlighted by Paola and Leeder (2011). The erosive processes captured by the LEM are broadly characterized as raindrop impact-induced diffusion and surface flow-induced shear stress. Unlike previous investigations, here the surface is continuously covered by overland flow, which is modeled as a flow network.

As described by the LEM, shear stress-driven erosion does not occur until a soil-specific flow rate is exceeded. The LEM-based analysis revealed that even for the considered situation where the morphological evolution is dominated by diffusive processes (and so the surface is not incised), the advective term in the LEM is still necessary to predict the surface evolution. Similarly to natural river networks at catchment scale and incised surfaces in previously reported laboratory experiments, a power-law relation was observed in the discharge exceedance probability for the experimental data. The intricate surface flow details captured by the detailed surface scans of the experimental flume were, however, not present in the modeled surface. Low-pass filtering of the measured and modeled surfaces markedly improved the agreement between the calculated flow networks. However, in that case, the discharge exceedance scaling relationships were not maintained. In general, the LEM could reproduce the low-pass filtered experimental results, i.e., small scale variability due surface roughness that increased over the course of the experiment is not present in the LEM, and had to be removed to obtain reasonable agreement between the experimental measurements and the model results.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, writing the original draft, investigation and modeling were done by MC. DB, AR and GS supervised the work and edited the manuscript. PP provided the laser scanner and supervised the scanning calibration. AC contributed to the spectral analysis. SJ guided the initial phases of experiment and further contributed to analyzing the rainfall patterns.

Funding

Financial support was provided by the Swiss National Science Foundation (200021-144320).

Acknowledgments

Jacques Roland Golay, Antoine Wiedmer, Pierre-Alain Hildenbrand, Htet Kyi Wynn and Julian Barry provided essential technical support for the execution of the experiment. We also appreciate the collaboration of the SAGRAVE company, Lausanne, Switzerland.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Banavar, J. R., Colaiori, F., Flammini, A., Maritan, A., and Rinaldo, A. (2001). Scaling, optimality, and landscape evolution. J. Stat. Phys. 104, 1–48. doi:10.1023/A:1010397325029