
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 26 May 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.860925
This article is part of the Research Topic Advances in the Application of Multi-Dimensional Geophysical Surveys in Earth and Environmental Sciences View all 8 articles
 Michael Commer1*
Michael Commer1* David L. Alumbaugh1
David L. Alumbaugh1 G. Michael Hoversten1
G. Michael Hoversten1 Evan S. Um1†
Evan S. Um1† Donald W. Vasco1†
Donald W. Vasco1† Michael Wilt1†
Michael Wilt1† Edward Nichols1†
Edward Nichols1† Pierpaolo Marchesini2†
Pierpaolo Marchesini2† Marie Macquet3†
Marie Macquet3†In geophysical inversions, lower and upper model parameter bounds are a means of solution stabilization. Further, constraints that intend to let only geologically plausible inverse solutions pass are amenable to lower and upper bounds. Reliable prior information is paramount to construct such bound constraints. It is common practice to narrow and widen bound intervals for regions of, respectively, more and less certain prior information. Contrary to this practice, we experiment with widened bound intervals in zones that are poorly resolved by a given survey configuration but where prior information would suggest structural anomalies of interest. The purpose of enlarged parameter bounds that correlate spatially with predefined targets is to let the inversion explore a larger solution space, thus increasing the potential to resolve otherwise hidden anomalies. Application of the method is based on a carbon-sequestration baseline (pre-injection) crosswell electromagnetic (EM) field survey at the Containment and Monitoring Institute Field Research Station (Alberta, Canada), where impeded measurements led to generally reduced sensitivities for the interwell region. Synthetic-data proofs of concept use augmented bounds designed to boost the resolution of artificial plume targets, indicating an enhanced illumination compared to constant bounds. Comparative field data inversions with spatially variable bounds constructed from prior resistivity and velocity information highlight non-horizontal baseline structures.
Geophysical inverse-modeling problems are usually hampered by data sparsity and data noise. At the same time, realistic earth models require a high degree of model discretization. The coincidence of these issues leads to a non-unique and thus ill-posed nature of solutions of pixel-based (many-parameter) inverse problems (e.g., Haber et al., 2010). A standard technique for addressing non-uniqueness is to regularize the solution-finding process through constraints that are imposed on the mathematical representation of the inverse solution (e.g., Jackson, 1979). The constrained inverse solution is commonly described as the minimization of a multi-component objective function, for example
consisting of a data component
In our experiments,
The literature on geophysical inversion usually motivates the introduction of constraints as a means to address non-uniqueness through allowing geological models that are perceived as plausible (Habashy and Abubakar, 2004; Abubakar et al., 2009; Sosa et al., 2013; Ogarko et al., 2021). Constraining the solution arising from the minimization of Eq. 1 is realized by the model-regularizing term
Minimizing the total error term
It has been argued that the inversion against a fixed reference model
The inversion experiments in this study pick up the concept of constraint balancing; however, we revert to the usage of bound constraints for their facilitation of prior-model fusion (Kim et al., 1999; Abubakar et al., 2008; Kim and Kim, 2011; Aghamiry et al., 2019; Ogarko et al., 2021). A priori knowledge with varying degrees of certainty lends itself to defining individual bounds a and b imposed on the model parameters
This contribution investigates a potential model resolution enhancement enabled through spatially variable bound constraints. Our approach is a simplification of the concepts by Yi et al. (2003) and Ogarko et al. (2021) because 1) we do not employ the parameter resolution matrix for bound construction, and 2) augmented bound intervals, that is, bounds that are enlarged with respect to a default, remain static throughout the inversion. The principal idea is to allow the inversion to venture out into an enlarged model space during all model-updating iterations. Regions of enlarged bounds reflect preconceived focus zones that are suggested by prior information. Hence, we also regard this method as a simple way of conveying prior model information about anomalous zones of interest to the inversion process. Synthetic and field data demonstrations are based on a crosswell EM baseline survey conducted within a geologic carbon sequestration (GCS) context.
The inverse-modeling studies of this work seek for a constrained solution using a non-linear conjugate-gradient (NLCG) scheme (e.g., Luenberger, 1984). Our NLCG implementation encompasses a three-dimensional (3D) finite-difference (FD) scheme for the forward modeling of CSEM data (Commer and Newman, 2008). The NLCG scheme minimizes an objective function of the form of Eq. 1 by performing a sequence of line-searches in model space, generating a sequence of model updates
Lower and upper parameter bounds
where x is the transformed parameter and n is a positive integer constant. Our studies employ a version realized by
Constant bounds may be most suitable for inversion applications where prior information is absent, that is, the bound interval
We do not employ a priori model information,
Our inversion operates on
Keep in mind that
For the case where the objective is to enhance the resolution in regions that exhibit resistive features in
where
For the following demonstrations, it is important to keep in mind that only the (resistive or conductive) nature of outstanding features in
The following section provides a synthetic-data and field-data proof-of-concept for the resolution-enhacing effect of spatially variable parameter bounds. The inverse modeling of crosswell EM data is based on surveys conducted at the Containment and Monitoring Institute Field Research Station (CaMI.FRS), located in Alberta, Canada. CaMI.FRS is a small-scale GCS test site for the investigation of monitoring techniques at shallow and intermediate injection depths (Um et al., 2020). An injector well and two observation wells are completed to a depth of 350 m (Figure 1A). Small volumes of CO2 will be injected into the basal Belly River Sandstone at depths up to 300 m. The basal Belly River sandstone ranges from 17 to 21 m thick and consists of fine- to medium-grained well to very-well sorted lithic arenite (sandstone with grain sizes 0.06–2 mm and over 50% rock fragments) (Iwuagwu and Lerbekmo, 1982).
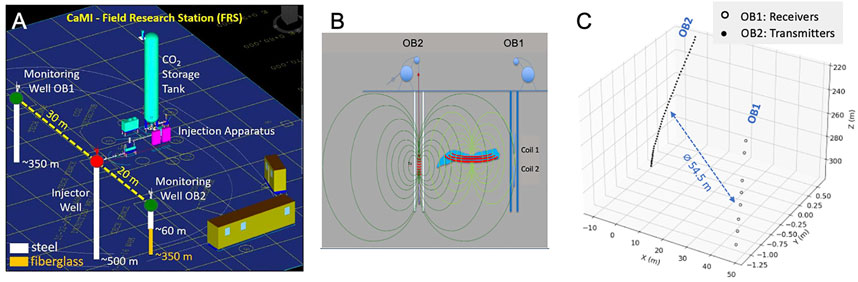
FIGURE 1. (A): Schematic view of CaMI.FRS site with injector and monitoring wells. (B): Schematic of a crosswell EM configuration. Primary EM fields are emitted in the transmitter well and recorded together with induced secondary vertical magnetic fields in an adjacent receiver well. Data processing steps separate the signals so that the rock electrical resistivity information is derived from the secondary fields. (C): Actual positions of the magnetic transmitter and receiver coils. The two wells OB1 and OB2 are deviated, with an average of 54.5 m separating the instrumented sections.
We first give a brief overview of the geophysical surveys conducted at CaMI.FRS. Both EM and seismic crosswell data were taken in order to characterize the pre-injection state. Our synthetic-data proof-of-concept replicates the EM survey geometry. The subsequent field-data proof-of-concept employs prior information in form of seismic images together with resistivity and velocity logs for the design of variable parameter bounds. Therefore, all prior information is introduced first.
Crosswell EM uses the principles of EM induction to interrogate the electrical resistivity between wells. As sketched in Figure 1B, a vertical magnetic dipole (VMD) induction coil placed in the transmitter well broadcasts sinusoidal EM signals into the formation. At the receiver well, the signals are detected, in our case via a double-coil receiver with two connected sensors separated by 5 m. Source and receiver usually traverse the wells with recordings triggered at regularly spaced intervals leading to a tomographic illumination of the interwell space.
Tomographic baseline crosswell EM data were collected over the depth section 200–320 m (Figure 1C) with a transmitter spacing of 2 m in observation borehole 2 (named OB2), thus leading to 59 source depth levels. The two-receiver string traversed 10 levels at intervals of 10 m in observation borehole 1 (OB1). Unfortunately, cross checks between signal amplitudes and receiver depth recordings revealed inconsistencies which rendered only 8 receiver sets per transmitter activation usable. While the cause remains unclear, we speculate that the bottom receiver of the double-sensor array might have buoyantly floated upwards, thus not keeping the constant reference separation (5 m) between the two sensors. Moreover, while the transmitter system operated at the two frequencies of 200 and 450 Hz, data noise turned out excessive at 450 Hz. Both issues reduced the usable data to a total of 454 complex magnetic-field data points which are the input to our field-data inversions presented below.
In addition to the data sparsity, another complication is caused by horizontal well deviations of the instrumented sections which max out at 7 m (OB2) and 0.5 m (OB1). Ensuing instrument rotations out of the horizontal plane are often neglected in academic crosswell EM studies. Given the dominating deviation of OB2, we incorporate source coil rotations in form of tilt and azimuth angles in the field-data inversions.
Croswell EM can be stymied by the signal-shielding nature of metal borehole casings, because large magnetic fields result from the transmitter coupling with hysteretic magnetic permeabilities of steel. If open holes (no casing present) cannot be realized, fiberglass casing avoids this coupling. At CaMI.FRS, the transmitter well (OB2) is steel-cased from the surface to 60 m and fiberglass-cased from 60 to 350 m, while OB1 is all steel-cased down to 350 m. The effects at frequencies below a few hundred Hz remain moderate for the received signals. Nevertheless, in the presence of weak geological effects on the data one wants to avoid any potentially overpowering casing effect. The casing effect at the receivers can be corrected for either in the course of data inversion, or it can be removed prior to the inversion process. Here we choose the latter in order to avoid the computationally demanding forward-modeling of casing effects during the inversion. The correction procedure essentially utilizes the fact that in the frequency domain one can approximate the casing effect by means of a source-signature correction with a complex factor (Wu and Habashy, 1994).
We outline the steps that correct for EM induction effects contained in receiver coils that are surrounded by steel casing. The main component is an appropriate reference model from which one can calculate non-casing reference data. The two resistivity logs in the two observation wells (Figure 2A) were employed to construct a 1D reference model. It involved fewer parameters than given by our 1D inversion presented below while being equivalent in terms of data fit. The predominantly horizontally layered geology at CaMI.FRS helps limit the error due to the approximate nature of the reference model.
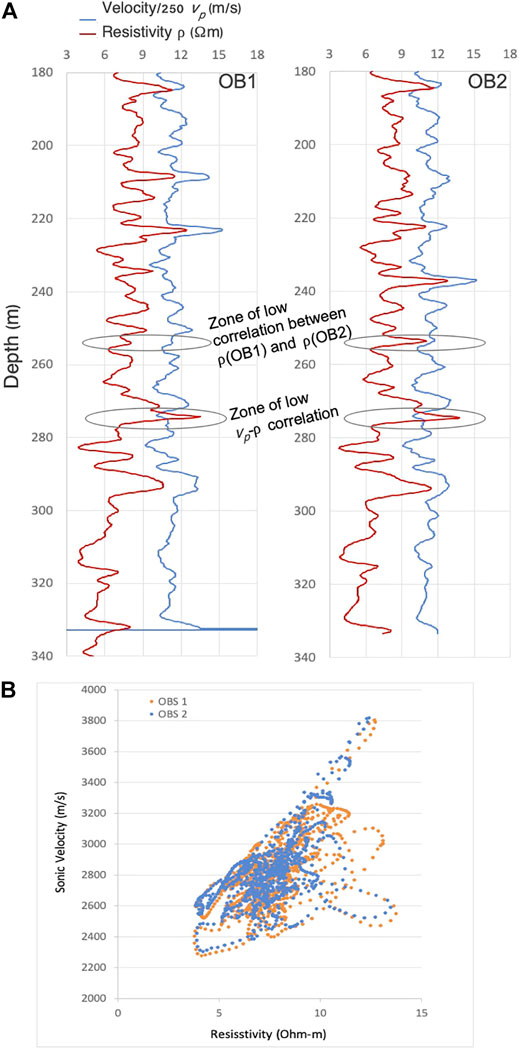
FIGURE 2. (A): Prior EM and seismic information at CaMI.FRS. Seismic-velocity (
For each common-receiver gather of the tomographic crosswell EM data, we extract the data pertaining to all transmitter depths that are in vertical proximity, here within 5 m of the depth of the receiver gather. These data are complex magnetic-field values containing the casing effect. Replicating their survey geometry with respect to the receiver depth, we calculate a corresponding non-casing data set through forward-modeling of the 1D reference model.
For each transmitter depth of a given receiver gather, we divide the non-casing reference data by its measured counterpart. This yields a set of estimated casing-correction factors which are also complex numbers. All correction factors of one receiver gather are averaged. The outcome is a best estimate for the magnetic-field attenuation and phase shift caused by the steel casing. The averaging is carried out for all individual receiver gathers, producing a set of location-dependent best-estimate correction factors. Making the correction depth-dependent intends to limit the impact on non-casing signal footprints one wants to retain as they contain for example effects due to local 3D structures.
The final step is the actual data correction. Each data point of a given receiver gather is multiplied by the gather’s correction factor, producing a common-receiver gather of corrected data. Applying the correction procedure to each receiver gather yields a tomographic data set of casing-corrected data that are also normalized for unit source moment. This set is the data input for the field-data inversions presented here. Image distortions due to this correction procedure are limited to the vicinity around the casing (Gao et al., 2008).
Compressional-wave velocity (
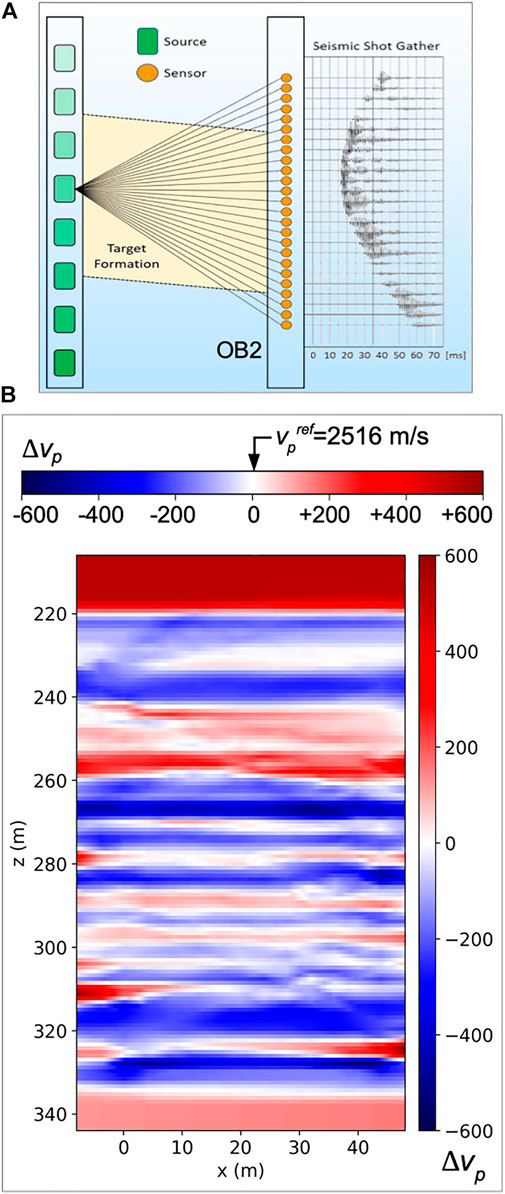
FIGURE 3. (A): Schematic view of crosswell seismic system. (B): 2D
Both the
The following inversion experiments demonstrate the benefits of spatially variable inversion constraints. Each case compares pairs of inversions, one using constant bounds, one using variable bounds. Synthetic EM data is generated using the field geometry of the CaMI.FRS baseline EM survey. A major focus of this survey involved the testing of new sensor hardware, which led to the issue that the employed operating frequency of f = 200 Hz is not optimal in terms of image resolution. The resolution can be estimated by the ratio between the transmitter-receiver separation,
The baseline survey’s configuration at CaMI.FRS involves an average transmitter-receiver separation of
Given these two survey impediments, resolution loss due to the low source frequency and the sparse receiver array, our synthetic-data inversions aim at investigating whether target-specific parameter-bound modifications can help alleviate the resulting low imaging capacity in order to produce satisfactory plume delineations. We assume the evolution of a CO2 plume due to an injection source near the center of the crosswell setup (Injector well in Figure 1A). Seismic imaging indicated a predominantly horizontally stratified background geology (Figure 3B). Therefore, underlying assumptions for the plume geometry involve an anisotropic hydraulic conductivity ratio that results in a greater horizontal flow and thus an ellipsoidal plume shape with the largest horizontal semiaxes along the x-axis (defining the well plane).
Our imaging studies are of a somewhat academic nature by assuming either purely electrically resistive or conductive CO2-induced anomalies. Laboratory studies indicate that much more differentiated electrical-conductivity alterations can occur due to potentially opposing effects due to ion content versus ion mobility that depend on pore water salinity, gas concentration, pressure, and temperature (Börner et al., 2015). Here, we restrict ourselves to two distinct cases: 1) a free CO2 phase acts as an electrical insulator and thus causes a resistive plume, and 2), at low pressures (shallow injection depths), a high ion content due to dissociation of carbonic acid results in a conductive plume.
Synthetic data generation follows the standard procedure of adding normally distributive random Gaussian noise to the real and imaginary components of the vertical magnetic fields (measured in A/m). Noise magnitudes are based upon 0.5% of the data amplitude and an additional noise floor of 10−11 A/m. For computational savings, we further exploit the reciprocity principle by swapping out transmitters and receivers so that the receiver well hosts 8 computational transmitters. While well deviations are accounted for, no sensor rotations are considered.
Our underlying premise is to employ bound constraints as a way of focusing the EM imaging by exploiting prior information. Our synthetic example simulates a case where prior information exists in form of a delineation of a focus zone, which could be the product of concurrent reservoir modeling. The bound constraints thus serve as a way of augmenting the geophysical model resolution in a zone that is of hydrogeological interest.
The zone of interest in our electrical-conductivity model will be a plume of ellipsoidal shape and with anomalous electrical conductivity relative to the background. We consider two cases, a resistive and a conductive plume. The ellipsoid’s semiaxes lengths (in meters) are (a, b, c) = (18.5, 10.5, 12.5) along the axes x, y, z, and it is centered at (x, y, z) = (22, 0, 257). White contour lines in Figure 4A outline the true target geometry. The colored ellipsoidal regions that occur incongruent to this actual geometry define the volume where lower and upper inversion parameter bounds are modified with respect to constant default bounds.
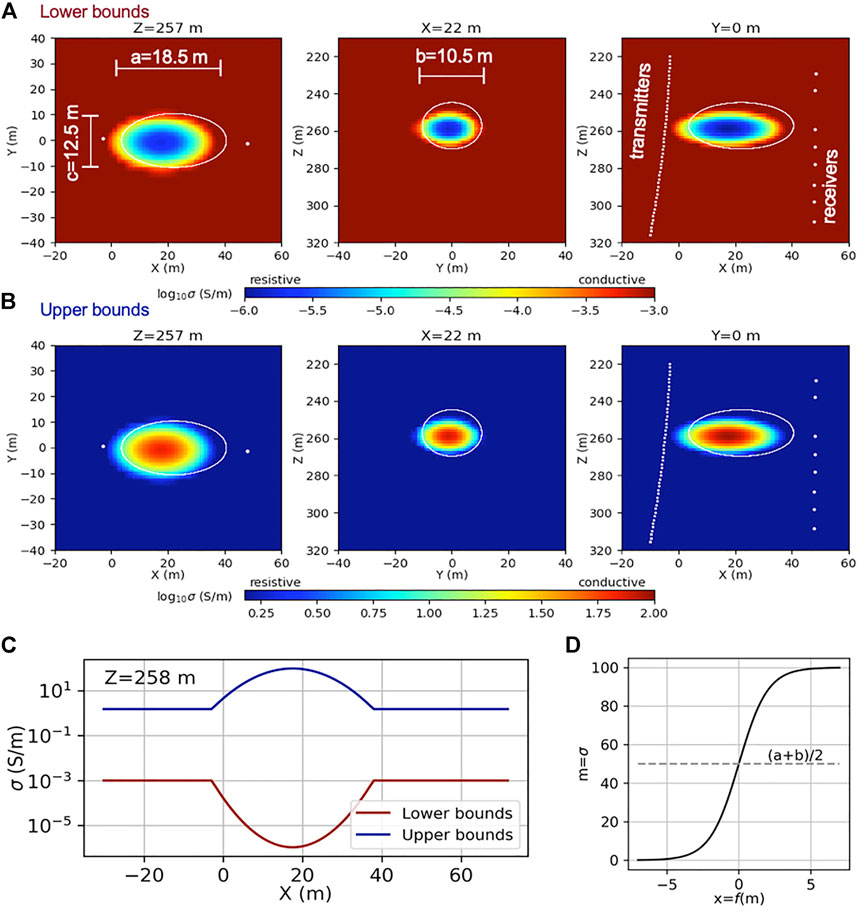
FIGURE 4. (A): Plume imaging for CaMI.FRS. Spatially variable lower and upper model parameter bounds constrain inversions for an ellipsoidal CO2 plume. Variable bounds occur over an ellipsoid that is different in shape and center coordinates to the true plume, the latter indicated by white contours and the semiaxes lengths (a,b,c). Crosswell instrument locations are projected. Lower parameter bounds span the electrical-conductivity range from 10−6 to 10−3 S/m. (B): Upper bounds range from 1.5 to 100 S/m. (C): Lower and upper bounds are paired such that constraints open up when traversing the ellipsoidal target region, here shown for the x-axis at (y,z) = (0, 258) m. (D): The logarithmic transformation function of Eq. 4 is exemplified for the bound interval
A prerequisite for designing modified bound constraints would be a reservoir flow model that approximates fluid saturations and thus plume evolution. While we do not carry out such flow-modeling, it is safe to assume that, at a minimum, a basic reservoir model will exist for the majority of GCS sites. However, depending on the degree of model refinement, there will always be some uncertainty associated with operational reservoir flow predictions. The incongruity between true and assumed plume boundaries is meant to simulate this uncertainty. To quantify the deviations, we assume that predictive flow modeling would deliver a plume estimate with the erroneous ellipsoid dimensions of (a, b, c) = (20.5, 12.5, 10.5). In addition, the center point is shifted to (x, y, z) = (18, 0, 260), which shall account for actual local preferential flow paths that would exceed the complexity of the available flow model.
Lower (Figure 4A) and upper (Figure 4B)
First, we assume the simplistic case where a free CO2 phase would act as an electrical insulator, thus causing a resistive plume. Figure 5A compares inversions using spatially constant bounds versus variable bounds. All inversions start with a homogeneous model of
with the constants

FIGURE 5. (A): Plume imaging for CaMI.FRS. Comparative inversions for an electrically resistive plume model. The upper, middle, and lower plot rows show, respectively, true model, inversion result using constant bounds, and inversion result using spatially variable bounds. (B): Comparative inversions for an electrically conductive plume model. The upper, middle, and lower plot rows show, respectively, true model, inversion result using constant bounds, and inversion result using spatially variable bounds. The corresponding variable lower and upper parameter bounds are shown by Figure 4. Elliptical contour lines in the images outline true (black) and assumed (green) plume boundaries. Assumed boundaries pertain to the ellipsoidal region defining the variable lower and upper parameter bounds. (C): Inversion of data set created from the background model using the variable bounds.
The 3D model outcome in Figure 5A (second plot row) results from constant parameter bounds
At low porewater salinities and injection levels that are shallow enough so that CO2 remains in the gaseous state, dissociation of carbonic acid causes higher ion contents. The resulting electrically conductive plume is simulated here at the injection depth of 257 m. The corresponding model in Figure 5B (true model in first plot row) uses the same background conductivity and plume geometry as the resistive plume. Now, the conductivity decreases from a maximum of 1.7 S/m at the ellipsoid center towards the background values at the borders.
Compared to a resistive anomaly, the sensitivity of VMD systems increases for a conductive anomaly. Similar to its resistive counterpart, the inversion with constant bounds produces a plume image that remains faint (Figure 5B, second row). However, the usage of the variable bounds achieves a clearer plume delineation (third row).
We emphasize that the variable-bounds concept has the mere goal of improving model resolution in terms of boosting the NLCG search process. It cannot alleviate a deficient data sensitivity. Insufficient sensitivity would cause solution instability. Preceding sensitivity studies therefore ensure that model parameters of target zones are well-resolved, regardless of any type of inversion constraints. A basic sensitivity check compares Hz-field responses calculated for the 59 receivers due to a selected source position located at z = 259 m (Figure 6). Amplitude (upper plot) and phase (lower plot) data are calculated for the background, where no ellipsoidal anomaly is present, and plotted together with the data containing the signal due to the resistive (blue lines) and conductive (red lines) plume. Percentage differences (dashed lines) between background and anomalous responses confirm that the sensitivity is higher for the conductive target (red dashed lines). While the degree of sensitivity is generally low, it is well above the assumed noise level (here 0.5%), thus validating that the sensitivity is sufficient for this kind of anomaly. Moreover, percentage differences (dashed lines) that are above noise level appear over a slightly larger depth section for phase than for amplitude. This sensitivity behavior made us set the data weights pertaining to the imaginary field component twice as high as for the real component. Since this is an arbitrary choice, it is likely that the plume imaging might be further optimized by means of additional trial inversions with proper differential data weighting.
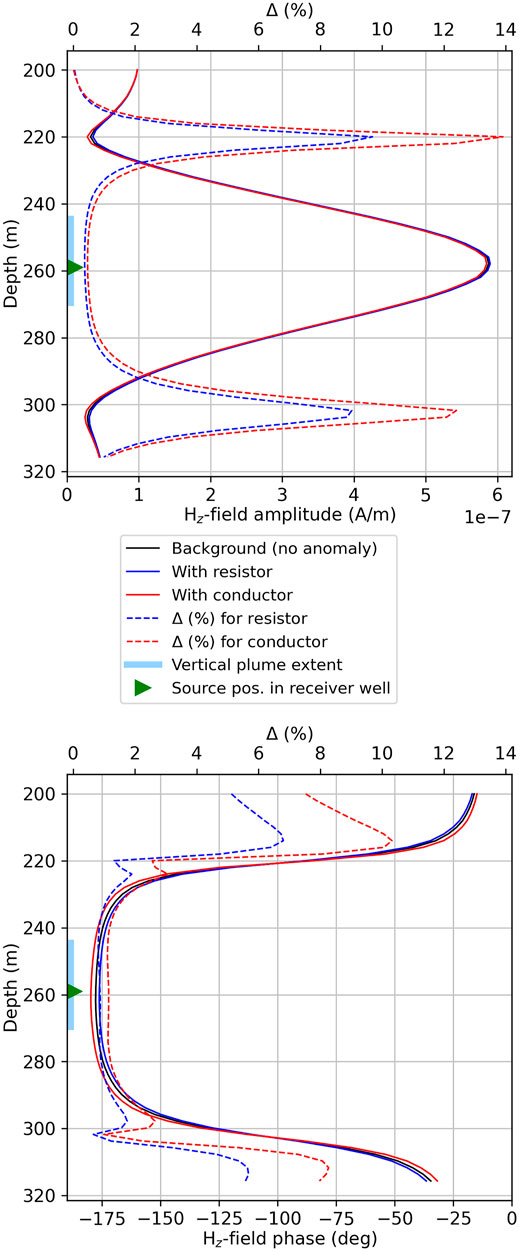
FIGURE 6. Sensitivity check in form of background-versus-anomaly forward modeling. The shown profile corresponds to one transmitter-receiver traverse. Hz-field amplitudes resulting from the background model (black lines) are compared against their counterparts calculated from the models with resistive (blue lines) and conductive (red lines) bodies. Dashed lines show percentage differences.
Figure 7A summarizes all four inversion instances (resistor and conductor, with constant and variable bounds) by showing the total RMS data fit against the model-updating iterations, the latter set to a maximum of 200. All inversions reach an RMS error below one. When facing generally low data sensitivities and such a similar general error convergence, the quality differences between different solutions are usually hardly discernible from individual data fits. Figure 7B exemplifies both initial and final fits produced by the variable-bound inversion for the conductive target. Here, maximal differences between the data fits at iterations 0 and 200 amount to 27% for amplitude and 31% for phase. Data fits for the corresponding constant-bound result (not shown here) are visually identical. These observations give rise to a verification of the solution consistency. Specifically, we want to ensure through two tests that 1) the anomalies are not an imaging artifact caused by the bound constraints, and 2) the solution is sufficiently independent of the starting model.
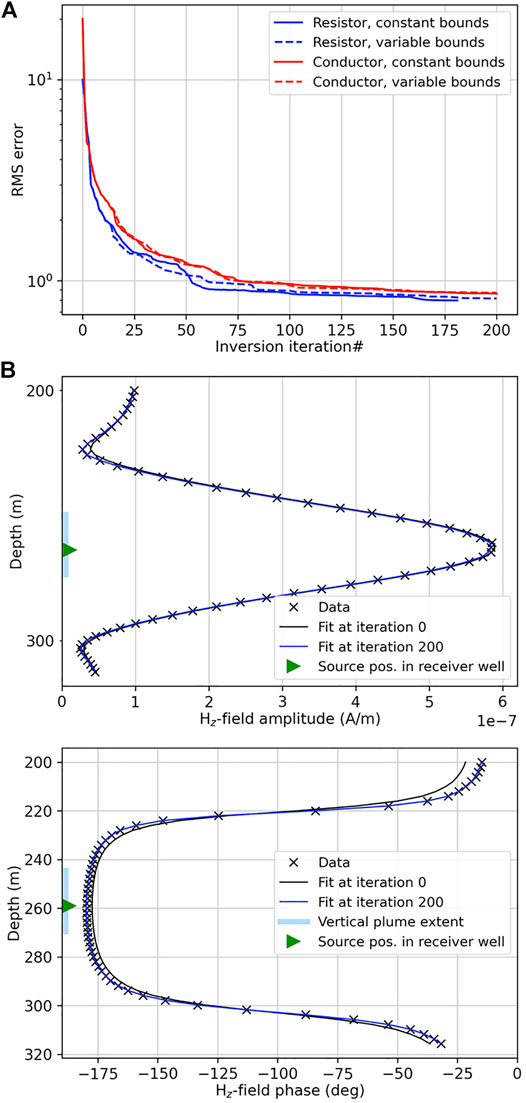
FIGURE 7. (A): Total RMS misfit for four synthetic-data inversions for a resistive and conductive plume, each comparing constant versus variable bounds. (B): Inverted data (symbols) and fits for the initial model guess (iteration 0) and the final model update (iteration 200) are shown as amplitudes and phases calculated from the vertical magnetic field. The shown profile corresponds to one transmitter-receiver traverse with its source located at z = 259 m. The vertical blue bar (left) indicates the vertical extent of the ellipsoidal plume.
The first test for solution consistency is in form of an inversion for the background model. For this check, the inverted data is calculated from the model without any anomalous ellipsoid present, that is, the data contains only the footprint of the background. At the same time, the inversion uses the variable bounds. Figure 5C shows the result of this test, where the x-y section exhibits a minor artifact reflecting the zone of the augmented bounds. However, generally, the final image indicates neither a resistive nor a conductive anomaly.
The second test verifies solution consistency over a range of starting model values. Figure 8A summarizes a sequence of 24 variable-bound inversion realizations for the conductive plume target. The starting
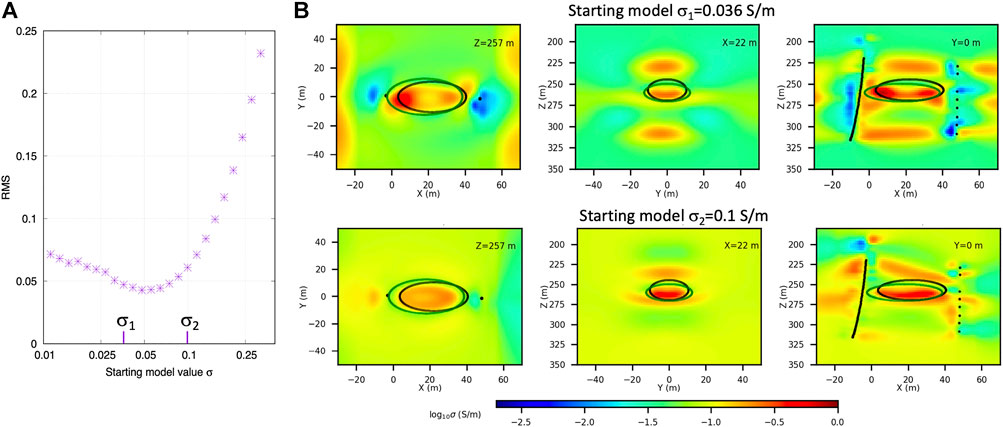
FIGURE 8. (A): Multiple inversion realizations for the conductive ellipsoidal anomaly (true model shown by Figure 5B, first row) using a range of homogeneous starting model values. The RMS error quantifies the difference between the true model and each inversion result. (B): Model reproductions exemplified for two starting-model values,
The following demonstration applies the concept of variable bounds to the 3D inversion of a baseline (pre-injection) field data set taken at CaMI.FRS. The well geometry is as shown by Figure 1. Here, we do not apply the reciprocity principle in order to honor the deviated transmitter well. The deviation causes transmitter coil rotations. Rotations are quantified by dip and azimuth angles, where maximum angles reach, respectively, 6.9° and 27.8°. Receiver rotations are negligible. The inverted data are vertical magnetic fields recorded at 8 receivers and sourced by 59 transmitters operating at 200 Hz.
No follow-up time-lapse data set is available at the time of writing. Since the measurements only contain the footprint of the background geology, we redefine the inversion objective. Instead of mapping fluid-induced anomalies, the design of bound constraints aims at identifying potential interwell zones of interest within the background geology. We first identify the nature of these anomalous zones through a 1D zonation. Using the optimization framework provided by the PEST protocol (Doherty, 2015), a sequence of 250 independent 1D inversion realizations with different starting models is carried out. No parameter smoothing constraints are imposed. Instead, each inversion is initiated with a different
Figure 9 compares the
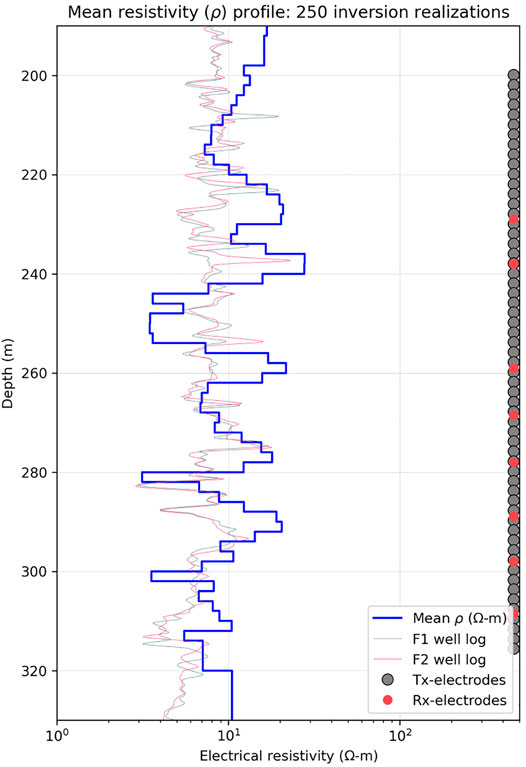
FIGURE 9. 1D resistivity well logs taken at CaMI.FRS. Also shown is the mean model calculated from 250 field-data inversion realizations. The final mean 1D model comprises parameters for 66 layers of fixed thickness. The vertical transmitter (grey) and receiver (red) electrode positions are projected onto the same line. Actual electrode distances are shown by Figure 1C.
Given that the VMD system exhibits better sensitivity towards conductive anomalies, we define the inversion objective to focus on possibly existing low-
We outline a four-step procedure for the design of target-adapted lower and upper parameter bounds for a constrained 3D inversion. The main principle is the widening of a given default bound interval
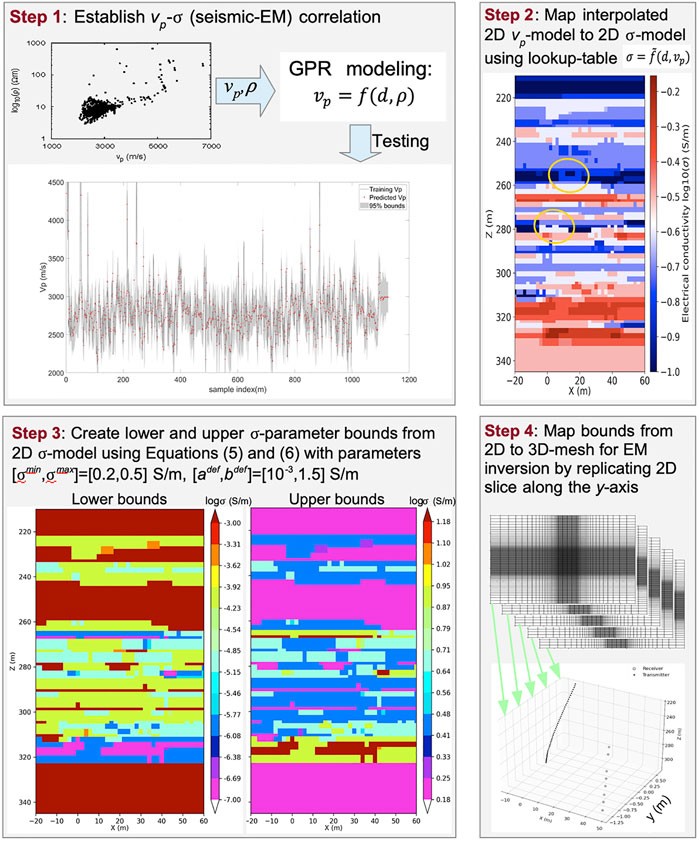
FIGURE 10. Workflow for creation of spatially variable 3D lower and upper conductivity parameter bounds for CaMI.FRS field data inversion. Lower bounds have a default (maximum) value of
Concurrent well logs of
Rearranging
The estimated 1D model of Figure 9 guides the definition of an approximate anomaly threshold. The estimated minimum layer resistivity amounts to
Note that augmented bounds cover the majority of the inversion domain, that is, in contrast to the central target given by the ellipsoid in Figure 4A, the bounds do not reflect a narrow focus zone. Also, we reiterate that while bound construction is based on prior assumptions about anomalously high
The bounds are discretized on the 2D x-z plane at y = 0. The 2D grid is replicated along all grid nodes of the y-axis in preparation for the subsequent 3D inversion. We choose 3D over 2D inversions based on earlier comparative studies on 2D versus 3D inversion of data containing actual 3D signatures. These studies have raised the concern that in the presence of actual 3D structures, the restriction to two model dimensions can lead to image artifacts (Papadopoulos et al., 2007; Nimmer et al., 2008; Hübert, 2012; Feng et al., 2014). To further limit potential artifacts, it is preferable to retain the actual 3D well deviations that are contained in the data.
Two comparative field data inversions employ the constant bounds
The initial model guess for both inversions is given by the final mean 1D model of Figure 9 (referred to as 1D model in the following). One could assume that the
The low final RMS misfit error of 1.78 achieved by the 1D model equals the starting RMS for the 3D inversions, confirming the dominating layered structure of the geology suggested by Um et al. (2020). Figure 11A summarizes the total error convergence. The variable-bound 3D inversion converges to a slightly lower final RMS and reaches the preset maximum iteration number (250), while the constant-bound inversion terminates after 173 iterations. However, final data fits are visually practically identical for both inversions, as evident in fits exemplified for one selected source depth (Figure 11B).
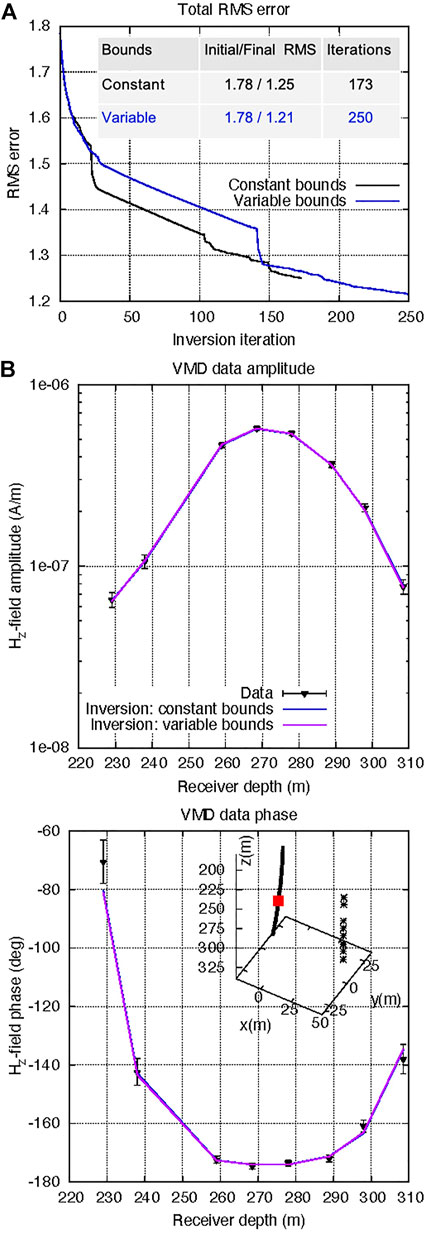
FIGURE 11. (A): Total RMS fitting error for CaMI.FRS field data inversion. (B): Data (symbols) and fits for inversions with constant bounds (blue lines) and variable bounds (purple lines). Real and imaginary vertical-magnetic fields are converted into amplitude and phase. The exemplified fits correspond to one transmitter-receiver traverse with the source located at z = 270 m (marked by red symbol).
It is now of interest to what degree variable bounds contribute to a better target inversion. While synthetic-data trials make an assessment straightforward, the absence of a ground truth in field-data inversions makes us revert to examining model differences. Figure 12 shows relative
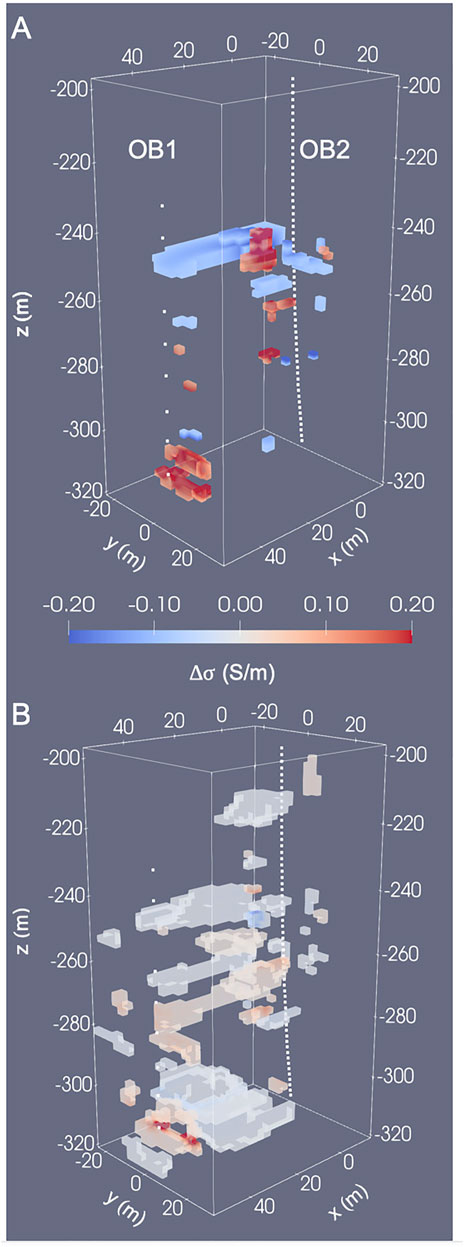
FIGURE 12. (A): Inversion of CaMI.FRS field data with variable parameter bounds. The inversion is initialized with the layered starting model (
Parameter constraints in form of spatially variable lower and upper bounds provide a straightforward way of incorporating spatial prior model information pointing to focus zones in an inversion workflow. Contrary to the common way of scaling the width of model parameter bounds with the uncertainty of prior information, we simply enlarge bounds in zones that host anticipated anomalies. The main purpose of prior information then reduces to the delineation of anomaly boundaries, without the need to quantify absolute properties exactly. While they cannot improve the lack of data sensitivity, widened bound intervals are a means of selectively increasing model fidelity in target zones. The approach essentially translates to scaling and steering the NLCG inversion’s search procedure in the model space so that local solution minima are more likely to be circumvented. It can accelerate solution convergence.
In time-lapse imaging related to GCS, reservoir flow modeling would provide the spatial a priori information for the design of location-dependent parameter bounds. Given that reservoir modeling of injection-induced hydrogeological state changes will likely accompany future GCS site management, it represents an inexpensive source of auxiliary information for constraining geophysical plume imaging. One may thus call the presented method a “poor people’s” alternative to a more sophisticated coupling by means of hydrogeophysical joint inversion; the latter would involve inverse modeling of a flow system interlinked with the EM data simulation (e.g., Commer et al., 2020).
In light of foreseeable economic limitations of long-term CCS monitoring, our synthetic-data study mimicked some inhibiting factors that actually occurred in the field. These are a suboptimal source frequency and resolution loss due to an incomplete data set. Despite these imposed shortcomings, fluid-induced conductivity alterations could still be mapped, suggesting that the variable-bounds concept can serve as a means to offset model resolution loss due to defective survey coverage to some degree.
Inversions with variable bounds applied to the CaMI.FRS baseline field data highlight that geophysical prior information, here seismic imaging and well logs, can be utilized for the design of target-specific parameter bounds. The presented inversions lend weight to indicators for correlated anomalies between
A final remark is that, as common in geophysical inversion problems of an underdetermined nature, multiple trial-and-error inversion realizations may be necessary to reduce the uncertainties of these results. Inversions might be further improved through optimized function parameters that control the spatial bound variation. In cases with a prohibitively large number of inversion realizations, Bayesian optimization with inequality constraints as presented by Gardner et al. (2014) might be a feasible alternative.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
MC: Writing, Editing, Conceptualization, Methodology. DA: Editing, Data acquisition, Supervision. GH: Methodology (GPR modeling). DV and PM: Methodology (seismic imaging). MW, EN, and EU: Data acquisition. MM: Project administration.
This research was supported by the U.S. Department of Energy, National Energy Technology Laboratory, CCSMR program, under the U.S. DOE Contract No. DE-AC02-05CH11231.
The author MM is employed by Carbon Management Canada. The author PM was employed by Silixa Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank Don Lawton, the CaMI Consortium, and all their partners for site access and the help received during field activities.
Abubakar, A., Habashy, T. M., Druskin, V. L., Knizhnerman, L., and Alumbaugh, D. (2008). 2.5D Forward and Inverse Modeling for Interpreting Low-Frequency Electromagnetic Measurements. Geophysics 73, F165–F177. doi:10.1190/1.2937466
Abubakar, A., Habashy, T. M., Li, M., and Liu, J. (2009). Inversion Algorithms for Large-Scale Geophysical Electromagnetic Measurements. Inverse Probl. 25, 123012. doi:10.1088/0266-5611/25/12/123012
Aghamiry, H. S., Gholami, A., and Operto, S. (2019). Implementing Bound Constraints and Total-Variation Regularization in Extended Full Waveform Inversion with the Alternating Direction Method of Multiplier: Application to Large Contrast Media. Geophys. J. Int. 218, 855–872. doi:10.1093/gji/ggz189
Alumbaugh, D. L., and Morrison, H. F. (1995). Monitoring Subsurface Changes over Time with Cross-Well Electromagnetic Tomographyt1. Geophys Prospect 43, 873–902. doi:10.1111/j.1365-2478.1995.tb00286.x
Börner, J. H., Herdegen, V., Repke, J.-U., and Spitzer, K. (2015). The Electrical Conductivity of CO2-bearing Pore Waters at Elevated Pressure and Temperature: a Laboratory Study and its Implications in CO2storage Monitoring and Leakage Detection. Geophys. J. Int. 203, 1072–1084. doi:10.1093/gji/ggv331
Commer, M., and Newman, G. A. (2008). New Advances in Three-Dimensional Controlled-Source Electromagnetic Inversion. Geophys. J. Int. 172, 513–535. doi:10.1111/j.1365-246X.2009.04216.x10.1111/j.1365-246x.2007.03663.x
Commer, M., Pride, S. R., Vasco, D. W., Finsterle, S., and Kowalsky, M. B. (2020). Imaging of a Fluid Injection Process Using Geophysical Data - a Didactic Example. Geophysics 85, W1–W16. doi:10.1190/geo2018-0787.1
de Groot‐Hedlin, C., and Constable, S. (2004). Inversion of Magnetotelluric Data for 2D Structure with Sharp Resistivity Contrasts. Geophysics 69, 78–86. doi:10.1190/1.1649377
Doherty, J. (2015). Calibration and Uncertainty Analysis for Complex Environmental Models. Brisbane, Australia: Watermark Numerical Computing.
Farquharson, C. G., Ash, M. R., and Miller, H. G. (2008). Geologically Constrained Gravity Inversion for the Voisey's Bay Ovoid Deposit. Lead. Edge 27, 64–69. doi:10.1190/1.2831681
Feng, D.-s., Dai, Q.-w., and Xiao, B. (2014). Contrast between 2D Inversion and 3D Inversion Based on 2D High-Density Resistivity Data. Trans. Nonferrous Metals Soc. China 24, 224–232. doi:10.1016/s1003-6326(14)63051-x
Gao, G., Alumbaugh, D., Zhang, P., Zhang, H., Levesque, C., Rosthal, R., et al. (2008). “Practical Implications of Nonlinear Inversion for Cross-Well Electromagnetic Data Collected in Cased-Wells,” in Paper Presented at the 78th SEG Annual Meeting, Las Vegas, NV, November 9-14.
Gardner, J. R., Kusner, M. J., Zhixiang, X., Weinberger, K. Q., and Cunningham, J. P. (2014). “Bayesian Optimization with Inequality Constraints,” in Proc. of the 31st Int. Conf. Machine Learning, Beijing, 937–945.32
Grayver, A. V., Streich, R., and Ritter, O. (2014). 3D Inversion and Resolution Analysis of Land-Based CSEM Data from the Ketzin CO2 Storage Formation. Geophysics 79, E101–E114. doi:10.1190/geo2013-0184.1
Habashy, T. M., and Abubakar, A. (2004). A General Framework for Constraint Minimization for the Inversion of Electromagnetic Measurements. Pier 46, 265–312. doi:10.2528/PIER03100702
Haber, E., Horesh, L., and Tenorio, L. (2010). Numerical Methods for the Design of Large-Scale Nonlinear Discrete Ill-Posed Inverse Problems. Inverse Probl. 26, 025002. doi:10.1088/0266-5611/26/2/025002
Hübert, J. (2012). From 2D to 3D Models of Electrical Conductivity Based upon Magnetotelluric Data, Experiences from Two Case Studies (Sweden: Uppsala University). Ph.D. Thesis.
Iwuagwu, C. J., and Lerbekmo, J. F. (1982). The Petrology of the Basal Belly River Sandstone Reservoir, Pembina Field, Alberta. Bull. Can. Petroleum Geol. 30, 187–207. doi:10.35767/gscpgbull.30.3.187
Jackson, D. D. (1979). The Use of A Priori Data to Resolve Non-uniqueness in Linear Inversion. Geophys. J. Int. 57, 137–157. doi:10.1111/J.1365-246X.1979.TB03777.X
Kim, H. J., and Kim, Y. (2011). A Unified Transformation Function for Lower and Upper Bounding Constraints on Model Parameters in Electrical and Electromagnetic Inversion. J. Geophys. Eng. 8, 21–26. doi:10.1088/1742-2132/8/1/004
Kim, H. J., Song, Y., and Lee, K. H. (1999). Inequality Constraint in Least-Squares Inversion of Geophysical Data. Earth Planet Sp. 51, 255–259. doi:10.1186/BF03352229
Luenberger, D. (1984). Linear and Nonlinear Programming. 2nd edition. Boston, Massachusetts, United States: Addison-Wesley.
Mackie, R. L., and Madden, T. R. (1993). Three-dimensional Magnetotelluric Inversion Using Conjugate Gradients. Geophys. J. Int. 115, 215–229. doi:10.1111/j.1365-246X.1993.tb05600.x
Medeiros, W. E., and Silva, J. B. C. (1996). Geophysical Inversion Using Approximate Equality Constraints. Geophysics 61, 1678–1688. doi:10.1190/1.1444086
Meju, M. A., Gallardo, L. A., and Mohamed, A. K. (2003). Evidence for Correlation of Electrical Resistivity and Seismic Velocity in Heterogeneous Near-Surface Materials. Geophys. Res. Lett. 30, 1373. doi:10.1029/2002GL016048
Newman, G. A., and Alumbaugh, D. L. (2000). Three-dimensional Magnetotelluric Inversion Using Non-linear Conjugate Gradients. Geophys. J. Int. 140, 410–424. doi:10.1046/j.1365-246x.2000.00007.x
Nimmer, R. E., Osiensky, J. L., Binley, A. M., and Williams, B. C. (2008). Three-dimensional Effects Causing Artifacts in Two-Dimensional, Cross-Borehole, Electrical Imaging. J. Hydrology 359, 59–70. doi:10.1016/j.jhydrol.2008.06.022
Ogarko, V., Giraud, J., Martin, R., and Jessell, M. (2021). Disjoint Interval Bound Constraints Using the Alternating Direction Method of Multipliers for Geologically Constrained Inversion: Application to Gravity Data. Geophysics 86, G1–G11. doi:10.1190/GEO2019-0633.1
Papadopoulos, N. G., Tsourlos, P., Tsokas, G. N., and Sarris, A. (2007). Efficient ERT Measuring and Inversion Strategies for 3D Imaging of Buried Antiquities. Near Surf. Geophys. 5, 349–361. doi:10.3997/1873-0604.2007017
Rasmussen, C. E., and Williams, C. K. I. (2006). Gaussian Processes for Machine Learning. Boston, MA: The MIT Press.
Sosa, A., Velasco, A. A., Velazquez, L., Argaez, M., and Romero, R. (2013). Constrained Optimization Framework for Joint Inversion of Geophysical Data Sets. Geophys. J. Int. 195, 1745–1762. doi:10.1093/gji/ggt326
Um, E. S., Marchesini, P., Wilt, M., Nichols, E., Alumbaugh, D. L., Vasco, D., et al. (2020). “Joint Use of Crosswell EM and Seismic for Monitoring CO2 Storage at the Containment and Monitoring Institute Field Site (CaMI): Baseline Surveys and Preliminary Results,” in Paper Presented at the 90th SEG Annual Meeting, Houston, TX, October 11-14.
Vasco, D. W., and Nihei, K. (2019). Broad Band Trajectory Mechanics. Geophys. J. Int. 216, 745–759. doi:10.1093/gji/ggy435
Wu, X., and Habashy, T. M. (1994). Influence of Steel Casings on Electromagnetic Signals. Geophysics 59, 378–390. doi:10.1190/1.1443600
Keywords: 3-D electrical resistivity imaging, crosswell EM, inversion constraints, lower and upper parameter bounds, CO2 sequestration monitoring
Citation: Commer M, Alumbaugh DL, Hoversten GM, Um ES, Vasco DW, Wilt M, Nichols E, Marchesini P and Macquet M (2022) Enhanced Multi-Dimensional Inversion Through Target-Specific Inversion Parameter Bounds With an Application to Crosswell Electromagnetic for Sequestration Monitoring. Front. Earth Sci. 10:860925. doi: 10.3389/feart.2022.860925
Received: 24 January 2022; Accepted: 02 May 2022;
Published: 26 May 2022.
Edited by:
Christof Kneisel, University of Wuerzburg, GermanyReviewed by:
Maysam Abedi, University of Tehran, IranCopyright © 2022 Commer, Alumbaugh, Hoversten, Um, Vasco, Wilt, Nichols, Marchesini and Macquet. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael Commer, bWNvbW1lckBsYmwuZ292
†These authors have contributed equally to this work and share last authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.