- 1College of Civil Engineering and Architecture, Guangxi University, Nanning, China
- 2Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning, China
- 3School of Civil and Architectural Engineering, East China University of Technology, Nanchang, China
- 4School of Architectural Engineering, Guangzhou City Construction College, Guangzhou, China
Collapse is one of the main dangers of tunnel construction using the drill-blast method. To assess the risk of collapse and provide a basis for risk control, a failure probability evaluation method for tunnel collapse based on a Bayesian network (BN) and normal cloud theory is proposed in this paper. First, typical tunnel collapse cases are analysed statistically based on the risk breakdown structure method, a Bayesian network model is built for drill-blast tunnel collapse and the causal relationships between the tunnel collapse and influential factors, such as geological factors and construction management factors, are revealed. Second, the multiple fault states of the risk factors are described using fuzzy numbers. A multi-state fuzzy conditional probability table of uncertain logical relationships between nodes is established using normal cloud theory to describe node failure probabilities. Finally, this paper will consider the entire life cycle of risk-prone events, including pre-incident, dynamic evaluation of the construction process and post-incident control. A typical tunnel collapse incident encountered during the construction of the Jinzuba Tunnel in Fujian was used as an example to verify the applicability of the method.
Introduction
With the vigorous development of highway and railway construction, road traffic has extended into mountainous areas, making tunnel construction larger-scale and more complex, especially in developing countries, such as China. Highway tunnel construction frequently has safety violations due to the various risk factors of the complex project environment. Collapse is one of the most frequent and harmful geological hazards during the construction of a tunnel. Because it is difficult to predict collapse, which is sudden and instantaneous, the constructors do not have enough time to escape. When a tunnel collapses, it can result in significant construction delays, economic loss, and even human casualties. As a result, it is necessary to investigate the risk mechanism of tunnel collapse by real-time safety analysis and considering accident scenarios, with the goal of providing decision support for ensuring the safety of tunnel construction.
To avoid major casualties and property loss due to violations of safety regulations, numerous researches have proposed risk-based analysis methods into safety management practices. There are two types of risk analysis: qualitative risk analysis and quantitative risk analysis (Khakzad et al., 2014). Qualitative methods include fault tree analysis (FTA) (Hyun et al., 2015), comprehensive evaluation methods (Zhang G.-H. et al., 2016), and others, which are simple and easy to use but do not provide consistent results (Chen et al., 2020). Quantitative methods include the analytic hierarchy process (AHP) (Hyun et al., 2015; Nezarat et al., 2015), support vector machines, decision trees, and others. Those methods can get a more accurate value of risks, but they can’t work unless detailed data is available (Chen et al., 2020). Hybrid methods, which combine qualitative and quantitative methods, have emerged as comprehensive and effective procedures for dealing with complex environments, using both qualitative and quantitative methods (D’Angelo et al., 2014; Golabchi et al., 2016).
A Bayesian network (BN) is a hybrid method for risk analysis that is, being increasingly applied (D’Angelo et al., 2014; Zhang et al., 2014). A BN model can be thought of as a data structure made up of nodes and edges. Nodes denote random variables and edges denote correlations (Chen et al., 2020). Compared to an AHP, a BN method is better at expressing the degree of influence of risk factors. A BN can qualitatively and quantitatively describe the dependence between variables and is suitable for knowledge representation and reasoning (Holický et al., 2013). In conventional BN analysis, the probability of occurrence of the root node is always regarded as a crisp value (Khakzad, 2013). Nevertheless, data in the construction engineering field are frequently subject to a variety of uncertainties, including incompleteness, randomness, inconsistency, fuzziness, and imprecision (Zhang et al., 2017). Therefore, group decision-making techniques are usually used to evaluate the occurrence probability of the root node. At present, fuzzy sets theory (Zadeh, 1965) is the most commonly used mathematical tool to address uncertainty, so fuzzy set theory is usually combined with a BN to improve its performance. In order to create a fuzzy BN, fuzzy set theory can be used to perform inference and belief propagation in a hybrid BN (Chen et al., 2020). A fuzzy BN is considered a very suitable tool in a probabilistic risk analysis domain (Zhang et al., 2014; Zhang L. et al., 2016).
However, once the membership function is specified in classical fuzzy set theory, one and only one accurate membership may be calculated for any given element in the universe to assess the uncertainty that the element belongs to the associated notion (Li et al., 2009). This goes against the spirit of a fuzzy set. Thus, Professor (Li et al., 2009) proposed a normal cloud model, which allows a stochastic disturbance of the membership degree encircling a determined central value. In contrast to fuzzy set theory, the elements of a qualitative concept are uncertain in a normal cloud model.
Combining a traditional cloud model with a BN has become increasingly popular in recent years (Chen et al., 2017; Wang et al., 2019). Chen et al. (2020) used a normal cloud model to discretize continuous monitoring and measurement data suitable for learning BNs. In the construction of mining tunnels, monitoring and measurement data include vault displacement, ground settlement, and horizontal convergence displacement. However, these data do not accurately reflect the actual construction situation and can only become one of the risk factors in the collapse risk assessment. Therefore, this paper innovatively applies a normal cloud model to convert the weight of each risk factor into a multistate conditional probability table to consider the impact of multiple factors on tunnel construction collapse. Compared with traditional dual-state risk factors, multistate risk factors can better reflect the actual situation of a construction site. However, as the status of risk factors increases, the establishment of a multistate conditional probability table becomes more complicated. For example, assuming each node has 4 states, the conditional probability table of child nodes with 4 parent nodes contains 256 combinations. Therefore, generating a multistate conditional probability table through a cloud model will greatly reduce the workload.
At present, the risk assessment method for highway tunnel construction in the China code is still relatively simple and cannot meet the needs of projects. It is necessary to develop a system decision-making method based on a multistate cloud Bayesian network (MCBN), aiming to guide the safety management of the entire life cycle of tunnel construction, including pre-accident, during-construction dynamic evaluation, and post-accident control. As a case study, a typical tunnel collapse hazard occurred during the construction of the Fujian Jinzhupa Tunnel in China. The results show that the proposed MCBN approach is feasible and has application potential.
Methodology
Bayesian Network
Since there are many introductions to the theory of Bayesian network (BN) (Li et al., 2017; Wu et al., 2022a), this article ignores such discussions. Assuming
Normal Cloud Model
A normal cloud model is a new cognition model of uncertainty proposed by Li et al. (2009). A normal cloud is an important cloud model based on the Gauss membership function. In practice, a normal distribution with relaxed conditions is coincident with the object world. Currently, it has been widely used in construction areas, such as tunnel excavation (Chen et al., 2020) and water inrush (Wang et al., 2019).
Cloud and Cloud Droplets
Given a qualitative concept B defined over a universe of discourse
In the formula, the distribution of x in U is called a cloud, and x is a cloud droplet.
A cloud can transform a qualitative concept to its quantitative value, which is composed of many cloud droplets. The droplets are in disorder, but when there are enough clouds, the overall characteristics of the qualitative concept are clearer (Wang, 2014). The grade of a certain degree of a cloud droplet reflects the fuzziness and randomness of a concept (Wang et al., 2019).
A Normal Cloud Model
A normal cloud model can be determined using numerical characteristics
Let X be the universe of discourse and B be a qualitative concept connected with X. If there is a number x, 1)
In the formula, the distribution of x in the universe X is called a normal cloud.
The Normal Cloud Generator
Typically, forward and backward transformations are used in the implementation of a standard cloud model. The goal of forwards normal cloud transformation (FNCT) is to generate a large number of cloud droplets. FNCT can generate the required cloud droplets. The normal cloud generator can be expressed as an algorithm given its numerical properties, as shown in Table 1.
Failure Probability Evaluation Method
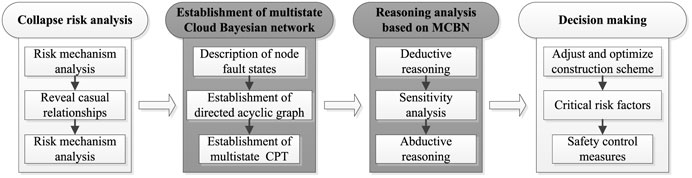
Using the powerful reasoning function in a multistate cloud Bayesian network (MCBN), deductive reasoning, abductive reasoning, and sensitivity analysis techniques can be used for safety analysis and management in the above three stages. This provides real-time and effective support to decision makers throughout the tunnel construction management process. The proposed approach includes the following four steps, as shown in Figure 1.
Collapse Risk Analysis
According to the collecting tunnel collapse cases and related researches (Zhou, 2008; Li, 2011; Chen et al., 2019; Wang et al., 2020; Zhang et al., 2020), and consulting experts in the field of tunnel engineering, the mechanisms of tunnel collapse are analysed.
Establishment of a Multistate Bayesian Network
Establishment of the DAG
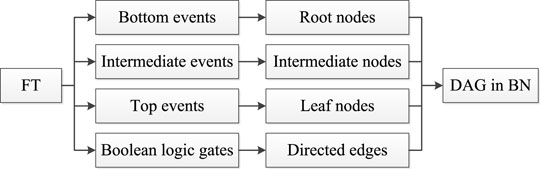
According to the research (Zhang L. et al., 2016), a qualified fault tree (FT) regarding tunnel construction safety can be used to provide effective prior knowledge for the establishment of the BN model’s DAG. Because the DAG structure in the MCBN is identical to that in a conventional BN, the DAG in the proposed MCBN is built by transforming the FT into the BN, as shown in Figure 2 (Khakzad et al., 2011).
Multistate Conditional Probability Table Construction
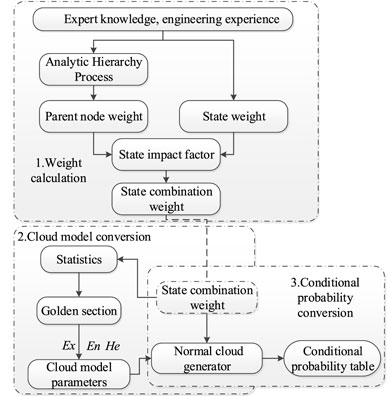
Because cloud theory is better than a Bayesian network in cognitive ability but worse in cognitive capability, this method combines the reasoning ability of a BN with the cognitive ability of a normal cloud model. The normal cloud generator is used to generate the MCPT using expert investigation. Since there are many introductions to the theory of MCPT (Wu et al., 2022a; Wu et al., 2022b), this article ignores such discussions. Figure 3 depicts an overview of the MCPT construction flowchart, which is divided into three sections: 1) weight calculation; 2) cloud model conversion; and 3) conditional probability conversion.
Reasoning Analysis Based on a Bayesian Network
Deductive Reasoning
The goal of deductive reasoning is to predict the probability distribution of risk events (leaf nodes) T given a set of risk factors (root nodes). Each risk factor’s current state is treated as evidence in an MCBN model. The probability distribution of tunnel collapse (T), represented by P (T = Ⅳ), is calculated using Eq. 4. P (T = Ⅳ) represents the highest risk probability.
where n is the number of the root nodes. Each root node Xi has four different states, denoted by “Ⅰ/Ⅱ/Ⅲ/Ⅳ.” Therefore, n root nodes have 4n combinations.
Sensitivity Analysis
Sensitivity analysis is a powerful method for detecting changes in the probability distribution of top events by varying the probability distribution of risk factors to measure the influence of each risk factor on tunnel collapse. In this research, the sensitivity performance measure (SPM) proposed by Zhang G.-H. et al. (2016) and shown in Eq. 5 is employed for sensitivity analysis.
Abductive Reasoning
In comparison to traditional risk-based methods such as AHP and FTA, the capabilities of abductive reasoning techniques for MCBN inference are unique and unrivaled. When an accident or failure occurs, abductive reasoning attempts to determine the posterior probability distribution of each risk factor. For fault diagnosis, the posterior probability distribution can be a reliable reference. The posterior probability distribution of risk factor Xi, represented by P (Xi = xi|T = Ⅳ), can be calculated using Eq. 6.
Case Study
To test the validity and applicability of the MCBN approach, this study examines the risk of tunnel collapse in a tunnel construction project.
Case Background
The Jinzhupa tunnel is a double-tube highway tunnel through the mountains connecting the Youxi and Jianning areas of Sanming City, China. The left and right tunnels are 771 and 782 m long, respectively. The entrance section of the tunnel is mainly composed of residual silty clay, a granite fully weathered layer, and a broken strong weathered layer. The main body of the cave is moderately weathered granite, which is affected by granite penetration. Affected by this, the rock mass is relatively broken, showing a very large or broken mosaic structure. The rock mass is broken and has varying degrees of weathering. During the construction process, tunnel collapse and water bursts easily occur.
Step 1: Risk/Hazard Identification of Tunnel Leakage and the DAG
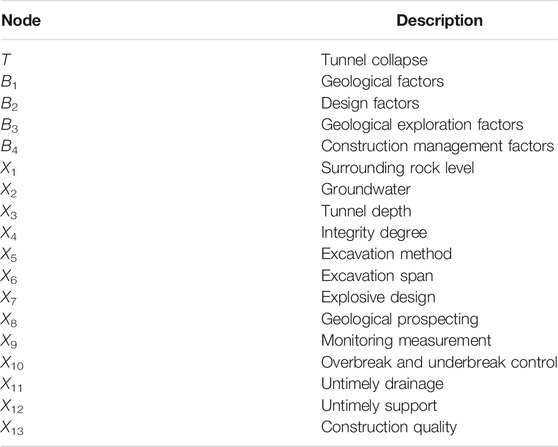
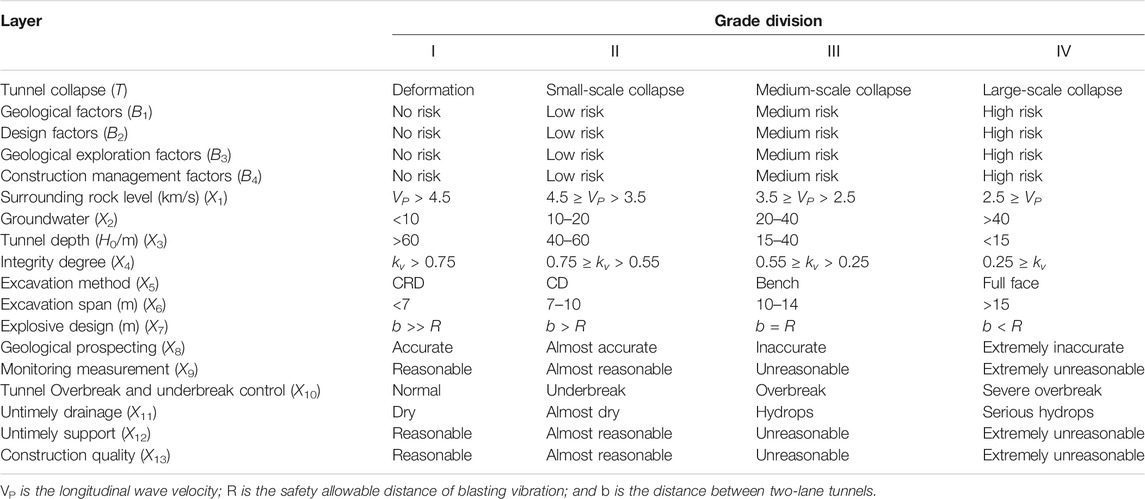
Tunnel collapse is considered a large potential geological hazard to the quality of tunnel construction. When a tunnel collapses, it can result in significant construction schedule delays, economic loss, and even human casualties. To precisely identify these influential factors, data from 120 tunnel collapse cases were collected and analyzed in accordance with the collapse risk analysis principles outlined in Collapse Risk Analysis. Concerning existing research results (Zhou, 2008; Li, 2011; Wang et al., 2020; Zhang et al., 2020), there are four main factors influencing tunnel collapse including: geological factors, design factors, geological exploration factors, and construction management factors. The DAG of the MCBN shown in Figure 4 is constructed by transforming the FT into a BN, as shown in Figure 2. The descriptions of all nodes are illustrated in Table 2. Meanwhile, the security status of each node is divided into 4 levels, denoted by I-IV, corresponding to fuzzy numbers 1–4 respectively, as shown in Table 3. These studies (Zhang et al., 2020; Wu et al., 2022a; Wu et al., 2022b) provide a detailed analysis of the risk factors.
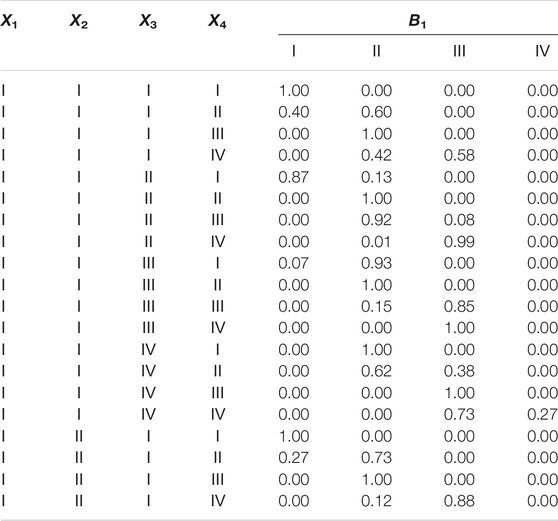
Step 2: Establish Multistate Conditional Probability Tables
As described in Section 3.2.3, the weight of each parent node is converted to a multistate conditional probability table (MCPT), as shown in Table 4 (due to the large number, only a portion is listed).
Step 3: Result Analysis
The created MCBN model can be updated with the root node state by actual conditions. This provides decision makers with effective support in real time for the whole process of safety and security before, including pre-accident, during-construction, and post-accident control.
Pre-Accident Control
Pre-accident control aims to optimize the tunnel construction plan and minimize the risk of tunnel collapse when economic conditions permit. During the proposal stage, the decision-maker lacks a thorough understanding of the actual situation regarding project risks. Despite being warned that there is a serious risk of tunnel collapse, they have no way of knowing the actual situation, let alone safety.
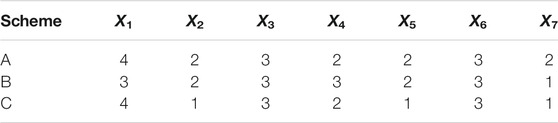
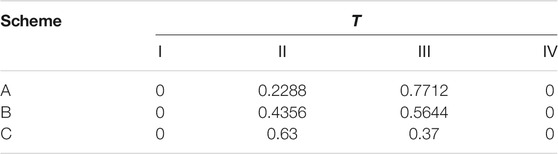
In the programme selection stage, decision-makers may face a choice of excavation method and tunnel location. Now, we have three schemes labeled as A, B, and C, as shown in Table 5. The current state of the parameters (Ⅰ, Ⅱ, Ⅲ, or Ⅳ) are entered into the MCBN as evidence, and then the outputs of the models are compared. From the perspective of safety and security, a scheme with a lower probability of tunnel collapse will make decision-makers more interested. The results shown in Table 6 demonstrate that Scheme C is the most competitive scheme since the predicted occurrence probability of tunnel collapse in Scheme C is lower than that in the other two schemes.
During-Construction Dynamic Evaluation
The goal of dynamic evaluation during construction is always to control the risk of collapse in order to ensure the safety of the construction. During the construction phase, decision-makers evaluate 13 factors (X1-X13) based on the actual on-site situation. Then the current states (Ⅰ, Ⅱ, Ⅲ, or Ⅳ) are entered into the MCBN model as given evidence. When the collapse risk value exceeds level III, building should be promptly halted for repair. Following the correction, an evaluation should be performed once again. Decision-makers can make corrections based on the results of sensitivity analysis. Construction will not begin until the danger level falls below level II. As a result, the construction may be constantly refined until the high potential safety concerns are managed. Furthermore, decision-makers must identify the important risk variables that have a stronger influence on the occurrence of construction failure, and those checkpoints should be prioritized during the construction phase. The MCBN can find essential construction parameters by using the sensitivity analysis approach in Bayesian inference.
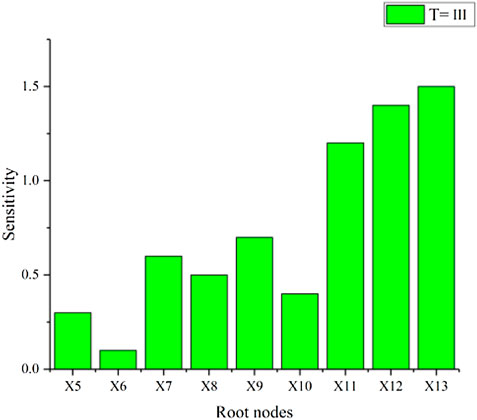
For example, in excavation section ZK242-695∼ZK242-705 of the Jinzhupa Tunnel, the values associated with the geological parameters are defined and then entered into MCBN as evidence for the given. The probability of collapse is shown in Table 7. The results indicate that the probable risk level for tunnel collapse is Class III, indicating that the tunnel construction should be corrected. Using Eq. 5, a sensitivity performance measure (SPM) of risk factors (X5–X13) is calculated. The findings demonstrate that X11 (Untimely drainage), X12 (Untimely support), and X13 (construction quality) are at the peak of the ranking for each indication, as shown in Figure 5. The occurrence of tunnel collapse is very sensitive to these three risk factors. Therefore, more focus must be placed on assuring the reasonable state of these building characteristics.
Post-Accident Control
After an accident or failure happens, the goal of post-accident control is to determine the most likely direct cause and then carry out real-time diagnostic and appropriate remedies. Under the current circumstances, policymakers consider it best practice to invite experts from the field to participate in expert group meetings. The field specialists then discuss the reasons of the accident and recommend immediate control measures. This will most likely miss the essential window for dealing with the situation, resulting in significant losses. We can mimic the evolution route of an accident in real time using the background reasoning approach in Bayesian inference (Zhang et al., 2014).
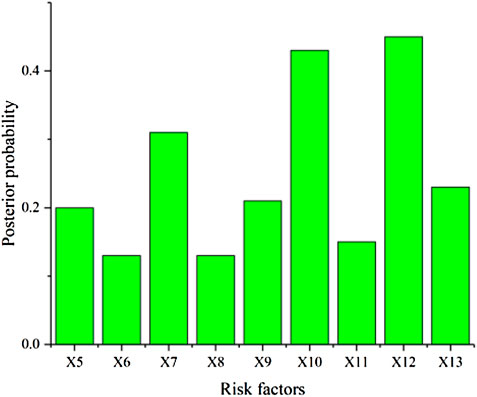
In excavation section ZK242-695∼ZK242-705 of the Jinzhupa Tunnel, the tunnel collapsed due to excessive rock fissures and dropping water seepage on the vault, as seen in Figures 6–9. Using Eq. 6, when a tunnel collapses, the posterior probability distribution of the risk factors (X5∼X13) may be determined, as shown in Figure 9. The results indicated that X12 (untimely support) and X10 (tunnel overbreak and underbreak control) are most likely to be the direct causes. Excessive excavation and untimely support, coupled with loose surrounding rock, led to the collapse accident. Therefore, the measures should be taken to reduce the collapse risk value. After the accident, this method can provide policymakers with a diagnostic analysis of the collapse and theoretical guidance for emergency rescue.
Discussion
1) A traditional Bayesian network is based on three assumptions: (a) The relationship between nodes is completely understood and fulfills the logical “AND” or “OR” relationship; (b) There are only two states, i.e., “YES” and “NO;” and (c) The root node’s failure probability is exactly determined. To characterize numerous failure situations of the nodes, the proposed model uses fuzzy numbers. The normal cloud model is used to build a multistate conditional probability table. Based on building a multi-state fuzzy conditional probability table, the logical relationships between nodes are described, which is able to reflect the uncertainty of the association between nodes. The problems associated with the three assumptions in traditional Bayesian networks are addressed.
2) Compared with the analytic hierarchy process, an MCBN model can not only carry out the static risk assessment but also carry out a dynamic risk assessment and perform sensitivity analysis on risk factors. During the construction process, it can always provide auxiliary opinions to decision-makers. Therefore, the safety of construction can be improved.
Conclusion and Future Work
This paper proposed an MCBN approach for failure probability evaluation. The results of the analysis express not only the likelihood of the data explicitly, but also the degree of uncertainty in the data, including its ambiguity and randomness. The model solves the problem of the difficulty in establishing a multistate conditional probability table. The MCBN model proposed in this paper can not only conduct dynamic risk assessment but also provide sensitivity analysis. The applicability of the method is verified by taking a typical tunnel collapse hazard in the construction of the Jinzhupa tunnel in China as an example. The results demonstrate the feasibility and application prospects of the method.
Compared to a traditional Bayesian network, an MCBN can better define the status of the impact factor. Moreover, compared to an ANN, an MCBN can conduct a dynamic risk assessment and provide a timely reference for decision-makers, thereby reducing casualties and economic losses. In addition, the advantages of a normal cloud model over a fuzzy set approach are also addressed.
The MCBN model proposed in this paper also has some limitations. During the construction process, the judgement of the state and weight of the risk factors still depends on the subjective consciousness of people. The objective of our subsequent research is to determine the weighting of risk factors based on several similar tunnel projects and to determine the status of the risk factors by monitoring the measured data.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
GM: Modification and Supervision. JL: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing—review and editing. WQ: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing—review and editing. BW: Modification and Supervision. SX: Modification and Supervision.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to appreciate the financial support from the National Natural Science Foundation of China (Grant Nos. 51678164 and 51478118), the Guangxi Natural Science Foundation Program (2018GXNSFDA138009).
References
Chen, C., Zhang, L., and Tiong, R. L. K. (2020). A Novel Learning Cloud Bayesian Network for Risk Measurement. Appl. Soft Comput. 87, 105947. doi:10.1016/j.asoc.2019.105947
Chen, F., Wang, Y., Wu, X., Xiao, D., and Zhang, L. (2017). Risk of Face Stability in Slurry Shield Tunneling Based on Hybrid Cloud-BN Model. J. Civ. Eng. Manag. 34, 73–79. (in Chinese). doi:10.14050/j.cnki.1672-9250.2005.03.002
Chen, W., Zhang, G., Wang, H., Zhong, G., and Wang, C. (2019). Evaluation of Possibility of Tunnel Collapse by Drilling and Blasting Method Based on T-S Fuzzy Fault Tree. Rock Soil Mech. 2019 (S1), 319–328. (in Chinese). doi:10.16285/j.rsm.2018.1712
D’Angelo, M. F. S. V., Palhares, R. M., Cosme, L. B., Aguiar, L. A., Fonseca, F. S., and Caminhas, W. M. (2014). Fault Detection in Dynamic Systems by a Fuzzy/Bayesian Network Formulation. Appl. Soft Comput. 21, 647–653. doi:10.1016/j.asoc.2014.04.007
Golabchi, A., Han, S., and Fayek, A. R. (2016). A Fuzzy Logic Approach to Posture-Based Ergonomic Analysis for Field Observation and Assessment of Construction Manual Operations. Can. J. Civ. Eng. 43, 294–303. doi:10.1139/cjce-2015-0143
Holický, M., Marková, J., and Sýkora, M. (2013). Forensic Assessment of a Bridge Downfall Using Bayesian Networks. Eng. Fail. Anal. 30, 1–9. doi:10.1016/j.engfailanal.2012.12.014
Hyun, K.-C., Min, S., Choi, H., Park, J., and Lee, I., (2015). Risk Analysis Using Fault-Tree Analysis (FTA) and Analytic Hierarchy Process (AHP) Applicable to Shield TBM Tunnels. Tunn. Undergr. Space Technol. 49 121-129. doi:10.1016/j.tust.2015.04.007
Khakzad, N., Khan, F., and Amyotte, P. (2011). Safety Analysis in Process Facilities: Comparison of Fault Tree and Bayesian Network Approaches. Reliability Eng. Syst. Saf. 96, 925–932. doi:10.1016/j.ress.2011.03.012
Khakzad, N., Khan, F., and Paltrinieri, N. (2014). On the Application of Near Accident Data to Risk Analysis of Major Accidents. Reliability Eng. Syst. Saf. 126, 116–125. doi:10.1016/j.ress.2014.01.015
Khakzad, N. (2013). Risk-based Design of Process Systems Using Discrete-Time Bayesian Networks. Reliability Eng. Syst. Saf. 109, 5–17. doi:10.1016/j.ress.2012.07.009
Li, D., Liu, C., and Gan, W. (2009). A New Cognitive Model: Cloud Model. Int. J. Intell. Syst. 24, 357–375. doi:10.1002/int.20340
Li, F. (2011). Risk Prediction and Control of Tunnel Collapse (China, Changsha: Central South University). Master’s Thesis(in Chinese).
Li, N., Feng, X., and Jimenez, R. (2017). Predicting Rock Burst hazard with Incomplete Data Using Bayesian Networks. Tunnelling Underground Space Techn. 61, 61–70. doi:10.1016/j.tust.2016.09.010
Nezarat, H., Sereshki, F., and Ataei, M. (2015). Ranking of Geological Risks in Mechanized Tunneling by Using Fuzzy Analytical Hierarchy Process (FAHP). Tunnelling Underground Space Techn. 50, 358–364. doi:10.1016/j.tust.2015.07.019
Wang, G., Xu, C., and Li, D. (2014). Generic normal Cloud Model. Inf. Sci. 280, 1–15. doi:10.1016/j.ins.2014.04.051
Wang, S., Li, L.-p., Shi, S., Cheng, S., Hu, H., and Wen, T. (2020). Dynamic Risk Assessment Method of Collapse in Mountain Tunnels and Application. Geotech. Geol. Eng. 38, 2913–2926. doi:10.1007/s10706-020-01196-7
Wang, X., Li, S., Xu, Z., Hu, J., Pan, D., and Xue, Y. (2019). Risk Assessment of Water Inrush in Karst Tunnels Excavation Based on normal Cloud Model. Bull. Eng. Geol. Environ. 78, 3783–3798. doi:10.1007/s10064-018-1294-6
Wu, B., Qiu, W., Huang, W., Meng, G., Nong, Y., and Huang, J. (2022b). A Multi-Source Information Fusion Evaluation Method for the Tunneling Collapse Disaster Based on the Artificial Intelligence Deformation Prediction. Arab. J. Sci. Eng. doi:10.1007/s13369-021-06359-z
Wu, B., Qiu, W., Qiu, W., Huang, W., Meng, G., Huang, J., et al. (2022a). Dynamic Risk Evaluation Method for Collapse Disasters of Drill-And-Blast Tunnels: a Case Study. Math. Biosci. Eng. 19, 309–330. doi:10.3934/mbe.2022016
Zhang, G.-H., Chen, W., Jiao, Y.-Y., Wang, H., and Wang, C.-T. (2020). A Failure Probability Evaluation Method for Collapse of Drill-And-Blast Tunnels Based on Multistate Fuzzy Bayesian Network. Eng. Geology. 276, 105752. doi:10.1016/j.enggeo.2020.105752
Zhang, G.-H., Jiao, Y.-Y., Chen, L.-B., Wang, H., and Li, S.-C. (2016). Analytical Model for Assessing Collapse Risk during Mountain Tunnel Construction. Can. Geotech. J. 53, 326–342. doi:10.1139/cgj-2015-0064
Zhang, L., Ding, L., Wu, X., and Skibniewski, M. J. (2017). An Improved Dempster-Shafer Approach to Construction Safety Risk Perception. Knowledge-Based Syst. 132, 30–46. doi:10.1016/j.knosys.2017.06.014
Zhang, L., Wu, X., Qin, Y., Skibniewski, M. J., and Liu, W. (2016). Towards a Fuzzy Bayesian Network Based Approach for Safety Risk Analysis of Tunnel-Induced Pipeline Damage. Risk Anal. 36, 278–301. doi:10.1111/risa.12448
Keywords: tunnel collapse, drill-blast method, cloud Bayesian network, collapse possibility, risk assessment
Citation: Meng G, Liu J, Qiu W, Wu B and Xu S (2022) A Failure Probability Evaluation Method for the Collapse of Drill-Blast Tunnels Based on a Multistate Cloud Bayesian Network. Front. Earth Sci. 10:856701. doi: 10.3389/feart.2022.856701
Received: 17 January 2022; Accepted: 28 February 2022;
Published: 15 March 2022.
Edited by:
Chaojun Jia, Central South University, ChinaReviewed by:
Zhang Cong, Central South University of Forestry and Technology, ChinaFu Helin, Central South University, China
Copyright © 2022 Meng, Liu, Qiu, Wu and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weixing Qiu, MTkxMDMwMjA0N0BzdC5neHUuZWR1LmNu
 Guowang Meng1,2
Guowang Meng1,2 Jialiang Liu
Jialiang Liu Weixing Qiu
Weixing Qiu Shixiang Xu
Shixiang Xu