The Strength Behavior and Desiccation Crack Development of Silty Clay Subjected to Wetting–Drying Cycles

It is commonly accepted that wetting–drying cycles have an effect on the soil strength behavior. Crack development in soil is observed by many engineers during wetting–drying cycles, which may give a good explanation for the change in soil strength. A series of laboratory tests were conducted in this study to investigate the desiccation crack development and the strength change law for silty clay subjected to different numbers of wetting–drying cycles. The results show that the desiccation cracks at the end of drying process developed in two stages: the stage of rapid growth and the stage of steady state. The change law of soil strength is similar to the cracking that decreases quickly in the former stage and slowly in the latter stage, which indicates that the cracking in the soil is the main reason for strength reduction. Based on the assumption of an isotropic and linear elastic soil mass at rest earth pressure conditions, an equation for the depth of desiccation cracking after different numbers of wetting–drying cycles was obtained with soil mechanics for unsaturated soils. Finally, the applicability of the equation was verified compared with the experiment results.

Introduction

Wetting–drying cycles are common in nature (Gao et al., 2019; Gao et al., 2020; Gao et al., 2021; Martin et al., 2021). The water content of soil changes during the process of repeated fluctuation of the groundwater level, which leads to the generation of wetting–drying cycles (Kilsby et al., 2009; Shi et al., 2014a). Influenced by wetting–drying cycles, the soil strength behavior will change, which may have negative effects on the safety of structures such as the underground storage (Shi et al., 2014b; Liu et al., 2018, Liu et al., 2020, Liu and Gao, 2020). It is reported that some structures were damaged by such cycles (Mshana et al., 1993; Leroueil, 2001; Chen et al., 2017; Chen et al., 2020). Therefore, it is significant to investigate the effect of wetting–drying cycles on the soil strength behavior.

Over the past decades, a number of experiments have been conducted to research the relationship between the soil strength behavior and wetting–drying cycles. The shear strength of clay affected by wetting–drying cycles was investigated by Rajiaram and Erbach et al. (1999) in the laboratory. The results showed that the soil strength of clay changes significantly with the wetting–drying cycles. In addition to clay, wetting–drying cycles have a negative effect on the strength of other kinds of soil. Goh et al. (2014) conducted a series of consolidated drained triaxial tests by using three different sand–kaolin mixtures which experienced multiple cycles of wetting–drying. The test results indicated that the samples on the wetting paths have lower shear strengths than those on the drying paths. In addition, to ascertain the performance of silty clay in pavement applications, Kampala et al. (2014) studied the durability of the calcium carbide residue and fly ash-stabilized silty clay against wetting–drying cycles. In general, soil strength will decrease when affected by wetting–drying cycles. It is because the soil structure is damaged during the cycles (Pires et al., 2007; Pires et al., 2008; Aldaood et al., 2014; Fan et al., 2019; Fan et al., 2020).

The desiccation cracks break the structure and integrality of soil and further reduce its strength during wetting–drying cycles (Shi et al., 2014a; Cao et al., 2016). The dynamic development of desiccation cracks in the expansive soil during wetting–drying cycles have been tested by Li et al. (2009), Li and Zhang et al. (2010), Li and Zhang et al. (2011), and Cao et al. (2016). The results showed that desiccation cracks developed in three stages: initial, primary, and steady state stages. In the initial stage, few cracks developed with the gradually decreasing water content. When the water content reached a critical value for crack initiation, cracks developed quickly and this was the beginning of the primary stage. As the water content approached the shrinkage limit of the soil, cracks developed slowly and reached a steady state. The cracks were found to be repeatable during three cycles of wetting–drying (Bronswijk, 1991; Kodikara and Choi, 2006). Yessiler et al. (2000) and Rayhani et al. (2008) investigated the surficial dimensions of cracks using the crack intensity factor, that is, the ratio of the surface area of cracks to the total surface area of the soil, in three compacted liner samples during wetting–drying cycles. Large amounts of cracking appeared in specimens with high fines content, and less cracking in soil with low fines content. The rules of crack development during wetting–drying cycles have been reported in the previous literature (Jiang et al., 2016; Liu et al., 2016; Lagroix and Guyodo, 2017; Kang et al., 2021). However, the mechanism behind the desiccation crack development during wetting–drying cycles rarely attracted the attention of engineers.

The objective of this study is to establish a mechanical model of the desiccation crack development, thereby to further explain the decrease of soil strength experienced wetting–drying cycles. The cracking in silty clay at the end of the drying process after different number of wetting–drying cycles was measured, and then, the strength of the samples was investigated with a series of consolidated undrain (CU) triaxial tests. Finally, the mechanism behind the desiccation crack development during wetting–drying cycles was analyzed.

Materials and Methods

Soil

The experiment was performed on undisturbed silty clay. The silty clay selected in the tests was taken from a slope in the Three Gorges Reservoir, located in the southwest of China. The mineralogical composition of the soil was determined by X-ray diffraction (XRD) using a D8 Advance X-ray diffractometer. The silty clay contained 28.39% quartz, 23.63% muscovite, 18.15% albite, 14.08% nontronite, 9.32% microcline, and 6.43% clinochlore. A series of basic geotechnical tests were performed to determine the natural density, natural water content, specific gravity, liquid limits, plastic limit, and void ratio for the soil, in accordance with the American Standard Test Method (ASTM Standard D4318-17, 2017). The physical properties of the soil are shown in Table 1.

TABLE 1

TABLE 1. Physical properties of soil.

Sample Preparation

More than twelve cylindrical samples with 39.1 mm in diameter and 80 mm in height were prepared by special tools, as shown in Figure 1.

FIGURE 1

FIGURE 1. Sample preparation.

Wetting–Drying Cycle Test

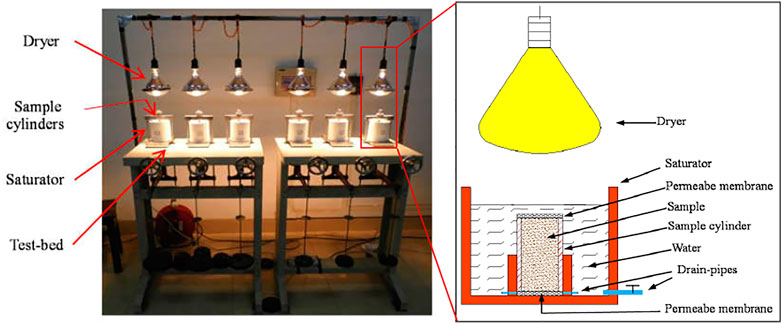
Soil samples were saturated and dried in a self-made apparatus including test-bed, saturators, dryers, and sample cylinders, as shown in Figure 2. Wetting process was to soak the samples in sample cylinders with the water level exceeding the top of the samples. It was found that 24 h of soaking was enough to reach saturation and to minimize entrapped air bubbles in the samples. The samples were dried by the dryer, which can heat soil to a temperature of 45°C. After 12.75 h of drying, the weight of the samples was not reduced.

FIGURE 2

FIGURE 2. Self-made test apparatus of wetting–drying cycles.

A wetting–drying cycle consisted of the following processes: 1) first, the samples were saturated by using the saturators as described previously; 2) the water inside the saturators was drained through drainpipes, and the samples were dried by using the dryer for 12.75 h until their weight reached to a constant; and 3) finally, the samples were saturated once again.

Twelve samples were divided into four groups (groups I, II, III, and IV) which were subjected to 0, 2, 4, and 8 consecutive wetting–drying cycles, respectively. There were three samples in each group.

Consolidated Undrained Triaxial Test

After the wetting–drying tests, a series of consolidated undrained (CU) triaxial tests were conducted to investigate the strength behavior of the four groups of samples which were at the saturated state, as shown in Figure 3. The type of the apparatus used in the CU triaxial tests was SJ-1A, made in China (Wang S. et al., 2020; Chen et al., 2021). The three samples in each group were consolidated for 24 h and then sheared under confining pressures of 50, 100, and 200 kPa, respectively. The shear test was performed until the axial strain ${\epsilon }_1$ reached 15% or the sample was destroyed completely (Wang J. et al., 2020; Tang et al., 2021; Wang et al., 2022).

FIGURE 3

FIGURE 3. Apparatus of consolidated undrained triaxial tests.

Results and Analysis

Crack Development

Figures 4A–D show the development of desiccation cracks on the soil surface at the end of each drying process. There were few cracks developed on the surface of the soil before wetting–drying cycles. After the first drying process, the length and width of the cracks increased. After the second drying process, the cracks developed continually, and a broad main crack appeared in the middle of the specimen surface. Within 3–8 cycles, the number of cracks did not change, and the width of the cracks developed very slowly. Therefore, it can be inferred that the desiccation cracks developed in two stages: the stage of rapid growth and stage of the steady state, in parallel with the increasing number of wetting–drying cycles. In the rapid growth stage, cracks developed quickly after the first and second cycles. As the cycle number approached more than two, cracks developed slowly and approached a steady state. Yessiler et al. (2000) also found that the development of cracks was not significant after the second wetting–drying cycle.

FIGURE 4

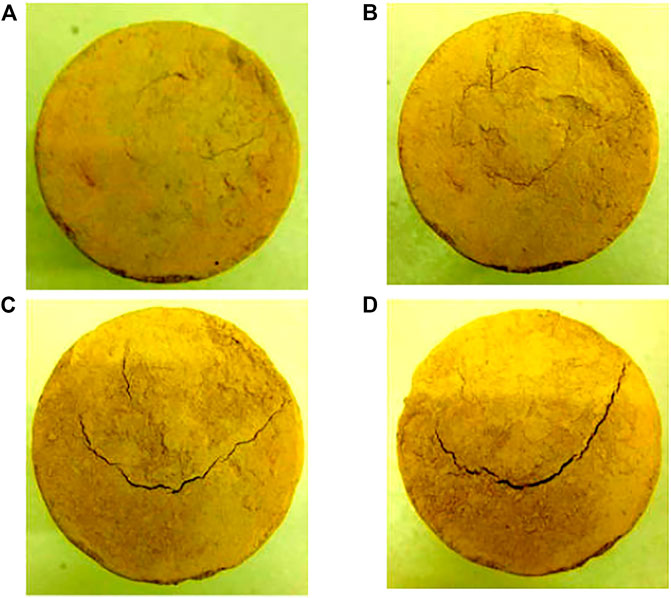
FIGURE 4. Crack development at the end of each drying process: (A) initial state, (B) after the first drying process, (C) after the second drying process, and (D) after the eighth drying process.

Stress–Strain Curves

Figures 5A–C illustrate the stress–strain curves for the twelve specimens in the CU triaxial shear test after different numbers of wetting–drying cycles. It should be noted that the curves of the three specimens in the group subjected to zero cycles were all strain-softening damage models, which is similar to the shearing behavior of over-consolidated soil (Ou et al., 2019; Wang et al., 2021a; Wang et al., 2021b). This is due to the fact that the structure and integrality of the specimens are not damaged before experiencing the wetting–drying cycles. When the axial strain approached approximately 7%, the deviator stress reached a peak value. In contrast, the strain-hardening damage model was observed for the nine specimens in groups II, III, and IV, which were subjected to 2, 4, and 8 wetting–drying cycles, respectively. This could be attributed to the structure and integrality of the specimens directly influenced by the cracks which were developed during wetting–drying cycles. Similar test results were reported by Pires et al. (2007), Pires et al. (2008). The experimental results show that the peak deviator stress of those three specimens of the group subjected to eight cycles is similar to the residual strength of the specimens of the group subjected to zero cycles, indicating that the soil structure of the group subjected to eight wetting–drying cycles was completely damaged.

FIGURE 5

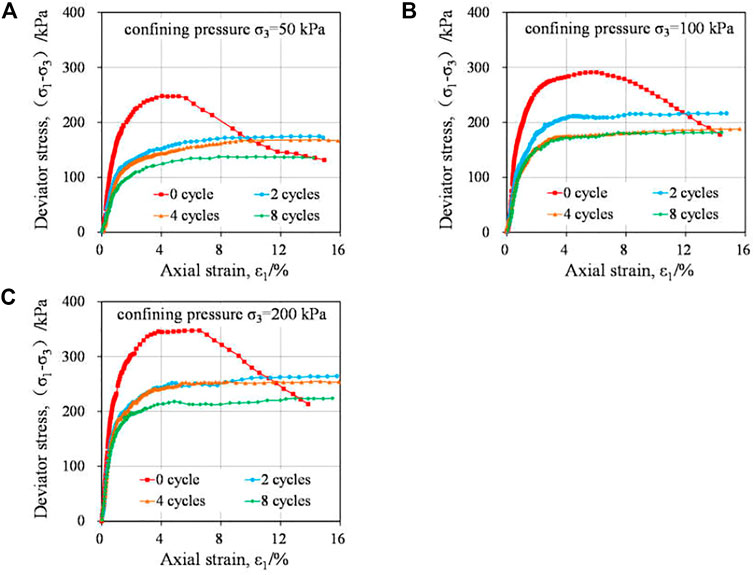
FIGURE 5. Stress-strain curves in the triaxial shear test: (A) σ₃ = 50 kPa, (B) σ₃ = 100 kPa, and (C) σ₃ = 200 kPa.

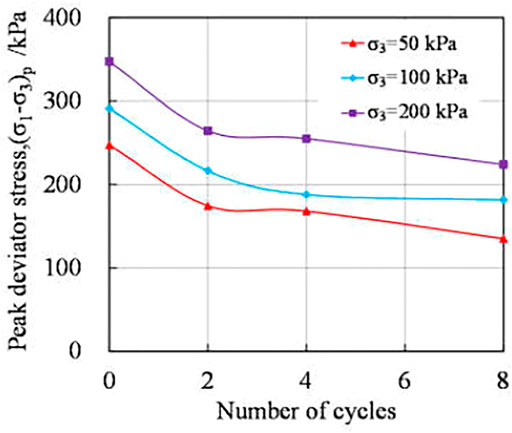
Peak Deviator Stress

The peak deviator stress of the twelve specimens after different number of cycles of wetting–drying could be obtained from Figure 5. When there is an obvious peak point in the stress strain curves in Figure 6, the peak value is taken as the peak deviator stress of the sample. However, when there is no obvious peak value in the curves, the deviator stress when the axial strain is 15% is taken as the peak deviator stress (ASTM Standard D7181, 2011). The peak deviator stress of the twelve specimens after different numbers of wetting–drying cycles was used in the comparison. Figure 6 presents the curves of the peak deviator stress and number of cycles. It is noticed that the larger the confining pressure is, the higher the peak deviator stress will be. This might be attributed to the bite force among the soil particle which becomes larger during the shear test with higher confining pressure. The bite force could contribute to the peak deviator stress. With an increasing number of wetting–drying cycles, the peak deviator stress decreases constantly. In detail, it decreases quickly in the first two cycles and markedly slowly in the subsequent cycles. The change rule is in line with the crack development in Figure 4, which indicates that the development of cracks is the main reason for the decrease of soil strength. The structure of specimens was terribly damaged in the first two cycles of wetting–drying by the cracks, and the peak deviator stress decreased notably accordingly. After two cycles, the cracks developed slowly, which caused the peak deviator stress to decrease slowly.

FIGURE 6

FIGURE 6. Curves of the peak deviator stress and number of wetting–drying cycles.

Mechanism Behind the Desiccation Crack Development During Wetting–Drying Cycles

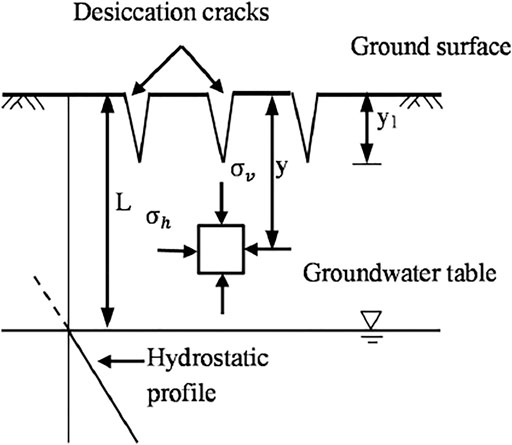
Generally, cracks mainly develop during the drying process, and do not develop during the wetting period (Li, 2009; Li and Zhang, 2010; Li and Zhang, 2011; Cao et al., 2016). Prior to discussing the mechanism behind the desiccation crack development during wetting–drying cycles, it is of value to discuss the development during the first drying process. This topic is discussed at rest earth pressure conditions (at K₀ state) as shown in Figure 7. Assume the underground water level decreases from the ground surface to somewhere underground of L meters depth, and the soil above the water level is dried.

FIGURE 7

FIGURE 7. Model of crack development in soil during the drying process.

The total vertical stress ${\sigma }_v$ in a leveled soil mass is calculated in the same way for both saturated and unsaturated soils (Figure 8). The total vertical stress ${\sigma }_v$ is called the overburden pressure, which is calculated as follows:

${\sigma }_v={\displaystyle \underset{0}{\overset{D}{\int }}\rho gdy},(1)$

where $\rho$ is the total density of soil, $g$ is the gravitational acceleration, y is the vertical distance from the ground surface, and D is the depth of soil under consideration.

FIGURE 8

FIGURE 8. Distribution of the matric suction during the drying process.

For a homogeneous soil mass, the total vertical stress can be expressed as follows:

${\sigma }_v=\rho gD,(2)$

Generally, the pore air pressure $u_a$ is equal to the atmospheric pressure. The pore water pressure $u_w$ above the groundwater table can either be estimated or measured. In some cases, the estimate can be based on hydrostatic conditions.

The horizontal pressure ${\sigma }_h$ at any depth below ground surface can be written as a ratio of the vertical pressure ${\sigma }_v$. Each of the pressures can be referenced to the pore air pressure $u_a$ (or the atmospheric pressure). The coefficient of earth pressure at rest, $K_0$, can be defined as follows:

$K_0=\frac{\left({\sigma }_h-u_a\right)}{\left({\sigma }_v-u_a\right)},(3)$

When $u_a=0$, $K_0={\sigma }_h/{\sigma }_v$, that is, the coefficient of earth pressure at rest for the saturated soil.

In saturated soil mechanics, the constitutive relations for the soil structure can be formulated in accordance with the generalized Hooke’s law using the effective stress variable $(\sigma -u_w)$. For an isotropic and linearly elastic soil structure, the constitutive relations in the x, y, and z directions can be described as follows:

$\{\begin{array}{c}{\epsilon }_x=\frac{\left({\sigma }_x-u_w\right)}{E}-\frac{u}{E}\left({\sigma }_y+{\sigma }_z-2u_w\right)\\ {\epsilon }_y=\frac{\left({\sigma }_y-u_w\right)}{E}-\frac{u}{E}\left({\sigma }_x+{\sigma }_z-2u_w\right)\\ {\epsilon }_z=\frac{\left({\sigma }_z-u_w\right)}{E}-\frac{u}{E}\left({\sigma }_x+{\sigma }_y-2u_w\right)\end{array},(4)$

where ${\epsilon }_x$, ${\epsilon }_y$, and ${\epsilon }_z$ are the normal strains in x, y and z directions, respectively; ${\sigma }_x$, ${\sigma }_y$, and ${\sigma }_z$ are the total normal stresses in x, y, and z directions, respectively; and E and u are the modulus of elasticity and Poisson’s ratio, respectively.

Fredlund et al. (Fredlund, 1976; Fredlund, 1979; Fredlund and Rahardjo, 1993) introduced the constitutive relations between saturated and unsaturated soil, using the appropriate stress state variables. The assumption is made that soil behaves as an isotropic and linear elastic material. The following constitutive relations are expressed in terms of stress state variables: $(\sigma -u_a)$ and $(u_a-u_w)$. The soil structure constitutive relations associated with the normal strains $\epsilon$ in the x, y, and z directions are as follows:

$\{\begin{array}{c}{\epsilon }_x=\frac{\left({\sigma }_x-u_a\right)}{E}-\frac{u}{E}\left({\sigma }_y+{\sigma }_z-2u_a\right)+\frac{\left(u_a-u_w\right)}{H}\\ {\epsilon }_y=\frac{\left({\sigma }_y-u_a\right)}{E}-\frac{u}{E}\left({\sigma }_x+{\sigma }_z-2u_a\right)+\frac{\left(u_a-u_w\right)}{H}\\ {\epsilon }_z=\frac{\left({\sigma }_z-u_a\right)}{E}-\frac{u}{E}\left({\sigma }_x+{\sigma }_y-2u_a\right)+\frac{\left(u_a-u_w\right)}{H}\end{array},(5)$

where H is the modulus of elasticity of the soil structure with respect to a change in matric suction, $(u_a-u_w)$. Thus, the stress ${\sigma }_h$ versus strain ${\epsilon }_h$ equation in the horizontal direction for a homogeneous, isotropic, unsaturated soil is given by the following equation:

${\epsilon }_h=\frac{\left({\sigma }_h-u_a\right)}{E}-\frac{u}{E}\left({\sigma }_v+{\sigma }_h-2u_a\right)+\frac{\left(u_a-u_w\right)}{H},(6)$

Eq. 6 applies to both horizontal directions.

For the at rest or $K_0$ condition in intact, homogeneous, unsaturated soil mass, the strain in the horizontal directions can be set to zero (i.e., ${\epsilon }_h=0$). Introducing ${\epsilon }_h=0$ into (6), the net horizontal stress can be written in terms of the vertical stress.

$\left({\sigma }_h-u_a\right)=\frac{u}{1-u}\left({\sigma }_v-u_a\right)-\frac{E}{\left(1-u\right)H}\left(u_a-u_w\right),(7)$

Eq. 7 can be normalized to the net vertical stress, and the equation takes the form for the coefficient of earth pressure at rest as follows:

$K_0=\frac{u}{1-u}-\frac{E}{\left(1-u\right)H}\frac{\left(u_a-u_w\right)}{\left({\sigma }_v-u_a\right)},(8)$

When the matric suction, $(u_a-u_w)$, goes to zero, Eq. 8 reverts to the form for a saturated soil (i.e., $K_0=\frac{u}{1-u}$). When matric suction is present in the soil, the horizontal stress is reduced. The reduction is also a function of the depth under consideration. At the shallow depths of the crack, a relatively small matric suction will cause the net horizontal stress to be zero and tend to be negative. If the soil cannot sustain any tensile strain, cracking of the soil will occur, commencing at the ground surface [22].

The depth of cracking in drying soil can be estimated using the coefficient of earth pressure at rest. The assumption is made that the at rest coefficient of earth pressure, $K_0$, is zero at the bottom of a crack. The above analysis assumes that the soil cannot sustain any tensile strain prior to failing. The depth of desiccation cracks, $y_1$, in the soil after the first drying process is taken into consideration as shown in Figure 8. At the bottom of the crack, the net horizontal stress is zero (i.e., $({\sigma }_v-u_a)=0$). Accordingly, (7) becomes

${\left({\sigma }_v-u_a\right)}_1=\frac{E}{uH}{\left(u_a-u_w\right)}_1,(9)$

where subscript, 1, represents the crack at the bottom after the first drying process. The net vertical stress, ${({\sigma }_v-u_a)}_1$, changes with the depth of the soil under consideration, as well as the matric suction, ${(u_a-u_w)}_1$.

The assumptions could be made concerning the matric suction variation with respect to depth. One typical matric suction profile is illustrated in Figure 8, which shows the negative pore water pressure as a linear function of the distance above the groundwater table (Fredlund and Rahardjo, 1993). The variable, $f_w$, is used to permit the pore water pressure to be represented as a percentage of the hydrostatic profile where a value greater than 1.0 signifies pore water pressures which are more negative than the hydrostatic profile. The matric suction ${(u_a-u_w)}_y$ at any depth, y, in the soil can be written as

${\left(u_a-u_w\right)}_y=f_w{\rho }_{w}g\left(L-y\right),(10)$

where ${\rho }_w$ is the density of water and L is the distance from ground surface to the water table. For a homogeneous soil, the net vertical stress ${({\sigma }_v-u_a)}_y$ at any depth, y, is written as

${\left({\sigma }_v-u_a\right)}_y=\rho gy,(11)$

Introduce (10) and (11) into (9), the depth of desiccation crack, $y_1$, after the first drying process is obtained as follows:

$y_1=\frac{L}{1+\frac{u\rho H}{f_w{\rho }_{w}E}},(12)$

Eq. 12 indicates that the depth of a desiccation crack depends on the matric suction and the elastic parameters of the soil.

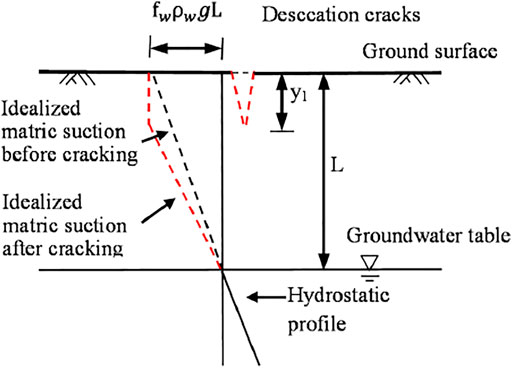
Through the cracking test results of Li et al. (2009), Li and Zhang et al. (2010), Li and Zhang et al. (2011), Ahmadi et al. (2012), Cao et al. (2016), and this study, it is found that the cracks cannot be recovered once they occur. After a wetting–drying cycle, the cracks will change the distribution of matric suction in the next drying process.

The soil at the cracks was exposed to the air, and thus, it can be considered that the matric suction in the depth of cracks equals to the matric suction on the ground surface (i.e., $(u_a-u_w)=f_w{\rho }_{w}gL$), while the matric suction under the bottom of cracks distributes linearly with the soil depth, as shown in Figure 8. Then the matric suction of the soil at any depth, y, is given as follows:

${\left(u_a-u_w\right)}_y=\{\begin{array}{c}{f}_w{\rho }_{w}gL,0\le y\le y_1\\ f_w{\rho }_{w}gL\frac{L-y}{L-y_1},y_1\le y\le L\end{array},(13)$

For a homogeneous soil, the net vertical stress at any depth, y, is written as Eq. 11. Substituting (11) and (13) into (9) gives an equation for the depth of cracking, $y_2$, at the end of drying process after the second wetting–drying cycle as follows:

$y_2=\frac{L}{1+\frac{u\rho H}{f_w{\rho }_{w}E}\left(1-\frac{y_1}{L}\right)},(14)$

where $0\mathrm{<}{y}_1\mathrm{<}L$ indicates $0\mathrm{<}(1-\frac{y_1}{L})\mathrm{<}1$. Compare (14) with (12), and it can be known that $y_1\mathrm{<}{y}_2$, suggesting that the crack development is deeper after the second wetting–drying cycle. Similarly, the crack depth, $y_n$, at the end of drying after “n” cycles of wetting–drying can be expressed as follows:

$y_n=\frac{L}{1+\frac{u\rho H}{f_w{\rho }_{w}E}\left(1-\frac{y_{n-1}}{L}\right)},(15)$

An equation for the depth of cracking, $y_n$, can be deduced from (12) and (15):

$y_n=L\frac{{\left(\frac{u\rho H}{f_w{\rho }_{w}E}\right)}^n-1}{{\left(\frac{u\rho H}{f_w{\rho }_{w}E}\right)}^{n+1}-1},(16)$

To illustrate the form of Eq. 16, the assumption is made that the total density of the soil is 1886 kg/m³ and the matric suction profile is equivalent to hydrostatic conditions. Lau et al. (1987) showed that E/H ratios are typically in the range of 0.15–0.20 for initially saturated clay.

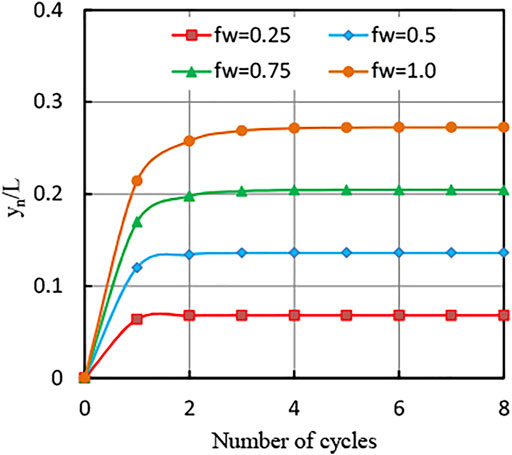
For an E/H ratio of 0.18 and a Poisson’s ratio of 0.35 of the soil, the anticipated depth of cracking at the end of drying process after “n” cycles of wetting–drying is shown in Figure 9.

FIGURE 9

FIGURE 9. Variations of $y_n/L$ with the number of wetting–drying cycles.

Figure 9 shows that the cracks develop quickly during the first wetting–drying cycle, then slow down with the increasing number of wetting–drying cycles, and finally approach a constant value. Moreover, the cracks occur mainly during the first two wetting–drying cycles, which is in line with the test results of this article, Cao et al. (2016), and Ahmadi et al. (2012). Generally, $f_w$ is related to the clay mineral content in the soil. $f_w$ increases with an increase in the clay mineral content, and accordingly, the crack becomes deeper. Thus, it is easy to explain why the cracks of silty clay in this study are smaller than that of expansive soil used in the experiment by Cao et al. (2016). To be specific, the clay mineral content of silty clay is smaller than that of the expansive soil. Hence, the law of crack development keeps accordance with the test results in this study. This indicates that Eq. 16 can be used to describe the crack development at the end of drying processes after different numbers of wetting–drying cycles.

Conclusion

In this study, a series of wetting–drying cycle tests and CU triaxial tests were first conducted to investigate the strength behavior and desiccation crack development of silty clay subjected to wetting–drying cycles. The results showed that the desiccation cracks developed rapidly in the first two cycles but slowly after two cycles, with the increasing number of wetting–drying cycles. The structure of silty clay was damaged by wetting–drying cycles. The peak deviator stress decreased quickly in the first two cycles and markedly slowly in the subsequent cycles, which is consistent with the development law of desiccation cracks. The main reason for the decrease of soil strength is the development of desiccation cracks. A new mechanics model of the desiccation crack development after different numbers of wetting–drying cycles was established with soil mechanics for unsaturated soils. In order to verify the applicability of the new model, charts with regard to the depth of desiccation cracking based on the equation were developed. Finally, the mechanism behind the desiccation crack development during wetting–drying cycles was analyzed.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization: YT; methodology: RZ and ZZ; formal analysis: YT; writing—original draft preparation: YT; writing—review and editing: YT, RZ, HC, and ZZ; and funding acquisition: YT.

Funding

The research work was supported by the National Natural Science Foundation of China (No. 51808083), the China Postdoctoral Science Foundation (No. 2020M673110), the Basic Research and Frontier Exploration Project of Chongqing of China (No. cstc2018jcyjAX0491), the Science and Technology Research Program of the Chongqing Municipal Education Commission (No. KJQN201800713), the Chongqing Postdoctoral Science Foundation (No. cstc2019jcyj-bshX0125), and the Opening Foundation of State Key Laboratory of Mountain Bridge and Tunnel Engineering (SKLBT-19-011).

Conflict of Interest

The author HC was employed by China Merchants Chongqing Communications Research & Design Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, H., Rahimi, H., and Rostami, M. E. (2012). Control of Swelling of Soil under Canal Lining by Wetting and Drying Cycles. Irrig. Drain. 61 (4), 527–532. doi:10.1002/ird.1666

CrossRef Full Text | Google Scholar

Aldaood, A., Bouasker, M., and Al-Mukhtar, M. (2014). Impact of Wetting-Drying Cycles on the Microstructure and Mechanical Properties of Lime-Stabilized Gypseous Soils. Eng. Geol. 174, 11–21. doi:10.1016/j.enggeo.2014.03.002

CrossRef Full Text | Google Scholar

ASTM Standard D7181-11 (2011). Standard test method for consolidated drained triaxial compression test for soils. West Conshohocken, PA: ASTM International. Available at: www.astm.org.

Google Scholar

ASTM Standard D4318-17 (2017). Standard Test Methods for Liquid Limit, Plastic Limit, Plastic Limit, and Plastic. West Conshohocken, PA: ASTM International. Available at: www.astm.org.

Google Scholar

Bronswijk, J. J. B. (1991). Drying, Cracking, and Subsidence of a clay Soil in a Lysimeter. Soil Sci. 152 (2), 92–99. doi:10.1097/00010694-199108000-00005

CrossRef Full Text | Google Scholar

Cao, L., Wang, Z., and Chen, Y. (2016). Unsaturated Seepage Analysis of Cracked Soil Including Development Process of Cracks. Adv. Mater. Sci. Eng. 2016, 1–13. doi:10.1155/2016/2684297

CrossRef Full Text | Google Scholar

Chen, Z. Q., He, C., Wu, D., and Xu, G. W. (2017). Fracture Evolution and Energy Mechanism of Deep-Buried Carbonaceous Slate. Acta Geotech. 79, 3667–3688. doi:10.1007/s11440-017-0606-5

CrossRef Full Text | Google Scholar

Chen, Z. Q., He, C., Yang, W. B., Guo, W. Q., Li, Z., and Xu, G. W. (2020). Impacts of Geological Conditions on Instability Causes and Mechanical Behavior of Large-Scale Tunnels: a Case Study from the Sichuan–Tibet Highway. China. B. Eng. Geol. Environ. 12 (6), 1–18. doi:10.1007/s11440-017-0606-5

CrossRef Full Text | Google Scholar

Chen, H. H., Li, L., Li, J. P., and Sun, D. A. (2021). A Generic Analytical Elastic Solution for Excavation Responses of an Arbitrarily-Shaped Deep Opening under Biaxial Iin-Ssitu Stresses. Int. J. Geomech. 21 (12), 04021241. doi:10.1061/(asce)gm.1943-5622.0002205

CrossRef Full Text | Google Scholar

Fan, J., Jiang, D., Liu, W., Wu, F., Chen, J., and Daemen, J. (2019). Discontinuous Fatigue of Salt Rock with Low-Stress Intervals. Int. J. Rock Mech. Mining Sci. 115 (3), 77–86. doi:10.1016/j.ijrmms.2019.01.013

CrossRef Full Text | Google Scholar

Fan, J., Liu, W., Jiang, D., Chen, J., Tiedeu, W. N., and Daemen, J. J. K. (2020). Time Interval Effect in Triaxial Discontinuous Cyclic Compression Tests and Simulations for the Residual Stress in Rock Salt. Rock Mech. Rock Eng. 53, 4061–4076. doi:10.1007/s00603-020-02150-y

CrossRef Full Text | Google Scholar

Fredlund, D. G., and Rahardjo, H. (1993). Soil Mechanics for Unsaturated Soils. New York: John Wiley & Sons.

Google Scholar

Fredlund, D. G. (1976). Density and Compressibility Characteristics of Air-Water Mixtures. Can. Geotech. J. 13 (4), 386–396. doi:10.1139/t76-040

CrossRef Full Text | Google Scholar

Fredlund, D. G. (1979). Second canadian Geotechnical Colloquium: Appropriate Concepts and Technology for Unsaturated Soils. Can. Geotech. J. 16 (1), 121–139. doi:10.1139/t79-011

CrossRef Full Text | Google Scholar

Gao, Y., Sun, D. a., Zhu, Z., and Xu, Y. (2019). Hydromechanical Behavior of Unsaturated Soil with Different Initial Densities over a Wide Suction Range. Acta Geotech. 14 (2), 417–428. doi:10.1007/s11440-018-0662-5

CrossRef Full Text | Google Scholar

Gao, Y., Sun, D. A., Zhou, A., and Li, J. (2020). Predicting Shear Strength of Unsaturated Soils over Wide Suction Range. Int. J. Geomech. 20 (2), 04019175. doi:10.1061/(ASCE)GM.1943-5622.0001555

CrossRef Full Text | Google Scholar

Gao, Y., Li, Z., Sun, D. A., and Yu, H. (2021). A Simple Method for Predicting the Hydraulic Properties of Unsaturated Soils with Different Void Ratios. Soil Tillage Res. 209 (3), 104913. doi:10.1016/j.still.2020.104913

CrossRef Full Text | Google Scholar

Goh, S. G., Rahardjo, H., and Leong, E. C. (2014). Shear Strength of Unsaturated Soils under Multiple Drying-Wetting Cycles. J. Geotech. Geoenviron. 140 (2), 1–5. doi:10.1061/(asce)gt.1943-5606.0001032

CrossRef Full Text | Google Scholar

Jiang, D., Fan, J., Chen, J., Li, L., and Cui, Y. (2016). A Mechanism of Fatigue in Salt under Discontinuous Cycle Loading. Int. J. Rock Mech. Mining Sci. 86 (7), 255–260. doi:10.1016/j.ijrmms.2016.05.004

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., and Zhang, Y. (2020). Creep Properties and Damage Constitutive Model of Salt Rock under Uniaxial Compression. Int. J. Damage Mech. 29 (6), 902–922. doi:10.1177/1056789519891768

CrossRef Full Text | Google Scholar

Kampala, A., Horpibulsuk, S., Prongmanee, N., and Chinkulkijniwat, A. (2014). Influence of Wet-Dry Cycles on Compressive Strength of Calcium Carbide Residue-Fly Ash Stabilized Clay. J. Mater. Civ. Eng. 26 (4), 633–643. doi:10.1061/(asce)mt.1943-5533.0000853

CrossRef Full Text | Google Scholar

Kang, Y., Fan, J., Jiang, D., and Li, Z. (2021). Influence of Geological and Environmental Factors on the Reconsolidation Behavior of fine Granular Salt. Nat. Resour. Res. 30 (1), 805–826. doi:10.1007/s11053-020-09732-1

CrossRef Full Text | Google Scholar

Kilsby, C., Glendinning, S., Hughes, P. N., Parkin, G., and Bransby, M. F. (2009). Climate-change Impacts on Long-Term Performance of Slopes. Proc. Inst. Civil Eng. Eng. Sustain. 162 (2), 59–66. doi:10.1680/ensu.2009.162.2.59

CrossRef Full Text | Google Scholar

Kodikara, J. K., and Choi, X. (2006). A Simplified Analytical Model for Desiccation Cracking of clay Layers in Laboratory Tests. Int. Conf. Unsaturated Soils 147, 2558–2569. doi:10.1061/40802(189)218

CrossRef Full Text | Google Scholar

Lagroix, F., and Guyodo, Y. (2017). A New Tool for Separating the Magnetic Mineralogy of Complex mineral Assemblages from Low Temperature Magnetic Behavior. Front. Earth Sci. 5, 61. doi:10.3389/feart.2017.00061

CrossRef Full Text | Google Scholar

Lau, J. T. K. (1987). Desiccation Cracking of Soils. Saskatoon, Sask, Canada: Department of Civil Engineering, University of Saskatchewan.

Google Scholar

Leroueil, S. (2001). Natural Slopes and Cuts: Movement and Failure Mechanisms. Géotechnique 51 (3), 197–243. doi:10.1680/geot.51.3.197.39365

CrossRef Full Text | Google Scholar

Li, J. H., and Zhang, L. M. (2010). Geometric Parameters and REV of a Crack Network in Soil. Comput. Geotech. 37 (4), 466–475. doi:10.1016/j.compgeo.2010.01.006

CrossRef Full Text | Google Scholar

Li, J. H., and Zhang, L. M. (2011). Study of Desiccation Crack Initiation and Development at Ground Surface. Eng. Geol. 123 (4), 347–358. doi:10.1016/j.enggeo.2011.09.015

CrossRef Full Text | Google Scholar

Li, J. H. (2009). Field Experimental Study and Numerical Simulation of Seepage in Saturated/unsaturated Cracked Soil. Hong Kong: The Hong Kong University of Science and Technology. Available at: respository.ust.hk/ir/Record/1783.1-5945.

Google Scholar

Liu, S., and Gao, X. (2020). Evaluation of the Anti-erosion Characteristics of an MICP Coating on the Surface of Tabia. J. Mater. Civ. Eng. 32 (10), 04020304. doi:10.1061/(asce)mt.1943-5533.0003408

CrossRef Full Text | Google Scholar

Liu, Q., Zhang, C., Torrent, J., Barrón, V., Hu, P., Jiang, Z., et al. (2016). Factors Controlling Magnetism of Reddish Brown Soil Profiles from Calcarenites in Southern Spain: Dust Input or Iin-Ssitu Pedogenesis? Front. Earth Sci. 4, 51. doi:10.3389/feart.2016.00051

CrossRef Full Text | Google Scholar

Liu, S., Yu, J., and Yasufuku, N. (2018). Physically Based Soil Water Characteristic Curves Function for Soils with Inner Porosity. Arch. Agron. Soil Sci. 65 (4), 537–548. doi:10.1080/03650340.2018.1511895

CrossRef Full Text | Google Scholar

Liu, S., Wang, R., Yu, J., Peng, X., Cai, Y., and Tu, B. (2020). Effectiveness of the Anti-erosion of an MICP Coating on the Surfaces of Ancient clay Roof Tiles. Const. Build. Mater. 243, 118202. doi:10.1016/j.conbuildmat.2020.118202

CrossRef Full Text | Google Scholar

Martin, B., Owen, A., Nichols, G. J., Hartley, A. J., and Williams, R. D. (2021). Quantifying Downstream, Vertical and Lateral Variation in Fluvial Deposits: Implications from the Huesca Distributive Fluvial System. Front. Earth Sci. 8, 564017. doi:10.3389/feart.2020.564017

CrossRef Full Text | Google Scholar

Naftali, S. M., Suzuki, A., and Kitazono, Y. (1993). Effects of Weathering on Stability of Natural Slopes in north-central Kumamoto. Soils Found. 33 (4), 74–87. doi:10.3208/sandf1972.33.4_74

CrossRef Full Text | Google Scholar

Ou, M. X., Dai, Z. F., Chen, Y. H., and D, Z. D. (2019). Load Transfer Model Considering Over-consolidation Ratio and Poisson Effect. J. Chongqing Univ. 43 (9), 101–108. (in Chinese with English Abstract). doi:10.11835/j.issn.1000-582X.2020.223

CrossRef Full Text | Google Scholar

Pires, L., Bacchi, O., and Reichardt, K. (2007). Assessment of Soil Structure Repair Due to Wetting and Drying Cycles through 2D Tomographic Image Analysis. Soil Tillage Res. 94 (2), 537–545. doi:10.1016/j.still.2006.10.008

CrossRef Full Text | Google Scholar

Pires, L. F., Cooper, M., Cássaro, F. A. M., Reichardt, K., Bacchi, O. O. S., and Dias, N. M. P. (2008). Micromorphological Analysis to Characterize Structure Modifications of Soil Samples Submitted to Wetting and Drying Cycles. Catena 72 (2), 297–304. doi:10.1016/j.catena.2007.06.003

CrossRef Full Text | Google Scholar

Rajiaram, G., and Erbach, D. C. (1999). Effect of Wetting and Drying on Soil Physical Properties. J. Terramech. 36 (1), 39–49. doi:10.1016/s0022-4898(98)00030-5

CrossRef Full Text | Google Scholar

Rayhani, M. H. T., Yanful, E. K., and Fakher, A. (2008). Physical Modeling of Desiccation Cracking in Plastic Soils. Eng. Geol. 97 (1-2), 25–31. doi:10.1016/j.enggeo.2007.11.003

CrossRef Full Text | Google Scholar

Shi, B.-x., Chen, S.-s., Han, H.-q., and Zheng, C.-f. (2014a). Expansive Soil Crack Depth under Cumulative Damage. Scientific World J. 2014 (12), 1–9. doi:10.1155/2014/498437

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, B.-x., Zheng, C.-f., and Wu, J.-k. (2014b). Research Progress on Expansive Soil Cracks under Changing Environment. Scientific World J. 2014, 1–6. doi:10.1155/2014/816759

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S., Zhong, Z., and Liu, X. (2020). Development of an Anisotropic Nonlinear Strength Criterion for Geomaterials Based on SMP Criterion. Int. J. Geomech. 20 (3), 04019183. doi:10.1061/(asce)gm.1943-5622.0001588

CrossRef Full Text | Google Scholar

Tang, Y., Zhang, H., Xu, J., Okubo, S., and Liu, X. (2021). Loading Rate Dependence of Rock Strength under Triaxial Compression. Front. Earth Sci. 9, 728366. doi:10.3389/feart.2021.728366

CrossRef Full Text | Google Scholar

Wang, J., Wang, T., Song, Z., Zhang, Y., and Zhang, Q. (2021a). Improved Maxwell Model Describing the Whole Creep Process of Salt Rock and its Programming. Int. J. Appl. Mech. 13 (10), 2150113. doi:10.1142/S1758825121501131

CrossRef Full Text | Google Scholar

Wang, J., Wang, X., Zhang, Q., Song, Z., and Zhang, Y. (2021b). Dynamic Prediction Model for Surface Settlement of Horizontal Salt Rock Energy Storage. Energy 235, 121421. doi:10.1016/j.energy.2021.121421

CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., Song, Z., Feng, S., and Zhang, Y. (2022). Nonlinear Creep Model of Salt Rock Used for Displacement Prediction of Salt Cavern Gas Storage. J. Energ. Storage 48, 103951. doi:10.1016/j.est.2021.103951

CrossRef Full Text | Google Scholar

Yessiler, N., Miller, C. J., Inci, G., and Yaldo, K. (2000). Desiccation and Cracking Behavior of Three Compacted Landfill Liner Soils. Eng. Geol. 57 (1-2), 105–121. doi:10.1016/s0013-7952(00)00022-3

CrossRef Full Text | Google Scholar