- 1School of Geosciences, University of Aberdeen, Aberdeen, United Kingdom
- 2WASM: Mineral, Energy and Chemical Engineering, Curtin University, Perth, WA, Australia
- 3Institute of Geosciences, Johannes Gutenberg University, Mainz, Germany
- 4National Research Council of Italy—Institute of Methodologies for Environmental Analysis (CNR—IMAA), Tito Scalo, Italy
- 5Department of Physics “Ettore Pancini”, University of Naples “Federico II”, Napoli, Italy
Imaging of fluid pathways is crucial to characterize processes taking place in hydrothermal systems, a primary cause of volcanic unrest and associated hazards. The joint imaging of seismic absorption and scattering is an efficient instrument to map fluid flow at crustal scale, and specifically in volcanoes; however, this technique has so far been applied to image volcanoes and hydrothermal systems at the kilometre scale. Here, we use data from a meter-scale, active seismic survey inside the shallow structure of the Solfatara crater to obtain the first frequency-dependent near-surface scattering and absorption model of a hydrothermal system. The Solfatara crater is the place used to monitor historic unrest at Campi Flegrei caldera (Italy), a high-risk volcano under continuous surveillance due to its closeness to a densely populated area. Improving the imaging of the shallow part of this system is crucial to broaden the understanding of unrest processes that are progressively characterizing other portions of the eastern caldera. The scattering contrasts highlight the primary structural feature, a fault separating the hydrothermal plume from zones of CO2 saturation nearing fumaroles. While high-absorption anomalies mark zones of high soil temperatures and CO2 fluxes, low-absorption anomalies indicate zones of very shallow upflow and are caused by contrasts between liquid-rich and vapour-rich fluids coming from mud pools and fumaroles, respectively. All maps show a SW-NE trend in anomalies consistent with fluid-migration pathways towards the eastern fumaroles. The results provide structural constraints that clarify mechanisms of fluid migration inside the crater. The techniques offer complementary geophysical images to the interpretation of hydrothermal processes and prove that seismic attenuation measurements are suitable to map fluid pathways in heterogeneous media at a detailed scale.
Introduction
Imaging hydrothermal systems in volcanic areas is crucial to forecasting phreatic eruptions (Mayer et al., 2016), assessing risks of edifice collapse (Rosas-Carbajal et al., 2016) and monitoring the possible evolution toward an unrest stage (Amoroso et al., 2018). Seismic attenuation measurements, like scattering and absorption that are suitable to map structures and feeding systems in volcanic settings (e.g., De Siena et al., 2016), could be applied to image hydrothermal systems. Scattering and absorption are the manifestations of the anelastic attenuation of coherent waves, i.e., the energy lost by seismic waves while propagating through a heterogeneous medium. The presence of fluids mainly controls absorption, triggered by fluid/squirt flow, internal friction, viscosity, and thermal relaxation mechanisms (Barton, 2006), while scattering is caused by the presence of heterogeneities and generally highlights tectonic interactions (De Siena et al., 2016) and lithological contrasts (Napolitano et al., 2020). At the sample scale, ultrasonic attenuation measurements are related to the physical rock properties (Vanorio et al., 2002; Di Martino et al., 2021). At crustal scale, seismic attenuation is a pivotal instrument to identify and track the location of fluid and melt reservoirs and, thus, to understand magmatic and hydrothermal processes in volcanic environments (e.g., De Siena et al., 2017a; De Landro et al., 2019). Frequency-dependent parameters like peak-delay time and the attenuation of coda waves are proven proxies of scattering attenuation and absorption (e.g., at Mount St Helens volcano—De Siena et al., 2016). These parameters have shown notable sensitivity to fluid-filled pathways and reservoirs, especially when using active-survey data (Prudencio et al., 2013; Ibáñez et al., 2020).
Peak-delay time (Pd) is a measurement of the strength of scattering (Takahashi et al., 2007) that has been recognised as a marker of scattering losses (Saito et al., 2002; Calvet and Margerin, 2013) and is sensitive to structural and geological features (e.g., Napolitano et al., 2020). Seismic wave propagation in volcanic areas is primarily affected by scattering that dissipates the energy of the coherent waves into coda waves (Sato et al., 2012). The attenuation of coda waves (Qc−1) measured from the decay of seismic envelope energy with time (Aki and Chouet, 1975) is a combination of intrinsic absorption and scattering losses. When coda waves enter the diffusive regime, coda attenuation directly measures absorption (Shapiro, 2000). The multiple scattering/diffusion approximation best describes seismograms in volcanic media, primarily if active sources produce the scattering in the media (Wegler, 2003; Prudencio et al., 2013).
The hydrothermal system of Campi Flegrei caldera (Southern Italy, Figure 1) is one of the best-studied and most hazardous in the world. Hydrothermal vents have progressively opened in the eastern caldera (Giudicepietro et al., 2021), entering the metropolitan city of Naples (∼1 million inhabitants). Hydrothermal activity is one of the causes of ground deformation and seismicity at the caldera (Vanorio et al., 2005; Troise et al., 2006; Cusano et al., 2008; Petrillo et al., 2019; Ricco et al., 2019) and the primary reason for the onset of recent earthquake swarms across the eastern caldera (Petrosino et al., 2018; Tamburello et al., 2019; Akande et al., 2021). There is debate around the source of fluids likely producing the recent unrest, whose inputs may be caused by either a deep contribution from a shallow magma sill (D’Auria et al., 2015; Chiodini et al., 2017), drying of the deep hydrothermal system (Moretti et al., 2018; Troise et al., 2019) or decarbonisation reaction from the caldera basement (Vanorio and Kanitpanyacharoen, 2015). However, there is a general agreement that in the upper 3 km hydrothermal processes are more likely taking place than magmatic ones, with the changes of permeability due to rainfalls receiving attention as a short-term trigger for seismicity and deformation (Akande et al., 2021; Petrosino and De Siena, 2021). Presently, degassing and seismicity are increasing due to the pressurisation and heating of the hydrothermal system, which triggers energy transfer from the fluids to the host rocks (Chiodini et al., 2021).
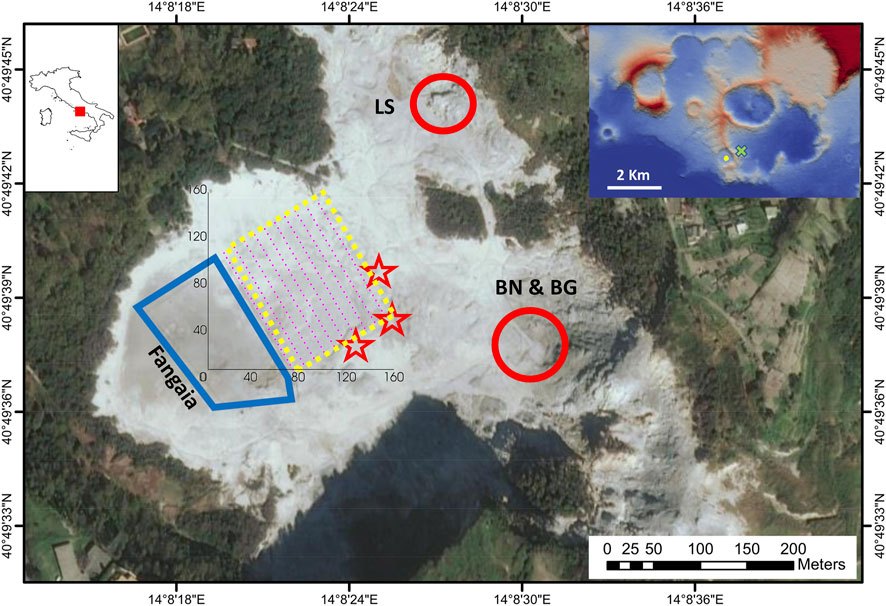
FIGURE 1. Solfatara Crater. The topography of Campi Flegrei is shown in the upper right corner, with the survey location in yellow and the Pisciarelli fumarole indicated by the green cross. The survey area of the active RICEN experiment is in the yellow box, with station locations in magenta. Main Hydrothermal features: Fangaia (mud pool, blue contour) and fumaroles (LS: Le Stufe, BN: Bocca Nuova, and BG: Bocca Grande; in red contours). The stars indicate other fumaroles closest to the survey area (after Serra et al., 2016). The inversion grid (black axes) extends between 0 and 160 m in the SN and WE directions. See figure SM-1 for a close-up on the location of stations and seismic shots.
Campi Flegrei goes through repeated unrest episodes (Kilburn et al., 2017), releasing carbon dioxide gases and high heat flow from the hydrothermal-magmatic system (Chiodini et al., 2007). The caprock has controlled fluid migrations since the 1980s (Vanorio and Kanitpanyacharoen, 2015; De Siena et al., 2017b; Calò and Tramelli, 2018). These fluid migrations to the surface towards the east caldera, produce seismic and geochemical responses, especially at the Solfatara crater (Di Luccio et al., 2015; De Siena et al., 2017b; Petrosino and De Siena, 2021). This crater formed about 4,000 years ago and, historically, is the first place where the volcano shows signs of unrest (Kilburn and McGuire, 2001). The Solfatara crater (Figure 1) is a tuff cone (graben-like structure) with 600 m in diameter, 100 m above sea level. Described as a maar-diatreme structure (Isaia et al., 2015), it was created by the interaction of supercritical fluids rising from depth and groundwater, leading to eruptions and tephra expulsion. High-angle normal faults and fractured rocks surround the Solfatara crater (Figure 1), guiding fluids from depth to fumaroles and mud pools (Bianco et al., 2004). The most active fumaroles across the caldera are located at Solfatara and across the Pisciarelli field, 400 m to the northeast. The two fields are likely connected, as inferred by field data, electromagnetic surveys, and gravity gradiometry (Troiano et al., 2014; Young et al., 2020). The increasing geochemical release and seismic activity between the Solfatara and Pisciarelli hydrothermal areas raise concerns over phreatic and hydrothermal eruptions (Chiodini et al., 2021; Giudicepietro et al., 2021).
Solfatara is a key region where the repeated unrest of the last 50 years has been monitored, becoming one of the best-known, best-monitored, and best-surveyed volcanic craters worldwide. Researchers have analysed the hydrothermal system at Solfatara by applying ambient noise tomography (e.g., Petrosino et al., 2012; Petrosino and De Siena, 2021), electrical resistivity tomography and self-potential (e.g., Byrdina et al., 2014; Gresse et al., 2017; Troiano et al., 2019), joint geochemical and thermal measurements (e.g., Tamburello et al., 2019; Chiodini et al., 2021); geodetic (e.g., D’Auria et al., 2015), gravity (Young et al., 2020), hydrogeological (e.g., Bruno et al., 2007) magnetotellurics (e.g., Troiano et al., 2014; Siniscalchi et al., 2019); volcano-tectonic (Isaia et al., 2015), seismic and tremor surveys (Saccorotti et al., 2007; Letort et al., 2012; Serra et al., 2016; Bruno et al., 2017; De Landro et al., 2017; Amoroso et al., 2018; Gammaldi et al., 2018; Giudicepietro et al., 2021), and seismic attenuation (De Landro et al., 2019). The first kilometre under Solfatara is imaged at very high resolution; however, there is still uncertainty about the structures that guide fluids from the deforming centre of the Solfatara caldera to its eastern side, specifically to the degassing Pisciarelli field (Young et al., 2020). At Solfatara, the absorption of seismic energy could be attributed mainly to wave-induced fluid flow, a mechanism known for producing significant attenuation in saturated porous rocks (Pride et al., 2004; Tisato and Quintal, 2013). Therefore, the spatial variation of scattering and absorption can be a marker of both structure and composition of the volcanic medium.
Most field imaging with absorption and scattering is in 2D, with no available results at the meter scale. This study offers the first example of 3D separation of seismic scattering from seismic absorption performed using the open-access code Multi-Resolution Attenuation Tomography (MuRAT3D). The active data from the Repeat Induced Earthquake and Noise (RICEN, Serra et al., 2016) experiment, performed inside the Solfatara crater in September 2013, offer the ideal dataset to image the shallowest hydrothermal system at Solfatara at the meter-scale. The results provide novel images that complement the available information, improving our insight into the shallow hydrothermal structures and revealing fluid pathway geometries around the main fumaroles.
Dataset
In this study, we used as input seismograms collected during the RICEN experiment (Serra et al., 2016). The network covers 90 × 115 m2 and comprises 240 sensors distributed over 10 lines (Yellow box in Figure 1). The distance between sensors is 5 m, with lines of 24 sensors distanced 10 m apart. The experiment was performed using a vibroseis seismic source from the 100 shot-points triggered; here, we used 20 shots evenly distributed, the best compromise between adequate coverage and avoiding redundancy (Supplementary Figure S1 in Supplemental Material).
The input velocity model is the one obtained by De Landro et al. (2017) using the full dataset of the RICEN array acquisition in a 160 × 160 × 30 m3 volume. The signals are sampled at a 1,000 Hz frequency rate. The seismograms were already pre-processed (cross-correlation with the vibroseis sweep to obtain a source-corrected signal and minimum phase filter to preserve causality; see Serra et al., 2016; De Landro et al., 2017 for details). The P-wave arrival times of each seismogram are the ones estimated by De Landro et al. (2017) and included in the header of the waveform files in SAC format. We selected 2,144 waveforms with source-station distances longer than 50 m. The analysis was carried out on the waveforms that complied with a coda to noise ratio higher than 3 (Supplementary Table S2). The P-wave energy is contained in the first 0.126 s from the P-wave picking and has frequencies above 45 Hz (De Landro et al., 2019). The start of the coda window was selected at 2 s from the origin time, with a length of 2 s (Figure 2).
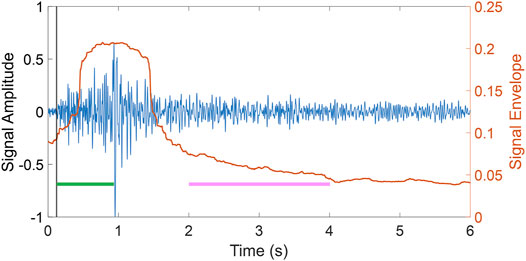
FIGURE 2. Signal example. Seismogram (blue) and its envelope (orange). The vertical black thin line marks the P-wave arrival. The coda window section is represented by the pink line, while the green line shows the peak delay measured on this seismogram.
We performed a preliminary study of the seismic signal and its spectrum over different windows to choose the suitable coda window (Supplementary Figures S2A,B). The choice of the coda windows complies with the assumption of stochastic waves contained in the coda section. We bandpass-filtered the seismograms by applying a Butterworth filter of order four in four frequency bands centred at 12, 18, 24, and 27 Hz. The coda waves contain stochastic information at this range of frequencies and are dominated by highly-scattered surface waves. The envelopes were computed through a smoothed Hilbert transform of the signal using a sliding window of the size of the sampling frequency (Figure 2).
Methods
Peak-Delay Measurements
We measured peak delay (Pd) as the time lag from the onset of the P-wave arrival to the maximum amplitude of the envelope (green line in Figure 2). In heterogeneous media, the peak delay should increase linearly with the travel time (Saito et al., 2002) and be related to the P-wave travel time (tt) in each frequency band f by:
where A(f) and B(f) are the coefficients of the linear fit (Pd_L) (Figure 3). Peak delay is mapped by measuring the variations of the logarithm of the Pd measures Log(Pd) relative to a linear trend:
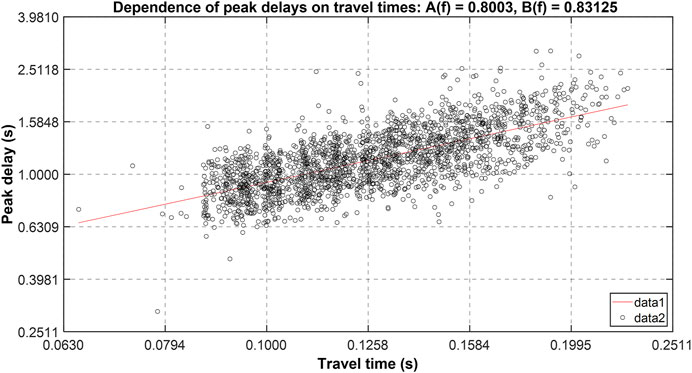
FIGURE 3. Peak-delay dependence on travel time at 18 Hz. Coefficients A and B define the linear fitting of the data with 95% confidence (A = 0.7668 ± 0.8338, B = 0.7941 ± 0.8684). Minimum and Maximum peak delay (0.3 and 5 s respectively) were set to avoid biases on the picking. Given this threshold, the data used for the analysis was reduced to 2081 seismograms at 18 Hz (Supplementary Table S2).
The data values above and below the linear trend represent the variations of the peak delay time, interpreted as high and low scattering (Takahashi et al., 2007). Areas with positive variations indicate that the ray path crosses strong heterogeneous zones (i.e., high scattering attenuation), while negative variations indicate either low scattering or strong absorption (Calvet et al., 2013). Peak delays are then mapped into space assuming sensitivity to the seismic ray, computed in the available velocity model (De Landro et al., 2017).
Coda Attenuation
The energy decay of the coda as a function of frequency and time (Aki and Chuoet, 1975) is given by:
where t is the lapse-time, S(f) is the frequency-dependent source factor, ∝ is a constant factor related to the geometrical spreading and Qc is the coda quality factor (inverse of coda attenuation). The coda decay method estimates Qc−1 values by linearizing this equation and obtaining a least-square fitting of the logarithm of the envelope energy at a given frequency versus lapse time (see Sketsiou et al., 2020 for the uncertainties associated with this linearization). A minimum correlation coefficient threshold of 0.8 was imposed for this fitting to select high-quality data. This threshold led to a further reduction of the data used for the analysis (1895 seismograms at 18 Hz); the cut was higher at lower frequencies (Supplementary Table S2).
The analysis is performed using the inversion approach described by De Siena et al. (2017a). However, this work uses 2D space-weighting functions (Prudencio et al., 2013; Del Pezzo et al., 2016) with the hypothesis that the entire energy of the coda window is contained (thus lost) inside the defined grid. MuRAT3D implements 3D multiple-scattering sensitivity kernels (Del Pezzo et al., 2018) based on Paasschen’s equations (Paasschens, 1997) (Supplementary Figure S3). To determine the input albedo and extinction length parameters, we followed the approach of Wegler (2003), assuming that the medium is fully diffusive (Scala et al., 2019). An iterative inversion (Gazzola et al., 2019) is used to obtain the Qc−1 values at each node. We tested the stability and resolution of the inversion at different grid node spacing through iterative regularizations and checkerboard tests (Supplementary Figures S3A–C). The best parametrization model corresponds to 11 × 11 × 7 nodes (grid spacing 16m × 16m × 5m). The anomalies are well reconstructed laterally; however, at depth, it is only possible to resolve a shallow section (upper ∼10m) for the coda.
Here, we interpret Qc−1 as a marker of seismic absorption, which is a common approach at a regional scale when a diffusive regime describes scattering (Calvet and Margerin, 2013; Prudencio et al., 2013; Sketsiou et al., 2020). Nonetheless, also at our very local scale, we checked that Qc−1 1) does not vary consistently with ray length (Calvet and Margerin, 2013) and 2) that Qc−1 has a linear correlation with frequency (Sketsiou et al., 2020) to validate this condition (Figure 4). The characteristic length after which the multiple scattering regime occurs is the scattering mean free path (Scala et al., 2019). The scattering mean free path must be larger than the wavelengths, and the source-receiver distance larger than the transport mean free path (Wegler, 2003). We measured an average scatter mean free path of ∼7.5 m in the area in a wide frequency range (10–40 Hz), which complies with these assumptions (see Supplementary Material S3). Scala et al. (2019) obtained a similar result, estimating a scattering mean free path of ∼10 m at 25 Hz in the Solfatara crater using surface waves. Their estimation of attenuation values using mean free path values assumes a homogeneous development of the coda in which the averaged elastic properties are independent of the location of source and receivers. In this study, we included sensitivity kernels in the inversion of coda attenuation values, which shows that only the first 10 m are resolved because of the close location of the events and stations at the surface (Del Pezzo et al., 2018).
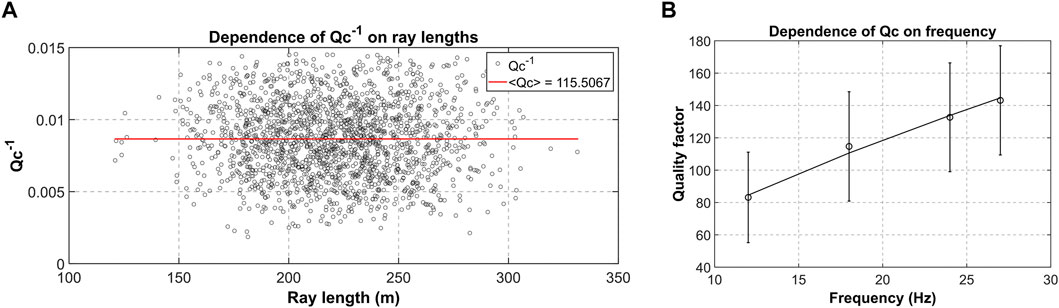
FIGURE 4. (A) Coda Attenuation Qc−1 dependency on ray length at 18 Hz (B) Qc values estimated at different frequencies.
Tomographic Procedures
Scattering attenuation is mapped by the regionalization of the peak delay measurements (see the workflow in Figure 5). The underlying principle is that the envelope of direct wave packets broadens due to multiple forward scattering by inhomogeneities (Markov approximation, Saito et al., 2002). We adopted the tomographic method developed by Takahashi et al. (2007) for mapping scattering as follows: 1) measure Pd for all the waveforms filtered at the study frequency bands; 2) cross-plot the Pd values against travel time (Figure 3); 3) perform a linear regression of the dependence of peak delay increasing with travel time; 4) allocate positive and negative variations of Pd with respect to the linear trend to identify strong and weak scattering, respectively; 5) map Pd in space using regionalization. The regionalization consisted of dividing the mapped volume into blocks, where each block is crossed by several rays, each ray has an allocated Pd value measured from its seismogram, and the average Pd of all these rays is given to the block. Then the variations between blocks are smoothed by taking the average of the mean Pd values between neighbour blocks. 6) Finally, we plot in 3D the spatial variations of peak delay (Figure 6).
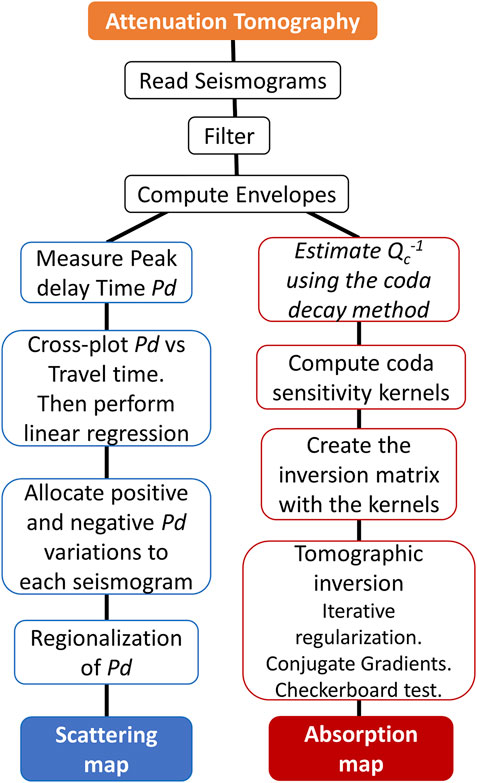
FIGURE 5. Workflow of the attenuation tomography methods applied to map peak delay (left side) and coda attenuation (right side) for imaging seismic scattering and absorption, respectively.
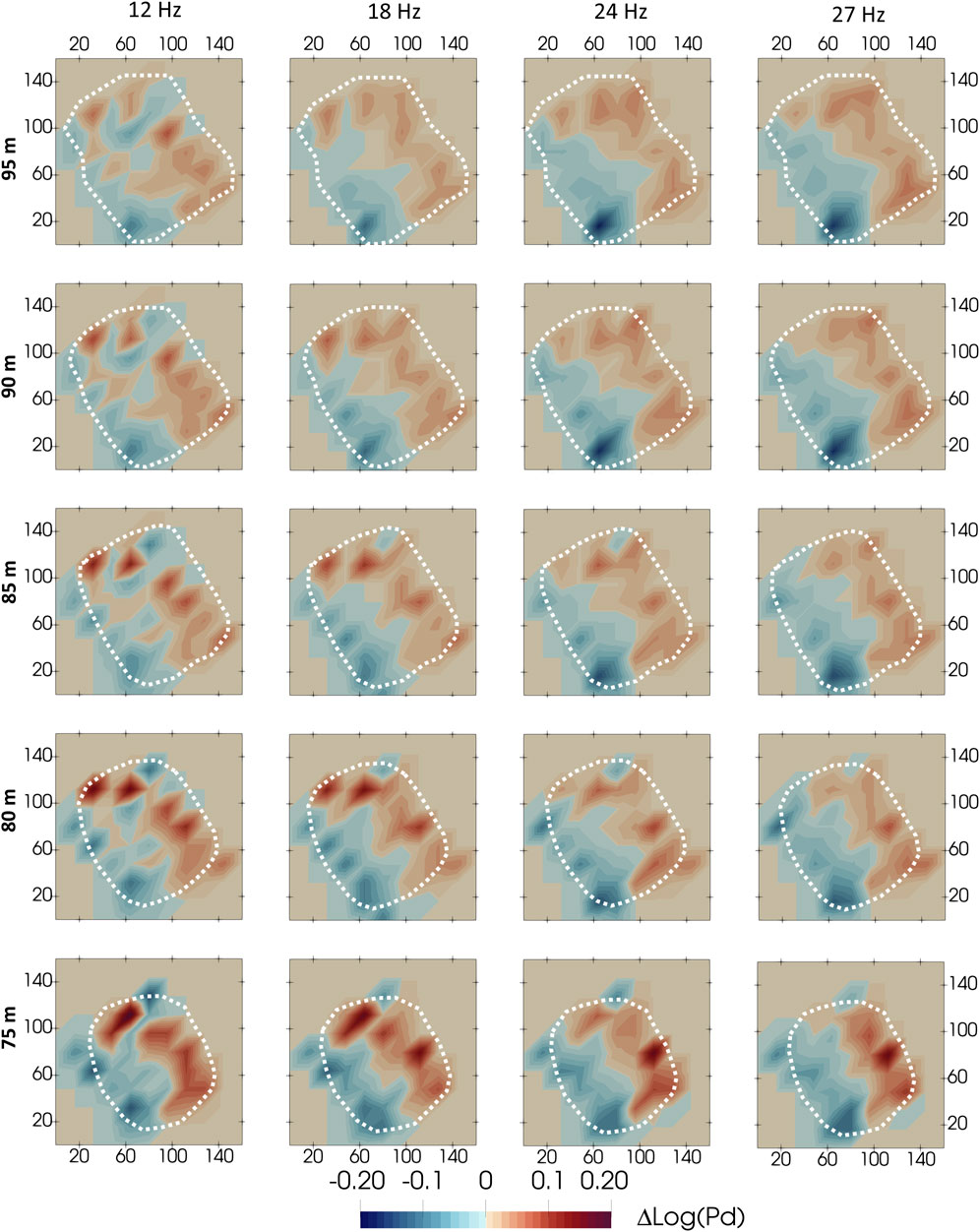
FIGURE 6. Peak delay variations at different frequencies. The white dashed polygon represents the resolution limits of the retrieved models based on the ray crossing.
Absorption is mapped by an inversion procedure of the coda attenuation measurements (see the workflow in Figure 5). The method is as follows: 1) compute the seismic envelopes at each study frequency; 2) compute Qc−1 from the least square fitting of the logarithm of the envelope versus time; 3) compute the sensitivity kernels for the event-station couples (Supplementary Figure S3); 4) create the inversion matrix G using the computed kernels; 5) perform the tomographic inversion. The linear inversion problem solves the general expression d = G(m); where the data vector d contains the Qc values measured for each seismogram, while the operator matrix G, which represents the mathematical relation between the observed and the modelled Qc−1, corresponds to the normalized sensitivity kernels. The model vector m contains the attenuation values Qc−1 for each block of the volume. The modelled Qc−1 are adjusted to satisfy the observed data by using an iterative regularization that leads to choosing adequate damping parameters using conjugate gradients (Aster et al., 2019; Gazzola et al., 2019). The final choice is performed by minimizing a cost function that includes data residuals and L2-norm misfit (Supplementary Figure S3B). 6) We produce a checkboard test to assess the accuracy of the inversion (Supplementary Figure S3A). These tests consist of alternating patterns of positive and negative anomalies that must be reconstructed, so that the areas with good recovery are assumed to be well constrained. 7) Finally, we plot the coda attenuation variations over the study volume (Figure 7).
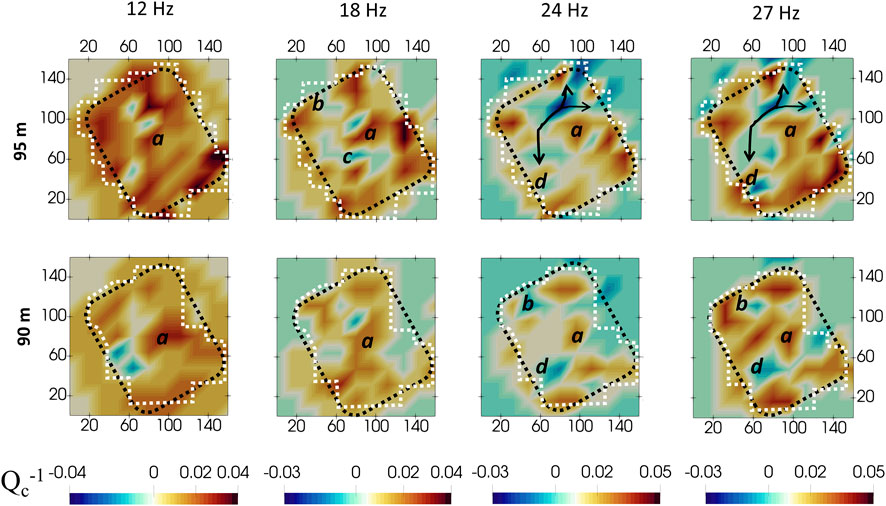
FIGURE 7. Coda attenuation variations at different frequencies. The white and black dashed polygon represents the resolved and survey area (Figure 1), respectively. We scaled the colour legend to the maximum and minimum for each frequency. The labels are described in the main text.
Results
Figures 6, 7 show the peak-delay and coda-attenuation variation maps. The maps occupy the extension of the input velocity model (Figure 1); however, for the peak delay maps, we only interpret the patterns in the area covered by the ray crossing, while for the coda attenuation maps the model resolution is delineated by the results of the checkerboard test. We present the results obtained in different frequency bands, as the size of the heterogeneities could change based on the wavelengths. For the peak-delay maps, we present depth slices every 5 m covering the entire study volume, while for the coda attenuation, we show only the first 10 m. Below this depth, the resolution of the results was inadequate (Supplementary Figure S3A) because:
1) The sources are located at the same elevation level of the stations (96–98 m), and coda waves mainly reverberate near source and receiver;
2) The first abrupt change in the velocity model, to which coda wave attenuation is extremely sensitive (Gabrielli et al., 2020), is around 85 m a.s.l. (De Landro et al., 2017);
3) Having a regular grid spacing smaller than 10 m on the vertical direction, coda waves do not propagate much at depth, as the wavelengths used are 4–8 times larger than the grid cell.
In the coda attenuation maps (Figure 7), the Qc−1 scale represents relative changes of coda attenuation resolved in the area, not an exact quantification of coda attenuation (for an average Qc value in the crater, see Figure 4B). In the inversion, we do not impose the condition of positive Qc−1 values, so we also obtain negative values. A description of the physics creating anomalous negative attenuation in volcanoes at Campi Flegrei caldera is given by De Siena et al. (2013). These negative anomalies are proven markers of deformation at regional and volcanic scales, marking interfaces inside the Tyrrhenian Sea (e.g., Nardoni et al., 2021) and Pollino fault network (Napolitano et al., 2020) and dike intrusions/fluid injections at Campi Flegrei (De Siena et al., 2017a). Such interfaces produce reverberations that contrast the diffusion approximation at specific frequencies, thus lowering coda attenuation. These reverberations can be related to the relative positions of source and interfaces. This has been proven via joint radiative transfer and eikonal equation modelling by Nardoni et al. (2021), who demonstrated that the presence of interfaces, like the Moho, in the medium creates reverberations that lower the inverted Qc−1 depending on the source location. At our scale, these could indicate lateral structural variations that could coincide with fluid-migration pathways.
The absorption models reveal geometries different from those observed in the peak delay map, an indication that coda attenuation and peak delay define different attenuation mechanisms and have different sensitivities. We merged and classified the absorption information from Qc−1 and the scattering information from peak delay in a parameter separation map (Figure 8) to discriminate fluid paths from fracture networks (De Siena et al., 2016; Napolitano et al., 2020). This map is divided into four quadrants: 1) Low Scattering/Low Absorption LS/LA, 2) High Scattering HS, 3) High Absorption HA, 4) High Scattering/High Absorption HS/HA, equivalent to the possible solutions of the attenuation model.
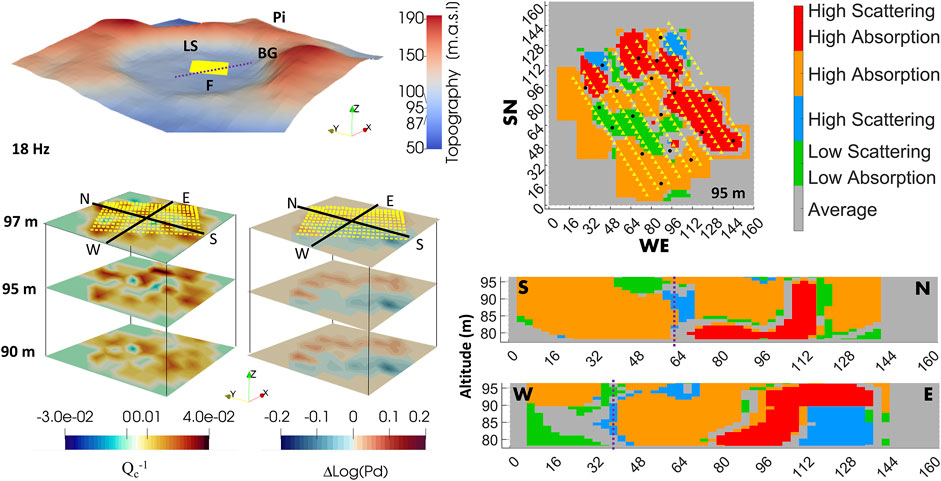
FIGURE 8. Left: The topography image indicates the location of the survey area (yellow rectangle), the main fumaroles, and the interpreted NW-SE fault from our results (dashed purple line). Absorption and scattering sections across the first 10 m are stacked below the topography, showing the trace of two vertical sections (SN and WE). Right: Parameter maps obtained at 18 Hz by separating the mapped values in their parameter space (the location of the stations and sources is indicated by the yellow triangles and the black circles, respectively).
Discussion
Layers of tuff deposits with similar rock properties but different fluid contents characterize the shallow Solfatara crater (table 1 in Petrosino et al., 2012). Thus, we assume that the changes observed in the absorption and scattering maps (Figures 6–8) are not affected by the lithology but are due to the fluid composition, temperature, and the alteration of the host rock caused by hydrothermal fluid and meteoric water infiltration. This rock alteration causes the lack of vegetation in the centre of the crater, where the survey took place (Figure 1). To the West of our study volume, there is the Fangaia mud pool. At depth, this zone is characterized by a conductive hydrothermal plume with meteoric water upwelling to the surface (Bruno et al., 2007), while towards the East there is a higher-resistivity zone attributed to the high CO2 saturation close to the fumaroles (<5 Ωm and 50–100 Ωm respectively, Byrdina et al., 2014).
The peak-delay maps (Figure 6) indicate the primary structural change in the zone. The change marks sharply the NW-SE-striking fault proposed by Bruno et al. (2007) in the middle of the crater, which appears as a resistive body in both electrical and magnetotelluric profiles. This buried fault (Isaia et al., 2015) is sealed by a mineralized clay-rich caprock with gaps at the surface due to the presence of the fault/fracture systems (Siniscalchi et al., 2019). Gammaldi et al. (2018) interpreted a fault of similar direction using 2D P-wave velocity images crossing the middle of the crater. They considered it the preferential gas migration path between the deeper hydrothermal source and the main fumaroles. The rocks are highly fractured in the eastern portion of the map (Isaia et al., 2015); here, the high scattering anomaly coincides with the area of most intense geothermal activity at Solfatara, that is also the one with the highest fumarole concentration. Young et al. (2020) delineated a low-gravity anomaly to the East of the crater (caused by the accumulation of two-phase fluid within highly-fractured and porous host rocks), and a moderate low gravity anomaly to the West that delimitates the Fangaia and is characterized by high CO2 fluxes. The survey area in this study is located between these two gravity anomalies. A preferential, active path for fluids is located along the SE and NE of the crater structure (described by Bruno et al., 2007 after Del Castillo et al., 1968). Apart from the prevalent NW-SE fault, the features in the maps follow a cross-cutting SW-NE trend, as inferred also by the very similar VP anomalies distribution retrieved in the depth range 15–27 m by De Landro et al. (2017). These anomalies are thus directed toward the Pisciarelli field (Isaia et al., 2015) in a way that is consistent with the existence of a migration pathway connecting the two regions (Young et al., 2020; Petrosino and De Siena, 2021).
Our Qc−1 model is satisfactorily resolved up to ∼87 m a.s.l. this is around ∼10 m below the surface (Figure 7). Laterally, the structure looks heterogenous, a product of the intense fluid saturation of the pore space in the area, especially at low frequencies (12 Hz). Letort et al. (2012) suggested that seismic noise sources at Solfatara are related to the presence of CO2 (and steam) bubbles and the propagation of these bubbles into the liquid layer. Saturated rocks strongly attenuate seismic energy when gas bubbles occupy part of the pore space (Tisato et al., 2015). In the highly-fractured and highly-porous rocks (up to 60%—Mayer et al., 2016) in Solfatara, the measured seismic absorption is likely related to these steam-to-liquid phase changes, taking place close to the surface (Chiodini, 2005). At 95 m, the coda attenuation maps show random features (Figure 7), likely due to the coexistence of downward flow of liquid water and upward flow of gas near the surface (Siniscalchi et al., 2019).
In Figure 7, the primary high Qc−1 anomalies (labelled “a”) correlate with the high soil temperature and high CO2 flux in the diffuse degassing area, as identified in the central part of the crater by Gresse et al. (2017). Interpretation of the low Qc−1 anomalies is more intriguing. They appear in the NW (“b”) and coincide with the low-frequency high-velocity body that Serra et al. (2016) derived from phase-velocity maps. Similar anomalies appear in correlation with the location of dike intrusions/fluid injections in the centre of the caldera, using data recorded during its major unrest (1983–1984—De Siena et al., 2017b). At 18 Hz, the narrow low Qc−1 anomaly (“c”) is thus inferred as the most likely location where the fluid flow from the NW-SE fault/fracture system, observed in the peak delay map, reaches the near-surface. Increasing frequencies and at the shallowest depth (95 m. a.s.l), the low-Qc−1 anomalies (“arrows”) go from S towards NE, pointing to the LS fumarole (Figure 1): this anomaly could indicate a connection between the mud pool and the fumaroles. These mud pools, found at both F and LS (Figure 8) are a combination of CO2 and steam bubbling through hot water (Gresse et al., 2017). We interpret the low Qc−1 anomaly “d” that appears at 24 and 27 Hz frequencies as the subsurface transition between the hot water/liquid-rich fluid coming from the Fangaia pool and the CO2/vapour-rich fluid from the plume below BG/BN fumaroles. This encounter point intensifies at depth, and it is most evident 90 m. a.s.l. It appears to be the SW portion of the area where hydrothermal circulation takes place (Bruno et al., 2007).
The area of the survey is characterized by 1) a high-absorption area and 2) a well-localized high-scattering and high-absorption area, while 3) there is no clear high-scattering zone, primarily a marker of sealing formations, like clays (Napolitano et al., 2020). The clay cap expected in this zone (Siniscalchi et al., 2019) is likely below our depth of penetration, as the fault/fracture system breaks it near the surface. These results suggest that the principal attenuation mechanism across the shallow hydrothermal is the fluid flow interaction on the highly porous and fractured rocks. In Figure 8, high absorption (in orange) increases towards the mud pools area, where the degassing is less intense. Here (i.e., the southern region of this model), we imaged strong variations of ΔLog(Pd) and Qc−1, especially at high frequencies. This observation is fully consistent with attenuation images by De Landro et al. (2019): they retrieved the lowest QP values in the investigated volume (i.e., the strongest attenuation) in this area, adjacent to the eastern part of the Fangaia mud-pool, where mineralized liquids saturate the shallow subsoil. The high-scattering/high-absorption zone (in red) appears below the main vents, where the degassing occurs.
In dry volcanic samples, the level of heterogeneity observed in coda waves produced by changes in pore space topology is already quite complex (Di Martino et al., 2021). At Solfatara, the host rocks are highly altered by intense hydrothermal alteration that increases porosity and permeability and reduces elastic wave velocity (Mayer et al., 2016), intensifying the attenuation responses. Once combined with evidence from rock physics, our maps could offer complementary information to retrieve fluid composition and saturation levels (e.g., Amoroso et al., 2017) at scales that bridge field seismology and rock observations.
The Solfatara crater has a unique significance, as it is where unrest episodes at Campi Flegrei have historically been monitored (Kilburn and McGuire, 2001). While vents continuously degas at its centre, the Pisciarelli fumarolic-hydrothermal area increased in 2009 on the outer eastern flank of the crater (Figure 1). Today, this is the most hazardous sector of the caldera, characterized by an active hydrothermal system often producing phreatic and small hydrothermal explosions (Isaia et al., 2021), and where fluids are progressively migrating east producing earthquakes (Petrosino and De Siena, 2021).
While the severity of a larger eruption is usually linked to a magmatic ejection, in this paper the mapped features are only produced by fluid flow interactions. From our study, it is impossible to determine if they are related to a magmatic source degassing at depth. Regardless, the scattering mapping of the hydrothermal system shows how a highly dipping fault is the primary contributor to fluid migration from depth (Figure 6). As previously highlighted by gravity gradiometry (Young et al., 2020), the fluid migrations feeding Pisciarelly are shallow (Figure 8) and start from the primary Solfatara feeder (Siniscalchi et al., 2019). Absorption marks the shallow pathways followed by these fluids, which migrate east towards Pisciarelli within the first few meters of the volcano (Figure 7). These traces likely extend further east, representing the most impending hazard for people leaving near the Solfatara crater.
Conclusion
We present scattering and absorption 3D models and an interpreted separation map of these attenuation parameters for the shallow hydrothermal system at Solfatara crater, inside Campi Flegrei caldera. The model delineates the NW-SE fault that separates fluids flowing through the mud pool (W) and vapor-filled structures near fumaroles (NE and SW). The lateral variations of absorption and scattering provide the first seismic evidence of fluid-migration pathways, previously inferred by field and gravity surveys. These fluids are generated under Fangaia and eventually reach the Pisciarelli fumaroles, outside the crater.
This work is the first application of 3D scattering and absorption imaging to a shallow hydrothermal system, providing models at meter-scale resolutions. The results depend on the complexity of the crater structure and support previous inferences about how these features constrain fluid migrations. On the other hand, within a relatively-homogeneous geological matrix, separating the attenuation mechanisms (i.e., scattering from absorption) demonstrated the high potential to detect fluid upflow and identify different fluid compositions. Our results offer a highly-resolved picture of the pathways taken by hazardous fluids to rise to surface and migrate east, from Solfatara towards the metropolitan city of Naples. This approach can improve modelling of very-shallow hydrothermal systems, especially if combined with different geophysical responses and interpreted using rock-physics observations.
Data Availability Statement
The version of the program MuRAT used to compute the analysis and the results presented here are available for download at https://github.com/PilarDiMartino/MuRAT_Solfatara (https://doi.org/10.5281/zenodo.5831367). The Solfatara catalogue is available on request.
Author Contributions
GD and VS performed preliminary analyses on the dataset, correcting for source functions, analysing data in frequency, and providing the seismic rays in the velocity model. MDM selected and analysed waveform data for the analysis, applied the MuRAT code, created all images and wrote the first draft of the paper. LDS enabled a fast implementation of the MuRAT code on the dataset, tested and commented results, and extended the first draft, including a more comprehensive volcanological discussion. The manuscript went through two successive reviews from all authors, which commented on methods and interpretation.
Funding
JGU provided funding for open-access publication fees, following the agreement with the Frontiers journal. MDM acknowledges the support of the Mainz Institute of Multiscale Modeling, which funded her research visit and training at the Johannes Gutenberg University of Mainz. The contribution of GD and VS was supported by the PRIN-FLUIDS project: “Detection and tracking of crustal fluid by multi-parametric methodologies and technologies” of the Italian PRIN-MIUR programme (grant no. 20174X3P29).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The analysis was performed using the MuRAT code available at https://github.com/LucaDeSiena/MuRAT.git.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.852510/full#supplementary-material
References
Akande, W. G., Gan, Q., Cornwell, D. G., and De Siena, L. (2021). Thermo‐Hydro‐Mechanical Model and Caprock Deformation Explain the Onset of an Ongoing Seismo‐Volcanic Unrest. J. Geophys. Res. Solid Earth 126 (3). doi:10.1029/2020jb020449
Aki, K., and Chouet, B. (1975). Origin of Coda Waves: Source, Attenuation, and Scattering Effects. J. Geophys. Res. 80 (23), 3322–3342. doi:10.1029/jb080i023p03322
Amoroso, O., Festa, G., Bruno, P. P., D'Auria, L., De Landro, G., Di Fiore, V., et al. (2018). Integrated Tomographic Methods for Seismic Imaging and Monitoring of Volcanic Caldera Structures and Geothermal Areas. J. Appl. Geophys. 156, 16–30. doi:10.1016/j.jappgeo.2017.11.012
Amoroso, O., Russo, G., De Landro, G., Zollo, A., Garambois, S., Mazzoli, S., et al. (2017). From Velocity and Attenuation Tomography to Rock Physical Modeling: Inferences on Fluid-Driven Earthquake Processes at the Irpinia Fault System in Southern Italy. Geophys. Res. Lett. 44 (13), 6752–6760. doi:10.1002/2016gl072346
Aster, R. C., Borchers, B., and Thurber, C. H. (2019). “Iterative Methods,” in Parameter Estimation and Inverse Problems. 1st ed (N: ElsevierCRC Press), 151–179. doi:10.1016/B978-0-12-804651-7.00011-0
Barton, N (2006). Rock Quality, Seismic Velocity, Attenuation and Anisotropy. Availbleat: https://doi-org.dbgw.lis.curtin.edu.au/10.1201/9780203964453.
Bianco, F., Del Pezzo, E., Saccorotti, G., and Ventura, G. (2004). The Role of Hydrothermal Fluids in Triggering the July–August 2000 Seismic Swarm at Campi Flegrei, Italy: Evidence from Seismological and Mesostructural Data. J. Volcano. Geotherm. Res. 133 (1–4), 229–246. doi:10.1016/s0377-0273(03)00400-1
Bruno, P. P. G., Maraio, S., and Festa, G. (2017). The Shallow Structure of Solfatara Volcano, Italy, Revealed by Dense, Wide-Aperture Seismic Profiling. Sci. Rep. 7 (1), 17386. doi:10.1038/s41598-017-17589-3
Bruno, P. P. G., Ricciardi, G. P., Petrillo, Z., Di Fiore, V., Troiano, A., and Chiodini, G. (2007). Geophysical and Hydrogeological Experiments from a Shallow Hydrothermal System at Solfatara Volcano, Campi Flegrei, Italy: Response to Caldera Unrest. J. Geophys. Res. 112 (B6), B06201. doi:10.1029/2006jb004383
Byrdina, S., Vandemeulebrouck, J., Cardellini, C., Legaz, A., Camerlynck, C., Chiodini, G., et al. (2014). Relations between Electrical Resistivity, Carbon Dioxide Flux, and Self-Potential in the Shallow Hydrothermal System of Solfatara (Phlegrean Fields, Italy). J. Volcanology Geothermal Res. 283, 172–182. doi:10.1016/j.jvolgeores.2014.07.010
Calò, M., and Tramelli, A. (2018). Anatomy of the Campi Flegrei Caldera Using Enhanced Seismic Tomography Models. Sci. Rep. 8 (1), 16254–16312. doi:10.1038/s41598-018-34456-x
Calvet, M., and Margerin, L. (2013). Lapse-Time Dependence of Coda Q: Anisotropic Multiple-Scattering Models and Application to the Pyrenees. Bull. Seismological Soc. America 103 (3), 1993–2010. doi:10.1785/0120120239
Calvet, M., Sylvander, M., Margerin, L., and Villaseñor, A. (2013). Spatial Variations of Seismic Attenuation and Heterogeneity in the Pyrenees: Coda Q and Peak Delay Time Analysis. Tectonophysics 608, 428–439. doi:10.1016/j.tecto.2013.08.045
Chiodini, G., Caliro, S., Avino, R., Bini, G., Giudicepietro, F., De Cesare, W., et al. (2021). Hydrothermal Pressure-Temperature Control on CO2 Emissions and Seismicity at Campi Flegrei (Italy). J. Volcanology Geothermal Res. 414, 107245. doi:10.1016/j.jvolgeores.2021.107245
Chiodini, G. (2005). Carbon Dioxide Diffuse Degassing and Estimation of Heat Release from Volcanic and Hydrothermal Systems. J. Geophys. Res. 110 (B8), B08204. doi:10.1029/2004jb003542
Chiodini, G., Selva, J., Del Pezzo, E., Marsan, D., De Siena, L., D’Auria, L., et al. (2017). Clues on the Origin of post-2000 Earthquakes at Campi Flegrei Caldera (Italy). Sci. Rep. 7 (1), 4472. doi:10.1038/s41598-017-04845-9
Cusano, P., Petrosino, S., and Saccorotti, G. (2008). Hydrothermal Origin for Sustained Long-Period (LP) Activity at Campi Flegrei Volcanic Complex, Italy. J. Volcanology Geothermal Res. 177 (4), 1035–1044. doi:10.1016/j.jvolgeores.2008.07.019
D’Auria, L., Massa, B., Cristiano, E., Del Gaudio, C., Giudicepietro, F., Ricciardi, G., et al. (2015). Retrieving the Stress Field within the Campi Flegrei Caldera (Southern Italy) through an Integrated Geodetical and Seismological Approach. Pure Appl. Geophys. 172 (11), 3247–3263. doi:10.1007/s00024-014-1004-7
De Landro, G., Serlenga, V., Amoroso, O., Russo, G., Festa, G., and Zollo, A. (2019). High Resolution Attenuation Images from Active Seismic Data: The Case Study of Solfatara Volcano (Southern Italy). Front. Earth Sci. 7, 295. doi:10.3389/feart.2019.00295
De Landro, G., Serlenga, V., Russo, G., Amoroso, O., Festa, G., Bruno, P. P., et al. (2017). 3D Ultra-high Resolution Seismic Imaging of Shallow Solfatara Crater in Campi Flegrei (Italy): New Insights on Deep Hydrothermal Fluid Circulation Processes. Sci. Rep. 7 (1), 3412. doi:10.1038/s41598-017-03604-0
De Siena, L., Amoruso, A., Pezzo, E. D., Wakeford, Z., Castellano, M., and Crescentini, L. (2017a). Space‐weighted Seismic Attenuation Mapping of the Aseismic Source of Campi Flegrei 1983–1984 Unrest. Geoph. Res. Lett. 44, 1740–1748.
De Siena, L., Calvet, M., Watson, K. J., Jonkers, A. R. T., and Thomas, C. (2016). Seismic Scattering and Absorption Mapping of Debris Flows, Feeding Paths, and Tectonic Units at Mount St. Helens Volcano. Earth Planet. Sci. Lett. 442, 21–31. doi:10.1016/j.epsl.2016.02.026
De Siena, L., Chiodini, G., Vilardo, G., Del Pezzo, E., Castellano, M., Colombelli, S., et al. (2017b). Source and Dynamics of a Volcanic Caldera Unrest: Campi Flegrei, 1983-84. Sci. Rep. 7 (1), 8099. doi:10.1038/s41598-017-08192-7
De Siena, L., Del Pezzo, E., Thomas, C., Curtis, A., and Margerin, L. (2013). Seismic Energy Envelopes in Volcanic media: In Need of Boundary Conditions. Geophys. J. Int. 195 (2), 1102–1119. doi:10.1093/gji/ggt273
Del Pezzo, E., De La Torre, A., Bianco, F., Ibanez, J., Gabrielli, S., and De Siena, L. (2018). Numerically Calculated 3D Space-Weighting Functions to Image Crustal Volcanic Structures Using Diffuse Coda Waves. Geosciences 8 (5), 175. doi:10.3390/geosciences8050175
Del Pezzo, E., Ibañez, J., Prudencio, J., Bianco, F., and De Siena, L. (2016). Absorption and Scattering 2-D Volcano Images from Numerically Calculated Space-Weighting Functions. Geophys. J. Int. 206 (2), 742–756. doi:10.1093/gji/ggw171
Di Luccio, F., Pino, N. A., Piscini, A., and Ventura, G. (2015). Significance of the 1982-2014 Campi Flegrei Seismicity: Preexisting Structures, Hydrothermal Processes, and hazard Assessment. Geophys. Res. Lett. 42 (18), 7498–7506. doi:10.1002/2015gl064962
Di Martino, M. D. P., De Siena, L., Healy, D., and Vialle, S. (2021). Petro-mineralogical Controls on Coda Attenuation in Volcanic Rock Samples. Geophys. J. Int. 226 (3), 1858–1872. doi:10.1093/gji/ggab198
Gabrielli, S., De Siena, L., Napolitano, F., and Del Pezzo, E. (2020). Understanding Seismic Path Biases and Magmatic Activity at Mount St Helens Volcano before its 2004 Eruption. Geophys. J. Int. 222 (1), 169–188. doi:10.1093/gji/ggaa154
Gammaldi, S., Amoroso, O., D'Auria, L., and Zollo, A. (2018). High Resolution, multi-2D Seismic Imaging of Solfatara Crater (Campi Flegrei Caldera, Southern Italy) from Active Seismic Data. J. Volcanology Geothermal Res. 357, 177–185. doi:10.1016/j.jvolgeores.2018.03.025
Gazzola, S., Hansen, P. C., and Nagy, J. G. (2019). IR Tools: a MATLAB Package of Iterative Regularization Methods and Large-Scale Test Problems. Numer. Algor 81, 773–811. doi:10.1007/s11075-018-0570-7
Giudicepietro, F., Chiodini, G., Avino, R., Brandi, G., Caliro, S., De Cesare, W., et al. (2021). Tracking Episodes of Seismicity and Gas Transport in Campi Flegrei Caldera through Seismic, Geophysical, and Geochemical Measurements. Seismol. Res. Lett. 92 (2A), 965–975. doi:10.1785/0220200223
Gresse, M., Vandemeulebrouck, J., Byrdina, S., Chiodini, G., Revil, A., Johnson, T. C., et al. (2017). Three-Dimensional Electrical Resistivity Tomography of the Solfatara Crater (Italy): Implication for the Multiphase Flow Structure of the Shallow Hydrothermal System. J. Geophys. Res. Solid Earth 122 (11), 8749–8768. doi:10.1002/2017jb014389
Ibáñez, J. M., Castro-Melgar, I., Cocina, O., Zuccarello, L., Branca, S., Del Pezzo, E., et al. (2020). First 2-D Intrinsic and Scattering Attenuation Images of Mt Etna Volcano and Surrounding Region from Active Seismic Data. Geophys. J. Int. 220 (1), 267–277. doi:10.1093/gji/ggz450
Isaia, R., Di Giuseppe, M. G., Natale, J., Tramparulo, F. D. A., Troiano, A., and Vitale, S. (2021). Volcano-tectonic Setting of the Pisciarelli Fumarole Field, Campi Flegrei Caldera, Southern Italy: Insights into Fluid Circulation Patterns and hazard Scenarios. Tectonics 40, e2020TC006227. doi:10.1029/2020tc006227
Isaia, R., Vitale, S., Di Giuseppe, M. G., Iannuzzi, E., D’Assisi Tramparulo, F., and Troiano, A. (2015). Stratigraphy, Structure, and Volcano-Tectonic Evolution of Solfatara Maar-Diatreme (Campi Flegrei, Italy). Geol. Soc. America Bull. 127 (9–10), 1485–1504. doi:10.1130/b31183.1
Kilburn, C. R., and McGuire, B. (2001). Italian Volcanoes (No. 1). Harpenden, England: Terra Publishing.
Letort, J., Roux, P., Vandemeulebrouck, J., Coutant, O., Cros, E., Wathelet, M., et al. (2012). High-resolution Shallow Seismic Tomography of a Hydrothermal Area: Application to the Solfatara, Pozzuoli. Geophys. J. Int. 189 (3), 1725–1733. doi:10.1111/j.1365-246x.2012.05451.x
Mayer, K., Scheu, B., Montanaro, C., Yilmaz, T. I., Isaia, R., Aßbichler, D., et al. (2016). Hydrothermal Alteration of Surficial Rocks at Solfatara (Campi Flegrei): Petrophysical Properties and Implications for Phreatic Eruption Processes. J. Volcanology Geothermal Res. 320, 128–143. doi:10.1016/j.jvolgeores.2016.04.020
Moretti, R., Troise, C., Sarno, F., and De Natale, G. (2018). Caldera Unrest Driven by CO2-induced Drying of the Deep Hydrothermal System. Sci. Rep. 8 (1), 8309. doi:10.1038/s41598-018-26610-2
Napolitano, F., De Siena, L., Gervasi, A., Guerra, I., Scarpa, R., and La Rocca, M. (2020). Scattering and Absorption Imaging of a Highly Fractured Fluid-Filled Seismogenetic Volume in a Region of Slow Deformation. Geosci. Front. 11 (3), 989–998. doi:10.1016/j.gsf.2019.09.014
Nardoni, C., De Siena, L., Cammarano, F., Magrini, F., and Mattei, E. (2021). Modelling Regional-Scale Attenuation across Italy and the Tyrrhenian Sea. Phys. Earth Planet. Interiors 318, 106764. doi:10.1016/j.pepi.2021.106764
Paasschens, J. C. J. (1997). Solution of the Time-dependent Boltzmann Equation. Phys. Rev. E 56, 1135–1141. doi:10.1103/physreve.56.1135
Petrillo, Z., D'Auria, L., Mangiacapra, A., Chiodini, G., Caliro, S., and Scippacercola, S. (2019). A Perturbative Approach for Modeling Short‐Term Fluid‐Driven Ground Deformation Episodes on Volcanoes: A Case Study in the Campi Flegrei Caldera (Italy). J. Geophys. Res. Solid Earth 124, 1036–1056. doi:10.1029/2018jb015844
Petrosino, S., Cusano, P., and Madonia, P. (2018). Tidal and Hydrological Periodicities of Seismicity Reveal New Risk Scenarios at Campi Flegrei Caldera. Sci. Rep. 8 (1), 13808–13812. doi:10.1038/s41598-018-31760-4
Petrosino, S., Damiano, N., Cusano, P., Di Vito, M. A., de Vita, S., and Del Pezzo, E. (2012). Subsurface Structure of the Solfatara Volcano (Campi Flegrei Caldera, Italy) as Deduced from Joint Seismic-Noise Array, Volcanological and Morphostructural Analysis: Subsurface Structure of Solfatara. Geochem. Geophys. Geosyst. 13 (7). doi:10.1029/2011gc004030
Petrosino, S., and De Siena, L. (2021). Fluid Migrations and Volcanic Earthquakes from Depolarized Ambient Noise. Nat. Commun. 12 (1), 6656. doi:10.1038/s41467-021-26954-w
Pride, S. R., Berryman, J. G., and Harris, J. M. (2004). Seismic Attenuation Due to Wave-Induced Flow. J. Geophys. Res. 109, B01201. doi:10.1029/2003JB002639
Prudencio, J., Del Pezzo, E., Garcia-Yeguas, A., and Ibanez, J. M. (2013). Spatial Distribution of Intrinsic and Scattering Seismic Attenuation in Active Volcanic Islands - I: Model and the Case of Tenerife Island. Geophys. J. Int. 195 (3), 1942–1956. doi:10.1093/gji/ggt361
Ricco, C., Petrosino, S., Aquino, I., Del Gaudio, C., and Falanga, M. (2019). Some Investigations on a Possible Relationship between Ground Deformation and Seismic Activity at Campi Flegrei and Ischia Volcanic Areas (Southern Italy). Geosciences 9 (5), 222. doi:10.3390/geosciences9050222
Rosas-Carbajal, M., Komorowski, J.-C., Nicollin, F., and Gibert, D. (2016). Volcano Electrical Tomography Unveils Edifice Collapse hazard Linked to Hydrothermal System Structure and Dynamics. Sci. Rep. 6 (1), 29899. doi:10.1038/srep29899
Saccorotti, G., Petrosino, S., Bianco, F., Castellano, M., Galluzzo, D., La Rocca, M., et al. (2007). Seismicity Associated with the 2004–2006 Renewed Ground Uplift at Campi Flegrei Caldera, Italy. Phys. Earth Planet. Interiors 165 (1–2), 14–24. doi:10.1016/j.pepi.2007.07.006
Saito, T., Sato, H., and Ohtake, M. (2002). Envelope Broadening of Spherically Outgoing Waves in Three Dimensional Random media Having Power Law Spectra. J. Geophys. Res. 107. doi:10.1029/2001jb000264
Sato, H., Fehler, M. C., and Maeda, T. (2012). Seismic Wave Propagation and Scattering in the Heterogeneous Earth. Second Edition. Springer Berlin Heidelberg. doi:10.1007/978-3-642-23029-5Seismic Wave Propagation and Scattering in the Heterogeneous Earth : Second Edition
Scala, A., Serra, M., Festa, G., and Roux, P. (2019). Insight into the Wave Scattering Properties of the Solfatara Volcano, Campi Flegrei, Italy. Front. Earth Sci. 7, 307. doi:10.3389/feart.2019.00307
Serra, M., Festa, G., Roux, P., Gresse, M., Vandemeulebrouck, J., and Zollo, A. (2016). A Strongly Heterogeneous Hydrothermal Area Imaged by Surface Waves: The Case of Solfatara, Campi Flegrei, Italy. Geophys. J. Int. 205 (3), 1813–1822. doi:10.1093/gji/ggw119
Shapiro, N. M. (2000). The Energy Partitioning and the Diffusive Character of the Seismic Coda. Bull. Seismological Soc. America 90 (3), 655–665. doi:10.1785/0119990021
Siniscalchi, A., Tripaldi, S., Romano, G., Chiodini, G., Improta, L., Petrillo, Z., et al. (2019). Reservoir Structure and Hydraulic Properties of the Campi Flegrei Geothermal System Inferred by Audiomagnetotelluric, Geochemical, and Seismicity Study. J. Geophys. Res. Solid Earth 124 (6), 5336–5356. doi:10.1029/2018jb016514
Sketsiou, P., Napolitano, F., Zenonos, A., and De Siena, L. (2020). New Insights into Seismic Absorption Imaging. Phys. Earth Planet. Interiors 298, 106337. doi:10.1016/j.pepi.2019.106337
Takahashi, T., Sato, H., Nishimura, T., and Obara, K. (2007). Strong Inhomogeneity beneath Quaternary Volcanoes Revealed from the Peak Delay Analysis ofS-Wave Seismograms of Microearthquakes in Northeastern Japan. Geophys. J. Int. 168 (1), 90–99. doi:10.1111/j.1365-246x.2006.03197.x
Tamburello, G., Caliro, S., Chiodini, G., De Martino, P., Avino, R., Minopoli, C., et al. (2019). Escalating CO2 Degassing at the Pisciarelli Fumarolic System, and Implications for the Ongoing Campi Flegrei Unrest. J. Volcanology Geothermal Res. 384, 151–157. doi:10.1016/j.jvolgeores.2019.07.005
Tisato, N., Quintal, B., Chapman, S., Podladchikov, Y., and Burg, J. P. (2015). Bubbles Attenuate Elastic Waves at Seismic Frequencies: First Experimental Evidence. Geophys. Res. Lett. 42 (10), 3880–3887. doi:10.1002/2015gl063538
Tisato, N., and Quintal, B. (2013). Measurements of Seismic Attenuation and Transient Fluid Pressure in Partially Saturated Berea sandstone: Evidence of Fluid Flow on the Mesoscopic Scale. Geophys. J. Int. 195 (1), 342–351. doi:10.1093/gji/ggt259
Troiano, A., Di Giuseppe, M. G., Patella, D., Troise, C., and De Natale, G. (2014). Electromagnetic Outline of the Solfatara-Pisciarelli Hydrothermal System, Campi Flegrei (Southern Italy). J. Volcanology Geothermal Res. 277, 9–21. doi:10.1016/j.jvolgeores.2014.03.005
Troiano, A., Isaia, R., Di Giuseppe, M. G., Tramparulo, F. D. A., and Vitale, S. (2019). Deep Electrical Resistivity Tomography for a 3D Picture of the Most Active Sector of Campi Flegrei Caldera. Sci. Rep. 9, 15124. doi:10.1038/s41598-019-51568-0
Troise, C., De Natale, G., and Kilburn, C. R. J. (2006). Mechanisms of Activity and Unrest at Large Calderas. London: Geological Society.
Troise, C., De Natale, G., Schiavone, R., Somma, R., and Moretti, R. (2019). The Campi Flegrei Caldera Unrest: Discriminating Magma Intrusions from Hydrothermal Effects and Implications for Possible Evolution. Earth-Science Rev. 188, 108–122. doi:10.1016/j.earscirev.2018.11.007
Vanorio, T., and Kanitpanyacharoen, W. (2015). Rock Physics of Fibrous Rocks Akin to Roman concrete Explains Uplifts at Campi Flegrei Caldera. Science 349 (6248), 617–621. doi:10.1126/science.aab1292
Vanorio, T., Prasad, M., Patella, D., and Nur, A. (2002). Ultrasonic Velocity Measurements in Volcanic Rocks: Correlation with Microtexture. Geophys. J. Int. 149 (1), 22–36. doi:10.1046/j.0956-540x.2001.01580.x
Vanorio, T., Virieux, J., Capuano, P., and Russo, G. (2005). Three-dimensional Seismic Tomography fromPwave andSwave Microearthquake Travel Times and Rock Physics Characterization of the Campi Flegrei Caldera. J. Geophys. Res. 110 (B3), B03201. doi:10.1029/2004jb003102
Wegler, U. (2003). Analysis of Multiple Scattering at Vesuvius Volcano, Italy, Using Data of the TomoVes Active Seismic experiment. J. Volcano. Geotherm. Res. 128 (1–3), 45–63. doi:10.1016/s0377-0273(03)00246-4
Keywords: scattering, absorption, hydrothermal system mapping, fluid migration pathways, seismic tomographic imaging
Citation: Di Martino MDP, De Siena L, Serlenga V and De Landro G (2022) Reconstructing Hydrothermal Fluid Pathways and Storage at the Solfatara Crater (Campi Flegrei, Italy) Using Seismic Scattering and Absorption. Front. Earth Sci. 10:852510. doi: 10.3389/feart.2022.852510
Received: 11 January 2022; Accepted: 28 February 2022;
Published: 31 March 2022.
Edited by:
Roberto Sulpizio, University of Bari Aldo Moro, ItalyReviewed by:
Giovanni Macedonio, Istituto Nazionale di Geofisica e Vulcanologia (INGV), ItalySilvia Massaro, Università degli Studi Aldo Moro, Italy
Copyright © 2022 Di Martino, De Siena, Serlenga and De Landro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luca De Siena, ldesiena@uni-mainz.de
 Maria Del Pilar Di Martino
Maria Del Pilar Di Martino