Reflection and Transmission of Inhomogeneous Plane Waves in Thermoelastic Media

We study the reflection and transmission coefficients of plane waves incident at an interface between two isotropic thermoelastic half spaces and compare them with those of the elastic case. The models include the classical-Biot (B) and extended Lord-Shulman (LS) theories, and predict reflected and transmitted fast-compressional (P), thermal (T) and shear (S) waves. The coefficients are formulated in terms of incidence and inhomogeneity angles, medium properties and potential functions. We consider different incident wave types and inhomogeneity angles to analyze the magnitude, phase and energy ratio of the plane waves, and perform a comparison with the isothermal (elastic) theory. The thermoelastic and elastic models predict different energy partitions between the P and S modes, satisfying the conservation of energy. The LS model exhibits higher T-wave thermal attenuation with increasing inhomogeneity angle at high frequencies, accordingly predicting more interference energy. The angle affects the energy partitions, particularly at the critical angle and near grazing incidence for an incident P wave, which satisfies the conservation of energy. Beyond the critical angle, the energy flux perpendicular to the interface of the isothermal model vanishes, while it is significant in the thermoelastic case. The T-wave magnitudes increase when the thermal conductivity (relaxation time) increases.

1 Introduction

The thermoelasticity theory couples the fields of elastic deformation and temperature and has been largely studied in several fields during the past decades, such as mechanics of materials, ultrasonics and to a much lesser extent in exploration geophysics (Zener, 1938; Savage, 1966; Armstrong, 1984; Veres et al., 2013; Wang and Li, 2013; Carcione et al., 2019). It is also of interest in geothermal applications (Buijze et al., 2019) and generally in the analysis of deep reservoirs, where temperature effects are important, mainly in relation to seismic-reflection technology, whose physics is based on the reflection and transmission (R/T) of waves.

Biot (1956) introduced the classical thermoelasticity theory, hereafter B theory, based on the parabolic Fourier heat conduction law, where the P or T waves propagate with unrealistic infinite phase speeds at high frequencies (Deresiewicz, 1957; Rudgers, 1990, Figures 1–3). Lord and Shulman (1967) introduced a relaxation term into the thermoelasticity equations to obtain finite wave velocities (hereafter LS theory), which led to the Maxwell-Cattaneo-Vernotte hyperbolic heat equation (Maxwell, 1867; Vernotte, 1948; Cattaneo, 1958). The involved relaxation time represents the time lag from imposing the temperature disturbance to the establishment of the steady-state regime. The LS theory predicts two compressional waves (P and T) and a shear wave having similar characteristics to the waves of poroelasticity (Biot, 1956), where the existence of the T wave has been verified experimentally (Ackerman et al., 1966; Jackson et al., 1970; McNelly et al., 1970) and numerically (Carcione et al., 2019; Wang Z.-W. et al., 2020). Green and Lindsay (1972) developed a similar thermoelasticity theory by introducing additional relaxation times. Generalized approaches, based on fractional derivatives, have been developed by Kumar et al. (2013) and Hobiny and Abbas (2020).

Research on reflection and transmission phenomena in elastic, anelastic and poroelastic media (e.g., Pilant, 1979) involves numerous approaches (Rokhlin et al., 1986; Denneman et al., 2002; Carcione, 2014; Wang E. et al., 2020). Here, we consider the theory of thermoelasticity, which is more general and provides realistic results. The reflection of thermoelastic waves at the free surface of an elastic half-space, based on the generalized Green-Lindsay theory, has been studied by Sinha and Elsibai (1996) and a similar problem has been attacked by Sharma et al. (2003) and Zenkour et al. (2013). Kumar and Sarthi (2006) solved the R/T problem, but ignoring energy dissipation, and Singh and Chakraborty (2013) assumed an initial stress at a solid-liquid interface, while Sharma (2018) considered a poroelastic/elastic interface. More recently, Sarkar and Mondal (2020) considered a stress-free and thermally insulated surface on the basis of the modified Green-Lindsay theory, but their formulation neglects the presence of inhomogeneous plane waves, violating Snell’s law, which is inappropriate but appears in many papers (e.g., Sinha and Elsibai, 1997; Wei et al., 2016; Sarkar et al., 2020). Wang et al. (2021) studied the scattering coefficients at a free surface in the framework of the thermo-poroelasticity theory.

First, we consider the B and LS theories, based on the Helmholtz potential function decomposition law, and obtain the respective inhomogeneous plane-wave solutions and dispersion relations. Then, using the boundary conditions and Snell’s law, we obtain the R/T coefficients for incident P and S waves at an interface between two thermoelastic media and compare them with the elastic case to illustrate the difference between the two theories and the influence of the inhomogeneity angle. Moreover, we verify the conservation of energy and discuss the variations of the coefficients as a function of the thermal conductivity and relaxation time.

2 Thermoelasticity

2.1 Governing Equations

The equations of thermoelasticity describe the relation between the stress-deformation and the temperature fields. We consider the generalized (LS) theory proposed by Lord and Shulman (1967). Let us define by u_i, i = x, y, z the displacement components and by T the increment of temperature field above the reference absolute temperature T₀ for the state of zero stress and strain. In a linear isotropic medium, combining the stress-strain and strain-displacement relations with the momentum conservation equation (Carcione et al., 2019), we obtain the displacement equation of motion and the law of heat conduction:

$\begin{array}{cc}\hfill & \left(\lambda +\mu \right)u_{j,ji}+\mu u_{i,jj}-\bar{\gamma }{T}_{,i}-\rho {\ddot{u}}_i=0,i,j=x,y,z,\hfill \\ \hfill & \bar{\kappa }{T}_{,jj}-c\left(\dot{T}+\tau \ddot{T}\right)-\bar{\gamma }{T}_0\left({\dot{u}}_{j,j}+\tau {\ddot{u}}_{j,j}\right)-q=0,\hfill \end{array}(1)$

where ρ is the mass density, $\bar{\kappa }$ is the thermal conductivity, c is the specific heat of the unit volume in the absence of deformation, τ is the relaxation time, q is the external heat source, a dot above a variable denotes time differentiation and the Einstein implicit summation is assumed. The thermal modulus is $\bar{\gamma }=(3\lambda +2\mu )\bar{\alpha }$, where λ and μ are the Lamé constants and $\bar{\alpha }$ is the linear thermal expansion coefficient. More details are given in Appendix A. In the B theory, τ = 0, and the heat equation is parabolic (diffusion-like), but it is hyperbolic (wave-like) in the LS theory.

2.2 Plane-Wave Solution

Let us consider that the displacement vector u can be described by a Helmholtz decomposition of the two potential functions:

$\mathbf{u}=\nabla \varphi +\nabla \times \left(\psi \widehat{\mathbf{n}}\right).(2)$

Substituting Eq. 2 into Eq. 1, we obtain

$\begin{array}{cc}\hfill & \left(\lambda +2\mu \right){\nabla }^2\varphi -\bar{\gamma }T=\rho \ddot{\varphi },\hfill \\ \hfill & \bar{\gamma }{T}_0\left({\nabla }^2\dot{\varphi }+\tau {\nabla }^2\ddot{\varphi }\right)=\bar{\kappa }{\nabla }^{2}T-c\left(\dot{T}+\tau \ddot{T}\right),\hfill \\ \hfill & \mu {\nabla }^2\psi -\rho \ddot{\psi }=0,\hfill \end{array}(3)$

where ∇² is the Laplacian operator and the plane-wave versions of the potential and temperature are

$\begin{array}{cc}\hfill & \varphi =A_{\varphi }\exp \left[\mathrm{i}\left(\omega t-\mathbf{k}\cdot \mathbf{x}\right)\right],\hfill \\ \hfill & T=A_T\exp \left[\mathrm{i}\left(\omega t-\mathbf{k}\cdot \mathbf{x}\right)\right],\hfill \end{array}(4)$

where A_ϕ and A_T are the amplitudes, ω is the angular frequency, t is the time variable, k is the complex wavenumber vector for the compressional waves (Chadwick, 1960; Jiao et al., 2019), x is the spatial vector and i² = −1, where

$\begin{array}{cc}\hfill \mathbf{k}& =\kappa \widehat{\mathbf{\kappa }}-\mathrm{i}\alpha \widehat{\mathbf{\alpha }},\hfill \\ \hfill \mathbf{k}\cdot \mathbf{k}& =k^2,\hfill \\ \hfill {\kappa }^2-{\alpha }^2& =\mathrm{R}\mathrm{e}\left(k^2\right),\hfill \\ \hfill 2\kappa \alpha \cos \gamma & =-\mathrm{I}\mathrm{m}\left(k^2\right),\hfill \end{array}(5)$

where Re (⋅) and Im (⋅) denote real and imaginary parts, respectively, γ is the inhomogeneity angle, κ and α are the magnitudes of the real wavenumber and attenuation vectors, respectively, and the directions of these vectors are

$\begin{array}{cc}\hfill & \widehat{\mathbf{\kappa }}=\left(\sin \theta ,\cos \theta \right),\hfill \\ \hfill & \widehat{\mathbf{\alpha }}=\left(\sin \left(\theta -\gamma \right),\cos \left(\theta -\gamma \right)\right),\hfill \end{array}(6)$

where the hat denotes a unit vector, θ is the angle between the real wavenumber vector and a line perpendicular to the interface. Thus, we can set

$\begin{array}{cc}\hfill & \varphi =A_{\varphi }\mathcal{E},T=A_T\mathcal{E},\hfill \\ \hfill & \mathcal{E}=\exp \left[\mathrm{i}\left(\omega t-x\left(\kappa \sin \theta -\mathrm{i}\alpha \sin \left(\theta -\gamma \right)\right)-z\left(\kappa \cos \theta -\mathrm{i}\alpha \cos \left(\theta -\gamma \right)\right)\right)\right].\hfill \end{array}(7)$

When γ is zero, the wave is homogeneous

$\begin{array}{cc}\hfill & \mathbf{k}=\left(\kappa -\mathrm{i}\alpha \right)\widehat{\mathbf{\kappa }}=k\widehat{\mathbf{\kappa }},\hfill \\ \hfill & v_{\mathrm{c}}=\frac{\omega }{k},\hfill \end{array}(8)$

where v_c is the complex velocity.

Substituting the plane waves Eq. 7 into Eqs. 3₁ and 3₂, using (5) we obtain

$\mathbf{H}\cdot \mathbf{A}=\left[\begin{array}{cc}\hfill \bar{\gamma }\hfill & \hfill k^2\left(\lambda +2\mu \right)-\rho {\omega }^2\hfill \\ \hfill \omega c\left(\mathrm{i}-\tau \omega \right)+\bar{\kappa }{k}^2\hfill & \hfill -\bar{\gamma }{T}_0\omega k^2\left(\mathrm{i}-\tau \omega \right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill A_T\hfill \\ \hfill A_{\varphi }\hfill \end{array}\right]=0.(9)$

The condition det(H) = 0 yields the dispersion equation

$k^4{L}_2-\left(L_0+L_1\right){\omega }^2{k}^2+{\omega }^4=0,(10)$

where

$\begin{array}{cc}\hfill {\left(L_0\right)}^{\text{LS}}& =\frac{\mathrm{i}\omega \bar{\kappa }}{c\left(1+\mathrm{i}\tau \omega \right)},{\left(L_0\right)}^{\mathrm{B}}=\frac{\mathrm{i}\omega \bar{\kappa }}{c},\hfill \\ \hfill L_1& =v_0^2+\frac{{\bar{\gamma }}^2}{\rho c}{T}_0,\hfill \\ \hfill L_2& =v_0^2{L}_0,\hfill \\ \hfill v_0^2& =\frac{\lambda +2\mu }{\rho }.\hfill \end{array}(11)$

Eq. 10 has the solutions

$k^2=\frac{{\omega }^2}{2L_2}\left[\left(L_0+L_1\right)\pm \sqrt{{\left(L_0+L_1\right)}^2-4L_2}\right].(12)$

There are two P-wave wavenumbers, a fast P-wave (minus sign) and a T-wave (plus sign). We have (Carcione, 2014, Eq. 3.34)

$\begin{array}{cc}\hfill & {\kappa }^2=\frac{1}{2}\left[\mathrm{R}\mathrm{e}\left(k^2\right)+\sqrt{{\left[\mathrm{R}\mathrm{e}\left(k^2\right)\right]}^2+{\left[\mathrm{I}\mathrm{m}\left(k^2\right)\right]}^2{\sec }^2\gamma }\right],\hfill \\ \hfill & {\alpha }^2=\frac{1}{2}\left[-\mathrm{R}\mathrm{e}\left(k^2\right)+\sqrt{{\left[\mathrm{R}\mathrm{e}\left(k^2\right)\right]}^2+{\left[\mathrm{I}\mathrm{m}\left(k^2\right)\right]}^2{\sec }^2\gamma }\right].\hfill \end{array}(13)$

For an inhomogeneous wave, the phase velocity and attenuation factor are (Carcione, 2014; Carcione et al., 2019)

$v_{\text{ph}}=\frac{\omega }{\kappa },A=\alpha .(14)$

For a homogeneous wave with γ = 0°, these quantities, expressed in terms of the real and imaginary parts of the complex velocity in Eq. 8, are

$v_{\text{ph}}={\left[\mathrm{R}\mathrm{e}\left(\frac{1}{v_{\mathrm{c}}}\right)\right]}^{-1},A=-\omega \mathrm{I}\mathrm{m}\left(\frac{1}{v_{\mathrm{c}}}\right),(15)$

and the attenuation coefficient is

$L=4\pi \frac{A{v}_{\text{ph}}}{\omega },(16)$

(Deresiewicz, 1957).

Similarly, considering an S plane wave

$\psi =A_{\psi }\mathcal{E},(17)$

where A_ψ is the amplitude and replacing Eq. 17 into (3)₃, we have

${\kappa }^2-{\alpha }^2-\mathrm{i}2\kappa \alpha \cos \gamma ={\omega }^2\frac{\rho }{\mu },(18)$

so that Im (k_S) = 0, and the corresponding wavenumber and phase velocity are

$k_{\mathrm{S}}=\omega \sqrt{\frac{\rho }{\mu }}\mathrm{a}\mathrm{n}\mathrm{d}{v}_{\mathrm{S}}=\sqrt{\frac{\mu }{\rho }},(19)$

respectively. The S wave is not affected by the thermal effects in (homogeneous) thermoelastic media.

3 Reflection and Transmission Coefficients

We consider the 2D case in the (x, z) plane, an interface defined by z = 0, the incidence media I (z > 0) and transmission media II (z < 0). The properties of medium II are represented with a prime superscript. The incident wave generates six waves, namely, three reflected and three transmitted, illustrated in Figure 1 where the subscripts 0, 1, 2 and 3 represent the incident, P, T and S waves, respectively.

FIGURE 1

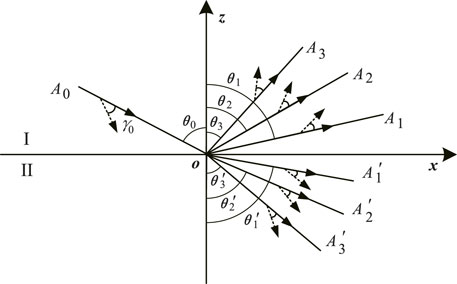
FIGURE 1. Reflection and transmission of plane waves at the interface separating two thermoelastic media. The solid and dashed arrows represent the propagation and attenuation directions, respectively.

3.1 Potential Functions

Consider an incident P wave, where the superscripts i, r and t represent incident, reflected and transmitted, respectively. Then, the potential functions are

$\begin{array}{cc}\hfill & {\varphi }^{\mathrm{I}}={\varphi }^{\mathrm{i}}+{\varphi }^{\mathrm{r}}=A_0{H}_0+\left(A_1{H}_1+A_2{H}_2\right),\hfill \\ \hfill & {\psi }^{\mathrm{I}}={\psi }^{\mathrm{r}}=A_3{H}_3,\hfill \\ \hfill & {\varphi }^{\text{II}}={\varphi }^{\mathrm{t}}=A_1^{\prime }{H}_1^{\prime }+A_2^{\prime }{H}_2^{\prime },\hfill \\ \hfill & {\psi }^{\text{II}}={\psi }^{\mathrm{t}}=A_3^{\prime }{H}_3^{\prime },\hfill \end{array}(20)$

where

$\begin{array}{cc}\hfill & H_0=\exp \left[\mathrm{i}\left(\omega t-\left(p_{0}x-q_{0}z\right)\right)\right],\hfill \\ \hfill & H_m=\exp \left[\mathrm{i}\left(\omega t-\left(p_{m}x+q_{m}z\right)\right)\right],\hfill \\ \hfill & H_m^{\prime }=\exp \left[\mathrm{i}\left(\omega t-\left(p_m^{\prime }x-q_m^{\prime }z\right)\right)\right],\hfill \end{array}(21)$

where A_m and $A_m^{\prime }$ are wave amplitudes, p_m and $p_m^{\prime }$ are horizontal wavenumbers, q_m and $q_m^{\prime }$ are vertical wavenumbers, and the subscripts 0, m = 1, m = 2 and m = 3 correspond to the incident, P, T and S waves, respectively. We consider Snell’s law which establishes the continuity of the horizontal wavenumbers (e.g., Carcione, 2014; Wang E. et al., 2020)

$p_0=p_m=p_m^{\prime },(22)$

where

$p_0=|{\kappa }_0|\sin {\theta }_0-\mathrm{i}|{\alpha }_0|\sin \left({\theta }_0-{\gamma }_0\right),(23)$

where θ₀ is the incidence angle and κ₀ and α₀ are given by Eq. 13 with k = k₀ and γ = γ₀ (see Figure 1). Generalized Snell’s law (Borcherdt, 2009, Eq. (5.2.20)) is

$\frac{\sin \left({\theta }_0\right)}{{\left(v_{\text{ph}}\right)}_0}=\frac{\sin \left({\theta }_m\right)}{{\left(v_{\text{ph}}\right)}_m}=\frac{\sin \left({\theta }_m^{\prime }\right)}{{\left(v_{\text{ph}}^{\prime }\right)}_m},|{\alpha }_0|\sin \left({\theta }_0-{\gamma }_0\right)=|{\alpha }_m|\sin \left({\theta }_m-{\gamma }_m\right)=|{\alpha }_m^{\prime }|\sin \left({\theta }_m^{\prime }-{\gamma }_m^{\prime }\right).(24)$

Because the phase velocities of the incident P (or T) and reflected P (or T) waves are the same, namely θ₀ = θ₁ (or θ₀ = θ₂), we get γ₀ = γ₁ (or γ₀ = γ₂) from Eqs. 12, 13. From Eqs 18 and Sharma (2018), we obtain

${\gamma }_3={\gamma }_3^{\prime }=\frac{\pi }{2}.(25)$

The reflection angle θ₂ (or θ₁) and transmission angles ${\theta }_1^{\prime }$ and ${\theta }_2^{\prime }$ satisfy

$\begin{array}{cc}\hfill & \sin \left({\theta }_m\right)=\sin \left({\theta }_0\right)\frac{{\left(v_{\text{ph}}\right)}_m}{{\left(v_{\text{ph}}\right)}_0},\sin \left({\theta }_m-{\gamma }_m\right)=\sin \left({\theta }_0-{\gamma }_0\right)\frac{|{\alpha }_0|}{|{\alpha }_m|},m=2\left(\mathrm{o}\mathrm{r}1\right),\hfill \\ \hfill & \sin \left({\theta }_n^{\prime }\right)=\sin \left({\theta }_0\right)\frac{{\left(v_{\text{ph}}^{\prime }\right)}_n}{{\left(v_{\text{ph}}\right)}_0},\sin \left({\theta }_n^{\prime }-{\gamma }_n^{\prime }\right)=\sin \left({\theta }_0-{\gamma }_0\right)\frac{|{\alpha }_0|}{|{\alpha }_n^{\prime }|},n=\mathrm{1,2},\hfill \end{array}(26)$

and

$\begin{array}{cc}\hfill & \tan \left({\theta }_m\right)=\frac{\mathrm{R}\mathrm{e}\left(p_0\right)}{\mathrm{R}\mathrm{e}\left(q_m\right)},\tan \left({\theta }_m-{\gamma }_m\right)=\frac{\mathrm{I}\mathrm{m}\left(p_0\right)}{\mathrm{I}\mathrm{m}\left(q_m\right)},m=2\left(\mathrm{o}\mathrm{r}1\right),\hfill \\ \hfill & \tan \left({\theta }_n^{\prime }\right)=\frac{\mathrm{R}\mathrm{e}\left(p_0\right)}{\mathrm{R}\mathrm{e}\left(q_n^{\prime }\right)},\tan \left({\theta }_n^{\prime }-{\gamma }_n^{\prime }\right)=\frac{\mathrm{I}\mathrm{m}\left(p_0\right)}{\mathrm{I}\mathrm{m}\left(q_n^{\prime }\right)},n=\mathrm{1,2},\hfill \end{array}(27)$

where q₀ is the vertical wavenumber of the incident wave, given by

$q_0=D_{\mathrm{R}}+\mathrm{i}{D}_{\mathrm{I}},D=\mathrm{p}\mathrm{v}\sqrt{k_0^2-p_0^2},(28)$

where D_R and D_I denote the real and imaginary parts of the complex quantity D, pv denotes the principal value and the calculations of the vertical wavenumber are similar for the reflected (q_m) and transmitted $(q_m^{\prime })$ waves. The reflected P (or T) wave is homogeneous if and only if the incident P (or T) wave is homogeneous. If θ_c is a critical angle for the transmitted P wave, namely ${\theta }_1^{\prime }=\pi /2$, the corresponding inhomogeneity angle is

$\tan \left({\gamma }_0\right)=\tan {\theta }_{\mathrm{c}}-\frac{2\mathrm{I}\mathrm{m}\left(k_1^{\prime 2}\right)}{\mathrm{I}\mathrm{m}\left(k_0^2\right)\sin \left(2{\theta }_{\mathrm{c}}\right)},(29)$

where k₀ and $k_1^{\prime }$ are the wavenumbers of the incident and transmitted P-waves. If the incident P wave is homogeneous (γ₀ = 0°) and not normally incident, using Eqs. 26, 29 the waves are homogeneous if and only if (Borcherdt, 2009)

$\begin{array}{cc}\hfill & {\sin }^2{\theta }_0\le \frac{\mathrm{I}\mathrm{m}\left(k_2^2\right)}{\mathrm{I}\mathrm{m}\left(k_0^2\right)}=\frac{k_2^2}{k_0^2},\frac{\mathrm{R}\mathrm{e}\left(k_0^2\right)}{\mathrm{I}\mathrm{m}\left(k_0^2\right)}=\frac{\mathrm{R}\mathrm{e}\left(k_2^2\right)}{\mathrm{I}\mathrm{m}\left(k_2^2\right)},\mathrm{r}\mathrm{e}\mathrm{fl}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{T}\mathrm{w}\mathrm{a}\mathrm{v}\mathrm{e},\hfill \\ \hfill & {\sin }^2{\theta }_0\le \frac{\mathrm{I}\mathrm{m}\left(k_m^{\prime 2}\right)}{\mathrm{I}\mathrm{m}\left(k_0^2\right)}=\frac{k_m^{\prime 2}}{k_0^2},\frac{\mathrm{R}\mathrm{e}\left(k_0^2\right)}{\mathrm{I}\mathrm{m}\left(k_0^2\right)}=\frac{\mathrm{R}\mathrm{e}\left(k_m^{\prime 2}\right)}{\mathrm{I}\mathrm{m}\left(k_2^{\prime 2}\right)},m=\mathrm{1,2},\hfill \end{array}(30)$

where the subscripts 1 and 2 correspond to the transmitted P and T waves, respectively. Then, substituting Eq. 20 into (3)₁, we obtain

$\begin{array}{cc}\hfill & T=-\frac{1}{\bar{\gamma }}\sum _{m=0}^2{\zeta }_m{A}_m{H}_m,\hfill \\ \hfill & T^{\prime }=-\frac{1}{{\bar{\gamma }}^{\prime }}\sum _{m=1}^2{\zeta }_m^{\prime }{A}_m^{\prime }{H}_m^{\prime },\hfill \end{array}(31)$

where

$\begin{array}{cc}\hfill & {\zeta }_m=\left(2\mu +\lambda \right)p_m^2-\rho {\omega }^2,\hfill \\ \hfill & {\zeta }_m^{\prime }=\left(2{\mu }^{\prime }+{\lambda }^{\prime }\right){p_m^{\prime }}^2-{\rho }^{\prime }{\omega }^2.\hfill \end{array}(32)$

On the other hand, for the incident S wave,

$\begin{array}{cc}\hfill & {\varphi }^{\mathrm{I}}={\varphi }^{\mathrm{r}}=A_1{H}_1+A_2{H}_2,\hfill \\ \hfill & {\psi }^{\mathrm{I}}={\psi }^{\mathrm{i}}+{\psi }^{\mathrm{r}}=A_0{H}_0+A_3{H}_3,\hfill \\ \hfill & {\varphi }^{\text{II}}={\varphi }^{\mathrm{t}}=A_1^{\prime }{H}_1^{\prime }+A_2^{\prime }{H}_2^{\prime },\hfill \\ \hfill & {\psi }^{\text{II}}={\psi }^{\mathrm{t}}=A_3^{\prime }{H}_3^{\prime },\hfill \end{array}(33)$

and, similarly,

$\begin{array}{cc}\hfill & T=-\frac{1}{\bar{\gamma }}\sum _{m=1}^2{\zeta }_m{A}_m{H}_m,\hfill \\ \hfill & T^{\prime }=-\frac{1}{{\bar{\gamma }}^{\prime }}\sum _{m=1}^2{\zeta }_m^{\prime }{A}_m^{\prime }{H}_m^{\prime },\hfill \end{array}(34)$

the corresponding expressions are given in Eqs. 21, 32. From Eq. 25, the incident S wave is inhomogeneous, and so are the reflected and transmitted S waves. The properties of the reflected and transmitted longitudinal waves generated by an incident S wave are analogous to those of the incident P wave in Eqs. 26, 30.

3.2 Zoeppritz Equations

At z = 0, the boundary conditions to be satisfied are the continuity of temperature, heat flux, and normal and tangential displacements and stresses (Ignaczak and Ostoja-Starzewski, 2010), i.e.,

$T=T^{\prime },\bar{\kappa }\frac{\partial T}{\partial z}={\bar{\kappa }}^{\prime }\frac{\partial T^{\prime }}{\partial z},u_z=u_z^{\prime },u_x=u_x^{\prime },{\sigma }_{zz}={\sigma }_{zz}^{\prime },{\sigma }_{xz}={\sigma }_{xz}^{\prime }.(35)$

Substituting Eqs. 2, 20 into the boundary conditions (35), we get the Knott equations (Knott, 1899) for the incident P wave

$\left[\begin{array}{cccccc}\hfill a_{11}\hfill & \hfill a_{12}\hfill & \hfill a_{13}\hfill & \hfill a_{14}\hfill & \hfill a_{15}\hfill & \hfill a_{16}\hfill \\ \hfill a_{21}\hfill & \hfill a_{22}\hfill & \hfill a_{23}\hfill & \hfill a_{24}\hfill & \hfill a_{25}\hfill & \hfill a_{26}\hfill \\ \hfill a_{31}\hfill & \hfill a_{32}\hfill & \hfill a_{33}\hfill & \hfill a_{34}\hfill & \hfill a_{35}\hfill & \hfill a_{36}\hfill \\ \hfill a_{41}\hfill & \hfill a_{42}\hfill & \hfill a_{43}\hfill & \hfill a_{44}\hfill & \hfill a_{45}\hfill & \hfill a_{46}\hfill \\ \hfill a_{51}\hfill & \hfill a_{52}\hfill & \hfill a_{53}\hfill & \hfill a_{54}\hfill & \hfill a_{55}\hfill & \hfill a_{56}\hfill \\ \hfill a_{61}\hfill & \hfill a_{62}\hfill & \hfill a_{63}\hfill & \hfill a_{64}\hfill & \hfill a_{65}\hfill & \hfill a_{66}\hfill \end{array}\right]\left[\begin{array}{c}\hfill A_1/A_0\hfill \\ \hfill A_2/A_0\hfill \\ \hfill A_3/A_0\hfill \\ \hfill A_1^{\prime }/A_0\hfill \\ \hfill A_2^{\prime }/A_0\hfill \\ \hfill A_3^{\prime }/A_0\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a_{17}\hfill \\ \hfill a_{27}\hfill \\ \hfill a_{37}\hfill \\ \hfill a_{47}\hfill \\ \hfill a_{57}\hfill \\ \hfill a_{67}\hfill \end{array}\right],(36)$

where

$\left\{\begin{array}{cc}\hfill & a_{11}=a_{12}=-a_{14}=-a_{15}=-a_{17}=p_0,a_{13}=-q_3,a_{16}=-q_3^{\prime },\hfill \\ \hfill & a_{21}=a_{27}=q_0,a_{22}=q_2,a_{23}=-a_{26}=p_0,a_{24}=q_1^{\prime },a_{25}=q_2^{\prime },\hfill \\ \hfill & a_{31}=a_{32}=-a_{37}=\rho {\omega }^2-2\mu p_0^2,a_{33}=2\mu p_3{q}_3,\hfill \\ \hfill & a_{34}=-\left({\rho }^{\prime }{\omega }^2-2{\mu }^{\prime }{p_1^{\prime }}^2\right),a_{35}=-\left({\rho }^{\prime }{\omega }^2-2{\mu }^{\prime }{p_2^{\prime }}^2\right),a_{36}=2{\mu }^{\prime }{p}_3^{\prime }{q}_3^{\prime },\hfill \\ \hfill & a_{41}=a_{47}=2p_0{q}_0,a_{42}=2p_2{q}_2,a_{43}=-\left(q_3^2-p_3^2\right),a_{44}=2\frac{{\mu }^{\prime }}{\mu }{p}_1^{\prime }{q}_1^{\prime },\hfill \\ \hfill & a_{45}=2\frac{{\mu }^{\prime }}{\mu }{p}_2^{\prime }{q}_2^{\prime },a_{46}=\frac{{\mu }^{\prime }}{\mu }\left({q_3^{\prime }}^2-{p_3^{\prime }}^2\right),\hfill \\ \hfill & a_{51}=a_{57}=q_0\left[\left(\lambda +2\mu \right)\left(p_0^2+q_0^2\right)-\rho {\omega }^2\right],a_{52}=q_2\left[\left(\lambda +2\mu \right)\left(p_2^2+q_2^2\right)-\rho {\omega }^2\right],\hfill \\ \hfill & a_{53}=a_{56}=0,a_{54}=\frac{{\bar{\kappa }}^{\prime }\bar{\gamma }}{\bar{\kappa }{\bar{\gamma }}^{\prime }}{q}_1^{\prime }\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_1^{\prime }}^2+{q_1^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],\hfill \\ \hfill & a_{55}=\frac{{\bar{\kappa }}^{\prime }\bar{\gamma }}{\bar{\kappa }{\bar{\gamma }}^{\prime }}{q}_2^{\prime }\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_2^{\prime }}^2+{q_2^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],\hfill \\ \hfill & a_{61}=-a_{67}=\left(\lambda +2\mu \right)\left(p_0^2+q_0^2\right)-\rho {\omega }^2,a_{62}=\left(\lambda +2\mu \right)\left(p_2^2+q_2^2\right)-\rho {\omega }^2,a_{63}=a_{66}=0,\hfill \\ \hfill & a_{64}=-\frac{\bar{\gamma }}{{\bar{\gamma }}^{\prime }}\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_1^{\prime }}^2+{q_1^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],a_{65}=-\frac{\bar{\gamma }}{{\bar{\gamma }}^{\prime }}\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_2^{\prime }}^2+{q_2^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right].\hfill \end{array}\right.(37)$

Similarly, we obtain the equations for the incident S wave, where A₀ is its amplitude in Eq. 36, and

$\left\{\begin{array}{cc}\hfill & a_{11}=a_{12}=-a_{14}=-a_{15}=p_0,a_{13}=a_{17}=-q_0,a_{16}=-q_3^{\prime },\hfill \\ \hfill & a_{21}=q_1,a_{22}=q_2,a_{23}=-a_{26}=-a_{27}=p_0,a_{24}=q_1^{\prime },a_{25}=q_2^{\prime },\hfill \\ \hfill & a_{31}=a_{32}=\rho {\omega }^2-2\mu p_0^2,a_{33}=a_{37}=2\mu p_0{q}_0,a_{34}=a_{35}=-\left({\rho }^{\prime }{\omega }^2-2{\mu }^{\prime }{p}_0^2\right),\hfill \\ \hfill & a_{36}=2{\mu }^{\prime }{p}_3^{\prime }{q}_3^{\prime },\hfill \\ \hfill & a_{41}=2p_1{q}_1,a_{42}=2p_2{q}_2,a_{43}=-a_{47}=p_0^2-q_0^2,\hfill \\ \hfill & a_{44}=2\frac{{\mu }^{\prime }}{\mu }{p}_1^{\prime }{q}_1^{\prime },a_{45}=2\frac{{\mu }^{\prime }}{\mu }{p}_2^{\prime }{q}_2^{\prime },a_{46}=-\frac{{\mu }^{\prime }}{\mu }\left({p_3^{\prime }}^2-{q_3^{\prime }}^2\right),\hfill \\ \hfill & a_{51}=q_1\left[\left(\lambda +2\mu \right)\left(p_1^2+q_1^2\right)-\rho {\omega }^2\right],a_{52}=q_2\left[\left(\lambda +2\mu \right)\left(p_2^2+q_2^2\right)-\rho {\omega }^2\right],\hfill \\ \hfill & a_{53}=a_{56}=a_{57}=0,a_{54}=\frac{{\bar{\kappa }}^{\prime }\bar{\gamma }}{\bar{\kappa }{\bar{\gamma }}^{\prime }}{q}_1^{\prime }\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_1^{\prime }}^2+{q_1^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],\hfill \\ \hfill & a_{55}=\frac{{\bar{\kappa }}^{\prime }\bar{\gamma }}{\bar{\kappa }{\bar{\gamma }}^{\prime }}{q}_2^{\prime }\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_2^{\prime }}^2+{q_2^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],\hfill \\ \hfill & a_{61}=\left(\lambda +2\mu \right)\left(p_1^2+q_1^2\right)-\rho {\omega }^2,a_{62}=\left(\lambda +2\mu \right)\left(p_2^2+q_2^2\right)-\rho {\omega }^2,\hfill \\ \hfill & a_{63}=a_{66}=a_{67}=0,a_{64}=-\frac{\bar{\gamma }}{{\bar{\gamma }}^{\prime }}\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_1^{\prime }}^2+{q_1^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right],\hfill \\ \hfill & a_{65}=-\frac{\bar{\gamma }}{{\bar{\gamma }}^{\prime }}\left[\left({\lambda }^{\prime }+2{\mu }^{\prime }\right)\left({p_2^{\prime }}^2+{q_2^{\prime }}^2\right)-{\rho }^{\prime }{\omega }^2\right].\hfill \end{array}\right.(38)$

Using the relations between displacement amplitudes and their ratios, we obtain

$R_m=\frac{A_m}{A_0}\frac{k_m}{k_0}=\left|R_m\right|\exp \left(\mathrm{i}{\vartheta }_m\right),T_m=\frac{A_m^{\prime }}{A_0}\frac{k_m^{\prime }}{k_0}=\left|T_m\right|\exp \left(\mathrm{i}{\vartheta }_m^{\prime }\right),(39)$

where k₀, k_m and $k_m^{\prime }$ (m = 1, 2, 3) represent the complex wavenumbers of incident, reflected and transmitted waves respectively. $\left|R_m\right|$ and $\left|T_m\right|$ define the reflection and transmission amplitudes, while ϑ_m and ${\vartheta }_m^{\prime }$ are the relative phase angles.

4 Energy-Flow Balance

Let us consider the balance of energy flux between the incident wave and the reflected and transmitted waves at a surface element of unit area where the energy flux is the scalar product of the surface traction and particle velocity. The time-averaged energy flux is (Carcione, 2014, Eq. 3.106)

$⟨F_i⟩=\frac{1}{2}\mathrm{R}\mathrm{e}\left({\sigma }_{ij}{\dot{u}}_j^{*}\right),i,j=x,z,(40)$

where $⟨\cdot ⟩$ denotes a temporal average over a period, the star is the complex conjugate, and each component is the sum of the components of the respective waves. The energy flux perpendicular to the interface is continuous across the interface, because of the continuity of stresses and displacements. Following Sharma (2018) and Wang E. et al. (2020), we consider the energy partition in the z-direction (perpendicular to the interface plane)

$⟨F_z⟩=\frac{1}{2}\mathrm{R}\mathrm{e}\left({\sigma }_{zz}{\dot{u}}_z^{*}+{\sigma }_{zx}{\dot{u}}_x^{*}\right).(41)$

In the following expressions, we have omitted the subscripts z for simplicity. Denoting by $⟨{\mathbf{F}}^{\mathrm{i}}⟩$ the energy flux of the incidence medium, we obtain

$⟨{\mathbf{F}}^{\mathrm{i}}⟩=⟨F_{ab}^{\mathrm{i}}⟩=\frac{1}{2}\mathrm{R}\mathrm{e}\left({\mathbf{P}}_{4\times 2}^{\mathrm{i}}\cdot {\mathbf{Q}}^{\mathrm{i}}{*}_{2\times 4}\right),a,b=\mathrm{0,1,2,3},(42)$

where

${\mathbf{P}}_{4\times 2}^{\mathrm{i}}=\left[\begin{array}{cc}\hfill {\sigma }_{zz}^{\left(0\right)}\hfill & \hfill {\sigma }_{xz}^{\left(0\right)}\hfill \\ \hfill {\sigma }_{zz}^{\left(1\right)}\hfill & \hfill {\sigma }_{xz}^{\left(1\right)}\hfill \\ \hfill {\sigma }_{zz}^{\left(2\right)}\hfill & \hfill {\sigma }_{xz}^{\left(2\right)}\hfill \\ \hfill {\sigma }_{zz}^{\left(3\right)}\hfill & \hfill {\sigma }_{xz}^{\left(3\right)}\hfill \end{array}\right],{\mathbf{Q}}_{2\times 4}^{\mathrm{i}}=\left[\begin{array}{cccc}\hfill {\dot{u}}_z^{\left(0\right)}\hfill & \hfill {\dot{u}}_z^{\left(1\right)}\hfill & \hfill {\dot{u}}_z^{\left(2\right)}\hfill & \hfill {\dot{u}}_z^{\left(3\right)}\hfill \\ \hfill {\dot{u}}_x^{\left(0\right)}\hfill & \hfill {\dot{u}}_x^{\left(1\right)}\hfill & \hfill {\dot{u}}_x^{\left(2\right)}\hfill & \hfill {\dot{u}}_x^{\left(3\right)}\hfill \end{array}\right],(43)$

where the diagonal element a = b = 0 of this matrix corresponds to the energy flux of the incident wave, and a = b = 1, 2, 3 to the reflected P, T, and S waves, whereas the off-diagonal elements are the interference fluxes between the incident and reflected waves.

In the transmission medium, the energy flux can be express as

$⟨{\mathbf{F}}^{\mathrm{t}}⟩=⟨F_{ab}^{\mathrm{t}}⟩=\frac{1}{2}\mathrm{R}\mathrm{e}\left({\mathbf{P}}_{3\times 2}^{\mathrm{t}}\cdot {\mathbf{Q}}^{\mathrm{t}}{*}_{2\times 3}\right),a,b=\mathrm{1,2,3},(44)$

where

${\mathbf{P}}_{3\times 2}^{\mathrm{t}}=\left[\begin{array}{cc}\hfill {\sigma }_{zz}^{\prime \left(1\right)}\hfill & \hfill {\sigma }_{xz}^{\prime \left(1\right)}\hfill \\ \hfill {\sigma }_{zz}^{\prime \left(2\right)}\hfill & \hfill {\sigma }_{xz}^{\prime \left(2\right)}\hfill \\ \hfill {\sigma }_{zz}^{\prime \left(3\right)}\hfill & \hfill {\sigma }_{xz}^{\prime \left(3\right)}\hfill \end{array}\right],{\mathbf{Q}}_{2\times 3}^{\mathrm{t}}=\left[\begin{array}{ccc}\hfill {\dot{u}}_z^{\prime \left(1\right)}\hfill & \hfill {\dot{u}}_z^{\prime \left(2\right)}\hfill & \hfill {\dot{u}}_z^{\prime \left(3\right)}\hfill \\ \hfill {\dot{u}}_x^{\prime \left(1\right)}\hfill & \hfill {\dot{u}}_x^{\prime \left(2\right)}\hfill & \hfill {\dot{u}}_x^{\prime \left(3\right)}\hfill \end{array}\right].(45)$

The diagonal elements are the energy fluxes of the transmitted P, T, and S waves. By scaling the energy flux with that of the incident wave $F_{00}^{\mathrm{i}}$, the relative energy ratios are

$E_{ab}^{\mathrm{i}}=\frac{⟨F_{ab}^{\mathrm{i}}⟩}{⟨F_{00}^{\mathrm{i}}⟩},\left(a,b=\mathrm{0,1,2,3}\right),E_{ab}^{\mathrm{t}}=\frac{⟨F_{ab}^{\mathrm{t}}⟩}{⟨F_{00}^{\mathrm{i}}⟩},\left(a,b=\mathrm{1,2,3}\right).(46)$

According to Eqs. 46 and 43 can be rewritten as

$\begin{array}{ll}\hfill {\mathbf{P}}_{4\times 2}^{\mathrm{i}}& =\left[\begin{array}{cc}\hfill 2\mu p_0^2-\rho {\omega }^2\hfill & \hfill 2\mu p_0{q}_0\hfill \\ \hfill \frac{A_1}{A_0}\left(2\mu p_1^2-\rho {\omega }^2\right)\hfill & \hfill -\frac{A_1}{A_0}2\mu p_1{q}_1\hfill \\ \hfill \frac{A_2}{A_0}\left(2\mu p_2^2-\rho {\omega }^2\right)\hfill & \hfill -\frac{A_2}{A_0}2\mu p_2{q}_2\hfill \\ \hfill -\frac{A_3}{A_0}2\mu p_3{q}_3\hfill & \hfill \frac{A_3}{A_0}\mu \left(q_3^2-p_3^2\right)\hfill \end{array}\right],\hfill \\ \hfill & {\mathbf{Q}}_{2\times 4}^{\mathrm{i}}=\omega \left[\begin{array}{cccc}\hfill -q_0\hfill & \hfill \frac{A_1}{A_0}{q}_1\hfill & \hfill \frac{A_2}{A_0}{q}_2\hfill & \hfill \frac{A_3}{A_0}{p}_3\hfill \\ \hfill p_0\hfill & \hfill \frac{A_1}{A_0}{p}_1\hfill & \hfill \frac{A_2}{A_0}{p}_2\hfill & \hfill -\frac{A_3}{A_0}{q}_3\hfill \end{array}\right].\hfill \end{array}(47)$

Eq. 45 is

$\begin{array}{ll}\hfill {\mathbf{P}}_{3\times 2}^{\mathrm{t}}& =\left[\begin{array}{cc}\hfill \frac{A_1^{\prime }}{A_0}\left(2{\mu }^{\prime }{p_1^{\prime }}^2-{\rho }^{\prime }{\omega }^2\right)\hfill & \hfill \frac{A_1^{\prime }}{A_0}2{\mu }^{\prime }{p}_1^{\prime }{q}_1^{\prime }\hfill \\ \hfill \frac{A_2^{\prime }}{A_0}\left(2{\mu }^{\prime }{p_2^{\prime }}^2-{\rho }^{\prime }{\omega }^2\right)\hfill & \hfill \frac{A_2^{\prime }}{A_0}2{\mu }^{\prime }{p}_2^{\prime }{q}_2^{\prime }\hfill \\ \hfill \frac{A_3^{\prime }}{A_0}2{\mu }^{\prime }{p}_3^{\prime }{q}_3^{\prime }\hfill & \hfill \frac{A_3^{\prime }}{A_0}\mu \left({q_3^{\prime }}^2-{p_3^{\prime }}^2\right)\hfill \end{array}\right],\hfill \\ \hfill & {\mathbf{Q}}_{2\times 3}^{\mathrm{t}}=\omega \left[\begin{array}{ccc}\hfill -\frac{A_1^{\prime }}{A_0}{q}_1^{\prime }\hfill & \hfill -\frac{A_2^{\prime }}{A_0}{q}_2^{\prime }\hfill & \hfill \frac{A_3^{\prime }}{A_0}{p}_3^{\prime }\hfill \\ \hfill \frac{A_1^{\prime }}{A_0}{p}_1^{\prime }\hfill & \hfill \frac{A_2^{\prime }}{A_0}{p}_2^{\prime }\hfill & \hfill \frac{A_3^{\prime }}{A_0}{q}_3^{\prime }\hfill \end{array}\right].\hfill \end{array}(48)$

The energy-balance equation in the z-direction at the interface is (Carcione, 2014, Eq. 6.116; Wang E. et al., 2020)

$E_{\text{sum}}=\left(\sum _{a=0}^3\sum _{b=0}^3{E}_{ab}^{\mathrm{i}}-E_{00}^{\mathrm{i}}\right)-\sum _{a=1}^3\sum _{b=1}^3{E}_{ab}^{\mathrm{t}}=-1,(49)$

where the sum of the vertical energy ratios result from the interaction between the incident wave and the three reflected waves, as well as interactions among the three reflected waves, is

$E_{\text{ir}}^{\mathrm{r}}=\sum _{b=1}^3\left[E_{b0}^{\mathrm{r}}+E_{0b}^{\mathrm{r}}+\left(\sum _{a=1}^3{E}_{ab}^{\mathrm{r}}-E_{bb}^{\mathrm{r}}\right)\right].(50)$

Similarly, the corresponding vertical interference energy ratio for the transmitted waves is

$E_{\text{ir}}^{\mathrm{t}}=\sum _{b=1}^3\left(\sum _{a=1}^3{E}_{ab}^{\mathrm{t}}-E_{bb}^{\mathrm{t}}\right).(51)$

Let us denote $E_{\text{ir}}=E_{\text{ir}}^{\mathrm{i}}-E_{\text{ir}}^{\mathrm{t}}$. The energy-flow balance verifies the reflection and transmission coefficients.

5 Examples

The effects of thermoelasticity and the inhomogeneity angle are illustrated by considering the magnitudes, phase angles and energy of the reflection and transmission coefficients. We assume the following reference properties of the incidence and transmission media:Incidence medium: ρ = 2054 kg/m³, c = 960 kg/(m s² K), $\bar{\kappa }$ = 10.5 m kg/(s³ K), $\bar{\alpha }$ = 0.33 × 10^–5 K⁻¹, T₀ = 300 K, v₀ = 2256.5 m/s, v_S = 1302 m/s.Transmission medium: ρ′ = 2600 kg/m³, c′ = 960 kg/(m s² K), ${\bar{\kappa }}^{\prime }$ = 10.5 m kg/(s³ K), ${\bar{\alpha }}^{\prime }$ = 0.33 × 10^–5 K⁻¹, $T_0^{\prime }$ = 300 K, $v_0^{\prime }$ = 3636.9 m/s, $v_{\mathrm{S}}^{\prime }$ = 2100 m/s.

v₀ and v_S are the elastic longitudinal and transverse wave velocities, consistent with Eqs 11₄ and 19. The relaxation time is

$\tau =\frac{\bar{\kappa }}{c{v}_0^2},(52)$

(Rudgers, 1990), equal to 2.15 and 0.83 ns for the incidence and transmission media, respectively. The corresponding velocities and densities used here are those of Pilant (1979), whose scattering coefficients in the isothermal case are represented in his Figures 12-3 and 12-4, while the thermoelasticity properties are taken from Carcione et al. (2019).

Figures 2, 3 show the phase velocities and attenuation coefficients of the P and T waves in the incidence and transmission media, as a function of frequency, respectively. The solid, dashed and dotted solid lines correspond to inhomogeneity angles of 0°, 40° and 80°, and the superscripts LS and B represent the Lord-Shulman and classical-Biot theories, respectively. We can see that the low-frequency behavior is almost the same, the T wave is strongly dissipative at low frequencies (Figures 2D, 3D), and that the P wave has a relaxation peak (Figures 2B, 3B) caused by the thermal effects at a relaxation frequency of approximately

$f_r=\frac{1}{2\pi \tau }.(53)$

The LS model predicts a finite high-frequency limit velocity and a lower velocity dispersion of the T wave, which is wave-like at high frequencies. Both the P and T waves have abnormal velocity behaviors at and beyond the inflexion point in the B case (velocity decreases) and T waves have infinite speed at high frequencies (Figures 2C, 3C). The thermal relaxation hardly affects the wave propagation at relatively low frequencies. It can be seen that inflexion points in the P-wave velocity occur at a frequency of approximately 100 MHz.

FIGURE 2

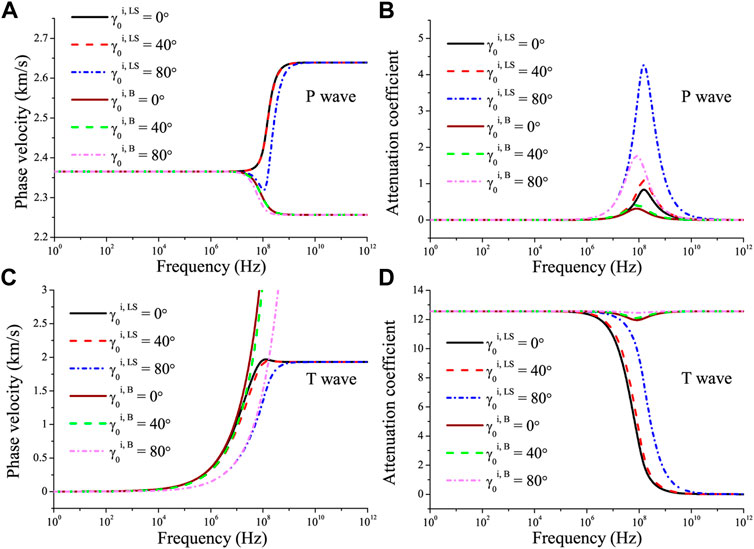
FIGURE 2. Phase velocity and attenuation coefficients of the P wave (A,B) and T wave (C,D) as a function of frequency in the incidence medium with different γ₀. The superscripts LS and B represent the Lord-Shulman and classical-Biot theories, respectively.

FIGURE 3

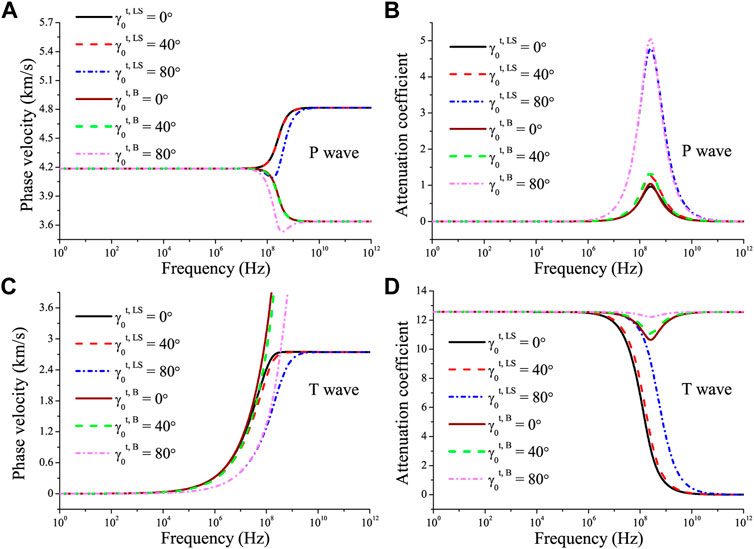
FIGURE 3. Phase velocity and attenuation coefficients of the P wave (A,B) and T wave (C,D) as a function of frequency in the transmission medium with different γ₀. The superscripts LS and B represent the Lord-Shulman and classical-Biot theories, respectively.

5.1 P-Wave Incidence

Figures 4, 5 show the absolute values of the reflection and transmission coefficients and the corresponding phase angles as a function of the incidence angle in the case of an incident P wave with a frequency of 100 MHz. The elastic case is also indicated. If the two media are elastic, there is a critical angle at approximately 40°. If the incident wave travels along the z-direction (vertical), an incident P wave will generate reflected and transmitted longitudinal waves without conversion to the shear modes. The incident P wave is homogeneous when γ₀ = 0°, and the behavior of the curves is close to that of the elastic case. We can see a pseudo critical angle at around 33° in the LS curves. Note that there is a converted S wave when the propagation angle is 0° and γ₀ is non-zero as shown in Figures 4B,D, the effects on the magnitudes are relatively strong at the critical angle, and the phases of the reflected P wave are reversed at large incidence angles.

FIGURE 4

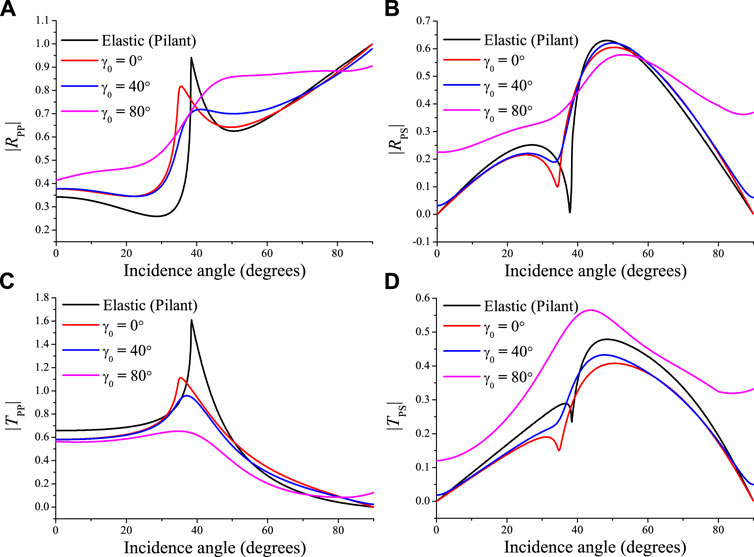
FIGURE 4. Absolute values of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves as a function of the P-wave incidence angle, corresponding to the elastic (black lines) and thermoelastic (color lines) cases at 100 MHz for different values of γ₀.

FIGURE 5

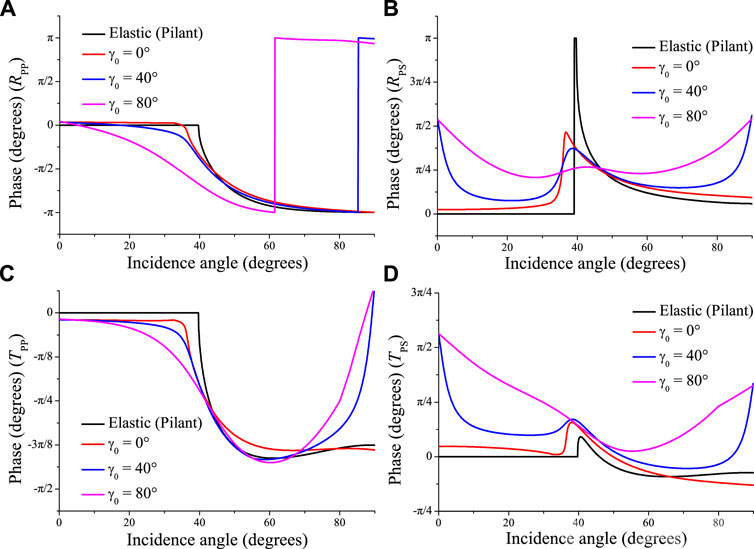
FIGURE 5. Same as Figure 4 but for the phase angles of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves.

The energy ratios are illustrated in Figure 6. Here, we plot the square root of the relative energy ratios to show the reflection and transmission, which is closer to the seismic response. The elastic phase and square root of the energy ratios are presented in Pilant (1979, Figure 12-3) and our results agree. The inhomogeneity angle affects the magnitudes of the reflected and transmitted waves (Figure 4) and consequently the energy partitions. In the elastic case, the energy flux perpendicular to the interface of the transmitted P wave (Figure 6C) vanish at the critical angle, because the wave propagates along the interface, carrying no energy flux in the vertical direction. The influence of γ₀ on the reflected P wave (Figure 6A) is evident at the critical angle, while the effect on the other waves is maximum near grazing incidence. The sum of all the energy ratios is −1, which implies energy conservation at the interface as shown in Figure 7.

FIGURE 6

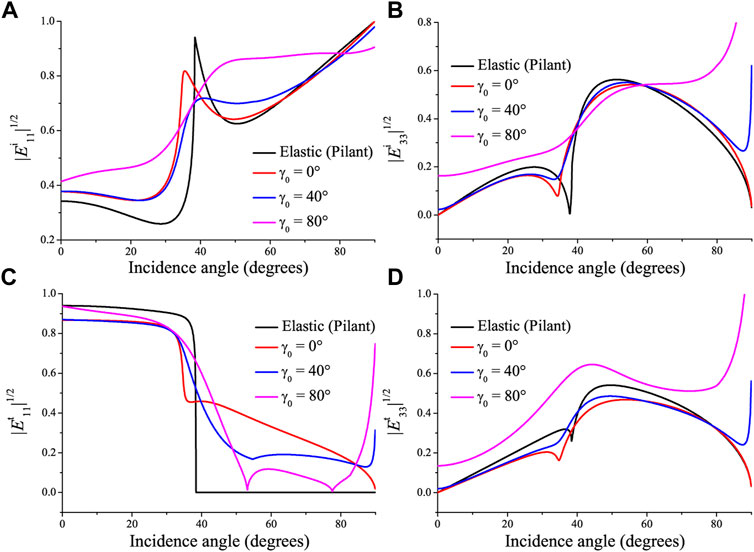
FIGURE 6. Same as Figure 4 but for the square root of the energy ratios of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves, considering the flux in the z-direction.

FIGURE 7

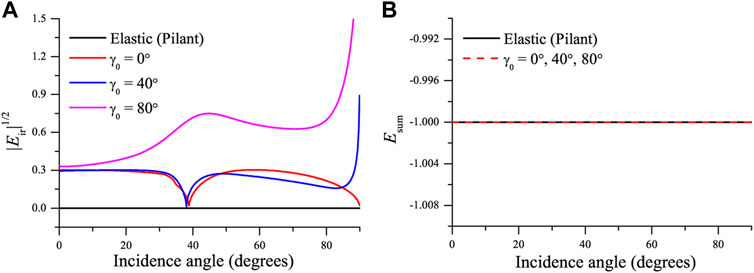
FIGURE 7. Square root of the interference energy (A) and the sum of the energy ratios (energy balance) (B) for an incident P wave (see Figure 4).

5.2 S-Wave Incidence

Next, we consider an incident S wave. Figures 8, 9 show the absolute values of the reflection and transmission coefficients and phase angles as a function of the incidence angle, and Figure 10 the corresponding energy ratios. Because the S-wave wavenumber k_S is real (see Eq. 19), the inhomogeneity angle has no effect (see Eq. 25) as can be seen in Figures 8–11 (the three curves overlap). The energy of the reflected and transmitted P waves, at approximately 35° and 20° in Figures 10A,C, vanishes in the elastic (lossless) case, where the wave propagates along the interface and, as for the P wave, the plane wave is evanescent. The curves in Figure 10 are identical to those of Pilant (1979, Figure 12-4). At the S-wave critical angle (38°), the energy ratio of the reflected S wave is 1 (Figure 10B), whereas the energy of other waves is zero, since the wave propagating along the interface carries no energy vertically. In the LS case, the behavior is analogous to the elastic case. However, there is transmission for all incidence angles and non-zero interference energy. Moreover, significant energy conversion occurs, as shown in Figure 11A, i.e., the LS model predicts more interference energy than the elastic one. The energy conservation at the interface is satisfied, as can be seen in Figure 11B. The same results have been illustrated at the free surface of double-porosity and two double-porosity media (Sharma, 2013; Wang E. et al., 2020).

FIGURE 8

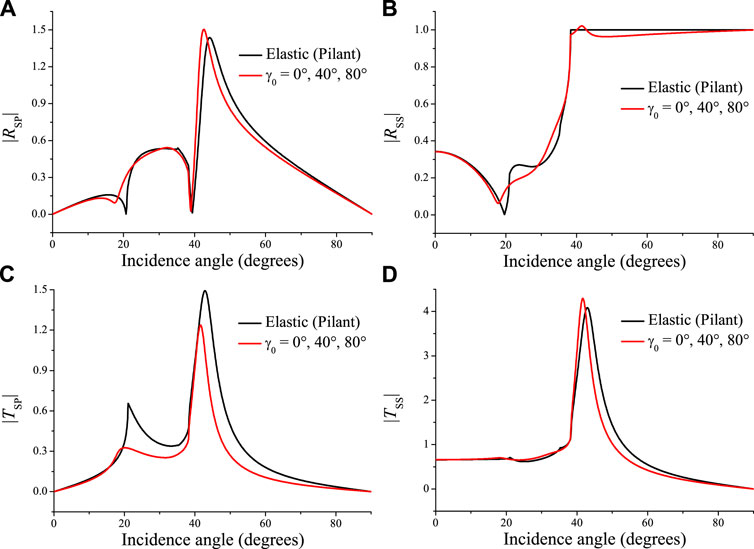
FIGURE 8. Absolute values of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves as a function of the S-wave incidence angle, corresponding to the elastic (black lines) and thermoelastic (red line) cases at 100 MHz for different values of γ₀.

FIGURE 9

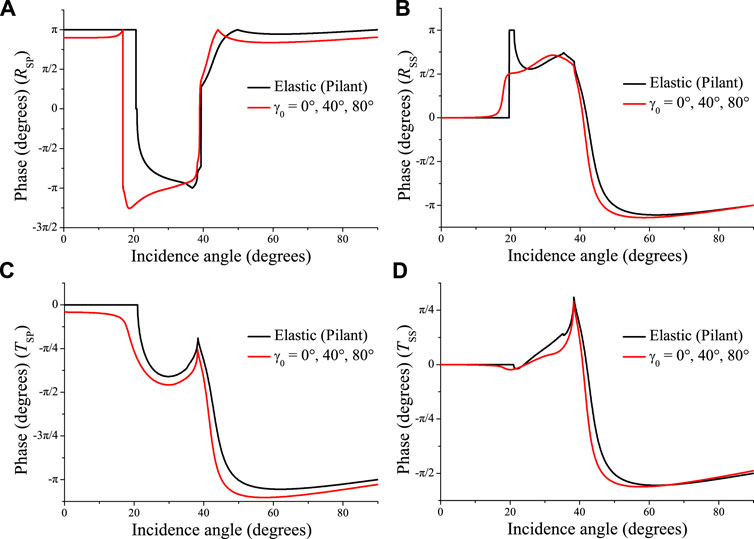
FIGURE 9. Same as Figure 8 but for the phase angles of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves.

FIGURE 10

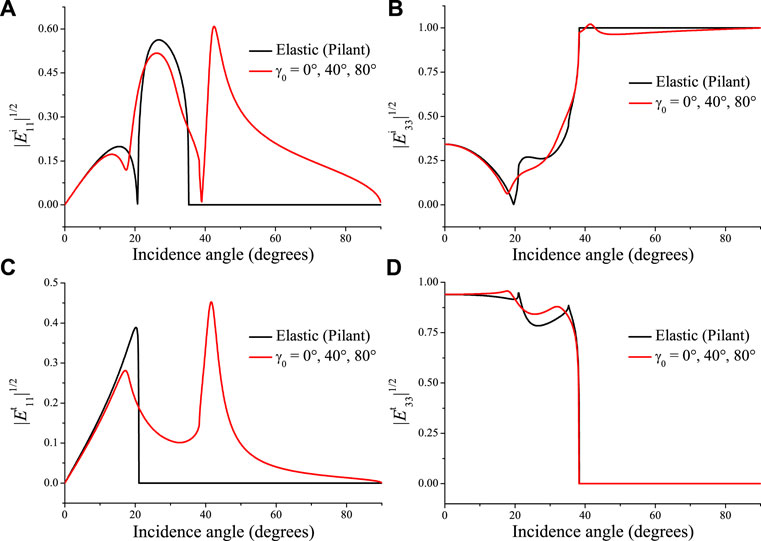
FIGURE 10. Same as Figure 8 but for the square root of the energy ratios of the reflected P (A), reflected S (B), transmitted P (C) and transmitted S (D) waves, considering the flux in the z-direction.

FIGURE 11

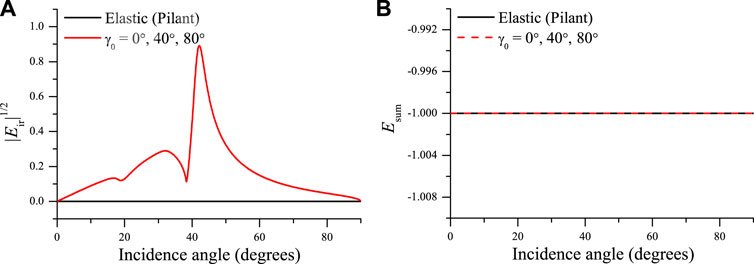
FIGURE 11. Square root of the interference energy (A) and the sum of the energy ratios (B) (see Figure 8).

5.3 Effect of the Thermal Conductivity (Relaxation Time)

Next, we study the effect of the relaxation time (see Eqs. 52, 53. Increasing $\bar{\kappa }$, we obtain a higher τ and a lower f_r (Carcione et al., 2019; Wang Z.-W. et al., 2020). The thermal conductivities of the incidence medium are assumed to be 0.5 m kg/(s³ K), 10.5 m kg/(s³ K) and 20.5 m kg/(s³ K), respectively, and that of the transmission medium is 10.5 m kg/(s³ K). Figures 12–15 show the effects of $\bar{\kappa }$ on the amplitudes and energy ratios. We observe that it affects more the T wave conversion in the case of an incident P wave (see Figures 12B,C). Higher $\bar{\kappa }$ enhances the T waves at the expense of the S waves for an incident S wave as shown in Figures 14, 15, where the T wave is weaker attenuated, according to Eqs. 52, 53 and curves of Figures 2D, 3D.

FIGURE 12

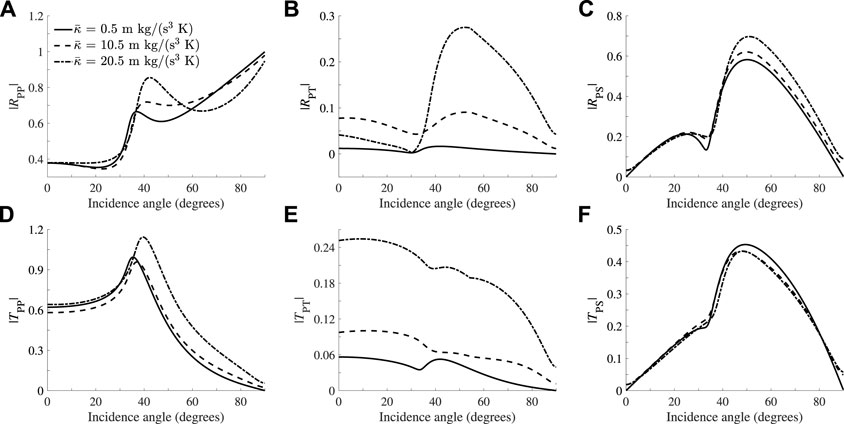
FIGURE 12. Absolute values of the reflected P (A), reflected T (B), reflected S (C), transmitted P (D), transmitted T (E) and transmitted S (F) waves as a function of the P-wave incidence angle at 100 MHz and γ₀ = 40°, where we vary the thermal conductivity of the incidence media.

FIGURE 13

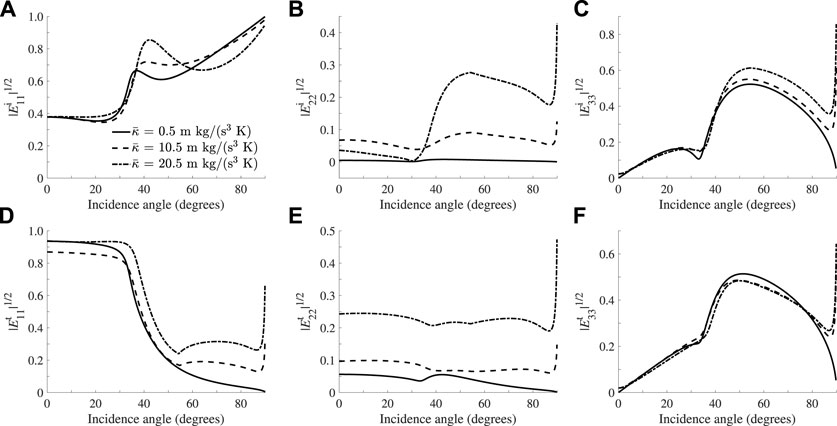
FIGURE 13. Same as Figure 12 but for the square root of the energy ratios of the reflected P (A), reflected T (B), reflected S (C), transmitted P (D), transmitted T (E) and transmitted S (F) waves, considering the flux in the z-direction.

FIGURE 14

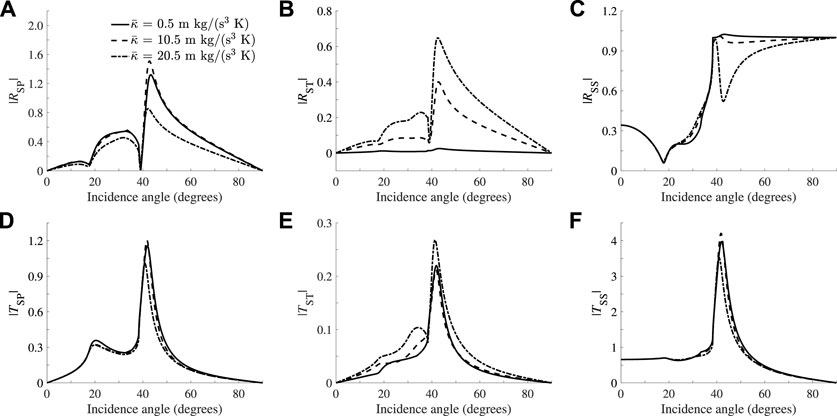
FIGURE 14. Same as Figure 12 but for the absolute values of the reflected P (A), reflected T (B), reflected S (C), transmitted P (D), transmitted T (E) and transmitted S (F) waves as a function of the S-wave incidence angle.

FIGURE 15

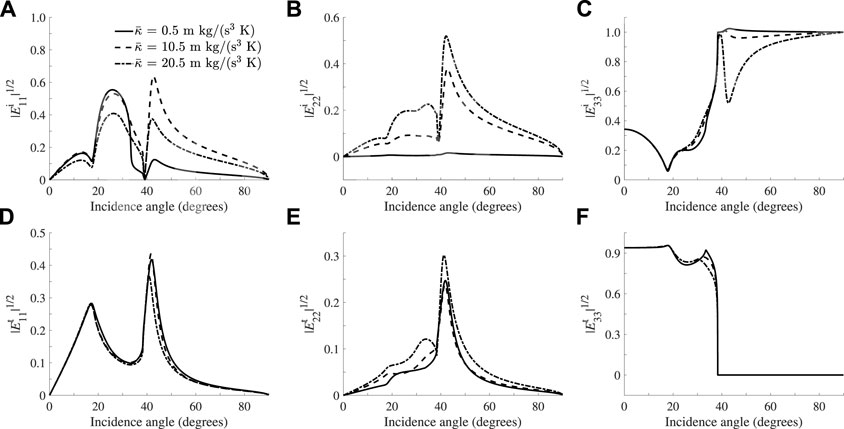
FIGURE 15. Same as Figure 14 but for the square root of the energy ratios of the reflected P (A), reflected T (B), reflected S (C), transmitted P (D), transmitted T (E) and transmitted S (F) waves, considering the flux in the z-direction.

6 Conclusion

We obtain the reflection and transmission coefficients at an interface separating two thermoelastic media, whose properties are based on the Lord-Shulman theory. Comparing these coefficients with those of the elastic (lossless) case, shows that critical angles, amplitudes and energy ratios, including interference fields, are affected by the presence of the thermal wave. Since the presence of this wave makes the media anelastic, the propagation and attenuation vectors of the incident wave do not necessarily coincide (inhomogeneous plane wave). The effect of the inhomogeneity angle is more noticeable at the critical angle and near grazing incidence angle for an incident P wave, and has no effect for an incident S wave, since the wavenumber of this wave is real. Then, we analyze the influence of the thermal conductivity (relaxation time) of the incidence media, which shows that this property affects the converted thermal wave more than the others, as expected. The calculations have been verified with the conservation of energy. This study is aimed to further improve the understanding of the behavior of the internal structure of the Earth, where the temperature effects are important.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

WH, L-YF, and JC contributed to conception and design of the study. WH wrote the first draft of the manuscript. WH, L-YF, JC, and TH wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The research is supported by the National Natural Science Foundation of China (Grant No. 41821002), 111 project “Deep-Superdeep Oil & Gas Geophysical Exploration” (B18055) and Innovation fund project for graduate students of China University of Petroleum (East China) (No. CXJJ-2022-17).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.850331/full#supplementary-material

References

Ackerman, C. C., Bertman, B., Fairbank, H. A., and Guyer, R. A. (1966). Second Sound in Solid Helium. Phys. Rev. Lett. 16 (18), 789–791. doi:10.1103/physrevlett.16.789

CrossRef Full Text | Google Scholar

Armstrong, B. H. (1984). Models for Thermoelastic Attenuation of Waves in Heterogeneous Solids. Geophysics 49 (7), 1032–1040. doi:10.1190/1.1441718

CrossRef Full Text | Google Scholar

Biot, M. A. (1956). Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 27 (3), 240–253. doi:10.1063/1.1722351

CrossRef Full Text | Google Scholar

Borcherdt, R. D. (2009). Viscoelastic Waves in Layered Media. Cambridge University Press.

Google Scholar

Buijze, L., van Bijsterveldt, L., Cremer, H., Paap, B., Veldkamp, H., Wassing, B. B. T., et al. (2019). Review of Induced Seismicity in Geothermal Systems Worldwide and Implications for Geothermal Systems in the Netherlands. Neth. J. Geosciences 98, 1–27. doi:10.1017/njg.2019.6

CrossRef Full Text | Google Scholar

Carcione, J. M. (2014). Wave fields in Real media. Theory and Numerical Simulation of Wave Propagation in Anisotropic, Anelastic and Porous media. 3rd ed. Elsevier.

Google Scholar

Carcione, J. M., Wang, Z.-W., Ling, W., Salusti, E., Ba, J., and Fu, L.-Y. (2019). Simulation of Wave Propagation in Linear Thermoelastic media. Geophysics 84 (1), T1–T11. doi:10.1190/geo2018-0448.1

CrossRef Full Text | Google Scholar

Cattaneo, C. (1958). Sur une forme de l’équation de la chaleur éliminant paradoxe d’une propagation instantantée. Comptes rendus de l’Académie des Sci. 247, 431–433.

Google Scholar

Chadwick, P. (1960). Thermoelasticity. The Dynamical Theory. Prog. Solid Mech. 1, 263–328. doi:10.1136/bmj.1.5165.56

CrossRef Full Text | Google Scholar

Denneman, A. I. M., Drijkoningen, G. G., Smeulders, D. M. J., and Wapenaar, K. (2002). Reflection and Transmission of Waves at a Fluid/porous‐medium Interface. Geophysics 67 (1), 282–291. doi:10.1190/1.1451800

CrossRef Full Text | Google Scholar

Deresiewicz, H. (1957). Plane Waves in a Thermoelastic Solid. The J. Acoust. Soc. America 29 (2), 204–209. doi:10.1121/1.1908832

CrossRef Full Text | Google Scholar

Green, A. E., and Lindsay, K. A. (1972). Thermoelasticity. J. Elasticity 2 (1), 1–7. doi:10.1007/bf00045689

CrossRef Full Text | Google Scholar

Hobiny, A. D., and Abbas, I. A. (2020). Fractional Order Thermoelastic Wave Assessment in a Two-Dimension Medium with Voids. Geomechanics Eng. 21 (1), 85–93.

Google Scholar

Ignaczak, J., and Ostoja-Starzewski, M. (2010). Thermoelasticity with Finite Wave Speeds. Oxford, United Kingdom: Oxford University Press.

Google Scholar

Jackson, H. E., Walker, C. T., and McNelly, T. F. (1970). Second Sound in NaF. Phys. Rev. Lett. 25 (1), 26–28. doi:10.1103/physrevlett.25.26

CrossRef Full Text | Google Scholar

Jiao, F., Wei, P., Zhou, X., and Zhou, Y. (2019). The Dispersion and Attenuation of the Multi-Physical fields Coupled Waves in a Piezoelectric Semiconductor. Ultrasonics 92, 68–78. doi:10.1016/j.ultras.2018.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Knott, C. G. (1899). III. Reflexion and Refraction of Elastic Waves, with Seismological Applications. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 48, 64–97. doi:10.1080/14786449908621305

CrossRef Full Text | Google Scholar

Kumar, R., and Sarthi, P. (2006). Reflection and Refraction of Thermoelastic Plane Waves at an Interface between Two Thermoelastic media without Energy Dissipation. Arch. Mech. 58 (2), 155–185.

Google Scholar

Kumar, R., Gupta, V., and Abbas, I. A. (2013). Plane Deformation Due to thermal Source in Fractional Order Thermoelastic media. Jnl Comp. Theo Nano 10 (10), 2520–2525. doi:10.1166/jctn.2013.3241

CrossRef Full Text | Google Scholar

Lord, H. W., and Shulman, Y. (1967). A Generalized Dynamical Theory of Thermoelasticity. J. Mech. Phys. Sol. 15 (5), 299–309. doi:10.1016/0022-5096(67)90024-5

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1867). On the Dynamical Theory of Gases. Philosophical Trans. R. Soc. Lond. 157, 49–88.

Google Scholar

McNelly, T. F., Rogers, S. J., Channin, D. J., Rollefson, R. J., Goubau, W. M., Schmidt, G. E., et al. (1970). Heat Pulses in NaF: Onset of Second Sound. Phys. Rev. Lett. 24 (3), 100–102. doi:10.1103/physrevlett.24.100

CrossRef Full Text | Google Scholar

Pilant, W. L. (1979). Elastic Waves in the Earth. New York: Elsevier Science Publishing Company.

Google Scholar

Rokhlin, S. I., Bolland, T. K., and Adler, L. (1986). Reflection and Refraction of Elastic Waves on a Plane Interface between Two Generally Anisotropic media. J. Acoust. Soc. America 79 (4), 906–918. doi:10.1121/1.393764

CrossRef Full Text | Google Scholar

Rudgers, A. J. (1990). Analysis of Thermoacoustic Wave Propagation in Elastic media. J. Acoust. Soc. America 88 (2), 1078–1094. doi:10.1121/1.399856

CrossRef Full Text | Google Scholar

Sarkar, N., and Mondal, S. (2020). Thermoelastic Plane Waves under the Modified green–lindsay Model with Two-Temperature Formulation. J. Appl. Mathematics Mech./Z. für Angew. Mathematik Mechanik 100 (11), 1–17. doi:10.1002/zamm.201900267

CrossRef Full Text | Google Scholar

Sarkar, N., Abo-Dahab, S. M., and Mondal, S. (2020). Reflection of Magneto-Thermoelastic Waves at a Solid Half-Space under Modified Green-Lindsay Model with Two Temperatures. J. Therm. Stresses 43 (9), 1083–1099. doi:10.1080/01495739.2020.1768991

CrossRef Full Text | Google Scholar

Savage, J. C. (1966). Thermoelastic Attenuation of Elastic Waves by Cracks. J. Geophys. Res. 71 (16), 3929–3938. doi:10.1029/jz071i016p03929

CrossRef Full Text | Google Scholar

Sharma, J. N., Kumar, V., and Chand, D. (2003). Reflection of Generalized Thermoelastic Waves from the Boundary of a Half-Space. J. Therm. Stresses 26 (10), 925–942. doi:10.1080/01495730306342

CrossRef Full Text | Google Scholar

Sharma, M. D. (2013). Effect of Local Fluid Flow on Reflection of Plane Elastic Waves at the Boundary of a Double-Porosity Medium. Adv. Water Resour. 61, 62–73. doi:10.1016/j.advwatres.2013.09.001

CrossRef Full Text | Google Scholar

Sharma, M. D. (2018). Reflection-refraction of Attenuated Waves at the Interface between a Thermo-Poroelastic Medium and a Thermoelastic Medium. Waves in Random and Complex Media 28 (3), 570–587. doi:10.1080/17455030.2017.1370154

CrossRef Full Text | Google Scholar

Singh, M. C., and Chakraborty, N. (2013). Reflection and Refraction of P-, SV- and thermal Wave, at an Initially Stressed Solid–Liquid Interface in Generalized Thermoelasticity. Appl. Math. Model. 37 (1-2), 463–475. doi:10.1016/j.apm.2012.03.008

CrossRef Full Text | Google Scholar

Sinha, S. B., and Elsibai, K. A. (1997). Reflection and Refraction of Thermoelastic Waves at an Interface of Two Semi-infinite media with Two Relaxation Times. J. Therm. Stresses 20 (2), 129–145. doi:10.1080/01495739708956095

CrossRef Full Text | Google Scholar

Sinha, S. B., and Elsibai, K. A. (1996). Reflection of Thermoelastic Waves at a Solid Half-Space with Two Relaxation Times. J. Therm. Stresses 19 (8), 749–762. doi:10.1080/01495739608946205

CrossRef Full Text | Google Scholar

Veres, I. A., Berer, T., and Burgholzer, P. (2013). Numerical Modeling of Thermoelastic Generation of Ultrasound by Laser Irradiation in the Coupled Thermoelasticity. Ultrasonics 53 (1), 141–149. doi:10.1016/j.ultras.2012.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Vernotte, P. (1948). Théorie continue et théorie moléculaire des phénomènes thermocinétiques. Comptes rendus de l’Académie des Sci. 227, 43–44.

Google Scholar

Wang, B. L., and Li, J. E. (2013). Hyperbolic Heat Conduction and Associated Transient thermal Fracture for a Piezoelectric Material Layer. Int. J. Sol. Structures 50 (9), 1415–1424. doi:10.1016/j.ijsolstr.2013.01.013

CrossRef Full Text | Google Scholar

Wang, E., Carcione, J. M., Yuan, Y., and Ba, J. (2021). Reflection of Inhomogeneous Plane Waves at the Surface of a Thermo-Poroelastic Medium. Geophys. J. Int. 224 (3), 1621–1639.

Google Scholar

Wang, E., Carcione, J. M., Ba, J., and Liu, Y. (2020a). Reflection and Transmission of Plane Elastic Waves at an Interface between Two Double-Porosity media: Effect of Local Fluid Flow. Surv. Geophys. 41 (2), 283–322. doi:10.1007/s10712-019-09572-6

CrossRef Full Text | Google Scholar

Wang, Z.-W., Fu, L.-Y., Wei, J., Hou, W., Ba, J., and Carcione, J. M. (2020b). On the Green Function of the Lord-Shulman Thermoelasticity Equations. Geophys. J. Int. 220 (1), 393–403. doi:10.1093/gji/ggz453

CrossRef Full Text | Google Scholar

Wei, W., Zheng, R., Liu, G., and Tao, H. (2016). Reflection and Refraction of P Wave at the Interface between Thermoelastic and Porous Thermoelastic Medium. Transp Porous Med. 113 (1), 1–27. doi:10.1007/s11242-016-0659-1

CrossRef Full Text | Google Scholar

Zener, C. (1938). Internal Friction in Solids II. General Theory of Thermoelastic Internal Friction. Phys. Rev. 53 (1), 90–99. doi:10.1103/physrev.53.90

CrossRef Full Text | Google Scholar

Zenkour, A. M., Mashat, D. S., and Abouelregal, A. E. (2013). The Effect of Dual-Phase-Lag Model on Reflection of Thermoelastic Waves in a Solid Half Space with Variable Material Properties. Acta Mechanica Solida Sinica 26 (6), 659–670. doi:10.1016/s0894-9166(14)60009-4

CrossRef Full Text | Google Scholar

Appendix A

Equations of Momentum Conservation and Heat Conduction

The strain (ϵ)-displacement (u) and constitutive relations (Biot, 1956) are

$2{ϵ}_{ij}=u_{i,j}+u_{j,i},$(A.1)

and

${\sigma }_{ij}=2\mu {ϵ}_{ij}+\left(\lambda ϵ-\bar{\gamma }T\right){\delta }_{ij}+f_{ij},$(A.2)

respectively, where ϵ = ϵ_ii, σ_ij are the stress components, δ_ij are the Kronecker components and f_ij are external stress forces, and the Einstein summation is asssumed.

The components of the equation of momentum conservation are

${\sigma }_{ij,j}=\rho {\ddot{u}}_i+f_i,$(A.3)

where f_i are the components of external body forces. Substituting the constitutive relations (A.2) into Eq. A.3 and using (A.1), in the absence of external body and stress forces, we obtain

$\left(\lambda +\mu \right)u_{j,ji}+\mu u_{i,jj}-\bar{\gamma }{T}_{,i}-\rho {\ddot{u}}_i=0.$(A.4)

On the other hand, the law of heat conduction is

$\bar{\kappa }{T}_{,jj}-c\left(\dot{T}+\tau \ddot{T}\right)-\bar{\gamma }{T}_0\left({\dot{u}}_{j,j}+\tau {\ddot{u}}_{j,j}\right)-q=0.$(A.5)

where T is the tempeature field and q a heat source.