Semi-Automated Inversion-Specific Data Selection for Volcano Tomography

1 Introduction

Seismic tomography is a technique that uses seismic data to build 2-D and 3-D models of the Earth’s interior. The most common application measures travel times and amplitudes of P- and S-waves produced by earthquakes or explosions and recorded at seismic stations. Tomography provides a forward model of how these waves have propagated through the Earth (generally, these waves follow “rays”) and uses data and models to invert, i.e., reconstruct in space for quantities like seismic velocity and attenuation on seismic wave-packets (Rawlinson et al., 2010; Koulakov, 2013; Rawlinson and Spakman, 2016). As the only technique available to scan the Earth at all scales, seismic tomography can be combined with other disciplines providing images and indirect measurements of Earth materials, from the Earth core to the shallow surface (Rawlinson et al., 2010). These techniques work when the amount of coherent waves preserved through propagation is sufficient across the seismic network and have found extensive success when applied to magmatic systems (Lees, 2007; Zandomeneghi et al., 2009; Koulakov, 2013; De Siena et al., 2017b). However, heterogeneity in these media produces multiple-scattering and diffusive wavefields that progressively deteriorate coherent-wave detection with distance. Researchers have thus developed tomographic techniques that in their forward model the sensitivity of coda waves (the waves scattered by this same heterogeneity) to the Earth structures (Del Pezzo et al., 2016, 2018), using them to image volcanoes (Prudencio, 2013; Prudencio et al., 2013; De Siena et al., 2017a).

Active seismic experiments offer ideal coverage to obtain highly-resolved tomographic images of volcanoes. The first applications date back to the 1980s, when travel-time tomography was applied to active data recorded across the Newberry and Medice Lake, in the Oregon and California Cascade Range, respectively (Achauer et al., 1988; Evans and Zucca, 1988). In the 1990s, active seismic experiments funded by national governments and international organisations have increased resolution on crustal volcanic structures. The feeding systems of Mt. Vesuvius [TOMOVES and MUREVES, Gasparini and Group (1998)] and Campi Flegrei [SERAPIS, Zollo et al. (2008)] are largely interpreted thanks to these surveys. In the last two decades active experiments have resolved the interior of Deception Island (TOMODEC 2005, Prudencio et al. (2013; 2015a)), Tenerife [TOMTEIDEVS, García-Yeguas et al. (2012); Prudencio (2013); Prudencio et al. (2015b)], Etna [TOMOETNA, Ibáñez et al. (2016)] and Santorini [PROTEUS, Hooft et al. (2019)]. Onshore, the most prominent active seismic experiments are iMuSH, at Mount St. Helens volcano, and MED-SUV, across several volcanic areas in the Mediterranean Sea. These are the only massive surveys where geophysical responses from both seismic and potential fields were collected (De Landro et al., 2017; Bedrosian et al., 2018; Siniscalchi et al., 2019; Ulberg et al., 2020). The corresponding images provide unique constraints on the shallow feeding systems and processes at these volcanoes, especially if used jointly with passive data (Battaglia et al., 2008).

Both coherent and incoherent waves have been extensively used at Deception Island (South Shetland Islands, Antarctica) primarily thanks to the TOMODEC2005 experiment, carried out during the austral summer of 2005 at Deception Island volcano (Ibáñez et al., 2017) (Figure 1). Over half a million seismic waveforms were produced by shots from a boat circling the island, and, especially, entering the central caldera, recorded by seismometers both on land and at the bottom of the sea (Prudencio et al., 2013). Deception Island is an ideal target for such an experiment for three primary reasons: 1) its morphology, with the navigable inner bay that allows ideal ray coverage on the central caldera; 2) the absence of anthropic noise (Lecocq et al., 2020); 3) a 360° spatial ray-coverage (Ibáñez et al., 2017), a unique feature when compared to other off-shore experiments, which generally provide directional ray coverage (Zollo et al., 2008). For these reasons, the corresponding travel-time, direct- and coda-wave attenuation show unprecedented resolution relative to other volcanic areas (Ben-Zvi et al., 2009; Zandomeneghi et al., 2009; Prudencio et al., 2013, 2015a; Del Pezzo et al., 2016, 2018). The dataset has a final, unique advantage: it is entirely available online (Ibáñez et al., 2017) and thus ideal for developing and testing automated and semi-automated data selection strategies.

FIGURE 1

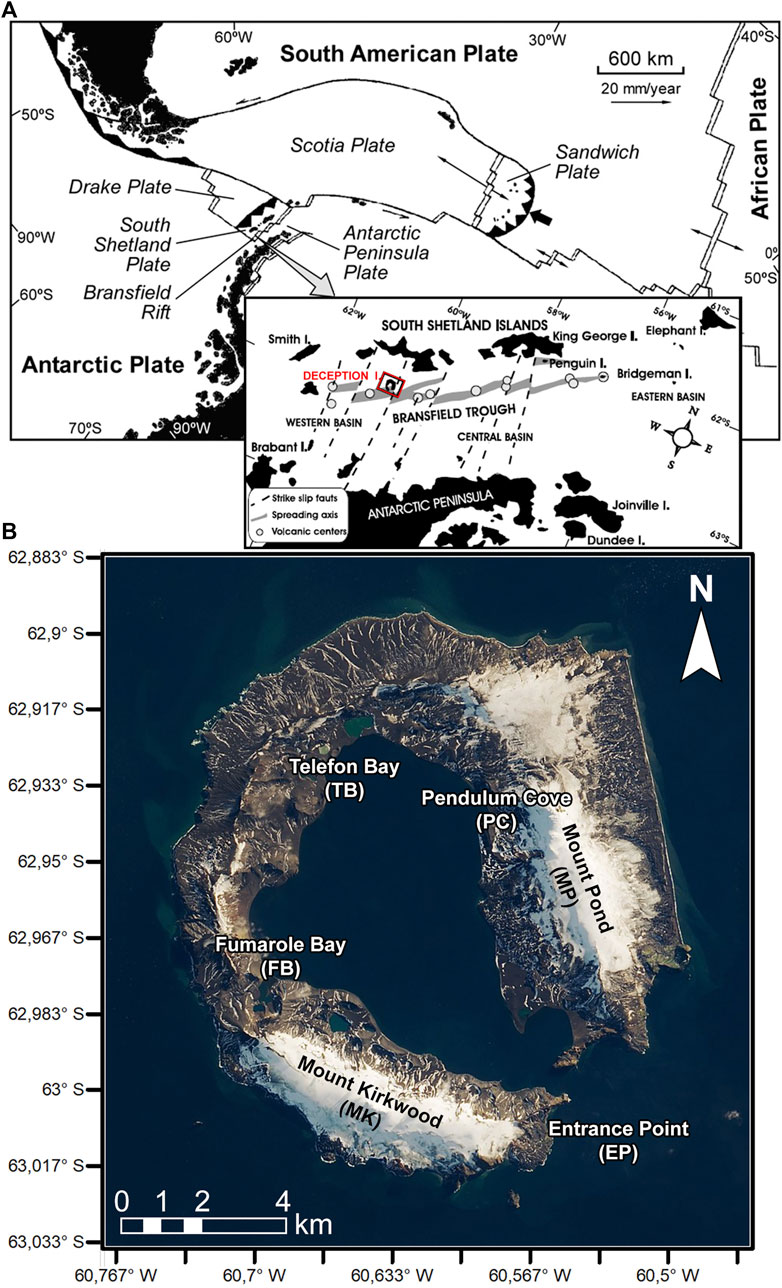
FIGURE 1. Simplified regional tectonic map and location of the South Shetland Islands (A) and map of Deception Island with toponymics (B).

There is uncertainty, or lack of benchmark strategies, about the best methods for the selection of waveforms necessary to perform seismic tomography using volcanic datasets; this is contrary to what happens at the global scale (Valentine and Woodhouse, 2010). Data selection strategies have generally been applied to passive seismo-volcanic datasets, and, when using active seismic data, they focus on travel times more than on amplitudes (De Landro et al., 2017). Strategies focused on amplitudes and, particularly, coda waves become increasingly necessary, as attenuation tomography is today a standard for imaging volcanoes (Prudencio et al., 2013, 2015a; Serlenga et al., 2016; De Siena et al., 2017a). Given the quantity of seismic traces produced by these experiments, an automatic or quasi-automatic system preliminary to inversion is necessary.

Automatic data processing strategies that focus on both travel-time and amplitude detection are generally applied to global seismic records (Valentine and Woodhouse, 2010). At smaller scales, they concentrate on phases and earthquake detection (Romero et al., 2016; Pang et al., 2019; Cortés et al., 2020). In volcanic media and especially in active seismic experiments, scattered waves dominate, with chaotic wave packets soon dominating seismic traces (Ibáñez et al., 2017). Semi-automated strategies provide better results in this case, especially if the expected medium heterogeneity is high (Bianco and Zaccarelli, 2009). These approaches combine two steps: dataset selection and application to imaging as a benchmark. The selection generally comprises several iterations, each depending on a single selection parameter (Cortés et al., 2015). It is necessary to set a-priori conditions specific to the inversion using standard practice from neural networks (Valentine and Woodhouse, 2010). Following each iteration, the obtained dataset must be applied to the corresponding imaging code to compare the results quantitatively with the same standard.

Given the increasing importance of coda techniques when imaging volcanoes, in this work, we present a quasi-automatic method for the selection of the best traces for coda-wave tomography using the TOMODEC2005 dataset. The open-access code MuRAT 1, previously applied in volcanic (Prudencio et al., 2015a; De Siena et al., 2016, 2017b; Gabrielli et al., 2020; Sketsiou et al., 2020) and tectonic setting (Borleanu et al., 2017; Napolitano et al., 2020), is used to perform data processing and inversion. The majority of the analysis focuses on reducing errors during the processing phases, reducing noise, increasing consistency between different node spacing and frequencies, and, especially, mitigating loss of information. We show that we reduce residuals by targeting the inversion results while increasing resolution on structures without any additional computational cost.

2 Data

The TOMODEC2005 experiment (Ibáñez et al., 2017) produced data that have been extensively used at Deception Island for velocity (Ben-Zvi et al., 2009; Zandomeneghi et al., 2009), attenuation, and scattering tomography (Prudencio et al., 2013, 2015a; Del Pezzo et al., 2016, 2018). Seismic waves produced at the volcano suffer high scattering, and waveforms recorded at stations can be described by the diffusion equation (Prudencio et al., 2013). In any coda-attenuation study, the waveforms must respect at least one condition: the envelope has to decrease exponentially from its main peak amplitude (Sato et al., 2012). The coda decay is controlled by coda attenuation (or inverse coda quality factor, $Q_c^{-1}$), which, in the diffusive approximation, is a measurement of seismic absorption, i.e., of the energy lost permanently by the interaction of the wave with the medium (Calvet and Margerin, 2013).

The starting dataset for this study is the subset of TOMODEC2005 used to perform attenuation tomography (Ibáñez et al., 2017). It comprises 20283 waveforms of different duration, each detected automatically knowing the time of the shot and corrected for the instrument function. The waveforms were then cut to 10 s from the time of the shot as signals always last less than this duration (Prudencio et al., 2015a). This dataset has been used to image seismic absorption by (Prudencio et al., 2013) with regular node spacing of 3 and 1 km. To verify the dataset quality, we made a first visual check (Valentine and Woodhouse, 2010). We subdivided the dataset into three groups: those with spurious signals (Figure 2A), those primarily characterised by null values (Figure 2B) and those visually identified as “good” (Figure 2C). These visual checks are standard in data selection. Still, the notion of “good” is qualitative, and operators should better follow standard seismological quality criteria, such as signal-to-noise ratio (Valentine and Woodhouse, 2010). However, these criteria do not target the ability of the dataset to perform a specific task, as imaging coda attenuation: such criteria could remove waveforms from datasets unnecessarily.

FIGURE 2

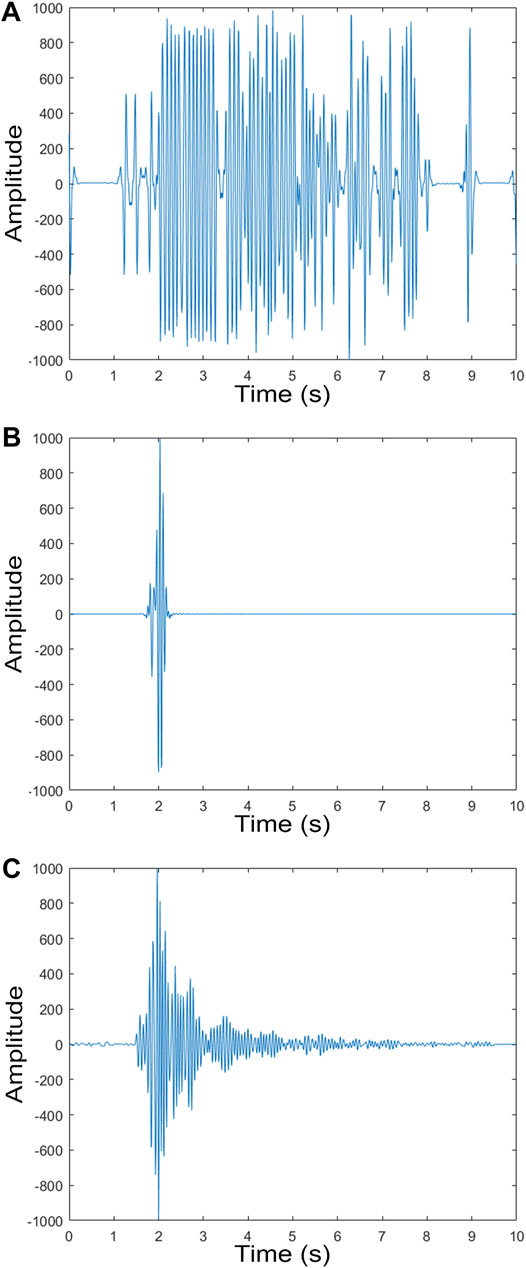
FIGURE 2. Traces example. (A): Trace with spurious signal; (B): Trace with null values; (C): Traces identified visually as being usable. All amplitudes are in counts.

3 Methods

3.1 Selection Criteria

The best way to test a dataset for tomography is to use them directly in the workflow necessary to obtain the final maps (Figure 3A). We start from the original dataset and a group of user-defined selection parameters. At each selection step (iteration) and for each frequency, we input waveforms into the MuRAT code (but the same procedure applies to any tomographic code), obtaining 2D images of coda attenuation (De Siena et al., 2016; 2017b). The user choice for the first four iterations is to exclude those waveforms:

1. characterised primarily by null values;

2. with a coda-window smaller than 4 seconds;

3. whose logarithmic coda decay had a small correlation coefficient relative to a line;

4. showing recurrent glitches at specific stations

FIGURE 3

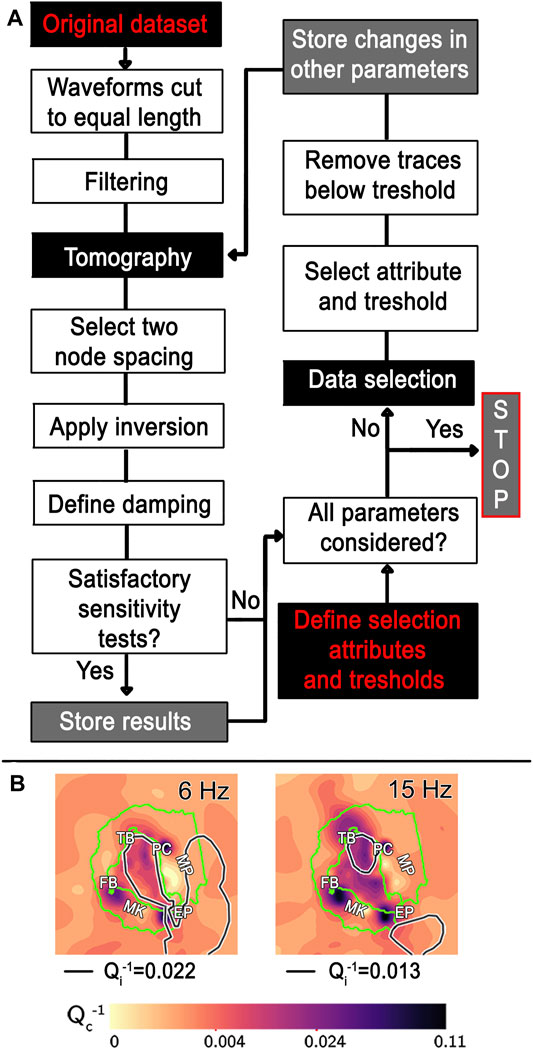
FIGURE 3. Workflow of the selection strategy and final improvement. (A) The workflow starts from the available original dataset and a user-dependent choice of selection parameters (black and red boxes). From the original dataset, the workflow develops a tomographic analysis whose results are stored after satisfactory recovery of synthetic anomalies. Successive iterations develop data selections until all selection parameters are considered, and save the variations in all parameters at all steps. The iterations stop after all parameters have been evaluated. (B) The results of the final iterations are compared with the contour of the homogeneous absorption $(Q_i^{-}1)$ bodies obtained at 6 and 16 Hz by Prudencio et al. (2013).

The four iterations are followed by the analysis of ten standard parameters (Table 2) used to select waveforms in seismic data processing–among those, we evaluate the discrimination potential of the signal-to-noise ratio (SNR). Each iteration provides a dataset that has been tested with chequerboard tests (Rawlinson and Spakman, 2016). The final results are stored only in case the sensitivity tests are satisfactory in the chosen portion of the medium (in our case, the central caldera). At each iteration all the previous parameters and the number of remaining traces are computed and stored again for comparisons (Tables 1–2).

TABLE 1

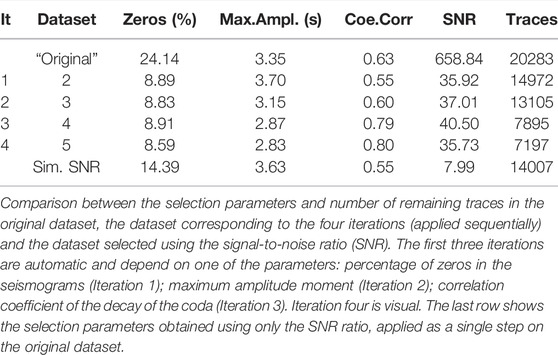
TABLE 1. Comparison between selection parameters at each selection iteration and relative to the signal-to-noise ratio.

TABLE 2

TABLE 2. Summary table of the additional parameters considered.

3.2 MuRAT Implementation and Testing

MuRAT analyses either Seismic Analysis Code data or text files associated with headers or external metadata, using as input an external file specifying parameters used for data processing and inversion (De Siena et al., 2014). The waveforms are filtered in four frequency bands, centred at 6 Hz, 9 Hz, 15 Hz and 21 Hz and with bandwidth one-third of the central frequency and considering a coda window of 4 s from the maximum peak amplitude (Del Pezzo et al., 2016). proves that at this lapse times the waves propagate diffusively, allowing to map seismic absorption with coda attenuation. Maps at lower frequencies cannot be obtained due to consistent surface-wave reverberations, affecting the hypotheses underlying the technique, i.e., that the wavefield is diffusive (Gabrielli et al., 2020). The anti-aliasing filter attenuates higher spectral bands hindering the tomographic analysis.

While the current release of the code can invert or regionalise for total attenuation (De Siena et al., 2017b), scattering attenuation (De Siena et al., 2016; Napolitano et al., 2020) and absorption (De Siena et al., 2017a; Gabrielli et al., 2020; Sketsiou et al., 2020) in 3D, we use the code exclusively to obtain 2D absorption images. This choice allows: (1) to compare more easily the results on a map, instead of having to search for specific sections in 3D where data selection could drastically change results; (2) compare with existing published maps of absorption obtained using the original dataset (Prudencio et al., 2013). After selecting the optimal damping parameters for the linearised inversions from the relation between residuals and solution norm, a first-order Tikhonov inversion is applied. At the end of the selection, the maps are tested by changing this parameter to one order of magnitude lower or higher than its value (Rawlinson and Spakman, 2016) (Supplementary Figures S2–5). For each iteration and test, chequerboard tests analogue to those used in (Prudencio et al., 2015a) show the sensitivity of the technique to space.

4 Results

For each dataset, we obtain four $Q_c^{-1}$ maps depending on frequencies at constant node spacing of 2 km (Figure 4) and 1 km (Figure 5). The input and output of the chequerboard test for each spatial resolution are shown in Figure 6.

FIGURE 4

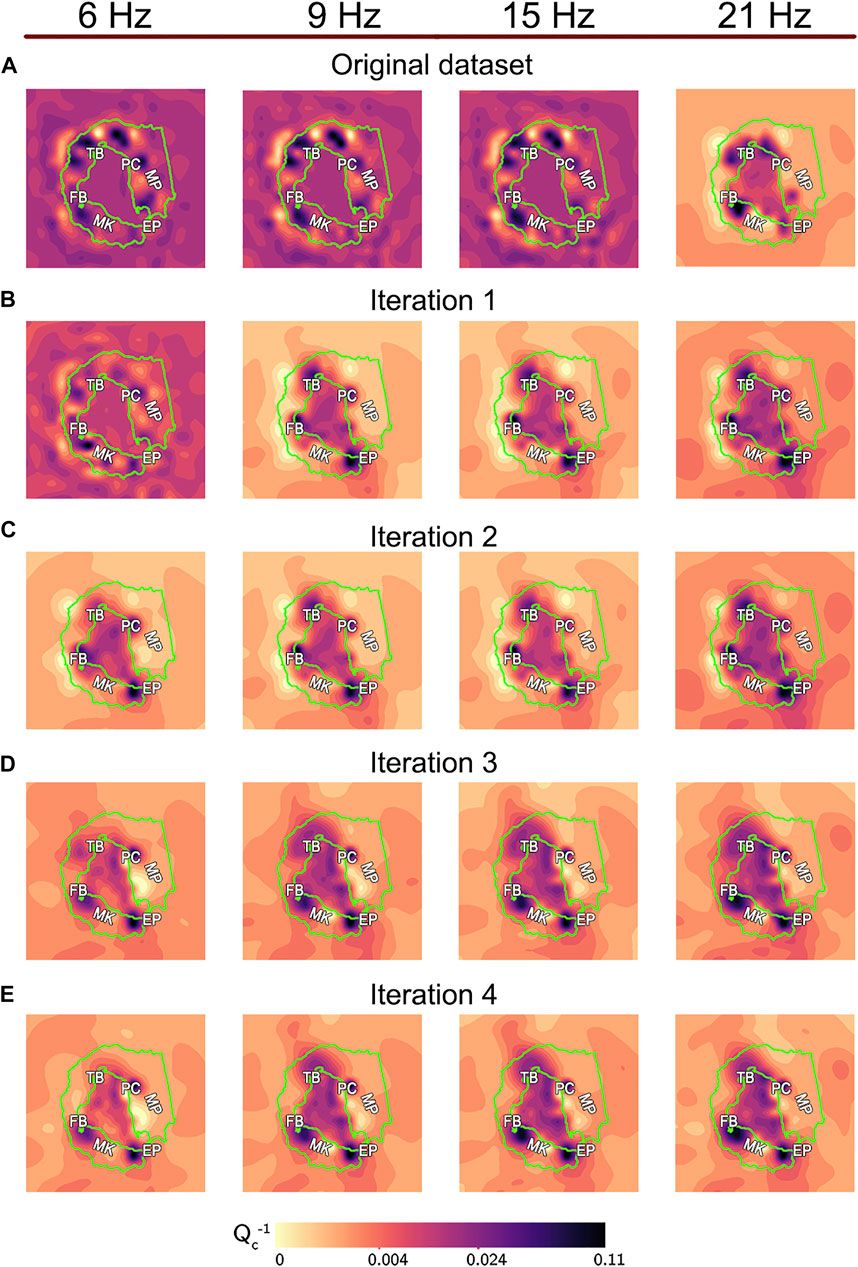
FIGURE 4. Maps of coda attenuation (Qc⁻¹) obtained with a node spacing of 2 km. Each panel corresponds to the results obtained with the original dataset (A), 20283 traces) or after removing traces: (B) with an average percentage of zeros greater then 40% (14972 traces); (C) whose main peak amplitude was later than 6 s (13105 traces); (D) having a coda decay correlation coefficient lower than 0.6 (7895 traces); (E) at stations with instruments producing spikes (7197 traces). TB: Telephone Bay; PC: Pendulum Cove; MP: Mount Pond; EP: Entrance Point; MK: Mount Kirkwood; FB: Fumarole Bay.

FIGURE 5

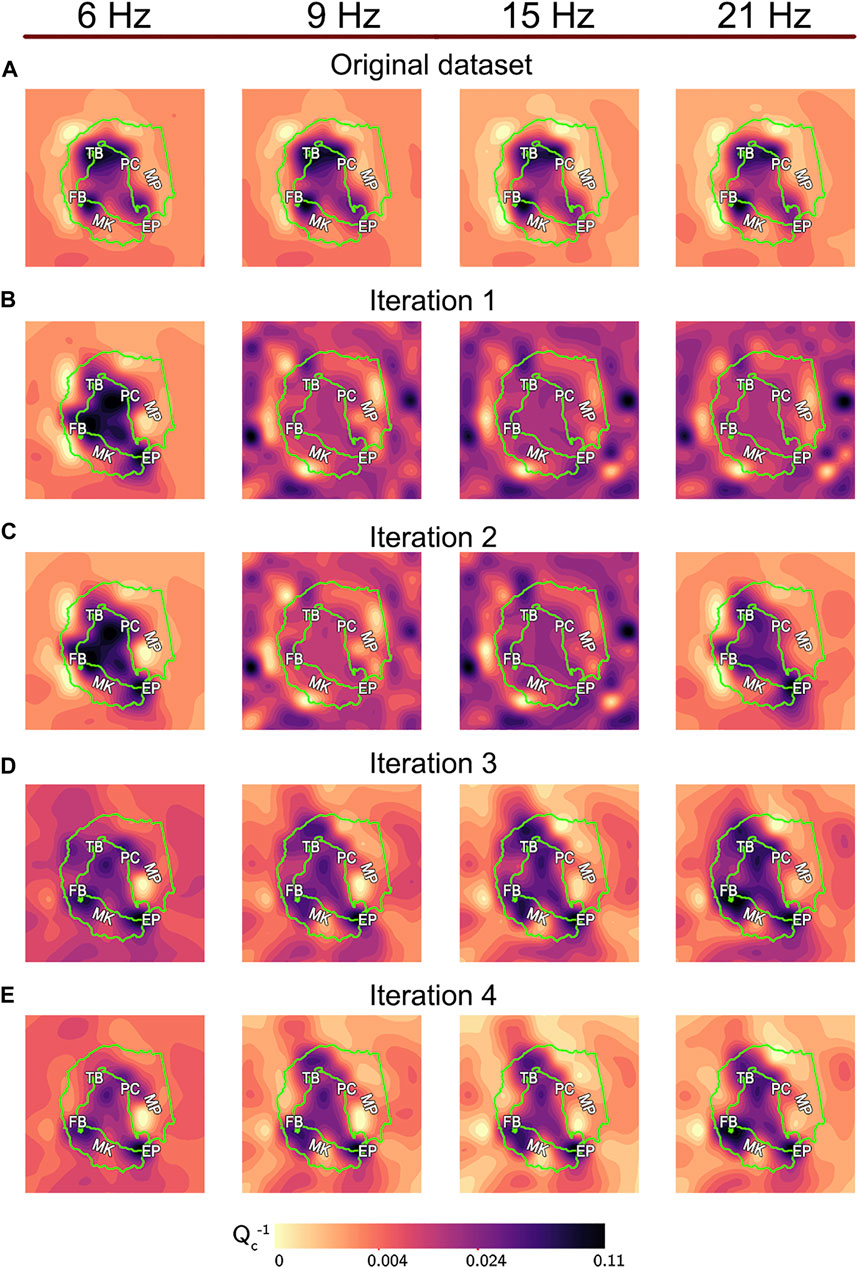
FIGURE 5. As for Figure 4 for a node spacing of 1 km. Each panel corresponds to a different iteration. TB: Telephone Bay; PC: Pendulum Cove; MP: Mount Pond; EP: Entrance Point; MK: Mount Kirkwood; FB: Fumarole Bay.

FIGURE 6

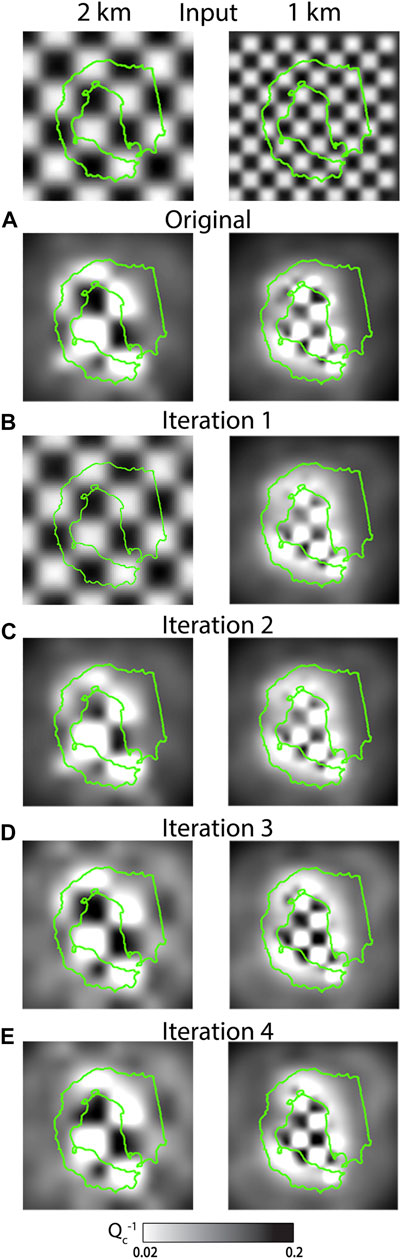
FIGURE 6. Chequerboard test input and output maps related to the datasets obtained after each iteration. The colorbar shows the variations of (Qc⁻¹).

4.1 Original Dataset: 20283 Traces

The original dataset comprises 20283 traces with a duration of 10 s each. We obtain eight attenuation maps - one for each frequency at 2 km (Figure 4A) and 1 km (Figure 5A) node spacing together with the associated chequerboard test (Figure 6A.

The models solved at 2 km show a pattern recognised in previous works: the best-resolved area only covers the inner bay (Port Foster), while the $Q_c^{-1}$ anomalies fall outside of it (Prudencio et al., 2015a; Del Pezzo et al., 2018) (Figure 6). Mapping frequencies from 6 to 15 Hz with a 1 km node spacing leads to variations primarily outside the resolved area, typical behaviour for a poorly-resolved model. The high-$Q_c^{-1}$ anomalies are distributed around the island, while the other anomalies focus on the northern (Telephone Bay) and western parts (Fumarole Bay) of the inner bay. Only the map at 21 Hz has a $Q_c^{-1}$ distribution consistent with the maps at 2 km. We followed up with numerical and visual analyses of the dataset, recognising several traces showing no exponential decrease from the peak (Figure 2A): these waveforms cannot be described by the diffusion model (Wegler and Lühr, 2001; Wegler, 2003).

4.2 Iteration 1: 14972 Traces

The first selection attribute is the percentage of time when the signal is equal to zero (Figure 2B). A signal that exactly equals zero indicates a malfunction of the instrument. Because the P-wave smoothed envelope lasts 4 s and the traces last 10 s, we remove traces with a percentage of zeroes higher than 40%, being this value greater than half of the coda window. The dataset obtained from this first iteration (Dataset 1) comprises 14972 waveforms with a zero-percentage value equal to 8.89%, from the 24.14% of the original dataset (Table 1).

The Qc⁻¹ anomalies obtained at 1 km node spacing (Figure 5B) are similar to those obtained in the previous step at 6 Hz; however, at the other frequencies, the maps seem to resolve the central part of the island. The primary anomalies are located in the inner bay, mainly north, northeast and west, in the areas of Telephone Bay, Pendulum Cove and Fumarole Bay, respectively (Figure 1A). Another anomaly is visible in the south, at the bay entrance (Entrance Point).

Apart from highlighting the sensitivity to anomalies of different sizes, displaying additional resolution tests allows evaluating the robustness of the results (Rawlinson and Spakman, 2016). Results at 1 km improve (Figure 5B), but those at 2 km worsen and become inconsistent, a sign of inversion instability. At 2 km resolution and 6 Hz, the Qc⁻¹ anomalies cover the inner bay, but at higher frequencies, the Qc⁻¹ anomalies are scattered across the island. In this case, the chequerboard test at 2 km is misleading, as it appears wholly solved. While it could be interpreted as an improvement, this is an unrealistic result as this remains an ill-posed problem that cannot have a solution that matches the input exactly (Aster et al., 2018). The most likely explanation is an inappropriate definition of the damping parameter for this iteration; however, the workflow still stores the results due to the success of the 1-km resolution results.

4.3 Iteration 2: 13105 Traces

The second selection parameter is the arrival time of the maximum peak amplitude relative to the origin, or peak delay, used as a measurement of scattering attenuation in volcanoes and faults (De Siena et al., 2016; Napolitano et al., 2020). This peak cannot be later than 6 s from the origin, given that we measure coda decay over a window of 4 seconds on 10-seconds-long waveforms. As a result, we obtained a dataset comprising 13105 traces with at least 4 seconds of coda-window (Dataset 2). After this selection, the average peak delay moves from 3.7 to 3.1 s (Table 1).

The results are shown in Figures 4C, 5C). For the first time, the Qc⁻¹ anomalies at 1 km resolution appear consistent at different frequencies. They are primarily located in four areas: Telephone Bay in the north; Pendulum Cove in the northeast; Fumarole Bay in the west; and Entrance Point in the south (Figure 1). However, at 2 km node spacing, only the anomalies at 6 and 21 Hz are consistent with each other and with those at 1 km. At 9 Hz and 15 Hz, the primary variations appear in an area not resolved by the chequerboard test.

The resolution tests give scientifically-meaningful results 6c. The most significant change from previous patterns is the general attenuation increase and smoother high-attenuation anomalies in the inner bay. Nevertheless, the $Q_c^{-1}$ maps still lack coherency between different frequencies and node spacing, suggesting that some undesired traces are still in the dataset.

4.4 Iteration 3: 7895 Traces

The following selection parameter is generally used to estimate the quality of each $Q_c^{-1}$ measurement: it is the correlation (Pearson) coefficient of the log-linear regression of the coda decay (Calvet and Margerin, 2013; Mayor et al., 2016; De Siena et al., 2017a). The parameter approaches one for perfect correlation and equals zero for the absence correlation. After the first two selections, there is a significant variation of this parameter (Table 1). The average correlation coefficient moves from 0.63 in the original dataset to 0.55 for Dataset 1 (largely because the presence of repeated zeroes stabilises the envelope correlation), then increases to 0.60 when using Dataset 2. In literature, a $Q_c^{-1}$ estimate is generally accepted when the correlation coefficient of the linear regression is greater than 0.60 (Calvet and Margerin, 2013). Iteration three removes all those traces with an average correlation coefficient value smaller than 0.6, creating Dataset 3. The average correlation value rises to 0.79, about 13% higher than the minimum values accepted in the literature (Table 1).

The results (Figures 4D, 5D) show for the first time homogeneous patterns between the maps at all frequencies and resolutions. At 1 km node spacing, the areas of highest $Q_c^{-1}$ are 3: in the northeast (Pendulum Cove), west-southwest (in between Fumarole Bay) and in the south (Entrance Point). This is the first iteration where a low $Q_c^{-1}$ anomaly appears in the Mount Kirkwood area, with a smaller extension at 6 Hz. In addition to all these punctual anomalies, a wide NNW-SSE orientated high $Q_c^{-1}$ anomaly covers the inner bay. The primary difference between 1 and 2 km node spacing is in the extent of the anomalies. Indeed, the high $Q_c^{-1}$ anomaly covers from Pendulum Cove to Telephone Bay in the northern area, while in the south, it covers the Neptune Bellows area completely. Additionally, a high $Q_c^{-1}$ anomaly is located in the west, near Fumarole Bay.

At 2 km resolution, a low $Q_c^{-1}$ anomaly appears at the south end of Mount Pond, while, between 21 and 9 Hz, another low $Q_c^{-1}$ anomaly is located east of Mount Kirkwood. Also, for the first time, all these anomalies fall in the resolved area (Figure 6D): this aspect, together with the similarities between maps at all frequencies and node spacing, suggests we could stop the selection process, which so far has been automatic. However, there are several differences between the last results and those obtained in the previous iterations. The most evident differences at 1 km are:

• the high $Q_c^{-1}$ anomaly in the Fumarole Bay area is shifted toward Mount Kirkwood;

• the low $Q_c^{-1}$ anomaly in the northern area is more defined and localised;

• a new low $Q_c^{-1}$ anomaly appears at the south end of Mount Pond.

At 2 km node spacing, we observe patterns similar to those of the previous step. The primary difference is at 21 Hz, where the low $Q_c^{-1}$ anomaly near Mount Kirkwood is replaced by a wider high $Q_c^{-1}$ anomaly that covers the Crater Lake area completely. Considering these differences, even if the chequerboard test highlights several areas better resolved than during previous iterations, we carried out a final visual analysis of the waveforms (Valentine and Woodhouse, 2010).

4.5 Iteration 4: 7197 Traces

The visual check shows that corrupted traces still occur in the dataset (Supplementary Figure S1). Making a cross-check between each station-waveform pair, we verified that this problem was station-dependent, and the automatic selections could not recognise the anomalous behaviour. In this last iteration, we removed all the waveforms recorded at those stations for a total of 689 traces (less than 10% of Dataset 3). After this procedure, Dataset four appears devoid of undesired traces from numerical and visual perspectives. Dataset four comprises 7197 seismic waveforms and has: (1) an average percentage of waveforms with null values equal to 8.59%; (2) an average maximum peak amplitude at 2.83 s and; (3) an average correlation coefficient value equal to 0.8 (Table 1). These values are very similar to those obtained in the previous iteration.

The results are shown in Figures 4E, 5E). At 2 km node spacing, the previously-discussed anomalies remain stationary but almost double in size. These anomalies are resolved in the chequerboard test at both 1 and 2 km node spacing 6. At 1 km, the highest-attenuation anomalies still cover the areas of Pendulum Cove, Fumarole Bay and Neptune Bellow. A broader high-attenuation anomaly trending NNW-SSE covers the inner bay. On the contrary, low-attenuation anomalies are located near Mt. Kirkwood and at the south end of Mt. Pound. We consider this the final dataset as the retrieved anomalies: 1) remain similar to those recovered from Dataset 3 (Figures 5D,E, 4D,E; 2) are consistent between different frequencies; 3) are similar when obtained using different node spacing; 4) occur across the well-resolved areas in the chequerboard tests.

4.6 Robustness Tests

We test the effective resolution of Dataset four by changing the optimal damping parameters for the linearised inversions at 6 and 15 Hz. Eight maps are generated using the damping parameters at one order of magnitude higher and lower than the value set using the L-curve corner for: (1) 6 Hz at 1 km (Supplementary Figure S2) and 2 km (Supplementary Figure S3) node spacing; (2) 15 Hz at 1 km (Supplementary Figure S4) and 2 km (Supplementary Figure S5) node spacing. This procedure estimates uncertainty more accurately, providing an additional tool to interpret the results.

The three high-attenuation anomalies at Pendulum Cove, Fumarole Bay and Neptune Bellow appear at 6 Hz and 1 km node spacing if using a damping one order of magnitude lower (0.11). At the same time, they result unsolved in the chequerboard test (Supplementary Figure S2). The anomalies are still visible by increasing damping one order of magnitude (11.8), but the chequerboard test cannot solve any part of the medium (Supplementary Figure S2). At 6 Hz and 2 km node spacing, lower damping (0.21) solves the entire chequerboard test, as we observed for Dataset 1 (Figure 6B). As in that case, the results appear under-damped (Supplementary Figure S3). Higher damping (21.6) outputs an unsolved chequerboard pattern.

At 15 Hz and 1 km node spacing, lower damping (0.11) produces results where two positive anomalies located south of Fumarole Bay and Pendulum Cove dominate the map. However, these areas are unsolved in the chequerboard test, while for a higher order of magnitude (11.8), the chequerboard test is completely unresolved (Supplementary Figure S4). In the last case (15 Hz, 2 km, Supplementary Figure S5), the chequerboard test looks completely solved for low damping, while at a higher order of magnitude (15.5), it is again wholly unresolved. All the maps obtained using different damping values show lower consistency and resolution than the original damping: we conclude that the selected damping is the best compromise to interpret the maps.

4.7 Alternative Attributes

Through our selections, we evaluate the average value of (Table 2):

• the mean amplitude of the noise windows (AmpNoise);

• the mean amplitude of the signal;

• the signal-to-noise-ratio value;

• the mean amplitude in the coda windows;

• the maximum power spectrum mean amplitude (MaxPowAmp);

• the frequency of the maximum power spectrum (MaxPowF);

• the mean auto-correlation value (AutoCorr);

• the spikes, i.e. the summation of all the value ≥500;

• the jumps, i.e. the average difference between a spike and the next value;

• the standard deviation of the Short Term Average vs. Long Term Average Standard Deviation.

These parameters are typically used for selecting waveforms in seismology (Valentine and Woodhouse, 2010). However, there is no apparent improvement in the maps when using these selection parameters, i.e., their application eventually only reduces the resolution by reducing coverage. Additionally, we observe no pattern in their changes between the different iterations. These parameters do not efficiently discriminate waveforms during the cleaning process; however, they might be essential for other techniques, such as travel-time tomography (Zandomeneghi et al., 2009).

4.8 Signal-to-Noise Ratio and Iteration Sequence

The chosen iteration order minimises the iteration number and avoids the excessive removal of waveforms. To verify the quality of the sequence, we used the signal-to-noise ratio (SNR), the first discrimination parameter used to select seismic waveforms in standard seismic applications (Valentine and Woodhouse, 2010). Noise is measured on a window of 1 s before the arrival of the P-wave. The SNR is normalized for the window used to compute the signal and noise amplitudes. For the TOMODEC2005 dataset, very high SNR values represent signals with spikes, contrary to common understanding. This value decreases from 658.84 in the original dataset to 35.73 in the final one, for a total of 14007 traces.

Table 1 shows that selecting data depending on the SNR worsens the fit and removes around 1000 additional waveforms without changing dramatically the correlation coefficient, the main marker of the quality of the data used to perform the tomography. These could still be waveforms suitable for a reliable tomographic image. We remove one-third of the dataset using only the SNR ratio (Table 1) (30.94%), causing: 1) a higher percentage of zeroes and a worse average correlation coefficient than in any iteration; 2) an average peak delay higher than any selected dataset except Dataset 2.

5 Discussion

While previous works show a single high-attenuation anomaly in the inner bay of the island (Prudencio et al., 2013; 2015a), our selection procedure highlights anomalies that spread from the centre of the bay to four areas: Telephone Bay, Pendulum Cove, Fumarole Bay and Entrance Point. All located across the caldera margin, some of these are the recognised locations of eruptions of the last century. One corresponds to the area occupied by the small island formed by the Telefon Bay eruption on 4 December 1967 (Smellie et al., 2002). A sub-glacial pyroclastic fissure produced by the 1969 eruption crosses Pendulum Cove (Smellie, 2002). On the contrary, Fumarole Bay is the location of the early volcanic edifice, the oldest exposed formation, and the area characterised by the highest ground temperatures across the island (Smellie et al., 2002). If interpreted with the extensive geochemical and geological records, these maps provide structural constraints to define the complex magmatic evolution of the island (Geyer et al., 2019).

The workflow highlights the need for inversion-specific data-selection strategies for volcanic imaging. If based only on standard attributes like the SNR ratio, the reduction in usable seismic waveforms leads to lower stability and robustness of the solution than with the current workflow (Table 1). A combination of standard and inversion-specific automatic selections followed by a visual analysis on the final dataset is a sequence that can be easily implemented on any active and passive dataset. The only time-consuming step remains the visual analysis. The automatic selection was unable to recognize about 10% of traces that were worsening residuals without adding useful information. While it was largely non-influential for a final interpretation of our results (compare panels d and e) in Figures 5D,E, 4, we cannot ensure that a fully automatic selection would be as successful with another dataset.

The sequence chosen to apply selection parameters is irrelevant if the last automatic selection is performed using the attribute that defines the data quality in the tomographic procedure. In our case, this parameter is the correlation coefficient of the coda decay. It is the quality of a P- or S-wave picks in travel-time tomography. A successful selection will substantially reduce the dataset without deteriorating the resolution in the area of interest, allowing to reconstruct smaller-scale details without redundancy in the data. In the procedure, we used the similarity between maps obtained at different frequencies as an additional marker of solution stability. This qualitative approach can be likely improved using a 2D correlation analysis.

While different frequencies theoretically map anomalies at different scales, these differences are usually minimal when using active data at volcanoes (Prudencio et al., 2013, 2015a,b; Ibáñez et al., 2017). However, a comparison with the local geology could confirm if the residual differences are linked to volcanic structures. The area resolved after the selection is smaller than the one resolved using Dataset 1 (Figure 6B) at 2 km node spacing, and generally interpreted in attenuation tomography studies (Prudencio et al., 2013, 2015a; Del Pezzo et al., 2018). However, our results demonstrate that this illumination likely overestimates the effective resolution potential of the dataset, primarily because the misfit between data and model is measured inadequately. The result can be the failed detection of primary features, as the NNW-SSE trend of the central high-attenuation anomaly. In Figure 3B, we compare the results obtained at the end of our iterations with the contour of the homogeneous bodies obtained by Prudencio et al. (2013), where such a trend is absent, especially at higher frequencies. NNW-SSE is the direction of extension of the Bransfield Strait underlined by the strike of several normal faults and alignment of the eruptive centres between 1967 and 1970 (Martí et al., 1996; Smellie et al., 2002; Geyer et al., 2019). This trend is just visible in velocity tomography maps (Zandomeneghi et al., 2009) and absent from previous attenuation studies (Prudencio et al., 2013; 2015a).

Seismic tomography models remain “just models” if they are not compared with the extensive interdisciplinary knowledge generally available at each volcano. This is particularly true at Deception Island, where researchers have provided some of the most extensive geological, geophysical, tectonic and geochemical reconstructions of magma feeding systems, especially for an ice-capped volcano that has erupted within the last century. Once compared to this extensive interdisciplinary knowledge within a geographic information system (GIS), the new model could provide a decisive piece to the puzzle of how this volcano has evolved, fed, and erupted. Apparently, the maps better fit geological and geochemical knowledge about the volcano (Martí et al., 1996; Geyer et al., 2019). They can thus provide an essential link between what we know from field and modelling studies and what we can image of the volcano interior.

This work is a stepping stone to produce more refined, sounder tomographic models of volcanoes. Active seismic experiments are rapidly becoming the standard in volcano tomography. Here, we demonstrate that efficient data selection strategies can retrieve stable and resolved anomalies that remain blurred without them. Once applied to other available active datasets, the workflow could reveal fine details of the volcanic structures that have remained invisible but could be essential to understand the volcano dynamics. Its application to passive seismicity is certainly more challenging, given the uncertainties associated with volcano seismicity detection and characterisation. At the same time, selection strategies targeting specific tomographic techniques could drastically improve detection of structures at hazardous volcanoes with decades of seismic records, like Mt. Etna (Italy) or Mount St. Helens (US), where data redundancy is most likely.

6 Conclusions and Future Outlooks

An inversion-specific semi-automated selection strategy applied to an active seismic dataset recorded at Deception volcano improves stability and robustness of tomographic maps exploiting amplitude information. The combination of standard and inversion-specific selection attributes improves images obtained with different node spacing and at multiple frequencies, showing a consistent picture of the volcano interior. These maps are compatible with existing attenuation maps. The inversion for coda attenuation using the final dataset shows higher resolution on the centre of the caldera at the expense of lateral illumination. The images highlight sites of eruptions and extensional trends, which, if confirmed by comparison with the extensive geological and geochemical records, could better link the present state of the caldera with its geological past.

Volcano tomography using active datasets is now well past its infancy. Our results demonstrate that it cannot simply rely on data-selection strategies taken from global tomography or seismic exploration in oil and gas. Attributes like coda attenuation are not part of standard processing procedures for seismic imaging. Our method focuses on object-oriented data quality, first evidencing the most prominent standard attributed biasing results (the percentage of zeroes across the dataset) and then selecting datasets to optimise the attributes used for the inversion. The results prove that using only standard quality assessments, as the signal-to-noise ratios, leads to trade-offs and unnecessary loss of information. The same procedure can be defined for any attribute used to do imaging, and the method is easily extendable to passive datasets that are more relevant for volcano-monitoring institutions. In the long-range, the adaptation of these workflows to the detection of seismic signals produced by the volcano could help the long-standing effort of the community to recognise pre-eruptive signals. Once combined with the increasing interdisciplinary knowledge available at Deception Island and other volcanoes, their implementation in passive tomography can help better constrain the interpretation of pre-existing structures, current processes and future eruptions by avoiding trade-offs from redundant data.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/RobertoGuardo/QcDataCleaning.

Author Contributions

RG designed the data cleaning code and its development, generated the maps and wrote the first draft text. LD guided the overarching research direction and contributed to data interpretation and manuscript writing.

Funding

RG acknowledges the financial support of the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) Argentina. TeMaS–Terrestrial Magmatic Systems Research Area of the Johannes Gutenberg University (Landesinitiative des Landes Rheinland-Pfalz) privided additional funding for the research.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are very grateful to Dr. Janire Prudencio for providing us with the original TOMODEC2005 dataset before its publication and helping us assess the starting dataset.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.849152/full#supplementary-material

Footnotes

¹MuRAT2D and MuRAT3D are open access Matlab codes available on GitHub, at https://lucadesiena.github.io/MuRAT/

References

Achauer, U., Evans, J. R., and Stauber, D. A. (1988). High-resolution Seismic Tomography of Compressional Wave Velocity Structure at Newberry Volcano, Oregon Cascade Range. J. Geophys. Res. 93, 10135–10147. doi:10.1029/jb093ib09p10135

CrossRef Full Text | Google Scholar

Aster, R. C., Borchers, B., and Thurber, C. H. (2018). Parameter Estimation and Inverse Problems. Amsterdam, Netherlands: Elsevier.

Google Scholar

Battaglia, J., Zollo, A., Virieux, J., and Dello Iacono, D. (2008). Merging Active and Passive Data Sets in Traveltime Tomography: the Case Study of Campi Flegrei Caldera (Southern Italy). Geophys. Prospect 56, 555–573. doi:10.1111/j.1365-2478.2007.00687.x

CrossRef Full Text | Google Scholar

Bedrosian, P. A., Peacock, J. R., Bowles-Martinez, E., Schultz, A., and Hill, G. J. (2018). Crustal Inheritance and a Top-Down Control on Arc Magmatism at Mount st helens. Nat. Geosci 11, 865–870. doi:10.1038/s41561-018-0217-2

CrossRef Full Text | Google Scholar

Ben-Zvi, T., Wilcock, W. S. D., Barclay, A. H., Zandomeneghi, D., Ibáñez, J. M., and Almendros, J. (2009). The P-Wave Velocity Structure of Deception Island, Antarctica, from Two-Dimensional Seismic Tomography. J. Volcanology Geothermal Res. 180, 67–80. doi:10.1016/j.jvolgeores.2008.11.020

CrossRef Full Text | Google Scholar

Bianco, F., and Zaccarelli, L. (2009). A Reappraisal of Shear Wave Splitting Parameters from Italian Active Volcanic Areas through a Semiautomatic Algorithm. J. Seismol 13, 253–266. doi:10.1007/s10950-008-9125-z

CrossRef Full Text | Google Scholar

Borleanu, F., De Siena, L., Thomas, C., Popa, M., and Radulian, M. (2017). Seismic Scattering and Absorption Mapping from Intermediate-Depth Earthquakes Reveals Complex Tectonic Interactions Acting in the Vrancea Region and Surroundings (Romania). Tectonophysics 706-707, 129–142. doi:10.1016/j.tecto.2017.04.013

CrossRef Full Text | Google Scholar

Calvet, M., and Margerin, L. (2013). Lapse-time Dependence of Coda Q: Anisotropic Multiple-Scattering Models and Application to the Pyrenees. Bull. Seismological Soc. America 103, 1993–2010. doi:10.1785/0120120239

CrossRef Full Text | Google Scholar

Cortés, G., Benitez, M. C., García, L., Álvarez, I., and Ibanez, J. M. (2015). A Comparative Study of Dimensionality Reduction Algorithms Applied to Volcano-Seismic Signals. IEEE J. Selected Top. Appl. Earth Observations Remote Sensing 9, 253–263.

Google Scholar

Cortés, G., Carniel, R., Lesage, P., Mendoza, M., and Della Lucia, I. (2020). Practical Volcano-independent Recognition of Seismic Events: Vulcan. Ears Project. Front. Earth Sci. 8, 702.

Google Scholar

De Landro, G., Serlenga, V., Russo, G., Amoroso, O., Festa, G., Bruno, P. P., et al. (2017). 3d Ultra-high Resolution Seismic Imaging of Shallow Solfatara Crater in Campi Flegrei (italy): New Insights on Deep Hydrothermal Fluid Circulation Processes. Sci. Rep. 7, 3412. doi:10.1038/s41598-017-03604-0

PubMed Abstract | CrossRef Full Text | Google Scholar

De Siena, L., Chiodini, G., Vilardo, G., Del Pezzo, E., Castellano, M., Colombelli, S., et al. (2017b). Source and Dynamics of a Volcanic Caldera Unrest: Campi Flegrei, 1983-84. Sci. Rep. 7, 8099. doi:10.1038/s41598-017-08192-7

PubMed Abstract | CrossRef Full Text | Google Scholar

De Siena, L., Amoruso, A., Pezzo, E. D., Wakeford, Z., Castellano, M., and Crescentini, L. (2017a). Space-weighted Seismic Attenuation Mapping of the Aseismic Source of Campi Flegrei 1983?1984 Unrest. Geophys. Res. Lett. 2017, n/a. doi:10.1002/2017GL072507

CrossRef Full Text | Google Scholar

De Siena, L., Calvet, M., Watson, K. J., Jonkers, A. R. T., and Thomas, C. (2016). Seismic Scattering and Absorption Mapping of Debris Flows, Feeding Paths, and Tectonic Units at Mount St. Helens Volcano. Earth Planet. Sci. Lett. 442, 21–31. doi:10.1016/j.epsl.2016.02.026

CrossRef Full Text | Google Scholar

De Siena, L., Thomas, C., and Aster, R. (2014). Multi-scale Reasonable Attenuation Tomography Analysis (Murat): An Imaging Algorithm Designed for Volcanic Regions. J. volcanology geothermal Res. 277, 22–35. doi:10.1016/j.jvolgeores.2014.03.009

CrossRef Full Text | Google Scholar

Del Pezzo, E., De La Torre, A., Bianco, F., Ibanez, J., Gabrielli, S., and De Siena, L. (2018). Numerically Calculated 3D Space-Weighting Functions to Image Crustal Volcanic Structures Using Diffuse Coda Waves. Geosciences 8, 175. doi:10.3390/geosciences8050175

CrossRef Full Text | Google Scholar

Del Pezzo, E., Ibanez, J., Prudencio, J., Bianco, F., and De Siena, L. (2016). Absorption and Scattering 2-D Volcano Images from Numerically Calculated Space-Weighting Functions. Geophys. J. Int. 206, 742–756.

Google Scholar

Evans, J. R., and Zucca, J. J. (1988). Active High-Resolution Seismic Tomography of Compressional Wave Velocity and Attenuation Structure at Medicine Lake Volcano, Northern California Cascade Range. J. Geophys. Res. 93, 15016–15036. doi:10.1029/jb093ib12p15016

CrossRef Full Text | Google Scholar

Gabrielli, S., De Siena, L., Napolitano, F., and Del Pezzo, E. (2020). Understanding Seismic Path Biases and Magmatic Activity at Mount st helens Volcano before its 2004 Eruption. Geophys. J. Int. 222, 169–188. doi:10.1093/gji/ggaa154

CrossRef Full Text | Google Scholar

García-Yeguas, A., Koulakov, I., Ibáñez, J. M., and Rietbrock, A. (2012). High Resolution 3d P Wave Velocity Structure beneath Tenerife Island (Canary Islands, spain) Based on Tomographic Inversion of Active-Source Data. J. Geophys. Res. Solid Earth 117.

Google Scholar

Gasparini, P., and Group, T. W. (1998). Looking inside Mt. Vesuvius. Eos Trans. AGU 79, 229. doi:10.1029/98eo00165

CrossRef Full Text | Google Scholar

Geyer, A., Álvarez-Valero, A. M., Gisbert, G., Aulinas, M., Hernández-Barreña, D., Lobo, A., et al. (2019). Deciphering the Evolution of Deception Island's Magmatic System. Sci. Rep. 9, 373. doi:10.1038/s41598-018-36188-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hooft, E. E. E., Heath, B. A., Toomey, D. R., Paulatto, M., Papazachos, C. B., Nomikou, P., et al. (2019). Seismic Imaging of Santorini: Subsurface Constraints on Caldera Collapse and Present-Day Magma Recharge. Earth Planet. Sci. Lett. 514, 48–61. doi:10.1016/j.epsl.2019.02.033

CrossRef Full Text | Google Scholar

Ibáñez, J. M., Díaz-Moreno, A., Prudencio, J., Zandomeneghi, D., Wilcock, W., Barclay, A., et al. (2017). Database of Multi-Parametric Geophysical Data from the TOMO-DEC experiment on Deception Island, Antarctica. Scientific data 4, 170128.

PubMed Abstract | Google Scholar

Ibáñez, J. M., Prudencio, J., Díaz-Moreno, A., Patanè, D., Puglisi, G., Lühr, B.-G., et al. (2016). The Tomo-etna experiment: an Imaging Active Campaign at Mt. etna Volcano. Context, Main Objectives, Working-Plans and Involved Research Projects. Ann. Geophys. 59, 0426.

Google Scholar

Koulakov, I. (2013). Studying Deep Sources of Volcanism Using Multiscale Seismic Tomography. J. Volcanology Geothermal Res. 257, 205–226. doi:10.1016/j.jvolgeores.2013.03.012

CrossRef Full Text | Google Scholar

Lecocq, T., Hicks, S. P., Van Noten, K., van Wijk, K., Koelemeijer, P., De Plaen, R. S., et al. (2020). Global Quieting of High-Frequency Seismic Noise Due to COVID-19 Pandemic Lockdown Measures. Science 369, 1338. doi:10.1126/science.abd2438

PubMed Abstract | CrossRef Full Text | Google Scholar

Lees, J. M. (2007). Seismic Tomography of Magmatic Systems. J. Volcanology Geothermal Res. 167, 37–56. doi:10.1016/j.jvolgeores.2007.06.008

CrossRef Full Text | Google Scholar

Martí, J., Vila, J., and Rey, J. (1996). Deception Island (Bransfield Strait, Antarctica): an Example of a Volcanic Caldera Developed by Extensional Tectonics. Geol. Soc. Lond. Spec. Publications 110, 253–265.

Google Scholar

Mayor, J., Calvet, M., Margerin, L., Vanderhaeghe, O., and Traversa, P. (2016). Crustal Structure of the Alps as Seen by Attenuation Tomography. Earth Planet. Sci. Lett. 439, 71–80. doi:10.1016/j.epsl.2016.01.025

CrossRef Full Text | Google Scholar

Napolitano, F., De Siena, L., Gervasi, A., Guerra, I., Scarpa, R., and La Rocca, M. (2020). Scattering and Absorption Imaging of a Highly Fractured Fluid-Filled Seismogenetic Volume in a Region of Slow Deformation. Geosci. Front. 11, 989–998. doi:10.1016/j.gsf.2019.09.014

CrossRef Full Text | Google Scholar

Pang, J., Cheng, F., Shen, C., Dai, T., Ning, L., and Zhang, K. (2019). Automatic Passive Data Selection in Time Domain for Imaging Near-Surface Surface Waves. J. Appl. Geophys. 162, 108–117. doi:10.1016/j.jappgeo.2018.12.018

CrossRef Full Text | Google Scholar

Prudencio, J., De Siena, L., Ibáñez, J. M., Del Pezzo, E., García-Yeguas, A., and Díaz-Moreno, A. (2015a). The 3D Attenuation Structure of Deception Island (Antarctica). Surv. Geophys. 36, 371–390. doi:10.1007/s10712-015-9322-6

CrossRef Full Text | Google Scholar

Prudencio, J. (2013). From 2D to 3D Attenuation Tomography in Volcanoes: The Study of Tenerife (Canary Islands) and Deception Island (Antarctica). Ph.D. thesis (Granada, Spain: Universidad de Granada).

Prudencio, J., Ibáñez, J. M., Del Pezzo, E., Martí, J., García-Yeguas, A., and De Siena, L. (2015b). 3d Attenuation Tomography of the Volcanic Island of Tenerife (Canary Islands). Surv. Geophys. 36, 693–716. doi:10.1007/s10712-015-9333-3

CrossRef Full Text | Google Scholar

Prudencio, J., Ibáñez, J. M., García-Yeguas, A., Del Pezzo, E., and Posadas, A. M. (2013). Spatial Distribution of Intrinsic and Scattering Seismic Attenuation in Active Volcanic Islands - II: Deception Island Images. Geophys. J. Int. 195, 1957–1969. doi:10.1093/gji/ggt360

CrossRef Full Text | Google Scholar

Rawlinson, N., Pozgay, S., and Fishwick, S. (2010). Seismic Tomography: a Window into Deep Earth. Phys. Earth Planet. Interiors 178, 101–135. doi:10.1016/j.pepi.2009.10.002

CrossRef Full Text | Google Scholar

Rawlinson, N., and Spakman, W. (2016). On the Use of Sensitivity Tests in Seismic Tomography. Geophys. J. Int. 205, 1221–1243. doi:10.1093/gji/ggw084

CrossRef Full Text | Google Scholar

Romero, J. E., Titos, M., Bueno, Á., Álvarez, I., García, L., Torre, Á. d. l., et al. (2016). Apasvo: a Free Software Tool for Automatic P-phase Picking and Event Detection in Seismic Traces. Comput. Geosciences 90, 213–220. doi:10.1016/j.cageo.2016.02.004

CrossRef Full Text | Google Scholar

Sato, H., Fehler, M. C., and Maeda, T. (2012). Seismic Wave Propagation and Scattering in the Heterogeneous Earth. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Serlenga, V., de Lorenzo, S., Russo, G., Amoroso, O., Garambois, S., Virieux, J., et al. (2016). A Three-Dimensional Qp Imaging of the Shallowest Subsurface of Campi Flegrei Offshore Caldera, Southern italy. Geophys. Res. Lett. 43, 11–209. doi:10.1002/2016gl071140

CrossRef Full Text | Google Scholar

Siniscalchi, A., Tripaldi, S., Romano, G., Chiodini, G., Improta, L., Petrillo, Z., et al. (2019). Reservoir Structure and Hydraulic Properties of the Campi Flegrei Geothermal System Inferred by Audiomagnetotelluric, Geochemical, and Seismicity Study. J. Geophys. Res. Solid Earth 124, 5336–5356. doi:10.1029/2018jb016514

CrossRef Full Text | Google Scholar

Sketsiou, P., Napolitano, F., Zenonos, A., and De Siena, L. (2020). New Insights into Seismic Absorption Imaging. Phys. Earth Planet. Interiors 298, 106337. doi:10.1016/j.pepi.2019.106337

CrossRef Full Text | Google Scholar

Smellie, J., López-Martínez, J., Headland, R., Hernández-Cifuentes, F., Maestro, A., Millar, I., et al. (2002). Geology and Geomorphology of Deception Island. Cambridge: British Antarctic Survey.

Google Scholar

Smellie, J. L. (2002). The 1969 Subglacial Eruption on Deception Island (Antarctica): Events and Processes during an Eruption beneath a Thin Glacier and Implications for Volcanic Hazards. Geol. Soc. Lond. Spec. Publications 202, 59–79. doi:10.1144/gsl.sp.2002.202.01.04

CrossRef Full Text | Google Scholar

Ulberg, C. W., Creager, K. C., Moran, S. C., Abers, G. A., Thelen, W. A., Levander, A., et al. (2020). Local Source Vp and vs Tomography in the Mount St. Helens Region with the Imush Broadband Array. Geochem. Geophys. Geosystems 21, e2019GC008888. doi:10.1029/2019gc008888

CrossRef Full Text | Google Scholar

Valentine, A. P., and Woodhouse, J. H. (2010). Approaches to Automated Data Selection for Global Seismic Tomography. Geophys. J. Int. 182, 1001–1012. doi:10.1111/j.1365-246x.2010.04658.x

CrossRef Full Text | Google Scholar

Wegler, U. (2003). Analysis of Multiple Scattering at Vesuvius Volcano, Italy, Using Data of the TomoVes Active Seismic experiment. J. volcanology geothermal Res. 128, 45–63. doi:10.1016/s0377-0273(03)00246-4

CrossRef Full Text | Google Scholar

Wegler, U., and Lühr, B.-G. (2001). Scattering Behaviour at Merapi Volcano (Java) Revealed from an Active Seismic experiment. Geophys. J. Int. 145, 579–592. doi:10.1046/j.1365-246x.2001.01390.x

CrossRef Full Text | Google Scholar

Zandomeneghi, D., Barclay, A., Almendros, J., Ibañez Godoy, J. M., Wilcock, W. S., and Ben-Zvi, T. (2009). Crustal Structure of Deception Island Volcano from P Wave Seismic Tomography: Tectonic and Volcanic Implications. J. Geophys. Res. Solid Earth 114. doi:10.1029/2008jb006119

CrossRef Full Text | Google Scholar

Zollo, A., Maercklin, N., Vassallo, M., Dello Iacono, D., Virieux, J., and Gasparini, P. (2008). Seismic Reflections Reveal a Massive Melt Layer Feeding Campi Flegrei Caldera. Geophys. Res. Lett. 35. doi:10.1029/2008gl034242

CrossRef Full Text | Google Scholar