Deformation Prediction of Tunnel-Surrounding Rock Considering the Time Effect of the Viscosity Coefficient: A Case of an NATM-Excavated Tunnel

Considering engineering problems such as complicated stress and the difficulty in controlling large deformation while a tunnel passes through a soft rock stratum, a theoretical prediction model of convergence deformation of tunnel-surrounding rock is proposed. Based on the longitudinal displacement profile curve reflecting the “space effect” of the excavation surface, the Hoek formula with better applicability was introduced to analyze and theoretically deduct the “time–space effect comprehensively.” By taking the influence of the “time effect” coefficient into account, an improved Nishihara model was established to derive the analytical equation of the viscoelastic–viscoplastic convergence of surrounding rock. Taking the Dingxi Tunnel of Wujing Expressway in Hunan Province, the physical and mechanical parameters of surrounding rock in the tunnel were firstly determined then they were used to calculate and predict the vault down of three typical sections with the scoping equation of surrounding rock deformation. Based on the calculation results, the causes of the differences between the measured and theoretical values were analyzed; moreover, it is indicated that the minimum root-mean-square error is 1.68, the minimum average error is 1.3%, and the correlation coefficient is 0.99. The comparison shows that the theoretical prediction results agree well with the corresponding field test results. The improved Nishihara model can accurately predict the final deformation of the surrounding rock. Simultaneously, it is also proved that the relevant parameters and the hypothesis and correlation of the nonlinear viscosity coefficient equation are reasonable, with particular effectiveness and applicability in practical engineering. This study is significant for further studying the tunnel-surrounding rock’s stability and accumulating theoretical and practical experience to develop rheological theory.

1 Introduction

In China, the center of tunnel construction is gradually shifting to the southwest and northwest. The construction difficulties are also shifting to high-stress areas with complex geology. Among them, carbonaceous shale is widely distributed in the strata of Southwest China. Because carbonaceous shale has the characteristics of obvious bedding development, low strength, and soft and easy disintegration, it has prominent rheological characteristics under a high-stress environment. Rheology is one of the important mechanical properties of rock, which is closely related to the long-term stability of rock mass engineering. Soft rock has distinct rheological properties. When tunnels cross such a layer, engineering problems, such as the complicated force and difficulty to control large deformation, are usually accompanied, severely restricting the construction and affecting the support’s long-term stability (Sun, 2007; Li et al., 2018). Therefore, scientific evaluation and prediction of surrounding rock deformation and stability according to the rheological characteristics of tunnel-surrounding rock are essential to guide on-site construction and feedback design and a necessary condition to ensure tunnel construction safety. At present, the rock rheological constitutive models used to describe the tunnel rock mass under excavation conditions mainly include (Song et al., 2018) the Kelvin, Bingham, Maxwell, Burgers, and Nishihara models. Among them, the Nishihara model can consider the viscoelastic characteristics of surrounding rock and the important characteristic of viscoplastic deformation. Therefore, the Nishihara model can describe the deformation of rock masses in tunnel engineering, such as sandstone, limestone, sandy shale, clay shale, and carbonaceous shale. To sum up, it is important to conduct further research on the deformation the mechanism of tunnel-surrounding rock under complex geological conditions, explore new methods for surrounding rock stability analysis, and establish a scientific prediction model, which can facilitate predictions of tunnel-surrounding rock deformation.

Some scholars have established constitutive creep models considering various effects by introducing different variables based on the Nishihara model (Shen et al., 2014; Li et al., 2014; Zhang et al., 2015; Li Z. Q. et al., 2017; Zhang J. X. et al., 2019). However, these models only consider the influence of a single variable and ignore the impact of time. At the same time, an improved Nishihara model was established based on the Nishihara model by considering different influencing factors, and it was also verified through the application. In the above aspects, a lot of important research work has been done to put forward many modified models for specific rock strata (Liu et al., 2017; Cao et al., 2017; Wang et al., 2018; Zhu et al., 2019; Jin et al., 2019; Wang et al., 2019; Li et al., 2020; Zhang L. et al., 2020). However, their general applicability is limited to a certain extent. In addition, based on the traditional Nishihara model, some scholars use a nonlinear viscoplastic body or clay tank to replace clay tank and viscoplastic body or use the series element method to establish the improved Nishihara model (Xu et al., 2015; Zhang et al., 2016; Ou and fang, 2017; Li Y. G. et al., 2017; Pu et al., 2017; Zhang Z. et al., 2020; Lin et al., 2020). Nonlinear improvements have been made to the existing models, but no research has been conducted on the time effects under nonlinear conditions. Considering the influence of time and stress on creep, some scholars established a nonlinear creep damage model and the corresponding constitutive equation (Feng et al., 2020; Liu W. et al., 2020; Yan et al., 2020; Liu Y. et al., 2020). However, they did not study the influence of this model on the damage and deformation of surrounding rocks.

Some scholars use the Nishihara model to study tunnel-surrounding rock deformation and deduce the analytical expression of tunnel-surrounding rock deformation based on the improved Nishihara model (Zhang, 2016; Xiao et al., 2017; Yu, X.Y. et al., 2018; Yu et al., 2019; Zhang B. et al., 2019, Zhang J.-Z. et al., 2019; Yu et al., 2020; Yu et al., 2019). In recent years, the prevalent artificial intelligence method (Huang et al., 2017; Zhou et al., 2017; Chen et al., 2019; Huang et al., 2020; Zhang K. et al., 2020; Zhu et al., 2020) provides a more potential development direction for tunnel construction deformation prediction. Combined with the application of deep learning algorithms and nonlinear theory, research on the multi-factor tunnel excavation system in complex geological environments shows excellent advantages (Melis et al., 2002; Huang et al., 2021; Huang et al., 2022). However, it is necessary to further combine the constitutive rock mass model and the viscoelastic plastic mechanics theory to give full play to this advantage.

In summary, previous scientific research achievements have made significant contributions to the optimization and improvement of the Nishihara model and the development of the prediction theory of tunnel-surrounding rock deformation, but there are still some shortcomings. In tunnel excavation, the surrounding rock will carry out stress redistribution from two dimensions of time and space. The time–space effect is an essential factor that must be considered in tunnel-surrounding rock deformation prediction. Therefore, based on the advantages of previous prediction methods, combined with the LDP curve reflecting the “spatial effect” of the excavation face, this study introduces the Hoek formula (Hoek, 2001) with better applicability to comprehensively analyze and theoretically deduce the “time–space effect”. Considering the time-space effect of the plastic viscosity coefficient, an improved Nishihara model is established to study the deformation process of surrounding rock in the process of tunnel excavation and support. The theoretical model is then established by rheological theory, and the convergence calculation formula of surrounding rock deformation is deduced. Finally, a comparative study is carried out combined with engineering cases to provide theoretical support and technical reference for the design and construction of tunnel engineering.

2 Viscoelastic–Viscoplastic Model

According to the previous engineering projects and indoor experimental research, the weak rheological properties surrounding rock with dissolution crack development, weak interlayer, gob, fault, and fracture zone are significant. Rheological properties of the weak surrounding rock are more susceptible to external forces, exhibiting nonlinear characteristics. The influence of viscous coefficients is not negligible, and it is closely related to the stress-strain state of surrounding rock. This study derived the analytical equation of the viscoelastic–viscoplastic convergence of surrounding rock based on the improved Nishihara model with the Matlab software.

2.1 Improved Nishihara Model

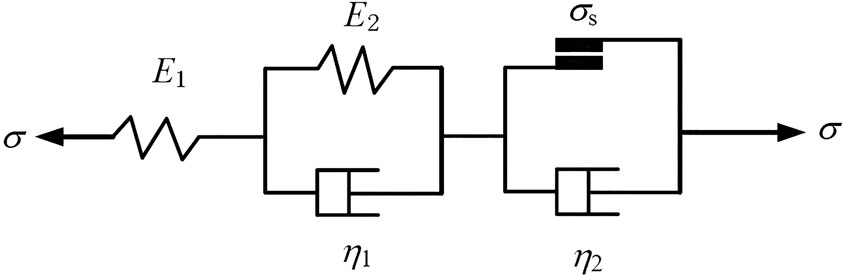
The traditional Nishihara model (Nishihara, 1957; Zhou et al., 2010) is composed of a Hooke body, Kelvin body, and Bingham body, as shown in Figure 1.

FIGURE 1

FIGURE 1. Nishihara model.

The viscosity coefficient ${\eta }_2$ in the traditional Nishihara model is replaced by the nonlinear viscoplastic coefficient $\eta \left(t\right)$ related to time, so the model becomes an unsteady Nishihara model. This study divides the model into two parts: the generalized Kelvin model and the nonlinear Bingham model. The viscoelastic and viscoplastic regions of the surrounding rock are analyzed. The improved Nishihara model is shown in Figure 2:where ${\eta }_1$, ${\eta }_2$, and $\eta \left(t\right)$ represent the coefficients of viscosity. $E_1$ and $E_2$ indicate the elastic modulus. ${\sigma }_s$ stands for the ultimate frictional resistance of St. Venant’s body.

FIGURE 2

FIGURE 2. Improved Nishihara model.

2.2 Basic Assumption

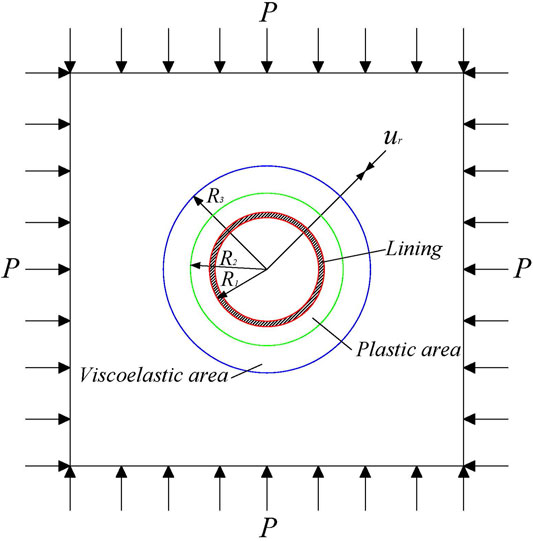
In this study, the calculation model assumes that the surrounding rock is a continuous isotropic rock mass mechanics model and does not consider the action of groundwater, and when the lateral pressure coefficient is λ(t), the viscoelastic plastic problem of stress and deformation of surrounding rock of a circular tunnel is assumed, and the original rock stress field is axisymmetric along the vertical direction. The viscoelastic–plastic surrounding rock mechanical model is shown in Figure 3. The radius of excavated tunnels is R₁, R₁-R₂, and R₂-R₃, representing ranges of the crack zone and plastic zone, while the elastic deformation zone should be from R₃ to infinity in theory.

FIGURE 3

FIGURE 3. Viscoelastic-plastic surrounding rock mechanic model.

In addition, many scholars have made theoretical assumptions and derivations based on experiments for the research on the expression of the nonlinear viscosity coefficient (Xiong et al., 2010; Yan et al., 2010). However, the results do not have universal adaptability. According to the nonlinear viscosity coefficient characteristics, this experiment is firstly expressed as Eq. 1: (whether it is a reasonable hypothesis, rationality will be verified in the sixth part of this study.)

$\eta \left(t\right)=\frac{t}{A+e^{-\frac{t}{B}}}(1)$

where A and B are constants related to the surrounding rock properties, which can be obtained from experimental data.

3 Viscoelastic Deformation Analysis

3.1 Generalized Kelvin Constitutive Equation

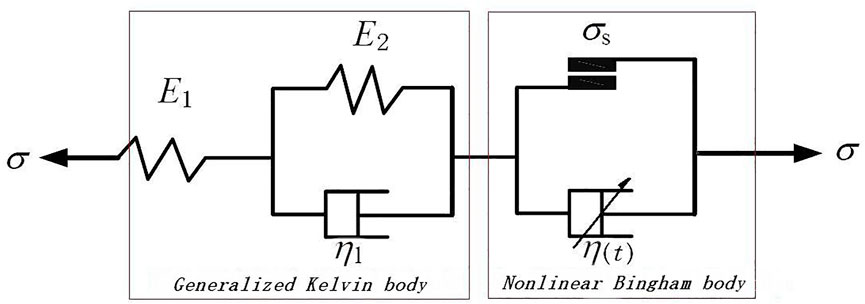
Based on the derivation method of the tunnel lining displacement in the Zhao et al. (2016), the theory and the relationship between “spatial effects” were improved by combining LDP curves, in which Hoek’s formula (Nishihara, 1957) was also introduced to conduct a comprehensive analysis and theoretical derivation of “space-time effects.”

The generalized Kelvin body analyzes the viscoelastic deformation. Considering that the shape changes only when the geometry undergoes elastoplastic deformation, it can be calculated because the volume deformation is almost negligible. According to the elastic mechanics, in the cylindrical coordinate system $(r,\theta ,z)$, due to the axial symmetry of the tunnel calculation model, all stress components are independent of the coordinate $\theta$, and the stress-strain is only a function of r, u. Therefore, the relationship between strain and displacement along the $(r,\theta )$ plane is as follows:

${\epsilon }_r=\frac{\partial u}{\partial r},{\epsilon }_{\theta }=\frac{u}{r}(2)$

${\epsilon }_{\theta }+{\epsilon }_r=\frac{u}{r}+\frac{\partial u}{\partial r}=0(3)$

then,

$u=\frac{A\left(t\right)}{r}(4)$

where $A\left(t\right)$ is a function of time, and substituting Eq. 4 into Eq. 2 yields:

${\epsilon }_r=\frac{\partial u}{\partial r}=-\frac{A\left(t\right)}{r},{\epsilon }_{\theta }=\frac{u}{r}=\frac{A\left(t\right)}{r^2}(5)$

The generalized Kelvin constitutive equation is transformed into a stress bias form, and the boundary condition, ${\sigma }_r={\sigma }_{\theta }=p,\overline{\sigma }=p$ when $r\to \infty$, is considered, and the axisymmetric condition can be expressed as follows:

$\frac{\partial }{\partial t}({\sigma }_r-p)+\frac{E_1+E_2}{{\eta }_1}({\sigma }_r-p)=-\frac{E_1\partial A\left(t\right)}{r^2\partial t}-\frac{E_1{E}_{2}A\left(t\right)}{r^2{\eta }_1}(6)$

where ${\sigma }_r$, ${\sigma }_{\theta }$, $\overline{\sigma }$—radial, circumferential, average stress;

${\epsilon }_r$, ${\epsilon }_{\theta }$—radial strain and circumferential strain;

$E_1$, $E_2$, ${\eta }_1$—instantaneous, viscous elastic modulus, and viscosity coefficient.

For the periphery of the tunnel, the “equivalent initial geo-stress” $p\left(x\right)$ corresponding to the displacement was introduced and substituted into Eq. 6 in the form of $p\left(x\right)=p_0\lambda \left(t\right)$. Considering the boundary condition of $r=r_0,\sigma =0$, the following relationship can be obtained:

$p_0\frac{d\lambda \left(t\right)}{dt}+\frac{E_1+E_2}{{\eta }_1}{p}_0\lambda \left(t\right)=\frac{E_{1}dA\left(t\right)}{r_0^{2}dt}-\frac{E_1{E}_{2}A\left(t\right)}{r_0^2{\eta }_1}(7)$

where $p_0$ is geo-stress.

3.2 Space Effect

To facilitate the study of the “space effects” of the working surface, we first consider the effects of elastic media. The “space effect” of the excavation surface is directly reflected in the radial displacement of the tunnel along the tunneling direction. This distribution curve is the longitudinal deformation profile curve, which is regarded as the LDP curve. At present, many scholars have made in-depth studies on LDP curves within the scope of “space effect.” Panet (1995) summarized the following approximate expressions by applying the finite-element analysis method of elasticity theory and combining the relationship between the measured radial displacement around the tunnel and the distance between the driving faces:

$\frac{u_m}{u_{m\infty }}=0.25+0.75\left[1-{\left(\frac{0.75}{0.75+x/R}\right)}^2\right](8)$

where R is the radius of the tunnel cave and x is the distance between the calculation section and the excavation face.

Hoek (1999) analyzed and fitted the field monitoring data of the Mingtam underground cavern project and summarized the following empirical expressions by using the related theory analysis method:

$\frac{u_m}{u_{m\infty }}={\left[1+e^{(-\frac{x}{1.1R})}\right]}^{-1.7}(9)$

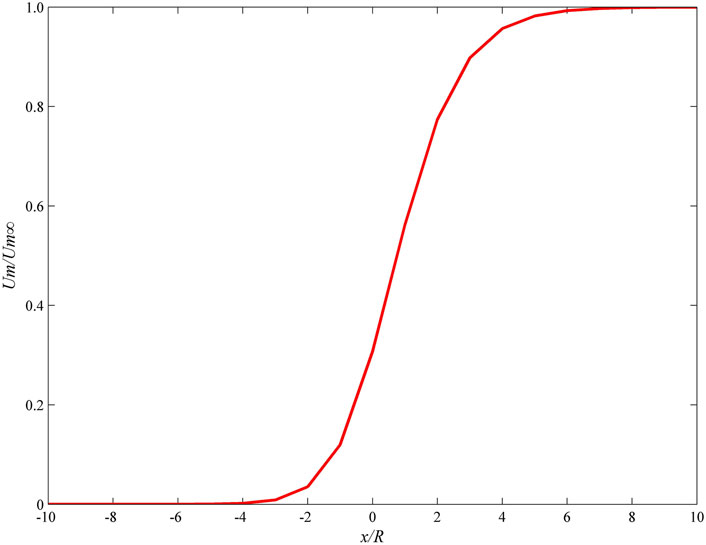
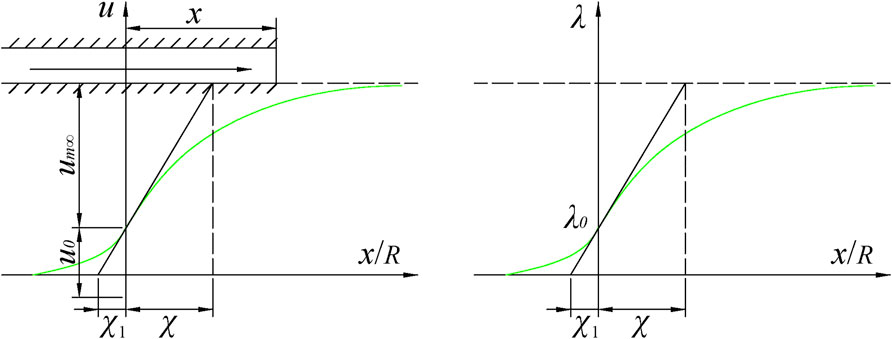
For the applicability of the above two formulas, Sun (2007) thinks that the Panet method overestimates the radial displacement of the tunnel, making it is easy to underestimate the supporting load in practical engineering and inducing the design unsafety. The result of the Hoek method agrees with the numerical analysis in the tunnel vault, waist, sidewall, and other parts, which shows that Hoek’s formula has stronger applicability and can better describe the “space effect” of the tunnel excavation surface. The radial displacement described by Hoek’s formula varies with the excavation surface, as shown in Figure 4.

FIGURE 4

FIGURE 4. Diagram of radial displacement described by Hoek formula changing with face excavation.

Therefore, this study transformed Hoek’s empirical formula:

Let $\chi =10x/\ln \left[\frac{1+e^{-\frac{x}{1.1R}}}{{\left[{(1+e^{-\frac{x}{1.1R}})}^{1.7}-1\right]}^{10}}\right]$, substitution Eq. 9:

The relationship between the radial displacement $u_m$ measured around the tunnel and the cross-section distance x measured at a distance from the working face is as follows:

$u_m=u_{m\infty }(1+e^{\frac{-x}{\chi }})(10)$

There is a relationship between $u_{m\infty }$ and constants $\chi$ as shown in Figure 5 below:

FIGURE 5

FIGURE 5. Radial displacement changes with the advancement of the tunneling surface.

Since the radial free displacement $u_0$ of surrounding rock had been generated before the excavation entry surface reached the cross-section of the survey point, the total displacement should be calculated as follows:

$u=u_{m\infty }+u_0=(u_{\infty }-u_0)(1+e^{\frac{-x}{\chi }})+u_0(11)$

If the equivalent initial geo-stress is $p\left(x\right)$, the relationship between displacement and equivalent initial geo-stress can be expressed as follows:

$u=\frac{1}{K_g}p\left(x\right)(12)$

Therefore, the above displacement should be proportional to the initial geo-stress, and Eq. 12 should be rewritten as follows:

$u=\frac{1}{K_g}{p}_0\lambda \left(x\right),p_0\lambda \left(x\right)=p_0\left(x\right)(13)$

where T is a constant relating to the characteristics of surrounding rock and the radius of the tunnel; Y is dimensionless.

Because $u_{\infty }=\frac{p_0}{K_g}$, then $u=u_{\infty }\lambda \left(x\right)$, after substituting Eq. 13 into Eq. 11:

$\lambda \left(x\right)=(1-\frac{u_0}{u_{\infty }})(1+e^{\frac{-x}{\chi }})+\frac{u_0}{u_{\infty }}(14)$

Let ${\lambda }_0=\frac{u_0}{u_{\infty }}$, as shown by Eq. 9, when $x/R=0$, then ${\lambda }_0=0.3078$. Then Eq. 14 can be simplified as:

$\lambda \left(x\right)=(1-{\lambda }_0)(1+e^{\frac{-x}{\chi }})+{\lambda }_0(15)$

According to Hoek’s empirical formula, the value of ${\lambda }_0$ is 0.3078. According to the symmetry and continuity of Figure 5, we can see that:

$\lambda \left(x\right)={\lambda }_0{e}^{\frac{-x}{{\chi }_1}},{\chi }_1=\frac{{\lambda }_0}{1-{\lambda }_0}\chi (16)$

3.3 Time Effect

Considering the influence of rock rheology, which has been neglected before, the Hoek formula is used to comprehensively analyze the “space effect” caused by the working face’s excavation and the “time effect” caused by the viscous effect of the surrounding rock. Assuming that the tunnel is driven forward at a continuous and uniform speed, and the driving speed is $\upsilon$, the simultaneous Eqs 15, 16 show that:

$\begin{array}{l}{\lambda }^e\left(t\right)=\{\begin{array}{l}1+(1-{\lambda }_0)e^{\frac{-t}{T_a}},t>0\\ {\lambda }_0{e}^{\frac{-t}{T_{a1}}},t\le 0\end{array}\\ T_a=\frac{\chi }{\upsilon },T_{a1}=\frac{{\chi }_1}{\upsilon },\end{array}(17)$

When $t>0$, the above ${\lambda }^e\left(t\right)$ expression is introduced into Eq. 7 to solve differential equations.

$\begin{array}{l}A\left(t\right)=-\frac{E_2{p}_0{r}_0^2{T}_a{\lambda }_0+E_2{p}_0{r}_0^2{T}_a-p_0{r}_0^2{\lambda }_0{\eta }_1+p_0{r}_0^2{\eta }_1}{E_1(T_a{E}_2-{\eta }_1)}{e}^{-\frac{t}{T_a}}\\ -\frac{p_0{r}_0^2{T}_a{\lambda }_0+p_0{r}_0^2{T}_a}{E_2{T}_a-{\eta }_1}{e}^{-\frac{t}{T_a}}+\frac{p_0{r}_0^2}{E_1}+\frac{p_0{r}_0^2}{E_2}+C{e}^{-\frac{E_2}{{\eta }_1}t}\end{array}(18)$

From the above formula, it can be seen that the displacement around the tunnel is $u^e=\frac{A\left(t\right)}{r}$; by taking into account $r=r_0$, Eq. 18 can be transformed into:

$\begin{array}{l}{u}^e=\frac{A\left(t\right)}{r_0}=-\frac{E_2{p}_0{r}_0{T}_a{\lambda }_0+E_2{p}_0{r}_0{T}_a-p_0{r}_0{\lambda }_0{\eta }_1+p_0{r}_0{\eta }_1}{E_1(T_a{E}_2-{\eta }_1)}{e}^{-\frac{t}{T_a}}\\ -\frac{p_0{r}_0{T}_a{\lambda }_0+p_0{r}_0{T}_a}{E_2{T}_a-{\eta }_1}{e}^{-\frac{t}{T_a}}+\frac{p_0{r}_0}{E_1}+\frac{p_0{r}_0}{E_2}+\frac{C}{r_0}{e}^{-\frac{E_2}{{\eta }_1}t}\end{array}(19)$

According to Eq. 19, when $t\to +\infty$, the limit displacement around the tunnel is $u_{\infty }^e=\frac{(E_1+E_2)p_0{r}_0}{E_1{E}_2}$ by calculating the upper limit. During the tunnel’s excavation, the surrounding rock in front of the working face is affected by the construction disturbance, promoting the redistribution of the stress in the surrounding rock, thus causing the initial displacement $u_0$ of the surrounding rock ahead.

To study the initial displacement, we should first discuss the case when $t\le 0$.

Equation 17 shows that when $t\le 0$, ${\lambda }^e\left(t\right)={\lambda }_0{e}^{\frac{-t}{T_{a1}}}$; when $t\to -\infty$, $A\left(t\right)=0$, so we can obtain:

$A\left(t\right)=u{e}^{\frac{(1-{\lambda }_0)t}{T_a{\lambda }_0}}(20)$

Because $u=\frac{\left[{\eta }_1+(E_1+E_2)T_{a1}\right]}{E_1(E_2{T}_{a1}+{\eta }_1)}{p}_0{\lambda }_0{r}_0^2$, when t = 0, there is:

$u_0=\frac{u}{r_0}=\frac{\left[{\eta }_1+(E_1+E_2)T_{a1}\right]}{E_1(E_2{T}_{a1}+{\eta }_1)}{p}_0{\lambda }_0{r}_0(21)$

Equation 21 shows that excavation speed directly affects the initial displacement $u_0$. If the tunneling speed is plodding, the viscous stress and strain of the surrounding rock will have enough time to be fully released. So, it can be concluded that as $\upsilon \to 0$, $T_{a1}=\frac{\chi }{\upsilon }\to \infty$. Then transform Eq. 21, then $u_0=\frac{\frac{\eta }{T_{a1}}+E_1+E_2}{E_1{E}_2+\frac{E_1\eta }{T_{a1}}}{p}_0{\lambda }_0{r}_0$, When $T_{a1}\to \infty$, $u_0\to \frac{E_1+E_2}{E_1{E}_2}{p}_0{\lambda }_0{r}_0$.

On the contrary, if the tunneling face is speedy, it is instantaneously annoying from infinity to the study’s monitoring section. The viscous stress-strain of the surrounding rock does not have sufficient time to release completely, and only the elastic deformation is emancipated. At this point, let us say: $\upsilon \to \infty$, then $T_{a1}=\frac{\chi }{\upsilon }\to 0$, so there is $u_0\to \frac{p_0{\lambda }_0{r}_0}{E_1}$. According to the above analysis, the initial displacement $u_0$ of the surrounding rock expressed by Eq. 20 is between the two extremes, namely:

$\frac{p_0{\lambda }_0{r}_0}{E_1}<u_0<\frac{E_1+E_2}{E_1{E}_2}{p}_0{\lambda }_0{r}_0(22)$

Let $E_{\infty }=\frac{E_1{E}_2}{E_1+E_2}$, the upper form is transformed into:

$\frac{p_0{\lambda }_0{r}_0}{E_1}<u_0<\frac{p_0{\lambda }_0{r}_0}{E_{\infty }}(23)$

Therefore, the viscoelastic deformation of the tunnel is $S^e=2(u^e-u_0)$.

4 Viscoelastic–Viscoplastic Deformation Analysis

4.1 Viscoplastic Deformation Analysis

In the process of tunnel excavation, besides the instantaneous elastic deformation released from the working face, the secondary stress generated by the stress redistribution of surrounding rock exceeds the yielding stress of the rock mass at that point, which results in the viscoplastic state that the deformation of surrounding rock increases with time. The “time effect” of rock rheology is related to viscoplastic flow in surrounding rock mass (Sun, 2007). This kind of viscous flow usually occurs in the weak surrounding rock with high stress, especially for the surrounding rock with well-developed joints and fissures and dissolution. It is also found that the nonlinear Bingham model is suitable for the rheological study of this kind of surrounding rock.

Considering that only when geo-materials undergo plastic deformation and volume deformation, the change of shape can be neglected, it is assumed that the volume of the plastic zone is constant, that is, the volume strain is zero. Then there are:

${\epsilon }_{\theta }+{\epsilon }_r=\frac{u^p}{r}+\frac{d{u}^p}{dr}=0(24)$

thus,

$u_p=\frac{A^p\left(t\right)}{r}(25)$

So the Bingham viscoplastic constitutive equation can be rewritten into the form of stress deviation. Furthermore, the boundary conditions are considered when $r\to \infty$, ${\sigma }_r={\sigma }_{\theta }=p,\overline{\sigma }=p$ and the axisymmetric state can be expressed as follows:

when $\sigma <{\sigma }_s$,

$\{\begin{array}{l}{\sigma }_r-\overline{\sigma }=-E({\epsilon }_r-\epsilon )\\ {\sigma }_{\theta }-\overline{\sigma }=-E({\epsilon }_{\theta }-\epsilon )\end{array}(26)$

Because there is no creep and stress relaxation in this case, we only analyze the second case

When $\sigma >{\sigma }_s$,

$\{\begin{array}{l}\frac{\partial ({\epsilon }_r-\overline{\epsilon })}{\partial t}=\frac{\partial ({\sigma }_r-\overline{\sigma })}{E\partial t}+\frac{({\sigma }_r-\overline{\sigma })-{\sigma }_s}{\eta \left(t\right)}\\ \frac{\partial ({\epsilon }_{\theta }-\overline{\epsilon })}{\partial t}=\frac{\partial ({\sigma }_{\theta }-\overline{\sigma })}{E\partial t}+\frac{({\sigma }_{\theta }-\overline{\sigma })-{\sigma }_s}{\eta \left(t\right)}\end{array}(27)$

When $r=r_0$, the ${\sigma }_r=0,\overline{\sigma }=p$, ${\epsilon }_r=-\frac{A^p\left(t\right)}{r_0^2},{\epsilon }_{\theta }=\frac{A^p\left(t\right)}{r_0^2}$ and axisymmetric conditions are substituted into Eq. 27, so $p$ is calculated in the form of $p=p\left(x\right)=p_0{\lambda }^p\left(t\right)$:

$\frac{d{A}^p\left(t\right)}{r_0^{2}dt}=\frac{p_{0}d{\lambda }^p\left(t\right)}{Edt}+\frac{p_0{\lambda }^p\left(t\right)-{\sigma }_s}{\eta \left(t\right)}(28)$

When $t<0$, the tunnel has not been excavated to the monitoring section, and the viscoplastic deformation of the surrounding rock of the section is minimal, which can be almost ignored. Therefore, it is only necessary to study the deformation after excavation. when $t>0$, $\lambda \left(t\right)=1+(1-{\lambda }_0)e^{\frac{-t}{T_a}}$ is substituted into Eq. 28 to get:

$\frac{d{A}^p\left(t\right)}{r_0^{2}dt}+\frac{p_0(1-{\lambda }_0)e^{-\frac{t}{T_a}}}{E{T}_a}-\frac{p_0\left[1+(1-{\lambda }_0)e^{-\frac{t}{T_a}}\right]+{\sigma }_s}{\eta \left(t\right)}=0(29)$

The above Eq. 29 is solved to obtain the expression $A^p\left(t\right)$ as follows:

$A^p\left(t\right)=\frac{p_0{T}_a{\lambda }_0{r}_0^2{e}^{-\frac{t}{T_a}}}{\eta \left(t\right)}-\frac{p_0{\lambda }_0{r}_0^2{e}^{-\frac{t}{T_a}}}{E}-\frac{p_0{T}_a{r}_0^2{e}^{-\frac{t}{T_a}}}{\eta \left(t\right)}+\frac{p_0{r}_0^2{e}^{-\frac{t}{T_a}}}{E}+\frac{r_0^2(p_0+{\sigma }_s)}{\eta \left(t\right)}t(30)$

$\eta \left(t\right)=\frac{t}{A+e^{-\frac{t}{B}}}$ is substituted into Eq. 30 can be obtained:

$u^p=\frac{p_0{T}_a{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{t}(A+e^{-\frac{t}{B}})-\frac{p_0{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{E}-\frac{p_0{T}_a{r}_0{e}^{-\frac{t}{T_a}}}{t}(A+e^{-\frac{t}{B}})+\frac{p_0{r}_0{e}^{-\frac{t}{T_a}}}{E}+r_0(p_0+{\sigma }_s)(A+e^{-\frac{t}{B}})(31)$

When $t\to +\infty$, $u_{\infty }^p=A^p\left(t\right)/r_0=\frac{r_0(p_0+{\sigma }_s)}{\eta \left(t\right)}t=A{r}_0(p_0+{\sigma }_s)$.

Therefore, the viscoplastic deformation of the tunnel is $S^p=2u^p$.

4.2 Viscoelastic–Viscoplastic Deformation Analysis

The viscoelastic theoretical solution of surrounding rock deformation mentioned above can be considered as the stress redistribution of surrounding rock after tunnel excavation is completed instantaneously with the elastic or elastic-plastic wave’s propagation velocity. The viscoelastic convergence expression of surrounding rock is $S^e=2(u^e+u_0)$, and the viscoplastic convergence expression is $S^p=2u^p$. Therefore, the analytical formula of viscoelastic–viscoplastic convergence of surrounding rock is developed as follows:

$\{\begin{array}{l}S=2(u^e+u^p+u_0)\\ u^e=-\frac{E_2{p}_0{r}_0{T}_a{\lambda }_0+E_2{p}_0{r}_0{T}_a-p_0{r}_0{\lambda }_0{\eta }_1+p_0{r}_0{\eta }_1}{E_1(T_a{E}_2-{\eta }_1)}{e}^{-\frac{t}{T_a}}\\ -\frac{p_0{r}_0{T}_a{\lambda }_0+p_0{r}_0{T}_a}{E_2{T}_a-{\eta }_1}{e}^{-\frac{t}{T_a}}+\frac{(E_2+E_1)p_0{r}_0}{E_1{E}_2}+\frac{C}{r_0}{e}^{-\frac{E_2}{{\eta }_1}t}\\ u^p=\frac{p_0{T}_a{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{t}(A+e^{-\frac{t}{B}})-\frac{p_0{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{E}-\frac{p_0{T}_a{r}_0{e}^{-\frac{t}{T_a}}}{t}\\ (A+e^{-\frac{t}{B}})+\frac{p_0{r}_0{e}^{-\frac{t}{T_a}}}{E}+r_0(p_0+{\sigma }_s)(A+e^{-\frac{t}{B}})\\ u_{\infty }^e=\frac{(E_1+E_2)p_0{r}_0}{E_1{E}_2},u_{\infty }^p=A{r}_0(p_0+{\sigma }_s),\frac{p_0{\lambda }_0{r}_0}{E_1}<u_0<\frac{p_0{\lambda }_0{r}_0}{E_{\infty }}\end{array}(32)$

where ${\sigma }_s$ is the yield stress; $E_{\infty }=\frac{E_1{E}_2}{E_1+E_2}$; ${\eta }_1$ is the viscosity coefficients; A and B are constants relating to the properties of the surrounding rock, and C is a constant.

In Eq. 32, excavation speed $\upsilon$ cannot approach infinity in tunnel engineering; the elastic deformation cannot be completed instantaneously in actual engineering, and the initial deformation $u_0$ can hardly be measured. Therefore, in order to make the calculated value more in line with the field monitored data, the above expression is simplified as $S_s=2(u^e+u^p)$ for calculation.

5 Case Analysis

According to the above analysis, if the initial stress state and mechanical parameters of surrounding rock before tunneling are given out, the deformation of the surrounding rock can be calculated according to the theoretical formula. This study verifies the rationality of theoretical derivation through the example of the Dingxi tunnel monitoring project of Wujing Expressway in Hunan Province and predicts the final deformation of surrounding rock.

5.1 Project Overview

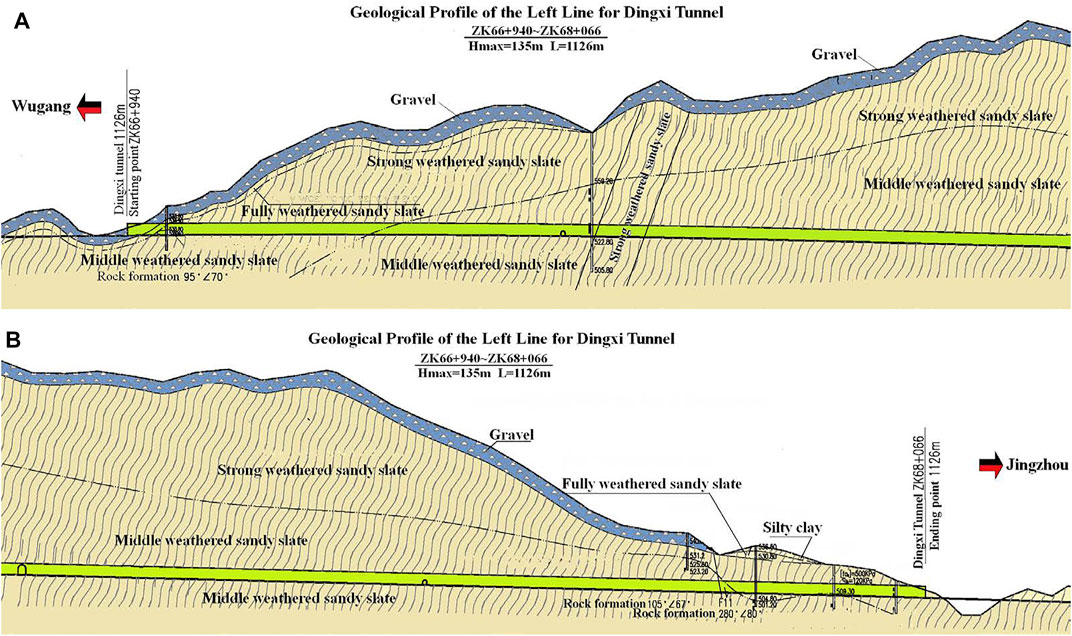
The Dingxi tunnel of the Wujing Expressway in Hunan Province is located in Huaihua City. The tunnel area is in a low mountainous landform with large terrain fluctuations, where the midline elevation is 510–648 m and the maximum height difference is about 148 m, as shown in Figure 6. The starting pile number of the left tunnel is ZK66 + 940-ZK68 + 066, with a length of 1,126 m, while the right tunnel is K66 + 926-K67 + 999 with a length of 1,073 m.

FIGURE 6

FIGURE 6. Geological profile of the left line of Dingxi tunnel. (A) Import side. (B) Exit side

In this case, three typical sections of ZK67 + 220 (Grade V), ZK67 + 500 (Grade VI), and ZK67 + 900 (Grade V) on the left line of the Dingxi tunnel are selected for research. The detailed geological evaluation is as follows:

(1) ZK67 + 220 section: the surrounding rock is the intensely weathered sandy slate, with a small amount of moderately weathered sandy slate. The joints and fissures of the rock mass are well developed, and the rock mass is broken.

(2) ZK67 + 500 section: the surrounding rock is the intensely weathered sandy slate, with developed joints and fissures, hard rock, and fragmented rock mass.

(3) ZK67 + 900 section: the wall rocks are primarily distributed in the fault fracture zone, and they were intensely weathered sandy slates.

5.2 Field Monitoring Test Scheme

The Layout of Measuring Points

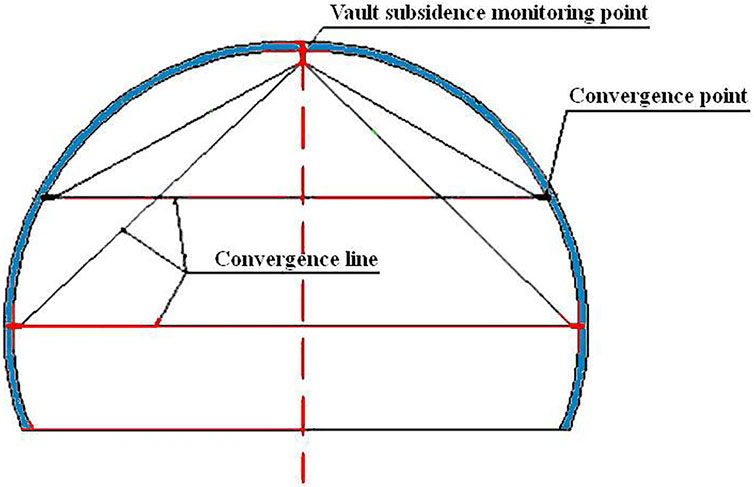
According to the type of surrounding rock, the tunnel’s depth, and the excavation method, measuring points were arranged in the tunnel wall along the longitudinal direction. The arrangement of measuring points and baselines was adjusted according to the specific construction scheme, and the distribution of measuring points should be set in the section where surrounding rock grades generally change.

The spacing distance between measuring points is 5–10 m. The layout of measuring points is shown in Figure 7.

FIGURE 7

FIGURE 7. Arrangement of measuring points for vault subsidence.

Measurement Frequency

The monitoring frequency in the experiment is to measure the data once a day.

Instruments and Equipment

The measuring base point is buried in the area outside the tunnel excavation longitudinal and transverse (3–5) times of tunnel diameter. According to the standard benchmark embedding method, two base points are buried for the mutual check. Therefore, the base point should be connected with the nearby benchmark to obtain the original elevation. A high-precision level observes the arch crown’s settlement, and the “four fixed principles” must be observed. In other words, it is necessary to refer to the following requirements: fixed construction personnel, fixed station position, fixed measurement duration, and fixed construction sequence, to ensure that the measurement accuracy meets the specification requirements. When the measuring points of the convergence measurement section are buried, the distance between the measuring points and the excavation surface should be less than 2 m. The first measurement should be carried out within 24 h after the last blasting. According to the relevant measurement frequency requirements, considering the influence of the ambient temperature, the data is read three times to ensure accuracy. The testing instruments and equipment are shown in Table 1.

TABLE 1

TABLE 1. Testing instruments and equipment.

5.3 Mechanical Parameters

Because the hydraulic fracturing method is simple and easy to operate in the testing process without needing to drill rock core samples or using exact electronic instruments, the testing depth can reach more than 5,000 m. Therefore, this study applies it to the initial in situ stress test of tunnel-surrounding rock.

The principle of the hydraulic fracturing method is to make the excellent wall break by increasing the water pressure based on the designed measurement depth of the hydraulic pump, then to determine the pressure and fracture direction of the characteristic point in the fracturing process, and calculate the initial stress state of the rock mass at the measurement point. Hydraulic fracturing is a two-dimensional testing method that can determine the maximum principal stress’s magnitude and direction and the minimum principal stress perpendicular from the borehole plane. Figure 8 illustrates hydraulic fracturing test device.

FIGURE 8

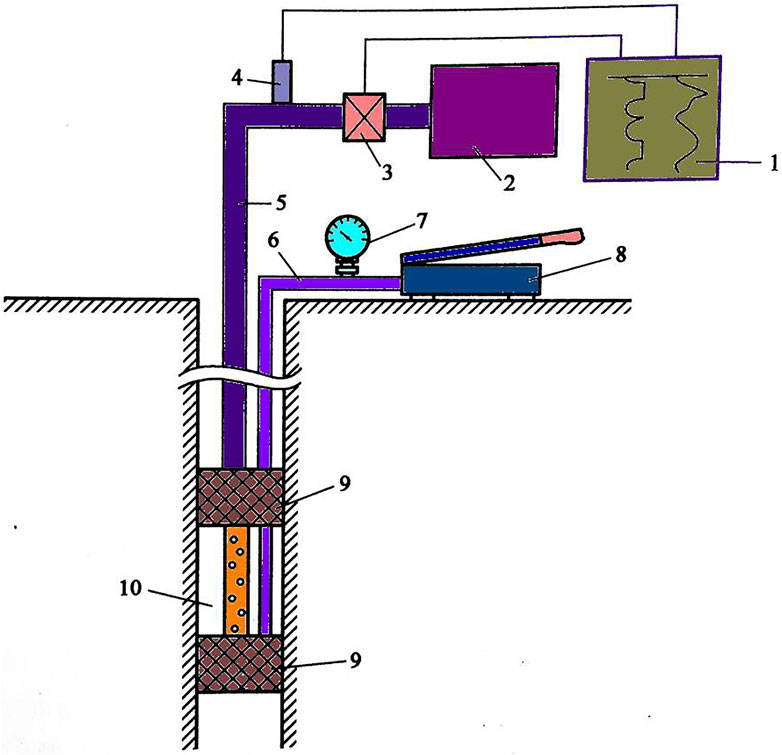
FIGURE 8. Schematic diagram of testing device for hydraulic fracturing method. 1-recorder, 2-high pressure pump, 3-flowmeter, 4-pressure gauge, 5-high pressure hose, 7-pressure gauge, 8-pump, 9-packer, 10-fracturing section.

According to the geological engineering report of the Dingxi tunnel, the in situ stress of three representative sections, ZK67 + 220, ZK67 + 500, and ZK67 + 900 on the left line, was measured with the hydraulic fracturing method. The self-weight stress value was calculated according to the designed thickness of overlying strata (${\sigma }_v=\rho gh$, rock bulk density $\rho =2.7g/c{m}^3$). The test results are shown in Table 2.

TABLE 2

TABLE 2. Measured values of initial in situ stress in Dingxi Tunnel.

Because the surrounding rock in this study area is intensely weathered sandy slate, it is suitable for the viscoelastic–viscoplastic rheological model. The mechanical parameters of the surrounding rock of the Dingxi tunnel are shown in Table 3. The model parameters in Table 3 were derived from the creep data under the corresponding stress by the formula $E_1=\frac{{\sigma }_0}{{\epsilon }_c\left(\infty \right)}$, $E_2=\frac{1}{\frac{{\epsilon }_c\left(\infty \right)+{\epsilon }_{cir}\left(\infty \right)}{\sigma }-\frac{1}{E_1}}$ and $\eta =\frac{E_{1}t}{\ln (1-\frac{E_1{\epsilon }_c\left(t\right)}{{\sigma }_0})}$.

TABLE 3

TABLE 3. Rheological mechanics parameters of surrounding rock of Dingxi Tunnel.

Because the design of the Dingxi tunnel is a three-center circular section, in order to ensure the accuracy of a theoretical calculation, it is necessary to convert the circular radius of the tunnel used in theoretical calculation into the equivalent circle radius using Eq. 33.

$r_0=\frac{{\left(\frac{b}{2}\right)}^2+H^2}{2H}(33)$

The equivalent radius of the Dingxi tunnel section is $r_0=7.03$ m, which was calculated by substituting b = 12.68 m and H = 10.08 m for the upper formula.

5.4 Calculation and Analysis

The vault settlement of ZK67 + 220, ZK67 + 500, and ZK67 + 900 sections was calculated by the analytic equation group $S_s=2(u^e+u^p)$ and compared with the measured results.

The simultaneous Eq. 32 was used to calculate all the parameters into the equation group $S_s=2(u^e+u^p)$, and the displacement expressions $S_s$ and ultimate displacement expressions $S_{\infty }$ of surrounding rock deformation can be obtained as follows:

$S_s=2\left[\begin{array}{l}-\frac{E_2{p}_0{r}_0{T}_a{\lambda }_0+E_2{p}_0{r}_0{T}_a-p_0{r}_0{\lambda }_0{\eta }_1+p_0{r}_0{\eta }_1}{E_1(T_a{E}_2-{\eta }_1)}{e}^{-\frac{t}{T_a}}-\frac{p_0{r}_0{T}_a{\lambda }_0+p_0{r}_0{T}_a}{E_2{T}_a-{\eta }_1}{e}^{-\frac{t}{T_a}}+\frac{(E_2+E_1)p_0{r}_0}{E_1{E}_2}+\frac{C}{r_0}{e}^{-\frac{E_2}{{\eta }_1}t}\\ +\frac{p_0{T}_a{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{t}(A+e^{-\frac{t}{B}})-\frac{p_0{\lambda }_0{r}_0{e}^{-\frac{t}{T_a}}}{E}-\frac{p_0{T}_a{r}_0{e}^{-\frac{t}{T_a}}}{t}(A+e^{-\frac{t}{B}})+\frac{p_0{r}_0{e}^{-\frac{t}{T_a}}}{E}+r_0(p_0+{\sigma }_s)(A+e^{-\frac{t}{B}})\end{array}\right](34)$

$S_{\infty }=2(u_{\infty }^e+u_{\infty }^p)=\frac{2(E_1+E_2)p_0{r}_0}{E_1{E}_2}+2\text{A}{r}_0(p_0+{\sigma }_s)(35)$

The Section of ZK67 + 220

The surrounding rock grade in this section is V, taking $A=0.19$, $B=0.58$, and the movement speed of the working face was $\upsilon =1.2m/d$. Monitoring can be started only when the driving distance of the working face exceeds 2 m of the cross-section of the measuring point. Therefore, when $T_a=3.5d$, it can be calculated using the formula $T_a=\chi /\upsilon$ (when $x=2,\chi =4.2$). The theoretical final settlement calculated by Eq. 35 is $S_{\infty }=$ 49.30 mm. However, due to the secondary lining of the section when $t=20d$, the final actual settlement measured in the field was $S=$ 48.97 mm. The comparison between the measured and theoretical values of the ZK67 + 220 section is shown in Figure 9.

FIGURE 9

FIGURE 9. Comparison of the measured and theoretical values for section ZK67 + 220.

The Section of ZK67 + 500

The surrounding rock grade for this section is IV, taking $A=0.14$, $B=0.28$, and the movement speed of the working face is $\upsilon =2.4m/d$. Monitoring can be started only when the driving distance of the working face exceeds 2 m of the cross-section of the measuring point. Therefore, when $T_a=1.75d$, it can be calculated using the $T_a=\chi /\upsilon$ (when $x=2,\chi =4.2$). The theoretical final settlement value calculated by Eq. 35 was $S_{\infty }=$ 36.77 mm. However, due to the secondary lining of the section when $t=20d$, the final actual settlement measured in the field was $S=$ 36.69 mm. The comparison between the measured and theoretical values of the ZK67 + 220 section is shown in Figure 10.

FIGURE 10

FIGURE 10. Comparison of the measured and theoretical values for section ZK67 + 500.

The Section of ZK67 + 900

The surrounding rock grade for this section is V, taking $A=0.29$, $B=0.49$, and the movement speed of the working face is $\upsilon =1.2m/d$. Monitoring can be started only when the driving distance of the working face exceeds 2 m of the cross-section of the measuring point. Therefore, when $T_a=3.5d$, it can be calculated using the formula $T_a=\chi /\upsilon$ (when $x=2,\chi =4.2$). The theoretical final settlement value calculated using Eq. 35 was $S_{\infty }=$ 53.70 mm. However, due to the secondary lining of the section when $t=20d$, the final actual settlement measured in the field was $S=$ 53.31 mm. The comparison between the measured and theoretical values of the ZK67 + 220 section is shown in Figure 11.

FIGURE 11

FIGURE 11. Comparison of the measured and theoretical values for section ZK67 + 900.

6 Discussion

In practical tunnel engineering, the instability and failure of surrounding rocks are closely related to the rheological properties of the rock mass, and the reasonable constitutive model is the key to studying the rheological properties. A new and improved Nishihara rheological model was presented, based on which the convergence formula of tunnel deformation was derived (Eq. 34) to be applied to the actual tunnel engineering. In this study, based on the residual calculation results, the R_MSE and the Mean Error (R_E) were calculated using the residual formula to evaluate the consistency of theoretical calculation results with real results and its calculation accuracy. The smaller the test standard value is, the more accurate the prediction result is, and the closer the theoretical calculation value is to the measured value. If the average error tends to “0,” the estimation is considered unbiased. The closer the correlation coefficient R² is to “1,” the higher the linear correlation between the theoretical and measured curves.

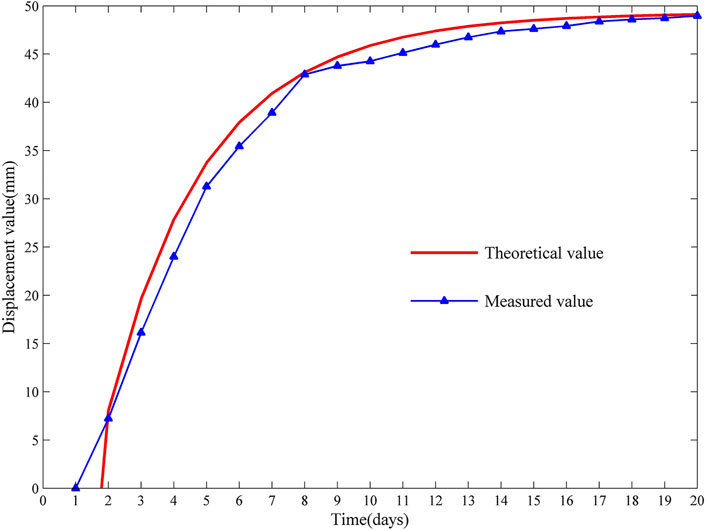
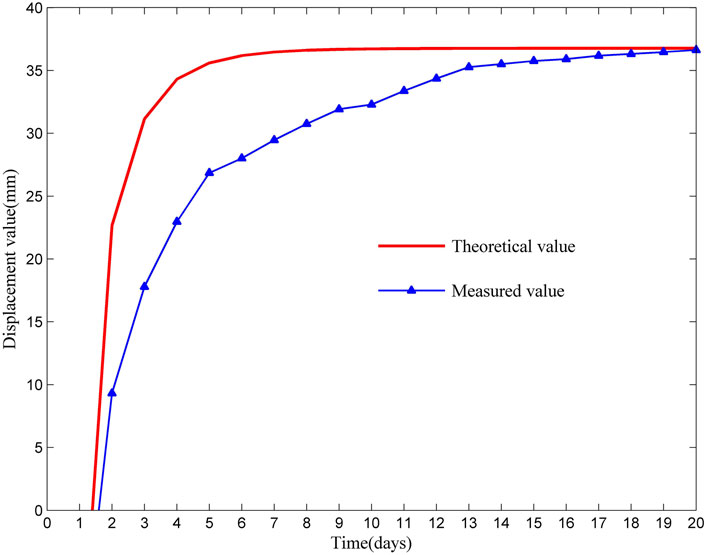
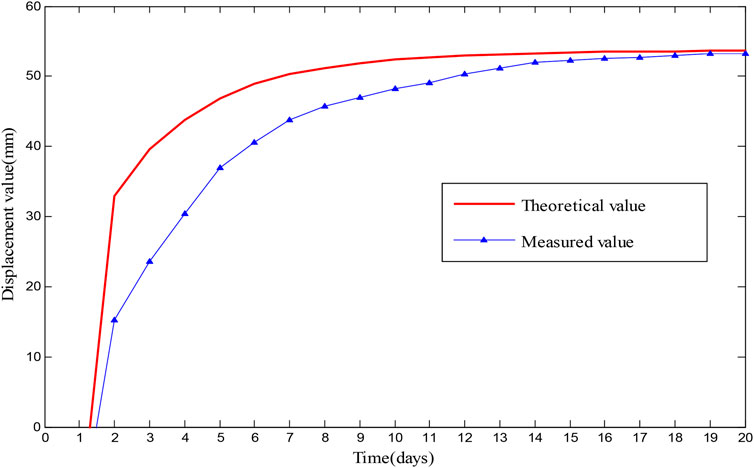
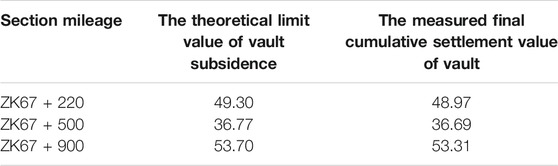
The following results are remarkable according to the comparative analysis of relevant parameters in Table 4 and Table 5. As shown in Table 4, the three sections’ final theoretical calculated values were all larger than the measured values, with a difference smaller than 0.73%, which can be considered very consistent. It can be seen from Table 5 that the root-mean-square error of the dislocation-time curves of the three sections was 7.26 mm, the maximum mean error was 5.01%, and the minimum correlation coefficient was 0.86. It was analyzed that firstly, in the field monitoring process, the secondary lining was applied on all three sections when T = 20 d, so the residual surrounding rock deformation cannot be effectively measured. The final measured settlement value was less than the final settlement value calculated by theory. Secondly, it was assumed that the surrounding rock’s elastic deformation is completed immediately after excavating the surrounding rock in the theoretical derivation of the model. However, due to the “time effect,” the viscoplastic deformation occurred slowly. “time effect” is also the fundamental reason for the massive difference in the settlement values at 12 d in Figures 10, 11. Thirdly, the faster driving speed of the section in Figure 9 and the shallower buried depth of the section in Figure 11 are also important reasons for the massive difference. Fourth, the existence of groundwater is significant to the stability of surrounding rock. The theoretical model in this paper does not consider the effect of groundwater, but there is gushing water in the tunnel during tunnel excavation. Fifth, the local variation of the excavation method and the uncertainty of construction disturbance are also factors that can not be ignored. In conclusion, the above accuracy evaluation indicates that the improved rheological model proposed in this study can provide a reference and theoretical basis for analyzing the stability of surrounding rock under similar conditions in other places.

TABLE 4

TABLE 4. Comparison between the measured and theoretical values.

TABLE 5

TABLE 5. Precision evaluation.

However, there are some limitations in this study to be further discussed. Firstly, due to the limited testing time and the number of test samples, this model’s validation was performed only by testing the deformation of the Dingxi tunnel. Therefore, some creep tests should be carried out on the rock mass of different tunnels in subsequent studies to verify the proposed improved rheological model. Secondly, rock mass fractures, groundwater, blasting, and other related factors were not considered in calculating the selected tunnel section. Considering these factors to make the improved rheological theory possible, it is a subject worthy of further study. Thirdly, the theoretical calculation results can only have particular reference significance in the tunnel’s surrounding rock with relatively single lithology, stable rock structure, and good integrity. However, in engineering practice, the deformation, instability, and failure of surrounding rock are complex processes controlled by several interrelated factors. To evaluate and predict the qualitative risk of the stable surrounding rock, the improved Nishihara model should further consider the coupling effect of many factors, such as joints and fractures in the rock mass, groundwater, lithologic differences, blasting, and lousy geology.

7 Conclusion

Based on the monitorization and measurement of the Dingxi Tunnel on Wujing Highway in Hunan Province, this study establishes an improved Nishihara model to forecast the surrounding rock deformation of the Dingxi Tunnel. The conclusions are as follows:

(1) Model establishment and theoretical derivation. By simultaneously considering the “time effect” of plastic viscosity coefficient and the “time-space effect” of the Hoek formula, an improved Nishihara model was established, and the viscoelastic–viscoplastic convergence analytical equation of surrounding rocks was derived.

(2) Application of the model. The comparison and verification show that the improved Nishihara model can accurately predict the final deformation of surrounding rock and further validate the assumptions and correlations of nonlinear viscosity coefficient equations. The correctness of the parameters indicates that this theoretical model has absolute validity and applicability in practical engineering.

(3) Limitations and prospecting of the model. The model is affected by excavation speed and buried depth under different geological conditions, and the forecast accuracy has certain limitations. Therefore, the critical point of research in the future is to deeply excavate and improve the model by combining in-depth learning and other methods.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

DH was responsible for determining the research purpose, organizing and reviewing the literature and previous research for discussion, determining the article structure, writing the draft manuscript, graphic conception, and implementation. XL, YL, and YW jointly agreed on the research objectives; provided supporting analysis and interpretation. LJ provided some modification suggestions and edited local text.

Funding

This research was supported by the National Natural Science Foundation of China (grant numbers: 51678226); the Natural Science Foundation of Hunan Province (grant numbers: 2021JJ50147, 2021JJ30078); the Science and Technology Innovation Project of Yiyang City (grant numbers: 2019YR02, 2020YR02); the Open Research Foundation of Hunan Provincial Key Laboratory of Key Technology on Hydropower Development (grant numbers: PKLHD202005). The support is gratefully acknowledged.

Conflict of Interest

DH and YW are employed by Power China Zhongnan Engineering Co. Ltd. LJ is employed by Changsha Metro Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, X., Zhao, J., and Li, Y. (2017). Viscoelastic-plastic Creep Constitutive Model of Frozen Soil. Emerging Mater. Res. 6 (2), 429–433. doi:10.1680/jemmr.16.00124

CrossRef Full Text | Google Scholar

Chen, R., Zhang, P., Wu, H., Wang, Z., and Zhong, Z. (2019). Prediction of Shield Tunneling-Induced Ground Settlement Using Machine Learning Techniques. Front. Struct. Civ. Eng. 13 (6), 1363–1378. doi:10.1007/s11709-019-0561-3

CrossRef Full Text | Google Scholar

Feng, W., Qiao, C., Niu, S., Yang, Z., and Wang, T. (2020). An Improved Nonlinear Damage Model of Rocks Considering Initial Damage and Damage Evolution. Int. J. Damage Mech. 29 (7), 1117–1137. doi:10.1177/1056789520909531

CrossRef Full Text | Google Scholar

Hoek, E. (1999). “Support for Very Weak Rock Associated With Faults and Shear Zones,” in Rock Support and Reinforcement Practice in Mining. Editors Villaescusa, , Windsor, , and Thompson, (Kalgoorlie, Australia: Balkema), 19—34.

Google Scholar

Huang, F., Cao, Z., Jiang, S.-H., Zhou, C., Huang, J., and Guo, Z. (2020). Landslide Susceptibility Prediction Based on A Semi-supervised Multiple-Layer Perceptron Model. Landslides 17, 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Huang, J., Jiang, S., and Zhou, C. (2017). Landslide Displacement Prediction Based on Multivariate Chaotic Model and Extreme Learning Machine. Eng. Geology. 218, 173–186. doi:10.1016/j.enggeo.2017.01.016

CrossRef Full Text | Google Scholar

Huang, F., Tao, S., Chang, Z., Huang, J., Fan, X., Jiang, S.-H., et al. (2021). Efficient and Automatic Extraction of Slope Units Based on Multi-Scale Segmentation Method for Landslide Assessments. Landslides 18, 3715–3731. doi:10.1007/s10346-021-01756-9

CrossRef Full Text | Google Scholar

Huang, F., Yan, J., Fan, X., Yao, C., Huang, J., Chen, W., et al. (2022). Uncertainty Pattern in Landslide Susceptibility Prediction Modelling: Effects of Different Landslide Boundaries and Spatial Shape Expressions. Geosci. Front. 13, 101317. doi:10.1016/j.gsf.2021.101317

CrossRef Full Text | Google Scholar

Jin, A., Wang, B., Zhao, Y., Wang, H., Feng, H., Sun, H., et al. (2019). Analysis of the Deformation and Fracture of Underground Mine Roadway by Joint Rock Mass Numerical Model. Arab J. Geosci. 12, 559. doi:10.1007/s12517-019-4741-1

CrossRef Full Text | Google Scholar

Li, D., Zhang, C., Ding, G., Zhang, H., Chen, J., Cui, H., et al. (2020). Fractional Derivative-Based Creep Constitutive Model of Deep Artificial Frozen Soil. Cold Regions Sci. Techn. 170, 102942. doi:10.1016/j.coldregions.2019.102942

CrossRef Full Text | Google Scholar

Li, X., Liu, E., Song, B., Liu, X., and Cesar de Sa, J. (2018). An Improved Nishihara Model for Frozen Loess Considering the Influence of Temperature. Adv. Mater. Sci. Eng. 2018, 1–10. doi:10.1155/2018/9073435

CrossRef Full Text | Google Scholar

Li, Y. G., Jin, L. Z., Tan, H., Li, Y. D., Liu, X. L., Mu, R., et al. (2017). An Experimental Study of Loading Rate Effects on Mechanical Characteristics of Cemented Paste Backfill. Water Resour. Hydropower Eng. 48 (7), 129–135. doi:10.1201/9781315166599-17

CrossRef Full Text | Google Scholar

Li, Y., Zhu, W., Fu, J., Guo, Y., and Qi, Y. (2014). A Damage Rheology Model Applied to Analysis of Splitting Failure in Underground Caverns of Jinping I Hydropower Station. Int. J. Rock Mech. Mining Sci. 71, 224–234. doi:10.1016/j.ijrmms.2014.04.027

CrossRef Full Text | Google Scholar

Li, Z. Q., Cao, W. Q., and Wang, X. L. (2017). Research on Thermal-Mechanical Creep Damage Model of Hard Brittle Rock. Ind. Construction 47 (06), 86–89. doi:10.13204/j.gyjz201706018

CrossRef Full Text | Google Scholar

Lin, H., Zhang, X., Wang, Y., Yong, R., Fan, X., Du, S., et al. (2020). Improved Nonlinear Nishihara Shear Creep Model with Variable Parameters for Rock-like Materials. Adv. Civil Eng. 2020 (3), 1–15. doi:10.1155/2020/7302141

CrossRef Full Text | Google Scholar

Liu, H. Z., Xie, H. Q., He, J. D., Xiao, M. L., and Zhuo, L. (2017). Nonlinear Creep Damage Constitutive Model for Soft Rocks. Mech. Time-depend Mater. 21 (1), 73–96. doi:10.1007/s11043-016-9319-7

CrossRef Full Text | Google Scholar

Liu, W., and Zhang, S. (2020). An Improved Unsteady Creep Model Based on the Time Dependent Mechanical Parameters. Mech. Adv. Mater. Structures 28 (12), 1838–1848. doi:10.1080/15376494.2020.1712624

CrossRef Full Text | Google Scholar

Liu, Y., Huang, D., Zhao, B., Wang, C., and Cen, D. (2020). Nonlinear Creep Behavior and Viscoelastic-Plastic Constitutive Model of Rock-Concrete Composite Mass. Adv. Civil Eng. 2020 (3), 1–14. doi:10.1155/2020/9059682

CrossRef Full Text | Google Scholar

Melis, M., Medina, L., and Rodríguez, J. M. (2002). Prediction and Analysis of Subsidence Induced by Shield Tunnelling in the Madrid Metro Extension. Can. Geotech. J. 39 (6), 1273–1287. doi:10.1139/t02-073

CrossRef Full Text | Google Scholar

Nishihara, M. (1957). Stress-Strain-Time Relations of Rocks. Doshisha Engng. Rev. 8, 32–55.

Google Scholar

Ou, Z.-f., and Fang, Y.-g. (2017). The Influence of Organic Matter Content on the Rheological Model Parameters of Soft Clay. Soil Mech. Found. Eng. 54 (4), 283–288. doi:10.1007/s11204-017-9470-4

CrossRef Full Text | Google Scholar

Panet, M. (1995). Le Calcul Des Tunnels Par La Methode Convergence-Confinement. Paris: Press de I'Ecole Nationale des Ponts et Chaussres, 75–100.

Google Scholar

Pu, S. Y., Rao, J. Y., Yang, K. Q., Huang, Z. H., and Liu, H. Q. (2017). Deformation Characteristics of Soil under Cyclic Loading. Rock Soil Mech. 38 (11), 188–197. doi:10.16285/j.rsm.2017.11.023

CrossRef Full Text | Google Scholar

Shen, C. H., Zhang, B., and Wang, W. W. (2014). A New Visco-Elastoplastic Creep Constitutive Model Based on Strain Energy Theory. Rock Soil Mech. 35 (12), 3430–3436. doi:10.13225/j.cnki.jccs.2014.0445

CrossRef Full Text | Google Scholar

Song, F., Wang, H., and Jiang, M. (2018). Analytically-based Simplified Formulas for Circular Tunnels with Two Liners in Viscoelastic Rock under Anisotropic Initial Stresses. Construction Building Mater. 175 (JUN.30), 746–767. doi:10.1016/j.conbuildmat.2018.04.079

CrossRef Full Text | Google Scholar

Sun, J. (2007). Rock Rheological Mechanics and its Advance in Engineering Applications. Chin. J. Rock Mech. Eng. 26 (6), 1081–1106. doi:10.1097/00000542-199411000-00017

CrossRef Full Text | Google Scholar

Wang, J., Wang, X., Zhan, H., Qiu, H., and Hu, S. (2019). A New Superlinear Viscoplastic Shear Model for Accelerated Rheological Deformation. Comput. Geotechnics 114 (Oct.), 103132.1–103132.10. doi:10.1016/j.compgeo.2019.103132

CrossRef Full Text | Google Scholar

Wang, X., Huang, Q., Lian, B., Liu, N., Zhang, J., and Lusquiños, F. (2018). Modified Nishihara Rheological Model Considering the Effect of Thermal-Mechanical Coupling and its Experimental Verification. Adv. Mater. Sci. Eng. 2018, 1–9. doi:10.1155/2018/4947561

CrossRef Full Text | Google Scholar

Xiao, Z. Q., Wang, X., Tang, D. S., Li, Z. P., Xu, C. Y., Zhou, P., et al. (2017). Calculation Method for the Radial Displacement of a Circular Tunnel Considering the Time Effect of the Viscosity Coefficient. Mod. Tunnelling Techn. 54 (06), 77–84. doi:10.13807/j.cnki.mtt.2017.06.011

CrossRef Full Text | Google Scholar

Xiong, L. X., Yang, L. D., and Zhang, Y. (2010). Non-stationary Burgers Model for Rock. Cent. South Univ (Sci Technol) 41 (02), 679–684.

Google Scholar

Xu, G. W., He, C., Hu, X. Y., and Wang, S. M. (2015). A Modified Nishihara Model Based on Fractional Calculus Theory and its Parameter Intelligent Identification. Rock Soil Mech. 36 (S2), 132–147. doi:10.16285/j.rsm.2015.S2.017

CrossRef Full Text | Google Scholar

Yan, B., Guo, Q., Ren, F., and Cai, M. (2020). Modified Nishihara Model and Experimental Verification of Deep Rock Mass under the Water-Rock Interaction. Int. J. Rock Mech. Mining Sci. 128, 104250. doi:10.1016/j.ijrmms.2020.104250

CrossRef Full Text | Google Scholar

Yan, Y., Wang, S. J., and Wang, E. Z. (2010). Creep Equation of Variable Parameters Based on Nishihara Model. Rock Soil Mech. 31 (10), 3025–3035. doi:10.16285/j.rsm.2010.10.019

CrossRef Full Text | Google Scholar

Yu, M., Liu, B., Sun, J., Feng, W., and Wang, Q. (2020). Study on Improved Nonlinear Viscoelastic-Plastic Creep Model Based on the Nishihara Model. Geotech Geol. Eng. 38 (3), 3203–3214. doi:10.1007/s10706-020-01217-5

CrossRef Full Text | Google Scholar

Yu, W., Pan, B., Zhang, F., Yao, S., and Liu, F. (2019). Deformation Characteristics and Determination of Optimum Supporting Time of Alteration Rock Mass in Deep Mine. KSCE J. Civ Eng. 23 (11), 4921–4932. doi:10.1007/s12205-019-0365-y

CrossRef Full Text | Google Scholar

Yu, X.-Y., Xu, T., Heap, M., Zhou, G.-L., and Baud, P. (2018). Numerical Approach to Creep of Rock Based on the Numerical Manifold Method. Int. J. Geomech. 18 (11), 04018153. doi:10.1061/(ASCE)GM.1943-5622.0001286

CrossRef Full Text | Google Scholar

Zhang, B., Hu, H., Yu, W., Liang, S., Li, J., and Lu, L. (2019). Timeliness of Creep Deformation in the Whole Visco-Elasto-Plastic Process of Surrounding Rocks of the Tunnel. Geotech Geol. Eng. 37 (2), 1007–1014. doi:10.1007/s10706-018-0668-7

CrossRef Full Text | Google Scholar

Zhang, J.-Z., Zhou, X.-P., and Yin, P. (2019). Visco-Plastic Deformation Analysis of Rock Tunnels Based on Fractional Derivatives. Tunnelling Underground Space Techn. 85, 209–219. doi:10.1016/j.tust.2018.12.019

CrossRef Full Text | Google Scholar

Zhang, J., Li, B., Zhang, C., and Li, P. (2019). Nonlinear Viscoelastic-Plastic Creep Model Based on Coal Multistage Creep Tests and Experimental Validation. Energies,12(18),3468. doi:10.3390/en12183468

CrossRef Full Text | Google Scholar

Zhang, K., Lyu, H.-M., Shen, S.-L., Zhou, A., and Yin, Z.-Y. (2020). Evolutionary Hybrid Neural Network Approach to Predict Shield Tunneling-Induced Ground Settlements. Tunnelling Underground Space Techn. 106:103594. doi:10.1016/j.tust.2020.103594

CrossRef Full Text | Google Scholar

Zhang, L., Yang, S., and Kłosowski, P. (2020). Unloading Rheological Test and Model Research of Hard Rock under Complex Conditions. Adv. Mater. Sci. Eng. 2020, 1–12. doi:10.1155/2020/3576181

CrossRef Full Text | Google Scholar

Zhang, Q. G., Liang, Y. C., Fan, X. Y., Li, G. Z., Li, W. T., Yang, B., et al. (2016). A Modified Nishihara Model Based on the Law of the Conservation of Energy and Experimental Verification. J. Chongqing Univ. 39 (3), 117–124. doi:10.11835/j.issn.1000-582X.2016.03.015

CrossRef Full Text | Google Scholar

Zhang, Q., Shen, M., and Ding, W. (2015). The Shear Creep Characteristics of a Green Schist Weak Structural Marble Surface. Mech. Adv. Mater. Structures 22 (9), 697–704. doi:10.1080/15376494.2011.584147

CrossRef Full Text | Google Scholar

Zhang, X. D. (2016). Study on Creep Effect of Tunnel Surrounding Rock Based on the Modified Visco-Elastoplastic Model and Lade-Duncan Criterion. Sci. Techn. Eng. 16 (18), 72–77.

Google Scholar

Zhang, Z., Liu, X., Cheng, L., Wu, S., and Zhang, B. (2020). A Rheological Constitutive Model for Damaged Zone Evolution of a Tunnel Considering Strain Hardening and Softening. Geomech. Geophys. Geo-energ. Geo-resour. 6, 56. doi:10.1007/s40948-020-00181-x

CrossRef Full Text | Google Scholar

Zhao, D., Jia, L., Wang, M., and Wang, F. (2016). Displacement Prediction of Tunnels Based on a Generalised Kelvin Constitutive Model and its Application in a Subsea Tunnel. Tunnelling Underground Space Techn. 54, 29–36. doi:10.1016/j.tust.2016.01.030

CrossRef Full Text | Google Scholar

Zhou, H. W., Wang, C. P., Han, B. B., and Duan, Z. Q. (2011). A Creep Constitutive Model for Salt Rock Based on Fractional Derivatives. Int. J. Rock Mech. Mining Sci. 48 (1), 116–121. doi:10.1016/j.ijrmms.2010.11.004

CrossRef Full Text | Google Scholar

Zhou, J., Shi, X., Du, K., Qiu, X., Li, X., and Mitri, H. S. (2017). Feasibility of Random-Forest Approach for Prediction of Ground Settlements Induced by the Construction of a Shield-Driven Tunnel. Int. J. Geomech. 17, 04016129. doi:10.1061/(ASCE)GM.1943-5622.0000817

CrossRef Full Text | Google Scholar

Zhu, H., Wang, X., Chen, X., and Zhang, L. (2020). Similarity Search and Performance Prediction of Shield Tunnels in Operation through Time Series Data Mining. Automation in Construction 114, 103178. doi:10.1016/j.autcon.2020.103178

CrossRef Full Text | Google Scholar

Zhu, Z.-y., Luo, F., Zhang, Y.-z., Zhang, D.-j., and He, J.-l. (2019). A Creep Model for Frozen Sand of Qinghai-Tibet Based on Nishihara Model. Cold Regions Sci. Techn. 167 (Nov), 102843.1–102843.9. doi:10.1016/j.coldregions.2019.102843

CrossRef Full Text | Google Scholar