
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 07 February 2022
Sec. Structural Geology and Tectonics
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.839084
This article is part of the Research Topic Advances in the Study of Natural Fractures in Deep and Unconventional Reservoirs View all 29 articles
 Jian Li1,2,3*
Jian Li1,2,3* Kewei Zu3,4*
Kewei Zu3,4* Qi Li1,2*
Qi Li1,2* Daqian Zeng3
Daqian Zeng3 Zhongchao Li4
Zhongchao Li4 Jixi Zhang4
Jixi Zhang4 Zhouliang Luo4
Zhouliang Luo4 Nanxin Yin5
Nanxin Yin5 Zhenjun Zhu1,2
Zhenjun Zhu1,2 Xiaojun Ding6
Xiaojun Ding6All stages of oil and gas exploration and development involve the study of in-situ stress. Since the traditional two-dimensional and three-dimensional homogeneous models can no longer fulfil the requirements of research and production, numerical simulation of the stress field has become an effective study method. In this study, we took the Jia 2 member in Puguang area as a case to establish a geological model and a mechanical model based on the tectonic framework and the distribution characteristics of the rock mechanical parameters, respectively, and loaded the model with the present-day in-situ stress state calculated from the logging data as the boundary conditions. The simulation results show that 1) the orientation of the maximum horizontal principal stress in the study area is near E-W, and the in-situ stress orientation is locally deflected due to the influence of faults; and 2) the magnitude of in-situ stress is predominantly affected by the burial depth and lithology, and the minimum horizontal principal stress, maximum horizontal principal stress, and differential stress are mainly concentrated in the ranges of 30–60, 50–80, and 10–40 MPa, respectively. We also analysed the opening sequence of the multiple fracture systems during development, using the present-day stress field model. The analysis revealed that the E-W fractures will open first, and the continuously increasing operating pressure will lead to formation breakdown, producing a fracture network.
In-situ stress is a natural force that objectively occurs in a rock mass (Jing et al., 2011). It is narrowly defined as the internal stress confined in the Earth’s crust (Xie et al., 2008), and broadly defined as the state of stress in the Earth in different geological periods. According to the time of occurrence, in-situ stress can be divided into paleo-stress and present-day in-situ stress. Paleo-stress typically refers to the stress before the Middle Pleistocene of the Quaternary, whereas the present-day in-situ stress refers to the stress state in the present formation (James, 1983; Zeng and Tian, 1998). Every process of oil and gas exploration, development, and production involves the study of in-situ stress. Paleo-stresses controlled the type of basin, as well as the generation, development, and combination, of geological structures. They also affected the migration and accumulation of oil and gas. Present-day in-situ stress influences the injection-production well arrangement, hydraulic fracturing plan, hydraulic fracture propagation, casing deformation, and wellbore stability in oil and gas development.
At present, the methods for evaluating in-situ stress states can be generally divided into three categories: field measurement and analysis, logging, and stress field numerical simulation. The field measurement and analysis methods are currently the most accurate means to obtain in-situ stress data, mainly including those based on casing stress relief (Cai et al., 1997; Qin et al., 2018), acoustic emission (Dong et al., 2009; Li and Dong, 2009), hydraulic fracturing (Zhou et al., 2015), differential strain, seismic velocity anisotropy (Cheng et al., 2008) and micro-seismic wave detection (Liu et al., 2006). These methods have high accuracy but the measurement points are discrete and not able to represent low-stress states of the whole or intact rock mass. Moreover, they cannot be applied on a large scale because of the high cost. In the logging method, the maximum horizontal principal stress orientation is detected by imaging logging based on the information on wellbore collapse and drilling-induced fractures. The maximum and minimum horizontal principal stress magnitudes are then calculated with the conventional logging data and the corresponding stress field model. Thus, the continuous variation patterns of the maximum and minimum horizontal principal stresses with depth are obtained. This method is easy to implement but the calculation results generally deviate from the true values to an extent; they need to be corrected with experimental results to improve the calculation accuracy. In addition, this method can only be applied to calculate the in-situ stress state in a single well, not the inter-well stress state. Numerical simulation of the stress field is one of the most effective methods to analyse the tectonic stress field quantitatively (Hu and Li, 2015). It is the preferred method to reconstruct the structural evolution process and the spatial distribution of stress fields. The currently available numerical simulation techniques include the finite element method, finite difference method, boundary element method, and discrete element method, among which the finite element method is the optimum for stress field modelling. In recent years, owing to the substantial development of finite element theory and software technology, the performance of this method has been significantly improved from qualitative analysis to quantitative calculation, from two-dimensional to three-dimensional. Similarly, it is necessary to combine the numerical simulation approach with other methods when calculating the distribution characteristics of the stress field.
Since the three-dimensional numerical simulation of the stress field can more realistically reflect the subsurface morphology, the three-dimensional finite element numerical simulation method has been widely applied in China to evaluate the differences in vertical stress caused by the weight of the overlying strata. However, when applying this method, researchers generally simulate the entire formation as a homogeneous body (Tan et al., 1997; Shen et al., 2004; Li et al., 2007; Su and Li, 2009; Sang et al., 2010; Tian et al., 2011; Zhan et al., 2011; Dai et al., 2013; Zeng et al., 2013; Meng et al., 2014; Zu et al., 2014; Hu and Li, 2015; Wang et al., 2015; Gong et al., 2021a), ignoring the heterogeneity of the layer due to the variations in sedimentary facies and lithology. Yet, strong heterogeneity can lead to redistribution of the in-situ stress magnitude and abrupt changes in the in-situ stress direction across the layer (Zeng et al., 2010; Zu et al., 2014; Gong et al., 2019; Gong et al., 2021b), thereby directly affecting the exploitation effect of the reservoir (Gao et al., 2000; Su and Li, 2009; Zeng et al., 2013; Li et al., 2019; Gong et al., 2021a; Gong et al., 2021b). This study attempted to establish a three-dimensional, heterogeneous present-day in-situ stress model for the Jia 2 member in Puguang area based on the tectonic framework, distribution of the rock mechanical parameters, and present-day in-situ stress state calculated from logging data, which can provide an essential basis for well pattern deployment and wellbore-instability prevention during drilling. As a next step, we applied this model to predict the fracture opening sequence to provide a foundation for designing a rational hydraulic fracturing plan.
The Puguang gas field is located in the north-eastern part of the Sichuan Basin, with an exploration area of 1,116 km2 (Xu et al., 2004; Qian and Zhong, 2009). To its north and east are the Micangshan thrust belt and Dabashan arcuate thrust belt, respectively. This gas field is not only controlled by the tectonic deformation of the basement of the Sichuan Basin, but also influenced by the deformation of the Micangshan and Dabashan thrust belts (Figure 1). The entire study area is developed with NE-trending structures. Several boundary faults running through this area divide the region into multiple secondary units, including two positive structures, the Maoba-Leiyinpu and Shuangshixi-Qingxichang structural belts, and two negative structures, the Puguang main body and Xuanhan syncline, showing a pattern of uplift and depression. Three major sets of décollements are developed, namely, from top to bottom, the gypsum salt rock from the lower part of the Leikoupo Formation to the fourth member of the Jialingjiang Formation, the Silurian shale, and the shale of the Cambrian Qiongzhusi Formation. The Puguang area has experienced the Caledonian, Hercynian, Indosinian, Yanshanian, and Himalayan orogenies successively. Before the Indosinian orogeny, tectonic movements in this area were dominated by vertical uplift and subsidence. Since the Indosinian epoch, the significant uplift and over-thrusting of the northern Daba Mountain and the Micang Mountains and their piedmont areas led to the uplift of the Puguang area, and its sedimentary facies transformed from marine to terrestrial (Liu et al., 2009). After entering the Yanshanian epoch, a large number of NE-SW-oriented structures were formed under the compression of the NW-SE-oriented structures developed between the late Yanshanian orogeny and early Himalayan orogeny, and a series of NW-SE-oriented structures were formed in the eastern Puguang area under the compression of the NE-SW-oriented structures developed during the late Himalayan orogeny (Tang et al., 2008; Zu et al., 2017).
The Puguang area is developed with gas-bearing systems of terrestrial and marine facies. Currently, the marine facies, Changxing and Feixianguan Formations, are the main production layers in the Puguang gas field. The Jialingjiang Formation is an important regional gas-producing formation in the Sichuan Basin with a good exploration prospect; the Jia 2 member has the best gas logging show. This layer has considerable undulations, with a burial depth between 2,500 and 5,500 m. The lithology of the Jia 2 member is complex, including dolostone, limestone, gypsum rock, and mudstone. According to the core analysis and testing data, the porosity of the dolostone is generally >2%, with an average of 5.8%; the maximum porosity of the limestone is 2.18%, and the average is 1.72%; and the permeability of the matrix is generally <0.25 × 10−3 μm2. Thus, this layer belongs to an ultralow-porosity and low-permeability reservoir.
In this study, we used the finite element method to perform numerical simulation of the tectonic stress field (Zeng et al., 2010; Gong et al., 2019; Gong et al., 2021b). This method is based on the variational principle and approximate interpolation discretization, breaking through the limitations of traditional numerical simulation that requires tectonic reconstruction from the aspects of geometry and kinematics. It can simulate heterogeneous geological features using the mechanical properties of different materials in the calculation. Moreover, the elements of the subdivided geological body are interconnected, and the number of elements can be set as required. The more divided the elements are, the closer the model is to the actual geological body. The whole body moves under the boundary stress, which significantly improves the accuracy of model operation. The finite element numerical simulation of the stress field includes three major steps: establishing a geological model, constructing a mechanical model, and analysing boundary conditions.
Establishing a geological model is the prerequisite and basis for numerical simulation. On the one hand, the geological model determines the framework of the mechanical model. On the other, the deviation between the geological model and the actual geological conditions determines the simulation accuracy, which is critical to the correct analysis of the in-situ stress distribution pattern.
The establishment of a geological model needs to follow certain principles:
1) When selecting the target horizon of the work area, the range of the work area shall be extended outward as far as possible, and the real tectonic relief in the work area should be reflected as much as possible based on the tectonic framework. At the same time, it is also necessary to refer to the distribution of sedimentary facies in the work area and divide the geological elements under the joint constraints of facies boundaries and faults.
2) Based on the regional stress state, the exterior of the geological body in the work area is wrapped with a regular cube, whose surface planes facing three directions are perpendicular to the three principal stress directions in the area, respectively.
3) Since numerous faults of different sizes are developed in the work area, displaying these faults one by one would generate excessive workload and also cause errors in software processing. Therefore, the faults need to be screened. The ones whose length is larger than 1 km that influence and reflect the tectonic pattern of the study area are retained, and the minor ones whose length is less than 1 km are ignored.
The geological model in this study was established based on the three-dimensional present-day tectonic framework of the Jia 2 member in the Puguang area. According to the single-well data of the Jia 2 member, the thickness of this layer ranges 146–293 m, with an average of 220 m; hence, the model thickness was set to 220 m.
Based on the geological model, the mechanical elements are divided and assigned with different rock mechanical parameters according to the distribution of the parameters (mainly the elastic modulus and Poisson’s ratio) that affect the state of the stress field across the layer. The rock mechanical parameters can be acquired using the static and dynamic methods. Since the parameters obtained by the static method are discrete and costly, the core data of the Jia 2 member in the Puguang area are limited, whereas the logging data are relatively abundant. Therefore, we mainly used the logging data to calculate the rock mechanical parameters in this study (Barree et al., 2009).
where E is the elastic modulus, GPa; μ is the Poisson’s ratio, dimensionless; ρ is the rock density, g/cm3; ts is the transverse wave time difference, μs/ft; and tp is the longitudinal wave time difference, μs/ft.
After fitting the single-well transverse waves with the multiple regression method, we calculated the rock mechanical parameters for 27 wells and established an equivalent mechanical model for a single well based on the litho-stratification data in the vertical direction. Among the rock mechanical parameters, the response of the rock’s elastic modulus to the in-situ stress distribution is more pronounced than the Poisson’s ratio [24]. Therefore, considering the calculation accuracy and the computing power of the workstation, the geological model was divided into different mechanical elements based on the criteria of elastic modulus: E ≥ 54 GPa, 54GPa > E ≥ 50 GPa, 50GPa > E ≥ 46 GPa, and 46GPa > E. To eliminate the influence of boundary effects, we confined the exterior of the modelled region with a rectangular frame as a loading and constraining object. The rectangular frame is a separate mechanical element whose rock mechanical parameters are determined based on the mean values of the internal geological body, and the corresponding elastic modulus and Poisson’s ratio are assigned to each mechanical element.
The treatment of faults is a critical issue. As the samples from fault zones are extremely loose and fragmented, their mechanical parameters cannot be obtained from rock mechanics experiments. According to the theory of tectonic deformation, the fault fracture zone, during its formation, is the dominant stress release zone of the entire geological body. After formation, it is the weakest part of the geological body. In previous studies, ∼40–70% Young’s modulus of the standard rock mass and a Poisson’s ratio with an increase of 0.02 were typically taken as the mechanical parameters of the fault zones. The more complex the tectonics of the study area, the more developed the faults, and the smaller the Young’s modulus and the larger the Poisson’s ratio of the fault zone (Chen and Tian, 1998; Wang et al., 1999; Zu et al., 2018).
On this basis, the mechanical model is subdivided into a grid. The geological body is represented by a finite number of elements interconnected by nodes and lines and transformed into a mathematical model for calculation. The element subdivision needs to be performed according to the geological characteristics; therefore, the same element cannot cross two different geological bodies. Because of if the acute angles is less than 5°, the software will not able to calculate the stress of the element around the corner. So, particularly small acute angles (<5°) in the modelled geological bodies and elements should be avoided. In this study, the strata of the Jia 2 member in the Puguang area were subdivided into 2.78 million elements.
For in-situ stress simulation, the boundary conditions mainly include stress boundary conditions and displacement boundary conditions. Since it is impossible to obtain accurate and reliable data on strain rate induced by the present-day in-situ stress state, we selected the stress boundary conditions as the boundary constraints of the finite element modelling in this study, i.e., the boundary conditions were calculated by loading the stress.
The present-day in-situ stress direction was obtained by analysing the orientation of drilling-induced fractures and the wellbore collapse direction from cross-dipole acoustic logs and dip meter logs of 30 wells in the Puguang area. The results show that the present-day maximum horizontal principal stress orientation is near E-W in the Jia 2 member. The present-day in-situ stress magnitude is calculated based on conventional logging data. According to the structural and geological characteristics of the Puguang area, we employed Huang’s model and the combined spring model to calculate the principal horizontal stress in 22 wells and obtained the average gradient of principal stress magnitude varying with depth in the Jia 2 member. The maximum horizontal principal stress σ1 had an average gradient of 0.0166 MPa/m, with an E-W orientation; and the minimum horizontal principal stress σ2 had an average gradient of 0.0115 MPa/m, with a N-S orientation. In addition, the gravity applied in the vertical direction and the constrained bottom were also boundary conditions for the loading calculations (Figure 2).

FIGURE 2. The boundary conditions of geo-stress in the second member of Jialingjiang formation, Puguang area.
The accuracy of model calculation results is evaluated by comparative analysis with actual data. The simulated in-situ stress direction was tested with the maximum horizontal principal stress direction calculated based on the wellbore collapse and drilling-induced fracture information from logging data interpretation (Table 1). The average error in the overall in-situ stress direction is 6.25°, and the maximum error in a single well does not exceed 15°. The simulated maximum and minimum principal stress magnitudes were tested with the in-situ stress magnitude calculated from the single-well data (Table 2). The overall maximum and minimum principal stress magnitudes have an average error of 7.29% and 8%, respectively, and the single-well error does not exceed 20%, indicating that the simulation results are reliable.

TABLE 1. Comparative the simulation results and the orientations of principal stress by measurement.
The simulation results reveal that the present-day in-situ stress state in the Jia 2 member of the Puguang area is dominated by E-W compressive stress (Figure 3). The minimum horizontal principal stress in the Jia 2 member is mainly concentrated between 30 and 60 MPa, the maximum horizontal principal stress is generally between 50 and 80 MPa (Figure 4), and the differential stress predominantly lies between 10 and 40 MPa (Figure 5). The in-situ stress distribution is remarkably controlled by the burial depth and lithology, and the overall distribution pattern of the maximum and minimum horizontal principal stresses is generally consistent. The high-value areas of principal stress magnitude are concentrated in the north-eastern and western Puguang area, where the tectonic deformation is less intense and the tectonic relief is gentle. The maximum and minimum horizontal principal stresses are small in the structurally high part of the central area.
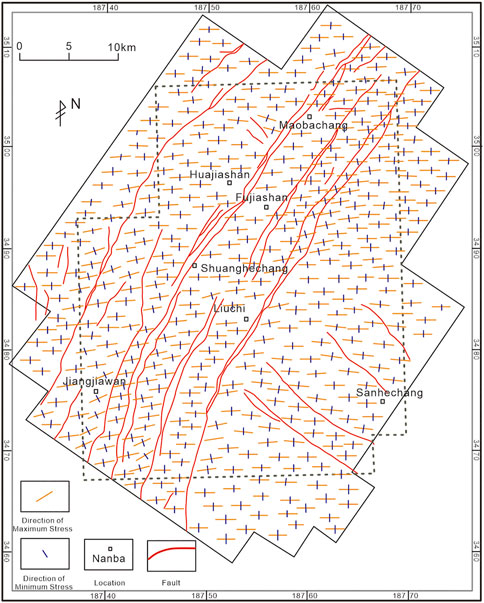
FIGURE 3. The distribution map of geo-stress directions in the second member of Jialingjiang formation, Puguang area.
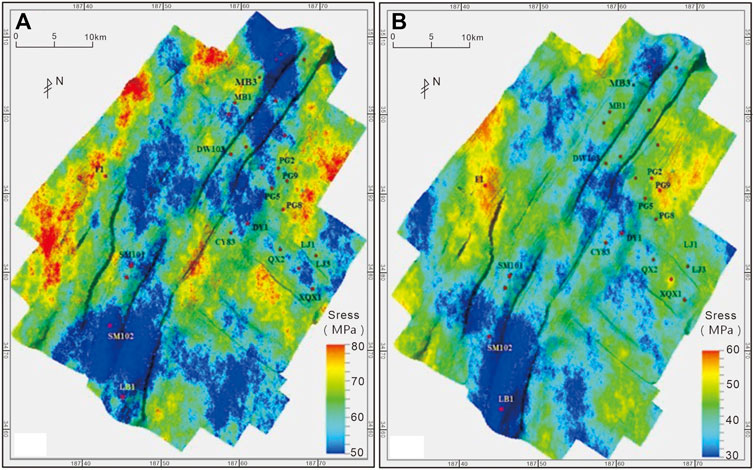
FIGURE 4. The contour maps of the numerical simulation geo-stress in the second member of Jialingjiang formation, Puguang area (A) the maximum horizontal principal stress (B) the minimum horizontal principal stress.
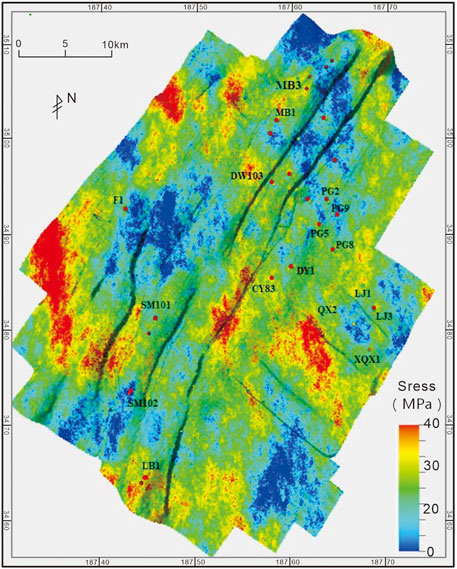
FIGURE 5. The contour map of horizontal differential stress numerical simulated in the second member of Jialingjiang formation.
The study and evaluation of in-situ stress are carried out throughout the exploration and development of oil and gas fields. Especially during oil and gas field development, the in-situ stress has a significant impact on the well pattern deployment, water injection development design, perforation scheme planning, and hydraulic fracturing treatment, as well as the later-stage casing deformation analysis and wellbore stability evaluation (Wan et al., 2009). In water injection development, it is critical to determine the fracture opening pressure. In particular, the fracture opening pressure and formation fracturing pressure in the areas with multiple fracture systems should be comprehensively considered (Zhao et al., 2015); their magnitudes are closely related to the in-situ stress. In this study, the opening pressure of the fractures with different orientations and the formation fracturing pressure were calculated based on the simulation results of the present-day stress field to determine the appropriate fracture opening sequence.
As Figure 3 shows, the in-situ stress orientation is locally deflected due to the influence of faults, and the effects of faults on the in-situ stress state are particularly prominent in the case of similar rock mechanical parameters (Zu et al., 2014). The fault zones are generally shattered zones manifested as weak geological bodies. Under the same regional compressive stress, the fault zone absorbs the stress and causes the deflection of the in-situ stress direction in surrounding areas. The trend of deflection gradually converges to the fault strike, and the deflection of in-situ stress direction is more significant at the fault tips than in the middle section of the fault, with a maximum local deflection of 20–30°. Because the state of the in-situ stress indeed varies between the elements separated by the fault, as a result, the defection pattern varies. When looking from the centre to any of the tip of the fault, on the left side around the fault tips, the orientation of the principle of the in-situ stress rotates clockwise, and on the opposite side, i.e., the right side, the orientation of the principle of the in-situ stress rotates anti-clockwise. In areas away from the fault, the degree of deflection gradually decreases. In addition, the scale of the fault and the angle between the fault strike and the regional maximum horizontal principal stress also affect the degree of present-day in-situ stress field deflection in the vicinity of the fault zone.
The strike, dip, and dipping direction of the tectonic fractures in the Jia 2 member of the Puguang area were counted by imaging logging, and the statistics (Figure 6) show that there are mainly three sets of tectonic fractures in the Jia 2 member, trending E-W, NW-SE, and N-W, respectively (Figure 6A). Among them, the near E-W fractures are high-angle fractures dipping towards due north or due south. Their dip is concentrated between 69.81° and 89.08°, with an average of 80°. The fractures with near NW-SE orientations dip towards NE or SW, with a value of 25–48° and an average of 40°. The near N-S trending fractures dip towards W, with a value of 20–40° and an average of 30° (Figure 6B).
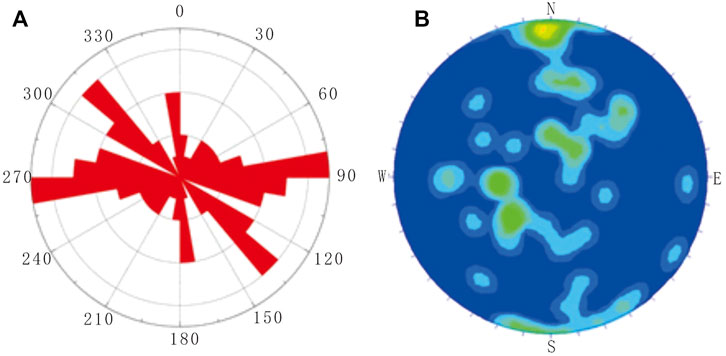
FIGURE 6. The statistic maps of structural fractures in the second member of Jialingjiang formation, Puguang area (A) the rose diagram of the fracture strike (B) The equal density map of the fracture dip directions and dips.
The opening pressure of each fracture system and the formation fracturing pressure can be calculated using the three-dimensional present-day stress field model, and the opening pressure of the fractures with different orientations can be expressed as (Zeng, 2004):
where
The formation fracturing pressure is (Zhao et al., 2015):
Pf is the formation fracturing pressure, Po is the pore fluid pressure, and
The calculation results show that the opening pressure of the fractures with near E-W, near N-S, and NW-SE orientations is concentrated in the ranges of 33–49, 78–107, and 84–117 MPa, respectively. In comparison, the formation fracturing pressure lies between 41 and 64 MPa, higher than the opening pressure of the near E-W fractures but lower than that of the other two sets of fractures. Therefore, during the hydraulic fracturing operation, the E-W fractures will open first and serve as the main seepage channels. As the fracturing pressure gradually increases, the formation will begin to rupture, producing a fracture network. A contour map of the fracture opening pressure in the Puguang area can be plotted based on the calculated opening pressures of different fracture systems (Figure 7). Designing the appropriate water injection pressure based on the fracture opening pressure in different areas is an effective measure to enhance oil and gas recovery.
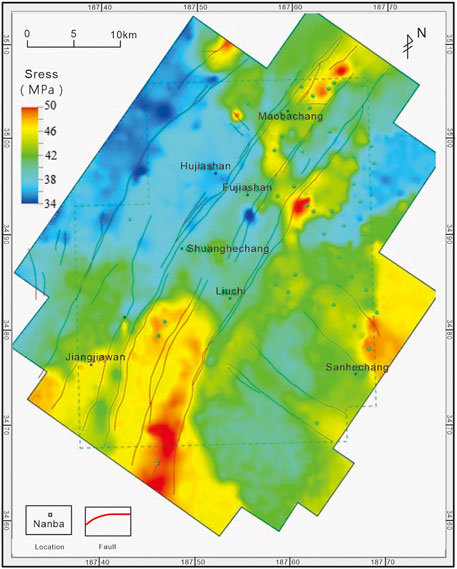
FIGURE 7. The contour map of E-W fracture opening pressure in the second member of Jialingjiang formation, Puguang area.
1) The numerical simulation results show that the present-day in-situ stress state in the Jia 2 member of the Puguang area is dominated by E-W compressive stress, and the in-situ stress orientation is locally deflected due to the influence of faults.
2) The minimum horizontal principal stress, maximum horizontal principal stress, and differential stress in the study area are mainly concentrated in the ranges of 30–60, 50–80, and 10–40 MPa, respectively, and the in-situ stress distribution is remarkably controlled by the burial depth and lithology.
3) Among the opening pressures of the fractures with different orientations in the Jia 2 member, calculated using the three-dimensional heterogeneous present-day in-situ stress model, the opening pressure of the near E-W fractures is the smallest, concentrated between 33 and 49 MPa, which is lower than the formation fracturing pressure. During hydraulic fracturing, the E-W fractures will open first and become the main seepage channels. The continuously increasing operating pressure will lead to formation breakdown, producing a fracture network.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
The first author JL is responsible for the idea and writing of this article, and the co-authors KZ, QL, DZ, ZZ, ZLi, JZ, ZLu, NY, and XD are responsible for the experimental part.
Authors KZ, ZLi, JZ, and ZLu were employed by the Zhongyuan Oilfield Branch Company. XD was employed by the China National Petroleum Corporation.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Barree, R. D., Gilbert, J. V., and Conway, M. (2009). “Stress and Rock Property Profiling for Unconventional Reservoir Stimulation,” in SPE Hydraulic Fracturing Technology Conference, Woodlands, TX, January 19, 2009 (OnePetro), 19–21. doi:10.2118/118703-MS
Cai, M. F., Qiao, L., Yu, B., and He, H. F. (1997). Results and Analysis of In-Situ Stress Measurement in Meishan Iron Mine. Chin. J. Rock Mech. Eng. 16 (3), 233–239.
Chen, B., and Tian, C. (1998). Numerical Simulation Technique for Structural Fractures in a Reservoir: Case Studies. Acta Petrolei Sinica 19, 50–54.
Cheng, Y. F., Shen, H. C., Zhao, Y. Z., Wang, J. Y., and Zhang, J. G. (2008). Study on the Earth Stress Field in Complex Fault Block——taking Xi-3 fault block in Beier Sag, Hailaer Basin as an example. J. Xi'an Shiyou Univ. (Natural Sci. Edition 0523, 15–20.
Dai, L. M., Li, S. Z., Lou, D., Suo, Y. H., Liu, X., Zhou, L. H., et al. (2013). Numerical modeling on the stress field in the Huanghua depression, Bohai Bay basin. Chin. J. Geophys. 56 (3), 929–942. doi:10.6038/cjg20130321
Dong, P., Han, D., Niu, Y., and Li, L. (2009). Object-Oriented Finite Element Programming for Multiphase Seepage in an Oil Reservoir. Rock Soil Mech. 30 (4), 1115–1130. doi:10.16285/j.rsm.2009.04.007
Gao, H., Liu, J., and Shen, L. (2000). Measuring Methods of Deep Formation Geostress and Its Application to Borehole Stability Analysis. Chin. J. Rock Mech. Eng. 19, 1124–1127.
Gong, L., Fu, X., Wang, Z., Gao, S., Jabbari, H., Yue, W., et al. (2019). A new approach for characterization and prediction of natural fracture occurrence in tight oil sandstones with intense anisotropy. Bulletin 103 (6), 1383–1400. doi:10.1306/12131818054
Gong, L., Gao, S., Liu, B., Yang, J., Fu, X., Xiao, F., et al. (2021a). Quantitative Prediction of Natural Fractures in Shale Oil Reservoirs. Geofluids, 15. doi:10.1155/2021/5571855
Gong, L., Wang, J., Gao, S., Fu, X., Liu, B., Miao, F., et al. (2021b). Characterization, controlling factors and evolution of fracture effectiveness in shale oil reservoirs. J. Pet. Sci. Eng. 203, 108655. doi:10.1016/j.petrol.2021.108655
Hu, Q., and Li, L. (2015). Numerical simulations of tectonic stress fields for Late Mesozoic-Paleogene extensional tectonics in western Shandong. Pet. Geology& Exp. 37, 259–266. doi:10.7603/s40972-015-0040-4
James, A. T. (1983). Correlation of natural gas by use of carbon isotopic distribution between hydrocarbon components. AAPG Bull. 67, 1176–1991. doi:10.1306/03b5b722-16d1-11d7-8645000102c1865d
Jing, F., Sheng, Q., Zhang, Y. H., and Liu, Y. K. (2011). Study advance on in-site geostress measurement and analysis of initial geostress field in China. Rock Soil Mech. 32 (S2), 51–58.
Li, J., Zeng, L., Li, W., Zhang, Y., and Cai, Z. (2019). Controls of the Himalayan deformation on hydrocarbon accumulation in the western Qaidam Basin, Northwest China. J. Asian Earth Sci. 174, 294–310. doi:10.1016/j.jseaes.2018.12.015
Li, Y. X., and Dong, B. C. (2009). In-situ stress measurement of reservoir using Kaiser effect of rock. Chin. J. Rock Mech. Eng. 28 (S1), 2802–2807.
Li, Z., Zeng, Z., Huang, Z., Liu, L., Wei, Z., and Zhang, K. (2007). Numerical Simulation of the Tectonic Stress Field and Forecasting of Fractures Based on MSC MARC. J. Geostress 13 (3), 233–238. doi:10.3969/j.issn.1006-6616.2007.03.005
Liu, Y., An, G., and Zhang, L. (2006). Confirming characteristics of ground stress field of Toutai oil field in Songliao Basin by microseismic wave method. Petroleim Geology. Oil Field Dev. Daqing 25, 29–30. doi:10.3969/j.issn.1000-3754.2006.03.010
Liu, Z., Mei, L., Guo, T., Fan, Y., Tang, J., and Shen, C. (2009). Characteristics and Differences of Hydrocarbon Accumulations in Marine Carbonate Rocks, Northeast Sichuan Basin: A Case Study from Puguang and Maoba Gas Fields. Pet. Explorat. Dev. 36 (5), 552–561. doi:10.3321/j.issn:1000-0747.2009.05.002
Meng, Q., Wang, T., Lü, J., Dong, Y., and Guo, B. (2014). Three-dimension numerical simulation for tectonic stress field of Tangshan fracture zone. J. Geodesy Geodynamics 34, 38–42.
Qian, Z., and Zhong, K. (2009). Sedimentary Facies and Reservoir Features of the Xujiahe Formation in Northeastern Sichuan Basin. Nat. Gas Industry 29 (6), 9–12. doi:10.3787/j.issn.1000-0976.2009.06.003
Qin, Y., Tang, H., Wu, Z., and Ge, X. (2018). A calculation model for 3D in-situ stress tensor of deep shale based on borehole wall stress relief method. Chin. J. Rock Mech. Eng. 37, 1468–1480. doi:10.13722/j.cnki.jrme.2018.0104
Sang, G. S., Xia, B., and Zhang, S. L. (2010). Numerical modeling of 3D tectonic stress field for the Xujiaweizi fault depression of Songliao basin. Geotectonica et Metallogenia 34 (2), 196–203. doi:10.3969/j.issn.1001-1552.2010.02.005
Shen, C., Mei, L., Liu, L., Zeng, Z., and Tang, J. (2004). Study of fault sealing by the 3-D paleo-tectonic numerical simulation. Pet. Geology& Exp. 26, 103–107. doi:10.3969/j.issn.1001-6112.2004.01.020
Su, Y., and Li, T. (2009). Effects studies of areal heterogeneity on oil-water displacement laws in extra-low permeability reservoirs. Pet. Geology. Recovery efficiency 16, 69–71. doi:10.3969/j.issn.1009-9603.2009.01.019
Tan, C., Wang, L., and Sun, B. (1997). An Approach to Numerical Simulation of 3-D Tectonic Stress Field of the Oil-Gas-Bearing Basin. J. Geostress 3 (1), 71–79.
Tang, D., Chen, X., and Zhang, X. (2008). Fault Systems and Their Tectonic Evolution in Xuanhan-Daxian Area, the Northeastern Sichuan Basin. Pet. Geology. Exp. 30 (1), 58–63. doi:10.3969/j.issn.1001-6112.2008.01.012
Tian, Y. P., Liu, X., Li, X., and Wei, M. (2011). Finite element method of 3-D numerical simulation on tectonic stress field. Earth Science—Journal China Univ. Geosciences 36 (2), 375–380. doi:10.3799/dgkx.2011.041
Wan, X. L., Gao, C. N., Wang, Y. K., Zhang, Z. H., Yan, H. L., and An, M. S. (2009). Coupled relationship between created and natural fractures and its implication to development. J. Geomechanics 15 (3), 245–252. doi:10.3969/j.issn.1006-6616.2009.03.006
Wang, K., Dai, J. S., Liu, H. L., Li, Q., and Zhao, L. B. (2015). Characteristic of current in-situ stress field in Keshen gas field. Tarim Basin. J. Cent. S. Univ. 46 (3), 941–951.
Wang, S., Song, H., and Liu, J. (1999). Numerical Modeling of Tectonic Stress Field in Tarim Basin and its Implication to Hydrocarbon Accumulation. Seismology Egology 21 (3), 268–273. doi:10.3969/j.issn.0253-4967.1999.03.010
Xie, R., Zhou, W., Deng, H., Wang, S., and Yan, C. (2008). Integrated Research Methods of In-Situ Stress Field Characteristics. Oil Drilling Prod. Tech. 30 (4), 32–35.
Xu, Y., He, Z., and Zeng, F. (2004). Characteristics of Gas Accumulation in Northeastern Sichuan Basin. Oil Gas Geol. 25 (3), 274–279. doi:10.3321/j.issn:0253-9985.2004.03.007
Zeng, L. (2004). Fissure and Its Seepage Characteristics in Low-Permeable Sandstone Reservoir. Chin. J. Geol. 39 (1), 11–17. doi:10.3321/j.issn:0563-5020.2004.01.002
Zeng, L., Su, H., Tang, X., Peng, Y., and Gong, L. (2013). Fractured tight sandstone oil and gas reservoirs: A new play type in the Dongpu depression, Bohai Bay Basin, China. Bulletin 97 (3), 363–377. doi:10.1306/09121212057
Zeng, L., and Tian, C. (1998). Tectonic stress field and the development of low permeability oil fields. Pet. Exploration Dev. 25, 91–93.
Zeng, L., Wang, H., Gong, L., and Liu, B. (2010). Impacts of the tectonic stress field on natural gas migration and accumulation: A case study of the Kuqa Depression in the Tarim Basin, China. Mar. Pet. Geology. 27 (7), 1616–1627. doi:10.1016/j.marpetgeo.2010.04.010
Zhan, Z. M., Chen, L. W., and Lu, Y. Z. (2011). Crustal dynamic parameters and 3D finite element model of North China. J. Geod. Geodyn 31, 28–32. doi:10.3969/j.issn.1671-5942.2011.z1.007
Zhao, X., Zeng, L., Jin, B., Jiao, J., Li, P., and Zhang, Y. (2015). Discussion on optimal injection pressure of fractured low-permeability sandstone reservoirs–A case study from Wangyao block in Ansai oilfield. Ordos Basin. Oil Gas Geology. 36, 855–861. doi:10.11743/ogg20150519
Zhou, J. B., Shi, X. D., Ding, Y. S., Kan, Y. K., and Shi, X. Y. (2015). The multi-parameter quantitative prediction of Reservoir fracture of fu-2 member in Tian 96 fault block of Jinhu sag. J. Geomechanics 21 (3), 341–350. doi:10.3969/j.issn.1006-6616.2015.03.004
Zu, K., Cheng, X., Luo, Z., Yin, N., and Wang, K. (2018). The Comparative Analysis of Different Methods for Fracture Prediction in Complex Carbonate Rock Reservoir. J. Geostress 24 (4), 465–473. doi:10.12090/j.issn.1006-6616.2018.24.04.048
Zu, K., Zeng, D., and Cheng, X. (2017). Forming Mechanism and Prediction of Structural Fractures in the Second Member of Jialingjiang Formation in Puguang Area. Xinjiang Petrol. Geol. 38 (4), 111–117. doi:10.7657/XJPG20170405
Keywords: Puguang area, geo-stress, finite element, numerical simulation, fracture opening pressure
Citation: Li J, Zu K, Li Q, Zeng D, Li Z, Zhang J, Luo Z, Yin N, Zhu Z and Ding X (2022) Prediction of Fracture Opening Pressure in a Reservoir Based on Finite Element Numerical Simulation: A Case Study of the Second Member of the Lower Triassic Jialingjiang Formation in Puguang Area, Sichuan Basin, China. Front. Earth Sci. 10:839084. doi: 10.3389/feart.2022.839084
Received: 19 December 2021; Accepted: 13 January 2022;
Published: 07 February 2022.
Edited by:
Lei Gong, Northeast Petroleum University, ChinaReviewed by:
Xing Zeng, Research Institute of Petroleum Exploration and Development (RIPED), ChinaCopyright © 2022 Li, Zu, Li, Zeng, Li, Zhang, Luo, Yin, Zhu and Ding. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian Li, cGhvZW5peC5saWppYW5AZ21haWwuY29t; Kewei Zu, enVrZXdlaTEyMzRAYWxpeXVuLmNvbQ==; Qi Li, bGlxaUBjdWdiLmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.