Study on Dynamic Response of Rock Slope With Inverse Non-Persistent Joints Under Earthquake

Based on the two-dimensional discrete element software UDEC, this article studied the dynamic response laws of rock slopes with inverse nonpersistent joints by the combination of different dip angles and spacing of joint and length of rock bridge under earthquake. The results showed that the existence of the joint surface had a significant impact on the dynamic response of the slope. When the dip angle of inverse nonpersistent joint increases or the joint spacing decreases, the PGA amplification factor of each monitoring point on the slope surface increases, and the influence range is mainly concentrated in the middle of the slope surface to the slope shoulder. Along the horizontal direction of the slope, closer to the shoulder of the slope, the PGA amplification factor increases with the increase of the joint dip angle and the decrease of rock bridge length and joint spacing; along the vertical direction, the PGA amplification coefficient curve increases first, then decreases, and then increases with the change of elevation, and the dynamic response of slope reacts the most violent where the joints are densely developed.

Introduction

Rock slope damage caused by the earthquake is a common geological disaster (Li et al., 2007). In the last century, the failure of rock slopes accounted for nearly 30% of all kinds of natural geological disasters caused by earthquakes. With the acceleration of the development in the western region of China, especially the construction of a number of large-scale infrastructure projects, the geological problems of rock slope disasters caused by earthquakes in the fields of highways, railways, cross-basin water transfer, and promoting urbanization in mountainous areas will be more prominent.

There are many factors controlling the seismic dynamic stability of rock slopes (Zhang et al., 2016), among which the spatial development characteristics and physical and mechanical properties of the internal structural plane play a major role. A large number of joints are usually developed in the rock mass, and the joints of the rock mass are not completely penetrated. The rock mass is cut into discontinuous bodies. At present, many scholars have made in-depth discussions on the influence of the bedding joint fissures developed in the rock mass on the stability of the slope rock mass and achieved certain results (Kang, 2018; Lin et al., 2019). However, in reality, the joints are abundant, and the research on the anti-dip discontinuous joints distributed in the slope is rarely reported. In addition, due to the suddenness and unpredictability of the earthquake, the dynamic response characteristics of the anti-dip discontinuous rock slope are very complex. In-depth exploration of this problem has very important practical significance and engineering value for dynamic stability evaluation, earthquake-induced landslide risk prediction, and engineering treatment of anti-dip intermittent jointed rock slope.

At present, the research methods of rock slope stability and dynamic response under earthquakes mainly include slope failure mechanism research based on earthquake damage experience (Guoxinag, 2012) (Guo et al., 2017), physical model test based on the shaking table test (Runqiu et al., 2013; Fan et al., 2016; Yang et al., 2018), and dynamic response research based on numerical analysis (Liu et al., 2012). At first, the research on slope stability from the perspective of actual seismic damage investigation mainly focused on the description and introduction of seismic damage (Yang, 2018). With the aggravation of seismic disasters, some scholars investigated the relationship between earthquakes and slope failure from the perspective of seismic damage statistics (Wang, 2001; Runqiu and Weile, 2008; Yin, 2009). Wang et al. put forward two improved calculation formulas for predicting the seismic collapse of rock and soil slopes by calculating and analyzing the comprehensive index values and comparing the calculated results with the seismic damage performance of natural slopes in historical earthquakes in China (Wang, 2001). Yin studied the development and distribution of geological disasters triggered by the '5.12′ Wenchuan earthquake (Yin, 2009). It was concluded that terrain slope is one of the controlling factors for the development of geological disasters, and most disasters are concentrated in the range of 20°–50°. Based on the statistics of collapse disasters in Wudu District of Gansu Province during Wenchuan earthquake, Chen pointed out that the thick strata with developed joints were the main factor inducing collapse (Chen, 2011). The shaking table test is an important means to simulate the response of the model under seismic load in the laboratory. The response of the model is studied by the similarity principle and dimensional analysis method (Xu, 2008; Xu, 2010; Xiao et al., 2017). Xu et al. designed and completed a 1:10 scale large-scale shaking table model test of the slope, revealing the instability mechanism of slope under seismic action (Xu, 2008). Yin focused on dissecting three typical examples of Niujuangou landslide-debris flow in Yingxiu, Wenchuan, located in the southwest part of the seismic rupture zone (initial epicenter), Beichuanchengxi landslide located in the middle part of the seismic rupture zone, and Qingchuandonghekou landslide-debris flow located in the northeast part of the seismic rupture zone, and analyzed the high-speed and long-distance characteristics of the seismic landslide (Yin, 2009). Xu et al. designed and completed a large-scale shaking table test with a ratio of 1:100 based on the typical slope of the " 5 · 12 ″ Wenchuan earthquake disaster area and systematically studied the seismic dynamic response characteristics of the model slope (Xu, 2010). Based on the prototype slope, Fu et al. designed a large-scale shaking table model test. By monitoring the axial force of anchor cable, soil pressure of pile body, slope acceleration, and slope displacement time history, they studied the seismic dynamic characteristics of the composite structure of the multi-level anchor cable frame beam and double-row anti-slide pile to strengthen the rock slope with a weak interlayer (Xiao et al., 2017). On the other hand, with the development of computer technology, numerical simulation technology has been widely used in seismic dynamic stability analysis of rock slopes (Liu et al., 2004; Potyondy and Cundall, 2004; Li, 2007; Guo et al., 2011; Camones et al., 2013). Liu et al. used UDEC to simulate the dynamic response of Huangmailin Phosphorite rock slope under explosion and compared with the field-measured results. The results showed that the numerical simulation results are in good agreement with the measured results (Liu et al., 2004). Li et al. compared the limit analysis method and the finite element numerical simulation method to solve the failure mechanism of the slope under earthquake action. The results showed that the numerical simulation method can better estimate the failure mechanism of the slope (Li, 2007). Guo et al. used the dynamic finite element method (DFEM) to analyze the vibration characteristics and dynamic response of rock and soil slope under seismic load, and combined DFEM with the vector sum analysis method (VSAM), the safety factor of slope at any time can be easily obtained (Guo et al., 2011). However, it involves engineering geology, seismic engineering, rock mechanics, and other disciplines, and the physical and mechanical properties of the research object are complex. Therefore, it is urgent to further deepen the understanding of the failure mechanism and dynamic response law of anti-dip intermittent jointed rock slopes under earthquake action.

In recent years, the two-dimensional discrete element software UDEC has shown significant advantages in simulating the response of jointed rock systems and rock masses under dynamic load conditions, and thus it has gradually become a powerful tool for geotechnical analysis and research. Based on UDEC 7.0, this article will study the influence of joint inclination, rock bridge length, and joint spacing on the dynamic response of anti-dip discontinuous jointed rock slopes under seismic conditions by inputting seismic waves, which provides a reference for the dynamic stability evaluation of such rock slopes.

Discrete Element Numerical Model Construction

Material Model and Parameter Determination

The numerical simulation uses UDEC 7.0 software. The slope constitutive model adopts Mohr–Coulomb model of the general rock model, considering plastic characteristics. The joint adopts contact-Coulomb slip model (joint model area), which needs to input joint cohesion and joint friction angle, joint normal stiffness and joint tangential stiffness, and other parameters. Among them, combined with the actual rock mass parameters, referring to the discrete element simulation analysis of Shentong (Shen et al., 2014), the normal stiffness of the joint will be determined which used the formula proposed by Cho (Cho et al., 2007):

$k_n=n\left[\frac{K+\left(4/3\right)G}{\mathrm{\Delta }{Z}_{\min }}\right]\begin{array}{cc}& \left(1\le \text{n}\le 10\right)\end{array},$

where k_n is the normal stiffness of the joint, Z_min is the minimum width of the area adjacent to the contact surface in the vertical direction, and K and G are the bulk modulus and shear modulus of the block, respectively. Considering the calculation efficiency, the maximum side length of the grid is set to 15 m. After many trial calculations and checks, the parameters are determined in Table 1.

TABLE 1

TABLE 1. Physico-mechanical parameters of the model slope.

Boundary Condition Setting and Seismic Wave Input

First, the velocity in the y-direction is fixed at the bottom of the model, and the velocity in the x-direction is fixed at both sides. The slope top and slope surface are free boundaries, and then the self-weight balance is calculated. In the dynamic response analysis of slope under seismic action, it is necessary to input seismic waves at the bottom of the model. In order to prevent the reflection of seismic waves at the boundary of the model, it is necessary to set the two sides of the model to the free field boundary and the bottom boundary to the viscous boundary.

Considering the complexity of the real slope geological structure, after reasonable generalization, the rock slope model with anti-inclination discontinuous joints is established, as shown in Figure 1. There are 21 monitoring points along the slope surface, horizontal direction, and vertical direction to monitor the acceleration of rock mass.

FIGURE 1

FIGURE 1. Diagram of the model and monitoring points of slope.

The first 60 s of the seismic wave measured at Mianzhuqing platform station in 2008 Wenchuan earthquake is used as the bottom of the horizontal seismic wave input model, and the acceleration time history curve is shown in Figure 2.

FIGURE 2

FIGURE 2. Acceleration time-history curve of the earthquake wave.

Slope Model Scheme

In UDEC, there are generally three steps to generate the final model:

1) Generate model geometry.

2) Define the constitutive model and material parameters.

3) Specify boundary conditions and initial conditions.

The influence of joint dip angle, rock bridge length, and joint spacing on the dynamic response of slope is studied by establishing five models with different joint dip angles, rock bridge length, and joint spacing. The parameters of each slope model are shown in Table 2, and the schematic diagram of slope model size and slope anti-dip discontinuous joint parameters is shown in Figure 3. Among them, D is the joint spacing, L_j is the joint length, L_r is the rock bridge length, and α is the joint dip angle (counterclockwise direction). The slope model with different joint dip angles, rock bridge length, and joint spacing is shown in Figure 4.

TABLE 2

TABLE 2. Model parameters.

FIGURE 3

FIGURE 3. Diagram of the model dimension and nonpersistent joint in the slope (unit: m).

FIGURE 4

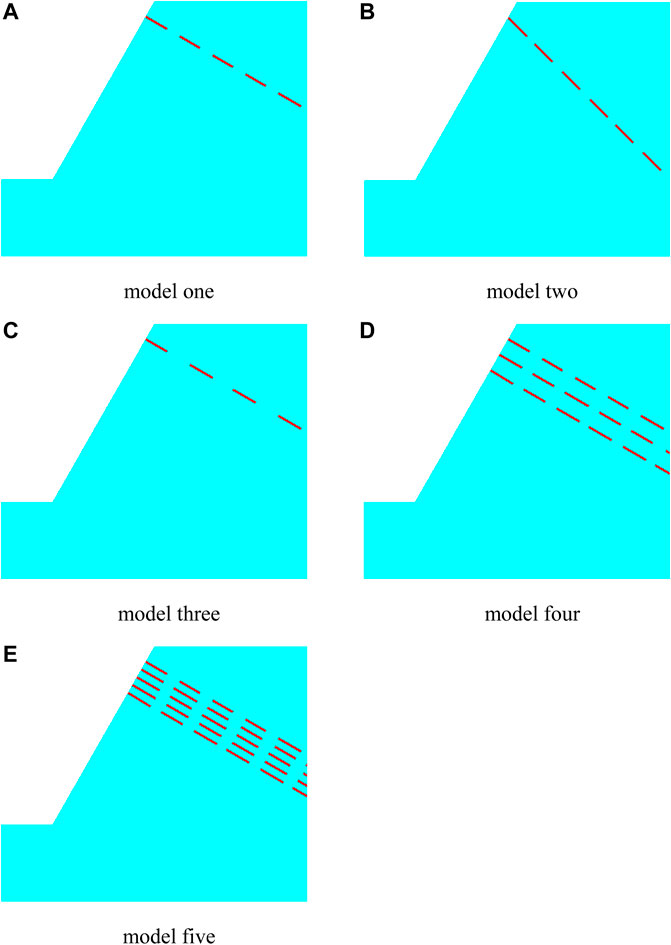
FIGURE 4. Sketches of simulation models. (A) Model 1 (B) Model 2. (C) Model 3. (D) Model 4. (E) Model 5.

Study on the Dynamic Response of Slope

According to the model set in Figure 4 and the monitoring point layout scheme in Figure 1, the acceleration time history curves of 21 monitoring points are obtained, and the dynamic response of slope under earthquake is studied. In this article, the PGA amplification factor is used to analyze peak ground acceleration (PGA). The ratio of peak acceleration of dynamic response to peak acceleration of the input seismic wave is defined as the PGA amplification factor.

Effect of Joint Inclination Difference

Under seismic action, the PGA amplification coefficients of nine monitoring points on the slope surface are shown in Figure 5A. The horizontal distance of monitoring points in the figure refers to the horizontal distance between the monitoring points and the origin of the lower-left corner coordinate of the model (as shown in Figure 3). The PGA amplification coefficients of monitoring points (points 9, 10, 11, 12, 13, and 14) along the horizontal direction of the slope are shown in Figure 5B. The PGA amplification coefficients of monitoring points (points 12, 15, 16, 17, 18, 19, 20, and 21) along the vertical direction of the slope are shown in Figure 5C. The joint dip angles of Model 1 and Model 2 are 30°and 45°, respectively, and there is the only difference in joint inclination between the two models.

FIGURE 5

FIGURE 5. PGA amplification factor of the monitoring points of slope. (A) Distribution of the PGA amplification factor at monitoring points along the slope surface. (B) Distribution of the PGA amplification factor at horizontal monitoring points. (C) Distribution of PGA amplification factor at vertical monitoring points.

It can be seen from Figure 5A that the PGA amplification first increases, then decreases, and then increases on the slope surface, and the acceleration amplification effect is the most significant at the shoulder position. When the dip angle of anti-dip discontinuous joints increases, the PGA amplification coefficient of each monitoring point on the slope surface increases, and the changing trend is significant from the middle of the slope surface to the top of the slope, while the change is relatively insignificant from the foot of the slope to the middle of the slope surface.

The dynamic response of the degree of rock mass along the horizontal direction is significantly correlated with the distance between rock mass and slope surface. As shown in Figure 5B, the PGA amplification coefficient decreases from the shoulder to the middle of the slope top and increases from the middle of the slope top to the trailing edge of the slope. With the increase of the joint dip angle, the PGA amplification coefficient of each monitoring point along the horizontal direction increases.

In the elevation direction, as shown in Figure 5C, with the increase of the joint surface, the maximum value of the PGA amplification coefficient increases. Due to the existence of the anti-inclined discontinuous joint surface, the PGA amplification coefficient does not show a monotonous increase with the increase of slope height but experiences a process of first increase, then decrease, and then increase, and the decrease occurs near the structural surface, indicating that when the seismic wave passes through the anti-inclined joint surface, the joint surface plays a certain degree of attenuation in its propagation.

Effect of Length Difference of Rock Bridge

The rock bridge lengths of Model 1 and Model 3 are 25 and 50 m, respectively, and only the rock bridge lengths are different between the two models.

It can be seen from Figure 6A that the PGA amplification coefficients of each monitoring point along the slope surface are basically the same, indicating that the difference in rock bridge length has no obvious effect on the PGA amplification coefficients of monitoring points along the same slope surface.

FIGURE 6

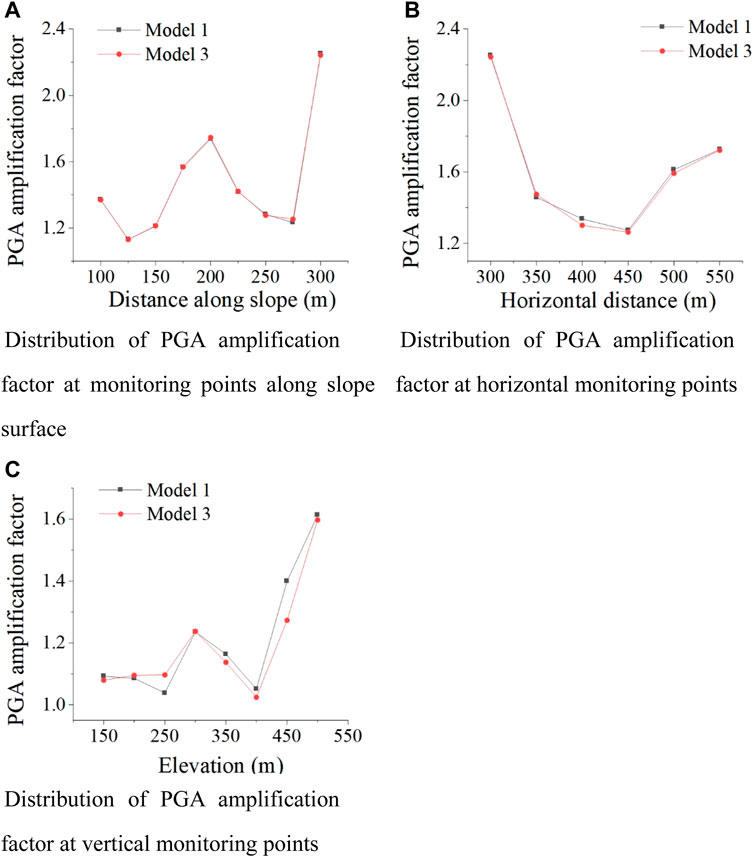
FIGURE 6. PGA amplification factor of the monitoring points of slope. (A) Distribution of the PGA amplification factor at monitoring points along the slope surface. (B) Distribution of the PGA amplification factor at horizontal monitoring points. (C) Distribution of the PGA amplification factor at vertical monitoring points.

In the horizontal direction, as shown in Figure 6B, with the increase of the length of the rock bridge, the PGA amplification coefficient of the slope decreases slightly, indicating that the increase of the length of the rock bridge has an influence on the dynamic response of the slope along the horizontal direction under a certain range.

Compared with the long slope, the slope with a shorter rock bridge length has bad slope stability, as shown in Figure 6C. In general, in the elevation direction, the PGA amplification factor is larger, and the length of the rock bridge is in negative correlation with the PGA amplification factor of monitoring points. The shorter the length of the rock bridge is, the greater the PGA amplification factor is, and the changing trend is significant from the middle of the slope to the top of the slope.

Effect of Joint Spacing Difference

The joint spacings of Model 4 and Model 5 are 35 and 17.5 m, respectively, and there is the only difference in joint spacing between the two models.

Joint spacing will affect the integrity of rock mass, thereby affecting slope stability. It can be seen from Figure 7A that when the anti-dip intermittent joint spacing decreases, the PGA amplification coefficient of each monitoring point on the slope surface increases, and the changing trend is significant from the middle of the slope surface to the shoulder of the slope, while the change is relatively insignificant at the foot of the slope. It can be seen that the smaller the joint spacing is, the worse the stability of the slope near the dense joint development is, and thus it is more prone to failure.

FIGURE 7

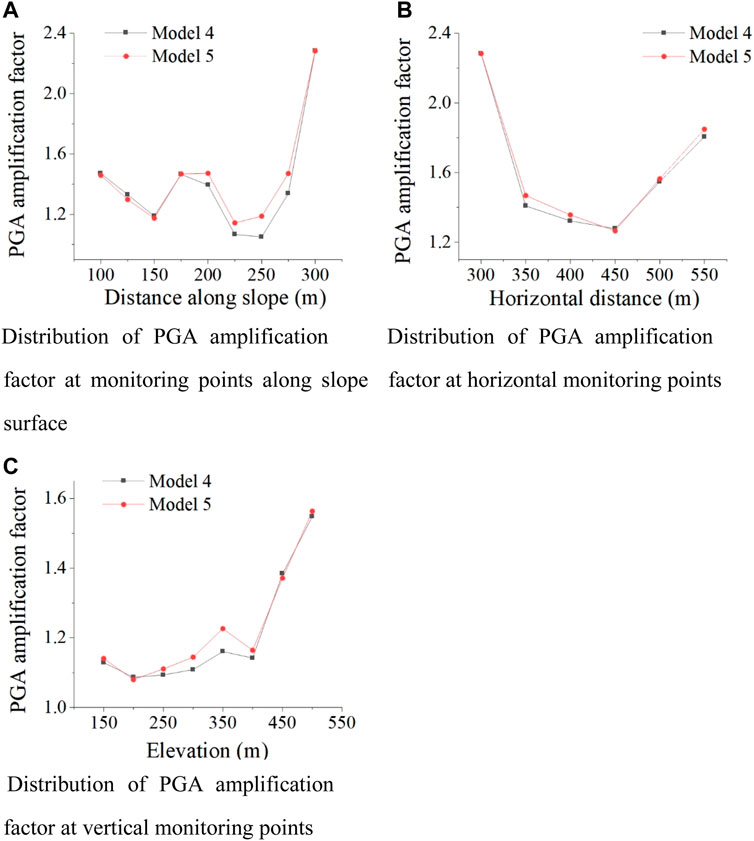
FIGURE 7. PGA amplification factor of the monitoring points of slope. (A) Distribution of the PGA amplification factor at monitoring points along the slope surface. (B) Distribution of the PGA amplification factor at horizontal monitoring points. (C) Distribution of the PGA amplification factor at vertical monitoring points.

Overall, as shown in Figure 7B, along the horizontal direction, with the decrease o joint spacing, the PGA amplification coefficient of each monitoring point of the slope increases slightly, but the influence range is mainly limited to the middle of the slope top to the trailing edge of the slope.

In the elevation direction, as shown in Figure 7C, there is a negative correlation between the joint spacing and the PGA amplification coefficient of the monitoring point. The smaller the joint spacing is, the greater the PGA amplification coefficient is, and the changing trend is the most significant in the middle of the slope. In general, the more intensive the joint surface develops, the worse the integrity of the slope rock mass and the worse its stability are; so, the seismic dynamic response is stronger.

It is concluded that when the seismic wave propagates in the fractured slope, the stress wave will produce reflection and refraction when it encounters intermittent joints. When the stress wave propagates to the surface of the slope, it will also produce reflection and refraction in the surface of the rock mass, which makes the stress wave in the rock mass occur local superposition, thus aggravating the dynamic response of the slope and making the slope stability worse.

Conclusion

Based on the two-dimensional discrete element software UDEC, this article has studied the dynamic response law of anti-dip intermittent jointed rock slopes with different combinations of joint inclination, rock bridge length, and joint spacing under seismic action.

The results have shown that the existence of the joint surface has a significant impact on the dynamic response of the slope. When the anti-inclined intermittent joint angle increases or the joint spacing decreases, the PGA amplification coefficient of each monitoring point on the slope surface increases, and the influence range is mainly concentrated in the middle of the slope surface to the shoulder. Along with the horizontal direction of the slope, closer to the shoulder, the PGA amplification coefficient increases with the increase of the joint dip angle and the decrease of rock bridge length and joint spacing. In the vertical direction, the PGA amplification coefficient curve generally shows a trend of first increase, then decrease, and then increase with the change of elevation, and the response is the strongest at the densely developed joints.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

GLX: conceptualization, methodology, software, validation, investigation, data curation, and writing—review and editing; WYH: software, validation, investigation, visualization, and writing and editing; RKH: investigation, visualization, and writing; ZL: writing—review and editing and funding acquisition; ZH: methodology, data curation, writing review and editing, and supervision.

Funding

This study was funded by the National Key R&D Program of China (No. 2017YFC1501001-03), the National Natural Science Foundation of China under No. 41977233, and the Scientific Research Foundation of Fuzhou University (No. XRC-18053).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Camones, L. A. M., Vargas, E. d. A., de Figueiredo, R. P., and Velloso, R. Q. (2013). Application of the Discrete Element Method for Modeling of Rock Crack Propagation and Coalescence in the Step-Path Failure Mechanism. Eng. Geology. 153, 80–94. doi:10.1016/j.enggeo.2012.11.013

CrossRef Full Text | Google Scholar

Chen, Y.-M., and Teng, G.-I. (2011). A Preliminary Discussion on the Characteristics of Landslide-Collapse Disaster Induced by Wenchuan Earthquake in Gansu and Countermeasures for Disaster Mitigation. Northwestern Seismological Journal 33 (B08), 451–455.

Google Scholar

Cho, N., Martin, C. D., and Sego, D. C. (2007). A Clumped Particle Model for Rock. Int. J. rock Mech. mining Sci. 44 (7), 997–1010. doi:10.1016/j.ijrmms.2007.02.002

CrossRef Full Text | Google Scholar

Fan, G., Zhang, J., Wu, J., and Yan, K. (2016). Dynamic Response and Dynamic Failure Mode of a Weak Intercalated Rock Slope Using a Shaking Table. Rock Mech. Rock Eng. 49 (8), 3243–3256. doi:10.1007/s00603-016-0971-7

CrossRef Full Text | Google Scholar

Guo, M., Ge, X., and Wang, S. (2011). Slope Stability Analysis under Seismic Load by Vector Sum Analysis Method. J. Rock Mech. Geotechnical Eng. 3 (3), 282–288. doi:10.3724/sp.j.1235.2011.00282

CrossRef Full Text | Google Scholar

Guo, S., Qi, S., Yang, G., Zhang, S., and Saroglou, C. (2017). An Analytical Solution for Block Toppling Failure of Rock Slopes during an Earthquake. Appl. Sci. 7 (10), 1008. doi:10.3390/app7101008

CrossRef Full Text | Google Scholar

Huang, R.-q., Li, G., and Ju, N.-p. (2013). Shaking Table Test on strong Earthquake Response of Stratified Rock Slopes. Chin. J. Rock Mech. Eng. 32 (5), 865–876.

Google Scholar

Huang, R.-q., and Li, W.-l. (2008). Research on Development and Distribution Rules of Geohazards Induced by Wenchuan Earthquake on 12th May, 2008 [J]. Chin. J. Rock Mech. Eng. 27 (12), 2585–2592. doi:10.3321/j.issn:1000-6915.2008.12.028

CrossRef Full Text | Google Scholar

Kang, B. (2018). Study on Failure Mode and Dynamic Response of Rock Slope with Non-persistent Joint under Earthquake. Rock Soil Mech. 39 (8), 3029–3037.

Google Scholar

Li, H., Xiao, K., and Liu, Y. (2007). Factor of Safety Analysis of Bedding Rock Slope under Seismic Load. Chin. J. Rock Mech. Eng. 26 (12), 2385–2394. doi:10.3321/j.issn:1000-6915.2007.12.002

CrossRef Full Text | Google Scholar

Li, X. (2007). Finite Element Analysis of Slope Stability Using a Nonlinear Failure Criterion. Comput. Geotechnics 34 (3), 127–136. doi:10.1016/j.compgeo.2006.11.005

CrossRef Full Text | Google Scholar

Lin, C.-H., Hung, C., Weng, M.-C., Lin, M.-L., and Uzuoka, R. (2019). Failure Mechanism of a Mudstone Slope Embedded with Steep Anti-dip Layered Sandstones: Case of the 2016 Yanchao Catastrophic Landslide in Taiwan. Landslides 16 (11), 2233–2245. doi:10.1007/s10346-019-01250-3

CrossRef Full Text | Google Scholar

Liu, Y., Deng, H., Huang, R. Q., Song, J. L., and Yuan, J. K. (2012). Numerical Simulation of Seismic Response of Anti-dumping Rock Slope Interbedded by Hard and Soft Layers. Hydrogeology Eng. Geology. 3, 30–37.

Google Scholar

Liu, Y., Li, H. B., Zhao, J., Li, J. R., and Zhou, Q. C. (2004). UDEC Simulation for Dynamic Response of a Rock Slope Subject to Explosions. Int. J. rock Mech. mining Sci. 41 (Suppl. 1). doi:10.1016/j.ijrmms.2004.03.106

CrossRef Full Text | Google Scholar

Potyondy, D. O., and Cundall, P. A. (2004). A Bonded-Particle Model for Rock. Int. J. rock Mech. mining Sci. 41 (8), 1329–1364. doi:10.1016/j.ijrmms.2004.09.011

CrossRef Full Text | Google Scholar

Shen, T., Wang, Y.-s., and Wu, L.-k. (2014). Discrete Element Simulation Analysis of Formation Mechanism of Xiaonanhai Landslide in Chongqing City. Rock Soil Mech. (in Chinese) 35 (S2), 667–675.

Google Scholar

Wang, Y.-q., Xin, X.-b., Gao, Y.-p., and Zhou, G.-s. (2001). Study on Comprehensive index Method for Predicting Earthquake-Induced Landslides. Chin. J. Geotech. Eng. 23 (3), 311–314.

Google Scholar

Xiao, F., Zhang, J.-J., and Zhou, L.-R. (2017). Shaking Table Test of Seismic Response of Slope Reinforced by Combination of Anti-slide Piles and Multi-Frame Foundation Beam with Anchor cable. Rock Soil Mech. 38 (2), 462–470. doi:10.16285/j.rsm.2017.02.020

CrossRef Full Text | Google Scholar

Xu, G.-X., Yao, L.-K., Gao, Z.-N., and Li, C.-H. (2008). Large-scale Shaking Table Model Test Study on Dynamic Characteristics and Dynamic Responses of Slope. Chin. J. Rock Mech. Eng. 27 (3), 624–632. doi:10.3321/j.issn:1000-6915.2008.03.025

CrossRef Full Text | Google Scholar

Xu, Q., Liu, H.-X., Zou, W., Fan, X.-M., and Chen, J.-J. (2010). Large-scale Shaking Table Test Study of Acceleration Dynamic Responses Characteristics of Slopes. Chin. J. Rock Mech. Eng. 29 (12), 2420–2428.

Google Scholar

Yang, G.-x., Wu, F.-q., Dong, J.-y., and Qi, S.-w. (2012). Study of Dynamic Response Characters and Failure Mechanism of Rock Slope under Earthquake. Chin. J. Rock Mech. Eng. 31 (4), 696–702. doi:10.16285/j.rsm.2017.0056

CrossRef Full Text | Google Scholar

Yang, G., Qi, S., Wu, F., and Zhan, Z. (2018). Seismic Amplification of the Anti-dip Rock Slope and Deformation Characteristics: A Large-Scale Shaking Table Test. Soil Dyn. Earthquake Eng. 115, 907–916. doi:10.1016/j.soildyn.2017.09.010

CrossRef Full Text | Google Scholar

Yang, Z.-P., Liu, S.-I., Liu, Y.-Q., He, C.-M., and Yang, W. (2018). Dynamic Stability Analysis of Bedding and Toppling Rock Slopes under Repeated Micro-seismic Action. Chin. J. Geotech Eng. 40 (7), 1277–1286. doi:10.11779/CJGE201807014

CrossRef Full Text | Google Scholar

Yin, Y.-P. (2009). Features of Landslides Triggered by the Wenchuan Earthquake. J. Eng. Geology. 17 (1), 29–38.

Google Scholar

Zhang, Z., Wang, T., Wu, S., and Tang, H. (2016). Rock Toppling Failure Mode Influenced by Local Response to Earthquakes. Bull. Eng. Geol. Environ. 75 (4), 1361–1375. doi:10.1007/s10064-015-0806-x

CrossRef Full Text | Google Scholar