Modelled sensitivity of Monte San Lorenzo ice cap, Patagonian Andes, to past and present climate

1 Introduction

The Southern Andes currently account for 8% of the total global mass loss from glaciers (Hugonnet et al., 2021). In particular, Patagonian glaciers are among the most climatically sensitive on Earth (Mackintosh et al., 2017), with an annual specific volume loss in excess of 1 m water equivalent (w.e.), the highest observed globally (Dussaillant et al., 2019; Zemp et al., 2019). However, sparse field measurements of glacier mass balance, ice thickness, basal ice conditions and ice velocity (including that from sliding versus deformation) limit our understanding of the dynamics of current ice-mass change and glacier-climate interactions. This data paucity impedes our ability to relate past glacier fluctuations explicitly to changes in palaeoclimate, as mass-balance sensitivities are poorly understood. Numerical glacier modelling can be applied to reconstruct glacier mass-balance distribution, glacier physical behaviour and properties in absence of measured empirical data. These models can be used to assess the sensitivity of an ice mass to both external climatic forcings (such as past temperature and precipitation) and physical parameters that impact ice flow and glacier mass balance (cf. Golledge et al., 2012; Doughty et al., 2013; Ziemen et al., 2016; Nielsen et al., 2018; Yan et al., 2018).

Small temperate ice caps in Patagonia, such as Monte San Lorenzo (MSL) (Figure 1; 47.58°S, 72.35°W, 3,706 m asl), typically have short response times and high climate sensitivity (Bahr et al., 1998), making them useful for understanding rapid changes in palaeoclimate and resultant glacier response. Notably, due to the strong west-east precipitation gradient across the Patagonian Andes (Garreaud et al., 2013), and their location further inland, the smaller ice caps such as MSL east of the main Patagonian icefields (72–73°W) may be limited by precipitation, and may therefore be more sensitive to change in this than glaciers further to the west.

FIGURE 1

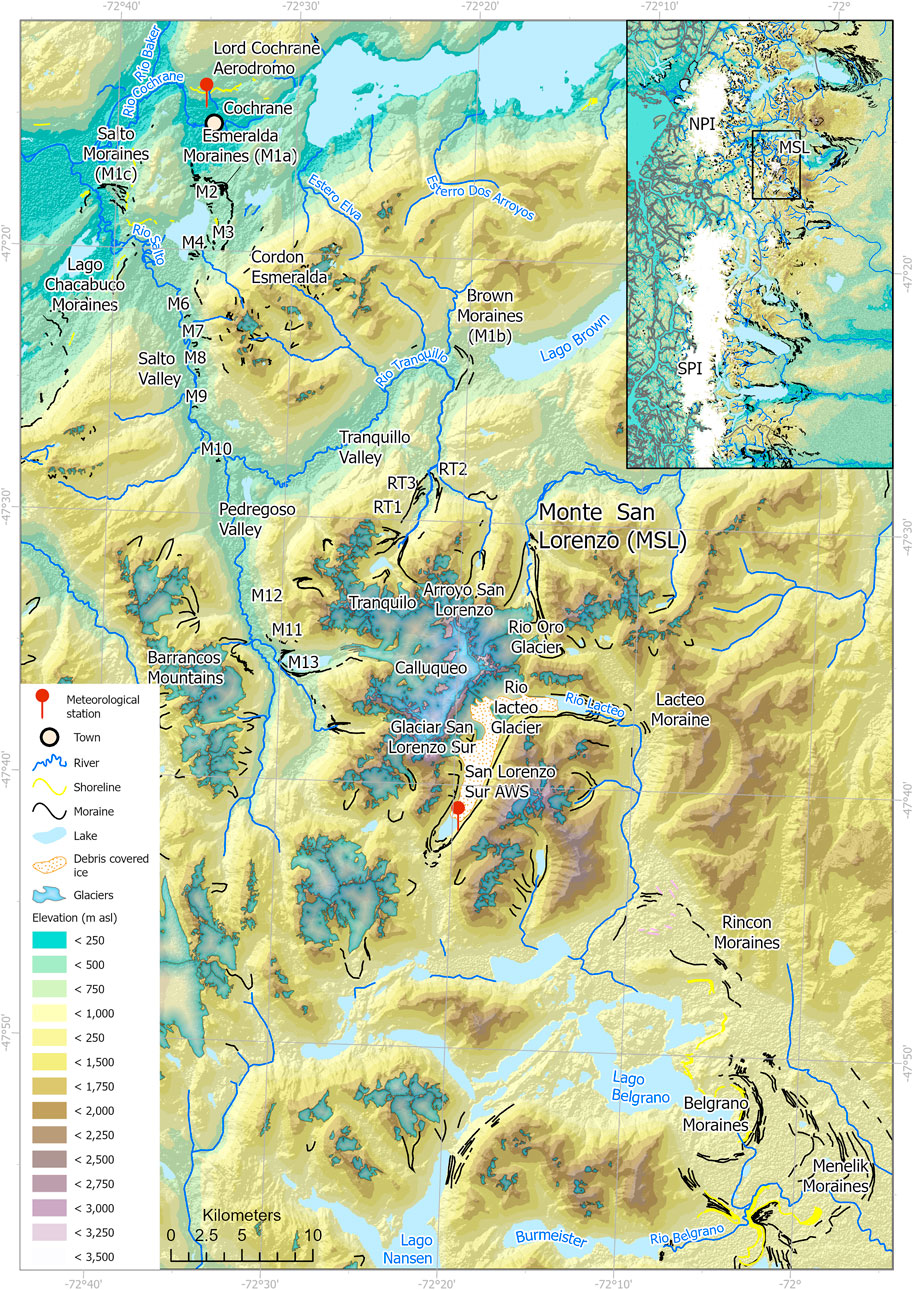
FIGURE 1. Map of the study area, with Monte San Lorenzo (MSL) and major placenames and geomorphological features mapped. Moraines, shorelines, rivers and lakes mapped in previous work (Davies and Glasser, 2012; Davies et al., 2018; 2020; Sagredo et al., 2018; Martin et al., 2019; 2022; Mendelová et al., 2020). For the inset, moraines and glaciers are from the compilation in Davies et al. (2020). Glacier outlines are derived from the Randolph Glacier Inventory v. 6.0 (Randolph Glacier Inventory Consortium et al., 2017), with a timestamp of 31.05.2003. Inset shows overview of Monte San Lorenzo (MSL), which lies to the southeast of the Northern Patagonian Icefield (NPI) and northeast of the Southern Patagonian Icefield (SPI). Moraine codes are after Martin et al. (2019), Mendelová et al. (2020), and Sagredo et al. (2018). AWS: Automatic weather station.

Geomorphological and chronological data collected from valleys around MSL show that glaciers receded rapidly through the Last Glacial-Interglacial Transition (LGIT; 15 to 11.7 ka BP; Lowe and Hoek, 2001) and Holocene (11.7 ka onwards; Rasmussen et al., 2014) (Sagredo et al., 2016, 2018; Davies et al., 2018; Martin et al., 2019, 2022; Thorndycraft et al., 2019; Mendelová et al., 2020). During this time, large-scale climatic events such as the Antarctic Cold Reversal (ACR) impacted Patagonia (Moreno et al., 2009; 2018; Tonello et al., 2009; Waldmann et al., 2010; Kilian and Lamy, 2012; Oehlerich et al., 2015; Quade and Kaplan, 2017; Kaplan et al., 2020). These climatic events resulted in changes in the Southern Westerly Winds, likely through the Southern Annular Mode (Boex et al., 2013; Moreno et al., 2018; Bendle et al., 2019; Kaplan et al., 2020; Morales et al., 2020; Moreno, 2020), driving changes in temperature and precipitation, which caused glacier fluctuations (Reynhout et al., 2019). However, the relative sensitivity of palaeo-glaciers to temperature and precipitation, and which of these forcings were the primary control on glacier mass balance at this time, remains unclear. There are few palaeoclimatic proxies available from Patagonia able to provide quantitative estimates of specific environmental conditions at particular times, especially in the study region (Kilian and Lamy, 2012; Massaferro and Larocque-Tobler, 2013). The available palaeoclimatic reconstructions often rely on qualitative comparisons (describing periods as hotter, colder, drier, wetter, for example) (Mansilla et al., 2016; Quade and Kaplan, 2017; McCulloch et al., 2020; Moreno, 2020). An improved understanding of present-day glacier dynamics and mass-balance sensitivities can inform our understanding of past glacier response to climate change.

In this study, we used the Parallel Ice Sheet Model (PISM) across a domain centred on the MSL ice cap, calibrated to match present-day ice extent, velocity and thickness. Our aim is firstly to quantify present-day physical glacier properties, ice dynamics (such as the proportion of ice deformation versus sliding and basal yield strength) and surface mass balance. Secondly, by comparing the LGIT landform record of outlet glaciers north of MSL (Martin et al., 2019; 2022) with results from PISM, we aim to gain insights into the palaeoclimatic controls on ice volume. We use model sensitivity experiments to assess the impact of surface air temperature, precipitation, snow and ice melt factors, bed strength and ice rheology on the simulated ice cap. These new data improve our understanding of the key controls on the behaviour of the present-day ice cap, its response to climatic perturbations, and provides climatic envelopes (the most likely mean ranges of temperature and precipitation) needed to drive glacial advances to moraines formed in the Late Glacial at the Monte San Lorenzo massif.

2 Study area and its geographic, climatic and glacial settings

2.1 Present-day glaciers of monte san lorenzo

South America is dominated on its western flank by the Andes, which extend for 68° of latitude from their northernmost point in tropical Columbia (12°N) to their southernmost extent in temperate Chile and Argentina (56°S) (Rodbell et al., 2009; Davies et al., 2020). There are three substantial icefields in the Patagonian Andes. The Northern Patagonian Icefield (NPI) covered 3,758 km² in the year 2000 (Barcaza et al., 2017). 90 km south of this lies the Southern Patagonian Icefield (SPI), which covered 12,485 km² in 2005 (Meier et al., 2018). Further south in Tierra del Fuego lies Cordillera Darwin (2,932 km² in 2005). Surrounding these larger icefields lie numerous glaciers, ice-capped volcanoes and small ice caps, including MSL and Sierra de Sangra (Meier et al., 2018).

MSL lies southeast of the Northern Patagonian Icefield (NPI), 70 km east of the main Andean chain (Figure 1). MSL is an isolated granodiorite to granitic massif (Ramos et al., 1982), and is the third highest peak (3,706 m) in the Patagonian Andes (Masiokas et al., 2009). Up to 102 ice bodies have been mapped on MSL’s flanks, covering 207 km² (Falaschi et al., 2013). Small glaciers also occupy the adjacent Cordon Esmeralda and Barrancos Mountains (Figure 1). The four largest glaciers at MSL are Rio Oro, Rio Lacteo, San Lorenzo Sur and Calluqueo (Martin et al., 2019). Glaciar Calluqueo is the largest, with an area of 45.3 km² (Falaschi et al., 2013), with its terminus reaching 600 m asl. Glaciar Calluqueo terminates on bedrock, but drains into the large, 3.5 km long proglacial Lago Calluqueo, which discharges into Rio Salto to the north. Glaciar Rio Lacteo in the east and Glaciar San Lorenzo are largely debris covered (Falaschi et al., 2021), and terminate in proglacial lakes. Glacier velocity mapping by Millan et al. (2022) indicates that the tongue of Calluqueo Glacier reaches velocities of up to 350 m a⁻¹, with slower flow of ∼100 m a⁻¹ in the tongue’s tributaries in the accumulation area. Glacier velocities are also available in the GoLIVE dataset (Fahnestock et al., 2016), which report very similar velocities profiles. Ice thicknesses reach 330 m at the ELA, with ice under 100 m thick in the accumulation area and on the glacier tongue (Millan et al., 2022). These glaciers have a majority of glacier area at low elevations, have small accumulation area ratios, and are correspondingly sensitive to small changes in equilibrium line altitude (ELA) (Falaschi et al., 2013, 2017). They are currently undergoing surface lowering in the lower ablation areas, with rates greater than 5 m a⁻¹ (Falaschi et al., 2017). Glacier area here has been decreasing at a mean rate of 0.8% a⁻¹ between 1985 and 2008 (Falaschi et al., 2013). Glacier mass balance determined from geodetic data is negative, with the west flank having a mass balance of -0.31 ± 0.16 m w. e. a⁻¹ (Falaschi et al., 2019).

Despite these recent observations, the glacier mass balance magnitude, distribution, and mass turnover, is poorly known for these glaciers. In the absence of field studies, ice-flow parameters and glacier flow dynamics (e.g., relative velocities from sliding and deformation) are also unclear. The glacier thermal regime, surface mass balance, distribution of temperate and cold-based ice is also unknown, as is the degree to which glaciers are sensitive to temperature and precipitation changes and the relative importance of these climate variables for driving past glacier change. To address these gaps in our understanding, we undertake a full simulation and investigation of the ice cap.

2.2 Present day temperature records

The nearest meteorological station to the MSL ice cap is located on the western lateral moraine of San Lorenzo Sur Glacier (47°42′S, 72°19′W, 1,140 m asl; Figure 1), from which Falaschi et al. (2015) report a mean annual air temperature of 3.8°C measured over the period from 2002 to 2013. The 0°C isotherm is at 1725 m asl (Falaschi et al., 2015), with a late-summer snowline between 1700–1750 m asl measured in the western sectors of the massif in February 2005 (Falaschi et al., 2013). The snowline is higher (1800 m) in the drier, eastern sectors of the massif (ibid.).

The nearest station recording both temperature and precipitation is at Lord Cochrane Aerodromo (47°15′S, 72°35′W, 182 m asl; Figure 1), 40 km north of MSL and 3,624 m below its summit (Direccion Meteologica de Chile, 2001). Temperature data recorded after 2000 are largely absent, however a full record from 1970 to 2000 documents a mean annual temperature of 9.4°C (ranging from 8.4°C to 10.8°C). The two mean annual temperature records from San Lorenzo Sur and Lord Cochrane Aerodromo at 1,140 m asl and 182 m asl respectively give a temperature lapse rate estimate of 0.0058°C m⁻¹. This is within the range observed across Patagonia (0.0048°C m⁻¹ to 0.0072°C m⁻¹) (Table 1).

TABLE 1

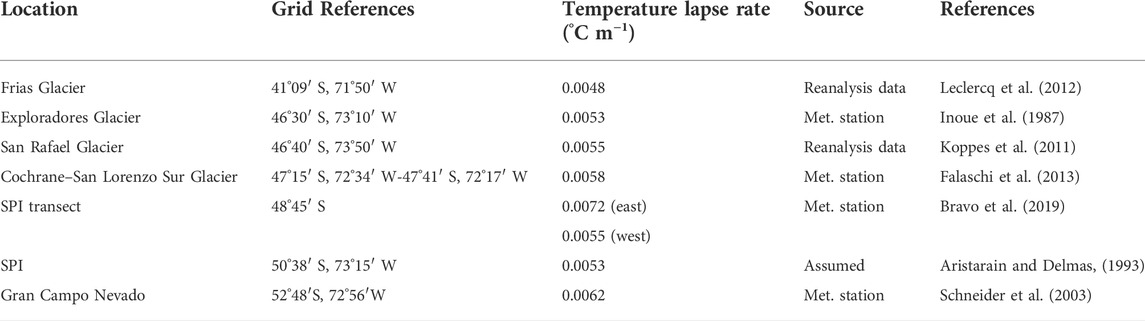
TABLE 1. Observed temperature lapse rates from across Patagonia. Lapse rate from Cochrane to San Lorenzo Glacier calculated by the authors, using data from Falaschi et al. (2013). SPI is Southern Patagonian Icefield.

2.3 Present-day precipitation records

The meteorological station at Lord Cochrane Aerodromo provides a mean annual precipitation of 726 mm a⁻¹ for 1970–2000 (range 522 mm –1,187 mm a⁻¹). There is a significant absence of precipitation measurements at higher elevations in the mountains to the east of the Patagonian icefields. Precipitation at MSL would be expected to be higher than these values obtained in the low valleys at Cochrane, due to the ice cap’s significant elevation, and in particular at Glaciar Calluqueo due to the west-facing accumulation catchment and the addition of wind-blown snow.

Annual accumulation on the windward, western side of the NPI at Glaciar San Rafael has been estimated to be between 4,800 and 10,000 mm (Fujiyoshi et al., 1987; Escobar et al., 1992; Carrasco et al., 2002), with similar annual precipitation recorded west of the Southern Andes (Schneider et al., 2003), and reflected in climate modelling (Garreaud et al., 2013). Mean precipitation rates over the eastern NPI for different elevations have been recently modelled to be 7,070 ± 790 mm a⁻¹ above 3,000 m, 5,480 ± 570 mm a⁻¹ from 2,000 to 2,500 m, and 3,720 ± 400 mm a⁻¹ below 1,000 m (Sauter 2020; Table 2). Values over the western NPI are higher, up to 7,930 ± 850 mm a⁻¹ above 3,000 m and 6,840 ± 680 mm a⁻¹ below 1,000 m. Such levels of precipitation are also reflected in river discharge models (Escobar et al., 1992).

TABLE 2

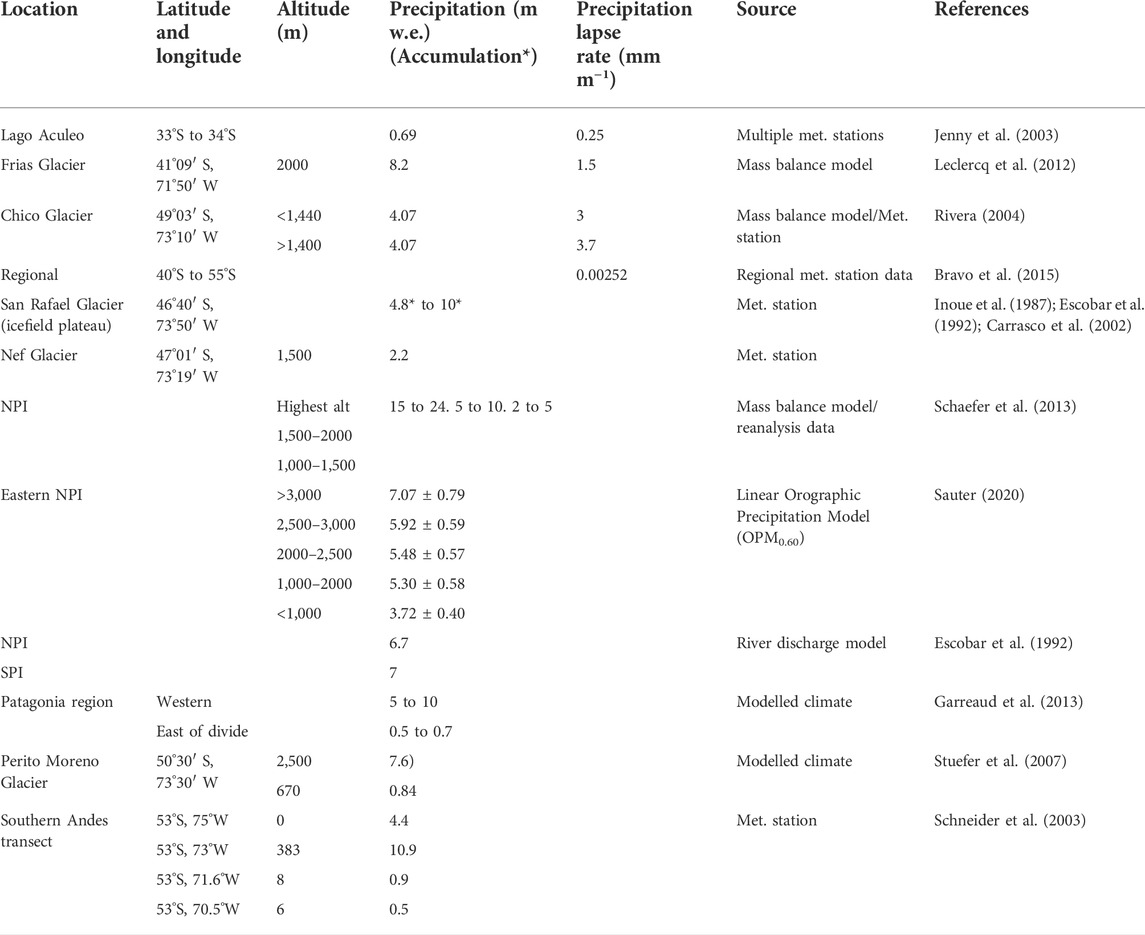
TABLE 2. Modelled and measured precipitation and accumulation data across Patagonia. NPI: Northern Patagonian Icefield. SPI: Southern Patagonian Icefield.

On a west-east transect, mean annual precipitation and accumulation values over the Southern Patagonian Icefield (SPI) range from 2,000 to 15,000 mm w. e. a⁻¹ (Inoue et al., 1987; Escobar et al., 1992; Carrasco et al., 2002; Garreaud et al., 2013; Schaefer et al., 2013), decreasing to between 7,600 mm and 2,500 mm w. e. a⁻¹ on the eastern outlet glaciers (Rivera 2004; Stuefer et al., 2007) (Table 2). Precipitation at Glaciar Tyndall (SPI; 51°15′S, 73°17′W) was modelled to be 7,100 ± 1,100 mm w. e. a⁻¹ for 2000–2016 (Weidemann et al., 2018).

On the eastern, lee side of the SPI, annual precipitation of 4,070 mm w. e. a⁻¹ was estimated based on stake measurements at Glaciar Chico (Rivera, 2004), and modelled to be 7,600 mm w. e. a⁻¹ at 2,500 m asl on Glaciar Perito Moreno (Stuefer et al., 2007). Ice core data from the accumulation area (2,600 m asl) of Glaciar Pío XI (SPI) from 2001 to 2005 yield accumulation rates of 3,400 to 7,100 mm w. e. a⁻¹, with an average of 5,800 mm w. e. a⁻¹ (Schwikowski et al., 2013), although these were not corrected for thinning due to glacier flow. For Glaciar Tyndall (SPI), the modelled mass balance in the accumulation area is 10,300 ± 1,800 mm w. e. a⁻¹ (Weidemann et al., 2018). These glaciers are located in the southern portions of the SPI, subject to the strong effect of the Southern Westerly Winds, and higher accumulation rates are expected. Across the SPI, measured snow accumulation reaches 15,400 mm w. e. a⁻¹ (Schaefer et al., 2015).

MSL’s location, 90 km inland from the Andes, lies at the edge of the rain shadow where there is a sharp contrast between vegetated and arid landscapes. This location has therefore a lower annual precipitation than that observed and modelled to its west. The mean annual measured precipitation at Cochrane is 726 mm a⁻¹ (1970–2000 AD). The measured precipitation at Cochrane shows a decreasing trend, and the longer annual mean from 1970–2021 is 688 mm a⁻¹. However, values after the year 2000 are not relevant to this study since we use the mean climate from 1970–2000 to initialise the model and to compare it with glacier outlines from the Randolph Glacier Inventory from 2003. Lower modelled and measured precipitation is also apparent at other low elevation sites east of the Andes range (Schneider et al., 2003; Stuefer et al., 2007; Garreaud et al., 2013). MSL sits at the northern edge of a break in the Andean range and therefore will experience less of a rain shadow effect than those regions latitudinally level with the higher-elevation NPI. However, its location 160 km inland from the coast, to the east of the mountains at the southern tip of the NPI, will still be factors contributing to lower levels of precipitation than at the NPI and SPI, which sit closer to the coast, receiving the full brunt of the precipitation-bearing Southern Westerly Winds.

Due to the scarcity of meteorological data from the Patagonian icefields and the surrounding region, in particular from ice masses at contrasting elevations, there are few measured precipitation lapse rates (those that are available are summarised in Table 2). These values are varied, ranging from 0.00252 mm m⁻¹–3.7 mm m⁻¹ (Jenny et al., 2003; Rivera, 2004; Leclercq et al., 2012; Bravo et al., 2015), likely due to the complex topography creating strongly site-specific precipitation gradients.

2.4 Ice dynamics during the Last Glacial-Interglacial transition

2.4.1 Antarctic cold reversal

During the Antarctic Cold Reversal (ACR; 14.5 to 12.8 ka; Blunier et al., 1997; Pedro et al., 2016), an enlarged, northwards-flowing Glaciar Calluqueo (with accumulation areas in the Barrancos Mountains and western Monte San Lorenzo) formed the substantial Salto and Esmeralda moraines at the mouth of the Pedregoso-Salto Valley, dated to 13.4 ka (Davies et al., 2018) (Figure 1; see panel ‘13 ka’ in Figure 2). This is the M1a moraine from Martin et al. (2019; 2022) and in Figure 1. These moraines are some 39 km from the current ice margin. Chironomid reconstructions from Lake Potrol Aike (52°S) and Antarctic ice-core records (Cuffey et al., 2016) both suggest a decrease in temperature of 3–4°C at this time (Massaferro and Larocque-Tobler, 2013). During the ACR, Glaciar Calluqueo terminated in the ice-dammed palaeolake Lago Chelenko with an outflow at 350 m asl (Figure 2) (Davies et al., 2018; 2020; Thorndycraft et al., 2019).

FIGURE 2

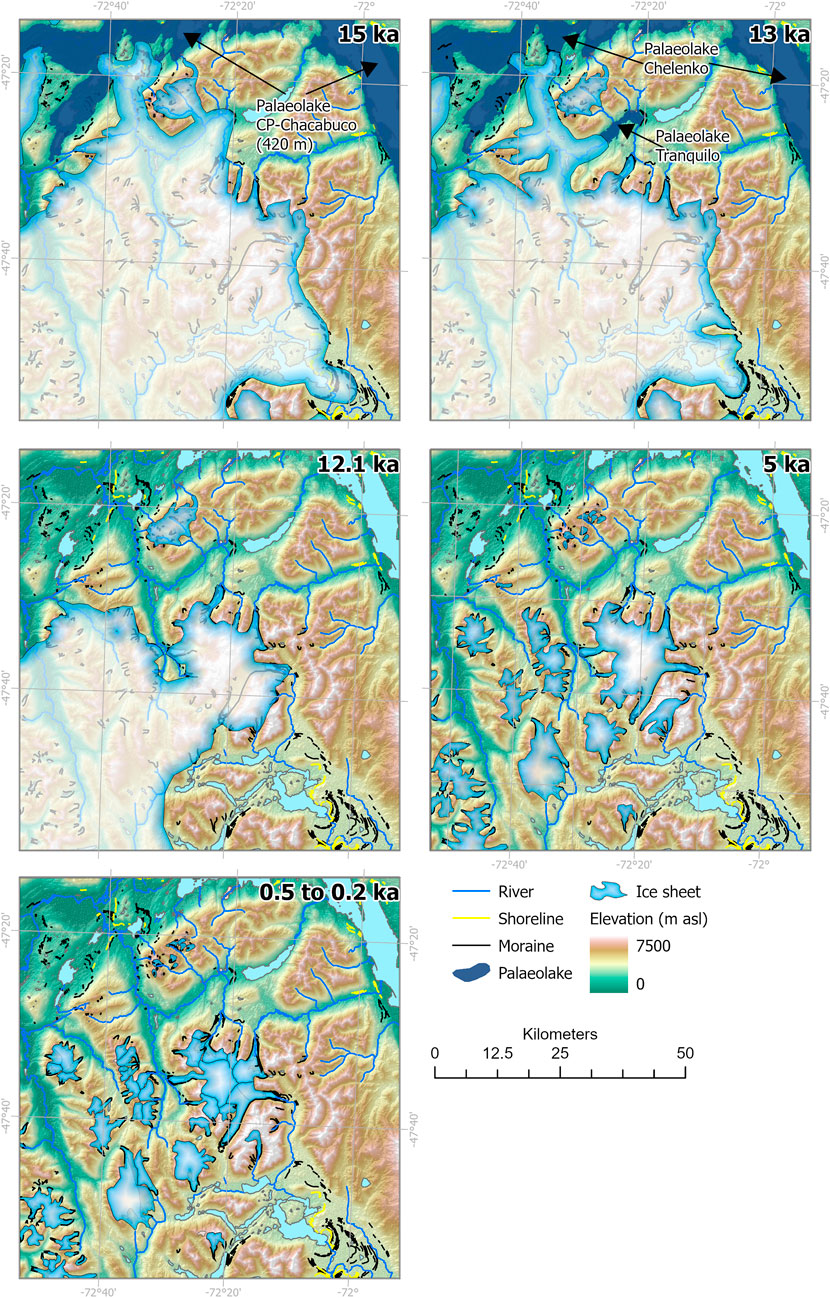
FIGURE 2. Empirical reconstruction of Monte San Lorenzo ice cap through the ACR (14.5–12.8 ka) Holocene, after numerous publications (Sagredo et al., 2016; 2018; Davies et al., 2018; 2020; Martin et al., 2019; 2022; Thorndycraft et al., 2019; Mendelová et al., 2020).

In the upper Tranquilo Valley, a series of inset moraines (RT1 to RT3, mean ages 13.8, 13.3 and 12.1 ka) also record stabilisation of much smaller northward-flowing MSL outlet glaciers during the ACR (Sagredo et al., 2016; 2018) (Figures 1, 2). The outermost moraines are only 14.3 km from the current ice margin. The RT1 to RT3 moraines are high above the level of any palaeolake in the study area. Below these moraines, perched deltas in the lower Tranquilo valley indicate that a palaeolake at 520 m asl existed in this valley also at this time (“Palaeolake Tranquilo”), which drained over the older Brown Moraines (M1b) into Lago Brown (Martin et al., 2019; Davies et al., 2020) (Figures 1, 2). Assuming no change in precipitation and an adiabatic lapse rate of 6.5°C/1,000 m, an estimated equilibrium line altitude (ELA) depression of 210 m would translate into temperature anomalies of just 1.6–1.8°C cooler than present during the ACR (Sagredo et al., 2016).

Outlet glaciers draining southeast from MSL also advanced during the ACR, reaching the Belgrano and Rincon moraines at 13.1 ± 0.6 ka (Mendelová et al., 2020) (Figures 1, 2). This suggests an advance of 30 km for Rio Lacteo and San Lorenzo Glacier.

2.4.2 Post-Antarctic cold reversal warming

The climate warmed across much of the Southern Hemisphere immediately following the ACR. Ice cores in Antarctica record a rapid temperature rise of 2.5°C in the century after 12.8 ka, with a bias of −2.75°C to −0.25°C compared with present day (Frieler et al., 2015; Cuffey et al., 2016). Changes in West Antarctic temperatures have been shown to be synchronous with cryospheric changes in Patagonia’s mid-latitudes (Cuffey et al., 2016; Bendle et al., 2019), with upwelling of warm deep water in the Southern Ocean a potential driver of warming across the mid and high-latitudes (Pedro et al., 2016). Sea surface temperatures at 46°S also record rapid warming at this time (Haddam et al., 2018). However, while there are some palaeoclimatic records of temperature and precipitation changes post-dating the ACR (Kilian and Lamy, 2012; Villa-Martínez et al., 2012; reviewed in Davies et al., 2020), the specific palaeoclimatic envelopes describing the prevailing climate at this time and in this region of Patagonia are poorly known. The relative sensitivity of the glacier mass balance to these changes and thus drivers of change are therefore poorly understood.

There is regional evidence of glacier recession immediately following the ACR. In the Pedregoso valley, recession of Glaciar Calluqueo is denoted by a series of nested moraines (M4 to M12). The ‘Moraine Mounds’ (M4) are located 5.2 km behind the Esmeralda Moraines (Martin et al., 2019 and Figure 1), dated to 12.8 ka (Glasser et al., 2012), and are 37 km from the present ice margin and above 350 m asl. By 12.5 ± 0.3 ka, Glaciar Calluqueo had receded to M9 (Martin et al., 2022). Lago Chelenko drained between 12.4 and 11.8 ka (Thorndycraft et al., 2019) (Figure 1), during the rapid post-ACR warming after 12.8 ka. The M12 moraines, lateral moraines just above the Holocene-age M13 moraines, are dated to 12.1 ± 0.4 ka. Recession over 50 km therefore occurred at a mean rate of 50.3 m yr⁻¹ between 12.8 (M4) and 12.1 ka (M12) (Martin et al., 2022).

Palaeolake Tranquilo drained when recession of Glaciar Calluqueo to the M12 moraine allowed a new outflow into Salto Valley (Martin et al., 2019; 2022). East of the MSL massif, the Lacteo lateral moraine, 20 km up-valley from the Rincon moraines (Figure 1), has a mean age of 12.4 ± 0.3 ka, supporting rapid recession following the ACR, followed by glacier stabilisation. Regional evidence of glacier stabilisation at this time is also supported by the formation of the RT5 Moraine in the Tranquilo valley at 12.2 ± 0.4 ka (Sagredo et al., 2018).

2.4.3 Mid-holocene and late holocene

A period of cooling during the mid-Holocene is reflected in the Antarctic ice-core record (from +0.4°C to +0.1°C from present day) (Frieler et al., 2015; Cuffey et al., 2016). During this mid-Holocene cooling, the glaciers around MSL advanced again, generally reaching the large moraines near the present-day outlet glacier termini (Davies et al., 2020), likely including the M13 moraines around Lago Calluqueo (Figures 1, 2). The moraines around the lake in the cirque in the upper Tranquilo valley date from 5.7 ka (Sagredo et al., 2016).

Across the icefield, these moraines were then re-occupied by glaciers during the Late Holocene (0.5–0.2 ka), evidenced by lichenometry (Garibotti and Villalba, 2017). Tree-ring records suggest that temperatures were 1–2°C cooler than present from 600 to 200 years ago in Patagonia (Villalba et al., 2005), driving this glacial advance (Kaplan et al., 2016). The Antarctic ice-core record shows cooler temperatures at this time, between 0.6°C and 1°C below present (Frieler et al., 2015; Cuffey et al., 2016).

2.5 Previous work modelling patagonian glaciers and icefields

Numerical modelling has previously been used to explore palaeo ice dynamics, glacier and mass-balance sensitivities in Patagonia. Model exploration of potential climates for past glacial advances so far has focused on the Last Glacial Maximum. Hulton et al. (1994) suggested that the ELA at the LGM was depressed by 160–560 m. A decade later, an updated coupled ice sheet/climate model suggested that at the LGM, the Patagonian Ice Sheet had an ice volume of 500,000 km³, with modelled ice velocities reaching 400 m a⁻¹ under a temperature decrease of 6°C and constant winds over the model domain (Hulton et al., 2002; Sugden et al., 2002).

A time-dependent model focused on the Northern Patagonian Icefield (45–48°S) suggested that an ELA lowering of 750–950 m occurred during the LGM (Hubbard et al., 2005), in order to reach the Fenix I-V moraines at Lago Buenos Aires. An ELA lowering of 900 m best matched the Fenix V moraine at 23,000 years BP. This model predicted a mean ice thickness of 1,130 m, drained by ice streams to the western and eastern margins. Forcing the model with temperature biases derived from an Antarctic ice core record suggested that the ice sheet rapidly shrank shortly after the LGM, with ice margin stabilisation during the Antarctic Cold Reversal (Hubbard et al., 2005).

More recently, a 2D ice sheet model applied over the Magallanes lobe in southern Patagonia suggested that summer temperatures were 4.5°C and 5.5°C cooler when the Magallanes lobe reached the inner and outer MIS two moraines respectively, with ∼25% less precipitation than at present (Peltier et al., 2021).

There are no presently published numerical modelling studies that focus on the Late Glacial period or the Antarctic Cold Reversal, though there has been some work on using glacier models to investigate Patagonian glacier response to Holocene climate change. Bravo et al. (2015) investigated glacier behaviour in the mid-Holocene (6,000 years BP) and pre-industrial period (1750 AD) using a degree-day glacier mass balance model. They used this to explore changes in glacier ELAs between the mid-Holocene and late Holocene. They showed that the modelled ELA was 20–30 m lower in the mid-Holocene relative to the pre-industrial period (Bravo et al., 2015).

Leclercq et al. (2012) used a long and detailed record of glacier length fluctuations at Glaciar Frías (Southern Patagonian Icefield) from 1639 AD to present. They used a simplified surface energy-balance model and a flowline model to account for the response of the glaciers to climatic forcing. They found that the overall glacier retreat (1,639–2009 AD) was best explained by a mean temperature increase of 1.2°C (Leclercq et al., 2012).

Ice-flow and surface-mass balance modelling has also been applied to some present-day glaciers, mostly across the main icefields. A full-Stokes ice-flow model (Elmer/Ice) applied over Glaciar San Rafael predicted low basal shear stresses (<25 kPa) and high surface velocities (7.6 km a⁻¹) (Collao-Barrios et al., 2018). This work suggested that most of the surface velocity is due to basal sliding of the glacier tongue.

3 Materials and methods

3.1 GlaRe reconstructions of equilibrium line altitude and palaeo-precipitation

Using empirical observations of the patterns of palaeoglacier recession and landsystem change north of MSL, based on geomorphological mapping, sedimentology and cosmogenic nuclide dating (at this site, mostly Glasser et al., 2012; Davies et al., 2018; Martin et al., 2019, 2022), it is possible to reconstruct the past ice surface and ELA for palaeoglaciers (Osmaston, 2005; Braithwaite, 2008; Rea, 2009; Sagredo et al., 2014). Due to the relationship between precipitation and temperature at the ELA of land-terminating glaciers (Ohmura et al., 1992; Bendle and Glasser, 2012; Chandler and Lukas, 2017), these data, when combined with existing temperature records, can be used to estimate palaeo-precipitation at glacier ELAs. We apply this method to Glaciar Calluqueo in the post-ACR period (see Supplementary Information for more details). These ELA-based, more simple precipitation reconstructions therefore provide a hypothesis for changes in the amount of precipitation during the period of rapid warming following the ACR. These can be compared with the precipitation and temperature changes required to force the glacier model to match mapped palaeoglacier extent.

In this study, the GlaRe ice-surface reconstruction GIS tool for ArcGIS (Pellitero et al., 2016) was used to calculate palaeo three-dimensional ice-surface for the present-day glacier and when the glacier occupied the post-ACR M12 (mean age 12.1 ± 0.4 ka) and M13 moraines (both limits from Martin et al. (2022); Figures 1, 2). GlaRe reconstructs a three-dimensional ice surface based upon a given bed topography and an element of the reconstructed ice margin (e.g. lateral or frontal moraine, or a trimline). This method assumes the present-day topography is the same as that of the palaeo-glacier bedrock topography. In this case, we used the bed topography provided in Carrivick et al. (2016). Once a palaeo-ice surface has been reconstructed, this can be used as the input to an automatic calculation of the glacier ELA.

The M12 and M13 moraine limits (Figure 1) were chosen because ice had separated from other glaciers and calving into palaeolakes had ceased. The GlaRe method is not appropriate for the ACR advance to the M1 moraine due to the lacustrine calving conditions at that time. The M13 limit is hypothesised to mark the advanced position of Glaciar Calluqueo at both the latest Holocene (0.2 ka) and during a regional mid-Holocene (5–6 ka) neoglaciation, in line with regional moraine patterns (Sagredo et al., 2016; Garibotti and Villalba, 2017).

The Accumulation Area Balance Ratio (AABR) method (Osmaston, 2005; Rea, 2009; Pellitero et al., 2015) is used in combination with the GlaRe tool (Pellitero et al., 2015; 2016) to calculate ELAs for the present-day glacier and the glacier when it occupied the M12 and M13 moraines. Balance ratios from 1.5 to 2.5 were used to provide a range of possible ELAs, with a representative ‘global’ value of 1.75 selected for comparison to present day empirical data (cf. Rea, 2009) (see Supplementary Information for more detail). The standard deviation of the ELAs calculated for different balance ratios provided an estimate of uncertainty in the ELA (cf. Osmaston, 2005). We refer to the ELAs reconstructed in this manner as GlaRe-ELAs to differentiate them from those modelled by PISM or measured during surface mass balance campaigns.

Palaeoglacier ELAs have been widely applied in palaeoclimate studies to reconstruct former climates (Bendle and Glasser, 2012; Sagredo et al., 2014; Chandler and Lukas, 2017). Once the 3D surface of the palaeoglacier has been reconstructed, and the ELA calculated, temperature at the ELA can be computed, for example, by calculating the height above the nearest weather station and applying a temperature lapse rate (for modern day glaciers). For palaeoglaciers, the temperature at the ELA can be calculated by bias-correcting the present-day measured mean climate against palaeoclimatic records for the relevant time period.

We calculated the temperature at Lord Cochrane Aerodromo at the time of each glacier stillstand by bias-correcting the Cochrane temperature record using surface air temperature data from Antarctic ice cores (Cuffey et al., 2016) (see Supplementary Information). This leads to a temperature reduction of 0.7°C during the Late Holocene (0.5–0.2 ka), 0.3°C during the Mid Holocene (5.7 ka, when Glaciar Calluqueo reached the M13 moraine), and 1.1°C at 12.1 ka BP (when Glaciar Calluqueo reached the M12 moraine). Secondly, we apply a lapse rate (0.0058°C m⁻¹) (calculated using data from Falaschi et al., 2013) to find the temperature at the height of the GlaRe-ELA at each of these time periods. We use a temperature uncertainty of ±0.45°C, which is obtained from present day temperature records at Lord Cochrane Aerodromo meteorological station.

Finally, we use the quantitative relationship between summer temperatures and precipitation at the GlaRe-ELA (Ohmura et al., 1992) to obtain estimates of palaeo-precipitation values for phases of glacier stabilisation at the M12 and M13 moraines (following Bendle and Glasser, 2012; Chandler and Lukas, 2017; Oien et al., 2021). An uncertainty in precipitation estimates is derived from the range in mean summer temperature.

3.2 Parallel ice sheet model description

We used the Parallel Ice Sheet Model (PISM), a three-dimensional, thermomechanically-coupled ice-sheet model, which has previously been thoroughly described (e.g., Bueler and Brown, 2009; Martin et al., 2011; Winkelmann et al., 2011; Aschwanden et al., 2012, 2016; Van Pelt and Oerlemans, 2012). PISM employs an enthalpy-based energy conservation scheme, combines the Shallow Ice and Shallow Shelf approximations (a ‘hybrid’ approximation), and considers both vertical deformation and longitudinal stretching within the ice. PISM also adopts a ‘pseudo-plastic’ law that relates basal ice velocity to basal shear stress to estimate basal sliding. Neumann boundary conditions are applied in the model at the grounded lateral ice margin, while Dirichlet boundary conditions are used at the domain edge (The PISM authors, 2017). Together, this numerical implementation means that fast-flowing outlet glaciers can be adequately simulated with manageable computation time (Aschwanden et al., 2016).

Similar to previous studies that used PISM to compute the evolution and sensitivity of ice caps and ice fields (e.g., Golledge et al., 2012; Ziemen et al., 2016; Jouvet et al., 2017; Schmidt et al., 2020; Žebre et al., 2021; Köse et al., 2022), our model for the MSL ice cap used boundary distributions for the ice thickness, bed topography, climate (surface mass balance) and basal heat flux from a combination of datasets, which we described below.

PISM was initialised with bed topography from Carrivick et al. (2016). In the absence of ice-thickness surveys of MSL outlet glaciers, ‘present-day’ ice thickness data was taken from a dataset derived from the output of a perfect-plasticity model (Carrivick et al., 2016). An ice thickness error of ±11% is reported, introduced in the model through the assumption that the ice behaves under perfect-plasticity and through the error in thickness resulting from the spatial interpolation from the ice thickness modelled at the glacier centreline to the ice thickness across the entire glacier width (Carrivick et al., 2016). This degree of error is in line with that observed globally when modelled ice thickness is compared with radar measurements (Li et al., 2012; James and Carrivick, 2016). A comparison of the Carrivick et al. (2016) model and Millan et al. (2022) dataset shows a good agreement between them, with an offset of ±20 m at the ELA. A bedrock DEM was produced for PISM initialisation by subtracting the modelled ice thickness from an ASTER GDEM in ArcMap v10.3.

Glacier mass balance is determined in PISM by the implementation of a positive degree day (PDD) model (Sato et al., 1984; Braithwaite and Olesen, 1989; 1990; Lang and Braun, 1990; Hock, 2003). The proportion of precipitation that falls as snow and the amount of snow and ice that melts is a product of the ice surface temperature and the number of positive degree days. Accumulation is dependent on precipitation and temperature, with 100% of precipitation assumed to be solid below 0°C, and linearly reduced to zero when air temperature is above 2°C. The melt factors for snow and ice (F_snow and F_ice in Table 3), representing the thickness of snow and ice melted per degree kelvin per PDD, can be tuned within PISM. Following melting, water may become refrozen based upon a predetermined refreeze fraction (Ø_refreeze in Table 3). Degree-day factor values of 3 and 8 mm w. e. were used for snow and ice respectively, in line with previous modelling studies and similar to those measured in Patagonia (cf. Supplementary Table S1).

TABLE 3

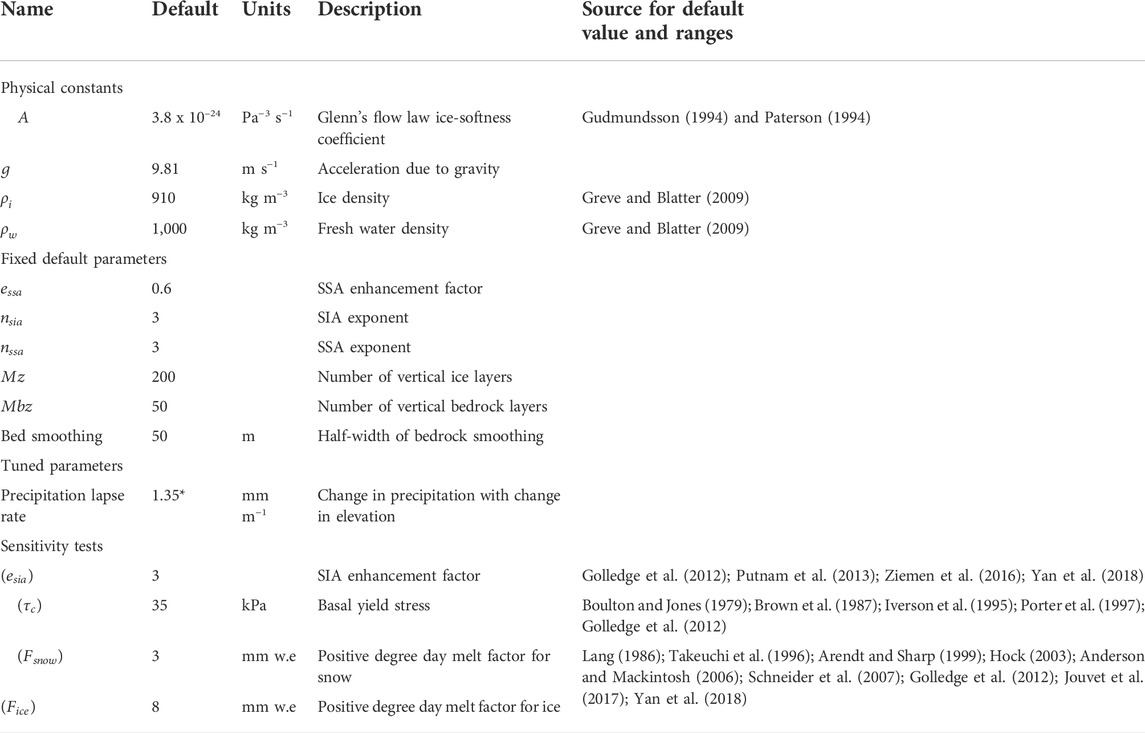
TABLE 3. Physical constants and parameter values used within the PISM model of the MSL ice cap. SIA is the Shallow Ice Approximation. SSA is the Shallow Shelf Approximation.

We applied a basal heat flux of 0.07842 W m^-2 based upon the relationship between basal heat flux and geology over a 2° by 2° equal area grid (Davies, 2013). The granitic lithology of the MSL massif may lead to a locally higher geothermal heat flux due to higher concentration of radioactive elements. However, there are no empirical data constraining this. Glacier outlines and drainage basins used for the model were derived for 2010–2011 (Davies and Glasser, 2012). Details of model initialisation and values and constants used for key parameters are provided in Table 3.

We ran the model using parallel computation, with processors distributed across 12 computational cores. This used a 250 (x, y) by 20 m (z) resolution gridded domain over an area of 80 km by 108 km (x, y), reflecting 138,993 horizontal grid cells, 200 vertical ice layers and 50 bedrock layers. For precipitation and temperature sensitivity experiments, where simulations produce a far greater volume of ice, we used a 500 m (x, y) resolution grid to enable feasible wall-clock run times of circa 24 h.

To spin up the model, we conducted a standardised PISM multiphase procedure (Aschwanden et al., 2013). The spin-up procedure computes an approximate steady state of the model under constant boundary conditions, which is achieved in three phases. First, a short (5-year) smoothing run was performed with simplified physics, using a non-sliding Shallow Ice Approximation (SIA) (Hutter, 1983). SIA accounts for flow by shear within the ice, neglecting longitudinal and transverse stresses. SIA is a simplified version of the Stokes equations for mass continuity and stress balance which describe the flow of glacier ice. Second, a longer (5000-year) run is done, without the ice geometry evolving. Third, SIA is run in parallel with a vertically integrated, sliding shallow shelf approximation (SSA) (Weis et al., 1999) forming a ‘hybrid’ model (Bueler and Brown, 2009), which accounts for flow caused by sliding of the ice over a weak substrate. This phase uses constant-climate conditions, and introduces a positive degree day (PDD) model to calculate the glacier mass balance, as well as the impact of geothermal heat flux at the ice-bed interface (The PISM authors, 2017). In this final phase, the ice geometry is allowed to evolve, and the model was run until an approximate equilibrium state of constant ice area and volume was reached (∼100–500 model years). The resulting spun up state was then used as the initial state for experimental runs.

An ensemble of 193 model runs was undertaken during model set up and testing. Two climate data evaluation, 11 model tuning runs and 38 sensitivity experiments were then run (Table 4). These tuning and sensitivity experiments used iterations of each variable to establish the key controls on the modelled icefield and to identify the envelope of parameter space in which the results agree most closely with the present-day observed icefield.

TABLE 4

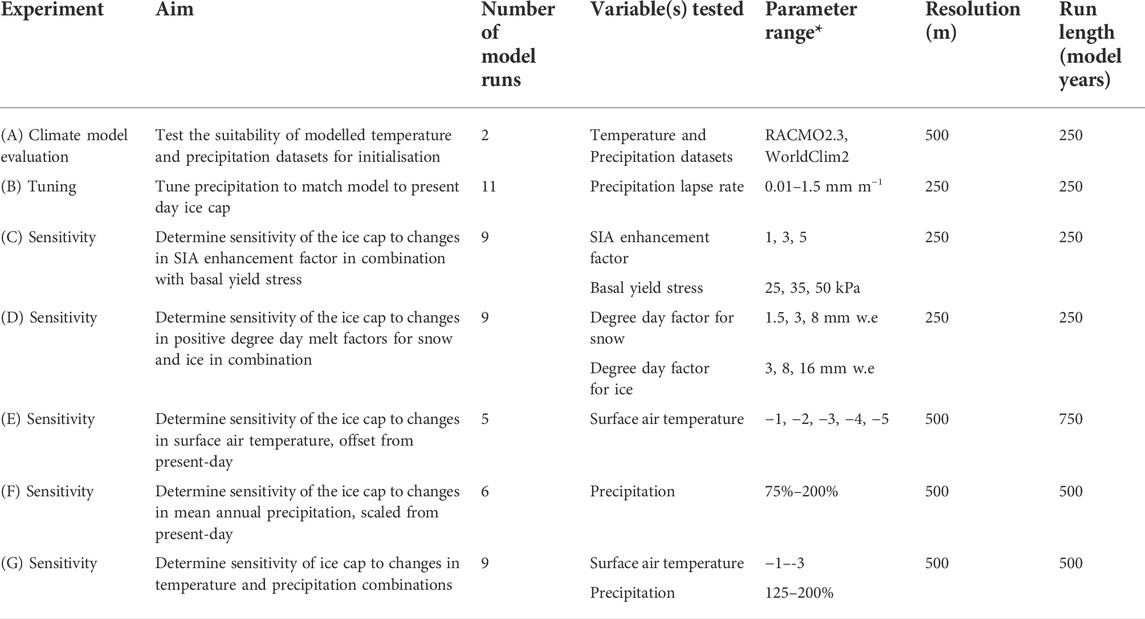
TABLE 4. Model tuning and sensitivity experiments performed in this study, documenting the number of model runs, variable(s) tested, range of parameters explored, the model resolution and model run lengths for each experiment. *references for selected parameters ranges are given under the respective variable in Table 3.

3.3 Climate forcing

We evaluated two climate data sets for model initialisation (Experiment A; Table 4). Two modelled climate gridded datasets, RACMO version 2.3 for Patagonia (RACMO2.3 PAT5.5) (Lenaerts et al., 2014) and WorldClim2 (Fick and Hijmans, 2017), were compared with measured meteorological station surface air temperature data from the western lateral moraine of Glaciar San Lorenzo Sur and temperature and precipitation data from Lord Cochrane Aerodromo (Figure 1). They were also compared with observed temperature lapse rates between these two meteorological stations (0.0058°C m⁻¹) (Falaschi et al., 2013) and across Patagonia (Table 1) (Inoue et al., 1987; Aristarain and Delmas, 1993; Schneider et al., 2003; Koppes et al., 2011; Leclercq et al., 2012; Bravo et al., 2019). This allowed us to evaluate the ability of both models to reproduce mean annual air temperature, temperature lapse rates, and the annual temperature cycle in the study area (Table 1; Supplementary Information). The results of this evaluation are shown in Section 4.2.

We also derived a gridded precipitation dataset using precipitation measured at Lord Cochrane Aerodromo meteorological station. The precipitation was varied with altitude, using a lapse rate, alongside the WorldClim2 surface air temperature dataset. The precipitation lapse rate was systematically varied (Experiment B) until the resulting precipitation distribution used to force the ice-flow model resulted in a steady state model simulation of an ice cap matching the present-day ice extent, thickness, velocity, and surface elevation change.

Palaeo-temperature at MSL across the LGIT was derived using relative temperature offsets from the West Antarctic Ice Sheet (WAIS) Divide surface air temperature reconstruction (Cuffey et al., 2016). Changes in West Antarctic temperatures have been shown to be synchronous with cryospheric changes in Patagonia’s mid-latitudes (Bendle et al., 2019), with upwelling of warm deep water in the Southern Ocean being a potential driver of warming across the mid and high-latitudes (Pedro et al., 2016). The degree of temporal temperature change across the ACR and the early Holocene as recorded in chironomid records (Massaferro and Larocque-Tobler, 2013; Massaferro et al., 2014) indicates that fluctuations in temperature are similar in the Patagonian mid-latitudes and in the WAIS Divide surface air temperature record (Cuffey et al., 2016).

3.4 Sensitivity experiments

Sensitivity experiments were undertaken to quantify the impact of PISM parameters on model output and explore glacier sensitivities to these variables. In Experiment C, the rheology of modelled ice was adjusted using an enhancement factor to account for variables which may cause increased softening within the ice, such as anisotropy or the inclusion of impurities or dust (Ritz et al., 1996; Parizek and Alley, 2004; Golledge et al., 2012). Values of 1, 3 and 5 were chosen (Table 4) to reflect the range of values used and found to fit empirical data in other ice modelling studies in mountain environments (Golledge et al., 2012; Putnam et al., 2013; Ziemen et al., 2016; Yan et al., 2018).

In Experiment C, bed strength was varied alongside ice rheology. A uniform fixed basal yield strength is applied to represent the strength of aggregate material at the ice-bed interface (The PISM authors, 2017). Values of 25 kPa, 35 kPa and 50 kPa were tested (Table 4), reflecting a range of measured values (Boulton and Jones, 1979; Brown et al., 1987; Iverson et al., 1995; Murray, 1997; Porter et al., 1997) and those tested in modelled mountain valley glaciers (Golledge et al., 2012). Previously published sensitivity analyses of ice rheology and basal yield strength reveals a co-dependency between variables (Golledge et al., 2012) and hence they were tested in combination.

In Experiment D, a range of degree-day factors for snow and ice, and their influence on glacier mass balance and ice volume, were explored. Finally, model sensitivity to temperature and precipitation were assessed (Experiments E, F, G) (Table 4). Glacier response to cooling was investigated in −1°C increments, alongside changes in precipitation, to explore factors that may have driven past glacier advances. When one or more variables were tested, the remaining variables were fixed to default values.

4 Results

4.1 GlaRe reconstructions of equilibrium line altitude and palaeo-precipitation

Using the GlaRe GIS based ice surface reconstruction tool (Pellitero et al., 2016) in combination with the AABR method (Osmaston, 2005; Pellitero et al., 2015), and applying a balance ratio of 1.75, the present-day (2003 AD) ELA of Glaciar Calluqueo is reconstructed as 1,615 ± 20 m asl (Table 5). Using a balance ratio of 1.5 resulted in no change to the GlaRe-ELA, and balance ratios of 2–2.5 resulted in only 25–50 m differences in the GlaRe-ELA, and so therefore the choice of balance ratio had little impact on our results. Using a 0.0058°C m⁻¹ temperature lapse rate appropriate for this region (calculated using data from Falaschi et al., 2013) produces a summer temperature at the present-day ELA of 6.9°C and a mean annual air temperature of 1.1°C. Using the summer air temperature-precipitation relationship at the ELA (Ohmura et al., 1992), this gives a precipitation value at the present-day GlaRe-ELA (1,615 m asl) of 2,932 ± 241 mm a⁻¹ w. e.

TABLE 5

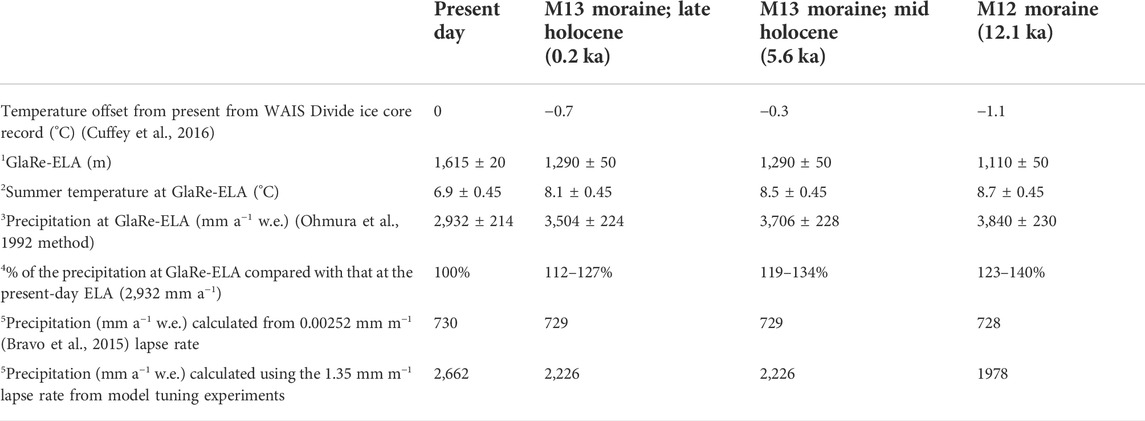
TABLE 5. ¹GlaRe-ELAs, rounded to the nearest 5 m, and the ²temperature and ³precipitation reconstructed at the GlaRe-ELA for the year 2010 glacier extent and for the M12 and M13 moraines. ⁴The percentage difference in precipitation at the GlaRe-ELA when compared with precipitation at the present-day GlaRe-ELA. ⁵The precipitation at each altitude is independently calculated using two precipitation lapse rates and precipitation data from Cochrane weather station.

The values for precipitation at the present-day GlaRe-ELA can be compared with that predicted at that altitude (1,615 ± 20 m asl) from various lapse rates. The precipitation at this elevation suggested by the precipitation lapse rate of Bravo et al. (2015) is far lower (730 mm a⁻¹ w. e.), which suggests that this lapse rate is too low in this region (Table 5). A lapse rate of 1.35 mm m⁻¹ (see Section 4.3) yields a precipitation of 2,662 mm a⁻¹ w. e., which is only 56 mm a⁻¹ w. e. Less than the minimum value predicted at the present-day GlaRe-ELA.

The GlaRe-ELA at the M13 glacier extent is 323 m lower, at 1,290 ± 50 m asl. With a −0.7°C temperature reduction as indicated by the Antarctic ice cores at 0.2–0.5 ka BP, this predicts an annual precipitation of 3,504 ± 224 mm a⁻¹ w. e., which is 12–27% higher than the precipitation that falls at the present-day GlaRe-ELA. At the M13 glacier extent in the mid-Holocene with a temperature 0.3°C lower than present, precipitation is calculated as 3,706 ± 228 mm a⁻¹. This indicates an increase in precipitation at the ELA of 19–34%. At 12.1 ka, when ice was at the M12 moraine, the GlaRe-ELA is 1,110 ± 50 m asl. At this time a −1.1°C temperature offset from present gives a precipitation value of 3,840 ± 230 mm a⁻¹. This is 23–40% more precipitation than falls at the present-day GlaRe-ELA.

4.2 Climate data evaluation (Experiment A)

Two modelled datasets, the Regional Atmospheric Climate Model (RACMO), version 2.3 for Patagonia (RACMO2.3 PAT5.5) (Lenaerts et al., 2014) and WorldClim2 (Fick and Hijmans, 2017), were investigated for their applicability to the study area and potential use to drive PISM spin-up to present-day conditions (Supplementary Figure S2). These two climate datasets were evaluated against average annual and monthly measured temperature and precipitation records from Lord Cochrane Aerodromo for the period 1970–2000 and temperature records from the metrological station at Glaciar San Lorenzo Sur (2002–2013; Falaschi et al., 2015) (Table 1; Table 6). The modelled climate data were assessed against seasonal temperature range as recorded in the meteorological station datasets, and against mean annual temperature and observed effective lapse rates at the weather stations in the local area and across Patagonia (Inoue et al., 1987; Aristarain and Delmas, 1993; Schneider et al., 2003; Koppes et al., 2011; Leclercq et al., 2012; Falaschi et al., 2013; Bravo et al., 2019) (cf. Table 1).

TABLE 6

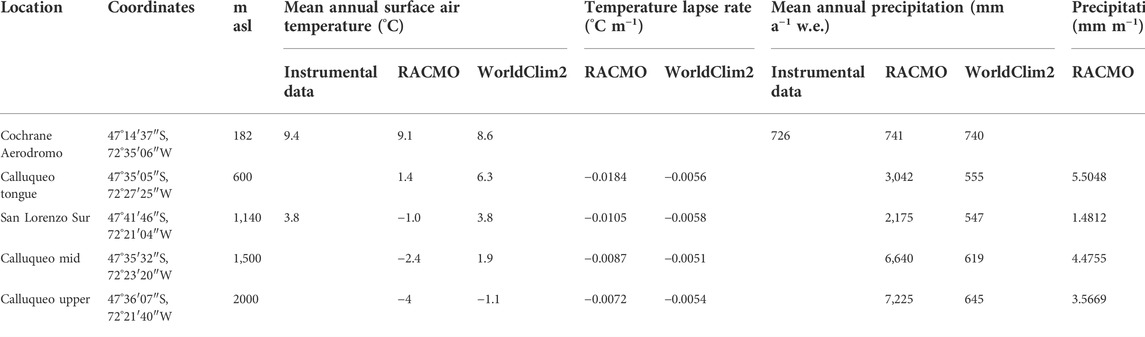
TABLE 6. Point climate data and calculated lapse rates from instrumental records, RACMO2.3 and WorldClim2. Lapse rates are calculated relative to Cochrane Aerodromo. Instrumental data from Cochrane Aerodromo meteorological station and WorldClim2 modelled climate data cover the period from 1970 to 2000. Modelled climate data from RACMO2.3 covers the period 1979 to 2000. Instrumental data from the metrological station at San Lorenzo Sur covers the period 2002–2013 (Falaschi et al., 2015).

We also considered whether the spatial resolution of the two datasets allowed the temperature variations across the mountain topography to be represented (see Supplementary Information for details). WorldClim2 produces temperatures (Table 6) and temperature lapse rates (0.0051–0.0056°C m⁻¹) that are within the range of those observed in Patagonia (Table 1). WorldClim2 also produces a close fit to the measured seasonal climate cycle at Cochrane Aerodromo (Supplementary Figure S1). The WorldClim2 temperature dataset was therefore used to force PISM under ‘present-day’ climate conditions, using mean annual and mean July surface air temperature from 1970 to 2000, with an applied 1.25 amplitude scaling factor to account for seasonality (see Supplementary Information for details).

The RACMO2.3 and WorldClim2 datasets both model mean annual precipitation at Cochrane Aerodromo to be slightly higher than the measured value. At Glaciar Calluqueo, both datasets were considered to be unrepresentative of precipitation (Table 6; Supplementary Figure S2). WorldClim2 provides mean annual precipitation values at Glaciar Calluqueo ranging from 555 to 645 mm a⁻¹, lower than instrumentally measured values at Cochrane Aerodromo. At Glaciar Calluqueo, RACMO2.3 models mean annual precipitation up to 7,725 mm a⁻¹. This is considered to be an unrealistically high value given measured and modelled precipitation levels across Patagonia (Table 2), precipitation predicted at the GlaRe-ELA using the Ohmura et al. (1992) method (Table 5), and MSL’s position inland of the Andes. Precipitation lapse rates calculated from RACMO2.3 point-data on Glaciar Calluqueo also give values higher than the few records from Patagonia (Table 2). Finally, initialising PISM using WorldClim2 and RACMO2.3 precipitation data (Experiment A) with WorldClim2 temperature data and ‘default’ parameter values (Table 3) produced models with too much and too little ice respectively in comparison with present-day ice extent (Supplementary Figure S3).

4.3 Tuning precipitation lapse rates (Experiment B)

A new gridded precipitation dataset was therefore created across the domain by applying a lapse rate to the mean precipitation value measured at Lord Cochrane Aerodromo (Supplementary Figure S2K). As lapse rates are poorly known and spatially variable in Patagonia (Table 2), an experiment with a range of simulated lapse rates was designed. In Experiment B, eleven simulations were therefore run in order to find the most appropriate lapse-rate value that forces the ice-flow model to best fit present-day observations of ice cap extent, volume and velocity (Figure 3). Due to the discrepancies around the ice cap (over-estimations in the north and south of the ice cap and underestimations of San Lorenzo and Rio Lacteo glaciers, which is likely related to debris cover), we aimed to obtain a best model fit with Glaciar Calluqueo (Figure 3B). This method allows precipitation values at MSL to be tuned while maintaining a realistic elevation dependence of precipitation across the domain. However, we note that the lapse-rate derived precipitation values do not capture spatially variable snow accumulation and ablation dynamics that are likely to be controlled by local topography and wind direction (see Supplementary Figure S2K). Further, while the prevailing wind conditions are usually a first-order control on snow accumulation, local terrain can significantly influence this (Małecki, 2015; Kavan et al., 2020).

FIGURE 3

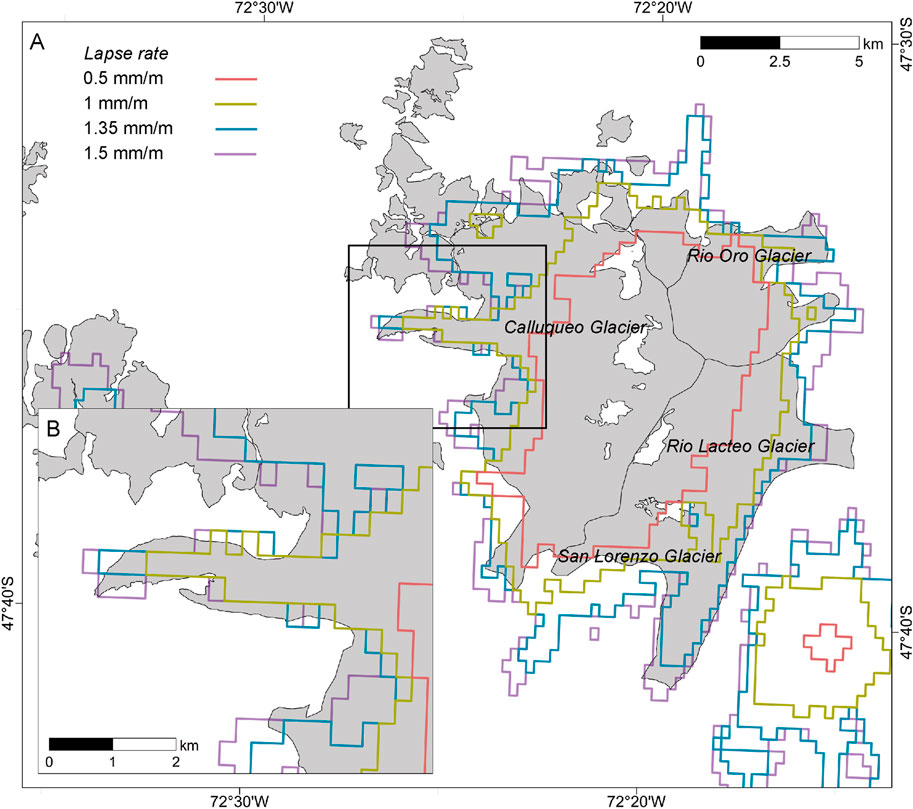
FIGURE 3. Experiment B. (A) Simulated ice extent produced by PISM forced using spatially variable precipitation datasets derived from different precipitation lapse rate values. The grey polygon indicates present day ice area from the RGI. (B) Inset map of an enlarged section of Glaciar Calluqueo.

Precipitation lapse rates from 0.1 to 1.5 mm m⁻¹ (11 simulations) were applied to the 30 years mean annual measured precipitation value at the Lord Cochrane Aerodromo weather station (Table 4). Default flow enhancement factor (3), basal yield strength (35 kPa) and degree-day factor values (3 mm w. e. snow and 8 mm w. e. ice) were used (Table 3) alongside a constant ‘present-day’ WorldClim2 temperature dataset (cf. Experiment A).

The simulated extent of the ice cap is significantly different when the ice-flow model is forced with the gridded precipitation datasets derived from different precipitation lapse rates (Figure 3A). The difference in ice thickness between simulations is negligible at the highest elevations and steepest topographies at the centre of the ice cap (less than 1 m), which is where ice is also thinnest (approximately 50 m). Where simulations extend down to lower elevations of Glaciar Calluqueo, the difference in thickness varies between 5 and 10 m, with highest lapse rate simulations producing thicker ice. The thickness of Glaciar Calluqueo along this bottom 4 km section for the 1.35 mm m⁻¹ lapse rate simulations is between 85 m and 100 m, similar to that modelled by Carrivick et al. (2016) (between 90 and 105 m).

The greatest difference in ice thickness between overlapping simulation outputs is at Glaciar San Lorenzo in the southeast. At its thickest point, the simulations with lapse rates of 1 mm m⁻¹, 1.35 mm m⁻¹ and 1.5 mm m⁻¹ have ice thickness of 334 m, 587 m and 628 m respectively. Where simulation outputs using lapse rates of 1.35 mm m⁻¹ and 1.5 mm m⁻¹ overlap along the lower 6 km of the glacier, the simulation forced by the higher lapse rate dataset is 40–47 m thicker along this length.

The best-fit lapse rate (1.35 mm m⁻¹) falls within the range of observed data (Table 2). This tuned dataset yields precipitation values at the ELA that are in line with those predicted by independent methods (see Section 4.1 and Table 5), providing additional confidence in the dataset. We note that it does not account for likely east-west gradients in the complex mountain topography of the study region, which are currently unquantified.

4.4 Sensitivity experiments

In Experiment C (9 simulations), the basal shear strength and ice rheology parameters were varied jointly (25 kPa, 35 kPa and 50 kPa and ice rheology of 1, 3 and 5; Table 4), whilst other parameters remained constant. This resulted in variations of ice thickness and extent (Supplementary Figure S4). A lower bed strength of 25 kPa initially leads to a longer and thinner glacier, with ice able to flow down-valley more readily. The simulations with the strongest bed strength resulted in a greater thickness of ice, which supports ablation better than the thinner glacier formed over a weaker bed (Supplementary Figure S4).

The flow enhancement factor accounts for the ‘softness’ of the ice and the ease with which it deforms. A flow enhancement factor of 3 produces a longer glacier profile than that produced using an enhancement factor of 1, as expected for ice that deforms more easily by internal shear (Supplementary Figure S4). A flow enhancement factor of 5 resulted in no further lengthening of the simulated glacier.

In Experiment D, the sensitivity of the modelled glaciers at MSL to changes in degree-day factors was investigated. Degree-day factors for snow of 1.5, 3 and 8 and 3, 8 and 16 for ice were chosen, to reflect the range observed globally (Lang, 1986; Takeuchi et al., 1996; Arendt and Sharp, 1999; Hock, 2003; Anderson B. et al., 2006; Möller et al., 2007; Schneider et al., 2007) and in line with previous mountain glacier modelling sensitivity studies (e.g., Golledge et al., 2012; Jouvet et al., 2017; Yan et al., 2018) (Supplementary Table S1). Setting low degree-day factors for snow and ice within PISM’s positive degree day model produces a greater ice extent, as outlet glaciers flowing into low altitude valleys experience less melt for the same surface air temperature. This results in ice being maintained in the valleys (Supplementary Figure S5). Increasing ice melt (using higher degree day factor for ice) causes a greater reduction in ice extent and volume than the same change in snow melt (Supplementary Figure S5).

In Experiment E, the impact of temperature change on the simulated icefield was investigated. Running constant-climate model simulations with step cooling from −1°C to −5°C uniformly across the domain illustrates how ice area and volume expands at an increasing rate with progressively colder simulations as the ELA lowers (Figure 4). Ice cover extends over areas of highest topography, alongside the growth of outlet glaciers into lower altitude valleys. Figure 4 shows how, under a −4°C to −5°C cooling from present-day, the rate of ice area growth begins to stabilise, while the rate of ice volume growth continues to increase. This is due to the distribution of ice growth at this stage of cooling. At −5°C, the large areas of high topography are ice-covered and have stable thicknesses. Ice growth is then primarily focused in the low altitude, steep-sided valleys where ice is topographically confined and grows to large thicknesses for relatively small increases in ice area.

FIGURE 4

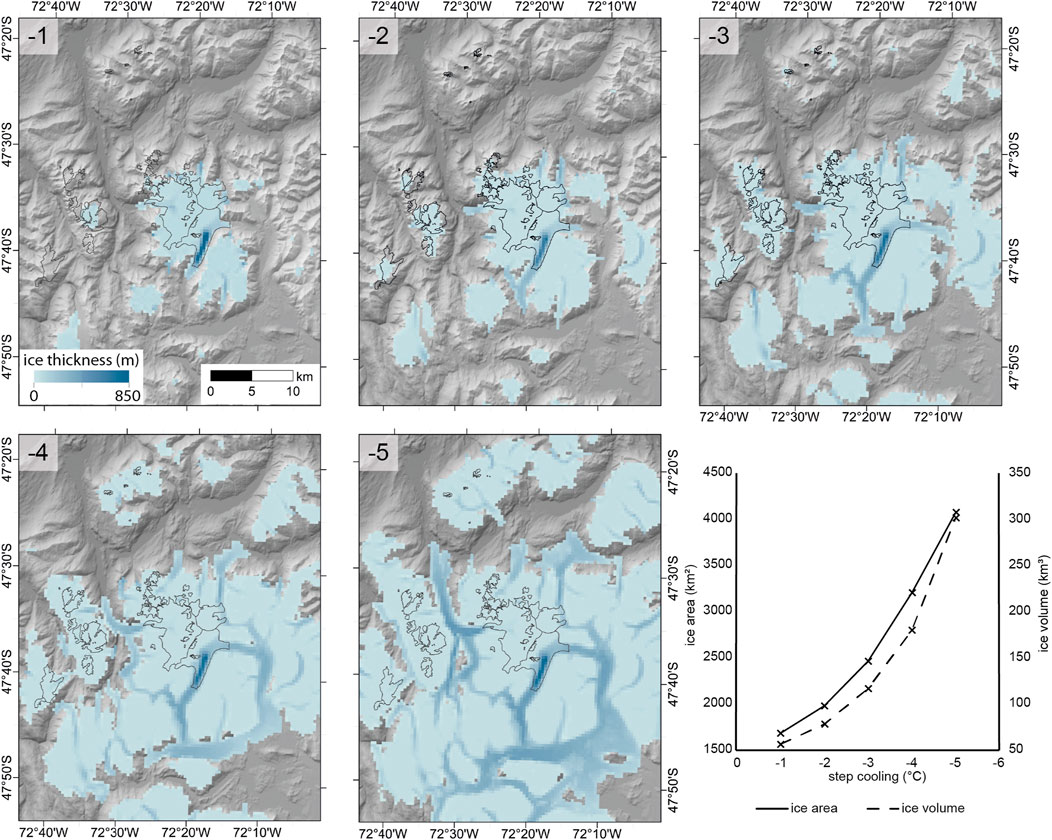
FIGURE 4. Experiment E. Model simulations of the MSL ice cap under surface air temperature step cooling of 1–5°C and present-day constant precipitation. Present-day ice extent shown as black outline. Graph shows modelled ice area and volume at equilibrium through five simulations under step cooling of −1 to −5°C.

For Experiment F, percentage scalings of 75%, 100%, 125%, 150%, 175% and 200% modern-day precipitation were applied across the domain to the “present-day” tuned precipitation dataset; a scaling of 100% is the present-day precipitation. Model simulations forced by increasing levels of precipitation demonstrate an increase in ice area and volume across the model domain (Figure 5). Unlike with progressively colder model simulations, glacierised area does not grow at an accelerating rate as precipitation increases; the rate of ice area increase slows under the wettest scenarios. However, ice volume increases relatively linearly, as outlet glaciers begin to occupy lower altitude valleys. This provides the topographic space for increasing ice volume growth with proportionally little increase in ice area.

FIGURE 5

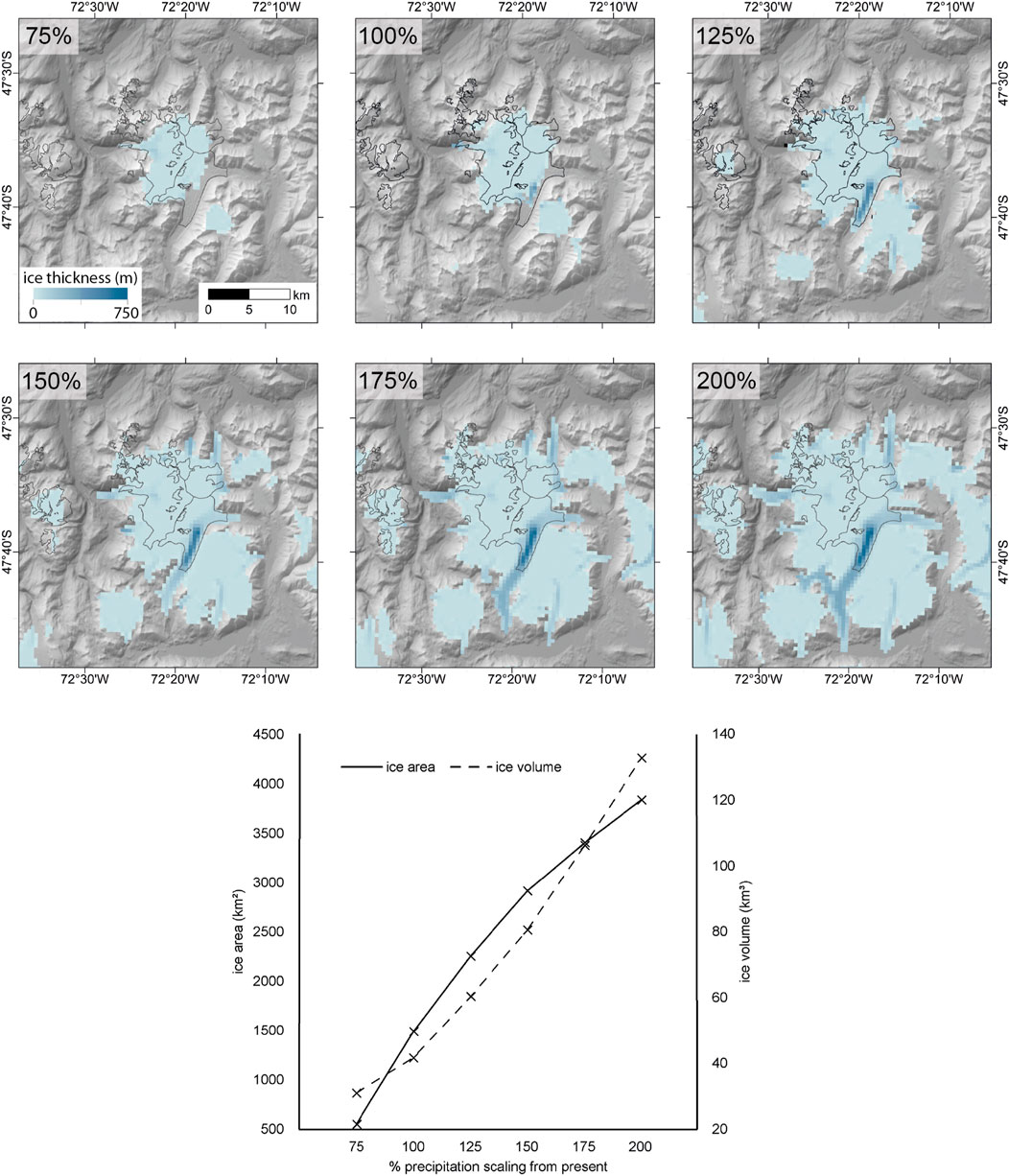
FIGURE 5. Experiment F. Model simulations of the MSL ice cap under increasingly scaled precipitation forcing from present-day. Surface air temperature is set constant to present-day. Present-day ice extent shown as black outline. Graph shows modelled ice area and volume at equilibrium through five simulations under increasingly scaled precipitation forcing.

Precipitation and temperature were varied in combination in Experiment G. Model simulations initialised with combinations of decreasing temperature and increasing precipitation, which may have been experienced by these glaciers during previous negative phases of the Southern Annular Mode during the LGIT and Holocene (Kaplan et al., 2020), lead to significant ice growth. While separately decreasing temperature by 3°C and scaling precipitation by 200% only lead to a relatively small increase in the length of Glaciar Calluqueo (ca 6 km from the present-day ice front) (experiments E and F, Figures 4, 5), combining these forcings together leads to a much greater increase in glacier length of 28 km (Figure 6). This difference in ice growth at colder temperatures is due to the increased proportion of precipitation falling as snow, combined with less annual ablation. The simulation of Glaciar Calluqueo growth also shows how the glacier bifurcates at the Salto-Tranquilo valley confluence, having sufficient mass to advance up a reverse-bed gradient and dam Palaeolake Tranquilo, providing some insight into the ice-flow dynamics and accumulation areas during the ACR and LGIT. In this advanced state there is also contribution of ice from accumulation areas on the Barrancos Mountains to the west and topographic highs to the south, as well as ice growth on Cordon Esmeralda (Figure 6).

FIGURE 6

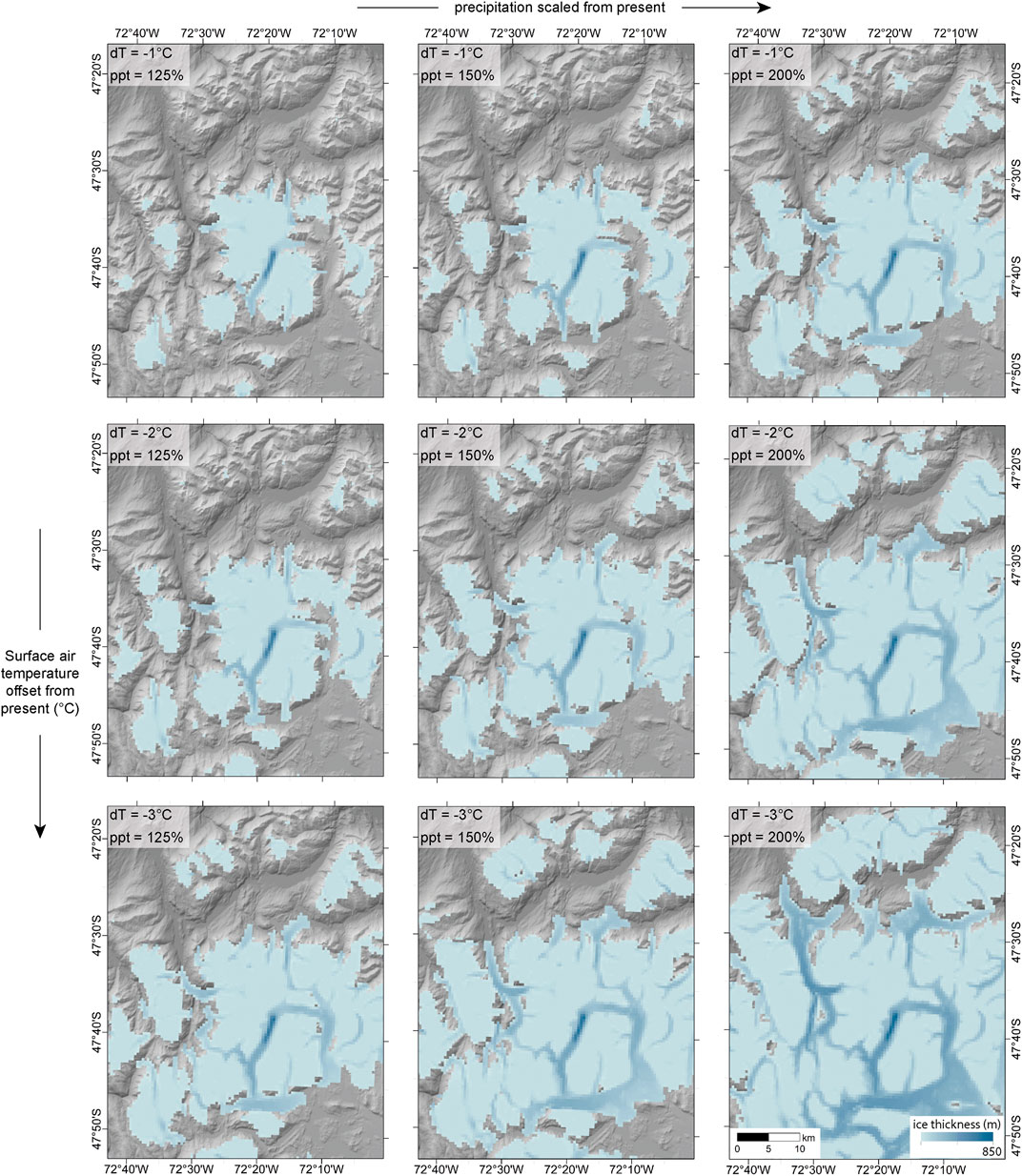
FIGURE 6. Experiment G. Model simulations of the MSL ice cap under combined surface air temperature step cooling of 1–3°C and precipitation scaling of 125%–200%.

4.5 Best-fit simulation of present-day Monte San Lorenzo ice cap

4.5.1 Climatic variability across Monte San Lorenzo

The WorldClim2 temperature dataset and a mean annual precipitation value of 726 mm a⁻¹ at 182 m asl, as measured at Lord Cochrane Aerodromo, with an applied lapse rate of 1.35 mm m⁻¹, produces a model output which best replicates the present-day ice cap (Figure 7A). This gives precipitation values at Glaciar Calluqueo of 1,220 mm a⁻¹ at the glacier tongue (545 m asl) and 2,660 mm a⁻¹ at the present-day GlaRe-ELA (1,615 ± 20 m asl). Precipitation increases to 5,480 mm a⁻¹ at the summit of the massif (3,706 m asl). Precipitation between ca 1,200 and 5,500 mm a⁻¹ at MSL, 70 km to the east of the NPI, falls within the range of the limited precipitation data available to the east of the Patagonian Icefield. The use of PISM’s default positive degree day melt factor values in this present-day simulation adds further confidence that the precipitation estimate is as realistic as we are able to produce, given the absence of empirical data.

FIGURE 7

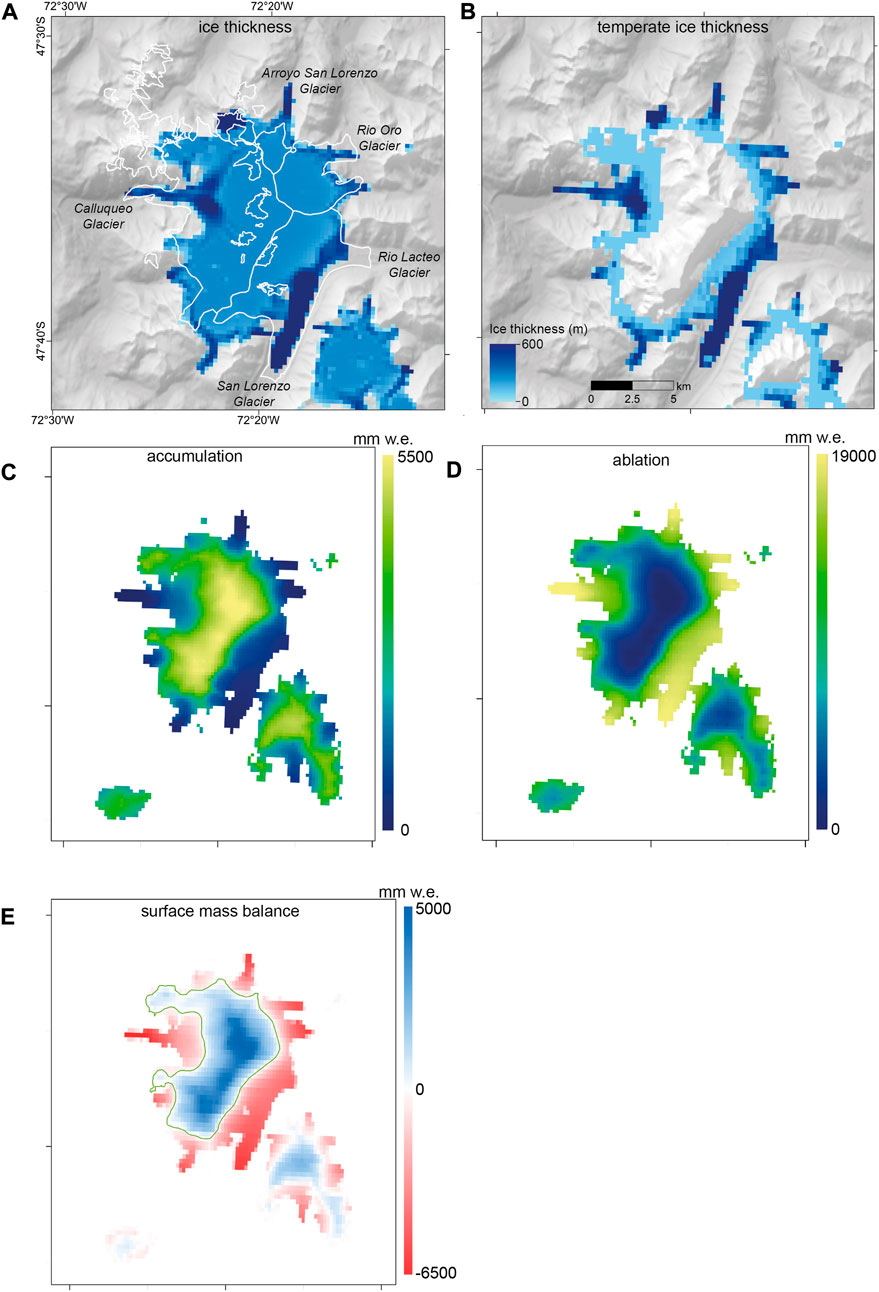
FIGURE 7. Total ice thickness (A) and temperate ice thickness (B) for the best-fit scenario of the modelled MSL ice cap. The white lines in (A) denotes the present-day ice extent and glacier catchment divides. Spatial distribution of annual accumulation (C), ablation (D) and surface mass balance (E) across the MSL ice cap. The green line in (E) denotes the Equilibrium Line. Tick marks represent latitude and longitude (as shown in panel A).

There is a good fit for the simulation at Glaciar Calluqueo, where the glacier underfits the observed geometry by only 250 m in length and width (Figure 7A). The simulation is within 75 m of the ice thicknesses predicted by Carrivick et al. (2016). The simulation overfits Glaciar Arroyo San Lorenzo to the north to a greater extent, by 2.5 km in glacier length (Figure 7A). This overfit is likely because the west-east spatial variation in precipitation across the ice cap is not well replicated by the precipitation lapse rate model dataset, making these high elevation valleys too wet. With the dominant precipitation source from the westerly winds, the north-east and south-east aspects of the valleys catchments are likely drier than the lapse rate derived precipitation dataset predicts. Reconstructing topographically controlled precipitation is especially difficult in mountain environments where topography is complex and changes dramatically over a small area.

The model underestimates the extent of the San Lorenzo and Rio Lacteo glaciers by 300 and 880 m respectively. These glaciers are covered by a thick layer of debris, which insulates the ice, reducing melting. PISM simulations do not account for this reduction in melt, and hence will simulate debris-covered glaciers to be lesser in extent than those observed.

4.5.2 Glacier mass balance

The present-day optimal-fit simulation of the MSL ice cap simulates grid cells with accumulation over the high peaks of up to 5.5 m w. e. a⁻¹ (Figure 7C). At an elevation of 3,000 to 2000 m asl, accumulation is between 4.5 and 2.5 m w. e. per grid cell, decreasing to 1 to 0.5 m w. e. at the tongues of the Calluqueo and San Lorenzo Sur glaciers (1,250–500 m asl). Ablation is up to 18 m w. e. on the tongue of Glaciar Calluqueo and 12.5 m w. e. on the flat plateau of Glaciar San Lorenzo Sur (Figure 7D). Ablation decreases with elevation up the ice cap, with a minimum of 0.5 mm w. e. annual ablation at the highest elevations.

Our model data provides a first indication of average mass balance conditions (1970–2000) at different locations on the icefield. The maximum measured annual surface mass balance of the MSL ice cap is a point measurement of 4.8 m w. e. at the massif’s peak, decreasing to zero at the equilibrium line between 1750 m asl and 2000 m asl (Figure 7E). The lowest mass balance occurs at the glacier tongues, with values of −3 m w. e. to −6.5 m w. e. in the lower ablation area of Glaciar Calluqueo. It should be acknowledged that in these simulations the ice cap is modelled to a state of equilibrium with climate (1970–2000). In reality outlet glaciers at MSL are receding and thinning (Falaschi et al., 2013; 2019), and therefore it would be expected that the distribution of mass balance is more negative. This is observed in mass balance measurements from geodetic data at Calluqueo Glacier from Falashci et al. (2019).

4.5.3 Ice velocity, basal sliding and temperate ice

Figure 8A shows a basal ice velocity up to ca 330 m a⁻¹, demonstrating basal sliding at the ice cap, in particular at locations of steepest bedrock slope, at Glaciar Calluqueo in the west and in the catchment of Glaciar San Lorenzo in the southeast. A marked similitude of basal and surface velocities (shown in Figures 8A,B) indicates that internal shear plays less of a role in ice flow and that the internal deformation velocity is negligible; rather, much of the ice velocity is derived through basal sliding.

FIGURE 8

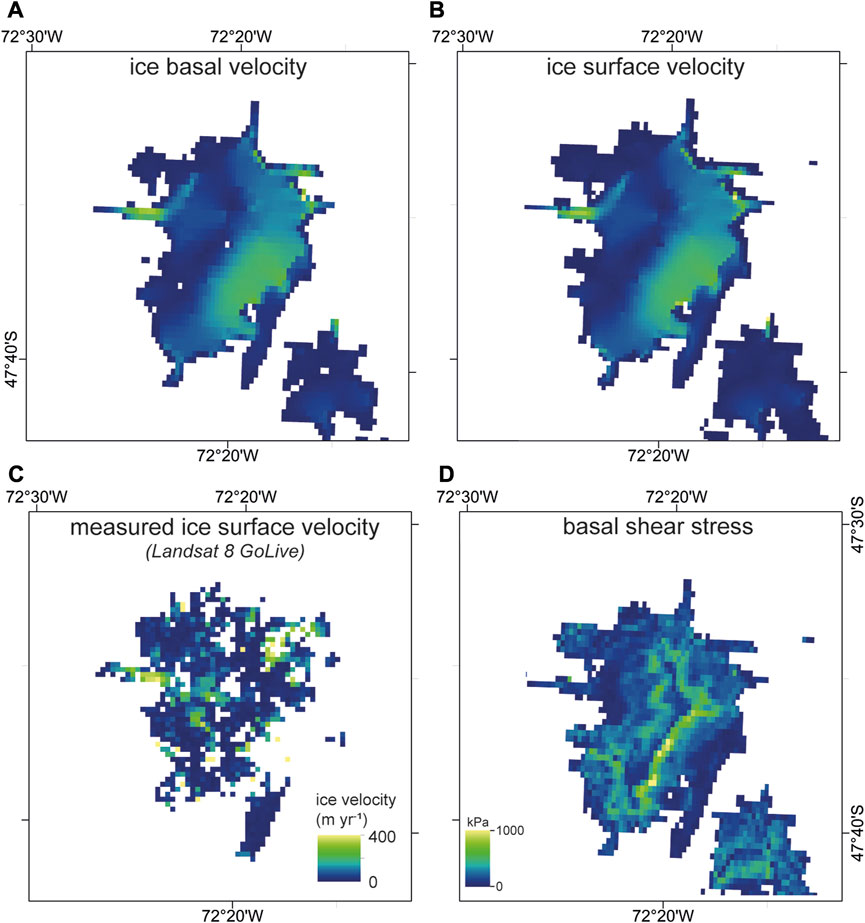
FIGURE 8. Basal ice (A) and surface ice (B) velocity of the modelled MSL ice cap. (C) Ice surface velocity of the MSL ice cap taken from the Global Land Ice Velocity Extraction from Landsat 8 (GoLIVE), Version 1 (image L8_231_093_032_2017_307_2017_339_RTT1, 3/11/2017 to 5/12/2017) (Fahnestock et al., 2016; Scambos et al., 2016). (D) Modelled basal shear stress opposing the driving stress resulting from gravity.

The simulation shows good agreement with observed ice surface velocity (Fahnestock et al., 2016; Scambos et al., 2016) (Figure 8C). The model replicates well the ice surface velocity field at Glaciar Calluqueo, particularly in the area of fast ice flow at the lower section of the glacier. The modelled ice surface velocities of 320–340 m a⁻¹ in this area shows a good agreement with the GoLIVE measured velocity of 340–390 m a⁻¹. The GoLive dataset shows two areas of faster flowing ice at higher elevations in the accumulation area of Glaciar Calluqueo, with velocities from 150 to 290 m a⁻¹ (Figure 8C). These fastest ice velocities occur in areas with steeply sloping, heavily crevassed ice. Modelled velocities here are lower, at a maximum of 70 m a⁻¹, perhaps due to domain resolution not picking up these highly topographically controlled areas of rapid ice flow, or because the areas are modelled as cold-based (Figure 7B). The rest of the accumulation area has low ice velocities, with good agreement between modelled ice surface velocities and GoLive velocities.

High basal shear stresses across the ice cap greater than the constant basal shear strength of 35 kPa (Figure 8D) enable basal sliding, facilitated by temperate ice at the pressure melting point. At Glaciar Calluqueo, basal shear stresses are between 50 kPa and 200 kPa (Figure 8D). Temperate ice is found at MSL’s outlet glaciers, where ice is thickest, the bed is insulated, and surface air temperature is warmer due to lower elevations (Figure 7). At highest elevations at the top of the massif, thinner ice and colder surface air temperatures thus results in cold-based ice, frozen to the bed and unable to slide.

4.6 Palaeoclimates and late glacial readvances

We examined the palaeoclimatic conditions required to explain past ice-cap extents by forcing the tuned simulation of the present-day ice cap with a suite of temperature and precipitation values, which was then assessed against ice cap extents reconstructed from empirical data (Sagredo et al., 2016; 2018; Davies et al., 2018, 2020; Martin et al., 2019; 2022; Mendelová et al., 2020) (Figure 2). Here, we evaluated the different temperature and precipitation values required to simulate mapped glacier extents through the Holocene and LGIT (Table 7). The WAIS Divide temperature (Cuffey et al., 2016) and ELA-based palaeo-precipitation reconstructions (Table 5) provide an independent indication of past climatic conditions for comparison.

TABLE 7

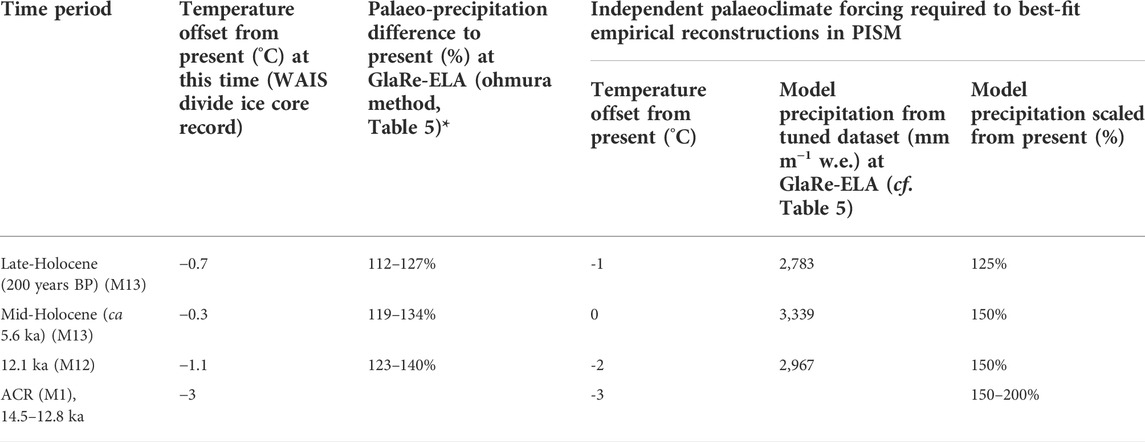
TABLE 7. Calculations of precipitation based upon GlaRe-ELA reconstructions following the method of Ohmura et al. (1992) under given temperature offsets from present (West Antarctic Ice Sheet (WAIS) Divide surface air temperature reconstruction (Cuffey et al., 2016). Temperature and precipitation forcing combinations which initialise the ice cap model to best fit empirical ice extent reconstructions are also listed.

4.6.1 Holocene advances

Figure 9 shows the best fit model simulations to reconstruct the ice extent for the Late-Holocene and mid-Holocene (A, B and C) (empirical reconstructions from Davies et al., 2020; 2018; Martin et al., 2019; 2022). During the mid- and Late-Holocene, periodically negative phases of the SAM brought cooler, wetter conditions to Patagonia (Abram et al., 2014; Reynhout et al., 2019; Kaplan et al., 2020), forcing glacier advances. In many cases, advances during the mid- and Late-Holocene re-occupied the same moraines, as seen at MSL.

FIGURE 9

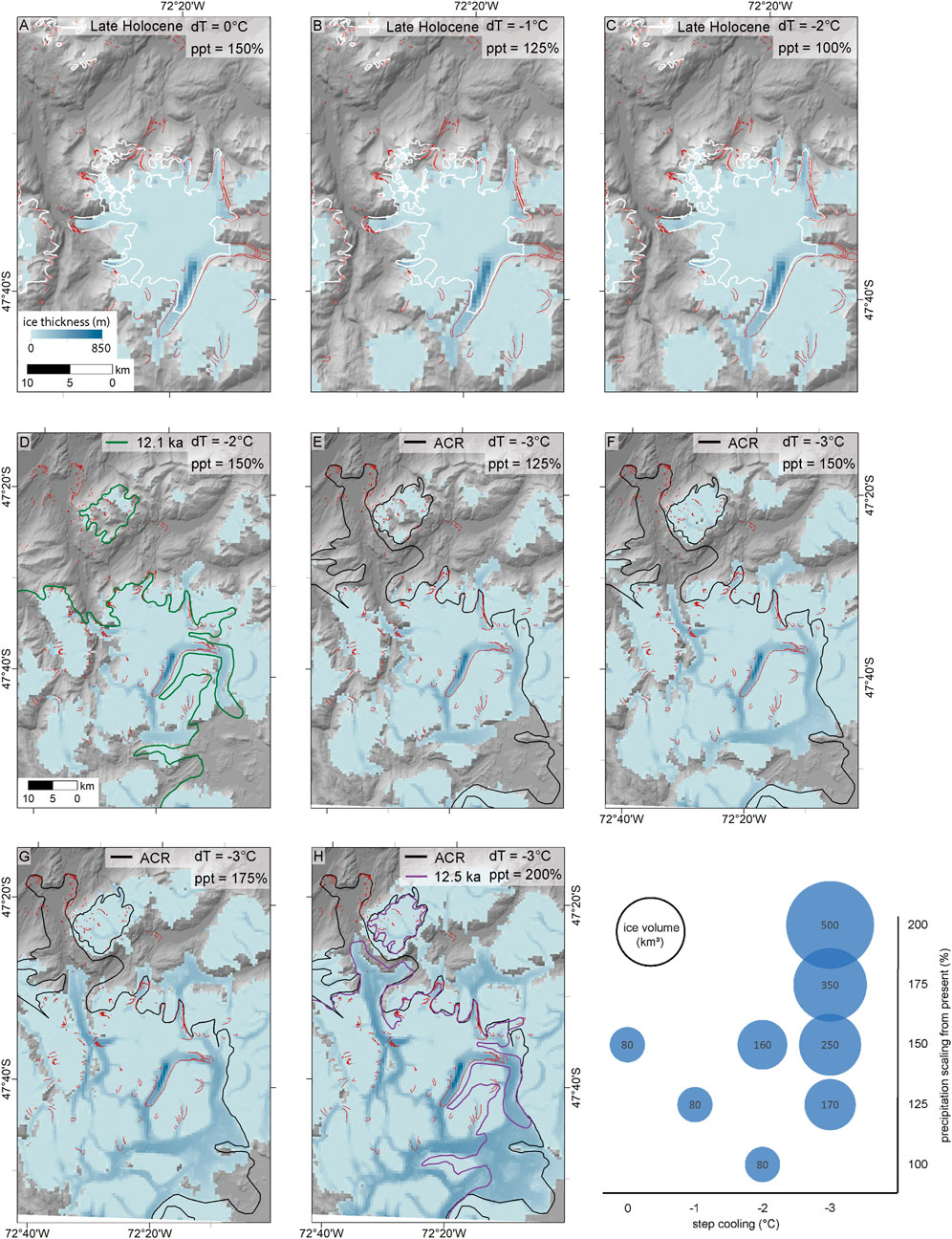
FIGURE 9. Model simulations of the MSL ice cap under combined surface air temperature step cooling of 1–3°C and precipitation scaling of 125%–200% to best fit palaeo ice mass reconstructions from the Late Holocene (A,B), mid-Holocene (B,C), ca 12.1 ka (D), 12.5 ka and the ACR (E-H). Moraines are shown in pink. Scatter plot shows how ice volume changes with different combinations of temperature and precipitation forcing.

For the Late-Holocene (ca 200 years BP), a combination of a temperature 1°C cooler than present and 125% of modern precipitation (Figure 9B; Table 7) most closely fits the empirical reconstruction and is in line with temperature offsets suggested by ice-core data (Cuffey et al., 2016) and our precipitation reconstructions using glacier equilibrium lines (Table 5). Model outputs suggests that ice surface velocities at Glaciar Calluqueo ranged between 250 m a⁻¹ and 400 m a⁻¹, similar to the modelled present-day glacier (Figure 6).

During the mid-Holocene (ca 5.6 ka) (Sagredo et al., 2016), a negative phase of the SAM brought increased precipitation to central Patagonia. A 0°C offset and 150% precipitation increase forced glacier advance to the mid-Holocene moraines (Figure 9A), which is similar again to the climatic variations suggested by palaeoclimatic ice-core data and Table 5. Modelled ice surface velocity was found to be slightly higher than present day on Glaciar Calluqueo, between 250 m a⁻¹ and 600 m a⁻¹ at their highest.

4.6.2 Advances during the last glacial-interglacial transition

The best fit model simulation to ice at the 12.1 ka reconstruction of Glaciar Calluqueo (Martin et al., 2022) requires model initialisation of −2°C and 150% precipitation from present, 0.9°C colder and >10% wetter than from the WAIS Divide temperature and ELA precipitation reconstruction (Figure 9D; Table 7). This envelope of palaeoclimatic conditions during the LGIT is the first available from numerical modelling for Patagonian icecaps. Modelled surface ice flowed significantly faster than the present-day, with the fastest ice flow on Glaciar Calluqueo between 1,000 m a⁻¹ and 1700 m a⁻¹.

The WAIS-Divide record suggests that surface air temperature at the ACR was up to 3°C colder than present in Antarctica, and Patagonian pollen and charcoal records indicate a cold and wet climate during this period (Moreno, 2004; Whitlock et al., 2007; Villa-Martínez et al., 2012). Model runs at -3°C from present and 200% present-day precipitation are not able to simulate the full extent of Glaciar Calluqueo at the ACR (Figure 9H), producing a glacier 16 km short of the ACR Esmeralda Moraine (cf. Davies et al., 2018). However, it does capture the growth of a substantial ice accumulation area in the Barrancos Mountains and Cordon Esmeralda, and gives insights into ice flow and dynamics during the ACR. Although the simulation in the Salto valley underfits, it does show a major advance, with accumulation in the adjacent high grounds, during the ACR. As Glaciar Calluqueo extended further down Pedregoso valley, ice velocities stabilised in comparison with those modelled for 12.1 and 12.5 ka, with maximum velocities between 500 m a⁻¹ and 525 m a⁻¹. Ice extending to the southeast of MSL flowed at lower velocities, between 150 m a⁻¹ and 250 m a⁻¹ at its fastest.

A temperature 3°C cooler and a 200% precipitation change relative to present matches the advance on the eastern side of the massif well, with the outlet glaciers reaching the ACR-dated Belgrano moraines (Mendelová et al., 2020) (cf. Figures 1, 9H). The −3°C offset and 150% precipitation increase simulation fits Glaciar Tranquilo in the north of MSL ice cap well as well (Figure 9F). Increasing precipitation to 200% results in an overfit here (Figure 9H), likely due to an overestimation of precipitation as the strong east-west orographic precipitation gradient is not taken into account. Given the northeast orientation of Glaciar Tranquilo’s catchment, a lower level of precipitation would be expected than is found within the lapse rate-derived precipitation dataset for the lee side of MSL.

The discrepancies seen between the model simulations of Glaciar Calluqueo and WAIS Divide-ELA climate reconstructions at the ACR are likely because at the ACR, ice was in a period of readvance during overall deglaciation from the LGM. The climate conditions at this point therefore reflect a readvance and stabilisation from an already large ice mass and are not cold enough to force the simulation to form such a significant mass of ice from the smaller modern MSL ice extent.

5 Discussion

5.1 Dynamics of Monte San Lorenzo ice cap

Our study provides a novel modelling approach to the analysis of the components of mass balance of a Patagonian ice cap. We show accumulation at MSL of up to 4.5 m w. e. at high elevations, decreasing to 1 m w. e. on the Glaciar Calluqueo tongue. Ablation in this high through-put system is 18 m w. e. on Glaciar Calluqueo tongue, and decreases to 0.5 m w. e. at the highest elevations. There are few comparative modelling or empirical studies available, but these values fall within the typical range expected east of the watershed. We show high ice velocities (320–340 m a⁻¹), driven by basal sliding. These velocities are in line with observations (Millan et al., 2022). Basal sliding throughout the year has also been suggested at Glacier Perito Moreno from field observations (Skvarca and Naruse, 1997) and from numerical modelling at Glaciar San Rafael (Collao-Barrios et al., 2018). However, at MSL, a basal layer of temperate ice with basal sliding is found only in the ablation areas, with cold-based ice and lower ice velocities at higher elevations. An exception to this occurs on the eastern side of the ice cap, where extremely steep headwalls lead to ice velocities between 80 and 200 m a⁻¹. MSL is sensitive to changes in basal yield shear strength (arising for example from an increase in basal meltwater input), which could result in dynamic thinning of the glacier.

5.2 Glacier sensitivity to climate

The sensitivity of glacier mass balance to changes in various climate variables, and the proportion to which each climate variable impacts glacier mass change, shows a wide spread across the globe (Mackintosh et al., 2017). Accumulation shows its highest sensitivity to temperature at the snow/rain threshold (usually between 0 and 3°C) (Anderson and Mackintosh, 2012). This relationship is strongest where precipitation is highest, such as in maritime environments (e.g., Purdie et al., 2008; Cullen and Conway, 2015). Temperate climate and low continentality (the difference in mean temperature between the warmest and coldest month) imply a larger proportion of the year with temperatures high enough for melt (Anderson and Mackintosh, 2012). These factors combined lead to a high mass turnover and result in maritime glaciers having the highest sensitivity to changes in climate (Meier et al., 2018; Oerlemans, 2005; Braithwaite et al., 2002).

Using our numerical model, it is possible to ascertain the relative sensitivity of the ice cap to temperature and precipitation changes. Our sensitivity experiments independently simulating the ice cap under step changes in temperature and precipitation show that a 1°C offset in surface air temperature is equivalent to a 21% change in precipitation in terms of obtaining the same change in ice volume. Glaciers with a higher change in precipitation equivalent to a 1°C change in temperature are less sensitive to precipitation; glaciers where a smaller percentage change in precipitation is required to force an equivalent glacier change to a 1°C change in temperature are more sensitive to precipitation. The global average is 25% precipitation change (Oerlemans, 2005).

We compare our results with other studies from across the Southern Hemisphere mid-latitudes. Here, a 1°C offset in surface air temperature is equivalent to a 20%–83% precipitation change (Figure 10) (Anderson et al., 2006; Bippus, 2007; Möller et al., 2007; Anderson et al., 2010; Anderson and Mackintosh, 2012). More maritime glaciers in New Zealand’s Southern Alps and in southern Patagonia are less sensitive to precipitation relative to temperature. For example, at Glaciar Perito Moreno (20% precipitation change equivalent to 1°C temperature change; Bippus, 2007) precipitation has a proportionally greater impact on glacier mass balance relative to temperature than at the more maritime Gran Campo Nevado (50% precipitation change equivalent to 1°C temperature change; Möller et al., 2007).

FIGURE 10

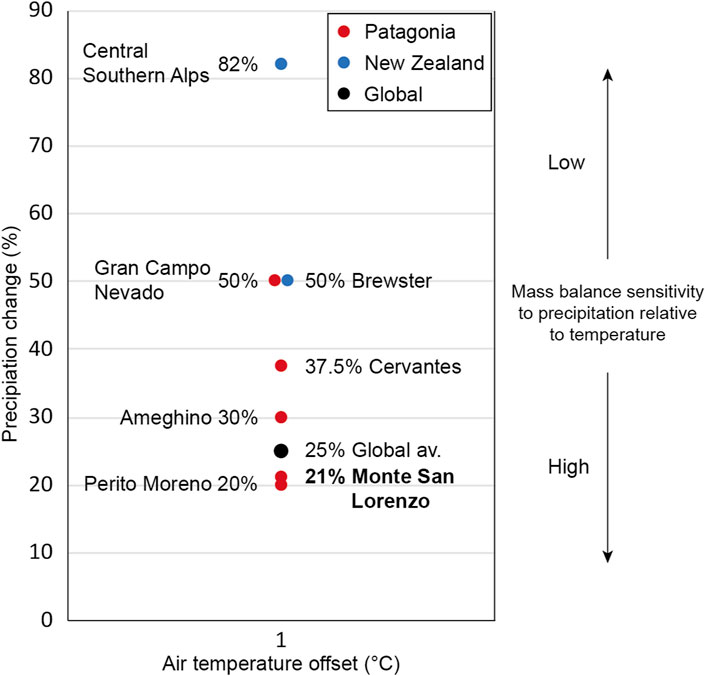
FIGURE 10. Precipitation change equivalent to 1°C change in air temperature at glaciers in Patagonia and New Zealand and a global average (black circle (Oerlemans, 2005),). Red circles are glaciers in Patagonia at Perito Moreno, Ameghino and Cervantes glaciers on the eastern side of the Southern Patagonian Andes (Bippus, 2007) the Gran Campo Nevado ice cap in southern Patagonia (53°S) (Möller et al., 2007) and the MSL ice cap (this study). Blue circles are glaciers in New Zealand’s Southern Alps at Brewster Glacier (Anderson et al., 2010) and an average of a collection of glaciers from the central Southern Alps, including Franz Joseph, Fox and Tazman Glaciers (Anderson and Mackintosh, 2012).

At the most strongly maritime glaciers, where there is a higher level of precipitation falling close to the snow/rain threshold temperature, the impact of a small change in temperature on mass balance, by changing the proportion of precipitation that falls as snow or rain, is exacerbated. Glaciers with comparatively higher mass balance sensitivity to precipitation compared with temperature are those with greater continentality, as is the case for MSL, on the eastern side of the Patagonian Andes. Therefore, at MSL, compared with the other Patagonian and New Zealand glaciers studied, and the global average, precipitation plays a greater role in mass balance than temperature.

Further, there are morphological contrasts between the Cervantes, Ameghino, MSL and Perito Moreno glaciers presented in Figure 10. Glaciar Perito Moreno and Glaciar Calluqueo have much higher accumulation area ratios (0.68 at Glaciar Calluqueo) and hence a smaller change in precipitation is needed for an equivalent mass balance change from a 1°C temperature variation. Although the dominant control on glacier mass balance is still temperature due to the strong empirical impact of temperature on accumulation (Anderson and Mackintosh, 2012), the precipitation changes observed at MSL will have a proportionally higher impact on mass balance than for many other glaciers in Patagonia.

5.3 Insights into ice dynamics during the last glacial-Interglacial transition

Empirical reconstructions of palaeo-ice dynamics (e.g., Figure 2), such as PATICE (Davies et al., 2020) or reconstructions of other ice sheets (Hughes et al., 2016; Batchelor et al., 2019; Dalton et al., 2020), rely on spatially limited data to constrain large areas of terrain. These reconstructions mostly rely on moraine limits in valleys and lowlands, with and without chronological control, to understand the extent and timing of former ice limits. They do not account for realistic ice-flow, especially in areas where bedforms such as mega-scale glacial lineations or drumlins are absent (cf. Clark et al., 2012). Ice volume and thickness are particularly challenging to constrain from these empirical data (Stokes et al., 2015; Davies, 2021). Numerical modelling provides additional data regarding past ice dynamics, including how glacier morphology evolves under different climates, especially in the upper reaches, where geomorphological data are absent.

In the case of Glaciar Calluqueo, numerical modelling provides information on glacier-tongue bifurcation at the junction of the Pedregoso and Tranquillo valleys. Our simulations showed the ice volume required to damn Río Tranquillo, forming Palaeolake Tranquillo. These simulations also illustrated the growth of multiple glacier accumulation zones across the Barrancos Mountains, with growing glaciers on Cordon Esmeralda that could have contributed ice during the LGIT. This helps to explain why the advance during the ACR was so much larger than that of Glaciar Tranquilo, which has a much smaller accumulation area. We are additionally able to gain insights into former ice velocities and mass balances, providing a deeper understanding of glacier-climate relationships and ice dynamics. These data are unavailable from the geomorphological record. Our numerical modelling experiments therefore add depth to the landform-derived reconstructions previously published in this area (Sagredo et al., 2016; 2018; Garibotti and Villalba, 2017; Davies et al., 2018, 2020; Martin et al., 2019; 2022; Mendelová et al., 2020).

We find that both cooler and wetter climates are needed to force readvances of these glaciers during the LGIT and Holocene, due to their temperate climate and high ablation rates. This supports previous work from proxy data, which shows that cooler, wetter conditions associated with changing Southern Westerly Winds are required to force Holocene advances (Moreno et al., 2018; Kaplan et al., 2020), though there are few direct quantitative records of precipitation available (Kilian and Lamy, 2012). The sensitivity of MSL to precipitation suggests that the rapid recession observed between 12.8 ka, when Glaciar Calluqueo was at the mouth of the valley (cf. Glasser et al., 2012) and 12.1 ka (Martin et al., 2022) was likely driven by both post-ACR temperature increase and a decrease in precipitation. At this time, a southward shift to ca 55°S in the Southern Westerly Winds is suggested by changing lake levels at Lago Cardiel (Quade and Kaplan, 2017), which would reduce precipitation at MSL (47.5°S). This would have contributed to the glacier’s rapid recession.

We are able to provide the first quantitative estimates for temperature and precipitation at key periods during the Late Glacial and Holocene. Firstly, meeting the readvance or stabilisation noted at 12.1 ka for Glaciar Calluqueo requires a cooling of 2°C and precipitation to increase to 150% of current values. An increase in precipitation at this time is likely, as noted by lake-level studies at Lago Cardiel, which increased to its hydrological maximum (136% of current level) by 11.3 ka (Quade and Kaplan, 2017). A readvance of glaciers at this time has been noted in other catchments (Mercer, 1968; 1976; Marden and Clapperton, 1995; Strelin and Malagnino, 2000; Glasser et al., 2012; Harrison et al., 2012; Menounos et al., 2013; Mendelová et al., 2020); however it has been queried whether this readvance was climatically driven or related to base level fall in ice-dammed lakes (Davies et al., 2020). Our modelled data suggests that a climatic driver (cooling and increased precipitation) is needed to force glaciers to readvance or stabilise at ∼11 to 12 ka, post-dating the ACR.

5.4 Insights into holocene palaeoclimates

Proxy palaeoclimatic evidence indicates less strong cooling during the Mid-Holocene readvance (5.6 ka) reconstructed for MSL (Sagredo et al., 2016), and we find that increasing precipitation to 150% of current values is required. There are widespread moraines around this region of Patagonia dating to the mid-Holocene, typically close to and just outside of those deposited during the Late Holocene readvances at 1–2 ka and 0.2–0.5 ka (Mercer, 1976; Fernandez et al., 2012; Nimick et al., 2016; Sagredo et al., 2016; Garibotti and Villalba, 2017; Reynhout et al., 2019; Davies et al., 2020). This period was a time of persistent negative Southern Annular Mode conditions, with an expansion northwards of the Southern Westerly Winds and a cold and wet climate forcing glacier growth (Moreno et al., 2018). This is in agreement with previous climate model simulations, which have suggested that during this mid-Holocene period (4–6 ka), cooling was limited, with changes of −0.2°C in the summer (the key time to influence ablation), −0.5°C in autumn, −0.4°C in winter, and warmer temperatures in the spring (0.2°C) (with respect to current values; Bravo et al., 2015). Bravo et al. (2015) argue that there was limited change in precipitation, but there was a seasonal shift, with more occurring in the principal accumulation season from October to April. While we did not change the seasonality in our sensitivity or palaeoclimate experiments, this would have a similar impact on the glaciers to increasing mean annual precipitation, by providing more accumulation, while summer cooling decreases ablation. Indeed, other studies have inferred increased precipitation at this time (Van Daele et al., 2016), so our reconstruction is in good agreement with results by Bravo et al. (2015) and Van Daele et al. (2016).

Finally, we find that a cooling of 1°C relative to today, together with a precipitation 125% of today’s values, is sufficient to force the readvance observed during the Late Holocene (0.2–0.5 ka). A readvance at this time is widely recognised in Patagonia (Masiokas et al., 2009; Davies and Glasser, 2012; Meier et al., 2018; Davies et al., 2020), with widespread deposition of moraines (Kaplan et al., 2016). Tree-ring and modelling-based temperature reconstructions agree with the ice-core record of cooling of 1–2°C at this time (Villalba et al., 2005; Kaplan et al., 2016). Our estimate is, however, one of the first quantified estimates of precipitation change during the Late Holocene in this region of Patagonia.

6 Conclusion

In this study, we used the Parallel Ice Sheet Model (PISM) to model a Patagonian ice cap. We undertook a series of experiments that used systematic iterations of different parameters within the model in order to establish the key controls on the modelled icefield and define the envelope of parameter space within which the results agree most closely with the present-day observed icefield. We were then able to define the palaeoclimatic envelopes that best approximate the mean palaeoclimatic conditions during readvances of the ice cap during the Late Glacial period.

We produced a simulation of the MSL ice cap matching present-day ice distribution, when initialised using the WorldClim2 modelled surface air temperatures and a precipitation dataset built from a tuned lapse rate (1.35 mm m⁻¹). This dataset results in mean annual precipitation at Glaciar Calluqueo, MSL, between 1,200 and 5,500 mm a⁻¹. These values are in line with sparse local measured records and regional modelled climate data.

Sensitivity experiments demonstrate that higher basal shear strength leads to a thicker and longer profile of Glaciar Calluqueo, due to the impact of ablation at low altitudes following rapid initial ice growth. Furthermore, they demonstrate a significant sensitivity of the model to changes in positive degree day snow and ice melt factors, with greater sensitivity to melting of ice in the ablation area than a reduction in mass input through snow melt in the accumulation area.

Cold-based ice, frozen to the bed, occupies higher elevations of the MSL ice cap (> ca 1,800 to 2,200 m asl), while temperate, warm-based ice is found at lower elevations in outlet glaciers. Temperate ice flows via basal sliding at up to 330 m a⁻¹, with negligible internal ice flow velocity. The simulated ice cap shows high surface mass flux, with ablation at outlet glacier tongues up to 18 m w. e. a⁻¹, and accumulation at highest elevations up to 5.5 m w. e. a⁻¹. Surface mass balance ranges from +4.8 m w. e. a⁻¹ to −6.5 m w. e. a⁻¹ with a simulated ELA between 1,750 m asl and 2,000 m asl.

Simulations initialised with a varied combination of temperature and precipitation values show that the model matched temperature and precipitation reconstructed from the WAIS Divide ice cores during the latest Holocene readvance. However, greater discrepancy is seen with simulations of greater ice extent, requiring further investigation through higher resolution and transient simulations. The MSL ice cap, situated to the east of the Andean cordillera with high continentality, is more sensitive to precipitation compared with temperature than the markedly maritime glaciers of the NPI and SPI, Gran Campo Nevado and glaciers of New Zealand’s Southern Alps. For MSL, a 1°C offset in surface air temperature is equivalent to a 21% change in precipitation. Our data suggest that palaeoenvironmental reconstructions and modelling of smaller ice caps east of the Andes could provide important insights into latitudinal shifts in the South Westerly Winds.

At 47°S, our modelling of Monte San Lorenzo demonstrates that cooler, wetter conditions are needed to drive reconstructed glacier advances at 0.2–0.5 ka, 5.6 ka and 12.1 ka, with temperature offsets of −1°C and 125% of modern precipitation (0.2–0.5 ka), 0°C and 150% precipitation (5.6 ka), and −2°C and 150% precipitation (12.1 ka). This new understanding of glacier sensitivity to temperature and precipitation change improves our ability to quantify the climatic drivers of past and present glacier fluctuations.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

This work was undertaken as part of a studentship awarded to JM at Royal Holloway University of London. The project was conceptualised, initialised and guided by BD and VT; the numerical modelling was undertaken by JM in collaboration with and guided by RJ.

Funding

JM was supported by a Natural Environment Research Council award NE/L002485/1.

Acknowledgments

Jan Leanarts is gratefully thanked for processing the RAMCO 2.3 climatic dataset for use in PISM. Nick Golledge is thanked for his advice and assistance in running PISM. We thank three reviewers for their constructive comments, which helped to improve the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.831631/full#supplementary-material

References

Abram, N. J., Mulvaney, R., Vimeux, F., Phipps, S. J., Turner, J., and England, M. H. (2014). Evolution of the Southern Annular Mode during the past millennium. Nat. Clim. Chang. 4, 564–569. doi:10.1038/nclimate2235

CrossRef Full Text | Google Scholar

Anderson, B., Lawson, W., Owens, I., and Goodsell, B. (2006). Past and future mass balance of ‘ka roimata o hine hukatere’ Franz Josef glacier, New Zealand. J. Glaciol. 52, 597–607. doi:10.3189/172756506781828449

CrossRef Full Text | Google Scholar

Anderson, B., and Mackintosh, A. (2012). Controls on mass balance sensitivity of maritime glaciers in the Southern Alps, New Zealand: The role of debris cover. J. Geophys. Res. 117. doi:10.1029/2011jf002064

CrossRef Full Text | Google Scholar

Anderson, B., Mackintosh, A., Stumm, D., George, L., Kerr, T., Winter-Billington, A., et al. (2010). Climate sensitivity of a high-precipitation glacier in New Zealand. J. Glaciol. 56, 114–128. doi:10.3189/002214310791190929

CrossRef Full Text | Google Scholar

Anderson, B., and Mackintosh, A. (2006). Temperature change is the major driver of late-glacial and Holocene glacier fluctuations in New Zealand. Geol. 34, 121–124. doi:10.1130/g22151.1

CrossRef Full Text | Google Scholar

Arendt, A., and Sharp, M. (1999). Energy balance measurements on a Canadian high Arctic glacier and their implications for mass balance modelling. Birmingham, UK: IAHS Publ., 165–172.

Google Scholar

Aristarain, A. J., and Delmas, R. J. (1993). Firn-core study from the southern Patagonia ice cap, South America. J. Glaciol. 39, 249–254. doi:10.3189/s0022143000015914

CrossRef Full Text | Google Scholar

Aschwanden, A., Aðalgeirsdóttir, G., and Khroulev, C. (2013). Hindcasting to measure ice sheet model sensitivity to initial states. Cryosphere 7, 1083–1093. doi:10.5194/tc-7-1083-2013

CrossRef Full Text | Google Scholar

Aschwanden, A., Bueler, E., Khroulev, C., and Blatter, H. (2012). An enthalpy formulation for glaciers and ice sheets. J. Glaciol. 58, 441–457. doi:10.3189/2012JoG11J088

CrossRef Full Text | Google Scholar

Aschwanden, A., Fahnestock, M. A., and Truffer, M. (2016). Complex Greenland outlet glacier flow captured. Nat. Commun. 7, 10524–10528. doi:10.1038/ncomms10524

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahr, D. B., Pfeffer, W. T., Sassolas, C., and Meier, M. F. (1998). Response time of glaciers as a function of size and mass balance: 1. Theory. J. Geophys. Res. 103, 9777–9782. doi:10.1029/98JB00507

CrossRef Full Text | Google Scholar

Barcaza, G., Nussbaumer, S. U., Tapia, G., Valdés, J., García, J.-L., Videla, Y., et al. (2017). Glacier inventory and recent glacier variations in the Andes of Chile, South America. Ann. Glaciol. 58, 166–180. doi:10.1017/aog.2017.28

CrossRef Full Text | Google Scholar

Batchelor, C. L., Margold, M., Krapp, M., Murton, D. K., Dalton, A. S., Gibbard, P. L., et al. (2019). The configuration of Northern Hemisphere ice sheets through the Quaternary. Nat. Commun. 10, 3713. doi:10.1038/s41467-019-11601-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Bendle, J. M., and Glasser, N. F. (2012). Palaeoclimatic reconstruction from lateglacial (younger dryas chronozone) cirque glaciers in snowdonia, north wales. Proc. Geologists'. Assoc. 123, 130–145. doi:10.1016/j.pgeola.2011.09.006

CrossRef Full Text | Google Scholar

Bendle, J. M., Palmer, A. P., Thorndycraft, V. R., and Matthews, I. P. (2019). Phased patagonian ice sheet response to southern Hemisphere atmospheric and oceanic warming between 18 and 17 ka. Sci. Rep. 9, 4133. doi:10.1038/s41598-019-39750-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Bippus, G. (2007). Modelling mass balance and climate sensitivity of glaciers of the southern Patagonia icefield. Available at: https://www.uibk.ac.at/acinn/theses/diploma-theses/bippus_gabriele_2007_dipl.pdf.

Google Scholar

Blunier, T., Schwander, J., Stauffer, B., Stocker, T., Dällenbach, A., Indermühle, A., et al. (1997). Timing of the antarctic cold reversal and the atmospheric CO2 increase with respect to the younger dryas event. Geophys. Res. Lett. 24, 2683–2686. doi:10.1029/97GL02658

CrossRef Full Text | Google Scholar

Boex, J., Fogwill, C., Harrison, S., Glasser, N. F., Hein, A., Schnabel, C., et al. (2013). Rapid thinning of the late pleistocene patagonian ice sheet followed migration of the southern westerlies. Sci. Rep. 3, 2118. doi:10.1038/srep02118

PubMed Abstract | CrossRef Full Text | Google Scholar

Boulton, G. S., and Jones, A. S. (1979). Stability of temperate ice caps and ice sheets resting on beds of deformable sediment. J. Glaciol. 24, 29–43. doi:10.3189/s0022143000014623

CrossRef Full Text | Google Scholar

Braithwaite, R. J. (2008). Temperature and precipitation climate at the equilibrium-line altitude of glaciers expressed by the degree-day factor for melting snow. J. Glaciol. 54, 437–444. doi:10.3189/002214308785836968

CrossRef Full Text | Google Scholar

Braithwaite, R. J., and Olesen, O. B. (1989). Calculation of glacier ablation from air temperature, west Greenland. Dordrecht: Springer, 219–233. doi:10.1007/978-94-015-7823-3_15

CrossRef Full Text | Google Scholar

Braithwaite, R. J., and Olesen, O. B. (1990). Response of the energy balance on the margin of the Greenland ice sheet to temperature changes. J. Glaciol. 36, 217–221. doi:10.3189/S0022143000009461

CrossRef Full Text | Google Scholar

Bravo, C., Quincey, D. J., Ross, A. N., Rivera, A., Brock, B., Miles, E., et al. (2019). Air temperature characteristics, distribution, and impact on modeled ablation for the South Patagonia Icefield. J. Geophys. Res. Atmos. 124, 907–925. doi:10.1029/2018jd028857

CrossRef Full Text | Google Scholar

Bravo, C., Rojas, M., Anderson, B. M., Mackintosh, A. N., Sagredo, E., and Moreno, P. I. (2015). Modelled glacier equilibrium line altitudes during the mid-Holocene in the southern mid-latitudes. Clim. Past. 11, 1575–1586. doi:10.5194/cp-11-1575-2015

CrossRef Full Text | Google Scholar

Brown, N. E., Hallet, B., and Booth, D. B. (1987). Rapid soft bed sliding of the Puget glacial lobe. J. Geophys. Res. 92, 8985–8997. doi:10.1029/jb092ib09p08985

CrossRef Full Text | Google Scholar

Bueler, E., and Brown, J. (2009). Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model. J. Geophys. Res. 114, F03008. doi:10.1029/2008jf001179

CrossRef Full Text | Google Scholar

Carrasco, J., Casassa, G., and Rivera, A. (2002). “Meteorological and climatological aspect of the southern patagonian icefield,” in The patagonian icefields. Editors G. Casassa, F. V Sepulveda, and R. M. Sinclair (New York: Kluwer-Plenum), 29–41.

CrossRef Full Text | Google Scholar

Carrivick, J. L., Davies, B. J., James, W. H. M., Quincey, D. J., and Glasser, N. F. (2016). Distributed ice thickness and glacier volume in southern South America. Glob. Planet. Change 146, 122–132. doi:10.1016/j.gloplacha.2016.09.010

CrossRef Full Text | Google Scholar

Chandler, B. M. P., and Lukas, S. (2017). Reconstruction of Loch Lomond Stadial (Younger Dryas) glaciers on Ben More Coigach, north‐west Scotland, and implications for reconstructing palaeoclimate using small ice masses. J. Quat. Sci. 32, 475–492. doi:10.1002/jqs.2941

CrossRef Full Text | Google Scholar

Clark, C. D., Hughes, A. L. C., Greenwood, S. L., Jordan, C., and Sejrup, H. P. (2012). Pattern and timing of retreat of the last British-Irish Ice Sheet. Quat. Sci. Rev. 44, 112–146. doi:10.1016/j.quascirev.2010.07.019

CrossRef Full Text | Google Scholar

Collao-Barrios, G., Gillet-Chaulet, F., Favier, V., Casassa, G., Berthier, E., Dussaillant, I., et al. (2018). Ice flow modelling to constrain the surface mass balance and ice discharge of San Rafael Glacier, Northern Patagonia Icefield. J. Glaciol. 64, 568–582. doi:10.1017/jog.2018.46

CrossRef Full Text | Google Scholar

Cuffey, K. M., Clow, G. D., Steig, E. J., Buizert, C., Fudge, T. J., Koutnik, M., et al. (2016). Deglacial temperature history of West Antarctica. Proc. Natl. Acad. Sci. U. S. A. 113, 14249–14254. doi:10.1073/pnas.1609132113

PubMed Abstract | CrossRef Full Text | Google Scholar

Cullen, N. J., and Conway, J. P. (2015). A 22 month record of surface meteorology and energy balance from the ablation zone of Brewster Glacier, New Zealand. J. Glaciol. 61, 931–946. doi:10.3189/2015jog15j004

CrossRef Full Text | Google Scholar

Dalton, A. S., Margold, M., Stokes, C. R., Tarasov, L., Dyke, A. S., Adams, R. S., et al. (2020). An updated radiocarbon-based ice margin chronology for the last deglaciation of the North American Ice Sheet Complex. Quat. Sci. Rev. 234, 106223. doi:10.1016/j.quascirev.2020.106223

CrossRef Full Text | Google Scholar

Davies, B. J., Darvill, C. M., Lovell, H., Bendle, J. M., Dowdeswell, J. A., Fabel, D., et al. (2020). The evolution of the Patagonian Ice Sheet from 35 ka to the present day (PATICE). Earth. Sci. Rev. 204, 103152. doi:10.1016/j.earscirev.2020.103152

CrossRef Full Text | Google Scholar

Davies, B. J. (2021). “Dating glacial landforms II: Radiometric techniques,” in Cryospheric geomorphology (Elsevier). doi:10.1016/B978-0-12-818234-5.00040-7

CrossRef Full Text | Google Scholar

Davies, B. J., and Glasser, N. F. (2012). Accelerating shrinkage of patagonian glaciers from the “little ice age” (∼AD 1870) to 2011. J. Glaciol. 58, 1063–1084. doi:10.3189/2012JoG12J026

CrossRef Full Text | Google Scholar

Davies, B. J., Thorndycraft, V. R., Fabel, D., and Martin, J. R. V. (2018). Asynchronous glacier dynamics during the antarctic cold reversal in central Patagonia. Quat. Sci. Rev. 200, 287–312. doi:10.1016/j.quascirev.2018.09.025

CrossRef Full Text | Google Scholar

Davies, J. H. (2013). Global map of solid Earth surface heat flow. Geochem. Geophys. Geosyst. 14, 4608–4622. doi:10.1002/ggge.20271

CrossRef Full Text | Google Scholar

Direccion Meteologica de Chile (2001). Estadistica climatologia tomo III.

Google Scholar

Doughty, A. M., Anderson, B. M., Mackintosh, A. N., Kaplan, M. R., Vandergoes, M. J., Barrell, D. J. A., et al. (2013). Evaluation of lateglacial temperatures in the southern Alps of New Zealand based on glacier modelling at irishman stream, ben ohau range. Quat. Sci. Rev. 74, 160–169. doi:10.1016/j.quascirev.2012.09.013

CrossRef Full Text | Google Scholar

Dussaillant, I., Berthier, E., Brun, F., Masiokas, M., Hugonnet, R., Favier, V., et al. (2019). Two decades of glacier mass loss along the Andes. Nat. Geosci. 12, 802–808. doi:10.1038/s41561-019-0432-5

CrossRef Full Text | Google Scholar

Escobar, F., Fernando, V., and Garin, C. (1992). “Water balance in the Patagonia icefield,” in Glaciological researches in Patagonia, 1990. Editors R. Naruse, and M. Aniya (Japanese Society of Snow and Ice), 109–119.

Google Scholar

Fahnestock, M., Scambos, T., Moon, T., Gardner, A., Haran, T., and Klinger, M. (2016). Rapid large-area mapping of ice flow using Landsat 8. Remote Sens. Environ. 185, 84–94. doi:10.1016/j.rse.2015.11.023

CrossRef Full Text | Google Scholar

Falaschi, D., Bolch, T., Rastner, P., Lenzano, M. G., Lenzano, L., Vecchio, A. L. O., et al. (2017). Mass changes of alpine glaciers at the eastern margin of the Northern and Southern Patagonian Icefields between 2000 and 2012. J. Glaciol. 63, 258–272. doi:10.1017/jog.2016.136

CrossRef Full Text | Google Scholar

Falaschi, D., Bravo, C., Masiokas, M., Villalba, R., and Rivera, A. A. A. (2013). First Glacier Inventory and recent changes in glacier area in the Monte san Lorenzo region (47°S), southern patagonian Andes, south America. Arct. Antarct. Alp. Res. 45, 19–28. doi:10.1657/1938-4246-45.1.19

CrossRef Full Text | Google Scholar

Falaschi, D., Lenzano, M. G., Villalba, R., Bolch, T., Rivera, A., and Lo Vecchio, A. (2019). Six decades (1958–2018) of geodetic glacier mass balance in Monte san Lorenzo, patagonian Andes. Front. Earth Sci. 7, 326. doi:10.3389/feart.2019.00326

CrossRef Full Text | Google Scholar

Falaschi, D., Rivera, A., Lo Vecchio Repetto, A., Moragues, S., Villalba, R., Rastner, P., et al. (2021). Evolution of surface characteristics of three debris-covered glaciers in the patagonian Andes from 1958 to 2020. Front. Earth Sci. 9. doi:10.3389/feart.2021.671854

CrossRef Full Text | Google Scholar

Falaschi, D., Tadono, T., and Masiokas, M. (2015). Rock glaciers in the patagonian Andes: An inventory for the Monte san Lorenzo (cerro Cochrane) massif, 47° S. Geogr. Ann. Ser. A Phys. Geogr. 97, 769–777. doi:10.1111/geoa.12113

CrossRef Full Text | Google Scholar

Fernandez, R., Anderson, J., Bertrand, S., and Wellner, J. (2012). Gualas glacier sedimentary record of climate and environmental change, golfo elefantes, western Patagonia (46.5° S). Holocene 22, 451–463. doi:10.1177/0959683611425545

CrossRef Full Text | Google Scholar

Fick, S. E., and Hijmans, R. J. (2017). WorldClim 2: New 1‐km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315. doi:10.1002/joc.5086

CrossRef Full Text | Google Scholar

Frieler, K., Clark, P. U., He, F., Buizert, C., Reese, R., Ligtenberg, S. R. M., et al. (2015). Consistent evidence of increasing Antarctic accumulation with warming. Nat. Clim. Chang. 5, 348–352. doi:10.1038/nclimate2574

CrossRef Full Text | Google Scholar

Garibotti, I. A., and Villalba, R. (2017). Colonization of mid- and late-Holocene moraines by lichens and trees in the Magellanic sub-Antarctic province. Polar Biol. 40, 1739–1753. doi:10.1007/s00300-017-2096-1

CrossRef Full Text | Google Scholar

Garreaud, R., Lopez, P., Minvielle, M., and Rojas, M. (2013). Large-scale control on the patagonian climate. J. Clim. 26, 215–230. doi:10.1175/JCLI-D-12-00001.1

CrossRef Full Text | Google Scholar

Glasser, N. F., Harrison, S., Schnabel, C., Fabel, D., and Jansson, K. N. (2012). Younger Dryas and early Holocene age glacier advances in Patagonia. Quat. Sci. Rev. 58, 7–17. doi:10.1016/j.quascirev.2012.10.011

CrossRef Full Text | Google Scholar

Golledge, N. R., Mackintosh, A. N. N., Anderson, B. M. M., Buckley, K. M. M., Doughty, A. M. M., Barrell, D. J. A. J. A., et al. (2012). Last glacial maximum climate in New Zealand inferred from a modelled southern Alps icefield. Quat. Sci. Rev. 46, 30–45. doi:10.1016/j.quascirev.2012.05.004

CrossRef Full Text | Google Scholar

Greve, R., and Blatter, H. (2009). Dynamics of ice sheets and glaciers. Springer.

Google Scholar

Gudmundsson, G. H. (1994). Converging glacier flow _ A case study: The unteraarglacier. Mitteilungen der Versuchsanstalt Fur wasserbau, hydrol. Und glaziologie an der Eidgenoss. Hochschule Zurich. Tech.

Google Scholar

Haddam, N. A., Siani, G., Michel, E., Kaiser, J., Lamy, F., Duchamp-Alphonse, S., et al. (2018). Changes in latitudinal sea surface temperature gradients along the Southern Chilean margin since the last glacial. Quat. Sci. Rev. 194, 62–76. doi:10.1016/j.quascirev.2018.06.023

CrossRef Full Text | Google Scholar

Harrison, S., Glasser, N. F., Duller, G. A. T., and Jansson, K. N. (2012). Early and mid-holocene age for the tempanos moraines, laguna san Rafael, patagonian Chile. Quat. Sci. Rev. 31, 82–92. doi:10.1016/j.quascirev.2011.10.015

CrossRef Full Text | Google Scholar

Hock, R. (2003). Temperature index melt modelling in mountain areas. J. Hydrol. X. 282, 104–115. doi:10.1016/S0022-1694(03)00257-9

CrossRef Full Text | Google Scholar

Hubbard, A., Hein, A. S., Kaplan, M. R., Hulton, N. R. J., and Glasser, N. (2005). A modelling reconstruction of the last glacial maximum ice sheet and its deglaciation in the vicinity of the northern patagonian icefield, south America. Geogr. Ann. Ser. A Phys. Geogr. 87, 375–391. doi:10.1111/j.0435-3676.2005.00264.x

CrossRef Full Text | Google Scholar

Hughes, A. L. C., Gyllencreutz, R., Lohne, Ø. S., Mangerud, J., and Svendsen, J. I. (2016). The last Eurasian ice sheets–a chronological database and time‐slice reconstruction, DATED‐1. Boreas 45, 1–45. doi:10.1111/bor.12142

CrossRef Full Text | Google Scholar

Hugonnet, R., McNabb, R., Berthier, E., Menounos, B., Nuth, C., Girod, L., et al. (2021). Accelerated global glacier mass loss in the early twenty-first century. Nature 592, 726–731. doi:10.1038/s41586-021-03436-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hulton, N. R. J., Purves, R. S., McCulloch, R. D., Sugden, D. E., and Bentley, M. J. (2002). The last glacial maximum and deglaciation in southern south America. Quat. Sci. Rev. 21, 233–241. doi:10.1016/S0277-3791(01)00103-2

CrossRef Full Text | Google Scholar

Hulton, N. R., Sugden, D. E., Payne, A., and Clapperton, C. (1994). Glacier modeling and the climate of Patagonia during the last glacial maximum. Quat. Res. 42, 1–19. doi:10.1006/qres.1994.1049

CrossRef Full Text | Google Scholar

Hutter, K. (1983). Theoretical glaciology, mathematical approaches to geophysics. D. D. Reidel.

Google Scholar

Inoue, J., Kondo, H., Fujiyoshi, Y., Yamada, T., and Fukami, H. (1987). Summer climate of the northern Patagonia icefield. Bull. glacier Res., 7–14.

Google Scholar

Iverson, N. R., Jansson, P., and Hooke, R. L. (1995). In-situ measurement of the strength of deforming subglacial till. J. Glaciol. 40, 497–503. doi:10.3189/s0022143000012375

CrossRef Full Text | Google Scholar

James, W. H. M., and Carrivick, J. L. (2016). Automated modelling of spatially-distributed glacier ice thickness and volume. Comput. Geosci. 92, 90–103. doi:10.1016/j.cageo.2016.04.007

CrossRef Full Text | Google Scholar

Jenny, B., Wilhelm, D., and Valero-Garcés, B. (2003). The Southern Westerlies in Central Chile: Holocene precipitation estimates based on a water balance model for Laguna Aculeo (33 50′ S). Clim. Dyn. 20, 269–280. doi:10.1007/s00382-002-0267-3

CrossRef Full Text | Google Scholar

Jouvet, G., Seguinot, J., Ivy-Ochs, S., and Funk, M. (2017). Modelling the diversion of erratic boulders by the Valais Glacier during the last glacial maximum. J. Glaciol. 63, 487–498. doi:10.1017/jog.2017.7

CrossRef Full Text | Google Scholar

Kaplan, M. R., Schaefer, J. M., Strelin, J. A., Denton, G. H., Anderson, R. F., Vandergoes, M. J., et al. (2016). Patagonian and southern south atlantic view of Holocene climate. Quat. Sci. Rev. 141, 112–125. doi:10.1016/j.quascirev.2016.03.014

CrossRef Full Text | Google Scholar

Kaplan, M. R., Strelin, J. A., Schaefer, J. M., Peltier, C., Martini, M. A., Flores, E., et al. (2020). Holocene glacier behavior around the northern Antarctic Peninsula and possible causes. Earth Planet. Sci. Lett. 534, 116077. doi:10.1016/j.epsl.2020.116077

CrossRef Full Text | Google Scholar

Kavan, J., Nývlt, D., Láska, K., Engel, Z., and Kňažková, M. (2020). High-latitude dust deposition in snow on the glaciers of James Ross Island, Antarctica. Earth Surf. Process. Landforms 45, 1569–1578. doi:10.1002/esp.4831

CrossRef Full Text | Google Scholar

Kilian, R., and Lamy, F. (2012). A review of Glacial and Holocene paleoclimate records from southernmost Patagonia (49–55°S). Quat. Sci. Rev. 53, 1–23. doi:10.1016/j.quascirev.2012.07.017

CrossRef Full Text | Google Scholar

Koppes, M., Conway, H., Rasmussen, L. A., and Chernos, M. (2011). Deriving mass balance and calving variations from reanalysis data and sparse observations, Glaciar San Rafael, northern Patagonia, 1950-2005. Cryosphere 5, 791–808. doi:10.5194/tc-5-791-2011

CrossRef Full Text | Google Scholar

Köse, O., Sarıkaya, M. A., Çiner, A., Candaş, A., Yıldırım, C., and Wilcken, K. M. (2022). Reconstruction of last glacial maximum glaciers and palaeoclimate in the central taurus range, Mt. Karanfil, of the eastern mediterranean. Quat. Sci. Rev. 291, 107656. doi:10.1016/j.quascirev.2022.107656

CrossRef Full Text | Google Scholar

Lang, H., and Braun, L. (1990). On the information content of air temperature in the context of snow melt estimation. Hydrol. Mt. Areas, 347–354.

Google Scholar

Lang, H. (1986). Forecasting meltwater runoff from snow-covered areas and from glacier basins. Dordrecht: Springer, 99–127. doi:10.1007/978-94-009-4536-4_5

CrossRef Full Text | Google Scholar

Leclercq, P. W., Pitte, P., Giesen, R. H., Masiokas, M. H., and Oerlemans, J. (2012). Modelling and climatic interpretation of the length fluctuations of Glaciar Frías (north Patagonian Andes, Argentina) 1639–2009 AD. Clim. Past. 8, 1385–1402. doi:10.5194/cp-8-1385-2012

CrossRef Full Text | Google Scholar

Lenaerts, J. T. M., Van Den Broeke, M. R., van Wessem, J. M., van de Berg, W. J., van Meijgaard, E., van Ulft, L. H., et al. (2014). Extreme precipitation and climate gradients in Patagonia revealed by high-resolution regional atmospheric climate modeling. J. Clim. 27, 4607–4621. doi:10.1175/jcli-d-13-00579.1

CrossRef Full Text | Google Scholar

Li, H., Ng, F., Li, Z., Qin, D., and Cheng, G. (2012). An extended “perfect-plasticity” method for estimating ice thickness along the flow line of mountain glaciers. J. Geophys. Res. 117, 1–11. doi:10.1029/2011JF002104

CrossRef Full Text | Google Scholar

Lowe, J. J., and Hoek, W. Z. (2001). Inter-regional correlation of palaeoclimatic records for the last glacial–interglacial transition: A protocol for improved precision recommended by the INTIMATE project group. Quat. Sci. Rev. 20, 1175–1187. doi:10.1016/S0277-3791(00)00183-9

CrossRef Full Text | Google Scholar

Mackintosh, A. N., Anderson, B. M., and Pierrehumbert, R. T. (2017). Reconstructing climate from glaciers. Annu. Rev. Earth Planet. Sci. 45, 649–680. doi:10.1146/annurev-earth-063016-020643

CrossRef Full Text | Google Scholar

Małecki, J. (2015). Snow accumulation on a small high‐arctic glacier svenbreen: Variability and topographic controls. Geogr. Ann. Ser. A Phys. Geogr. 97, 809–817. doi:10.1111/geoa.12115

CrossRef Full Text | Google Scholar

Mansilla, C. A., McCulloch, R. D., and Morello, F. (2016). Palaeoenvironmental change in southern Patagonia during the lateglacial and Holocene: Implications for forest refugia and climate reconstructions. Palaeogeogr. Palaeoclimatol. Palaeoecol. 447, 1–11. doi:10.1016/j.palaeo.2016.01.041

CrossRef Full Text | Google Scholar

Marden, C. J., and Clapperton, C. M. (1995). Fluctuations of the south patagonian ice-field during the last glaciation and the Holocene. J. Quat. Sci. 10, 197–209. doi:10.1002/jqs.3390100302

CrossRef Full Text | Google Scholar

Martin, J. R. V., Davies, B. J., and Thorndycraft, V. R. (2019). Glacier dynamics during a phase of Late Quaternary warming in Patagonia reconstructed from sediment-landform associations. Geomorphology 337, 111–133. doi:10.1016/j.geomorph.2019.03.007

CrossRef Full Text | Google Scholar

Martin, J. R. V., Thorndycraft, V. R., Davies, B. J., and Rodes, A. (2022). Rapid glacier recession at Monte san Lorenzo (Patagonia) in response to abrupt southern Hemisphere warming 13.0–12.0 ka BP. J. Quat. Sci. doi:10.1002/jqs.3463

CrossRef Full Text | Google Scholar

Martin, M. A., Winkelmann, R., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., et al. (2011). The potsdam parallel ice sheet model (PISM-PIK) – Part 2: Dynamic equilibrium simulation of the antarctic ice sheet. Cryosphere 5, 727–740. doi:10.5194/tc-5-727-2011

CrossRef Full Text | Google Scholar

Masiokas, M. H., Rivera, A., Espizua, L. E., Villalba, R., Delgado, S., and Aravena, J. C. (2009). Glacier fluctuations in extratropical South America during the past 1000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 281, 242–268. doi:10.1016/j.palaeo.2009.08.006

CrossRef Full Text | Google Scholar

Massaferro, J., Larocque-Tobler, I., Brooks, S. J., Vandergoes, M., Dieffenbacher-Krall, A., and Moreno, P. (2014). Quantifying climate change in Huelmo mire (Chile, Northwestern Patagonia) during the Last Glacial Termination using a newly developed chironomid-based temperature model. Palaeogeogr. Palaeoclimatol. Palaeoecol. 399, 214–224. doi:10.1016/j.palaeo.2014.01.013

CrossRef Full Text | Google Scholar

Massaferro, J., and Larocque-Tobler, I. (2013). Using a newly developed chironomid transfer function for reconstructing mean annual air temperature at Lake Potrok Aike, Patagonia, Argentina. Ecol. Indic. 24, 201–210. doi:10.1016/j.ecolind.2012.06.017

CrossRef Full Text | Google Scholar

McCulloch, R. D., Blaikie, J., Jacob, B., Mansilla, C. A., Morello, F., De Pol-Holz, R., et al. (2020). Late glacial and Holocene climate variability, southernmost Patagonia. Quat. Sci. Rev. 229, 106131. doi:10.1016/j.quascirev.2019.106131

CrossRef Full Text | Google Scholar

Meier, W. J.-H., Grießinger, J., Hochreuther, P., and Braun, M. H. (2018). An updated multi-temporal glacier inventory for the Patagonian Andes with changes between the Little Ice Age and 2016. Front. Earth Sci. 6, 1–21. doi:10.3389/feart.2018.00062

CrossRef Full Text | Google Scholar

Mendelová, M., Hein, A. S., Rodes, A., Smedley, R. K., and Xu, S. (2020). Glacier expansion in central Patagonia during the antarctic cold reversal followed by retreat and stabilisation during the younger dryas. Quat. Sci. Rev. 227, 106047. doi:10.1016/j.quascirev.2019.106047

CrossRef Full Text | Google Scholar

Menounos, B., Clague, J. J., Osborn, G., Davis, P. T., Ponce, F., Goehring, B., et al. (2013). Latest Pleistocene and Holocene glacier fluctuations in southernmost Tierra del Fuego, Argentina. Quat. Sci. Rev. 77, 70–79. doi:10.1016/j.quascirev.2013.07.008

CrossRef Full Text | Google Scholar

Mercer, J. H. (1976). Glacial history of southernmost South America. Quat. Res. 6, 125–166. doi:10.1016/0033-5894(76)90047-8

CrossRef Full Text | Google Scholar

Mercer, J. H. (1968). Variations of some patagonian glaciers since the late-glacial. Am. J. Sci. 266, 91–109. doi:10.2475/ajs.266.2.91

CrossRef Full Text | Google Scholar

Millan, R., Mouginot, J., Rabatel, A., and Morlighem, M. (2022). Ice velocity and thickness of the world’s glaciers. Nat. Geosci. 15, 124–129. doi:10.1038/s41561-021-00885-z

CrossRef Full Text | Google Scholar

Möller, M., Schneider, C., and Kilian, R. (2007). Glacier change and climate forcing in recent decades at Gran Campo Nevado, southernmost Patagonia. Ann. Glaciol. 46, 136–144. doi:10.3189/172756407782871530

CrossRef Full Text | Google Scholar

Morales, M. S., Cook, E. R., Barichivich, J., Christie, D. A., Villalba, R., LeQuesne, C., et al. (2020). Six hundred years of South American tree rings reveal an increase in severe hydroclimatic events since mid-20th century. Proc. Natl. Acad. Sci. U. S. A. 117, 16816–16823. doi:10.1073/pnas.2002411117

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno, P. I., François, J. P., Villa-Martínez, R. P., and Moy, C. M. (2009). Millennial-scale variability in Southern Hemisphere westerly wind activity over the last 5000 years in SW Patagonia. Quat. Sci. Rev. 28, 25–38. doi:10.1016/j.quascirev.2008.10.009

CrossRef Full Text | Google Scholar

Moreno, P. I. (2004). Millennial‐scale climate variability in northwest Patagonia over the last 15 000 yr. J. Quat. Sci. 19, 35–47. doi:10.1002/jqs.813

CrossRef Full Text | Google Scholar

Moreno, P. I. (2020). Timing and structure of vegetation, fire, and climate changes on the Pacific slope of northwestern Patagonia since the last glacial termination. Quat. Sci. Rev. 238, 106328. doi:10.1016/j.quascirev.2020.106328

CrossRef Full Text | Google Scholar

Moreno, P. I., Vilanova, I., Villa-Martínez, R., Dunbar, R. B., Mucciarone, D. A., Kaplan, M. R., et al. (2018). Onset and evolution of southern annular mode-like changes at centennial timescale. Sci. Rep. 8, 3458. doi:10.1038/s41598-018-21836-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, T. (1997). Assessing the paradigm shift: Deformable glacier beds. Quat. Sci. Rev. 16, 995–1016. doi:10.1016/S0277-3791(97)00030-9

CrossRef Full Text | Google Scholar

Nielsen, L. T., Aðalgeirsdóttir, G., Gkinis, V., Nuterman, R., and Hvidberg, C. S. (2018). The effect of a Holocene climatic optimum on the evolution of the Greenland ice sheet during the last 10 kyr. J. Glaciol. 64, 477–488. doi:10.1017/jog.2018.40

CrossRef Full Text | Google Scholar

Nimick, D. A., McGrath, D., Mahan, S. A., Friesen, B. A., and Leidich, J. (2016). Latest pleistocene and Holocene glacial events in the colonia valley, northern Patagonia icefield, southern Chile. J. Quat. Sci. 31, 551–564. doi:10.1002/jqs.2847

CrossRef Full Text | Google Scholar

Oehlerich, M., Mayr, C., Gussone, N., Hahn, A., Hölzl, S., Lücke, A., et al. (2015). Lateglacial and Holocene climatic changes in south-eastern Patagonia inferred from carbonate isotope records of Laguna Potrok Aike (Argentina). Quat. Sci. Rev. 114, 189–202. doi:10.1016/j.quascirev.2015.02.006

CrossRef Full Text | Google Scholar

Oerlemans, J. (2005). Extracting a climate signal from 169 glacier records. Science 308, 675–677. doi:10.1126/science.1107046

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohmura, A., Kasser, P., and Funk, M. (1992). Climate at the equilibrium line of glaciers. J. Glaciol. 38, 397–411. doi:10.1017/s0022143000002276

CrossRef Full Text | Google Scholar

Oien, R. P., Rea, B. R., Spagnolo, M., Barr, I. D., and Bingham, R. G. (2021). Testing the area–altitude balance ratio (AABR) and accumulation–area ratio (AAR) methods of calculating glacier equilibrium-line altitudes. J. Glaciol., 68, 357–368. doi:10.1017/jog.2021.100

CrossRef Full Text | Google Scholar

Osmaston, H. (2005). Estimates of glacier equilibrium line altitudes by the Area×Altitude, the Area×Altitude balance ratio and the Area×Altitude balance index methods and their validation. Quat. Int. 138–139, 22–31. doi:10.1016/j.quaint.2005.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Parizek, B. R., and Alley, R. B. (2004). Ice thickness and isostatic imbalances in the ross embayment, west Antarctica: Model results. Glob. Planet. Change 42, 265–278. doi:10.1016/J.GLOPLACHA.2003.09.005

CrossRef Full Text | Google Scholar

Paterson, W. S. B. (1994). The physics of glaciers, 480.

Google Scholar

Pedro, J. B., Bostock, H. C., Bitz, C. M., He, F., Vandergoes, M. J., Steig, E. J., et al. (2016). The spatial extent and dynamics of the Antarctic Cold Reversal. Nat. Geosci. 9, 51–55. doi:10.1038/ngeo2580

CrossRef Full Text | Google Scholar

Pellitero, R., Rea, B. R., Spagnolo, M., Bakke, J., Hughes, P., Ivy-Ochs, S., et al. (2015). A GIS tool for automatic calculation of glacier equilibrium-line altitudes. Comput. Geosci. 82, 55–62. doi:10.1016/j.cageo.2015.05.005

CrossRef Full Text | Google Scholar

Pellitero, R., Rea, B. R., Spagnolo, M., Bakke, J., Ivy-Ochs, S., Frew, C. R., et al. (2016). GlaRe, a GIS tool to reconstruct the 3D surface of palaeoglaciers. Comput. Geosci. 94, 77–85. doi:10.1016/j.cageo.2016.06.008

CrossRef Full Text | Google Scholar

Peltier, C., Kaplan, M. R., Birkel, S. D., Soteres, R. L., Sagredo, E. A., Aravena, J. C., et al. (2021). The large MIS 4 and long MIS 2 glacier maxima on the southern tip of South America. Quat. Sci. Rev. 262, 106858. doi:10.1016/j.quascirev.2021.106858

CrossRef Full Text | Google Scholar

Porter, P. R., Murray, T., and Dowdeswell, J. A. (1997). Sediment deformation and basal dynamics beneath a glacier surge front: Bakaninbreen, Svalbard. Ann. Glaciol. 24, 21–26. doi:10.3189/s0260305500011873

CrossRef Full Text | Google Scholar

Purdie, H. L., Brook, M. S., and Fuller, I. C. (2008). Seasonal variation in ablation and surface velocity on a temperate maritime glacier: Fox Glacier, New Zealand. Arct. Antarct. Alp. Res. 40, 140–147. doi:10.1657/1523-0430(06-032)[purdie]2.0.co;2

CrossRef Full Text | Google Scholar

Putnam, A. E. E., Schaefer, J. M. M., Denton, G. H. H., Barrell, D. J. A. J. A., Birkel, S. D. D., Andersen, B. G. G., et al. (2013). The last glacial maximum at 44°S documented by a 10Be moraine chronology at lake ohau, southern Alps of New Zealand. Quat. Sci. Rev. 62, 114–141. doi:10.1016/j.quascirev.2012.10.034

CrossRef Full Text | Google Scholar

Quade, J., and Kaplan, M. R. (2017). lake-level stratigraphy and geochronology revisited at Lago (lake) Cardiel, Argentina, and changes in the southern hemispheric westerlies over the last 25 ka. Quat. Sci. Rev. 177, 173–188. doi:10.1016/j.quascirev.2017.10.006

CrossRef Full Text | Google Scholar

Ramos, V. A., Niemeyer, H., Skarmeta, J., and Muñoz, J. (1982). Magmatic evolution of the austral patagonian Andes. Earth. Sci. Rev. 18, 411–443. doi:10.1016/0012-8252(82)90047-2

CrossRef Full Text | Google Scholar

Randolph Glacier Inventory Consortium, Arendt, A., Bliss, A., Bolch, T., Cogley, J. G., Gardner, A., et al. (2017). Randolph Glacier inventory–a dataset of global glacier outlines: Version 6.0: Technical report, global land ice measurements from space. Colorado, USA: Digit. Media.

Google Scholar

Rasmussen, S. O., Bigler, M., Blockley, S. P., Blunier, T., Buchardt, S. L., Clausen, H. B., et al. (2014). A stratigraphic framework for abrupt climatic changes during the last Glacial period based on three synchronized Greenland ice-core records: Refining and extending the INTIMATE event stratigraphy. Quat. Sci. Rev. 106, 14–28. doi:10.1016/j.quascirev.2014.09.007

CrossRef Full Text | Google Scholar

Rea, B. R. (2009). Defining modern day Area-Altitude Balance Ratios (AABRs) and their use in glacier-climate reconstructions. Quat. Sci. Rev. 28, 237–248. doi:10.1016/j.quascirev.2008.10.011

CrossRef Full Text | Google Scholar

Reynhout, S., Sagredo, E. A., Kaplan, M. R., Aravena, J. C., Martini, M. A., Moreno, P. I., et al. (2019). Holocene glacier fluctuations in Patagonia are modulated by summer insolation intensity and paced by Southern Annular Mode-like variability. Quat. Sci. Rev. 220, 178–187. doi:10.1016/j.quascirev.2019.05.029

CrossRef Full Text | Google Scholar

Ritz, C., Fabre, A., and Letréguilly, A. (1996). Sensitivity of a Greenland ice sheet model to ice flow and ablation parameters: Consequences for the evolution through the last climatic cycle. Clim. Dyn. 13, 11–23. doi:10.1007/s003820050149

CrossRef Full Text | Google Scholar

Rivera, A. (2004). Mass balance investigations at glaciar Chico, southern Patagonia icefield. Chile. South. Patagon. Icefield, Chile.

Google Scholar

Rodbell, D. T., Smith, J. A., and Mark, B. G. (2009). Glaciation in the Andes during the lateglacial and Holocene. Quat. Sci. Rev. 28, 2165–2212. doi:10.1016/j.quascirev.2009.03.012

CrossRef Full Text | Google Scholar

Sagredo, E. A., Kaplan, M. R., Araya, P. S., Lowell, T. V., Aravena, J. C., Moreno, P. I., et al. (2018). Trans-Pacific glacial response to the Antarctic Cold Reversal in the southern mid-latitudes. Quat. Sci. Rev. 188, 160–166. doi:10.1016/j.quascirev.2018.01.011

CrossRef Full Text | Google Scholar

Sagredo, E. A., Lowell, T. V., Kelly, M. A., Rupper, S., Aravena, J. C., Ward, D. J., et al. (2016). Equilibrium line altitudes along the Andes during the Last millennium: Paleoclimatic implications. Holocene 27, 1019–1033. doi:10.1177/0959683616678458

CrossRef Full Text | Google Scholar

Sagredo, E. A., Rupper, S., and Lowell, T. V. (2014). Sensitivities of the equilibrium line altitude to temperature and precipitation changes along the Andes. Quat. Res. 81, 355–366. doi:10.1016/j.yqres.2014.01.008

CrossRef Full Text | Google Scholar

Sato, A., Takahashi, S., Naruse, R., and Wakahama, G. (1984). Ablation and heat balance of the yukikabe snow patch in the daisetsu mountains, hokkaido, Japan. Ann. Glaciol. 5, 122–126. doi:10.3189/1984AoG5-1-122-126

CrossRef Full Text | Google Scholar

Scambos, T., Fahnestock, M., Moon, T., Gardner, A., and Klinger, M. (2016). Global land ice velocity extraction from Landsat 8 (Go-LIVE), version 1, 10. Boulder, Colorado USA: NSIDC Natl. Snow Ice Data Center, N5ZP442B.

Google Scholar

Schaefer, M., Machguth, H., Falvey, M., and Casassa, G. (2013). Modeling past and future surface mass balance of the Northern Patagonia Icefield. J. Geophys. Res. Earth Surf. 118, 571–588. doi:10.1002/jgrf.20038

CrossRef Full Text | Google Scholar

Schaefer, M., Machguth, H., Falvey, M., Casassa, G., and Rignot, E. (2015). Quantifying mass balance processes on the southern Patagonia icefield. Cryosphere 9, 25–35. doi:10.5194/tc-9-25-2015

CrossRef Full Text | Google Scholar

Schmidt, L. S., Ađalgeirsdóttir, G., Pálsson, F., Langen, P. L., Guđmundsson, S., and Björnsson, H. (2020). Dynamic simulations of Vatnajökull ice cap from 1980 to 2300. J. Glaciol. 66, 97–112. doi:10.1017/jog.2019.90

CrossRef Full Text | Google Scholar

Schneider, C., Glaser, M., Kilian, R., Santana, A., Butorovic, N., and Casassa, G. (2003). Weather observations across the southern Andes at 53°S. Phys. Geogr. 24, 97–119. doi:10.2747/0272-3646.24.2.97

CrossRef Full Text | Google Scholar

Schneider, C., Kilian, R., and Glaser, M. (2007). Energy balance in the ablation zone during the summer season at the gran Campo Nevado ice cap in the southern Andes. Glob. Planet. Change 59, 175–188. doi:10.1016/j.gloplacha.2006.11.033

CrossRef Full Text | Google Scholar

Schwikowski, M., Schläppi, M., Santibañez, P., Rivera, A., and Casassa, G. (2013). Net accumulation rates derived from ice core stable isotope records of Pío XI glacier, Southern Patagonia Icefield. Cryosphere 7, 1635–1644. doi:10.5194/tc-7-1635-2013

CrossRef Full Text | Google Scholar

Skvarca, P., and Naruse, R. (1997). “Dynamic behavior of glaciar Perito Moreno, southern Patagonia,” in Annals of glaciology. Editor I. M. Whillans, 24, 268–271.

CrossRef Full Text | Google Scholar

Stokes, C. R., Tarasov, L., Blomdin, R., Cronin, T. M., Fisher, T. G., Gyllencreutz, R., et al. (2015). On the reconstruction of palaeo-ice sheets: Recent advances and future challenges. Quat. Sci. Rev. 125, 15–49. doi:10.1016/j.quascirev.2015.07.016

CrossRef Full Text | Google Scholar

Strelin, J. A., and Malagnino, E. C. (2000). Late-glacial history of Lago argentino, Argentina, and age of the puerto bandera moraines. Quat. Res. 54, 339–347. doi:10.1006/qres.2000.2178

CrossRef Full Text | Google Scholar

Stuefer, M., Rott, H., and Skvarca, P. (2007). Glaciar Perito Moreno, Patagonia: Climate sensitivities and glacier characteristics preceding the 2003/04 and 2005/06 damming events. J. Glaciol. 53, 3–16. doi:10.3189/172756507781833848

CrossRef Full Text | Google Scholar

Sugden, D. E., Hulton, N. R. J., and Purves, R. S. (2002). Modelling the inception of the Patagonian icesheet. Quat. Int. 95, 55–64. doi:10.1016/s1040-6182(02)00027-7

CrossRef Full Text | Google Scholar

Takeuchi, Y., Naruse, R., and Skvarca, P. (1996). Annual air-temperature measurement and ablation estimate at Moreno Glacier, Patagonia. Bull. glacier Res. 14, 23–28.

Google Scholar

The PISM authors (2017). PISM, a parallel ice sheet model, manual version 1.0. Available at: https://pism-docs.org/sphinx/manual/.

Google Scholar

Thorndycraft, V. R., Bendle, J. M. J. M., Benito, G., Davies, B. J. B. J., Sancho, C., Palmer, A. P. A. P., et al. (2019). Glacial lake evolution and Atlantic-Pacific drainage reversals during deglaciation of the Patagonian Ice Sheet. Quat. Sci. Rev. 203, 102–127. doi:10.1016/j.quascirev.2018.10.036

CrossRef Full Text | Google Scholar

Tonello, M. S., Mancini, M. V., and Seppä, H. (2009). Quantitative reconstruction of Holocene precipitation changes in southern Patagonia. Quat. Res. 72, 410–420. doi:10.1016/j.yqres.2009.06.011

CrossRef Full Text | Google Scholar

Van Daele, M., Bertrand, S., Meyer, I., Moernaut, J., Vandoorne, W., Siani, G., et al. (2016). Late Quaternary evolution of Lago Castor (Chile, 45.6° S): Timing of the deglaciation in northern Patagonia and evolution of the southern westerlies during the last 17 kyr. Quat. Sci. Rev. 133, 130–146. doi:10.1016/j.quascirev.2015.12.021

CrossRef Full Text | Google Scholar

Van Pelt, W. J. J., and Oerlemans, J. (2012). Numerical simulations of cyclic behaviour in the parallel ice sheet model (PISM). J. Glaciol. 58, 347–360. doi:10.3189/2012jog11j217

CrossRef Full Text | Google Scholar

Villa-Martínez, R., Moreno, P. I., and Valenzuela, M. A. (2012). Deglacial and postglacial vegetation changes on the eastern slopes of the central Patagonian Andes (47°S). Quat. Sci. Rev. 32, 86–99. doi:10.1016/j.quascirev.2011.11.008

CrossRef Full Text | Google Scholar

Villalba, R., Masiokas, M. H., Kitzberger, T., and Boninsegna, J. A. (2005). “Biogeographical consequences of recent climate changes in the southern Andes of Argentina,” in Global change and mountain regions (Springer), 157–166.

CrossRef Full Text | Google Scholar

Waldmann, N., Ariztegui, D., Anselmetti, F. S., Coronato, A., and Austin, J. A. (2010). Geophysical evidence of multiple glacier advances in Lago Fagnano (54°S), southernmost Patagonia. Quat. Sci. Rev. 29, 1188–1200. doi:10.1016/j.quascirev.2010.01.016

CrossRef Full Text | Google Scholar

Weidemann, S. S., Sauter, T., Malz, P., Jaña, R., Arigony-Neto, J., Casassa, G., et al. (2018). glacier mass changes of lake-terminating grey and Tyndall glaciers at the southern Patagonia icefield derived from geodetic observations and energy and mass balance modeling. Front. Earth Sci. 6, 81. doi:10.3389/feart.2018.00081

CrossRef Full Text | Google Scholar

Weis, M., Greve, R., and Hutter, K. (1999). Theory of shallow ice shelves. Contin. Mech. Thermodyn. 11, 15–50. doi:10.1007/s001610050102

CrossRef Full Text | Google Scholar

Whitlock, C., Moreno, P. I., and Bartlein, P. (2007). Climatic controls of Holocene fire patterns in southern South America. Quat. Res. 68, 28–36. doi:10.1016/j.yqres.2007.01.012

CrossRef Full Text | Google Scholar

Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., et al. (2011). The potsdam parallel ice sheet model (PISM-PIK) – Part 1: Model description. Cryosphere 5, 715–726. doi:10.5194/tc-5-715-2011

CrossRef Full Text | Google Scholar

Yan, Q., Owen, L. A., Wang, H., and Zhang, Z. (2018). Climate constraints on glaciation over high-mountain asia during the last glacial maximum. Geophys. Res. Lett. 45, 9024–9033. doi:10.1029/2018GL079168

CrossRef Full Text | Google Scholar

Žebre, M., Sarıkaya, M. A., Stepišnik, U., Colucci, R. R., Yıldırım, C., Çiner, A., et al. (2021). An early glacial maximum during the last glacial cycle on the northern Velebit Mt. (Croatia). Geomorphology 392, 107918. doi:10.1016/j.geomorph.2021.107918

CrossRef Full Text | Google Scholar

Zemp, M., Huss, M., Thibert, E., Eckert, N., McNabb, R., Huber, J., et al. (2019). Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 568, 382–386. doi:10.1038/s41586-019-1071-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Ziemen, F. A., Hock, R., Aschwanden, A., Khroulev, C., Kienholz, C., Melkonian, A., et al. (2016). Modeling the evolution of the juneau icefield between 1971 and 2100 using the parallel ice sheet model (PISM). J. Glaciol. 62, 199–214. doi:10.1017/jog.2016.13

CrossRef Full Text | Google Scholar