Key Processes on Triggering the Moderate 2020/21 La Niña Event as Depicted by the Clustering Approach

The 2020/21 La Niña was not well predicted by most climate models when it started in early-mid 2020. This paper adopted an El Niño-Southern Oscillation (ENSO) ensemble prediction system to evaluate the key physical processes in the development of this cold event by performing a clustering analysis of 100 ensemble member predictions 1 year in advance. The abilities of two clustering approaches were first examined in regard to capturing the development of the 2020/21 La Niña event. One approach was index clustering, which adopted only the 12-month Niño3.4 indices in 2020 as an indicator, and the other was pattern clustering through contrasting the evolution of sea surface temperature (SST) anomalies over the tropical Pacific in 2020 for clustering. Pattern clustering surpasses index clustering in better describing the evolution over the off-equatorial and equatorial regions during the 2020/21 La Niña. Consequently, based on the pattern clustering approach, a comparison of the selected most (five best) and least (five worst) representative ensemble members illustrated that the predominance of anomalous southeasterly winds over the central equatorial Pacific in spring 2020 played a crucial role in initiating the moderate La Niña event in 2020/21, by preventing the development of westerly winds over the warm pool. Moreover, the inherent spring predictability barrier (SPB) was still a major challenge for improving the prediction skill of the 2020/21 La Niña event when the prediction occurred across the spring season.

Introduction

The El Niño-Southern Oscillation (ENSO), the largest interannual signal in the climate system, is a typical coupled atmosphere-ocean phenomenon with time scales of approximately 2–7 years (Ren et al., 2020). ENSO not only affects weather and climate anomalies in the equatorial Pacific but also affects other parts of the world through atmospheric teleconnections (Trenberth et al., 1998); therefore, successful prediction of ENSO has always been a hot topic (Luo et al., 2016; Song et al., 2021).

Since the 1960s, domestic and foreign scholars have established numerous theories regarding the onset and development of ENSO (Bjerknes, 1969; Wyrtki, 1975; Jin, 1997; Weisberg and Wang, 1997; Picaut et al., 1997); these theories offer much assistance in predicting and studying ENSO. With the increase in computing power and the introduction of techniques such as data assimilation (Evensen, 2004; Zheng and Zhu, 2010), current climate models can realize the effective prediction of El Niño and La Niña events 6–12 months in advance (Jin et al., 2008; Barnston et al., 2012; Ludescher et al., 2013; Zhang and Gao, 2016; Zheng and Zhu, 2016; Ren et al., 2017; 2020; Zhang et al., 2020). However, there are also many problems in ENSO prediction, such as ENSO diversity (Xie et al., 2018; Ren et al., 2018) which indicates that various and complex forcing and feedback mechanisms exist throughout the entire process of ENSO onset and development (Kang et al., 2017), and this diversity still cannot be described well by current coupled models (Cai et al., 2018). Moreover, ENSO prediction skills were lower in the 2000s than in the 1980s or 1990s (Barnston et al., 2012; Zheng et al., 2016), even with an increase in ocean observations, especially in the equatorial tropical Pacific (Kumar et al., 2015). In addition, due to asymmetric ENSO features, the predictability between El Niño and La Niña events is distinctively different (Hu et al., 2019). First, the successful prediction of La Niña has not received the same attention as that of El Niño (Barnston et al., 2012). Feng et al. (2015) recognized that La Niña events are less predictable because of their weaker intensity and more features; Larson and Kirtman (2019) pointed out that El Niño events are more predictable from the aspect of the signal-to-noise ratio. Furthermore, most current models have a faster decline across the boreal spring in the prediction skill of La Niña events than for El Niño events (Lopez and Kirtman 2014).

The 2020/21 La Niña was not well predicted by most climate models when it started in early mid 2020 (IRI website at https://iri.columbia.edu/), which indicates that the onset and development of this event were complicated and that this event is worth exploring carefully. Furthermore, Zheng et al. (2021) pointed out that the 2020/21 La Niña event was responsible for the extremely cold winter in China, but they did not describe the key processes in this event and generally attributed them to atmospheric and oceanic processes. In this work, we utilized a clustering approach called pattern clustering because it is better and more reasonable for depicting the physical evolution of the tropical Pacific when compared with the traditional clustering approach called index clustering. This paper attempted to compare the information in an ENSO ensemble prediction system between the best and worst prediction members obtained by pattern clustering and found characteristics and key processes for this event. The paper is organized as follows: In Section 2, the selected model, data sources and methods are described. In Section 3, the comparison of the two clustering approaches is discussed. In Section 4, the main results through pattern clustering are reported. Finally, in Section 5, a conclusion and discussion are given.

Model, Datasets and Methods

Model

This paper adopted the ENSO ensemble prediction system (EPS) developed at the Institute of Atmospheric Physics (IAP), Chinese Academy of Sciences (Zheng et al., 2006; Zheng et al., 2009; Zheng and Zhu, 2016), to evaluate the key processes of the 2020/21 La Niña event. This system utilizes the ensemble Kalman filter (EnKF) data assimilation method (Zheng and Zhu, 2010), which is based on an intermediate coupled model, and establishes ENSO real-time prediction (Zheng and Zhu, 2015) by taking the initial uncertainty and the uncertainty in the prediction process into account (Zheng et al., 2009). The implementation of a 20-year retrospective 12-month ensemble forecast experiment proved that the EPS can successfully predict the possibility of ENSO events 1 year in advance (Zheng and Zhu, 2016).

Datasets

Based on this model using the same initial conditions but different stochastic model error perturbations, we obtained 100 ensemble members that predict a 12-month lead from January 2020. The prediction results contained monthly data of physical quantities such as the sea surface temperature anomaly (SSTA), 20°C isotherm depth anomaly (Z20), zonal wind stress anomaly (Tauxa), and meridional wind stress anomaly (Tauya). This dataset has a longitude interval of 2° and an unequal latitude interval of 0.5°. The SSTA in the observation data was derived from the monthly extended reconstruction of SST data (ERSST v5) (Huang et al., 2017), with a horizontal resolution of 2°, and the monthly wind stress data were from the NECP–DOE (National Centers for Environmental Prediction–Department of Energy) Reanalysis II (Kanamitsu et al., 2002), with a global T62 Gaussian grid (192 × 94).

Methods

Clustering analysis, a statistical approach, is widely used in ENSO research and related studies. Cassou and Terray (2001) pointed out the asymmetrical role of El Niño and La Niña in influencing the winter atmospheric variability of the North Atlantic/Europe using K-means clustering. Singh and Delcroix (2013) indicated that the EP El Niño (maximum anomalous warm center in the equatorial eastern Pacific) and CP El Niño (same as EP El Niño but in the equatorial central Pacific) have different recharge and discharge processes through hierarchical clustering analysis. Zhao et al. (2020), using clustering analysis, demonstrated that the Pacific meridional mode (PMM) has two types, which have different characteristics on the impact of ENSO. As a classification method in machine learning, clustering usually includes K-nearest neighbor (KNN) clustering, K-means clustering and hierarchical clustering. In this paper, the principle of the KNN clustering algorithm was adopted; that is, we selected the k-training samples nearest to the input sample in the feature space, and we could also select abnormal values compared with the input sample. Therefore, this paper aims to find the closest and farthest prediction members to the observations. The distance between the prediction members and observation sample is calculated based on the Euclidean distance. The calculation formula is as follows:

${\mathit{d}}_{\mathit{ij}}\mathrm{=}\sqrt{{\displaystyle \sum _{\mathit{k=1}}^{\mathit{p}}{\mathrm{(}{\mathit{x}}_{\mathit{ik}}\mathrm{-}{\mathit{x}}_{\mathit{jk}}\mathrm{)}}^{\mathrm{2}}}}(1)$

In this formula, i and j represent two different samples, which can be regarded as the prediction and observation, respectively, k represents the corresponding elements between the two samples, and p is the total number of samples.

To obtain members closer to the observations from the ensemble members, two different clustering approaches were adopted, namely, index clustering and pattern clustering. The former was based on 12-month Niño3.4 (170°W-120°W, 5°S-5°N) indices for clustering to obtain different degrees of similarity in the actual evolution of the Niño3.4 index among ensemble members and only utilized the SSTA-based index for clustering, called as index clustering. The latter realized clustering by using the 12-month Pacific anomalous SST (120°E-80°W, 30°S-30°N) evolution, and it is referred to pattern clustering. At the same time, this paper adopted principal component analysis (PCA) which is an unsupervised machine learning method commonly used in dimensionality reduction, to reduce the amount of calculation of pattern clustering. In this work, we regarded the 12-month Pacific SSTA field as a whole, which was the input of the PCA, and extracted an explanation variance of 90% to represent the evolution of the 12-month Pacific SSTA. Finally, the output of PCA was performed for clustering analysis.

The Ability of Index Clustering and Pattern Clustering to Represent La Niña’s Development in 2020/21

As indicated by Zheng et al. (2021), the moderate 2020/21 La Niña event originated from the cold SSTA of the equatorial eastern Pacific in May 2020, gaining strength and spreading westward under the easterly wind anomaly in the autumn, and since October 2020, the Niño3.4 index exceeded −1.0°C and reached its peak in the boreal winter.

To find ensemble members that were closer to the development of the 2020/21 La Niña event, this paper utilized two clustering approaches (index clustering and pattern clustering) to obtain the top five best ensemble members, which were mostly similar to the observations, called the best prediction members (Figure 1). On the one hand, the ensemble mean of the model indicated that the equatorial Pacific developed into an El Niño event in 2020, while in reality it developed into a La Niña event, which was completely opposite of the observations, illustrating that the model starting from January also failed to predict the 2020/21 La Niña event. On the other hand, the best members selected by the two clustering approaches had temporal variations in the Niño3.4 index similar to the observations, and there were few obvious differences in index evolution between the two methods. Furthermore, it was necessary to find a better method, such as the evolution of sea surface temperature or the wind field, to distinguish these two approaches.

FIGURE 1

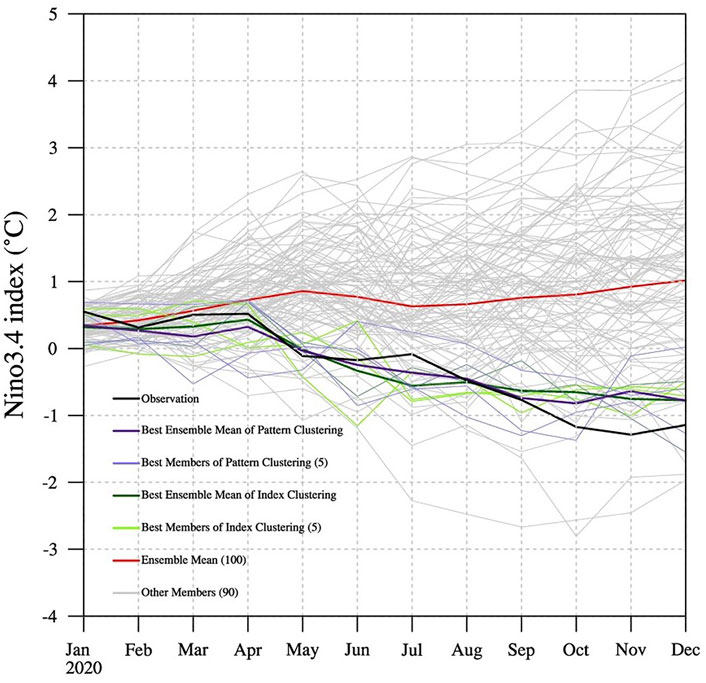
FIGURE 1. The temporal variation in the Niño3.4 index in 2020 of the observations (black line) and of the best prediction members selected by the two clustering methods. The red line represents the ensemble mean from all 100 ensemble members. The green lines represent the best five ensemble members (light) with the ensemble-mean forecast (dark) selected by index clustering, the purple lines represent the best five ensemble members (light) with the ensemble-mean forecast (dark) selected by pattern clustering, and other gray lines are other residual ensemble members.

The SSTA distributions obtained by the two clustering approaches were further explored, and we not only paid attention to the evolution of the SSTA within the equator (Figure 2) but also showed the evolutionary characteristics of the SSTA outside the equator (Figure 3). The onset time of this La Niña event was May 2020 based on observations of the anomalous development of the cold SSTA of this La Niña event within the equator as mentioned in previous work (Zheng et al., 2021). The cold SSTA gradually spread westward over time, reaching La Niña status (i.e., the Niño 3.4 index exceeded -0.5°C) in August, and approached its peak in November 2020, forming a moderate La Niña event (Figure 1). The cold anomaly center was located near 135°W, and the entire equatorial western Pacific always had a warm SSTA. Both clustering approaches could show the cold SSTA in the equatorial central and eastern Pacific in the boreal winter of 2020, but only pattern clustering could describe westward propagation of the cold SSTA, which was closer to the realistic 2020/21 La Niña evolution, while the variation in the cold SSTA in index clustering tended to be locally generated in the central equatorial Pacific. In addition, when describing the anomalous sea temperature in the western equatorial Pacific, index clustering from March to June obviously had a cold SSTA, which was somewhat different from the actual situation.

FIGURE 2

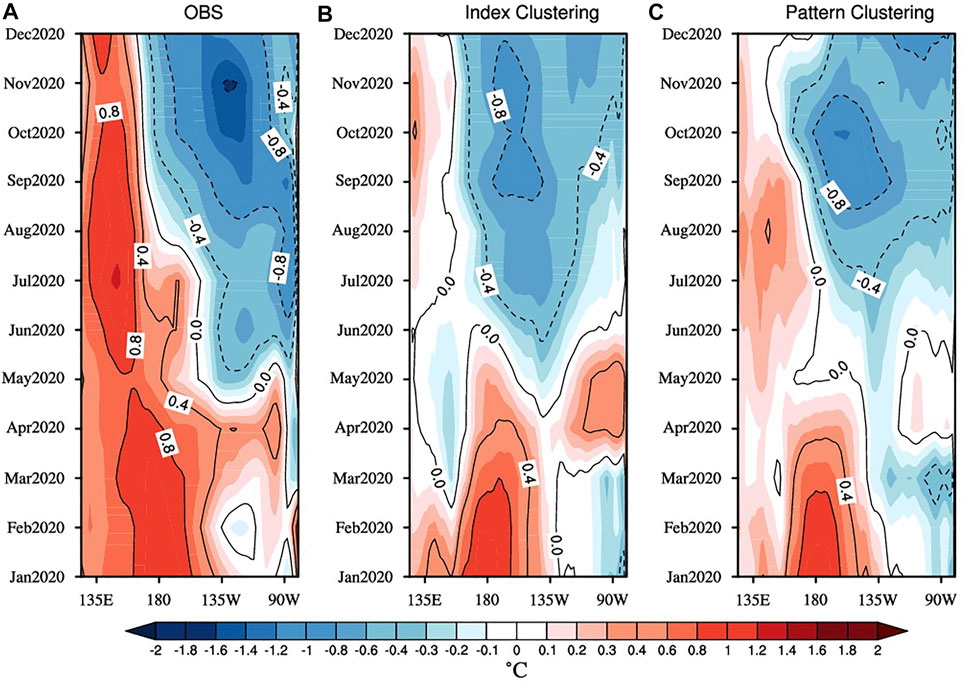
FIGURE 2. Temporal evolution of the SSTA along the equatorial Pacific (averaged between 5°S and 5°N) in 2020 for (A) observations, (B) the ensemble mean of the best prediction members by index clustering, and (C) the ensemble mean of the best prediction members by pattern clustering. The contour interval is 0.4°C.

FIGURE 3

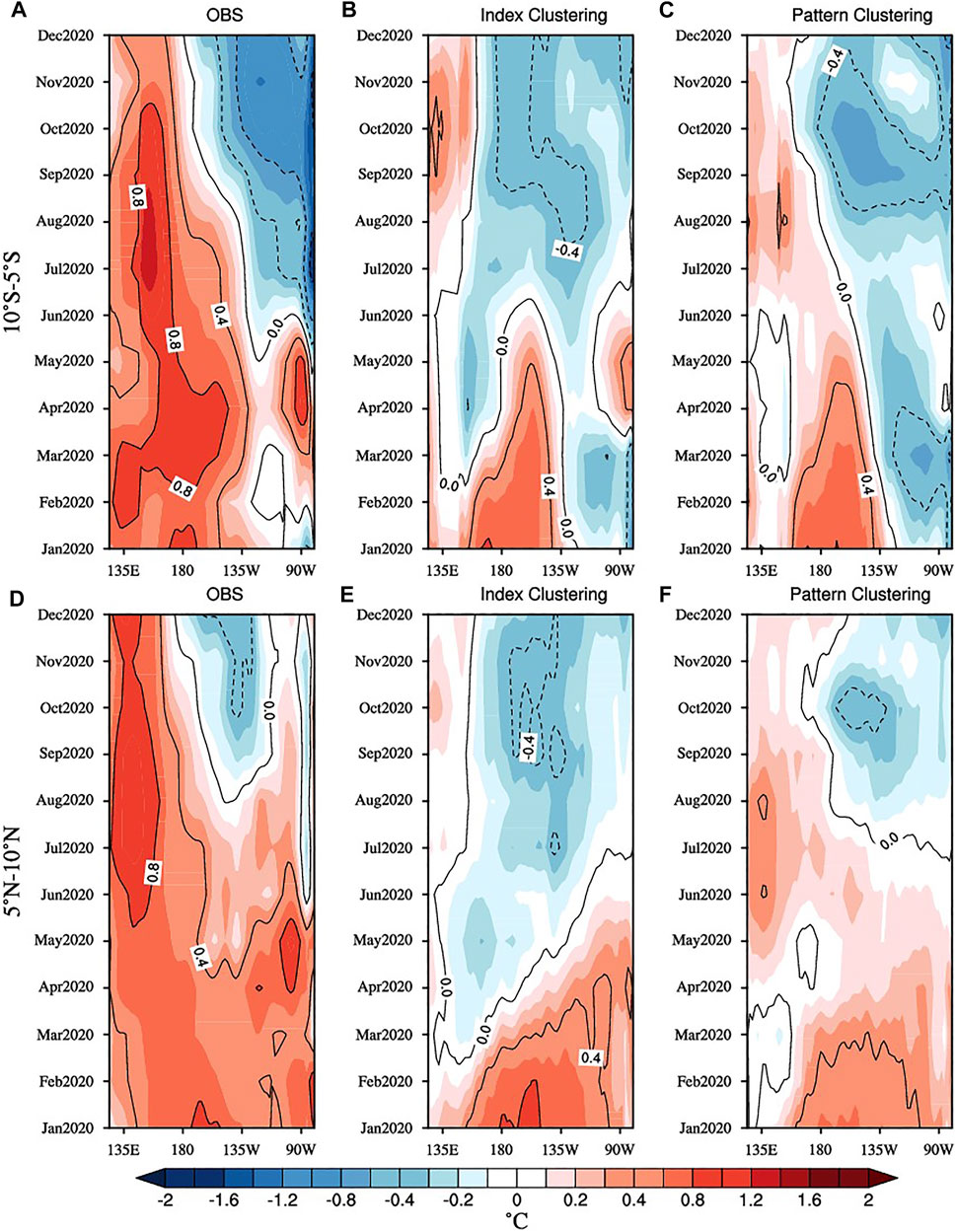
FIGURE 3. Temporal evolution of the SSTA along the off-equatorial Pacific (averaged between 10°S and 5°S and between 5°N and 10°N) in 2020 for (A,D) observations, (B,E) the ensemble mean of the best prediction members by index clustering, and (C,F) the ensemble mean of the best prediction members by pattern clustering. The contour interval is 0.4°C.

Furthermore, from the evolution of the SSTA outside the equator, we also found that there were apparent differences between the two clustering approaches (Figure 3). First, in observing the evolutionary characteristics of the SSTA south and north of the equator (Figures 3A,D), we found that the cold SSTA south of the equator began to spread westward from June, which corresponded to the time when the cold SSTA in the equator began to develop. For the two clustering approaches, index clustering compared with pattern clustering had two propagation paths of a cold SSTA south of the equator (Figures 3B,E) and eastward propagation of a cold SSTA north of the equator (Figures 3C,F), which were both inconsistent with the observational facts. Therefore, the best members selected by pattern clustering were closer to the observations regardless of observing the variation in the SSTA within or outside the equator.

To further examine the differences between the two clustering approaches from another perspective, we focused on the evolution of the anomalous wind field. Since the cold SSTA south of the equator mentioned above was closely related to this La Niña event, the variation in the anomalous wind field south of the equator was mainly considered (Figure 4). The mean wind anomalies in Figures 4B,C were obtained by the ensemble mean of the best prediction members in index clustering and pattern clustering based on SSTA differences, respectively. From observations, it could be found that the eastern Pacific in the Southern Hemisphere basically maintained a state of southerly wind anomaly, which was conducive to transporting cold water south of the equator to the equator. For the two clustering approaches, even though the prediction results of wind stress were weaker than the observations (Zheng and Zhu, 2016), from the difference map (pattern clustering minus index clustering), it could be determined that the best prediction members selected by pattern clustering could better reflect the southerly wind anomaly, especially in the area near 135°W. In summary, regardless of the evolution of the SSTA or of the anomalous wind field, pattern clustering was more in line with the observational facts and was more conducive to discussing the developmental characteristics of this event.

FIGURE 4

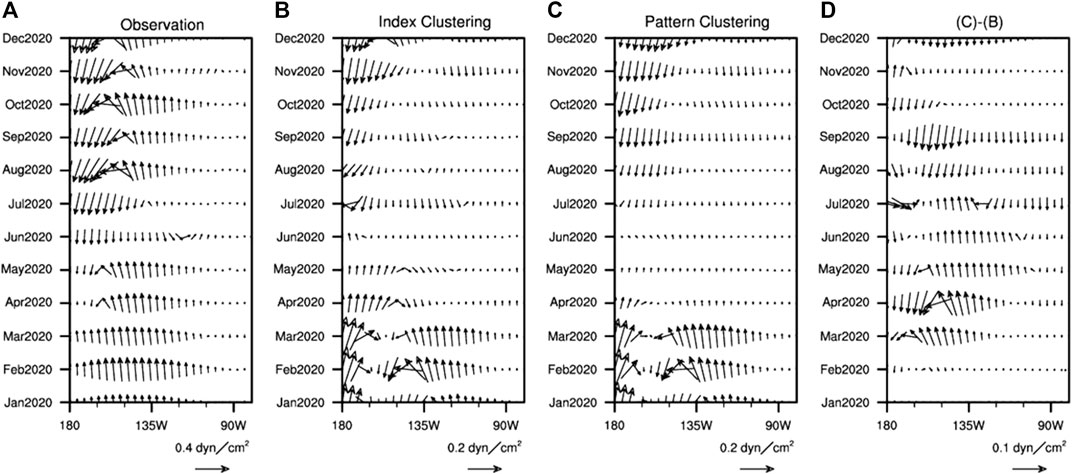
FIGURE 4. Temporal evolution of wind stress anomalies along the equatorial Pacific (averaged between 10°S and EQ) in 2020 for (A) observations, (B) the ensemble mean of the best prediction members by index clustering, (C) the ensemble mean of the best prediction members by pattern clustering, and (D) ensemble mean of the best prediction members by pattern clustering minus ensemble mean of the best prediction members by index clustering (i.e., (C)–(B)).

Key Processes of the 2020/21 La Niña Event Revealed by Pattern Clustering

Based on the above comparison, this paper utilized pattern clustering to select the best and worst prediction members, and the evolution of the Niño3.4 index of the two sets is shown in Figure 5. Through the comparison of the best and worst prediction members, we could analyze which key process could trigger this La Niña event. First, the prediction results of the evolution of the SSTA and anomalous wind field from January to May for the best and worst prediction members are displayed in Figure 6. From the observations, the entire equatorial Pacific was warm in the west and cold in the east in January, and it was one of the structures most likely to produce the “spring predictability barrier” (SPB) (Webster and Yang, 1992; Yu et al., 2009), a phenomenon in which most ENSO prediction models suffer a sharp decrease in prediction skill across the spring season (Latif et al., 1994). Currently, the SPB is still a major challenge in ENSO prediction (Zheng and Yu, 2017). When we focused on the variation in the Niño 3.4 index of the ensemble mean and observations (Figure 1), apparent discrepancies appeared after spring, which displayed an obvious SPB phenomenon in the 2020/21 La Niña event. Second, even under the action of an easterly wind anomaly in the eastern equatorial Pacific, the development of the cold SSTA in this area was interrupted from January to March, mainly because the strength of the coupled ocean-atmosphere system is weak in boreal spring, which is one of the possible reasons for the SPB phenomenon (Zebiak and Cane, 1987; Webster, 1995). Therefore, it is difficult to have good coordination between the wind field and sea temperature. After spring, the cold SSTA developed again and was accompanied by the transportation of cold water south of the equator. In summary, this event actually exhibited a characteristic: the uncoordinated ocean-atmosphere configuration structure formed by the large-scale warm SSTA in the western equatorial Pacific and the general easterly wind anomaly in the equatorial region. This uncoordinated ocean-atmosphere coupled structure appeared in spring and was superimposed on the weak coupled strength of the ocean-atmosphere, which further increased the difficulty of prediction starting at this time, and it may be one of the reasons why many models starting in spring failed to predict the 2020/2021 La Niña event. From the perspective of the best and worst prediction members, there were two completely opposite development situations, that is, the best (worst) prediction members showed the gradual weakening (strengthening) of the westerly wind anomaly in the western equatorial Pacific, and correspondingly showed that this anamaly was beneficial to the development of the cold (warm) SSTA in the equatorial eastern Pacific; therefore, the different variation of the Niño3.4 index between the best and worst prediction members formed two totally opposite events (Figure 5).

FIGURE 5

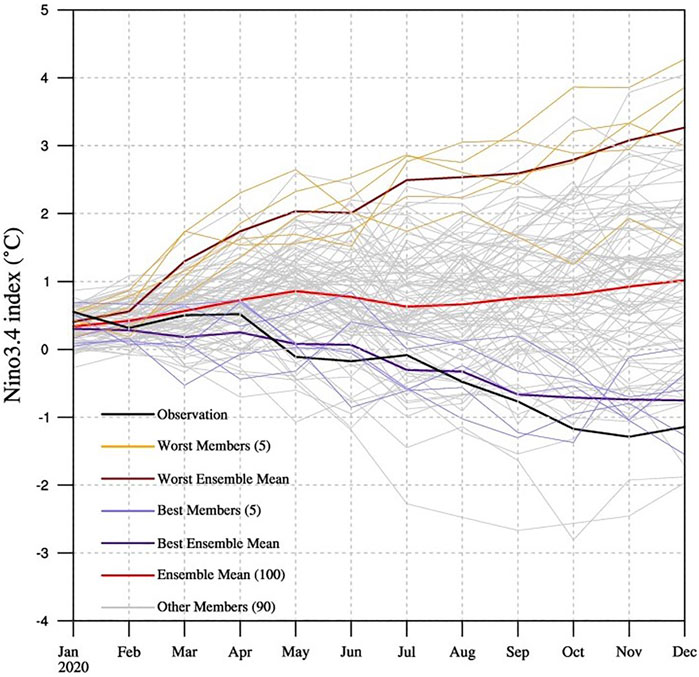
FIGURE 5. The temporal variation in the Niño3.4 index in 2020 of observations (black line) and of the best and worst prediction members selected by pattern clustering. The red line represents the ensemble mean from all 100 ensemble members. The purple lines represent the best five ensemble members (light) with the best ensemble-mean forecast (dark), the orange lines represent the worst five ensemble members with the worst ensemble-mean forecast (dark red line), and the gray lines represent other ensemble members.

FIGURE 6

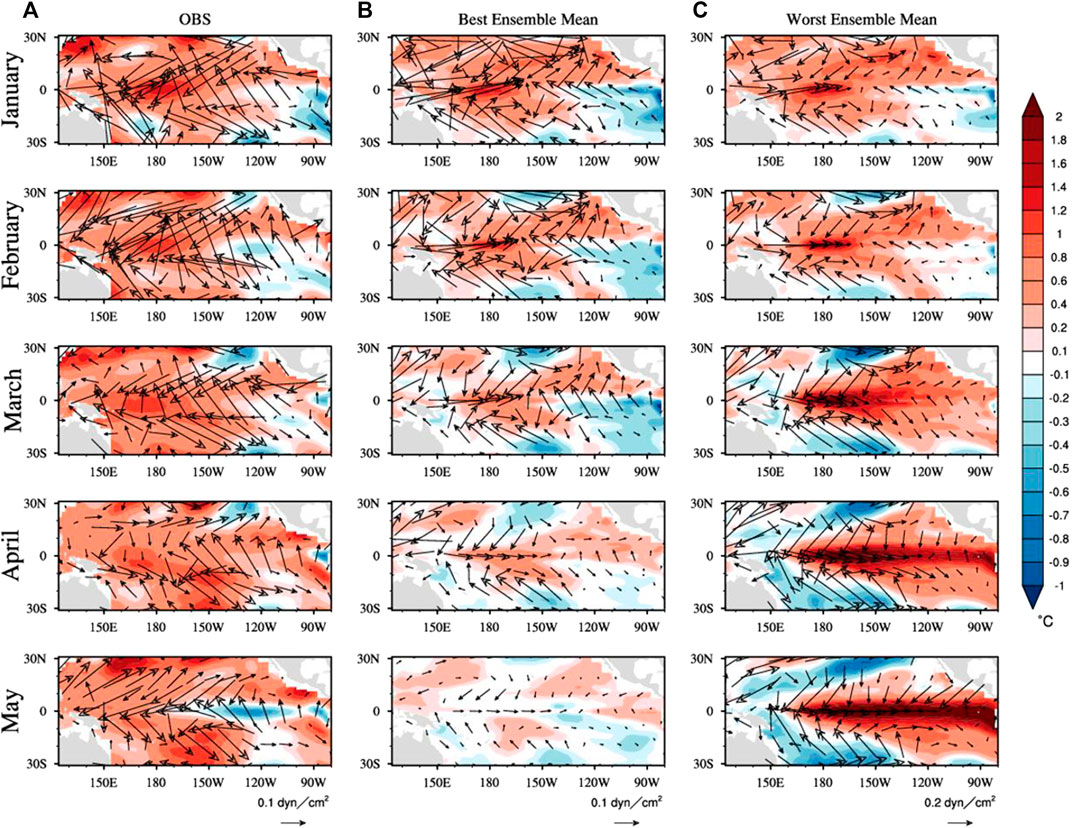
FIGURE 6. Temporal evolution of wind stress anomalies (vectors) and SSTA (shading) (30°S-30°N, 120°E-80°W) from January to May 2020 [(A): observations; (B): the ensemble mean of the best prediction members by pattern clustering; and (C): the ensemble mean of the worst prediction members by pattern clustering].

We further explored the reason for the opposite development of the best prediction members and the worst prediction members using pattern clustering. Figure 6 shows that in January, the ocean-atmosphere configuration (wide range of warm SSTA in the tropical Pacific and westerly wind anomaly in the western Pacific) of the best and worst prediction members can easily develop into the state of El Niño, and the cold SSTA in the eastern equatorial Pacific was relatively weak compared with the large-scale warm SSTA; however, the configuration developed into the La Niña event in the best prediction members. One possible reason for this development may be that its cold SSTA in the eastern equatorial Pacific was obviously stronger than the worst prediction members in January 2020 (Figure 6). Furthermore, we analyzed the Hovmoller diagrams (Figure 7), which are profile diagrams first proposed by Hovmöller in 1949 to reflect the temporal variation of atmospheric variables (Hovmöller, 1949) and are now widely used in the analysis of zonal or meridional variation characteristics of ENSO events (Feng et al., 2015; Lian et al., 2017; Lian and Chen, 2021; Hu et al., 2019; Zheng et al., 2021). At the starting time of the forecast (January 2020), the most obvious differences between the worst prediction members and the best prediction members in the four variables (Taux, Tauy, SSTA, and Z20) were the cold SSTA located in the southeast Pacific. Even though there were southerly wind anomalies in this region, the cold SSTA of the worst prediction members was weaker than that of the best prediction members. It was easier for the cold SSTA of the best prediction members to occupy the equatorial region, thereby establishing the Bjerknes feedback (Bjerknes, 1969), leading to the westward development of cold SSTA in the eastern equatorial region, weakening the westerly wind anomaly, and thus establishing the easterly wind anomaly. Therefore, the best prediction members successfully predicted that the cold SSTA in the southeast Pacific explained why the best and worst prediction members had completely opposite development directions.

FIGURE 7

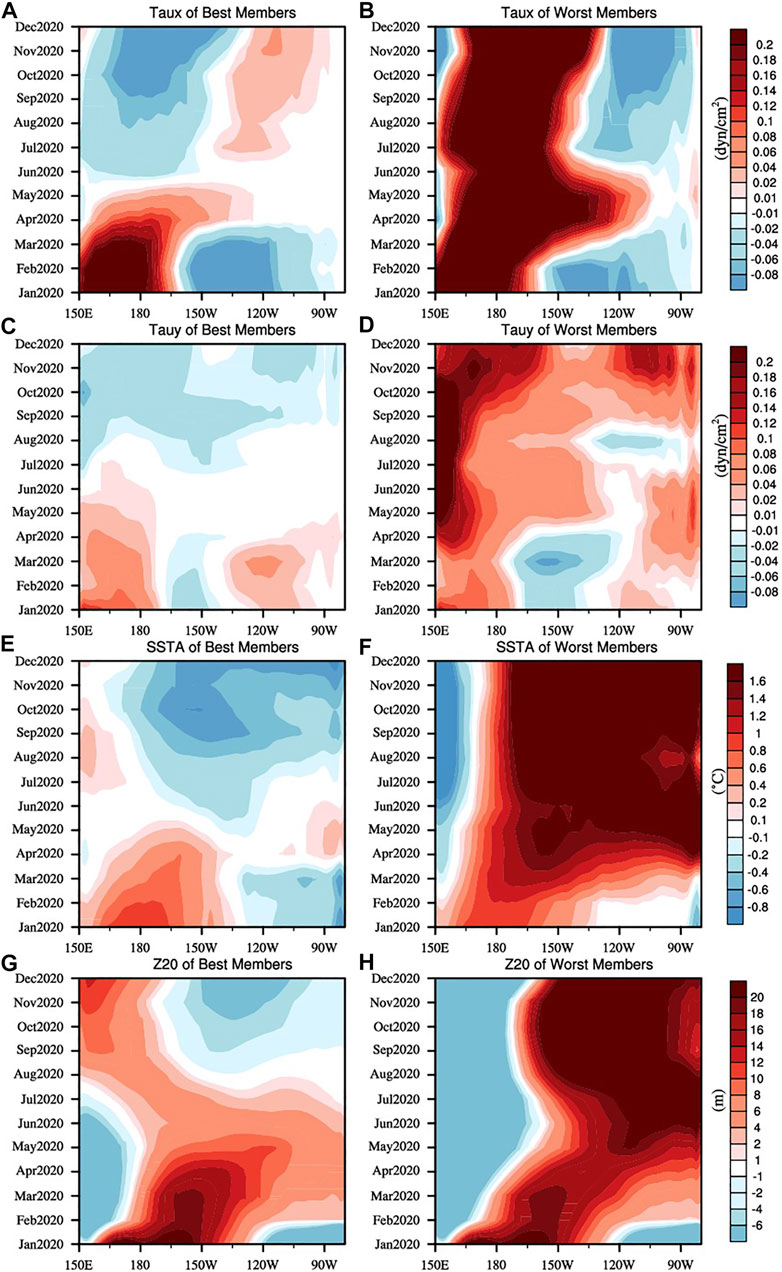
FIGURE 7. Temporal variation of Taux, Tauy, SSTA, and Z20 of the ensemble mean of the best prediction members (i.e., (A,C,E,G)) and the worst prediction members by pattern clustering (i.e. (B,D,F,H)) along the 10°S to the equator.

Moreover, the discrepancies between the best and worst prediction members deserve further discussion to determine the specific time and sequence of apparent differences in variables (Taux, Tauy, SSTA, and Z20) and to further find the different roles of the atmosphere and ocean in the development of this La Niña event. Therefore, the difference diagrams along the equatorial Pacific (from 5°S to 5°N) between the best prediction members and the worst prediction members are shown in Figure 8 (ensemble mean of the best prediction members minus ensemble mean of the worst prediction members). Based on the discussion above, the anomalous cold water from the best prediction members in the southeast Pacific flowed into the equatorial region under the impact of the southerly wind anomaly, and by February, there were differences in SSTA compared with the worst prediction members. The atmosphere responded quickly to the differences; Figure 8 shows the negative and positive values of the anomalous zonal wind and meridional wind, respectively, and the most obvious areas of the differences were near the date line. Therefore, for the best prediction members, it manifested as the strengthening of a southeasterly wind anomaly near the date line, and it was this anomalous wind field condition that was conducive to the appearance of the cold SSTA in the central and eastern equatorial Pacific and the northward transportation of cold water south of the equator. Correspondingly, apparent differences in the thermocline depth anomaly appeared after spring. The discrepancies between the best and worst prediction members emerged in the spring season. On the one hand, this was the result of the cold SSTA in the Southern Hemisphere under the influence of the southerly wind anomaly, and on the other hand, it actually reflected the SPB phenomenon of this model in this cold event. Furthermore, the differences between the best and worst prediction members also emphasized the dominant role of surface signals in the development of the moderate 2020/21 La Niña event.

FIGURE 8

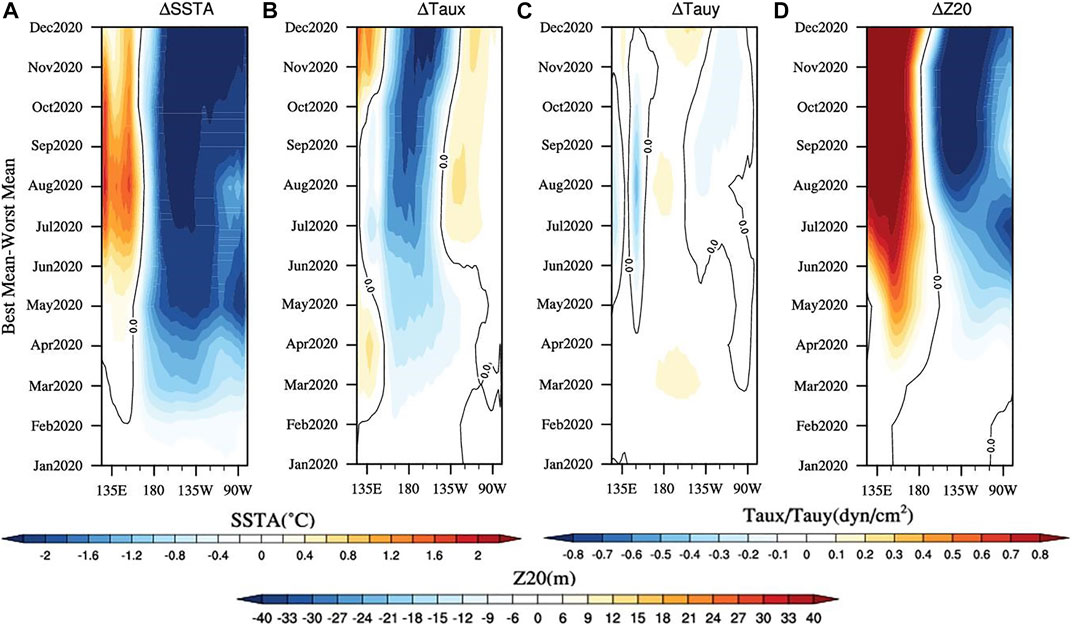
FIGURE 8. Temporal evolution of the differences (ensemble mean of the best prediction members minus ensemble mean of the worst prediction members) of four variables along the equatorial Pacific (averaged between 5°S and 5°N) in 2020 for (A) ΔSSTA, (B) ΔTaux, (C) ΔTauy, and (D) ΔZ20.

Discussion and Conclusion

Clustering using traditional index types could not accurately describe the evolution of the entire event, and clustering analysis using the evolution of the anomalous sea temperature field (120°E-80°W, 30°S-30°N) better fit the physical changes of the actual event; for such a coupled system, both the SSTA field and the anomalous wind field showed a better fit with the observation. The development of the 2020/21 La Niña event had an obvious SPB. In spring, there was an obvious inconsistency in ocean-atmosphere coordination, and the strength of the coupled ocean-atmosphere system was weak; therefore, the cold SSTA in the equatorial eastern Pacific in spring did not develop even under the action of an easterly wind anomaly, leading to the occurrence of cold-warm-cold variation in the SSTA in the equatorial eastern Pacific. This uncoordinated coupled ocean-atmosphere structure explains the failure of many models starting in the spring of 2020 to predict the event and indicates its complexity. The best members predicted by pattern clustering were closer to the actual observations, indicating that the development of this event was closely related to the cold SSTA south of the equator and the southeasterly wind anomaly in this region, which were the key processes of the 2020/21 La Niña event and the reason for opposite development between the best prediction members and the worst prediction members. Previous works (Min et al., 2017; Hua and Su, 2020) demonstrated that the important role of the southeast Pacific in the prediction of the ENSO event, and the failure to predict the cold SSTA in the southeast Pacific among the worst prediction members may be the reason for the obvious SPB phenomenon in this model. Moreover, this event also showed the dominant role of the surface signals.

A very obvious difference between the ensemble mean and the observation after spring (Figure 1) is the apparent performance of the SPB of this model, that is, the prediction skills suffer a sharp decline after the spring season, and at the same time, as mentioned in previous discussions, the atmosphere-ocean configuration of the equatorial Pacific in early 2020 was uncoordinated, which made it more difficult to determine the development direction of this event. Therefore, the prediction results starting in January are worthwhile for analyzing the specific performance and role of the SPB phenomenon in this event. From the discussion of the best and worst prediction members, it was found that successful predictions for the cold SSTA in the southeast Pacific would be extremely beneficial in overcoming the SPB phenomenon, thereby significantly improving prediction skills across the spring season, though only for this cold event.

In this work, we highlighted the importance of the SPB in predicting the 2020/21 La Niña event and the primary role of surface signals in the development of this event. However, this paper only explained the key processes of this event from a qualitative perspective, and the specific role of the wind field needs further study. At the same time, when comparing the best and worst prediction members by pattern clustering, apparent differences appeared in the spring season, and the relationship between this and the SPB and whether all of the obvious differences in each prediction of the ensemble prediction system appeared in spring are worthy of further exploration.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://psl.noaa.gov/data/gridded/data.noaa.ersst.v5.html; and https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.gaussian.html.

Author Contributions

W-TC is mainly responsible for the drawing of the paper graphics and article writing, and FZ is mainly responsible for the supply of data, the construction and revision of the paper, furthermore, H-XF is responsible for the revision and comment of the paper.

Funding

This work was supported by the Key Research Program of Frontier Sciences, CAS (Grant No. ZDBS-LY-DQC010), the National Natural Science Foundation of China (Grant Nos. 41876012; 42175045), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB42000000).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barnston, A. G., Tippett, M. K., L'Heureux, M. L., Li, S., and DeWitt, D. G. (2012). Skill of Real-Time Seasonal ENSO Model Predictions during 2002-11: Is Our Capability Increasing. Bull. Amer. Meteorol. Soc. 93 (5), 631–651. doi:10.1175/BAMS-D-11-00111.1

CrossRef Full Text | Google Scholar

Bjerknes, J. (1969). Atmospheric Teleconnections from the Equatorial Pacific. Mon. Wea. Rev. 97 (3), 163–172. doi:10.1175/1520-0493(1969)097<0163:atftep>2.3.co;2

CrossRef Full Text | Google Scholar

Cai, W., Wang, G., Dewitte, B., Wu, L., Santoso, A., Takahashi, K., et al. (2018). Increased Variability of Eastern Pacific El Niño under Greenhouse Warming. Nature 564 (7735), 201–206. doi:10.1038/s41586-018-0776-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Cassou, C., and Terray, L. (2001). Dual Influence of Atlantic and Pacific SST Anomalies on the North Atlantic/Europe winter Climate. Geophys. Res. Lett. 28 (16), 3195–3198. doi:10.1029/2000GL012510

CrossRef Full Text | Google Scholar

Evensen, G. (2004). Sampling Strategies and Square Root Analysis Schemes for the EnKF. Ocean Dyn. 54 (6), 539–560. doi:10.1007/s10236-004-0099-2

CrossRef Full Text | Google Scholar

Feng, L., Zheng, F., Zhu, J., and Liu, H. (2015). The Role of Stochastic Model Error Perturbations in Predicting the 2011/12 Double-Dip La Niña. SOLA 11, 65–69. doi:10.2151/sola.2015-014

CrossRef Full Text | Google Scholar

Hovmöller, E. (1949). The Trough-And-Ridge Diagram. Tellus 1 (2), 62–66. doi:10.1111/j.2153-3490.1949.tb01260.x

CrossRef Full Text | Google Scholar

Hu, J., Duan, W., and Zhou, Q. (2019). Season-dependent Predictability and Error Growth Dynamics for La Niña Predictions. Clim. Dyn. 53, 1063–1076. doi:10.1007/s00382-019-04631-5

CrossRef Full Text | Google Scholar

Hua, L.-J., and Su, J.-Z. (2020). Southeastern Pacific Error Leads to Failed El Niño Forecasts. Geophy. Res. Lett. 47 (17). doi:10.1029/2020GL008764

CrossRef Full Text | Google Scholar

Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., et al. (2017). Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 30 (20), 8179–8205. doi:10.1175/JCLI-D-16-0836.1

CrossRef Full Text | Google Scholar

Jin, E. K., Kinter, J. L., Wang, B., Park, C.-K., Kang, I.-S., Kirtman, B. P., et al. (2008). Current Status of ENSO Prediction Skill in Coupled Ocean-Atmosphere Models. Clim. Dyn. 31 (6), 647–664. doi:10.1007/s00382-008-0397-3

CrossRef Full Text | Google Scholar

Jin, F.-F. (1997). An Equatorial Ocean Recharge Paradigm for ENSO. Part I: Conceptual Model. J. Atmos. Sci. 54 (7), 811–829. doi:10.1175/1520-0469(1997)054<0811:AEORPF>2.0.CO;2

CrossRef Full Text | Google Scholar

Kanamitsu, M., Ebisuzaki, W., Woollen, J., Yang, S.-K., Hnilo, J. J., Fiorino, M., et al. (2002). NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Amer. Meteorol. Soc. 83 (11), 1631–1644. doi:10.1175/BAMS-83-11-1631

CrossRef Full Text | Google Scholar

Kang, X., Zhang, R.-H., Gao, C., and Zhu, J. (2017). An Improved ENSO Simulation by Representing Chlorophyll-Induced Climate Feedback in the NCAR Community Earth System Model. Sci. Rep. 7 (1), 17123. doi:10.1038/s41598-017-17390-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, A., Chen, M., Xue, Y., and Behringer, D. (2015). An Analysis of the Temporal Evolution of ENSO Prediction Skill in the Context of the Equatorial Pacific Ocean Observing System. Mon. Wea. Rev. 143 (8), 3204–3213. doi:10.1175/MWR-D-15-0035.1

CrossRef Full Text | Google Scholar

Larson, S. M., and Kirtman, B. P. (2019). Linking Preconditioning to Extreme ENSO Events and Reduced Ensemble Spread. Clim. Dyn. 52, 7417–7433. doi:10.1007/s00382-017-3791-x

CrossRef Full Text | Google Scholar

Latif, M., Barnett, T. P., Cane, M. A., Flügel, M., Graham, N. E., von Storch, H., et al. (1994). A Review of ENSO Prediction Studies. Clim. Dyn. 9 (4-5), 167–179. doi:10.1007/bf00208250

CrossRef Full Text | Google Scholar

Lian, T., and Chen, D. (2021). The Essential Role of Early-spring westerly Wind Burst in Generating the Centennial Extreme 1997/98 El Niño. J. Clim. 34 (20), 1–38. doi:10.1175/JCLI-D-21-0010.1

CrossRef Full Text | Google Scholar

Lian, T., Tang, Y., Zhou, L., Islam, S. U., Zhang, C., Li, X., et al. (2017). Westerly Wind Bursts Simulated in CAM4 and CCSM4. Clim. Dyn. 50 (3-4), 1353–1371. doi:10.1007/s00382-017-3689-7

CrossRef Full Text | Google Scholar

Lopez, H., and Kirtman, B. P. (2014). WWBs, ENSO Predictability, the spring Barrier and Extreme Events. J. Geophys. Res. Atmos. 119 (17), 114–210. doi:10.1002/2014JD021908

CrossRef Full Text | Google Scholar

Ludescher, J., Gozolchiani, A., Bogachev, M. I., Bunde, A., Havlin, S., and Schellnhuber, H. J. (2013). Improved El Nino Forecasting by Cooperativity Detection. Proc. Natl. Acad. Sci. 110 (29), 11742–11745. doi:10.1073/PNAS.1309353110

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, J.-J., Yuan, C., Sasaki, W., Behera, S. K., Masumoto, Y., Yamagata, T., et al. (2016). Current Status of Intraseasonal–Seasonal-To-Interannual Prediction of The Indo-Pacific Climate. Indo-Pacific Clim. Variability Predictability,World Scientific Ser. Asia-Pacific Weather Clim. 7, 63–107. doi:10.1142/9789814696623_0003

CrossRef Full Text | Google Scholar

Min, Q., Su, J., and Zhang, R. (2017). Impact of the South and North Pacific Meridional Modes on the El Niño-Southern Oscillation: Observational Analysis and Comparison. J. Clim. 30 (5), 1705–1720. doi:10.1175/JCLI-D-16-0063.1

CrossRef Full Text | Google Scholar

Picaut, J., Masia, F., and du Penhoat, Y. (1997). An Advective-Reflective Conceptual Model for the Oscillatory Nature of the ENSO. Science 277 (5326), 663–666. doi:10.1126/science.277.5326.663

CrossRef Full Text | Google Scholar

Ren, H.-L., Jin, F.-F., Song, L., Lu, B., Tian, B., Zuo, J., et al. (2017). Prediction of Primary Climate Variability Modes at the Beijing Climate Center. J. Meteorol. Res. 31 (1), 204–223. doi:10.1007/s13351-017-6097-3

CrossRef Full Text | Google Scholar

Ren, H.-L., Scaife, A. A., Dunstone, N., Tian, B., Liu, Y., Ineson, S., et al. (2018). Seasonal Predictability of winter ENSO Types in Operational Dynamical Model Predictions. Clim. Dyn. 52, 3869–3890. doi:10.1007/s00382-018-4366-1

CrossRef Full Text | Google Scholar

Ren, H.-L., Zheng, F., Luo, J.-J., Wang, R., Liu, M., Zhang, W., et al. (2020). A Review of Research on Tropical Air-Sea Interaction, ENSO Dynamics, and ENSO Prediction in China. J. Meteorol. Res. 34 (1), 43–62. doi:10.1007/s13351-020-9155-1

CrossRef Full Text | Google Scholar

Singh, A., and Delcroix, T. (2013). Eastern and central Pacific ENSO and Their Relationships to the Recharge/discharge Oscillator Paradigm. Deep Sea Res. Oceanographic Res. Pap. 82, 32–43. doi:10.1016/J.DSR.2013.08.002

CrossRef Full Text | Google Scholar

Song, Y., Shu, Q., Bao, Y., Yang, X., and Song, Z. (2021). The Short-Term Climate Prediction System FIO-CPS v2.0 and its Prediction Skill in ENSO. Front. Earth Sci. 9. doi:10.3389/feart.2021.759339

CrossRef Full Text | Google Scholar

Trenberth, K. E., Branstator, G. W., Karoly, D., Kumar, A., Lau, N.-C., and Ropelewski, C. (1998). Progress during TOGA in Understanding and Modeling Global Teleconnections Associated with Tropical Sea Surface Temperatures. J. Geophys. Res. 103 (C7), 14291–14324. doi:10.1029/97JC01444

CrossRef Full Text | Google Scholar

Webster, P. J. (1995). The Annual Cycle and the Predictability of the Tropical Coupled Ocean-Atmosphere System. Meteorl. Atmos. Phys. 56 (1-2), 33–55. doi:10.1007/BF01022520

CrossRef Full Text | Google Scholar

Webster, P. J., and Yang, S. (1992). Monsoon and ENSO: Selectively Interactive Systems. Q.J R. Met. Soc. 118 (507), 877–926. doi:10.1002/QJ.49711850705

CrossRef Full Text | Google Scholar

Weisberg, R. H., and Wang, C. (1997). A Western Pacific Oscillator Paradigm for the El Niño-Southern Oscillation. Geophys. Res. Lett. 24 (7), 779–782. doi:10.1029/97GL00689

CrossRef Full Text | Google Scholar

Wyrtki, K. (1975). El Niño-The Dynamic Response of the Equatorial Pacific Oceanto Atmospheric Forcing. J. Phys. Oceanogr. 5 (4), 572–584. doi:10.1175/1520-0485(1975)005<0572:ENTDRO>2.0.CO;2

CrossRef Full Text | Google Scholar

Xie, S.-P., Peng, Q., Kamae, Y., Zheng, X.-T., Tokinaga, H., and Wang, D. (2018). Eastern Pacific ITCZ Dipole and ENSO Diversity. J. Clim. 31 (11), 4449–4462. doi:10.1175/JCLI-D-17-0905.1

CrossRef Full Text | Google Scholar

Yu, Y., Duan, W., Xu, H., and Mu, M. (2009). Dynamics of Nonlinear Error Growth and Season-dependent Predictability of El Niño Events in the Zebiak-Cane Model. Q.J.R. Meteorol. Soc. 135 (645), 2146–2160. doi:10.1002/QJ.526

CrossRef Full Text | Google Scholar

Zebiak, S. E., and Cane, M. A. (1987). A Model El Niñ-Southern Oscillation. Mon. Wea. Rev. 115 (10), 2262–2278. doi:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2

CrossRef Full Text | Google Scholar

Zhang, R.-H., and Gao, C. (2016). The IOCAS Intermediate Coupled Model (IOCAS ICM) and its Real-Time Predictions of the 2015-2016 El Niño Event. Sci. Bull. 61 (13), 1061–1070. doi:10.1007/s11434-016-1064-4

CrossRef Full Text | Google Scholar

Zhang, R.-H., Yu, Y., Song, Z., Ren, H.-L., Tang, Y., Qiao, F., et al. (2020). A Review of Progress in Coupled Ocean-Atmosphere Model Developments for ENSO Studies in China. J. Ocean. Limnol. 38 (4), 930–961. doi:10.1007/s00343-020-0157-8

CrossRef Full Text | Google Scholar

Zhao, J., Kug, J.-S., Park, J.-H., and An, S.-I. (2020). Diversity of Pacific Meridional Mode and its Distinct Impacts on El Niño-Southern Oscillation. Geophys. Res. Lett. 47 (19), doi:10.1029/2020gl088993

CrossRef Full Text | Google Scholar

Zheng, F., Fang, X. H., Zhu, J., Yu, J. Y., and Li, X. C. (2016). Modulation of Bjerknes Feedback on the Decadal Variations in ENSO Predictability. Geophys. Res. Lett. 43 (24), 12560–12568. doi:10.1002/2016GL071636

CrossRef Full Text | Google Scholar

Zheng, F., and Yu, J.-Y. (2017). Contrasting the Skills and Biases of Deterministic Predictions for the Two Types of El Niño. Adv. Atmos. Sci. 34 (12), 1395–1403. doi:10.1007/s00376-017-6324-y

CrossRef Full Text | Google Scholar

Zheng, F., Yuan, Y., Ding, Y., Li, K., Fang, X., Zhao, Y., et al. (2021). Extreme Cold Events from East Asia to North America in Winter 2020/21. Adv. Atmos. Sci.. doi:10.1007/s00376-021-1033-y

CrossRef Full Text | Google Scholar

Zheng, F., and Zhu, J. (2010). Coupled Assimilation for an Intermediated Coupled ENSO Prediction Model. Ocean Dyn. 60 (5), 1061–1073. doi:10.1007/s10236-010-0307-1

CrossRef Full Text | Google Scholar

Zheng, F., and Zhu, J. (2016). Improved Ensemble-Mean Forecasting of ENSO Events by a Zero-Mean Stochastic Error Model of an Intermediate Coupled Model. Clim. Dyn. 47 (12), 3901–3915. doi:10.1007/s00382-016-3048-0

CrossRef Full Text | Google Scholar

Zheng, F., and Zhu, J. (2015). Roles of Initial Ocean Surface and Subsurface States on Successfully Predicting 2006-2007 El Niño with an Intermediate Coupled Model. Ocean Sci. 11 (1), 187–194. doi:10.5194/os-11-187-2015

CrossRef Full Text | Google Scholar

Zheng, F., Zhu, J., Wang, H., and Zhang, R.-H. (2009). Ensemble Hindcasts of ENSO Events over the Past 120 Years Using a Large Number of Ensembles. Adv. Atmos. Sci. 26 (2), 359–372. doi:10.1007/s00376-009-0359-7

CrossRef Full Text | Google Scholar

Zheng, F., Zhu, J., Zhang, R.-H., and Zhou, G.-Q. (2006). Ensemble Hindcasts of SST Anomalies in the Tropical Pacific Using an Intermediate Coupled Model. Geophys. Res. Lett. 33 (19), L19604. doi:10.1029/2006GL026994

CrossRef Full Text | Google Scholar