Study on Long-Term Variation Characteristics of Geomagnetic Cutoff Rigidities of Energetic Protons Caused by Long-Term Variation of Geomagnetic Field

As a parameter that quantitatively measures the shielding effect of the Earth’s magnetic field on energetic particles, the geomagnetic cutoff rigidities will change significantly with the long-term change of geomagnetic field. In this article, by using the numerical simulation method, combined with the variation trend of the Earth’s main field International Geomagnetic Reference Field (IGRF) model and the energetic particles’ windows (EPWs), the variation characteristics of the cutoff rigidities of geomagnetic energetic particles in the vertical direction from 1965 to 2025 were studied. The study found that there is a close relationship between the cutoff latitude corresponding to the cutoff rigidities and the background magnetic field intensity, but they are not in a simple linear relationship. The changes of the cutoff rigidities and geomagnetic field in the northern and southern hemispheres are asymmetric. The weakening of the geomagnetic field will push the cutoff latitudes toward the near equatorial region in the southern hemisphere, but for northern hemisphere the phenomenon is not always credible. In the northern hemisphere, the areas of EPWs will decrease at a relative rate of 0.03%/yr, but in the southern hemisphere, it will increase at a rate of about 0.05%/yr to 0.12%/yr. The long-term trajectory of the positions of the EPWs’ central points do not correspond to geomagnetic poles, nor the magnetic dip poles, relatively speaking, its position is closer to the geomagnetic poles. The study can be used for a long-term forecasting of cutoff rigidities caused by background geomagnetic field variations.

1 Introduction

Energetic particles play a useful key-role in space weather storms forecasting (Mavromichalaki et al., 2006) and in the specification of magnetic properties of coronal mass ejections (CMEs), shocks, and ground level enhancements (GLEs). Meanwhile, the ionosphere and atmosphere of the Earth can be affected by the energetic particles which enter the magnetosphere at low altitudes (Nesse Tyssøy et al., 2013; Galand, 2001). Furthermore, energetic particles are major space weather phenomena that can produce hazardous effects in the near-Earth space environment. Understanding the physical processes of the energetic particles has both scientific and practical significance, considering their serious impact on the space environment and space systems (e.g., harming the spacecrafts in the inner magnetosphere) (Koons et al., 1998; Baker and D., 2000). Therefore, the study of the coupling mechanism between interplanetary and magnetospheric energetic particles is an important issue in solar terrestrial space physics.

Energetic protons are the main component of cosmic rays, and the interplanetary energetic particles can penetrate the protective layer of electronic components, resulting in single-event inversion, which poses a threat to the health of astronauts. At the same time, it will also reduce the service life of solar cells and affect polar short wave communication. In serious cases, it will cause damage to electronic components, cause satellite failure, and even completely destroy the satellite (Baker and D, 2000; Koons et al., 1998). Also, the variation of the energetic particle environment can affect the airplane routes across the polar region (Alken et al., 2020). Also, some researchers found that the cosmic rays can affect the climate (Kirkby, 2007), which will have a long-term variation.

The access of energetic protons into the magnetosphere is controlled by the magnetic field. As the first barrier of the Earth, the geomagnetic field can effectively prevent the entry of interplanetary energetic particles and reduce the radiation of energetic particles in near-Earth space. Störmer (1955) first theoretically described the behavior by assuming that the magnetic field is a dipole field. In a pure dipole magnetic field, particles are shielded by a potential barrier from an inner forbidden region whose boundary is defined by the following equation as (Störmer, 1955):

$r=\sqrt{\frac{Mq}{mvc}}\frac{{\cos }^2\lambda }{1+\sqrt{1+{\cos }^3\lambda }},(1)$

where M is the dipole moment, λ is the geomagnetic latitude, r is the radial distance from the center of the dipole with the unit of r being Re (the Earth radii), m is the mass, c is the speed of light, q is the charge of particles, and v is the particle speed. In order to predict the energetic particles transporting to a specific location through the magnetosphere, the concept of geomagnetic rigidity is used. The geomagnetic rigidity is defined as R = mvc/q. As a parameter that quantitatively measures the shielding effect of the Earth’s magnetic field on energetic particles, the geomagnetic cutoff rigidity describes the rigidities threshold of energetic charged particles when they pass through the geomagnetic shielding effect and reach the observation points (Smart and Shea, 2005). From Eq. 1, the cutoff rigidity at any point in space can be expressed as

$R\left(\text{GV}\right)=\frac{C}{r^2}\frac{{\cos }^4\lambda }{{\left(1+\sqrt{1+{\cos }^3\lambda }\right)}^2},(2)$

where constant C = 60 is derived by the dipole model (Kress et al., 2010), and GV is the unit of the rigidity.

This equation can give the global cutoff rigidities simply and quickly, but because the dipole magnetic field cannot completely and accurately describe the real Earth’s background magnetic field, especially in the period of intense magnetospheric activity, such as magnetic storm and substorm, the Earth’s magnetic field will be compressed or stretched, resulting in the reduction of the effectiveness of the geomagnetic field described by the dipole magnetic field. With the continuous improvement of numerical simulation calculation, the global cutoff rigidities distribution image is given. At the same time, with the continuous progress of satellite observation technology and the continuous improvement of numerical simulation calculation, it is found that the cutoff rigidities of energetic particles corresponding to latitude should be calculated by more complex formulas (Dmitriev et al., 2010). Meanwhile, due to the long-term variation of the geomagnetic field, especially the geomagnetic change has accelerated significantly in recent years (Alken et al., 2020), the shielding effect of the geomagnetic field on energetic particles will change significantly, resulting in the change of the background energetic particle environment caused by the entry of solar/galactic cosmic rays into the magnetosphere. Therefore, it is necessary to remeasure the cutoff rigidities of energetic particles caused by the change of magnetic field. Although some researchers (Shea, 1971; Bhattacharyya and Mitra, 1997; Kudela and Bobik, 2004; Smart and Shea, 2009; Dorman et al., 2017; Cordaro et al., 2018, 2019) have studied the cutoff rigidities of energetic particles for the long-term variation of the geomagnetic field, their research either used the earlier geomagnetic field model until the year 2000 (Shea and Smart, 2001) or did not give the difference behavior for different hemispheres. Some authors calculated the cutoff rigidities only for one or several stations (Shea and Smart, 2001) or the limited area (Cordaro et al., 2018, 2019). Shea et al. (1987) studied the cosmic ray vertical cutoff rigidities as a function Mcllwain L-parameter for different epochs of the geomagnetic field, while the Mcllwain L-parameter cannot give the three-dimensional locations exactly. Dorman et al. (2017) studied this problem for the entire global world using the numerical simulation method, but they did not give a parameter relationship to evaluate the background change of high-energy particles.

All studies did not give the overall change of the cutoff latitude, nor the quantitative parameters were used to study its change trend, especially the change of the central point corresponding to the cutoff latitude, which has not even received any research and attention. Since not many articles on the change of the cutoff rigidities are available, we consider this article of utmost importance. This article will study this problem from different aspects, especially the inconsistency between the change of cutoff rigidities and the long-term change of the geomagnetic field. Using the newest IGRF model and more refined grid division (compared with the grid 5 × 15 in latitude and longitude (Bhattacharyya and Mitra, 1997)), this article will focus on the overall change at different times. At the same time, we will study its geometric center point and explore the correlation between them in combination with the change of the position of the magnetic poles.

The following parts of this article will discuss different contents, respectively. The second section will introduce the numerical simulation method. The third section shows the inconsistency of the change trend by analyzing the change of geomagnetic field and cutoff rigidities. Finally, a brief summary and discussion are made.

2 Simulation Method

The equation of charged particle’s motion in the magnetosphere can be written as

$\frac{d\mathbf{p}}{dt}=q\mathbf{v}\times \mathbf{B},(3)$

where p is the relativistic momentum of the particle, v is the velocity, q is the charge, and B is the magnetic field. Here, the electric field is ignored. Following Smart et al. (2000), we calculate charged particle trajectories time backward. If a particle can reach the boundary of the magnetosphere before its total trajectory path length exceeds 1000 Re, the rigidity is considered an allowed rigidity (Kress et al., 2004). However, if the particle intersects the solid Earth or the particle is still moving in the magnetosphere after its total trajectory path length exceeds 1000 Re, the rigidity is considered a forbidden one.

The lowest rigidity above which all rigidities are allowed is denoted as the upper cutoff rigidity R_max, and the highest rigidity below which all rigidities are forbidden is denoted as the lower cutoff rigidity R_min. From a rigidity much higher than the possible R_max to a rigidity much lower than the possible R_min, we scan the rigidity values at the discrete intervals δR = 0.001 GV. In this way, we obtain the values of R_max and R_min, and the allowed and forbidden rigidities between R_max and R_min are denoted as δR_allowed and δR_forbidden, respectively. Thus, the effective cutoff rigidity, R_eff, is calculated with the formula

$R_{e\mathit{ff}}=R_{\mathit{m}\mathit{a}\mathit{x}}-\sum _{R_{\mathit{m}\mathit{i}\mathit{n}}}^{R_{\mathit{m}\mathit{a}\mathit{x}}}\delta R_{allowed}.(4)$

In our numerical method, Eq. 3 is integrated with the fourth order Runge–Kutta method. The step size in time is set to be equal to 0.01 of particles’ gyro-period throughout the trajectory (Kress et al., 2004). We consider that the particles access the position from the vertical direction. So, the initial velocities $v_{x_i}$ (x_i = x, y, z) of the particles at the given position x, y, and z are

$v_{x_i}=v\frac{x_i}{\sqrt{x^2+y^2+z^2}},(5)$

where v is the initial velocity of particles, and the altitude of the position is set to be 450 km as the initial position, according to Smart and Shea (2003). In addition, the inner boundary is set to be 1.0R_e from the Earth center. The x, y, and z coordinates are applicable when using the magnetospheric coordinates which are right-handed, orthogonal, and Earth-centered coordinate systems (Smart et al. (2000)). The coordinates we use here are the GEO (geographic coordinate system) and GSM (geocentric solar-magnetospheric).

It should be noted that during the numerical simulation with the main field of International Geomagnetic Reference Field (IGRF) as the background magnetic field, the inner and outer boundaries are set at a radial distance of an Earth radius. At the same time, because IGRF is the Earth’s main field, the magnetopause-type given by Tsyganenko (Tsyganenko, 1995, 1996; Tsyganenko and Stern, 1996) is not suitable to describe the simple IGRF magnetopause. Therefore, in the simulation process, we only use the total time and total distance of particle motion and the maximum range of particle motion in three-dimensional, rather than using the magnetopause-type given by Tsyganenko as the outer boundary. At the same time, as the dependence of cutoff rigidities on latitude is significantly greater than that on longitude, but the longitude dependence of geomagnetic field change is obvious, in order to analyze the global spatial change characteristics with high precision, we use the latitude direction interval of 1 degree and longitude direction of 10 degrees to grid the world. The temporal and spatial evolution characteristics of global vertical cutoff rigidities are calculated. For the detailed numerical simulation process of calculating the cutoff rigidities, please refer to Chu and Qin (2016).

Considering the change of the long-term geomagnetic field, here, we only use the main field as the background field for numerical simulation. The main field model we used here is the International Geomagnetic Reference Field (IGRF) model (http://www.ngdc.noaa.gov/IAGA/vmod/igrf.html). The model is a standard mathematical description of the Earth’s main magnetic field and its secular variation. The IGRF model is standardized for a particular year, reflecting the most accurate measurements available at that time and indicating a small-scale, slow time variation of the Earth’s magnetic field. The model is usually updated every 5 years to make sure the results given by the model are the most accurate at present. In December 2019, the 13th generation of the International Geomagnetic Reference Field (IGRF) was released by the International Association of Geomagnetism and Aeronomy (IAGA) Division V Working Group (V-MOD). This model updates the previous generation with a definitive main field model for epoch 2015, a main field model for epoch 2020, and a predictive linear secular variation for 2020 to 2025 (Alken et al., 2020). Since the moving speed of the pole was accelerated in the 1960s, we set the time range for our study after 1965. Meanwhile, since the dipole point has crossed the primary meridian in recent years and the IGRF 13 model can deduce the magnetic field data in 2025, we will continue our research until 2025. To calculate the main sources contribution of the geomagnetic field and coordinate transformations, we use the source code package GEOPACK-2008 provided by Tsyganenko. All the aforementioned computer codes for magnetospheric field and coordinate transformation calculations are downloaded from the website http://geo.phys.spbu.ru/tsyganenko/modeling.html.

3 Simulation Results and Discussion

Since the change of cutoff rigidities is mainly caused by the change of the Earth’s magnetic field, the long-term variation characteristics of the IGRF magnetic field are given here first.

3.1 Long-Term Variation of Geomagnetic Field

Here, we will focus on only two aspects: the change of global magnetic field intensity and the movement of magnetic poles. The movement of magnetic poles includes the magnetic dip poles and geomagnetic poles in both northern and southern hemispheres. According to the article by Alken et al. (2020), the geomagnetic poles are calculated from the three dipole Gauss coefficients and correspond to where the magnetic dipole axis intersects a sphere of mean Earth radius 6371.2 km. The magnetic dip poles are defined as the locations where the main magnetic field as a whole is normal to the Earth’s surface, represented by the WGS84 reference ellipsoid. They can be defined as the locations where the magnetic field component tangent to the ellipsoid vanishes.

For the convenience of picture expression, we will give the image of background magnetic field in limited years and give the change information. Figure 1 shows the global contour map of the total field intensity at the altitude of 450 km at an interval of 20 years from 1965 to 2025. The map shows that Siberia and the Southern Ocean between Australia and Antarctic in the southern hemisphere own the largest field intensities. Also, South America, which is known as the South Atlantic Anomaly (SAA), is the region of significantly weaker field. Usually, in this region, because the radiation environment of energetic particles is much higher than that in other areas, many payloads will be shut down in this area to ensure the safety of satellite operation. Interestingly, Terra-Nova et al. (2019) found that a region which is close to SAA minimum longitude has a second minimum intensity. This region can be found at the Earth’s surface, but it cannot be found at our simulation height (450 km). The global contour map of variation of the total field intensity is given in Figure 1. From the figure, we can find that the global magnetic field intensity has two obvious reduction regions from 1965 to till date. However, the global background magnetic field intensity does not always decrease, especially in the eastern hemisphere, and there is also an obvious enhancement, but the enhancement range is not so large compared with the weakening range.

FIGURE 1

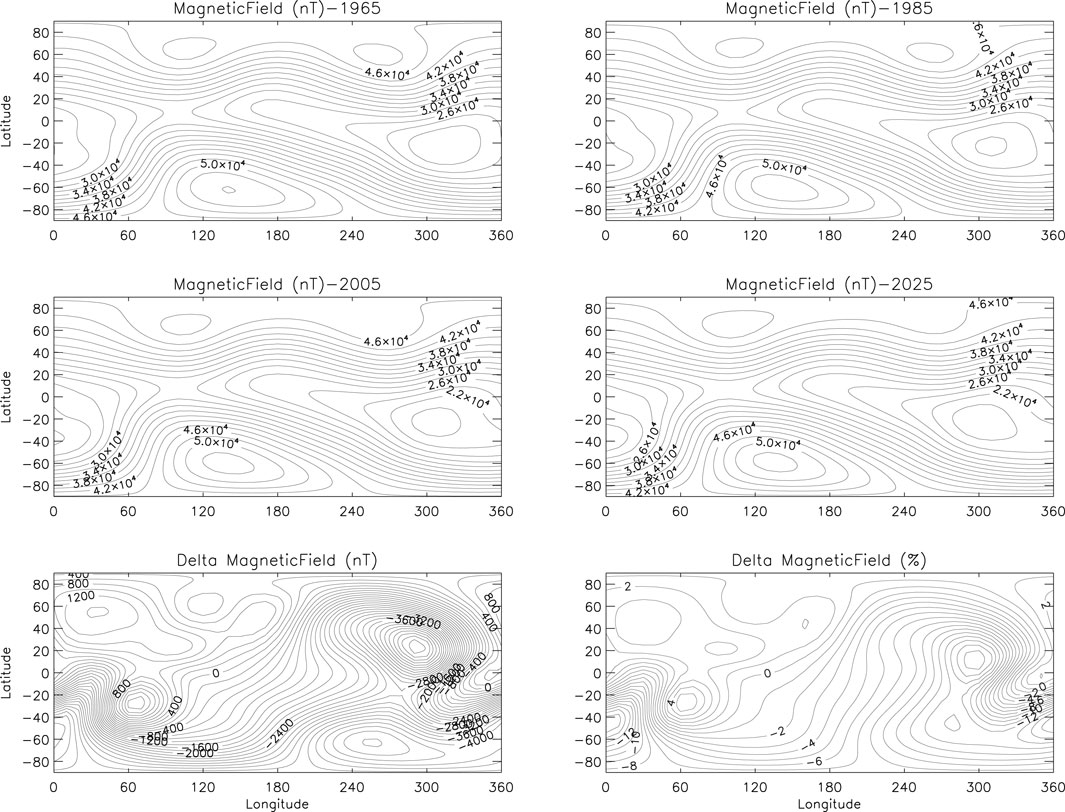
FIGURE 1. Contour of the background magnetic field calculated by the IGRF 13 model from 1965 to 2025 by every 20 years and absolute and relative changes of the magnetic field contour image.

The position with the strongest relative decrease is in the magnetic equatorial regions of North and South America and the outer boundary of the SAA region, in which the outer boundary of the SAA region decreases most strongly, with a relative change of about 15%.

Figure 2 is the pole positions of the IGRF magnetic field for different years from 1900 to 2025 with the time resolution of 5 years. The blue dots are the magnetic dip poles, and the red ones are the geomagnetic poles. The data are from the article by Alken et al. (2020). There are significant differences between the two due to the non-dipolar structure of the Earth’s magnetic field. For more than a century, the change of the dip poles is more obvious than that of the geomagnetic poles. Usually, when the interplanetary and magnetospheric coupling mechanism is studied, the geomagnetic poles are used, as they can be used to specify the relative orientation of the Earth’s magnetic field with respect to the Sun.

FIGURE 2

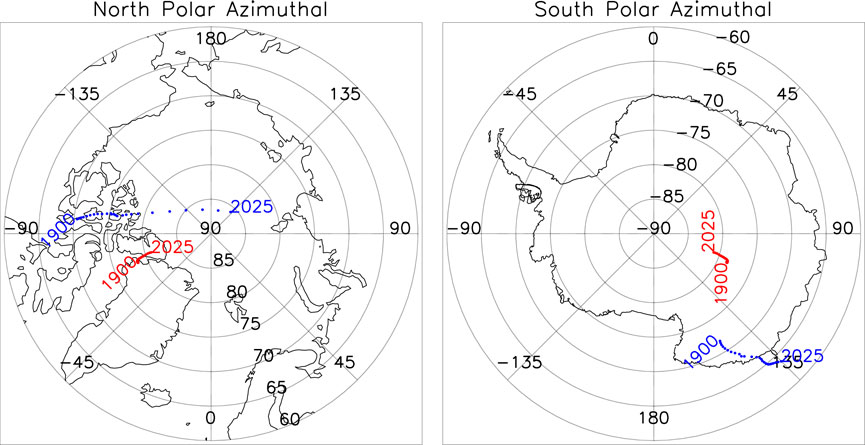
FIGURE 2. Center location of the IGRF magnetic field for different years from 1900 to 2025 with the time resolution of 5 years. The blue dots are the magnetic dip pole centers, and the red ones are the geomagnetic pole centers. The data are from the article by Alken et al. (2020).

3.2 Long-Term Variation of Cutoff Rigidities

The cutoff rigidities penumbra is an effective concept, which can reflect the motion of energetic particles at the observation position. The rigidity penumbra is shown in Figures 3, 4 for the north and south hemispheres for different years. These two figures show the maximum, minimum, and effective cutoff rigidity at intervals of 1 MeV for the calculation of the rigidity at an altitude of 450 km, determined by trajectory calculations. In this illustration, black indicates forbidden rigidities, and white indicates allowed rigidities. The transmission of energetic particles changes from fully allowed at rigidities above the maximum cutoff rigidity, R_max, to partly allowed in the cosmic ray penumbra, to totally forbidden at rigidities below the minimum cutoff rigidity, R_min. In addition, they are either allowed or forbidden to access with rigidities between R_max and R_min, so it is named the penumbra area. The panels from top to bottom represent the changes of the penumbra of the cutoff rigidities at the same location in 1965, 1985, 2005, and 2025, respectively. Because the cutoff rigidities are not symmetrical about the magnetic equator or geographical equator and in order to compare the cutoff rigidities of the same order, we selected observation points with different longitude and latitude in the northern and southern hemispheres for comparative analysis. The geographical longitude and latitude of the observation point in the northern hemisphere are 30 and 300, while in the south hemisphere they are −50 and 300, respectively. By comparing different years, it can be found that from 1965 to 2025, the effective, maximum, and minimum cutoff rigidities of the same location in the northern hemisphere show an increasing trend. While, the trend in the southern hemisphere is the opposite, showing a decreasing trend. In the northern hemisphere, the effective cutoff rigidities changed from 4.234 GV in 1965 to 5.257 GV in 2025, which represents an increase of 24%. At the same time, the southern hemisphere changed from 6.763 to 4.482 GV, which represents a decrease of 34%.

FIGURE 3

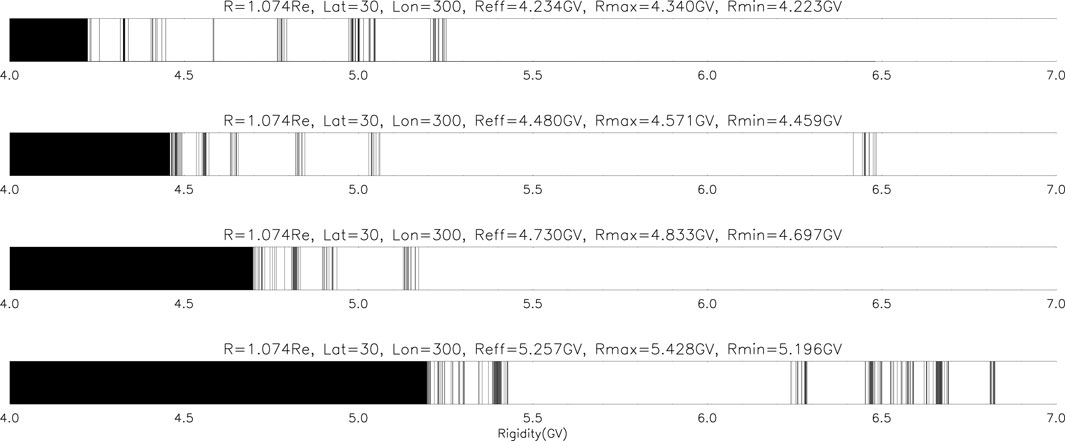
FIGURE 3. Illustration of the geomagnetic cutoff rigidities penumbra. This figure shows the maximum, minimum, and effective cutoff rigidity at an interval of 1 MeV for the calculation of the rigidity at an altitude of 450 km, determined by trajectory calculations. In this illustration, black indicates forbidden rigidities, and white indicates allowed rigidities. Note that the cutoff is not sharp and that as the rigidity is decreased. The transmission of cosmic rays changes from fully allowed at rigidities above the maximum computed cutoff, R_max, to partly allowed in the cosmic ray penumbra, to totally forbidden at rigidities below the minimum computed cutoff, R_min. In addition, they are either allowed or forbidden to access with rigidities between R_max and R_min, so it is named the penumbra area. The panel from top to bottom represents the changes of the penumbra of the cutoff rigidities at the same location in 1965, 1985, 2005, and 2025, respectively.

FIGURE 4

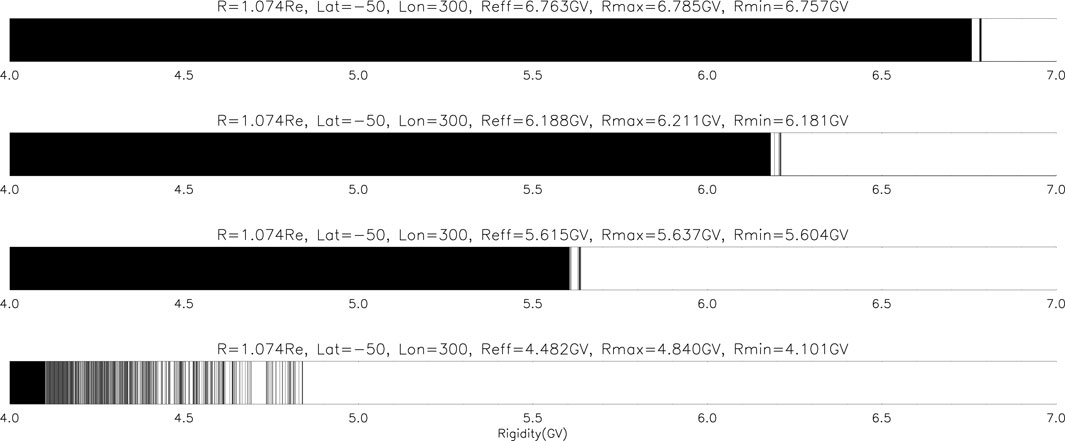
FIGURE 4. Same as Figure 3 but for different hemisphere.

Then, we expand the study scope to the global world. From Figure 5, which shows the variation of the global cutoff rigidities, it can be seen that there are mainly four regions of change in cutoff rigidities worldwide. Some regions of the northern hemisphere show that the cutoff rigidities decrease with the weakening of the magnetic field; however, there are also some regions where the cutoff rigidities increase while the magnetic field becomes weaker. Figures 6, 7 show the histogram of variation of background geomagnetic field and cutoff rigidities with the longitude and latitude between 1965 and 2025. The upper panel indicates that the relative change of the magnetic field changes with the longitude/latitude, and the lower panel indicates the relationship between the relative change of cutoff rigidities and longitude/latitude. The longitude and latitude distribution images corresponding to the changes of magnetic field and cutoff rigidities show that there is a deviation of about 60 degrees in longitude, and the dependence on the latitude is basically with expectations in the southern hemisphere. But, in the northern hemisphere, the relationship between the two is complex, which shows an anticorrelation relationship, which is puzzling. At the same time, although the second minimum intensity region of the magnetic field at the simulation altitude is not shown in the magnetic field distribution map, it can be found that the cutoff rigidities in this region have changed significantly (Longitude 0, about 30 south latitude). This finding is exciting because it shows that the magnetic field in the bottom region plays a decisive role in the motion of energetic particles. This also means that in the numerical simulation of energetic particles, especially in the process of single particles, it is necessary to reasonably and carefully set the inner boundary to prevent the deviation of particle motion caused by unreasonable boundary setting.

FIGURE 5

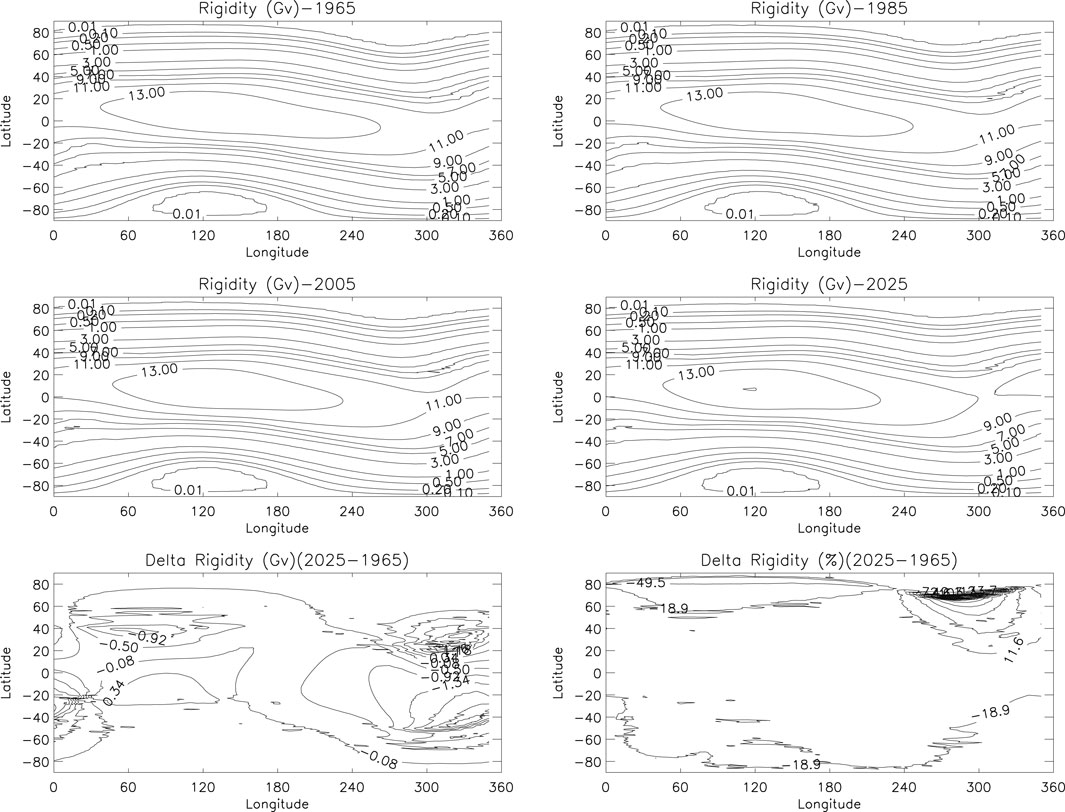
FIGURE 5. Global contour of cutoff rigidities from 1965 to 2025 by every 20 years and their absolute and relative changes contour image.

FIGURE 6

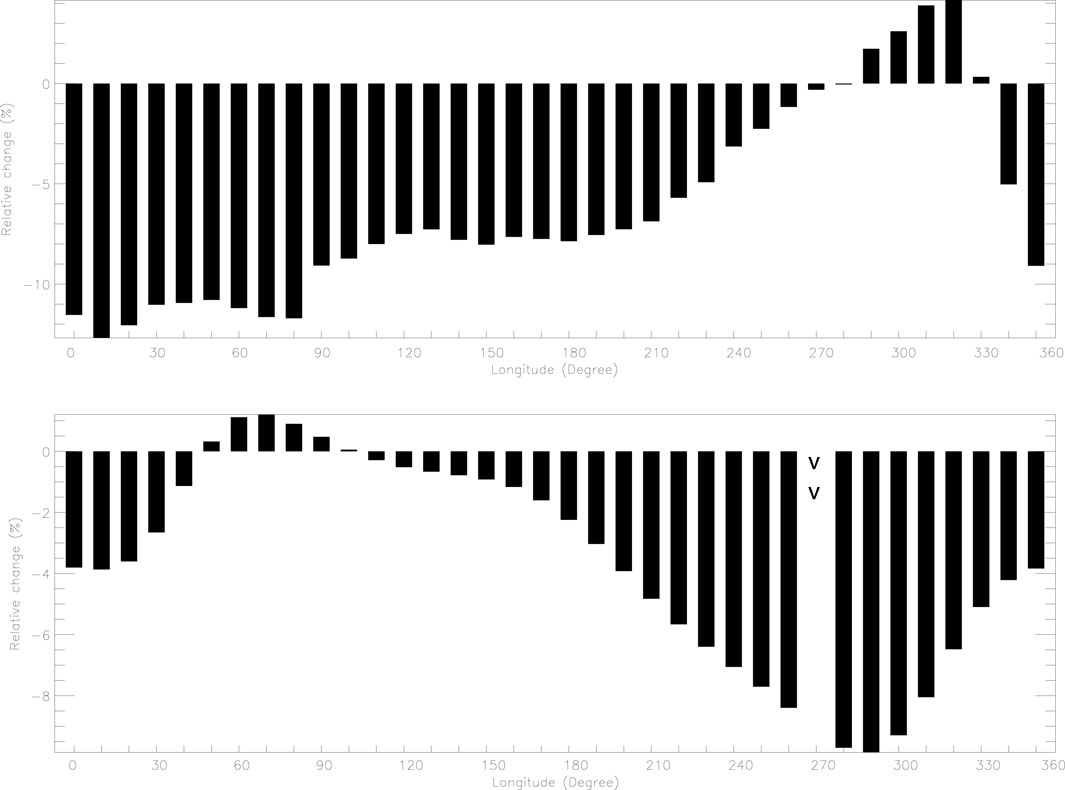
FIGURE 6. Histogram of variation of background geomagnetic field and cutoff rigidities with the longitude between 1965 and 2025. The upper panel indicates that the relative change of the magnetic field changes with the longitude, and the lower panel indicates the relationship between the relative change of cutoff rigidities and longitude.

FIGURE 7

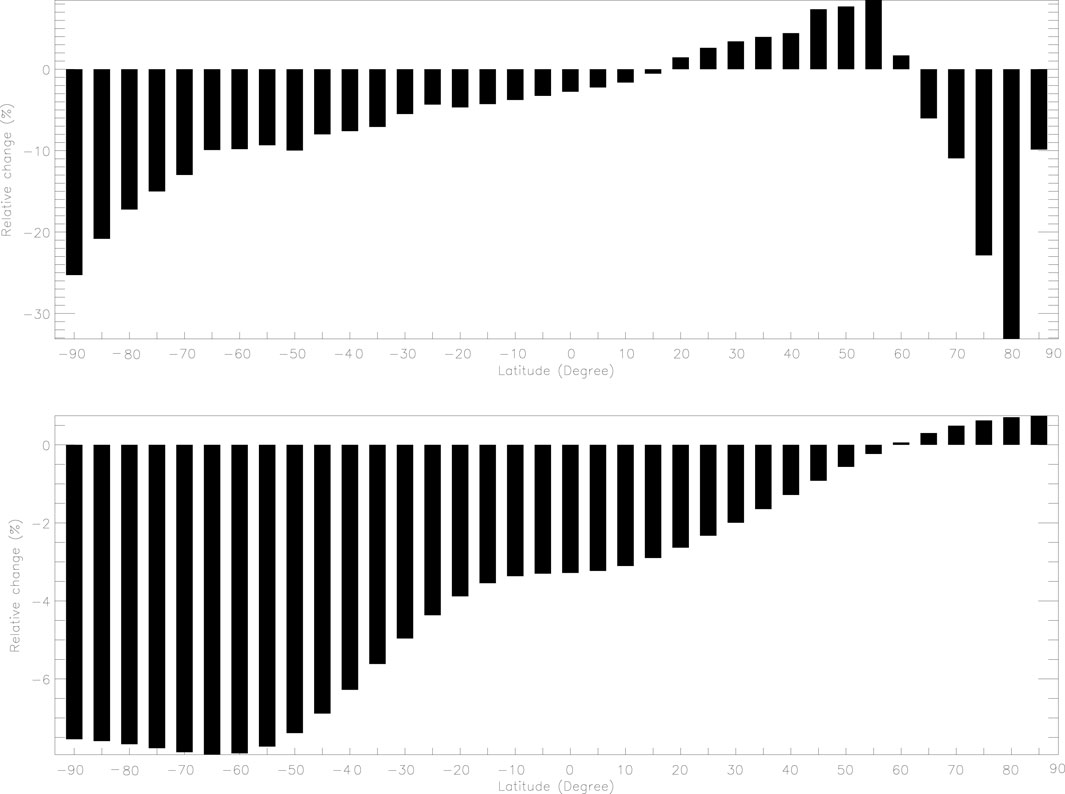
FIGURE 7. Histogram of variation of background geomagnetic field and cutoff rigidities with the latitude between 1965 and 2025. The upper panel indicates that the relative change of magnetic field changes with the latitude, and the lower panel indicates the relationship between the relative change of cutoff rigidities and latitude.

In order to illustrate the dependence of the change of cutoff rigidities caused by the change of the magnetic field, the relationship of the variation of the global rigidities and the global geomagnetic field is shown in Figure 8. It can be easily found that normally the decrease of the magnetic field cannot always lead to the decrease of the cutoff rigidities. For the global grids with the spatial resolution by 1 for latitude and 10 for longitude, nearly 40% of the changes of these two parameters are inconsistent. When the magnetic field becomes intense, 16.543 9% of the cutoff rigidities will become smaller, while 23.173 7% will become larger. Also, when the magnetic field becomes smaller, 11.694 3% of the cutoff rigidities will become smaller, while 48.572 7% will become larger.

FIGURE 8

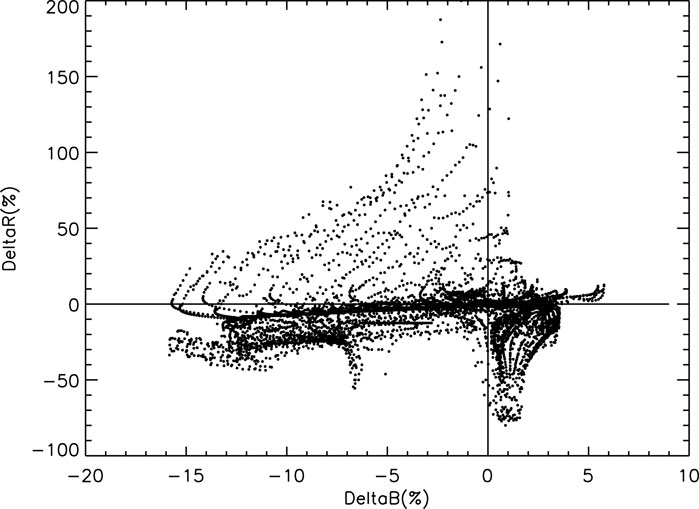
FIGURE 8. Relationship of the variation of the global rigidities and the global geomagnetic field. For the global grids with the spatial resolution by 1 for latitude and 10 for longitude, nearly 40% of the changes of these two parameters are inconsistent. Also, when the magnetic field becomes intense, 16.5439% of the cutoff rigidities will become smaller, while 23.1737% will become larger. Also when the magnetic field becomes smaller, 11.6943% of the cutoff rigidities will become smaller, while 48.5727% will become larger.

Figure 9 shows the cutoff latitude boundary with a cutoff rigidity of 200 MV in the northern and southern hemispheres (the cutoff latitude boundary is calculated by spline interpolation here). Different colors represent the simulation results of the background magnetic field in different years. The colors “black,” “yellow,” “red,” “pink,” “green,” “sky blue,” and “blue” represent 1965, 1975, 1985, 1995, 2005, 2015, and 2025, respectively. The left one is the boundary of the EPW in the northern hemisphere, and the right one is in the southern hemisphere. The cutoff latitude boundary image shown in the figure can be fitted with ellipses, and the eccentricity of ellipses in the northern and southern hemispheres is different. Obviously, the boundary curve in the southern hemisphere is similar to that of a circle, while in the northern hemisphere is more inclined to the shape of an ellipse, and the elliptical eccentricity in the northern hemisphere is greater than that in the southern hemisphere; this result is consistent with the result given by Dmitriev et al. (2010). The cutoff latitude boundary corresponding to the cutoff rigidities changes obviously with the magnetic field, especially in the northern hemisphere. However, this variable situation brings some difficulties to our study because it is difficult to determine how the global energetic particles radiation environment will change through the cutoff latitudes. Therefore, we introduced the concept of energetic particles’ windows.

FIGURE 9

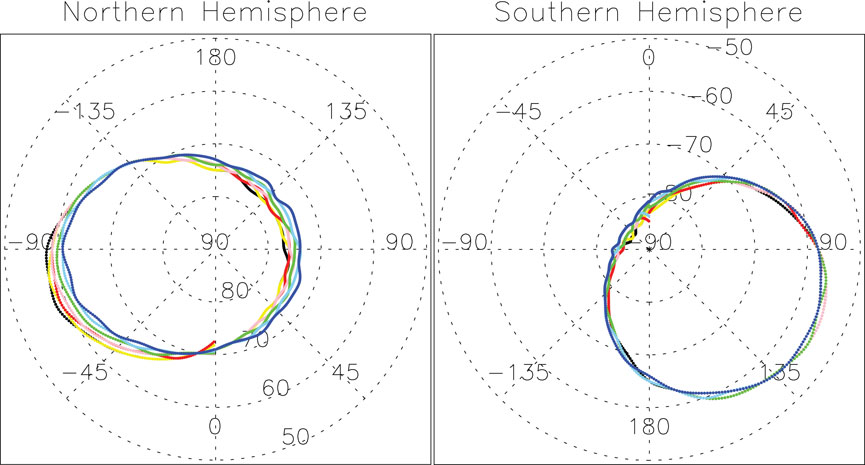
FIGURE 9. Image of EPWs with 200 MV under different background magnetic fields for different years which are marked with different colors. The colors “black,” “yellow,” “red,” “pink,” “green,” “sky blue,” and “blue” represent 1965, 1975, 1985, 1995, 2005, 2015, and 2025, respectively. The left one is the boundary of the EPW in the northern hemisphere, and the right one is in the southern hemisphere.

3.3 The Energetic Particles’ Windows

As a concept corresponding to the cutoff rigidities, the cutoff latitude is expressed as the latitude boundary corresponding to the same cutoff rigidities. From the aforementioned global contour of cutoff rigidities, it can be found that when the cutoff rigidity is smaller than 11GV, the cutoff latitudes can form a closed curve. Different from the method of using the cutoff latitudes, we here define a region, energetic particles’ windows (EPWs), where the vertical cutoff rigidities of energetic particles are less than or equal to a threshold value, R_t. A simple example is given in Figure 10; the shaded region indicates the EPWs with the threshold R_t = 200 MV, and the big black dot indicates the center of the window. By calculating the area above the cutoff latitudes, the variation characteristics of the cutoff rigidities can be evaluated (Refer to Chu and Qin (2016) for detailed description).

FIGURE 10

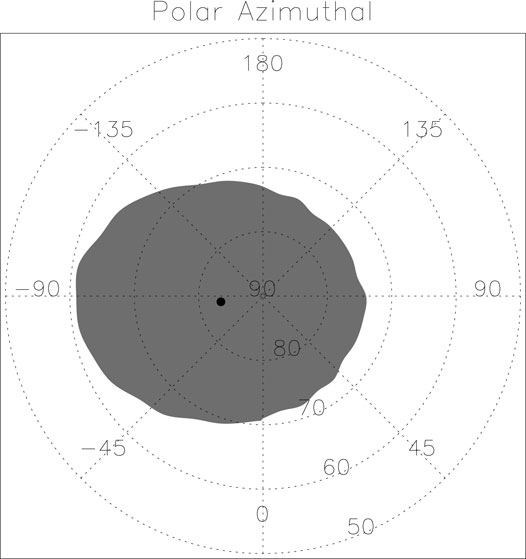
FIGURE 10. Schematic diagram of EPWs defined in the article. Here, we use 200 MV as the cutoff rigidity, and the black dot represents the center of the EPW.

3.4 Area Variation Characteristics Corresponding to Cutoff Latitudes

The areas and the centers of the EPWs can give us a better understanding of the coupling processing between the interplanetary and the magnetosphere. In this chapter, the area of the EPWs will be studied. Figure 11 shows changes of the EPWs’ area with time under different background magnetic fields for both the north and south hemispheres. The colors “black,” “red,” “orange,” “pink,” “green,” “sky blue,” “blue,” “violet,” “gray,” and “purple” represent 0.1, 1, 2, 3, 4, 5, 6, 7, 8, and 9 GV, respectively. It is expected that when the intensity of the background magnetic field becomes weaker, the cutoff rigidities at the same location will become smaller, resulting in the shift of the cutoff latitude boundary to the equator. However, the change trends in the northern and southern hemispheres are obviously different. Next, we will give the time change rate of the area corresponding to EPWs. Although the change trend of EPWs’ area in the northern and southern hemisphere is obviously different, when we select the standard, we take 1965 as the reference for both the northern and southern hemispheres. All of the information is given in Figure 11. Compared with the temporal change rate of EPWs’ area in the northern and southern hemisphere, the temporal change rate in the southern hemisphere is greater than that in the northern hemisphere. Figure 12 shows the area temporal change rate of EPWs corresponding to different rigidities obtained by polynomial fitting. The slope of the line obtained by first-order polynomial fitting in the northern hemisphere is less than 0, and the absolute value of the slope becomes smaller with the increase of the rigidities. The slope of the line varies between −0.03/yr and −0.004/yr. While in the southern hemisphere, they are large than 0, and the slope of the line becomes larger and larger when the rigidities increase. The maximal value is 0.12/yr, and the minimum is 0.056/yr. These parameters suggest that due to the change of the background magnetic field, the radiation flux of energetic particles in the southern hemisphere will increase by 5.6 to 12% in hundred years. In the northern hemisphere, the value will be around −3%. In combination with the change trend of the northern and southern hemispheres, from a global perspective, as shown in Figure 13, the radiation flux of energetic particles of different rigidities will increase by 1.1% to 5.6% in hundred years. Although its impact may be limited in the short term, when its time scale reaches a millennium or even longer, the radiation environment will change dramatically. Kudela and Bobik (2004) used the simulation method under the model geomagnetic field (n = 2+) and found that the maximum cutoff rigidity decreased from about 24 to 17 GV between 0 and 2000 years which means the time change rate is about 0.015%/yr. This value is obviously smaller than our simulation results which means that the variation maybe much more complex than what we expect. The linearity maybe impossible to claim with reliability accepted approach abnormal development of behavior of geomagnetic cutoff rigidity (Dorman et al., 2017); however, we can still use this method to evaluate the change of cutoff rigidities, as these values have the same order.

FIGURE11

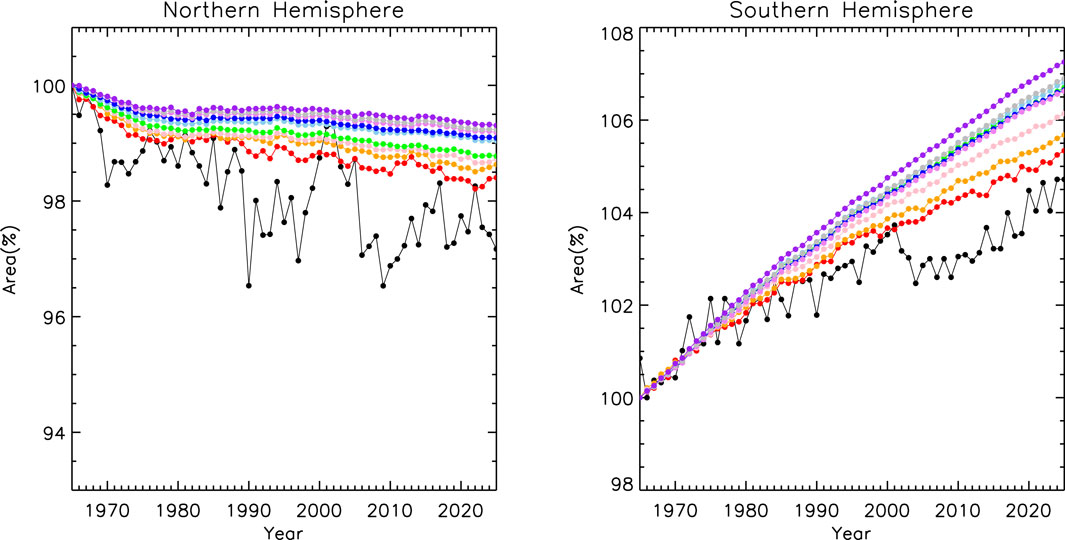
FIGURE11. Changes of the EPWs’ area with time under different background magnetic fields for both the north and south hemispheres. The colors “black,” “red,” “orange,” “pink,” “green,” “sky blue,” “blue,” “violet,” “gray,” and “purple” represent 0.1, 1, 2, 3, 4, 5, 6, 7, 8, and 9 GV, respectively.

FIGURE 12

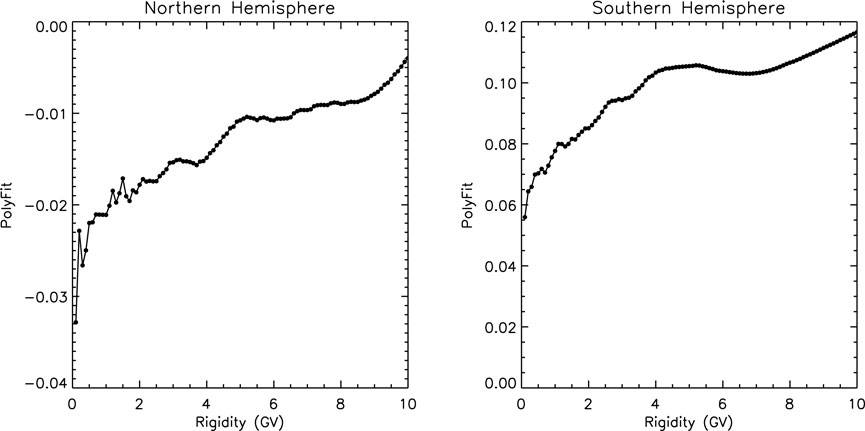
FIGURE 12. Area time change rate of EPWs corresponding to different rigidities obtained by polynomial fitting.

FIGURE 13

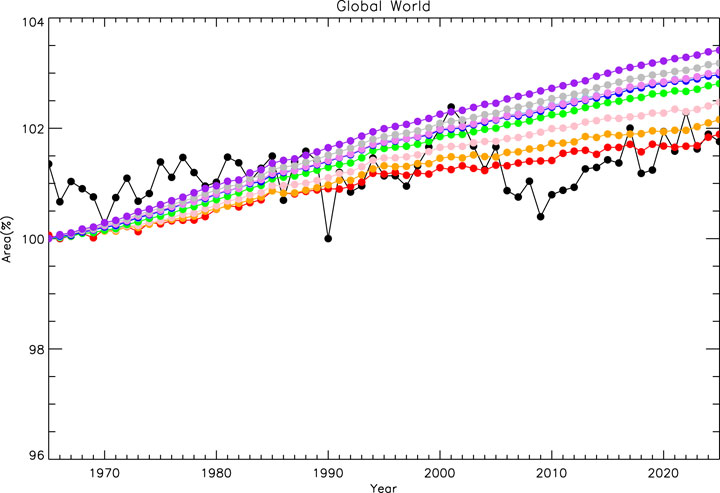
FIGURE 13. Same as Figure 11 but for the global world.

The pitch angle dependence of the cutoff rigidities that is carried out by our group (Chu et al., 2021) shows that the energetic particles corresponding to the cutoff rigidities tend to reach the observation points along the opposite direction of the magnetic field. This suggests that compared with the northern hemisphere, a large number of particles will tend to reach near-Earth space from the southern hemisphere. With the time goes, the flux of energetic particles in the southern hemisphere will be significantly higher than that in the northern hemisphere.

3.5 Variation Characteristics of EPWs’ Center Points

As one of the characteristics of geomagnetic field variation, by the end of 2019, the longitude of the magnetic dipolar pole in the north hemisphere has crossed the prime meridian (Alken et al., 2020) and also the geomagnetic poles are always in motion. Therefore, it will be very meaningful for us to study the corresponding relationship between the central point of the EPWs and the magnetic pole point. The center of the EPWs is the geometric center, and we do not perform any weighting here. For the area surrounded by the above cutoff latitude, the longitude and latitude information of its geometric center can be calculated. As an important parameter, Dmitriev et al. (2010) used satellite observation results to fit the longitude and latitude coordinates of the center point of the cutoff latitude elliptic boundary. Here, we directly use the numerical simulation method to obtain the longitude and latitude information of the central points. Combined with the analysis of Figures 2, 14, we can find that the central points of EPWs are closer to the magnetic pole point of geomagnetic rather than the magnetic pole point of the dipole magnetic field. This is easy to understand because IGRF gives the main geomagnetic field, not a simple dipole magnetic field. Although the dipole magnetic field plays a major role, the influence of other orders cannot be ignored. Combined with the paleomagnetic data, it can be obtained that the dipole moment of the geomagnetic field has decreased by nearly 1/4 in the past 1000 years. In sharp contrast to the decrease of the dipole moment, the non-dipole part of the geomagnetic field has increased rapidly. For 100 years, quadrupole and octupole are enhanced by 95% and 74%, respectively (Courtillot and Mouel, 1988; WEI and XU, 2001; Kudela and Bobik, 2004).

FIGURE 14

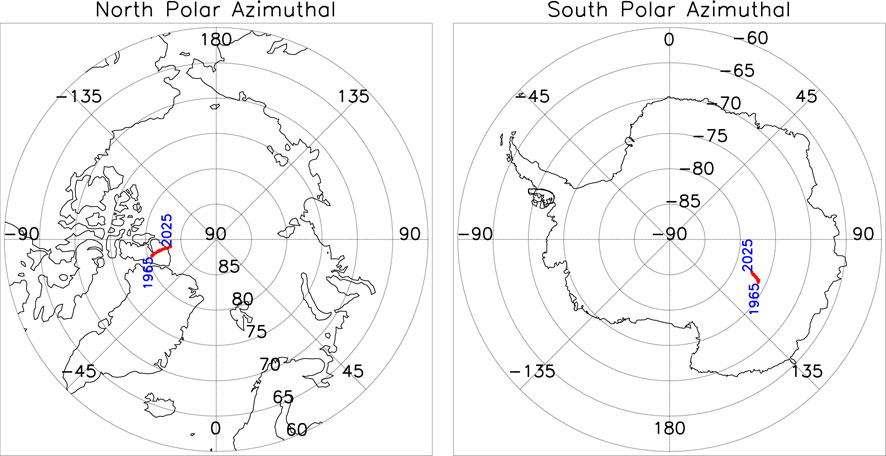
FIGURE 14. Central location of the EPW for the rigidity of 1 GV for different years from 1965 to 2025 with the time resolution of 1 year.

Meanwhile, compared with the position of the magnetic pole, the central points of EPWs are closer to the geographical north pole in the northern hemisphere, but in the southern hemisphere, the situation is just the opposite, and the central points of EPWs are closer to the low latitudes.

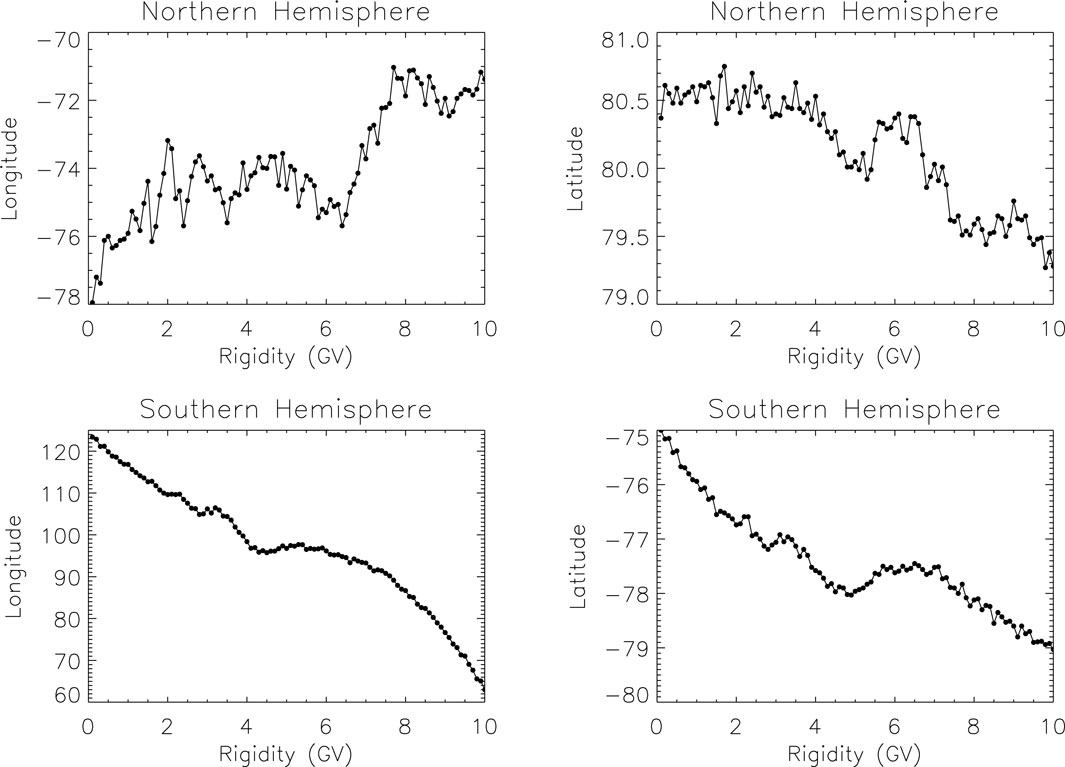
The central points of EPWs are usually close to the morning and dusk side, not on the day side or night side. This phenomenon may be due to the fact that the cusp region in the northern and southern hemispheres is usually on the dawn and dusk side, not on the day or night side. The cusp region is still the central region from where energetic particles enter the near-Earth space. Another interesting phenomenon is the relationship between the particle’s rigidity and the longitude and latitude of the EPWs’ center. Figure 15 shows the center location of the EPW for different rigidities. It can be found that in the south hemisphere, the longitude of the center points changes obviously with the particle’s rigidity; however, the situation in the northern hemisphere is somewhat different, and its change is not so strong. This may be because the Earth’s magnetic field is not very effective in restraining or shielding the very high energy particles, especially when the energetic particles enter near-Earth space from the southern hemisphere. As this problem does not belong to the main content of this article, it will not be discussed in detail here and will be studied in the future works.

FIGURE 15

FIGURE 15. Central location of the EPW for different rigidities.

4 Conclusion

A good description of energetic particle precipitation requires a good view that covers the temporal and spatial variation of the cutoff rigidities. The main purpose of this article was to present the variation of the cutoff rigidities caused by the background magnetic field for a long term. This investigation considers the fact that the geomagnetic field is not static but constantly changing in time and space. In this article, the vertical geomagnetic cutoff rigidities were calculated numerically by solving the trajectories of energetic particles in the geomagnetic field (IGRF-13 model) from 1965 to 2025 every year. Our numerical simulations show that there is a close relationship between the cutoff latitude corresponding to the cutoff rigidities and the background magnetic field intensity, but they are not in a simple relationship. The changes of the cutoff rigidities and geomagnetic field in the northern and southern hemispheres are asymmetric. For the grids of 1 × 10 in latitude and longitude, nearly 40% of the changes between the magnetic field intensity and the cutoff rigidities are inconsistent, which means when the magnetic field intensity becomes smaller/larger, 40% of the corresponding cutoff rigidities will become larger/smaller. From 1965 to 2025, the maximum cutoff rigidity decreased from 6.9 to 3.9 GV which occurred in the southern hemisphere of (330, −45), and the maximum cutoff rigidity increased from 7.2 to 10.0 GV in the northern hemisphere of (320, 21). On the other hand, by defining the energetic particles windows (EPWs), the areas and the centers of the EPWs were studied. The time change rate of the EPWs’ areas is between −0.03/yr and −0.004/yr in the northern hemisphere, while in the southern hemisphere, it is 0.12/yr and the minimum is 0.056/yr, compared to the time change rate of about 0.015%/yr from 0 to 2000 years suggested by the article by Kudela and Bobik (2004). The long-term trajectory of the geomagnetic north poles does not correspond to the positions of the central point of EPWs. The weakening of the geomagnetic field will push the cutoff latitude toward the near equatorial region in the south hemisphere, but for the north hemisphere, the phenomenon is not always credible.

The energetic particles outside the magnetosphere tend to enter the near-Earth space in the direction antiparallel to the magnetic field other than in the direction along the magnetic field lines which combined the result that with the weakening of the magnetic field, in the southern hemisphere, the area of the EPWs will become larger and larger, and the radiation caused by the solar and cosmic energetic particles will be more intense. We have a reason to believe that the central position of the aurora may change with the movement of the central point of the energetic particles’ windows (EPWs.)

In the future work, the non-vertical cutoff rigidities caused by the geomagnetic fields will be studied, to find out whether the dependence of the cutoff rigidities at different angles on the background magnetic field is the same, also to combine the in situ spacecraft observations such as NOAA and China Seismo-Electromagnetic Satellite (CSES), and to make out the differences between the simulation and observations.

Moreover, the knowledge acquired from cutoff rigidities in the near-Earth space and the sources of energetic particles’ precipitation from the interplanetary should provide new insights for both the terrestrial and interplanetary researchers. Collaborations between scientists involved in these different fields are crucial for a better understanding of coupling between interplanetary and near-Earth space. It is hoped that our study can provide some useful suggestions of coupling mode and coupling efficiency, etc.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

WC and YY put forward relevant ideas. WC performed the numerical simulation and carried out most of the analysis and wrote the manuscript. GQ provided part simulation codes, and others helped to review the manuscript and gave modification suggestions.

Funding

Our work was partly supported by the National Key R and D Program of China (Grant No. 2018YFC1503502-05) and the APSCO Earthquake Research Project Phase II and ISSI-BJ (2019IT-33).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge IAGA for the source code of the IGRF model (http://www.ngdc.noaa.gov/IAGA/vmod/igrf.html) and Dr. Nikolai Tsyganenko for the source code of the GEOPACK-2008 (http://geo.phys.spbu.ru/tsyganenko/Geopack-2008.html). We thank the useful discussion with Dr. Yang Wang from School of Science, Harbin Institute of Technology, Shenzhen. Additionally, the authors also wish to thank the reviewers for their constructive comments that helped to improve the scholarly quality of the article.

References

Alken, P., Thébault, E., Beggan, C. D., Amit, H., and Zhou, B. (2020). International Geomagnetic Reference Field: the Thirteenth Generation. Earth Planets and Space 73.

Google Scholar

Baker, D. N. (2000). The Occurrence of Operational Anomalies in Spacecraft and Their Relationship to Space Weather. IEEE Trans. Plasma Sci. 28, 2007–2016. doi:10.1109/27.902228

CrossRef Full Text | Google Scholar

Bhattacharyya, A., and Mitra, B. (1997). Changes in Cosmic ray Cut-Off Rigidities Due to Secular Variations of the Geomagnetic Field. Ann. Geophys. 15, 734–739. doi:10.1007/s00585-997-0734-6

CrossRef Full Text | Google Scholar

Chu, W., Qin, G., ang Song Xu, J. H., Zeren, Z., and Shen, X. (2021). A Study on Non-vertical Geomagnetic Cutoff Rigidity of Magnetosphere Energetic Particles during Geomagnetic Quiet Period. Chin. J. Geophys. 64, 410–418.

Google Scholar

Chu, W., and Qin, G. (2016). The Geomagnetic Cutoff Rigidities at High Latitudes for Different Solar Wind and Geomagnetic Conditions. Ann. Geophys. 34, 45–53. doi:10.5194/angeo-34-45-2016

CrossRef Full Text | Google Scholar

Cordaro, E. G., Venegas, P., and Laroze, D. (2018). Latitudinal Variation Rate of Geomagnetic Cutoff Rigidity in the Active Chilean Convergent Margin. Ann. Geophys. 36, 275–285. doi:10.5194/angeo-36-275-2018

CrossRef Full Text | Google Scholar

Cordaro, E. G., Venegas-Aravena, P., and Laroze, D. (2019). Variations of Geomagnetic Cutoff Rigidity in the Southern Hemisphere Close to 70°W (South-Atlantic Anomaly and Antarctic Zones) in the Period 1975-2010. Adv. Space Res. 63, 2290–2299. doi:10.1016/j.asr.2018.12.019

CrossRef Full Text | Google Scholar

Courtillot, V., and Le Mouel, J. L. (1988). Time Variations of the Earth's Magnetic Field: From Daily to Secular. Annu. Rev. Earth Planet. Sci. 16, 389–476. doi:10.1146/annurev.ea.16.050188.002133

CrossRef Full Text | Google Scholar

Dmitriev, A. V., Jayachandran, P. T., and Tsai, L.-C. (2010). Elliptical Model of Cutoff Boundaries for the Solar Energetic Particles Measured by Poes Satellites in December 2006. J. Geophys. Res. 115, a–n. doi:10.1029/2010JA015380

CrossRef Full Text | Google Scholar

Dorman, L., Gvozdevsky, B., Belov, A., Gushchina, R., and Yanke, V. (2017). “The Secular Variations of Cosmic ray Cutoff Rigidities, Caused by century Variations in Geomagnetic Field, and Cosmic ray Variations,” in 35th International Cosmic Ray Conference. doi:10.22323/1.301.0067

CrossRef Full Text | Google Scholar

Galand, M. (2001). Introduction to Special Section: Proton Precipitation into the Atmosphere. J. Geophys. Res. 106, 1–6. doi:10.1029/2000ja002015

CrossRef Full Text | Google Scholar

Kirkby, J. (2007). Cosmic Rays and Climate. Surv. Geophys. 28, 333–375. doi:10.1007/s10712-008-9030-6

CrossRef Full Text | Google Scholar

Koons, H., Mazur, J., Selesnick, R., Blake, J., Fennell, J., Roeder, J., et al. (1998). The Impact of the Space Environment on Space Systems. paper presented 6th Spacecraft Charging Tech. 1, 7–11.

Google Scholar

Kress, B. T., Hudson, M., Perry, K., and Slocum, P. (2004). Dynamic Modeling of Geomagnetic Cutoff for the 23-24 November 2001 Solar Energetic Particle Event. Geophys. Res. Lett. 31. doi:10.1029/2003GL018599

CrossRef Full Text | Google Scholar

Kress, B. T., Mertens, C. J., and Wiltberger, M. (2010). Solar Energetic Particle Cutoff Variations during the 29-31 October 2003 Geomagnetic Storm. Space Weather 8, a–n. doi:10.1029/2009SW000488

CrossRef Full Text | Google Scholar

Kudela, K., and Bobik, P. (2004). Long-term Variations of Geomagnetic Rigidity Cutoffs. Sol. Phys. 224, 423–431. doi:10.1007/s11207-005-6498-9

CrossRef Full Text | Google Scholar

Mavromichalaki, H., Souvatzoglou, G., Sarlanis, C., Mariatos, G., Plainaki, C., Gerontidou, M., et al. (2006). Space Weather Prediction by Cosmic Rays. Adv. Space Res. 37, 1141–1147. doi:10.1016/j.asr.2005.03.159

CrossRef Full Text | Google Scholar

Nesse Tyssøy, H., Stadsnes, J., Søraas, F., and Sørbø, M. (2013). Variations in Cutoff Latitude during the January 2012 Solar Proton Event and Implication for the Distribution of Particle Energy Deposition. Geophys. Res. Lett. 40, 4149–4153.

Google Scholar

Shea, M. A. (1971). “Changes in Neutron Monitor Response and Vertical Cutoff Rigidities Resulting from Secular Variations in the Geomagnetic Field,” in 12th International Cosmic Ray Conference (ICRC12) (Hobart: University of Tasmania), Vol. 3, 859–864.

Google Scholar

Shea, M. A., Smart, D. F., and Gentile, L. C. (1987). Estimating Cosmic ray Vertical Cutoff Rigidities as a Function of the McIlwain -parameter for Different Epochs of the Geomagnetic Field. Phys. Earth Planet. Interiors 48, 200–205. doi:10.1016/0031-9201(87)90145-2

CrossRef Full Text | Google Scholar

Shea, M., and Smart, D. (2001). Vertical Cutoff Rigidities for Cosmic ray Stations since 1955. Int. Cosmic Ray Conf. (Hamburg, Germany) 10, 4063.

Google Scholar

Smart, D. F., and Shea, M. A. (2005). A Review of Geomagnetic Cutoff Rigidities for Earth-Orbiting Spacecraft. Adv. Space Res. 36, 2012–2020. doi:10.1016/j.asr.2004.09.015

CrossRef Full Text | Google Scholar

Smart, D. F., and Shea, M. A. (2009). Fifty Years of Progress in Geomagnetic Cutoff Rigidity Determinations. Adv. Space Res. 44, 1107–1123. doi:10.1016/j.asr.2009.07.005

CrossRef Full Text | Google Scholar

Smart, D. F., Shea, M. A., and Flückiger, E. O. (2000). Magnetospheric Models and Trajectory Computations. Space Sci. Rev. 93, 305–333. doi:10.1007/978-94-017-1187-6_15

CrossRef Full Text | Google Scholar

Smart, D. F., and Shea, M. A. (2003). The Space-Developed Dynamic Vertical Cutoff Rigidity Model and its Applicability to Aircraft Radiation Dose. Adv. Space Res. 32, 103–108. doi:10.1016/s0273-1177(03)90376-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Störmer, C. (1955). The Polar aurora. Walton St. Oxford OX2 6DP United Kingdom: Clarendon Press. doi:10.1002/qj.49708235123

CrossRef Full Text | Google Scholar

Terra-Nova, F., Amit, H., and Choblet, G. (2019). Preferred Locations of Weak Surface Field in Numerical Dynamos with Heterogeneous Core-Mantle Boundary Heat Flux: Consequences for the South Atlantic Anomaly. Geophys. J. Int. 217, 1179–1199. doi:10.1093/gji/ggy519

CrossRef Full Text | Google Scholar

Tsyganenko, N. A. (1996). Effects of the Solar Wind Conditions in the Global Magnetospheric Configurations as Deduced from Data-Based Field Models. In International Conference on Substorms (France; Versailles) 389, 181.

Google Scholar

Tsyganenko, N. A. (1995). Modeling the Earth's Magnetospheric Magnetic Field Confined within a Realistic Magnetopause. J. Geophys. Res. 100, 5599–5612. doi:10.1029/94ja03193

CrossRef Full Text | Google Scholar

Tsyganenko, N. A., and Stern, D. P. (1996). Modeling the Global Magnetic Field of the Large-Scale Birkeland Current Systems. J. Geophys. Res. 101, 27187–27198. doi:10.1029/96ja02735

CrossRef Full Text | Google Scholar

Wei, Z.-G., and Xu, W.-Y. (2001). Drifts and Intensity Variations of the Geomagnetic Field. Chin. J. Geophys. 44, 496–505. doi:10.1002/cjg2.167

CrossRef Full Text | Google Scholar