Quantitative Evaluation and Diagnosis of Water Resources Carrying Capacity (WRCC) Based on Dynamic Difference Degree Coefficient in the Yellow River Irrigation District

In order to effectively deal with the uncertainty between evaluation samples and evaluation criteria, and quantitatively identify the water resources carrying capacity (WRCC) and its obstacle factors in the Yellow River irrigation district, a calculation method of dynamic difference degree coefficient varying with evaluation sample was proposed, and then an evaluation and diagnosis model of WRCC was established. The results applied to the Dagong irrigation district showed that the overall WRCC of five counties in the irrigation district were improved from 2010 to 2017, especially since 2013. The improvement magnitudes of Changyuan County, Fengqiu County, and Hua County were significantly higher than those of Xun County and Neihuang County. In 2017, Fengqiu County, Changyuan County, Hua County, Xun County, and Neihuang County were in water resources critical overloaded status, and the connection number values were 0.231, 0.163, 0.120, −0.293, and −0.331, respectively, which is consistent with the fact that their distances become farther from the main stream of the Yellow River. In addition, the utilization ratio of water resources, available water resources amount per capita, GDP per capita, and water deficient ratio in each county belonged to the middle or strong obstacle index over a long period of time. They were the crucial obstacle factors of WRCC in the Dagong irrigation district, as well as the core and difficult points of water resources management. In some counties, the effective irrigation area ratio, effective utilization coefficient of irrigation water, and water consumption ratio of the ecological environment gradually developed from strong obstacle to weak or strong promotion index. These were important reasons for the improvement of their carrying situation, reflecting their control of agricultural and ecological water consumption. In short, the results of the case study suggest that the model established in this study is conducive to the identification of water resources’ carrying status and its key obstacle factors in the Yellow River irrigation district, and can be applied to the evaluation and regulation of resources and environment carrying capacity.

Introduction

The Yellow River irrigation district plays a key role in national food security and regional water security in China (Ren et al., 2018; Xiong et al., 2021; Yin et al., 2021). However, due to the conflicting issues in water resources supply and demand, in combination with a fragile ecological environment and severe water problems in the Yellow River basin, the sustainable development of the Yellow River irrigation district is significantly restricted at present (Gonçalves et al., 2007; Jia et al., 2013; Miao et al., 2015). Water resources carrying capacity (WRCC) is a key index to quantify the sustainability of regional water resources utilization. Therefore, accurate evaluation and diagnosis of obstacle factors for WRCC in the Yellow River irrigation district are of great significance to ensure the coordinated development of water resources, the social economy, and the ecological environment (Pereira et al., 2007; Zhang X. et al., 2020; Jin et al., 2021).

Over the past 3 decades, WRCC has become a hot and difficult issue in the field of sustainable water resources utilization (Wang et al., 2013; Peng et al., 2021; Qi et al., 2021). Gong and Jin (2009) established a fuzzy comprehensive evaluation model of WRCC. Wang et al. (2018) constructed an evaluation model of WRCC based on entropy and synergy theories. Similarly, Dai et al. (2019) used a system dynamics model to evaluate WRCC. Song et al. (2020) assessed WRCC using the catastrophe series method. Wu et al. (2020) built an evaluation model of WRCC based on cloud model. Furthermore, Zhao et al. (2021) established an evaluation and influencing factor analysis model of WRCC based on the theoretical framework of pressure support, damage recovery, and recession promotion. However, previous studies on WRCC evaluation have mostly focused on cities or regions, while those focusing on irrigation districts are scarce (Kang et al., 2019; Zhang et al., 2019; He et al., 2021). In addition, research on the obstacle factor diagnosis of WRCC is even less common (Cui et al., 2018). Therefore, it is urgent to establish an effective evaluation and diagnosis model, as well as accurately identify the level and obstacle factors of WRCC in the Yellow River irrigation district.

The WRCC system is affected by many factors, including water resources, the social economy, and the ecological environment, and is a typically complex system (Yang et al., 2015; Wang et al., 2019; Liao et al., 2020). At present, the multi-index system comprehensive evaluation is an effective method of WRCC evaluation by constructing an evaluation index system and evaluation model (Zhang et al., 2019; Peng and Deng, 2020; Zuo et al., 2021). However, most models are unable to fully consider the uncertainty between evaluation samples and evaluation criteria, resulting in the deviations of evaluation results (Jin et al., 2008). Set pair analysis (SPA) is a new system uncertainty analysis method which fully reflects the certainty and uncertainty relationships between evaluation samples and evaluation criteria by the same-different-inverse structure of connection number for the set pair constructed by these two sets (Zhao, 2000; Kumar and Garg, 2016; Chong et al., 2017). This method has been widely used to comprehensively evaluate water resources system problems (Wang et al., 2009; Li et al., 2019; Zhang et al., 2021). Yang et al. (2014) used SPA to evaluate the vulnerability of water resources system. Roy and Datta (2019) studied the adaptive management of coastal aquifers based on SPA and entropy theory. In addition, Su et al. (2019) conducted water security evaluation using SPA and scenario simulation. Similarly, Lyu et al. (2021) coupled SPA and fuzzy number to assess the risk of urban water quality. Wan et al. (2021) built a river health evaluation and prediction model based on SPA and extension theory. Nevertheless, the majority of studies only reflect the evaluation results based on the connection number components (Li et al., 2021). Thus, it is difficult to obtain the value of the complete connection number, which results in a loss of information, thereby limiting the development of SPA. Moreover, the key is to reasonably determine the difference degree coefficient of the connection number.

As a key part of the connection number, the difference degree coefficient is used to quantitatively describe the uncertainty of the constructed set pair at the micro level (Zhao, 2000; Wang et al., 2009; Pan et al., 2017). This has a significant impact on the evaluation results. Several researchers have reported on the calculation methods of the difference degree coefficient. For example, Li et al. (2009) deduced and optimized the difference degree coefficient using the target value of the connection number. Tang (2009) proposed an expert estimation method of the difference degree coefficient. Furthermore, Pan et al. (2016) and Li et al. (2021) respectively constructed the trapezoidal and triangular fuzzy numbers of the difference degree coefficient, and determined the variation range of difference degree coefficient at a given cut set level. Jin et al. (2019a, 2019b) allocated the difference degree coefficient in proportions using grey correlation degree and full partial certainty, respectively. However, the majority of these methods are relatively rough and only obtain an approximate value or an interval range of difference degree coefficients (Tang, 2009; Pan et al., 2016; Li et al., 2021). In fact, accurately calculating the value of the difference degree coefficient remains difficult, which leads to large deviations between the research results and reality. In addition, this coefficient should be determined in combination with evaluation sample information. Therefore, at present, there is a need for the development of an effective method with which to calculate the difference degree coefficient.

In this study, based on the theoretical analysis and practical investigation of the water resources carrying characteristics in the Yellow River irrigation district, an evaluation index system and evaluation grade criteria were built. Additionally, a method to calculate the dynamic difference degree coefficient varying with the evaluation sample was also proposed, and the value of the complete connection number was obtained. Then, a model was established to quantitatively evaluate the WRCC and diagnose its key obstacle factors in the Yellow River irrigation district. Furthermore, this model was further applied to the Dagong irrigation district in Henan Province, China. The results provide scientific support for water resources management and decision-making in the Yellow River irrigation district.

Materials and Methods

Evaluation and Diagnosis Model of WRCC Based on Dynamic Difference Degree Coefficient

The evaluation and diagnosis model of WRCC in the Yellow River irrigation district based on dynamic difference degree coefficient was constructed according to the following steps (Figure 1):

FIGURE 1

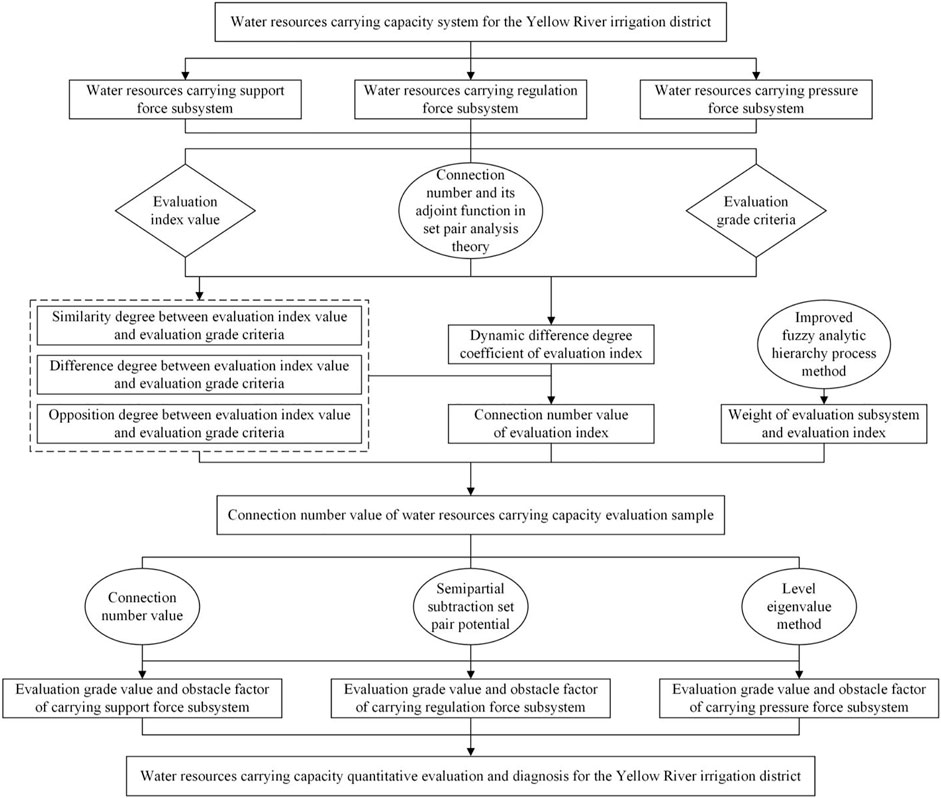
FIGURE 1. Construction process of evaluation and diagnosis model for water resources carrying capacity (WRCC) in the Yellow River irrigation district based on dynamic difference degree coefficient.

Step 1: Based on the structural and functional analysis of WRCC system (Jin et al., 2018; Liao et al., 2020), combined with the results of practical study, expert consultation, and literature review in the Yellow River irrigation district (Zhang et al., 2019; Zhang X. Y. et al., 2020; Jin et al., 2021), an evaluation index system {x_kj|k = 1, 2, 3; j = 1, 2, … , n_k} was established. The evaluation index sample set was set as {x_ikj|i = 1, 2, … , m; k = 1, 2, 3; j = 1, 2, … , n_k}, where x_ikj denotes the value of index j in subsystem k for sample i, m denotes the number of evaluation samples, k = 1, 2, 3 denotes the water resources carrying support force subsystem, carrying pressure force subsystem, and carrying regulation force subsystem, respectively, and n_k denotes the number of indexes in subsystem k. In addition, in this study, the WRCC in the Yellow River irrigation district was divided into three evaluation grades (Cui et al., 2018; Li et al., 2021) {s_gkj|g = 1, 2, 3; k = 1, 2, 3; j = 1, 2, … , n_k}, where g = 1, 2, 3 denotes the water resources loadable status, critical overloaded status, and overloaded status, respectively.

Step 2: The improved fuzzy analytical hierarchy process based on accelerating genetic algorithm (AGA-FAHP) (Jin et al., 2004) was used to determine the weight of subsystem and that of each evaluation index {w_kj|k = 1, 2, 3; j = 1, 2, … , n_k}.

For subsystem k, experts were invited to compare the importance of each index in this subsystem to the WRCC in the irrigation district, and the fuzzy complementary judgment matrix A^k = (a^k_jl)_nk×nk was obtained. This matrix met 0 ≤ a^k_jl ≤ 1 and a^k_jl + a^k_lj = 1, a^k_jl = 0.5, indicating that index j was as important as index l, a^k_jl > 0.5, indicating that index j was more important than index l, and vice versa. Furthermore, the AGA-FAHP was used to verify and modify the consistency of A^k and calculate the weight of each evaluation index w_kj. If A^k satisfies additive transitivity, then (Song and Yang, 2003):

$\left(a_{jq}^k-0.5\right)+\left(a_{ql}^k-0.5\right)=\left(a_{jl}^k-0.5\right),k=\mathrm{1,2,3};j,q,l=\mathrm{1,2},\dots ,n_k(1)$

where A^k denotes the fuzzy consistency judgment matrix, (a^k_{jl ‒} 0.5) describes the importance of index j compared with index l, and the fuzzy consistency judgment matrix meant that this preference of importance could be transmitted. Moreover, if A^k meets complete consistency, then (Song and Yang, 2003):

${\displaystyle \sum _{j=1}^{n_k}{\displaystyle \sum _{l=1}^{n_k}\left|0.5\left(n_k-1\right)\left(w_{kj}-w_{kl}\right)+0.5-a_{jl}^k\right|/n_k^2}}=0(2)$

where the left term in Eq. 2 is the consistency index of A^k. If this index did not exceed a certain critical value, it would indicate that A^k had satisfactory consistency. Otherwise, A^k should be modified. The modified matrix was B^k = (b^k_jl)_nk×nk, and the sorting weight of the element in B^k was still set as {w_kj|k = 1, 2, 3; j = 1, 2, … , n_k}. Hence, B^k satisfies the following equation (Jin et al., 2004):

$\begin{array}{l}\min CIC\left(n_k\right)={\displaystyle \sum _{j=1}^{n_k}{\displaystyle \sum _{l=1}^{n_k}\left|b_{jl}^k-a_{jl}^k\right|/n_k^2+}}{\displaystyle \sum _{j=1}^{n_k}{\displaystyle \sum _{l=1}^{n_k}\left|0.5\left(n_k-1\right)\left(w_{kj}-w_{kl}\right)+0.5-b_{jl}^k\right|}}/n_k^2\\ \mathrm{s}.\mathrm{t}.\{\begin{array}{l}{b}_{jj}^k=0.5,k=\mathrm{1,2,3};j=\mathrm{1,2},\dots ,n_k\\ 1-b_{lj}^k=b_{jl}^k\in \left[a_{jl}^k-d,a_{jl}^k+d\right]\cap \left[\mathrm{0,1}\right],\\ k=\mathrm{1,2,3};j=\mathrm{1,2},\dots ,n_k;l=j+1,j+2,\dots ,n_k\\ {\displaystyle \sum _{j=1}^{n_k}{w}_{kj}=1.0,w_{kj}\in \left[\mathrm{0,1}\right],k=\mathrm{1,2,3};j=\mathrm{1,2},\dots ,n_k}\end{array}\end{array}(3)$

which represents the optimal fuzzy consistency judgment matrix for A^k. Here, CIC(n_k) is the consistency index coefficient and d is a parameter that usually takes the value within [0, 0.5]. The sorting weight {w_kj|k = 1, 2, 3; j = 1, 2, … , n_k} and the upper triangular elements in B^k were the optimization variables. Accelerating genetic algorithm (AGA) is a general global optimization method and it is effective in solving Eq. 3. In addition, when CIC(n_k) was less than a certain critical value, A^k was considered to have satisfactory consistency, and the obtained sorting weight of each evaluation index was acceptable. Otherwise, d should be adjusted. Based on a large number of simulation tests and relevant studies (Jin et al., 2004; Cui et al., 2018), a critical value of 0.20 was selected in this study.

Step 3: SPA is an original theory of uncertainty quantitative analysis proposed by Chinese scholar Zhao Keqin in 1989 (Zhao, 2000). The foundation of SPA was the connection number u of the set pair constructed by two sets with a common attribute, and the certainty and uncertainty relationships of the set pair were quantitatively described by a same-different-inverse structure. Specifically, according to SPA, the certainty of the set pair was divided into two aspects of similarity and opposition, which were quantitatively expressed by a and c, respectively. Furthermore, the uncertainty of the set pair was divided into the uncertainty at a macro level, which was measured by b, and that at the micro level, which was depicted by I. The ternary connection number u, which was commonly used, is expressed as follows (Yang et al., 2014):

$u=a+bI+cJ(4)$

where a, b, and c denote the similarity degree, difference degree, and opposition degree components of connection number u, respectively, which were used to quantitatively express the degrees of the same property, different property, and inverse property for the constructed set pair, a + b + c = 1. I denotes the difference degree coefficient and its value varies with the relationship type of the set pair. The set pair constructed in this study belonged to the positive-negative type, and I generally took the value within [‒1, 1]. J denotes the opposition degree coefficient, which generally takes ‒1 for the set pair of positive-negative type (Wang et al., 2009; Cui et al., 2018).

Based on SPA and the practical problem of WRCC evaluation in the Yellow River irrigation district, two sets of evaluation index value and evaluation grade criteria constituted a set pair. According to the variable fuzzy set of the proximity between index value and grade criteria, the connection number of evaluation index was calculated. Specifically, the initial ternary connection number component u_gikj between WRCC evaluation index sample value x_ikj and grade criteria s_gkj (g = 1, 2, 3) in the irrigation district were, respectively, as follows (Jin et al., 2008):

$u_{1ikj}=\{\begin{array}{l}1,s_{0kj}\le x_{ikj}\le s_{1kj}\text{for}\text{positive}\text{index},\hfill \\ \text{or}{s}_{0kj}\ge x_{ikj}\ge s_{1kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ 1-2\left(x_{ikj}-s_{1kj}\right)/\left(s_{2kj}-s_{1kj}\right),s_{1kj}<x_{ikj}\le s_{2kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{1kj}>x_{ikj}\ge s_{2kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ -1,s_{2kj}<x_{ikj}\le s_{3kj}\text{for}\text{positive}\text{index},\hfill \\ \text{or}{s}_{2kj}>x_{ikj}\ge s_{3kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \end{array}(5)$

$u_{2ikj}=\{\begin{array}{l}1-2\left(s_{1kj}-x_{ikj}\right)/\left(s_{1kj}-s_{0kj}\right),s_{0kj}\le x_{ikj}\le s_{1kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{0kj}\ge x_{ikj}\ge s_{1kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ 1,s_{1kj}<x_{ikj}\le s_{2kj}\text{for}\text{positive}\text{index},\hfill \\ \text{or}{s}_{1kj}>x_{ikj}\ge s_{2kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ 1-2\left(x_{ikj}-s_{2kj}\right)/\left(s_{3kj}-s_{2kj}\right),s_{2kj}<x_{ikj}\le s_{3kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{2kj}>x_{ikj}\ge s_{3kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \end{array}(6)$

$u_{3ikj}=\{\begin{array}{l}-1,s_{0kj}\le x_{ikj}\le s_{1kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{0kj}\ge x_{ikj}\ge s_{1kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ 1-2\left(s_{2kj}-x_{ikj}\right)/\left(s_{2kj}-s_{1kj}\right),s_{1kj}<x_{ikj}\le s_{2kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{1kj}>x_{ikj}\ge s_{2kj}\text{for}\text{negative}\text{index}\hfill \\ 1,s_{2kj}<x_{ikj}\le s_{3kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{2kj}>x_{ikj}\ge s_{3kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \end{array}(7)$

where the larger the value of positive (negative) index, the higher (lower) the evaluation grade. s_1kj and s_2kj denote the critical value between grade 1 and grade 2, and that between grade 2 and grade 3, respectively, for index j in subsystem k. s_0kj and s_3kj denote the other critical values of grade 1 and grade 3, respectively.

The initial ternary connection number component u_gikj depended on whether the evaluation index sample value x_ikj belonged to the same interval, adjacent interval, or separated interval of evaluation grade g, and took 1, the value within [‒1, 1], or ‒1, respectively. Therefore, u_gikj can be regarded as a relative difference degree function for the variable fuzzy set of the proximity between index value and grade criteria, the corresponding relative membership degree is as follows (Chen, 2005):

$a_{ikj}^{\ast }=0.5+0.5u_{1ikj},b_{ikj}^{\ast }=0.5+0.5u_{2ikj},c_{ikj}^{\ast }=0.5+0.5u_{3ikj},i=\mathrm{1,2},\dots ,m;k=\mathrm{1,2,3};j=\mathrm{1,2},\dots ,n_k(8)$

Furthermore, the final ternary connection number components a, b, and c of the WRCC evaluation index in the irrigation district were obtained using Eq. 8 after normalization as follows (Jin et al., 2008; Cui et al., 2018):

$a_{ikj}=a_{ikj}^{\ast }/\left(a_{ikj}^{\ast }+b_{ikj}^{\ast }+c_{ikj}^{\ast }\right),b_{ikj}=b_{ikj}^{\ast }/\left(a_{ikj}^{\ast }+b_{ikj}^{\ast }+c_{ikj}^{\ast }\right),c_{ikj}=c_{ikj}^{\ast }/\left(a_{ikj}^{\ast }+b_{ikj}^{\ast }+c_{ikj}^{\ast }\right)(9)$

Step 4: According to SPA and the expression of connection number u in Eq. 4, the difference degree coefficient I was the link that transformed difference degree b to similarity degree a or opposition degree c under certain conditions. It was considered to be an important connector between the theoretical model of connection number and the practical research question. Therefore, how to scientifically determine I was a key and challenging problem when calculating the value of the complete connection number. However, the value process of difference degree coefficient I was highly uncertain and complex and few studies had been published at present.

The difference degree coefficient I was essential to quantitatively describe the uncertainty of set pair at the micro level (Zhao, 2000; Wang et al., 2009; Pan et al., 2017), while an important source of the uncertainty was the information carried by sample data. In addition, the physical meaning of I can be interpreted as the level of difference degree b transformed to similarity degree a or opposition degree c, wherein the direction (transformed to a or c) and magnitude should be closely related to the proximity between evaluation sample value and each evaluation grade. That was, the larger the value of a (or c), the more b transformed to a (or c). Therefore, I should vary continuously and dynamically with the practical sample value of research question. In this study, the set pair composed of WRCC evaluation index sample value x_ikj and grade criteria s_gkj in the Yellow River irrigation district belonged to the positive-negative type, where the value range of I was [‒1, 1] (Zhao, 2000; Zhang, 2020a; Jin et al., 2021). Furthermore, when I was within [0, 1], this indicated that b transformed to a, whereas when I was within [‒1, 0], indicating that b transformed to c, and the absolute value of I reflected the transformed magnitude. In other words, the difference degree coefficient I_ikj in this study continuously and dynamically changed with the evaluation index sample value x_ikj, as shown in Figure 2. Specifically, when x_ikj was closer to the critical value s_0kj of grade 1, I_ikj was closer to 1. When x_ikj was closer to the critical value s_1kj between grades 1 and 2, I_ikj was closer to 1/3. When x_ikj was closer to the critical value s_2kj between grades 2 and 3, I_ikj was closer to ‒1/3. Moreover, when x_ikj was closer to the critical value s_3kj of grade 3, I_ikj was closer to ‒1. Based on SPA and the above analysis, this study proposed a method for calculating the dynamic difference degree coefficient of the ternary connection number as follows:

$I_{ikj}=\{\begin{array}{l}1-2\left(x_{ikj}-s_{0kj}\right)/3\left(s_{1kj}-s_{0kj}\right),s_{0kj}\le x_{ij}\le s_{1kj}\mathbf{for}\mathbf{positive}\mathbf{index}\text{,}\hfill \\ \mathbf{or}{s}_{0kj}\ge x_{ikj}\ge s_{1kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ -2\left[x_{ikj}-\left(s_{1kj}+s_{2kj}\right)/2\right]/3\left(s_{2kj}-s_{1kj}\right),s_{1kj}<x_{ikj}\le s_{2kj}\mathbf{for}\mathbf{positive}\mathbf{index},\hfill \\ \mathbf{or}{s}_{1kj}>x_{ikj}\ge s_{2kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \\ -1+2\left(s_{3kj}-x_{ikj}\right)/3\left(s_{3kj}-s_{2kj}\right)\text{,}{s}_{2kj}<x_{ikj}\le s_{3kj}\mathbf{for}\mathbf{positive}\mathbf{index}\text{,}\hfill \\ \mathbf{or}{s}_{2kj}>x_{ikj}\ge s_{3kj}\mathbf{for}\mathbf{negative}\mathbf{index}\hfill \end{array}(10)$

FIGURE 2

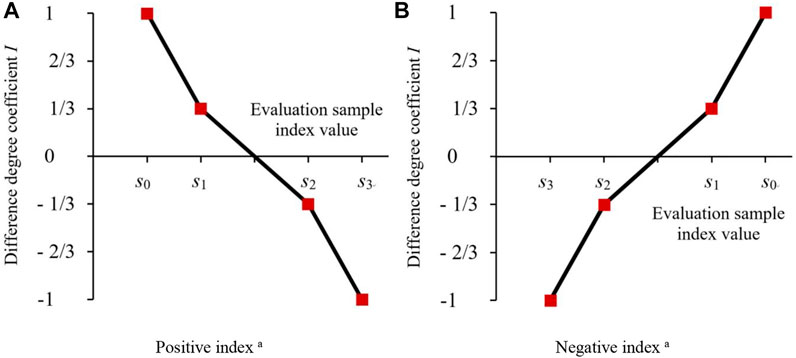
FIGURE 2. Value process for dynamic difference degree coefficient of the ternary connection number changes with evaluation index sample value. The larger the value of positive (negative) index, the higher (lower) the evaluation grade.

Step 5: The ternary connection number u_ikj of index j in subsystem k for WRCC evaluation sample i was calculated by substituting the results obtained by Eqs. 5‒10) into Eq. 4 (Zhao, 2000; Jia et al., 2013):

$u_{ikj}=a_{ikj}+b_{ikj}{I}_{ikj}+c_{ikj}J,i=\mathrm{1,2},\dots ,m;k=\mathrm{1,2,3};j=\mathrm{1,2},\dots ,n_k(11)$

Combined with the weight w_kj of index j in subsystem k obtained by Eq. 3, the ternary connection number u_ik of subsystem k for sample i was calculated as follows (Jin et al., 2008):

$u_{ik}={\displaystyle \sum _{j=1}^{n_k}{w}_{kj}{a}_{ikj}}+{\displaystyle \sum _{j=1}^{n_k}{w}_{kj}{b}_{ikj}}{I}_{ikj}+{\displaystyle \sum _{j=1}^{n_k}{w}_{kj}{c}_{ikj}}J,i=\mathrm{1,2},\dots ,m;k=\mathrm{1,2,3}(12)$

Finally, the ternary connection number u_i of WRCC evaluation sample i in the Yellow River irrigation district was obtained according to the following equation (Cui et al., 2018):

$u_i={\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}{a}_{ikj}}}+{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}{b}_{ikj}}{I}_{ikj}}+{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}{c}_{ikj}}J},i=\mathrm{1,2},\dots ,m(13)$

where w_k denotes the weight of subsystem k, which can be calculated using the AGA-FAHP.

The evaluation grade value of WRCC in the irrigation district was calculated based on the connection number value u obtained by Eq. 13, wherein u∈[‒1, 1]. Furthermore, u was divided into three levels according to the critical values of evaluation index grade criteria, which corresponded to water resources overloaded status u∈[‒1.000, ‒0.667), critical overloaded status u∈[‒0.667, 0.667], and loadable status u∈(0.667, 1.000], respectively.

To compare with the connection number value u, the evaluation grade value h_i of sample i was calculated using the level eigenvalue method (Zhou et al., 2022) in Eq. 14. h was also divided into three levels according to the critical values of evaluation index grade criteria, which corresponded to water resources overloaded status h∈(2.5, 3.0], critical overloaded status h∈[1.5, 2.5], and loadable status h∈[1.0, 1.5), respectively.

$h_i={\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}}}{a}_{ikj}+2{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}}}{b}_{ikj}+3{\displaystyle \sum _{k=1}^3{\displaystyle \sum _{j=1}^{n_k}{w}_k{w}_{kj}}}{c}_{ikj},i=\mathrm{1,2},\dots ,m(14)$

Step 6: The main obstacle factors hindering the improvement of WRCC in the Yellow River irrigation district were diagnosed based on the connection number value u_ikj of evaluation index calculated using Eq. 11. It can be proven that u_ikj∈[‒1, 1], and based on the principle of equal division, the evaluation indexes were divided into five types. They were strong obstacle u_ikj∈[‒1.0, ‒0.6), middle obstacle u_ikj∈[‒0.6, ‒0.2), weak obstacle u_ikj∈[‒0.2, 0.2], weak promotion u_ikj∈(0.2, 0.6], and strong promotion indexes u_ikj∈(0.6, 1.0]. Moreover, the strong or middle obstacle index was the factor that seriously hindered the improvement of WRCC, and at the same time, the key focus of water resources regulation and control in the irrigation district.

For comparison with the connection number value u, the set pair potential of connection number for evaluation index was used to diagnose the obstacle factors of WRCC. According to SPA, set pair potential reflected the overall development trend of set pair at the macro level (Zhao, 2000; Zhou et al., 2022). To quantitatively describe this trend, Cui et al. (2018) constructed the subtraction set pair potential s₁(u) of the ternary connection number in Eq. 15, the basic idea was to allocate b to a and c according to the proportions of a/(a+b + c) and c/(a+b + c), respectively:

$s_1\left(u_{ikj}\right)=\left[a_{ikj}+b_{ikj}{a}_{ikj}/\left(a_{ikj}+b_{ikj}+c_{ikj}\right)\right]-\left[c_{ikj}+b_{ikj}{c}_{ikj}/\left(a_{ikj}+b_{ikj}+c_{ikj}\right)\right](15)$

In addition, the partial connection number reflected the overall development trend of set pair at the micro level (Zhao, 2000). From the perspective of same-different-inverse transformation based on the partial connection number, to transform the similarity component of b to a, (a+b) should be regarded as a whole of the similarity and should not include the opposition degree c. Therefore, it was more reasonable to take a/(a+b) as the proportion of b allocated to a than a/(a+b + c) in Eq. 15. Similarly, to transform the opposition component of b to c, (c + b) should be regarded as a whole of the opposition and should not include the similarity degree a. It was more reasonable to consider c/(c + b) as the proportion of b allocated to c than c/(a+b + c) in Eq. 15. Therefore, based on the subtraction set pair potential and further combined with the idea of the partial connection number, a new adjoint function of the ternary connection number, the semipartial subtraction set pair potential s₂(u) was proposed (Jin et al., 2021):

$s_2\left(u_{ikj}\right)=\{\begin{array}{l}-1,a_{ikj}+b_{ikj}=0\\ 1,b_{ikj}+c_{ikj}=0\\ \left[a_{ikj}+b_{ikj}{a}_{ikj}/\left(a_{ikj}+b_{ikj}\right)\right]-\left[c_{ikj}+b_{ikj}{c}_{ikj}/\left(c_{ikj}+b_{ikj}\right)\right],\\ a_{ikj}+b_{ikj}\ne 0\mathrm{and}{b}_{ikj}+c_{ikj}\ne 0\end{array}(16)$

It can be seen that s₂(u_ikj)∈[‒1, 1], according to the principle of equal division, s₂(u_ikj) was divided into five levels. They were inverse potential s₂(u_ikj)∈[‒1.0, ‒0.6), partial inverse potential s₂(u_ikj)∈[‒0.6, ‒0.2), symmetrical potential s₂(u_ikj)∈[‒0.2, 0.2], partial identical potential s₂(u_ikj)∈(0.2, 0.6], and identical potential s₂(u_ikj)∈(0.6, 1.0], respectively. Furthermore, the index of partial inverse potential or inverse potential was diagnosed as the main obstacle factor hindering the improvement of WRCC and also the important object of water resources management in the Yellow River irrigation district (Li et al., 2021).

Study Area

The evaluation and diagnosis model of WRCC based on dynamic difference degree coefficient was applied to the Dagong ecological irrigation district in Henan Province, China. The level of WRCC and key obstacle factors were quantitatively identified in the typical Yellow River irrigation district. The Dagong irrigation district was located in the north of the Yellow River (Figure 3), with a design irrigation area of 190,000 ha and a land area of 2,886 km². It was a large-scale Yellow River irrigation district in Henan Province (Zhang et al., 2019; Du et al., 2020). This irrigation district included Neihuang County, Xun County, Hua County, Changyuan County, and Fengqiu County, all of these were advanced counties of grain production in China. The main planting crops included wheat, rice, and corn, while intercropping crops included peanuts, millet, beans, cotton, and sesame (Zhang X. et al., 2020). In recent years, with the rapid development of the social economy in the irrigation district, the demand for water resources for agriculture, life, secondary and tertiary industries, and ecology had continuously increased, which resulted in a prominent contradiction between limited supply and increased demand for water resources (Gonçalves et al., 2007; Pereira et al., 2007; Jia et al., 2013). In summary, the water resources situation in the Dagong irrigation district was severe.

FIGURE 3

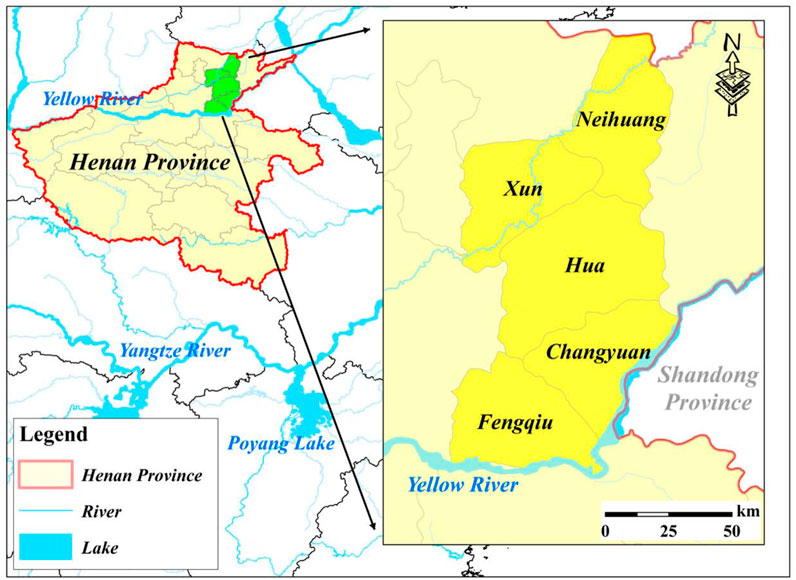
FIGURE 3. Location of the Dagong ecological Yellow River irrigation district in Henan Province, China.

Results and Discussion

Establishment of WRCC Evaluation Index System in Irrigation District

According to the evaluation target and construction principle of evaluation index system (Gong and Jin, 2009; Song et al., 2011; Chang et al., 2020), and combined with the influencing factors of the real process for WRCC in the ecological Yellow River irrigation district, the WRCC system was divided into three subsystems. They were water resources carrying support force subsystem, carrying pressure force subsystem, and carrying regulation force subsystem, respectively (Cui et al., 2018; Jin et al., 2018; Li et al., 2021). Moreover, based on the comprehensive analysis of carrying characteristics for these three subsystems, the actual development of water resources, the social economy, and the ecological environment in the Dagong irrigation district, as well as relevant research (Du et al., 2020; Zhang X. et al., 2020; Jin et al., 2021), an evaluation index system (three subsystems, a total of nine indexes X₁—X₉), and the corresponding evaluation grade criteria (water resources loadable, critical overloaded, and overloaded status) are listed in Table 1. In addition, the weights of subsystem and each evaluation index were determined using the AGA-FAHP in Eq. 3, together with relevant studies (Du et al., 2020; Zhang X. et al., 2020) (Table 1).

TABLE 1

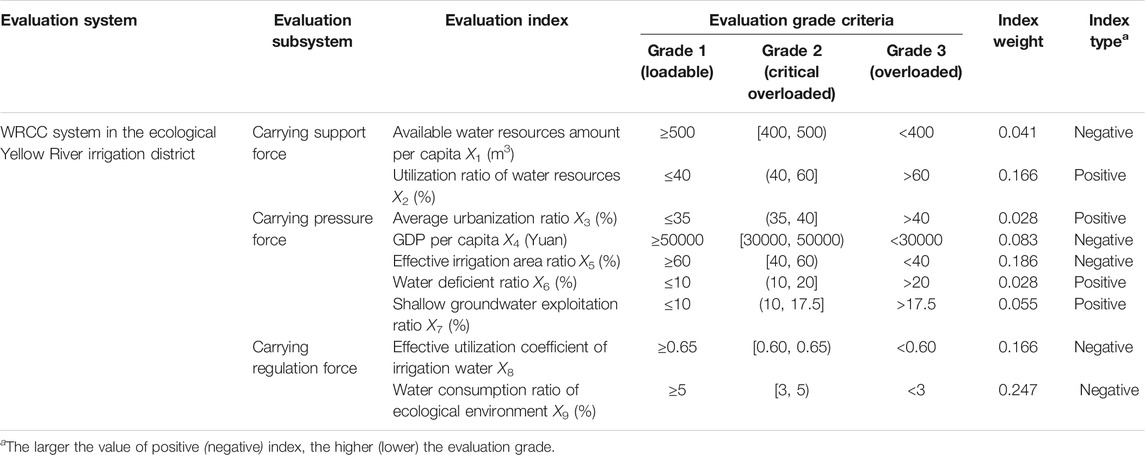
TABLE 1. Evaluation index system and evaluation grade criteria of water resources carrying capacity (WRCC) in the ecological Yellow River irrigation district (Du et al., 2020; Zhang X. et al., 2020; Jin et al., 2021).

In this study, the sample data of WRCC evaluation index in the Dagong irrigation district were obtained from the Henan Water resources Bulletin (2010–2017), the Henan Statistical Yearbook (2011–2018), and phased achievements of the third national survey and evaluation of water resources utilization in Henan Province, China.

Evaluation and Analysis of WRCC for Five Counties in Irrigation District

The sample data of nine WRCC evaluation indexes for five counties in the Dagong irrigation district from 2010 to 2017, and the corresponding evaluation grade criteria in Table 1, were substituted into Eq. 5‒9 to obtain the connection number components of each index. Furthermore, the dynamic difference degree coefficient of the connection number for each index was calculated in combination with Figure 2 and Eq. 10. Then, according to the index weight in Table 1 and Eq. 11‒13, the connection number values of evaluation index, subsystem, and WRCC were calculated. Meanwhile, the evaluation grade value according to the level eigenvalue method was obtained using Eq. 14. Finally, the evaluation results of WRCC in the Dagong irrigation district are shown in Figures 4‒6.

FIGURE 4

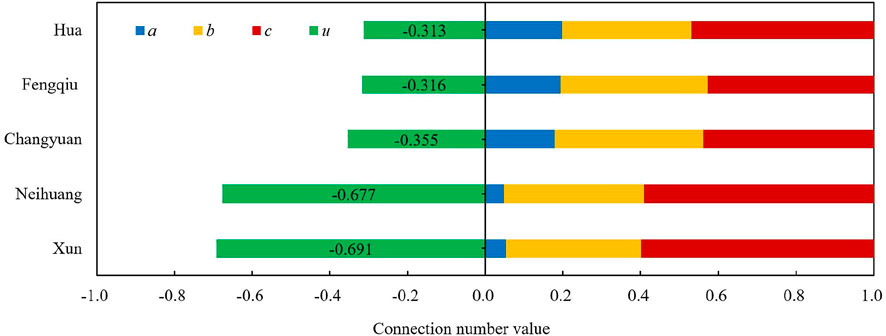
FIGURE 4. Average values of connection number u and its components a, b, and c for water resources carrying capacity (WRCC) evaluation from 2010 to 2017 in the Dagong irrigation district.

(1) According to the average value of WRCC evaluation connection number u from 2010 to 2017 for each county (Figure 4), from the perspective of multi-year average, Xun County and Neihuang County belonged to the water resources overloaded status (‒1.000 ≤ u < ‒0.667), while the other three counties were in critical overloaded status (‒0.667 ≤ u ≤ 0.667). The results are consistent with those of Du et al. (2020) and Zhang et al. (2021). It indicates that although the carrying status of the five counties has been different over the years, the overall carrying situation in the Dagong irrigation district is serious. Thus, there is a need to analyze the driving mechanism of WRCC in different counties, identify the key factors hindering the improvement of WRCC, and then take the corresponding measures.

In addition, it can be seen that from the average value of the connection number component (Figure 4), the multi-year average values of opposition degree c for the five counties were all significantly larger than those of similarity degree a, which was consistent with the above evaluation result of severe water resources carrying situation for these five counties. Moreover, the average values of a in Hua County, Fengqiu County, and Changyuan County were relatively higher (0.198, 0.193, and 0.179, respectively), while those of c in Xun County and Neihuang County were relatively larger (0.598 and 0.591) (Figure 4). These results were consistent with the above result that the WRCC in Hua County, Fengqiu County, and Changyuan County were stronger than those in Xun County and Neihuang County.

(2) It can be seen from the evaluation results of two methods (Figure 5), the changing trends of the evaluation grade values of WRCC for five counties from 2010 to 2017 calculated by connection number method were consistent with those of level eigenvalue method. Furthermore, the changing range and the differences in grade value year to year obtained by connection number were more significant than level eigenvalue. It shows that the evaluation method of the connection number based on the dynamic difference degree coefficient can fully excavate and make use of the information carried by sample data. Furthermore, the uncertainty of the WRCC system can be accurately quantified by the dynamic difference degree coefficient varying with the actual evaluation sample, and the value of the complete connection number can be directly determined. Therefore, the WRCC evaluation method proposed in this study has a higher sensitivity and accuracy, and the evaluation results are reasonable and reliable.

FIGURE 5

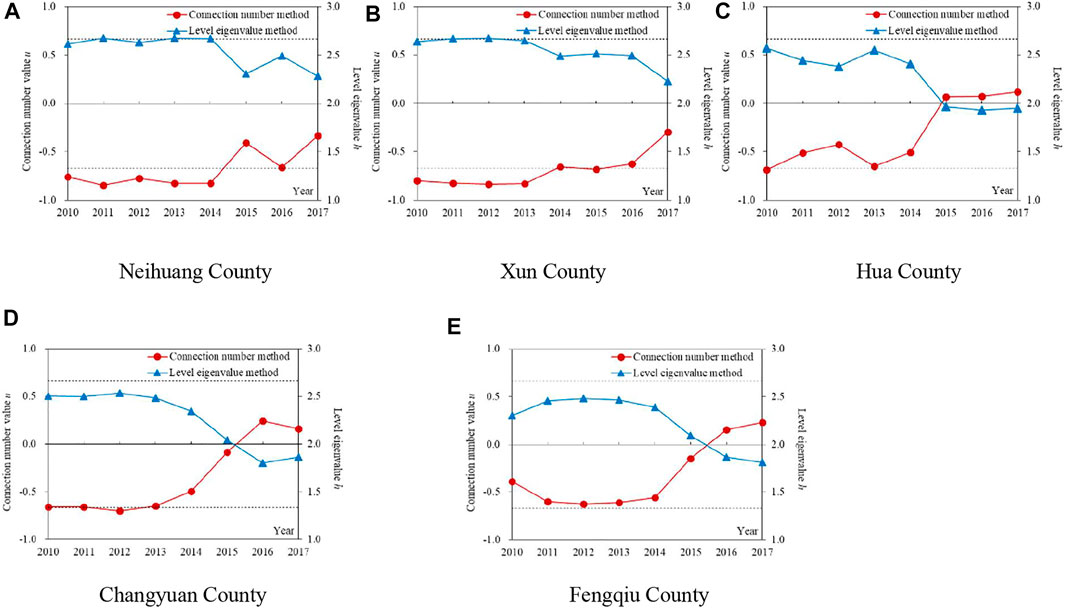
FIGURE 5. Evaluation grade values of two methods for water resources carrying capacity (WRCC) from 2010 to 2017 in the Dagong irrigation district. The two dashed lines from top to bottom in the figures represent the boundary of connection number value for water resources loadable and critical overloaded status (0.667), and that for critical overloaded and overloaded status (‒0.667) in each county, respectively.

(3) According to the connection number values and the corresponding grade values of WRCC evaluation for each county from 2010 to 2017 (Figures 6, 7), from the perspective of overall development in the irrigation district, from 2010 to 2017, most counties were in water resources overloaded status (‒1.000 ≤ u < ‒0.667), some belonged to critical overloaded status (‒0.667 ≤ u ≤ 0.667), and others were in loadable status (0.667 < u ≤ 1.000). Furthermore, the number of overloaded counties decreased from three in 2010 to zero in 2017, and the average value of the connection number for the five counties decreased from ‒0.656 in 2010 to ‒0.022 in 2017. After 2013, the average value from 2010 to 2013 and that from 2014 to 2017 were ‒0.681 (overloaded) and ‒0.260 (critical overloaded), respectively. Additionally, in 2016 and 2017, the connection number values of the three counties (Fengqiu County, Changyuan County, and Hua County) were larger than zero and approached loadable status (Figure 6). The WRCC in the irrigation district were significantly improved and. it indicates that although the carrying situation in the Dagong irrigation district is severe in recent years, it has developed in a favorable direction as a whole (Zhang et al., 2019; Jin et al., 2021). Thus, there is a need to continuously strengthen the scientific measures of water resources regulation. In addition, the Dagong irrigation district may not have paid enough attention to water resources management before 2013, resulting in the exploitation of water resources far exceeding the available amount. The WRCC system is unbalanced and the WRCC is weak. However, since the implementation of the strictest water resources management system in China (Zuo et al., 2014; Wang et al., 2018), the carrying situation in the irrigation district has been improved markedly, which is consistent with the studies of Du et al. (2020) and Zhang X. et al. (2020).

FIGURE 6

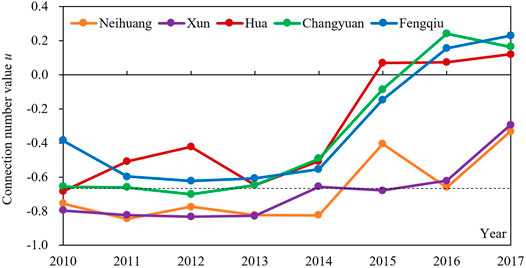
FIGURE 6. Connection number values of water resources carrying capacity (WRCC) evaluation from 2010 to 2017 in the Dagong irrigation district. The dashed line in the figure represents the boundary of the connection number value for water resources critical overloaded and overloaded status (‒0.667) in the irrigation district.

FIGURE 7

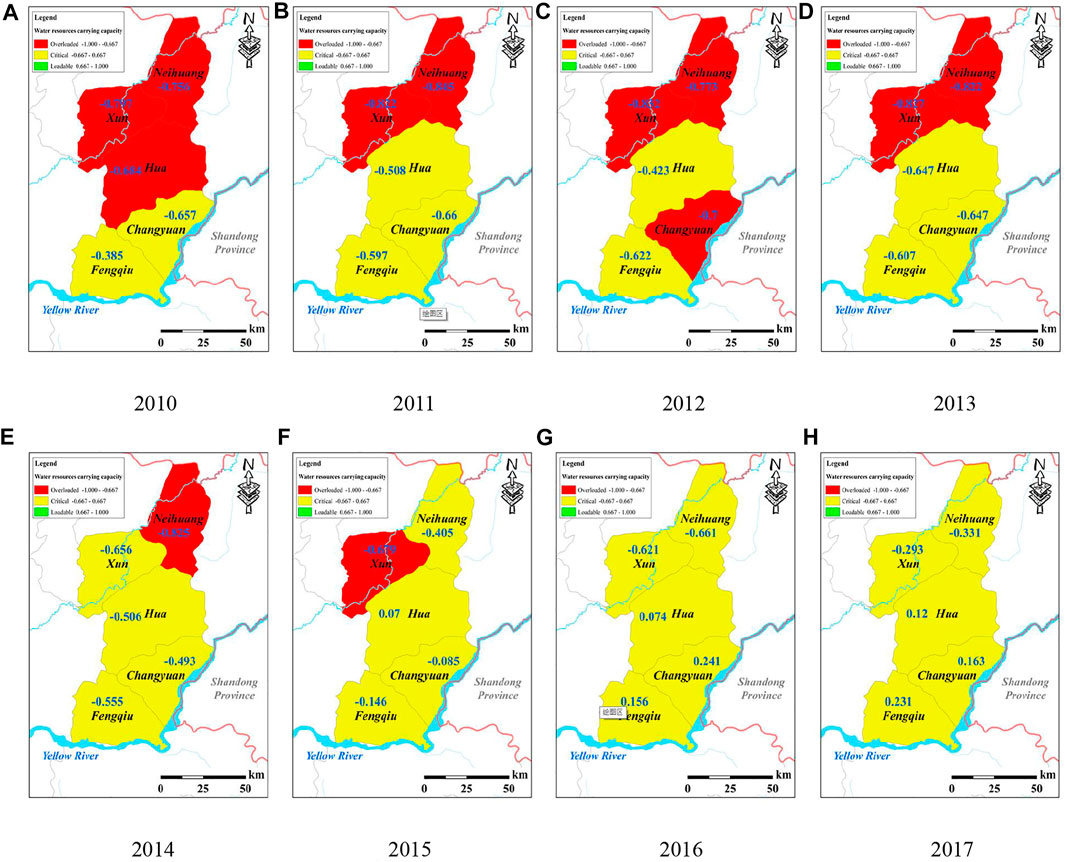
FIGURE 7. Spatial distributions of water resources carrying capacity (WRCC) evaluation grade values from 2010 to 2017 in the Dagong irrigation district.

From the perspective of each county, from 2010 to 2017, the WRCC of the five counties tended to be improved, wherein the magnitudes in Hua County, Changyuan County, and Fengqiu County were significantly higher than Neihuang County and Xun County, especially since 2015. Also, the connection number value in Neihuang County decreased from 2015 to 2016, reflecting the decline of WRCC (Figure 6). The average values of the connection number from 2015 to 2017 in Hua County, Changyuan County, and Fengqiu County were 0.088, 0.106, and 0.080, respectively, all greater than zero, while those in Neihuang County and Xun County were ‒0.466 and ‒0.531, which were close to the edge of overloaded status. Moreover, in 2017, the order of carrying status in the five counties from excellent to poor was Fengqiu County, Changyuan County, Hua County, Xun County, and Neihuang County, with the corresponding connection number values of 0.231, 0.163, 0.120, ‒0.293, and ‒0.331, respectively. It is consistent with the fact that these five counties become farther away from the main stream of the Yellow River (Figure 7). Therefore, the WRCC in each county is significantly related to its distance from the Yellow River (Jin et al., 2021).

In reality, there are many upstream and downstream management units of the backbone projects in the Dagong irrigation district, wherein their relationships are complex and difficult to coordinate, and the upstream water resources supply conditions cannot meet the downstream demand (Zhang X. Y. et al., 2020). Taking Neihuang County at the downstream end of the irrigation canal system as an example, this county needs to apply to the Dagong management office of Xinxiang City and coordinate with the water conservancy bureaus of the upstream counties for water resources use (Song and Zhang, 2018). There are many intermediate links that make it extremely difficult to use water resources. In addition, Neihuang County has only been able to divert water once a year in flood season since 2009, with a time of 1 week. Furthermore, the Yellow River diversion and storage projects are dry most of the time (Zhang, 2017). Combined with the statistical data, in 2017, the available water resources amount per capita in Fengqiu County, Changyuan County, Hua County, Xun County, and Neihuang County are 340.00 m³, 298.50 m³, 280.56 m³, 178.49 m³, and 278.00 m³, respectively. Correspondingly, the average water deficient ratios from 2010 to 2017 are 27.91%, 29.91%, 45.60%, 54.89%, and 41.04%, respectively. The above results are also consistent with the studies of Zhang et al. (2015) and Du et al. (2020), indicating that the WRCC of Changyuan County and Fengqiu County have begun to be strengthened since 2014, and the WRCC in the Dagong irrigation district improved in 2017, and the exceptions are Neihuang County and Xun County. Therefore, to promote the WRCC of each county in the Dagong irrigation district to a direction of improvement, this study further analyzes the change of the connection number value for each evaluation index year to year, and diagnoses the main obstacle factors of WRCC.

Affected by many factors such as nature, the economy, society, population, science and technology, the WRCC system in irrigation district is a typical complex system with great uncertainty, mainly including a kind of fuzzy uncertainty due to the uncertainty of the boundary between evaluation samples and evaluation criteria. In this study, SPA is applied to the WRCC evaluation in the Yellow River irrigation district, two sets of evaluation index value and evaluation grade criteria constitute a set pair, and the certainty and uncertainty of their proximity are quantitatively analyzed from three aspects of the same (the evaluation sample value is at the same level as the evaluation level), different (adjacent level) and inverse (separated level). Specifically, SPA divides the certainty of this set pair into similarity and opposition components, which are quantitatively described by a and c, respectively. In addition, the uncertainty between similarity and opposition is divided into the uncertainty at the macro level, measured by b, and that at the micro level, measured by I. Therefore, the calculation method of dynamic difference degree coefficient I varying with evaluation sample proposed in this study, quantifies the uncertainty at the micro level of the set pair constituted by index value and grade criteria. From the perspective of information utilization, this method retains the extremely important information of the variation range of sample data for the research objective. In a word, this study further considers the boundary fuzzy uncertainty of WRCC system in the Yellow River irrigation district, making the evaluation results more comprehensive, more objective, and closer to reality.

Diagnosis of WRCC Obstacle Factors for Five Counties in Irrigation District

The changes of WRCC for each county in recent years were analyzed and discussed above. Then, the obstacle factors of WRCC were diagnosed by the connection number value and semipartial subtraction set pair potential of evaluation index to provide a basis for water resources regulation and control in the Dagong irrigation district.

(1) The connection number value of evaluation index was calculated using the connection number components and difference degree coefficients according to Eq. 11. The average values of the connection number for each index from 2010 to 2017 for five counties in the irrigation district are listed in Table 2. As shown in Table 2, there were six, six, five, two, and three strong obstacle indexes (‒1.0 ≤ u < ‒0.6) in Neihuang County, Xun County, Hua County, Changyuan County, and Fengqiu County, respectively, on average for many years. Nevertheless, there were zero, zero, one, one, and one strong promotion indexes (0.6 < u ≤ 1.0), respectively. These results were consistent with the above results that the WRCC of Fengqiu County, Changyuan County, and Hua County were stronger than Neihuang County and Xun County (Figures 4, 7). It indicates that the numbers of strong obstacle indexes and the strong promotion indexes determined by the connection number value in this study can reflect the overall carrying situation of each county. The more the strong obstacle index and the less the strong promotion index, the worse the carrying status, and vice versa.

TABLE 2

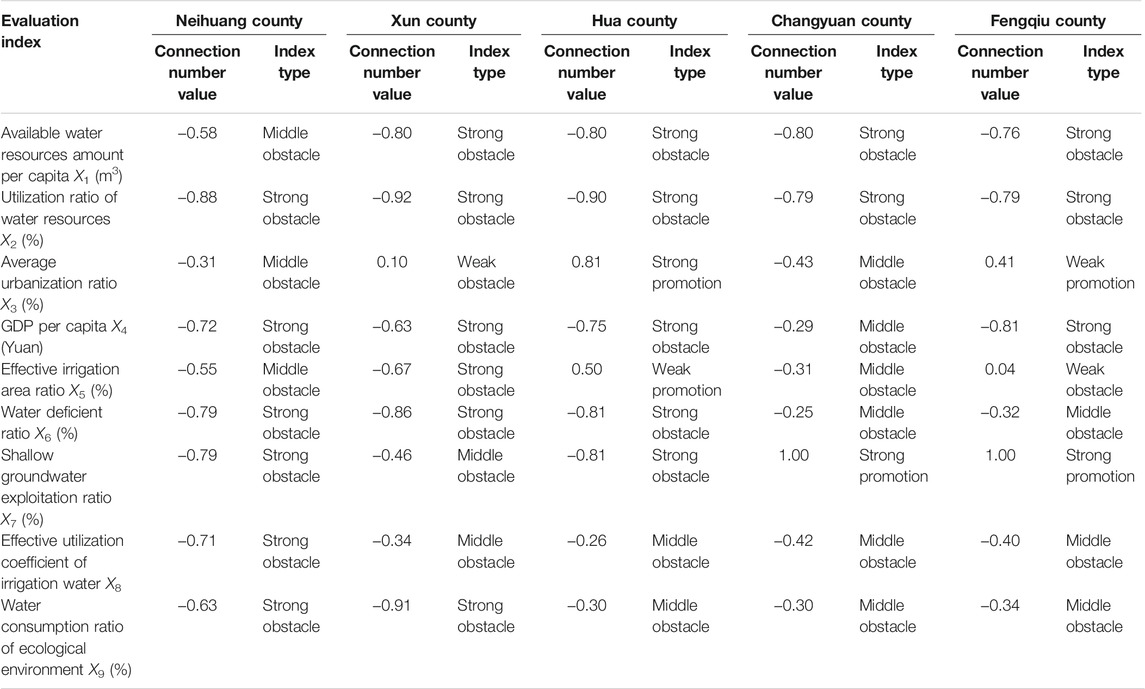
TABLE 2. Average values of connection number for water resources carrying capacity (WRCC) evaluation index from 2010 to 2017 in the Dagong irrigation district.

Over the years, the utilization ratio of water resources X₂ was a strong obstacle index, available water resources amount per capita X₁, GDP per capita X₄, and water deficient ratio X₆ were strong or middle obstacle indexes for the five counties (Table 2). These are the key factors that hinder the improvement of WRCC in the Dagong irrigation district, and also the important objects of WRCC regulation and control. Meanwhile, the annual variations of the connection number value for these indexes are so small that they are difficult to be improved and regulated.

(2) The connection number values of nine WRCC evaluation indexes from 2010 to 2017 for five counties in the Dagong irrigation district, and the semipartial subtraction set pair potential calculated by Eq. 16, are shown in Figure 8. The change of the connection number value for each index was analyzed and the key influencing factors of carrying status in each county were identified. Moreover, the strong obstacle index and middle obstacle index were the main reasons for weak WRCC, which can be diagnosed as the obstacle factors of WRCC and key objects to be improved.

FIGURE 8

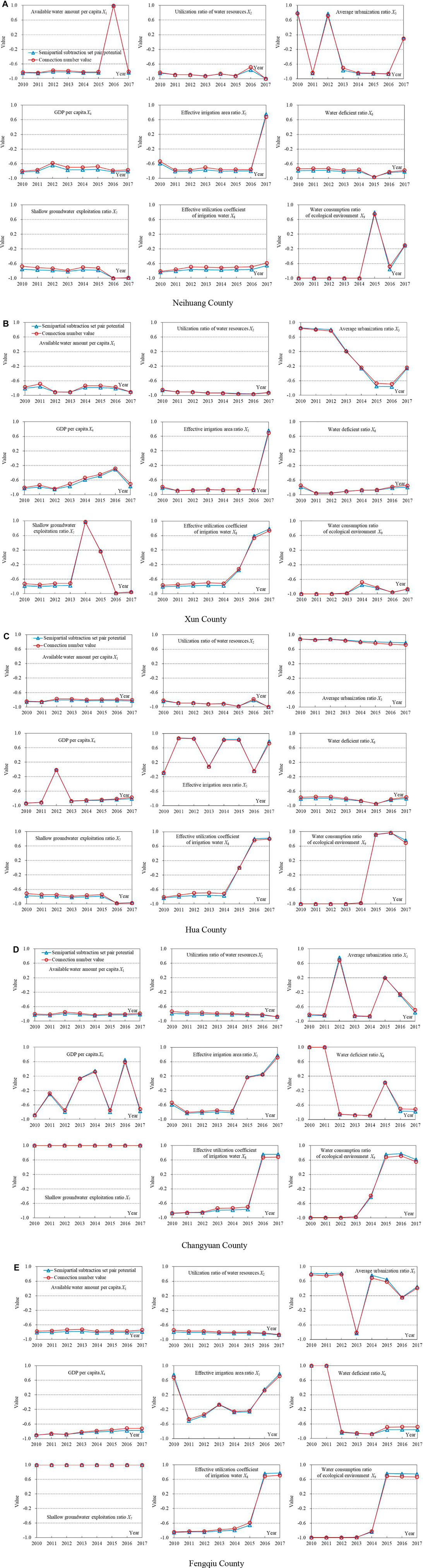
FIGURE 8. Connection number values of water resources carrying capacity (WRCC) evaluation index from 2010 to 2017 in the Dagong irrigation district. The four dashed lines from top to bottom in the figures represent the boundary of connection number value for strong promotion and weak promotion types (0.6), and those for weak promotion and weak obstacle (0.2), weak obstacle and middle obstacle (‒0.2), and middle obstacle and strong obstacle (‒0.6) in each county, respectively.

The change trend of the connection number value for each index from 2010 to 2017 was consistent with the semipartial subtraction set pair potential for the five counties, while the overall variation range of the connection number value was larger. However, when the value varied markedly during 2 years, the range of the set pair potential was greater (Figure 8). For example, the connection number values of water consumption ratio of ecological environment X₉ for Hua County in 2016 and 2017 were 0.97 and 0.69 (the absolute difference was 0.28), respectively, while the set pair potential were 0.97 and 0.76 (0.21) respectively. In addition, the connection number values of average urbanization ratio X₃ for Fengqiu County in 2013 and 2014 were ‒0.81 and 0.68 (the absolute difference was 1.49), respectively, while the set pair potential were ‒0.83 and 0.76 (1.59) respectively. It indicates that the connection number value determined by the calculation method of dynamic difference degree coefficient proposed in this study is reasonable and reliable, and can more sensitively and accurately identify the change of carrying status for evaluation index.

The obstacle factors of WRCC (the connection number value u < ‒0.2) in Neihuang County were X₁, X₂, X₄, X₅, X₆, X₇, and X₈ (Figure 8A). It reflected that in recent years, this county was generally in water resources overloaded status because of the less water resources amount, large population, low economic level, high urbanization degree, less effective irrigation area, and low utilization coefficient of irrigation water (Zhang et al., 2017). Furthermore, the reasons for the change in carrying situation were analyzed to guide water resources management, according to the connection number value of index. The improvement of WRCC in 2015 (Figure 5A) was mainly due to the water consumption ratio of ecological environment X₉ developed from strong obstacle (the connection number value was ‒1.00) in 2014 to the strong promotion (0.74) in 2015 (Figure 8A). Additionally, the carrying status worsened again in 2016 (Figure 5A) because the shallow groundwater exploitation ratio X₇ further deteriorated from strong obstacle (‒0.72) in 2015 to the largest strong obstacle (‒1.00) in 2016, and meanwhile X₉ deteriorated from strong promotion (0.74) in 2015 to strong obstacle (‒0.68) in 2016 (Figure 8A). Therefore, the main season for the declined WRCC from 2015 to 2016 is the sharp drop of water resources supply for the ecological environment, followed by the continuous degree increase of groundwater exploitation. Moreover, the reason for the improvement of WRCC in 2017 was that the average urbanization ratio X₃, effective irrigation area ratio X₅, and X₉ were improved (Figure 5A and 8A) (Song and Zhang, 2018). Therefore, the key measures to improve the severe water resources carrying situation in Neihuang County are to reasonably control the levels of shallow groundwater exploitation and urban development, and to increase the effective irrigation area and water resources consumption for ecological environment.

The obstacle factors in Xun County were X₁, X₂, X₄, X₆, X₇, and X₉ (Figure 8). Furthermore, the main reasons for the overloaded status from 2010 to 2013 (Figure 5B) were that the water resources amount was low, the population was large, the economic level was low, and the effective irrigation area was small (Figure 8) (Jin et al., 2021). The slight improvement of WRCC since 2014 (Figure 5B) was due to the effective irrigation area ratio X₅ and effective utilization coefficient of irrigation water X₈ gradually developed from strong obstacle to strong promotion. Nevertheless, at the same time, the average urbanization ratio X₃ degenerated from middle obstacle to strong obstacle, and the shallow groundwater exploitation ratio X₇ gradually degenerated from strong promotion to weak obstacle and even strong obstacle (Figure 8). It indicated that in recent years, the increase of effective irrigation area had promoted the improvement of WRCC in Xun County. Meanwhile, the rapid development of urbanization and the increasingly high rates of groundwater exploitation had limited the magnitude of improvement, which should be paid attention to. These were consistent with research of Zhang X. et al. (2020), who found that Xun County was in the edge of overloaded status. This may be due to the fact that, for satisfying the water consumption of social and economic development, the expansion of groundwater funnel had not been effectively controlled. In addition, this county is located at the downstream end of the canal system in the Dagong irrigation district (Figure 7), and the upstream water supply condition cannot meet the downstream water demand, resulting in the poor WRCC.

The obstacle factors in Hua County were X₁, X₂, X₄, X₆, and X₇ (Figure 8). In addition, the approaching overloaded status from 2010 to 2014 (Figure 5C) was mainly due to the less water resources amount, large population, low economic level, and high degree of water resources utilization (Figure 8) (Zhang, 2017). Therefore, supplementing the amount of water resources, accelerating social and economic development, promoting water saving level, and controlling water resources exploitation are effective means to improve the carrying situation. The WRCC increased significantly from 2015 to 2017 (Figure 5C) because of the improvement in the effective utilization coefficient of irrigation water X₈ and water consumption ratio of ecological environment X₉. X₈ gradually developed from strong obstacle before 2015 to weak obstacle and strong promotion thereafter, while X₉ was improved from strong obstacle in 2014 to strong promotion in 2017 (Figure 8). These are directly related to the control of agricultural and ecological water consumption by the policy of “three red lines,” and reflect the effectiveness and necessity of the strictest water resources management system in China (Zuo et al., 2014; Zhang et al., 2015). Furthermore, according to the investigation, the amount of water diversion from the Yellow River in Hua County has been about 70 million m³ since 2007, without taking into account the normal water supply, excessive water resources were stored in reservoirs. This effectively alleviates the problem of farmland irrigation, improves the ecological environment, and guarantees the sustainable and stable development of the social economy in this county. In addition, the average urbanization ratio X₃ remained the index of strong promotion type for a long time (Figure 8). The appropriate urbanization level is an important factor to ensure excellent carrying status in Hua County (Figure 7).

The obstacle factors in Changyuan County were X₁, X₂, X₃, X₄, and X₆ (Figure 8). Furthermore, the carrying status was improved from near overloaded to critical overloaded from 2014 to 2017 (Figure 5D). This was mainly because the effective irrigation area ratio X₅ gradually developed from strong obstacle in 2014 to weak promotion and strong promotion. Meanwhile, the effective utilization coefficient of irrigation water X₈ and water consumption ratio of ecological environment X₉ were improved from strong obstacle to strong promotion (Figure 8). It shows that since the implementation of the strictest water resources management system, this county has scientifically adjusted the agricultural and ecological water consumption, and the effects are remarkable (Dou and Wang, 2017; Zhang et al., 2017). However, the connection number values of average urbanization ratio X₃, GDP per capita X₄, and water deficient ratio X₆ fluctuated markedly over the years, and they all belonged to the index of middle obstacle type (Figure 8 and Table 2), which should be paid close attention as obstacle factors. The shallow groundwater exploitation ratio X₇ was always strong promotion (Figure 8), indicating that Changyuan County has strictly controlled the degree of groundwater exploitation for a long time (Song et al., 2020). This is a crucial factor for guaranteeing its relatively excellent water resources carrying situation (Figure 7).

The obstacle factors in Fengqiu County were X₁, X₂, X₄, and X₆ (Figure 8). It can be seen that the less water resources amount, large population, and low economic level significantly restricted the improvement of its WRCC (Zhang, 2017; Jin et al., 2021). Therefore, transferring and supplementing the water resources and promoting the economic development are powerful measures to strengthen the WRCC. Similar to Changyuan County, Fengqiu County gradually developed from near overloaded status to critical overloaded status from 2014 to 2017 (Figure 5e), which was mainly due to that the effective irrigation area ratio X₅, effective utilization coefficient of irrigation water X₈, and water consumption ratio of ecological environment X₉ were improved from middle obstacle or strong obstacle to strong promotion (Figure 8). It suggests that this county has strictly carried out the control of “red lines” on agricultural and ecological water consumption (Zhang et al., 2015), fully ensuring the effective improvement of its carrying situation. Moreover, the average urbanization ratio X₃ quickly recovered to weak promotion and strong promotion after deteriorating to strong obstacle in 2013, while the water deficient ratio X₆ was not improved after worsening to strong obstacle in 2012 from strong promotion in 2010 and 2011. The shallow groundwater exploitation ratio X₇ was the index of strong promotion type for a long time (Figure 8) (Song et al., 2020). It reflects that the appropriate levels of groundwater exploitation and urbanization are key factors to ensure the strong WRCC in Fengqiu County (Figure 7). Meanwhile, it is necessary to take measures, such as adding water supply, decreasing water consumption, or increasing water use efficiency, to reduce the water deficient ratio and then strengthen the WRCC.

In summary, the evaluation and diagnosis results obtained in this study are consistent with the real water resources carrying situation in the Dagong irrigation district under the current policy environment (Xu, 2020; Fan et al., 2021; Qin, 2021). According to the construction standard of ecological irrigation district, and great concerns about ecological civilization construction and new water resources management concept in China, the administrative departments should further improve the water resources allocation of each county in the irrigation district and conduct other relevant works. So as to realize that there are water resources for supplementing source in flood season and those for irrigation in non-flood season, on the basis of guaranteeing the domestic and industrial water supply.

Conclusion

In order to deal with the uncertainty between evaluation samples and evaluation criteria, a connection number model of WRCC evaluation was established. Furthermore, taking account of the information carried by sample data, a calculation method of dynamic difference degree coefficient varying with the actual evaluation sample was also proposed. As a result, a quantitative evaluation and obstacle factor diagnosis model of WRCC in the Yellow River irrigation district was constructed. In addition, an empirical study was carried out in the Dagong ecological irrigation district, and the following main conclusions were obtained:

1) The results of WRCC evaluation and diagnosis in a typical irrigation district were consistent with the real situation and existing studies, indicating that the connection number evaluation and diagnosis method based on dynamic difference degree coefficient was effective and reliable. These results provided important scientific support for water resources allocation and management in the Yellow River irrigation district.

2) Although the WRCC in the Dagong irrigation district remained severe, it had been improved as a whole since 2013. Five counties of the irrigation district were all in water resources critical overloaded status by 2017. Moreover, the WRCC of Fengqiu County, Changyuan County, Hua County, Xun County, and Neihuang County became weaker in turn, which was consistent with the fact that they were further away from the main stream of the Yellow River.

3) The utilization ratio of water resources, available water resources amount per capita, GDP per capita, and water deficient ratio belonged to the index of strong or middle obstacle type. These were the main obstacle factors of WRCC, as well as the key and difficulty of water resources regulation and control for the Dagong irrigation district.

4) The connection number model based on dynamic difference degree coefficient proposed in this study can identify the relatively certain water resources carrying situation and its crucial obstacle factors in irrigation district, and can be applied to resources, environment, ecology carrying capacity fields, and other set pair system problems.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YC prepared, created, and presented the published work; applied statistical, mathematical, and computational technique to analyze or synthesize study data. LZ, LJ, and YC conceptualized and formulated overarching research goals and aims; developed and designed the methodology; and was involved in project administration, and funding acquisition. GW, BZ, and WN curated, visualized, and presented the data. All authors were involved in critical review, commentary, and revision.

Funding

This study was financially supported by the National Natural Science Foundation of China (Grant No. 52109009) and National Key Research and Development Program of China (Grant No. 2018YFC0407206), the Natural Science Foundation of Anhui Province, China (Grant No. 2108085QE254), and the Fundamental Research Funds for the Central Universities (Grant Nos. JZ2021HGTA0165, JZ2020HGQA0202, JZ2021HGQB0281).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the handling editor and the reviewers, for their reviews and valuable comments that significantly improved the quality of this paper.

References

Chang, T., Li, J. Q., Jin, J. L., Chen, L., Dong, T., Chen, M. L., et al. (2020). Multi-dimensional Water Resources Carrying Capacity Evaluation index System for Water Flow System Function. Water Resour. Prot. 36, 44–51. doi:10.3880/j.issn.1004-6933.2020.01.007

CrossRef Full Text | Google Scholar

Chen, S. Y. (2005). Theories and Methods of Variable Fuzzy Sets in Water Resources and Flood Control System. Dalian: Dalian University of Technology Press.

Google Scholar

Chong, T., Yi, S., and Heng, C. (2017). Application of Set Pair Analysis Method on Occupational hazard of Coal Mining. Saf. Sci. 92, 10–16. doi:10.1016/j.ssci.2016.09.005

CrossRef Full Text | Google Scholar

Cui, Y., Feng, P., Jin, J., and Liu, L. (2018). Water Resources Carrying Capacity Evaluation and Diagnosis Based on Set Pair Analysis and Improved the Entropy Weight Method. Entropy 20, 359. doi:10.3390/e20050359

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, D., Sun, M., Xu, X., and Lei, K. (2019). Assessment of the Water Resource Carrying Capacity Based on the Ecological Footprint: a Case Study in Zhangjiakou City, North China. Environ. Sci. Pollut. Res. 26, 11000–11011. doi:10.1007/s11356-019-04414-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Dou, M., and Wang, Y. (2017). The Construction of a Water Rights System in China that Is Suited to the Strictest Water Resources Management System. Water Supply 17, 238–245. doi:10.2166/ws.2016.130

CrossRef Full Text | Google Scholar

Du, X. F., Li, Y. B., and Zhang, X. Y. (2020). Study on Water Resources Carrying Capacity of Ecological Diversion Irrigation District in the Lower Reaches of the Yellow River. Hydro-Science Eng. (2), 22–29. doi:10.12170/20200209001

CrossRef Full Text | Google Scholar

Fan, X. C., Qin, J. T., Xu, L., Liu, S. R., Gu, S. W., and Lyu, M. C. (2021). Construction and Empirical Analysis of the Evaluation index System for the Water-Saving Level of Large-Sized Irrigation Districts. Trans. Chin. Soc. Agric. Eng. 37, 99–107. doi:10.11975/j.issn.1002-6819.2021.20.011

CrossRef Full Text | Google Scholar

Song, F., Yang, X., and Wu, F. (2020). Catastrophe Progression Method Based on M-K Test and Correlation Analysis for Assessing Water Resources Carrying Capacity in Hubei Province. J. Water Clim. Change 11, 556–567. doi:10.2166/wcc.2018.114

CrossRef Full Text | Google Scholar

Gonçalves, J. M., Pereira, L. S., Fang, S. X., and Dong, B. (2007). Modelling and Multicriteria Analysis of Water Saving Scenarios for an Irrigation District in the Upper Yellow River Basin. Agric. Water Manage. 94, 93–108. doi:10.1016/j.agwat.2007.08.011

CrossRef Full Text | Google Scholar

Gong, L., and Jin, C. (2009). Fuzzy Comprehensive Evaluation for Carrying Capacity of Regional Water Resources. Water Resour. Manage. 23, 2505–2513. doi:10.1007/s11269-008-9393-y

CrossRef Full Text | Google Scholar

He, L., Du, Y., Wu, S., and Zhang, Z. (2021). Evaluation of the Agricultural Water Resource Carrying Capacity and Optimization of a Planting-Raising Structure. Agric. Water Manage. 243, 106456. doi:10.1016/j.agwat.2020.106456

CrossRef Full Text | Google Scholar

Jia, Z., Wu, Z., Luo, W., Xi, W., Tang, S., Liu, W. L., et al. (2013). The Impact of Improving Irrigation Efficiency on Wetland Distribution in an Agricultural Landscape in the Upper Reaches of the Yellow River in China. Agric. Water Manage. 121, 54–61. doi:10.1016/j.agwat.2013.01.003

CrossRef Full Text | Google Scholar

Jin, J. L., Wei, Y. M., and Ding, J. (2004). Fuzzy Comprehensive Evaluation Model Based on Improved Analytic Hierarchy Process. J. Hydraulic Eng. 35 (3), 65–70. doi:10.13243/j.cnki.slxb.2004.03.011

CrossRef Full Text | Google Scholar

Jin, J. L., Wu, K. Y., and Wei, Y. M. (2008). Connection Number Based Assessment Model for Watershed Water Security. J. Hydraulic Eng. 39, 401–409. doi:10.3321/j.issn:0559-9350.2008.04.003

CrossRef Full Text | Google Scholar

Jin, J. L., Dong, T., Li, J. Q., Zhang, L. B., and Li, H. (2018). Water Resources Carrying Capacity Evaluation Method under Different Carrying Standards. Adv. Water Sci. 29, 31–39. doi:10.14042/j.cnki.32.1309.2018.01.004

CrossRef Full Text | Google Scholar

Jin, J. L., Zhang, H. Y., Chen, M. L., Cui, Y., and Ning, S. W. (2019a). Evaluation and Diagnosis of Agricultural Drought Vulnerability Based on Grey Correlation and Connection Number Coupling. J. Catastrophol. 34, 1–7. doi:10.3969/j.issn.1000-811X.2019.01.001

CrossRef Full Text | Google Scholar

Jin, J. L., Zhang, H. Y., Chen, M. L., Wang, H. R., Cui, Y., and Ning, S. W. (2019b). Evaluation of Regional Agricultural Drought Vulnerability Coupled with Dynamic Connection Number and Full Partial Certainty. J. Beijing Normal Univ. (Nat. Sci.) 55, 724–730. doi:10.16360/j.cnki.jbnuns.2019.06.008

CrossRef Full Text | Google Scholar

Jin, J. L., Shen, S. X., Cui, Y., Zhang, X. Y., He, P., and Ning, S. W. (2021). Dynamic Evaluation of Water Resources Carrying Capacity in the Yellow River Diversion Irrigation District Based on Semipartial Subtraction Set Pair Potential. 52 507–520. doi:10.13243/j.cnki.slxb.20200561

CrossRef Full Text | Google Scholar

Kang, J., Zi, X., Wang, S., and He, L. (2019). Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water 11, 999. doi:10.3390/w11050999

CrossRef Full Text | Google Scholar

Kumar, K., and Garg, H. (2016). TOPSIS Method Based on the Connection Number of Set Pair Analysis under Interval-Valued Intuitionistic Fuzzy Set Environment. Comp. Appl. Math. 37, 1319–1329. doi:10.1007/s40314-016-0402-0

CrossRef Full Text | Google Scholar

Li, Z. Y., Wu, M., Liu, Z. Y., Li, D. P., and Guo, C. (2009). A New Approach to I in Connection Number and Application in Water Quality Assessment. J. Sichuan Univ. (Engineer. Sci. Ed.) 41, 8–13. doi:10.15961/j.jsuese.2009.01.002

CrossRef Full Text | Google Scholar

Li, M., Zheng, T., Zhang, J., Fang, Y., Liu, J., Zheng, X., et al. (2019). A New Risk Assessment System Based on Set Pair Analysis - Variable Fuzzy Sets for Underground Reservoirs. Water Resour. Manage. 33, 4997–5014. doi:10.1007/s11269-019-02390-w

CrossRef Full Text | Google Scholar

Li, Z., Jin, J., Cui, Y., Zhang, L., Wu, C., Ning, S., et al. (2021). Dynamic Evaluation of Regional Water Resources Carrying Capacity Based on Set Pair Analysis and Partial Connection Number. J. Hydraulic Eng.. doi:10.2166/ws.2021.371

CrossRef Full Text | Google Scholar

Liao, X., Ren, Y., Shen, L., Shu, T., He, H., and Wang, J. (2020). A "Carrier-Load" Perspective Method for Investigating Regional Water Resource Carrying Capacity. J. Clean. Prod. 269, 122043. doi:10.1016/j.jclepro.2020.122043

CrossRef Full Text | Google Scholar

Lyu, H.-M., Shen, S.-L., and Zhou, A. (2021). The Development of IFN-SPA: A New Risk Assessment Method of Urban Water Quality and its Application in Shanghai. J. Clean. Prod. 282, 124542. doi:10.1016/j.jclepro.2020.124542

CrossRef Full Text | Google Scholar

Miao, Q., Shi, H., Gonçalves, J. M., and Pereira, L. S. (2015). Field Assessment of basin Irrigation Performance and Water Saving in Hetao, Yellow River basin: Issues to Support Irrigation Systems Modernisation. Biosyst. Eng. 136, 102–116. doi:10.1016/j.biosystemseng.2015.05.010

CrossRef Full Text | Google Scholar

Pan, Z. W., Jin, J. L., and Zhou, R. X. (2016). Assessment Method Using Connection Number Based on Trapezoidal Fuzzy Numbers and its Application. Adv. Sci. Technol. Water Resour. 36, 69–74. doi:10.3880/j.issn.1006-7647.2016.05.013

CrossRef Full Text | Google Scholar

Pan, Z., Wang, Y., Jin, J., and Liu, X. (2017). Set Pair Analysis Method for Coordination Evaluation in Water Resources Utilizing Conflict. Phys. Chem. Earth, Parts A/B/C 101, 149–156. doi:10.1016/j.pce.2017.05.009

CrossRef Full Text | Google Scholar

Peng, T., and Deng, H. (2020). Comprehensive Evaluation on Water Resource Carrying Capacity Based on DPESBR Framework: A Case Study in Guiyang, Southwest China. J. Clean. Prod. 268, 122235. doi:10.1016/j.jclepro.2020.122235

CrossRef Full Text | Google Scholar

Peng, T., Deng, H., Lin, Y., and Jin, Z. (2021). Assessment on Water Resources Carrying Capacity in Karst Areas by Using an Innovative DPESBRM Concept Model and Cloud Model. Sci. Total Environ. 767, 144353. doi:10.1016/j.scitotenv.2020.144353

PubMed Abstract | CrossRef Full Text | Google Scholar

Pereira, L. S., Gonçalves, J. M., Dong, B., Mao, Z., and Fang, S. X. (2007). Assessing basin Irrigation and Scheduling Strategies for Saving Irrigation Water and Controlling Salinity in the Upper Yellow River Basin, China. Agric. Water Manage. 93, 109–122. doi:10.1016/j.agwat.2007.07.004

CrossRef Full Text | Google Scholar

Qi, P., Xia, Z., Zhang, G., Zhang, W., and Chang, Z. (2021). Effects of Climate Change on Agricultural Water Resource Carrying Capacity in a High-Latitude basin. J. Hydrol. 597, 126328. doi:10.1016/j.jhydrol.2021.126328

CrossRef Full Text | Google Scholar

Qin, T. (2021). Comprehensive Evaluation of Water Resources Security in Dagong Yellow River Diversion Irrigation Area of Henan Province. Zhengzhou: North China University of Water resources and Electric Power.

Google Scholar

Ren, D., Xu, X., Engel, B., and Huang, G. (2018). Growth Responses of Crops and Natural Vegetation to Irrigation and Water Table Changes in an Agro-Ecosystem of Hetao, Upper Yellow River basin: Scenario Analysis on maize, sunflower, Watermelon and Tamarisk. Agric. Water Manage. 199, 93–104. doi:10.1016/j.agwat.2017.12.021

CrossRef Full Text | Google Scholar

Roy, D. K., and Datta, B. (2019). Adaptive Management of Coastal Aquifers Using Entropy-Set Pair Analysis-Based Three-Dimensional Sequential Monitoring Network Design. J. Hydrol. Eng. 24, 04018072. doi:10.1061/(ASCE)HE.1943-5584.0001765

CrossRef Full Text | Google Scholar

Song, G. X., and Yang, D. L. (2003). Methods for Identifying and Improving the Consistency of Fuzzy Judgment Matrix. Syst. Eng. 21, 110–116.

Google Scholar

Song, D. J., and Zhang, L. X. (2018). Investigation and Suggestions on the Current Situation of Dagong Yellow River Diversion Irrigation District. Henan Water Resour. South-to-North Water Diversion 47 (5), 25–26.

Google Scholar

Song, X.-m., Kong, F.-z., and Zhan, C.-s. (2011). Assessment of Water Resources Carrying Capacity in Tianjin City of China. Water Resour. Manage. 25, 857–873. doi:10.1007/s11269-010-9730-9

CrossRef Full Text | Google Scholar

Song, Q. X., Li, J., Miao, H. C., Gao, Y. Y., Wang, Z. P., and Chen, F. (2020). Analysis of Groundwater Exploitation Potential in the north Region of Yellow River in Henan Province. Yellow River 42, 67–72. doi:10.3969/j.issn.1000-1379.2020.08.014

CrossRef Full Text | Google Scholar

Su, Y., Gao, W., and Guan, D. (2019). Integrated Assessment and Scenarios Simulation of Water Security System in Japan. Sci. Total Environ. 671, 1269–1281. doi:10.1016/j.scitotenv.2019.03.373

CrossRef Full Text | Google Scholar

Tang, Y. P. (2009). The Methods to Fetch I in Difference Degree Coefficient of Set Pair Analysis and its Applications. Math. Pract. Theor. 39, 67–70.

Google Scholar

Wan, X., Yang, T., Zhang, Q., Yan, X., Hu, C., Sun, L., et al. (2021). A Novel Comprehensive Model of Set Pair Analysis with Extenics for River Health Evaluation and Prediction of Semi-arid basin - A Case Study of Wei River Basin, China. Sci. Total Environ. 775, 145845. doi:10.1016/j.scitotenv.2021.145845

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Jin, J., Ding, J., and Li, Y. (2009). A New Approach to Water Resources System Assessment - Set Pair Analysis Method. Sci. China Ser. E-technol. Sci. 52, 3017–3023. doi:10.1007/s11431-009-0099-z

CrossRef Full Text | Google Scholar

Wang, S., Yang, F.-L., Xu, L., and Du, J. (2013). Multi-scale Analysis of the Water Resources Carrying Capacity of the Liaohe Basin Based on Ecological Footprints. J. Clean. Prod. 53, 158–166. doi:10.1016/j.jclepro.2013.03.052

CrossRef Full Text | Google Scholar

Wang, Y., Wang, Y., Su, X., Qi, L., and Liu, M. (2019). Evaluation of the Comprehensive Carrying Capacity of Interprovincial Water Resources in China and the Spatial Effect. J. Hydrol. 575, 794–809. doi:10.1016/j.jhydrol.2019.05.076

CrossRef Full Text | Google Scholar

Wu, C., Zhou, L., Jin, J., Ning, S., Zhang, Z., and Bai, L. (2020). Regional Water Resource Carrying Capacity Evaluation Based on Multi-Dimensional Precondition Cloud and Risk Matrix Coupling Model. Sci. Total Environ. 710, 136324. doi:10.1016/j.scitotenv.2019.136324

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X.-j., Zhang, J.-y., Gao, J., Shahid, S., Xia, X.-h., Geng, Z., et al. (2018). The New Concept of Water Resources Management in China: Ensuring Water Security in Changing Environment. Environ. Dev. Sustain. 20, 897–909. doi:10.1007/s10668-017-9918-8

CrossRef Full Text | Google Scholar

Xiong, L., Xu, X., Engel, B., Huang, Q., Huo, Z., Xiong, Y., et al. (2021). Modeling Agro-Hydrological Processes and Analyzing Water Use in a Super-large Irrigation District (Hetao) of Arid Upper Yellow River basin. J. Hydrol. 603, 127014. doi:10.1016/j.jhydrol.2021.127014

CrossRef Full Text | Google Scholar

Xu, M. J. (2020). Analysis and Prediction of Cultivated Land Grain Efficiency in Typical Yellow River Diversion Irrigation Area of Henan Province. Tianjin: Tiangong University.

Google Scholar

Yang, X.-H., He, J., Di, C.-L., and Li, J.-Q. (2014). Vulnerability of Assessing Water Resources by the Improved Set Pair Analysis. Therm. Sci. 18, 1531–1535. doi:10.2298/TSCI1405531Y

CrossRef Full Text | Google Scholar

Yang, J., Lei, K., Khu, S., and Meng, W. (2015). Assessment of Water Resources Carrying Capacity for Sustainable Development Based on a System Dynamics Model: A Case Study of Tieling City, China. Water Resour. Manage. 29, 885–899. doi:10.1007/s11269-014-0849-y

CrossRef Full Text | Google Scholar

Yin, Z., Ottlé, C., Ciais, P., Zhou, F., Wang, X., Jan, P., et al. (2021). Irrigation, Damming, and Streamflow Fluctuations of the Yellow River. Hydrol. Earth Syst. Sci. 25, 1133–1150. doi:10.5194/hess-25-1133-2021

CrossRef Full Text | Google Scholar

Wang, Y., Cheng, H., and Huang, L. (2018). Water Resources Carrying Capacity Evaluation of a Dense City Group: A Comprehensive Water Resources Carrying Capacity Evaluation Model of Wuhan Urban Agglomeration. Urban Water J. 15, 615–625. doi:10.1080/1573062X.2018.1529805

CrossRef Full Text | Google Scholar

Zhang, Y. F., Guo, W., Xu, J. X., and Zhang, X. Y. (2015). Optimal Allocation to Water Resources of the Yellow River Irrigation District of Dagong Based on the Strictest Managerical System of Water Resources. J. North China Univ. Water Resour. Electric Power (Natural Sci. Ed.) 36, 28–32. doi:10.3969/j.issn.1002-5634.2015.03.007

CrossRef Full Text | Google Scholar

Zhang, S., Xiang, M., Yang, J., Fan, W., and Yi, Y. (2019). Distributed Hierarchical Evaluation and Carrying Capacity Models for Water Resources Based on Optimal Water Cycle Theory. Ecol. Indicators 101, 432–443. doi:10.1016/j.ecolind.2019.01.048

CrossRef Full Text | Google Scholar

Zhang, Q., Xu, P., Chen, J., Qian, H., Qu, W., and Liu, R. (2021). Evaluation of Groundwater Quality Using an Integrated Approach of Set Pair Analysis and Variable Fuzzy Improved Model with Binary Semantic Analysis: A Case Study in Jiaokou Irrigation District, East of Guanzhong Basin, China. Sci. Total Environ. 767, 145247. doi:10.1016/j.scitotenv.2021.145247

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J. (2017a). Study on Coordinated Development of Typical Area Irrigated by the Yellow River Based on Sustainable Theory. Zhengzhou: North China University of Water resources and Electric Power.

Google Scholar

Zhang, X., Du, X., and Li, Y. (2020). Comprehensive Evaluation of Water Resources Carrying Capacity in Ecological Irrigation Districts Based on Fuzzy Set Pair Analysis. Dwt 187, 63–69. doi:10.5004/dwt.2020.25287

CrossRef Full Text | Google Scholar

Zhang, X. Y., Du, X. F., Xu, J. X., and Zhang, Z. Q. (2019). Analysis of Water Resources Carrying Capacity in Dagong Yellow River Diversion Irrigation Area Based on Ecology. Yellow River 41, 49–52+57. doi:10.3969/j.issn.1000-1379.2019.06.011

CrossRef Full Text | Google Scholar

Zhang, X. Y., Qin, T., Yang, Q. X., Du, X. F., Yang, L. B., and Liu, X. M. (2020). Method of Evaluating Safety for Water Usage and its Application to Water Use in Irrigation Districts in the Lower Reach of the Yellow River. J. Irrig. Drain. 39, 18–24. doi:10.13522/j.cnki.ggps.2020184

CrossRef Full Text | Google Scholar

Zhang, Y. S., Lu, Z. G., Wang, M., Qin, H. X., Wang, Y. P., He, G., et al. (2017). Calculation and Analysis of Irrigation Water Use Efficiency of Henan Province. China Rural Water Hydropower (1), 9–12+17.

Google Scholar

Zhao, Y., Wang, Y., and Wang, Y. (2021). Comprehensive Evaluation and Influencing Factors of Urban Agglomeration Water Resources Carrying Capacity. J. Clean. Prod. 288, 125097. doi:10.1016/j.jclepro.2020.125097

CrossRef Full Text | Google Scholar

Zhao, K. Q. (2000). Set Pair Analysis and its Preliminary Application. Hangzhou: Zhejiang Science and Technology Press.

Google Scholar

Zhou, R., Jin, J., Cui, Y., Ning, S., Bai, X., Zhang, L., et al. (2022). Agricultural Drought Vulnerability Assessment and Diagnosis Based on Entropy Fuzzy Pattern Recognition and Subtraction Set Pair Potential. Alexandria Eng. J. 61, 51–63. doi:10.1016/j.aej.2021.04.090

CrossRef Full Text | Google Scholar

Zuo, Q., Jin, R., Ma, J., and Cui, G. (2014). China Pursues a Strict Water Resources Management System. Environ. Earth Sci. 72, 2219–2222. doi:10.1007/s12665-014-3369-4

CrossRef Full Text | Google Scholar

Zuo, Q., Guo, J., Ma, J., Cui, G., Yang, R., and Yu, L. (2021). Assessment of Regional-Scale Water Resources Carrying Capacity Based on Fuzzy Multiple Attribute Decision-Making and Scenario Simulation. Ecol. Indicators 130, 108034. doi:10.1016/j.ecolind.2021.108034

CrossRef Full Text | Google Scholar