Long-term Performance Evaluation and Economic Analysis for Deep Borehole Heat Exchanger Heating System in Weihe Basin

To reduce carbon emission and achieve carbon neutrality, deep geothermal energy has been widely extracted for building heating purpose. In recent years, deep borehole heat exchanger (DBHE) heating system has gained more attention, especially in densely populated urban areas in Weihe Basin, northern China. The long-term performance and the economic feasibility are essential for the system application. In this work, the DBHE model implemented in OpenGeoSys software is verified against an analytical solution and a comprehensive economic analysis approach is further proposed. Then the short-term thermal performance tests are conducted to obtain the tentative heat extraction capacity for long-term simulation. The long-term simulations are further performed with the heat pump unit under the adjusted tentative heat extraction rate imposed on the DBHE. Finally, a comprehensive economic analysis is applied to the DBHE heating system over 15 heating seasons. Results show that the minimum coefficient of performance value of the heat pump is 4.74 over the operation of 15 heating seasons. With the increase of depth for the DBHE, the total electricity consumption of heat pumps and circulation pumps has a prominent promotion. With the comprehensive approach of economic analysis, the depth of 2,600 m has the lowest levelized cost of total heating amount, which is the best system design for the application in Weihe Basin. The present results are specific to the conditions in Weihe Basin, but the proposed economic analysis approach is generic.

1 Introduction

Considering the restriction of global warming imposed by The Paris Agreement 2015, countries worldwide are firmly devoted to pursuing a rapid transition toward renewable energy (De La Peña et al., 2022). In recent years, the European Union (Rodrigues et al., 2022), China (Zhao et al., 2022), and many other countries (Salvia et al., 2021) all made ambitious pledges to reach carbon neutrality by 2060 or earlier. To make sure the carbon emission target can be achieved, the environmentally friendly, highly efficient renewable energy solution will play a more crucial role in the future (Zhao and You, 2020). In view of the high proportion of building energy consumption within the whole energy usage worldwide (Ürge-Vorsatz et al., 2015), especially the huge amount of energy consumed for building heating and hot water supply (about 40% or even more in Europe) (Dias and Costa, 2018; Lin and Lin, 2019), it is of great importance to propose more renewable energy solutions for building heating, especially in cold regions. Compared with other renewable energy sources, geothermal energy gains lots of attention in serving as a building heating source for its stability, versatility, and extensive availability (Anderson and Rezaie, 2019; Lund and Toth, 2021) in the last few decades.

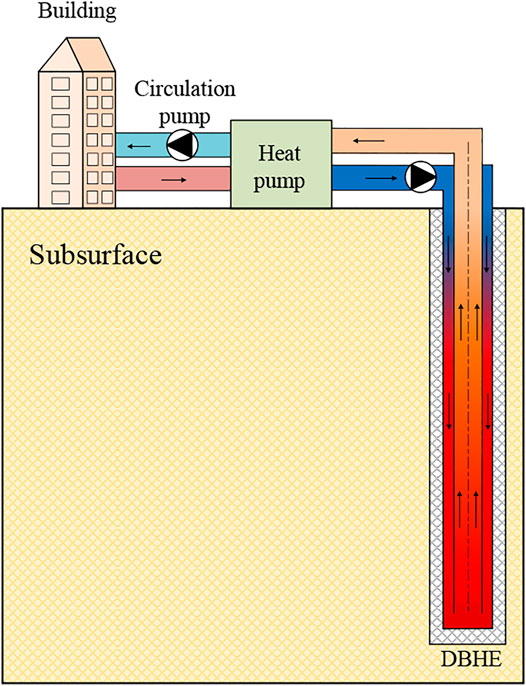
The history of people directly using geothermal energy could be traced back to ancient times, and the natural or artificial hot springs are usually used for baths or heating. Since the concept of ground source heat pump (GSHP) has been proposed in the last century, the shallow borehole heat exchanger (BHE) is then introduced to many projects for wide use (Ozgener et al., 2007). The shallow BHE coupled geothermal heat pump system can extract/inject energy from/to subsurface for building heating/cooling. One of the advantages of the system is that it does not rely on the local hydrothermal geothermal resource due to the closed loop in the subsurface. Thus, this shallow geothermal utilization technology has had a rapid development in the last decades. However, in densely populated regions, several hundreds of BHEs are needed to meet the large heating demand. This requires a colossal drilling area (Javadi et al., 2019) on the ground surface. Besides, due to the unbalanced heating and cooling demand in cold regions, the soil thermal balance (Soltani et al., 2019) is very difficult to maintain, making the system unsustainable in long-term operation (Chen et al., 2020b). These two aspects largely constrain the system application in a densely populated area where heating demand is larger. To efficiently utilize the geothermal energy for heating purposes in densely populated cold regions, an approach of the deep borehole heat exchanger (DBHE, see Figure 1) is proposed (Kohl et al., 2002), and several pioneered projects were executed (Morita et al., 1992; Kohl et al., 2000) at the end of the last century. The DBHE usually has a depth of 2,000∼3,000 m and a coaxial pipe installed in the borehole (Śliwa and Kotyza, 2003; Chen et al., 2019a), leading to a large heat exchange surface area with the surrounding subsurface.

FIGURE 1

FIGURE 1. Schematic diagram of the DBHE heating system.

The related pilot applications show that the DBHE heating system has satisfactory performance, while it has a high initial drilling cost that may lack economic potential, especially in Europe (Sapinska-Sliwa et al., 2016).

Under the constraints of large building-heating demand and limited land area in China’s densely populated urban area, the DBHE heating technology has been widely applied in northern China. It has gained lots of attention from both the Chinese government and the heating market in recent years. Starting from 2017, there are a few DBHE heating pilot projects reported in northern China (Huang et al., 2020), most of which are located in Xi’an city, Weihe Basin (Wang et al., 2017; Deng et al., 2019). The related experimental field tests indicated that the average coefficient of performance (COP) of the DBHE-coupled GSHP heating system can reach 4.58 (Deng et al., 2020). Considering the concentrated heating load and low drilling cost in China heating market, the DBHE heating technology is of good feasibility to extract deep geothermal energy, serving as the primary building heating source in the future.

To further investigate the heat extraction performance of the DBHE heating system, considerable research about the DBHE system has been conducted in the last few years. With analytical (Luo et al., 2019; Pan et al., 2019) and numerical approaches (Kong et al., 2017; Fang et al., 2018; Song et al., 2018), researchers developed several simulation tools to investigate and quantify the performance of the DBHE and the response of surrounding soil/rock. Some commercial software, such as FLUENT (Li et al., 2020) and COMSOL (Hu et al., 2020), are also applied to simulate the heat transfer process of the DBHE system. Using the FEFLOW software, Le Lous et al. (2015) performed a series of detailed numerical investigations to study the heat extraction performance of the DBHE under different design parameters and geological conditions. The results indicated that increasing the drilling depth of pipe accounts for the considerable heat extraction of the DBHE. By introducing the Laplace transformation and Stehfest inversion technology, Beier (2020) proposed a novel analytical method to simulate coupled thermal-hydraulic process of the DBHE system, in which the geothermal gradient in the subsurface can be considered. Nevertheless, the geological properties are the same along the whole DBHE length in the analytical solution. To investigate the impact of geological parameters (Liu et al., 2020) on the system’s long-term sustainability, Cai et al. (2018) developed a 2D numerical model and validated the model against the field data. Xu et al. (2020) further conducted a series of scenarios, which demonstrated the impact of intermittent heating mode on the DBHE heat extraction performance. Pan et al. (2020) performed an economic analysis for the DBHE system by using an analytical solution proposed by Beier et al. (2014), while the variation of heat pump performance was not taken into account.

Due to the time-consuming simulations in the fully discretized 3D model, most related research on the DBHE system are focused on the short-term operation (e.g., one heating season or 1 year). In addition, few studies can be found on the economic analysis of the DBHE system, which actually largely affects the system applicability in the long term. Based on the related sensitivity analysis results of the DBHE, the drilling depth has been proved by researchers that a more extended depth will bring higher outlet temperature and higher heat extraction capacity. Nevertheless, the drilling depth is constrained with higher drilling costs for the deeper rock. Another critical knowledge gap in simulating the DBHE is that the simulation of the DBHE only contains the subsurface part but ignores the corresponding influence on the heat pump system. In this context, the investigations on heat extraction performance and sustainability of the DBHE-based long-term simulations, considering the interaction with heat pump system, are of great significance for its economic analysis and the selection of design parameters.

In our previous work (Chen et al., 2019a; Cai et al., 2021), a numerical model established by OpenGeoSys (OGS) software was developed for simulating the coaxial DBHE and surrounding soil. The model had been validated against experimental data measured from several pilot projects in Xi’an, Weihe Basin (Cai et al., 2021). In these studies, the accuracy of our model simulating the long-term heat extraction performance of a DBHE and the surrounding subsurface is thoroughly illustrated. In contrast, further economic analysis with the performance of the heat pump system involved has not been carried out yet. In this context, a series of scientific questions are raised for the DBHE heating system: How can a long-term performance evaluation be conducted when the heat pump characteristic in the DBHE heating system is considered? How does a comprehensive economic analysis affect the decision-making for the DBHE system in designing the optimal drilling depth? With the initial and operating costs considered, which depth of the DBHE is more economically sustainable against others in Weihe Basin?

In this paper, the aforementioned scientific questions were analyzed by a series of elaborated numerical simulations. The DBHE system model was constructed with the OpenGeoSys software (Kolditz et al., 2012) and further deployed based on the actual geological parameters in Weihe Basin. Through the constructed numerical model, thermal performance tests of the DBHE system were carried out, and the tentative heat extraction capacities of the DBHE were evaluated. After that, the long-term heat extraction performance of the DBHE system with different depths was analyzed in detail. In the next step, a comprehensive economic analysis for the DBHE was investigated during long-term operation, and the electricity consumption of the heat pump and circulation pump was also evaluated. At the end of the article, practical suggestions of drilling depth are made for the design of the DBHE heating systems.

2 Methodology

2.1 Dual Continuum FEM Method in OpenGeoSys

In the present model framework for DBHE simulation, many researchers tend to select numerical approaches since they are more capable of handling the flexible initial and boundary conditions that emerge from the field study. The numerical DBHE model used in this study is implemented by using Dual Continuum Finite Element Method (DC-FEM) (Al-Khoury et al., 2010; Shao et al., 2016) in the open-source software OpenGeoSys (OGS) (Kolditz et al., 2012). In the field of deep coaxial borehole heat exchanger simulation, the coaxial pipe with an annular inlet (CXA) is recommended for heat extraction (Chen et al., 2019a). The governing equations for the fluid inside the centered and annular borehole read:

$\begin{array}{ccc}\hfill {\rho }_f{c}_f\frac{\partial T_i}{\partial t}+{\rho }_f{c}_f{\mathbf{v}}_i\cdot \nabla T_i=\nabla \cdot \left({\Lambda }_i\cdot \nabla T_i\right)+H_i& \hfill & \hfill \\ \hfill \mathrm{B}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}):& \hfill & \hfill \end{array}(1)$

$\begin{array}{ccc}\hfill q_{n{T}_i}=-{\Phi }_{\mathit{io}}\left(T_o-T_i\right)\mathrm{o}\mathrm{n}{\Gamma }_i& \hfill & \hfill \end{array}(2)$

$\begin{array}{ccc}\hfill {\rho }_f{c}_f\frac{\partial T_o}{\partial t}+{\rho }_f{c}_f{\mathbf{v}}_o\cdot \nabla T_o=\nabla \cdot \left({\Lambda }_o\cdot \nabla T_o\right)+H_o& \hfill & \hfill \\ \hfill \mathrm{B}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}):& \hfill & \hfill \end{array}(3)$

$\begin{array}{ccc}\hfill q_{n{T}_o}=-{\Phi }_{\mathit{io}}\left(T_i-T_o\right)-{\Phi }_{\mathit{og}}\left(T_g-T_o\right)\mathrm{o}\mathrm{n}{\Gamma }_o& \hfill & \hfill \end{array}(4)$

where ρ_f and c_f refer to the density and specific heat capacity of the circulation fluid, respectively. The H and Γ are the heat sink/source term and heat transfer boundary. The v_i and v_o denote the flow velocity of fluid in the inner and outer pipes, respectively. Φ_io refers to the heat transfer coefficient between inner and outer pipes while Φ_og denotes the heat transfer coefficient between the outer pipe and grout (Diersch et al. 2011).

The term of hydrodynamic thermal dispersion tensor Λ reads:

${\Lambda }_f=\left({\lambda }_f+{\rho }_f{c}_f{\beta }_L\Vert {\mathbf{v}}_f\Vert \right)\mathbf{I}(5)$

where β_L denotes the longitudinal heat dispersivity and I refers to the identity matrix. The v_f is the Darcy velocity of groundwater flow in the subsurface.

The governing equations for the grout surrounding the outer pipe and the soil surrounding the borehole are given as follows:

$\begin{array}{ccc}\hfill {\rho }_g{c}_g\frac{\partial T_g}{\partial t}=\nabla \cdot \left({\lambda }_g\cdot \nabla T_g\right)+H_g& \hfill & \hfill \\ \hfill \mathrm{B}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}):& \hfill & \hfill \end{array}(6)$

$\begin{array}{ccc}\hfill q_{n{T}_g}=-{\Phi }_{\mathit{og}}\left(T_o-T_g\right)-{\Phi }_{\mathit{gs}}\left(T_s-T_g\right)\mathrm{o}\mathrm{n}{\Gamma }_g& \hfill & \hfill \end{array}(7)$

$\begin{array}{ccc}\hfill {\rho }_s{c}_s\frac{\partial T_s}{\partial t}=\nabla \cdot \left({\Lambda }_s\cdot \nabla T_s\right)+H_s& \hfill & \hfill \\ \hfill \mathrm{B}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{T}\mathrm{y}\mathrm{p}\mathrm{e}):& \hfill & \hfill \end{array}(8)$

$\begin{array}{ccc}\hfill q_{n{T}_s}=-{\Phi }_{\mathit{gs}}\left(T_g-T_s\right)\mathrm{o}\mathrm{n}{\Gamma }_s& \hfill & \hfill \end{array}(9)$

in which the detailed calculation of heat transfer coefficient Φ between soil and borehole can be found in Diersch et al. (2011).

Following the DC-FEM approach, the simulation domain is divided into two compartments, including the line elements representing boreholes and the 3D prism elements standing for the surrounding subsurface. All the governing equations inside the borehole (Eqs. 1, 3, 6) are solved on 1D line elements and the surrounding subsurface equation (Eq. 8) is solved in 3D prism elements. The heat flux between each component inside the borehole and between the surrounding subsurface is calculated by the temperature difference and the corresponding heat transfer coefficient. They are explicitly linked and solved together with the governing equations in the numerical model. Compared with the fully discretized 3D model, the number of elements can be significantly reduced through the model implementation with DC-FEM technology (Al-Khoury et al., 2010). More detailed documentation on benchmarks and tutorials of DBHE modeling features can be found on the official website of OpenGeoSys (Bilke et al., 2020).

2.2 Model Verification

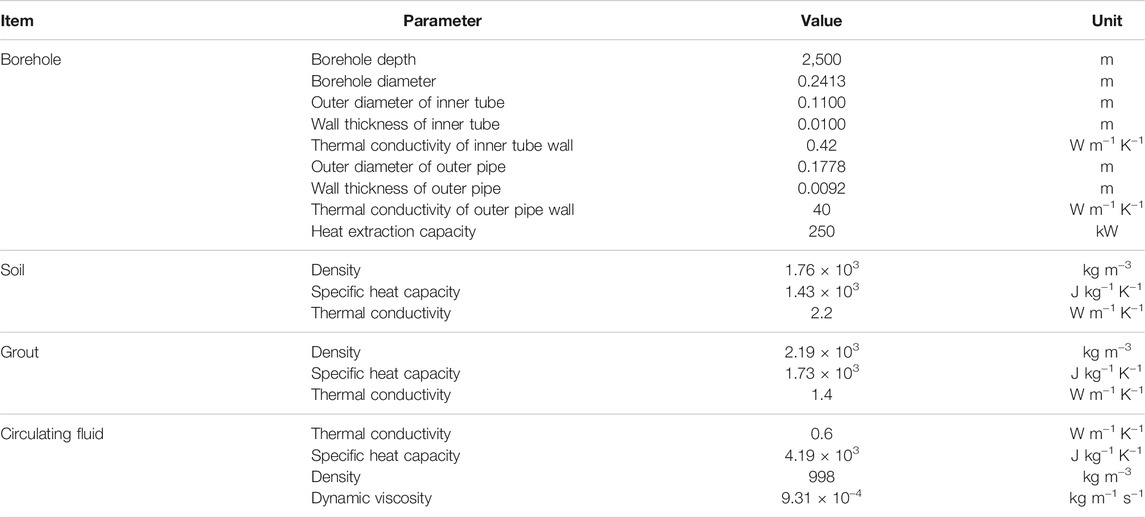
The BHE model implemented in OpenGeoSys software has previously been verified against analytical solution by Chen et al. (2020b, 2021) and monitoring data from actual projects in Europe (Meng et al., 2019; Chen et al., 2020a). The related calculation model is proved to be of the capability to reproduce the variation of long-term heat extracting performance for the DBHE system. As for the DBHE model, a thorough model validation has been conducted based on a multi-DBHE pilot project in Xi’an (Cai et al., 2021). In this study, the DBHE model established in OpenGeoSys considering the geothermal gradient is also verified based on the analytical DBHE solution proposed by Beier (2020). The setting of related parameters can be found in Table 1 and the operation time is set as one entire heating season.

TABLE 1

TABLE 1. Detailed parameters of the simulated DBHE for both OpenGeoSys and Beier’s model

The verification results (see Figure 2) show that the circulation temperatures calculated by the OpenGeoSys match well against Beier’s model. At the end of the heating season, the maximum difference between the results calculated by two models is no more than 0.57°C (less than 2.2%). Throughout the simulation, the inlet and outlet temperatures calculated by the OpenGeoSys are slightly higher than Beier’s model, which can be explained by the different calculation method in non-dimensional number within the DBHE between the OpenGeoSys and Beier’s model. This verification ensures that our model has enough accuracy and can be used in investigating the long-term performance of the DBHE.

FIGURE 2

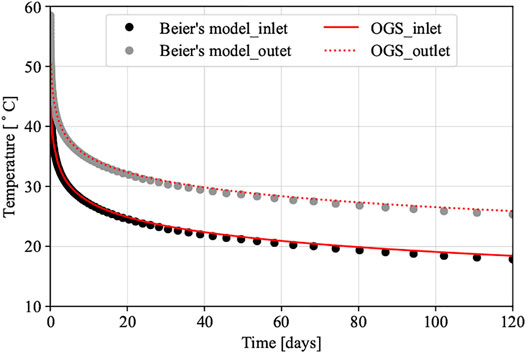
FIGURE 2. Verification of the proposed DBHE model based on OpenGeoSys against Beier’s analytical solution.

2.3 Model Configuration

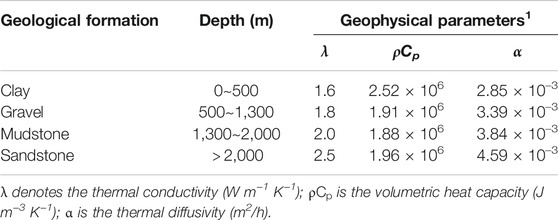
Based on the parameter settings in Table 1, the models in this study are then further extended for several different drilling depths from approximately 2,000 to 3,000 m to meet our purpose in solving the scientific questions proposed in Section 1. According to the published geological data (Ren et al., 2020) and in situ test results from realistic projects (Cai et al., 2021), the scenarios are configured based on the geological conditions and geothermal features in Weihe Basin (see Table 2).

TABLE 2

TABLE 2. Detailed geophysical parameters of Weihe Basin, China

For the boundary conditions of the model, the average ambient air temperature of 14.8°C (Dirichlet type) and typical geothermal heat flux 65 mW/m² (Neumann type) are imposed at the top and bottom surface of the domain, respectively. Moreover, based on the assumption of homogeneous media in the subsurface, the typical linear geothermal gradient in Xi’an is set as 35.0°C/km (Ren et al., 2020), serving as the initial condition of the model. To prevent the thermal plume from interfering with the domain boundary, the domain size is set to be 300 × 300 × (depth + 200) m. The mesh density and time step size of the simulation are chosen based on our previous work (Cai et al., 2021), in which the time step size of the simulation is first chosen to be 1 h in the heating season and later increased to 6 h during the recovery period. Furthermore, the heat pump and water pump units are introduced to our model. The performance curve of the heat pump is selected from a reference sample of heat pump manufacturer (Hein et al., 2016), which will be explained in detail in the next section. All the aforementioned simulation scenarios are all run for 15 years, which is the typical life-cycle span of an HVAC (heating, ventilation, and air conditioning) system in China (Chen S. et al., 2019).

3 Long-Term Economic Evaluation Approach

In this section, a comprehensive approach for the long-term economic evaluation of the DBHE heating system (see Figure 1) is proposed, in which the heat extraction performance, electricity consumption of heat pump and circulation pump, and initial costs are all taken into account.

To facilitate the economic analysis and not hinder the correctness of the main conclusion, several assumptions made in this study are listed as follows:

• The economic analysis of the DBHE heating system will just focus on the variation of performance of heat source side, which contains the DBHE, circulation pump of heat source, and heat pump. The range of drilling depth is set from 2,000 to 3,000 m in corroding to the technical regulation for DBHE heating system in Shaanxi Province (DBJ61/T166, 2020). Also, the prescriptive heating season for Weihe Basin, Shaanxi, lasts 4 months, from November 15 to the next March 15.

• The circulation temperatures for user side and building heating load are supposed to be constant so that the performance of heat pump will be just in correlation to the inlet temperature of heat pump on the source side. According to the reference sample (Hein et al., 2016), the COP of heat pump is defined as

$CO{P}_{hp}=a_1+b_1\times T_{in,hp}(10)$

where a₁ and b₁ are the coefficients, which are 3.925 and .083, respectively.

Based on the definition of COP, the hourly electricity cost of heat pump is calculated as

$C_{hp,h}=\frac{Q_{DBHE}}{CO{P}_{hp}-1}\times \mathrm{\Delta }t\times E_p(11)$

where Q_DBHE is the heat extraction rate of the DBHE (kW). Δt is the operation time, and the interval used in this work is 1 h. E_p is the electricity price, which is set to 0.7669 Yuan/kWh (Shaanxi, 2018).

• The DBHE will suffer a performance attenuation during long-term operation. Therefore, for the DBHE heating system equipped with different depths of boreholes, the index used in this study is to let the COP of the heat pump be at the same level at the end of the running period. Also, to prevent pollution on deep groundwater resources, the anti-freeze solution is not allowed to add to the DBHE system (DBJ61/T166, 2020). Thus, the inlet temperature of the DBHE should not fall below 0°C to prevent freeze in pipes. With these assumptions, the maximum heat extraction capacity will be obtained for the convenience of further economic analysis.

• The geological conditions for simulation are set as the typical values of Weihe Basin. Based on our previous work (Chen C. et al., 2019), the existence of groundwater flow does not provide a notable increase of heat extraction for the DBHE so that the groundwater flow is not introduced. The drilling cost data are acquired from a local drilling company in Xi’an and summarized to a quadratic polynomial form according to the suggestions from Lukawski et al. (2014). The estimation of drilling cost (unit: Yuan) reads:

$C_{drilling}=a_2+b_2\times D+c_2\times D^2(12)$

where D is the drilling depth (m). a₂, b₂, and c₂ are the coefficients, which are 850,909, −890, and 0.536, respectively.

• The electricity consumption of circulation pump is calculated based on the flow friction of the DBHE, which is determined by the Darcy–Weishbach equation. The pump efficiency is set as 85%.

$F_{DBHE}=f\times \frac{D}{d_e}\times \frac{\rho v^2}{2}(13)$

in which d_e is the equivalent diameter of pipe.

Based on the classic calculation method in hydrology, the equivalent diameter of pipe is determined by

$d_e=\frac{4A}{X}(14)$

where A and X are the flow cross-sectional area and perimeter of the flow area, respectively.

The Darcy friction factor f is calculated by Churchill correlation (Churchill, 1977):

$f^{-1}={\left(\frac{1}{{\left[\left({\left(\frac{8}{\mathrm{R}\mathrm{e}}\right)}^{10}+{\left(\frac{\mathrm{R}\mathrm{e}}{36500}\right)}^{20}\right)\right]}^{1/2}}+{\left[2.21\left(\ln \frac{\mathrm{R}\mathrm{e}}{7}\right)\right]}^{10}\right)}^{1/5}(15)$

Based on the similar concept of levelized cost of energy and evaluation criterion in shallow GSHP system (Cui et al., 2019), a novel index of levelized cost of heating capacity (LCOH) is proposed for the DBHE heating system in this study. The heat extraction capacity of the DBHE and electricity consumption of corresponding heat pumps and water pumps are all involved in this index, in which the dynamic COP of heat pump and circulation resistance are considered. The definition of LCOH index for the DBHE heating system reads:

$LCOH=\frac{C_{ini.}+{\sum }_{i=1}^N\frac{C_{ann.}}{{\left(1+r\right)}^i}}{{\sum }_{i=1}^N\frac{Q_{tot.}}{{\left(1+r\right)}^i}}(16)$

where C_ini. and C_ann. are initial cost and annual cost of the DBHE heating system, respectively. N is the typical operation period of HVAC system, which is set to 15 years (Chen S. et al., 2019). r is the discount rate, which is 6% for typical HVAC system (Khadra et al., 2020). Q_tot. is the total heating amount supplied from the DBHE heating system to the building sector, including the heat extraction of the DBHE, and the power consumed by heat pumps and circulation pumps. Based on this economic evaluation approach and related index, the economic analysis for the DBHE heating system in Weihe Basin will be carried out in the next section.

4 Results

In this section, the long-term heat extraction performance of the DBHE with different depths will be assessed and thorough economic analysis for the DBHE heating system will be executed following the approach proposed in Section 3.

4.1 Determination of Tentative Heat Extraction Capacity for Different Depths

Generally, there are two types of boundary conditions imposing on the DBHE, including fixed inlet temperature and fixed heat extraction rate, which correspond to the so-called thermal performance test and thermal response test (Choi et al., 2019). For a certain depth of the DBHE, to quantify its tentative heat extraction capacity, the boundary condition of fixed inlet temperature is chosen for the DBHE in this section. All inlet temperatures are fixed at 4°C, which is the threshold of circulation temperature in the heat pump unit (Cai et al., 2021). The flow rate of circulation fluid is 0.01 m³/s for different depths of the DBHE, including 2,000, 2,200, 2,400, 2,600, 2,800, and 3,000 m. The other DBHE parameter setting and subsurface properties are listed in Table 1 and Table 2.

The outlet temperature evolution of six DBHEs with different depths over the first heating season is presented in Figure 3. For all the tentative tests with the chosen parameters for the DBHE with different depths, the outlet temperatures tend to have a rapid dropdown at the first couple of days. For example, the outlet temperature of the DBHE with 3,000 m decreases by 10.85°C in the first 60 days, while the temperature drop is only 0.95°C in the next 60 days. The trend of outlet temperature variation indicates that the heat extraction rate of the DBHE after 60 days does not change too much, from 587.02 to 548.45 kW for the DBHE with 3,000 m depth.

FIGURE 3

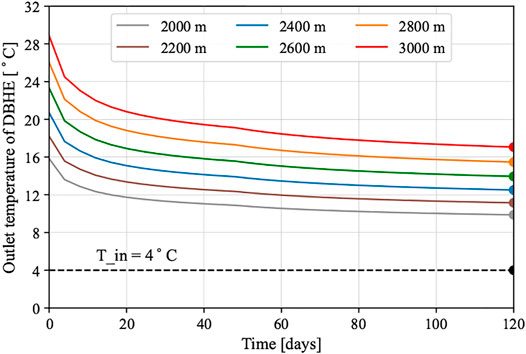
FIGURE 3. Thermal performance test of heat extraction capacity for the DBHE with different drilling depths.

When looking into the outlet temperatures among DBHEs with different depths, it has a higher value with deeper depth. While reaching the end of the heating season (marked in Figure 3), the outlet temperatures for six different depths are 9.87, 11.15, 12.51, 13.95, 15.47, and 17.06°C, respectively. In a conservative way of calculating tentative heat extraction capacity, the corresponding values are calculated according to the temperature difference at the end of heating season in Figure 3. It is found that the calculated tentative heat extraction capacity increases with the increment of drilling depth of the DBHE. From the depth of 2,000–3,000 m, the tentative heat performance capacity (black numbers above the bar) increases by 122.3%, from 246.72 to 548.45 kW. This implies that a deeper DBHE has a more considerable heat extraction potential.

4.2 Long-Term Heat Extraction Performance of the DBHE With Different Depths

In a more practical case, the inlet temperature of DBHE cannot be fixed in long-term operation, while the heating demand is usually kept fixed. Therefore, for long-term simulation of the DBHE, the fixed heat extraction rate is imposed to mimic real-world projects. In this section, the fixed heat extraction rate is imposed according to the calculated tentative heat extraction capacities from short-term thermal performance tests in the previous section. If the temperature drop of circulation temperature after the long-term operation is too large (below 0°C and have a risk of freeze) or too small (the DBHE can provide higher heating capacity), the heat extraction capacity will be adjusted until a proper value is obtained. It also needs to be mentioned that the flow rate for each DBHE with different depths is not the same. It is designed based on both the heat extraction rate and the typical temperature difference consumed by evaporator in heat pump. By adopting the official engineering standard in China (GB50189, 2015), the typical temperature difference of heat exchanger (evaporator) equipped in the heat pump unit is set to 10°C.

The variation of circulation temperature of the DBHE with different depth under 15-year operation is presented in Figure 4. It is worth noting that the temperature dropdown of several scenarios in Figure 4A is too large (below 0°C) to maintain the system operation, which means the tentative heat extraction capacities are slightly overestimated by the short-term thermal performance test. Therefore, the heat extraction rates used in long-term simulation for the DBHE with shallower depths are conducted with a slight reduction (no more than 5%; see the red values in Figure 6) of original tentative values. The evolution of circulation temperature with the adjusted heat extraction capacity is depicted in Figure 4B.

FIGURE 4

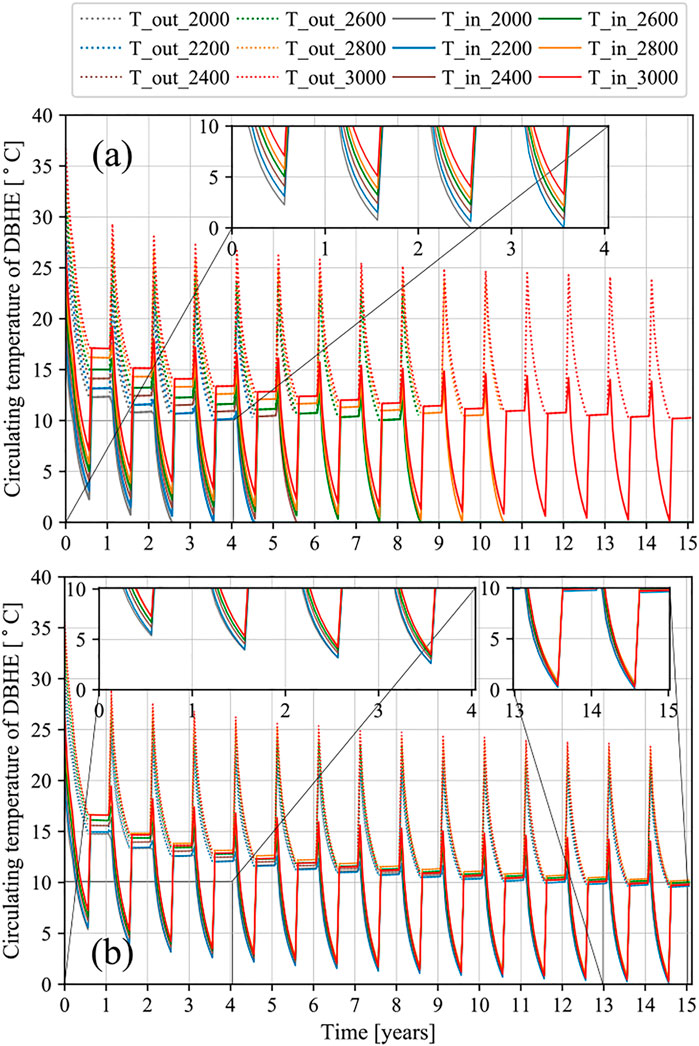
FIGURE 4. Long-term heat extraction performance of the DBHE (A) with the tentative heat extraction capacity (B) with the adjusted heat extraction capacity.

In Figure 4A, the inlet temperatures for scenarios with the depth from 2,000 to 2,800 m have a quick drop-down to under zero and the system will not work anymore due to the freezing of circulation fluid. As for the scenario with 3,000 m depth of the borehole, the long-term performance of the DBHE system under its corresponding tentative heat extraction capacity just reached 0°C inlet temperature threshold at the end of the 15th heating season. This indicates that the corresponding heat extraction rate has reached the upper limit of heat extraction potential. However, for the other five scenarios, this tentative heat extraction rate is beyond these upper potentials and is unsustainable in 15 years.

To make all the scenarios fully conform to the inlet temperature and COP index, Figure 4B presents the circulation fluid temperature evolution with adjusted heat extraction rate. Under the adjusted heat extraction rate, the inlet temperatures at the end of the last heating season are higher than 0°C for all six scenarios.

Furthermore, Figure 5 illustrates the soil temperature profiles at the depth of 200 m above each DBHE bottom for all the six scenarios at the first and 15th year. As shown in Figure 5A,B, the soil temperature in the subsurface surrounded the DBHE suffers severe drop-down compared with the initial value, which is caused by the heat extraction of the DBHE. After 15-year operation, the thermally affected radius of every DBHE is about 60 m. In every year, the heating season lasts 4 months, then another 8 months to recovery. Figure 5C,D shows the temperature distribution after the first and last year. It can be seen that the soil temperature around each DBHE has a recovery effect. For example, for the 2,000 m DBHE, the soil temperature at the end of the last recovery season is 69.8°C, which is 51.9°C higher than the temperature value at the end of the last heating season.

FIGURE 5

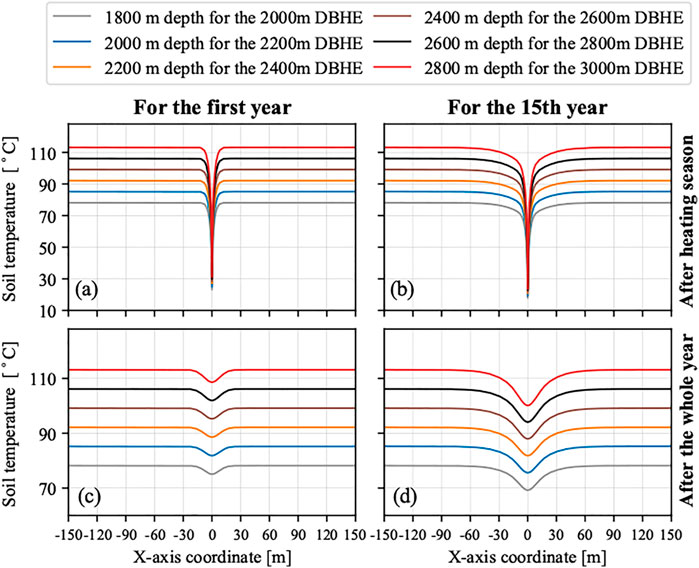
FIGURE 5. Soil temperature distribution for the DBHE with different drilling depths (A) at the end of the first heating season; (B) at the end of the last heating season; (C) at the end of first year; (D) at the end of last year.

For the six scenarios, the adjusted heat extraction rates presented in Figure 6 can be regarded as the upper limit of the heat extraction capacity. For the DBHE with depth of 2,000 m, the adjusted heat extraction rate is 5% lower than the tentative value predicted by the short-term thermal performance test. With the increased depth, the tentative heat extraction rate is more close to the upper limit of heat extraction potential. The reduction proportion of tentative heat extraction rate is gradually decreased from 4 to 1% for the depth varied from 2,200 to 2,800 m. Finally, by applying this adjusted heat extraction rate, all the circulation temperatures under different drilling depths of DBHE are at the same level, which is of an excellent agreement to the inlet temperature and COP criterion.

FIGURE 6

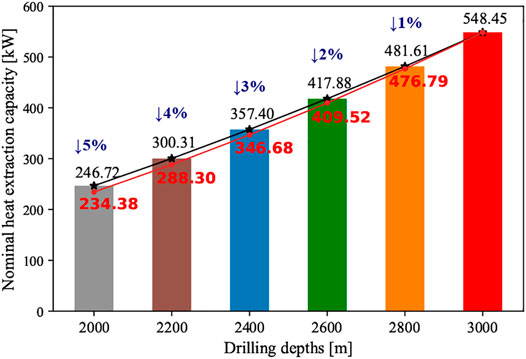
FIGURE 6. Determination of tentative heat extraction capacity for the DBHE with different drilling depths.

4.3 Variation of COP in Long-Term Operation

To conduct a comprehensive economic analysis for the DBHE heating system, the variation of performance of heat pump is of significance to be evaluated. Based on the assumption in Section 3, the COP of heat pump is only changed according to the outlet temperature of DBHE.

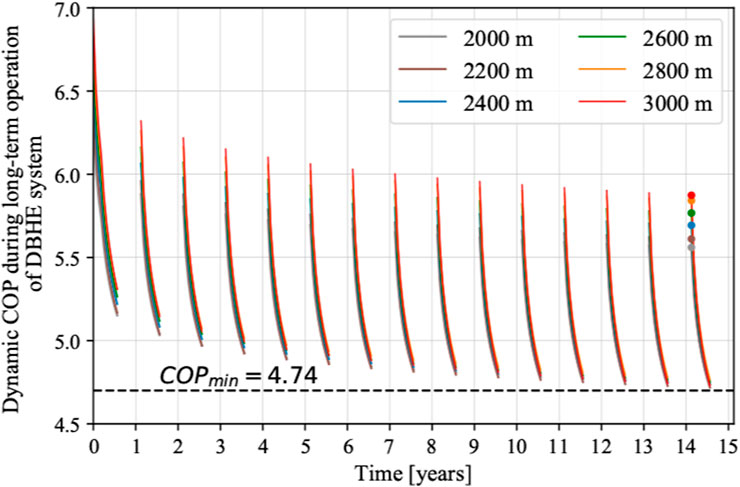
With the adjusted heat extraction rate imposed on the DBHE, the heat pump COP values over 15 heating seasons are presented in Figure 7 for the six different DBHE depths. In the first year of operation, the DBHE heating system with a deeper drilling borehole has a higher COP value of the heat pump. The COP for the scenario with 3,000 m depth of DBHE is 5.95, while the COP for the system with 2,000 m depth of DBHE is just 5.59. As the operation goes on, the COP values among the DBHE heating system with different drilling depths tend to be identical. The DBHE heating system with a deeper drilling depth maintains a larger COP in a couple of days at the beginning of every heating season. At the last heating season, the COP value for DBHE depth from 2,000 to 3,000 m increases from 5.56 to 5.87. Over the operation of 15 heating seasons, the minimum COP value of the heat pump is 4.74 for all six scenarios. It proved that using the DBHE heating system can have very high efficiency. Nevertheless, the applicability of the DBHE heating system in Weihe Basin is not only determined by the high efficiency of the system but also the sustainable economic feasibility.

FIGURE 7

FIGURE 7. Variation of COP for the DBHE heating system with different drilling depths.

4.4 Variation of Operational Costs and Overall Economic Analysis for the DBHE Heating System

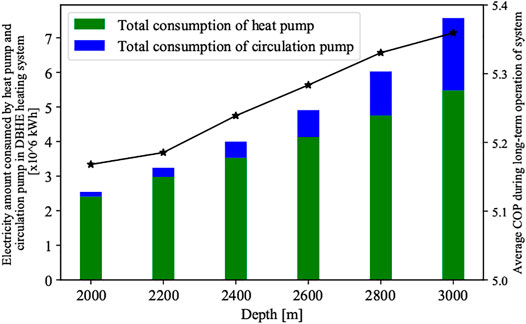
Based on the long-term heat extraction capacity determined in Section 4.2, economic analyses for the DBHE heating system are performed over long-term operation. In this section, according to the calculation method stated in 3, the consumption of heat pump and circulation pump can be addressed based on the circulation temperature variation of the DBHE and electricity price. The corresponding parameters of Weihe Basin in 3 are used for the calculation of consumption. The total accumulated electricity consumption of heat pump and circulation pump during 15 heating seasons and also the average COP of heat pump are presented in Figure 8.

FIGURE 8

FIGURE 8. Electricity amount consumed by heat pump and circulation pump in the DBHE heating system.

It can be seen in Figure 8 that the total electricity consumption of the circulation pump considerably rises with a deeper drilling depth of the DBHE. For the DBHE heating system with depth of 2,000 m, the total electricity consumption of heat pump and circulation pump is 2.40 × 10⁶ kWh and 1.35 × 10⁵ kWh, while for the 3,000 m DBHE, it was 5.48 × 10⁶ kWh for the electricity consumption of heat pump and 2.09 × 10⁶ kWh for the circulation pump. The total electricity consumption by heat pump and circulation pump increases by 2.28 and 15.5 times, respectively. The significant increment of electricity consumed by circulation pump can be explained by the higher circulation flow rate (0.013 m³/s) for the 3,000 m DBHE, compared with flow rate (0.0056 m³/s) of 2,000 m DBHE. In addition, the reason for higher total electricity consumption by heat pump is the outlet temperature from the DBHE. As indicated by Figure 4B, after operation of 15 heating seasons, the average outlet temperature of 3,000 m DBHE is a little higher than the others, leading to about one times increase based on the 2,000 m DBHE. Also, the black line gives the variation of COP of the DBHE heating system with different drilling depths. The DBHE system with deeper depth produces a higher heat extraction amount and has a similar variation trend of circulation temperature. The slight increment of outlet temperature will result in higher COP for the heat pump and less power consumed. This phenomenon can also explain the slow increase in the total electricity consumption of heat pumps from the aspects of COP. In total, the consumption of heat pumps and circulation pumps has a prominent promotion with a deeper drilling depth of the DBHE.

From the aforementioned investigation, it is clearly known that the DBHE heating system with deeper drilling depth has higher considerable heat extraction rate while it assumes more electricity on heat pump and circulation pump. Therefore, a combined economic analysis for the DBHE heating system during long-term operation is necessary to illustrate the system applicability. Figure 9A depicts the LCOH and net present value (NPV) for the DBHE heating system with different depths. With deeper depth of the DBHE, the LCOH of the DBHE heating system tends to decrease from 0.594 Yuan (2,000 m) to 0.568 Yuan (2,600 m). Then the LCOH shows a slow increase to 0.573 Yuan (3,000 m), which means that the DBHE heating system with a drilling depth of 2,600 m has the slowest LCOH. For the DBHE heating system with depth of 2,600 m, its levelized cost of total heating amount is lower than other systems with shallower or deeper depths, which can give reference to parameter design in applying the DBHE heating system in Weihe Basin. Figure 9B illustrates the NPV variation over long-term operation of the DBHE with the depth of 2,600 m. It can be seen that the NPV value shows an approximate-linear increase over the operation of 15 years. After 10-year operation, the NPV turns to be higher than zero, which illustrates that the pay-off time of the 2,600 m DBHE is around 10 years.

FIGURE 9

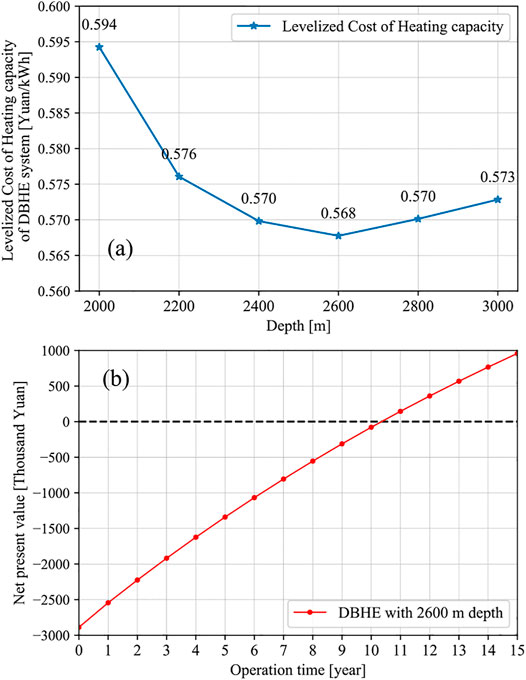
FIGURE 9. The LCOH (A) and NPV (B) value for the DBHE heating system with different drilling depths.

5 Discussion

5.1 Comparison With Other Published DBHE Models

In comparison with other two-dimensional DBHE models (Nian et al., 2019; Brown et al., 2021), the 3D DBHE model presented in this work is also well applicable in modeling the heat extraction performance of the DBHE (Kong et al., 2017), especially for the flexible boundary conditions and segmented soil properties. Furthermore, the proposed model has been validated by several experimental data, including northwestern and northeastern China (Huang et al., 2020; Cai et al., 2021), and other regions (Chen et al., 2020a).

It is worth noting that there are no hydraulic governing equations in the current DBHE model, which means the thermal properties of the circulation fluid cannot be changed according to the pressure values. This assumption is reasonable for a DBHE system with a depth shallower than 3 km under a normal geothermal gradient as concluded by Chen et al. (2019). For a DBHE system with a depth more than 3 km and a very high geothermal gradient (Doran et al., 2021), the pressure- and temperature-dependent heat transfer coefficients have to be taken into account in the DBHE simulation. However, this is not the case discussed in this work in Weihe Basin. In Weihe Basin, the average geothermal gradient is lower than 0.04°C/m (Ren et al., 2020). For a specific case with a very higher geothermal gradient, e.g., in Tibet, China, the system utilized for geothermal heat extraction could be hydrothermal system or enhanced geothermal system instead of a closed-loop system to have better performance and efficiency.

5.2 Replicability and Applicability of the Proposed Evaluation Method

Although this study presents a thorough and comprehensive approach to evaluate the economic feasibility for the DBHE heating system, the related conclusion is very site specific, totally based on the local parameters in Weihe Basin. For other regions, a similar approach should be performed according to the local conditions, most notably the drilling cost, geological properties, and operation period. In addition, with the urgent need for the reduction of carbon emission, the carbon trade market will make a difference in evaluating the economic feasibility of renewable energy technology. Using geothermal energy as its energy source will profit more because it can earn an extra carbon index sold in the carbon trade market.

6 Conclusion

In this study, a series of numerical models based on the typical geological conditions in Weihe Basin, China, have been carried out to simulate the long-term heat extraction performance. The economic feasibility of the DBHE heating systems with different drilling depths has been evaluated as well. Short-term thermal performance tests have been conducted to get the tentative heat extraction capacity and the adjusted heat extraction rates used for long-term performance simulation of the DBHE. Then, according to the local electricity price and calculation of power assumed by the heat pump and circulation pump, a combined economic analysis for the DBHE heating system is performed based on the long-term simulation results. To be more specific:

• For a deeper DBHE, the calculated tentative heat extraction rate by thermal performance test is much higher. The tentative heat performance capacity increases from 246.72 kW of 2,000 m DBHE to 548.45 kW of 3,000 m DBHE.

• The tentative heat extraction slightly overestimates the upper limit of heat extraction potential of the DBHE. A slight reduction (no more than 5%) gives a more reasonable heat extraction rate for the long-term operation of the DBHE.

• With the adjusted heat extraction rate imposed on the DBHE, the DBHE heating system with a deeper drilling borehole has a higher COP value of the heat pump in the first year of operation. Over the operation of 15 heating seasons, the minimum COP value of the heat pump is 4.74 for all six scenarios.

• The total electricity consumption of heat pumps and circulation pumps have a prominent promotion with a deeper drilling depth of the DBHE. For the depth of 2,600 m, its LCOH is lower than other systems with other depths, so that it is the better choice for application in Weihe Basin.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

WC: conceptualization, methodology, software, validation, writing—original draft, visualization. FW: conceptualization, formal analysis, project administration, funding acquisition, supervision. JJ: methodology, investigation, validation. ZW: methodology, visualization. JL: formal analysis, investigation. CC: methodology, software, validation, writing—review and editing.

Funding

This research is financially supported by the Key Research and Development Project of Shaanxi Province (2020ZDLSF06-08), as well as the Open Project of Key Laboratory of Coal Resources Exploration and Comprehensive Utilization (KF 2021-1), which is funded by the Chinese Ministry of Natural Resources.

Conflict of Interest

Author JL was employed by the company Shaanxi Coal Geology Group Company Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors CC.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank Prof. Zhanli Ren for his helpful advice on selecting geological parameters of Weihe Basin and Prof. Beier for his public MATLAB program on the analytical solutions. Also, the authors would like to thank all the reviewers and editors for their constructive comments on this paper.

Abbreviations

BHE, borehole heat exchanger; COP, coefficient of performance; DBHE, deep borehole heat exchanger; FEM, finite element method; GSHP, ground source heat pump; HVAC, heating, ventilation, and air conditioning; LCOH, levelized cost of heating capacity; NPV, net present value.

References

Al-Khoury, R., Kölbel, T., and Schramedei, R. (2010). Efficient Numerical Modeling of Borehole Heat Exchangers. Comput. Geosciences 36, 1301–1315. doi:10.1016/j.cageo.2009.12.010

CrossRef Full Text | Google Scholar

Anderson, A., and Rezaie, B. (2019). Geothermal Technology: Trends and Potential Role in a Sustainable Future. Appl. Energ. 248, 18–34. doi:10.1016/j.apenergy.2019.04.102

CrossRef Full Text | Google Scholar

Beier, R. A., Acuña, J., Mogensen, P., and Palm, B. (2014). Transient Heat Transfer in a Coaxial Borehole Heat Exchanger. Geothermics 51, 470–482. doi:10.1016/j.geothermics.2014.02.006

CrossRef Full Text | Google Scholar

Beier, R. A. (2020). Thermal Response Tests on Deep Borehole Heat Exchangers with Geothermal Gradient. Appl. Therm. Eng. 178, 115447. doi:10.1016/j.applthermaleng.2020.115447

CrossRef Full Text | Google Scholar

Bilke, L., Shao, H., Chen, S., and Cai, W. (2020). OpenGeoSys Tutorial. Available at: https://www.opengeosys.org/docs/userguide/basics/introduction/.

Google Scholar

Brown, C. S., Cassidy, N. J., Egan, S. S., and Griffiths, D. (2021). Numerical Modelling of Deep Coaxial Borehole Heat Exchangers in the Cheshire basin, UK. Comput. Geosciences 152, 104752. doi:10.1016/j.cageo.2021.104752

CrossRef Full Text | Google Scholar

Cai, W., Wang, F., Chen, S., Chen, C., Liu, J., Deng, J., et al. (2021). Analysis of Heat Extraction Performance and Long-Term Sustainability for Multiple Deep Borehole Heat Exchanger Array: A Project-Based Study. Appl. Energ. 289, 116590. doi:10.1016/j.apenergy.2021.116590

CrossRef Full Text | Google Scholar

Cai, W., Wang, F., Liu, J., Wang, Z., and Ma, Z. (2019). Experimental and Numerical Investigation of Heat Transfer Performance and Sustainability of Deep Borehole Heat Exchangers Coupled with Ground Source Heat Pump Systems. Appl. Therm. Eng. 149, 975–986. doi:10.1016/j.applthermaleng.2018.12.094

CrossRef Full Text | Google Scholar

Chen, C., Cai, W., Naumov, D., Tu, K., Zhou, H., Zhang, Y., et al. (2021). Numerical Investigation on the Capacity and Efficiency of a Deep Enhanced U-Tube Borehole Heat Exchanger System for Building Heating. Renew. Energ. 169, 557–572. doi:10.1016/j.renene.2021.01.033

CrossRef Full Text | Google Scholar

Chen, C., Shao, H., Naumov, D., Kong, Y., Tu, K., and Kolditz, O. (2019a). Numerical Investigation on the Performance, Sustainability, and Efficiency of the Deep Borehole Heat Exchanger System for Building Heating. Geothermal Energy 7, 18. doi:10.1186/s40517-019-0133-8

CrossRef Full Text | Google Scholar

Chen, S., Cai, W., Witte, F., Wang, X., Wang, F., Kolditz, O., et al. (2020a). Long-term thermal Imbalance in Large Borehole Heat Exchangers Array-A Numerical Study Based on the Leicester Project. Energy and Buildings 231, 110518. doi:10.1016/j.enbuild.2020.110518

CrossRef Full Text | Google Scholar

Chen, S., Witte, F., Kolditz, O., and Shao, H. (2020b). Shifted thermal Extraction Rates in Large Borehole Heat Exchanger Array–A Numerical experiment. Appl. Therm. Eng. 167, 114750. doi:10.1016/j.applthermaleng.2019.114750

CrossRef Full Text | Google Scholar

Chen, S., Zhang, Q., Li, H., Mclellan, B., Zhang, T., and Tan, Z. (2019b). Investment Decision on Shallow Geothermal Heating & Cooling Based on Compound Options Model: A Case Study of china. Appl. Energ. 254, 113655. doi:10.1016/j.apenergy.2019.113655

CrossRef Full Text | Google Scholar

Choi, W., Kikumoto, H., and Ooka, R. (2019). Critical Comparison between thermal Performance Test (Tpt) and thermal Response Test (Trt): Differences in Heat Transfer Process and Extractable Information. Energ. Convers. Management 199, 111967. doi:10.1016/j.enconman.2019.111967

CrossRef Full Text | Google Scholar

Churchill, S. W. (1977). Comprehensive Correlating Equations for Heat, Mass and Momentum Transfer in Fully Developed Flow in Smooth Tubes. Ind. Eng. Chem. Fundamentals 16, 109–116. doi:10.1021/i160061a021

CrossRef Full Text | Google Scholar

Cui, Y., Zhu, J., Twaha, S., Chu, J., Bai, H., Huang, K., et al. (2019). Techno-economic Assessment of the Horizontal Geothermal Heat Pump Systems: A Comprehensive Review. Energ. Convers. Management 191, 208–236. doi:10.1016/j.enconman.2019.04.018

CrossRef Full Text | Google Scholar

DBJ61/T166 (2020). Technical Regulation for Medium Deep Geothermal Buried Pipe Heating System. Shaanxi Province: Department of Housing and Urban-Rural Development. [Dataset].

Google Scholar

De La Peña, L., Guo, R., Cao, X., Ni, X., and Zhang, W. (2022). Accelerating the Energy Transition to Achieve Carbon Neutrality. Resour. Conservation Recycling 177, 105957.

Google Scholar

Deng, J., He, S., Wei, Q., Li, J., Liu, H., Zhang, Z., et al. (2020). Field Test and Optimization of Heat Pumps and Water Distribution Systems in Medium-Depth Geothermal Heat Pump Systems. Energy and Buildings 209, 109724. doi:10.1016/j.enbuild.2019.109724

CrossRef Full Text | Google Scholar

Deng, J., Wei, Q., Liang, M., He, S., and Zhang, H. (2019). Field Test on Energy Performance of Medium-Depth Geothermal Heat Pump Systems (Md-ghps). Energy and Buildings 184, 289–299. doi:10.1016/j.enbuild.2018.12.006

CrossRef Full Text | Google Scholar

Dias, J. M., and Costa, V. A. (2018). Adsorption Heat Pumps for Heating Applications: A Review of Current State, Literature Gaps and Development Challenges. Renew. Sustainable Energ. Rev. 98, 317–327. doi:10.1016/j.rser.2018.09.026

CrossRef Full Text | Google Scholar

Diersch, H.-J., Bauer, D., Heidemann, W., Rühaak, W., and Schätzl, P. (2011). Finite Element Modeling of Borehole Heat Exchanger Systems: Part 1. Fundamentals. Comput. Geosciences 37, 1122–1135. doi:10.1016/j.cageo.2010.08.003

CrossRef Full Text | Google Scholar

Doran, H. R., Renaud, T., Falcone, G., Pan, L., and Verdin, P. G. (2021). Modelling an Unconventional Closed-Loop Deep Borehole Heat Exchanger (Dbhe): Sensitivity Analysis on the Newberry Volcanic Setting. Geothermal Energy 9, 1–24. doi:10.1186/s40517-021-00185-0

CrossRef Full Text | Google Scholar

Fang, L., Diao, N., Shao, Z., Zhu, K., and Fang, Z. (2018). A Computationally Efficient Numerical Model for Heat Transfer Simulation of Deep Borehole Heat Exchangers. Energy and Buildings 167, 79–88. doi:10.1016/j.enbuild.2018.02.013

CrossRef Full Text | Google Scholar

Gb50189 (2015). Design Standard for Energy Efficiency of Public Buildings. PR China: Ministry of Housing and Urban-Rural Development. [Dataset].

Google Scholar

Hein, P., Kolditz, O., Görke, U.-J., Bucher, A., and Shao, H. (2016). A Numerical Study on the Sustainability and Efficiency of Borehole Heat Exchanger Coupled Ground Source Heat Pump Systems. Appl. Therm. Eng. 100, 421–433. doi:10.1016/j.applthermaleng.2016.02.039

CrossRef Full Text | Google Scholar

Hu, X., Banks, J., Wu, L., and Liu, W. V. (2020). Numerical Modeling of a Coaxial Borehole Heat Exchanger to Exploit Geothermal Energy from Abandoned Petroleum wells in Hinton, Alberta. Renew. Energ. 148, 1110–1123. doi:10.1016/j.renene.2019.09.141

CrossRef Full Text | Google Scholar

Huang, Y., Zhang, Y., Xie, Y., Zhang, Y., Gao, X., and Ma, J. (2020). Field Test and Numerical Investigation on Deep Coaxial Borehole Heat Exchanger Based on Distributed Optical Fiber Temperature Sensor. Energy 210, 118643. doi:10.1016/j.energy.2020.118643

CrossRef Full Text | Google Scholar

Javadi, H., Ajarostaghi, S. S. M., Rosen, M. A., and Pourfallah, M. (2019). Performance of Ground Heat Exchangers: A Comprehensive Review of Recent Advances. Energy 178, 207–233. doi:10.1016/j.energy.2019.04.094

CrossRef Full Text | Google Scholar

Khadra, A., Hugosson, M., Akander, J., and Myhren, J. A. (2020). Economic Performance Assessment of Three Renovated Multi-Family Buildings with Different HVAC Systems. Energy and Buildings 224, 110275. doi:10.1016/j.enbuild.2020.110275

CrossRef Full Text | Google Scholar

Kohl, T., Brenni, R., and Eugster, W. (2002). System Performance of a Deep Borehole Heat Exchanger. Geothermics 31, 687–708. doi:10.1016/s0375-6505(02)00031-7

CrossRef Full Text | Google Scholar

Kohl, T., Salton, M., and Rybach, L. (2000). “Data Analysis of the Deep Borehole Heat Exchanger Plant Weissbad (Switzerland),” in Proceedings World Geothermal congress. Kyushu-Tohoku, Japan, 3459–3464.

Google Scholar

Kolditz, O., Bauer, S., Bilke, L., Böttcher, N., Delfs, J.-O., Fischer, T., et al. (2012). Opengeosys: an Open-Source Initiative for Numerical Simulation of Thermo-Hydro-Mechanical/chemical (Thm/c) Processes in Porous media. Environ. Earth Sci. 67, 589–599. doi:10.1007/s12665-012-1546-x

CrossRef Full Text | Google Scholar

Kong, Y., Chen, C., Shao, H., Zhonghe, P., Liangping, X., and Jiyang, W. (2017). Principle and Capacity Quantification of Deep-Borehole Heat Exchangers. Chin. J. Geophys. 60, 4741–4752. doi:10.6038/cjg20171216

CrossRef Full Text | Google Scholar

Le Lous, M., Larroque, F., Dupuy, A., and Moignard, A. (2015). Thermal Performance of a Deep Borehole Heat Exchanger: Insights from a Synthetic Coupled Heat and Flow Model. Geothermics 57, 157–172. doi:10.1016/j.geothermics.2015.06.014

CrossRef Full Text | Google Scholar

Li, C., Guan, Y., Liu, J., Jiang, C., Yang, R., and Hou, X. (2020). Heat Transfer Performance of a Deep Ground Heat Exchanger for Building Heating in Long-Term Service. Renew. Energ. 166, 20–34. doi:10.1016/j.renene.2020.11.111

CrossRef Full Text | Google Scholar

Lin, J., and Lin, B. (2019). The Actual Heating Energy Conservation in china: Evidence and Policy Implications. Energy and Buildings 190, 195–201. doi:10.1016/j.enbuild.2019.03.004

CrossRef Full Text | Google Scholar

Liu, J., Wang, F., Cai, W., Wang, Z., and Li, C. (2020). Numerical Investigation on the Effects of Geological Parameters and Layered Subsurface on the thermal Performance of Medium-Deep Borehole Heat Exchanger. Renew. Energ. 149, 384–399. doi:10.1016/j.renene.2019.11.158

CrossRef Full Text | Google Scholar

Lukawski, M. Z., Anderson, B. J., Augustine, C., Capuano, L. E., Beckers, K. F., Livesay, B., et al. (2014). Cost Analysis of Oil, Gas, and Geothermal Well Drilling. J. Pet. Sci. Eng. 118, 1–14. doi:10.1016/j.petrol.2014.03.012

CrossRef Full Text | Google Scholar

Lund, J. W., and Toth, A. N. (2021). Direct Utilization of Geothermal Energy 2020 Worldwide Review. Geothermics 90, 101915. doi:10.1016/j.geothermics.2020.101915

CrossRef Full Text | Google Scholar

Luo, Y., Guo, H., Meggers, F., and Zhang, L. (2019). Deep Coaxial Borehole Heat Exchanger: Analytical Modeling and thermal Analysis. Energy 185, 1298–1313. doi:10.1016/j.energy.2019.05.228

CrossRef Full Text | Google Scholar

Meng, B., Vienken, T., Kolditz, O., and Shao, H. (2019). Evaluating the thermal Impacts and Sustainability of Intensive Shallow Geothermal Utilization on a Neighborhood Scale: Lessons Learned from a Case Study. Energ. Convers. Management 199, 111913. doi:10.1016/j.enconman.2019.111913

CrossRef Full Text | Google Scholar

Morita, K., Bollmeier, W. S., and Mizogami, H. (1992). An experiment to Prove the Concept of the Downhole Coaxial Heat Exchanger (DCHE) in Hawaii. Los Angeles, United States: Geothermal Resources Council.

Google Scholar

Nian, Y.-L., Cheng, W.-L., Yang, X.-Y., and Xie, K. (2019). Simulation of a Novel Deep Ground Source Heat Pump System Using Abandoned Oil wells with Coaxial Bhe. Int. J. Heat Mass Transfer 137, 400–412. doi:10.1016/j.ijheatmasstransfer.2019.03.136

CrossRef Full Text | Google Scholar

Ozgener, L., Hepbasli, A., and Dincer, I. (2007). A Key Review on Performance Improvement Aspects of Geothermal District Heating Systems and Applications. Renew. Sustainable Energ. Rev. 11, 1675–1697. doi:10.1016/j.rser.2006.03.006

CrossRef Full Text | Google Scholar

Pan, A., Lu, L., Cui, P., and Jia, L. (2019). A New Analytical Heat Transfer Model for Deep Borehole Heat Exchangers with Coaxial Tubes. Int. J. Heat Mass Transfer 141, 1056–1065. doi:10.1016/j.ijheatmasstransfer.2019.07.041

CrossRef Full Text | Google Scholar

Pan, S., Kong, Y., Chen, C., Pang, Z., and Wang, J. (2020). Optimization of the Utilization of Deep Borehole Heat Exchangers. Geothermal Energy 8, 1–20. doi:10.1186/s40517-020-0161-4

CrossRef Full Text | Google Scholar

Ren, Z., Liu, R., Ren, W., Qi, K., Yang, G., Cui, J., et al. (2020). Distribution of Geothermal Field and its Controlling Factors in the Weihe basin. ACTA GEOLOGICA SINICA 94, 1938–1949. doi:10.1111/1755-6724.14458

CrossRef Full Text | Google Scholar

Rodrigues, R., Pietzcker, R., Fragkos, P., Price, J., McDowall, W., Siskos, P., et al. (2022). Narrative-driven Alternative Roads to Achieve Mid-century Co2 Net Neutrality in Europe. Energy 239, 121908. doi:10.1016/j.energy.2021.121908

CrossRef Full Text | Google Scholar

Salvia, M., Reckien, D., Pietrapertosa, F., Eckersley, P., Spyridaki, N.-A., Krook-Riekkola, A., et al. (2021). Will Climate Mitigation Ambitions lead to Carbon Neutrality? An Analysis of the Local-Level Plans of 327 Cities in the EU. Renew. Sustainable Energ. Rev. 135, 110253. doi:10.1016/j.rser.2020.110253

CrossRef Full Text | Google Scholar

Sapinska-Sliwa, A., Rosen, M. A., Gonet, A., and Sliwa, T. (2016). Deep Borehole Heat Exchangers—A Conceptual and Comparative Review. Int. J. Air-Conditioning Refrigeration 24, 1630001. doi:10.1142/s2010132516300019

CrossRef Full Text | Google Scholar

Shaanxi, P. G. (2018). Notice of Shaanxi Provincial price bureau on Adjusting Shaanxi Power Grid Electricity price. Available at: http://sndrc.shaanxi.gov.cn/zjww/jgcs/jgc/lsxx/jgysbbz/zyspjg/dl/aAj2Yj.htm.

Google Scholar

Shao, H., Hein, P., Sachse, A., and Kolditz, O. (2016). Geoenergy Modeling II: Shallow Geothermal Systems. Berlin, Germany: Springer.

Google Scholar

Śliwa, T., and Kotyza, J. (2003). Application of Existing wells as Ground Heat Source for Heat Pumps in Poland. Appl. Energ. 74, 3–8. doi:10.1016/S0306-2619(02)00125-3

CrossRef Full Text | Google Scholar

Soltani, M., Kashkooli, F. M., Dehghani-Sanij, A., Kazemi, A., Bordbar, N., Farshchi, M., et al. (2019). A Comprehensive Study of Geothermal Heating and Cooling Systems. Sustainable Cities Soc. 44, 793–818. doi:10.1016/j.scs.2018.09.036

CrossRef Full Text | Google Scholar

Song, X., Wang, G., Shi, Y., Li, R., Xu, Z., Zheng, R., et al. (2018). Numerical Analysis of Heat Extraction Performance of a Deep Coaxial Borehole Heat Exchanger Geothermal System. Energy 164, 1298–1310. doi:10.1016/j.energy.2018.08.056

CrossRef Full Text | Google Scholar

Ürge-Vorsatz, D., Cabeza, L. F., Serrano, S., Barreneche, C., and Petrichenko, K. (2015). Heating and Cooling Energy Trends and Drivers in Buildings. Renew. Sustainable Energ. Rev. 41, 85–98.

Google Scholar

Wang, Z., Wang, F., Liu, J., Ma, Z., Han, E., and Song, M. (2017). Field Test and Numerical Investigation on the Heat Transfer Characteristics and Optimal Design of the Heat Exchangers of a Deep Borehole Ground Source Heat Pump System. Energ. Convers. Management 153, 603–615. doi:10.1016/j.enconman.2017.10.038

CrossRef Full Text | Google Scholar

Xu, T., Hu, Z., Feng, B., Feng, G., Li, F., and Jiang, Z. (2020). Numerical Evaluation of Building Heating Potential from a Co-axial Closed-Loop Geothermal System Using Wellbore–Reservoir Coupling Numerical Model. Energy Exploration & Exploitation 38, 733–754. doi:10.1177/0144598719889799

CrossRef Full Text | Google Scholar

Zhao, N., and You, F. (2020). Can Renewable Generation, Energy Storage and Energy Efficient Technologies Enable Carbon Neutral Energy Transition? Appl. Energ. 279, 115889. doi:10.1016/j.apenergy.2020.115889

CrossRef Full Text | Google Scholar

Zhao, X., Ma, X., Chen, B., Shang, Y., and Song, M. (2022). Challenges toward Carbon Neutrality in china: Strategies and Countermeasures. Resour. Conservation Recycling 176, 105959. doi:10.1016/j.resconrec.2021.105959

CrossRef Full Text | Google Scholar

Nomenclature

A flow cross-sectional area (m²)

C economic cost (Yuan)

c specific heat capacity (J kg⁻¹ K⁻¹)

D drilling depth (m)

d_e equivalent diameter of the pipe (m)

E_q electricity price (Yuan/kWh)

F flow friction (Pa)

f Darcy friction factor

H heat sink/source term (W m⁻³)

I identity matrix (–)

K roughness of pipe (mm)

L length of pipe (m)

N integer (–)

P power (kW)

Q heat extraction amount (kW)

q_n heat flux (W m⁻²)

r discount rate

Re Reynolds number (–)

T temperature (°C)

t time (h)

v vector of flow velocity (m s⁻¹)

X perimeter of the flow area (m)

α thermal diffusivity (m² h⁻¹)

β_L longitudinal heat dispersivity (m)

Γ boundary

λ thermal conductivity (W m⁻¹ K⁻¹)

Λ thermal hydrodynamic dispersion tensor (W m⁻¹ K⁻¹)

Φ heat transfer coefficient (W m⁻¹ K⁻¹)

ρ density (kg m⁻³)

Θ Darcy friction factor (–)

Δ difference operator

∇ nabla vector operator

∑ integral operator

f circulation fluid in borehole

g grout

hp heat pump

i inner pipe (outflow)

in inlet

max maximum

o outer pipe (inflow)

out outlet

s soil/rock