Investigating Anzali Wetland Sediment Estimation Using the MPSIAC Model

The adverse effects of upland erosion impact the Anzali Wetland in Iran. The Modified Pacific South-west Inter Agency Committee model (MPSIAC) was used to estimate the sediment yield in the watershed. The watershed was divided into twelve sub-watersheds based on the geomorphologic features and waterway orientations (Sw₀-Sw₁₁). To investigate the effect of different factors on erosion and sedimentation, data were digitized using ArcGIS software. The effective factor weights were determined using the MPSIAC model, and the total sediment yield was calculated for each sub-watershed. Results showed that the amount of particulate sediment in the critical sub-watersheds Sw₆ and Sw₉ was 777.9 and 730.2 t km⁻². yr⁻¹, respectively. Based on erosion and sedimentation results, the sub-watershed erosion was prioritized as Sw₆> Sw₉> Sw₄> Sw₁> Sw₀> Sw₅> Sw₂> Sw₈> Sw₃> Sw₁₁ > Sw₇> Sw₁₀. Both model inputs (precipitation) and outputs (sediment) at different parts of the watershed were assessed via point observations data. Comparison of correlation values reveals that the correlation between the simulated and sampling values was strong in sub-watershed 1 (R² < 0.8). EF, RMSE, nRMSE, CRM, and MAE were 0.23, 16.74 tons per year, 5.05%, 0.55, and −3.6, respectively, which indicates the model’s high performance in Sw₀. Areas with insufficient cover and bare soil showed a high correlation with the final erosion model. Thus, land-use classes, such as dense vegetation and good pastures, correspond to areas with low erosion. Conversely, bare soils and poor pastures were located on the eroded flats.

1 Introduction

Soil erosion and degradation is a severe environmental problem that is a critical hazard for environmental bodies. Faulty agricultural practices, high annual precipitation, and land-use changes in northern Iran are vital environmental factors that accelerate soil erosion (Noori et al., 2016). Sediment production due to soil erosion directly affects the life in the Anzali Wetland by causing severe morphological changes (JICA, 2005). The approximate location of the Anzali Wetland and its watershed is between N 36°55′ to 37°32′ and E 48°45′ to °49°42′ and is located in northern Iran along the coast of the Caspian Sea. The Anzali Wetland covers 193 km² in the Guilan Province and was registered in the Ramsar Convention International Wetlands list in 1975 (Khalili Vavdare et al., 2019). Although it is internationally known as an essential habitat for migratory water birds, it was added to the Montreux Record of degraded wetlands in 1993 (JICA, 2005). The adverse effects of upland erosion are related to anthropogenic activities, such as wastewater sedimentation and solid waste generation. Furthermore, critical damage to the wetland facilities due to transported and suspended loads into reservoir lakes has caused high economic costs due to poor water quality (Refahi, 1996; Wang et al., 2003).

One of the significant threats to the global economic and environmental sustainability is soil erosion and high sediment yields, which are affected by lithology, the area of watersheds, climate, hydrology, ground cover, and land use (Milliman and Syvitski, 1992; Zhang et al., 2010; Zhu and Li, 2014), and have different effects on erosion (Parehkar et al., 2013). Erosion, by each factor, can cause further problems for downstream watersheds, such as wetlands. Although erosion cannot be entirely prevented, reducing its volume, extent, and rate may be practically possible. Given the complexity of soil erosion, all the effective parameters should be identified and determined. Several empirical, numerical, and experimental methods have been developed to estimate watershed sediment yields (Onstad and Foster, 1975; Heininger and Cullmann, 2015).

Several soil erosion methods have been analyzed to watershed sediment yield or sediment rate studies (Eisazadeh et al., 2012), including empirical, numerical, and experimental models (Amini et al., 2010; Amiri, 2010; Najm et al., 2013; Noori et al., 2016; Pourkarimi et al., 2017; Zarei and Amiri, 2017; Brooshkeh et al., 2018; Noori et al., 2018; Zarei et al., 2019), as well as sensitivity analysis (Behnam et al., 2011) or chronological models (Abbasi, 2019; Khalili Vavdare et al., 2019). Empirical estimation methods were first developed to analyze the effects of agricultural practices (Eisazadeh et al., 2012; Noori et al., 2016) due to their simple structure and ease of application. The method applied statistical information analysis with digitalization by utilizing geographic information systems (GISs), remote sensing (RS), and satellite imagery to estimate sheet and rill erosion in watersheds. In this method, soil erosion is simply estimated as an empirical evaluation of the calibrated coefficients. Empirical methods have been widely used to estimate the sediment yield and erosion (Nearing et al., 2015).

To date, the Pacific South-west Inter-Agency Committee (PSIAC) model has been developed primarily for application in mostly arid and semi-arid regions in the United States, which have the same environmental conditions as Iran (Sadeghi, 1993). The main model inputs are surface geology, soil, climate, runoff, topography, ground cover, land use, upland erosion, and channel erosion. Subsequently, various modifications have been suggested to enhance the model performance. The results of these modifications are summarized in new models, such as the Modified Pacific South-west Inter-Agency Committee (MPSIAC) model. The difference is that nine governing equations were used in MPSIAC. Unlike the PSIAC model, the sediment yield is assumed to be directly proportional to the total numerical values assigned to the nine MPSIAC model factors. The MPSIAC model (PSAIC, 1986) estimates the long-term average annual erosion rate as a product of the sediment yield in sloped areas based on rainfall patterns, soil characteristics, topography, land cover, and management practices. Ndomba et al. (2013) estimated the amount of sedimentation in ungauged catchments in southwestern Tanzania through a study using the PSIAC model. The BIAS values in the calibration and validation periods were equal to 7.88 and 18.12%, respectively, which indicate the model’s efficiency in simulating the sediment of the catchment.

Subsequently, modified models have widely and successfully investigated watersheds around the world. By developing and integrating this model into ArcGIS and RS (Daneshvar and Bagherzadeh, 2012; Noori et al., 2018), some attempts were made to investigate and assess this integrated model for the evaluation of sediment yields and soil erosion in the Iranian watersheds (Mirakhorlo and Rahimzadegan, 2018; Shojaei et al., 2019). On the other hand, some studies have been conducted to compare different models such as EPM, PSIAC, and MPSIAC to estimate the sedimentation yield (Mirakholro and Rahimzadegan, 2018; Zarei et al., 2019). Abdullah et al. (2017) used MPISIAC, EMP, and RUSLE empirical models to investigate the amount of erosion in the Um-Niga region of Kuwait. The results showed that the RUSLE model did not have good accuracy, but the MPSIAC and EMP models had acceptable and close results. Between these two models, the MPSIAC model had more spatial accuracy. Bayat et al. (2020) assessed the accuracy and distribution of erosion layers from the EPM and MPSIAC models compared with the BLM model as terrestrial reality values in the Shahriari watershed, Iran. Examination of statistical indicators showed that the correlation of erosion classes of the MPSIAC model with the BLM output (as a terrestrial reality map) is higher than the EPM model. Also, the results of evaluating the accuracy of MPSIAC and EPM models showed that the value of the kappa coefficient in the MPSIAC model was higher than that of the EPM model.

Also, in several studies, soil nutrients and organic carbon were investigated using the MPSIAC model (Heshmati et al., 2012; Elsey-Quirk et al., 2019). Tangestani (2006) compared EPM and PSIAC models in GIS for erosion and sediment yield assessment in the Afzar Catchment, Fars Province, Iran. Noori et al. (2016) compared EPM and MPSIAC models in GIS and RS for erosion and sediment yield assessment in Dez watershed, Iran. Both studies were in arid and semi-arid climate. The results suggested that models such as MPSIAC have high efficiency in calculating sediment yields in arid and semi-arid regions such as Iran. Ramezani et al. (2018) studied the status of erosion and sedimentation in the watershed of Baranjestanak Dam in the Ghaemshahr city, Iran, by using MPSIAC and EMP experimental methods. The studied basin was in a low erosion class. The results showed that the MPSIAC model was more accurate than the experimental EPM model as it uses more parameters (Ramezani et al., 2018).

In the past, the Anzali Wetland was much deeper, but it has shallowed due to sedimentation. The total sediment inflow to the wetland is estimated at approximately 5,227.4 t km⁻² year⁻¹ (Khalili Vavdare et al., 2019). Sedimentation studies of the wetland were conducted to understand the dominant sediment origin and estimate the sedimentation rate for the ongoing management and conservation of the Anzali Wetland. Due to the good performance of the MPSIAC model in estimating the amount of erosion and sediment in the watersheds and the lack of insufficient related research on the Anzali watershed, this model was selected to investigate the status of the Anzali watershed. The present study was conducted to evaluate erosion and assess the current sedimentation rate and pattern in the Anzali Wetland. This research is aimed to monitor sedimentation to determine the relationship between the effective parameters and sediment yields in the Anzali watershed.

2 Materials and Methods

2.1 Study Area

As shown in Figure 1, in the present study, the Anzali Wetland and its watershed were considered as the study area. The watershed has an area of approximately 3,740 km² (Zare Khosheghbal et al., 2013a). There are 15 rivers originating from the Talesh Mountains that discharge into this wetland, and ten major river systems notably influence the sedimentation and environment of the wetland. These rivers are perennial and originate from the Alborz Mountains to the south. The annual mean discharge into the wetland is estimated to be approximately 76 m³ s⁻¹, or 2,400 MCM. Because of the geographical location, these streams significantly affect the inflowing annual sediment load that pours into the wetlands (Zare Khosheghbal et al., 2013b).

FIGURE 1

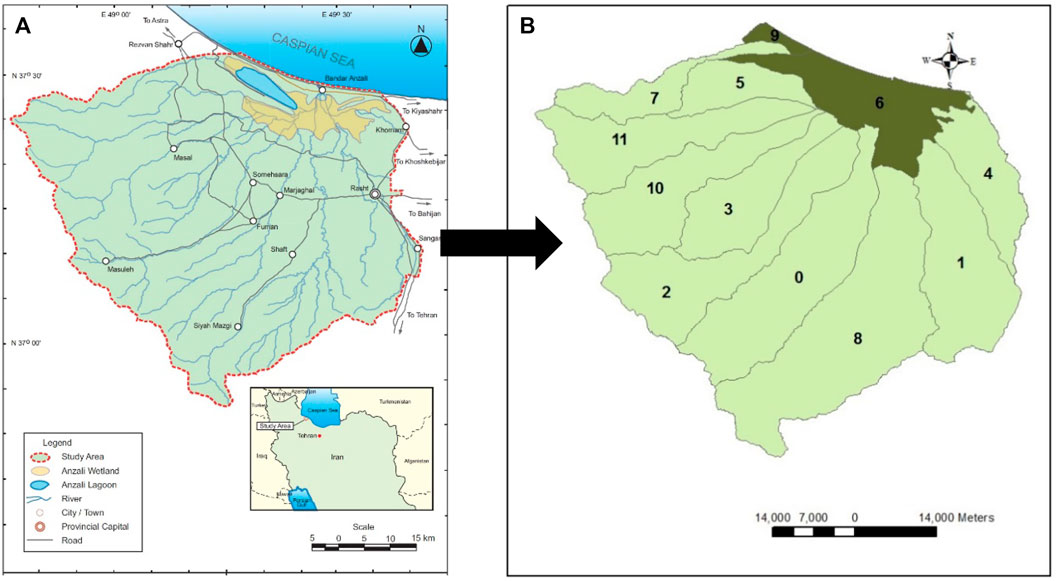
FIGURE 1. Location of the Anzali watershed (A) showing the twelve sub-watershed divisions (Sw₀-Sw₁₁) (B).

The northern region of Iran, where the Anzali Wetland is located, has a Caspian or Hyrcanian climate with a precipitation of 400–2000 mm yr⁻¹. The evaporation rate increases from west to east with a regional average of 800 mm. The temperature is mild, ranging from −0.8 to 37.3°C with an average of 17°C. The natural slope is less than 1% in the plains dipping toward the Anzali Wetland, and the slope of the mountainous area increases to more than 25% from the boundary of the plains up to 2,500 to 3,000 m in elevation.

2.2 The MPSIAC Model

The MPSIAC model, considering the modification used by Johnson and Gebhardt (1982), is an appropriate method to measure watershed sediment yields in Iran. This model has been successfully applied by researchers to estimate the watershed sediment yields in semi-arid areas of Iran (Khaledian, et al., 2012; Refahi, 1996; Heydarian, 1996). The erosion quantities, which are calculated in every sub-watershed, will be considered in relation to influential parameters.

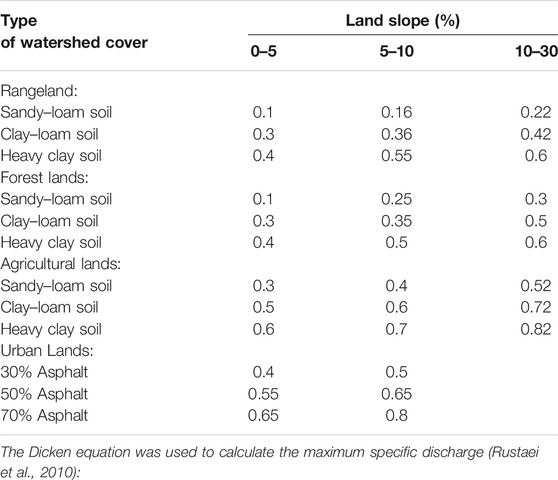
In this model, the nine effective factors influencing erosion and sediment production include surface geology (X₁), soil (X₂), climate (X₃), runoff (X₄), topography (X₅), ground vegetation or land cover (X₆), land use (X₇), upland erosion (X₈), and river erosion or channel erosion (X₉). According to the intended purpose of MPSIAC models, the study area of the watershed should be divided into hydrological units (sub-watersheds), land component units, or equal geomorphological working units. As shown in Table 1, the model factors are ranked based on the corresponding tables that are compacted. In the MPSIAC model, five sediment yield classes or Qs are defined based on the nine factor value summation (R) using Eq. 1.

$Q_s=38.77e^{0.0353R},(1)$

where Q_s is the deposition rate (m³. km⁻²). The Anzali watershed was divided into twelve sub-watersheds based on the geomorphologic features and waterway orientations. To investigate the effect of different factors on erosion and sedimentation, data such as geological layer parameters, watershed slopes, the elevation from sea level, the distance from rivers and roads, rainfall, and land use were digitized in ArcGIS 10.4.1 software, which demonstrates the relative superiority of this model compared to other experimental methods. The effective factor weights were determined using the MPSIAC model, and the total amount was calculated for each region. Finally, the amount of sediment was determined using Eq. 1.

TABLE 1

TABLE 1. Determining the annual sediment yield and erosion class by using the MPSIAC model.

Given the status and characteristics of each element, including rock type, slope, direction, vegetation, land use, rainfall, and soil, factor scores were determined (Khalili Vavdare et al., 2019). First, the score of each factor was determined according to the results of the factor characteristics study. The erosion intensity was then classified as one from these five classes: very low, low, medium, high, and very high, and a qualitative erosion severity map was prepared (Table 1).

The work is executed as follows:

1) Prepare the maps, such as

 a) Aerial photos of the Anzali watershed at a scale of 1:100,000

 b) Soil map of the area at a scale of 1:100,000

 c) Digital Landsat satellite data related to the Anzali watershed

 d) Geological map of the region at a scale of 1:100,000

2) Digitize the maps using GIS

3) Divide the watershed and identify working units

4) Model with MPSIAC

To model with MPSIAC, the nine required factors must be examined and analyzed. All practical factors in the model are dimensionless. A brief explanation of the model components is presented as follows.

2.2.1 Surface Geology (X₁)

The first component relates to a geologic erosion index (X₁) called the surface geology factor, which is determined based on the types of rocks and their characteristics, such as their hardness, fracture habit, and weathering conditions. The value of this factor ranges from 0 to 10 (Refahi, 1996; Tangestani, 2006). To prepare this index, the geological map was first digitized at a scale of 1:100000 over the studied area. Then, for further analysis, the relevant map was prepared as a raster model by weighing the lithological units based on the sensitivity of each unit in ArcView 10.4.1 software.

2.2.2 Soil (X₂)

The soil factor (X₂) is equal to 16.67 × k, where k denotes the soil erodibility factor in the universal soil loss equation (USLE) and depends on the soil texture and amount of lime, gravel, silt, and organic matter. These characteristics were obtained from a soil report of the area. Each characteristic was then applied to the corresponding nomogram, and the k value was obtained. Morgan and Nalepa (1982) proposed the numbers shown in Table 2 for the erodibility coefficient (k) of different soils.

TABLE 2

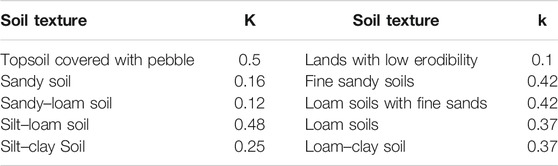
TABLE 2. Erodibility coefficient (k) for different soil textures (Morgan and Nalepa, 1982).

The soil in the area was mainly alluvial and forested. The soil erodibility range was measured according to Table 2 and was found to be between 2.7 and 5.4, with an average of 4.1.

2.2.3 Climate (X₃)

The climate factor (X₃) was estimated using a 6-h precipitation amount with a 2-year return period (P2) in mm. In this study, the climate factor was based on 30 years of rainfall records from 1976 to 2005. Meteorological information and statistics from regional stations were used to determine the 6-h rainfall with a 2-year return period. Using the full 24-h rain period and Eq. 2, the maximum rainfall in 6 h with a return period of 2 yr was estimated (Alizadeh Gorji, 2006) to be 71 mm. By placing this value in Eq. 2, the maximum weather factor score was set at 14.3 mm.

$P_{10}^{60}\left(0.3710+0.6184t^{0.4484}\right)\left(0.4524+0.2471\ln \left(T-0.6\right)\right)=P_T^t,(2)$

where t is the duration of precipitation (h), T is the return period (yr), and $P_{10}^{60}$ is in millimeters.

2.2.4 Runoff (X₄)

The runoff factor (X₄) in Eq. 1 was obtained from Eq. 3, in which the total average runoff (R₀) in mm was interpolated from measurements at the meteorological stations shown in Figure 1. The special peak discharge (determined from the peak discharge in the hydrological units divided by area) (Q_p) in m³ s ⁻¹ km⁻² for a period of 30 years (1976–2005) was used for long-term simulations, and the corresponding values for each of 5-year period were used for short-term simulations. The estimated runoff depth at the watershed exit point is the result of the runoff participation of all the waterways in the watershed. However, the obtained number cannot truly represent the watershed runoff. To solve this problem, the watershed runoff coefficient was first calculated using hydrological equations, and the runoff depth of each hydrological unit was calculated using Eq. 3.

$R=C.P,(3)$

where R is the annual runoff depth (mm), C is the runoff coefficient, and P is the rainfall depth (mm). The runoff coefficient depends on the physical characteristics of the watershed, and its value can be obtained from Table 3.

$Q=C.A^{0.75},(4)$

$Q_p=Q/A,(5)$

TABLE 3

TABLE 3. Runoff coefficients for different watersheds.

In Eqs 4 and 5, Q is the peak discharge (m³ s⁻¹), A is the watershed area (km²), and Q_p is the special peak discharge (cubic meters per second per square kilometer). The runoff factor score of each watershed unit was calculated using the specific peak discharge and annual runoff height of each hydrological unit in the Anzali watershed.

2.2.5 Topography (X₅)

X₅ is a topographic factor determined based on the average watershed slope (S) (%). The average slope map was generated from a digital elevation model (DEM) using ArcGIS 10.4.1. To determine the topographic factor, a slope map was prepared using the DEM of the area. To prepare this model, topographic maps at a scale of 1:100,000 and the 3D Analyst add-on function in ArcGIS were used to extract a slope map. Then, in each hydrology unit, the post factor and height were calculated by placing the average slope of each unit.

2.2.6 Ground Cover (X₆)

Vegetation, litter, and rocks are the main features of ground cover (X₆). The bare ground factor (P_b) is a representative of these three features. To determine the ground cover factor, a vegetation density map prepared by the Japan International Cooperation Agency (JICA) was utilized. Subsequently, the vegetation map was overlain with the map of hydrological units, and then the bare and uncovered grounds were quantified in each hydrological unit. Ultimately, the resulting number was placed in 0.2 × P_b, and the ground cover factor score was determined.

2.2.7 Land-Use (X₇)

The land-use factor (X₇) was estimated based on the plant canopy (P_c) (%) using the equation 20 - 0.2P_c. To determine P_c, a relationship between the canopy and Normalized Difference Vegetation Index (NDVI) was developed for this area according to equation 64.1 NDVI + 15.9. The final land-use map is shown in Figure 2B. In this study, to determine the land-use factor, a land-use map was prepared by JICA. The results overlapped with the hydrological unit maps. After completing the studies with field operations, the percentage of canopy cover of each unit was calculated, and the land-use factor score was determined based on the above equation.

FIGURE 2

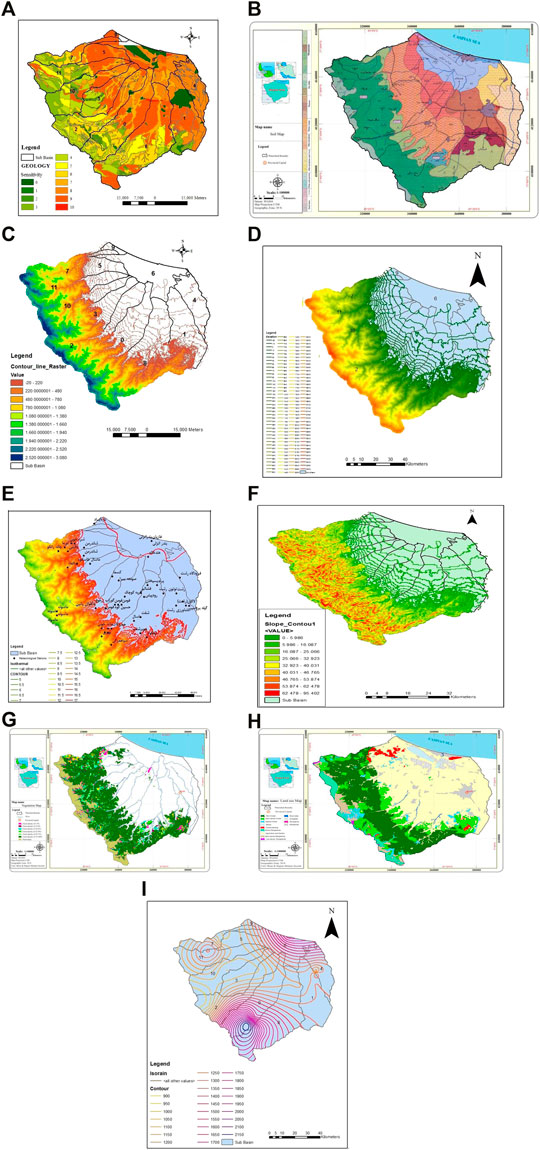
FIGURE 2. (A) Geology, (B) Type of land, (C) Contour, (D) DEM, (E) Isotherm, (F) Slope-contour, (G) Ground cover, (H) Land use, (I) Isorain.

2.2.8 Upland Erosion (X₈)

The upland erosion (X₈) factor was obtained based on the method suggested by the Bureau of Land Management (BLM). The first six factors in the soil surface factors (SSF1–SSF6) were obtained from field observations. The seventh factor, SSF7, was estimated from precipitation and gully formation. The value of each of these factors ranged from 0 to 15. The total SSF score was derived by summing the values of all seven factors (SSF1–SSF7), and the upland erosion factor (X8) was obtained from Eq. 6 (Johnson and Gebhardt, 1982).

${\mathrm{X}}_{\mathrm{8}}=0.25\mathrm{SSF},(6)$

To investigate the role of the above factors in sediment production, surface erosion was evaluated in the watershed, including rainfall, laminar, furrow, and moat erosion. Due to the importance of this factor in sediment production, its score varied between 0 and 25. If no erosion was observed on the ground, a score of zero was given, and if more than 50% of the ground comprised ditches, a score of 25 was given. Erosion status factors at the watershed level are shown in Table 4.

TABLE 4

TABLE 4. Determining the score related to the current status of erosion for sediment production.

2.2.9 Channel Erosion (X₉)

The channel erosion factor (X9) was determined based on the gully erosion factor by using the BLM method and by considering the relation between annual rainfall (in mm) and gully erosion improvement. X₉ was calculated using the equation 1.67 × SSF₇. SSF₇ was obtained from the method suggested by the BLM (Johnson and Gebhardt, 1982).

Finally, in the MPSIAC model, the sum of the nine factors was expressed by R, and the rate of the sediment yield was predicted using the following equation: 38.77e0.0353R, where Q_s is the rate of the sediment yield in each sub-watershed in m³ km⁻² y⁻¹.

The required information layers were produced to implement and prepare the MPSIAC. First, a topographic layer of the Anzali watershed at a scale of 1:100,000 is shown in Figure 2D. The 24-h and 6-h rainfall return periods for 10 years, calculated in each sub-watershed, is required to generate the climate layer. Then, 10 years of rainfall and temperature data from the meteorological stations in the Anzali watershed were gathered, and then, isorain and isotherm data were produced, as shown in Figure 2. Specific land-use layers using satellite imagery from 2015, geological layers using maps (Figure 2A) at a scale of 1:100,000, slope paths (Figures 2C,F), and their depth using topographic maps and precipitation using meteorological information were prepared.

These current maps were adjusted according to the model format, and all maps were superposed. A digital map was then prepared from different data. After digitization, all the required model maps were transformed from a linear to grid structure with a cell size of 50 m × 50 m. Using the information layers created and based on the structure of each model, the necessary processing was performed, and the initial model information layers (sediment production map) were prepared. Then, the different factor weights were determined in the MPSIAC model, and the values of the total effective factors were calculated for each region. Finally, the amount of erosion and sediment were determined. Figure 2 is attached with high quality maps as a Supplementary Material.

2.3 Model Validation

For validation, 19 years of rainfall data (2003–2020) and sediment load were measured in the meteorological reference stations, and reference hydrometers of 12 sub-basins were collected. Precipitation data was used to simulate the sediment of the MPSIAC model. Since climatic data in each study is one of the most uncertain parameters and access to annual information of other model parameters was not possible and also assuming that effective values in sediment estimation using the MPSIAC model are constant, the only factor of change was rainfall, so for each year during this period, the sediment load was predicted and estimated. Observational and simulation values of the sediment load were compared by using a graphical method (R2) and statistical indices such as root mean square error (RMSE) (Hyndman Rob and Koehler, 2006), normalized root mean square error (nRMSE) (Willmott and Matsuura, 2005), mean error (MAE) (Schaeffer, 1980), coefficient of residual mass (CRM) (Wallis and Todini, 1975), and model efficiency (EF) (Loague and Green, 1991). Both data sets were transferred to the coordinate plates to employ the graphical method, and R2 is calculated automatically in an Excel worksheet.

3 Results and Discussion

In the first step, the results of the influential parameter in determining the sediment yield should be determined, the details of which are explained in detail in the Materials and Methods section. An explanation of these nine factor results is briefly presented.

3.1 Model Parameters

3.1.1 Geology

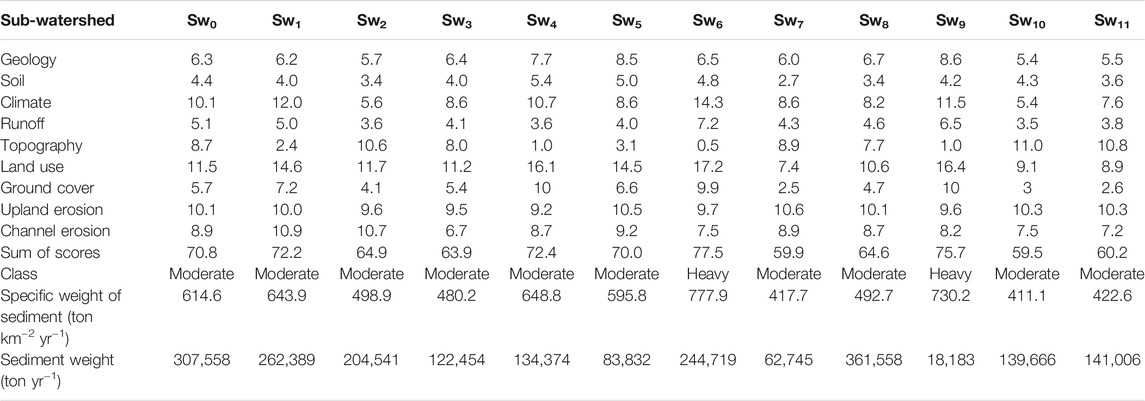
The Anzali watershed has great geological diversity comprising 101 lithological units. Most of the northern part of the watershed is composed of Quaternary (IV) formations, which are highly sensitive to erosion. The Quaternary materials consist of in situ or discontinuous materials, sediment deposits, or transition discontinuities. Geologically, the rock units in most of the study area belong to the Quaternary period and predominantly have a loose structure and unconsolidated particles that erode during rainfall and snowmelt. Surface, furrow, and massif erosion transport sediment to the secondary and main waterways, and the Anzali Wetland (Khalili Vavdare et al., 2019). Using the raster map of geological units, the surface geological factor score in each sub-watershed was calculated. Based on the results, sub-watersheds 5 and 9 had the highest susceptibility to erosion (Sw₅ and Sw₉).

3.1.2 Soil

Most soils were alluvial and forested. Soil erodibility ranged between 2.7 and 5.4, with an average of 4.1.

3.1.3 Climate

The climate of the Anzali Wetland is semi-humid to humid. The Alborz mountain range in the southern part of the Caspian Sea causes mild weather and heavy rainfall. Climate scores range from 5.4 (Sw₁₀) to 14.3 (Sw₆), with an average of 9.3 in the Anzali watershed.

3.1.4 Runoff

Because the Anzali watershed was divided into twelve sub-watersheds based on physiographic (hydrological) conditions, it can be inferred that the highest area and elevation were related to sub-watersheds 8 (Pasikhan) (Sw₈) and 11 (Sw₁₁) (Morghak), respectively. Using yearly rainfall values, the values of runoff height, volume, and flow coefficient of each sub-watershed were determined. The highest annual rainfall was related to sub-watersheds 0, 6, and 9. Sub-watersheds 9 (Kenareh) (Sw₉) and 6 (Bandar Anzali) (Sw₆) showed the highest runoff factors, and sub-watersheds 4 (Khamam-Rud) (Sw₄) and 10 (Khalakai) (Sw₁₀) showed the lowest amount of this factor. The wetland catchment area is the rainiest region in Iran, and the Anzali Wetland is a wet point in this watershed. Most rainfall was observed in sub-watersheds 0, 6, and 8 (Sw₀, 6, and 8). Based on 24- and 6-h rainfall with a return period of 2 years, the score of the weather factor was calculated for each sub-watershed as shown in Table 5.

TABLE 5

TABLE 5. Runoff factor parameter.

3.1.5 Topography

After digitizing the topographic maps of the area and preparing a slope map, the average watershed slope was determined to be approximately 25%, with a slope range of zero to 6% occupying the most significant area. Furthermore, more than half of the watershed area had a slope of less than 16%. The average slope of the sub-watersheds was obtained using GIS, and the topographic factor score was calculated. The highest topographic factor score was related to sub-watersheds 10 (Khalakai) (Sw₁₀) and 11 (Morghak) (Sw₁₁), which can be attributed to the high average slope of these sub-watersheds.

3.1.6 Ground Cover

In Table 7, the score of ground cover ranges from 2.5 in Sw₈ to 10 in Sw_5,10. The average score of this parameter is 6.

3.1.7 Land Use

Land use was divided into thirteen different units, as shown in Figure 2. Farms and orchards cover the largest area of the watershed. Based on the results, the land-use factor varied in different units, which is attributed to different vegetation and variable density throughout the watershed. The highest land-use factor score was related to sub-watersheds 6 and 9 (Sw_6,9), which are downstream of the main watershed and its agricultural sector. The upstream part of the watershed was less sensitive to erosion because of the dense and semi-dense forest cover.

3.1.8 Upland Erosion

One of the determining factors in weathering and erosion of rocks is their inherent mineral properties. The sensitivities were classified from 1 to 10, which denote the most resistant (1) and sensitive (10) to erosion, respectively. Formations with a sensitivity of 9 occupied the highest percentage of the watershed area. The number zero was related to the wetland and asphalt. Arabkhedri et al. (2009) calculated the suspended load of a country’s watershed and found that watersheds with high suspended sediment loads mainly have sensitive marl lithology, such as the one found in the Anzali Wetland watershed. The soil surface factor of them can be determined using the BLM method (Table 6). Sub-watersheds 10 and 11 (Sw₁₀ and Sw₁₁) showed the highest and sub-watersheds 5 and 3 showed the lowest erosion and river erosion values. Sw in the tables represents the sub-watershed, and the subscript values refer to the sub-watershed number.

TABLE 6

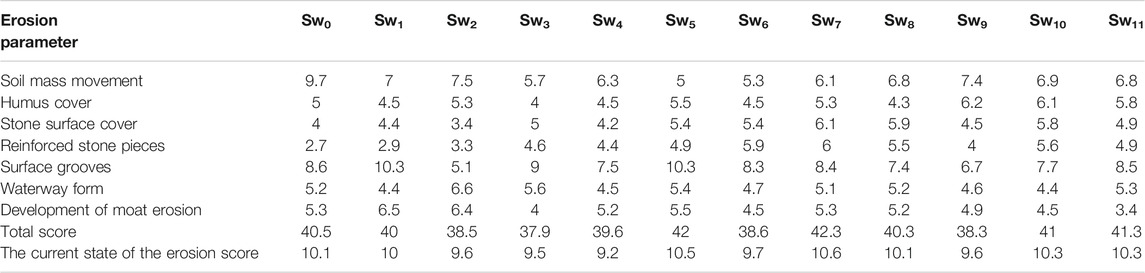
TABLE 6. Determination of the soil surface factor score by using the BLM method and determination of the current erosion factor score.

3.1.9 Channel Erosion

According to Table 7, channel erodibility ranged between 6.7 (Sw₂) and 10.9 (Sw₄) with an average of 8.6.

TABLE 7

TABLE 7. The score of nine parameters and amount of sediments in each sub-watersheds.

3.1.10 Sediment Flux

The scores of nine parameters in twelve sub-watersheds and the total scores are shown in Table 6. The highest score corresponded to sub-watershed 6 (Sw₆). Overall, climatic factors and the current erosion status were identified as the most critical factors in sediment production. To calculate the sediment rate, the weighted average degree of sedimentation in each sub-watershed was used. As seen in Table 6, the minimum, maximum, and mean sedimentation rates were determined as 59.5, 77.5, and 67.6%, respectively, for the entire watershed. In most watersheds with medium and high sedimentation rates, attention must be paid to the erosion status and the application of protection measures.

3.2 Sediment Yield

Based on the results, the mean sediment yield varied from 143.75 in Sw₁ to 176.18 in the Sw₃ sub-watershed, with a sediment production of 5,360.43 and 6,242.05 m³ yr⁻¹, respectively. The Sw₀ sub-watershed had the highest sediment yield (10,976.81 m³ yr⁻¹), which can be attributed to the larger surface area of this sub-watershed compared to the other sub-watersheds (Table 6).

As shown in Table 7 and Table 8, the amount of particulate sediment in the most critical sub-watersheds 6 and 9 (Sw_6,9) were found to be 777.9 and 730.2 t km⁻² yr⁻¹, respectively. Due to geological sensitivity, topographic conditions, heavy rainfall, and high river erosion, sediment production was higher in these units. Abdi et al. (2011) concluded that if the geological formations exposed to the watershed surface are sensitive to erosion, the watershed sediment production could be high in mountainous and steep regions with humid climate and considerable rainfall.

TABLE 8

TABLE 8. The sedimentation rate of hydrological units of the Anzali catchment based on the MPSIAC model.

3.3 Erosion Prioritize

The importance of intensified erosion in the Anzali watershed is far less than that of natural erosion. However, grazing and upstream pasture degradation effectively intensify peak flooding and runoff and increase its severity. Based on erosion and sediment studies conducted in the Anzali watershed, the sub-watershed erosion prioritization is as follows:

Sw₆> Sw₉> Sw₄> Sw₁> Sw₀> Sw₅> Sw₂> Sw₈> Sw₃> Sw₁₁ > Sw₇> Sw₁₀

Similar to the sediment yield, the soil losses were classified into five erosion classes. Results showed that the amount of soil loss varied from <215 to >1,900 m³ km⁻² yr⁻¹, classified as “very slight” to “severe” classes. Based on the results, 68.97% of the surface area was related to the ‘slight’ class, with average soil losses of 215–615 m3 km⁻² yr⁻¹ (Table 7). The mean soil losses in the study area varied from 522.46 in Sw₆ to 677.63 in the Sw₃ sub-watershed. Additionally, based on the sediment delivery ratio (SDR) results, it ranged from 0.23 in the Sw₀ to 0.29 in the Sw₆ sub-watershed (Table 8).

The amount of sedimentation in each hydrological unit of the Anzali watershed determined by zoning and overlap in GIS are presented in Table 8. If the specific sediment weight is assumed to be 1.3 t m⁻³, the total annual sediment that will flow to the wetland will be 2,083,026 t yr⁻¹ and the amount of specific sediment will be 6,734.5 t km⁻² yr⁻¹. The amount of water erosion in most watersheds in Iran is reported to be between 8 and 16 tons per hectare per year (Mahdian, 2004).

Water erosion is intensified by vegetation loss due to overgrazing, and the presence of formations sensitive to marl erosion reinforces it. With the intensification of this type of erosion, soil permeability is reduced, soil fertility is lost, and the vegetation cover is further destroyed. Eventually, the ground is prepared for the desertification of the region and intensification of wind activity. In addition, with the passage of floods over the marl formations and sediment transfer to the alluvial plain followed by evaporation, salts are precipitated, increasing soil salinity. It should be noted that water erosion plays a role in desert development in the study area, exacerbating the water erosion effect. Therefore, desertification should be controlled in this region.

Despite the region’s sensitivity to water erosion, there is potential to control the types of erosion in the study area. By realizing this potential, effective steps can be taken to control regional desertification. According to the results, an average erosion rate was determined as 8.5 t ha⁻² yr⁻¹, and sub-watersheds 1 and 2 have the highest rates with an average of approximately 10.9 t ha⁻² yr⁻¹. Among the geomorphological facies, Musil facies with erosion equivalent to Sw₅ (10.6 t ha⁻² yr⁻¹) differs from other facies. Sedimentation rates start from approximately 411 t km⁻² yr⁻¹ in Sw₁₀ which is upstream of the watersheds and reach a maximum of 777 t km⁻² yr⁻¹ in Sw₆. Sub-watersheds Sw_6,9 with high levels of sediment (>750 t km⁻² yr⁻¹) had the highest amount of sediment production. The average amount of maximum sedimentation in the entire region was 6,743 t ha⁻¹ km⁻². In the watershed outlets, the amount of erosion increased, covering many land-use classes.

One of the most important factors in erosion and sediment production in the Anzali watershed is the type of geological formation, especially in the watershed outlets. The presence of sensitive marl formations, which are ubiquitous in some areas at the surface and in some places, has also appeared in the erosion path, facilitating natural erosion in the region. However, runoff due to rock outcrops upstream and their accumulation in the watershed outlet provide the grounds for erosion intensification.

As can be seen in Figures 3A,B, the erosion rates were high in the middle and eastern study areas, which can be attributed to the geology and scattered vegetation cover. Because the main lithologies of these areas are thick-bedded limestone, shale, and siltstone, they are not resistant to erosion. However, the erosion rate in the northern part of the study area was lower than that in the middle and southern parts because of the forest and vegetation cover, as well as resistant geologic formations.

FIGURE 3

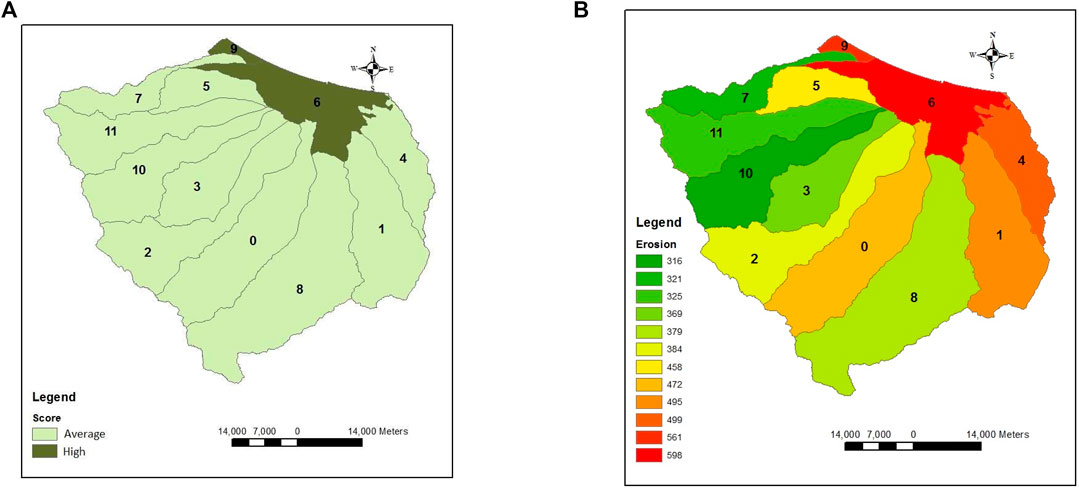
FIGURE 3. Spatial distribution of erosion intensity resulted from the MPSIAC model: (A) qualitive erosion, (B) sedimentation yields of the Anzali watershed.

Table 8 presents the ratios of the area and sediment to the total area and total sediment. The highest sediment ratio was related to sub-watersheds 0 and 8, which also had the highest area ratio. Land-use parameters have been the most practical erosion modeling tool in most watersheds.

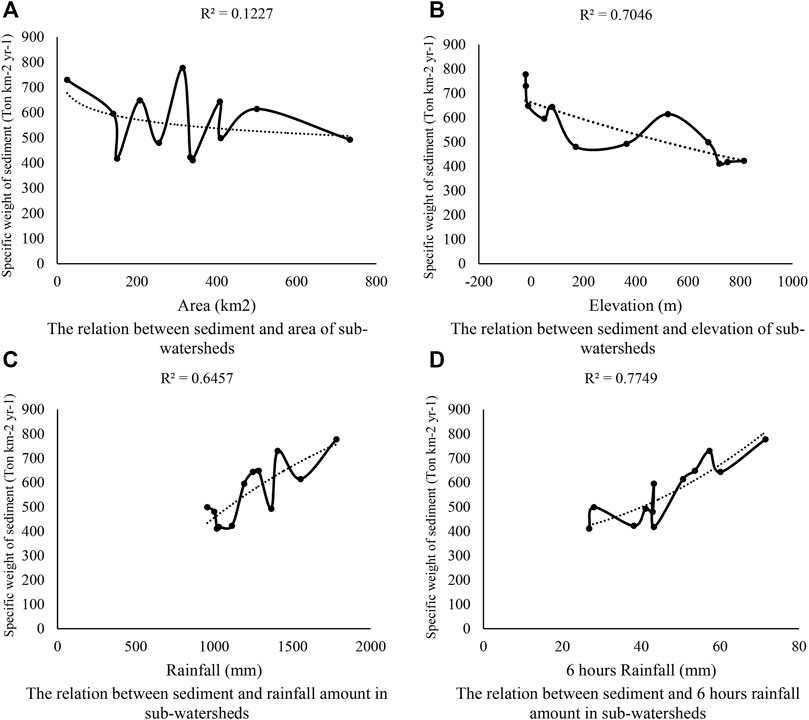
Therefore, with predicted sediment yields of events, effective parameters were fitted with the specific sediment weights (Figures 4A,D) in the model. The new coefficient and exponent were used to calculate the sediment yield, and the results showed a close correlation with the observed event data. The predicted annual sediment yield also showed a 17.6% difference from the observed sediment yield. In these figures, the polynomial function had a better regression coefficient. The results also indicated that land units with smaller areas were more sensitive to erosion and sediment yields. The accuracy regression line (R²) of the generated map was 0.13–0.78. In Table 9, results comparing different factors in Anzali catchment units are presented. As it turns out, land use is the main parameter in the sedimentation process.

FIGURE 4

FIGURE 4. The relation between sedimentation and climatology of the sub-watershed.

TABLE 9

TABLE 9. Results of comparing different factors in Anzali catchment units.

The simulated sediment and sampling values were analyzed and tested to validate the MPSIAC model. Comparison of correlation values reveals that the correlation between the simulated and sampling values is strong in sub-basin 1 (R² < 0.8). Besides, the performance value of the model (EF) also indicates the accuracy of the data fit and varies from infinite negative in the worst case to one at the time of complete data fit. RMSE analysis of sediment values shows these values are in the acceptable range 16.74 tons per year. Since the nRMSE level is less than 10, this model has an excellent performance in estimating the sediment load. Also, according to the classification by Jamieson et al. (1991), nRMSE is less than 10% in the excellent category, and nRMSE between 10 and 20% is in a good category. Also, the closer the EF, RMSE, and nRMSE values are to zero, the better the simulation model performs. CRM values also show that this statistic is close to zero (CRM = 0.55), which indicates the model’s high performance. Since the results of these indicators in all sub-basins have a more or less similar trend, it is enough to examine the statistical indicators in one sub-basin (Sw₀).

Sedimentation was directly related to rainfall, with runoff being the highest amount in this period. This shows that sedimentation is sensitive to runoff, as illustrated in Figure 4A.

4 Conclusion

The watershed of the Anzali Wetland is the primary source of the wetland sediment load, especially the upper watershed, which contributes approximately to 80% of the total sediment load (approximately 1,339,000 tons/year). Overgrazing, deforestation, and limited erosion control are among the main causes of erosion in the watershed. One of the most important climatic parameters increasing erosion in the region is short-term rainfall, which is a characteristic of all climates in Iran, especially in the Anzali watershed. This wetland has expanded significantly in the past but has been gradually filled by alluvial and deltaic sediments of the Sefidrood, Rasht, Fooman, and Masal rivers. Therefore, taking protective measures to reduce the sediment entering the wetland is a necessary and vital measure for the future.

The model results showed that the erosion areas are highly correlated with the regional lithology, soil, and vegetation status. Areas with poor cover and bare soil also showed high correlation with the final erosion model. This means that land-use classes, such as dense vegetation and good pastures, correspond to areas with low erosion. Conversely, bare soils and poor pastures are located on severely eroded surfaces. The amount of sediment based on the MPSIAC model was estimated to be approximately 5,227.4 t km⁻² yr⁻¹, which is consistent with the values measured by using the Cs ionomeric method. The MPSIAC model and GIS software allowed us to identify the factors affecting sediment production in a better, faster, and more accurate way by examining the various model layers to prevent further sediment production.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.736125/full#supplementary-material

References

Abbasi, A. (2019). 210Pb and 137Cs Based Techniques for the Estimation of Sediment Chronologies and Sediment Rates in the Anzali Lagoon, Caspian Sea. J. Radioanal. Nucl. Chem. 322, 319–330. doi:10.1007/s10967-019-06739-8

CrossRef Full Text | Google Scholar

Abdi, P., Feiznian, S., and Peyrowan, H. R. (2011). “Evaluation of Erodibility of Marl Lithologies of Zanjan Province Using EPM Model and GIS,” in The 7th Conference of Engineering Geology and the Environment (Shahrood city, Iran: Industrial Shahrood University). (in Persian).

Google Scholar

Abdullah, M., Feagin, R., and Musawi, L. (2017). The Use of Spatial Empirical Models to Estimate Soil Erosion in Arid Ecosystems. Environ. Monit. Assess. 189, 78. doi:10.1007/s10661-017-5784-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Alizadeh Gorji, Gh. (2006). Estimation of Erosion and Sediment Using MPSIAC Model in GIS Environment (Case Study: Kalijan-Rastagh Basin), Faculty of Humanities and Social Sciences. Master Thesis. Tabriz city, Iran: University of Tabriz. (In Persian).

Google Scholar

Amini, S., Rafiei, B., Khodabakhsh, S., and Heydari, M. (2010). Estimation of Erosion and Sediment Yield of Ekbatan Dam Drainage basin with EPM, Using GIS. Iranian J. Earth Sci. Available at: http://ijes.mshdiau.ac.ir/article_522730.html.

Google Scholar

Amiri, K. (20102010). Estimate of Erosion and Sedimentation in Semi-arid Basin Using Empirical Models of Erosion Potential within a Geographic Information System. Air Soil Water Res., 3. doi:10.4137/aswr.s3427

CrossRef Full Text | Google Scholar

Arabkhedri, M., Valikhojini, A., Hakimkhani, S. H., Charkhabi, A. H., and Telvari, A. (2009). Estimation Sediment Yield and Preparation Sediment Yield Map for Iran, Final Report of Research Project. Tehran city, Iran: Soil Conservation and Watershed Management Research Center of Iran. (in Persian).

Google Scholar

Bayat, R., Arabkhedri, M., Arabkhedri, M., Behnam, N., and Gerami, Z. (2020). Performance Evaluation of EPM and MPSIAC Models for Determination of Erosion Status of Shahriari Watershed. jsaeh 7 (3), 1–16. doi:10.29252/jsaeh.7.3.1

CrossRef Full Text | Google Scholar

Behnam, N., Parehkar, M., and PaziraC, E. (20112011). Sensitivity Analysis of MPSIAC Model. J. Rangeland Sci. 1 (No. 4), 295–302. doi:10.33899/regs.2011.6426

CrossRef Full Text | Google Scholar

Brooshkeh, E., Sokouti, R., Arab Khedri, M., and Nabi Pey Lashkarian, S. (2018). Comparative Efficacy of Some Empirical Models to Estimate Sediment Yield in Small Catchments. AgricultForest 64 (2), 163–173. Podgorica. doi:10.17707/AgricultForest.64.2.12

CrossRef Full Text | Google Scholar

Daneshvar, M. R. M., and Bagherzadeh, A. (2012). Evaluation of Sediment Yield in PSIAC and MPSIAC Models by Using GIS at Toroq Watershed, Northeast of Iran. Front. Earth Sci. 6, 83–94. doi:10.1007/s11707-011-0189-7

CrossRef Full Text | Google Scholar

Eisazadeh, L., Sokouti, R., Homaee, M., and Pazira, E. (2012). Comparison of Empirical Models to Estimate Soil Erosion and Sediment Yield in Micro Catchments. Eurasian J. Soil Sci. 1, 28–33. Available at: http://ejss.fesss.org/10.18393/ejss.2012.1.028-033.

Google Scholar

Elsey-Quirk, T., Graham, S. A., Mendelssohn, I. A., Snedden, G., Day, J. W., Twilley, R. R., et al. (2019). Mississippi River Sediment Diversions and Coastal Wetland Sustainability: Synthesis of Responses to Freshwater, Sediment, and Nutrient Inputs. Estuarine, Coastal Shelf Sci. 221, 170–183. doi:10.1016/j.ecss.2019.03.002

CrossRef Full Text | Google Scholar

Heshmati, M., Arifin, A., Shamshuddin, J., and Majid, N. M. (2012). Predicting N, P, K and Organic Carbon Depletion in Soils Using MPSIAC Model at the Merek Catchment, Iran. Geoderma 175-176, 64–77. doi:10.1016/j.geoderma.2011.12.028

CrossRef Full Text | Google Scholar

Heydarian, S. (1996). “Assessment of Erosion in Mountain Regions,” in Paper presented at the proceedings of 17th Asian conference on remote sensing.

Google Scholar

Hyndman, R. J., and Koehler, A. B. (2006). Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 22 (4), 679–688. doi:10.1016/j.ijforecast.2006.03.001

CrossRef Full Text | Google Scholar

Jamieson, P. D., Porter, J. R., and Wilson, D. R. (1991). A Test of the Computer Simulation Model ARCWHEAT1 on Wheat Crops Grown in New Zealand. Field Crops Res. 27, 337–350. doi:10.1016/0378-4290(91)90040-3

CrossRef Full Text | Google Scholar

JAPAN international cooperation agency (2005). The Study on Integrated Management for Ecosystem Conservation of the Anzali Wetland in the Islamic republic of iran. Final Report: Executive Report. Available at: https://openjicareport.jica.go.jp/pdf/11784097.pdf.

Google Scholar

Johnson, C., and Gebhardt, K. (1982). Predicting Sediment Yields from Sagebrush Rangelands [Pacific Southwest Inter-Agency Committee Prediction Procedure, Southwest Idaho]. Agric Rev Manuals. Available at: https://agris.fao.org/agrissearch/search.do?recordID=US19830947628.

Google Scholar

Khaledian, Y., Kiani, F., and Ebrahimi, S. (2012). The Effect of Land Use Change on Soil and Water Quality in Northern Iran. J. Mt. Sci. 9 (6), 798–816. doi:10.1007/s11629-012-2301-1

CrossRef Full Text | Google Scholar

Khalili Vavdare, S., Sedghi, H., and Sarraf, A. (2019). Determination of Sedimentation Rate in Anzali Lagoon of Northern Iran Using 137Cs Tracer Technique. Appl. Ecol. Env. Res. 17 (1), 1337–1347. doi:10.15666/aeer/1701_13371347

CrossRef Full Text | Google Scholar

Loague, K., and Green, R. E. (1991). Statistical and Graphical Methods for Evaluating Solute Transport Models: Overview and Application. J. Contaminant Hydrol. 7, 51–73. doi:10.1016/0169-7722(91)90038-3

CrossRef Full Text | Google Scholar

Mahdian, M. H. (2004). “Study of Lands Degradation in Iran,” in Proceedings of the Third National Conference of Erosion & Sediment (Tehran, Iran, 226–231. (In Persian).

Google Scholar

Milliman, J. D., and Syvitski, J. P. M. (1992). Geomorphic/tectonic Control of Sediment Discharge to the Ocean: the Importance of Small Mountainous Rivers. J. Geology. 100 (525–544), 525–544. doi:10.1086/629606

CrossRef Full Text | Google Scholar

Mirakhorlo, M. S., and Rahimzadegan, M. (2018). Application of Sediment Rating Curves to Evaluate Efficiency of EPM and MPSIAC Using RS and GIS. Environ. Earth Sci. 77, 723. doi:10.1007/s12665-018-7908-2

CrossRef Full Text | Google Scholar

Morgan, K. M., and Nalepa, R. (1982). Application of Aerial Photographic and Computer Analysis to the USLE for Areawide Erosion Studies. J. Soil Water Conserv 37, 347–350. Available at: https://www.jswconline.org/content/37/6/347.

Google Scholar

Najm, Z., Keyhani, N., Rezaei, Kh., Naeimi Nezamabad, A., and Vaziri, S. H. (20132013). Sediment Yield and Soil Erosion Assessment by Using an Empirical Model of MPSIAC for Afjeh & Lavarak Sub-watersheds, Iran. Earth 2 (1), 14–22. doi:10.11648/j.earth.20130201.13

CrossRef Full Text | Google Scholar

Ndomba, P. M. (2013). Validation of PSIAC Model for Sediment Yields Estimation in Ungauged Catchments of Tanzania. Ijg 04, 1101–1115. doi:10.4236/ijg.2013.47104

CrossRef Full Text | Google Scholar

Nearing, M. A., Unkrich, C. L., Goodrich, D. C., Nichols, M. H., and Keefer, T. O. (2015). Temporal and Elevation Trends in Rainfall Erosivity on a 149 Km 2 Watershed in a Semi-arid Region of the American Southwest. Int. Soil Water Conservation Res. 3, 77–85. doi:10.1016/j.iswcr.2015.06.008

CrossRef Full Text | Google Scholar

Noori, H., Karami, H., Farzin, S., Siadatmousavi, S. M., Mojaradi, B., and Kisi, O. (20182018). Investigation of RS and GIS Techniques on MPSIAC Model to Estimate Soil Erosion. Nat. Hazards 91, 221–238. doi:10.1007/s11069-017-3123-9

CrossRef Full Text | Google Scholar

Noori, H., Siadatmousavi, S. M., and Mojaradi, B. (2016). Assessment of Sediment Yield Using RS and GIS at Two Sub-basins of Dez Watershed, Iran. Int. Soil Water Conservation Res. 4, 199–206. doi:10.1016/j.iswcr.2016.06.001

CrossRef Full Text | Google Scholar

Onstad, C., and Foster, G. (1975). Erosion Modeling on a Watershed. Trans. ASAE 18 (2), 288–0292. doi:10.1007/s11069-017-3123-910.13031/2013.36572

CrossRef Full Text | Google Scholar

Pacific Southwest Inter-Agency Committee (PSIAC) (1986). Water Management Subcommittee on American Society of Civil Engineers (ASCE), Report No. HY 12. Available at: https://www.scirp.org/(S(lz5mqp453edsnp55rrgjct55))/reference/ReferencesPapers.aspx?ReferenceID=1566226.Factors Affecting Sediment Yield in the Pacific Southwest Area and Selection and Evaluation of Measures for Reduction of Erosion and Sediment Yield

Google Scholar

Parehkar, A., Behnam, N., and Shokrabadi, M. (2013). An Investigation Survey on MPSIAC Model to Predict Sediment Yield in Iran. Rjees 5 (6), 342–349. doi:10.19026/rjees.5.5709

CrossRef Full Text | Google Scholar

P. Heininger, and J. Cullmann (Editors) (2015). Sediment Matters—The Challenges (Heidelberg: Springer). Available at: https://b-ok.cc/book/2570195/07c988.

Google Scholar

Pourkarimi, M., Mahmoudi, S., Masihabadi, M., Pazira, E., and Moeini, A. (2017). Use of MPSIAC and EPM to Estimate Sediment Yield and Erosion - a Case Study of a Watershed of the Second Urban Phase, Mashhad, Khorasan Province. AgricultForest 63 (4), 201–213. Podgorica. doi:10.17707/AgricultForest.63.4.21

CrossRef Full Text | Google Scholar

Refahi, H. G. (1996). Water Erosion and Conservation. Tehran: University Of Tehran Publication.

Google Scholar

Rustaei, Sh., Rasooli, A. A., and Ahmadzadeh, H. (2010). Erosion and Sediment Modeling of Ajabshir tea Castle Catchment Using Satellite Data in GIS Environment. Geogr. Dev. 18, 178–159. (In Persian). doi:10.22111/gdij.2010.1125

CrossRef Full Text | Google Scholar

Sadeghi, H. (1993). “Comparison of Some Erosion Potential and Sediment Yield Assessment Models in Ozon-Dareh Sub-catchment,” in Proceedings of the National Conference on Land Use Planning (Tehran, Iran.

Google Scholar

Schaeffer, D. L. (1980). A Model Evaluation Methodology Applicable to Environmental Assessment Models. Ecol. Model. 8, 275–295. doi:10.1016/0304-3800(80)90042-3

CrossRef Full Text | Google Scholar

Shojaei, Sh., Noura, M. R., and Habibi Mood, Sh. (2019). Estimation of Sedimentation and Erosion Using MPSIAC, FSM and Direct Measurement Methods in Gabric Watershed, South-Eastern of Iran. Q. J. Environ. Erosion Res. Available at: http://dorl.net/dor/20.1001.1.22517812.1397.8.4.5.8.

Google Scholar

Tangestani, M. H. (2006). Comparison of EPM and PSIAC Models in GIS for Erosion and Sediment Yield Assessment in a Semi-arid Environment: Afzar Catchment, Fars Province, Iran. J. Asian earth Sci. 27 (5), 585–597. doi:10.1016/j.jseaes.2005.06.002

CrossRef Full Text | Google Scholar

Wallis, J. R., and Todini, E. (1975). Comment upon the Residual Mass Curve Coefficient. J. Hydrol. 24, 201–205. doi:10.1016/0022-1694(75)90080-3

CrossRef Full Text | Google Scholar

Wang, G., Gertner, G., Fang, S., and Anderson, A. B. (2003). Mapping Multiple Variables for Predicting Soil Loss by Geostatistical Methods with TM Images and a Slope Map. Photogramm Eng. Remote Sensing 69 (8), 889–898. doi:10.14358/PERS.69.8.889

CrossRef Full Text | Google Scholar

Willmott, C., and Matsuura, K. (2005). Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 30, 79–82. doi:10.3354/cr030079

CrossRef Full Text | Google Scholar

Zare khosheghbal, M., Charkhabi, A. H., Sharifi, F., and Ghazban, F. (2013a). An Investigation of Sediment Pollution in the Anzali Wetland. Polish J. Environ. Study 22 (1), 283–288. Available at: http://www.pjoes.com/An-Investigation-of-Sediment-Pollution-r-nin-the-Anzali-Wetland,88979,0,2.html.

Google Scholar

Zare khosheghbal, M., Sharifi, F., and Ghazban, F. (2013b). Using C¹⁴ Isotope in Determining Sedimentation Rate in Non–turbulent Aquatic Environment. Ann. Biol. Res. 4 (1), 219–225. Available at: https://www.scholarsresearchlibrary.com/abstract/using-c14-isotope-in-determining-sedimentation-rate-in-nonturbulent-aquatic-environment-7214.html.

Google Scholar

Zarei, A. R., and Amiri, M. J. (2017). Evaluation of Soil Losses and Sediment Yield Using Modified PSIAC Model. Iran Agric. Res. 36 (1), 111–116. doi:10.22099/iar.2017.4035

CrossRef Full Text | Google Scholar

Zarei, A. R., Mokarram, M., and Shabani, A. (2019). Evaluation of Sediment Yield (Qs) in Bishezard Watershed Located Southwest of Iran, Using PSIAC and MPSIAC Models. Ijgenvi 18 (1), 1. doi:10.1504/IJGENVI.2019.098890

CrossRef Full Text | Google Scholar

Zhang, X., Cao, W., Guo, Q., and Wu, S. (2010). Effects of Landuse Change on Surface Runoff and Sediment Yield at Different Watershed Scales on the Loess Plateau. Int. J. Sediment Res. 25 (3), 283–293. doi:10.1016/S1001-6279(10)60045-5

CrossRef Full Text | Google Scholar

Zhu, C., and Li, Y. (2014). Long-term Hydrological Impacts of Land Use/land Cover Change from 1984 to 2010 in the Little River Watershed, Tennessee. Int. Soil Water Conservation Res. 2 (2), 11–21. doi:10.1016/S2095-6339(15)30002-2

CrossRef Full Text | Google Scholar